Refinable C¹ spline elements for irregular quad layout

Abstract

Building on a result of U. Reif on removable singularities, we construct C¹ bi-3 splines that may include irregular points where less or more than four tensor-product patches meet. The resulting space complements PHT splines, is refinable and the refined spaces are nested, preserving for example surfaces constructed from the splines. As in the regular case, each quadrilateral has four degrees of freedom, each associated with one spline and the splines are linearly independent. Examples of use for surface construction and isogeometric analysis are provided.

1. Introduction

Geometrically continuous G^k spline complexes and generalized subdivision surfaces are the two most popular families of constructions for filling multi-sided holes in a regular tensor-product spline lattice. Although many properties of subdivision surfaces can be computed by spectral analysis, their representation as an infinite sequence of ever smaller smoothly-connected surface rings complicates their inclusion into existing industrial design infrastructure and the use of standard integration rules in their analysis. The finitely many polynomial spline patches of a G^k spline complex are typically more convenient and fit well into the CAD pipeline. However, refining a G^k spline complex requires careful book keeping. For, what used to be an edge where patches join with G^k continuity is now split into two. To represent the same spline complex, the pieces further away from the multi-sided hole have to remember to join using G^k rules rather than the regular C^k rules that the immediate regular neighborhood seems to prescribe. If we ignore the book keeping, we can refine G^k spline complexes, but the resulting spaces are not nested. That is, an initial surface or function may not have an exact representation in refined form. By contrast, refinement of subdivision functions yields nested spaces by construction.

Can we combine, for multi-sided configurations, a finite representation with simple nested refinability? After developing a solution, we realized that it was rather similar to work already published in U. Reif’s PhD thesis [Rei93, Rei97]. Reif proposed to project bi-cubic C¹ splines into a subspace that, despite being singular at the central point of the n-sided cap, guarantees tangent continuity at the central, irregular point and C¹ continuity everywhere else. Inconveniently, the projected space has fewer degrees of freedom near the irregularity than in the surrounding regular spline regions; and these degrees of freedom can not be symmetrically distributed as proper control points. Our variant of Reif’s construction applies one localized 2 × 2 split (see Fig. 1a) so that the resulting degrees of freedom are uniformly distributed and so that

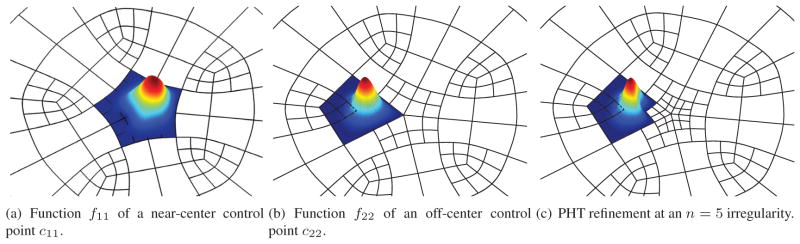
Figure 1.

Piecewise bi-cubic refinable C¹ basis functions f_ij. On quadrilaterals adjacent to irregular points, the basis functions of the spline space consist of 2 × 2 C¹-connected polynomial pieces. Surface and analysis space consist of linear combinations Σc_ijf_ij with control points c_ij.

• regardless of the valences of its vertices, each quadrilateral of the input quad mesh is associated with four degrees of freedom.

In the regular case, where all the vertices of a quad have valence four, these four degrees of freedom are the B-spline control points of bicubic splines with double knots. Fig. 1a,b show basis functions near irregular points and the local split of the quad mesh that provides the full four degrees of freedom despite the projection. The splines complement and are naturally compatible with bi-cubic PHT splines [DCL⁺08, LDC10, KXCD15] for localized refinement. Fig. 1c illustrates a basis function near a PHT-refined n = 5 neighborhood.

1.1. Related Literature

In the 1990s, a number of C¹ surface constructions were based on singularities at the vertices [Pet91, War92, PN93, NP94, Rei95a, Rei97] including constructions of curvature continuous surfaces [BR97, Rei95b]. A major contribution of Reif’s singular construction [Rei97] was a proof showing that the corner singularity is removable by a local change of variables; and that the resulting surface is tangent continuous at and near the central irregular point where more of fewer than four tensor-product patches come together. More recently, in the context of iso-geometry, Takacs and Jüttler [TJ12] analyzed singular spline constructions, but did not draw the connection to the earlier surface constructions. They observed that specific linear combinations of singular splines can be sufficiently regular for isogeometric analysis and closed with the prediction that “main targets for further analysis are approximation properties on singular domains”. The monograph [PR08] characterizes subdivision surfaces as smooth spline surfaces with singularities at the irregular points and establishes the differential-geometric properties of subdivision surfaces at the singularities. Subdivision functions have repeatedly been used as finite elements [COS00, CSA⁺02, Bar13, NKP14]. The linear independence of Loop and Catmull-Clark subdivision splines, except for the cube mesh, was proven in [PW06].

Reif’s construction is based on bicubic splines with double knots. These functions have been generalized for local refinement using T-corners where coarse and fine splines meet. The local refinability of these PHT splines [DCL⁺08, LDC10, KXCD15] nicely complements the ability we focus on: to create multi-sided blends.

Overview

Section 2 collects the notation and setup for constructing the splines near irregularities. Section 3 derives the splines. Section 4 discusses their properties: C¹ smoothness, refinability and linear independence of the functions associated with the four degrees of freedom of each quadrilateral. Section 5 discusses two uses of the splines.

2. Definitions and Setup

We consider a network of quadrilateral facets or quads. The nodes where four quads meet are called regular, else irregular nodes. An irregular node must not be a direct neighbor of an irregular node, but may be a diagonal neighbor within the same quad. If the assumption fails, one Catmull-Clark-refinement step can enforce the requirement.

Except where the construction switches to the PHT construction to accommodate local refinement, every quad ℓ is associated with four basis functions, hence four degrees of freedom, $c_{ij}^{\ell }\in {ℝ}^d$, i, j ∈ {1, 2}. Surface and analysis space will consist of linear combinations Σc_ijf_ij with control points c_ij. We obtain basis functions $f_{ij}^k$, for example, by setting $c_{ij}^{\ell }=1$ and all other coefficients to zero and then applying the Algorithm of Section 3. It is convenient to define the basis function $f_{ij}^k$ piecewise by tensor-product polynomials b of bi-degree 3 in Bernstein-Bézier (BB) form

$$b(u,v):=\sum _{i=0}^3\sum _{j=0}^3{b}_{ij}{B}_i^3(u)B_j^3(v),(u,v)\in \square :={[\mathrm{0..1}]}^2,$$

where $B_k^3(t):=\left(\begin{array}{c}3\\ k\end{array}\right){(1-t)}^{3-k}{t}^k$ are the Bernstein-Bézier (BB) polynomials of degree 3 and b_ij are the BB coefficients [Far02, PBP02].

3. Construction

Since the regular C¹ bi-3 tensor-product spline and the construction of PHT splines are well-known, we focus on constructing the BB patches of irregular quads surrounding the irregular node. Even this construction is remarkably simple.

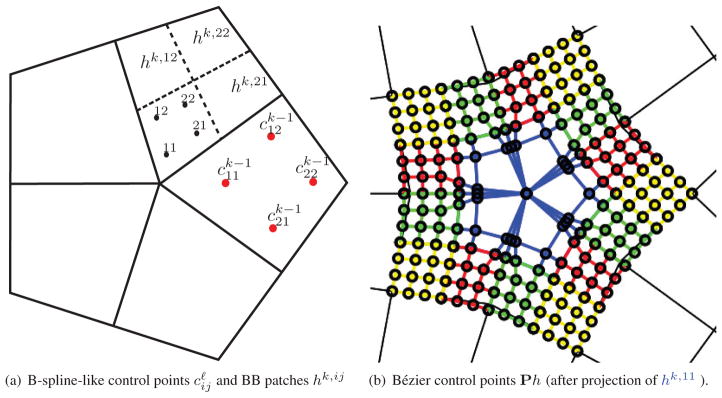
Given the four degrees of freedom $c_{ij}^k$ of each quad k, we can convert the C¹ bi-3 tensor-product splines to their BB form: set the four interior BB-coefficient $a_{ij}^k:=c_{ij}^k$ or i, j ∈ {1, 2}. Then the remaining coefficients $a_{ij}^k$ are determined as averages to join patches with C¹ continuity. Patches a^k corresponding to an irregular quad are split into four at u = v = 1/2. This yields 2×2 sub-patches (see Fig. 2a): h^k,ij := Sa^k, i, j ∈ {1, 2}. The split S is equivalent to deCasteljau’s algorithm. We complete the construction by projecting into one plane the relevant BB-coefficients of the sub-patches immediately surrounding the irregular node.

Figure 2.

Construction at an irregular node of valence n = 5. (a) Input: B-spline-like control points c, intermediate subpatches h^k,ij and the subscripts {11, 12, 21, 22} of the inner Bézier control points of h^k,11. (b) Output: Bézier points $b_{\alpha \beta }^{k,ij}$ obtained by projection P of the bi-3 patches h^k,11(u, v).

Algorithm.

Spline construction at an irregular node.

Input: B-spline-like control points $c_{ij}^k$, i, j ∈ {1, 2}, k = 0, …, n − 1 (see Fig. 2a) of quadrilaterals surrounding an n ≠ 4-valent node.

Output: A C1 spline complex consisting of 4n polynomial pieces bk,αβ that is singularly parameterized at the central point (Fig. 2b). Conversion to BB form: set $a_{ij}^k:=c_{ij}^k$ for i, j ∈ {1, 2} and then compute the remaining coefficients $a_{ij}^k$, i, j ∈ {0, 1, 2, 3} of the bicubic BB-patches ak(u, v), k = 1, …, n, as averages of the $c_{ij}^k$ so that the ak join C1 except at the irregular point $a_{00}^k$ that we set to the average of the surrounding control points $a_{00}^k:={\sum }_{k=1}^n{c}_{11}^k/n$. Subdivide the patches ak to get sub-patches hk,ij := Sak, i, j ∈ {1, 2}. When i +j > 2 then bk,ij := hk,ij. Only the subpatches hk,11 that include the central point still require work. Abbreviating $h_{\alpha \beta }:=h_{\alpha \beta }^{k,11}$, we apply the projection P (cf. [Rei97, Sect.6]): $$\left(\begin{array}{c}{b}_{11}\\ b_{21}\\ b_{12}\end{array}\right):=\mathbf{P}\left(\begin{array}{c}{h}_{11}\\ h_{21}\\ h_{12}\end{array}\right):=\left(\begin{array}{ccc}{\mathbf{P}}_1& {\mathbf{P}}_2& {\mathbf{P}}_3\\ {\mathbf{P}}_4& {\mathbf{P}}_5& {\mathbf{P}}_6\\ {\mathbf{P}}_7& {\mathbf{P}}_8& {\mathbf{P}}_9\end{array}\right)\left(\begin{array}{c}{h}_{11}\\ h_{21}\\ h_{12}\end{array}\right)$$ (1) where ${\mathbf{P}}_{\nu }(j,k):=p_{\nu }^{j-k}$, for ν = 1, …, 9, and j, k = 0, …, n − 1, φn := 2π/n, ψ := arg((1 + iβsinφn)e−iφn/2), β := 1/10, $p_1^j=p_2^j=p_3^j=p_4^j=p_7^j=1/3n,p_5^j=p_9^j=(1+3cos(j{\phi }_n))/3n$, $p_6^j=(1+3cos(2\psi +j{\phi }_n))/3n,p_8^j=(1+3cos(2\psi -j{\phi }_n))/3n$. Average $b_{10}^k:=(b_{11}^k+b_{11}^{k+1}/2)$ for all edges and set $b_{00}^k:={\sum }_{k=1}^n{b}_{11}^k/n$ for all vertices of valence n.

4. Properties

Smoothness, namely the C¹ continuity of the resulting surface, follows immediately from [Rei97, Theorem 1.2]. For 1 < p < 4, the L^p norms of the main curvatures the singularly parameterized surfaces are finite at and near the irregular points [Rei97, Theorem 1.4]. Refinability means that applying B-spline subdivision to the control net c and then applying the Algorithm yields the same surface as applying the Algorithm followed by subdividing the resulting Bézier patches by deCasteljau’s algorithm. Abbreviating the Algorithm as PSc, refinability is therefore equivalent to showing that the following diagram commutes:

$$\begin{array}{ccc}\mathbf{PS}c& \stackrel{\mathbf{S}}{\to }& \mathbf{SPS}c\\ \downarrow \mathbf{P}& & \downarrow \mathbf{P}\\ \mathbf{PS}c& \stackrel{\mathbf{S}}{\to }& \mathbf{SPS}c\end{array}$$ (2)

Commutativity follows since, by definition of a projection, PPS = PS and PSPS = SPS, and S keeps a projected function unchanged.

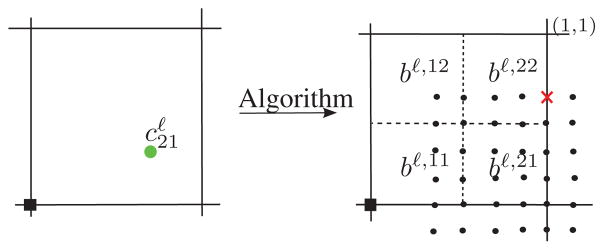
To prove linear independence of the functions $f_{ij}^k$ associated with the control point $c_{ij}^k$, we first observe that the regular PHT elements are linearly independent, i.e. there is a functional that is one for one element and zero for all other elements (by definition they are not supported near the irregularity). Hence, to reproduce the zero function, we may set their coefficients to zero and remove them from consideration. Of the functions associated with an irregular quad, $f_{22}^k$ is also regular, hence can also be removed. For the remaining 3n functions $f_{11}^k,f_{12}^k$ and $f_{21}^k$ associated with one n-sided hole, consider their sub-patches b^k,22, k = 0, …, n − 1. Let b^k,22(1, 1) be the corner point not shared with any b^k,ij , i +j < 4 and denote by ${\mathcal{F}}^{\ell }({\partial }_2^2)$ the functional acting on the patch b^ℓ,22 of a function by twice differentiating in the second variable followed by evaluation at (1, 1). Then ${\mathcal{F}}^{\ell }({\partial }_2^2)f_{ij}^k=0$ for all $f_{ij}^k$ except for $f_{21}^{\ell }$ (see Fig. 3) and, symmetrically, ${\mathcal{F}}^{\ell }({\partial }_1^2)f_{ij}^k=0$ except for $f_{12}^{\ell }$. This leaves only the maps $f_{00}^k$ for consideration of dependence. Linear independence follows since ${\mathcal{F}}^{\ell }({\partial }_2^2{\partial }_1^2)f_{11}^k=0$ (differentiation twice in each variable) unless k = ℓ.

Figure 3.

Nonzero BB coefficients ● of the basis function $f_{21}^{\ell }$. The coefficient marked additionally with an × is nonzero only for $f_{21}^{\ell }$. It is zero for $f_{12}^k$ or $f_{11}^k$, k = 0, …, n − 1 and for $f_{21}^k$, k ≠ ℓ.

5. Some uses

In this section, we illustrate two uses of the C¹ spline elements for irregular quad layout.

Surface construction from a quad mesh

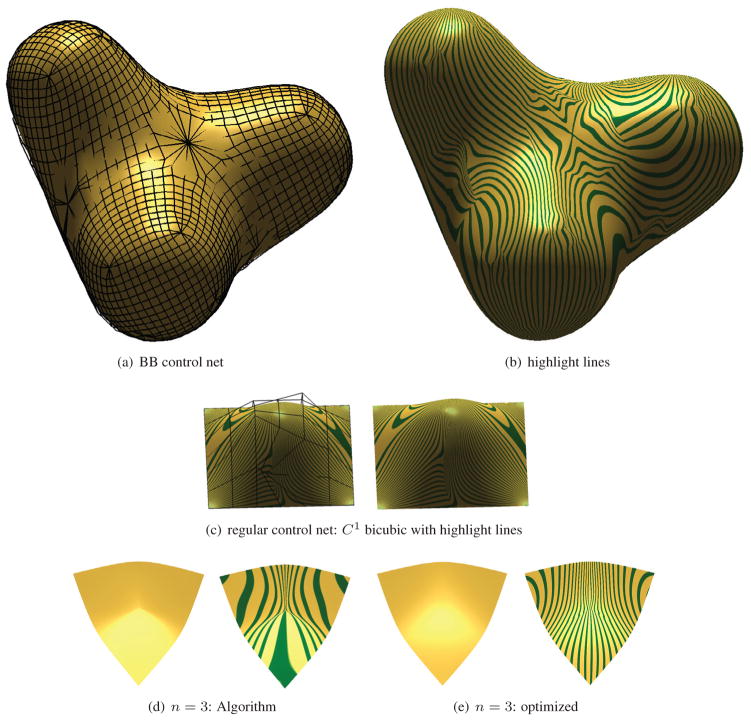
Fig. 4c illustrates that, depending on the choice of coefficients, regular tensor-product bi-3 splines with double knots can have a poor highlight line distributions. The simple default choice of interpreting the quad-mesh vertices as bi-3 B-spline coefficients and inserting knots to obtain the $c_{ij}^k$ often yields good highlight lines in regular spline regions. For irregular neighborhoods, the surfaces generated by the Algorithm are only of moderate quality (see Fig. 4b,d). However, Fig. 4e shows that we one can choose functionals and optimize the coefficient placement near irregularities to generate surfaces of reasonable quality. We do not discuss this further since more research is required to see whether one can consistently obtain good shape with a simple recipe for different valences. While the resulting surfaces are still not ‘class A’, their highlight line distribution may be acceptable where IGA might be deployed, such as the inside surfaces of a car door.

Figure 4.

(a,b)Surface with 3,5 and 6-sided singularly-covered neighborhoods. (c) Regular control net and highlight lines on a regular C¹ bi-3 spline surface. (d,e) 3-neighborhood improved by optimizing coefficient positions.

Isogeometric analysis

Next, we test the C¹ singular splines as isogeometric elements on two model problems: Poisson’s equation on the square and the Scorderlis-Lo roof benchmark problem of the shell obstacle course [BSL⁺85]. The latter demonstrates that the weak form of differential equations up to fourth order can be solved with the new finite elements.

Example 1

We solve Poisson’s equation:

$$\text{find}u:\mathrm{\Omega }\to ℝ:\{\begin{array}{ll}-\mathrm{\Delta }u=f\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=0\hfill & \text{on}\partial \mathrm{\Omega }.\hfill \end{array}$$ (3)

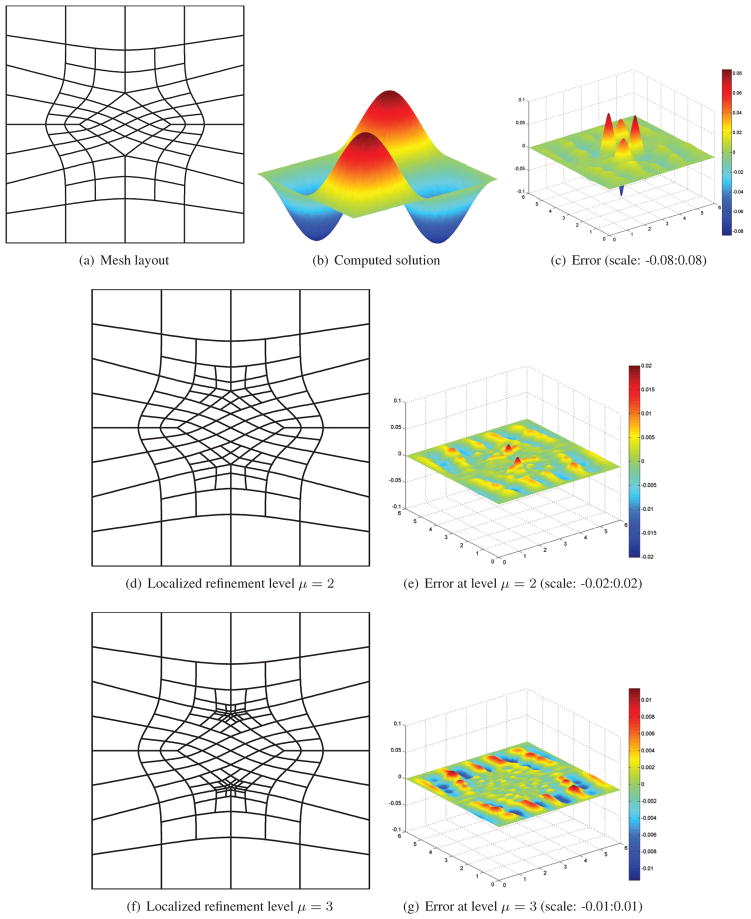
on the square Ω := {(x, y) ∈ ℝ² : 0 < x < 6, 0 < y < 6} with f := (4π²/9) sin((πx)/3) sin((πy)/3). The exact solution is u = 2sin((πx)/3) sin((πy)/3). We intentionally create a simple irregular partition of the square to be able to compare the convergence when computing with irregular layout to the well-known error reduction under refinement by 2⁻⁴ on the regular layout. For the simple(st) irregular parition, we insert irregular points of valence 3 and of valence 5 as shown in Fig. 5a. We numerically solve Equation (3) by Galerkin’s Method and assemble the stiffness matrix and the right-hand-side of the PDE system based on the Bézier coefficients of the splines.

Figure 5.

Poisson’s equation on the square [0, 6]². (d) and (f) increase refinement local to the 5-valent points.

Table 1 lists the L², L^∞ and H¹ errors of isogeometric analysis on the irregular layout Fig. 5a. This irregular layout is then uniformly refined. Solving, for comparison, the equation using tensor-product cubic spline that is five times uniformly refined yields L², L^∞ and H¹ errors of 7.2e-7, 4.9e-7 and 4.8e-05. That is, the error after ℓ = 5-fold refinement differs by roughly one order of magnitude in favor of the regular spline. Correspondingly, the convergence rates for the singular construction are almost the same as those for the regular spline refinement, namely almost 2⁴ for the L² norm and L^∞ norm and close to 2³ for the H¹ norm.

Table 1.

Error and approximate convergence rate (a.c.r.) in the L², L^∞ and H¹ norms for Poisson’s equation on the square [0, 6]².

ℓ	||u − uh||L2	a.c.r. ||·||L2	||u − uh||L∞	a.c.r. ||·||L∞	||u − uh||H1	a.c.r. ||·||H1
1	0.0625	-	0.0826	-	0.4568	-
2	0.0098	6.4	0.0194	4.3	0.1448	3.2
3	9.7e-04	10.1	0.0015	12.9	0.0225	6.4
4	7.17e-5	13.5	1.3e-4	11.5	0.0033	6.8
5	5.29e-06	13.56	9.87e-06	13.1	4.78e-04	6.9

Table 2 list the L², L^∞ and H¹ errors and the corresponding convergence rate measured for local PHT-type refinement Fig. 5(d,f). Fig. 5(c,e,g) illustrates that maximal errors decrease with each local refinement. Since the local refinement is applied to reduce the maximal error, the L^∞ norm decreases while, as expected, the L² and H¹ errors do not change much.

Table 2.

Local refinement level μ: error and approximate convergence rate in the L², L^∞ and H¹ norms for Poisson’s equation on the square [0, 6]².

μ	||u − uh||L2	a.c.r. ||·||L2	||u − uh||L∞	a.c.r. ||·||L∞	||u − uh||H1	a.c.r. ||·||H1
1	0.0625	-	0.0826	-	0.4568	-
2	0.0213	2.9	0.0199	4.15	0.1920	2.38
3	0.019	1.12	0.011	1.81	0.1304	1.47

Example 2

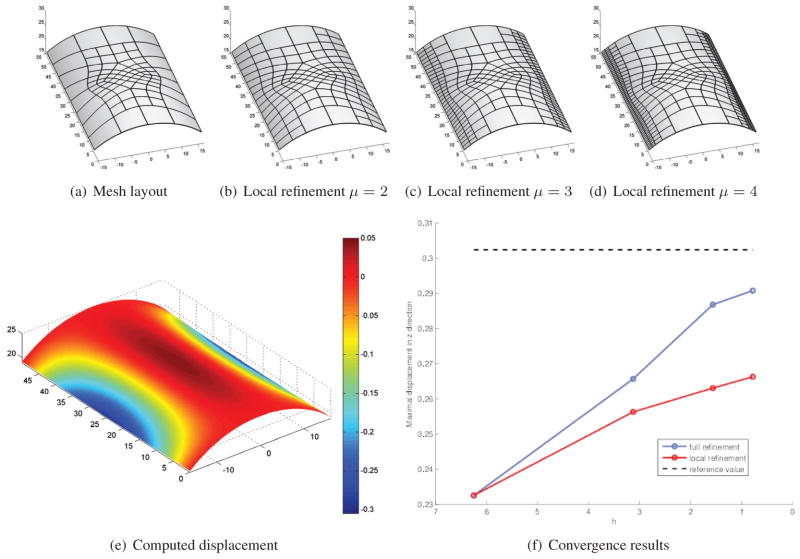
Next, we solve the Scorderlis-Lo roof benchmark problem in Koiter’s shell model [Koi70] under Kirchhof-Love assumptions. This is a fourth order PDE hence requires smoothness of the elements in the weak formulation. The displacement vector field of the thin shell is found by minimizing the total potential energy function, which depends on membrane strain, bending strain, body force and traction, Young modulus and Poisson’s ratio (see e.g.[COS00]).

With x and y our C¹ bicubic splines and z the analytical height function, we modeled the roof as x := (x, y, z(x, y)). The quality of the computation is measured in Fig. 6f by tracking the maximum displacement (of the midpoint on the edge aligned with the cylinder’s axis). While local refinement along the boundary alone Fig. 6[a–d] only makes little progress, under uniform refinement the value converges quickly to the benchmark value.

Figure 6.

Convergence of the displacement of the Scordelis-Lo roof to the benchmark.

6. Conclusion

We rediscovered and modified a construction of U. Reif to obtain a smooth spline complex where less or more than four tensor-product patches meet. Starting with a quad mesh, our modification yields a uniform distribution of degrees of freedom: each quadrilateral has four degrees of freedom and each degree of freedom is represented as a coefficient associated with one spline function. These spline functions are linearly independent. The resulting space complements PHT splines, is refinable and the refined spaces are nested. That is, surfaces constructed from the splines are unchanged under refinement.