Quantification of Private Information Leakage from Phenotype-Genotype Data: Linking Attacks

Abstract

Studies on genomic privacy have traditionally focused on identifying individuals using DNA variants. In contrast, molecular phenotype data, such as gene expression levels, are generally assumed free of such identifying information. Although there is no explicit genotypic information in them, adversaries can statistically link phenotypes to genotypes using publicly available genotype-phenotype correlations, for instance, expression quantitative trait loci (eQTLs). This linking can be accurate when high-dimensional data (many expression levels) are used, and the resulting links can then reveal sensitive information, for example, an individual having cancer. Here, we develop frameworks for quantifying the leakage of individual characterizing information from phenotype datasets. These can be used for estimating the leakage from large datasets before release. We also present a general three-step procedure for practically instantiating linking attacks and a specific attack using outlier gene-expression levels that is simple yet accurate. Finally, we describe the effectiveness of this outlier attack under different scenarios.

1 INTRODUCTION

Genomic privacy has recently emerged as an important issue, particularly in light of a surge in biomedical data acquisition ^1–3. Among these, molecular phenotype datasets, like functional genomics measurements, substantially grow the list of the quasi-identifiers⁴ which may lead to re-identification and characterization of individuals^4–6. In general, statistical analysis methods are used to discover genotype-phenotype correlations^7,8, which can be utilized by an adversary for linking the entries in genotype and phenotype datasets, thereby revealing sensitive information. The availability of a large number of correlations increases the possibility of linking^9,10.

Protecting the privacy of participating individuals has emerged as an important issue in genotype-phenotype association studies. Several studies addressed the problem of detecting whether an individual, with known genotype, has participated in a study¹¹ raising privacy concerns^12–15. We refer to these systematic breaches as “detection of a genome in a mixture” attacks (Supplementary Fig. 1). However, as the number and size of phenotype and genotype datasets increase, the detection of individuals in them will be irrelevant since any individual will already have their genotype or phenotype information stored in a dataset, i.e., participation will already be known. This opens up a new route to breaching privacy: An adversary can now aim at cross-referencing multiple, seemingly independent, genotype and phenotype datasets and pinpointing an individual to characterize her sensitive phenotypes. It is most certain that as personal genomics gains more prominence, the attackers will aim at linking different datasets in order to reveal sensitive information. We will refer to these attacks as “linking attacks”^4,5. One well-known example of these is the attack that matched the entries in Netflix Prize Database and the Internet Movie Database¹⁶. For research purposes, Netflix released an anonymized dataset of movie ratings of thousands of viewers. This dataset was assumed to be secure as the viewer’s names were removed. However, Narayanan et al used the Internet Movie Database, in which the identities of many users are public but only some of their movie choices are available, and linked it to the Netflix dataset. This revealed the identities and personal movie preference information of many users in the Netflix dataset. This attack is underpinned by the fact that both Netflix and the Internet Movie Database host millions of individuals and any individual who is in one dataset is very likely to be in the other dataset. As the size and number of the genotype and phenotype datasets increase, the number of potentially linkable datasets will increase (Supplementary Note).

2 RESULTS

2.1 Linking Attack Scenario

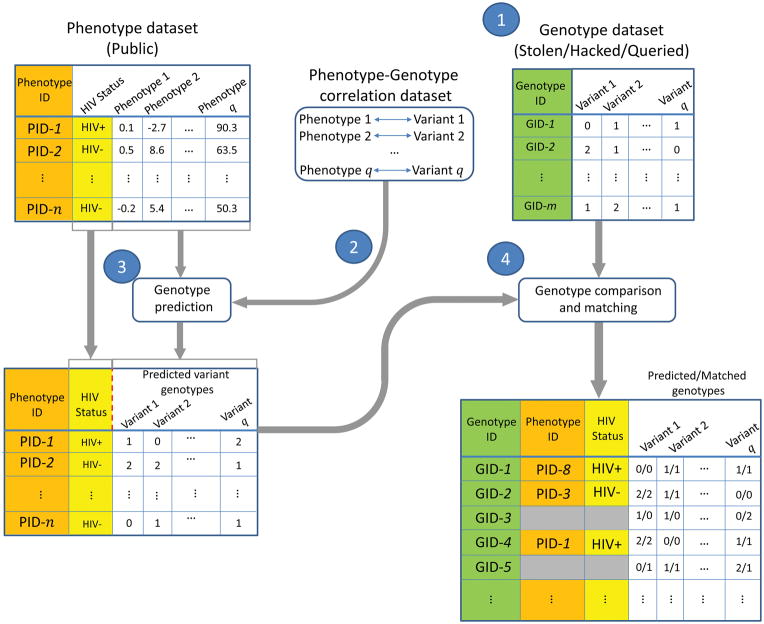
In the linking attacks, the attacker aims at characterizing sensitive information about a set of individuals in a stolen genotype dataset (Fig. 1). For each individual, she aims at querying the publicly available anonymized phenotype datasets in order to characterize, for example, their HIV status. For this, she utilizes a public quantitative trait loci (QTL) dataset that contains genotype-phenotype correlations. She statistically predicts genotypes using the phenotypes and QTLs. Then she compares the predicted genotypes to the genotype dataset and links the entries that have good genotype concordance. The sensitive information for the linked individuals is revealed to the attacker.

Figure 1.

Illustration of the linking attack. The publicly available anonymized phenotype dataset contains q phenotype measurements and the HIV Status for a list of n individuals. The genotype dataset contains the variant genotypes for m individuals whose identities are known. The genotype-phenotype correlation dataset contains q phenotypes, variants, and their correlations. The attacker predicts the variant genotypes for n individuals in phenotype dataset using the phenotype measurements. The attacker then links the phenotype dataset to the genotype dataset by matching the predicted genotypes to the genotype dataset. The linking potentially reveals the HIV status for the subjects in the genotype dataset. The IDs and HIV Status are colored to illustrate how the linking combines the entries in the two datasets. The grey-shaded columns are not used for linking.

Among the QTL datasets, the abundance of expression QTL (eQTL) datasets makes them most suitable for linking attacks. In an eQTL dataset, each entry contains a gene, a variant, and correlation coefficient, denoted by ρ, between the expression levels and genotypes (Fig. 2, Supplementary Fig. 2). For reporting results and for performing mock linking attacks, we use the eQTLs and gene expression levels from the GEUVADIS Project¹⁷, and the genotypes from the 1000 Genomes Project¹⁸ as representative datasets.

Figure 2.

Illustration of computation of the individual characterizing information (ICI) and correct predictability of genotypes. Given an eQTL where genotype of variant V₁ is correlated with expression of gene 1 (E₁), joint distribution of genotype and expression illustrates the correlation (ρ) indicated by the line fit. Computation of marginal and conditional genotype distributions from the joint distribution are illustrated. ICI for the variant genotype g₁ is computed as the logarithm of reciprocal of the genotype frequency. For n variant genotypes, each genotype contributes to ICI additively with the logarithm of reciprocal of the genotype frequency: −log(V₁ = g₁) − log(V₂ = g₂) − ··· −log(V_n = g_n). The predictability of the genotype given expression level is e is computed in terms of the entropy of conditional genotype distribution, given expression level e. The conditional distribution is built by slicing the joint distribution at expression level e (Indicated by red colored illustrations).

2.2 Genotype Predictability and Information Leakage

We assume that the attacker will behave in a way that maximizes her chances of correctly characterizing the greatest number of individuals. Thus, she will try and predict the genotypes, using the phenotype measurements, for the largest set of variants that she believes she can predict correctly. The most obvious way is by first sorting the genotype-phenotype pairs with respect to decreasing strength of correlation then predicting the genotypes for each variant (Supplementary Fig. 3). The attacker will encounter a tradeoff: As she goes down the list, more individuals can be characterized (more genotypes can characterize more individuals) but it also becomes more likely that she makes an error in the prediction since the genotype-phenotype correlations decrease. This tradeoff can also be viewed as the tradeoff between precision (fraction of the linkings that are correct) and recall (fraction of individuals that are correctly linked). We propose two measures, cumulative individual characterizing information (ICI) and genotype predictability (π), to study this tradeoff.

ICI can be interpreted as the total amount of information in a set of variant genotypes that can be used to pinpoint an individual in a linking attack. This quantity depends on the joint frequency of the variant genotypes. For example, if the set contains many common genotypes, they will not be very useful for pinpointing individuals. On the other hand, rare variant genotypes give more information. Thus, the information content of a set of genotypes is inversely proportional to the joint frequency of the genotypes. We utilize this property to quantify ICI in terms of genotype frequencies (Online Methods, Fig. 2, Supplementary Fig. 4). In order to estimate the joint frequency of variant genotypes, we assume that the variant genotypes are distributed independently (Online Methods, Supplementary Note).

For a set of variants, π measures how predictable genotypes are given the gene expression levels. Since genotypes and expression levels are correlated, knowledge of the expression enables one to predict the genotype more accurately than predicting without such information. In order to quantify the predictability, we use an information theoretic measure for randomness left in genotypes, given gene expression levels (Online Methods, Fig. 2). This has several advantages over using reported correlation coefficients for quantifying predictability. Although the correlation coefficient is a measure of predictability, it is computed differently in different studies and there is no easy way to combine and interpret the correlation coefficients for joint predictability of multiple eQTL genotypes. On the other hand, joint predictability can be easily quantified using π as it fits naturally to the information theoretic formulations (Online Methods). Furthermore, the predictability estimated via π can accommodate the non-linear relationships between genotype and phenotype–unlike the correlation coefficient, which generally measures linear relationships.

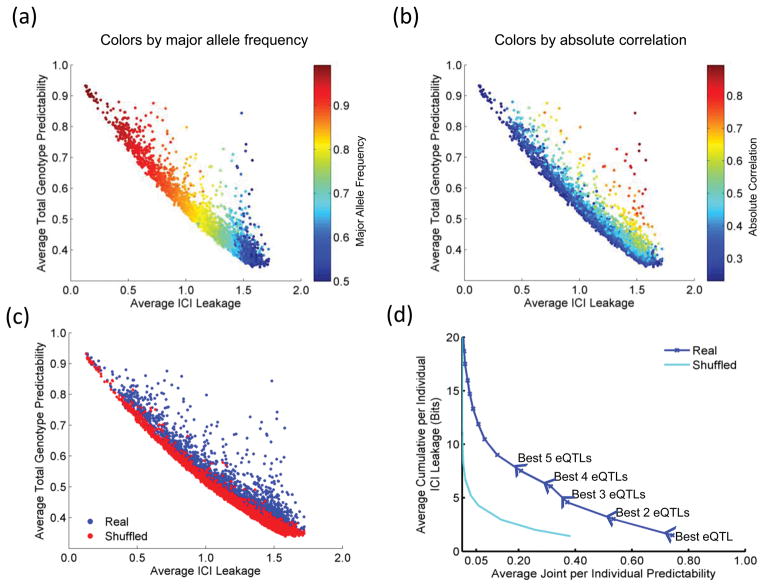
We first considered each eQTL and evaluated the genotype predictability versus the characterizing information leakage. We computed, for each eQTL in the GEUVADIS dataset, average predictability and average ICI over all the individuals (Fig. 3a). Most of the data points are spread along the anti-diagonal: eQTL variants with high major allele frequencies have high predictability and low ICI; and vice versa for variants with lower frequencies (Fig. 3b). This is expected because the genotypes of the high frequency variants can be predicted, on average, easily (most individuals will harbor one dominant genotype) and consequently do not deliver much characterizing information and vice versa for the eQTLs with lower frequency alleles. In order to evaluate how much gene expression levels contribute to predictability of genotypes, we use a shuffled eQTL dataset. The predictability versus ICI leakage for the eQTLs in the shuffled eQTL dataset (Online Methods) is dominantly on the anti-diagonal (Fig. 3c). This is also expected as the predictabilities for shuffled eQTL genotypes depend mainly on how frequently they occur in the population (major frequency genotypes bring low ICI). On the other hand, the real eQTLs (Fig. 3b) deviate from the anti-diagonal, compared to shuffled eQTLs, which shows that expression supplies much information for predicting eQTL genotypes (Fig. 3c). The eQTLs with high correlation have substantially higher ICI and greater predictability. These results illustrate the fact that π measures the total effect of genotype frequencies and expression levels on the predictability of genotypes.

Figure 3.

Estimates of ICI leakage versus predictability. The plots show, for each eQTL, the information leakage (x-axis) versus correct genotype predictability (y-axis). The dots are colored with respect to: (a) the major allele frequency (b) absolute correlation of the eQTL (c) real versus shuffled eQTL datasets. (d) The average cumulative ICI leakage versus joint genotype predictability is shown when multiple eQTLs are utilized with shuffled eQTL dataset. The arrows on the plot indicate the increasing numbers of eQTLs used in estimated joint predictability and cumulative ICI leakage.

When multiple genotypes are utilized, the information leakage is greatly increased. To study this, we computed ICI and predictability for increasing numbers of eQTLs (Supplementary Note, Fig. 3d). As expected, the predictability decreases with increasing ICI leakage. Inspection of mean predictability versus mean cumulative ICI enables us to estimate the number of vulnerable individuals at different predictability levels. For example, at 20% predictability, there is approximately 8 bits of cumulative ICI leakage. At this level of leakage, the adversary can pinpoint an individual, with 20% accuracy, within a sample of 2⁸ = 256 individuals. Thus, within any sample of 256 individuals, we expect the attacker to correctly link 51 (20% of 256) individuals. Although the attacker would not know which individuals are correctly linked, she can estimate reliability of linkings, as discussed later, and focus on the most reliable ones. At 5% predictability, the leakage is 11 bits and the attacker can pinpoint an individual in a sample of 2¹¹ = 2048 individuals. This corresponds to approximately 100 individuals getting correctly linked (5% of 2048). Auxiliary information can be easily added into ICI. For example, gender information, which can be predicted with high accuracy from many molecular phenotype datasets, brings 1 bit of additional auxiliary information to ICI (Supplementary Note).

2.3 Framework for Linking Attacks

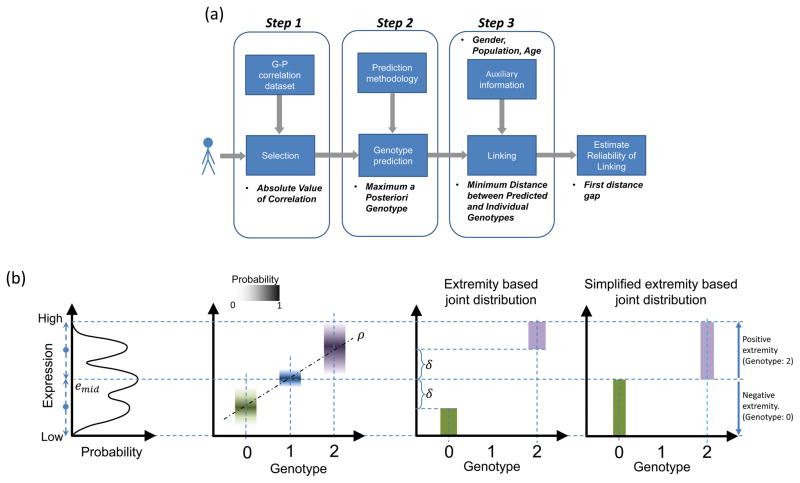
We present a three-step framework for practical instantiation of linking attacks (Fig. 4a). This framework can be used to perform mock linking attacks on datasets to assess their privacy risks. We use this framework to simulate mock attacks in the following sections for assessing their accuracies. The input is the phenotype measurements for an individual, who is being queried for a match to individuals in the genotype dataset (Fig. 1). In the first step, the attacker selects the QTLs, which will be used in linking. The selection of QTLs can be based on different criteria. As discussed earlier, the genotype predictability (π) is the most suitable QTL selection criterion. Although the attacker cannot practically compute predictability using only the QTL list, any function of predictability would still be useful to the attacker for selecting QTLs. For example, the most accessible criterion is selection based on the absolute strength of association, |ρ|, between the phenotypes and genotypes. The second step is genotype prediction for the selected QTLs by modeling the genotype-phenotype distribution (Fig 4b). The third and final step of a linking attack is comparison of the predicted genotypes to the genotypes of the individuals in genotype dataset to identify the individual that best matches to the predicted genotypes. In this step, the attacker links the predicted genotypes to the individual in the genotype dataset (Online Methods).

Figure 4.

Illustration of genotype-expression associations and linking attacks (a) Illustration of the three step linking process: selecting phenotypes and genotypes to be used in linking (step one), predicting the genotypes (step two), linking predicted genotypes to the genotype dataset (step three). The attacker can also estimate the reliabilities of the linkings using the first distance gap metric. (b) Schematic representation of expression-genotype relationships and simplifications. The trimodal gene expression distribution and the joint genotype-expression distribution are shown. The conditional distribution of expression given each genotype is illustrated with box plots in different colors corresponding to each genotype. The genotypes and expression levels are correlated (ρ) as indicated by the line fit. In the extremity-based joint distribution, when the genotype value is 0, a uniform probability is assigned for expression values where extremity is smaller than δ (Green rectangle). For a genotype value 1, no probability is assigned. When genotype value is 2, the probability is uniformly distributed over expression values for which extremity is greater than δ (Purple rectangle). Simplified extremity-based model utilizes the same distribution by setting δ to 0. In this case, when genotype is 0, joint probability is distributed uniformly over expression levels with negative extremity (Green rectangle). When genotype is 2, uniform probability is assigned to expression levels with positive extremity (Purple Rectangle).

2.4 Individual Characterization by Linking Attacks

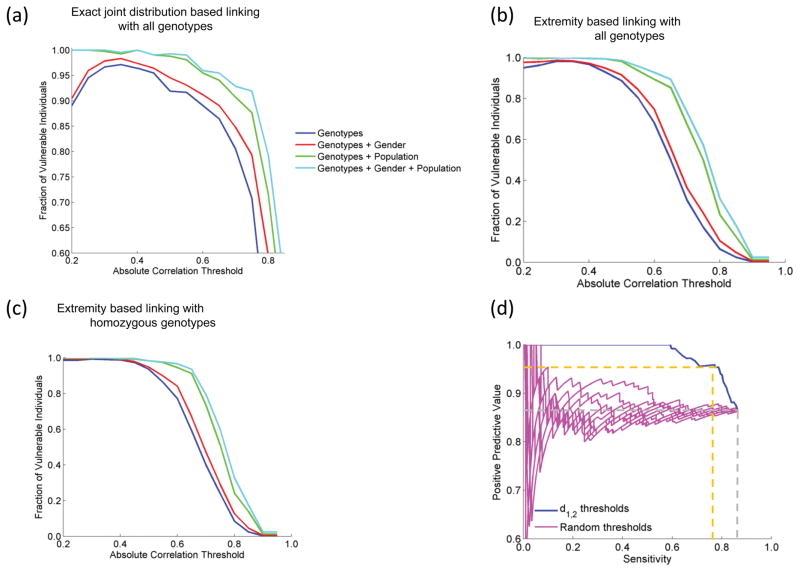
Using the three-step approach, we first evaluated the accuracy of linking using a genotype prediction model where the attacker knows exact joint genotype-expression distribution (Supplementary Note). Although not very realistic, this scenario is useful as a baseline reference for comparison of linking accuracy. The attacker builds the posterior distribution of genotypes given expression levels from the joint distribution. Finally, she predicts each genotype by selecting the genotype with maximum a posteriori probability (Supplementary Note, Supplementary Fig. 5) and links the predicted genotypes to the individual whose genotypes match best. For several eQTL selections with changing correlation threshold, the linking accuracy is above 95% and approaches 100% when auxiliary information is available (Fig. 5a).

Figure 5.

Accuracy of linking attacks. (a) Accuracy of linking with genotype predictions where exact genotype-expression distributions are known (baseline attack). The absolute correlation threshold (x-axis) versus the fraction of vulnerable individuals (y-axis) is plotted. Red, green, and cyan plots show linking accuracy with gender, population, and gender and population as auxiliary information, respectively. (b) Linking accuracy with extremity based linking with all genotypes. (c) Linking accuracy with extremity-based linking with homozygous genotypes. (d) Sensitivity versus positive predictive value of linkings chosen with changing d_1,2, threshold, for the eQTL selection where overall linking accuracy is 84%, in comparison to the random selections of linkings.

In general, knowledge or correct reconstruction of the exact joint genotype-expression distribution may not be possible because the genotype-phenotype correlation coefficient alone is not sufficient to reconstruct the genotype distribution given the expression levels. The attacker can, however, utilize a priori knowledge about the genotype-expression relation and build the joint distributions using models with varying complexities and parameters (Online Methods, Supplementary Note, Supplementary Fig. 6). We focus on a highly simplified model where the attacker exploits the knowledge that the extremes of the gene expression levels (highest and smallest expression levels) are observed with extremes of the genotypes (homozygous genotypes). We use a measure, termed extremity, to quantify the outlierness of expression levels (Online Methods, Supplementary Note, Supplementary Fig. 7a, b and 8). Based on the extremity of expression level and the gradient of association, the attacker first builds an estimate of the joint genotype-expression distribution, then constructs the posterior distribution of genotypes and finally chooses the genotype with the maximum a posterior probability (Online Methods, Supplementary Note, Fig. 4b).

The extremity based prediction methodology assigns zero probability to the heterozygous genotype. Thus, it assigns only homozygous genotypes to variants, for which the associated gene’s expression level has absolute extremity higher than a threshold. With this approach, the genotype prediction accuracy increases with increasing absolute correlation threshold (Supplementary Fig. 7c). We performed linking attack using this prediction method (in 2nd step of linking). In the 1st step of the attack, we used absolute correlation (|ρ|) and extremity thresholds (|δ|) for eQTL selection. The linking accuracy is higher than 95% for most eQTL selections (Fig 4b, Supplementary Fig. 7d). We also observed that changing extremity threshold does not affect the linking accuracy substantially compared to changing absolute correlation threshold. We thus focus on attack scenarios where the absolute extremity threshold is set to zero. This also simplifies the attack scenario by removing one parameter from genotype prediction. We performed linking attack with this model where we used the correlation-based eQTL selection in step 1, then extremity-based genotype prediction in step 2. In the step 3, we evaluated two distance measures for linking the predicted genotypes to the individuals in genotype dataset (Online Methods, Supplementary Fig. 9). More than 95% of the individuals (Fig. 5b,c) are vulnerable for most of the parameter selections, which is more accurate compared to the baseline linking attack (Fig 5a). When the auxiliary information is used, the fraction of vulnerable individuals is 100% for most of the eQTL selections. We also observed that the extremity attack may link close relatives to each other, which can create potential privacy concerns for the family (Supplementary Note, Supplementary Fig. 10a). These results show that linking attack with extremity-based genotype prediction, although technically simple, can be extremely effective in characterizing individuals.

We evaluated whether the attacker can estimate the reliability of the linkings. We observed that the measure we termed, first distance gap, denoted by d_1,2, serves as a good reliability estimate for each linking. We computed the positive predictive value (PPV) versus sensitivity of the linkings with varying d_1,2 thresholds. For the eQTL selection where overall linking accuracy is 84%, the attacker can link a large fraction (79%) of the individuals at a PPV higher than 95% (Online Methods, Fig. 5d, Supplementary Fig. 10b).

We also studied several biases that can affect linking accuracy. First, when the eQTL discovery sample set is different from the samples set on which linking attack is performed, the accuracies are still very high (Supplementary Note, Supplementary Fig. 10c). Moreover, attacks are accurate when there is mismatch between the tissue or population of eQTL discovery sample set and those of linking attack sample set (Supplementary Note, Supplementary Table 1a, b). In addition, we observed that the extremity attack is still effective when genotype sample size is very large (Supplementary Note, Supplementary Fig. 10d).

3 DISCUSSION

In genomic privacy, it is necessary to consider the basic premise of sharing any type of information: there is always an amount of sensitive information leakage in every released dataset¹⁹. It is therefore essential for the genomic data sharing and publishing mechanisms to incorporate statistical quantification methods to objectively quantify risk estimates before the datasets are released. The quantification methodology and the analysis framework presented here can be used for analysis of the information leakage when the correlative relations between datasets can be exploited for performing linking attacks (Supplementary Note, Supplementary Fig. 11).

In the context of linking attacks, an individual’s existence in two seemingly independent databases (e.g., phenotype and the genotype) can cause a privacy concern when an attacker statistically links the databases using the a priori information about correlation of entries in the databases. The methods that we propose can be integrated directly into the existing risk assessment and management strategies. One such strategy is k-anonymization and its extensions^20–22. This technique performs anonymization of the datasets by ensuring that no combination of the features (e.g., predicted genotypes) can be used to pinpoint an individual to less than k individuals. This is done by censoring the entries or by noise addition into the dataset. The estimates of genotype predictability and ICI leakages can be used to select which entries in the phenotype dataset should be anonymized so as to achieve anonymity. This maximizes the utility of the anonymized dataset by focusing only on the data points that leak the most characterizing information. In addition, as the anonymization process can focus only on the sources of highest leakage, this cuts down compute requirements²³ and increase efficiency of anonymization. Another approach is to serve phenotypic data from a statistical database. In this context, differential privacy has been proposed as an optimal way for privacy-aware data serving²⁴. In a differentially private database, release mechanisms are used to query the database and share statistics of the underlying data. The individual records in the database are not shared. To ensure the privacy of the database, the release mechanisms keep track of the leakage in the past queries and limit access to the database. For phenotype databases, the ICI leakage can be incorporated into the release mechanisms so that the total leakage can be tracked. It is also worth noting that anonymized data publishing and serving mechanisms may substantially decrease the biological utility of the data²⁵. Thus, it is necessary to integrate measures of biological utility of the anonymized datasets as another quantity in the risk assessment.

8 ONLINE METHODS

8.1 Genotype, Expression, and eQTL Datasets

The eQTL, expression, and genotype datasets contain the information for linking attack (Supplementary Fig. 2). The eQTL dataset is composed of a list of gene-variant pairs such that the gene expression levels and variant genotypes are significantly correlated. We will denote the number of eQTL entries with q. The eQTL (gene) expression levels and eQTL (variant) genotypes are stored in q × n_e and q × n_v matrices e and v, respectively, where n_e and n_v denotes the number of individuals in gene expression dataset and individuals in genotype dataset. The kth row of e, e_k, contains the gene expression values for kth eQTL entry and e_k,j represents the expression of the kth gene for jth individual. Similarly, kth row of v, v_k, contains the genotypes for kth eQTL variant and v_k,j represents the genotype (v_k,j ∈ {0,1,2}) of k variant for jth individual. The coding of the genotypes from homozygous or heterozygous genotype categories to the numeric values is done according to the correlation dataset (Online Methods). We assume that the variant genotypes and gene expression levels for the kth eQTL entry are distributed randomly over the samples in accordance with random variables (RVs) which we denote with V_k and E_k, respectively. We denote the correlation between the RVs with ρ(E_k, V_k). In most of the eQTL studies, the value of the correlation is reported in terms of a gradient (or the regression coefficient) in addition to the significance of association (p-value) between genotypes and expression levels.

8.2 Quantification of Characterizing Information and Predictability

The genotype RV V_k takes 3 different values, {0,1,2}, where the genotype coding is done by counting the number of alternate alleles in the genotype. Given that the genotype is g_k,j, we quantify the individual characterizing information in terms of self-information²⁶ of the event that RV takes the value g_k,j:

$$\mathit{ICI}\left(V_k=g_{k,j}\right)=I\left(V_k=g_{k,j}\right)=-{log}_2(p\left(V_k=g_{k,j}\right))$$ (1)

where V_k is the RV that represents the kth eQTL genotype, p(V_k = g_k,j) is the probability (frequency) of that V_k takes the value g_k,j, and ICI denotes the individual characterizing information. Given multiple eQTL genotypes, assuming that they are independent, the total individual characterizing information is simply summation of those:

$$\mathit{ICI}\left(\{V_1=v_{1,j},V_2=v_{2,j},\dots ,V_N=v_{N,j}\}\right)=-\sum _{k=1}^N{log}_2\left(p(V_k=v_{k,j})\right).$$ (2)

The genotype probabilities are estimated by the frequency of genotypes in the genotype dataset. We measure the predictability of eQTL genotypes using an entropy-based measure. Finally, the base of the logarithm that is used determines the units in which ICI is reported. When the base two logarithm is used as above, the unit of ICI is bits.

Given the genotype RV, V_k, and the correlated gene expression RV, E_k,

$$\pi (V_k\mid E_k=e)=exp(-H(V_k\mid E_k=e))$$ (3)

where π denotes the predictability of V_k given the gene expression level e, and H denotes the entropy of V_k given gene expression level e for E_k. The extension to multiple eQTLs is straightforward. For the kth individual, given the expression levels e_k,j for all the eQTLs, the total predictability is computed as

$$\begin{array}{l}\pi (\{V_k\},\{E_k=e_{k,j}\left\}\right)=exp(-H(\{V_k\}\mid \{E_k=e_{k,j}\}\left)\right)\\ =exp\left(-\sum _{k}H(V_k\mid E_k=e_{k,j})\right)\end{array}$$ (4)

In addition, this measure is guaranteed to be between 0 and 1 such that 0 represents no predictability and 1 representing perfect predictability. The measure can be thought as mapping the prediction process to a uniform random guessing where the average correct prediction probability is measured by π.

8.3 Extremity-Based MAP Genotype Prediction

Using an estimate of the joint distribution, the attacker can compute the a posteriori distribution of genotypes given gene expression levels. To quantify the extremeness of expression levels, we use a statistic we termed extremity. For the gene expression levels for k^th eQTL, e_k, extremity of the j^th individual’s expression level, e_k,j, is defined as

$$\mathit{ext}(e_{k,j})=\frac{\text{rank}\text{of}{e}_{k,j}\text{in}\{e_{k,1},e_{k,2},\dots ,e_{k,n_e}\}}{n_e}-\mathrm{0.5.}$$ (5)

Extremity can be interpreted as a normalized rank, which is bounded between −0.5 and 0.5. The average median extremity is uniformly distributed among individuals (Supplementary Fig. 7a). In addition, around half of the genes (10,000) in each individual have extremity value exceeding 0.3. Also, around 1000 genes have an absolute extremity exceeding 0.45 (Supplementary Fig. 7b). In other words, each individual harbors a substantial number of genes whose expressions are at the extremes within the population. These can potentially serve as quasi-identifiers. It is worth noting, however, that not all of these extreme genes are associated with eQTLs.

Following from the above discussion, the adversary builds the posterior distribution for kth eQTL genotypes as

$$P(V_k=0\mid E_k=e_{k,j})=\{\begin{array}{ll}1\hfill & \text{if}\left|\mathit{ext}\right(e_{k,j}\left)\right|>\delta ,\mathit{ext}\left(e_{k,j}\right)\times \mathrm{\rho }(E_k,V_k)<0\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (6)

$$P(V_k=2\mid E_k=e_{k,j})=\{\begin{array}{ll}1\hfill & \text{if}\left|\mathit{ext}\right(e_{k,j}\left)\right|>\delta ,\mathit{ext}\left(e_{k,j}\right)\times \mathrm{\rho }(E_k,V_k)>0\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (7)

$$P(V_k=1\mid E_k=e_{k,j})=0.$$ (8)

From the a posteriori probabilities, when the sign of the extremity and the reported correlation are the same, the attacker assigns the genotype value 2, and otherwise, genotype value 0. Finally, the genotype value 1 is never assigned in this prediction method, i.e., the a posteriori probability is zero. As yet another way of interpretation, the genotype prediction can be interpreted as a rank correlation between the genotypes and expression levels and choosing the homozygous genotypes that maximize the absolute values of the rank correlation. Thus, this process can be generalized as a rank correlation based prediction. The posterior distribution of genotypes in equations (6–8) can be derived from a simplified model of the genotype-expression distribution that utilizes just one parameter (Online Methods). We used the posterior genotype probabilities in extremity-based predictions and assessed the genotype prediction accuracy. As expected, the accuracy of genotype predictions increases with increasing correlation thresholds (Supplementary Fig. 7c). The slight decrease of genotype accuracy at correlation thresholds higher than 0.7 is caused by the fact that the accuracy (fraction of correct genotype predictions within all genotypes) is not robust at very small number of SNPs. Although we expect very high accuracy, even one wrong prediction among a small number of total genotypes decreases the accuracy significantly.

8.4 First Distance Gap Statistic Computation

In the linking step, the attacker computes, for each individual, the distance to all the genotypes in the genotype dataset, and then identifies the individual with smallest distance. Let d_j,(1) and d_j,(2) denote the minimum and second minimum genotype distances (among d^H(ṽ_·,j,v_·,a) for all a) for jth individual. We propose using the difference between these distances, termed first distance gap statistic, as a measure of the linking reliability. For this, the attacker computes the following difference:

$$d_{1,2}(j)=d_{j,(2)}-d_{j,(1)}$$ (9)

First distance gap can be computed without the knowledge of the true genotypes, and is immediately accessible by the attacker with no need for auxiliary information (Supplementary Fig. 9). The basic motivation for this statistic comes from the observation that the first distance gap for correctly linked individuals are much higher compared to the incorrectly linked individuals.

8.5 eQTL Identification with Matrix eQTL

To identify eQTLs, we used the Matrix eQTL²⁷ method. We first generated the testing and training sample lists by randomly picking 210 and 211 individuals, respectively, for testing and training sets. We then separated the genotype and expression matrices into training and testing sets. Matrix eQTL is run to identify the eQTLs using the training dataset. In order to decrease the run time, Matrix eQTL is run in cis-eQTL identification mode. After the eQTLs are generated, we filtered out the eQTLs whose FDR (as reported by Matrix eQTL) was larger than 5%. We finally removed the redundancy by ensuring that each gene and each SNP is used only once in the final eQTL list. To accomplish this, we selected the eQTL that is correlated with highest association with each gene. The association statistic reported by Matrix eQTL was used as the measure of the strength of association between expression levels and genotypes. A similar procedure is applied when eQTLs for 30 trios are identified.

8.6 Modeling the Genotype-Phenotype Distribution

In the second step of the linking attack, the genotype predictions are performed. As intermediary information, the genotype predictions are used as input to the third step (Fig. 4a), where linking is performed. The main aim of attacker is to maximize the linking accuracy (not the genotype prediction accuracy), which depends jointly on the genotype prediction accuracy and the accuracy of the genotype matching in the 3rd step. Other than the accuracy of linking, another important consideration, for risk management purposes, is the amount of auxiliary input data (like training data for prediction model) that the genotype prediction takes. The prediction methods that require high amount of auxiliary data would decrease the applicability of the linking attack as the attacker would need to gather extra information before performing the attack. On the other hand, the prediction methods that require little or no auxiliary data makes the linking attack much more realistic and prevalent. It is therefore useful, in the context of risk management strategies, to study complexities of genotype prediction methods and to evaluate how these translate into assessing the accuracy and applicability of the linking attack. We study different simplifications of genotype prediction, and illustrate different levels of complexity for genotype prediction.

The attacker estimates the posterior distribution of genotypes and utilizes the maximum a posteriori estimate of the genotype as the general prediction method. For this, she must first model the joint genotype-phenotype distribution and then build the posterior distribution of genotypes (Supplementary Fig. 6a). The first level of the model can be built by decomposing the conditional distribution of expression (given genotypes) with independent variances and means (Supplementary Fig. 6b). Assuming that the mean and variance are sufficient statistics for the conditional distributions (e.g., normally distributed), the joint distributions can be modeled when the 6 parameters (3 means and 3 variances) are trained. The training can be performed using unsupervised methods like expectation maximization, or it can be performed using training data. This would, however, increase the required auxiliary data and decrease the applicability of the linking attack. A simplification of the model can be introduced by assuming that the variances of the conditional expression distributions are the same for each genotype (Supplementary Fig. 6c). This decreases the number of parameters to be trained to 4 (3 means and 1 variance). An equally complex model with 4 parameters can be built assuming that the conditional distributions are uniform at non-overlapping ranges of expression (Supplementary Fig. 6d). This model requires 4 parameters (e₁,e₂,e₃,e₄) to be trained. This model can be further simplified into a model which requires only one parameter (Supplementary Fig. 6e). In this model, uniform probability is assigned when homozygous genotypes is observed and expression level is higher (or lower) than e_mid. In addition, zero probability is assigned when heterozygous genotypes are observed. Depending on the direction of genotype-expression gradient, the expression levels higher than e_mid associate with one of the homozygous genotypes and expression levels lower than e_mid associate with the other homozygous genotype. This simplified model is exactly the distribution that is utilized in the extremity-based genotype prediction. In the extremity based prediction, we estimate e_mid simply as the mid-point of the range of gene expression levels within the expression dataset (Supplementary Note).

8.7 Datasets

The normalized gene expression levels for 462 individuals and the eQTL dataset are obtained from the GEUVADIS mRNA Sequencing Project¹⁷. The eQTL dataset contains all the significant (Identified with a false discovery rate of at most 5%) gene-variant pairs with high genotype-expression correlation. To ensure that there are no dependencies between the variant genotypes and expression levels, we used the eQTL entries where gene and variants are unique. In other words, each variant and gene are found exactly once in the final eQTL dataset. The shuffled (randomized) eQTL datasets in comparisons are generated by shuffling the gene names in the gene-variant pairs in eQTL dataset. This way the gene and variant matchings are randomized. The genotype, gender, and population information datasets for 1092 individuals are obtained from 1000 Genomes Project¹⁸. For 421 individuals, both the genotype data and gene expression levels are available. For the tissue analysis, the publicly available significant eQTLs for 6 tissues that are computed by the GTex project are downloaded from the GTex Portal. The HAPMAP CEU trio expression and genotype datasets are obtained from the HAPMAP project web site.

8.8 Code Availability

Analysis code that is used to generate results can be obtained from http://privaseq.gersteinlab.org

Supplementary Material

Supplementary Figures. Supplementary Table 1.

Linking accuracy of extremity-based linking attack using the eQTLs are identified in different populations and different tissues and comparison with Schadt et al method. (a) The table shows the linking accuracies (for populations shown in the rows) when the eQTLs that are identified using data (indicated in each column) from different populations. (b) The linking accuracy of individuals from the GEUVADIS Project when eQTLs identified from different tissues are used in linking. (c) Linking attack accuracy comparison. The table shows linking accuracy for Schadt et al and extremity-based linking attack methods. Each row corresponds to a different number of data points in the training datasets that is input to Schadt et al method.