Challenges and promises for translating computational tools into clinical practice

Abstract

Computational modeling and associated methods have greatly advanced our understanding of cognition and neurobiology underlying complex behaviors and psychiatric conditions. Yet, no computational methods have been successfully translated into clinical settings. This review discusses three major methodological and practical challenges (A. precise characterization of latent neurocognitive processes, B. developing optimal assays, C. developing large-scale longitudinal studies and generating predictions from multi-modal data) and potential promises and tools that have been developed in various fields including mathematical psychology, computational neuroscience, computer science, and statistics. We conclude by highlighting a strong need to communicate and collaborate across multiple disciplines.

Introduction

Computational modeling has greatly contributed to understanding cognitive processes underlying our decision-making. By providing a mechanistic account of the processes, computational modeling allows us to generate quantitative predictions and test them in a precise manner. Computational modeling also provides a framework for studying the neural mechanisms of complex behaviors. Ever since reinforcement learning models were shown to well describe phasic activity changes in midbrain dopamine neurons [1], computational modeling has been widely combined with electrophysiological data and human functional magnetic resonance imaging (fMRI) signals to identify brain regions implementing specific cognitive processes [2,3]. A systematic line of research based on the computational framework suggests that the brain has multiple systems for decision-making [4,5]: the Pavlovian system, which sets a strong prior on our actions when we are faced with rewards or punishments and the instrumental system, which is further divided into habitual (i.e., model-free; efficient but inflexible) and goal-directed (model-based; effortful but flexible) systems. While the Pavlovian system has been traditionally regarded as purely model-free, new ample evidence suggests Pavlovian learning might also involve model-based evaluation [6].

There is a growing consensus that computational modeling can also be helpful to understand psychiatric disorders. Computational models can break maladaptive behaviors into distinct cognitive components, and the model parameters associated with the components can be used to understand the latent cognitive sources of their deficits. Therefore, computational modeling can provide a useful framework in understanding comorbidity among psychiatric disorders in a systematic way. Such a framework can specify psychiatric conditions with basic dimensions of neurocognitive functioning and offer a novel approach to assess and diagnose psychiatric patients [7–10].

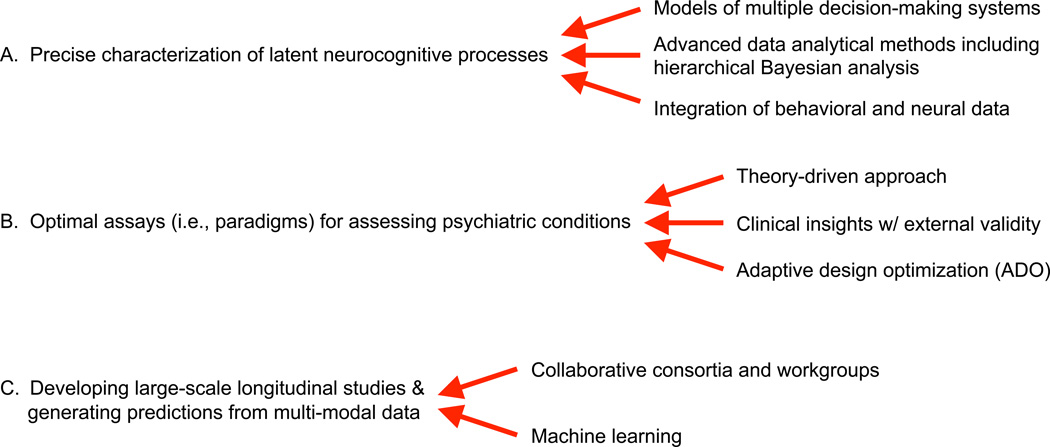
Despite the growing enthusiasm, no computational assays or methods have influenced clinical practice yet. There remain several major methodological and practical challenges that need to be solved for translating computational modeling tools into clinical practice. In this article, among many others, we focus on the following challenges as summarized in Figure 1: (A) precise characterization of latent neurocognitive processes, (B) development of optimal assays for assessing psychiatric conditions, (C) development of large-scale longitudinal studies and generating predictions using multi-modal and multi-dimensional data. In the following sections, we provide a general overview of each challenge and discuss how we can potentially address them. Our review focuses on computational modeling of human decision-making and fMRI studies, which are most relevant to the challenges we consider. We also briefly review how mathematical psychologists and computational neuroscientists have independently attempted to understand psychiatric disorders using computational methods. We hope this article will help researchers in each field identify strengths of the other field and stimulate further communication and interaction between the fields. There are some important topics that are not addressed in this article including biophysically-based models and readers can refer to existing review papers on the topics [11–13]. Because of space limit, our review excludes a survey of model comparison methods and mathematical details of Bayesian data analysis, which are covered in other reviews [14–16].

Figure 1.

Promising approaches to address three major changes for translating computational tools into clinical practice

A. Precise characterization of latent neurocognitive processes

Early applications of computational modeling to psychiatric populations were initiated by mathematical psychologists. Traditionally they focused on identifying cognitive processes embedded in a cognitive or decision-making task. Mathematical psychologists including Batchelder, Townsend, Ratcliff, Neufeld, and Treat advocated as well as empirically demonstrated that computational modeling can be used to assess clinical populations [17]. The computational approach began to receive additional attention as Busemeyer and Stout [18] developed the Expectancy-Valence Learning (EVL) model for the Iowa Gambling Task (IGT) and apply the EVL to several clinical populations [19]. The model has been subsequently revised to improve its performance, which led to a newer version called the Prospect Valence Learning (PVL) model [20,21]. Despite criticism on the IGT for its complicated design and performance heterogeneity [22], the PVL model showed good model-fits and simulation performance [e.g., 23] and it has been applied to several populations with substance dependence [for a review and detailed findings see, 24]. For example, modeling approaches on the IGT revealed reduced loss aversion among heroin users compared to healthy individuals, which was robust across all models we tested [23]. Computational models have also been used to decompose performance of clinical populations on the Balloon Analogue Risk Task (BART) [25], the Go/Nogo task [26], and speeded choice-response time tasks [27].

Independently, computational neuroscientists including Montague, Dayan, Dolan, Friston, and colleagues have put efforts to build computational accounts of (ab)normal cognition and its biological underpinnings (a.k.a. Computational Psychiatry) [8,28,29]. They built computational frameworks and used the method called model-based fMRI [3] or model-based electroencephalography [30] (among other methods) in which internal states predicted by computational models are used to identify brain regions that presumably implement a particular cognitive/computational process. Many applications to psychiatric disorders [31–34] have been built around the Bayesian decision framework that offers a Bayesian account of decision-making [35]. In addition, recent studies using model-based fMRI significantly enhanced our understanding of the neurobiological mechanisms underlying reinforcement learning and decision-making in the brain [for recent reviews see, 12,36].

Once we build a computational model, the next important step is parameter estimation. Getting accurate estimates of the key model parameters is critical for phenotyping computational processes precisely. Currently the state of the art for parameter estimation is hierarchical hierarchical Bayesian analysis (HBA) that pools information across individuals and captures similarities and differences among individuals in a hierarchical way [15,37]. Hierarchical methods are particularly useful when the amount of information is small or insufficient for precise parameter estimation at the individual level. Hierarchical methods, whether Bayesian or non-Bayesian [e.g., 38] often lead to very similar parameter estimates (personal communication). Because assumptions and priors for HBA and non-Bayesian hierarchical methods are different, the choice for a hierarchical method may depend on the computational model concerned. However, we believe HBA has several advantages over non-Bayesian methods such as its more flexible assumptions and finding full posterior distributions instead of point estimates (thus providing maximum information about parameter estimates). HBA also allows us to compare clinical and non-clinical groups by comparing their posterior distributions [15,23]. Recent development of tools [39] and tutorials [15,16] also facilitated its usage.

While HBA is already widely accepted and used in cognitive science and mathematical psychology, hierarchical methods including HBA have been only recently adopted in computational/cognitive neuroscience field and non-hierarchical maximum likelihood estimation (MLE) is still often used. Using simulated behavioral data and actual behavioral/fMRI data, Ahn et al. [40] empirically showed how HBA is superior to non-hierarchical MLE methods. While individual MLE estimates, which are based only on each individual’s data, were often driven toward parameter bounds (e.g., learning rate = 0), HBA reliably recovered the true parameters of simulated data. Using HBA also improved the fMRI signal compared to using individual MLE (i.e., higher peak activation and larger regions of activation), presumably because HBA improved the characterization of individual differences.

There still remain major challenges for HBA and associated hierarchical methods. Assuming a single hyper-group across a modest number of individuals (e.g., ~50) might be valid [c.f., 41], but the assumption might be invalid when fitting large samples (e.g., ~1000) with a single hyper-group [42]. Non-parametric Bayesian methods [43] that let the data determine the number of hyper-groups as well as group assignment and estimate parameters simultaneously could be a great solution, but it is computationally very challenging. Alternatively, Bayesian hierarchical mixture approaches [e.g., 44], or HBA of each subgroup that is clustered by behavioral indices, might provide practical compromises. Another important direction is to integrate neural and behavioral measures into a single hierarchical Bayesian framework so that neural and behavioral data can mutually constrain each other and simultaneously inform the parameter estimates of a computational model [45].

B. Developing assays for improving the assessment of psychiatric conditions

Behavioral performance on a decision-making task entails multiple cognitive processes (e.g., valuation of reward/risk, outcome evaluation, action selection) and interaction of multiple decision-making systems including Pavlovian and instrumental (habitual and goal-directed) systems [46]. Thus, it is important to develop and employ assays (i.e., tasks) that will allow us to maximally decompose the underlying processes and reveal the interactions of the decision-making systems.

Historically, there have been mainly two approaches. Clinicians developed or adopted emotionally engaging tasks based on their clinical experience and intuitions to mimic naturalistic risk-taking behaviors. The tasks include the delay discounting task (DDT) [47], the IGT [48], the BART [49], and the Cambridge Gambling Task [50] that had widespread success in classifying clinical populations from healthy individuals (i.e., external validity). However, the complexity of the tasks makes it challenging to decompose its cognitive processes at the behavioral level. Behavioral economists and computational neuroscientists, on the other hand, typically start with difficult goals: Understanding specific constructs (e.g., valuation of reward) or the interactions among the decision-making systems [6] is a primary goal, and tasks are designed accordingly. Examples include decision problems between two monetary gambles [for a review see, 51], decision-making tasks [52–54] teasing apart the contribution of goal-directed and habitual systems, and the orthogonalized Go/Nogo task [55] examining the interactions between Pavlovian and instrumental systems. While early monetary decision-making tasks probing specific reward/risk constructs had limited success in distinguishing clinical populations from healthy controls [51], recent studies using theory-guided decision-making tasks have revealed specific cognitive processes and neural correlates associated with psychiatric conditions [54,56,57].

While being excited about past success applying decision-making probes to psychiatric patients, we are still in need of improving the assays. Considering clinical patients having reduced cognitive capacity and attention span, some of the decision-making tasks are too long or cognitively too challenging to be used in clinical settings. Thus, it is possible that some of the decision-making deficits could be attributed to their general intelligence or working memory capacity, rather than targeted neurocognitive processes. We believe both clinical experience and up-to-date knowledge of neuro-circuitry of specific psychiatric conditions can guide us to design tasks that are not only emotionally engaging [51] but also decomposable.

A promising computational approach to shorten the length of a task or improve the efficiency of information gain is the use of adaptive design optimization (ADO) [58]. In a typical experiment, when designing a task for probing specific processes, researchers make a priori decisions on experimental design (e.g., number of trials, amount of reward/punishment in gambling tasks, delays between stimuli). Then, we identify the best-fitting model and estimate its model parameters (see section B for more details on these issues). In contrast, ADO finds the optimal design “on the fly” that maximizes information gain based on data collected from preceding trials, presents the optimized stimuli on the current trial, observes outcomes, and updates the priors for experimental parameters into posteriors using a Bayesian framework. Recent advances in computer hardware and algorithms make it tractable to do Bayesian updating within a reasonable time scale (e.g., within 1sec). ADO has already been successfully applied to identifying best-fitting models in gambling paradigms [59] and DDT [60], as well as to optimally assess visual acuity using the contrast sensitivity function [61]: The studies demonstrated that ADO substantially reduced the number of trials required to do model comparisons or parameter estimation, or dramatically increased test-retest reliability compared to a non-ADO procedure [61]. These results suggest that implementation of ADO-based experiments might potentially benefit psychiatric research, especially those utilizing neuroimaging methods in saving time and scanning cost.

ADO methods are new and there remain several empirical issues to be addressed. ADO procedures naturally tend to make decisions maximally difficult over trials and change the statistics of the choice set (e.g., the range of gains and losses). Therefore, during ADO-based experiments, participants might be more likely to make random choices with difficult options, behave very differently [62], or experience more negative feelings compared to during non-ADO experiments. To address the concerns, several adjustments have been used: inserting easy trials between tough trials [61], stopping data collection when the same small subset of trials are presented repeatedly, and reducing the number of required trials for convergence by running simulations and identifying an optimal set of choices prior to experimentation [60]. However, additional future studies are needed to determine whether ADO produces systematic differences in choice patterns by examining the inter- and intra-personal differences across ADO and non-ADO sessions.

C. Developing large-scale longitudinal studies and generating predictions using multi-modal and multi-dimensional data

From a clinical perspective, the efforts and approaches listed above eventually boil down to a question: Can we predict clinical outcomes using these neuro-computational markers? To make predictions that generalize to new samples and identify predictors of a psychiatric condition, large sample sizes using longitudinal studies are needed. There already exist several consortia and working groups that provide imaging and genetic data from a large number of individuals, including the Enhancing Neuroimaging Genetics through Meta-Analysis (ENIGMA; http://enigma.ini.usc.edu), the IMAGEN (http://www.imagen-europe.com), the Pediatric Imaging, Neurocognition, and Genetics (PING; http://pingstudy.ucsd.edu) Study, and Brain Genomics Superstruct (https://dataverse.harvard.edu/dataverse/GSP) projects. However, sample sizes or clinical phenotypes publicly available through the consortia are still limited, and there remains a critical need to develop large-scale longitudinal studies in various psychiatric conditions. In drug addiction, the National Institute on Drug Abuse (NIDA) is launching the Adolescent Brain Cognitive Development (ABCD) Study (http://addictionresearch.nih.gov/adolescent-brain-cognitive-development-study), which will longitudinally track 10,000 adolescents over 10 years, and the study will include substance use, neuroimaging, and genomic measures. The NIDA will share the database through their data repository and we anticipate it will allow researchers interested in drug addiction to evaluate the utility of their tools.

Such a large longitudinal dataset contains many millions of variables; thus consideration of multiple comparisons would be essential to minimize Type I and II errors in associated classical statistics. Recent reports suggest that cross-validated machine learning may well serve as a promising approach for effective analysis of such big datasets [63,64]. However, how to integrate neural (e.g., genomic variations and brain-based measures) and behavioral (e.g., model parameters and survey scores) measures in a principled way for generating predictions is still a topic of active research. For example, Whelan et al. [65] conducted a longitudinal study aiming to predict future alcohol misuse by using regression-based machine learning. The study incorporated a wide spectrum of measures including genetic variations, functional/structural MRI, gray matter volume, cognitive tasks, personality surveys, and family history. Although their machine learning method (penalized logistic regression) produced generalizable and relatively accurate predictions, the approach essentially treated all modalities and measures within each modality equally, whereas in reality there is a complex interplay among genetic, environmental, and other unidentified factors [66]. There is a strong need to identify multivariate methods that are suited for this type of multi-modal dataset.

Discussions/Conclusions

Although we have discussed three key aspects of future challenges, we acknowledge that the list is not exhaustive. Another important practical challenge is a search for cost-effective markers. While neuroimaging and genomic measures are promising biomarkers for psychiatric disorders, many practitioners might not be able to afford the cost. Thus, finding markers that are affordable yet predictive of clinical outcomes would have important practical implications [63]. Preliminary literature suggests that eye movements including spontaneous eye blinks [e.g., 67] and pupil diameter [68] could potentially serve as surrogate measures (also see [69]) but the field is still in its infancy.

A potential way to reduce the cost of imaging markers is the application of machine learning approaches to fMRI time-series data. A dominant way of analyzing fMRI data is the voxel-wise general linear model (GLM) approach, which can lead to substantial loss of power in case of model mis-specification [e.g., 70]. Two recent studies demonstrated that the use of unmodeled fMRI time-series data combined with machine learning can produce rapid fMRI classifiers for autism spectrum disorder [71] or political attitudes [72]. They used single-stimulus measurements (approximately 20 seconds of time-series data) as regressors, which contained enough information to make reliable classifications.

Computationally inspired measures have yet to undergo large-scale validation and a lot of serious work remains to be done (e.g., test-retest reliability, validation of computational methods and findings using simulated and real data across diverse populations, understanding the regulatory environment critical for translating scientific tools into clinical practice). We strongly believe that solving these challenges requires close communication and collaboration between people in multiple areas. Clinicians, mathematical psychologists, computational neuroscientists, computer scientists, statisticians, and researchers in related fields have their own expertise and can provide their unique (or overlapping) contributions to tackle these technical and practical challenges. For example, clinical insights and experience can greatly inform the design of computational assays for clinical populations. Also, knowledge in neurobiological underpinnings of psychiatric conditions and decision neuroscience can be essential in every step of computational psychiatric research. Collaboration with people in computer science and statistics will be also critical to identify cutting-edge computational and statistical algorithms that are suited for multi-modal datasets. Also, workshops and meetings that can facilitate communication between multiple areas would mutually benefit each area.

Highlights.

• Computational approaches provide novel insights into psychiatric conditions

• There exist several challenges for translating the approaches into clinical tools

• This review discusses three major methodological and practical challenges

• Highlighting a need to communicate and collaborate across multiple disciplines