Likelihood-Based Inference for Discretely Observed Birth-Death-Shift Processes, with Applications to Evolution of Mobile Genetic Elements

Summary

Continuous-time birth-death-shift (BDS) processes are frequently used in stochastic modeling, with many applications in ecology and epidemiology. In particular, such processes can model evolutionary dynamics of transposable elements — important genetic markers in molecular epidemiology. Estimation of the effects of individual covariates on the birth, death, and shift rates of the process can be accomplished by analyzing patient data, but inferring these rates in a discretely and unevenly observed setting presents computational challenges. We propose a multi-type branching process approximation to BDS processes and develop a corresponding expectation maximization algorithm, where we use spectral techniques to reduce calculation of expected sufficient statistics to low dimensional integration. These techniques yield an efficient and robust optimization routine for inferring the rates of the BDS process, and apply broadly to multi-type branching processes whose rates can depend on many covariates. After rigorously testing our methodology in simulation studies, we apply our method to study intrapatient time evolution of IS6110 transposable element, a genetic marker frequently used during estimation of epidemiological clusters of Mycobacterium tuberculosis infections.

1. Introduction

Continuous-time branching processes are widely used in stochastic modeling of population dynamics, with applications in biology, genetics, epidemiology, quantum optics, and nuclear fission (Renshaw, 2011). One of the most widely used classes of branching processes are birth-death (BD) processes, a simple yet flexible model for single-species population dynamics. The popularity of BD processes is in part attributable to their well-understood mathematical properties. To accurately model behavior in many applications, however, it is often necessary to consider systems with more than one species — bivariate or other multi-type processes are commonly used to model phenomena such as competition, predation, or infection (Renshaw, 2011). Multi-type branching processes form one class of models that can accommodate populations with multiple types, but these models pose considerable computational challenges for statistical inference. Our work introduces new methods to overcome these challenges, enabling likelihood-based inference in partially observed, multi-type branching processes.

Many statistically relevant quantities are available in closed form for birth-death processes and several of its variants, including transition probabilities, stationary distributions, and moments (Bailey, 1964; Keiding, 1975; Crawford and Suchard, 2012). The ability to compute finite-time transition probabilities enables likelihood-based inference for discretely observed or partially observed BD processes, since the observed likelihood is a function of these transition probabilities. Evaluating this likelihood is necessary in maximum likelihood estimation as well as in many Bayesian inferential procedures. Recent work by Doss et al. (2013) and Crawford et al. (2014) introduces techniques to additionally compute conditional moments of BD sufficient statistics for linear and general birth-death-immigration processes, enabling calculation of the expected complete-data likelihood necessary in an expectation-maximization (EM) algorithm (Dempster et al., 1977).

Unfortunately, methods to evaluate finite-time transition probabilities and conditional moments are not known in the multi-type setting, and generalizing the techniques available in the single-species case is nontrivial. Without these quantities, likelihood-based estimation is limited to simulation-based inference via Monte Carlo EM or MCMC (Golinelli et al., 2006) and asymptotic approximations, such as moment-based estimating equations (Catlin et al., 2001). However, these approaches have shortcomings. MCMC approaches require augmenting the state space by high-dimensional latent variables and become computationally prohibitive when the state space is large. Moment-based methods are statistically less efficient than likelihood-based approaches and thus often inappropriate for smaller datasets, requiring a large number of observations to produce meaningful standard errors and confidence intervals.

In this paper, we extend the analysis of Doss et al. (2013), deriving previously unavailable numerical solutions to transition probabilities and conditional moments for discretely observed, multi-type branching processes. This enables us to evaluate the observed likelihood, as well as to reduce the challenging computation of expected complete-data log-likelihood necessary in an EM algorithm to efficient evaluation of expected sufficient statistics by low-dimensional integration. Our EM algorithm can be applied in settings where the data are assumed to be generated from independent, continuous-time multi-type branching processes, observed at discrete and possibly irregularly spaced time points, whose rates can be a function of many process-specific covariates.

Though our methodology applies broadly, we focus attention to estimating the rates of a birth-death-shift (BDS) process which allows a simultaneous birth and death, or shift event, to occur. The BDS process adds the possibility of shift events to the standard BD framework, and is useful for modeling systems that allow for elements to switch locations or types. For example, in epidemiological applications, interaction between infected and susceptible populations can be captured as a shift event, involving a simultaneous increase and decrease in the respective populations. Spatial BDS processes have also been studied to improve Metropolis-Hastings algorithms for perfect sampling (Huber, 2012) relevant to a range of spatial statistical applications; see Illian et al. (2008) for an overview. Our motivation stems from the BDS process proposed by Rosenberg et al. (2003) to model evolution of transposons — mobile genetic elements that can replicate, die, or shift locations along the genome. While previous methods have inferred rates of this process from data under restrictive model assumptions, our method is the first to enable inference without compromising the model. In particular, previous analyses either did not allow multiple events to occur per observation interval or could not model shift events, while our work successfully addresses both issues. We derive an EM algorithm for discretely observed multi-type branching processes, and assess its performance in several simulation studies. Finally, we apply our algorithm to estimate rates of the IS6110 transposon in the Mycobacterium tuberculosis genome as a function of relevant covariates.

2. Methodology

Our motivation stems from a birth-death-shift process proposed by Rosenberg et al. (2003) to model evolutionary dynamics of transposable elements or transposons — genomic mobile sequence elements. Each transposon can (1) duplicate, with the new copy moving to a new genomic location; (2) shift to a different genomic position; or (3) be removed and lost from the genome, independently of all other transposons. These events occur at instantaneous rates proportional to the total transposon copy number at that time. Thus, transposons evolve according to a linear birth-death-shift (BDS) process in continuous time.

The process of transposon evolution within a host is observable by serially genotyping the organism of interest, e.g., Mycobacterium tuberculosis as in Rosenberg et al. (2003). The number and chromosomal position of the IS6110 element in the M. tuberculosis genome can be visualized using restriction fragment length polymorphism (RFLP). This technique entails restriction endonuclease digestion of the M. tuberculosis DNA which is run in an agarose gel, southern blotting and probing with a peroxidase labeled IS6110 probe. Birth, death, and shift events are thus detectable via changes in the number and size of the bands where the IS6110 elements are located.

Estimating the rates based on observed changes at genotyping times in this experimental setup corresponds to inference in a discretely observed linear BDS process. That is, we assume each element behaves independently, and that overall rates of each event are proportional to total copy number k. Together with the time-homogeneity assumption, waiting times until occurrence of an event are distributed exponentially with rate kη, where η = λ+μ+ν. When an event occurs, the probability that it is birth, death, or shift is given by λ/η, ν/η, and μ/η respectively. The BDS process is therefore a continuous-time Markov chain (CTMC).

The states in our process $\tilde{\mathbf{x}}\in {\{0,1\}}^S≔\tilde{\Omega }$ can be represented as binary vectors, where S is the number of possible locations transposons may occupy along the genome, 0's denote unoccupied sites, and 1's correspond to sites occupied by a transposon. Now, denote the 2^S × 2^S infinitesimal generator of this CTMC as $\mathbf{Q}=\left\{q_{{\tilde{\mathbf{x}}}_1,{\tilde{\mathbf{x}}}_2}\right\}$, where $q_{{\tilde{\mathbf{x}}}_1,{\tilde{\mathbf{x}}}_2}$ denotes the instantaneous rate of jumping to ${\tilde{\mathbf{x}}}_2$ beginning from ${\tilde{\mathbf{x}}}_1$, with ${\tilde{\mathbf{x}}}_1$, ${\tilde{\mathbf{x}}}_2\in \tilde{\Omega }$. To write the entries of Q, first define $C^{+}\left(\tilde{\mathbf{x}}\right)$ as the set of all configurations with one additional site occupied relative to $\tilde{\mathbf{x}}$. Thus, $C^{+}\left(\tilde{\mathbf{x}}\right)$ contains states corresponding to one birth event beginning with $\tilde{\mathbf{x}}$. Similarly $C^{\to }\left(\tilde{\mathbf{x}}\right)$ contains states where one additional site is occupied and one originally occupied site is no longer occupied, and $C^{-}\left(\tilde{\mathbf{x}}\right)$ contains states where one originally occupied site in $\tilde{\mathbf{x}}$ is no longer occupied. Then $\mid C^{+}\left({\tilde{\mathbf{x}}}_1\right)\mid =S-k$, $\mid C^{-}\left({\tilde{\mathbf{x}}}_1\right)\mid =k$, and $\mid C^{\to }\left({\tilde{\mathbf{x}}}_1\right)\mid =\mid C^{+}\left({\tilde{\mathbf{x}}}_1\right)\mid \times \mid C^{-}\left({\tilde{\mathbf{x}}}_1\right)\mid$, and finally the entries of the generator Q are given by

$$q_{{\tilde{\mathbf{x}}}_1,{\tilde{\mathbf{x}}}_2}=\frac{\lambda }{\mid C^{+}\left({\tilde{\mathbf{x}}}_1\right)\mid }{1}_{\{{\tilde{\mathbf{x}}}_2\in C^{+}({\tilde{\mathbf{x}}}_1\left)\right\}}+\frac{\nu }{\mid C^{\to }\left({\tilde{\mathbf{x}}}_1\right)\mid }{1}_{\{{\tilde{\mathbf{x}}}_2\in C^{\to }({\tilde{\mathbf{x}}}_1\left)\right\}}+\frac{\mu }{\mid C^{-}\left({\tilde{\mathbf{x}}}_1\right)\mid }{1}_{\{{\tilde{\mathbf{x}}}_2\in C^{-}({\tilde{\mathbf{x}}}_1\left)\right\}}.$$ (1)

2.1 BDS process with covariates

We are interested in inference when the data consist of m independent processes $\left\{{\tilde{\mathbf{X}}}^p\left(t\right)\right\}$, p = 1, …, m, each discretely observed at times 0 = t_p,0 < t_p,1 < … < t_p,n(p). We assume each $\left\{{\tilde{\mathbf{X}}}^p\right(t\left)\right\}$ process evolves according to a linear BDS model with per-particle instantaneous birth rate λ_p ⩾ 0, shift rate ν_p ⩾ 0, and death rate μ_p ⩾ 0. The data, observations from each process, are points in the previously defined state space, with ${\tilde{\mathbf{X}}}^p\left(t\right)\in \tilde{\Omega }$ for any fixed p and t. For example, in transposon evolution, each patient p is genotyped at n(p)+1 observation times, and at each given time, the 1's present in the data vector correspond to locations in the gel currently occupied by transposons. The observed data corresponding to a given process $\left\{{\tilde{\mathbf{X}}}^p\right(t\left)\right\}$ can thus be collected in a S × {n(p) + 1} matrix with columns corresponding to observation times, and the full observed dataset can be collected into a $S\times {\sum }_{p=1}^m\left\{n\right(p)+1\}$ matrix: $\mathbf{Y}=\left\{{\tilde{\mathbf{X}}}^1\left(t_{1,0}\right),\dots ,{\tilde{\mathbf{X}}}^1\left(t_{1,n\left(1\right)}\right),\dots ,{\tilde{\mathbf{X}}}^m\left(t_{m,0}\right),\dots ,{\tilde{\mathbf{X}}}^m\left(t_{m,n\left(m\right)}\right)\right\}$.

The rates of each process are determined by a vector of c covariates ${\mathbf{z}}_p=(z_{p,1},z_{p,2},\dots ,z_{p,c})\in {\mathbb{R}}^c$ through a log-linear model log(λ_p) = β^λ · z_p, log(ν_p) = β^ν · z_p, log(μ_p) = β^μ · z_p, where β ≔ (β^λ, β^ν, β^μ) are the regression coefficients and · represents a vector product. For instance, in an epidemiological study, these covariates may contain patient-specific disease process and demographic information. The observed data log-likelihood is obtained by summing over transitions in each process and summing over all processes:

$${\tilde{\ell }}_o(\mathbf{Y};\beta )=\sum _{p=1}^m\sum _{j=0}^{n\left(p\right)-1}\log {\tilde{p}}_{{\tilde{\mathbf{X}}}^p\left(t_{p,j}\right),{\tilde{\mathbf{X}}}^p\left(t_{p,j+1}\right)}(t_{p,j+1}-t_{p,j};{\theta }_p),$$ (2)

where θ_p = (λ_p, ν_p, μ_p) and ${\tilde{p}}_{{\tilde{\mathbf{x}}}_1,{\tilde{\mathbf{x}}}_2}(t;\theta )={\text{Pr}}_{\theta }\left\{\tilde{\mathbf{X}}\right(t)={\tilde{\mathbf{x}}}_2\mid \tilde{\mathbf{X}}(0)={\tilde{\mathbf{x}}}_1\}$ denotes a transition probability of the BDS process. We are interested in computing the maximum likelihood estimates (MLEs) of parameters β of the BDS process. Notice that if the transition probabilities were available for given λ, ν, μ, and t values, one could maximize the likelihood in (2) using standard off-the-shelf optimization procedures. However, due to the large state space of all possible configurations of occupied sites, analysis of these transition probabilities is intractable. To approximate the BDS model likelihood above, we introduce a two-type branching process with computationally tractable transition probabilities that are numerically close to the transition probabilities of the BDS model over any time interval. The following sections detail the correspondence between the BDS model and the two-type branching process.

2.2 State space reduction

The size of the original state space $\mid \tilde{\Omega }\mid =2^S$ quickly becomes unmanageable as S grows so that analysis using the rate matrix defined in (1) becomes unwieldy for all but small values of S. Previous work by Doss et al. (2013) addresses this issue by collapsing the state space to one dimension, distilling the data to copy number counts at each observation time. In this simplified setting, they develop tools for inference in a discretely observed birth-death-immigration framework. However, this approximate model ignores particle shifts which do not affect the total copy number, rendering the shift rate unidentifiable. Further, collapsing the state space in this way violates the Markov assumption in the BDS model. In particular, waiting times between birth and death events are exponentially distributed under the model in Doss et al. (2013), but under the BDS model with shift events, the waiting time between a birth and death no longer follows an exponential distribution.

Instead of ignoring shifts, we propose a reduction of the state space into a two-dimensional representation $\Omega \in \mathbb{N}\times \mathbb{N}$. Elements of this reduced space are pairs X(t) = (x_old, x_new) ∈ Ω tracking the number of originally occupied and newly occupied sites at the end of each observation interval. As an example, assume six particles are present initially at time t₀, and a shift and a birth occur before the first observation t₁, and a death occurs before a second observation at t₂. When considering the first interval [t₀, t₁), we have {X(t₀) = (6, 0),X(t₁) = (5, 2)}, but over [t₁, t₂), we now have {X(t₁) = (7, 0),X(t₂) = (6, 0)}, since all seven particles at t₁ comprise the initial population in the second interval. This seemingly inconsistent definition of the state at X(t₁) is not a problem: we will see that all necessary computations occur across disjoint intervals, so that our reduced representation of the original process needs only to be defined consistently for any given pair of consecutive observations.

Formally, this state space transformation is a mapping $\psi :\tilde{\Omega }\times \tilde{\Omega }\to \Omega \times \Omega$ on consecutive pairs of observations in $\tilde{\Omega }$ to the reduced state space that can be computed $\psi :\left\{\tilde{\mathbf{X}}\right(t_1),\tilde{\mathbf{X}}(t_2\left)\right\}\mapsto \left\{\right(a,0),(b,c\left)\right\}=\left\{\mathbf{X}\right(t_1),\mathbf{X}(t_2\left)\right\}$, where $a={\sum }_{j=1}^S{\tilde{X}}_j\left(t_1\right)$ is the total number of initially occupied sites in $\tilde{\mathbf{X}}\left(t_1\right)$, $b={\sum }_{j=1}^S{1}_{\left\{{\tilde{X}}_j\right(t_2)={\tilde{X}}_j(t_1\left)\right\}}{\tilde{X}}_j\left(t_1\right)$ is the number of initially occupied sites that remain occupied, and $c={\sum }_{j=1}^S{1}_{\left\{{\tilde{X}}_j\right(t_2)-{\tilde{X}}_j(t_1)=1\}}$ is the number of newly occupied sites in $\tilde{\mathbf{X}}\left(t_2\right)$ not present in $\tilde{\mathbf{X}}\left(t_1\right)$. Note that while ψ significantly reduces the size of the state space, the mapping discards information about specific particle locations, which is uninformative to inferring birth, death, and shift rates due to symmetry induced by particle independence. The number of changes in locations between observations — the data relevant to our estimation task — is preserved in the image of ψ.

2.3 A two-type branching process model

Working now in the space Ω, we can treat x_old and x_new as particle types in a two-type branching process. Let a_j(k, l) be the rate of producing k type 1 particles and l type 2 particles, beginning with one type j particle, j = 1, 2. Then the nonzero rates defining the two-type branching process corresponding to the birth-death-shift model are given by a₁(1, 1) = λ, a₁(0, 1) = ν, a₁(0, 0) = μ, a₁(1, 0) = −(λ + ν + μ), a₂(0, 2) = λ, a₂(0, 1) = −(λ + μ), a₂(0, 0) = μ. This characterization enables us to apply a generating function approach to obtain transition probabilities of the process. Defining X_j(t) as the number of type j particles at time t, we consider the generating function

$$\begin{array}{cc}\hfill {\varphi }_{jk}(t,s_1,s_2)& =\mathrm{E}\left\{s_1^{X_1\left(t\right)}{s}_2^{X_2\left(t\right)}\mid X_1\left(0\right)=j,X_2\left(0\right)=k\right\}\hfill \\ \hfill & =\sum _{l=0}^{\infty }\sum _{m=0}^{\infty }{p}_{(j,k),(l,m)}\left(t\right)s_1^l{s}_2^m.\hfill \end{array}$$ (3)

Using the Kolmogorov backward equations, we derive equations and a closed form solution for ϕ_jk (see Appendix A). With ϕ_jk available, we see from (3) that the transition probabilities p_(j,k),(l,m)(t) can then be obtained by differentiating and setting s₁, s₂ = 0, but without an analytical expression for these derivatives, repeated numerical differentiation is inefficient and numerically unstable. Instead, we map our domain [0, 1] × [0, 1] to the boundary of the complex unit circle by setting s₁ = e^2πiw1, s₂ = e^2πiw2 so that the generating function becomes a Fourier series ${\varphi }_{jk}(t,e^{2\pi iw1},e^{2\pi iw2})={\sum }_{l,m=0}^{\infty }{p}_{(j,k),(l,m)}\left(t\right)e^{2\pi ilw1}{e}^{2\pi imw2}$. Applying a Riemann sum approximation to the integral corresponding to coefficients given by the Fourier inversion formula, we can compute the transition probabilities using

$$\begin{array}{cc}\hfill p_{(j,k),(l,m)}\left(t\right)& ={\int }_0^1{\int }_0^1{\varphi }_{jk}(t,e^{2\pi i{w}_1},e^{2\pi i{w}_2})e^{-2\pi il{w}_1}{e}^{-2\pi im{w}_2}d{w}_{1}d{w}_2\hfill \\ \hfill & \approx \frac{1}{N^2}\sum _{u=0}^{N-1}\sum _{v=0}^{N-1}{\varphi }_{jk}(t,e^{2\pi iu∕N},e^{2\pi iv∕N})e^{-2\pi ilu∕N}{e}^{-2\pi imv∕N}.\hfill \end{array}$$ (4)

Choice of a larger N leads to a finer and thus more accurate Riemann sum approximation of the integral, and also allows us to compute transition probabilities to and from a larger total particle population of either type. The Fast Fourier transform (FFT) enables efficient computation of these coefficients (Henrici, 1979), and in our application and simulation studies, we find that a grid size as small as N = 16 yields accurate results. With transition probabilities available, we may closely approximate ${\tilde{\ell }}_o(\mathbf{Y};\beta )$ by the branching process likelihood

$${\ell }_o(\mathbf{Y};\beta )=\sum _{p=1}^m\sum _{j=0}^{n\left(p\right)-1}\log p_{{\mathbf{X}}^p\left(t_{p,j}\right),{\mathbf{X}}^p\left(t_{p,j+1}\right)}(t_{p,j+1}-t_{p,j};{\theta }_p),$$ (5)

so that maximizing (5) also maximizes the observed likelihood in (2) by proxy.

3. EM algorithm for the BDS process

With transition probabilities of the process available, it is already possible to produce MLEs of the covariate effects associated with birth, death, and shift rates by numerical maximization of the observed likelihood. However, an EM algorithm approach often outperforms off-the-shelf optimization procedures in missing data problems, offering a significantly faster and more robust solution. Let ℓ_c(X, β) denote the complete data log-likelihood, X the complete data, and Y the available observations. The EM algorithm begins with an initial parameter estimate β₀, and then at each j^th iteration, updates the estimate by setting β_j = argmax_β E_βj−1 {ℓ_c(X, β) | Y}. Each iteration involves a computation of the expectation term called the E-step, followed by a maximization of the expectation called the M-step.

3.1 E-step

The fully observed BDS process is a continuous-time Markov chain, so its complete-data log-likelihood can be written as

$${\ell }_c(\mathbf{X};\beta )=\sum _{p=1}^m\left\{b_p\log {\lambda }_p+f_p\log {\nu }_p+d_p\log {\mu }_p-({\lambda }_p+{\mu }_p+{\nu }_p)\sum _{k=0}^{\infty }k{\tau }_p\left(k\right)+\sum _{k=0}^{\infty }\log {\tau }_p\left(k\right)\right\},$$ (6)

where τ_p(k) is the total time process X^p(t) spends with total copy number $X_1^p\left(t\right)+X_2^p\left(t\right)=k$, b_p is the total number of births, f_p the number of shifts, and d_p the number of deaths for each patient p = 1, …, m — these quantities are the complete data sufficient statistics (Guttorp, 1995). Notice the final term in (6) is constant with respect to the parameters. We see that in order to obtain the expected complete-data log-likelihood, we need to calculate only expected births — E_β {b_p | Y}, shifts — E_β {f_p | Y}, deaths — E_β {d_p | Y}, and particle time — E_β {R_p | Y}, where the last quantity is defined

$${\mathrm{E}}_{\beta }\{R_p\mid \mathbf{Y}\}≔{\mathrm{E}}_{\beta }\left\{{\int }_{t_{p,0}}^{t_{p,n\left(p\right)}}{X}_1\left(s\right)+X_2\left(s\right)ds\mid \mathbf{Y}\right\}={\mathrm{E}}_{\beta }\left\{\sum _{k=0}^{\infty }k{\tau }_p\left(k\right)\mid \mathbf{Y}\right\}.$$

By independence of the p processes and linearity of expectations, each expectation breaks into sums of expectations over the observation intervals. Further, by homogeneity it suffices that for all non-negative integers j, k, l, m, we can calculate the quantities

$$e_{jk,lm}^{+}\left(t\right)=\mathrm{E}\{b_{p,t}\mid {\mathbf{X}}^p(0)=(j,k),{\mathbf{X}}^p(t)=(l,m\left)\right\},$$

$$e_{jk,lm}^{\to }\left(t\right)=\mathrm{E}\{f_{p,t}\mid {\mathbf{X}}^p(0)=(j,k),{\mathbf{X}}^p(t)=(l,m\left)\right\},$$

$$e_{jk,lm}^{-}\left(t\right)=\mathrm{E}\{d_{p,t}\mid {\mathbf{X}}^p(0)=(j,k),{\mathbf{X}}^p(t)=(l,m\left)\right\},$$

$$e_{jk,lm}^{\ast }\left(t\right)=\mathrm{E}\{R_{p,t}\mid {\mathbf{X}}^p(0)=(j,k),{\mathbf{X}}^p(t)=(l,m\left)\right\}.$$

Dependence of these quantities on rates λ_p, ν_p, μ_p is suppressed for simplicity. As noticed by Minin and Suchard (2008) and Doss et al. (2013), it is easier to work via restricted moments

$$m_{jk,lm}^{+}\left(t\right)=\mathrm{E}\{b_{p,t}{1}_{\left\{{\mathbf{X}}^p\right(t)=lm\}}\mid {\mathbf{X}}^p(0)=(j,k\left)\right\}=\sum _{n=0}^{\infty }n{q}_{jk,lm}^{+}(n,t),$$

$$m_{jk,lm}^{\to }\left(t\right)=\mathrm{E}\{f_{p,t}{1}_{\left\{{\mathbf{X}}^p\right(t)=lm\}}\mid {\mathbf{X}}^p(0)=(j,k\left)\right\}=\sum _{n=0}^{\infty }n{q}_{jk,lm}^{\to }(n,t),$$

$$m_{jk,lm}^{-}\left(t\right)=\mathrm{E}\{d_{p,t}{1}_{\left\{{\mathbf{X}}^p\right(t)=lm\}}\mid {\mathbf{X}}^p(0)=(j,k\left)\right\}=\sum _{n=0}^{\infty }n{q}_{jk,lm}^{-}(n,t),$$

$$m_{jk,lm}^{\ast }\left(t\right)=\mathrm{E}\{R_{p,t}{1}_{\left\{{\mathbf{X}}^p\right(t)=lm\}}\mid {\mathbf{X}}^p(0)=(j,k\left)\right\}={\int }_{x=0}^{\infty }x\mathrm{d}{q}_{jk,lm}^{\ast }(x,t),$$

where

$$q_{jk,lm}^{\ast }(x,t)=\mathrm{Pr}\{R_{p,t}⩽x,{\mathbf{X}}^p(t)=(l,m)\mid {\mathbf{X}}^p(0)=(j,k\left)\right\},$$

$$q_{jk,lm}^{+}(n,t)=\mathrm{Pr}\{b_{p,t}=n,{\mathbf{X}}^p(t)=(l,m)\mid {\mathbf{X}}^p(0)=(j,k\left)\right\},$$

and q^→, q⁻ are defined analogously. The conditional expectations can then be recovered after dividing by transition probabilities, i.e. $e_{jk,lm}^{+}\left(t\right)=m_{jk,lm}^{+}\left(t\right)∕p_{jk,lm}\left(t\right)$.

These restricted moments can be computed with a similar approach used to obtain transition probabilities. We begin by defining the pseudo-generating functions: for expected births, let $g_{jk,lm}^{+}(r,t)={\sum }_{n=0}^{\infty }{q}_{jk,lm}^{+}(n,t)r^n$. Ignoring notational dependence on individual patients for simplicity, we define the joint generating function

$$\begin{array}{cc}\hfill & H_{jk}^{+}(r,s_1,s_2,t)=\mathrm{E}\left\{r^{b_t}{s}_1^{X_1\left(t\right)}{S}_2^{X_2\left(t\right)}\mid \mathbf{X}\left(0\right)=(j,k)\right\}\hfill \\ \hfill & =\sum _l\sum _m\sum _n\text{Pr}\{b_t=n,\mathbf{X}(t)=(k,l)\mid \mathbf{X}(0)=(j,k\left)\right\}{r}^n{s}_1^l{s}_2^m\hfill \\ \hfill & =\sum _l\sum _m{g}_{jk,lm}^{+}(r,t)s_1^l{s}_2^m.\hfill \end{array}$$

Pseudo-generating functions for shifts and deaths are defined analogously, and the pseudo-generating function for particle time is defined as

$$\begin{array}{cc}\hfill H_{jk}^{\ast }(r,s_1,s_2,t)& =\sum _l\sum _m{\int }_{x=0}^{\infty }{e}^{-rx}\mathrm{d}{q}_{jk,lm}^{\ast }(x,t)s_1^l{s}_2^m\hfill \\ \hfill & ≔\sum _l\sum _m{V}_{jk,lm}(r,t)s_1^l{s}_2^m,\hfill \end{array}$$

where $V_{jk,lm}(r;t)={\int }_0^{\infty }{e}^{-rx}\mathrm{d}{q}_{jk,lm}^{\ast }(x;t)$ is the Laplace-Stieltjes transform of $q_{jk,lm}^{\ast }(x;t)$. In each case we can define series whose coefficients are our quantities of interest by partial differentiation:

$$G_{jk}^{+}(s_1,s_2,t)={\phantom{\mid }\frac{d}{dr}{H}_{jk}^{+}(r,s_1,s_2,t)\mid }_{r=1}=\sum _l\sum _m\left\{\sum _{n}n{q}_{jk,lm}^{+}(n,t)\right\}{s}_1^l{s}_2^m=\sum _l\sum _m{m}_{jk,lm}^{+}\left(t\right)s_1^l{s}_2^m.$$ (7)

$G_{jk}^{\to }$ and $G_{jk}^{-}$ are defined analogously, and the expression for particle time is instead differentiated at r = 0:

$$G_{jk}^{\ast }(s_1,s_2,t)={\phantom{\mid }\frac{d}{dr}{H}_{jk}^{\ast }(r,s_1,s_2,t)\mid }_{r=0}=\sum _l\sum _m\left\{{\int }_{x=0}^{\infty }x\mathrm{d}{q}_{jk,lm}^{\ast }(x,t)\right\}{s}_1^l{s}_2^m=\sum _l\sum _m{m}_{jk,lm}^{\ast }\left(t\right)s_1^l{s}_2^m.$$ (8)

We see that given expressions for $H_{jk}^{+}$, $H_{jk}^{\to }$, $H_{jk}^{-}$, and $H_{jk}^{\ast }$, the coefficients corresponding to moments $m_{jk,lm}^{+}$, $m_{jk,lm}^{\to }$, $m_{jk,lm}^{-}$, $m_{jk,lm}^{\ast }$ can then be numerically computed using FFT analogously to (4). For notational simplicity, we use G_jk when referring collectively to $G_{jk}^{+}$, $G_{jk}^{\to }$, $G_{jk}^{-}$, and $G_{jk}^{\ast }$, and similarly define H_jk.

Having reduced our task to computing H_jk, we define H₁ ≔ H₁₀(r, s₁, s₂, t) and H₂ ≔ H₀₁(r, s₁, s₂, t). Particle independence then yields $H_{jk}=H_1^j{H}_2^k$. In all cases, H₂ is analytically available, and we derive an ordinary differential equation for H₁, summarized in the theorem below. We present the result for a branching process with rates corresponding to the birth-death-shift model, but such systems of equations are available for an arbitrary time-homogeneous multi-type branching process.

Theorem 1: Let {X_t} be a two-type branching defined by the rates in Section 2.3. Denote particle time and the number of births, shifts, and deaths over the interval [0, t) by R_t, b_t, f_p, and d_t respectively. Define the generating functions corresponding to births as

$$\begin{array}{cc}\hfill & H_1^{+}(r,s_1,s_2,t)=E\left\{r^{b_t}{s}_1^{X_1\left(t\right)}{s_2}^{X_2\left(t\right)}\mid \mathbf{X}\left(0\right)=(1,0)\right\}\mathit{and}\hfill \\ \hfill & H_2^{+}(r,s_1,s_2,t)=E\left\{r^{b_t}{s}_1^{X_1\left(t\right)}{s_2}^{X_2\left(t\right)}\mid \mathbf{X}\left(0\right)=(0,1)\right\}.\hfill \end{array}$$

Then $H_2^{+}=y_b+$

$${\left\{\frac{-\lambda r}{2\lambda r{y}_b-\lambda -\mu }+\left(\frac{1}{s_2-y_b}+\frac{\lambda r}{2\lambda r{y}_b-\lambda -\mu }\right)e^{-(2y_b\lambda r-\lambda -\mu )t}\right\}}^{-1},$$

where $y_b=(\lambda +\mu +\sqrt{{\lambda }^2+2\lambda \mu +{\mu }^2-4\lambda \mu r})∕\left(2\lambda r\right)$, and $H_1^{+}$ satisfies

$$\frac{d}{dt}{H}_1^{+}(t,s_1,s_2,r)=\lambda r{H}_1^{+}{H}_2^{+}+\nu H_2^{+}+\mu -(\lambda +\mu +\nu )H_1^{+},$$ (9)

subject to initial condition H₁(r, s₁, s₂, 0) = s₁.

Analogous equations for shifts, deaths, and particle time along with detailed derivations are included in Appendix B.

This theorem shows that for each of the sufficient statistics, necessary computations for H_jk reduce to solving a single ordinary differential equation, and because we can evaluate H_jk, we can also easily differentiate H_jk numerically, yielding solutions G_jk.

To summarize, with $H_{jk}^{+}$, $H_{jk}^{-}$, $H_{jk}^{\to }$, $H_{jk}^{\ast }$ now available, we may obtain the restricted moments by computing the coefficients in the power series $G_{jk}^{+}$, $G_{jk}^{-}$, $G_{jk}^{\to }$, $G_{jk}^{\ast }$. These coefficients are recovered using a Riemann approximation to the Fourier inversion formula analogous to formula (4). We are thus able to compute all necessary quantities appearing in the expected complete-data log-likelihood ${\mathrm{E}}_{\tilde{\beta }}\left\{{\ell }_c\right(\mathbf{X},\beta )\mid \mathbf{Y}\}$. Recall that sufficient statistics for each patient b_p, f_p, d_p, and R_p break up over intervals: i.e. the total number of births b_p is equal to the sum of the number of births over each disjoint interval [t_p,j−1, t_p,j), with j = 1, …, n(p). Further, by the Markov property, the conditional expectation of the number births over an interval [t₁, t₂) given Y depends only on the states of the process at the endpoints of the interval:

$$\mathrm{E}(b_{p,t_2-t_1}\mid \mathbf{Y})=\mathrm{E}\{b_{p,t_2-t_1}\mid {\mathbf{X}}^p(t_1),{\mathbf{X}}^p(t_2\left)\right\}=e_{{\mathbf{X}}^p\left(t_1\right),{\mathbf{X}}^p\left(t_2\right)}^{+}(t_2-t_1)=\frac{m_{{\mathbf{X}}^p\left(t_1\right),{\mathbf{X}}^p\left(t_2\right)}^{+}(t_2-t_1)}{p_{{\mathbf{X}}^p\left(t_1\right),{\mathbf{X}}^p\left(t_2\right)}(t_2-t_1)},$$ (10)

and the same is true for the other sufficient statistics. Therefore, for each process p,

$${\mathrm{E}}_{\tilde{\beta }}(b_p\mid \mathbf{Y})=\sum _{i=1}^{n\left(p\right)}{e}_{{\mathbf{X}}^p\left(t_{p,i-1}\right),{\mathbf{X}}^p\left(t_{p,1}\right)}^{+}(t_{p,i-1}-t_{p,i};{\tilde{\lambda }}_p,{\tilde{\nu }}_p,{\tilde{\mu }}_p),$$ (11)

with $\log \left({\tilde{\lambda }}_p\right)={\tilde{\beta }}^{\lambda }\cdot z_p$, $\log \left({\tilde{\nu }}_p\right)={\tilde{\beta }}^{\nu }\cdot z_p$, $\log \left({\tilde{\mu }}_p\right)={\tilde{\beta }}^{\mu }\cdot z_p$, and we obtain ${\mathrm{E}}_{\tilde{\beta }}(f_p\mid \mathbf{Y})$, ${\mathrm{E}}_{\tilde{\beta }}(d_p\mid \mathbf{Y})$ analogously. Finally, combining (11), (10), (6) and denoting ${\tilde{\theta }}_p=({\tilde{\lambda }}_p,{\tilde{\nu }}_p,{\tilde{\mu }}_p)$, the expected complete-data log likelihood up to a constant is equal to

$${\mathrm{E}}_{\tilde{\beta }}\left\{{\ell }_c\right(\mathbf{X},\beta )\mid \mathbf{Y}\}\propto$$ (12)

$$\sum _{p=1}^m\left[\sum _{j=1}^{n\left(p\right)}\left\{\frac{m_{{\mathbf{X}}^p\left(t_{p,j-1}\right),{\mathbf{X}}^p\left(t_{p,j}\right)}^{+}(t_{p,j}-t_{p,j-1};{\tilde{\theta }}_p)}{p_{{\mathbf{X}}^p\left(t_{p,j-1}\right),{\mathbf{X}}^p\left(t_{p,j}\right)}(t_{p,j}-t_{p,j-1};{\tilde{\theta }}_p)}\log {\lambda }_p+\frac{m_{{\mathbf{X}}^p\left(t_{p,j-1}\right),{\mathbf{X}}^p\left(t_{p,j}\right)}^{\to }(t_{p,j}-t_{p,j-1};{\tilde{\theta }}_p)}{p_{{\mathbf{X}}^p\left(t_{p,j-1}\right),{\mathbf{X}}^p\left(t_{p,j}\right)}(t_{p,j}-t_{p,j-1};{\tilde{\theta }}_p)}\log {\nu }_p+\frac{m_{{\mathbf{X}}^p\left(t_{p,j-1}\right),{\mathbf{X}}^p\left(t_{p,j}\right)}^{-}(t_{p,j}-t_{p,j-1};{\tilde{\theta }}_p)}{p_{{\mathbf{X}}^p\left(t_{p,j-1}\right),{\mathbf{X}}^p\left(t_{p,j}\right)}(t_{p,j}-t_{p,j-1};{\tilde{\theta }}_p)}\log {\mu }_p-\frac{m_{{\mathbf{X}}^p\left(t_{p,j-1}\right),{\mathbf{X}}^p\left(t_{p,j}\right)}^{\ast }(t_{p,j}-t_{p,j-1};{\tilde{\theta }}_p)}{p_{{\mathbf{X}}^p\left(t_{p,j-1}\right),{\mathbf{X}}^p\left(t_{p,j}\right)}(t_{p,j}-t_{p,j-1};{\tilde{\theta }}_p)}({\lambda }_p+{\mu }_p+{\nu }_p)\right\}\right].$$ (13)

3.2 M-step

To complete an M-step, we use an efficient Newton-Raphson (N-R) algorithm to maximize the expectation $g\left(\beta \right)=E_{\tilde{\beta }}\left\{{\ell }_c\right(\mathbf{X},\beta )\mid \mathbf{Y}\}$. Each N-R step recursively updates parameters using the following equation:

$${\beta }_{\mathit{new}}={\beta }_{\mathit{cur}}-{\left\{\mathbf{H}g\right({\beta }_{\mathit{cur}}\left)\right\}}^{-1}\nabla g\left({\beta }_{\mathit{cur}}\right),$$ (14)

where ▽_g denotes the gradient vector and H_g denotes the Hessian matrix of g(β). Fortunately, compact analytical forms for these quantities are available. First, we collect complete data sufficient statistics across processes into the following vectors:

$${\mathbf{U}}^T=\left(E_{\tilde{\beta }}\right(b_{1,t_{1,n\left(1\right)}}\mid \mathbf{Y}),\dots ,E_{\tilde{\beta }}(b_{m,t_{m,n\left(m\right)}}\mid \mathbf{Y}\left)\right),$$

$${\mathbf{V}}^T=\left(E_{\tilde{\beta }}\right(f_{1,t_{1,n\left(1\right)}}\mid \mathbf{Y}),\dots ,E_{\tilde{\beta }}(f_{m,t_{m,n\left(m\right)}}\mid \mathbf{Y}\left)\right),$$

$${\mathbf{D}}^T=\left(E_{\tilde{\beta }}\right(d_{1,t_{1,n\left(1\right)}}\mid \mathbf{Y}),\dots ,E_{\tilde{\beta }}(d_{m,t_{m,n\left(m\right)}}\mid \mathbf{Y}\left)\right),$$

$${\mathbf{P}}^T=\left(E_{\tilde{\beta }}\right(R_{1,t_{1,n\left(1\right)}}\mid \mathbf{Y}),\dots ,E_{\tilde{\beta }}(R_{m,t_{m,n\left(m\right)}}\mid \mathbf{Y}\left)\right).$$

If we aggregate covariate vectors for each process in a c × p matrix Z = (z₁, …, z_m) and process-specific rates into vectors λ = (λ₁, …, λ_m), ν = (ν₁, …, ν_m),μ = (μ₁, …, μ_m), then the gradient and Hessian can be expressed as

$$\nabla g\left(\beta \right)=(-{\mathbf{Z}}^T\{\text{diag}\left(\mathbf{P}\right)\lambda +\mathbf{U}\},-{\mathbf{Z}}^T\{\text{diag}\left(\mathbf{P}\right)\nu +\mathbf{V}\},-{\mathbf{Z}}^T\{\text{diag}\left(\mathbf{P}\right)\mu +\mathbf{D}\left\}\right),$$ (15)

$$\mathbf{Hg}\left(\beta \right)=-\left(\begin{array}{ccc}\hfill {\mathbf{Z}}^T\text{diag}(\mathbf{P}\cdot \lambda )\mathbf{Z}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\mathbf{Z}}^T\text{diag}(\mathbf{P}\cdot \nu )\mathbf{Z}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\mathbf{Z}}^T\text{diag}(\mathbf{P}\cdot \mu )\mathbf{Z}\hfill \end{array}\right).$$ (16)

In our experience the M-step generally converges in fewer than ten N-R steps. Availability of closed form solutions (15) and (16) yields very fast execution of each N-R step — the computational cost of the M-step is negligible compared to the E-step.

3.3 Accelerating E-step calculations for intervals with no change

In our birth-death-shift application, we may avoid the relatively costly E-step calculations for some intervals by approximating the probability of observing no changes with the probability that no event occurs in the underlying complete process. This leads to computational efficiency gains in settings such as our application where many intervals feature no observed changes.

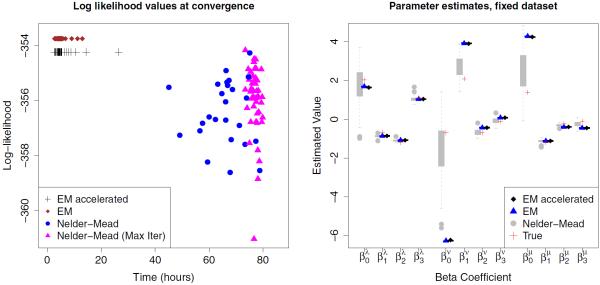
It is very unlikely that events occur in a time interval [t₁, t₂) yet no change is observed so that X(t₁) = X(t₂). For instance, if 12 elements are present initially and a death followed by a birth occur, then we almost always observe X(t₁) = (12, 0),X(t₂) = (11, 1) unless the element added by the birth occupies the exact location that was previously occupied by the element that dies. This scenario would leave the observed state unchanged, X(t₁) = X(t₂) = (12, 0), but has exceedingly low probability: the already small but non-negligible probability that more than one event occurs is then multiplied by 1/(S – 11), the probability of the birth occurring in a specific location (recall S is very large). Therefore, it is numerically accurate to treat intervals with no observed changes as if no changes in the latent continuous-time process occur. In this case, the transition probability is easily calculated, given by the tail of an exponential distribution p_{(12,0),(12,0)} (t₂ −t₁) = e^{−12(λ+μ+ν)(t₂−t₁)}. In addition to efficient closed-form transition probability calculation, the expected sufficient statistics necessary for the E-step are known in this setting. If no events occur, we know that $e_{(k,0),(k,0)}^{+}\left(t\right)=e_{(k,0),(k,0)}^{\to }\left(t\right)=e_{(k,0),(k,0)}^{-}\left(t\right)=0$, and that the expected particle time is $e_{(k,0),(k,0)}^{\ast }\left(t\right)=kt$. This is not only faster computationally but also more numerically stable, avoiding the division of numerically calculated restricted moments by numerically calculated transition probabilities. We verify this efficient implementation in our simulation studies as illustrated in Figure 4.

Figure 4.

The left plot shows converged log-likelihood values using EM, accelerated EM, and Nelder-Mead optimization. The right plot shows parameter estimates produced by the EM, accelerated EM, and Nelder-Mead algorithms, with true parameters values shown as crosses. This figure appears in color in the electronic version of this article.

3.4 Implementation

Our algorithms are implemented in R package bdsem, available at https://github.com/jasonxu90/bdsem. The EM algorithm implementation accommodates panel data settings with unevenly spaced discrete observations and includes functions for MLE inference using other methods, as well as code for simulating from the BDS process. The software is accompanied by a vignette that steps through simplified versions of all simulation studies included in this paper.

4. Results

We begin with a simulation study to check that transition probabilities for the two-type branching process described in Section 2.3 coincide with those of the BDS model. We compare our generating function computations to Monte Carlo estimates of transition probabilities obtained by simulating from the BDSmodel, and also include a comparison to the FM method presented in (Rosenberg et al., 2003).

4.1 Comparison with frequent monitoring

The FM model allows at most one event to occur per interval. Thus, over an observation interval [t_i, t_i+1) beginning with k particles, the probabilities of a birth, death, and shift have closed forms (λ/η)e^{−kη(t_i+1−t_i)}, (μ/η)e^{−kη(t_i+1−t_i)}, and (ν/η)e^{−kη(t_i+1−t_i)} respectively, where η = λ + ν + μ. The probability of no event occurring is given by e^{−kη(t_i+1−t_i)}, and all other transition probabilities are zero under the FM assumption.

We compute Monte Carlo approximations of transition probabilities from 2000 realizations of a BDS process without covariates, with rates λ = 0.0188, μ = 0.0147, ν = 0.00268 equal to estimates of transposable element birth, death, and shift rates obtained by Rosenberg et al. (2003) using FM. We begin each simulation with an initial population size of 10, and record the state of the process after simulating for dt units of time, varying dt from 0.5 to 10.

In Figure 2, we see that as the length of an observation interval increases, FM approximations become inaccurate, while those obtained using our method remain within the narrow Monte Carlo confidence intervals. However, notice that the probability that no event occurs remains accurate even under the FM approximation, supporting the efficient implementation of our EM algorithm described in Section 3.3. Figure C-1 in the Appendix C demonstrates that our method also reliably calculates other transition probabilities that are set to 0 by the FM method, and these computations remain accurate when we vary the rates of the process.

Figure 2.

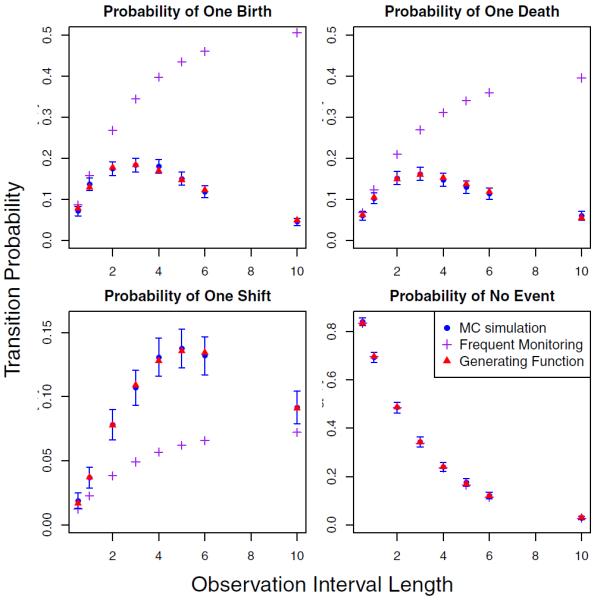
Transition probability approximations. BDS transition probabilities are approximated with two methods — the FM method, shown with crosses, and the generating function method, depicted with triangles. We depict Monte Carlo estimates of the BDS transition probabilities with circles; vertical segments indicate their corresponding Monte Carlo confidence intervals. This figure appears in color in the electronic version of this article.

Further, these discrepancies in numerical transition probabilities between methods indeed translate to differences in estimated rates. To see this, we generate a partially observed dataset and infer rates using both methods. We simulate from the BDS process with λ = 0.07, μ = 0.12, ν = 0.02 to resemble the dynamics of the real dataset we will analyze in the next section, and record 200 discretely observed states of the process evenly spaced dt time units apart. Each simulated interval begins with an initial population size drawn uniformly between 1 and 15, and this data generating process is repeated to produce three datasets corresponding to inter-observation intervals of lengths dt = (0.2, 0.4, 0.6). We infer the MLE rates for each of the three discretely observed datasets using the generating function method and under the frequent modeling assumption, and repeat the entire procedure for 200 trials.

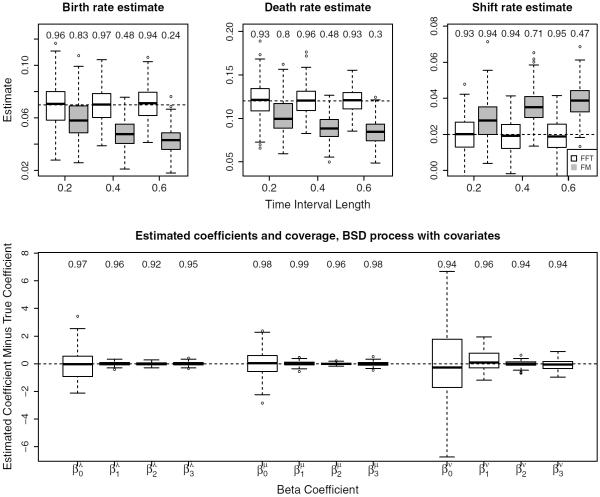
In the top row of Figure 3, we see that our generating function approach successfully recovers the MLE estimates, and coverage of 95% confidence intervals remains close to 0.95 as we increase the length of time intervals between observations. The FM method performs somewhat reasonably for shorter observation intervals, but the bias in these approximate MLEs becomes stark as dt increases, with 95% confidence interval coverage probability dropping as low as 0.24.

Figure 3.

MLE parameter estimates on simulated data. The top row displays estimates of global birth, death, and shift rates in the simple BDS for three datasets, each with observation interval lengths dt = (0.2, 0.4, 0.6). True parameter values used to initialize simulations marked by horizontal dashed line, and results using the FM method are included in gray. Monte Carlo coverage probabilities for 95% confidence intervals are displayed above box plots. The bottom row displays estimated coefficients using EM in the BDS process with covariates, shifted by true values.

We can also check the accuracy of restricted moment computations via simulation by verifying the equality $\mathrm{E}(N_t^{+}\mid X_0=i,j)={\sum }_{k,l}\mathrm{E}(N_t^{+},1_{xt=kl}\mid x_0=i,j)$ for expected births, and analogous expressions for other expected sufficient statistics. The left hand side is empirically approximated by a Monte Carlo average of the number of births over many realizations of the process, while the restricted moments on the right hand side are computed via our generating function approach (see Appendix C, Figure C-2).

4.2 Estimation of parameters in BDS model with covariates

With accurate transition probabilities and restricted moments available, we are ready to infer coefficients in the BDS model with covariate-dependent rates using the EM algorithm. We begin by generating a simulated dataset resembling the real data consisting of observations corresponding to 100 “patients,” each with three covariates z_p,1, z_p,2, z_p,3 ~ Unif{(0, 2) × (6, 10) × (4, 6)}. An illustration of the format of these data, which reflects the format of the real dataset we later analyze, is provided in Table 1. We then simulate patient-specific BDS processes, beginning with rates λ_p, ν_p, μ_p log-linearly related to a true vector of coefficients β. We collect between 2 and 7 observations per patient, each spaced dt = 0.4 apart. Each simulated observation interval begins with an initial population uniformly drawn between 2 and 14. Finally, we choose true values of the effect sizes so that averaging over patients, the overall birth, shift, and death rates of the process are similar to previous studies (Rosenberg et al., 2003; Doss et al., 2013).

Table 1.

Visualization of data format with covariates z_i, i = 1, 2, 3.

Patient	Time	# Bands	Shift	z 1	z 2	z 3
1	0	9	no	1.3	6.3	4.2
	0.4	9	no	1.3	6.3	4.2
	0.8	10	no	1.3	6.3	4.2
	1.2	10	no	1.3	6.3	4.2
	1.6	10	yes	1.3	6.3	4.2
	2.0	10	no	1.3	6.3	4.2
2	0	14	no	0.7	9.1	5.5
	0.4	14	no	0.7	9.1	5.5
	0.8	13	no	0.7	9.1	5.5
3	⋮	⋮	⋮	⋮	⋮	⋮

The algorithm is initialized with β₀ ~ N {β, diag(0.5β)}, and the entire procedure of generating the dataset and inferring rates via EM is repeated 150 times. In the bottom row of Figure 3, we see that the MLEs are again unbiased estimates of the true values, with corresponding confidence interval coverage staying close to 95%. Our EM algorithm not only successfully recovers the true parameters, but also outperforms generic optimization. We choose to compare against the Nelder-Mead (NM) algorithm, as it proved to be the most robust among the methods available via the optim function in R; a similar choice of NM for comparison to EM implementations is motivated in (Lange and Minin, 2013). In this experiment, we generate one fixed dataset as described in the procedure above from the BDS model with covariates and initialize each method with identical initial parameter values and convergence criteria, using a relative tolerance of ϵ = 1 × 10⁻⁶. We repeat this procedure over 100 sets of initial parameters.

Figure 4 displays the log-likelihood values achieved by each algorithm at convergence, as well as values in which Nelder-Mead terminated at an iteration limit set at 2000 steps. We see that in every case, the EM algorithm is significantly faster and finds a better optimum than NM. Further, the wide range of converged log-likelihood values suggests that NM is sensitive to initial conditions — an undesirable feature in this fixed data setting. We also verify that EM and accelerated EM arrive at the same parameter estimates and log-likelihood values at convergence up to specified relative tolerance. The increase in efficiency is not seen here: in these simulated examples, generating function computations are always performed and cached at each iteration, rather than bypassed for candidate intervals described in Section 3.3. In our application in the following section, we find that accelerating EM runs approximately six times as fast as its nonaccelerated counterpart.

Our EM approach is not only more stable in terms of the maximized log-likelihood, but also in terms of parameter estimates. The right panel of Figure 4 shows that estimates for each coefficient differ by no more than 0.01 across disparate initial conditions under both EM implementations, while a range of estimates are produced by the Nelder-Mead algorithm.

Note that for some coefficients, estimates produced by NM appear to lie closer to the “true” parameters used to generate the data. We believe this to be an artifact of centering initial parameter values for both algorithms around the true parameters. Indeed, MLEs corresponding to the likelihood surface of a given synthetic dataset generally do not coincide exactly with the inputs used to simulate the data. The fact that EM consistently finds a better optimum in terms of log-likelihood suggests that this is the case.

4.3 Mycobacterium tuberculosis transposable element evolution

We apply our EM algorithm to infer covariate-dependent birth, death, and shift rates of the M. tuberculosis transposon IS6110, a frequently used marker to track M. tuberculosis in the community (McEvoy et al., 2007). The marker serves as a DNA fingerprint, and in community-based studies patients that share the same or similar M. tuberculosis genotypes are considered as part of the same transmission chain (Van Embden et al., 1993; Kato-Maeda et al., 2011). However, such inference relies on a fairly precise understanding of within-host evolutionary dynamics: for instance, if a DNA marker changes very rapidly, isolates from the same source will be strongly differentiated, and the severity of outbreaks would be underestimated without accounting for the high change rate. Understanding the rates of change of IS6110 -based genotypes is thus critical toward the interpretation and design of such studies (Tanaka and Rosenberg, 2001), which in turn provide important information toward designing policy decisions such as control and intervention programs.

We analyze data from an ongoing study of the transmission and pathogenesis of M. tuberculosis patients in a community study in San Francisco (Cattamanchi et al., 2006). The database includes all culture positive tuberculosis cases reported to the San Francisco Department of Public Health. We included patients with more than one M. tuberculosis isolate from specimens sampled more than 10 days apart, genotyped with IS6110 restriction fragment length polymorphism (RFLP) analysis. Our dataset contains 252 observation intervals corresponding to 196 unique patients observed at 452 time points. Average time between sampling times is 0.35 years, with the longest interval being 2.35 years. Of the 252 intervals, 29 feature endpoints with distinct genotypes. Additional summary statistics are included in Appendix D.

This dataset was analyzed by Rosenberg et al. (2003) under the FM assumption, but these authors necessarily discarded all intervals with more than one change in RFLP bands, as these intervals with “complex changes” are not possible under their restricted model. A later investigation by Doss et al. (2013) relaxes this assumption, allowing for multiple births or deaths to occur, but ignores RFLP band locations entirely, working instead only with total copy numbers evolving under a linear birth-death process. Under this birth-death model, the shift rate becomes unidentifiable, and the study instead infers covariate effects of birth and death rates. Our new method allows for a more principled and complete analysis, utilizing the full dataset without compromising any original modeling assumptions.

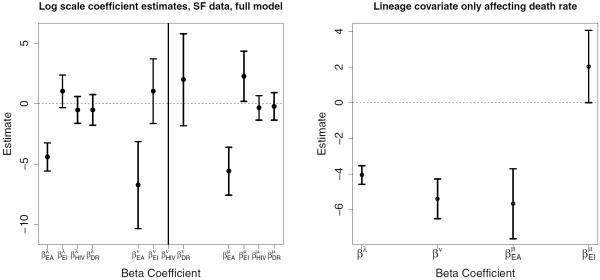
We begin by applying our EM algorithm to the simple BDS model with a single birth, death, and shift rate of IS6110 for all patients. We estimate the MLE rates $\widehat{\lambda }=0.0156$, $\widehat{\nu }=0.00426$, $\widehat{\mu }=0.0187$, with associated 95% confidence intervals (0.00929, 0.0251), (0.00145, 0.0125), and (0.0177, 0.0301) respectively; results were not sensitive to parameter initializations. These estimates are interpretable as the change rate of IS6110 per copy, per year, and our results are consistent with previous estimates in the literature: for all rates, confidence intervals overlap those obtained in the frequent monitoring approach in (Rosenberg et al., 2003) as well as those obtained in the BD model (Doss et al., 2013). Similarly to Doss et al. (2013) which estimates μ = 0.0207, our estimate of death rate $\widehat{\mu }$ allowing for multiple events between observations is higher than μ = 0.0147 obtained under the FM assumption. This is to be expected, as there are multiple intervals in which IS6110 count drops by more than 1 in the dataset. Although confidence intervals overlap, our estimate $\widehat{\nu }$ is noticeably higher than the previous result ν = 0.00268, with the upper end of our confidence interval almost twice as large as the upper end of the 95% FM confidence interval [0, 0.00654). Again, our analysis allows consideration of intervals that can be explained by at least two genotype changes that were either omitted in earlier studies or interpreted as a single birth event.

In addition to estimating the BDS rates globally, Doss et al. (2013) investigated rates as functions of several covariates in a panel data setting, and their findings in the birth-death framework suggest that M. tuberculosis lineage (Gagneux et al., 2006) may have a statistically significant effect on the rates of the process. We reexamine the effect of lineage on the rates in the full BDS model, considering 109 patients infected with Euro-American (EU) lineage strains, 54 patients with East-Asian (EA) strains, and 25 patients with Indo-Oceanic (IO) strains. We combine EU and IO lineages, because Doss et al. (2013) found that the number of IO samples was not sufficient to recover rates for this lineage. Following Doss et al. (2013), we also include HIV infection status of each patient (HIV) and drug resistance status of the M. Tuberculosis strain (DR). These attributes are coded as binary covariates: EI_p = 1 if patient p is infected with the EU or IO strain and 0 otherwise, so that intercept terms ${\beta }_0^{\lambda }$, ${\beta }_0^{\mu }$, ${\beta }_0^{\nu }$ correspond to the EA strain. The variable HIV_p = 1 if patient p is infected with HIV and 0 otherwise, and DR_p = 1 if patient p is infected with a drug-resistant strain, and 0 otherwise. Covariates are log-linearly related to birth, death, and shift rates: $\log {\lambda }_p={\beta }_0^{\lambda }+{\beta }_1^{\lambda }{\text{EI}}_p+{\beta }_2^{\lambda }{\text{HIV}}_p+{\beta }_3^{\lambda }{\text{DR}}_p$, $\log {\mu }_p={\beta }_0^{\mu }+{\beta }_1^{\mu }{\text{EI}}_p+{\beta }_2^{\mu }{\text{HIV}}_p+{\beta }_3^{\mu }{\text{DR}}_p$, $\log {\nu }_p={\beta }_0^{\nu }+{\beta }_1^{\nu }{\text{EI}}_p+{\beta }_2^{\nu }{\text{HIV}}_p+{\beta }_3^{\nu }{\text{DR}}_p$.

We estimate coefficients in the full log-linear model described above, as well as in several simpler models, using the EM algorithm. The simpler models differ from the full model by either excluding the HIV and DR covariates, or excluding all covariates for specified global or “simple” rates. For instance, the model labeled “Lineage only, simple ν” in Table 2 has five parameters $\beta =({\beta }_0^{\lambda },{\beta }_1^{\lambda },{\beta }_0^{\mu },{\beta }_1^{\mu },{\beta }^{\nu })$, and rates defined as $\log {\lambda }_p={\beta }_0^{\lambda }+{\beta }_1^{\lambda }{\text{EI}}_p$, log ν_p = log ν = β^ν, $\log {\mu }_p={\beta }_0^{\mu }+{\beta }_1^{\mu }{\text{EI}}_p$. Estimates in all cases are not sensitive to starting values. A summary and model comparison via the Bayesian Information Criterion (BIC) (Schwarz, 1978) is included in Table 2, which selects the model including only the lineage covariate for modeling death rate μ. Coefficient estimates are displayed graphically for the full model as well as the best model selected by BIC in Figure 5. While we choose not to report coefficient estimates from each model for brevity, in all models, the confidence interval for ${\beta }_{EI}^{\mu }$ does not contain zero, indicating that strain lineage has a statistically significant effect on the death rate. The estimate ${\beta }_{EI}^{\widehat{\mu }}=2.028$ under the best model indicates that in Euro-American and Indo-Oceanic lineages loss of IS6110 element occurs exp(2.028) = 7.599 times faster than in their East-Asian counterpart. Our analysis affirms the result suggested by Doss et al. (2013) in the simpler BD framework: M. tuberculosis lineage needs to be taken into consideration when studying disease transmission using IS6110 genotypes.

Table 2.

Model comparison via $\text{BIC}\approx -2\widehat{L}+k\ln n$. We also fit the log-linear model of Doss et al. (2013), which includes separate indicator variables for Euro-American and Indo-Oceanic lineages. Models described as “lineage only” do not include HIV, DR covariates, and rates described as “simple” are global to all patients, not influenced by covariates in the model.

Model	# Par	Log-likelihood	BIC
Full, EU, IO lineages	15	−119.845	330.01
Full	12	−120.498	313.25
Full, simple ν	9	−122.455	299.10
Lineage covariate only	6	−123.649	293.42
Lin. only, simple ν	5	−123.717	277.54
Lin. only, simple λ, ν	4	−124.472	273.02
Simple λ, ν, μ	3	−127.914	273.90

Figure 5.

Coefficient estimates and 95% confidence intervals in full model and best model according to BIC. Notice intervals corresponding to ${\beta }_{EI}^{\mu }$ do not contain 0.

5. Discussion

In this paper, we have developed an EM algorithm for inference in a discretely observed, multi-type branching process framework. We focus our attention on fitting BDS processes to panel data, driven by the problem of estimating evolutionary dynamics of IS6110 — a genetic marker that plays an important role in DNA fingerprinting of M. tuberculosis. Our method allows for log-rates to be linear combinations of many patient-specific covariates, and is flexible enough to capture the full range of dynamics between observation times by approximating the BDS process with a two-type branching process. To our knowledge, there is no other method of comparable accuracy for fitting BDS processes in this setting.

The generating functions and numerical techniques we derive to calculate previously unknown transition probabilities and restricted moments are helpful tools toward probabilistic characterization of such processes more generally. We demonstrate how our generating function approach leads to maximum likelihood estimation and evaluation of expected complete-data log-likelihood within an EM algorithm, but note that these calculations also arise in a variety of other statistical prediction and estimation techniques. For example, tractability of the likelihood via our methods allows for their use in Bayesian inference.

Several problems associated with our numerical methods remain open. First, although we empirically show that our branching process approximation to the discretely observed BDS likelihood is highly accurate, rigorous characterization of this approximation is lacking. Filling this theoretical gap is an interesting avenue for future research. Second, our method has potential numerical limitations in settings with very large populations. Computing transition probabilities to population sizes up to N of any particle type typically requires N^p differential equations to be solved, where p is the number of particle types. Although efficient numerical solvers evaluate each ODE in fractions of a second, requiring millions of evaluations becomes prohibitive within an iterative algorithm. However, because the support of transition probabilities is often concentrated unless observation intervals are very long, future work may harness this sparsity to accelerate computations.

Our covariate-specific rate analysis reaffirms previous indication in the simplified BD framework that strain lineage has a significant effect on the death rate (Doss et al., 2013), although the large confidence intervals suggest that this lineage effect is somewhat marginal. Indeed, more data would be required to be certain in the result, but our principled analysis is assuring in that any spurious findings can now be attributed to limited, noisy data rather than to model misspecification. The possibility of differences in rates of genetic marker evolution across lineages is important in epidemiological studies. For example, similar IS6110 genotypes across multiple individuals infected with EA lineage of M. tuberculosis do not provide strong evidence of these individuals belonging to the same transmission chain, because of the slow change rate of IS6110 in the EA lineage. Failing to account for this may lead to inferring false relationships among genotypically similar clusters of patients.

The BDS model we consider is general enough so that our methods can be applied to studying evolution of any transposable element. Such studies are not limited to infectious disease surveillance, as studying evolution of transposable elements in eukaryotes is also of great interest (Biémont, 2010). Beyond the BDS framework, the tools we develop for fitting branching processes are transferable to many settings. For example, our methodology is applicable to compartmental models, a class of well-known multi-type branching processes that finds applications in modeling cancerous growth, bacterial evolution, and cellular differentiation in systems such as hematopoiesis (Golinelli et al., 2006).

Figure 1.

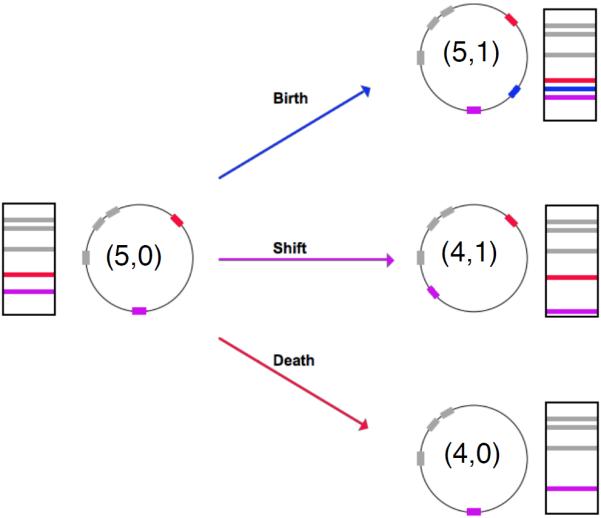
Illustration of the three types of transposition—birth, death, shift—along a genome, represented by circles. Transposons, depicted by filled rectangles along the circles/genomes, correspond to observable gel bands, denoted by horizontal lines in the rectangles next to each circle diagram. Numbers within each circle represent each configuration X(t) in the notation introduced in Section 2.2. More specifically, we call the gel band on the left our initial configuration and set the number of particles of type 1 to the number of bands, 5, and the number of particles of type 2 to 0. On the right set of diagrams, a birth event keeps the number of type 1 particles intact and increments the number of type 2 particles by one, a death event changes the number of type 1 particles from five to four and keeps the number of type 2 particles at zero, and finally a shift event decreases the number of type 1 particles by one and increases the number of type 2 particles by one.