Multi-Site, Multi-Vendor Validation of the Accuracy and Reproducibility of Proton-Density Fat- Fraction Quantification at 1.5T and 3T using a Fat-Water Phantom

Abstract

Purpose

To evaluate the accuracy and reproducibility of quantitative chemical shift-encoded MRI (CSE-MRI) to quantify proton-density fat-fraction (PDFF) in a fat-water phantom across sites, vendors, field strengths and protocols.

Methods

Six sites (three vendors: GE/Philips/Siemens) participated in this study. A phantom containing multiple vials with various oil-water suspensions (PDFF:0–100%) was built, shipped to each site and scanned at 1.5T and 3T using two CSE protocols per field strength. Confounder-corrected PDFF maps were reconstructed using a common algorithm. To assess accuracy, PDFF bias and linear regression with the known PDFF were calculated. To assess reproducibility, measurements were compared across sites, vendors, field strengths and protocols using analysis of covariance (ANCOVA), Bland-Altman analysis and the intra-class correlation coefficient (ICC).

Results

PDFF measurements showed overall absolute bias (across sites, field strengths and protocols)=0.22% with 95% CI:(0.07%,0.38%), and R²>0.995 relative to the known PDFF at each site, field strength and protocol (slopes: 0.96–1.02, intercepts: −0.56%–1.13%). ANCOVA did not show effects of field strength (p=0.36), or protocol (p=0.19). There was a significant effect of vendor (F=25.13,p=1.07×10⁻¹⁰), with bias= −0.37% (Philips) and −1.22% (Siemens) relative to GE. The overall ICC was 0.999.

Conclusion

CSE-based fat quantification is accurate and reproducible across sites, vendors, field strengths and protocols.

INTRODUCTION

Chemical shift-encoded (CSE) techniques for MRI-based quantification of triglyceride concentration have shown great promise for early diagnosis, quantitative grading and treatment monitoring of nonalcoholic fatty liver disease (NAFLD) (1). These techniques enable non-invasive liver fat quantification for both research (eg: clinical trials for drug development) and clinical applications. However, for CSE liver fat quantification techniques to provide a valid quantitative imaging biomarker, their accuracy (low bias and high linearity relative to an accepted reference), precision (high test-retest repeatability) and reproducibility (low variability under different experimental conditions) must be demonstrated (2).

By addressing all relevant confounding factors, including T₁ (3) and $T_2^{\ast }$ relaxation (4,5), multi-peak spectral complexity of fat (5), noise bias (3), phase errors (6), and temperature effects (7), CSE fat quantification techniques enable accurate measurement of the proton density fat-fraction (PDFF), a quantitative imaging biomarker of tissue triglyceride concentration (1). The accuracy (using spectroscopy or liver biopsy as the reference) and precision (using test-retest repeatability) of CSE methods for liver PDFF quantification have been demonstrated in multiple single-site studies over the past decade (8–13).

Recent research efforts have focused on validating the reproducibility of PDFF quantification. The effect of different echo time combinations was assessed by Levin et al. (14). Reproducibility across field strengths (1.5T and 3T) has been demonstrated by Artz et al (15) and Hansen et al (16) on a single vendor, and reproducibility across field strengths and two vendors at a single site has been demonstrated by Kang et al (17). Mashhood et al. assessed the reproducibility of liver PDFF quantification across five sites, five magnets and three vendors (18). This study also included preliminary fat-water phantom analysis, although the phantoms employed were limited in scope (only three PDFF values), and the analysis of the phantoms did not directly assess reproducibility across sites. Direct demonstration of reproducibility in fat-water phantoms across multiple sites, vendors, platforms and field strengths has yet to be performed. Phantom-based studies enable validation of PDFF techniques in a controlled setting and enables more comprehensive assessment of reproducibility than is possible with human subjects. Multi-center validation is necessary to assess reproducibility of PDFF quantification, as needed in multi-center clinical trials (eg: for drug development) as well as for quality assurance across different clinical sites.

Therefore, the purpose of this work was to test the accuracy and reproducibility of PDFF measurements across multiple sites, vendors, and field strengths using a fat-water phantom and a common reconstruction algorithm that corrects for all relevant confounding factors.

METHODS

Phantom construction

An agar-based fat-water phantom consisting of 11 cylindrical glass vials (diameter=25 mm, height=90 mm) with multiple oil-to-water concentrations (PDFF = 0%, 2.6%, 5.3%, 7.9%, 10.5%, 15.7%, 20.9%, 31.2%, 41.3%, 51.4%, 100%) was constructed (7,19). Each of the oil-water emulsions (40ml total) included: deionized water, peanut oil, agar (2% w/v), sodium dodecyl sulfate (SDS, 43mM), sodium chloride (43mM), sodium benzoate (3mM), and copper sulfate (1.0mM). The PDFF=0% vial was built with no SDS (since a surfactant is not needed for this vial), and the PDFF=100% vial contained only peanut oil. The cap of each vial was lined using silicone gel for improved sealing. Throughout the duration of the study (14 months), the phantom was kept at room temperature without special storage instructions at each site.

Imaging sites

After construction, the phantom was scanned at Site 1. The phantom was then shipped to and scanned at five additional imaging sites over a 14-month period (between October 2014 and November 2015). The scanner vendors included GE (two sites), Philips (two sites), and Siemens (two sites), each with 1.5T and 3T platforms (Table 1). To complete the study (December 2015) and to assess the integrity of the phantom, as well as any drift in PDFF values, the phantom was shipped back to Site 1 and re-scanned at both field strengths.

Table 1.

Magnets and coils used in this study

Site (vendor)	1.5T scanner	1.5T coil	3T scanner	3T coil
Site 1 (GE)	HDxt	Single-channel head coil	MR750	Single-channel head coil
Site 2 (GE)	HDxt	Single-channel head coil	HDxt	Single-channel head coil
Site 3 (Philips)	Achieva	Single-channel head coil	Ingenia	Single-channel head coil
Site 4 (Philips)	Achieva	8-channel head coil	Achieva	6-channel head coil
Site 5 (Siemens)	Aera	Single-channel head coil	Tim Trio	Single-channel head coil
Site 6 (Siemens)	Avanto	12-channel head coil	Tim Trio	12-channel head coil

Imaging protocol

At each site and scanner, vials were placed in the scanner room at least 30 minutes prior to scanning, for temperature stabilization. Next, vials were placed contiguously on the scanner table, parallel to the main magnetic field. Data acquisition was performed at both 1.5T and 3T using each site’s version of a multi-echo 3D spoiled gradient echo (SGRE) CSE sequence (9,12,20), which included two different acquisition protocols to test the reproducibility across different acquisition parameters. The sequence parameters were chosen to reflect clinical imaging parameters used in previous studies (9,11,12), while providing sufficient spatial resolution for relatively small vials. Two six-echo protocols were chosen at each field strength and approximately matched across sites. Protocol 1 generated approximately in-phase and opposed-phase water and fat signals: TE₁≈ΔTE≈2.30ms (1.5T), TE₁≈ΔTE≈1.15ms (3T), and protocol 2 used the shortest echoes typically achievable in 3D liver CSE imaging: TE₁≈1.10–1.20ms, ΔTE 2.00ms (1.5T) or ΔTE≈1.00ms (3T). All data were acquired in the axial plane (perpendicular to the long axes of the vials), at 6 echo times to enable $T_2^{\ast }$ correction, and using a small flip angle (2°–3°) to minimize T₁ bias. The multi-echo acquisitions were performed using monopolar readouts, except for 3T imaging at sites 5 and 6 where bipolar readouts were used because monopolar pulse sequences with adequate imaging parameters were not available. Specific imaging parameters are provided in Table 2.

Table 2.

Chemical Shift-Encoded protocols used in this study at six sites including three MRI vendors: GE (sites 1–2), Philips (sites 3–4), and Siemens (sites 5–6). All protocols consisted of 6 echoes obtained in either one or two echo trains, without parallel imaging acceleration, and with a single average.

Site	Field	Protocol	TE1 (ms)	ΔTE (ms)	ETL	Readout	Flip (°)	TR (ms)	Number of Slices	Slice (mm)	FOV (cm2)	Matrix	In-plane resolution (mm2)
1	1.5T	1	2.30	2.31	6	monopolar	3	16.6	24	4	30.0×21.0	256×179	1.2×1.2
1	1.5T	2	1.20	1.98	6	monopolar	3	14.9	24	4	32.0×22.4	192×134	1.7×1.7
1	3T	1	1.15	1.17	3	monopolar	2	9.2	24	4	40.0×28.0	240×168	1.7×1.7
1	3T	2	1.24	1.00	3	monopolar	2	8.0	24	4	32.0×22.4	192×134	1.7×1.7
2	1.5T	1	2.30	2.07	6	monopolar	3	15.9	24	4	32.0×22.4	224×157	1.4×1.4
2	1.5T	2	1.06	2.00	6	monopolar	3	13.6	24	4	32.0×22.4	224×157	1.4×1.4
2	3T	1	1.28	1.08	3	monopolar	3	9.2	24	4	32.0×22.4	240×157	1.3×1.4
2	3T	2	1.22	1.02	3	monopolar	3	8.8	24	4	32.0×22.4	224×157	1.4×1.4
3	1.5T	1	2.30	2.30	3*	monopolar	3	17.0	28	4	30.0×21.0	108×75	2.8×2.8
3	1.5T	2	1.19	1.80	3*	monopolar	3	15.0	28	4	32.0×22.4	116×79	2.8×2.8
3	3T	1	1.15	1.15	3	monopolar	3	9.1	28	4	32.0×22.4	200×140	2.0×2.0
3	3T	2	1.10	1.00	3	monopolar	3	8.0	28	4	32.0×22.4	160×112	2.0×2.0
4	1.5T	1	2.30	2.30	4**	monopolar	3	21.0	28	4	30.0×21.0	120×84	2.5×2.5
4	1.5T	2	1.22	1.80	4**	monopolar	3	16.0	28	4	32.0×22.0	128×88	2.5×2.5
4	3T	1	1.15	1.15	4**	monopolar	3	11.0	28	4	32.0×22.4	160×112	2.0×2.0
4	3T	2	1.10	1.00	4**	monopolar	3	10.0	28	4	32.0×22.4	160×112	2.0×2.0
5	1.5T	1	2.30	2.30	6	monopolar	3	17.0	28	4	30.0×20.6	192×132	1.6×1.6
5	1.5T	2	1.14	1.76	6	monopolar	3	15.0	28	4	32.0×22.0	192×132	1.7×1.7
5	3T	1	1.13	1.25***	6	bipolar	3	9.0	28	4	32.0×23.0	192×138	1.7×1.7
5	3T	2	1.10	1.10	6	bipolar	3	8.0	28	4	32.0×23.0	192×138	1.7×1.7
6	1.5T	1	2.30	2.42	6	monopolar	3	17.0	28	4	32.0×22.0	192×132	1.7×1.7
6	1.5T	2	1.20	2.00	6	monopolar	3	15.0	28	4	32.0×22.0	192×132	1.7×1.7
6	3T	1	1.15	1.15	6	bipolar	3	8.3	28	4	32.0×22.0	192×132	1.7×1.7
6	3T	2	1.20	1.04	6	bipolar	3	8.0	28	4	32.0×22.0	192×132	1.7×1.7

^*Two 6-echo bipolar acquisitions with opposite polarities were combined to form one synthetic monopolar dataset using the even echoes from one bipolar acquisition, and the odd echoes from the other.

^**These acquisitions obtained 8 echoes in two interleaved echo trains (4 echoes each), but only the first 6 echoes were used in PDFF reconstruction, for consistency with the remaining sites.

^***This acquisition used non-uniformly spaced TEs: 1.13ms, 2.32ms, 3.60ms, 4.90ms, 6.15ms, 7.38ms (average ΔTE=1.25ms).

PDFF reconstruction and measurement

Complex-valued echo images were sent to a central site (Site 1) for reconstruction of PDFF maps. The reconstruction included correction for the multi-peak fat spectrum (5,21), $T_2^{\ast }$ relaxation (single $T_2^{\ast }$, common for water and fat) (5,22), and temperature-related frequency shifts (7). For temperature correction, a room temperature of ~22°C was assumed, and a common frequency shift of 0.1 ppm was applied for all acquisitions at all sites, resulting in a shift of 3.50 ppm between water and the main (i.e. CH₂) fat peak. In combination with the multi-peak fat spectrum, this resulted in a six-peak fat model (21,23) with frequency shifts relative to the water peak (ppm): −3.90, −3.50, −2.70, −2.04, −0.49, 0.50, respectively, and relative amplitudes: 0.087, 0.694, 0.128, 0.004, 0.039, 0.048, respectively.

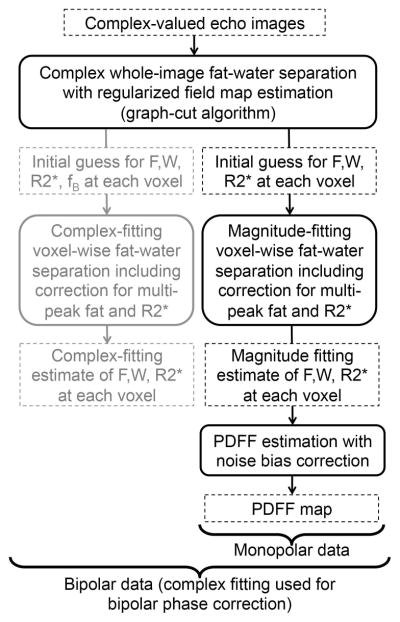
PDFF mapping was performed in a two-step process by first using complex fitting (to obtain approximate water-fat separation with full 0–100% PDFF range), followed by magnitude fitting initialized with the results from complex fitting (to avoid phase errors in the PDFF estimation) (6,22). A flow chart of the entire algorithm is shown in Figure 1. In the first step, complex fitting was performed using a regularized B₀ field map estimation approach with a graph-cuts based algorithm. The purpose of this step was to provide a true 0–100% PDFF range while avoiding artifactual discontinuities in the estimated B₀ field map, which can result in erroneous assignments of the fat and water signals (fat-water swaps) (24). In the second step, magnitude fitting was performed (initialized with the complex fitting results from the previous step) using a voxel-by-voxel nonlinear least-squares algorithm to obtain fat-only and water-only images. Finally, PDFF maps were calculated from the fat-only and water-only images using magnitude discrimination in order to avoid noise bias effects (3). The same offline reconstruction algorithm was used for the data acquired on each scanner at each of the six sites. For each PDFF map, measurements were performed by placing an ROI (~3cm²) on each of the vials, averaging over the three central slices of the vial.

Figure 1.

Workflow of the data processing algorithm used for PDFF mapping.

For bipolar readout acquisitions (25), linear phase offsets (applied to the even echoes and modeled as ϕ(x) = ϕ₀ + xϕ₁, where x is the readout direction) were estimated and corrected automatically prior to PDFF mapping, by minimizing the difference (root sum of squares over the entire images) in estimated water and fat amplitude between magnitude and complex fitting:

$$\underset{{\varphi }_0,{\varphi }_1}{min}\sum _{qs.t.R_{2,q}^{\ast }<100s^{-1}}\left[{(\mid W_{q,\mathit{complex}}\mid -\mid W_{q,\mathit{magn}}\mid )}^2+{(\mid F_{q,\mathit{complex}}\mid -\mid F_{q,\mathit{magn}}\mid )}^2\right]$$ (1)

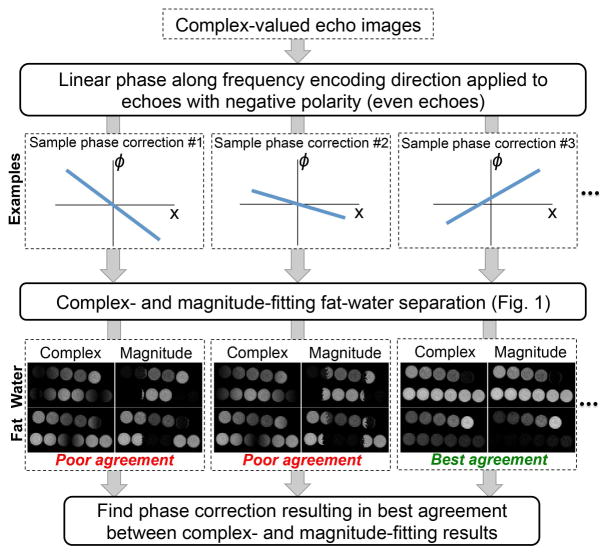
where W_q,complex and W_q,magn are the estimates of water signal at voxel q using complex and magnitude fitting, respectively, F_q,complex and F_q,magn are the estimates of fat signal at voxel q using complex and magnitude fitting, respectively, and $R_{2,q}^{\ast }$ is the $R_2^{\ast }=1/T_2^{\ast }$ estimate (magnitude fitting) at voxel q. The phase correction algorithm is restricted to voxels with moderate $R_2^{\ast }(<100{\mathrm{s}}^{-1})$, to avoid unstable phase correction due to noisy voxels, where $R_2^{\ast }$ can be arbitrarily high. Note that it is not necessary that the phase correction algorithm for bipolar gradients completely eliminate phase errors. Rather, this algorithm must be sufficient to enable complex fitting with moderate errors over the entire PDFF range 0–100%, to provide a suitable initialization for the subsequent magnitude fitting, as described above. Note that the final PDFF estimation (after phase correction) is not restricted in the range of $R_2^{\ast }$. The bipolar phase correction algorithm is outlined in Figure 2.

Figure 2.

Workflow of the phase correction algorithm used in this work for bipolar acquisitions. This algorithm performs phase correction along the readout direction, seeking the linear phase correction ϕ(x)= ϕ₀+xϕ₁ (applied to the even echoes) that results in the best match between fat-water separated images obtained from complex- and magnitude-fitting, respectively. The algorithm is initialized by sampling a discrete grid on the space of ϕ₀ and ϕ₁. Starting from the optimum point within the initial grid, the method then applies a descent algorithm to find a locally optimum solution where complex-fitting and magnitude-fitting provide the most similar fat-water separations.

Statistical analysis

The overall bias for all PDFF measurements was calculated with respect to the true PDFF (known from the phantom construction). Further, the linearity of the PDFF measurements (relative to the true PDFF) was assessed using linear regression analysis.

To assess reproducibility, multi-way analysis of covariance (ANCOVA), Bland-Altman analysis, and intra-class correlation coefficient (ICC) analysis were performed. In order to jointly assess the effects of vendor, field strength and protocol on the measured PDFF, a multi-way ANCOVA was performed, using the known PDFF as a covariate. To assess reproducibility across protocols, PDFF measurements from protocols 1 and 2 were compared using Bland-Altman analysis, at all sites and both field strengths. Similarly, 1.5T PDFF measurements were compared to 3T measurements using Bland-Altman analysis to assess reproducibility across field strengths, and PDFF measurements from each of the sites 2–6 were compared to those from site 1 using Bland-Altman analysis to assess reproducibility across sites. In ANCOVA and Bland-Altman analyses, PDFF bias was calculated in absolute percentage points. Additionally, all measured PDFF values were compared across sites, vendors, field strengths and protocols using the two-way random, single-measure ICC.

Finally, to assess the potential phantom and scanner drift over the study (October 2014 – December 2015), Bland-Altman analysis was performed to compare the PDFF measurements obtained at site 1 at the beginning (October 2014) and at the end (December 2015) of the study.

Statistical analysis was performed in Microsoft Excel (Version 14.5.5, 2011), Matlab (Mathworks, Natick, MA), and R (26).

RESULTS

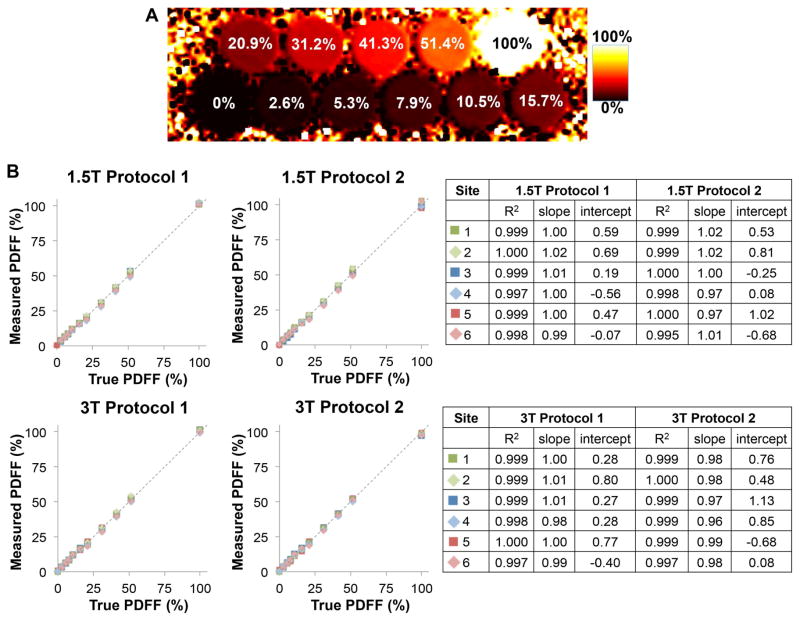
PDFF maps from all sites were reconstructed successfully (see Figure 3A). Further, the complex echo images and reconstructed maps used in this work have been made publicly available under Ref. (27). These data are provided as Matlab (Mathworks, Natick, MA) structures, following the convention used by the ISMRM Fat-Water Toolbox (28).

Figure 3.

Phantom PDFF mapping demonstrates accurate fat quantification at all sites, vendors, field strengths and protocols. A) Representative PDFF map. B) Linear regression analysis showing high correlation, slope close to 1 and intercept close to 0 for all acquisitions.

The overall bias in the measured PDFF (across over all measurements at all sites, field strengths and protocols), relative to true PDFF, was 0.22% with 95% CI: (0.07%,0.38%). Linear regression results comparing the measured PDFF to the true PDFF are shown in Figure 3B. PDFF measurements at each site, field strength and protocol were highly correlated with the known PDFF (R²>0.995), with a slope close to 1 (between 0.96 and 1.02) and intercept close to zero (between 0.56% and 1.13%).

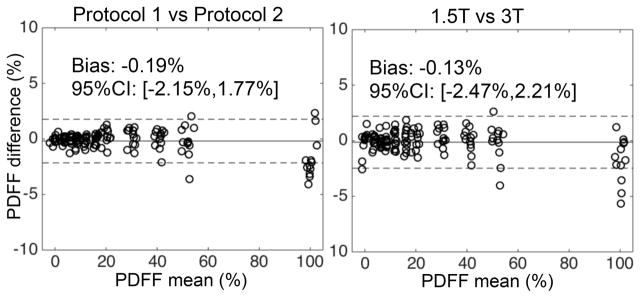
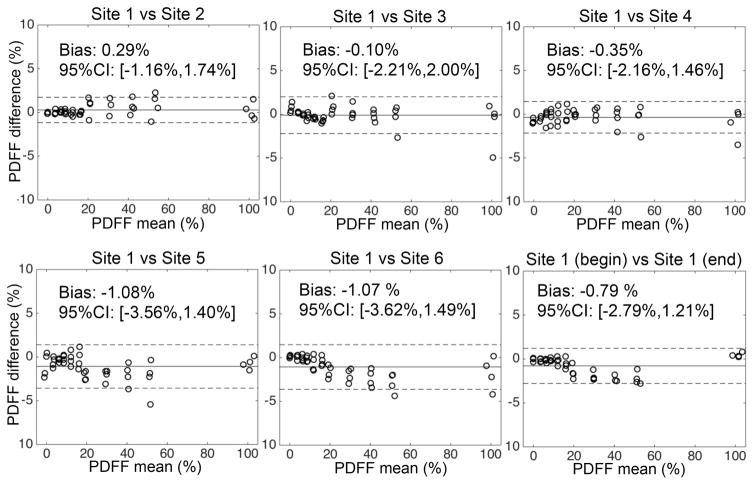
ANCOVA analysis demonstrated no significant effect of field strength (F=0.83, p=0.36), or protocol (F=1.73, p=0.19) on the measured PDFF. There was a significant effect of vendor (F=25.13, p=1.07×10⁻¹⁰). Using the measurements from GE (sites 1 and 2) as a reference, each of the remaining vendors resulted in the following effect on PDFF (mean ± standard error): Philips (sites 3 and 4): −0.37% ± 0.18%, Siemens (sites 5 and 6): −1.22% ± 0.18%. Bland-Altman analyses evaluating the reproducibility across protocols and field strengths are shown in Figure 4. Bland-Altman analyses evaluating the reproducibility across sites and vendors are shown in Figure 5. The measured ICC over all sites, vendors, field strengths and protocols was ICC=0.999, with 95% CI=0.997–1.000.

Figure 4.

Bland-Altman analysis comparing PDFF measurements across protocols and across field strengths demonstrate reproducible fat quantification, for all sites and vendors in this study.

Figure 5.

Bland-Altman analysis between PDFF measurements from sites 2–6 and those from site 1 (measured at the beginning of the project) demonstrates reproducible fat quantification with low bias across sites. Bland-Altman analysis between PDFF measurements from site 1 at the beginning and end of the project demonstrates integrity of the phantom and lack of drift in PDFF values.

Bland-Altman analysis (also shown on Figure 5) of the PDFF measurements performed at site 1 at the beginning and at the end of the study showed low bias (−0.79%) and a 95% confidence interval of (−2.79%, 1.22%).

DISCUSSION

This study demonstrated both the accuracy (ie: low bias and high linearity) and the reproducibility of CSE-based PDFF quantification across six sites with three different MRI vendors, at both 1.5T and 3T, and using two different acquisition protocols with different echo times. Further, it has demonstrated the utility of an agar-based fat-water phantom to validate the acquisitions performed at multiple sites and over an extended time period (14 months). These results are important for the widespread dissemination of CSE fat quantification techniques, both for research and clinical application, as well as for meta-analysis across different studies.

These results confirm the fundamental nature of PDFF, which can be measured accurately across a wide range of platforms and pulse sequences, and they demonstrate the accuracy of the confounder-corrected approach used in this work. We speculate that the PDFF biases observed across vendors (which were small, but significant) may be partly due to variability in temperature between sites. Even higher accuracy and reproducibility might be achieved by measuring the phantom temperature during the scan and adjusting the fat-water frequency shift accordingly. However, the excellent accuracy and reproducibility observed in this study without control for specific temperature variations across sites demonstrates the utility of the proposed approach and its potential for further multi-center validation studies and quality assurance. Additionally, our results suggest that any errors due to temperature variations across exams and sites are small.

The results from this study are in good agreement with previous accuracy and reproducibility studies in preliminary phantom studies (19) and in patient studies, which have demonstrated accuracy in multiple platforms (8–13), and have shown promising reproducibility results across sites, vendors and field strengths (15,18). This study adds to this body of work by demonstrating reproducibility in a controlled setting and in a more comprehensive manner than can be achieved with human studies.

The discrepancies in PDFF measurements (ANCOVA and Bland-Altman analysis) observed in this study were between −1.22% and 0.29%. These effects are small compared to the range of PDFF values measured in this work (0–100%), as well as compared to the range of PDFF values observed in the liver (roughly 0–50%) (8,9,11,12). Further, the observed discrepancies are on the order of the precision (test-retest repeatability) of liver PDFF quantification observed in recent studies (95% CI ranging between ±0.4% and ±2.7%) (8,10,11,29). Importantly, recent weight loss studies have demonstrated decreases in measured liver fat with diet (average PDFF decreases of 4.7–4.8% between the beginning and the end of the interventions) (30,31). Thus, the results of the current study suggest the feasibility of longitudinal liver PDFF measurements across different sites, vendors, field strengths and protocols.

This study had several limitations. The use of head coil acquisitions without parallel imaging acceleration likely resulted in higher signal-to-noise ratio (SNR) than that obtained using phased-array torso coil with parallel imaging acceleration as commonly performed in abdominal imaging, although this was likely compensated in part by the increased spatial resolution (eg: 4mm slices) used in this work. Although the accuracy and reproducibility of PDFF measurement at different sites may depend on the underlying SNR, the evaluation of this effect was beyond the scope of this study.

Another limitation of this study is the presence of differences in the acquisition parameters across sites. Even though this study attempted to establish similar protocols at all sites, substantial differences remained between acquisition parameters at different sites (eg: echo time combinations, readout polarities, or repetition times). However, the accuracy and reproducibility observed in this study across sites and protocols are particularly encouraging for the development and widespread dissemination of PDFF as a quantitative imaging biomarker.

This study used a centralized PDFF reconstruction based on a two-step process: a complex fitting algorithm to provide full PDFF range (0–100%), followed by a magnitude fitting algorithm. This magnitude fitting step was initialized with the results from complex fitting in order to maintain the full PDFF range but avoiding PDFF bias related to phase errors in the acquired images. Finally, the PDFF maps were estimated from the magnitude fitting fat-only and water-only images. Importantly, relying on magnitude fitting for PDFF quantification provides insensitivity to phase errors, at the cost of reduced SNR (particularly for certain echo time combinations) (6,32). Although advanced “hybrid” techniques have been proposed, which combine complex and magnitude fitting results in the final PDFF estimate, these techniques rely on specific assumptions on the size and location of phase errors (6,32). Given the broad range of sites, vendors and platforms employed in this study, PDFF estimates were obtained directly from the final magnitude fitting results in order to accommodate the expected variability of phase errors in the acquired images. Further, we expect that this approach may have applicability for future multi-center, multi-vendor clinical studies.

The use of a centralized PDFF reconstruction enabled a unified comparison of the acquisitions performed at each site and vendor, however each vendor’s own PDFF reconstruction algorithm was not tested in this study. PDFF reconstructions using vendor-specific algorithms were not always available from all sites and vendors, therefore this analysis was not feasible in this work. Additionally, the fat-water phantom employed in this study did not include the presence of iron, which is well known to shorten $T_2^{\ast }$ in iron-overloaded livers and can confound PDFF quantification. It is expected that confounder-corrected PDFF quantification, which accounts for $T_2^{\ast }$ decay, will remain accurate in the presence of moderate iron levels (4,19,33). In future work, it will be desirable to perform phantom and in vivo studies to determine the limits of accurate and reproducible PDFF quantification in the presence of greater degrees of iron overload.

Fat-water phantoms provide a powerful tool for validation and quality assurance of fat quantification techniques. Potential applications of this type of phantom study include the multi-center validation of novel fat quantification techniques, multi-center clinical trials (eg: for drug development) and for quality assurance at clinical sites.

In summary, the development of quantitative imaging biomarkers such as PDFF requires validation across different vendors, sites and platforms. This work demonstrates excellent accuracy and reproducibility of confounder-corrected PDFF quantification in a fat-water phantom across six sites, three vendors, two field strengths, two acquisition protocols, and twelve magnets.