Statistical Approaches for Enhancing Causal Interpretation of the M to Y Relation in Mediation Analysis

Abstract

Statistical mediation methods provide valuable information about underlying mediating psychological processes, but the ability to infer that the mediator variable causes the outcome variable is more complex than widely known. Researchers have recently emphasized how violating assumptions about confounder bias severely limits causal inference of the mediator to dependent variable relation. Our article describes and addresses these limitations by drawing on new statistical developments in causal mediation analysis. We first review the assumptions underlying causal inference and discuss three ways to examine the effects of confounder bias when assumptions are violated. We then describe four approaches to address the influence of confounding variables and enhance causal inference, including comprehensive structural equation models, instrumental variable methods, principal stratification, and inverse probability weighting. Our goal is to further the adoption of statistical methods to enhance causal inference in mediation studies.

The many citations of articles outlining mediation methods demonstrate the popularity and fruitfulness of mediation as a tool to understand underlying processes. An examination of every empirical article within a 6-month period in 2007 in Personality and Social Psychology Bulletin (PSPB) revealed that 41% of the articles tested mediation in at least one study (Kashy, Donnellan, Ackerman, & Russell, 2009); from 2005 to 2009, 59% of articles in the Journal of Personality and Social Psychology (JPSP) and 65% in PSPB included at least one mediation test (Rucker, Preacher, Tormala, & Petty, 2011); and 16% of articles in Psychological Science published in 2011 to 2012 included mediation analyses (Hayes & Scharkow, 2013). In JPSP, Baron and Kenny’s (1986) article on mediation is the single most cited article (Quinones-Vidal, Lopez-Garcia, Penaranda-Ortega, & Tortosa-Gil, 2004)—20,326 times, according to Web of Science in June 2013.

Past Associate Editor and regular publisher in JPSP, Robert Cialdini (2009) noted that journal editors place increasing importance on mediation. Associate Editor of the Journal of Experimental Social Psychology, Jamin Halberstadt (2010) stated in a Society for Personality and Social Psychology listserve email that,

• I will desk reject all papers that are unlikely to survive the review process, or do not on their face satisfy the standards or goals of the Journal. This includes, in my opinion … studies with no insight into psychological mechanism.

In his editorial as incoming editor of JPSP, Eliot Smith (2012) further highlighted the importance of mediation for social psychology and stated that

• explanation of observed effects in terms of underlying processes is almost a signature of articles that JPSP has historically published. Only rare articles demonstrate an effect without making at least some progress toward identifying the contributing processes. The most common approach to identifying those processes is mediation analysis. Thus recent developments in both the theory and the methods of mediation analysis are particularly significant for this journal. (pp. 1–2)

Mediation analysis provides an optimal way to test mechanisms based on theory (MacKinnon, 2008; Mark, 1990). By hypothesizing theoretical mechanisms, researchers generate hypotheses about different causal mechanisms and thus create an extensive pattern of predictions. After testing these hypotheses, the researcher can compare the actual pattern of results against the results predicted by different theoretical causal process models (MacKinnon, 2008; Mark, 1990; Rosenbaum, 1984). Despite its popularity, however, mediation analysis has been severely criticized because of the limited conclusions regarding causal mediation effects. As summarized by Bullock, Green, and Ha (2010), “In practice, it is often impossible to draw conclusions about mediation without invoking strong and untestable assumptions. And even when these assumptions are invoked, the data requirements for persuasive mediation analysis typically entail drawing on numerous studies” (p. 550). Therefore, we seek to provide strategies addressing a primary criticism of mediation analysis—the difficulty of demonstrating the mediator causes the dependent variable. Information on methods to address other limitations of mediation analysis such as moderator effects and measurement error can be found in other sources (e.g., Bullock et al., 2010; MacKinnon, 2008).

In most applications of mediating variables in experimental social psychology, researchers randomly assign participants to experimental conditions and measure both the mediating mechanism and dependent variable. Researchers then conduct statistical analyses to provide estimates for the models summarized in Figure 1. Random assignment of participants to levels of the X variable enables causal interpretation of the estimated X to Y relation—the c effect in Panel A of Figure 1, and the estimated X to M relation—the a effect in Panel B of Figure 1. However, randomization of participants to levels of X but not M fails to provide a causal interpretation of the b relation, as described below.

Figure 1.

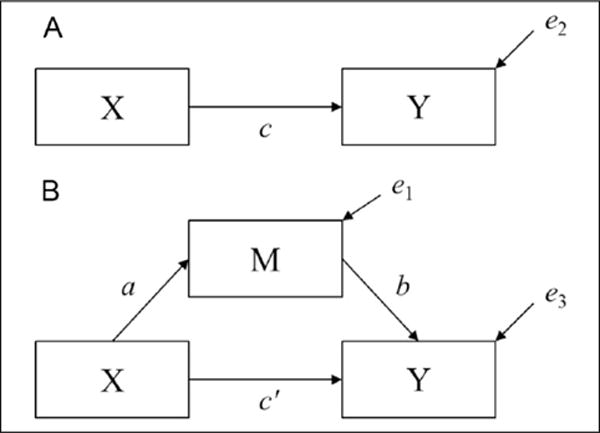
X to Y model (Panel A) and X to M to Y mediation model (Panel B).

To illustrate, three regression equations comprise the single mediator model (shown in Figure 1):

$$\mathrm{M}=i_1+a\mathrm{X}+e_1,$$ (1)

$$\mathrm{Y}=i_2+c\mathrm{X}+e_2,$$ (2)

$$\mathrm{Y}=i_3+c\prime \mathrm{X}+b\mathrm{M}+e_3,$$ (3)

where X is the independent variable, M is the mediator, and Y is the outcome variable; i₁, i₂, and i₃ are the intercepts in each Equation; and e₁, e₂, and e₃ are the residuals. In Equation 1, regress the dependent mediating variable M on X and the coefficient a represents the relation between X and M. (These coefficients represent sample estimates of population parameters). In Equation 2, regress the dependent variable Y on X and the c coefficient represents the relation between X and Y, or the total effect. In Equation 3, regress Y simultaneously on X and M; c′ represents the relation between X and Y, adjusting for M, representing the direct effect of X, or the effect of X not mediated by M; b represents the effect of M on Y adjusting for X. The quantity ab is the causal estimator of the mediated effect (also called the indirect effect), if the five following requirements are met: (a) No confounding of the X to Y relation, (b) no confounding of the X to M relation, (c) no confounding of the M to Y relation, and (d) no effects of X that confound the M to Y relation (VanderWeele & Vansteelandt, 2009). A confounder variable relates to other variables such that its omission from statistical analysis leads to biased estimates of effects. It is also assumed that (e) no interaction exists between X and M affecting Y, although adding the interaction to Equation 3 provides an estimate of this relation if desired. Randomization of participants to levels of X removes the possibility of confounding of the relation of X to M and X to Y, but fails to resolve the assumption of no confounding of the M to Y relation or the assumption of effects of X on other confounders that may affect Y. Even for experimental mediation designs in which researchers randomly assign participants to levels of X, the relation between M and Y—the b effect—fails to provide a clear interpretation as a causal effect, providing a limitation of analyses to identify mediating mechanisms as now described by many researchers (Bullock et al., 2010; Holland, 1988; MacKinnon, 2008).

In summary, the purpose of this article is twofold. First, we describe the problem with causal inference in the mediation analysis of experimental social-psychological studies using nontechnical language relevant for substantive researchers. Second, we summarize strategies to improve the causal interpretation of the b coefficient in mediation analysis using developments in statistical causal inference and provide demonstrations, syntax, and output for these procedures in the supplemental materials. We hope to persuade researchers to consider optimal statistical mediation analysis techniques to enhance causal inference.

Causal Inference in Mediation Analysis

In an experiment perfectly demonstrating causal inference, the same participant partakes in both the experimental and control conditions simultaneously and provides an assessment of the dependent variable in each condition. Comparing the assessment for an individual participant between conditions in the experiment yields the causal effect. Although within-subjects designs enable the same participant to partake in both conditions, carryover effects affect measurement of the dependent variable. Furthermore, the same participant cannot simultaneously partake in the experimental and control groups (which would eliminate carryover effects), a problem called the fundamental problem of causal inference (Holland, 1988). Given the impossibility of a participant simultaneously participating in both conditions, causal inference requires alternative methods. For the case of mediation, issues are even more complex as described below.

Counterfactual and Potential Outcomes Model

Although not commonly taught in graduate psychology courses, the counterfactual or potential outcomes model (Hernán & Robins, 2015; Neyman, 1923/1990; Pearl, 2009; Robins & Greenland, 1992; Rubin, 1974, 1977) provides a way to interpret evidence for causal relations. This philosophical approach makes explicit that the fundamental problem of causal inference arises from the primary goal to know the unique causal effect for each participant. Knowing the individual causal effect, however, requires the impossible because it logically implies that each participant must simultaneously serve in all conditions. This philosophical approach considers the effect of each condition on an individual, not just the condition in which the individual participated. For example, to know the effects of social class during childhood on health, a person would have to grow up in a lower social class and have their health assessed, while also growing up in a higher social class and have their health assessed. The difference between the two health assessments provides causal evidence for the effects of social class on health for that person. Clearly, however, a person cannot simultaneously grow up in both lower and upper class settings, that is, a person cannot typically participate in each condition and provide an assessment of the dependent variable in each condition.

Therefore, central to modern causal inference is the counterfactual—the potential effects of each condition on the participant, not just the condition in which they served. The counterfactual approach suggests that valid causal inference occurs only when a participant’s value on the dependent variable (or mediator) in the experimental condition is compared with that same participant’s value on the dependent variable (or mediator) in the control condition. These models are called potential outcome models, because they consider all the potential conditions in which a participant could serve, not just the condition in which they served.

The next strongest alternative to a participant simultaneously serving in each condition would be to have identical participants serve in the control and experimental groups, but again, this is impossible as participants are not identical. Instead, researchers randomly assign participants to conditions and compare the condition averages, rather than a participant’s assessment in each condition. Random assignment operates under the assumption that participant differences that potentially confound the experimental effects are randomly dispersed across conditions and therefore are not confounds. Accordingly, researchers use the average causal effect—examining group average differences as a function of the experimental manipulation, rather than one participant’s difference on the dependent variable between conditions. The key idea of random assignment to conditions to remove individual difference confounders is widely accepted in psychology and a cornerstone of causal inference methods.

The potential outcomes approach provides a way to address the no confounding variables assumption (or the no omitted variables assumption as it is sometimes called in psychology to reflect important variables that are omitted from an analysis) of a mediation analysis (MacKinnon, 2008) by considering how the mediated relation differs with and without confounds. The no confounding variables assumption presumes that no other variables confound the relation between the predictor and outcome variables. In the single mediator model, omitted variables which potentially affect the X to M and M to Y relations introduce confounder bias because an omitted variable could correlate with both X and M. Randomization of participants to levels of X removes confounder bias in the X to M and X to Y relation. So randomization enables causal interpretation of the a coefficient (the relation between X and M) and c coefficient (the total relation between X and Y), as noted by Holland (1988) in the application of the counterfactual approaches to mediation (Rubin, 1974; Sobel, 2008).

However, because of the influence of potential omitted confounding variables on the M to Y relation, the b coefficient cannot be interpreted as a causal effect even when X is randomized, because researchers cannot randomize the value of M but instead participants self-select their values of M. This inability to randomly assign M means that omitted variables could potentially confound this relation. The c′ coefficient is also not an accurate estimator of the causal effect of X on Y, adjusting for M because of the potential for other variables to affect the M to Y relation, due to the correlational nature of that relation. Thus, the inability to randomly assign participants to M limits the interpretation of b as a causal effect (Bullock et al., 2010; MacKinnon, 2008; Robins & Greenland, 1992; Winship & Morgan, 1999).

As an example from cognitive dissonance research, assume that the X variable represents whether participants either receive a manipulation to invoke dissonance or a no manipulation control.¹ The mediator, M, measures dissonance arousal, and Y measures attitude change. Due to the randomization of X, confounders fail to provide an alternative explanation of the effect of the manipulation on dissonance arousal or on attitude change. However, the level of dissonance arousal was not directly randomized. Participants who received the manipulation were not randomly assigned a value of the dissonance arousal and participants in the control condition were not randomly assigned to a dissonance arousal value. In both groups, participants self-select a level of dissonance arousal which potentially occurs due to confounding variables in each group that are not randomized. As a result, confounders of the M to Y relation potentially exist that cause both dissonance arousal and attitude change. Furthermore, these confounders may also exist as the true underlying mediating variable, not dissonance arousal. For example, anxiety potentially confounds the M (dissonance arousal) to Y (attitude change) relation. Attitude change through dissonance arousal may exist either because anxiety correlates with both variables or because anxiety truly mediates the X to Y relation. In social psychological research, many variables potentially confound the M to Y relation.

The assumptions of no confounding bias as applied to the X to M and M to Y relations are more formally known as the sequential ignorability assumption (Imai, Keele, & Tingley, 2010; Imai, Keele, & Yamamoto, 2010; Lynch, Cary, Gallop, & Ten Have, 2008; Ten Have et al., 2007). The sequential ignorability assumption contains two parts: Part A corresponds to the ignorability of omitted confounding variables in the X to M and X to Y relations, which allows for the causal interpretation of the a and c coefficients, respectively, and Part B corresponds to the ignorability of omitted confounding variables in the M to Y relation which allows for the causal interpretation of the b and c′ coefficients.

The sequential ignorability Part A assumption presumes that no variables confound the X to M and X to Y relation; this enables causal interpretation of the X to M and X to Y effects. Designs in which researchers randomly assign participants to levels of X uphold this assumption. The same logic applies to the sequential ignorability Part B assumption that no variables confound the M to Y relation. This sequential ignorability Part B assumption, however, rests on the premise that researchers randomly assign participants to the level of M, which is unlikely because typically researchers only randomize X, not M. Figure 2 presents an example of a single mediator model with a single confounder of the X to M relation and a single confounder of the M to Y relation.

Figure 2.

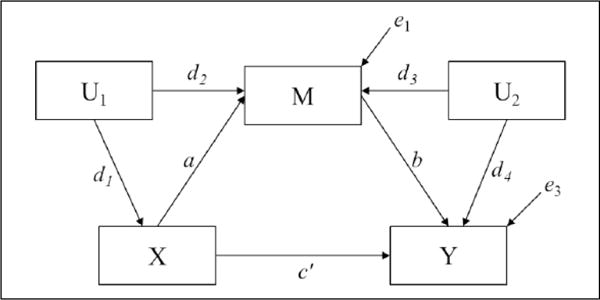
X to M to Y mediation model with a single confounder of X to M (U₁) and a single confounder of M to Y (U₂).

If both assumptions of sequential ignorability prove true (and no confounders exist as caused by the manipulation), then the ordinary least squares estimator for the mediated effect, ab, yields a causal mediation effect (Imai, Keele, & Tingley, 2010; Imai, Keele, & Yamamoto, 2010; Pearl, 2012). Random assignment to both X and M ensures this situation. When both parts of the sequential ignorability assumption prove true, then the mediated (indirect) effect exists as a natural mediated (indirect) effect in the potential outcome framework (Pearl, 2001; Robins & Greenland, 1992). The natural mediated effect is the mediated effect on Y at the value of M that the participant would have if that participant was in the treatment condition compared with the value of M that the participant would have in the control condition.²

Cases can exist in which the sequential ignorability assumption Part B is appropriate, such as in applied psychological research where researchers select mediators because theory and prior empirical research demonstrated repeatedly that they cause the outcome variable. In this case, researchers consider the b coefficient as known, and because of this causal relation of M to Y, changing M should lead to changes in Y. Even in this case, however, it is possible that the relation of M to Y is not completely causal or even spurious, particularly if researchers base the “known” M to Y relation on correlational research between M and Y. Researchers can address the sequential ignorability assumption by discussing the substantive theoretical and empirical research for evidence of a true causal relation between M and Y, and whether the self-selection of M likely occurs. Researchers can thoroughly describe confounding variables that may provide alternative interpretations of a hypothesized mediating process—which often occurs in the discussion section of research articles. Considerable differences likely exist in the validity of the ignorability assumption for different mediators such as norms, attitudes, physiology, behaviors, cognitions, and other mediators in social psychology. As mentioned above, for many applied mediation studies, compelling evidence based on extensive research likely supports a causal relation of M to Y, thus why the manipulation targeted M.

In summary, experimental studies provide evidence for the causal relation of X to M but not the M to Y relation, because participants are not randomized to levels of M. Several articles critiquing mediation analysis in psychology emphasized the important implications of violating the sequential ignorability assumption (Bullock et al., 2010; Imai, Keele, & Tingley, 2010, MacKinnon, 2008). In particular, when ignoring sequential ignorability, researchers could identify an incorrect mediator, an observed mediation relation could arise due to a confounder that predicts M and Y, and/or a mediation relation could be hidden by a confounding variable. In particular, the violation of this assumption importantly implies that most mediation analyses may find evidence for incorrect mediators without researchers being aware of this problem. This problem intensifies when basic social psychological research translates into applied social psychology interventions targeting a particular mediator.

Given the importance of the sequential ignorability assumption, what possible options exist for researchers to improve causal inference from a research study? We first describe methods to investigate confounder bias by examining the effect of a confounder on the estimate of the observed mediated effect to answer the following questions: “What size of a confounder effect would make an observed mediated effect zero?” and “What size of a confounder effect would make a nonexistent mediated effect appear significant?” Second, we outline the rationale of four major methods to improve causal inference from a mediation study: comprehensive structural equation models, instrumental variables, principal stratification, and inverse probability weighting, to answer the question “What statistical methods provide more accurate estimates of mediation effects?”

Dissonance Data Example

We use a dissonance example to illustrate the methods described in this article, based on the Harmon-Jones, Brehm, Greenberg, Simon, and Nelson (1996) study on cognitive dissonance. We chose this article because it clearly investigates mediators of cognitive dissonance and it included values that could be used as effect size measures. In this simulated data example, X is a binary variable representing randomization to either of two conditions in which one condition was designed to induce cognitive dissonance. The dependent variable is attitude change and the mediator is dissonance arousal measured by physiological galvanic skin response. In other words, the manipulation (X) causes dissonance arousal (M) and dissonance arousal causes attitude change (Y). We also generated two confounding variables for the relation of M to Y—anxiety (U₁) and desire to please the experimenters (U₂). We refer to this example through the article to provide an empirical example of the statistical methods described to enhance causal inference. The data set and analyses are provided in the supplemental materials.

In the simulated data set, the manipulation (X) affected attitudes (Y): c = 0.74, SE = .31, t = 2.37, p = .02. The manipulation also affected dissonance arousal (M): a = 1.15, SE = .28, t = 4.10, p < .001. Dissonance arousal (M) affected attitudes (Y): b = 0.59, SE = .14, t = 4.27, p < .001, even when adjusted for the manipulation (X). The adjusted effect of the manipulation was not statistically significant: c′ = 0.06, SE = .31, t = 0.20, p = .84, when including M. The value of c′ dropped (c′ = 0.06) compared with c (c = 0.74). The mediated effect estimate is ab = (1.15) (0.59) = c − c′ = 0.74 − 0.06 = 0.68 with upper and lower confidence limits of 0.23 and 1.19, so the mediated effect was statistically significant. We use the data (available in the supplemental materials) to illustrate the methods described below. First, we use plots of sensitivity to confounder bias to demonstrate how much an observed mediated effect could be affected by unobserved confounders. Second, we use statistical methods that address possible confounding in the example.

Investigating Confounder Bias in the Mediated Effect

Sensitivity analysis assesses how violations of assumptions of a statistical analysis, such as confounding of the relation of M to Y, affect research conclusions. In this section, we assume that researchers randomize participants to X, as in most experimental social psychological studies, so we can focus on confounding of the M to Y relation. We discuss three sensitivity analysis methods to assess the effects of hypothetical confounder bias below.

Average causal mediation effect (ACME)

One way to investigate the sensitivity of model results to confounding variables assesses how large a confounder effect on the M to Y relation must be to invalidate conclusions about mediation (Frank, 2000; Li, Bienias, & Bennett, 2007; Lin, Psaty, & Kronmal, 1998; Rosenbaum, 2002). Thus, researchers can explore the sensitivity of mediation results to a confounder by systematically increasing the correlation between the errors in Equation 2 for the model predicting M and Equation 3 for the model predicting Y and evaluating the degree to which the mediated effect estimate changes as described by Imai, Keele, and Tingley (2010). A confounder of the M and Y relation leads to a correlation in the error in these two equations. Imai, Keele, and Tingley (2010) provided an R program to conduct mediation analysis and plot how the estimate of the mediated effect changes as a function of how much a confounder affects the correlation between the error terms in the model predicting M and Y (see supplemental materials).

To use the dissonance example, the extent to which a con-founder of anxiety (or any confounder) affects the mediated effect of dissonance on attitude change could be investigated by systematically varying the correlation between residuals in the equations predicting dissonance arousal (M) and attitude change (Y) and then assessing the mediated effect. The correlation between the residuals reflects the size of a possible theoretical confounding variable such as anxiety. Accordingly, these analyses show how the mediated effect changes as a function of the size of the confounder effect on M and Y. The computer program available from Imai, Keele, and Tingley (2010) and described in the supplemental materials automatically generates possible values of the correlation between residuals corresponding to confounding. Using the sample dissonance data (see supplemental materials), a correlation between residuals of about .51 renders the mediated effect equal to zero. Such a large correlation needed to reduce a mediated effect to zero suggests the inability of the confounder to affect the mediated relation. See Figure S1 in the supplemental materials, which shows the confounder bias plot using the Imai, Keele, and Tingley (2010) method.

VanderWeele’s (2010) confounder bias method

VanderWeele (2008, 2010) developed a second way to probe bias in mediation relations using two parameters: γ and δ. The γ coefficient corresponds to the relation of an unobserved binary confounder to Y and the δ coefficient reflects the difference in prevalence of the confounder variable, U, for participants with the same value of M in the experimental versus control groups. In other words, the researcher must identify a range of possible values for the regression coefficient relating a binary confounder to the dependent variable and a range of possible values for the difference in the proportion of participants for whom the confounder variable exists for participants with the same value of the mediator in the experimental and control groups. The extent to which a confounder affects the mediated effect estimate can be obtained by subtracting the value γδ from the estimate of the mediated effect, thus yielding an estimate of the mediated effect with the influence of the confounding variable removed. This approach easily assesses the sensitivity of results to confounder bias but requires the identification of reasonable values for the two parameters of interest, γ and δ. This method can also be used for a continuous confounder by interpreting γ as the effect on Y for a one standard deviation change in the confounder and δ as difference between groups for a one standard deviation change between treatment and control groups.

For the dissonance example with anxiety as a confounder, the coefficient γ is the relation of a binary confounder of anxious or not to the outcome variable (attitudes) and the coefficient δ is the difference in the proportion of persons who experience anxiety in the experimental versus control conditions at the same level of dissonance arousal (M). To obtain an estimate of the mediated effect with the confounder (anxiety) removed, first generate a value of γ, the regression coefficient between anxiety (binary confounder) with attitudes (Y) based on prior research or guesses about its value. Then generate a value for δ for the difference between the proportions of participants with the confounder of anxiety in the two groups, that is, the proportion of anxious persons in the experimental condition minus the proportion of anxious persons in the control condition at a value of dissonance arousal. Multiply the coefficient, δ, by γ and subtract that value from the estimated mediated effect in the sample to obtain the mediated effect unconfounded by anxiety. If prior research exists from which to select values of γ and δ, researchers can use best guesses based on the maximum and minimum values possible. For the dissonance example and a confounder of whether a participant had taken anti-anxiety medication, γ is a hypothetical regression coefficient predicting attitude change by mediation of .30 and δ is the difference in the proportion of persons who took anti-anxiety medication between the two groups of .05 for a bias of .02. The corrected mediated effect would then be .68 minus .02 or .66. Researchers can also plot the value of the mediated effect as a function of γ and δ to show when the mediated effect is zero. For the dissonance example data (syntax available in the supplemental materials), the plot (Figure S2 in the supplemental materials) shows that a confounder effect would have to be very large to reduce the mediated effect to zero for the dissonance data.

Left out variables error method (LOVE)

The LOVE method (Mauro, 1990) to investigate confounder bias calculates two correlations using a hypothesized confounder: (a) the correlation between a confounder and Y and (b) the correlation between a confounder and M that make an observed mediated effect zero (MacKinnon, Cox, Miocevic, & Kisbu-Sakarya, 2012). The metric of correlation between the confounder and M and Y likely makes this method easy for psychologists to understand intuitively because of prior experience with correlation coefficients. The size of the correlation coefficients enables researchers to identify the size of correlations of the confounder and M and the confounder and Y that would cause the mediated effect to become zero.

To illustrate the LOVE method using the dissonance example (see supplemental materials), the mediated effect will change as the correlation between an unobserved con-founder such as anxiety and dissonance and the correlation between anxiety and attitude change. Formulas for calculating a new mediated effect for different values of the correlation of a confounder and Y and the confounder and M are described in Cox, Kisbu-Sakarya, Miocevic, and MacKinnon (2013). As demonstrated in Figure S3 for the dissonance data example, a correlation of anxiety and dissonance of .54 and a correlation of anxiety and attitude of .60 would reduce the observed mediated effect to zero. The large correlations necessary to reduce the observed mediated effect to zero suggest that confounding is an unlikely explanation of the mediated effect. In another situation, application of this method may suggest a mediated effect would be reduced to zero for relatively low correlations with a confounder consistent with confounder bias as an alternative interpretation of the mediated effect.

Statistical Methods to Address Causal Inference

Several statistical methods improve causal conclusions from experimental mediation studies, including comprehensive structural equation models (Bollen, 1989), instrumental variable methods (Holland, 1988; Sobel, 2008), principal stratification (Frangakis & Rubin, 2002; Jo, 2008), and inverse probability weighting (Robins, Hernán, & Brumback, 2000), which we discuss below.

Comprehensive structural equation models

To address the influence of confounding variables, a researcher could include measures of all relevant confounding variables in the statistical analysis of mediation. The challenge underlying this method is given by Hubert Blalock’s (1979) presidential address to the American Sociological Society: “Reality is sufficiently complex that we will need theories that contain upwards of fifty variables if we wish to disentangle the effects of numerous exogenous and endogenous variables on the diversity of dependent variables that interest us” (p. 881). Such comprehensive models include all statistical influences on the mediating and dependent variables in a research study. A structural equation model would then be estimated to address the confounding variables problem (MacKinnon, 2008). For example, if two possible confounders exist as shown in Figure 2, estimate the model in Figure 2 and include the paths relating the confounding variables to X, M, and Y (though with randomization the path from the confounder U₁ to M should be zero). In this way, the estimates of the paths in the mediation model are adjusted for relevant variables. With randomization of X, confounders related to the X and M variables are unnecessary, but possible confounders of the M to Y relation exist. So in this context, include all variables related to M and Y to adjust for confounders. If another mediating process is operating then specify and estimate additional mediational pathways corresponding to the additional mediators.

To illustrate using the dissonance data example (see supplemental materials), researchers include measures of all variables related to the mediator and outcome such as the two confounding variables for the relation of M to Y anxiety (U₁) and desire to please the experimenters (U₂) generated for the example. Because of random assignment, neither of these variables should be related to X but could be related to the mediator and dependent variables. Once specified, the entire model is estimated and, assuming a well-fitting model, an estimate of the mediated effect is obtained by taking the product of the a and b paths in the structural equation model. For the dissonance data example, the mediated effect from the structural equation model was 0.63 compared with 0.68 without adjustment for the two confounders.

In summary, one statistical solution to improving the causal interpretation of the M to Y relation in mediation estimates a comprehensive model that contains relevant variables. Even if not all relevant variables are available, including the most important confounders likely improves the accuracy of the estimate of the b coefficient. This larger, more general model requires comprehensive clarification of the relations between variables which also strengthens the theoretical model. To date, experimental research rarely includes additional covariates in statistical models but non-experimental research frequently uses covariates. Including measures of competing, alternative, and potentially confounding mediators to help identify the true mediator should be an easy approach for social psychologists to implement. The challenge with this approach is that it assumes that all confounders are included in the comprehensive model and that each mediator is measured equally well so that the variance accounted for by each mediator is not due to one variable’s superior measurement. Regardless, comprehensive models provide a way of minimizing the extent to which confounds explain a mediation relation.

One practical application of comprehensive models is to add relevant variables in the regression equations predicting M and Y using SAS, SPSS or programs specific for mediation analysis (Hayes, 2013; MacKinnon, 2008; Valeri & VanderWeele, 2013). These models are helpful for controlling for possible confounding variables but contain limitations, such as the requirement for all confounders to be measured and the assumption that all variables are measured equally well. Structural equation modeling is the best approach to comprehensive modeling because it allows for latent variables to improve measurement of constructs as well as more complicated mediation relations such as mediators in a sequence, multiple mediators, and multiple dependent variables. Structural equation programs now compute mediated effects for any model and the Mplus program includes causal estimators of mediated effects (Muthén & Muthén, 2012).

Instrumental variable methods

Instrumental variable methods address the influence of confounding variables but require that a variable exists that reflects random assignment and the variable relates to Y only via its influence on M (Angrist, Imbens, & Rubin, 1996; Angrist & Krueger, 2001; Bound, Jaeger, & Baker, 1995; Hanushek & Jackson, 1977; MacKinnon, 2008; Shadish, Cook, & Campbell, 2002; Stolzenberg & Relles, 1990, 1997). In some examples, the instrumental variable exists as a naturally occurring variable that reflects random assignment but an instrumental variable can also represent random assignment to conditions. When researchers randomize X, using X as an instrumental variable provides an estimate of the causal relation between M and Y. In the instrumental variable method, X predicts M, and the predicted values of M then predict Y. The coefficient relating the predicted value of M to Y is the causal estimator of the b coefficient relating M to Y under certain assumptions described below. Note that X is treated as more than an independent variable representing assignment to conditions; X is now called an instrumental variable or instrument that represents a randomized manipulation to change the mediator. That M can be considered randomized from its prediction by X removes the influence of any confounding variable on the relation of M to Y. A recent review (Bollen, 2012) outlines the application of instrumental variable methods in the social sciences.

The instrumental variables approach requires several assumptions to enable causal interpretation of the b coefficient, which make it very difficult to appropriately apply instrumental variable methods (see MacKinnon, 2008; Shadish et al., 2002). This approach assumes that randomization of X leads to changes in M such that the stronger the relation of X to M, the better the instrument. The ideal instrument has a correlation of 1 between X with M, which makes X statistically, but perhaps not conceptually, indistinguishable from M.

The exclusion restriction assumption requires that M completely mediates the effect of X on Y such that the inclusion of M eliminates the relation between X and Y. Complete mediation may be unrealistic with real data from many social psychology studies. Nevertheless, the instrumental variable method is an ideal method for social psychology because it reflects randomization of a single factor that affects a single mediator which leads to a causal change in the dependent variable. Finding these manipulations that target only the mediator of interest—and not other mediators—and with effects on the outcome entirely through the mediator requires a challenging precision of theory from a sustained program of research.

The dissonance example (see supplemental materials) illustrates the difficulty of using instrumental variable methods in social psychology. Using the instrumental variable method, a manipulation would need to be devised that changed dissonance arousal but did not have an effect on attitude change other than through dissonance arousal. So the predicted value of dissonance arousal from the experimental manipulation would then be used to predict attitude change. The resulting path relating predicted dissonance arousal to attitude change would estimate the corresponding causal effect. It is difficult to conceive of such a detailed manipulation to change only the mediator causally related to attitude change. However, this type of causal inference approach illustrates the challenging task of identifying a true mediator.

Assuming that the manipulation X does not have a direct effect on Y, the instrumental variables method can be applied to the dissonance example data. First estimate the relation of X to M and then use the predicted value of M to predict Y, which yields a coefficient of .65 which is the instrumental variable estimator of the relation of M to Y. The coefficient is slightly larger than .59 which was the coefficient from ordinary least squares regression for these data.

One benefit of using instrumental variable methods to enhance causal interpretation of the M to Y relation is that not all confounders need to have been measured. However, researchers interested in using the instrumental variables method need to, in the theoretical stage of the research process, think carefully about what manipulation would change a single mediator that entirely explains how the manipulation affects the dependent variable. This approach requires the entire effect of the manipulation on Y to go through the mediator.

Principal stratification

A recent method to strengthen causal inference in mediation studies arose from the theoretical classification of different possible individual response patterns for how X affects M and M affects Y. Related to the instrumental variables method, it often includes the exclusion restriction assumption. In principal stratification approaches, researchers identify subsets of participants based on how M could change in response to experimental manipulation X or control. For example, in a two-group experimental manipulation versus control study there four different types of hypothetical responses across X to M as described by Jo (2008): (a) never-changers: participants whose mediator fails to change regardless of whether they participated in the experimental or control condition; (b) forward-changers: participants whose mediator changes only if they received the manipulation; (c) backward-changers: participants whose mediator changes only if they participated in the control condition; and (d) always-changers: participants whose mediator changes regardless if they participated in either the experimental or control condition. These four groups of participants are hypothetical and orthogonal to the experiment so their classification exists independently of random assignment and as a result the omitted variables that confound the M to Y relation do not influence the mediated effect using principal stratification.

Most studies using principal stratification assume monotonicity—such that no backward-changers exist due to the unlikeliness that the mediator would change for participants in the control condition because they fail to receive the experimental manipulation to influence the mediator. Applications of the principal stratification method also assume the exclusion restriction that the mediator transmits the entire effect of the manipulation. Given the three possible remaining stratifications, researchers estimate the mediated effect by comparing proportions in different strata and the means within and between these stratifications (Angrist et al., 1996; Frangakis & Rubin, 2002; Jo, 2008).

For example, for dichotomous variables X and M, observed participant data in the experimental condition are divided into participants who change or do not change on Y. The participants in the experimental condition who change theoretically consist of two hypothetical groups, forward-changers and always-changers. The participants in the experimental condition who do not change consist of the hypothetical group of never-changers. In the control condition, the participants who have observed data consistent with change consist of the hypothetical group of always-changers and the participants in the control group who did not change are either in the hypothetical group of forward-changers or never-changers. Recall that forward-changers are participants who would change if exposed to the manipulation so the persons in the control group who do not change could be these forward-changers. Researchers then use the difference in observed means of Y in each of the conditions and the percentage of forward-changers to obtain an estimate of the causal mediated effect. Researchers compare the observed changers in the experimental condition to the observed changers in the control condition because forward-changers and always-changers comprise the experimental condition changers whereas only always-changers comprise the control condition changers, so the difference in the proportion reflects only forward-changers.

Here, we provide an example using the dissonance design (see supplemental materials), and assume “change” refers to “increases in dissonance.” Researchers randomly assign participants to receive a dissonance inducing manipulation or no dissonance control, and then assess whether they experience dissonance arousal (measured as yes, M = 1 vs. no, M = 0) and attitude change. Participants in the control condition that changed dissonance arousal (X = 0, M = 1) are always-changers and the proportion in the control condition equaled 0.42. Participants in the manipulation condition with observed change in dissonance arousal (X = 1, M = 1), are always-changers and forward-changers and the proportion in the manipulation condition equaled 0.85. The difference in always-changers and forward-changers in the manipulation condition (0.85), minus the proportion of always-changers in the control condition (0.42) equals the proportion of forward-changers (0.43). Dividing the difference in mean attitude change between manipulation and control condition, (0.44 – 0.33), by the proportion of forward-changers gives an estimate of the mediated effect in the group of forward-changers (1.73). In the principal stratification approach, a large proportion of forward-changers and a large manipulation effect for forward-changers provide evidence for mediation (Jo, 2008).

In new developments for these models, researchers use covariates to obtain information about the mediator stratifications to identify parameters in the model, such as propensity score methods to help define stratifications (Jo, Stuart, MacKinnon, & Vinokur, 2011; Stuart, Perry, Le, & Ialongo, 2008). The principal stratification method typically applies to designs with categorical mediators, which undermines its usefulness, as most mediators in social psychology are continuous. Nevertheless, the method is one of the first applied causal mediation approaches and future work may extend it to continuous mediating variables.

The benefits to using principal stratification methods to enhance causal interpretation of the M to Y relation include clearly addressing that different types of participants with different responses to an experimental manipulation exist. These different types of participants are hypothetical although observed measures of these persons might exist which could be treated as moderators of mediation effects. Moderation in these types of models lies outside the scope of this article but find more on these issues in other articles (Jo, 2008; Jo et al., 2011). Correctly identifying the different types of participants, satisfying the no backward-changers assumption, and studying mediators that drive the entire effect pose significant challenges to this approach.

Inverse probability weighting

Using observed covariates to measure confounder effects and adjust analyses to remove the confounder bias is another approach to obtaining effects adjusted for confounders (Robins et al., 2000). These analyses enable researchers to create an artificial data set without confounder bias and then conduct analyses on the confounder-free data. The goal of these analyses is to generate the potential outcome data for a research study described earlier. In this method, researchers develop a statistical model for the prediction of the mediator based on covariate information and use a weighting method whereby each participant’s contribution to the analysis is weighted by the extent to which confounder bias affects their individual data. The weights are constructed by obtaining numerator and denominator probabilities corresponding to the standardized residual for each participant. That is, the standardized residual for each participant is converted to the probability on the normal distribution. The model without these predictors and only including X provides the probability for the numerator of the weight. To find the denominator, a model with all covariates and X provides the probability for the denominator of the weight. The ratio of these weights is then used in a subsequent weighted least squares regression analysis thereby adjusting for potential confounders of the M to Y relation (Coffman, 2011; Coffman & Zhong, 2012). The b coefficient from the weighted analysis estimates the effect of M and Y adjusted for confounding. If the model includes all confounders, then the b coefficient reflects the causal relation.

For most research studies, a large number of covariates are used to calculate weights including demographic variables and potential confounding variables. Several other methods to estimate weights for inverse probability weighting exist for situations with large weights (Cole & Hernán, 2008), including truncating weights at a certain value. The problem underlying large weights occurs if denominator probabilities get extremely small which yields weights for some participants 100 times the weight for other participants.

This inverse probability weighting method assumes no unmeasured confounders but the method does not require that M mediates the entire effect of X on Y, the exclusion restriction, as for the instrumental variables method. To date, this method has been rarely used in psychology (Coffman & Kugler, 2012; VanderWeele, Hawkley, Thisted, & Cacioppo, 2011), but it is becoming more common in epidemiology and the health sciences. The inverse probability weighting method provides a straightforward opportunity for researchers to adjust for confounder bias in social psychological experiments by including measures of confounders in their research.

For the dissonance data example (see supplemental materials), a regression equation predicting M from X alone provided the numerator of the weight for each participant and the regression equation predicting M with X and U₁ and U₂ gives information for the denominator of the weight for each participant. The weight for each participant equals the numerator divided by the denominator and measures the extent to which the participant’s data are confounded. A weighted least squares regression then yielded the b coefficient of 0.56 rather than 0.59 in the unweighted analysis.

A benefit to using inverse probability weighting methods to enhance causal interpretation of the M to Y relation is that confounder effects can be removed from the mediated effect, therefore providing a cleaner estimate of the mediated effect. Furthermore, this method does not require M to carry the entire effect of X on Y. That this method requires the measurement of all important confounders, however, poses a challenge to researchers. Nevertheless, the inverse probability weighting method holds promise for social psychologists because it provides a straightforward strategy to including information on possible confounders in statistical analysis.

Discussion

This article raises the question of the best method to assess true underlying causal mediation relations among variables. Strong mediation theories in social psychology rely on both statistical and experimental mediation methods. Traditional statistical mediation approaches typically use a randomized experimental design, whereby the estimates of the X to M and X to Y estimate causal relations, but the estimate of the M to Y relation is correlational, thus limiting the ability to infer causality for the M to Y relation, given that unmeasured variables potentially confound the M to Y relation. The approaches described in this article assume randomization to levels of X, though we acknowledge that randomization may be compromised in some settings by missing data, experimenter bias, and imperfect manipulations. Similarly, we did not directly address the issue of measurement error besides mentioning the usefulness of latent variable modeling in structural equation modeling (Ledgerwood & Shrout, 2011; MacKinnon, 2008).

In this article, we described several approaches to improving causal inference from a mediation study. These methods address the problem of how omitted or confounding variables could affect observed mediation relations. We focused on methods that could be used for individual studies though we acknowledge that the accumulation of evidence for a mediation theory requires a program of research. Research design is an important component providing evidence for mediation (Pirlott & MacKinnon, 2013), but any research design needs to address the potential confounding of M on Y when the M to Y relation is correlational.

We discussed two major approaches to enhance causal inference—sensitivity to confounder bias and statistical methods. Researchers can investigate how confounder bias potentially changes observed results via sensitivity analysis. By considering possible confounding variables, researchers can examine whether (a) the size of a confounder effect is large enough to explain the mediated effect, (b) it appears that the mediated effect remains even when considering large confounder effects, or (c) the confounder increased the observed mediated effect. This third type of effect occurs if a confounder had an opposite relation with the mediator and the dependent variable.

Each approach has strengths and challenges. The LOVE plots are likely the most straightforward for social psychologists because investigation of bias as function of a possible correlation between a confounder and the mediating and dependent variables is more familiar than the coefficients for the VanderWeele (2008, 2010) method and the correlated errors of the Imai, Keele, and Tingley (2010) method. The VanderWeele method also requires definition of important coefficients, one relating a possible confounder to the outcome and then the difference in the confounder variable between the control and experimental groups. A strength of the Imai et al. method is that it is included as part of a computer program that computes direct and indirect effects in the potential outcome framework as well as making the plots. The program computes causal estimators for different types of outcome variables such as for a binary dependent variable so it is useful for many different types of variables. Both the Imai et al. and the VanderWeele methods apply to the potential outcome model so they are also relevant for studies with a binary dependent variable. Nevertheless, probably the easiest place for social psychologists to start is the consideration of possible confounders of the M to Y relation and then what are likely correlations between confounders and M and Y so that they can be explored with the LOVE plots.

We also described statistical approaches to improve causal conclusions from a research study including structural equation modeling, instrumental variable methods, principal stratification, and inverse probability weighting. Each of these methods bears different strengths and weaknesses, as summarized in Table 1. Details for each method can be found in the citations in this article. The instrumental variables method requires that all of the effect of the manipulation on Y is through the mediator but not that researchers measure all confounders. The current requirement of a binary mediator and complete mediation reduces the usefulness of the principal stratification method. It is likely that all these methods will be improved and evaluated as researchers seek more accurate estimation of mediation effects in experimental designs.

Table 1.

Summary of Strengths, Weaknesses, and Required Assumptions of Each Technique.

Technique and overview	Strengths	Weaknesses
Comprehensive structural equations models	Requires clarification of when and how variables are related in a comprehensive model	Assumption: Each mediator is measured equally well so that the variance accounted for by each mediator is not due to one variable’s superior measurement
Include measures of all relevant confounding variables in the statistical analysis of mediation	Includes (possibly latent) measures of competing, alternative, and potentially confounding mediators to help identify the true mediator	Assumption: No unmeasured confounders
	X, M, and Y can be continuous or dichotomous although randomization of X is likely dichotomousa
Instrumental variables	Not all confounders need to have been measured	Assumption: Randomization of X leads to changes in M such that the stronger the relation of X to M, the better the instrument. The ideal instrument has a correlation of 1.00 between X with M, which makes X statistically, but perhaps not conceptually, indistinguishable from M
Assuming no direct effect of X on Y, uses the effect of X on M to predict Y from M	X, M, and Y can be continuous or dichotomous although randomization of X is likely dichotomous to represent a random predictor	Assumption: exclusion restriction, is that M completely mediates the effect of X on Y such that when M is considered there is no relation between X and Y.
Principal stratification	Clearly addresses that there are different types of participants with different responses to an experimental manipulation.	Assumption: Monotonicity assumption is made such that there are no backward-changers because it is unlikely that the mediator would change for participants in the control condition because they are unexposed to the experimental manipulation to influence the mediator
Classification of different possible individual response patterns for how X affects M and M affects Y		Assumption: exclusion restriction that the entire effect of the manipulation on the dependent variable is through the mediator. Assumption: X and M dichotomous
Inverse probability weighting	Does not require that the entire effect of X on Y is through M	Assumption: No unmeasured confounders
Use observed covariates to measure confounder effects and adjust analyses to remove the confounder bias	Confounder effects can be removed from the mediated effect, therefore providing a cleaner estimate of the mediated effect

Note: More detail on the methods can be found in the citations for each method.

^aNeed potential outcome approaches for the most accurate estimation of mediation with combinations of categorical and continuous M and Y (Imai, Keele, & Tingley, 2010; Valeri & VanderWeele, 2013) and see also the more recent version of MPIus (Muthen & Muthen 2012) for causal mediation effect estimation in a structural equation modeling framework.

The inverse probability weighting method allows for a large number of variables to be included in the calculation of weights and provides estimates of causal effects in the potential outcome model and does not necessitate that the mediator carries the entire effect of X to Y. However, this method also assumes that researchers measured and included in the weighted analysis all relevant confounders and requires the development of weights for every relation not randomized and or susceptible to confounding.

The easiest of these methods to implement is likely the development of a comprehensive model including measured potential confounders and mediators, and more complex models can be specified in structural equation modeling. However, sample size may limit the number of variables included in a model and the structural equation model estimation is not generally the same as the potential outcomes model. It is also important to note that not all covariates should be included in the comprehensive or inverse probability weighting models and other methods that use covariates. In general, if there is a variable that is caused by the manipulation, then the methods will reduce effects because they will be treated as if they are a confounding variable. Some care must be taken that covariates are variables collected at the baseline and are not affected by the manipulation in a way that will bias mediation estimation. Despite these limitations, comprehensive models and inverse probability weighting are two methods that could be routinely applied by social psychologists.

Our overall goal was to encourage researchers to routinely consider confounders of mediation relations and measure them in research studies. Additional causal inference methods similar to those discussed in this article also exist in development (Manski, 2007), including methods not requiring counterfactuals but lead to similar approaches (Geneletti, 2007), a method called g-estimation that is related to inverse probability weighting (Loeys et al., 2013; Vansteelandt, 2009) and methods based on stochastic probability causal models (Steyer, 2005). The capability of these causal inference approaches for accurate mediation analysis will likely continue to be evaluated over the next decade.

Experimental mediation designs randomizing both X and M present an alternative statistical approach addressing causality when M is measured, yet bears another set of challenges with few demonstrations in the literature (e.g., Word, Zanna, & Cooper, 1974). Although this approach minimizes the risk of confounders in the M to Y relation, it encumbers other challenges regarding experimental manipulation of M (see Bullock et al., 2010), such as the mere manipulation of mediators that occur in the “black box”—attitudes, perceptions, physiology.

As in any research endeavor, the researcher seeks to infer the true state of affairs from a sample of data. Mediation analysis presents a particularly challenging case because researchers can typically randomize only one of the three variables in the mediation theory and randomization of X fails to ensure the causality of M on Y. In psychology and many other disciplines, mediating variables are a cornerstone to scientific progress because they explain how nature operates (Kashy et al., 2009; MacKinnon, 2008; Spencer, Zanna, & Fong, 2005). Modern statistical methods for causal inference are improving and combining these methods with precise experiments addresses the challenge of demonstrating that M causes Y.