Let technology do the work: Improving prediction of massive transfusion with the aid of a smartphone application

Abstract

BACKGROUND

The use of massive transfusion protocols (MTPs) is now common in civilian trauma settings, and early activation of MTP has been shown to increase survival of MTP recipients. Numerous MTP prediction tools have been developed; however, they are often cumbersome to use efficiently or have traded predictive power for ease of use. We hypothesized that a highly accurate predictor of massive transfusion could be created and incorporated into a smartphone application that would provide an additional tool for clinicians to use in directing the resuscitation of critically injured patients.

METHODS

Data from all trauma admissions since the inception of MTP were put in place at Grady Memorial Hospital in Atlanta, Georgia, were collected. A predictive model was developed using the least absolute shrinkage and selection operator (LASSO) and 10-fold cross validation. Data were resampled over 500 iterations, each using a unique and random subset of 80% of the data for model training and 20% for validation.

RESULTS

The trauma registry contained 13,961 cases between 2007 and November 2011, of which 10,900 were complete and 394 received MTP. Of 44 input terms, only the mechanism of injury, heart rate, systolic blood pressure, and base deficit were found to be important predictors of massive transfusion. Our model has an area under the receiver operating curve of 0.96 (against data not used during model training) and accurately predicted MTP status for 97% of all patients. The model accurately discriminated full MTPs from MTP activations that did not meet criteria for massive transfusion. While complex to calculate by hand, our model has been packaged into a mobile application, allowing for efficient use while minimizing potential for user error.

CONCLUSION

We have developed a highly accurate model for the prediction of massive transfusion that has potential to be easily accessed and used within a simple and efficient mobile application for smartphones.

LEVEL OF EVIDENCE

Prognostic/epidemiologic study, level III.

The use of massive transfusion protocols (MTPs) has become common in civilian trauma centers based on published military experience detailing aggressive component therapy and damagecontrol resuscitation.¹ Grady Memorial Hospital (GMH) implemented an MTP in 2007, which, to date, has been used to guide resuscitation in more than 500 patients.² Patients requiring MTP generally have greater injury severity and a significantly higher mortality rate than non-MTP patients, even with the potential benefits of organized implementation of damage-control resuscitation principles using MTPs. Indeed, a recent study evaluated risk factors and system errors associated with mortality within their MTP and found that the only significant predictor for improved survival was early emergency department MTP activation, suggesting a significant need for early prediction of the requirement for massive transfusion.³

A related problem with the use of an MTP is its resource intensive nature. In our center, implementation of the MTP required the blood bank to increase the inventory of prethawed AB plasma, in addition to the preparation of packages before they may be required, which has led to an increased amount of cryoprecipitate wastage. Furthermore, an MTP activation typically requires two blood bank technologists to concentrate solely on preparing and issuing products for the protocol and a dedicated “runner” from the nursing or support staff. These immediate requirements do not take into consideration the administrative efforts such as additional blood bank testing, anesthesia/nursing transfusion documentation, and auditing that must be performed following termination of an MTP. As such, overuse of the protocol leads, globally, to inefficient patient care.

Prediction algorithms within the medical and surgical fields tend to be cumbersome, requiring memorization of scoring systems that use some element of basic mathematics, introducing opportunity for operator error. For ease of bedside use, continuous predictors (i.e., systolic blood pressure [SBP] and heart rate [HR]) are often artificially forced into discrete variables (i.e., HR > 120 or SBP < 90) for easy tally. While improving simplicity, this discretization often reduces predictive power.^4–6 With most medical personnel routinely carrying sophisticated portable computers (smartphones), the need for excessively simplifying algorithms to enable bedside “finger counting” is no longer a requirement. Furthermore, the use of technology to aid clinical judgment is likely to reduce time to procedure activation and calculation error. As such, we hypothesized that a statistically powerful and accurate predictor of massive transfusion could be created and incorporated into a smartphone application that would provide an additional tool for clinicians to use in directing the resuscitation of critically injured patients.

PATIENTS AND METHODS

Data Collection

After institutional review board approval was obtained, data from all trauma admissions since the inception of formal damage-control resuscitation principles was put in place, in the form of an MTP, at GMH in Atlanta, Georgia, were collected.² These data are maintained within the Department of Surgery for Emory University at GMH. All predictive points used were admission values. Base deficit (BD) used was from the first recorded hospital value—generally within 4 hours of admission.

Model Development and Validation

Predictive models in the medical sciences are often developed using statistical techniques known as ordinary least squares (OLS) regressions. While OLS can provide unbiased estimates of model coefficients, this often comes at the expense of increased variances and overfitting, known as a bias-variance tradeoff. By definition, overfitting provides better fits to the specific data set used (R² always increases with model complexity); however, incorporating “noise” by overfitting ultimately reduces predictive power of the model when confronted with new data.⁷

For this study, a supervised regression algorithm was used, termed the “least absolute shrinkage and selection operator” or LASSO. The details of LASSO have been previously described.⁸ Briefly, LASSO performs L1-constrained least squares regressions that reduce overfitting by imposing a “penalty” on each parameter. While introducing a small amount of bias relative to the OLS coefficients, penalization can reduce variance and improve prediction. This penalty effectively shrinks less important variable coefficients to zero, resulting in a reduction in model complexity (the source of overfitting) and retains only important parameters useful for prediction. Thus, LASSO estimates model coefficients while performing a type of model selection, yielding less complex, more interpretable and predictive models.

Tenfold cross-validation was used to tune the magnitude of the penalty (λ) to achieve optimal predictive efficacy.⁹ λ was determined such that deviance over the 10-fold cross-validation was minimized, and λ was increased as much as possible to reduce complexity while keeping model deviance within 1 SD of its minimum, an approach that has been demonstrated to optimize predictions.¹⁰

Improving Efficiency of Data Use

To use data most efficiently while maximizing prediction and performing appropriate model validation, the previously mentioned process was repeated over 500 iterations, each time using a random subset of 80% of the complete data for model training and withholding 20% for model validation. Thus, the final model represents the mean of the model coefficients calculated for each of the 500 iterations.

Model Validation

An important aspect of model validation for predictive models is whether the model was validated against the same data used for training or against new data unseen during model development. For numerous reasons, it is usually erroneous to perform validation against the same data used for training.⁷ Thus, as mentioned previously, a sampling procedure was used, whereby model training and validation were performed on 500 unique samples of the data set, with each run training the model on a randomly chosen subset of 80% of the data and validating on the 20% withheld from the training. Area under the receiver operating curve (AUROC) is calculated as the mean of the AUROCs of these 500 iterations, and each individual run provides an ROC built using data entirely unseen during the particular model training process. Thus, reported AUROC is representative of the sensitivity and specificity of our model to predict MTP given new data and not data used during model development.

Development of a Mobile Application

Given the complexity of the predictive model, performing appropriate calculations by hand to determine expected probability of requiring MTP is infeasible in a hospital setting. We therefore developed a mobile application that can be installed on modern smartphones and requires only that the user input patient values via simple slide bars on the touch screen. For research purposes, such as prospective analyses of MTP activation, the mobile application can be modified to collect patient data and appropriately deliver data directly to a database over the “cloud.” Such a scenario lends itself naturally to the opportunity for the model to continuously train itself, improving with each use that which is submitted to the server. For example, with each new complete case that is submitted to the server, the model can be rerun, coefficients can be slightly modified accordingly, and a slightly updated equation can be inserted automatically into the mobile application, particularly if the application is Web based. While this idea is perhaps unconventional in medical practice, the idea of “machine learning” is quite common in robotics,⁷ engineering science, and the Web-based e-mail services that most people use everyday. Indeed, this type of automated model updating or machine learning will likely continue to become an every increasing component of all industries, including medicine.

Statistical Analyses

All statistical analyses, model development, and model validation were performed using the R statistical environment (R Foundation for Statistical Computing, Vienna, Austria; http://www.R-project.org). Simple unadjusted bivariate comparisons were performed with Student’s t tests. LASSO regression was performed using the “glmnet” package for R,¹⁰ and AUROC were calculated using the “ROCR” package.¹¹

RESULTS

Patient Demographics

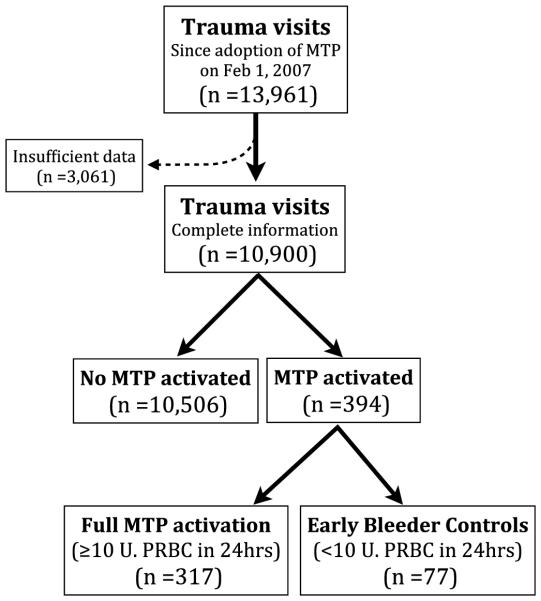
A total of 13,961 trauma activations were identified in the hospital’s trauma registry since the inception of the MTP at GMH in February 2007. Of these, 3,061 patients had missing data critical to the model development process, and these patients were excluded from the analysis (Fig. 1). Of the 10,900 patients included in the analysis, 8,409 (77%) were male, and 394 (3.6%) received MTP. Males were significantly more likely to receive MTP after injury (323 of 8,409, 3.8% males, vs. 71 of 2,491, 2.9% females; p = 0.023), and MTP patients were slightly younger (35.6 years vs. 39.5 years, p < 0.001). On average, MTP patients had significantly worse BDs (−12.7 vs. −4.4, p < 0.001), lower SBP (105 vs. 136, p < 0.0001), increased HR (113 vs. 92, p < 0.0001), and higher Injury Severity Score (ISS) (25.5 vs. 10.3, p < 0.0001). While the greatest number of MTP activations followed blunt trauma, patients with gunshot wounds (GSWs) were most likely to receive MTP (189 of 8,542, 2.2% blunt, vs. 178 of 1,795, 9.9% GSWs; p < 0.0001). Other pertinent demographic data are detailed in Table 1.

Figure 1.

Flow diagram of trauma registry data used in this study.

TABLE 1.

Demographics of MTP and Non-MTP Trauma Visits

	MTP	Non-MTP	p
Demographic	n = 394	n = 10,506	<0.001
Male (%)	82.9	77.0	0.02
Age, mean (SD)	35.6 (14.5)	39.5 (16.3)	<0.001
Pulse rate	113.7 (28.6)	92.2 (20.9)	<0.001
SBP	105.3 (31.1)	136.2 (26.2)	<0.001
BD	−12.7 (6.3)	−4.4 (2.7)	<0.001
ISS	25.5 (13.2)	10.4 (8.9)	<0.001
PRBC given in 24 h	19.4 (13.4)	—
Survival, %	58.1	95.1	<0.001
MOI
Blunt, %	48.0	79.5	<0.001
Age	40.1 (16.3)	41.3 (16.7)	0.320
Pulse	113.5 (29.8)	91.7 (20.7)	<0.001
SBP	103.7 (30.6)	137.4 (26.0)	<0.001
BD	−13.2 (5.5)	−4.3 (2.5)	<0.001
ISS	30.7 (13.7)	10.6 (9.0)	<0.001
PRBC given in 24 h	20.4 (12.8)	—
Survival, %	45.0	95.4	<0.001
GSW, %	45.2	15.4	<0.001
Age	30.3 (12.2)	31.1 (12.2)	0.410
Pulse	115.7 (26.6)	93.6 (22.0)	<0.001
SBP	107.9 (31.1)	132.2 (27.2)	<0.001
BD	−12.1 (6.9)	−4.8 (3.2)	<0.001
ISS	21.2 (10.0)	10.8 (8.2)	<0.001
PRBC given in 24 h	19.0 (13.9)	—
Survival, %	68.6	92.3	<0.001
SW, %	6.8	5.1	0.009
Age	38.9 (11.0)	35.5 (12.4)	0.130
Pulse	101.2 (30.0)	96.1 (20.1)	<0.001
SBP	99.4 (33.6)	129.3 (25.3)	<0.001
BD	−13.7 (7.7)	−5.0 (3.1)	<0.001
ISS	17.8 (14.0)	6.2 (7.2)	<0.001
PRBC given in 24 h	15.8 (14.8)	—
Survival, %	81.5	98.7	<0.001

p values are calculated using Student’s t test for differences in means and two-proportion z test for differences in proportions.

Early Bleeding Control

As previously mentioned, efficient use of an MTP is important in a busy trauma center, and overuse can waste resources. As prediction of massive transfusion is inexact, a proportion of activations will never require massive transfusion by its most accepted definition (10 U of packed red blood cell [PRBC] transfusion in 24 hours). Patients in whom the 10-U minimum was not reached and who survived their resuscitation were considered to have early bleeding control (EBC). Of the 394 MTP activations, 77 achieved EBC (Table 2) and received a mean of 6.4 U of PRBCs in 24 hours versus 22.6 in “appropriate” MTP activations (p < 0.0001). Relative to appropriate MTP activations, EBC had less severe BD (−7.9 vs. −13.9, p < 0.001), higher SBP (112 mm Hg vs. 103 mm Hg, p < 0.0001), and lower ISS (21.9 vs. 26.4, p = 0.002). They were also more likely to occur following MTP activation because of stab wounds (SWs) (10 of 27, 37%) versus blunt trauma (27 of 189, 14%, p = 0.008) or GSW (40 of 178, 22%, p = 0.160).

TABLE 2.

Demographics of EBCs and Complete MTP Activations

	Complete MTP	EBC	p
Demographic, %	n = 317	n = 77	<0.001
Male, %	77.9	90.9	0.023
Age, mean (SD)	36.0 (15.6)	34.0 (12.5)	0.235
Pulse	114.4 (29.7)	110.7 (23.8)	<0.001
SBP	103.6 (31.1)	112.3 (30.0)	0.025
BD	−13.9 (6.2)	−7.9 (4.1)	<0.001
ISS	26.4 (13.5)	21.9 (10.8)	0.002
MOI, n (%)
Blunt, %	162 (51.1)	27 (35.1)	0.012
GSW, %	138 (43.5)	40 (51.9)	0.183
SW, %	17 (5.3)	10 (13.0)	0.018
PRBC given in 24 h	22.6 (13.15)	6.4 (2.16)	<0.001
Survival, %	51.1	87.0	<0.001

p values are calculated using Student’s t test for differences in means and two-proportion z test for differences in proportions.

Predicting Probability of MTP

The predictive model was developed over 500 independent iterations using LASSO and 10-fold cross-validation for choosing model complexity. In each run, the LASSO algorithm reduces less important predictive variables to zero while keeping only variables with greater predictive capacity. Variables initially incorporated into the LASSO algorithm included age, sex, mechanisms of injury (MOIs), ISS, BD, HR, SBP as well as their interactions and second-order terms to account for nonlinearity. Of note, HR and SBP were incorporated into the model as the natural logarithm of the ratio of the two values ${\log }_e\left(\frac{HR}{SBP}\right)$. MOI was coded as three mutually exclusive groups (blunt, GSW, and SW) and one nonmutually exclusive “penetrating” variable, which included GSW and SW. Of all the single variables, interaction terms, and second-order terms (44 in total), LASSO retained eight as optimal for prediction. Of these predictors, BD, BD² and ${\log }_e\left(\frac{HR}{SBP}\right)$ are the most important predictors, with interaction terms between these and the MOI also being important (Table 3). The first half of the predictive model can be represented by the logistic equation:

$$IntermediateProbability=IPr=\frac{e^{\beta \cdot X}}{1+e^{\beta \cdot X}}$$ (Eq. 1)

where β represents the vector of coefficients in Table 3 and X represents the vector of centered and scaled values of each predictor for a given patient. Table 3 provides the fixed values to center and scale each patient variable (e.g., subtract the fixed centering value in Table 3 from the patient value for the respective predictor and then scale by dividing the centered value by the respective scaling factor).

TABLE 3.

Predictor Coefficient and Centering/Scaling Values

	Coefficient		Variable
Predictor	β value	SD	Center	Scale
Intercept	−4.972	0.111	0	1
BD	−1.551	0.101	−4.702	3.280
GSW	0.142	0.224	0	1
Ln(HR / SBP)	0.591	0.060	−0.377	0.340
Ln(HR / SBP) × BD	0.180	0.028	1.451	2.387
BD × GSW	−0.074	0.0001	−0.905	2.693
BD × SW	0.037	0.033	−0.282	1.496
Ln(HR / SBP) × blunt	0.098	0.045	−0.312	0.332
BD2	−0.367	0.058	32.843	62.176

GSW, SW and blunt are coded as 0 (negative) or 1 (positive) for the respective MOI. Center and scale values are based on mean and SDs from the entire data set of 10,900 visits.

To determine probability of requiring MTP given a patient’s IPr value, we fit a logarithmic curve to the proportion of patients in our cohort who received MTP at or above a specified IPr against the full spectrum (0–1) of potential IPr values. The result is a well-fit logarithmic function (R² = 0.97) that describes the probability that a patient will receive MTP given that patient’s calculated IPr. The final model to calculate the probability of MTP for a patient with a set of clinical values, X, for the β co-efficients in the IPr calculation can be written out as follows: Probability (MTP|X) = 0.1473 × 1 n(IPr|X) + 0.791 (Eq. 2). Because a more discrete prediction is often desirable rather than a probability value on a continuous scale, we developed a four-tiered response based on the distribution of patient IPr values. These categories represent relative probability of MTP, namely, very low (IPr < 0.018), low (0.018 ≤ IPr < 0.070), moderate (0.070 ≤ IPr < 0.270), and high (IPr ≥ 0.27).

Predictive Performance and Validation

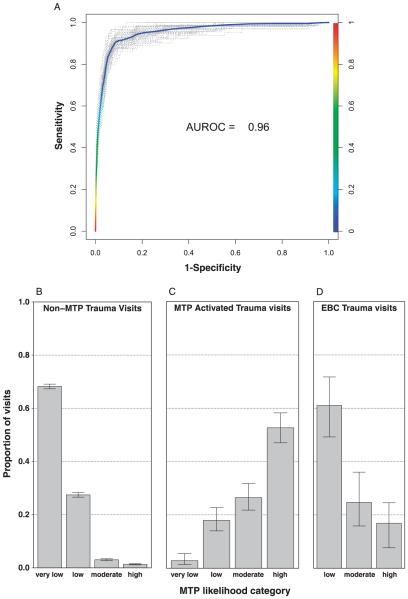
With each iteration used in the model development, we measured the sensitivity and specificity of the model to predict MTP against the random 20% of the data that were left out during that particular iteration. Thus, we report the sensitivity and specificity as the mean of the AUROCs of the 500 iterations, each of which is based on prediction of data entirely unseen during model development. Our model demonstrates very high sensitivity and specificity with an AUROC of 0.96 (95% confidence interval, 0.927–0.983; Fig. 2A). Furthermore, when forcing results out of a continuous “probability of MTP” distribution and into a dichotomous “positive/negative” for MTP result (cutoff IPr of >0.27 for positive MTP), our model correctly predicted MTP status for a mean of 97% of the test cohorts across the 500 iterations.

Figure 2.

Model validation and predictive performance. Model sensitivity and specificity (A) were measured for each of 500 development runs and mean area under the curve of the 500 runs was calculated. For each run, 20% of the data was randomly selected and withheld from model training. Model sensitivity and specificity were measured against this 20% for each run. For ease of visualization, 10% of the 500 runs were randomly chosen and plotted in A. Proportions of non-MTP trauma visits (B), MTP activated trauma visits (C), and EBCs (D) are plotted by their predicted MTP likelihood category. Error bars represent 95% confidence intervals using Wilson’s score method with continuity correction.

Using the four MTP probability categories mentioned previously, the predictive model correctly categorized 95.6% of non-MTP trauma visits as “very low” or “low” and only 3.0% and 1.4% as moderate or high probability of MTP, respectively (Fig. 2B). In contrast, 80.1% of MTP visits were categorized as “high” or “moderate,” with only 17.9% and 2.8% categorized as “low” or “very low” probability of MTP, respectively (Fig. 2C).

Detection of EBC

A fraction of MTP activations (19.5%) do not result in complete massive transfusion (EBC).We sought to determine if our predictive algorithm could differentiate between EBCs and appropriate MTP activations. Indeed, 61.0% of the EBCs were classified as either “low” (44.2%) or “very low” (16.8%), while 24.6% and 14.2% were classified as “moderate” or “high” probability of MTP, respectively (Fig. 2D).

Mobile Application

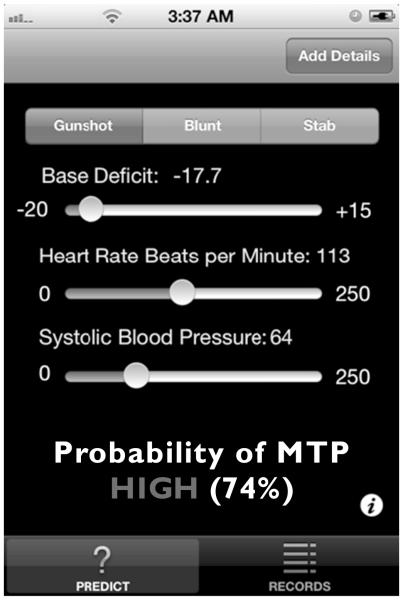
The complexity of the model described previously proibits simple hand calculations at the bedside. We developed a very simple to use mobile application for touch screen smartphones or tablets, which enables rapid assessment of a patient’s likelihood of requiring MTP without the need for recalling cumbersome scoring systems or finger counting. Rather, the practitioner need only to input the MOI, HR, SBP, and BD, and the application performs all of the mathematics, providing the user with a “very low,” “low,” “moderate” or “high” likelihood of requiring MTP as well as the actual probability as predicted by our model (Fig. 3) Furthermore, as briefly discussed previously, by embedding our model into a mobile application, data can be continuously streamed to a database in the “cloud.” With such a setup, there is great potential for the model to be “rerun” with each new case that is uploaded to the server, and in so doing, the model can be set to automatically modify itself slightly—based on the new data. Over time, such a process of “machine learning” can yield an ever increasingly powerful model for prediction purposes.

Figure 3.

Mobile application for MTP prediction: Our model has been packaged into a mobile application that can be installed on modern smartphones. The application requires only that the user input only the method of injury, BD, HR, and SBP and outputs a probability of MTP on both a continuous scale (%) and a categorical scale (high, moderate, low, very low).

DISCUSSION

Clinical decision support tools are ubiquitous within hospital settings. A number of such tools have been developed for early prediction of MTP.^3,12,13 The Trauma Associated Severe Hemorrhage (TASH) and Assessment of Blood Consumption (ABC) scoring systems are perhaps the most widely used. These and numerous other scoring systems have been recently reviewed by Maegele et al.¹⁴ Briefly, the TASH score is based on a 28-point system and incorporates 8 unique variables (hemoglobin, base excess, SBP, pulse, positive FAST, clinically unstable pelvic fracture, open or dislocated fracture, and sex). The continuous variables are discretized and weighted such that more extreme values confer a greater TASH score (e.g., hemoglobin of <12, 11, 10, 9, or 7 add 2, 3, 4, 6, or 8 points to the TASH score, respectively). Once calculated, the TASH score is then placed into a logistic equation to obtain the probability of MTP. The ABC score in contrast is a much simpler four-point system where the presence of each criteria (penetrating mechanism, SBP < 90 mm Hg, pulse > 120 beats/min, and positive FAST finding) adds a single point for a maximum of four points, and each additional point increases the likelihood of massive transfusion. For example, an ABC score of 1 confers a likelihood of approximately 10%, while a 2 gives a likelihood of nearly 40%. The difference between a 2 and a 3 is minimal, with a 3 giving an increase of approximately 5% over a 2, and a 4 gives a reported likelihood of 100%.

These two scoring systems, which have been very useful to clinicians over the years, demonstrate general weaknesses often found in “manual tally” systems, with the TASH score being somewhat cumbersome (and thus could also benefit from incorporation into modern technology) and the ABC score somewhat simplified. Furthermore, the discretization of continuous to categorical variables suggests tradeoff where some amount of predictive power is compromised for increased simplicity and usability.

In an era where nearly every individual on a medical team is carrying powerful technology, in the form of a smartphone or tablet, the need to make the tradeoff between predictive power and simplicity has been greatly reduced. Accordingly, we have used LASSO regression and developed a predictive model that is 97% accurate to predict MTP activation. While, historically, it would not be feasible to use this predictive model at the bedside, it becomes extremely simple, straightforward, and highly efficient when embedded into a smartphone application. Indeed, with the aid of modern technology, any trained or untrained practitioner should be able to determine a patient’s probability of requiring the activation of an MTP, given only a few simple vital statistics for a patient, including the method of injury (blunt, GSW, or SW), HR, SBP, and BD.

While the predictive model described here has been built upon an excellent data source and sound statistics, it is not without its weaknesses. As in every predictive model for MTP, the outcome upon which the model is trained (e.g., MTP positive vs. negative) is based on physician discretion and not on any purely biologic or laboratory outcome. Indeed, the primary reason to develop such a predictive tool is to aid the physician in accurately deciding when and for whom to activate MTP. Thus, our data set undoubtedly contains cases where MTP may have been warranted but was never activated, and inherent in the data exists a certain amount of error in the training outcome that is necessarily incorporated into the model. This is an unavoidable consequence of developing models with outcomes prone to human decision and error. Furthermore, while validation was performed using robust resampling methods so that training and validation were never performed using the same cases, all of the data used for training and validation throughout each iteration originate from a single data set. Thus, it is important to perform further validation on a data set developed within an institution outside of our own and to prospectively evaluate this tool within our own (currently underway) and other institutions.

Increasingly sophisticated clinical decision support tools will become more and more available to clinicians for bedside use. This study demonstrates that such a tool can be designed for prediction of massive transfusion. Prospective validation of this tool is currently being undertaken at our institution. Indeed, as the tool can be modified to routinely learn and update its parameters, it is anticipated that its accuracy will increase over time. At the current time, while we do not advocate that this model or any model for that matter be used as the sole clinical decision making tool, we anticipate that this will be very helpful to support clinical decisions in real time. By providing both an overall probability of MTP for a patient as well as a classification of “very low,” “low,” “moderate” or “high” likelihood of requiring MTP, we feel that the physician will have adequate flexibility to determine how best to use the results of the application with each patient. Furthermore, because 17.9% of MTP activations were classified as “low” and 2.8% as “very low” while only 3.0% and 1.4% of non-MTP patients were classified as “moderate” or “high” probability of MTP, respectively, the model demonstrates superior ability to rule out (vs. rule in) MTP in a given patient. Either way, however, our model, when embedded into a mobile application, will provide the clinician with a very fast, simple-to-use aid to support clinical decisions regarding whether to activate MTP. Moreover, because our model demonstrated ability to classify approximately 60% EBCs as “low” or “very low” probability of requiring MTP, use of our model and application may provide further discriminatory power to reduce unnecessary activation of MTP. Because time to MTP activation is one of the most important factors for patient outcome and overuse is a strain on already overtaxed resources, accurate and highly efficient prediction will be an important tool to increase survival in trauma patients.