Abstract
The regulation of glucagon secretion in the pancreatic α-cell is not well understood. It has been proposed that glucose suppresses glucagon secretion either directly through an intrinsic mechanism within the α-cell or indirectly through an extrinsic mechanism. Previously, we described a mathematical model for isolated pancreatic α-cells and used it to investigate possible intrinsic mechanisms of regulating glucagon secretion. We demonstrated that glucose can suppress glucagon secretion through both ATP-dependent potassium channels (KATP) and a store-operated current (SOC). We have now developed an islet model that combines previously published mathematical models of α- and β-cells with a new model of δ-cells and use it to explore the effects of insulin and somatostatin on glucagon secretion. We show that the model can reproduce experimental observations that the inhibitory effect of glucose remains even when paracrine modulators are no longer acting on the α-cell. We demonstrate how paracrine interactions can either synchronize α- and δ-cells to produce pulsatile oscillations in glucagon and somatostatin secretion or fail to do so. The model can also account for the paradoxical observation that glucagon can be out of phase with insulin, whereas α-cell calcium is in phase with insulin. We conclude that both paracrine interactions and the α-cell's intrinsic mechanisms are needed to explain the response of glucagon secretion to glucose.
Keywords: insulin, pancreatic α-cell, glucagon, islet, somatostatin, pancreatic δ-cell
pancreatic islets consist of three main endocrine cell types that work together to control glucose homeostasis: α-cells, β-cells, and δ-cells. Pancreatic α-cells release glucagon primarily in response to low blood glucose levels, whereas pancreatic β-cells secrete insulin when blood glucose is elevated. Pancreatic δ-cells release somatostatin, which is an inhibitor of both insulin and glucagon secretion. Although glucose-stimulated insulin secretion is relatively well understood, glucose suppression of glucagon secretion remains a puzzle (28).
Does glucose suppress glucagon secretion directly through intrinsic mechanisms or indirectly through extrinsic mechanisms? This question is part of an ongoing debate in α-cell dynamics. There is evidence that islet cells release a variety of factors that can modulate glucagon secretion, such as insulin (53, 68), Zn+ (22, 41), γ-aminobutyric acid (GABA) (23, 64, 79), and somatostatin (24, 34, 72). However, paracrine regulators do not inhibit secretion below the basal rate (28), and glucagon secretion is maximally suppressed at glucose concentrations that are too low to stimulate insulin or somatostatin secretion (66, 77). These data point to a role for intrinsic regulation at low glucose concentrations. There is evidence that glucose can directly regulate glucagon secretion through ATP-sensitive K+ channels (KATP) (26, 31, 52, 82) or a store-operated current (SOC) (50, 76).
Previously, we investigated intrinsic mechanisms of regulating glucagon secretion and showed that both KATP channels and SOC are capable of suppressing glucagon secretion, albeit in different ways (78). Following the hypothesis of Zhang et al. (82), KATP channels suppress secretion in the model by closing when glucose raises the ATP/ADP ratio, as in β-cells. In contrast to β-cells, however, the resulting depolarization reduces spike amplitude by inactivating Na+ and Ca2+ channels. This decreases Ca2+ influx and reduces glucagon secretion. Following the hypothesis of Liu et al. (50), glucose regulates glucagon secretion in the model through SOC by activating the sarcoendoplasmic reticulum calcium ATP ase (SERCA), which pumps Ca2+ in to the endoplasmic reticulum (ER). When glucose is elevated, the ER fills, turning off SOC, and the consequent hyperpolarization reduces secretion (50). Although the electrical effects of the two mechanisms are opposite, we proposed that SOC and KATP work together to modulate glucagon secretion. For that model of α-cell dynamics, we neglected the role of paracrine inhibitors of glucagon secretion to focus on the intrinsic mechanisms.
In this study, we investigate how insulin and somatostatin can regulate glucagon secretion by combining previously published mathematical models of α-cells (78) and β-cells (5, 6) with a new model of δ-cells to create an islet model: the β/α/δ (BAD) model. We show that the model can reproduce experimental data demonstrating that the inhibitory effect of glucose remains even when paracrine modulators do not act on the α-cell. Based on this finding, we conclude that the role of paracrine interactions in the islet is to modulate the α-cell's intrinsic response to glucose. We also demonstrate how paracrine interactions synchronize α-cells to produce pulsatile oscillations in glucagon secretion. We find that the pancreatic β-cells serve as a pacemaker for the islet to drive oscillations in glucagon and somatostatin secretion.
MATERIALS AND METHODS
Model.
The BAD model for pancreatic islets contains one representative cell of each type (extended to several α-cells for Fig. 12) as well as the interactions between them (Fig. 1). β-Cells are coupled by gap junctions, allowing individual β-cells to synchronize. Therefore, the model β-cell represents all of the β-cells in the islet. However, α- and δ-cells are not coupled by gap junctions, so the α- and δ-cells in the model represent the average behavior of the cells of their respective types, which may all be doing different things.
Fig. 12.
A and B: if glucagon is secreted from 5 uncoupled α-cells, total glucagon secretion is flat. Paracrine effects are suppressed by fixing to 0, r−2a to 0.001, and to 2.7 nS. C and D: however, if the same cells are coupled by paracrine effects, total glucagon secretion is oscillatory. α-Cell heterogeneity was modeled by having different JGK and κ values for the 5 α-cells: JGK,a1 = 0.2, JGK,a2 = 0.1, JGK,a3 = 0.15, JGK,a4 = 0.25, JGK,a5 = 0.3, κa1 = 0.003, κa2 = 0.005, κa3 = 0.003, κa4 = 0.005, and κa5 = 0.003.
Fig. 1.
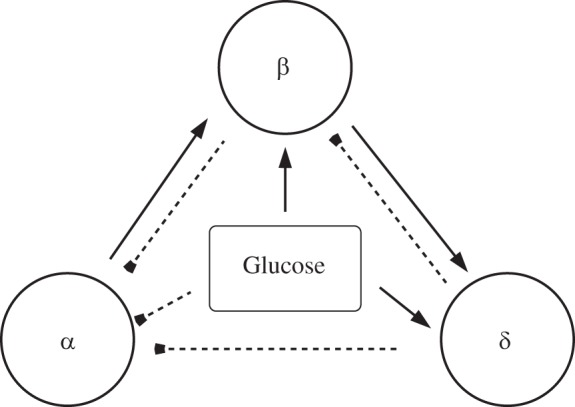
Paracrine interactions among α-, β-, and δ-cells in the pancreatic islet. Solid lines with arrowheads indicate stimulation; dashed lines with blunt ends indicate inhibition. Glucose is assumed to directly affect all islet cells.
Pancreatic β-cells secrete by exocytosis of insulin-containing granules, which involves a cascade of complex steps such as docking, priming, fusing, and release of insulin. A detailed kinetic model for insulin secretion that includes these processes was developed by Chen et al. (14). We now add this model of exocytosis to the dual-oscillator model for pancreatic β-cells described previously by Bertram and colleagues (5, 6). The dual-oscillator model contains three interacting components, electrical/Ca2+, glycolytic, and mitochondrial, that combine to produce slow oscillations in membrane potential, cytosolic Ca2+, and metabolism. With the addition of the exocytosis model, insulin secretion also oscillates. For some simulations (Figs. 3–7) that do not involve oscillations, a simplified electrical spiking model was used.
Fig. 3.
Voltage, calcium, and insulin secretion for 1 (A–C), 7 (D–F), and 11 mM glucose (G–I). The β-cell is hyperpolarized in 1 mM glucose (A). Calcium and secretion are low (B and C). Raising glucose (7 mM) depolarizes the cell (D), causing an increase in calcium (E) and insulin secretion (F). Finally, raising glucose further (11 mM) increases the frequency and amplitude of the spikes (G). More calcium enters the cell, and more insulin is secreted (H and I).
Fig. 7.
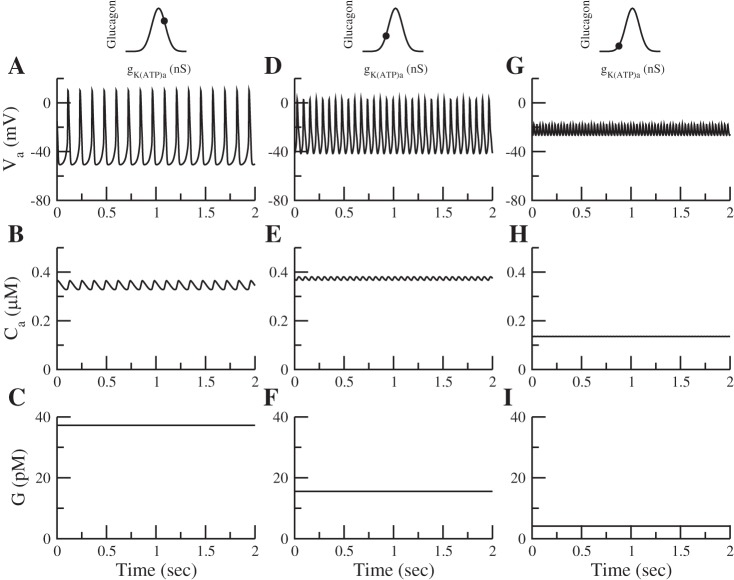
Glucose can inhibit glucagon secretion through store-operated current (SOC) independently of KATP channels, somatostatin, and insulin. A: glucose can inhibit secretion in islets without functional KATP channels (solid curved line) and in islets without functional KATP channels or somatostatin (dashed curved line). B: = 0.025 nS, as in Fig. 6. In G1, kSERCA = 0.05 ms, making gSOC ≈ 0.015 nS. In G7, kSERCA = 0.5 ms, making gSOC decrease to 0. is replaced by a constant background K+ conductance of 0.3 nS, and g KATPd is replaced by a constant K+ conductance of 0.29 nS. Somatostatin secretion is assumed to respond to glucose via a KATP-independent amplifying factor (see Eq. A19 in the appendix) (81). Relation of KATP conductance to the bell-shaped curve is the same as in Fig. 5.
The α-cell model is taken from Watts and Sherman (78). The contribution of KATP channels to glucagon secretion is the same as in this study (78). Figure 2A shows the behavior of the α-cell as a function of the KATP conductance, gKATPa; the subscripted letter a denotes that this is the conductance in the α-cell. The lines in Fig. 2A represent constant voltages, and the circles represent the minimum and maximum voltages during spiking. Starting on the far right, as gKATPa is decreased, action potentials are produced. A further decrease in gKATPa decreases the amplitude of the action potential. Figure 2B reprises from Watts and Sherman (78) the fundamental feature of α-cell secretion; as gKATPa decreases, glucagon secretion first increases and then decreases. The increase is due to the initiation of spiking, whereas the decrease results from reduced spike amplitude, and ultimately loss of spiking, as Na+ and Ca2+ channels inactivate.
Fig. 2.
A and C: diagrams showing the repertoire of behaviors of the α-cell (A) and δ-cell (C) models as a function of the ATP-sensitive K+ channel (KATP) conductance. Line represents constant voltages, and ○ and ● represent stable and unstable spiking oscillations, respectively. Corresponding pairs of lower and upper circles represent the minimum and maximum voltages during spiking. B: as glucose increases, gKATPa decreases and glucagon secretion first increases then decreases. D: as gKATPd decreases, somatostatin secretion increases monotonically.
The contribution of SOC (not shown) is qualitatively the same as in Watts and Sherman (78), but the conductance has been made an order of magnitude smaller; we show below that this is sufficient to account for data on secretion in the absence of KATP channels and when SERCA is blocked. At very low gKATPa, the cell settles on a depolarized plateau that does not support secretion.
Finally, we have added a kinetic model of exocytosis similar to the one used for the β-cells. Adding the exocytosis model was necessary to correctly model the inhibition of granule priming by somatostatin, as described below (see Eq. 10).
The δ-cell model is adapted from the α-cell model. We have removed the T-type Ca2+ current, which is absent in mouse δ-cells (26), and modified the parameters of the remaining ionic currents to shift the dependence of the electrical activity to the left. The dependence of the electrical activity as a function of the δ-cell KATP conductance, gKATPd, is shown in Fig. 2C. As in the α-cell, action potentials are produced when gKATPd is decreased, but there is limited inactivation even when KATP conductance is 0. As a result, somatostatin secretion monotonically increases as gKATPd decreases (Fig. 2D). Accordingly, somatostatin secretion increases monotonically with glucose. Somatostatin secretion is modeled as a function of microdomain Ca2+ (Eq. A18 in the appendix). The above changes are the minimal ones needed to make the dose-response curve monotonic, but the model should be considered provisional, as it does not include important features such as R-type calcium channels and calcium-induced calcium release (81).
Equations not described here for the three cell types are located in the appendix. The parameters of the β-cell and δ-cell can be found in Tables 1 and 2, respectively. Although each cell type has its own set of electrical, calcium, and secretion equations, we make the simplifying assumption that insulin, glucagon, and somatostatin are secreted into a common, well-mixed space. The concentrations of insulin (I), glucagon (G), and somatostatin (S) in this compartment are given by the following equations:
| (1) |
| (2) |
| (3) |
Table 1.
Parameters for the β-cell
| Parameter | Value |
|---|---|
| gK(Ca),b | 280 pS |
| k4,b | 150 |
| sm,b | 10 |
| gK,b | 1,800 pS |
| kPMCA b | 0.2 ms−1 |
| B | 1 ms−1 |
| nCa,b | 590 |
| vm,b | −6 mV |
| gCa,b | 7 pS |
| τn | 5 ms |
| JGK,b | 0.4 μM ms−1 |
Table 2.
Parameters for the δ-cell
| Parameter | Value |
|---|---|
| gNa,d | 5 nS |
| gKA,d | 0.5 nS |
| vCaPQ,d | −15 mV |
| NPQ | 0.1 |
| fV pq,d | 0.00226 |
| gCaPQ,d | 0.7 nS |
| gK.d | 7.5 nS |
| kPQ | 40 |
| fVl,d | 0.00340 |
| Bas | 0.0009 |
where JIS is the rate of insulin secretion, JGS is the rate of glucagon secretion, JSS is the rate of somatostatin secretion, vc is the volume of the compartment, and fb, fa, and fd are the rates of hormone clearance from the compartment. Because the parameters, especially the effective compartment sizes and clearance rates, are not known, we have chosen them to allow hormone concentrations to build up and decay on the time scale of oscillations in Figs. 9, 10, and 12. Figure 11 shows that no oscillations are seen if those constraints are violated.
Fig. 9.
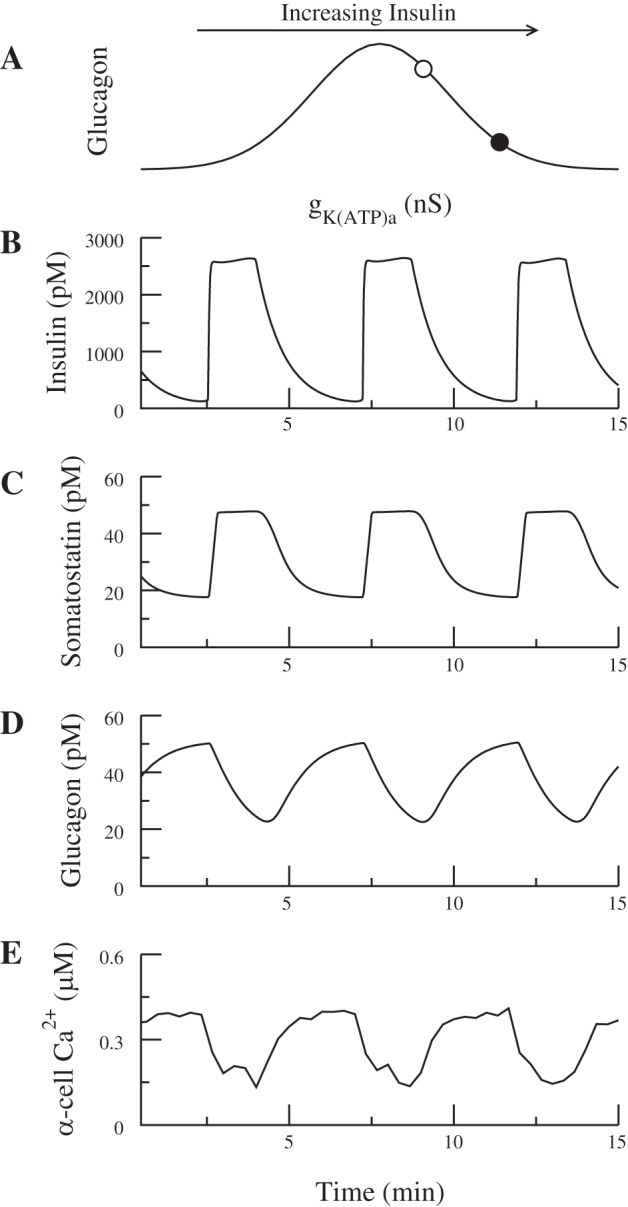
Oscillatory insulin secretion acts as a pacemaker to synchronize hormone oscillations. A: the α-cell is assumed to have gKATPa on the right side of the schematic bell-shaped dose-response curve (○). Insulin lowers α-cell Ca2+ when it increases gKATPa and decreases glucagon secretion (●). B and C: in-phase insulin and somatostatin secretion. D and E: both Ca2+ and glucagon are anti-phase with insulin. In this simulation ka = 0.0889, ra = 0.1, = 7,000 pS, and gKATPd = 0.26 nS. As insulin oscillates, gKATPa varies between 0.24 and 0.28 nS.
Fig. 10.
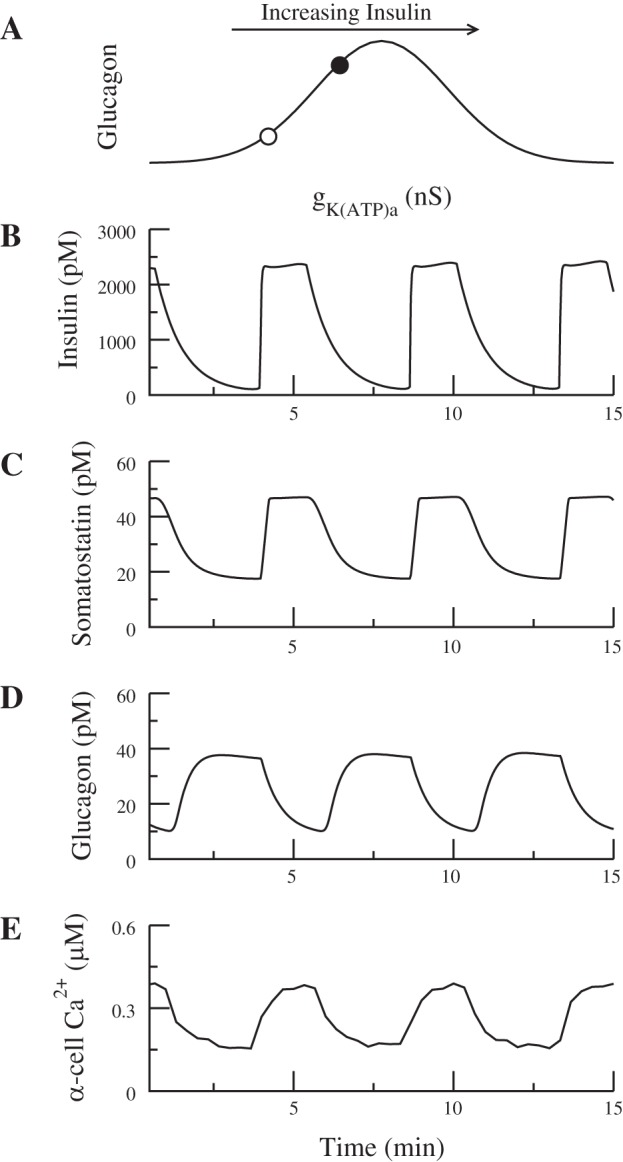
A: in elevated glucose, the α-cell is assumed to have gKATPa on the left side of the schematic bell-shaped dose-response curve (○); insulin increases α-cell Ca2+ by increasing gKATPa (●). B and C: in-phase insulin and somatostatin secretion. D and E: somatostatin suppresses glucagon secretion by a direct effect on exocytosis, which trumps the rise in Ca2+ so that glucagon is anti-phase with insulin. In this simulation, ka = 0.0148, ra = 5, = 7,000 pS, and gKATPd = 0.26 nS. As insulin oscillates, gKATPa varies between 0.04 and 0.08 nS (compare with Fig. 2A).
Fig. 11.
A–C: glucagon oscillations may not be observed if the turnover of hormones is too rapid. For this simulation, the parameters for the flux out of the compartment were increased for all 3 hormones. (fb = 5,000, fa = 300, fd = 0.006, = 7,000 pS, and gKATPd = 0.26 nS). D–F: glucagon does not oscillate if β-cells exhibit fast bursting oscillations. Note the time scale is now in seconds. [gK(Ca) = 500 pS, JGK = 0.8, = 8,500 pS, and gKATPd = 0.26 nS]. Relation of KATP conductance to the bell-shaped curve is the same as in Fig. 10.
Next, we describe the interactions between the cells that are included in the model. The β-cell modifies glucagon secretion by increasing KATP channel activity (22, 48); therefore, the conductance of the α-cell KATP channels (gKATPa) depends on the concentration of insulin in the common space. The equation for gKATPa is
| (4) |
where EffIa is the effect of insulin on the α-cell and is the maximal conductance of the KATP channels. EffIa is an increasing function of insulin and is given by the following phenomenological equation
| (5) |
We neglect the recently described additional effect of insulin to lower cAMP (18), which is subsumed under the effects of somatostatin (see below). The implications of a separate effect of insulin on cAMP are addressed in the discussion.
There is also evidence that the β-cell stimulates somatostatin secretion (13). Moreover, one of the implications of our simulations is that synchrony between insulin and somatostatin is only possible if β-cells stimulate δ-cells. One possible mechanism is a Cl− channel activated by GABA. It has been shown in both rat and human islets that GABA is coreleased with insulin in large, dense core granules (10, 11).
For simplicity, instead of adding equations for GABA, we model the conductance of the GABA current as depending on insulin concentration in the compartment. IGABA is given by the following equation:
| (6) |
where EffId is the effect of GABA on the δ-cell, is the maximal conductance of the GABA channel, and vGABA is the reversal potential. Because GABA is coreleased with insulin, we assume that GABA is an increasing function of insulin and model EffId by the following phenomenological equation
| (7) |
Somatostatin inhibits insulin and glucagon secretion by reducing cAMP, which works primarily through a direct effect to reduce exocytosis but secondarily through activation of G protein-coupled inwardly rectifying potassium (GIRK) channels (15, 29, 30, 34, 42, 80). The GIRK current IGIRKx is given by the following equation
| (8) |
where x = a or b for the α- or β-cell, respectively, EffSx is the effect of somatostatin, is the maximal conductance of GIRK, and vGIRK is the reversal potential. EffSx is an increasing function of somatostatin and is given by the following phenomenological equation
| (9) |
Somatostatin inhibits exocytosis both by inhibiting adenylate cyclase, which lowers cAMP levels (16, 70), and through a pathway independent of cAMP (29, 42). In the model, somatostatin inhibits exocytosis by increasing the parameter that governs the rate of depriming of granules, r−2x, where x = a or b for α- or β-cell, respectively. The equation for r−2x is
| (10) |
Similar results would be obtained if somatostatin were assumed to reduce the rate of priming r2x. See Eq. A6 in the appendix for additional equations governing exocytosis.
cAMP likely has other effects on ion channels, especially calcium channels, which may be helpful for explaining the regulation of glucagon secretion by acetylcholine and glucagon-like peptide-1 (56) but are not needed here.
Glucagon increases insulin secretion by increasing cAMP levels (40, 67, 70). In the model, glucagon increases the parameter that governs the rate of priming granules, r2,b. The equation for r2,b is
| (11) |
Similar results would be obtained if glucagon were assumed to increase the rate of resupplying granules, r3,b (see Eq. A7 in the appendix). Parameters for the paracrine interactions are in Table 3.
Table 3.
Parameters for paracrine interactions
| Parameter | Value |
|---|---|
| fb | 2,000 |
| fd | 0.003 |
| vGABA | 0 mV |
| ḡGIRK,b | 10 pS |
| ra | 4.5 s−1 |
| fa | 150 |
| ḡGABA | 0.1 nS |
| ḡGIRK,a | 0.025 nS |
| VGIRK | −80 mV |
| rb | 0.002 s−1 |
In human islets, it has been reported that α-cells modulate insulin secretion by secreting acetylcholine (55, 63). We have not modeled this here, as the effects would be very similar to those of glucagon in the cases we simulate, where both would increase insulin secretion when α-cells are active. However, it would be important for other situations, such as selective loss of one of those receptors on β-cells.
The differential equations were solved numerically with the variable step size method CVODE implemented in the XPPAUT software package (19) with absolute and relative tolerances 10−10.
RESULTS
Model responses to different levels of glucose.
To test the model's response to changing glucose levels, we simulated the voltage, calcium, and secretion from each cell type for 1, 7, and 11 mM glucose (Figs. 3–5). The change in glucose was modeled as a decrease in the conductance of the KATP channels for each cell type and an increase in the rate of the SERCA pump (kSERCA) in the α-cell. The parameter values used for these simulations are shown in Table 4. For simplicity, we consider a case in which the β-cells have spiking activity but no slow metabolic oscillations.
Fig. 5.
Voltage, calcium, and glucagon secretion for 1 (A–C), 7 (D–F), and 11 mM glucose (G–I). A: the α-cell is electrically active in low glucose. B and C: both calcium and secretion are high. D: raising glucose (7 mM) reduces the amplitude of the spikes. E and F: calcium is unchanged, whereas glucagon secretion is decreased. G–I: increasing glucose more (11 mM) causes depolarized small spikes (G), a reduction in calcium (H), and a further reduction in secretion (I). Schematic of glucagon secretion rate vs. KATP conductance and KATP level for corresponding level of glucose is shown at top (●).
Table 4.
| G1 | G7 | G11 | |
|---|---|---|---|
| 3 nS | 0.6 nS | 0.15 nS | |
| gKATPb | 150 pS | 85 pS | 25 pS |
| gKATPd | 0.29 nS | 0.27 nS | 0.18 nS |
| kSERCA | 0.05 | 0.5 | 0.5 |
G1, 1 mM glucose; G7, 7 mM glucose; G11, 11 mM glucose; KATP, ATP-sensitive K+ channel; SERCA, sarcoendoplasmic reticulum calcium ATP ase.
The β-cell is electrically silent in low glucose (Fig. 3A). Raising glucose depolarizes the cell and produces electrical activity (Fig. 3D). Action potentials bring in calcium, and insulin is secreted (Fig. 3, E and F). A further increase in glucose further increases spike frequency, cytosolic calcium, and insulin secretion (Fig. 3, G–I).
The δ-cell has a similar response to glucose (Fig. 4). In low glucose, the δ-cell is silent (Fig. 4A) but still has some basal secretion (Fig. 4C). Increasing glucose depolarizes the cell (Fig. 4D), increases calcium influx (Fig. 4E), and increases somatostatin secretion (Fig. 4F). Increasing glucose further increases the frequency of spiking (Fig. 4G), causing an increase in calcium and secretion (Fig. 4, H and I).
Fig. 4.
Voltage, calcium, and somatostatin secretion for 1 (A–C), 7 (D–F), and 11 mM glucose (G–I). The δ-cell is silent in 1 mM glucose (A). Calcium is low (B), but there is a basal level of secretion (C). Raising glucose (7 mM) depolarizes the cell (D), raises calcium (E), and increases somatostatin secretion (F). Finally, raising glucose even further (11 mM) increases the frequency of the spikes (G). Calcium influx and somatostatin secretion increase further (H and I).
We have chosen KATP conductance in low glucose to be near the peak of the dose-response curve for glucagon secretion (see Fig. 2D and the schematic insets in Fig. 5). With this choice, glucagon secretion generally decreases with glucose (Fig. 5C). In 1 mM glucose, the α-cell produces large-amplitude spikes (Fig. 5A) and releases glucagon (Fig. 5C). Raising glucose decreases the amplitude of the spikes (Fig. 5D). Although calcium is roughly the same (Fig. 5E), glucagon secretion decreases (Fig. 5F). This decrease is due to the closure of P/Q-type calcium channels, which have been linked to glucagon secretion and the inhibitory effects of insulin and somatostatin. Increasing glucose more causes small depolarized spikes (Fig. 5G), a reduction in calcium, and a further reduction in secretion (Fig. 5, H and I). The decrease in spike amplitude with glucose has been seen experimentally (31, 82).
Effect of somatostatin on glucagon secretion.
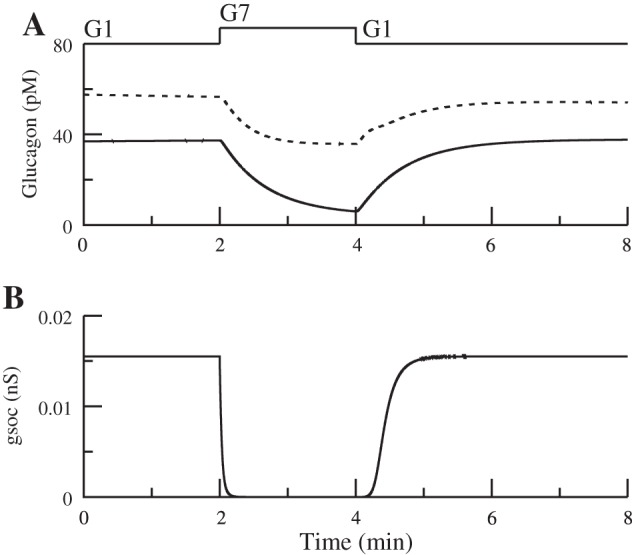
The role of somatostatin as an inhibitor of glucagon secretion was recently studied in vitro (15) using somatostatin-knockout islets (Sst−/−). It was shown that the absence of somatostatin resulted in an overall increase in glucagon secretion, but the inhibitory effect of glucose remained. Our model can reproduce the main features of this experiment, as shown in Fig. 6. In Sst+/+ islets, increasing glucose from 1 (G1) to 7 mM (G7) decreases glucagon secretion (Fig. 6A, solid line) while increasing somatostatin and insulin secretion (Fig. 6, B and C). Although glucagon secretion is higher in Sst−/− islets, glucose is still able to inhibit secretion (Fig. 6A, dashed line). Sst−/− islets are modeled by fixing to 0 and r−2x to 0.001, removing the effects of somatostatin from the islet. Increasing the glucose concentration decreases the conductance of the KATP channels for all three islet cell types. For this simulation, we again assume for simplicity that there are no metabolic oscillations and that KATP conductance is constant. Therefore, the change in glucose concentration was modeled as a change in , gKATPb, and gKATPd, where
Fig. 6.

Somatostatin tonically inhibits both glucagon and insulin secretion. In Sst+/+ islets (solid curved line), increasing glucose decreases glucagon secretion (A) while increasing somatostatin (B) and insulin secretion (C). Although insulin and glucagon are both higher in Sst−/− islets (dashed curved line; A and C), glucose still retains its inhibitory effect on glucagon secretion (compare with the 4th figure in Ref. 15). Parameters are as follows for 1 mM glcuose (G1): = 3 nS, gKATPb = 150 pS, gKATPd = 0.29 nS, and kSERCA = 0.05; for 7 mM glucose (G7): = 0.6 nS, gKATPb= 85 pS, gKATPd= 0.27 nS, kSERCA = 0.5, and = 0.025 nS throughout. Relation of KATP conductance to bell-shaped curve is the same as in Fig. 5.
x = a, b, and d, and gKATPa is given by Eq. 4).
Pancreatic α-cells have also been proposed to contain a SOC, which is affected by increasing glucose. SOC is an inward current with a conductance that decreases as ER Ca2+ increases:
| (12) |
where cer∞ represents Cer-dependent activation. In low glucose the ER is relatively depleted because of limited SERCA activation. Increasing glucose activates SERCA and fills the ER, which reduces SOC. This effect of SERCA activity was modeled by a change in the rate of SERCA pump activity, kSERCA (see Eq. A11 in the appendix). Although somatostatin no longer affects the islets in this simulation, glucose still inhibits glucagon secretion through the closure of KATP channels, the inactivation of a SOC, and insulin.
Although SOC is present in Fig. 6, it does not play a major role in reducing glucagon secretion, but another experiment (15) showed that glucose still suppressed glucagon secretion in the absence of KATP channels and somatostatin, using SUR1−/− islets and pertussis toxin. Based on this data, it was argued that there exists another mechanism that contributes to glucose suppression of glucagon secretion. We proposed previously (78) that this unknown mechanism is SOC, and we now extend this by including paracrine effects. In addition, we found that SOC can be effective even with much smaller conductance (0.015 nS) than was used by Watts and Sherman (78).
The first step in modeling SUR1−/− islets is to remove the KATP current. However, in the absence of any other change, this would result in α-cells that are permanently depolarized. We propose that some other K+ conductance must be upregulated to prevent this from happening. Therefore, we replaced KATP with a constant K+ conductance (0.28 nS). Figure 7A shows that glucose can suppress secretion in the absence of KATP channels both with (solid line) and without (dashed line) the inhibitory effect of somatostatin by deactivating SOC current. Figure 7B shows that only a small SOC current is needed; it is sufficient to assume that gSOC is ∼0.015 nS in 1 mM glucose and decreases to zero in 7 mM glucose.
The simulations of Figs. 6 and 7 suggest that, although somatostatin and insulin have large effects on α-cells, these paracrine factors are not themselves responsible for the glucose sensitivity of glucagon secretion. We address this further in the discussion.
Disturbed glucagon secretion in diabetes.
Recently, biobreeding diabetic rats, an animal model of type 1 diabetes (T1D), were used to investigate impaired counterregulation of glucagon secretion during hypoglycemia (44). In the diabetic rats, glucagon secretion was reduced during hypoglycemia, but somatostatin receptor antagonism restored glucagon secretion to the level of the control rats.
To investigate this, we assume that intrinsic glucose sensing by α-cells and central nervous system signaling are intact in T1D and ask how a loss of insulin secretion would affect glucagon secretion. As in Fig. 5, we assume that glucagon secretion decreases when glucose is raised. In this configuration, insulin, provided its main effect is to open KATP channels, would increase glucagon secretion in 7 mM glucose, and its loss would do the opposite. If this were the only consequence of losing insulin, postprandial glucagon would go down, whereas it was observed to increase in T1D (12, 60, 74). However, in our model, loss of β-cell activity would also reduce somatostatin secretion (Fig. 1). We choose paracrine parameters such that the latter effect dominates and glucagon is above normal (G7 responses in Fig. 8).
Fig. 8.
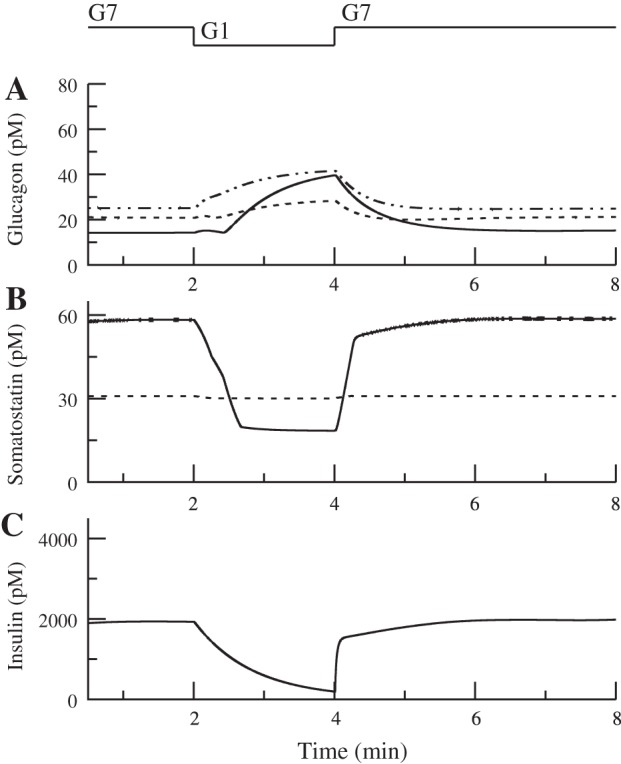
In control islets, reducing glucose from 7 to 1 mM decreases somatostatin and insulin secretion (solid curved line; B and C) and increases glucagon secretion (solid curved line; A), as shown by the intraislet hormone concentrations. In the absence of insulin, corresponding to severe diabetes, somatostatin is below control in G7 and above control in G1 (dashed line; B). In this case, the basal level of somatostatin was increased (bas = 0.0015). Glucagon secretion is above control in G7 and below control in G1 (dashed line; A). Blocking somatostatin receptors increases glucagon secretion, especially in G1 (dotted and dashed line; A). Relation of KATP conductance to the bell-shaped curve is the same as in Fig. 5.
Achieving reduced glucagon secretion at low glucose in T1D is more subtle. The loss of insulin would have little or no effect on glucagon and somatostatin secretion in 1 mM glucose. Therefore, we assume, as argued in Karimian et al. (44), that somatostatin secretion is exaggerated in T1D, possibly because the number of δ-cells is increased (see G1 responses in Fig. 8B) (71). With this assumption added, the model exhibits both reduced glucagon secretion in low glucose and increased glucagon secretion in high glucose. It also reproduces the findings in Karimian et al. (44) that glucagon secretion in low glucose can be restored by blocking somatostatin receptors (see G1 responses in Fig. 8A; also see the discussion for consideration of other possibilities).
Synchronized hormone oscillations.
We now investigate the role of paracrine effects in hormone oscillations, which have been recorded in high glucose (20 mM) in both isolated islets and the perfused rat pancreas (27, 36, 37, 65). Insulin and somatostatin oscillate in phase with each other but out of phase with glucagon. To study this, we now include a glycolytic oscillator in the β-cells to drive insulin oscillations (see Eq. A4 in the appendix).
Pulsatile insulin secretion depends on two distinct characteristics of β-cells. First, insulin secretion is driven by an intrinsic oscillatory mechanism dependent on glucose metabolism and ion channels (4, 73). Second, within an islet, individual β-cells are coupled to neighboring β-cells by gap junctions (2, 3, 35).
This coupling allows the β-cells to secrete in synchrony, and the intrinsic oscillation makes the secretion pulsatile. Glucagon and somatostatin secretion are not pulsatile without the influence of insulin because the α-cell and δ-cell models lack an intrinsic slow oscillator and can only produce spikes of action potentials. Although Ca2+ oscillations have been observed in α-cells (7, 8, 57, 61), these cells are not coupled by gap junctions like β-cells and are not synchronized. Below (Fig. 12), we come back to the possibility that α-cells contain an intrinsic oscillatory mechanism, but first we examine whether paracrine interactions alone can account for oscillations in glucagon and somatostatin.
In the model, glucagon secretion is influenced both indirectly through the postulated effects of insulin to open KATP chanels and directly by the postulated effect of somatostatin to inhibit exocytosis (Fig. 1). Somatostatin is always inhibitory, independent of glucose concentration, but the direction of the insulin effect is ambiguous. That is, the relationship between KATP conductance and glucagon secretion was shown to be a bell-shaped function of the prevailing KATP conductance (82). The intrinsic response of the isolated α-cell in the model similarly produces a bell-shaped curve as gKATPa is varied, as shown in Watts and Sherman (78) and repeated here in Fig. 2A. Thus, a glucose-mediated decrease in gKATPa or an insulin-mediated increase in gKATPa can either increase or decrease glucagon secretion, depending on the starting gKATPa level.
In Fig. 9A (○), gKATPa is chosen such that it is on the right side of the glucose dose-response curve. Then, increasing insulin lowers α-cell Ca2+ and decreases secretion (Fig. 9A, ●). Consequently, both glucagon secretion and α-cell Ca2+ are anti-phase with insulin (Fig. 9, D and E). Also, because of the stimulatory effect of the β-cell on somatostatin secretion, insulin and somatostatin oscillate in phase with each other (Fig. 9, B and C).
A recent study, however, reported that α-cell Ca2+ is in phase with β-cell Ca2+ at 20 mM glucose (49) and hence, presumably in phase with insulin. In Fig. 10A, we show that this can happen if the α-cell has KATP conductance such that the open circle is on the left-hand side of the bell (Fig. 10A). In this case, insulin increases α-cell Ca2+ by increasing gKATPa. This would normally be expected to increase glucagon secretion (Fig. 10A, ●), but somatostatin overcomes the effect of Ca2+ and is able to suppress glucagon secretion through its direct effect on exocytosis. Therefore, glucagon secretion is anti-phase with insulin (Fig. 10D), whereas Ca2+ is in phase (Fig. 10E). As in Fig. 9, insulin and somatostatin secretion are in phase with each other (Fig. 10, B and C).
Although it may seem paradoxical for α-cell Ca2+ to be out of phase with glucagon, the configuration of Fig. 10 avoids another paradox that would afflict Fig. 9. In that case, gKATPa places the α-cell just to the right of the peak of the glucagon secretion curve in high glucose. That means that at low glucose, the physiologically relevant case, the α-cell would be far to the right of the peak of its glucose dose-response curve. Then, increases in glucose would increase glucagon secretion unless they are counterbalanced by another effect. In low glucose, the paracrine inhibition from somatostatin would be relatively weak and limited in its ability to serve this function.
Oscillations in glucagon are not universally observed. For example, in Nadal et al. (57) no oscillations were observed, and there was no synchrony among α- or δ-cells. Thus, although the structure of islet cell interactions depicted in Fig. 1 is favorable for coordinated hormone oscillations, it is not sufficient. Fig. 11, A–C, shows one way that oscillations can fail to occur. If turnover of hormones in the interstitial space is too rapid, the concentration will not build up and dissipate slowly as insulin rises and falls. Another way oscillations could fail to appear is if the β-cells exhibit fast, rather than slow, electrical oscillations (Fig. 11, D–F). In this case, insulin secretion does not exhibit slow oscillations, so glucagon and somatostatin cannot oscillate.
Intrinsic glucagon pulsatility.
As stated earlier, there is some evidence that isolated α-cells are oscillatory, suggesting that they may contain an intrinsic glycolytic oscillator (7, 8, 62). However, α-cells are extremely heterogeneous (39, 57, 61) and not coupled by gap junctions like β-cells. We propose that paracrine interactions are needed to synchronize glucagon oscillations even if some or all of the α-cells are intrinsically oscillatory. To test this hypothesis, we extended the model to include five α-cells in addition to the one representative β-cell and one representative δ-cell. The equations for the glycolytic oscillator from (5) were added to the α-cell model (see Eq. A4 in the appendix). Heterogeneity was incorporated by giving each cell a different value for the parameter JGK, which is the rate of the enzyme glucokinase, and κ, which controls the speed of the glycolytic oscillations; many other parameters could have been used for this illustration.
Figure 12A shows the glucagon secretion from the five individual α-cells without the inhibitory effects of insulin or somatostatin. The lack of paracrine interactions was modeled by fixing the conductance of the GIRK and KATP channels and the rate of depriming of granules in the α-cells. Three of the α-cells are oscillating, whereas two are spiking but not undergoing slow oscillations. We included both oscillating and nonoscillating α-cells since it is likely that only a subset of individual α-cells contain oscillations in secretion. The total glucagon secretion from the islet is nearly static (Fig. 12B). However, if we run the same simulation and include the paracrine effects, glucagon secretion becomes pulsatile. In contrast to Fig. 12A, Fig. 12C shows that each individual cell is secreting in an oscillatory fashion, and this secretion is synchronized. Since the individual α-cells are now synchronized, the total glucagon secretion is pulsatile (Fig. 12D). This indicates that another role of paracrine effects is to tame the heterogeneity of α-cells.
DISCUSSION
This study continues the investigation begun by us (78) on the roles of intrinsic and paracrine factors in the regulation of glucagon secretion. In the first paper, we showed that two intrinsic mechanisms, KATP channels and SOC channels, could each account for the reduction of glucagon secretion by glucose. In the current study, we have added models for β- and δ-cells to investigate paracrine effects in intact pancreatic islets.
We have shown that this BAD model can account for experiments in which the effects of somatostatin are absent due to genetic knockout (Fig. 6) or pretreatment with pertussis toxin (Fig. 7). In the latter case, KATP channels were also absent (due to genetic knockout), but responsiveness to glucose remained. To the extent that insulin acts by modulating KATP channels, this simulation also demonstrates that glucose can inhibit glucagon secretion independently of insulin secretion. The model shows that the residual glucose sensitivity could be accounted for by the effect of glucose to fill the ER and reduce SOC current. However, recent evidence suggests that insulin may act independently of KATP channels by reducing cAMP (18), so SOC may not be solely responsible for the decrease in secretion in the experiments corresponding to Fig. 7.
The model shows that SOC can affect glucagon secretion even when the conductance is rather small, much smaller than we used previously (78). Thus, although there is no direct electrophysical evidence for the existence of SOC current in α-cells, it is possible that it would be difficult to detect experimentally unless other factors, such as somatostatin and KATP channels, are absent or nonfunctional.
One prediction of the model highlighted in Fig. 7 is that some other K+ channel likely compensates for the loss of KATP channels. Two possible candidates are the two-pore domain K+ channel TWIK-related acid-sensitive K+ channel 1 (17) and GIRK (42). Similarly, it is not clear what mechanisms mediate the increase by glucose of somatostatin secretion in δ-cells when KATP is knocked out. It has been suggested that calcium-induced calcium release increases somatostatin secretion, provided that KATP conductance is reduced sufficiently (81). In the absence of detailed information about the pathway, we have simply assumed that secretion increases when glucose rises.
We have chosen intrinsic α-cell parameters such that glucose decreases glucagon secretion and parameters for the paracrine effects that preserve this response (Figs. 3–5). With this starting point, extreme loss of insulin secretion, as in type 1 or advanced type 2 diabetes, can result in exaggerated postprandial glucagon secretion at the same time as impaired glucagon response to hypoglycemia, even if intrinsic glucose sensing in the α-cells and external signaling are intact (Fig. 8). The postprandial hyperglucagonemia in that simulation results from reduced drive to the δ-cells from the β-cells. Alternatively, if insulin lowers cAMP in δ-cells (18), that would likely be sufficient to account for postprandial hyperglucagonemia independent of any alteration in δ-cells, as β-cells far outnumber δ-cells.
Impaired glucagon response to low glucose was modeled as a consequence of exaggerated somatostatin secretion in the chronic absence of insulin, as described previously (44, 71). Given this, the model shows that the counterregulatory response can be rescued by somatostatin receptor antagonism (44).
However, there is also evidence that δ-cell number is reduced in diabetes (32). An alternative model for glucagon counterregulation is the “switch-off hypothesis,” which holds that α-cells require a reduction in an inhibitory signal (insulin or somatostatin) coinciding with the reduction in glucose to be adequately stimulated (20). Under normal conditions, insulin and somatostatin would decrease along with glucose, but this would not occur in type 1 diabetes, which may account for the impaired counterregulation without needing to assume increased somatostatin secretion. The switch-off has been modeled under the assumption that α-cells stimulate δ-cells with a delay and thus indirectly inhibit themselves. When insulin decreases acutely, the α-cells are transiently disinhibited because of the delay (20, 21). We have not modeled this, concentrating instead on possible steady-state mechanisms.
Another major focus was how islets produce pulses of insulin and somatostatin secretion in antisynchrony with those of glucagon. The relevant experiments were carried out at high glucose (20 mM), where we assume that SOC is negligible.
Within an islet, β-cells are electrically coupled to their neighbors through gap junctions (2, 3, 35). This coupling allows the β-cells to secrete in synchrony, generating pulses of insulin secretion. On the other hand, α- and δ-cells are not coupled through gap junctions, but we have shown that β-cells can synchronize and drive pulses of glucagon and somatostatin secretion.
The model suggests that β-cells stimulate somatostatin secretion, which is sufficient to account for synchronous oscillations of somatostatin and insulin. In the model, this stimulation comes from GABA, which is cosecreted with insulin (10, 11) and modeled simply as proportional to insulin secretion. Other possible mechanisms include ATP (33) and urocortin 3 (75) or any other paracrine factor that oscillates in synchrony with insulin. The mechanism of urocortin stimulation would be different from GABA, an increase in cAMP rather than direct activation of an ion channel, but has been postulated to have the same end result, a rise in cytosolic calcium in δ-cells that would increase somatostatin secretion (see Fig. 9 in Ref. 75). In the absence of paracrine modulators, somatostatin secretion is static, since we assume that individual δ-cells produce spikes of electrical activity but no slow oscillations [some may (see Ref. 8), but in the absence of synchrony they will not produce islet-wide pulsatility]. However, somatostatin secretion oscillates in synchrony with insulin when the δ-cell is stimulated by the β-cell (Figs. 9, B and C, and 10, B and C). Thus, β-cells can drive pulses of somatostatin secretion in sufficiently high glucose. An alternative hypothesis is that α-cells stimulate the δ-cells with a delay (1, 20), as discussed above in connection with impaired counterregulation in diabetes. See also the model of Hong at al. (38), which includes a positive α- to δ-cell interaction. This mechanism could also work to make the glucagon and somatostatin oscillations antisynchronous and the somatostatin and insulin oscillations synchronous.
Like somatostatin, glucagon secretion is expected to be static when uncoupled from paracrine effects. We have shown that oscillations in glucagon secretion can be driven by the β-cell, but the δ-cell is needed to guarantee that these oscillations are out of phase with insulin. Under the assumption that insulin secretion modulates KATP channels, its effect on the α-cell can change depending on the KATP conductance in the absence of modulation by insulin. If the KATP conductance is near or to the right of the peak of the bell-shaped curve, as in Fig. 9A, then increasing insulin would reduce secretion. Therefore, inhibition from insulin is all that is necessary to produce antisynchrous oscillations in glucagon secretion (Fig. 9D). However, if the α-cell KATP conductance is far to the left of the peak, as in Fig. 10A, then increasing insulin would increase secretion. In this case, the inhibitory effect of somatostatin can overcome the rise in Ca2+ produced by the effect of insulin to produce antisynchronous oscillations in glucagon (Fig. 10D). Again, insulin could also contribute by reducing cAMP (18). However, oscillations in α-cell Ca2+ would be out of phase with glucagon secretion (Fig. 10E). Although this seems paradoxical, recall that the observations were made in high glucose; the configuration of Fig. 10 is more likely than that of Fig. 9 to be compatible with reduction of glucagon secretion by KATP closure in the physiological range of low glucose.
If α-cells are able to oscillate due to intrinsic mechanisms, then glucagon secretion would still be static when uncoupled from paracrine interactions (Fig. 12B). Since α-cells are not coupled by gap junctions like β-cells, some other mechanism must exist to synchronize glucagon secretion in order for islets to produce pulses of secretion. We have shown that paracrine effects are sufficient to synchronize glucagon oscillations (Fig. 12D).
Anti-phase oscillations have been seen in vitro in high glucose levels (20 mM) (27, 36, 37, 65) and in vivo (25, 45, 54). However, the purpose of these asynchronous oscillations is unclear. Perhaps having these oscillations helps keep glucose levels in the appropriate range. It is well known that pulsatile insulin secretion helps the liver function more efficiently, but it is not clear whether pulsatile glucagon secretion would be beneficial (see Ref. 69 for a recent review of the literature on this question).
In addition to possibly inadequate coupling (as in Figs. 11 and 12), another barrier to pulsatile glucagon secretion is heterogeneity of α-cells. Whereas δ-cells are also presumably heterogeneous, this is likely of less consequence, as their secretion depends monotonically on KATP conductance; α-cells, in contrast, have a nonmonotonic dose-response curve (Fig. 2B), which allows the direction as well as the magnitude of the glucose dependence to vary. Indeed, the results in Figs. 9 and 10 depend on the α-cells having the same KATP conductance or at least being tightly clustered in the same region.
However, two recent studies have shown that whereas in some α-cells cytosolic Ca2+ decreased with glucose, the majority increased Ca2+ (46, 47). We propose that insulin and/or somatostatin could help suppress α-cells that secrete inappropriately at high glucose. However, a full exploration of heterogeneity requires a model with hundreds of α-cells to generate distributions of parameters and outcomes. This is more readily done with a simplified model. Preliminary results with such a model (Watts M and Sherman A, unpublished observations) indicate that moderate heterogeneity can be overcome by averaging over the population, but extreme heterogeneity can eliminate intrinsic modulation completely, leaving only paracrine regulation.
GRANTS
This work was supported by the Intramural Research Program of the National Institutes of Health (National Institute of Diabetes and Digestive and Kidney Diseases).
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
M.W., J.H., and O.K. performed experiments; M.W. and A.S. interpreted results of experiments; M.W. prepared figures; M.W. drafted manuscript; M.W., J.H., O.K., and A.S. approved final version of manuscript; A.S. conception and design of research; A.S. edited and revised manuscript.
APPENDIX
The BAD model combines the dual-oscillator model (DOM) for β-cells, our recent α-cell model, a new model for δ-cells, and the interactions between them. Since a complete mathematical description of the DOM and α-cell model has been published previously, only the key elements of the model are described here. The equations for the interactions between the cells can be found in the main text, and the parameters can be found in Table 3.
β-Cell model.
The DOM consists of three interacting compartments, electrical/calcium, glycolytic, and mitochondrial, and accounts for the three main oscillatory behaviors of islets: fast electrical bursting, slow glycolytic bursting, and compound bursting (4–6). The electrical/calcium component contains the membrane potential (Vb), the Hodgkin-Huxley gating variable for the voltage dependent K+ channels (n), cytosolic calcium (cb), Ca2+ within a microdomain of L-type Ca2+ channels (cmdL,b) and Ca2+ stored internally in the ER (cER). The equation for the plasma membrane potential is
| (A1) |
and the calcium equations for the cell are
| (A2) |
| (A3) |
where JL,b and JR,b are molar Ca2+ influx through open L- and R-type Ca2+ channels, fc and fmd are the fraction of free Ca2+ in the cytosol and microdomain, B is the transport rate constant of Ca2+ between the cytosol and the microdomain, and JER,b and Jm are Ca2+ flux out of the ER and mitochondria.
After entering the cell, glucose is metabolized in glycolysis. It is phosphorylated to glucose 6-phosphate (G6P) by glucokinase (GK), isomerized to fructose 6-phosphate (F6P), and then phosphorylated a second time to fructose-1,6-bisphosphate (FBP) by phosphofructokinase-1 (PFK-1), the key enzyme that controls glycolytic oscillations. F6P is assumed to be in equilibrium with G6P; therefore, the equations for the glycolytic component are
| (A4) |
where JPFK and JGPDH are the PFK and glyceraldehyde 3-phosphate dehydrogenase (GPDH) reaction rates and JGK is the glucokinase rate, which is treated as a parameter of the model.
The final component describes the reactions in the mitochondria, which metabolizes the carbons from glucose and produces most of the ATP in the cell. The mitochondrial component has four variables: mitochondrial NADH concentration (NADHm), mitochondrial ADP concentration (ADPm), mitochondrial calcium concentration (cm), and the inner membrane potential (ψm). We use the rate of GPDH, which is in equilibrium with FBP, as the input into the mitochondria. That rate satisfies
| (A5) |
We added a kinetic model for granule exocytosis to the DOM to model insulin secretion from the β-cell. The kinetic model was taken from Chen et al. (14). The exocytosis cascade describes the interaction between the insulin-containing granules and the plasma membrane inside the β-cell and is divided into seven steps. It is assumed that a granule has to dock to the membrane from a reserve pool, be primed, and move to the microdomain of an L-type Ca2+ channel before it can bind with Ca2+ and fuse with the cell membrane. The number of granules in pool i is given by the following:
| (A6) |
States 1–6 contain vesicles in the docked and primed states, state F is the number of granules in the fused state, and state R is the number of granules ready to be released. The resupply rate (r3b) is assumed to be modulated through an amplifying signal generated from glucose metabolism or other cellular reactions. Here, the amplifying signal comes from the mitochondrial compartment, specifically, the variable JO, which is the oxygen consumption at the final stage of the electron transport chain, during which NADH is converted to NAD+. We use this variable because mitochondrial metabolism has been shown to be important for amplification of insulin secretion (51). The equation for the resupply rate is
| (A7) |
To add exocytosis to the DOM, microdomain calcium was modified by the following equation:
| (A8) |
This function scales the Ca2+ in the microdomain to be more in line with the microdomain Ca2+ concentrations used by Chen et al. (14). The rate of insulin secretion JIS is given by the following equation:
| (A9) |
The form of the DOM is adapted from Bertram et al. (4). Some parameters were added or changed to interface the oscillatory and exocytotic components. In particular, microdomain calcium, which was not included previously, was added, which required calcium channel parameters to be modified to match the calcium affinity of exocytotic calcium sensing. In addition, some calcium channel parameters were adjusted to make the model more robust to changes in calcium and KATP conductances. Parameters that have been changed from those in Bertram et al. (4) and Chen et al. (14) can be found in Table 1.
α-Cell model.
Unlike the β-cell model, the α-cell model (78) currently contains only one compartment: the electrical/calcium compartment. There are 15 variables: the membrane potential (Va), 11 Hodgkin-Huxley gating variables for the voltage-dependent Ca2+ and K+ channels, cytosolic Ca2+ (ca), Ca2+ within the microdomain of PQ-type Ca2+ channels (cmdPQ,a), and Ca2+ stored in the ER (cER,a). The equation for the plasma membrane potential (Va) is
| (A10) |
and the calcium equations for the cell are
| (A11) |
where JT,a, JL,a, and JPQ,a are molar Ca2+ influx through open T-, L-, and PQ-type Ca2+ channels.
The kinetic model for granule exocytosis was added to the α-cell model as a replacement for the glucagon secretion equations. This change was necessary to model somatostatin's effect on exocytosis. The equations are the same as the β-cell equations (see Eq. A6 above), with the exception that we do not include a mitochondrial compartment and assume that the resupply rate (r3,a) depends only on calcium:
| (A12) |
The rate of glucagon secretion is
| (A13) |
To test the effects of heterogeneity on glucagon oscillations (Figs. 7 and 8), we added the glycolytic compartment from Bertram et al. (5) to the α-cell model. Along with the equations for G6P and FBP (Eqs. 4 and 5), the following equation for ADP was added:
| (A14) |
where γ is given by the following equation:
| (A15) |
ADP is affected by cytosolic Ca2+ and glycolysis. The Ca2+ effect is through the factor (1 − ca/0.45), whereas input from glycolysis is incorporated through γ.
δ-Cell model.
The δ-cell model was modified from the α-cell model in Watts and Sherman (78) and contains 13 variables because there are no T-type Ca2+ channels. The equation for the plasma membrane potential (Vd) is
| (A16) |
and the calcium equations for the cell are
| (A17) |
We modeled somatostatin secretion as depending on Ca2+ in the microdomains surrounding P/Q-type Ca2+ channels, since these channels have been linked to somatostatin secretion (9). The rate of secretion is expressed as
| (A18) |
following the formulation in Pedersen and Sherman (59). For Fig. 7, we assume that somatostatin secretion responds to glucose via a KATP-independent amplifying factor. In this case, the secretion equation becomes
| (A19) |
where Amp = 1 in 1G and 2 in 7G.
REFERENCES
- 1.Ajmera I, Swat M, Laibe C, Le Novere N, Chelliah V. The impact of mathematical modeling on the understanding of diabetes and related complications. CPT Pharmacometrics Syst Pharmacol 2: e54, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Benninger RK, Head WS, Zhang M, Satin LS, Piston DW. Gap junctions and other mechanisms of cell-cell communication regulate basal insulin secretion in the pancreatic islet. J Physiol 589: 5453–5466, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Benninger RK, Zhang M, Head WS, Satin LS, Piston DW. Gap junction coupling and calcium waves in the pancreatic islet. Biophys J 95: 5048–5061, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bertram R, Satin L, Pedersen MG, Luciani D, Sherman A. Interaction of glycolysis and mitochondrial respiration in metabolic oscillations of pancreatic islets. Biophys J 92: 1544–1555, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bertram R, Satin L, Zhang M, Smolen P, Sherman A. Calcium and glycolysis mediate multiple bursting models in pancreatic islets. Biophys J 87: 3074–3087, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bertram R, Sherman A, Satin LS. Metabolic and electrical oscillations: partners in controlling pulsatile insulin secretion. Am J Physiol Endocrinol Metab 293: E890–E900, 2007. [DOI] [PubMed] [Google Scholar]
- 7.Berts A, Ball A, Gylfe E, Hellman B. Suppression of Ca2+ oscillations in glucagon-producing alpha 2-cells by insulin/glucose and amino acids. Biochim Biophys Acta 1310: 212–216, 1996. [DOI] [PubMed] [Google Scholar]
- 8.Berts A, Gylfe E, Hellman B. [Ca]2+ oscillations in pancreatic islet cells secreting glucagon and somatostatin. Biochem Biophys Res Commun 208: 644–649, 1995. [DOI] [PubMed] [Google Scholar]
- 9.Braun M, Ramracheya R, Amisten S, Bengtsson M, Moritoh Y, Zhang Q, Johnson PR, Rorsman P. Somatostatin release, electrical activity, membrane currents and exocytosis in human pancreatic delta cells. Diabetologia 52: 1566–1578, 2009. [DOI] [PubMed] [Google Scholar]
- 10.Braun M, Ramracheya R, Bengtsson M, Clark A, Walker JN, Johnson PR, Rorsman P. Gamma-aminobutyric acid (GABA) is an autocrine excitatory transmitter in human pancreatic beta-cells. Diabetes 59: 1694–1701, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Braun M, Wendt A, Karanauskaite J, Galvanovskis J, Clark A, MacDonald PE, Rorsman P. Corelease and differential exit via the fusion pore of GABA, serotonin, and ATP from LDCV in rat pancreatic beta cells. J Gen Physiol 129: 221–231, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Brown RJ, Sinaii N, Rother KI. Too much glucagon, too little insulin: time course of pancreatic islet dysfunction in new-onset type 1 diabetes. Diabetes Care 31: 1403–1404, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Brunicardi FC, Kleinman R, Moldovan S, Nguyen TH, Watt PC, Walsh J, Gingerich R. Immunoneutralization of somatostatin, insulin, and glucagon causes alterations in islet cell secretion in the isolated perfused human pancreas. Pancreas 23: 302–308, 2001. [DOI] [PubMed] [Google Scholar]
- 14.Chen YD, Wang S, Sherman A. Identifying the targets of the amplifying pathway for insulin secretion in pancreatic beta-cells by kinetic modeling of granule exocytosis. Biophys J 95: 2226–2241, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cheng-Xue R, Gomez-Ruiz A, Antoine N, Noel LA, Chae HY, Ravier MA, Chimienti F, Schuit FC, Gilon P. Tolbutamide controls glucagon release from mouse islets differently than glucose: involvement of K(ATP) channels from both α-cells and δ-cells. Diabetes 62: 1612–1622, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Claro A, Grill V, Efendic S, Luft R. Studies on the mechanisms of somatostatin action on insulin release. IV. Effect of somatostatin on cyclic AMP levels and phosphodiesterase activity in isolated rat pancreatic islets. Acta Endocrinol (Copenh) 85: 379–388, 1977. [PubMed] [Google Scholar]
- 17.Dadi PK, Luo B, Vierra NC, Jacobson DA. TASK-1 Potassium Channels Limit Pancreatic α-Cell Calcium Influx and Glucagon Secretion. Mol Endocrinol 29: 777–787, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Elliott AD, Ustione A, Piston DW. Somatostatin and insulin mediate glucose-inhibited glucagon secretion in the pancreatic α-cell by lowering cAMP. Am J Physiol Endocrinol Metab 308: E130–E143, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ermentrout B. Simulating, Analyzing, and Animating Dynamical Systems: A Guide to XPPAUT for Researchers and Students. Philadelphia, PA: SIAM, 2002. [Google Scholar]
- 20.Farhy LS, Du Z, Zeng Q, Veldhuis PP, Johnson ML, Brayman KL, McCall AL. Amplification of pulsatile glucagon counterregulation by switch-off of α-cell-suppressing signals in streptozotocin-treated rats. Am J Physiol Endocrinol Metab 295: E575–E585, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Farhy LS, McCall AL. Pancreatic network control of glucagon secretion and counterregulation. Methods Enzymol 467: 547–581, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Franklin I, Gromada J, Gjinovci A, Theander S, Wollheim CB. Beta-cell secretory products activate α-cell ATP-dependent potassium channels to inhibit glucagon release. Diabetes 54: 1808–1815, 2005. [DOI] [PubMed] [Google Scholar]
- 23.Franklin IK, Wollheim CB. GABA in the endocrine pancreas: its putative role as an islet cell paracrine-signalling molecule. J Gen Physiol 123: 185–190, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Gerich JE, Lovinger R, Grodsky GM. Inhibition by somatostatin of glucagon and insulin release from the perfused rat pancreas in reponse to arginine, isoproterenol and theophylline: evidence for a preferential effect on glucagon secretion. Endocrinology 96: 749–754, 1975. [DOI] [PubMed] [Google Scholar]
- 25.Goodner CJ, Walike BC, Koerker DJ, Ensinck JW, Brown AC, Chideckel EW, Palmer J, Kalnasy L. Insulin, glucagon, and glucose exhibit synchronous, sustained oscillations in fasting monkeys. Science 195: 177–179, 1977. [DOI] [PubMed] [Google Scholar]
- 26.Göpel SO, Kanno T, Barg S, Rorsman P. Patch-clamp characterisation of somatostatin-secreting -cells in intact mouse pancreatic islets. J Physiol 528: 497–507, 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Grapengiesser E, Salehi A, Qader SS, Hellman B. Glucose induces glucagon release pulses antisynchronous with insulin and sensitive to purinoceptor inhibition. Endocrinology 147: 3472–3477, 2006. [DOI] [PubMed] [Google Scholar]
- 28.Gromada J, Franklin I, Wollheim CB. Alpha-cells of the endocrine pancreas: 35 years of research but the enigma remains. Endocr Rev 28: 84–116, 2007. [DOI] [PubMed] [Google Scholar]
- 29.Gromada J, Høy M, Buschard K, Salehi A, Rorsman P. Somatostatin inhibits exocytosis in rat pancreatic alpha-cells by G(i2)-dependent activation of calcineurin and depriming of secretory granules. J Physiol 535: 519–532, 2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Gromada J, Hoy M, Olsen HL, Gotfredsen CF, Buschard K, Rorsman P, Bokvist K. Gi2 proteins couple somatostatin receptors to low-conductance K+ channels in rat pancreatic α-cells. Pflugers Arch 442: 19–26, 2001. [DOI] [PubMed] [Google Scholar]
- 31.Gromada J, Ma X, Hoy M, Bokvist K, Salehi A, Berggren PO, Rorsman P. ATP-sensitive K+ channel-dependent regulation of glucagon release and electrical activity by glucose in wild-type and sur1−/− mouse alpha-cells. Diabetes 53, Suppl 3: S181–S189, 2004. [DOI] [PubMed] [Google Scholar]
- 32.Guardado Mendoza R, Perego C, Finzi G, La Rosa S, Capella C, Jimenez-Ceja LM, Velloso LA, Saad MJ, Sessa F, Bertuzzi F, Moretti S, Dick EJ Jr, Davalli AM, Folli F. Delta cell death in the islet of langerhans and the progression from normal glucose tolerance to type 2 diabetes in nonhuman primates (baboon, papio hamadryas). Diabetologia 58: 1814–1826, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Gylfe E, Tengholm A. Neurotransmitter control of islet hormone pulsatility. Diabetes Obes Metab 16, Suppl 1: 102–110, 2014. [DOI] [PubMed] [Google Scholar]
- 34.Hauge-Evans AC, King AJ, Carmignac D, Richardson CC, Robinson IC, Low MJ, Christie MR, Persaud SJ, Jones PM. Somatostatin secreted by islet delta-cells fulfills multiple roles as a paracrine regulator of islet function. Diabetes 58: 403–411, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Head WS, Orseth ML, Nunemaker CS, Satin LS, Piston DW, Benninger RK. Connexin-36 gap junctions regulate in vivo first- and second-phase insulin secretion dynamics and glucose tolerance in the conscious mouse. Diabetes 61: 1700–1707, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Hellman B, Salehi A, Grapengiesser E, Gylfe E. Isolated mouse islets respond to glucose with an initial peak of glucagon release followed by pulses of insulin and somatostatin in antisynchrony with glucagon. Biochem Biophys Res Commun 417: 1219–1223, 2012. [DOI] [PubMed] [Google Scholar]
- 37.Hellman B, Salehi A, Gylfe E, Dansk H, Grapengiesser E. Glucose generates coincident insulin and somatostatin pulses and antisynchronous glucagon pulses from human pancreatic islets. Endocrinology 150: 5334–5340, 2009. [DOI] [PubMed] [Google Scholar]
- 38.Hong H, Jo J, Sin SJ. Stable and flexible system for glucose homeostasis. Phys Rev E Stat Nonlin Soft Matter Phys 88: 032711, 2013. [DOI] [PubMed] [Google Scholar]
- 39.Huang YC, Rupnik M, Gaisano HY. Unperturbed islet alpha-cell function examined in mouse pancreas tissue slices. J Physiol 589: 395–408, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Ikeuchi M, Cook DL. Glucagon and forskolin have dual effects upon islet cell electrical activity. Life Sci 35: 685–691, 1984. [DOI] [PubMed] [Google Scholar]
- 41.Ishihara H, Maechler P, Gjinovci A, Herrera PL, Wollheim CB. Islet β-cell secretion determines glucagon release from neighbouring α-cells. Nat Cell Biol 5: 330–335, 2003. [DOI] [PubMed] [Google Scholar]
- 42.Kailey B, van de Bunt M, Cheley S, Johnson PR, MacDonald PE, Gloyn AL, Rorsman P, Braun M. SSTR2 is the functionally dominant somatostatin receptor in human pancreatic β- and α-cells. Am J Physiol Endocrinol Metab 303: E1107–E1116, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Karimian N, Qin T, Liang T, Osundiji M, Huang Y, Teich T, Riddell MC, Cattral MS, Coy DH, Vranic M, Gaisano HY. Somatostatin receptor type 2 antagonism improves glucagon counterregulation in biobreeding diabetic rats. Diabetes 62: 2968–2977, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lang DA, Matthews DR, Burnett M, Ward GM, Turner RC. Pulsatile, synchronous basal insulin and glucagon secretion in man. Diabetes 31: 22–26, 1982. [DOI] [PubMed] [Google Scholar]
- 46.Le Marchand SJ, Piston DW. Glucose suppression of glucagon secretion: metabolic and calcium responses from α-cells in intact mouse pancreatic islets. J Biol Chem 285: 14389–14398, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Le Marchand SJ, Piston DW. Glucose decouples intracellular [Ca]2+ activity from glucagon secretion in mouse pancreatic islet α-cells. PLoS One 7: e47084, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Leung YM, Ahmed I, Sheu L, Gao X, Hara M, Tsushima RG, Diamant NE, Gaisano HY. Insulin regulates islet alpha-cell function by reducing KATP channel sensitivity to adenosine 5′-triphosphate inhibition. Endocrinology 147: 2155–2162, 2006. [DOI] [PubMed] [Google Scholar]
- 49.Li J, Yu Q, Ahooghalandari P, Gribble FM, Reimann F, Tengholm A, Gylfe E. Submembrane ATP and Ca2+ kinetics in α-cells: unexpected signaling for glucagon secretion. FASEB J 29: 3379–3388, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Liu YJ, Vieira E, Gylfe E. A store-operated mechanism determines the activity of the electrically excitable glucagon-secreting pancreatic α-cell. Cell Calcium 35: 357–365, 2004. [DOI] [PubMed] [Google Scholar]
- 51.MacDonald MJ, Fahien LA, Brown LJ, Hasan NM, Buss JD, Kendrick MA. Perspective: emerging evidence for signaling roles of mitochondrial anaplerotic products in insulin secretion. Am J Physiol Endocrinol Metab 288: E1–E15, 2005. [DOI] [PubMed] [Google Scholar]
- 52.MacDonald PE, Marinis YZ, Ramracheya R, Salehi A, Ma X, Johnson PR, Cox R, Eliasson L, Rorsman P. A KATP channel-dependent pathway within α-cells regulates glucagon release from both rodent and human islets of langerhans. PLoS Biol 5: 1236–1247, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Maruyama H, Hisatomi A, Orci L, Grodsky GM, Unger RH. Insulin within islets is a physiologic glucagon release inhibitor. J Clin Invest 74: 2296–2299, 1984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Menge BA, Gruber L, Jorgensen SM, Deacon CF, Schmidt WE, Veldhuis JD, Holst JJ, Meier JJ. Loss of inverse relationship between pulsatile insulin and glucagon secretion in patients with type 2 diabetes. Diabetes 60: 2160–2168, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Molina J, Rodriguez-Diaz R, Fachado A, Jacques-Silva MC, Berggren PO, Caicedo A. Control of insulin secretion by cholinergic signaling in the human pancreatic islet. Diabetes 63: 2714–2726, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Montefusco F, Pedersen MG. Mathematical modelling of local calcium and regulated exocytosis during inhibition and stimulation of glucagon secretion from pancreatic alpha-cells. J Physiol 593: 4519–4530, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Nadal A, Quesada I, Soria B. Homologous and heterologous asynchronicity between identified alpha-, beta- and delta-cells within intact islets of Langerhans in the mouse. J Physiol 517: 85–93, 1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Pedersen MG, Sherman A. Newcomer insulin secretory granules as a highly calcium-sensitive pool. Proc Natl Acad Sci USA 106: 7432–7436, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Pörksen S, Nielsen LB, Kaas A, Kocova M, Chiarelli F, Orskov C, Holst JJ, Ploug KB, Hougaard P, Hansen L, Mortensen HB; Hvidøre Study Group on Childhood Diabetes. Meal-stimulated glucagon release is associated with postprandial blood glucose level and does not interfere with glycemic control in children and adolescents with new-onset type 1 diabetes. J Clin Endocrinol Metab 92: 2910–2916, 2007. [DOI] [PubMed] [Google Scholar]
- 61.Quesada I, Todorova MG, Alonso-Magdalena P, Beltrá M, Carneiro EM, Martin F, Nadal A, Soria B. Glucose induces opposite intracellular Ca2+ concentration oscillatory patterns in identified alpha- and beta-cells within intact human islets of Langerhans. Diabetes 55: 2463–2469, 2006. [DOI] [PubMed] [Google Scholar]
- 62.Quoix N, Cheng-Xue R, Mattart L, Zeinoun Z, Guiot Y, Beauvois MC, Henquin JC, Gilon P. Glucose and pharmacological modulators of ATP-sensitive K+ channels control [Ca2+]c by different mechanisms in isolated mouse alpha-cells. Diabetes 58: 412–421, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Rodriguez-Diaz R, Dando R, Jacques-Silva MC, Fachado A, Molina J, Abdulreda MH, Ricordi C, Roper SD, Berggren PO, Caicedo A. Alpha cells secrete acetylcholine as a nonneuronal paracrine signal priming beta cell function in humans. Nat Med 17: 888–892, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Rorsman P, Berggren PO, Bokvist K, Ericson H, Mohler H, Ostenson CG, Smith PA. Glucose-inhibition of glucagon secretion involves activation of GABAA-receptor chloride channels. Nature 341: 233–236, 1989. [DOI] [PubMed] [Google Scholar]
- 65.Salehi A, Qader SS, Grapengiesser E, Hellman B. Pulses of somatostatin release are slightly delayed compared with insulin and antisynchronous to glucagon. Regul Pept 144: 43–49, 2007. [DOI] [PubMed] [Google Scholar]
- 66.Salehi A, Vieira E, Gylfe E. Paradoxical stimulation of glucagon secretion by high glucose concentrations. Diabetes 55: 2318–2323, 2006. [DOI] [PubMed] [Google Scholar]
- 67.Samols E, Marri G, Marks V. Promotion of insulin secretion by glucagon. Lancet 2: 415–416, 1965. [DOI] [PubMed] [Google Scholar]
- 68.Samols E, Stagner JI. Intra-islet regulation. Am J Med 85: 31–35, 1988. [DOI] [PubMed] [Google Scholar]
- 69.Satin LS, Butler PC, Ha J, Sherman AS. Pulsatile insulin secretion, impaired glucose tolerance and type 2 diabetes. Mol Aspects Med 42: 61–77, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Schuit FC, Pipeleers DG. Regulation of adenosine 3′,5′-monophosphate levels in the pancreatic B cell. Endocrinology 117: 834–840, 1985. [DOI] [PubMed] [Google Scholar]
- 71.Strowski MZ, Blake AD. Function and expression of somatostatin receptors of the endocrine pancreas. Mol Cell Endocrinol 286: 169–179, 2008. [DOI] [PubMed] [Google Scholar]
- 72.Strowski MZ, Parmar RM, Blake AD, Schaeffer JM. Somatostatin inhibits insulin and glucagon secretion via two receptors subtypes: an in vitro study of pancreatic islets from somatostatin receptor 2 knockout mice. Endocrinology 141: 111–117, 2000. [DOI] [PubMed] [Google Scholar]
- 73.Tornheim K. Are metabolic oscillations responsible for normal oscillatory insulin secretion? Diabetes 46: 1375–1380, 1997. [DOI] [PubMed] [Google Scholar]
- 74.Unger RH, Orci L. The role of glucagon in the endogenous hyperglycemia of diabetes mellitus. Annu Rev Med 28: 119–130, 1977. [DOI] [PubMed] [Google Scholar]
- 75.van der Meulen T, Donaldson CJ, Cceres E, Hunter AE, Cowing-Zitron C, Pound LD, Adams MW, Zembrzycki A, Grove KL, Huising MO. Urocortin3 mediates somatostatin-dependent negative feedback control of insulin secretion. Nat Med 21: 769–776, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Vieira E, Salehi A, Gylfe E. Glucose inhibits glucagon secretion by a direct effect on mouse pancreatic alpha cells. Diabetologia 50: 370–379, 2007. [DOI] [PubMed] [Google Scholar]
- 77.Walker JN, Ramracheya R, Zhang Q, Johnson PR, Braun M, Rorsman P. Regulation of glucagon secretion by glucose: paracrine, intrinsic or both? Diabetes Obes Metab 13, Suppl 1: 95–105, 2011. [DOI] [PubMed] [Google Scholar]
- 78.Watts M, Sherman A. Modeling the pancreatic α-cell: dual mechanisms of glucose suppression of glucagon secretion. Biophys J 106: 741–751, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Wendt A, Birnir B, Buschard K, Gromada J, Salehi A, Sewing S, Rorsman P, Braun M. Glucose inhibition of glucagon secretion from rat alpha-cells is mediated by GABA released from neighboring beta-cells. Diabetes 53: 1038–1045, 2004. [DOI] [PubMed] [Google Scholar]
- 80.Yoshimoto Y, Fukuyama Y, Horio Y, Inanobe A, Gotoh M, Kurachi Y. Somatostatin induces hyperpolarization in pancreatic islet alpha cells by activating a G protein-gated K+ channel. FEBS Lett 444: 265–269, 1999. [DOI] [PubMed] [Google Scholar]
- 81.Zhang Q, Bengtsson M, Partridge C, Salehi A, Braun M, Cox R, Eliasson L, Johnson PR, Renström E, Schneider T, Berggren PO, Göpel S, Ashcroft FM, Rorsman P. R-type Ca(2+)-channel-evoked CICR regulates glucose-induced somatostatin secretion. Nat Cell Biol 9: 453–460, 2007. [DOI] [PubMed] [Google Scholar]
- 82.Zhang Q, Ramracheya R, Lahmann C, Tarasov A, Bengtsson M, Braha O, Braun M, Brereton M, Collins S, Galvanovskis J, Gonzalez A, Groschner LN, Rorsman NJ, Salehi A, Travers ME, Walker JN, Gloyn AL, Gribble F, Johnson PR, Reimann F, Ashcroft FM, Rorsman P. Role of KATP channels in glucose-regulated glucagon secretion and impaired counterregulation in type 2 diabetes. Cell Metab 18: 871–882, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]