Abstract
The optical properties of bovine ocular tissues have been determined at laser wavelengths in the near-infrared (NIR) region. The inverse adding doubling (IAD), Kubelka–Munk (KM), and inverse Monte Carlo (IMC) methods were applied to the measured values of the total diffuse transmission, total diffuse reflection, and collimated transmission to determine the optical absorption and scattering coefficients of the bovine cornea, lens and retina from 750 to 1,000 nm using a CW Ti:sapphire laser. The optical properties obtained from these three methods have been compared and are discussed.
Keywords: Lasers, Bovine ocular tissues, Optical properties
Introduction
Recently, there has been considerable interest in the accurate measurement of the optical properties of ocular tissues, particularly the scattering and absorption coefficients. The fundamental optical properties of biological tissues can be used for the diagnosis of various diseases and ocular maladies. Since medical laser applications for ocular diseases have steadily increased over the past several years, it is critical to have a clear understanding of the fundamental optical properties of ocular tissues. The optical properties may indeed influence the distribution and propagation of light in a tissue medium. Unfortunately, a systematic study of ocular tissue optical properties is lacking. Therefore, in this article we present an in-depth characterization of the optical properties of bovine cornea, lens, and retina.
A number of researchers have reported the optical properties of ocular tissues [1–5] from various species such as bovine and porcine. Furthermore, there have been studies contrasting different models to track the light distribution in particular tissues [6–8]. Previously, the characterization of bovine ocular tissues in the visible region was performed; here, we extend the scope of that study into the near-infrared (NIR) using the three models: (a) inverse adding doubling (IAD), (b) inverse Monte Carlo (IMC), and (c) Kubelka–Munk (KM). Through a comparison of the three models, a clearer sense of the optical properties may be obtained. We employed two integrating spheres to measure the diffuse reflectance, diffuse transmittance, and collimated transmittance for the cornea, lens, and retina of bovine eyes from 750 to 1,000 nm lines from CW Ti:sapphire laser. These values are subsequently applied to these models to determine scattering and absorption coefficients of bovine corneal, lens, and retinal tissues in the NIR.
Background theory and computational models
The quantitative distribution of light intensity in biological media can be obtained from the solution of the radiative transport equation [9]
| (1) |
where I(r, s) is the intensity per unit length at the target location r in the s direction (s is the unit directional vector), μa and μs are the absorption and scattering coefficients, respectively, p(s, s′) is the phase function, representing contributions due to scattering from the direction s′ to s, and Ω′ is the solid angle. The first term on the right-hand side represents the loss in intensity per unit length in the s direction due to absorption and scattering, whereas the second term denotes the gain per unit length due to scattering in the s′ direction. Although Eq. (1) is difficult to solve analytically for biological media due to the inherent inhomogeneities and irregularities in their physical shapes, an approximate solution can be obtained by assuming homogeneity and regular geometry of the medium, and thereby an estimate of light intensity distribution is reached by solving the radiative transport equation.
The form of the phase function p(s, s′) is usually not known a priori for experimental applications, especially in the case of biological media. The Henyey–Greenstein phase function, however, provides a good approximation for turbid media:
| (2) |
where ν=cos(θ), and θ is the scattering angle between s and s′. The Henyey–Greenstein phase function depends only on the scattering anisotropy coefficient, g, which is defined as the mean of the scattering angle:
| (3) |
The scattering anisotropy coefficient may also be obtained through the more practical expression: [10]
| (4) |
The value of g ranges from −1 for complete backward scattering to +1 for complete forward scattering. The anisotropy value of 0 indicates isotropic scattering. The phase function is normalized so its integral over all space is unity.
In order to solve the transport Eq. (1), values of μa, μs, and g are required. Therefore, an appropriate experimental method is necessary to measure these fundamental optical properties. It is, however, impossible to directly measure both absorption or scattering in a single experiment. This difficult problem of separating the scattering from the absorption in the total attenuation of light flux propagating through a turbid medium such as biological tissue had been resolved by using different theoretical models, as well as numerical and computational techniques.
Kubelka–Munk (KM) method
The one-dimensional, two-flux KM model [11] has been widely used to determine both the absorption and scattering coefficients of biological media [12–17], provided the scattering is significantly dominant over the absorption. This model provides rather simple mathematical expressions for determining the optical parameters from the measured values of diffuse reflectance and transmission. In the past, researchers have applied the diffusion approximation to the transport equation to successfully characterize biological media [14, 15], most notably, utilizing the experimental method described by Van Gemert et al. for determining the absorption and scattering coefficients.
Inverse adding doubling (IAD) method
Even though an analytical solution to Eq. (1) does not exist for samples such as tissues, an elaborate numerical solution is possible using the Monte Carlo (MC) simulation technique [1, 18, 19]. Furthermore, an important numerical approach known as the IAD [10] method is employed to solve the radiative transport equation [9]. Both the IAD method and MC simulation technique have provided more accurate estimates of optical properties (μa, μs, g) for biological tissues than any other models previously used. Since the details are available in the literature, only a synopsis of the IAD method is provided here. Two dimensionless quantities used in the entire process of IAD are the albedo (a) and optical depth (τ) which are defined as follows:
| (5) |
and
| (6) |
where t is the physical thickness of the sample entered into the program in millimeters. The measured values of the total diffuse reflectance (Rd), total diffuse transmittance (Td), and unscattered collimated transmittance (Tc) are applied to the IAD algorithm in order to determine the optical absorption and scattering coefficients of freshly harvested ocular tissues.
Inverse Monte Carlo (IMC) method
The MC method has been used to describe a variety of stochastic phenomena that require simulation of random processes. In the case of turbid media, the inhomogeneities and varying refractive indices may be modeled by using this method. As the photons travel through the tissue medium, they may be scattered or absorbed. Using a large number of photons, these events may be tracked, and outcomes are tabulated in accordance with probability density distributions.
The inverse problem is termed the IMC method. In this scheme, the Rd and Td are used to determine the μa and μs, which are modeled by a stochastic simulation of light interaction with biological media. This method has been employed by several researchers to calculate absorption and scattering coefficients [8, 20]. The IMC calculations were performed using the MagicLight algorithm developed by I. V. Yaroslavsky [21]. In this article, we present the scattering and absorption coefficients of the cornea, lens, and retina of bovine ocular tissues from 750 to 1,000 nm, and compare the values obtained using different models.
Materials and methods
Ocular tissue preparation
Samples of bovine ocular tissues were provided by a local beef packer plant. A pair of eyes were enucleated fresh and transported in ice (within 1 h) to the research laboratory. Immediately upon arrival at the research laboratory, fresh (never frozen) whole eyes were dissected on ice with phosphate buffered saline (PBS) to separate and remove the desired ocular tissues for optical measurements. The eye was carefully dissected to allow access to the inner structures of the eye (e.g., vitreous humor). The eye was cut and separated into the anterior segment containing the cornea and the posterior cup containing the retina and the optic nerve. The cornea, lens, and retina were dissected and studied separately. The entire neurosensory retina was detached from the optic nerve and washed with PBS to remove any remaining retinal pigmented epithelial cells from the back surface. Removal of the retina from the posterior eye cup occurs last in the dissection. Tissue samples were mounted between glass slides and spacers are used to ensure samples were not distorted due to excessive compression. Individual sample thicknesses were measured. The data was collected at room temperature within 2 h from the sample preparation.
Measurement of diffuse reflectance and transmittance
The total diffuse reflectance (Rd), total diffuse transmittance (Td), and collimated transmittance (Tc) were measured using two identical integrating spheres (Oriel model 70674). The tissue sample was placed in a specially designed holder which fit on the ports connecting the integrating spheres. The measurements were performed on the bovine lens, cornea, and retina from 750 to 1,000 nm in increments of 50 nm.
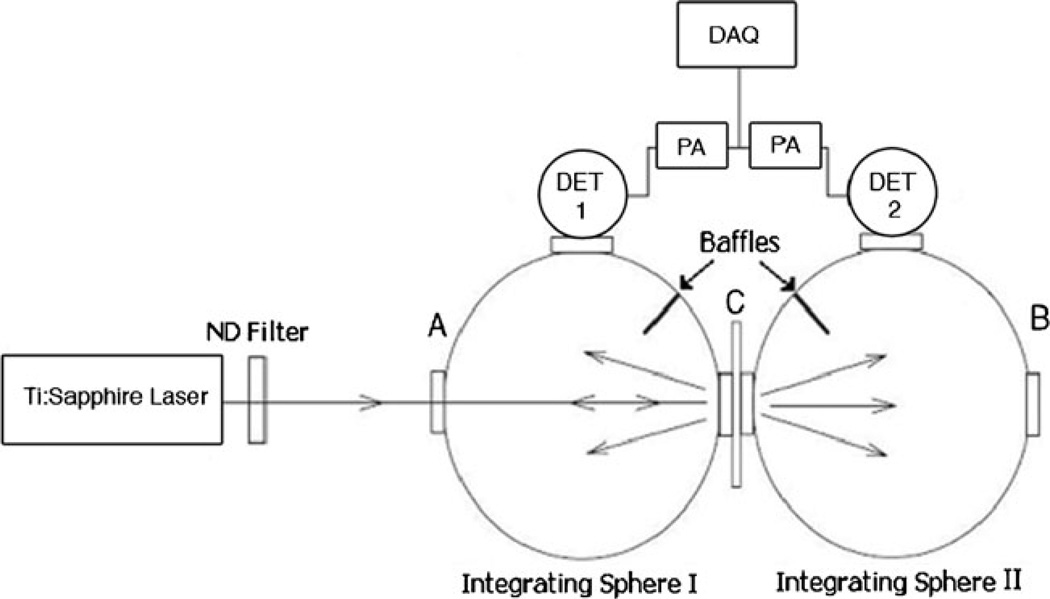
The schematic of the experimental setup for measuring the total diffuse reflectance and total diffuse transmittance is shown in Fig. 1 and is the same as was used in our previous work [21]. The laser beam was directed into the entrance port A of integrating sphere 1 (Oriel 70674) whose exit port is coupled with the entrance port of integrating sphere 2. The sample was mounted at the coupling port C. The exit port B of integrating sphere 2 was blocked by a cap with a reflective surface identical to that of the integrating spheres. The diameter of each sphere was 6 in. and each port had a diameter of 1.5 in. Light leaving the sample was reflected multiple times from the inner surfaces of the spheres before reaching the InGaAs detectors. The inner surfaces of the spheres are coated with a layer of barium sulfate to ensure a highly reflective Lambertian surface.
Fig. 1.
Experimental schematic for the diffuse reflection and transmission measurements of bovine ocular tissues. DET detector, PA preamplifier, DAQ data acquisition card
Reflecting baffles within the spheres shielded the detectors from light directly leaving the sample. The reflected and transmitted light intensities were detected by two identical InGaAs detectors (EG&G Judson model J16D-M204-R05M-60) mounted at the measuring ports of integrating spheres 1 and 2. The detector signals were enhanced with preamplifiers (EG&G Judson PA9) to decrease the signal-to-noise ratio. The signals were measured through a LABView analog signal recorder by way of a data acquisition card (NI ENET 1963) connected to a computer. The measured light intensities from each detector was then utilized to determine the total diffuse reflectance (Rd) and total diffuse transmittance (Td) by the following expressions:
| (7) |
and
| (8) |
where Xr is the reflected intensity detected by the remittance detector with the sample at C, Zr is the incident intensity detected by the remittance detector without the sample at C and with the reflective surface at the exit port C of the integrating sphere 1, Xt is the transmitted intensity detected by the transmittance detector with the sample at C and Zt is the incident intensity detected by the transmittance detector with no sample at C and with a reflective surface at B, and Y is the correction factor for the stray light measured by the detectors with no sample at C nor a reflective surface at B.
Measurement of collimated transmittance
The unscattered collimated transmittance (Tc) was measured to determine the total attenuation coefficient. The collimated laser beam intensities were measured by placing an integrating sphere approximately 1 m behind the sample to minimize the detection solid angle of the scattered photons, and the sample mounted at Port B of the reflectance sphere. Tc was calculated by the following relation:
| (9) |
where Xc is the collimated light intensity detected by a detector attached to the measuring port C of the integrating sphere and Zc is the incident light intensity detected with no sample in the light path; the reflective surface was placed at the exit port B of the integrating sphere in both cases.
Data analysis
Kubelka–Munk (KM) method
The KM coefficients, K and S, can be expressed in terms of μa and μs in the following forms:
| (10) |
where g is the scattering anisotropy coefficient. These coefficients can be expressed in terms of sample thickness (t), diffuse reflectance (Rd), and diffuse transmittance (Td) as follows [17]:
| (11) |
where
| (12) |
The collimated transmittance (Tc) can be written in terms of the absorption and scattering coefficients following Beer’s law:
| (13) |
where t is the sample thickness and measured in centimeters. By combining Eqs. (10) through (12), we can solve for the values of μa, μs, and g.
Inverse adding doubling (IAD) method
In order to obtain the values of μa and μs using the IAD method [10], the measured values of Rd, Td, and Tc were supplied to the IAD algorithm. The IAD algorithm iteratively chooses the values for the dimensionless quantities: a and τ, defined in Eqs. (5) and (6), respectively, and then adjusts the value of g until it matches the measured values of Rd and Td. The values of a and τ provided by the IAD method are then used to calculate μa and μs using Eqs. (5) and (6). Returned values are selected when the error tolerance has been achieved, where the error function is defined as
| (14) |
The default tolerance is set at 0.0001.
Inverse Monte Carlo (IMC) method
The scattering, absorption, and scattering anisotropy coefficients are obtained using a Monte Carlo (MC) simulation. The simulation involves tracking of a large number of photons through a turbid medium and keeps a tally of the absorption and scattering events using a probability distribution. This is an iterative process. The values of Rd, and Td, are measured experimentally. In the IMC mode, these values are provided as an initial set of inputs. The MC simulation is performed using a gradient algorithm and takes into account sphere parameters, geometries of the sample, and the incident beam to calculate Rd, Td, and Tc. Returned calculated values are then selected by minimizing a squared error function,
| (15) |
If the difference is smaller than the error threshold as determined by the program, δ<0.0004, the values of μa, μs, and g are validated.
Results and discussion
Measurements of Rd, Td, and Tc were repeated five times on the bovine lens, corneal and the retinal tissues from two samples in the region of 750 to 1,000 nm in 50 nm. The refractive indices used for our calculations were 1.37 for cornea, 1.40 for lens, and 1.34 for retina, and a range of 0.85–0.99 for the scattering anisotropy coefficient (g) [2]. Using the KM method, the experimental values were used to calculate the μa, μs for comparison. The experimental values of Rd, Td, Tc, and accepted values for the index of refraction and the scattering anisotropy coefficient, were input into the IAD program. The output of the IAD program provided the dimensional quantities a and τ, defined by Eqs. (5) and (6), respectively. The absorption and scattering coefficients were then calculated from the values of a and τ. Furthermore, the same initial values of Rd, Td, and Tc were also used in the MagicLight [21] inverse Monte Carlo program to obtain values for the coefficients. Figures 2, 3, 4, 5, 6, and 7 show the results for each tissue type, cornea, lens, and retina, as obtained by each method with the standard deviations with the specific values reported in Tables 1, 2, 3, 4, 5, and 6. C1, L1, and R1 denote the cornea, lens and retina of the first sample; C2, L2, and R2 denote the cornea, lens and retina of the second. KM denotes values obtained through the Kubelka–Munk method, IAD denotes those obtained through inverse adding doubling, and IMC denoted those obtained through inverse Monte Carlo.
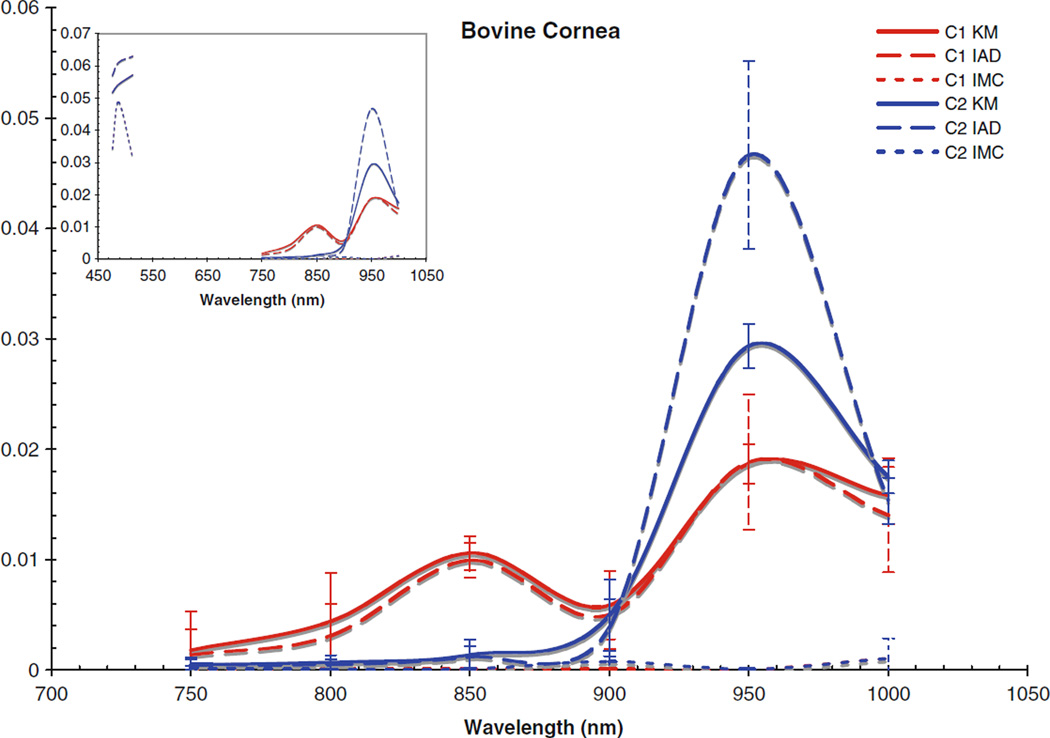
Fig. 2.
Absorption coefficient for bovine cornea. Inset includes data from the visible region
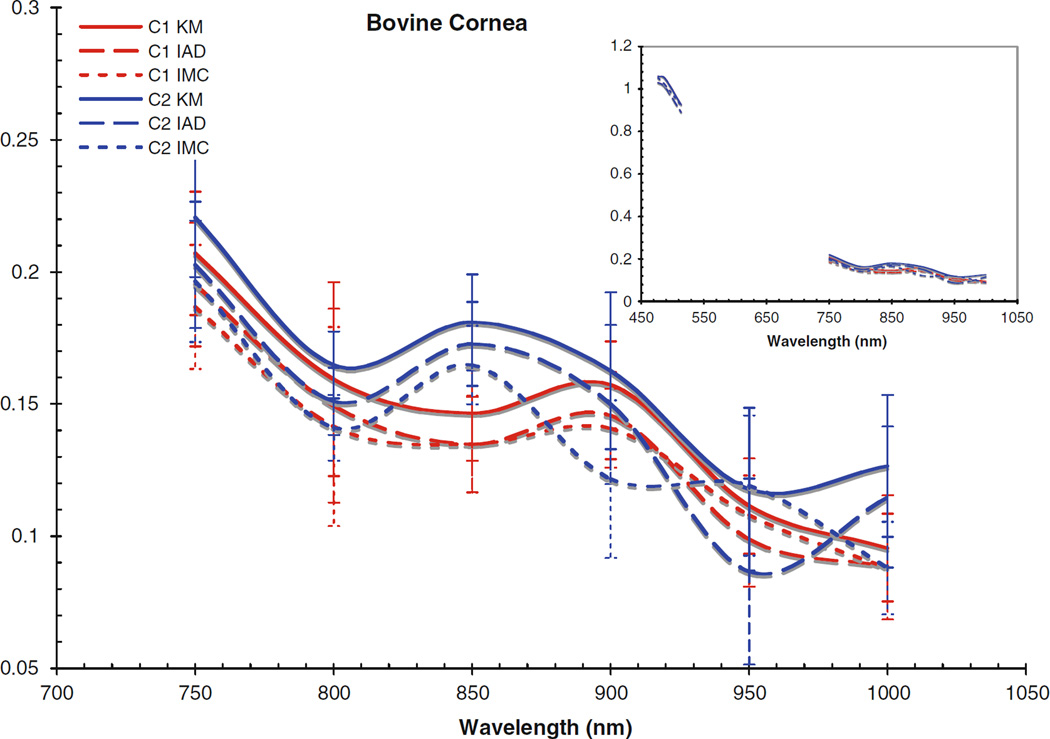
Fig. 3.
Scattering coefficient for bovine cornea. Inset includes data from the visible region
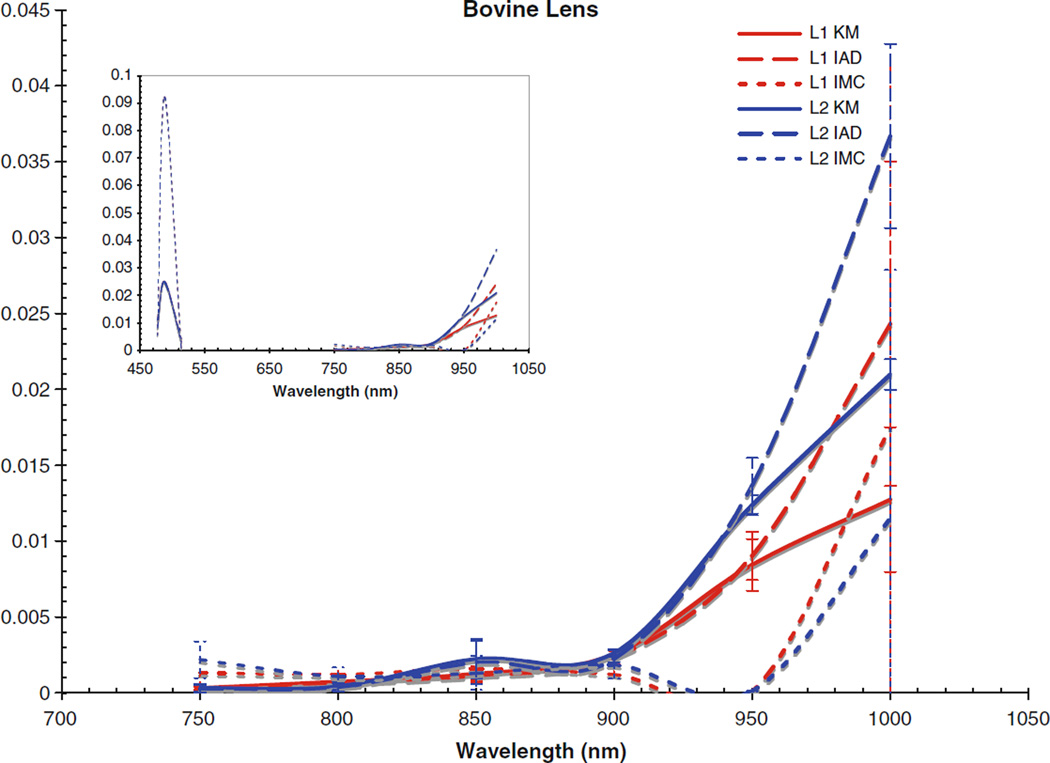
Fig. 4.
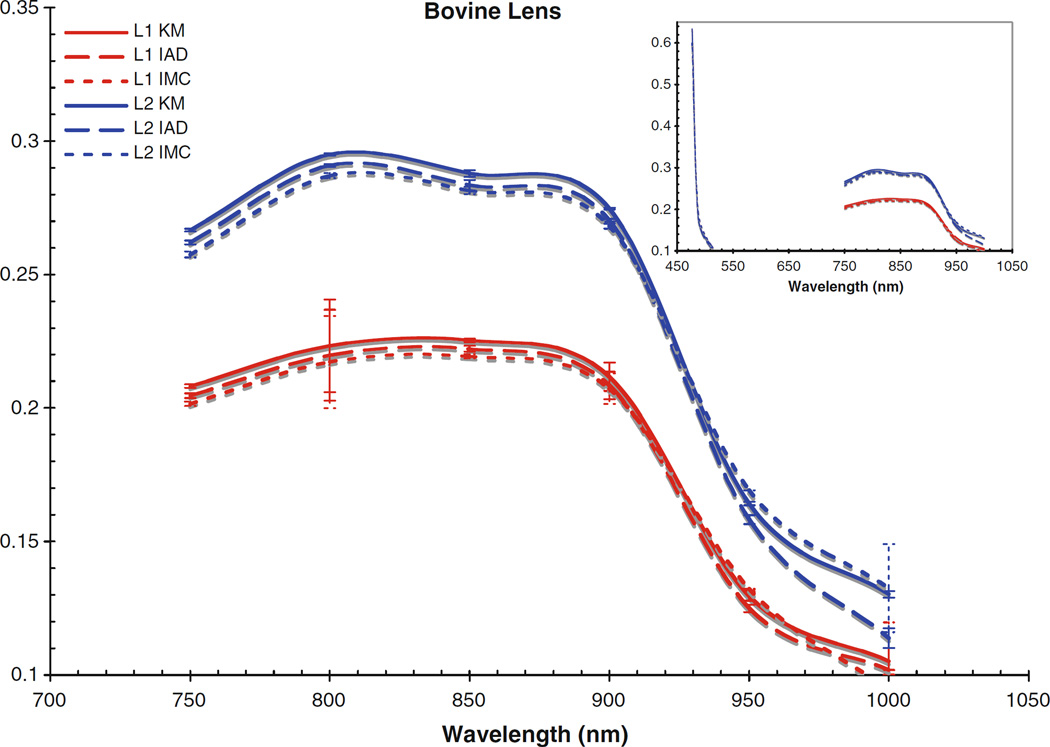
Absorption coefficient for bovine lens. Inset includes data from the visible region
Fig. 5.
Scattering coefficient for bovine lens. Inset includes data from the visible region
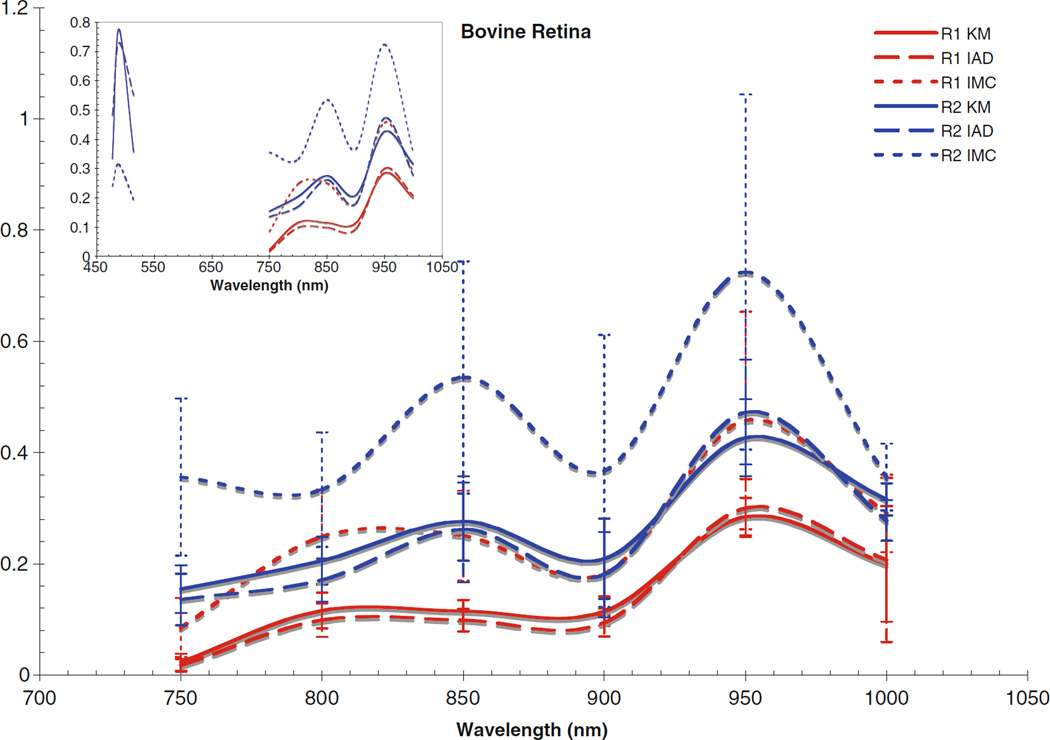
Fig. 6.
Absorption coefficient for bovine retina. Inset includes data from the visible region
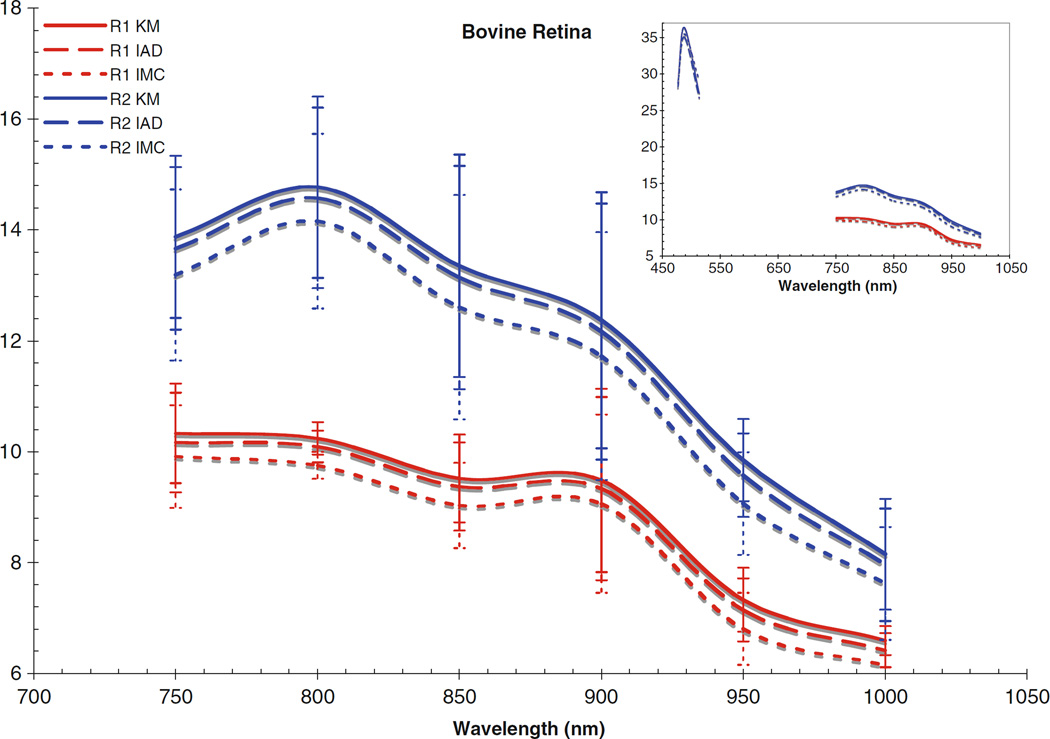
Fig. 7.
Scattering coefficient for bovine retina. Inset includes data from the visible region
Table 1.
Absorption and scattering coefficients for bovine cornea from sample 1
| Wavelength | KM | IAD | IMC | |||
|---|---|---|---|---|---|---|
| μa(mm−1) | μs(mm−1) | μa(mm−1) | μs(mm−1) | μa(mm−1) | μs(mm−1) | |
| 750 nm | 0.0018 | 0.2070 | 0.0014 | 0.1952 | 0.0000 | 0.1868 |
| 800 nm | 0.0044 | 0.1594 | 0.0031 | 0.1493 | 0.0001 | 0.1415 |
| 850 nm | 0.0106 | 0.1466 | 0.0100 | 0.1347 | 0.0001 | 0.1348 |
| 900 nm | 0.0059 | 0.1572 | 0.0050 | 0.1457 | 0.0001 | 0.1408 |
| 950 nm | 0.0187 | 0.1114 | 0.0188 | 0.0989 | 0.0000 | 0.1080 |
| 1,000 nm | 0.0158 | 0.0954 | 0.0140 | 0.0886 | 0.0011 | 0.0880 |
Table 2.
Absorption and scattering coefficients for bovine cornea from sample 2
| Wavelength | KM | IAD | IMC | |||
|---|---|---|---|---|---|---|
| μa(mm−1) | μs(mm−1) | μa(mm−1) | μs(mm−1) | μa(mm−1) | μs(mm−1) | |
| 750 nm | 0.0005 | 0.2205 | 0.0005 | 0.2026 | 0.0002 | 0.1964 |
| 800 nm | 0.0007 | 0.1648 | 0.0005 | 0.1510 | 0.0000 | 0.1411 |
| 850 nm | 0.0014 | 0.1809 | 0.0012 | 0.1727 | 0.0001 | 0.1648 |
| 900 nm | 0.0050 | 0.1626 | 0.0038 | 0.1498 | 0.0008 | 0.1216 |
| 950 nm | 0.0293 | 0.1178 | 0.0467 | 0.0866 | 0.0001 | 0.1192 |
| 1,000 nm | 0.0175 | 0.1266 | 0.0153 | 0.1148 | 0.0011 | 0.0880 |
Table 3.
Absorption and scattering coefficients for bovine lens from sample 1
| Wavelength | KM | IAD | IMC | |||
|---|---|---|---|---|---|---|
| μa(mm−1) | μs(mm−1) | μa(mm−1) | μs(mm−1) | μa(mm−1) | μs(mm−1) | |
| 750 nm | 0.0003 | 0.2082 | 0.0003 | 0.2046 | 0.0013 | 0.2016 |
| 800 nm | 0.0008 | 0.2233 | 0.0007 | 0.2198 | 0.0012 | 0.2172 |
| 850 nm | 0.0013 | 0.2253 | 0.0011 | 0.2222 | 0.0016 | 0.2194 |
| 900 nm | 0.0025 | 0.2117 | 0.0023 | 0.2085 | 0.0012 | 0.2073 |
| 950 nm | 0.0084 | 0.1295 | 0.0090 | 0.1250 | 0.0001 | 0.1322 |
| 1,000 nm | 0.0127 | 0.1052 | 0.0243 | 0.1020 | 0.0175 | 0.0946 |
Table 4.
Absorption and scattering coefficients for bovine lens from sample 2
| Wavelength | KM | IAD | IMC | |||
|---|---|---|---|---|---|---|
| μa(mm−1) | μs(mm−1) | μa(mm−1) | μs(mm−1) | μa(mm−1) | μs(mm−1) | |
| 750 nm | 0.0003 | 0.2666 | 0.0003 | 0.2621 | 0.0022 | 0.2575 |
| 800 nm | 0.0004 | 0.2950 | 0.0004 | 0.2908 | 0.0011 | 0.2871 |
| 850 nm | 0.0022 | 0.2878 | 0.0020 | 0.2834 | 0.0013 | 0.2815 |
| 900 nm | 0.0026 | 0.2747 | 0.0023 | 0.2703 | 0.0019 | 0.2681 |
| 950 nm | 0.0124 | 0.1642 | 0.0137 | 0.1582 | 0.0001 | 0.1692 |
| 1,000 nm | 0.0210 | 0.1303 | 0.0367 | 0.1138 | 0.0115 | 0.1325 |
Table 5.
Absorption and scattering coefficients for bovine retina from sample 1
| Wavelength | KM | IAD | IMC | |||
|---|---|---|---|---|---|---|
| μa(mm−1) | μs(mm−1) | μa(mm−1) | μs(mm−1) | μa(mm−1) | μs(mm−1) | |
| 750 nm | 0.0230 | 10.3293 | 0.0178 | 10.1686 | 0.0855 | 9.9128 |
| 800 nm | 0.1161 | 10.24O2 | 0.0988 | 10.0927 | 0.2487 | 9.7534 |
| 850 nm | 0.1154 | 9.5182 | 0.0987 | 9.3700 | 0.2505 | 9.0291 |
| 900 nm | 0.1145 | 9.4814 | 0.0943 | 9.3341 | 0.1819 | 9.0601 |
| 950 nm | 0.2849 | 7.3289 | 0.3004 | 7.1465 | 0.4579 | 6.8024 |
| 1,000 nm | 0.2000 | 6.5931 | 0.2069 | 6.4199 | 0.2907 | 6.1491 |
Table 6.
Absorption and scattering coefficients for bovine retina from sample 2
| Wavelength | KM | IAD | IMC | |||
|---|---|---|---|---|---|---|
| μa(mm−1) | μs(mm−1) | μa(mm−1) | μs(mm−1) | μa(mm−1) | μs(mm−1) | |
| 750 nm | 0.1543 | 13.8759 | 0.1357 | 13.6664 | 0.3561 | 13.1876 |
| 800 nm | 0.2055 | 14.7708 | 0.1709 | 14.5771 | 0.3331 | 14.1565 |
| 850 nm | 0.2759 | 13.3528 | 0.2620 | 13.1376 | 0.5352 | 12.6070 |
| 900 nm | 0.2090 | 12.3679 | 0.1806 | 12.1662 | 0.3670 | 11.7236 |
| 950 nm | 0.4265 | 9.8491 | 0.4727 | 9.5764 | 0.7247 | 9.0652 |
| 1,000 nm | 0.3157 | 8.1511 | 0.2778 | 7.9609 | 0.3558 | 7.6259 |
The computed scattering coefficients for all tissues and wavelengths agree very well, as can be seen in the figures. There is a wider degree of variation among the differently computed scattering coefficients, particularly in the IMC values of μs. This is likely due to the fact that the scattering influence of the tissue was so weak in this wavelength region; also, the IMC algorithm tended to converge to a solution for smaller computational photon packets (100’s or 1,000’s of photons). Despite this difficulty in achieving the optical coefficients using IMC, the results for μa do not vary so differently from those obtained through the other methods as to be unuseful as an indication to the scattering properties of the tissues. Indeed, the data obtained through IMC serves to highlight how well KM and IAD agree in their approximation of the scattering coefficients for these types of samples.
The corneas and lenses of both samples proved to be much more scattering than absorbing in the region of interest, which is expected per their biological function in the nearby visible spectrum. The retinas also had much higher scattering coefficients, nearly greater by an order of magnitude than the absorption coefficient. The corneas and lenses also showed more variance between measurements at a single wavelength in the scattering coefficients than the absorption coefficients over the spectrum, although this may be due to the extreme lowness of the absorbing power of these tissues in this region.
Of the tissue types investigated, the retinas had the highest values of μa and μs and showed the most variance in both coefficients, which is due to the high concentration of photopigments in the rods and cones. While these photoactive molecules serve the purpose of interacting with visible light so that the neural pathways associated with sight are triggered, it is well known that these pigments can still be scattering in the infrared region [22]. Indeed, mapping changes in the infrared reflectance has recently become a valid method of tracking the triggering events in the retina [23]. It is widely held that the infrared signal reflected is truly a good indication of the photochemical signaling in the retina because the hemoglobin present in the vasculature behind the retina does not interact with infrared light very strongly, although it is still unclear specifically which photopigments within the retinal layers are most responsible for a reflectance signal due to backscattering [23, 24]. The actual values of the absorption and scattering coefficients for the retinal tissues reported in this study have importance for practical applications requiring the prediction of light transport through tissue, e.g., in the design of treatment modalities for photodynamic therapy in the eye where the degree of interaction with light at the target sites may vary. Variable concentrations of photopigments obviously complicates the laser dosimetry for such treatment modes, because the amount of light delivered will have to be adjusted based on the amount of absorbing chromophores in order to achieve some standard clinical effect. Values in this region are of particular importance because of the recent interest in laser and scanning technologies in the infrared. Despite the small disagreements between the differently computed values, the general trends for interaction with light are clear for each tissue type. The cornea becomes slightly more absorbent and less scattering occurs as the wavelength reaches out into the infrared. The lens absorbs very weakly throughout the whole region, only becoming slightly more absorbent at 950 and 1,000 nm. There is an almost inverse correlation between the absorption and scattering influence of the lens, as the scattering coefficients remained rather constant until 950 and 1,000 nm, where they decreased. The retinas showed similar trends, with slight increases in μa towards the infrared and corresponding slight decreases in μs.
Comparing the coefficients to our previous work in the visible region [25], as shown in the figure insets for context, it can be seen that both cornea samples had noticeably lower values for μa and μs in the NIR than was found in the visible region. Conversely, the lenses and retinas had μa values in the NIR which were very similar to the visible region. The retinas were seen to have μs values that were slightly lower than in the visible region, and the lenses had μs values that were slightly higher; however, the difference between the two regions was not that great.
Conclusions
Optical characterization was performed for bovine corneas, lenses, and retinas using the double integrating sphere setup. The absorption and scattering coefficients computed using the Kubelka–Munk, inverse adding doubling, and inverse Monte Carlo techniques were compared and found to be in agreement. The values in the near-infrared were also compared to those found in the visible spectrum.
Acknowledgments
This work was supported by the NSF-sponsored Center for Biophotonics Science and Technology at UC Davis under Cooperative Agreement No. PHY 0120999. The authors would like to thank Scott Prahl (Oregon Medical Laser Center) for the use of the IAD source code, Steven L. Jacques (Oregon Medical Laser Center), and Lihong Wang (Washington University, St. Louis, MO) for the use of the source code for the Monte Carlo model. The source codes for both of these programs are available at http://omlc.ogi.edu/software/. Additionally, we would like to thank Ilya Yaroslavsky for use of the MagicLight algorithm for integrating sphere measurements. We also thank Dr. Kelly Nash for her insightful input.
References
- 1.Hammer M, Roggan A, Schweitzer D, Muller G. Optical properties of ocular tissues, an in vitro study using the double-integrating-sphere technique and inverse Monte Carlo simulation. Phys Med Biol. 1995;40:963–978. doi: 10.1088/0031-9155/40/6/001. [DOI] [PubMed] [Google Scholar]
- 2.Sardar DK, Swanland GY, Yow RY, Thomas RJ, Tsin ATC. Optical properties of ocular tissues in the near infrared region. Lasers Med Sci. 2007;22:46–52. doi: 10.1007/s10103-006-0421-y. [DOI] [PubMed] [Google Scholar]
- 3.van den Berg TJ, Spekreijse H. Near infrared light absorption in the human eye media. Vis Res. 1997;37:249–253. doi: 10.1016/s0042-6989(96)00120-4. [DOI] [PubMed] [Google Scholar]
- 4.Vos JJ, Munnik AA, Boogaard J. Absolute spectral reflectance of the fundus oculi. J Opt Soc Am. 1965;55:573–574. [Google Scholar]
- 5.Maher EF. Transmission and absorption coefficients for ocular media of the rhesus monkey. USAF School of Aerospace Med Brooks AF Base, TX, Report SAM-TR-78-32. 1978 [Google Scholar]
- 6.Bashkatov AN, Genina EA, Kochubey VI, Gavrilova AA, Kapralov SV, Grishaev VA, Tuchin VV. Optical properties of human stomach mucosa in the spectral range from 400 to 2000 nm: prognosis for gastroenterology. Med Laser Appl. 2007;22:95–104. [Google Scholar]
- 7.Gebhart SC, Lin WC, Mahadevan-Jansen A. In-Vitro determination of normal and neoplastic human brain tissue optical properties using inverse-adding doubling. Phys Med Biol. 2006;51:2011–2027. doi: 10.1088/0031-9155/51/8/004. [DOI] [PubMed] [Google Scholar]
- 8.Yaroslavsky AN, Schulze PC, Yaroslavsky IV, Schober R, Ulrich F, Schwarzmaier HJ. Optical properties of selected native and coagulated human brain tissues in vitro in the visible and near-infrared spectral range. Phys Med Biol. 2002;47:2059–2073. doi: 10.1088/0031-9155/47/12/305. [DOI] [PubMed] [Google Scholar]
- 9.Chandrasekhar S. Radiative transfer. Dover, New York: 1960. [Google Scholar]
- 10.Prahl SA, Van Gemert MJC, Welch AJ. Determining the optical properties of turbid media by using the adding-doubling method. Appl Opt. 1993;32:559–568. doi: 10.1364/AO.32.000559. [DOI] [PubMed] [Google Scholar]
- 11.Kubelka P. New contributions for the optics of intensely light-scattering materials. J Opt Soc Am. 1948;38:448–457. doi: 10.1364/josa.38.000448. [DOI] [PubMed] [Google Scholar]
- 12.Wan S, Anderson RR, Parish JA. Analytical modeling for the optical properties of the skin with in vitro and in vivo applications. Photochem Photobiol. 1981;34:493–499. doi: 10.1111/j.1751-1097.1981.tb09391.x. [DOI] [PubMed] [Google Scholar]
- 13.Ertefai S, Profio AE. Spectral transmittance and contrast in breast diaphanography. Med Phys. 1985;12:393–400. doi: 10.1118/1.595701. [DOI] [PubMed] [Google Scholar]
- 14.Reynolds L, Johnson CC, Ishimaru A. Diffuse reflectance from a finite blood medium: application to the modeling of fiberoptic catheters. Appl Opt. 1978;15:2059–2067. doi: 10.1364/AO.15.002059. [DOI] [PubMed] [Google Scholar]
- 15.Groenhuis RJA, Ferwerda HA, Ten Bosch JJ. Scattering and absorption of turbid materials determined from reflection measurements. 1: theory. Appl Opt. 1983;22:2456–2462. doi: 10.1364/ao.22.002456. [DOI] [PubMed] [Google Scholar]
- 16.van Gemert MJC, Welch AJ, Star WM, Motamedi M. Tissue optics for a slab geometry in diffusion approximation. Lasers Med Sci. 1987;2:295–302. [Google Scholar]
- 17.Kottler F. Turbid media with plane-parallel surfaces. J Opt Soc Am. 1960;50:483–490. [Google Scholar]
- 18.Hourdakis J, Perris A. A Monte Carlo estimation of tissue optical properties for use in laser dosimetry. Phys Med Biol. 1995;40:351–364. doi: 10.1088/0031-9155/40/3/002. [DOI] [PubMed] [Google Scholar]
- 19.Jacques SL, Wang L. Monte Carlo modeling of light transport in tissues. In: Welch AJ, van Gemert MJC, editors. Opticalthermal response of laser-irradiated tissue. New York: Plenum; 1995. [Google Scholar]
- 20.Sardar DK, Mayo ML, Glickman RD. Optical characterization of melanin. J Biomed Opt. 2001;6:404–411. doi: 10.1117/1.1411978. [DOI] [PubMed] [Google Scholar]
- 21.Yaroslavsky I, et al. Inverse hybrid technique for determining the optical properties of turbid media from integrating-sphere measurements. Appl Opt. 1996;35:6797–6809. doi: 10.1364/AO.35.006797. [DOI] [PubMed] [Google Scholar]
- 22.Abramoff M, Kwon Y, et al. Visual stimulus-induced changes in human near-infrared fundus reflectance. Investig Ophthalmol Vis Sci. 2006;47:715–721. doi: 10.1167/iovs.05-0008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Tsunoda K, Oguchi Y, et al. Mapping cone-and rod-induced retinal responsiveness in macaque retina by optical imaging. Investig Ophthalmol Vis Sci. 2004;45:3820–3826. doi: 10.1167/iovs.04-0394. [DOI] [PubMed] [Google Scholar]
- 24.Hanazono G, Tsunoda K, et al. Intrinsic signal imaging in macaque retina reveals different types of flash-induced light reflectance changes of different origins. Investig Ophthalmol Vis Sci. 2007;48:2903–2912. doi: 10.1167/iovs.06-1294. [DOI] [PubMed] [Google Scholar]
- 25.Sardar D, Yust B, et al. Optical absorption and scattering of bovine cornea, lens and retina in the visible region. Lasers Med Sci. 2009;24:839–847. doi: 10.1007/s10103-009-0677-0. [DOI] [PMC free article] [PubMed] [Google Scholar]