Abstract
Population structure inference with genetic data has been motivated by a variety of applications in population genetics and genetic association studies. Several approaches have been proposed for the identification of genetic ancestry differences in samples where study participants are assumed to be unrelated, including principal components analysis (PCA), multi-dimensional scaling (MDS), and model-based methods for proportional ancestry estimation. Many genetic studies, however, include individuals with some degree of relatedness, and existing methods for inferring genetic ancestry fail in related samples. We present a method, PC-AiR, for robust population structure inference in the presence of known or cryptic relatedness. PC-AiR utilizes genome-screen data and an efficient algorithm to identify a diverse subset of unrelated individuals that is representative of all ancestries in the sample. The PC-AiR method directly performs PCA on the identified ancestry representative subset and then predicts components of variation for all remaining individuals based on genetic similarities. In simulation studies and in applications to real data from Phase III of the HapMap Project, we demonstrate that PC-AiR provides a substantial improvement over existing approaches for population structure inference in related samples. We also demonstrate significant efficiency gains, where a single axis of variation from PC-AiR provides better prediction of ancestry in a variety of structure settings than using ten (or more) components of variation from widely used PCA and MDS approaches. Finally, we illustrate that PC-AiR can provide improved population stratification correction over existing methods in genetic association studies with population structure and relatedness.
Keywords: PCA, admixture, cryptic relatedness, pedigrees, GWAS
Introduction
Ancestry inference with genetic data is an essential component for a variety of applications in genetic association studies, population genetics, and both personalized and medical genomics. Advances in high-throughput genotyping technology have allowed for an improved understanding of continental-level and fine-scale genetic structure of human populations, as well as other organisms. Principal components analysis (PCA) [Patterson et al., 2006; Price et al., 2006] has been the prevailing approach in recent years for both population structure inference and correction of population stratification in genome-wide association studies (GWAS) with high-density single nucleotide polymorphism (SNP) genotyping data. Other widely used methods for inference on genetic ancestry include multi-dimensional scaling (MDS) [Purcell et al., 2007], a dimension reduction method similar to PCA, and model-based methods, such as STRUCTURE [Pritchard et al., 2000], FRAPPE [Tang et al., 2005], and ADMIXTURE [Alexander et al., 2009], for proportional ancestry estimation in samples from admixed populations.
Genetic studies often include related individuals; however, most existing population structure inference methods fail in the presence of relatedness. For example, the top principal components from PCA, as well as the top dimensions from MDS, can reflect family relatedness rather than population structure when applied to samples that include relatives [Price et al., 2010]. Model-based ancestry estimation methods similarly fail in the presence of relatedness as they are not able to distinguish between ancestral groups and clusters of relatives [Thornton and Bermejo, 2014]. For certain family-based study designs with known pedigrees, the population structure inference method proposed by Zhu et al. [2008], where SNP loadings calculated from a PCA on pedigree founders are used to obtain principal components values for genotyped offspring, can be used. However, this approach, which we refer to as “FamPCA,” fails in the presence of cryptic or misspecified relatedness and is not applicable to most GWAS where genealogical information on sample individuals is often incomplete or unavailable. The FamPCA method requires genotype data to be available for pedigree founders, which can be prohibitive for many genetic studies. In addition, inference on population structure is limited to the ancestries in the subset of genotyped founders, which may lack sufficient diversity to be representative of the ancestries in the entire sample [Chen et al., 2013].
We address the problem of population structure inference and correction in samples with related individuals. We do not put constraints on how the individuals might be related, and we allow for the possibility that genealogical information on sample individuals could be partially or completely missing. We propose a method, which we call PC-AiR (principal components analysis in related samples), for inference on population structure from SNP genotype data in general samples with related individuals. The PC-AiR method implements a fast and efficient algorithm for the identification of a diverse subset of mutually unrelated individuals that is representative of the ancestries in the entire sample. Axes of variation are inferred using this ancestry representative subset, and coordinates along the axes are predicted for all remaining sample individuals based on genetic similarities with individuals in the ancestry representative subset. The top axes of variation (principal components) from PC-AiR are constructed to be representative of ancestry and robust to both known or cryptic relatedness in the sample. A remarkable feature of PC-AiR is the method’s ability to identify a diverse and representative subset of individuals for ancestry inference using only genome-screen data from the sample, without requiring additional samples from external reference population panels or genealogical information on the study individuals.
We assess the robustness and accuracy of PC-AiR for inference on genetic ancestry in simulation studies with both related and unrelated individuals under various types of population structure settings, including admixture. We also directly compare PC-AiR to existing population structure inference methods using both simulated data and real genotype data from the Mexican Americans in Los Angeles, California (MXL) and African American individuals in the southwestern USA (ASW) population samples of release 3 of phase III of the International Haplotype Map Project (HapMap) [International HapMap 3 Consortium, 2010]. The population structure inference methods to which we compare PC-AiR are: (1) PCA with the EIGENSOFT [Price et al., 2006] software, (2) MDS with the PLINK [Purcell et al., 2007] software, (3) the model-based ancestry estimation methods FRAPPE [Tang et al., 2005] and ADMIXTURE [Alexander et al., 2009], and (4) FamPCA [Zhu et al., 2008] as implemented in the KING [Manichaikul et al., 2010] software. We also perform simulation studies to assess population structure correction with PC-AiR in GWAS with relatedness and ancestry admixture. We compare type-I error when using principal components from PC-AiR to other widely used population stratification correction methods including: (1) the EIGENSTRAT [Price et al., 2006] method, which uses PCA with EIGENSOFT to correct for population structure, and (2) the linear mixed model methods EMMAX [Kang et al., 2010] and GEMMA [Zhou and Stephens, 2012], which use variance components and an empirical genetic relationship matrix to simultaneously account for both population structure and relatedness among sample individuals.
Methods
Overview of the PC-AiR Method
Let the set be a sample of outbred individuals who have been genotyped in a genome-screen. An essential component of the PC-AiR method for population structure inference in the presence of relatedness is to use genome-screen data to partition into two non-overlapping subsets, and , i.e. with , where is a subset of mutually unrelated individuals who are representative of the ancestries of all individuals in , and is a “related subset” of individuals who have at least one relative in . We allow for individuals in to be related to each other in addition to having relatives in . PC-AiR uses measures of pairwise relatedness and ancestry divergence calculated using SNP genotype data from the autosomal chromosomes for the identification of , without requiring external reference panels or genealogical information. Population structure inference on the entire set of sample individuals, , is then obtained by first directly performing PCA on the selected ancestry representative subset, , and then predicting values along the components of variation for all individuals in the related subset, , based on genetic similarities with the individuals in . In the following subsections, we describe the PC-AiR method in detail.
Population Genetic Modeling Assumptions
The population genetic modeling assumptions we make are weak and are satisfied by commonly used models of population structure, such as the Balding-Nichols model [Balding and Nichols, 1995]. The individuals in set are assumed to have been sampled from a population with ancestry derived from K ancestral subpopulations. Let be the set of autosomal SNPs in the genome-screen, and for SNP , denote to be the vector of subpopulation-specific allele frequencies, where is the allele frequency at SNP s in subpopulation . We assume that the are random variables that are independent across s but with possible dependence across the k’s, with mean and covariance for every s, where 1 is a length K column vector of 1’s, and ΘK is a K × K matrix. In genetic models incorporating population structure, the allele frequency parameter ps is typically interpreted as an “ancestral” allele frequency, or some average of allele frequencies across subpopulations. Although we allow ΘK to be completely general, including allowing for non-zero covariances across subpopulations, a special case is the Balding-Nichols model, where ΘK is a diagonal matrix with (k, k)-th element equal to θk ⩾ 0, and θk is Wright’s standardized measure of variation, FST, for subpopulation k [Wright, 1949]. We allow for sample individuals to have admixed ancestry from the K subpopulations, and we denote to be the ancestry vector for individual , where is the proportion of ancestry across the autosomal chromosomes from subpopulation k for individual i, with for all k, and . In most contexts, the parameters K, ΘK, ps and ps for all , and ai for all will be unknown. The goal of PC-AiR is to obtain inference on ancestry, i.e. the ai’s, for all sample individuals in the presence of known or cryptic relatedness.
Relatedness Inference in Structured Populations
PC-AiR uses kinship coefficients to measure genetic relatedness between all pairs of individuals in , where the kinship coefficient for individuals i and j, which we denote as ϕij, is defined to be the probability that a random allele selected from i and a random allele selected from j at a locus are identical-by-descent (IBD). When the genealogy of the sample individuals is known, PC-AiR can use theoretical or pedigree-based kinship coefficients, and a number of software packages [Abney, 2009; Zheng and Bourgain, 2009] are available for obtaining kinship coefficients for pairs of individuals according to a specified genealogy. However, genealogical information on sample individual is often unknown, incomplete, or misspecified, and PC-AiR can also use empirical kinship coefficients estimated from genome-screen data for samples with cryptic relatedness that must be genetically inferred. It is important to note that relatedness estimators that assume population homogeneity, such as those implemented in the widely used PLINK software [Purcell et al., 2007] or obtained via a standard genetic relationship matrix (GRM) [Yang et al., 2010], are biased in samples from structured populations. Therefore, we do not recommended using kinship estimators developed for homogenous populations with PC-AiR as they have been demonstrated to give inflated relatedness estimates in samples with population structure [Manichaikul et al., 2010; Thornton et al., 2012], where (1) unrelated pairs of individuals with similar ancestry can have kinship-coefficient estimates corresponding to values that are expected for close relatives, and (2) related individuals can have a systematic inflation in their estimated degree of relatedness.
To use the PC-AiR method when pedigree relationships are unknown or incomplete, we recommend using empirical kinship coefficient estimates from methods that have been developed for samples from structured populations. One such estimator is KING (kinship-based inference for GWASs)-robust [Manichaikul et al., 2010]. KING-robust was developed for relatedness inference in samples from populations with discrete substructure, and it is a consistent estimator of the kinship coefficient for a pair of outbred individuals from the same subpopulation. This estimator, however, will generally be negatively biased for pairs of individuals that have different ancestries. Despite this bias, the KING-robust estimator is typically able to separate close relatives with similar ancestry from unrelated individuals, which is often sufficient for the PC-AiR method. Additionally, the PC-AiR method exploits the negative bias of the KING-robust estimator to gain insight on ancestry differences among individuals, as discussed in more detail in the following subsection.
Estimated kinship coefficients from the recently proposed REAP [Thornton et al., 2012] and RelateAdmix [Moltke and Albrechtsen, 2014] methods can also be used by PC-AiR. Both of these methods offer improved relatedness inference over KING-robust in samples with admixed ancestry by using external reference population panels such as HapMap. REAP and RelateAdmix, however, may not be suitable for some studies as they require (1) some prior knowledge about the ancestries that are likely present in the sample, and (2) appropriate reference panels with suitable surrogates for the ancestral subpopulations. KING-robust does not require external reference panels and can be used with PC-AiR for admixed samples with cryptic relatedness when the REAP and RelateAdmix methods may not be practical.
Measuring Ancestry Divergence with Genome-Screen Data
Pairwise measures of genetic relatedness, such as kinship coefficients, among individuals in a sample can be used for selecting a subset of mutually unrelated individuals [Staples et al., 2013]. In structured samples, however, identifying a subset of unrelated individuals based solely on relatedness measures can result in a subset that lacks sufficient diversity for population structure inference on the entire sample, as it may not be representative of the ancestries of all individuals. For the identification of an ancestry representative subset of mutually unrelated individuals, PC-AiR incorporates measures of ancestry divergence in addition to the previously discussed kinship coefficients used as measures of genetic relatedness.
Consider a pair of individuals i, who have non-missing genotype data at the set of autosomal SNPs in a genome-screen, and let denote the total number of SNPs in this set. Additionally, let the random variables gis and gjs be the number of copies of the reference allele that individuals i and j each have, respectively, at SNP ; thus, gis and gjs take values of 0, 1, or 2. To measure ancestry divergence between a pair of unrelated individuals i and j, we use the estimator
| (1) |
where is an indicator for individual i being heterozygous at SNP s, i.e. is 1 if gis = 1 and is 0 otherwise, and is similarly defined for individual j. Equation (1) is equivalent to the KING-robust estimator [Manichaikul et al., 2010] that has been proposed for estimating kinship coefficients of related individuals in samples from discrete subpopulations. Here we consider the KING-robust estimator under the general population genetic modeling assumptions previously discussed for i and j with admixed ancestry from K ancestral subpopulations, and the limiting behavior of this estimator is derived in Appendix A. For unrelated individuals i and j from the same subpopulation, as . However, when i and j have different ancestral backgrounds, is generally a negatively biased estimator of kinship, and this bias provides a useful measure of ancestry divergence between pairs of individuals. The magnitude of the negative bias depends on how different the ancestries are for the pair of individuals. The estimator has more extreme negative values when (1) the θk values are large, (2) i and j have large ancestry proportion differences, or (3) either i or j has an ancestry proportion that is close to 1 from one of the K subpopulations. For the special case when i and j are non-admixed and have ancestry from different subpopulations k and k′, the limiting value of the estimator reaches an extreme negative value with
| (2) |
PC-AiR uses the estimator given by Equation (1) for inference on ancestry divergence for all pairs of individuals i, who are not inferred to be related based on the kinship coefficient measures discussed in the previous subsection.
Identification of an Ancestry Representative Subset
We now provide details on how PC-AiR uses both the relatedness and ancestry divergence measures discussed in the previous two subsections for the identification of , a mutually unrelated subset of individuals that is representative of the ancestries of all individuals in the sample . Let be the kinship coefficient measure that is chosen for relatedness inference on a pair of individuals i, . When the genealogy of the sample individuals is known, could be a pedigree-based kinship coefficient, and when the genealogy is partially or completely unknown, should be an empirical kinship coefficient estimate from a relatedness estimation method that allows for population structure, e.g. the KING-robust estimator of Equation (1), REAP, or RelateAdmix. In order to identify all pairs of relatives in , a relatedness threshold, τϕ, is chosen such that i and j are designated to be related by the PC-AiR method if . When pedigree-based kinship coefficients are used with PC-AiR, all unrelated pairs have τϕ should be set to 0. When empirical kinship coefficient estimates are used, there is some noise in the estimation, and τϕ can be set to an approximate upper bound that is expected for the chosen kinship coefficient estimator for an unrelated pair. For example, when using KING-robust for relatedness inference, i.e. using we have found that 0.025 is an approximate upper bound with dense SNP genotyping data for unrelated pairs with the same ancestry, and setting τϕ = 0.025 works well in practice for identifying relatives with similar ancestry up to third-degree (and some fourth-degree) in a variety of population structure settings with ancestry admixture. For all sample individuals , we calculate as a measure of the total kinship individual i has with inferred relatives in the sample, where is the indicator that individual j is inferred to be related to i.
PC-AiR uses to infer ancestry divergence for all pairs of individuals i, who are not inferred to be relatives. We showed that is close to 0 for unrelated pairs with similar ancestry, while unrelated pairs with different ancestry have values that are systematically negative. We define a pair of individuals i and j to be “divergent” if they have different ancestral backgrounds, i.e. , where −τκ is the expected lower bound of for a pair of unrelated individuals with the same ancestry. Since the distribution of for unrelated pairs with the same ancestry is expected to be symmetric around 0, the vast majority of these pairs should satisfy when is large, where 0.025 is the previously mentioned approximate upper bound for unrelated pairs. We have found that setting −τκ = −0.025 works well in practice for identifying unrelated pairs of individuals with different ancestries. For all sample individuals , we calculate , the number of divergent ancestry pairs that individual i is a member of. Small δi values generally correspond to individuals with ancestry that is similar to the ancestries of many other individuals in , while the highest δi values generally correspond to individuals with unique ancestry and/or individuals with an ancestry proportion close to 1 from one of the subpopulations.
The algorithm used by PC-AiR for partitioning the set based on measures of ancestry divergence and kinship is presented in Appendix B. It is both fast and efficient, and the two subsets returned from the algorithm are the ancestry representative and mutually unrelated subset, , and the related subset, , where each individual in has at least one relative in . The algorithm is constructed in such a way that one individual from any set of mutually related individuals in is included in , with priority given to the individual who is a member of the most divergent ancestry pairs (large δi). This helps to ensure that every ancestry in is represented by some individual(s) in , while simultaneously satisfying the requirement that individuals in are also mutually unrelated. It also favors choosing the individuals with the highest ancestry proportions from each of the K subpopulations for . These individuals will be at the extremes of the K − 1 dimensional space spanned by the axes of variation representing the ancestries in , and selecting them for helps to avoid shrinkage in prediction of principal component values for individuals in . Secondary priority for inclusion in is given to individuals that share the most genetic information with their collection of relatives in (large γi), also allowing for better prediction of principal component values for relatives in .
Genetic Similarity Matrix for PC-AiR
The traditional PCA approach for population structure inference with genetic data, e.g., the EIGENSOFT method, performs PCA on standardized genotypes, where the standardized genotype value for individual i at SNP s is given by
| (3) |
and will typically be an allele frequency estimate for SNP s calculated using all sample individuals. The PC-AiR method also uses standardized genotypes, but the allele frequencies used for the standardization are calculated using only the unrelated individuals selected for . The standardized genotype values for PC-AiR are calculated from Equation (3) by setting , where
| (4) |
is the subset of individuals in who have non-missing genotype data at SNP s, and is the number of individuals in . In samples with related individuals and population structure, we have found that using the estimator provides better ancestry inference with PC-AiR than using allele frequency estimates calculated from the entire sample, which can be heavily influenced by the correlated genotypes among relatives. For any individual with a missing genotype value at SNP s, zis is set to 0, i.e. gis is set equal to , an estimate of its expected value. Provided that individuals with high levels of missingness are excluded from the analysis as a result of standard quality control [Laurie et al., 2010], a small percentage of mean imputed genotypes should not bias the results.
In addition to standard quality control filtering of SNPs with poor quality, minor allele frequency (MAF) filtering of rare variants is recommended for PC-AiR. LD pruning of SNPs, similar to what has been recommended for standard PCA [Patterson et al., 2006; Price et al., 2006], may also be beneficial, as high-density genotyping arrays contain clusters of highly correlated SNPs which can have strong influence on individual PCs in some settings [Novembre et al., 2008]. Let be the number of SNPs in the filtered set , and let n, nu, and nr be the number of individuals in set and subsets and , respectively, with n = nu + nr. We construct 𝗭, an standardized genotype matrix for , with (i, s)-th entry equal to zis, ordered such that the first nu rows correspond to individuals in , and the remaining nr rows correspond to individuals in . The standardized genotype matrix for is the submatrix 𝗭u corresponding to the first nu rows of 𝗭. Similarly, the submatrix 𝗭r is the standardized genotype matrix for corresponding to the last nr rows of 𝗭.
Similar to the traditional PCA approach, PC-AiR obtains a genetic similarity matrix (GSM) for population structure inference from standardized genotypes. It is important to note that PCA applied to a GSM that includes all individuals in , as in the traditional PCA approaches, leads to artifactual principal components for ancestry due to confounding from correlated genotypes among relatives, i.e. genetic similarities are reflecting alleles shared IBD among relatives. To protect against confounding caused by sample relatedness, PC-AiR instead calculates a GSM using only the mutually unrelated sample individuals who were selected to be included in the ancestry representative subset, . The empirical nu × nu GSM for calculated with the standardized genotype matrix 𝗭u is
| (5) |
and the (i, j)-th entry of provides a measure of the average genetic similarity across the autosomes for individuals i, .
Population Structure Inference in Related Samples with PC-AiR
To obtain principal components that are ancestry representative for a set containing related individuals, the PC-AiR method first performs a PCA [Jackson, 1991; Jolliffe, 1986] using genome-screen data from only those individuals selected to be in the mutually unrelated ancestry representative subset, . PCA applied to the real symmetric GSM from Equation (5) results in the eigendecomposition , where is an nu × nu matrix whose dth column vector, , is the dth principal component (axis of variation), and is a corresponding nu × nu diagonal matrix of eigenvalues. By construction, individuals in are mutually unrelated and have diverse ancestry, so the top principal components of are expected to be representative of ancestry. An SNP weight matrix giving the relative influence of each SNP on each of the nu axes of variation can be obtained as , and from the form of the eigendecomposition given above, it can be shown [Heath et al., 2008] that the matrix of principal components can alternatively be written as
| (6) |
Once PCA has been performed on the subset , the PC-AiR method predicts principal components values for the related subset, , by replacing 𝗭u, the standardized genotype matrix for individuals in , with 𝗭r, the standardized genotype matrix for individuals in , in Equation (6). The nr × nu matrix of predicted principal components for , which we denote as 𝗤r, is thus given by
| (7) |
The dth column vector of the matrix 𝗤r corresponds to PC-AiR’s predicted coordinates along the dth axis of variation for the individuals in . We define Γ to be the n × nu matrix of the combined principal components for and , where
| (8) |
The column vectors of Γ are the principal components (axes of variation) of the set obtained from the PC-AiR method. The genetic structure that is reflected by all of the principal components for PC-AiR are found using only the ancestry representative subset, , and thus the top principal components from Γ are designed to be representative of ancestry in , even in the presence of known or cryptic relatedness.
Simulation Studies
We perform simulation studies in which both population and pedigree structure are simultaneously present in order to (1) assess the accuracy and robustness of the PC-AiR method for population structure inference in the presence of relatedness, (2) evaluate correction for population stratification with PC-AiR in genetic association studies with cryptic structure, and (3) compare the performance of PC-AiR to existing methods. We simulate a variety of population structure settings, including admixture and ancestry-related assortative mating, with differentiation between populations ranging from subtle to large. We evaluate population structure inference for five different relationship configurations, where each configuration corresponds to a specific setting of genealogical relationships among the sample individuals. In all simulation studies considered, pedigree information on the sample individuals is hidden and genetic relatedness is inferred from the genotype data with the PC-AiR method using the KING-robust kinship estimator in Equation (1).
Population Structure Settings
The population structure settings we consider are similar to the settings in Price et al. [2006], where PCA was performed with the EIGENSOFT software in unrelated samples for inference on and adjustment for population structure in GWAS, except that our simulation studies include related individuals. We consider population structure settings where individuals have ancestry derived from two populations, and the allele frequencies at 100,000 SNPs for each of these two populations are generated using the Balding-Nichols model [Balding and Nichols, 1995]. More precisely, for each SNP s, the allele frequency ps in the ancestral population is drawn from a uniform distribution on [0.1, 0.9], and the allele frequency in population k ℰ {1, 2} is drawn from a beta distribution with parameters ps(1 − θk)/θk and (1 − ps)(1 − θk)/ θk. In all simulations, we set θ1 and θ2 equal to a common value, FST. We consider FST values of 0.01 and 0.1, respectively, to generate allele frequencies from closely related and divergent populations.
For both FST values considered, we simulate three population structure settings. Population structures I and II both consist of individuals sampled from an admixed population formed from populations 1 and 2. For population structure I, all unrelated individuals and pedigree founders have ancestry proportions a from population 1 and (1 – a) from population 2, with the parameter a for each individual drawn from a uniform distribution on [0, 1]. Population structure II is similar to population structure I, but with the ancestry parameter, a, drawn from a beta distribution with mean 0.4 and standard deviation 0.1 for 50% of the unrelated individuals and pedigree founders, and with mean 0.6 and standard deviation 0.1 for the other 50%. All founders within the same pedigree have a drawn from the same beta distribution for population structure II. Population structure III consists of non-admixed individuals, where 50% of the unrelated individuals and pedigrees are sampled from population 1, and the other 50% are sampled from population 2. Both population structure settings II and III have ancestry-related assortative mating, i.e., the mating of founder individuals in every pedigree occurs with individuals who have either the same (population structure III) or similar (population structure II) ancestry, while population structure I has random mating that is independent of ancestry.
Relationship Configurations
Four of the five relationship configurations simulated include both related and unrelated individuals. Relationship configuration I consists of 200 unrelated individuals and 200 individuals from 10 four-generation pedigrees, where each pedigree has a total of 20 individuals (Figure S1). Relationship configuration II is comprised of 280 unrelated individuals with 20 parent-offspring trios, and relationship configuration III includes 260 unrelated individuals with 20 sibling pairs. Relationship configuration IV includes only unrelated individuals and more distant relatives, and is comprised of 500 unrelated individuals, 12 first cousin pairs, 12 first cousin trios, and 10 first cousin quartets. To sample pedigree relationships within a given setting of population structure, we simulate genotypes for pedigree founders under Hardy-Weinberg equilibrium (HWE) according to the chosen population structure setting and then drop alleles down the pedigree. Relationship configuration V is 320 unrelated individuals without any family structure. We include the unrelated sample setting in our simulation studies in order to evaluate any potential loss in population structure inference with the PC-AiR method compared to standard PCA in a setting where standard PCA is appropriate and has been previously demonstrated to perform well.
Results
Subtle Population and Pedigree Structure
We first considered samples with subtle population structure, where the ancestry of the sample individuals is derived from two closely related populations. We set FST to 0.01 (a typical value for divergent European populations) and generated genotype data under population structure I for each of the five relationship configurations. Population structure inference with PC-AiR was compared to that of standard PCA with the EIGENSOFT software. To assess the performance of the two methods, we included the top principal components (axes of variation) from each method as predictors for the true simulated ancestry of the sample individuals in a linear regression model, and the proportion of ancestry explained, as measured by R2, was used to evaluate prediction accuracy. We also compared the efficiency of PC-AiR to EIGENSOFT by assessing the number of top axes of variation required to attain an R2 of at least 0.99 for ancestry. It should be noted that since the data in the simulation studies contained only one added dimension of population structure, an optimal method would require only a single axis of variation for complete ancestry inference. Both PC-AiR and EIGENSOFT were provided only genotype data without any additional pedigree information on the sample individuals.
Figure 1 displays the population structure inference results for relationship configuration I from both PC-AiR and EIGENSOFT. Figure 1B displays the top two axes of variation obtained by EIGENSOFT, which almost entirely reflected pedigree structure in the sample. The ten spikes of points radiating from the center cluster in the figure correspond to the individuals who are members of the ten pedigrees, and the cluster of points in the center of the plot corresponds to the 200 individuals who do not have any relatives in the sample. In contrast, the top two axes of variation from PC-AiR were not confounded by family structure, as illustrated in Figure 1A, and the top axis explained ancestry in the sample nearly perfectly, with an R2 of 0.993 (Figure 1C). Figure 1D shows that the top axis of variation from EIGENSOFT did not reflect population structure and did not adequately capture the ancestry of the sample individuals, with an R2 of only 0.133. The efficiency for population structure inference of both methods is illustrated in Figure 1E, where the proportion of ancestry explained (R2 values) for each of the top axes of variation is displayed. EIGENSOFT required the top 51 axes to be included as predictors in a linear regression model to achieve an R2 of at least 0.99 for ancestry. In contrast, a single axis of variation from PC-AiR had an R2 greater than 0.99, thus demonstrating a substantial improvement in efficiency with PC-AiR over EIGENSOFT in this setting with both subtle population structure and relatedness.
Figure 1.
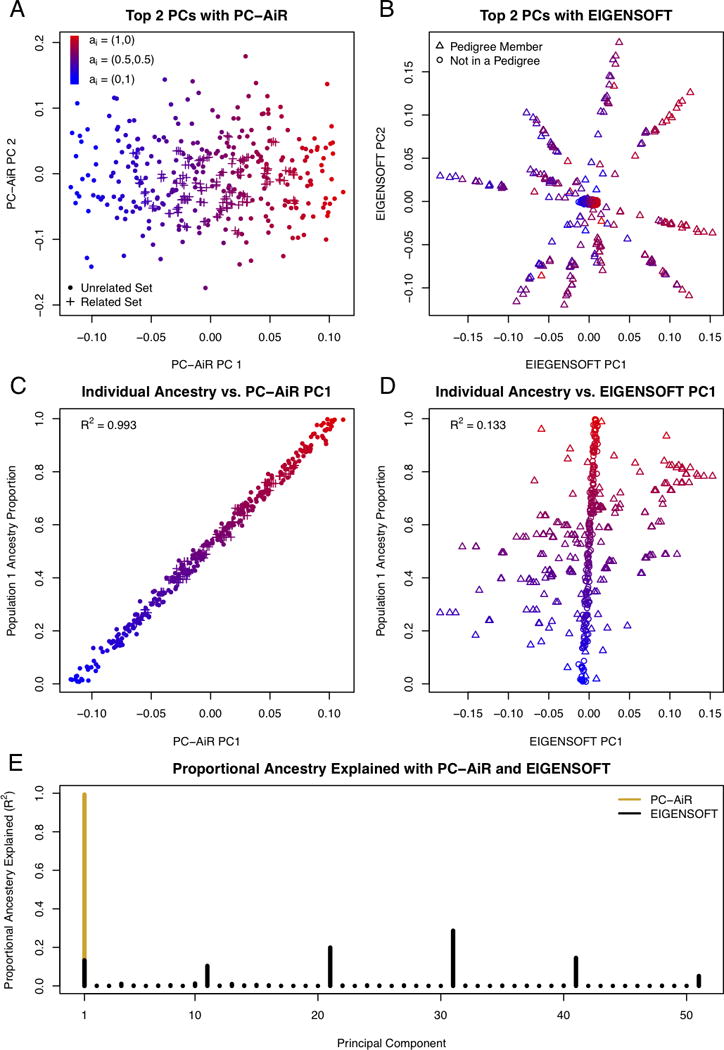
Comparison of PC-AiR and EIGENSOFT for Relationship Configuration I and Population Structure I with FST = 0.01.
(A and B) Scatter plots of principal components 1 and 2 from PC-AiR (A) and EIGENSOFT (B), respectively. (C and D) Scatter plots of the simulated population 1 ancestry proportions vs. coordinates along principal component 1 for each individual from PC-AiR (C) and EIGENSOFT (D), respectively. (A–D) The color of a point represents the simulated ancestry of an individual; red for population 1, blue for population 2, and an intermediate color for an admixed individual. (A and C) A dot represents an individual in the mutually unrelated ancestry representative set, and a plus represents an individual in the related set. (B and D) A circle represents an individual not in a pedigree, and a triangle represents an individual who is a member of a pedigree. (E) Barplot of the efficiency of PC-AiR and EIGENSOFT. Each bar represents the proportion of ancestry explained (R2 value) by each principal component from PC-AiR (gold) and EIGENSOFT (black), until a cumulative R2 of 0.99 is achieved.
The performance of PC-AiR and EIGENSOFT was also assessed for the remaining relationship configurations under population structure I. Population structure inference results for relationship configurations II and III are presented in Figures S2 and S3. The top axes of variation from EIGENSOFT were influenced by relatedness, as expected; however, since relationship configurations II and III have substantially less pedigree structure than relationship configuration I, there was some improvement in ancestry prediction with the top axis in each of these two settings, with R2 values of 0.870 and 0.933, respectively. For both of these relationship configurations, the top 21 axes of variation from EIGENSOFT were required to attain an R2 of at least 0.99 for predicting ancestry. In comparison, the PC-AiR analysis was robust to the relatedness in the sample, and the single top axis of variation from both relationship configurations attained an R2 value greater than 0.99. The results for relationship configuration IV, which consists of unrelated individuals and third-degree relatives, are presented in Figure S4. Accurate ancestry inference was obtained from the top axis of variation from both methods, with R2 values of 0.989 and 0.993 for PC-AiR and EIGENSOFT, respectively. Interestingly, the top axis of variation from EIGENSOFT attained a marginally higher R2 with ancestry than PC-AiR’s in this setting; however, as seen in Figure S4B, EIGENSOFT’s 2nd axis of variation reflected family structure in the sample. In fact, the 2nd through 35th axes of variation from EIGENSOFT all reflected familial structure in the sample, which could be problematic if these axes were incorrectly interpreted as representing population structure. In contrast, no axes beyond the first one from PC-AiR represented any identifiable sample structure. For relationship configuration V, PC-AiR accurately identified all sample individuals to be unrelated, i.e. the ancestry representative subset, , was the entire sample, , so the PC-AiR method reduced to standard PCA, and inference with either PC-AiR or EIGENSOFT was essentially identical. The R2 for ancestry with the top axis of variation from both methods was greater than 0.99, illustrating that there is no loss in accuracy or efficiency compared to standard PCA when using PC-AiR for population structure inference in samples where all individuals are unrelated.
We also evaluated the performance of PC-AiR and EIGENSOFT under population structures II and III with FST set to 0.01 for each of the relationship configurations, and the results are given in Table 1. Under population structure II, a single axis of variation from PC-AiR provided much better prediction of ancestry than using ten (or more) axes from EIGENSOFT for each of the four relationship configurations with related samples, including relationship configuration IV that consists of only unrelated individuals and third-degree relatives. For population structure III where individuals are sampled from discrete populations and there is no admixture, the top axis of variation from PC-AiR fully explained the ancestry, attaining an R2 > 0.99, for each of the relationship configurations. This was also true of EIGENSOFT, except for relationship configuration I, where 22 axes of variation were required to reach an R2 of at least 0.99. For relationship configuration V, where all sample individuals were unrelated, PC-AiR and EIGENSOFT gave identical results, with the top axis from both methods fully explaining the true ancestry.
Table 1.
Proportion of Ancestry Explained (R2) by PC-AiR and EIGENSOFT in Simulation Studies
| Relationship Configuration | Population Structure | FST | PC-AiR da = 1 |
EIGENSOFT | |||
|---|---|---|---|---|---|---|---|
| d = 1 | d = 4 | d = 10 | d*b | ||||
| I | I | 0.01 | 0.993 | 0.133 | 0.145 | 0.165 | 51 |
| 0.1 | 0.999 | 0.977 | 0.977 | 0.993 | 10 | ||
| II | 0.01 | 0.949 | 0.302 | 0.360 | 0.402 | 51 | |
| 0.1 | 0.998 | 0.741 | 0.741 | 0.755 | 41 | ||
| III | 0.01 | 0.999 | 0.832 | 0.832 | 0.832 | 22 | |
| 0.1 | 0.999 | 0.998 | 0.998 | 0.998 | 1 | ||
| II | I | 0.01 | 0.994 | 0.870 | 0.871 | 0.872 | 21 |
| 0.1 | 0.999 | 0.999 | 0.999 | 0.999 | 1 | ||
| II | 0.01 | 0.942 | 0.259 | 0.313 | 0.320 | 21 | |
| 0.1 | 0.998 | 0.983 | 0.983 | 0.984 | 21 | ||
| III | 0.01 | 0.999 | 0.990 | 0.990 | 0.990 | 1 | |
| 0.1 | 0.999 | 0.999 | 0.999 | 0.999 | 1 | ||
| III | I | 0.01 | 0.990 | 0.933 | 0.933 | 0.936 | 21 |
| 0.1 | 0.999 | 0.999 | 0.999 | 0.999 | 1 | ||
| II | 0.01 | 0.922 | 0.220 | 0.230 | 0.250 | 21 | |
| 0.1 | 0.997 | 0.992 | 0.992 | 0.993 | 1 | ||
| III | 0.01 | 0.998 | 0.995 | 0.995 | 0.995 | 1 | |
| 0.1 | 0.999 | 0.999 | 0.999 | 0.999 | 1 | ||
| IV | I | 0.01 | 0.989 | 0.993 | 0.993 | 0.994 | 1 |
| 0.1 | 0.999 | 0.999 | 0.999 | 0.999 | 1 | ||
| II | 0.01 | 0.921 | 0.747 | 0.747 | 0.762 | 23 | |
| 0.1 | 0.996 | 0.998 | 0.998 | 0.998 | 1 | ||
| III | 0.01 | 0.997 | 0.998 | 0.999 | 0.999 | 1 | |
| 0.1 | 0.999 | 0.999 | 0.999 | 0.999 | 1 | ||
d denotes the number of axes of variation included as predictors in the linear regression model to determine the R2 value for either PC-AiR or EIGENSOFT.
d* is the number of axes of variation from EIGENSOFT that are required to either match the R2 value of the first axis of variation from PC-AiR or achieve an R2 of 0.99, whichever is smaller.
Relatedness and Admixture from Divergent Populations
We also conducted simulation studies with relatedness and admixture from divergent populations. We considered relationship configuration I and population structure II, where we set FST to 0.1 (a value representative of continental-level ancestry differences) in the Balding-Nichols model to simulate allele frequencies at SNPs derived from two divergent populations. We evaluated and compared the performance of PC-AiR to PCA with the EIGENSOFT software, MDS with the PLINK software, and the two model-based methods ADMIXTURE and FRAPPE for proportional ancestry estimation. As in the previous subsection, no genealogical information on the sample individuals was provided to any of the analysis methods, so the FamPCA method could not be used as it is restricted to settings with known pedigrees. The ADMIXTURE and FRAPPE software analyses were conducted with the correct number of populations specified.
The population structure inference results for each method considered are shown in Figure 2, where each panel is a plot of the simulated population 1 ancestry proportions against the inferred ancestry from one of the methods. The top axis of variation from PC-AiR had an R2 of 0.998 and provided nearly perfect inference on ancestry for the sample individuals (Figure 2A). Similar to the EIGENSOFT results for the simulations with subtle population structure and relatedness, the top axis of variation did not adequately reflect the ancestry in this related sample with admixture from divergent populations, attaining an R2 of only 0.741 (Figure 2B). ADMIXTURE and FRAPPE gave identical ancestry proportion estimates for all individuals in the simulation, and Figure 2D shows estimated proportional ancestry plotted against the simulated ancestry proportions from population 1. These model-based ancestry estimation methods were confounded by the pedigree structure in the sample and performed similarly to PCA, with an R2 of only 0.730. While the top dimension of MDS achieved an R2 of 0.785 and provided some improvement in predicting ancestry over both of the model-based methods as well as the top axis of variation from EIGENSOFT, it was also confounded by sample relatedness, as shown in Figure 2C.
Figure 2.
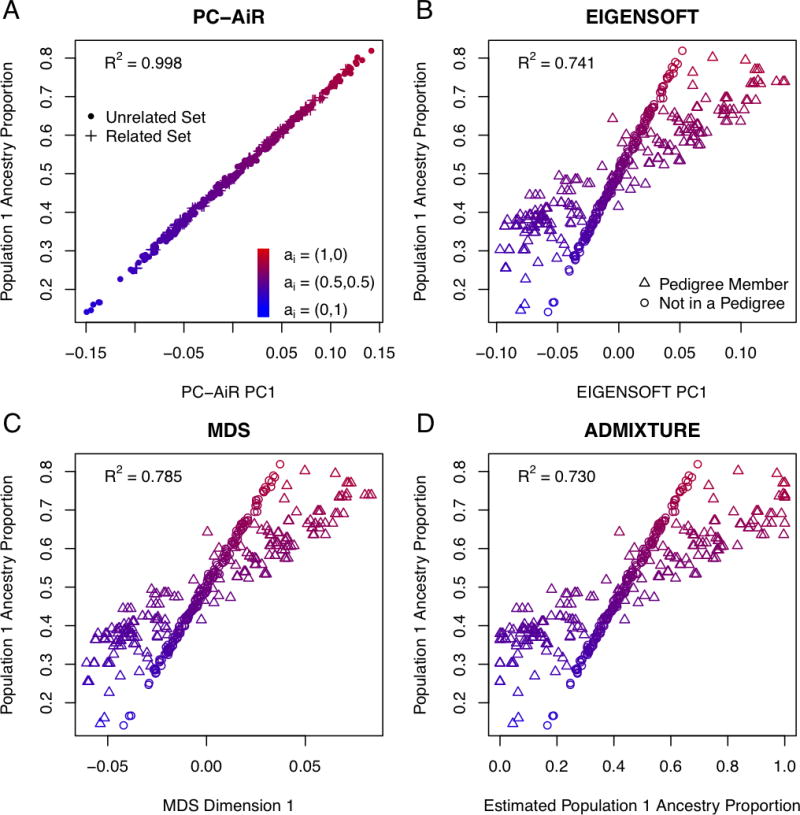
Population Structure Inference Results for Relationship Configuration I and Population Structure II with FST = 0.1.
Scatter plots of the simulated population 1 ancestry proportions for each individual are plotted against: (A) coordinates along principal component 1 from PC-AiR, (B) coordinates along principal component 1 from EIGENSOFT, (C) coordinates along dimension 1 from MDS, and (D) the estimated ancestry proportions from ADMIXTURE for the inferred population with the highest R2. The color of a point represents the simulated ancestry of an individual; red for population 1, blue for population 2, and an intermediate color for an admixed individual. (A) A dot represents an individual in the mutually unrelated ancestry representative set, and a plus represents an individual in the related set. (B–D) A circle represents an individual not in a pedigree, and a triangle represents an individual who is a member of a pedigree.
We also evaluated the performance of PC-AiR and EIGENSOFT for all combinations of relationship configurations and population structure settings with FST set to 0.1 (Table 1). For all settings considered, the top axis of variation from PC-AiR gave nearly perfect ancestry inference, attaining an R2 > 0.99. The extent to which PCA with EIGENSOFT was confounded by the relatedness depended on how complex the pedigree structure was; however, a single axis of variation from PC-AiR always performed as well as or better than using ten axes of variation from EIGENSOFT for ancestry prediction.
Ancestry Inference and Prediction in Related Samples with Reference Panels
Reference population panels are commonly used for improved ancestry inference in unrelated samples from admixed populations, such as African Americans and Hispanics. We conducted a simulation study evaluating population structure inference with reference panels in admixed samples with relatedness. We considered the same simulation study discussed in detail in the previous subsection, but we now included reference panels consisting of 50 unrelated individuals randomly sampled from each of the two underlying populations. The same population structure methods from the previous subsection were used, and the results are displayed in Figure S5. Ancestry inference with EIGENSOFT, MDS, ADMIXTURE, and FRAPPE was substantially improved by including the reference panels as compared to the analyses without them, but PC-AiR still outperformed all methods, with the top axis of variation achieving an R2 of 0.999 with ancestry. The analyses with ADMIXTURE and FRAPPE, which were run supervised with the reference population samples included as fixed groups and specified in the analysis, gave identical results to each other as they did in the unsupervised analysis discussed in the previous subsection, and the estimated ancestry proportions had an R2 of 0.973 with the simulated ancestries. Similarly, the top axis of variation from each of EIGENSOFT and MDS reached R2 values of 0.970 and 0.979 respectively.
Interestingly, from the previous subsection we have that the top axis of variation from PC-AiR without including additional reference population samples had an R2 of 0.998 and thus provided better ancestry inference than all of the competing methods with the reference panels. Even with the inclusion of reference panels, there remained some bias in ancestry inference for all methods, except for PC-AiR, that was induced by the presence of related individuals in the sample. This can be seen in Figure S5, where the inferred ancestries for individuals with relatives in the sample were systematically biased for each of the competing methods. We have found that conducting separate supervised individual ancestry analyses with ADMIXTURE (or FRAPPE) for each of the admixed samples, i.e. analyses with genotype data from a single admixed sample individual and all individuals in the reference population panels included, can remove the bias caused by sample relatedness, known or cryptic, as long as the reference panel samples are appropriate surrogates for the underlying populations. We performed separate individual analyses that were supervised with ADMIXTURE for each sample individual, and the estimated ancestries attained an R2 of 0.999, the same as PC-AiR.
Recent work [Chen et al., 2013; Ma and Amos, 2012] has shown that ancestry proportions can be predicted from principal components analysis in unrelated samples. Using the methodology described in Chen et al. [2013], principal components from PC-AiR can similarly provide accurate prediction of ancestry proportions in samples with relatedness (Figure S6). Despite the fact that PC-AiR can provide accurate ancestry inference without using reference population samples, we recommend including reference panels when predicting ancestry proportions from principal components, as we have found that ancestry proportion estimates will be biased if individuals with 100% ancestry from each of the underlying populations are not available for the PCA.
Correcting for Structure in Genetic Association Studies
We also performed simulation studies to compare population structure correction in genetic association studies with PC-AiR to existing approaches. Allele frequencies were generated at 100,000 null SNPs for two ancestral populations with FST set to 0.1. We define to be the absolute difference in the reference allele frequencies between ancestral populations 1 and 2 at SNP s. We also define three classes of SNPs based on Ds, where SNPs with Ds < 0.2, 0.2 ≤ Ds < 0.4, and Ds ⩾ 0.4 were considered to have “low differentiation,” “moderate differentiation,” and “high differentiation,” respectively. Of these 100,000 SNPs, approximately 70%, 25%, and 5% of the SNPs were lowly, moderately, and highly differentiated. Genotype data was generated under population structure II for sample individuals related according to relationship configuration I, and for each individual i in the sample, a quantitative trait value yi was simulated according to the model where is the genome-wide ancestry proportion from population 1 for individual i, gi is the number of alleles individual i has at the causal SNP, and εi ~ N(0, 1) is a random environmental effect assumed to be acting independently on individuals. The frequency of the selected casual variant in populations 1 and 2 was 0.13 and 0.17, respectively.
The following statistical methods were evaluated for genetic association testing: linear regression without ancestry adjustment; EIGENSTRAT; linear regression with principal components from PC-AiR included as fixed effects; GEMMA [Zhou and Stephens, 2012] and EMMAX [Kang et al., 2010], which are “exact” and “approximate” linear mixed effects model methods, respectively, that use an empirical genetic relationship matrix to capture both population and pedigree sample structure; and EMMAX with principal components from EIGENSOFT or PC-AiR included as fixed effects. For the association analyses, each null SNP was included as a fixed effect in the statistical models and was tested for association with the simulated quantitative trait. The genomic control inflation factor [Devlin and Roeder, 1999] λGC was used to evaluate confounding due to unaccounted for sample structure, where λGC ≈ 1 indicates appropriate correction for population and family structure, while λGC > 1 indicates elevated type-I error.
The results of the simulations are given in Table 2. As expected, all of the association tests using linear regression models have inflated type 1 error since these methods either (1) do not account for any of the sample structure, or (2) account for population structure but not relatedness. Including a single principal component from PC-AiR in the linear regression model results in a lower λGC compared to EIGENSTRAT with the top ten principal components for all classes of SNPs. This is due to the top PC from PC-AiR nearly perfectly explains ancestry (R2 = 0.998), while the top 10 PCs from EIGENSOFT have an R2 of only 0.672 for ancestry because of the relatedness in the sample. The mixed model approaches considered, EMMAX and GEMMA, are also not properly calibrated, with λGC > 1 for SNPs with moderate to high differentiation, and λGC < 1 for SNPs with low differentiation. EMMAX with the top ten PCs from EIGENSOFT included as fixed effects is still not properly calibrated due to insufficient correction for population stratification. However, including a single PC from PC-AiR as a fixed effect with EMMAX results in appropriate calibration of the association test statistics, with λGC = 1 for all classes of SNPs.
Table 2.
Genomic Control λGC for Association Testing Simulation Study
| Method | Highlya Differentiated | Moderatelyb Differentiated | Lowlyc Differentiated |
|---|---|---|---|
|
| |||
| Linear Regression | 3.16 | 1.82 | 1.25 |
| EIGENSTRAT with 10 PCs | 1.19 | 1.12 | 1.07 |
| Linear Reg. + 1 PC from PC-AiR | 1.04 | 1.05 | 1.05 |
| GEMMA | 1.35 | 1.10 | 0.95 |
| EMMAX | 1.32 | 1.08 | 0.94 |
| EMMAX + 10 PCs from EIGENSOFT | 1.07 | 1.02 | 0.98 |
| EMMAX + 1 PC from PC-AiR | 1.00 | 1.00 | 1.00 |
Highly differentiated SNPs have allele frequency differences ⩾ 0.4 between the two ancestral populations.
Moderately differentiated SNPs have allele frequency differences < 0.4 and ⩾ 0.2 between the two ancestral populations.
Lowly differentiated SNPs have allele frequency differences < 0.2 between the two ancestral populations.
Population Structure Inference in Admixed HapMap Samples
HapMap MXL Data
We analyzed high-density SNP genotype data from the Mexican Americans in Los Angeles, California (MXL) population sample of HapMap 3 for population structure inference. We applied PC-AiR, EIGENSOFT, MDS, ADMIXTURE, and FamPCA to the 86 genotyped individuals, and we compared the population structure inference results of these methods to a supervised individual ancestry estimation analysis with ADMIXTURE that included continental reference population panels. For the supervised analysis with ADMIXTURE, the number of ancestral populations was set to 3, for which the HapMap CEU (Utah residents with ancestry from northern and western Europe from the Centre d’Etude du Polymorphisme Human collection) and YRI (Yoruba in Ibadan, Nigeria) samples were included as the reference population panels for European and African ancestry, respectively, and for which the Human Genome Diversity Project (HGDP) [Li et al., 2008] samples from the Americas were included for Native American ancestry. The analyses were based on the set of 150,872 autosomal SNPs that were genotyped in both the HapMap and HGDP datasets. To protect against potential confounding due to relatedness in the supervised ancestry analysis, a separate ADMIXTURE analysis was conducted for each of the HapMap MXL individuals, where each analysis included a single HapMap MXL individual and the reference population panels. All methods, except for FamPCA, were only provided the SNP genotype data on the sample individuals for population structure inference, without any additional information on the pedigree relationships. The FamPCA method was also provided the documented pedigrees in the HapMap MXL which includes 24 genotyped trios, 5 families with two genotyped individuals, and 4 families with a single genotyped individual. The PC-AiR method used the KING-robust kinship coefficient estimator in Equation (1) and the relatedness threshold τϕ = 0.025 to infer genetic relatedness in the sample, and a MAF filter of 5% was used on SNPs for population structure inference.
Figure 3F presents a bar plot of the results from the supervised individual ADMIXTURE ancestry analysis. In the bar plot of ancestry proportion estimates, individuals (vertical bars) are arranged in increasing order (left to right) of genome-wide European ancestry proportion. Our proportional ancestry estimates were similar to the results from previous supervised analyses of this data [Gravel et al., 2013; Thornton et al., 2012]. HapMap MXL individuals have modest African ancestry with little variation, with a mean of 6% and a standard deviation (SD) of 1.8%. The sample individuals are largely derived from European and Native American ancestry, with means of 49.9% (SD=14.8%) and 44.1% (SD=14.8%) respectively. Since the European and Native American ancestry proportions are predominant, nearly perfectly negatively correlated (with a correlation of −0.99), and quite variable, ranging from 18.0% to 91.0% and from 4.2% to 80.4% respectively, we expected that an optimal population structure inference method would require only a single axis of variation to explain these two ancestries in the HapMap MXL.
Figure 3.
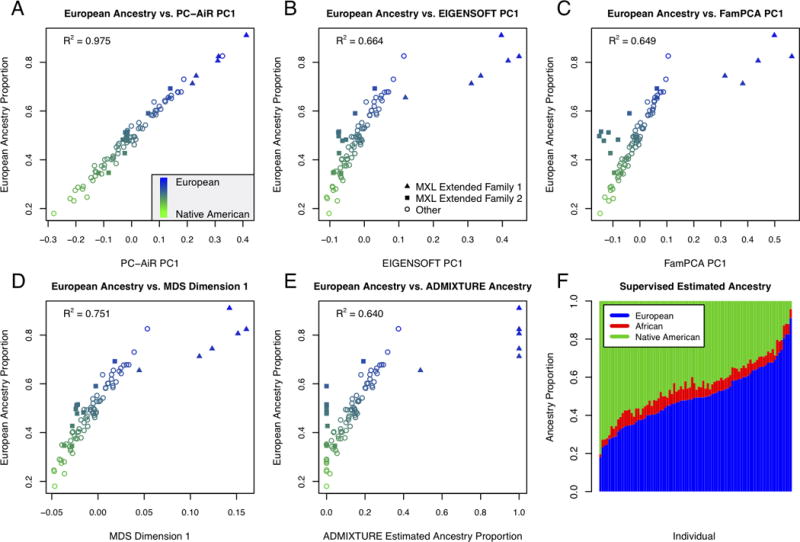
Comparison of Population Structure Inference for the HapMap MXL Sample.
Scatter plots of the European ancestry proportions estimated from a supervised individual ancestry analysis with ADMIXTURE for each individual are plotted against: (A) coordinates along principal component 1 from PC-AiR, (B) coordinates along principal component 1 from EIGENSOFT, (C) coordinates along principal component 1 from FamPCA, (D) coordinates along dimension 1 from MDS, and (E) the estimated ancestry proportions from an unsupervised analysis with ADMIXTURE for the inferred population with the highest R2. The color of a point represents the ancestry of an individual as estimated from a supervised individual ancestry analysis with ADMIXTURE; blue for European, green for Native American, and an intermediate color for an admixed individual. Individuals who are members of MXL Extended Family 1 or 2 are plotted as triangles or squares, respectively, and remaining individuals are plotted as circles. (F) Individual ancestry estimates for 86 HapMap MXL samples from a supervised individual ancestry analysis with ADMIXTURE. Each individual is represented by a vertical bar; estimated European (HapMap CEU), African (HapMap YRI), and Native American (HGDP samples from the Americas) ancestry proportions are shown in blue, red, and green, respectively.
The population structure inference results for European and Native American ancestry in the HapMap MXL are given in Table 3. PC-AiR’s top axis of variation was nearly perfectly correlated with European (and Native American) ancestry, as estimated from the supervised individual ADMIXTURE ancestry analysis, with an R2 of 0.98 (Figure 3A). In contrast, the top axis of variation from each of EIGENSOFT, FamPCA, and MDS had an R2 for European ancestry of only 0.66, 0.65, and 0.75 respectively. For the unsupervised ADMIXTURE analysis that did not include reference panels, the highest R2 for either European or Native American ancestry with any estimated ancestry component was only 0.64. Figures 3B, 3C, 3D, and 3E illustrate that ancestry inference in the HapMap MXL for each of these competing methods was confounded by relatedness, including the FamPCA method, which was provided the documented pedigree relationships. Ancestry inference with FamPCA was confounded by cryptic relatedness present in the HapMap MXL including a previously reported [Thornton et al., 2012] extended pedigree consisting of two smaller documented pedigrees, which are labeled in Figure 3 as MXL Extended Family 1. Without being provided any pedigree information, a single axis of variation from PC-AiR gave better prediction of both European and Native American ancestry than the top ten axes from EIGENSOFT, MDS, and FamPCA, as shown in Table 3. Remarkably, without using any reference population samples the top axis of variation from PC-AiR gave comparable ancestry inference on European and Native American ancestry to a supervised ancestry analysis that included reference panels, similar to the results from the simulation studies.
Table 3.
Population Structure Inference Results for HapMap MXL and ASW
| R2 Values | ||||||
|---|---|---|---|---|---|---|
| Ancestry | da | PC-AiR | EIGENSOFTb | MDSc | FamPCAd | ADMIXTUREe |
| MXL Sample | ||||||
| European | 1 4 10 |
0.975 – – |
0.664 0.914 0.924 |
0.751 0.935 0.943 |
0.649 0.969 0.970 |
0.640 – – |
| Native American | 1 4 10 |
0.977 – – |
0.661 0.908 0.911 |
0.748 0.929 0.932 |
0.651 0.968 0.969 |
0.633 – – |
| MXL + ASW Sample | ||||||
| European | 2 4 10 |
0.988 – – |
0.858 0.868 0.963 |
0.892 0.899 0.970 |
0.862 0.878 0.987 |
0.615 – – |
| Native American | 2 4 10 |
0.995 – – |
0.953 0.958 0.987 |
0.962 0.967 0.989 |
0.951 0.961 0.996 |
0.866 – – |
| African | 2 4 10 |
0.999 – – |
0.996 0.996 0.999 |
0.997 0.997 0.999 |
0.997 0.997 0.999 |
0.990 – – |
Population structure inference results from each method were compared to ancestry estimates from a supervised individual ancestry analysis with ADMIXTURE including reference population panels.
d denotes the number of axes of variation included as predictors in the linear regression model to determine the R2 value for each of the methods.
PCA was performed with the EIGENSOFT software.
MDS was implemented in the PLINK software.
FamPCA is the Zhu et al. [2008] method as implemented in the KING [Manichaikul et al., 2010] software.
An unsupervised ADMIXTURE analysis was conducted without including reference population panels. FRAPPE results were identical to ADMIXTURE.
Combined HapMap ASW and MXL Data
To evaluate the performance of the population structure inference methods in an admixed population structure setting with three predominant continental ancestries and relatedness, we considered an analysis of the combined HapMap ASW (African American individuals in the southwestern USA) and MXL samples. Similar to our ancestry estimation analysis of the HapMap MXL, we also conducted a supervised individual ADMIXTURE analysis for the 87 genotyped individuals in the HapMap ASW with reference population panels included for European, Native American, and African ancestries. Figure S7A shows a barplot of the results from the supervised individual ADMIXTURE ancestry analysis of the HapMap MXL and ASW samples, which illustrates that these populations have very different ancestral backgrounds. Most of the HapMap ASW ancestry is African, with a mean of 77.5% (SD=8.4%). There is also a large European ancestry component, with a mean of 20.5% (SD=7.9%); however, unlike the HapMap MXL, there is very little Native American ancestry in the HapMap ASW, with a mean of only 1.9% (SD=3.5%). Since there are three predominant continental ancestries in the combined HapMap ASW and MXL samples, we expected that an optimal method would require two axes of variation to fully explain continental population structure.
We applied each of the dimension reduction methods (i.e. PC-AiR, EIGENSOFT, MDS, and FamPCA) to the combined HapMap ASW and MXL samples and compared the results to the supervised individual ancestry analysis with ADMIXTURE that included the reference population panels; results are shown in Table 3. All of the methods were able to fully explain the African ancestry with two axes of variation, achieving R2 values greater than 0.99. For European ancestry, PC-AiR’s top two axes of variation achieved an R2 value of 0.99, while the top two axes from each of the competing population structure methods had R2 values less than 0.90. With an R2 value greater than 0.99, PC-AiR’s top two axes of variation also explained Native American ancestry better than the top two axes from EIGENSOFT, MDS, and FamPCA, with corresponding R2 values of 0.95, 0.96, and 0.95, respectively. These results are illustrated in Figure 4, where we can see that the top two axes of variation from each of these methods, except PC-AiR, were confounded by relatedness. In fact, the top ten axes of variation from EIGENSOFT, MDS, and FamPCA were highly confounded by pedigree structure, whereas axes beyond the top two from PC-AiR did not represent any identifiable structure and appear to be random noise (Figures S8 – S12). As a consequence, the top ten axes of variation from both EIGENSOFT and MDS were not able to explain European and Native American ancestry as well as the top two axes from PC-AiR. Intersetingly, FamPCA required ten axes of variation to match PC-AiR’s top two, despite FamPCA being provided the documented pedigree information for both the HapMap MXL and ASW samples (Table 3). PC-AiR appropriately accounted for both the known and cryptic relatedness in the sample for optimal and efficient inference on ancestry with only two axes of variation.
Figure 4.
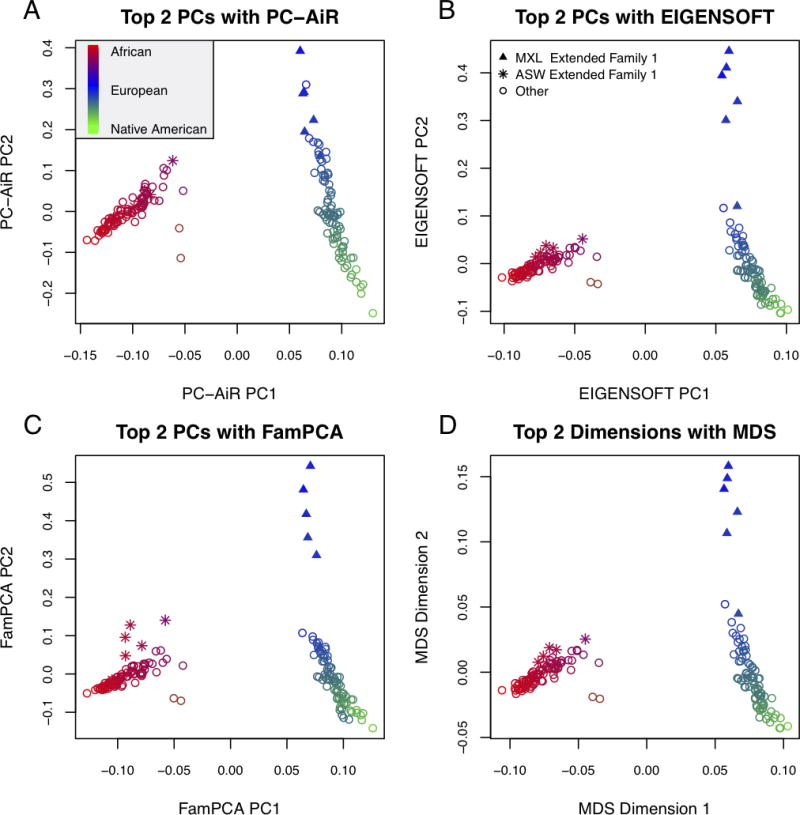
Comparison of Population Structure Inference for the HapMap MXL and ASW Combined Sample. Scatter plots of the top two axes of variation from PC-AiR (A), EIGENSOFT (B), FamPCA (C), and MDS (D). The color of a point represents the ancestry of an individual as estimated from a supervised individual ancestry analysis with ADMIXTURE; blue for European (HapMap CEU), red for African (HapMap YRI), green for Native American (HGDP samples from the Americas), and an intermediate color for an admixed individual. Individuals who are members of MXL Extended Family 1 or ASW Extended Family 1 are plotted as triangles or stars, respectively, and remaining individuals are plotted as circles.
We also performed an unsupervised ancestry analysis with ADMIXTURE and FRAPPE without including reference panel samples and we compared the results to the supervised ADMIXTURE analysis. ADMIXTURE and FRAPPE performed identically to each other, as expected, and a barplot of the estimated ancestry proportions from the unsupervised ancestry analysis is given in Figure S7B. Two of the three components of ancestry essentially distinguish the ASW from the MXL samples, while the third was completely confounded by pedigree structure. These estimated ancestry components were able to attain an R2 value of 0.99 for African ancestry, but the R2 values were only 0.87 for Native American ancestry and 0.62 for European ancestry, thus performing the worst of all the methods for ancestry inference in the combined HapMap MXL and ASW samples.
Assessment of Computation Time
The computation time for PC-AiR depends on both the sample size and the number of markers being analyzed. To analyze a simulated sample of 800 individuals, where 400 individuals are from 20 pedigrees and the remaining 400 individuals are unrelated, with 100K, 50K, and 20K SNPs required 28.5s, 14.8s, and 6.3s, respectively, on a 2.5 GHz laptop with 8 GB memory. The PC-AiR analysis of the HapMap data with 150,872 SNPs required 1.8s for the MXL sample with 86 individuals and 3.9s for the combined ASW and MXL sample with 173 individuals. All computation times refer to the time to run the PC-AiR algorithm, and do not include the time to estimate the measures of relatedness and divergence. The KING software implements a highly efficient algorithm for obtaining relatedness/divergence estimates that can be used with PC-AiR, with estimates for millions of pairs of individuals can be performed in a matter of minutes.
Discussion
Genetic ancestry inference has been motivated by a variety of applications in population genetics, genetic association studies, and other genomic research areas. Advancements in array-based genotyping technologies have largely facilitated the investigation of genetic diversity at remarkably high levels of detail, and a variety of methods have been proposed for the identification of genetic ancestry differences among unrelated sample individuals using high-density genome-screen data. It is common, however, for genetic studies to have sample structure that is due to both population stratification and relatedness, and existing population structure inference methods can fail in related samples. We developed PC-AiR, a method for robust population structure inference in the presence of known or cryptic relatedness. PC-AiR applies a computationally efficient algorithm that uses pairwise measures of kinship and ancestry divergence from genome-screen data for the identification of a diverse subset of mutually unrelated individuals that is representative of the ancestries in the entire sample. Principal components that are representative of ancestry are obtained by performing PCA directly on genotype data from individuals selected for the ancestry representative subset, while coordinates along the axes of variation for the remaining individuals in the sample are predicted based on genetic similarities with the diverse subset. The PC-AiR method does not require the genealogy of the sampled individuals to be known, and it can be used across a variety of study designs, ranging from population based studies where individuals are assumed to be unrelated to family based studies with partially or completely unknown pedigrees.
In simulation studies with a broad range of population structure settings, including ancestry admixture, and with sample individuals related according to a variety of genealogical configurations, we demonstrated that the top axes of variation from PC-AiR were nearly perfectly correlated with ancestry. In contrast, widely used methods for population structure inference performed poorly in the presence of relatedness, including the PCA method implemented in the EIGENSOFT software, MDS as implemented in PLINK software, and model-based ancestry estimation methods ADMIXTURE and FRAPPE. We also applied PC-AiR and competing methods to the admixed HapMap MXL and ASW population samples. Without using any reference population panels or pedigree information on the sample individuals, the top two axes of variation from PC-AiR nearly perfectly explained proportional European, Native American, and African ancestry in the HapMap MXL and ASW samples as compared to a supervised individual ancestry analysis with ADMIXTURE that included reference population panels. In contrast, all other population structure inference methods were confounded by relatedness, including the FamPCA method which was provided the documented pedigree relationships but was unable to appropriately account for cryptic relatedness in the sample. While PC-AiR can use documented pedigree relationships, we recommend using empirical genetic relatedness estimates obtained from genome-wide SNP genotype data in lieu of pedigree-based kinship measures, as mis-specification of pedigree relationships can lead to inaccurate ancestry inference and poor performance, similar to what we observed with FamPCA in the presence of cryptic relatedness in the HapMap samples.
Performing PCA with genome-wide SNP weights that are calculated from external reference panels has recently been proposed [Chen et al., 2013] for certain admixed populations. This approach, however, requires prior knowledge about the ancestries of the individuals in the sample, which may be partially or completely unknown, as well as having available reference population panels with suitable surrogates for the underlying ancestral populations. Nevertheless, the PC-AiR method can also easily incorporate SNP-weights from external reference panels for population structure inference. For example, by designating samples from external reference panels to be the ancestry representative subset in the PC-AiR algorithm, principal components for individuals in the target sample for population structure inference will be calculated based solely on SNP weights from the reference panels. A potential limitation of using SNP weights from external reference panels, however, is that inference on population structure will be limited to the ancestries of individuals selected from the reference panels, which may not be representative of the ancestries of all individuals in the sample. An attractive alternative approach that we recommend is to perform a PC-AiR analysis on the study sample combined with the external reference panels. Genome-screen data could then be used by the algorithm implemented in PC-AiR for the identification of an ancestry representative subset from the combined set of reference population and sample individuals. With this approach, ancestries from both the reference panels and the sample would then be allowed to contribute to the SNP weights, which would help to ensure that all ancestries in the sample are adequately represented for inference on population structure.
Linear mixed models (LMMs) have recently emerged as a powerful and effective approach for association mapping in samples with population structure as well as family structure or cryptic relatedness [Yang et al., 2014]. LMMs have previously been evaluated in samples with subtle population structure [Price et al., 2010; Wu et al., 2011] and have been shown to have appropriate control over type-I error. We evaluated the performance of LMMs in simulation studies where sample individuals have ancestry derived from divergent populations, and our simulation results showed that widely used LMM approaches for association mapping, such as EMMAX and GEMMA, can have an increase in type-I error due to under-correction of SNPs with moderate to high differentiation in allele frequencies between ancestral population, as well as a loss of power due to overcorrection of SNPs with little to no differentiation. This result illustrates potential problems with existing LMM approaches for association mapping in recently admixed populations, where a large proportion of SNPs are expected to have substantial allele frequency differences between the underlying ancestral populations. For example, African Americans have genetic contributions from European and African ancestral populations, and in a comparative analysis of allele frequencies at 1.4 million autosomal SNPs for European (CEU) and West African (YRI) samples in HapMap, we found that approximately 10% of the SNPs were highly differentiated, with allele frequency differences greater than 0.4, while 26% were moderately differentiated, with allele frequency differences between 0.2 and 0.4. Our simulation studies also illustrated that including principal components from PC-AiR as fixed effects in LMMs resulted in appropriate calibration of association test statistics at all SNPs in related admixed samples, protecting against inflated type-I error at highly and moderately differentiated SNPs.
The challenges of inferring genetic ancestry in related samples have been well documented [Patterson et al., 2006; Price et al., 2010]. To our knowledge, PC-AiR is the first method to provide robust population structure inference and correction in the presence of known or cryptic relatedness without requiring reference population panels, external SNP loadings, or genealogical information on the sample individuals. We have implemented the PC-AiR method in an R package that is freely downloadable (see Web Resources).
Supplementary Material
Acknowledgments
This study was supported in part by the National Institutes of Health grants K01 CA148958 and P01 HG0099568 (to T.T.).
Appendix A Derivation of the KING-Robust Parameter Value for Unrelated Pairs of Individuals in the Presence of Admixture
Here we derive the limiting value for the KING-robust kinship coefficient estimator for an outbred unrelated pair of individuals i and j under our general population genetic modeling assumptions. Recall that gis is the number of copies of the reference allele that individual i has at SNP s, and thus gis can take values 0, 1, or 2 and has unconditional expectation . We assume that the ancestral allele frequencies, ps for , are independent and identically distributed (i.i.d.) random variables from some unspecified distribution on [0, 1]. Under this assumption, the unconditional expectation of gis is the same for every choice of , and if we assume that genotypes at different SNPs are independent, then
| (A1) |
as . Note that the independence of SNPs assumption can be relaxed for Equation (A1), and a sufficient condition would be that the effective number of independent SNPs tends to ∞. In what follows, we derive each of the expectations in Equation (A1) conditional on ps, and we show that the limiting value of does not depend on ps, implying that the i.i.d. assumption can also be relaxed.
As in Thornton et al. [2012], we define the quantity μis to be one half of the expectation of gis, conditional on individual i’s ancestry, ai, and the vector of subpopulation-specific allele frequencies, ps, at SNP s:
| (A2) |
The quantity μis can be interpreted as the individual-specific allele frequency for individual i at SNP s, and it is a linear combination of the subpopulation-specific allele frequencies weighted by individual i’s autosomal ancestry proportions from each of the ancestral subpopulations. In Thornton et al. [2012], both ai and ps are treated as fixed quantities. Here, we similarly treat the ancestry vectors as fixed, and we implicitly condition on ai and aj throughout what follows, but we allow ps to be a random vector with the properties and Cov[ps] = ps(1 − ps)ΘK for all under our population genetic modeling assumptions. Therefore, we calculate the following:
| (A3) |
| (A4) |
The expectations and can be obtained directly from the observed genotype probabilities for individual i conditional on ps; however, it should be noted that these probabilities are not what is expected under HWE based on individual i’s individual specific allele frequencies, μis. The observed genotype probabilities take into account that individual i inherits one allele from the mother of i, M(i), and one allele from the father of i, P(i), at every locus. In the presence of recent admixture there can be departure from HWE in the observed genotype frequencies despite individual i being outbred; if individual i’s parents do not have the same ancestry, then individual i will have excess heterozygosity. Using the observed genotype probabilities, we can calculate
| (A5) |
where μM(i)s and μP(i)s are the allele frequencies at SNP s for i’s mother and father respectively. To obtain , we note that the expectation of an indicator function is just the probability of the event it indicates, so
| (A6) |
Since we are only considering unrelated individuals, the genotype values gis and gjs are independent conditional on the vector of subpopulation allele frequencies, so . Therefore, we can calculate
| (A7) |
Plugging the appropriate expectations into Equation (A1) and simplifying, we get that
| (A8) |
In what follows, we look at this quantity in more detail to demonstrate that it may be either a negatively or positively biased estimate of 0 for a pair of unrelated individuals.
When the parents of individual i have the same ancestry, ai = aM(i) = aP(i), and when the parents of individual j have the same ancestry, aj = aM(j) = aP(j), then Equation (A8) simplifies to
| (A9) |
This scenario could correspond to a population with discrete substructure but can also occur in a population with admixture. If i and j also have the same ancestry, then ai = aj and . However, if i and j have different ancestry, then the limiting value is systematically negative, and the magnitude of this negative value is large when i and j have very different ancestry proportions. For the special case when the parents of an individual have very different ancestry, the limiting value can become positive. To see this, consider the extreme example where the parents of individual i are from different subpopulations, and the parents of individual j are from different subpopulations. In this setting , so Equation (A8) simplifies to
| (A10) |
If i and j have no common ancestry from any subpopulation, then , otherwise the limiting value is positive, and the magnitude is large if i and j have similar ancestry proportions. In general, the limiting value of decreases as ai and aj become more different or as either of the pairs (aM(i), aP(i)) or (aM(j), aP(j)) become more similar. Properties of the underlying ancestral populations also affect the magnitude of this bias. When the ancestral subpopulations are highly divergent, as measured by large values on the diagonal of ΘK, the absolute magnitude of the bias will increase.
As discussed in the main text, PC-AiR uses the bias of the estimator to identify which individuals are to be given priority to be included in the ancestry representative subset. Individuals that have a large number of negative pairwise estimates have different ancestry from many others in the samples and will be selected by the PC-AiR algorithm to ensure that the ancestry representative subset is both diverse and representative of all ancestries in the sample.
Appendix B PC-AiR Algorithm for Partitioning into and
Compute: and for all .
Initialize the two subsets to be and , where Ø is the empty set.
-
Compute: .
If , continue to step (4), otherwise go to step (10).
-
Identify , the subset of individuals in with the most relatives in .
If , where is the number of elements in , go to step (5). Otherwise set and go to step (8).
-
Identify , the subset of individuals in that are members of the least divergent ancestry pairs.
If , go to step (6). Otherwise set and go to step (8).
-
Identify , the subset of individuals in that have the minimum total kinship with their inferred relatives.
If , go to step (7). Otherwise set and go to step (8).
Randomly select one element from and define this element to be the set .
Define the sets: and .
Update and and return to step (3).
The algorithm has completed.
Footnotes
Web Resources
PC-AiR is implemented in the R language and is available from Bioconductor (http://www.bioconductor.org) as part of the GENESIS package.
The authors have no conflicts of interest to declare.
References
- Abney M. A graphical algorithm for fast computation of identity coefficients and generalized kinship coefficients. Bioinformatics. 2009;25(12):1561–1563. doi: 10.1093/bioinformatics/btp185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alexander DH, Novembre J, Lange K. Fast model-based estimation of ancestry in unrelated individuals. Genome Research. 2009;19(9):1655–1664. doi: 10.1101/gr.094052.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balding DJ, Nichols RA. A method for quantifying differentiation between populations at multi-allelic loci and its implications for investigating identity and paternity. Genetica. 1995;96:3–12. doi: 10.1007/BF01441146. [DOI] [PubMed] [Google Scholar]
- Chen C-Y, Pollack S, Hunter DJ, Hirschhorn JN, Kraft P, Price AL. Improved ancestry inference using weights from external reference panels. Bioinformatics. 2013;29(11):1399–1406. doi: 10.1093/bioinformatics/btt144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Devlin B, Roeder K. Genomic control for association studies. Biometrics. 1999;55(4):997–1004. doi: 10.1111/j.0006-341x.1999.00997.x. [DOI] [PubMed] [Google Scholar]
- Gravel S, Zakharia F, Moreno-Estrada A, Byrnes JK, Muzzio M, Rodriguez-Flores JL, Kenny EE, Gignoux CR, Maples BK, Guiblet W, et al. Reconstructing native american migrations from whole-genome and whole-exome data. PLoS Genetics. 2013;9(12):e1004023. doi: 10.1371/journal.pgen.1004023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heath SC, Gut IG, Brennan P, McKay JD, Bencko V, Fabianova E, Foretova L, Georges M, Janout V, Kabesch M, et al. Investigation of the fine structure of european populations with applications to disease association studies. European Journal of Human Genetics. 2008;16(12):1413–1429. doi: 10.1038/ejhg.2008.210. [DOI] [PubMed] [Google Scholar]
- International HapMap 3 Consortium. Integrating common and rare genetic variation in diverse human populations. Nature. 2010;467(7311):52–58. doi: 10.1038/nature09298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson JE. A User’s Guide to Principal Components. New York: John Wiley; 1991. [Google Scholar]
- Jolliffe IT. Principal Component Analysis. Springer-Verlag; 1986. [Google Scholar]
- Kang HM, Sul JH, Zaitlen NA, Kong S-y, Freimer NB, Sabatti C, Eskin E, et al. Variance component model to account for sample structure in genome-wide association studies. Nature Genetics. 2010;42(4):348–354. doi: 10.1038/ng.548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laurie CC, Doheny KF, Mirel DB, Pugh EW, Bierut LJ, Bhangale T, Boehm F, Caporaso NE, Cornelis MC, Edenberg HJ, et al. Quality control and quality assurance in genotypic data for genome-wide association studies. Genetic Epidemiology. 2010;34(6):591–602. doi: 10.1002/gepi.20516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li JZ, Absher DM, Tang H, Southwick AM, Casto AM, Ramachandran S, Cann HM, Barsh GS, Feldman M, Cavalli-Sforza LL, et al. Worldwide human relationships inferred from genome-wide patterns of variation. Science. 2008;319(5866):1100–1104. doi: 10.1126/science.1153717. [DOI] [PubMed] [Google Scholar]
- Ma J, Amos CI. Principal components analysis of population admixture. PloS One. 2012;7(7):e40115. doi: 10.1371/journal.pone.0040115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manichaikul A, Mychaleckyj JC, Rich SS, Daly K, Sale M, Chen WM. Robust relationship inference in genome-wide association studies. Bioinformatics. 2010;26(22):2867–2873. doi: 10.1093/bioinformatics/btq559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moltke I, Albrechtsen A. Relateadmix: a software tool for estimating relatedness between admixed individuals. Bioinformatics. 2014;30(7):1027–1028. doi: 10.1093/bioinformatics/btt652. [DOI] [PubMed] [Google Scholar]
- Novembre J, Johnson T, Bryc K, Kutalik Z, Boyko AR, Auton A, Indap A, King KS, Bergmann S, Nelson MR, et al. Genes mirror geography within europe. Nature. 2008;456(7218):98–101. doi: 10.1038/nature07331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patterson N, Price AL, Reich D. Population structure and eigenanalysis. PLoS Genetics. 2006;2(12):e190. doi: 10.1371/journal.pgen.0020190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, Reich D. Principal components analysis corrects for stratification in genome-wide association studies. Nature Genetics. 2006;38(8):904–909. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
- Price AL, Zaitlen NA, Reich D, Patterson N. New approaches to population stratification in genome-wide association studies. Nature Reviews Genetics. 2010;11(7):459–463. doi: 10.1038/nrg2813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard JK, Stephens M, Donnelly P. Inference of population structure using multilocus genotype data. Genetics. 2000;155(2):945–959. doi: 10.1093/genetics/155.2.945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MA, Bender D, Maller J, Sklar P, De Bakker PI, Daly MJ, et al. Plink: a tool set for whole-genome association and population-based linkage analyses. The American Journal of Human Genetics. 2007;81(3):559–575. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Staples J, Nickerson DA, Below JE. Utilizing graph theory to select the largest set of unrelated individuals for genetic analysis. Genetic Epidemiology. 2013;37(2):136–141. doi: 10.1002/gepi.21684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang H, Peng J, Wang P, Risch NJ. Estimation of individual admixture: analytical and study design considerations. Genetic Epidemiology. 2005;28(4):289–301. doi: 10.1002/gepi.20064. [DOI] [PubMed] [Google Scholar]
- Thornton T, Tang H, Hoffmann TJ, Ochs-Balcom HM, Caan BJ, Risch N. Estimating kinship in admixed populations. The American Journal of Human Genetics. 2012;91(1):122–138. doi: 10.1016/j.ajhg.2012.05.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornton TA, Bermejo JL. Local and global ancestry inference and applications to genetic association analysis for admixed populations. Genetic Epidemiology. 2014;38(S1):S5–S12. doi: 10.1002/gepi.21819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S. The genetical structure of populations. Annals of Eugenics. 1949;15(1):323–354. doi: 10.1111/j.1469-1809.1949.tb02451.x. [DOI] [PubMed] [Google Scholar]
- Wu C, DeWan A, Hoh J, Wang Z. A comparison of association methods correcting for population stratification in case–control studies. Annals of Human Genetics. 2011;75(3):418–427. doi: 10.1111/j.1469-1809.2010.00639.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J, Benyamin B, McEvoy BP, Gordon S, Henders AK, Nyholt DR, Madden PA, Heath AC, Martin NG, Montgomery GW, et al. Common snps explain a large proportion of the heritability for human height. Nature Genetics. 2010;42(7):565–569. doi: 10.1038/ng.608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J, Zaitlen NA, Goddard ME, Visscher PM, Price AL. Advantages and pitfalls in the application of mixed-model association methods. Nature Genetics. 2014;46(2):100–106. doi: 10.1038/ng.2876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng Q, Bourgain C. Kininbcoef: Calculation of kinship and inbreeding coefficients. 2009 ( http://galton.uchicago.edu/mcpeek/software/index.html)
- Zhou X, Stephens M. Genome-wide efficient mixed-model analysis for association studies. Nature Genetics. 2012;44(7):821–824. doi: 10.1038/ng.2310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu X, Li S, Cooper RS, Elston RC. A unified association analysis approach for family and unrelated samples correcting for stratification. The American Journal of Human Genetics. 2008;82(2):352–365. doi: 10.1016/j.ajhg.2007.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


