Density Functional Tight Binding: values of semi-empirical methods in an ab initio era

Abstract

Semi-empirical (SE) methods are derived from Hartree-Fock (HF) or Density Functional Theory (DFT) by neglect and approximation of electronic integrals. Thereby, parameters are introduced which have to be determined from reference calculations and/or by fitting to available experimental data. This leads to computational methods that are about 2–3 orders of magnitude faster than the standard HF/DFT methods using medium sized basis sets while being about 3 orders of magnitude slower than empirical force field methods (Molecular Mechanics: MM). Therefore, SE methods are most appropriate for a specific range of applications. These include the study of systems that contain a large number of atoms and therefore being too large for ab initio or DFT methods and also problems where dynamic or entropic effects are particularly important. In the latter case, the errors made by considering a very limited number of molecular structures or neglecting entropic contributions can be much larger than the accuracy lost due to the use of SE methods. Another area where SE methods are attractive concerns the analysis of systems for which reliable MM models are not readily available. Therefore, even in an era when rapid progress is being made in ab initio methods, there is considerable interest in further developing SE methods. We illustrate this point by focusing on the discussion of recent development and application of the Density Functional Tight Binding method.

Graphical abstract

Introduction

Density Functional Tight Binding (DFTB) denotes a series of computational models derived from Density Functional Theory (DFT). The starting point is a molecular reference density ρ₀, which is constructed from a superposition of densities ρ_a from the neutral atoms ‘a’ that compose the molecule, cluster or solid of interest. The DFT total energy is expanded in a Taylor series around this reference density up to a specific order, and the total energy is written as:

$$E[\rho ]=E^0[{\rho }_0]+E^1[{\rho }_0,\delta \rho ]+E^2[{\rho }_0,{(\delta \rho )}^2]+E^3[{\rho }_0,{(\delta \rho )}^3]+\cdots$$ (1)

The truncation at a specific order leads to models DFTB1,¹ DFTB2² (formerly referred to as SCC-DFTB) and DFTB3^3–6 that contain the respective terms in Eq. 1, which are subject to further approximations. These approximations, described in detail in recent reviews,^7–9 introduce two parameters per element type in the E² and E³ terms, which can be computed from DFT and two parameters in E¹ per element type, which define the atomic orbital basis set and neutral atomic densities. The E⁰ term, however, is represented as pairwise potentials and fitted to either ab initio or experimental data; this is the reason that DFTB is characterized as a semi-empirical (SE) method.¹

In terms of computational efficiency, SE methods like DFTB are midway between ab initio/DFT and empirical force field methods (Molecular Mechanics: MM): they are roughly three orders of magnitude faster than DFT (with a medium sized basis set)² and three orders of magnitude slower than empirical force field methods. Without further algorithmic improvements (e.g., linear-scaling methods), both DFTB and DFT methods show an O(N³) scaling. This means that, with a given computational cost, DFTB is able to treat systems with 10 times more atoms or can perform Molecular Dynamics (MD) at a three orders of magnitude longer time scale than DFT. For example, it is common to use DFT for systems up to 100 atoms to carry out MD simulations on the picosecond time scale, while using DFTB the time scale is readily extended to nano-seconds. In biological applications, the systems to be treated are usually too large for pure DFT or SE methods, therefore QM/MM approaches¹⁰ are used and the similar difference in the accessible time scale applies.

In contrast to DFT-GGA functionals, which are often parametrized as well, DFTB requires element and element-pair specific parameters; the number of parameters, however, is much smaller than in MM approaches. DFTB is a quantum method and therefore is able to describe bond breaking and formation events, i.e., it is able to treat chemical reactions. Moreover, DFTB is able to compute all molecular properties similar to DFT, such as electronic excitation energies, infrared (IR) and Raman spectra etc., which are not directly available from empirical force field based calculations. In practice, however, due to approximations inherent to DFTB, care has to be exercised for molecular property calculations, especially those that depend sensitively on polarizability (see below).

For organic and biological applications, the most recent model is the DFTB3 approach with parameters called 3OB (www.dftb.org). The method has been discussed in detail recently^5,6,8,9 and the performance has been investigated for O, N, C, H containing molecules in great detail.⁶ For many properties, DFTB3/3OB shows a comparable performance to DFT-GGA with medium sized basis sets, which suggests to apply DFTB3/3OB instead of DFT/DZP for large organic/biomolecular systems due to computational efficiency considerations, especially for initial mechanistic explorations. In fact, there are cases where DFTB3/3OB performs better than DFT/DZP, such as for proton transfer reactions where the accuracy of barrier heights and proton affinities is crucial.⁶ However, there are also several notable exceptions: (i) There are cases where DFTB3 is known to be less robust than DFT. For example, proton affinities of certain nitrogen-containing molecules are in notable error, therefore careful testing and calibration prior to application is required; another example is that DFTB3 has limited transferability for phosphate chemistry and therefore has to be parameterized in a reaction-specific manner.^11,12 (ii) DFTB3 does not give energies and vibrational frequencies with the same level of accuracy as DFT, therefore two parametrizations, one focusing on energetics and one with emphasis on vibrational frequencies have been published.⁶ (iii) The minimal basis inherent to DFTB3 limits the accuracy of computed IR and Raman intensities,^13,14 which indicates that further developments are necessary to improve related properties such as polarizability and its derivatives with respect to nuclear displacements. For more detailed discussions, see Refs. 8,9.

One of the challenges for deriving robust and accurate SE methods is the availability of high-quality data sets (based on either experiments or accurate computations) that can be used for the parametrization. For main-group elements based compounds, large benchmark datasets are available, such as those collected by Grimme et al.¹⁵ and Hobza et al. for thermodynamic/kinetic properties and non-covalent interactions.¹⁶ Sets of this kind have been used to benchmark and calibrate DFT functionals, which show quite a varying degree of accuracy for different chemical problems. Similarly, these benchmark sets can be used for the parametrization and testing of DFTB and other semi-empirical methods,¹⁷ as done, for example, for the parametrization of DFTB3 for O, N, C and H using Grimme’s GMTKN-24 benchmark compilation.⁶ For transition metal ions, the amount of relevant and accurate experimental data is limited and the accuracy of ab initio/DFT calculations also remains less clear compared to main group elements.^18–22 Therefore, the parameterization of SE methods for transition metals has been lagging behind. Nevertheless, considering the importance of metal in (bio)chemistry, this remains an important direction worth pursuing.

Finally, since DFTB is derived from DFT and in particular uses a GGA exchange-correlation functional (PBE), DFTB also inherits all the well known limitations of DFT-GGA, as discussed in detail recently.^8,9 For example, since the efficiency of DFTB allows to treat rather large QM regions, the issue of dispersion becomes important. In QM/MM schemes, the van der Waals interactions between the QM and MM regions and within the MM region are taken care of by the MM force field terms, while the QM region, when treated with pure DFT/GGA, is lacking the dispersion interactions. Accordingly, we have proposed to augment DFTB with a damped empirical dispersion correction more than a decade ago,²³ and we have demonstrated that this is not only important for the stability of DNA, where the dispersion interactions are well-known, but also for peptides and proteins, which otherwise may assume quite different secondary and tertiary structures^24,25 (also see discussion below for non-natural peptides). In two recent studies by other investigators,^17,26 it was shown that DFTB2 and DFTB3 augmented with empirical dispersions are promising for the description of non-covalent interactions involving large molecules, especially considering the computational efficiency. For example, with the D3 empirical dispersion model, DFTB3 was found to give comparable performance to SCS-MP2 for non-covalent interactions for large molecules²⁶ (but with a very small fraction of computational cost).

Application areas

As mentioned above, SE methods in general and DFTB in particular are midway between ab initio/DFT and MM methods in terms of computational efficiency. Therefore, they are particularly useful in applications where (i) ab initio/DFT is computationally too expensive but a quantum chemical treatment is required (e.g., chemical reactions and excitation spectra), (ii) popular MM models lack the required accuracy or transferability. In the following, we discuss several recent applications of DFTB that fall into these two categories, focusing on studies from our groups.

DFTB: an efficient alternative to DFT for chemical processes in the condensed phase

Quantum chemical applications are often based on energy minimized molecular structures. Those are the starting points for computing reaction energies and barriers, where the latter can be determined by applying reaction path or transition state optimization techniques. The same techniques can also be applied to study large biological molecules using QM/MM methods.¹⁰ The main challenge in condensed phase applications arises due to the overwhelmingly complex energy landscape, where often one or a few energy stationary points are not sufficient for understanding the (reactive) processes of interest. As shown by several authors,^27–29 a use of static approaches based on optimized geometries can lead to substantial errors in the reaction energy of up to 30 kcal/mol and in the barrier height of more than 5 kcal/mol. Therefore, the calculation of free energy differences becomes mandatory.

Free energy simulations typically require an extensive sampling of the configurational space, which is difficult to accomplish with brute force ab initio QM(/MM) calculations.³⁰ Accordingly, several useful approaches have been developed as valuable alternatives in practical applications. One approach is the QM-FE set of methods of Yang and co-workers,³¹ in which the thermal fluctuations of the QM region and MM region are decoupled; this approach is expected to work well when the QM region does not have large anharmonic motions. As a different approach, dual-level methods have been proposed in which proper sampling is carried out with an inexpensive QM/MM potential (e.g., SE/MM or EVB/MM), and the energetics are refined at the higher QM/MM level based on either minimum energy path^32,33 or single-step free energy perturbation.^34–36 The statistical convergence of these dual-level methods depends on whether the potential energy surfaces at the two QM/MM levels have good overlaps. In ‘paradynamics’,³⁷ for example, the ‘reference potential’ at the EVB level is iteratively refined such that it approaches the high level QM potential for the process of interest. The alternative is to develop reliable SE approaches that give good descriptions of the general energy landscape as compared to high-level QM methods. Coupling such SE/MM potential functions and efficient enhanced-sampling techniques^38,39 such as umbrella-sampling-replica-exchange can be a powerful way to provide a reliable reference surface for accurate free energy calculations. This consideration motivated us to continue developments of the DFTB approach over the past decade.

A similar situation is observed for property (e.g., spectra) calculations. For example, since vibrational or optical spectra are highly dependent on the molecular geometry, the use of a single conformer for the chromophore is often too severe a limitation. Here again SE(/MM) methods can be applied to improve spectra calculations by an extensive sampling of relevant chromophore and environment conformations.

In the following, we illustrate these points with a few specific applications where DFTB is used as the SE method.

Reactions that explicitly involve a large number of groups

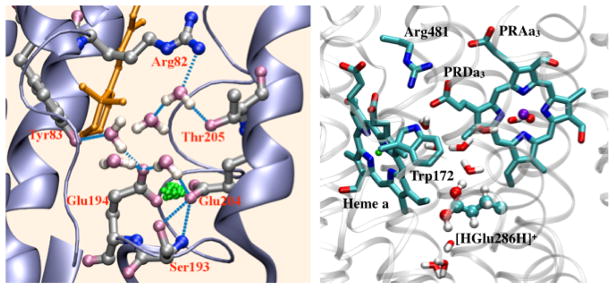
For some biological applications, a significant number of groups are explicitly involved in the process of interest, leading to large QM regions that contain ~100 atoms. Good examples include long-range proton transfers, proton-coupled-electron transfers, and chemistry catalyzed by multi-metal active sites. Moreover, the reactive groups often exhibit significantly anharmonic motions during the reaction, making the computations even more challenging for expensive ab initio QM/MM simulations. For those problems, efficient SE/MM methods that balance computational accuracy and efficiency are particularly useful. Compared to carefully parameterized reactive force fields such as MS-EVB,⁴⁰ the accuracy of SE/MM for very specific systems might be less impressive, however, a SE/MM approach is much less restrictive in terms of the type of chemical processes it describes and applicability of the model in different environments. This is illustrated in the recent application of the DFTB/MM approach to several proton transfer processes in enzymes such as carbonic anhydrase (CA), bacteriorhodopsin (bR) and cytochrome c oxidase (CcO). The DFTB/MM calculations were required to discuss the potential relevance of hydroxide transfer in CA,⁴¹ an intermolecular proton bond model for the proton storage site in bR,^42,43 and a concerted proton transfer mechanism in CcO⁴⁴ (Fig.1). Once a new mechanistic hypothesis is established, either new experimental studies or calculations with new reactive MM model can be carried out.

Figure 1.

DFTB/MM simulations have been crucial to describe the chemical structure of the proton storage site of bacteriorhodopsin^42,43 (left) and the concerted proton transfer pathway in Cytochrome c Oxidase (right), which implicates a transiently doubly protonated glutamate.⁴⁴

A relevant issue in these applications concerns the reliability of DFTB for treating water in different protonation states and environments. As discussed in several recent publications,^45–48 there are several limitations of the DFTB3 model for treating bulk water and solvated proton/hydroxide. For example, a notable level of oversolvation of water and an excess proton/hydroxide in water has been noted in several studies. Therefore, improving the performance of DFTB3 for these systems is one of the important topics for current research. On the other hand, it is also worth emphasizing that for the purpose of comparing free energy profiles along different proton transfer pathways in biomolecules, our experience suggests that the oversolvation effect is unlikely to have a significant impact. In a recent study, for example, we compared the potentials of mean force (PMFs) for the translocation of a proton through a model ion channel⁴⁹ calculated with DFTB3/3OB and its variant, which was adjusted to eliminate the oversolvation effects of bulk water and solvated proton through a simple reverse Monte Carlo approach. The difference in the computed PMF barriers is about 1–2 kcal/mol, which is a small effect for most mechanistic investigations.

Sampling of optical and vibrational spectra

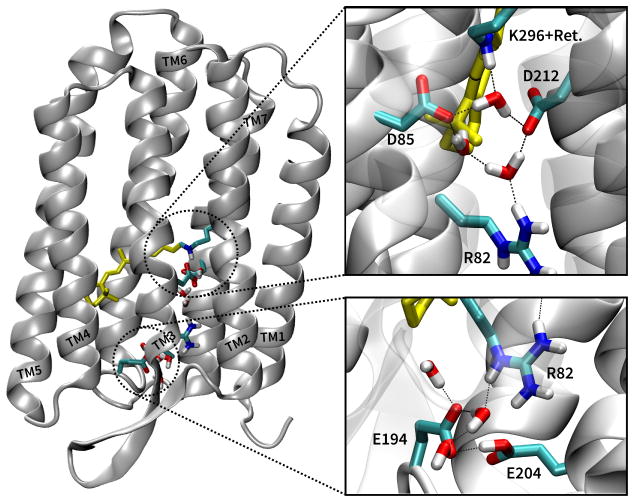
In quantum chemistry, optical and vibrational properties are usually computed for optimized geometries. This is also done for complex biomolecules using QM/MM calculations, where the chromophore of interest is treated at a QM level, while the remainder of the protein is described with MM. For flexible molecules or molecules embedded in a protein, the geometry optimization based approach may not always lead to useful results. This calls for a calculation of spectra based on MD trajectories. Tavan and coworkers have reviewed different techniques that can be applied to compute vibrational (IR) spectra using MD trajectories.^50,51 Nevertheless, static approaches based on one or a few optimized geometries may work in specific cases, e.g., when the relevant local substructures only fluctuate around an average conformation. The fact that different approaches are appropriate for different situations is illustrated by the light-activated proton pump bacteri-orhodopsin (bR: Fig. 2), a membrane protein that pumps protons through the cell membrane after photo-isomerization of the retinal-chromophore.

Figure 2.

The structure of bR (left), showing the retinal chromophore (yellow) and the active site (upper right), which consists of a hydrogen bonding network that connects the retinal with two aspartates (D85 and D12) and three water molecules. The proton release group (PRG) consists of two glutamates (E194 and E204), several water molecules and arginine 82 (lower right).

In the ground state of the photocycle,⁵² the chomophore in bR is hydrogen bonded via a water molecule to two negatively charged aspartic acid side chains. Since DFTB provides an accurate description of the retinal geometry,⁵³ we have used DFTB/MM to optimize the structure of bR^54–60 and other retinal proteins like rhodopsin^61,62 and sensory rhodopsin II (SRII). For bR, the optimized structure of the active site seems to be a good model for the average structure. We have tested this hypothesis using MD simulations, sampling the structures and computing excitation energies along the MD trajectories.⁵⁵ The results showed that the absorption maximum of the sampled spectrum coincides very well with excitation energy computed from the optimized structure. Analysis of the trajectories showed that this is due to the very stable hydrogen bonding network formed by several charged groups and three water molecules. Moreover, using optimized structures, we were able to reproduce vibrational frequencies of the carbonyl stretches of the aspartic acid side chains upon protonation,⁵⁸ as well as the excited states energies computed using ab initio MRCI for the QM region^54–57

Following photoexcitation, the retinal chromophore isomerizes from a trans to the cis form, and the intermediate states called K, L are visited, before a proton, initially located on the retinal chromphore, is transferred to D85 (Fig. 2). This is the first proton transfer (PT) event, investigated in detail using DFTB/MM.^63–66 To study this PT, we have used geometry optimization and reaction path methods, since entropic effects were known to be small. Again, this first PT step seems to be an example where traditional geometry optimization techniques work well.

However, the crystal structures of L give conflicting geometrical information, not only about the position of water molecules but also for the orientation of the retinal itself. Further, it turned out that the structures modeled with QM/MM at low and high temperatures are different, therefore the crystal structures determined at low temperatures (cryo-trapped) do not seem to be appropriate for computing spectral properties determined experimentally at room temperature.⁶⁰ This problem is even more pronounced in the K state, where vibrational spectra have been found to be very much dependent on the temperature. This is related to very different retinal geometries at various temperatures, which lead to different vibrational properties. Here, simple optimization techniques cannot reproduce this effect and DFT methods are at their limits, since MD trajectories in the nanosecond regime are required.

Following K and L, the protein reaches the M state, where the first proton transfer from retinal to D85 occurs, and a proton is released to the extracellular side. The nature of the release site has been debated and recently two models have evolved. The first model involves a protonated water cluster between the glutamates E194/E204 and arginine 82,⁶⁷ while the second model has the excess proton shared between the glutamates.^42,43 Experimentally a broad continuum absorption between 1800 and 2200 cm⁻¹ has been observed, which in principle can be associated with either protonate water clusters or a delocalized proton between the pair of glutamates. DFT/MM calculations initially seemed to show that this continuum absorption is related to a protonated water cluster.⁶⁸ However, those DFT/MM calculations only included the water cluster in the QM (DFT) region, and therefore the proton was trapped therein. Enlarging the QM region by including the glutmates 194 and 204 in both DFTB/MM and B3LYP/MM simulations showed that the proton rapidly left the water cluster and became delocalized between the glutamates.^42,43 The reason for this fast transition is a significant energy difference of more than 10 kcal/mol in favor of the proton being delocalized between the glutamates. DFTB/MM simulations explicitly showed that this delocalized proton leads to a broad IR absorption band in the relevant spectroscopic region. It is worth noting that the continuum feature is dependent on the thermal delocalization of the shared proton, and a geometry optimization followed by a normal mode analysis would result in a single peak in the mid-IR, as illustrated by studies of protonated water clusters.⁶⁹

Finally, we emphasize again that minimal basis set methods such as DFTB likely find limitations for quantitative calculation of IR or Raman intensities. Although absolute dipole moments and even molecular polarizabilities can be improved using post-SCF procedures, the response of these properties with respect to nuclear displacements is still deficient.^13,14 Therefore, a careful testing using relevant model systems should be conducted before application to complex systems.

Long range electron/charge transfers

Marcus theory^70–73 and its extensions^74–78 have been very successful in describing charge transfer (CT) in a multitude of molecular systems. Within the assumption of weak electronic coupling between donor and acceptor, the rate of charge transfer can be obtained in the high-temperature non-adiabatic limit as

$$k_{DA}=\frac{\langle H_{DA}^2\rangle }{\hslash }\sqrt{\frac{\pi }{\lambda k_{B}T}}exp\left(-\frac{{(\mathrm{\Delta }G+\lambda )}^2}{4\lambda k_{B}T}\right).$$ (2)

Here ΔG is the free energy difference between the initial and the final states, λ is the reorganization energy, which can be estimated using QM, MM, QM/MM or even simpler models. H_DA is the electronic coupling between the donor and acceptor sites, and there are several quantum chemical approaches to compute them.⁷⁹ The most simple yet robust approach however, is to use a fragment molecular orbital (FMO) based scheme where only the donor/acceptor frontier orbitals (HOMOs in case of hole, LUMOs in case of electron transfer) are explicitly involved. This is a computationally inexpensive and numerically stable procedure and therefore well-suited to computing the electronic couplings along extended molecular dynamics trajectories. We recently illustrated that the couplings can also be computed very efficiently using DFTB, without losing accuracy with respect to full DFT-FMO methods.^80,81 This allows to compute couplings and evaluate Eq. 2 for large systems along extended MD trajectories, as done for example for the organic compound Alq₃,82 which is used for organic light-emitting diode materials.

Once the coupling elements are available, the charge transport properties can also be studied based on Landaure currents sampled along extended MD trajectories.⁸³ Indeed, both types of models, Marcus theory for hopping transport and Landauer for coherent transport, have been applied successfully in many areas. However, they presuppose a time scale separation and a specific charge transport mechanism. In other words, the typical approximations concern the localization of charge to donor/acceptor in the limiting states, that the electronic and nuclear degrees of freedom are well separated in time scale, and that the process is either adiabatic or non-adiabatic.

Based on DFTB/MM, a multi-scale methodology has been derived that bridges these two simulation regimes, i.e., it provides an unbiased description of CT at a greatly reduced effort in the calculation of the electronic structure problem by using some of the concepts of Marcus theory.^84,85 The methodology starts with a fragmentation of the molecular system, which works well when the electronic structure is build up from molecular orbitals localized on these fragment. A prototypical example is hole transfer in DNA, where the relevant electronic subsystem is build up from the HOMO orbitals on the individual bases, i.e., the super-molecular wave function can be described as a superposition of base-HOMOs (see Fig. 3).

Figure 3.

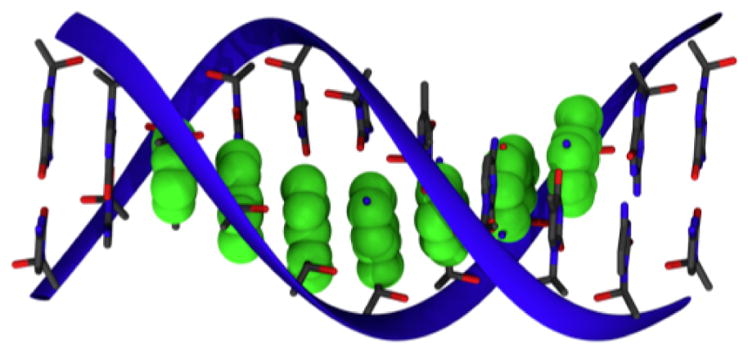
The HOMO orbitals on the guanine bases are shown in green. For an ideal structure (poly-GT), the HOMO on the DNA strand is delocalized over several guanines, i.e. this HOMO can be modeled as a superposition of HOMO’s of the individual bases.

This DFTB/MM based FMO electronic structure description is then used in non-adiabatic propagation schemes, where the nuclei and the electrons are propagated simultaneously according to the Newton/Schrödinger equations of motion. This approach is conceptually similar to standard ab initio non-adiabatic dynamics methods, although with greatly reduced computational cost, and it provides an unbiased description of different charge transport mechanisms depending on the material, its dynamical behavior and environmental influences. We used both Ehrenfest-type and surface hopping approaches to simulate coupled dynamics of several systems,^84,85 which included NA, proteins and peptides. First studies of organic materials are currently under way in our laboratory. In particular, the application to fast hole transfer in the protein photolyase demonstrated the advantage of the method.⁸⁶ In that case, the time scale separation between electronic and nuclear degrees of freedom seemed to be invalid, which led to a drastic breakdown of Marcus theory, while a non-adiabatic dynamics method was able to predict the experimentally observed behavior.

DFTB: an alternative to empirical force field models

Molecular mechanical force fields have been successfully applied to a variety of systems and are nowadays an indispensable tool for gaining deeper insights into the structural, dynamical and energetic properties of biomolecules and complex materials. With these widespread applications, however, the limits of popular non-polarizable empirical force fields have also become increasingly clear. In the following, we touch upon several examples where a carefully calibrated SE method can be a valuable alternative.

Availability of MM parameters

A practically relevant issue is the availability of force field parameters. Accurate parametrization is often a tedious process and therefore MM parameters are not always available for the system of interest. While standard protein, lipid and DNA parameters have been developed and refined over the past few decades, for more specialized systems parameters may be missing or of questionable quality. This concerns, for example, protein cofactors, which are often not straightforward to parametrize due to extended π-conjugation. In such cases, it might be more practical to apply a QM/MM approach using a SE based QM method due to the sampling requirements.

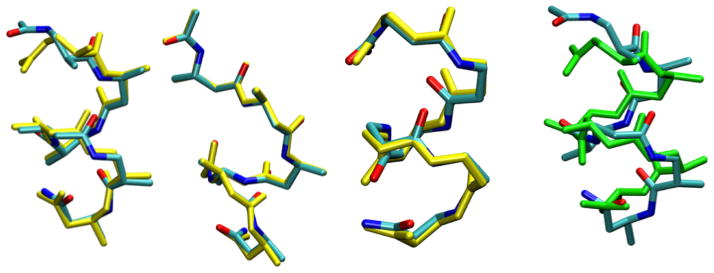
A second example concerns non-natural peptides. Many non-natural ‘foldamers’⁸⁸ such as peptoids, β-peptides and mixed α, β-peptides have found increasingly broad applications, thus it is of interest to develop effective simulation protocols for understanding their structural, dynamical and potentially assembly behaviors. Unlike for natural biopolymers, there has not been a systematic set of efforts to develop, benchmark and refine MM force fields^89–93 for non-natural biopolymers; we have demonstrated that it is not always a good practice to simply “borrow” MM parameters from force fields for natural biopolymers to describe non-natural peptides.^94,95 Therefore, this represents an area where efficient and reliable SE/MM methods are particularly needed. As shown in several previous studies, the DFTB approach provides encouraging descriptions for the conformational properties of several β-peptides⁸⁷ (Fig. 4) as compared to popular DFT methods such as B3LYP. Regarding the impact of including empirical dispersion in DFTB, the effects on the calculated structure and conformational energies for several β-peptides were found to be generally small; this is probably because the larger number of atoms in the β-amino acids causes dispersion to saturate more quickly as a function of the number of residues compared to natural peptides. Nevertheless, in several cases, including dispersion led to substantially different structures with a backbone RMSD on the order of 1 Å (see Fig. 4). With further improvements in the rotational barriers (see below), we anticipate that DFTB/MM simulations in which the solvent environment (e.g., water-methanol mixture) is described by classical models, will find many applications.

Figure 4.

Overlay of DFTB2 and B3LYP/6-31G* optimized structures (yellow) for several β-peptides studied in Ref. 87; only the backbone is shown for clarity. The backbone RMSD varies between 0.17 and 0.37 Å. Also shown on the far right is the overlay of DFTB2 structures with (green) and without including the empirical dispersion for one β-peptide sequence; the backbone RMSD is 1.0 Å. See text and Ref.⁸⁷ for the discussion of dispersion effects.

Dynamic/solvent-accessible metal sites

Metal ions play important structural and catalytic roles in biology. For a metal site with well-defined coordination sphere and structure, reliable MM models can be developed.⁹⁶ In many cases, however, the metal site is (partially) solvent exposed and the coordination sphere of the metal is likely to change during the reactive process.^97,98 For those problems, neither a MM model or an ab initio QM/MM model is ideal, and a SE/MM model is again needed to strike the proper balance between computational accuracy and efficiency. A recent example from our group concerns the analysis of catalytic promiscuity in the alkaline phosphatase (AP) enzymes, which feature a solvent-exposed bi-metallic zinc site. Using a carefully calibrated DFTB/MM model,⁹⁹ including the use of a new QM-MM electrostatic Hamiltonian,¹⁰⁰ we showed that the AP enzymes are able to stabilize phosphoryl transition states of different nature in a single active site.¹⁰¹ Since solvent polarization was found to play a major role, the results would have been difficult to obtain without an adequate sampling of the solvent redistributions during the phosphoryl transfers. The advantage of DFTB over other SE models (e.g., AM1) for the description of the bimetallic zinc site was also illustrated in these applications.

Localized polarization effects

The need to go beyond fixed-charge models has been realized in many areas of chemical and biomolecular applications. This is potentially important in highly heterogeneous environments, such as the air/water interface and the interior of proteins. The active site of bR is a particularly relevant example. As shown by several authors, standard non-polarizable force fields are not able to describe the active site hydrogen-bonding structure as shown in Fig. 2. The hydrogen bonds between retinal and nearby water molecules are easily broken, leading to a direct salt bridge between the retinal and an aspartate,^102–104 which in turn leads to different spectroscopic properties. Similarly, overestimation of the stability of internal salt-bridge interactions in cytochrome c oxidase by non-polarizable force fields has been discussed.^105,106 The importance of including polarization effects for the description of protein/peptide stability^107–111 and protein-ligand interactions^112–116 has been highlighted by several groups.

As a result of these and related observations, there is considerable effort in developing transferable polarizable force fields in a systematic fashion. This is far from straightforward, especially for highly flexible systems like biomolecules. An alternative, therefore, is to employ a carefully calibrated quantum model, to either directly simulate the system of interest or to update the partial charges along MD simulations. For realistic applications, full QM calculations at the ab initio level remains challenging, despite recent progress in linear scaling QM methods. There are several promising linear-scaling SE methods based on either AM1¹¹⁷ or DFTB,¹¹⁸ although much remains to be done to calibrate these models for a balanced treatment of non-covalent interactions and conformational (torsional) energetics.

In the near future, therefore, it appears more realistic to expect that QM/MM methods are used to treat local polarization effects such as the situation described above for bR and CcO. For this purpose, SE/MM again is attractive due to the ease with MD sampling; DFTB/MM simulations have indeed been shown to be effective to treat the bR active site.¹⁰² When even more extensive sampling is desired, an alternative is to carry out essentially classical MD simulations, with the partial charges for the site of interest updated based on DFTB/MM calculations at a given update frequency. We note that DFTB is particularly suitable in this context because reliable atomic charge schemes have been developed¹¹⁹ which can be used to improve the MM charges for specific proteins and protein conformations. Although atomic charges themselves are not observables, the quality of the charge scheme is manifested in terms of the accuracy in the resulting multipole moments and electrostatic interactions that can be computed ‘on the fly’ during MD simulations. It is also possible to further improve the description of local electrostatics and polarization using post-SCF corrections to alleviate some limitations associated with the minimal basis approximations.^13,14

Concluding Remarks

In this short perspective, we attempt to use several rather unique applications of DFTB(/MM) applications to highlight that it is valuable to continue developing semi-empirical (SE) methods in an “ab initio era”. Systematically improving the efficiency and accuracy of ab initio/DFT methods is of clear long-term importance. In practical applications, however, it is worth noting that the typical computational resources would limit ab initio/DFT based QM or QM/MM calculations to subnanoseconds even with a modest basis set such as double-zeta-plus-polarization (DZP). With this level of basis sets and sampling, the uncertainties associated with ab initio/DFT based QM(/MM) simulations might be comparable or even larger than carefully calibrated SE(/MM) simulations. This consideration is one of the main driving forces behind our continuing developments of the DFTB models over the past decade or so.

The computational efficiency of SE methods in general and DFTB in particular is midway between ab initio/DFT and empirical force fields models. Therefore, as we discussed in this article, SE(/MM) methods are most useful to problems where sampling is particularly important or properties are not straightforward to compute from existing empirical force field models. Examples include “delocalized” chemical reactions (e.g., long-range proton/electron transfers) in the condensed phase, spectra calculations in biomolecules, active sites in proteins that implicate metal ions or strong polarization effects, and structural properties of non-natural biopolymers.

In terms of the status of SE methods, we focus on the discussion of the DFTB models in this article; for the discussion of other SE methods, see, for example, Refs.^120–122 The latest DFTB3 model with the 3OB parameterization generally leads to very reliable structural properties for organic systems, and the energetics are also often comparable to DFT-GGA using medium sized basis sets. Therefore, DFTB3/3OB can be used to study a broad range of organic and biomolecular systems instead of DFT-GGA/DZP, especially for initial mechanistic explorations. On the other hand, it is always important to perform benchmark calculations for the specific system of interest since DFTB3 in the current form is less robust than DFT-GGA and has several known limitations.^{8,9,11,45–47} For many practical applications, an effective integration of DFTB3/MM and ab initio/DFT/MM approach is likely most productive, and there is considerable need in developing novel methods that facilitate such integration. This can be particularly important for systems that implicate metal ions, for which DFTB appears to provide more reliable descriptions than existing SE models and therefore is well-suited as the low-level QM method that guides the sampling in a multi-level framework.

One issue being investigated actively in our groups has to do with the underestimation of Pauli repulsion due to the minimal basis and the use of PBE exchange functional in DFTB. This results in a slightly too dense packing of weakly bonded systems and an underestimation of rotational barriers; the issue can be particularly severe for highly charged systems, as exemplified by the hydration of hydroxide. Finally, there is considerable effort in improving the description of non-covalent interactions in DFTB by going beyond the monopole approximation.^118,123 With a balanced description of conformational and non-covalent energetics, along with other algorithmic developments such as linear-scaling, the next generation of DFTB model is poised to be a powerful method uniquely suited for a broad range of chemical and biological applications, even in an ab initio era.

Figure 5.

DFTB/MM simulations^99,101 suggested that transition states of different nature are stabilized in a single enzyme active site. Stabilization provided by water molecules accessible to the active site were shown to play a major role in such “catalytic plasticity”.