DISCOVERING PATIENT PHENOTYPES USING GENERALIZED LOW RANK MODELS

Abstract

The practice of medicine is predicated on discovering commonalities or distinguishing characteristics among patients to inform corresponding treatment. Given a patient grouping (hereafter referred to as a phenotype), clinicians can implement a treatment pathway accounting for the underlying cause of disease in that phenotype. Traditionally, phenotypes have been discovered by intuition, experience in practice, and advancements in basic science, but these approaches are often heuristic, labor intensive, and can take decades to produce actionable knowledge. Although our understanding of disease has progressed substantially in the past century, there are still important domains in which our phenotypes are murky, such as in behavioral health or in hospital settings. To accelerate phenotype discovery, researchers have used machine learning to find patterns in electronic health records, but have often been thwarted by missing data, sparsity, and data heterogeneity. In this study, we use a flexible framework called Generalized Low Rank Modeling (GLRM) to overcome these barriers and discover phenotypes in two sources of patient data. First, we analyze data from the 2010 Healthcare Cost and Utilization Project National Inpatient Sample (NIS), which contains upwards of 8 million hospitalization records consisting of administrative codes and demographic information. Second, we analyze a small (N=1746), local dataset documenting the clinical progression of autism spectrum disorder patients using granular features from the electronic health record, including text from physician notes. We demonstrate that low rank modeling successfully captures known and putative phenotypes in these vastly different datasets.

1. Introduction

1.1. Learning phenotypes from the electronic health record

With the advent and proliferation of electronic health records, phenotyping has become a popular mechanism with which to define patient groups based on shared characteristics- typically for conducting observational studies, defining quality metrics, or targeting clinical interventions. Current phenotyping methods vary: some rely on rules crafted from domain knowledge, others relying on statistical learning, and some employ hybrid approaches.^1,2 Regardless of the method, phenotyping has clear utility when the resulting groups are well defined, but may fail when the situation is unclear. Instead of presupposing phenotypes, recent work has leveraged advances in unsupervised learning to discover phenotypes from the data.^3,4

A major barrier to applying machine learning approaches to phenotype discovery using health records data is that these data are often sparse, biased by non-random missingness, and heterogeneous.³ An emerging framework, Generalized Low Rank Modeling (GLRM), offers a potential solution to address these limitations. Specific low rank models have already been successfully applied to various biomedical problems.^4,5,6 However, no prior study has considered low rank modeling as an overarching framework with which to perform phenotype discovery via models tailored to the qualities of the dataset at hand. Here, we demonstrate the use of this flexible framework to discover phenotypes in two datasets of different quality, granularity, and which represent diverse clinical situations.

1.2. Standardizing hospital care using phenotype discovery has high impact

Each year, Americans are admitted to hospitals over 37 million times, in aggregate spending more than 175 million days as inpatients.⁷ In addition, hospitalizations cost the US economy $1.3 trillion dollars annually.⁸ In light of this enormous impact, improvements in hospital care can yield dramatic results. For example, the Institute of Medicine estimated that up to 98,000 patients die each year from preventable medical errors.⁹ Recent coordinated efforts to improve safety resulted in a staggering 1.3 million fewer patients harmed, 50,000 lives saved, and $12 billion in health spending avoided.¹⁰ These efforts shared a simple premise: uncovering common phenotypes bridging diverse inpatient cohorts can drive substantial improvements in care and outcomes.¹⁰ Given that phenotype discovery is such a critical step towards improving hospital care, existing methods for subgroup discovery are often slow and labor-intensive. For example, the codification of sepsis has taken decades¹¹, despite the fact that it contributes to as many as 1 out of every 2 hospital deaths¹² and is the single most expensive cause of US hospitalization.¹³

1.3. Autism spectrum disorder phenotypes are poorly defined and badly needed

Autism spectrum disorder (ASD) is a leading cause of mental illness in children, with an estimated 52 million cases globally.¹⁴ In the United States, its prevalence has been estimated to be as high as 1 in 68, resulting in $11.5 billion in social costs^15,16. ASD has eluded precise characterization of either its biological underpinnings or its clinical presentation, leading to substantial challenges in diagnosis and treatment, particularly in light of a wide range of heterogeneous phenotypes and comorbidities¹⁷. Although symptoms of the disorder are commonly present by age 18 months, ASD is typically not diagnosed until age 4 or later, after significant irreversible impairments in learning and neurodevelopment have already occurred¹⁵. Even after diagnosis, the progression of ASD is different across individuals, which has led to efforts to define subgroups that are at differential risk of comorbidities.¹⁸ A systematic and data-driven approach for phenotype discovery can precisely characterize this heterogeneous disorder and its progression over time.

2. Methods

We analyze two datasets of different sizes, feature granularity, data-types, domains, and timelines. Instead of taking a one-size-fits-all approach, we create a tailored low rank model within the generalized low rank model framework to account for the specific qualities of each dataset and then fit the model to discover hidden phenotypes.

2.1. Generalized low rank models

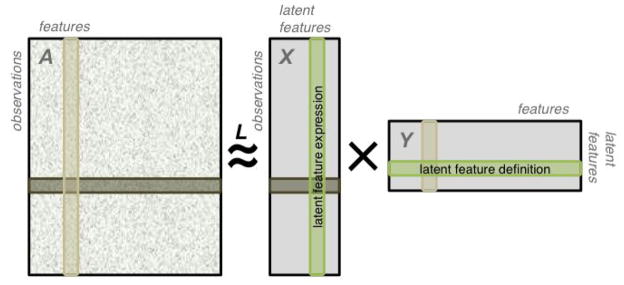
The idea behind low rank models is to represent high-dimensional data in a transformed lower-dimensional space. Generalized low rank models¹⁹ begin with a matrix or data table A that is populated with n samples or observations (rows) of m different features (columns; Figure 1). These features may take values from different sets (e.g. some may be real numbers, others true/false, enumerated categories, etc.) and each observation may have missing values for some features. The number of features in the dataset is referred to as its dimensionality.

FIGURE 1.

A data matrix is approximated as the product of two matrices. By construction, the resulting approximation is of lower algebraic rank. The data matrix A may contain features of different data-types and missing entries, as illustrated here. Each row of X is an encoding of an observation in A in the latent feature space. Each column of Y is an encoding of a feature of A in the latent feature space.

We approximate A by XY, where X ∈ ℜ^n×k and Y ∈ ℜ^k×m (Figure 1). We interpret the rows of this “tall and skinny” X as observations from A represented in terms of the k new latent features. We interpret each row of the “short and wide” Y as a representation of one of the k latent features in terms of the m original features. In a sense, Y encodes a transformation from the original features into the latent features.

To find X and Y, we pose the following optimization problem:

$$\underset{X,Y}{min}\sum _{i,j\in \mathrm{\Omega }}{l}_{ij}(A_{ij},{(XY)}_{ij})+r_X(X)+r_Y(Y)$$ (1)

This expression consists of two parts: a loss function and regularizers. The loss

$$L=\sum _{i,j\in \mathrm{\Omega }}{l}_{ij}(A_{ij},{(XY)}_{ij})$$ (2)

is a measure of the accuracy of our approximation of the data. Different losses may be more or less appropriate for different types of data (to reflect different noise models), so we allow the loss to be decomposed over the different elements of the dataset to account for heterogeneity in the types of features present. In addition, we only calculate the loss over the set Ω, which represents the non-missing entries in our dataset. This strategy allows us to ‘borrow’ statistical power from partially-filled or incomplete observations where other methods would discard the entire observation. The regularizers r_x and r_y constrain or penalize the latent feature representation. Using appropriate regularization can prevent overfitting and improve model interpretability.

To impute missing or hidden values, we solve: ${\widehat{A}}_{ij}=\mathit{arg}\underset{a\in \alpha }{min}{l}_{ij}(a,{(XY)}_{ij})$, where α represents the set of possible values that a can take (e.g. if a is a boolean feature, α = {1, −1}).

Particular choices of losses and regularizations result in many well known models. For instance, using $L(A,XY)={\Vert A-XY\Vert }_2^2$ and no regularization is mathematically equivalent to principal components analysis (PCA). A well-written and detailed description of GLRM and the kinds of models that can be created using this framework can be found in the seminal work by Udell et. al.¹⁹

2.2. Hospitalization dataset and phenotype discovery model

We used data from the 2010 National Inpatient Sample, the largest all-payer nationally representative dataset of US hospitalizations.²⁰ Each hospitalization record includes a variety of fields providing information about patient diagnoses (up to 25 different ICD-9-CM codes) and procedures (up to 15 ICD-9-CM procedure codes), as well as demographics, admission/discharge/transfer events, and comorbidities (a set of 30 AHRQ comorbidity measures, e.g. AIDS). For efficiency, we processed the dataset to consolidate the ~18,000 ICD-9-CM diagnosis and procedure codes into a total of 516 Clinical Classification Software (CCS) codes.²¹ Additionally, we used 44 variables regarding patient demographics, admission circumstances, hospitalization outcome, and patient comorbidity. We expanded all categorical variables into sets of boolean dummy variables (one for each possible value) to yield a total of 557 boolean, continuous, and ordinal features. We focused specifically on adult hospitalizations (age ≥ 18 years) as the causes, demographics, and outcomes of pediatric hospitalizations differ substantially. To speed computation, we selected a random subsample of 100,000 hospitalizations to fit our models to.

Hospitalization records contain a diversity of data-types. We measured the accuracy of the approximation for different data elements by data-type appropriate loss functions, e.g. quadratic loss for real-valued variables such as age, hinge losses for boolean variables such as presence or absence of procedures. Real, categorical, ordinal, and boolean, and periodic data-types are familiar to most researchers, and appropriate losses for these kinds of variables are known in the machine learning and optimization communities.¹⁹

We defined an epistemic boolean variable as a boolean variable where we have a lopsided confidence about whether a true value actually indicates truth or a false value actually indicates falsehood. For example, consider diagnoses: if a clinician codes a patient for a diagnosis, it is highly likely that that patient experienced the condition that the code represents -- in other words, we are confident that “True” means true. On the other hand, if a patient did not receive a particular diagnosis, that variable would simply be missing in that patient’s hospitalization record. In reality, we are less sure that the patient did not experience that condition because it may have escaped diagnosis, remained unrecognized, or simply gone uncoded. We developed a loss function to account for lopsided epistemic uncertainty of this sort. Correct predictions are not penalized regardless. Our loss function for epistemic booleans is a generalization of the boolean hinge loss and is defined as follows:

$$l(a,u)=(w_F{1}_{\{-1\}}(a)+w_T{1}_{\{1\}}(a))\ast max(1+au,0)$$ (3)

where 1_A(x) is an indicator function for x ∈ A. When w_T > w_F, this loss function penalizes false negatives more than false positives, reflecting our greater certainty about observations labeled as “True” compared to those labeled as “False”.

In light of the divergent scales and domains of the features, all loss functions and regularizers were adjusted for scaling and offsets.¹⁹

2.3. Autism spectrum disorder dataset and phenotype discovery model

We used data from the Stanford Translational Research Integrated Database Environment (STRIDE), a de-identified patient dataset that spans 18 years and more than 1.2 million patients who visited Stanford Hospital & Clinics. From all patients in STRIDE, we identified 1746 patients with at least 2 autism spectrum disorder (ASD) related visits (visits assigned a 299.* ICD9 code). For these patients, we analyzed billing data from all visits (ICD9 and CPT codes), prescribed drugs, as well as mentions of clinical concepts in their medical notes found using our previously described text annotation pipeline.²² We restricted our analysis to data recorded when these 1746 patients were at most 15 years old because we are interested in modeling ASD phenotypes in children and adolescents. We generated a feature vector for each patient by calculating the frequency of occurrence of each visit-associated ICD9 code, prescribed drug, and medical concept mentioned in any note of that patient, binned by 6 month intervals (Figure 2). To capture the nature of this data, we used a Poisson loss over all elements in the dataset. This low rank model specification is mathematically equivalent to Poisson PCA.²³

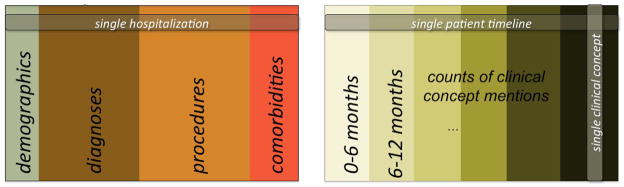
FIGURE 2.

Illustration of the hospitalization (left) and ASD (right) datasets. For each ASD patient, we created a vector from the frequency of occurrence of each concept (C-1, C-2…) mentioned in their medical notes, ICD9 codes associated with a visit (ICD9-1, ICD9-2…) and medications prescribed (DRUG-1, DRUG-2…) within each 6 month period of their medical history captured in our database.

2.4. GLRM implementation

To fit our models, we used the Julia package LowRankModels²⁴, which implements the algorithm described by Udell et. al.¹⁹ This software employs a general purpose, fast, and effective procedure called alternating proximal gradient descent to solve a broad class of optimization problems. Although model-specific solvers (i.e. algorithms that take advantage of the structure of a particular GLRM) could be faster, this general-purpose software allowed us to rapidly iterate through model design decisions and test choices of parameters and robustness.

The Julia LowRankModels package is still under active development. We dedicated substantial effort to learning and clarifying the code, contributing bug fixes, adding needed features, and optimizing performance. Our contributions will accelerate our future work and the work of other researchers using low rank models.

3. Results

3.1. Tailored low rank models outperform PCA

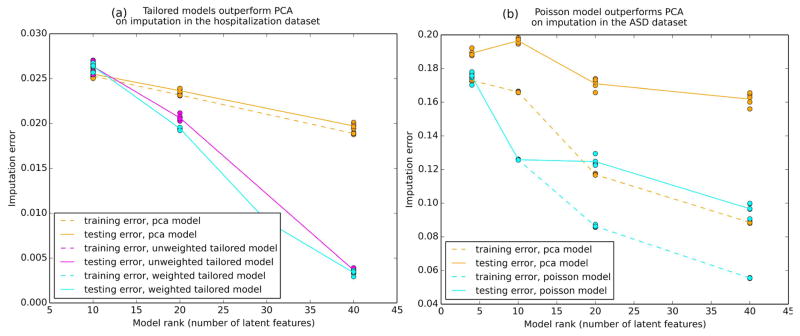
As an intrinsic evaluation, we benchmarked our tailored models against naive low rank models (PCA) of equal rank by artificially hiding a portion of the elements in the dataset and judging each model’s ability to correctly impute the missing values. This procedure was repeated in a 5-fold cross validation for each model (Figure 3). In both datasets, the tailored models outperformed PCA in terms of the imputation error for held out values. Imputation errors are evaluated using a merit function specific to the data, not the model. While minimizing the merit function is the ultimate goal, models are fit using loss functions because the merit function is generally nonsmooth and nonconvex.

FIGURE 3.

Training and testing imputation error in 5-fold cross validation of each model across a range ranks. The tailored models perform better than their naive counterpart (PCA). Imputation error is mean-normalized within each feature and by the number of data entries tested over.

3.2. Low rank models discover hospitalization phenotypes

We began our analysis of our hospitalization model by inspecting the latent features. Recall that each latent feature in a low rank model is a row vector in the computed matrix Y. Each entry in this vector corresponds to the influence of an original feature within this latent feature. We examined the representation of the original features in terms of the latent features by clustering the latent feature representations of the original features (the columns of the matrix Y). Hierarchical clustering clearly reproduced known associations between diagnoses, procedures, comorbidities, and demographics (not shown).

To discover phenotypes, we clustered the low rank representation of our subsample of the NIS dataset (the matrix X). We chose a hierarchical cluster cutpoint for eight clusters of hospitalizations and compared cluster characteristics (Table 1) in terms of the original feature space. The eight clusters had widely divergent baseline characteristics and could be well defined within recognizable hospital phenotypes. For example, patients in clusters 4 and 5 were nearly all young females who were hospitalized for pregnancy and childbirth. They differed in that patients in cluster 5 had a slightly longer length of stay, likely associated with the marked difference in the need for C-sections (6.2% for cluster 4 vs 88.4% for cluster 5). Cluster 1 appeared to contain patients hospitalized for orthopedic procedures, while cluster 2 largely included patients with psychiatric or substance abuse hospitalization -- the most common procedure was alcohol detoxification (16.7%). Cluster 7 was nearly exclusively patients undergoing procedures for acute myocardial infarction with a 91.0% rate of cardiac percutaneous transluminal coronary angioplasty. Clusters 6 and 8 included medically complex patients with cluster 6 having a high mortality (8.1%) with a younger mean age of 61 years.

TABLE 1.

Hospitalization phenotypes closely mirror common reasons for hospitalization.

	Sample Clusters
	1	2	3	4	5	6	7	8
	n = 759 (9.2%)	n = 527 (6.4%)	n = 2,807 (33.9%)	n = 629 (7.6%)	n = 302 (3.6%)	n = 2,311 (27.9%)	n = 177 (2.1%)	n = 779 (9.4%)
Phenotype	ORTHO	PSYCH	INFECT	EASY OB	HARD OB	SEVERE	AMI	COMPLEX
									p-value
Age	63 (17)	45 (13)	62 (19)	27 (6)	30 (6)	61 (18)	63 (12)	71 (16)	<0.001
Female	58.4%	44.4%	56.7%	100%	99.3%	53.6%	31.6%	48.3%	<0.001
LOS	3.6 (3.1)	4.2 (4.2)	4.1 (4.6)	2.3 (1.4)	3.5 (3.0)	6.9 (9.0)	2.9 (2.7)	5.4 (4.4)	<0.001
Mortality	0%	0.2%	0.2%	0%	0%	8.1%	1.7%	0.5%	<0.001
Cost	48.8 (50.4)	16.0 (18.0)	23.4 (23.9)	10.5 (6.6)	18.8 (19.3)	55.2 (81.7)	65.6 (41.9)	36.0 (38.3)	<0.001
Principal Diagnosis									<0.001
#1	OA (29.4%)	Mood d/o (17.8%)	PNA (5.8%)	OB traum. (26.6%)	Prior Csxn (23.3%)	Sepsis (5.2%)	AMI (48.6%)	CHF (11.7%)
#2	Back pain (16.2%)	EtOH d/o (14.2%)	COPD (4.6%)	Preg. Comp (12.6%)	Birth Comp (13.9%)	Biliary dz (3.7%)	CAD (42.4%)	AKI (5.5%)
#3	LL Fxr (7.1%)	Substance (8.7%)	Sepsis (3.7%)	Birth comp (12.2%)	Breach (10.9%)	Rehab (3.4%)	Dev. Compl (4.5%)	HTN compl (5.3%)
#4	Hip Fxr (6.2%)	Schizo. (8.0%)	Angina (3.7%)	Prol. Preg. (10.7%)	Fetal distr. (8.9%)	Complic. (2.7%)	Conduction (0.6%)	Dev compl (4.6%)
#5	Dev Comp (5.4%)	Pancreatic (4.6%)	Dysrhythm (3.6%)	Nml. Preg. (8.0%)	Preg HTN (7.6%)	CVA (2.6%)	Dysrhytm (0.6%)	Sepsis (4.5%)
Principal procedure									<0.001
#1	Knee arth. (22.4%)	None (64.7%)	None (64.9%)	Deliv. Assist (53.1%)	C-sxn (88.4%)	None (19.0%)	PTCA (91.0%)	None (40.8%)
#2	Spinal fus (12.5%)	Etoh detox (16.7%)	Card. Cath (3.5%)	OB lac rep (26.2%)	Deliv Assist (4.3%)	EGD (5.4%)	Other heart (3.4%)	Dialysis (11.4%)
#3	Hip replac (11.9%)	Ventilation (3.4%)	Other cath (2.4%)	C-sxn (6.2%)	Tubes tie (2.3%)	Ventilation (4.4%)	Card cath (1.7%)	Blood Tx (6.0%)

Ortho: orthopedics; Psych: psychiatric; Infect: infection; Easy OB: uncomplicated obstectrics; Hard OB: complex obstetrics; Severe: severe medical illness; AMI: acute myocardial infarction; Complex: complex medical illness; LOS: length of stay; OA: osteoarthritis; LLL lower extremity; Fxr: fracture; Dev Comp: device complication; D/O: disorder; EtOH: alcohol; Schizo: schizophrenia; PNA: pneumonia; COPD: chronic obstructive pulmonary disease; OB: obstetrical; Preg: pregnancy; Comp: complication; Csxn: Ceasarean section; Fetal distr: detal distress; HTN: hypertension; Dz: disease; Complic: complication; CVA: cerebrovascular disease; CAD: coronary artery disease; CHF: congestive heart failure; AKI: acute kidney injury; Arth: arthroscopy; Spinal fus: spinal fusion; Hip replac: hip replacement; Detox: detoxification; Card cath: cardiac catheterization; OB lac rep: laceration repair; EGD: esophagoduodenoscopy; PTCA: percutaneous coronary angioplasty; Blood tx: blood transfusion

3.3. Phenotypes discovered from a low rank model of ASD progression

To discover ASD phenotypes we first examined the composition of the latent features in our models. Regardless of the parameterization or the rank, the primary effect that we observed in our latent feature vectors was differential enrichment for original features coming from different 6-month time-bins (Figure 4). For instance, the second latent feature shown has relatively high weights on original features corresponding to medical concepts observed in patients during the second time bin, while the first has relatively high weights on original features corresponding to clinical concepts observed in patients during the fourth time bin. This “useage timeline” effect was evident in all models we considered, regardless of rank.

FIGURE 4.

Each panel represents one latent feature vector in the matrix Y. Vertical gray lines are manually overlaid boundaries between time bins. Time bins are ordered temporally from left to right. The weights of the original features in each latent feature representation are predominantly associated according to the time bin in which each original feature was recorded, and not by clinical similarity between the original features.

To discover phenotypes, we clustered the low rank representations of our ASD dataset (the matrix X). Using k-means clustering, we derived cluster centroids (phenotypes) in terms of their latent feature representations (each phenotype is a vector in ℜ^k). To inspect these in terms of our original features, we multiplied each phenotype vector by the matrix Y. The derived phenotypes were not differentially enriched for specific clinical concepts. Instead, these “temporal phenotypes” grouped patients by the timings of their interactions with the healthcare system.

4. Discussion

4.1. Hospital phenotypes suggest streamlining or compartmentalizing hospital organization

Our analysis of a nationally-representative hospitalization administrative dataset revealed that low rank modeling could identify clinically distinguishable hospital phenotypes. These phenotypes are immediately familiar to clinicians and hospital administrators with each cluster representing recognizable ‘wards’ or ‘service lines’ provided by hospitals. For example, it distinguished patients primarily admitted for orthopedic surgeries from those admitted for substance abuse or psychiatric diagnoses, essentially rediscovering hospitals’ ‘orthopedics’ and ‘psychiatric’ wards. Our approach also identified sub-phenotypes within larger classes. For example, hospitalizations for childbirth are the most common reason for US inpatient stays, and our results revealed two subtypes within the obstetric population differentiated by their need for procedural intervention. Our current results establish the validity of using the low rank modeling approach for identifying known hospital phenotypes with the hope that extending this approach will yield the discovery of new phenotypes for which streamlined care pathways can be implemented.

4.2. Time-binning masks phenotype signals in ASD dataset

In our ASD model, we saw that the discovered phenotypes were not differentially enriched for specific clinical concepts. However, the phenotypes were not the product of random noise--they succeeded in capturing the primary source of variation in the data, which was temporality. Analysis of the latent features revealed that mentions of different clinical concepts within a time bin are more associated with each other than mentions of the same clinical concept with itself in another time bin. The model remarkably learned these associations without any a priori knowledge that the features represented time-binned counts. The model successfully detected a clear structure in the data, although that structure reflects an artifact of featurization and the clinical challenges associated with early diagnosis in ASD. There may be clinically relevant phenotypes present in the data, but our analysis shows that this signal is masked by time-binning. Our result is emblematic of what lies at the crux of low-rank models: the algorithm will discover the clearest and most robust signals, whether or not these signals are meaningful to the user’s research interest or insight. Thus low rank models should be used to understand the profile of the dataset in order to inform future data collection or featurization. In our case, our result suggests that we should employ a different featurization method in future studies or that we should incorporate time explicitly, perhaps using tensor factorization or a convolutional approach.

4.3 Summary

In this study, we applied a novel and flexible machine learning method -- generalized low rank modeling -- to two very different datasets. Instead of forcing the same model onto different datasets or creating specific methods with little hope of reuse, we built two unique models united by one overarching framework and software package. Furthermore, we demonstrated different approaches to analyzing low rank models and used these techniques to discover phenotypes present in the data.

Accelerating the process of phenotype discovery has high potential to improve care and outcomes for patients, but additional work in the validation and care standardization of such phenotypes is still required. Nonetheless, using such a high-throughput approach for finding patient subgroups could dramatically shorten the time necessary to make new discoveries, especially when applied to massive datasets documenting poorly understood phenomena.