Joint analysis of multiple traits in rare variant association studies

SUMMARY

The joint analysis of multiple traits has recently become popular since it can increase statistical power to detect genetic variants and there is increasing evidence showing that pleiotropy is a widespread phenomenon in complex diseases. Currently, the majority of existing methods for the joint analysis of multiple traits test association between one common variant and multiple traits. However, the variant-by-variant methods for common variant association studies may not be optimal for rare variant association studies due to the allelic heterogeneity as well as the extreme rarity of individual variants. Current statistical methods for rare variant association studies are for one single trait only. In this paper, we propose an Adaptive Weighting Reverse Regression (AWRR) method to test association between multiple traits and rare variants in a genomic region. AWRR is robust to the directions of effects of causal variants and is also robust to the directions of association of traits. Using extensive simulation studies, we compare the performance of AWRR with canonical correlation analysis (CCA), Single-TOW, and the Weighted Sum Reverse Regression (WSRR). Our results show that, in all of the simulation scenarios, AWRR is consistently more powerful than CCA. In most scenarios, AWRR is more powerful than Single-TOW and WSRR.

Introduction

There is increasing evidence showing that pleiotropy, the effect of one variant on multiple traits, is a widespread phenomenon in complex diseases (Sivakumaran et al., 2011). Furthermore, in genetic association studies of complex diseases, multiple related traits are usually measured. For example, hypertension is evaluated using systolic and diastolic blood pressures, the Metabolic Syndrome is based on observing three of five criteria (Sattar et al., 2008), and neuropsychiatric disorders depend on a range of overlapping clinical characteristics (O'Reilly et al., 2012). Although most published genome-wide association studies (GWAS) analyze each of the related traits separately, the joint analysis of multiple traits not only can increase statistical power to detect genetic variants (Solovieff et al., 2013; Stephens, 2013; Yang & Wang, 2012; Zhou & Stephens, 2014), but can also be crucial to understand the genetic architecture of the disease of interest (Aschard et al., 2014). Thus, the joint analysis of multiple traits has recently become popular. Several statistical methods for the joint analysis of multiple traits have been developed. These methods can be roughly divided into three groups: regression methods, combining test statistics from univariate analysis, and dimension reduction methods. Regression methods include mixed effects models (Korte et al., 2012; Zhou & Stephens, 2014) and reverse regression models (O'Reilly et al., 2012; Yan et al., 2013). By modeling the covariance structure of correlated traits and dependence structure between individuals, mixed effects models not only can incorporate multiple correlated traits, but also can be robust to population stratification. Reverse regression models consider genotypes as the response variable and all the traits as independent variables, therefore, reverse regression models do not need to know the complex distributions of the traits and can be applied to a large number of mixed types of traits. For combining the test statistics from univariate analysis, one first obtains univariate test statistics by performing association tests for each trait individually and then combines the univariate test statistics by linear combinations (O'Brien, 1984; van der Sluis et al., 2013; Yang et al., 2010). The dimension reduction methods include canonical correlation analysis (CCA) (Tang & Ferreira, 2012), principal components of traits (PCT) (Aschard et al., 2014), and principal components of heritability (PCH) (Klei et al., 2008; Lange et al., 2004; Ott & Rabinowitz, 1999). CCA is to find a linear combination of traits and a linear combination of genotypes at multiple variants such that the correlation between the two linear combinations reaches its maximum. PCT is the principal component analysis to the traits. The PCT methods are usually based on the first PC or first few PCs of the traits (Feng et al., 2007; Klei et al., 2008). Aschard et al. (2014) showed that contrary to the widespread practice, tests based on only the first few PCs often have low power, whereas combining signals across all PCs can have greater power. PCH is to find a linear combination of multiple traits such that this linear combination has the maximum heritability.

Almost all of the aforementioned methods are to test association between one common variant and multiple traits. However, the variant-by-variant methods for common variant association studies may not be optimal for rare variant association studies due to the allelic heterogeneity as well as the extreme rarity of individual variants (Li & Leal, 2008). Recent studies show that complex diseases are caused by both common and rare variants (Bodmer & Bonilla, 2008; Kang et al., 2010; Pritchard, 2001; Pritchard & Cox, 2002; Stratton & Rahman, 2008; Teer & Mullikin, 2010; Walsh & King, 2007). Next-generation sequencing technology allows sequencing of the whole genome of large groups of individuals, and thus makes rare variant association studies feasible (Andres et al., 2007; Metzker, 2010). Recently, statistical methods for rare variant association studies with a single trait have been developed by summarizing genotype information from multiple variants. These methods include burden tests (Li & Leal, 2008; Madsen & Browning, 2009; Morgenthaler & Thilly, 2007; Price et al., 2010; Zawistowski et al., 2010), quadratic tests (Neale et al., 2011; Sha et al., 2012; Wu et al., 2011), and combined tests (Derkach et al., 2013; Lee et al., 2012; Sha & Zhang, 2014). Burden tests collapse rare variants in a genomic region into a single burden variable and then regress the trait on the burden variable to test for the cumulative effects of rare variants in the region. These tests implicitly assume that all rare variants are causal and that the directions of the effects are all the same. Quadratic tests include tests with statistics of quadratic form of score vector, as well as adaptive weighting methods. These tests are robust to the directions of the effects of causal variants and are less affected by neutral variants than burden tests. Burden tests can only outperform quadratic tests when most of the rare variants are causal and the directions of the effects of causal variants are all the same. Combined tests combine information from burden tests, quadratic tests, and possibly other tests aiming to have advantages of multiple tests.

In this article, we propose an adaptive weighting reverse regression (AWRR) method to test association between multiple traits and rare variants in a genomic region. In AWRR, we first propose adaptive weights to collapse genotypes. Then, we use the score test to test association based on the reverse regression, in which collapsed genotypes is treated as the response variable and multiple traits are treated as independent variables. Using extensive simulation studies, we compare the performance of AWRR with CCA, Single-TOW, and the Weighted Sum Reverse Regression (WSRR). In Single-TOW, we first calculate the TOW statistic (Sha et al., 2012) to test the association between each trait and variants in a genomic region and then the statistic of Single-TOW is the largest of TOW statistics. In WSRR, we first calculate the weighted sum (Madsen & Browning, 2009) of genotypes at variants in a genomic region and then the statistic of WSRR is the score test statistic under reverse regression model, in which the weighted sum of genotypes is the response variable and traits are predictor variables. Our results show that, in all of the simulation scenarios, AWRR is consistently more powerful than CCA. In most scenarios, AWRR is more powerful than Single-TOW and WSRR.

Method

We consider a sample with n unrelated individuals. Each individual has K (potentially correlated) traits and has been genotyped at M variants in a genomic region. Let y_ik denote the k^th trait value of the i^th individual. Let x_im denote the genotype score of the m^th variant of the i^th individual, where x_im is the number of minor alleles of the i^th individual carried at the m^th variant. We denote Y_i = (y_i1,…,y_iK)^T as the K traits for the i^th individual. We propose an adaptive weighting reverse regression (AWRR) method to test the null hypothesis H₀: none of the K traits are associated with the M variants in the genomic region. For constructing the test statistic of AWRR, we first collapse the M dimensional genotype (x_i1,…,x_iM) into a one dimensional number $x_i=\sum _{m=1}^M{w}_m{x}_{im}$, where w_m is the adaptive weight for the m^th variant. The adaptive weight w_m should satisfy the properties that w_m should be large if the m^th variant has strong association with the K traits and w_m should have different signs for risk and protective variants. Then, the statistic of AWRR is the score test statistic under the reverse regression model $x_i={\beta }_0+\sum _{k=1}^K{\beta }_k{y}_{ik}+{\epsilon }_i$. In details, the AWRR method has the following steps.

1. We define a weight W_m for the m^th variant such that W_m will be large if the m^th variant has strong association with the K traits and W_m will be also large if the m^th variant is a rare variant. For these purposes, we propose $W_m=\frac{1}{\sqrt{p_m(1-p_m)}}{T}_m$, where p_m is the minor allele frequency of the m^th variant and T_m is the score statistic to test the null hypothesis H₀:β₁=⋯=β_K = 0 under the reverse regression model $\text{log}\frac{p_{im}}{1-p_{im}}={\beta }_0+{\beta }_1{y}_{i1}+\cdots +{\beta }_K{y}_{iK}$, where we assume a dominant model p_im = Pr(x_im=1) = Pr(x_im=2). In fact, for rare variants, x_im essentially is 0 or 1. The score statistic is given by $T_m=U_m^T{V}_m^{-1}{U}_m$, where $U_m=\sum _{i=1}^n{Y}_i(x_{im}-{\overline{x}}_m)$ and $V_m=\frac{1}{n}\sum _{i=1}^n{(x_{im}-{\overline{x}}_m)}^2\sum _{i=1}^n(Y_i-\overline{Y}){(Y_i-\overline{Y})}^T$, where ${\overline{x}}_m=\frac{1}{n}\sum _{i=1}^n{x}_{im}$, and $\overline{Y}=\frac{1}{n}\sum _{i=1}^n{Y}_i$. Under the null hypothesis, T_m follows a χ² distribution with degrees of freedom K. However, W_m does not consider the direction of the effects of causal variants.

2. In this step, we will define a direction of W_m. We first select a trait (the selected trait denoted as the k̃^th trait). We use sign(ρ(y_k̃,x_m)) to denote the direction of the associations of the m^th variant, where y_k̃ = (y_1k̃,…,y_nk̃)^T and x_m = (x_1m,…,x_nm)^T. If the k̃^th trait has no association with the M variants, the directions of the association will be random. In order to try to avoid random directions, we propose to choose the trait that has the strongest association with the M variants. Let $T_{TOW}^k$ denote the statistic of TOW (Sha et al., 2012) to test association between the k^th trait and the M variants. $T_{TOW}^k$ is defined as $T_{TOW}^k=\sum _{i=1}^n(y_{ik}-{\overline{y}}_k)(x_i^o-{\overline{x}}^o)$, where $x_i^o={\sum }_{m=1}^M{w}_m^o{x}_{im}$ and $w_m^O={\sum }_{i=1}^n(y_{ik}-{\overline{y}}_k)(x_{im}-{\overline{x}}_m)/{\sum }_{i=1}^n{(x_{im}-{\overline{x}}_m)}^2$. We choose the k̃^th trait such that $T_{TOW}^{\tilde{k}}={\text{max}}_{1\le k\le K}{T}_{TOW}^k$.

3. The final weight for the m^th variant is given by w_m = sign(ρ(y_k̃,x_m))W_m. Let $x_i=\sum _{m=1}^M{w}_m{x}_{im}$. Then, we consider the reverse regression model $x_i={\beta }_0+\sum _{k=1}^K{\beta }_k{y}_{ik}+{\epsilon }_i$. We apply a score test to test the null hypothesis H₀:β₁ =⋯= β_K = 0. The score statistic is given by T_AWRR = u^TV⁻¹u, where $u=\sum _{i=1}^n(x_i-\overline{x})Y_i,V=\frac{1}{n}\sum _{i=1}^n{(x_i-\overline{x})}^2\sum _{i=1}^n(Y_i-\overline{Y}){(Y_i-\overline{Y})}^T,\overline{x}=\frac{1}{n}\sum _{i=1}^n{x}_i$, and $\overline{Y}=\frac{1}{n}\sum _{i=1}^n{Y}_i$.

4. In this step, we evaluate the p-value of T_AWRR. Since w_m depends on the trait values and the genotype scores, T_AWRR does not follow a χ² distribution with degrees of freedom K. We use a permutation procedure to evaluate the p-value of T_AWRR. In each permutation, we randomly shuffle Y₁,…,Y_n and keep the genotypes of each individual unchanged. We repeat step 1 to step 3 based on each permutated data. Let $T_{AWRR}^0$ denote the test statistic of T_AWRR based on the original data and $T_{AWRR}^{\mathit{\text{per}}}$ denote the test statistic based on the permuted data. Then the p-value of the test T_AWRR is the proportion of the number of permutations with $T_{AWRR}^{\mathit{\text{per}}}\ge T_{AWRR}^0$.

Comparison of Tests

We compare the performance of the proposed test AWRR with those of the canonical correlation analysis (CCA) (Tang & Ferreira, 2012), the Single-TOW method (Sha et al., 2012), and the Weighted Sum Reverse Regression (WSRR) method (Madsen & Browning, 2009).

CCA method

although the asymptotical distribution of the CCA statistic works well for common variants, it is very conservative for rare variants. Thus, we propose to use a permutation procedure to evaluate the p-value of the CCA statistic.

Single-TOW method

let $T_{TOW}^k$ denote the statistic of TOW (Sha et al., 2012) to test association between the k^th trait and the M variants. The statistic of Single-TOW is given by $T_{\mathit{\text{Single}}-TOW}={\text{max}}_{1\le k\le K}{T}_{TOW}^k$. The p-value of T_Single-TOW is evaluated by a permutation procedure.

WSRR method

let $X_i=\sum _{m=1}^M{w}_m{x}_{im}$, where $w_m=1/\sqrt{p_m(1-p_m)}$ and p_m is the minor allele frequency of the m^th variant. We consider the reverse regression model $X_i={\beta }_0+\sum _{k=1}^K{\beta }_k{y}_{ik}+{\epsilon }_i$. The statistic of WSRR, T_WSRR, is the score test statistic to test the null hypothesis H₀:β₁ =⋯=β_K = 0. Under the null hypothesis, T_WSRR follows a χ² distribution with degrees of freedom K.

Simulation

Our simulations follow that of Sha et al. (2012). In detail, the empirical Mini-Exome genotype data provided by the genetic analysis workshop 17 (GAW17) are used for simulation studies. This dataset contains genotypes of 697 unrelated individuals on 3205 genes. We conduct two sets of simulations. In the first set of simulations, we choose four genes: ELAVL4, MSH4, PDE4B, and ADAMTS4 with 10, 20, 30, and 40 variants, respectively. We merge the four genes to form a super gene (Sgene1) with 100 variants (Sha et al., 2012). In the second set of simulations, we choose ten genes: ELAVL4, FAM73A, PSMB4, FSHR, GMCL1, HNMT, GALNT13, NEUROD1, MYEOV2, and TWF2 with 10 variants in each of them. We merge the ten genes to form a super gene (Sgene2) with 100 variants. In our simulation studies, we generate genotypes based on the genotypes of 697 individuals in the Sgene1 and Sgene2. To generate a qualitative disease affection status, we use a liability threshold model based on a quantitative trait. For a qualitative trait, an individual is defined as affected if the individual’s corresponding quantitative trait is at least one standard deviation larger than the phenotypic mean. This yields a prevalence of 16% for the simulated disease in the general population. In the following, we describe how to generate a quantitative trait.

To evaluate the type I error, we generate K traits of an individual independent of the genotypes by using

$$Y={(y_1,\dots ,y_K)}^T=\sqrt{\rho }\mathrm{B}u+\sqrt{1-\rho }\epsilon ,$$

where u = (u₁,…,u_nu)^T ~ MVN (0,I) is a vector of n_u independent standard normal latent variables, ε = (ε₁,…, ε_K)^T ~ MVN (0,I) is a vector of errors, B is a K×n_u loading matrix, the values of n_u and B are based on two variance models: (1) n_u = 1, B = (1,…,1)^T and (2) n_u = 2, $\mathrm{B}=\left[\begin{array}{cc}\hfill e_{[K/2]}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill e_{K-[K/2]}\hfill \end{array}\right]$. Thus, Y ~ MVN(0,Σ), where Σ = ρBB^T + (1−ρ)I.

To evaluate power, we consider that all causal variants are rare (MAF<0.01). We randomly choose n_c rare variants as causal variants, where n_c is determined by the percentage of causal variants among rare variants. Denote n_r and n_p as the number of risk rare variants and protective rare variants, respectively, where n_r+n_p = n_c. Let $x_{qi}^r$ and $x_{ji}^p$ denote the genotypic scores of the q^th risk rare variant and the j^th protective rare variant for the i^th individual, respectively. Suppose that causal variants have impact on L traits among the K traits. Among the L traits, there are L_p traits positively correlated with risk variants and there are L_n traits negatively correlated with risk variants. Let h denote the heritability of all the n_c rare causal variants on each of the L traits. Generate n_c random numbers r₁,…,r_nc from a uniform distribution between 0 and 1. The heritability of the i^th causal variant is given by $h_i=\raisebox{1ex}{$h{r}_i$}\!\left/ \!\raisebox{-1ex}{$\sum _{j=1}^{n_c}{r}_j$}\right.$. Under this assumption, we simulated K traits by

$$y_{ik}=\{\begin{array}{cc}\sum _{q=1}^{n_r}{\beta }_{kq}^r{x}_{qi}^r-\sum _{j=1}^{n_p}{\beta }_{kj}^p{x}_{ji}^p+{\epsilon }_{ik},\hfill & 1\le k\le L_p\hfill \\ -(\sum _{q=1}^{n_r}{\beta }_{kq}^r{x}_{qi}^r-\sum _{j=1}^{n_p}{\beta }_{kj}^p{x}_{ji}^p)+{\epsilon }_{ik},\hfill & L_p+1\le k\le L,\hfill \\ {\epsilon }_{ik},\hfill & L<k\le K\hfill \end{array}$$

where ε_i = (ε_i1,…,ε_iK)^T can be generated in the same way as generating traits of evaluating type I error, ${\beta }_{kq}^r$ and ${\beta }_{kj}^p$ are constants and their values depend on the heritability.

Results

For type I error evaluation, we only consider the first set of simulations, but consider different sample sizes, different significance levels, different variance models and different types of traits. In each simulation scenario, the p-values of AWRR, Single-TOW and CCA are estimated by 10,000 permutations (the p-values of WSRR are estimated by a χ² distribution) and the type I error rates of all of the four tests are evaluated using 10,000 replicated samples. For 10,000 replicated samples, the 95% confidence intervals (CIs) for the type I error rates at the nominal levels 0.05 and 0.01 are (0.046, 0.054) and (0.008, 0.012), respectively. The estimated type I error rates of the four tests are summarized in Tables 1, 2, S1 and S2. From these tables, we can see that only two estimated type I error rates of CCA are not within the CIs and these two type I error rates (one is 0.0126 for nominal level 0.01 in Table 1, and the other one is 0.05505 for nominal level 0.05 in Table S1) are very close to the upper bounds of the corresponding CIs, which indicates that the four tests are all valid.

Table 1.

The estimated type I error rates of four methods for quantitative traits under variance model 1. 10,000 replicates are used. This set of simulations is based on Sgene1.

	Sample size
		500	1000	2000
α = 0.05	CCA	0.0518	0.0519	0.04645
	Single-TOW	0.04995	0.05255	0.0506
	WSRR	0.0464	0.0506	0.0496
	AWRR	0.0519	0.0527	0.0531
α = 0.01	CCA	0.012	0.00845	0.0126
	Single-TOW	0.0117	0.00965	0.012
	WSRR	0.0081	0.009	0.0097
	AWRR	0.01075	0.0097	0.01135

Table 2.

The estimated type I error rates of four methods for qualitative traits under variance model 1. 10,000 replicates are used. This set of simulations is based on Sgene1.

	Sample size
		500	1000	2000
α = 0.05	CCA	0.052	0.0527	0.04985
	Single-TOW	0.0519	0.0534	0.05
	WSRR	0.0502	0.0493	0.0487
	AWRR	0.054	0.0505	0.05265
α = 0.01	CCA	0.0101	0.01115	0.00955
	Single-TOW	0.0109	0.01165	0.01115
	WSRR	0.0106	0.0092	0.0106
	AWRR	0.00955	0.00965	0.012

For power comparisons, we consider 10 traits and we assume that all causal variants are rare. For each type of traits and each variance model, we consider different values of heritability, different percentages of protective variants, and different percentages of causal variants. In each of the simulation scenarios, the p-values of AWRR, Single-TOW and CCA are estimated using 1,000 permutations (the p-values of WSRR are estimated by a χ² distribution) and the power of all of the four tests is evaluated using 500 replicated samples at a significance level of 0.05.

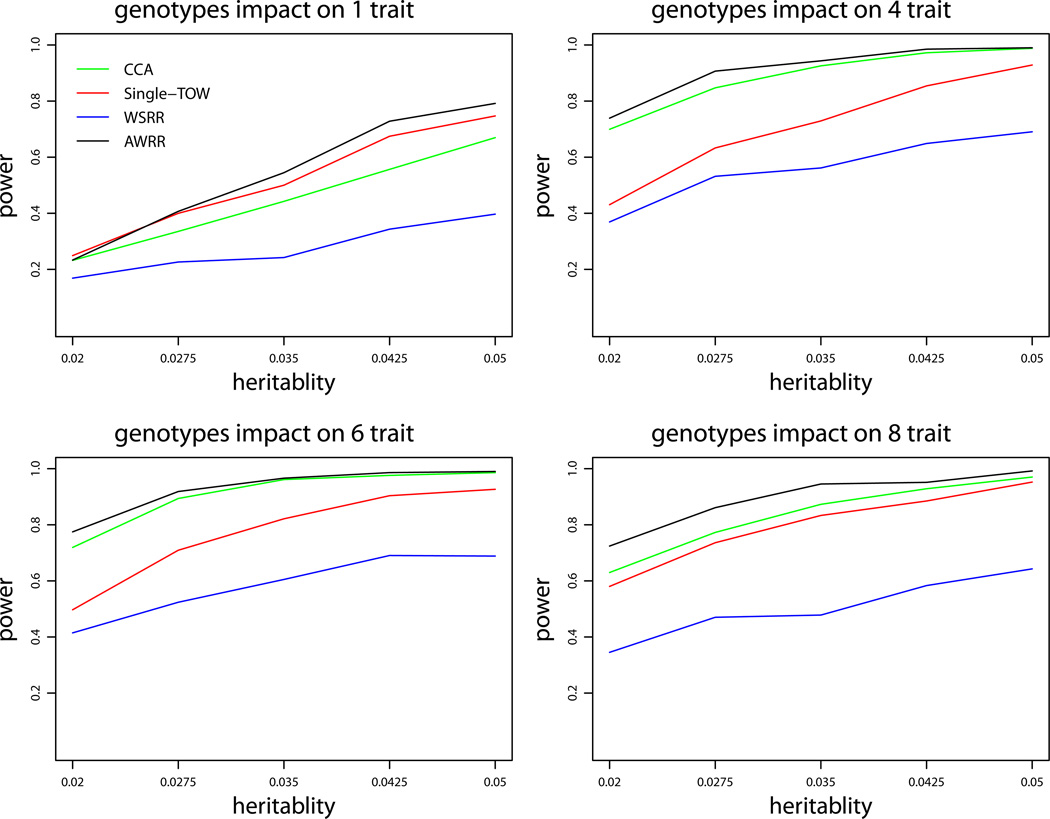
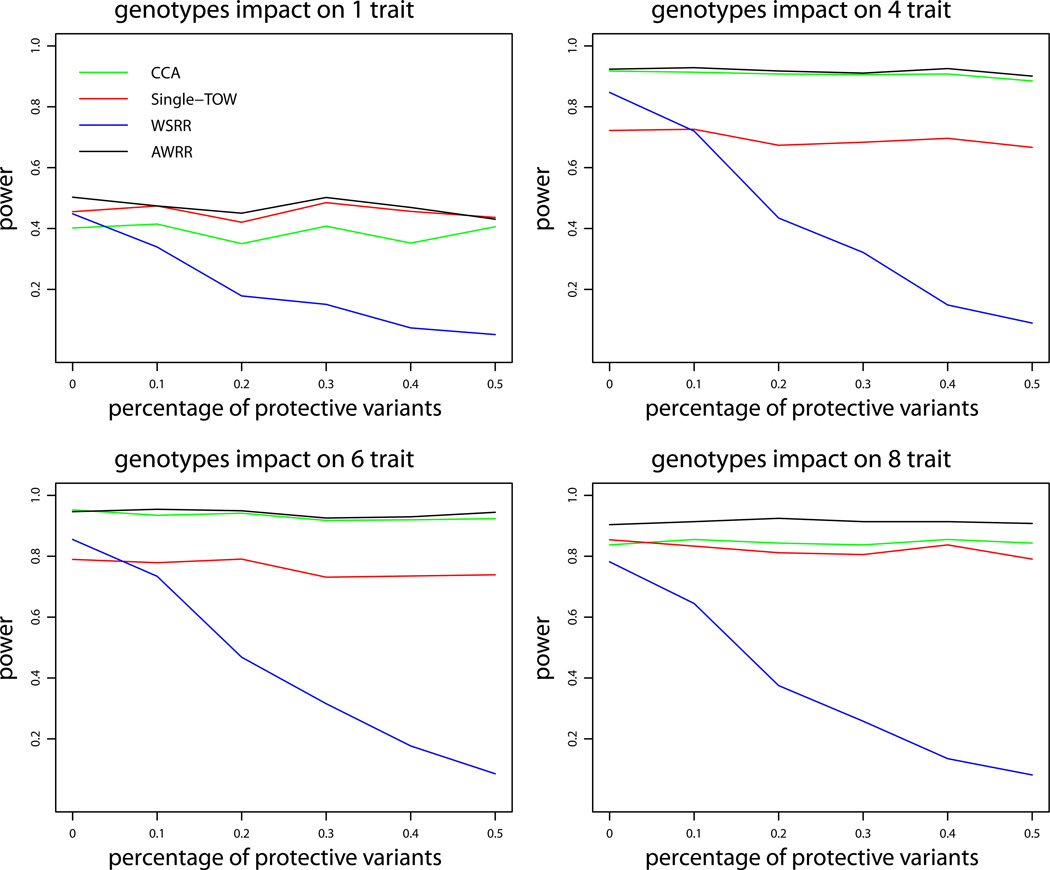
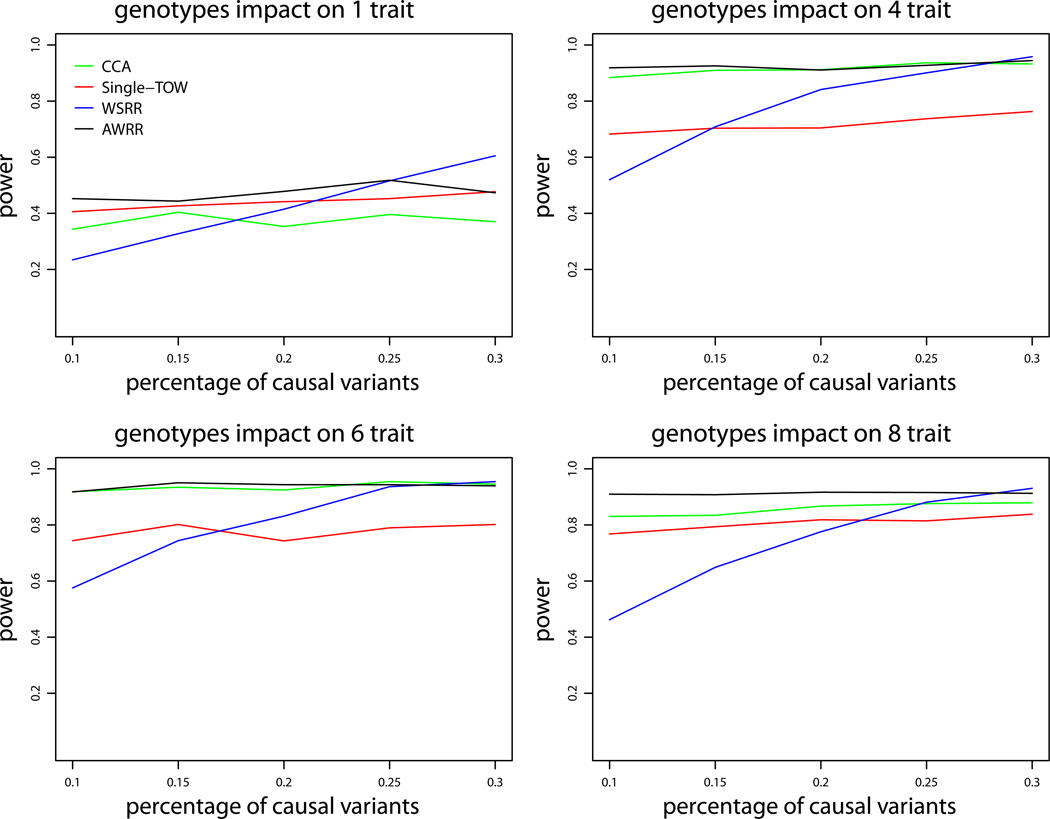
We first consider the first set of simulations for quantitative traits under variance model 1. Figure 1 provides the power comparisons of the four tests (WSRR, AWRR, CCA and Single-TOW) for the power as a function of heritability. This figure shows that WSRR is the least powerful one and AWRR is the most powerful one. It is little complicated to compare the power of Single-TOW with the power of CCA. When genotypes impact on only one trait, Single-TOW is more powerful than CCA; otherwise, CCA is more powerful than Single-TOW. Since Single-TOW only depends on the trait that has the strongest association with genotypes, it is more favorable for Single-TOW when genotypes impact on fewer traits. Power comparisons of the four tests for the power as a function of percentage of protective variants are given by Figure 2. This figure shows that, with an increasing percentage of protective variants, the power of WSRR decreases while the power of the other three methods does not change. Other patterns of the power comparisons are similar to those shown in Figure 1. The power comparisons of the four tests for the power as a function of the percentage of causal variants are given by Figure 3. As shown in this figure, with an increasing percentage of causal variants, the power of WSRR increases while the power of the other three methods does not change. WSRR is the least powerful method when the percentage of causal variants is small (≤ 0.15), while WSRR is the most powerful test when the percentage of causal variants is large (≥ 0.3). The patterns of the power comparisons of CCA, AWRR and Single-TOW are similar to those shown in Figure 1.

Figure 1.

Power comparisons of the four tests (WSRR, AWRR, CCA and Single-TOW) for the power as a function of heritability for quantitative traits under variance model 1. The sample size is 1000 and ρ = 0.5. The percentage of the causal variants is 0.1. All causal variants are risk variants. The total number of traits is 10. This set of simulations is based on Sgene1.

Figure 2.

Power comparisons of the four tests (WSRR, AWRR, CCA and Single-TOW) for the power as a function of percentage of protective variants for quantitative traits under variance model 1. The sample size is 1000, the percentage of causal variants is 0.2, the total heritability is 0.03, and ρ = 0.5. The total number of traits is 10. This set of simulations is based on Sgene1.

Figure 3.

Power comparisons of the four tests (WSRR, AWRR, CCA and Single-TOW) for the power as a function of the percentage of causal variants for quantitative traits under variance model 1. The sample size is 1000 and ρ = 0.5, and the total heritability is 0.03. All causal variants are risk variants. The total number of traits is 10. This set of simulations is based on Sgene1.

Under the first set of simulations, we also compare the powers of the four methods for quantitative traits under variance model 2 and for qualitative traits under variance models 1 and 2. These results are given in Figures S1–S9. For each type of trait, the patterns of the power comparisons are similar under variance models 1 and 2. For qualitative traits, CCA is consistently less powerful than Single-TOW and AWRR because CCA is designed for quantitative traits. For qualitative traits, the powers of AWRR, Single-TOW, and CCA decrease with the increase of the percentage of protective variants, although decrease not as fast as that of WSRR. As pointed out by Wu et al. (2011) and Sha et al. (2012), the decrease in the powers of AWRR, Single-TOW, and CCA in the presence of both risk and protective variants is due to the fact that protective variants lower MAFs in cases and thus make observing rare variants in the cases more difficult. The larger decrease in power of WSRR is additionally driven by the sensitivity to the direction of the effect due to aggregation of genotypes.

Under the second set of simulations, we compare the powers of the four methods for quantitative traits under variance model 1. Results are given in Figures S10–S12. Comparing Figures S10–S12 with Figures 1–3, the patterns of the power comparisons under the second set of simulations are very similar to those under the first set of simulations. Under the second set of simulations, we also compare the powers of the four methods for quantitative traits under variance model 2 and for qualitative traits under variance models 1 and 2 (results are not shown). Results also show that the patterns of the power comparisons under the second set of simulations are very similar to those under the first set of simulations.

In summary, for all simulation scenarios, AWRR is consistently more powerful than CCA and the power of WSRR increases with an increasing percentage of causal variants or with a decreasing o percentage of protective variants. For quantitative traits, the powers of AWRR, CCA and Single-TOW are robust to the percentage of protective variants and to the percentage of causal variants, while for qualitative traits, the powers of AWRR, CCA and Single-TOW decrease with the increasing of the percentage of protective variants and are relatively robust to the percentage of causal variants.

Discussion

In this article, we proposed the AWRR method to perform joint analysis of multiple traits in rare variant association studies based on the following reasons: (1) the development of next-generation sequencing technology has made directly testing all rare variants feasible and (2) there is increasing evidence showing that pleiotropy is a widespread phenomenon in complex diseases and multiple related traits are usually measured in genetic association studies of complex diseases. We used extensive simulation studies to compare the performance of AWRR with CCA, WSRR and Single-TOW. Our results showed that AWRR has correct type I error rates, is robust to the directions of the association of causal variants for quantitative traits, and is robust to the percentage of causal variants. AWRR is consistently more powerful than CCA. AWRR is more powerful than Single-TOW and WSRR in most simulation scenarios.

Our simulation studies showed that the performance of each of AWRR, WSRR and Single-TOW depends strongly upon the number of traits impacted by genetic variants, the percentage of protective variants, and the percentage of causal variants. And no method demonstrates consistently good power. To increase the robustness of the test, we can combine AWRR, WSRR and Single-TOW aiming to have advantages of the three methods. Let p_AWRR, p_WSRR and p_Single-TOW denote the p-values of AWRR, WSRR, and Single-TOW, respectively. The combined test statistic can be defined as T_combined = min{p_AWRR,p_WSRR,p_Single-TOW}. However, the performance of the combined test needs further investigation.

In association studies based on unrelated individuals, it has been long recognized that population stratification can seriously confound association results (Knowler et al., 1988; Lander & Schork, 1994). Several methods have been developed to control for population stratification for association studies based on unrelated individuals. These methods include the GC approach (Devlin & Roeder, 1999; Devlin et al., 2001; Reich & Goldstein, 2001), the PC approach (Bauchet et al., 2007; Chen et al., 2003; Price et al., 2006; Zhang et al., 2003; Zhu et al., 2002), and the MLM approach (Kang et al., 2010; Zhang et al., 2010). Like most association tests based on unrelated individuals, AWRR is subject to bias due to population stratification. To make AWRR robust to population stratification, we can use the PC approach. Let P_i = (p_i1,…,p_iL)^T denote the first L PCs of the genotypes at a set of genomic markers for the i^th individual. In step 3 of AWRR, we can use the residuals of the regression x_i = α + β^TP_i + ε_i to replace x_i and use the residuals of the regression $y_{ik}={\alpha }_k+{\beta }_k^T{P}_i+{\epsilon }_{ik}$ to replace y_ik. The performance of using the PC approach to control for population stratification in AWRR also needs further investigation.

The computation time required for running AWRR depends on the sample size, the number of variants in the genomic region, the number of traits, and the number of permutations. The running time of AWRR with 1000 permutations on the data set with 1000 individuals, 10 traits, and 100 variants in the genomic region on a laptop with four Intel Cores @ 2.00GHz and 4 GB memory is no more than 0.5s. To perform genome-wide studies, we can first select genomic regions that show evidence of association based on a small number of permutations (e.g. 1000), and then a large number of permutations can be used to test the selected regions.