Tradeoffs in the Design of Health Plan Payment Systems: Fit, Power and Balance

Abstract

In many markets, including the new U.S. Marketplaces, health insurance plans are paid by risk-adjusted capitation, sometimes combined with reinsurance and other payment mechanisms. This paper proposes a framework for evaluating the de facto insurer incentives embedded in these complex payment systems. We discuss fit, power and balance, each of which addresses a distinct market failure in health insurance. We implement empirical metrics of fit, power, and balance in a study of Marketplace payment systems. Using data similar to that used to develop the Marketplace risk adjustment scheme, we quantify tradeoffs among the three classes of incentives. We show that an essential tradeoff arises between the goals of limiting costs and limiting cream skimming because risk adjustment, which is aimed at discouraging cream-skimming, weakens cost control incentives in practice. A simple reinsurance system scores better on our measures of fit, power and balance than the risk adjustment scheme in use in the Marketplaces.

1. Introduction

Payments to private health plans in regulated insurance markets are complex, often mixing an array of mechanisms aimed at achieving the dual goals of constraining cost growth and limiting the distortions created by selection. When considered in isolation, features like prospective or concurrent risk adjustment, capitation, and reinsurance each have clear theoretical links to addressing particular inefficiencies. However, these features are widely used as components of larger payment systems, and the net insurer incentives created by such combinations have been essentially unexplored, both theoretically and empirically. Given the prominence of these regulatory mechanisms in both private and publicly subsidized health insurance markets in the US and elsewhere, the issue is of tremendous practical importance. The relatively small body of prior work assessing the de facto incentives in real-world payment systems for cost control and selection is surprising, since constraining cost growth has attracted significant policy interest in recent years, and over the same period there has been a surge of empirical and theoretical work in economics on adverse selection in health insurance markets.¹

We show that an essential tradeoff arises between the goals of limiting costs and limiting cream skimming because risk adjustment, which is the dominant regulatory tool aimed at discouraging cream-skimming, is in fact tied to a plan’s realized costs, and therefore affects cost control incentives. In practice, the conditions used to determine risk adjustment are established during provider-patient interactions in which a bill (claim) is generated. For example, under Medicare’s private plan option called Medicare Advantage a single physician office visit at which a patient receives a new diagnosis of “diabetes without complications” changes a patient’s risk score and results in an additional payment of approximately $1,500 annually from Medicare to the private health plan enrolling that individual. But the visit generating the diagnosis, and the follow-up events the visit triggers, such as further diagnostic testing, are components of cost to the plan, creating a link between payments a plan receives from risk adjustment and the plan’s realized costs. Thus, utilization affects both costs and risk-adjusted payments, implying that insurers are compensated at least in part for their patients’ utilization, and therefore not fully incentivized to restrain utilization as intended.

This paper proposes a framework for evaluating the de facto insurer incentives embedded in the regulations and payment systems that govern health insurance markets. We illustrate application of the framework by evaluating the risk adjustment and reinsurance scheme used in the ACA Marketplaces, and some variants on that policy. We classify incentives for analyzing payment schemes along three dimensions that capture the main regulatory concerns in health insurance markets, including containing adverse selection, controlling costs, and eliminating margins of distortion across different types of services. Specifically, we study what we refer to as the fit, power and balance of payment systems.

The notions of fit and power are well-established in the prior literature. Fit refers to how well variation across enrollees in plan costs is explained by variation in payments, and is intended to characterize the susceptibility of the payment system to cream-skimming by insurers (e.g. Van de ven and Ellis 2000 and Breyer, Bundorf and Pauly 2012). Higher fit reduces the incentive for insurers to discourage less profitable consumers from enrolling in their plan, as it compensates plans for attracting more expensive consumer types. Power is meant in the sense of the power of a contract (Laffont and Tirole 1993): it describes how the payer or regulator compensates expenditure by plans on the margin. The widespread adoption of capitation in private markets and public insurance systems in the 1980’s and its continued use today is the clearest evidence of implicit interest in contract power in these markets.

A small body of prior work has investigated the tension between incentives for cream skimming and cost reduction. This literature has primarily described the tradeoff between a prospective payment system, which maximizes incentives for cost control but may induce adverse selection, and a cost-reimbursement system, which reduces power but conveys fewer incentives to select more profitable enrollees (Newhouse, 1996). Van Barneveld et al. (2001) consider various forms of “risk sharing” between a regulator and insurers that combine prospective and retrospective components.² Our analysis emphasizes that the risk-adjusted component, which has traditionally been viewed as having no impact on cost control incentives, may affect insurer incentives for cost control in practice.³ We show that this is particularly relevant when risk adjustment is based on concurrent utilization, as in the case of the Marketplaces.

The most explicit consideration of the effect of risk adjustment on the power of a payment system was by McClellan (1997) who assessed the de facto utilization incentives in Medicare’s Prospective Payment System, which paid hospitals for Medicare admissions on the basis of Diagnosis-Related Groups (DRGs). McClellan showed that in practice the Prospective Payment System included a large retrospective component, with approximately 55 cents of each dollar in hospital costs recovered in higher payments on average. In our terms, the power of the hospital DRG-PPS system was .45. Unlike our focus here, the implicit tension between fit and power was not considered by McClellan.

Balance assesses the differences in power across various types of medical services. If medical events in one area of care impact insurance plan payment more than medical events in another area, the power of the payment system will be greater in the second area than in the first.⁴ We show that even if risk adjustment succeeds in removing the incentive for insurers to distort benefits to attract a particular set of enrollees, it can create new incentives to distort benefits conditional on a fixed set of enrollees.

The first main contribution of this paper is to highlight the de facto incentives embedded in payment schemes that feature capitation with risk adjustment and reinsurance. Traditionally, diagnostic risk adjustment has been viewed as fitting payments to expected costs without sacrificing this cost-control incentive, under the premise that risk adjustment compensates for patient characteristics rather than services provided (Pope et al., 2011). We argue here that the de facto properties of a capitation payment depend crucially on the details, such as whether risk adjustment is prospective (based on diagnoses in the prior plan year) or concurrent (based on diagnoses in the current plan year). The conceptual framework we introduce forms a foundation for empirically evaluating the tradeoffs embedded in real-world payment systems. In addition, we take a first step towards operationalizing the concepts of power, fit, and balance, though we expect future work to refine how these three characteristics are measured in various settings. We describe, for example, how power and balance can be easily measured with simulation methods applied to claims data that trace out how variation in healthcare utilization maps to variation in payments in even complex payment systems.

We illustrate the notion of de facto tradeoffs by applying our framework to the current Marketplace payment system. Using two years of claims from the same database of insureds used to calibrate Marketplace risk adjustment by the Department of Health and Human Services, we randomly eliminate healthcare events and measure the extent to which insurer payments and costs respond under various payment schemes. The Marketplace payment system is particularly complex so we take it apart to assess the partial contribution of some of its key features, such as the decision to pay plans with a concurrent rather than a prospective risk adjustment formula.

We find that, consistent with the expressed intentions of the Marketplace regulators, concurrent risk adjustment confers dramatically better fit than would prospective risk adjustment in this setting. Concurrent risk adjustment in isolation more than doubles the fit compared to prospective risk adjustment. However, we show that it does so at the cost of reducing power—that is, the incentive to constrain spending—dramatically. Further, our simulations reveal that both forms of risk adjustment feature significant imbalance. For example, the average power for inpatient services in the concurrent risk adjustment systems used in Marketplaces is about .62, but power for the top ten major diagnostic categories ranges from .18 to .92, implying that the marginal reimbursement rate across these categories ranges from 82 cents on the dollar to 8 cents on the dollar. This is a margin of potential distortion that to our knowledge has been ignored in past treatments of risk adjustment.

The second main contribution of this paper is to challenge the conventional wisdom that risk adjustment should be the preferred mechanism for linking payments to expected costs without weakening insurer incentives to control costs. A few recent studies have pointed to potential problems with risk adjustment including favorable selection (Brown et al 2014, Newhouse et al. 2012) and manipulable coding (Geruso and Layton 2015; Kronick and Welch 2014), though such studies have not evaluated the performance of risk adjustment relative to an alternative payment scheme. One of our most striking findings is that in terms of our measures of fit, power and balance, the diagnosis-based concurrent risk adjustment that is slated for indefinite use in the Marketplaces beginning in 2017 fares poorly relative to other feasible payment policies. For example, prospective risk adjustment combined with reinsurance performs on par with the planned policy in terms of fit and power, but rates significantly better in balance. Even a simple reinsurance program alone rates favorably compared to the planned 2017 payment scheme: When considered singly, reinsurance that tracks a temporary (2014 to 2016) program currently in use in the Marketplaces provides a similar fit, is more powerful, and is better balanced than the planned payment system, which is based on concurrent risk adjustment alone.⁵ This finding exposes the extent to which the incentives created by risk adjustment have been widely misunderstood. The results stand in stark contrast to the near universal preference for diagnostic risk adjustment over reinsurance in health systems in the US and abroad, and point to the need for further analysis.

More broadly, our framework sheds new light on a fundamental tension in health plan payment between the dual goals of cost control and combatting selection, even though it does not equip us to measure total welfare associated with various payment system alternatives. In contrast to prior studies examining inefficiencies due to selection that have focused on an isolated distortion (e.g. cream-skimming in Frank, Glazer, and McGuire 2000 or price distortions in Einav, Finkelstein and Cullen 2010), quantifying welfare here is difficult because our notion of the relevant welfare margins is broader than what is usually examined in the literature. It includes for example, optimal spending in healthcare relative to other goods.⁶ Our focus on the characteristics of fit, power, and balance—which relate to specific regulatory concerns—complements this prior literature and allows us to make progress on comparing payment systems without, for example, solving the intractable problem of determining optimal healthcare spending. Our framework shows how the use of concurrent risk adjustment in the Marketplaces relative to the alternative prospective risk adjustment decreases power (weakening cost containment incentives) while simultaneously improving fit (better addressing cream-skimming incentives). Quantifying these effects is useful, even though the framework cannot evaluate how much a better fit is “worth” in terms of a sacrifice in power. We envision that tradeoff as being assessed by a regulator’s objective function, which will vary across market settings. And as we show, the payment policy proposed for long-term use in Marketplaces is dominated by another feasible alternative.

These findings are important for the continued reform of US health insurance markets, which increasingly follow models of managed competition. While our framework and proposed metrics do not encompass all objectives of health plan payment systems, our quantitative results present a clear set of considerations and benchmarks for regulators and policymakers aiming to simultaneously address concerns about selection and cost control in markets for private plans in Medicare, Medicaid, and the Marketplaces. We develop a method to “grade” health plan payment incentives with simple simulations. Our main purposes are to incorporate the full set of plan payment features into fit and incentive comparisons, and, to show how the complex incentive effects of risk adjustment and other plan features can be operationalized for purpose of policy analysis.

The remainder of the paper proceeds as follows. Section 2 defines fit, power and balance, and develops the rationale for these measures as grades of a payment system. Section 3 describes our data and how we operationalize the payment schemes in the context of Marketplaces. Results are in Section 4. Section 5 discusses the implications of our analysis for plan payment policy and research, and Section 6 contains some brief conclusions.

2. Fit, Power and Balance of a Payment System

This section develops the rationale and explicit definitions for our three measures of payment systems: fit, power and balance. Sections 2.1 and 2.2 begin by defining fit and power and then describing the tradeoff between the two. Section 2.3 extends the power analysis to more than one service by defining balance, and shows under what conditions a balanced system is (second) best.

2.1 Fit

Fit describes how well payments to plans track plans’ costs. Fit has long been an object of interest among regulators and researchers because, conceptually, fit is tied to a payment scheme’s ability to address adverse selection and cream skimming (Van de Ven and Ellis 2000). By matching payments to costs irrespective of health state, better fit mitigates incentives for insurers to cream-skim the healthiest, lowest-cost consumers among the insurance pool, perhaps by distorting the benefits package (Breyer, Bundorf and Pauly, 2012). Better fit also flattens the firm’s perceived cost curve, reducing the Akerlof (1970) selection problem of feedback from average costs into prices that was highlighted in Einav, Finkelstein, and Cullen (2010).

An R² measure has been widely applied as a criterion for evaluating the fit of risk adjustment algorithms (Breyer, Bundorf and Pauly, 2012). For example, for the risk adjustment system used in the Marketplaces, risk adjustment parameters were chosen as the coefficients maximizing the R² in a regression of costs on a hierarchical list of medical conditions. After R-squared the next most popular measure is the mean absolute prediction error (MAPE) with its linear rather than quadratic loss function and as applied, for example in Van Barneveld et al. (2001). While our focus in the analysis that follows is on R², for illustration we also present some results using Cumming’s Prediction Measure (Cumming et al., 2002), which is a MAPE measure of fit.

Arguments for the less-common alternatives to R-squared are generally made on statistical rather than economic grounds.⁷ One line of critique of R-squared measures argues that “only predictable costs matter” in assessing alternative risk adjustment models. However, “predictability” is not a simple matter to incorporate into metrics of payment system performance, generally requiring a set of assumptions about what is predictable, and by whom.⁸ For the purpose of illustrating the incentive tradeoffs that are the focus of the paper, we follow the published literature and regulatory interest in summarizing fit primarily in an R² measure, though we expect future work to refine this metric.

Consider N individuals in a market indexed by i, i = 1,…,N. Cost for individual i is x_i, and the average cost in the population is $\overline{\mathrm{x}}$. The payment system (which could be composed of diagnostic, demographic, and cost-related elements) leads to a payment of p_i for person i. We define the fit of the payment system as:

$$\mathrm{Fit}=1-\frac{{\sum }_{\mathrm{i}}{\left({\mathrm{x}}_{\mathrm{i}}-{\mathrm{p}}_{\mathrm{i}}\right)}^2}{{\sum }_{\mathrm{i}}{\left({\mathrm{x}}_{\mathrm{i}}-\overline{\mathrm{x}}\right)}^2}$$ (1)

The fit measure in (1), analogous to an R², is the portion of the variance in costs explained by the payment system. A capitation payment system that just returns the population mean spending as the payment for each person, ${\mathrm{p}}_{\mathrm{i}}=\overline{\mathrm{x}}$, covers costs on average but explains none of the variance in cost and so would have a fit of zero. A plan would then have strong incentives to skimp on quality or coverage to deter demand from the sicker enrollees. A cost-based payment system in which p_i = x_i explains all of the variance in cost and has a fit equal to one.

Following Zhu et al. (2013) and McGuire et al. (2014) we adopt a metric that captures the R² of all aspects of the payment system, not merely the risk adjustment component. The generalization in (1) accommodates the evaluation of many types of payment mechanisms, including reinsurance, capitation with risk adjustment, and “mixed systems” which blend capitation and cost-based reimbursement by setting payments equal to a weighted average of individual costs and population average costs. A mixed system is relatively simple to implement in practice and can be easily characterized in terms of power and balance. A mixed system therefore serves as a convenient and relevant standard against which to compare the performance of the more complex alternatives involving risk adjustment. Consider a 50/50 mixed system setting payment equal to the half the population average plus half the cost that the individual incurs. This generates ${\mathrm{p}}_{\mathrm{i}}=.5\overline{\mathrm{x}}+.5{\mathrm{x}}_{\mathrm{i}}$. For this 50/50 mixed system, fit is .75, following Equation (1). Intuitively, since deviations are squared in the fit measure, cutting the deviations exactly in half captures 75 percent of the variance in costs. Writing the mixed system in general form with a weight of λ on the population mean cost and (1−λ) on the individual’s realized cost, the fit of a mixed system is

$$\mathrm{Fit}(\mathrm{\lambda })=1-\frac{{\sum }_{\mathrm{i}}{\left({\mathrm{x}}_{\mathrm{i}}-\mathrm{\lambda }\overline{\mathrm{x}}-(1-\mathrm{\lambda }){\mathrm{x}}_{\mathrm{i}}\right)}^2}{{\sum }_{\mathrm{i}}{\left({\mathrm{x}}_{\mathrm{i}}-\overline{\mathrm{x}}\right)}^2}=1-{\mathrm{\lambda }}^2.$$ (2)

Thus, if a mixed payment system weights the population mean at .8 and the individual realized costs at .2, the payments explain 36% of the variance in health care costs.

The fit of payment systems combining risk adjustment and a mixed system can be calculated analytically if the R² of the risk adjustment algorithm is known. Suppose a risk adjustment system on its own has an R² equal to R²_RA.⁹ If the risk adjusted capitation payment, denoted ${\mathrm{p}}_{\mathrm{i}}^{\mathrm{RA}}$, gets a weight λ and a person’s realized cost gets a weight (1− λ) in the payment system, then fit is:

$$\mathrm{Fit}(\mathrm{RA},\mathrm{\lambda })=1-\frac{{\sum }_{\mathrm{i}}{({\mathrm{x}}_{\mathrm{i}}-{\mathrm{\lambda }\mathrm{p}}_{\mathrm{i}}^{\mathrm{RA}}-(1-\mathrm{\lambda }){\mathrm{x}}_{\mathrm{i}})}^2}{{\sum }_{\mathrm{i}}{({\mathrm{x}}_{\mathrm{i}}-\overline{\mathrm{x}})}^2}=1-\frac{{\mathrm{\lambda }}^2{\sum }_{\mathrm{i}}{({\mathrm{x}}_{\mathrm{i}}-{\mathrm{p}}_{\mathrm{i}}^{\mathrm{RA}})}^2}{{\sum }_{\mathrm{i}}{({\mathrm{x}}_{\mathrm{i}}-\overline{\mathrm{x}})}^2}=1-{\mathrm{\lambda }}^2(1-{{\mathrm{R}}^2}_{\mathrm{RA}}),$$ (3)

where the latter equality follows from the definition of R²_RA. For example, if the risk adjustment explains 10 percent of the variance and the population weight λ is .50, the fit of the payment system is 1 − .25(.90) = 77.5 percent.

For more complex payments systems, such as when reinsurance combines with risk adjustment, fit will need to be evaluated empirically via Equation (1).

2.2 Power

We use the term power as it is used in contract theory, to describe the share of costs at the margin born by the health plan.¹⁰ Power in health insurance contracts is tightly linked to the goal of cost control, as it describes the payment system’s impact on the insurer’s marginal incentive to limit healthcare spending. Insurers are in a position to materially affect consumers’ decisions over healthcare spending–for example by limiting quantity via patient cost sharing and gatekeeping and by increasing the patient’s shadow price of care in certain clinical areas via long waits or limited networks. Plans can also affect utilization via provider incentives—for example, via utilization review, selective contracting, setting provider reimbursement on a FFS basis versus a capitated basis, or adjusting FFS prices paid for various services.¹¹

Plans face many competing incentives with respect to cost containment. It is important to note that power reflects only the cost containment incentives that are built into the payment system.¹² Power is not intended to capture, for example, how restricting access to providers may impact consumers’ valuation of a plan, which insurers would also take into account when designing gatekeeping arrangements. Nor does it account for the practical and regulatory constraints on restricting access to certain types of “necessary” or non-discretionary medical services. Consumer preferences over care and medical practice norms would interact with consideration of power in an insurer’s plan design. But power is a feature of the payment system only. It characterizes how a plan’s expenditures impact a plan’s net payment from the regulator. This connection is non-obvious when it comes to risk adjustment, and our definition and method of operationalizing power is intended to expose the full incentives in a payment scheme.

In health insurance markets, contracts are generally less than full-powered; for example, in many settings, including the ACA Marketplaces, insurers reinsure against large losses. Therefore, for insured individuals with spending above some threshold level of claims, there are weakened incentives for the insurer to limit claims. Further, as we show below, any risk adjustment system in health insurance which uses diagnoses linked to claims will have less than full power.¹³ Power is therefore likely to vary considerably away from full (i.e., 1.0) in this setting, with potentially substantial impacts on plan incentives for healthcare spending.

If an insurer’s payment p_i is invariant to changes in realized costs x_i, as it would be in a plan paid by an age-gender only risk adjustment system, the power of the payment system would be at the maximum of 1.0. Conversely, in a cost-based system where payment tracked costs exactly, the power would be 0. Away from these polar cases of payment systems, the change in payment for a person with respect to a change in cost for a person could vary over people and vary over ranges of cost. For example, the first health care event in a diagnostic area will trigger higher payment, but subsequent ones may not. In general, the derivative, dp_i/dx_i, will depend on various factors, including levels of spending, and could differ for different categories of spending.

At the population level, characterizing a payment system as applied to a group of N enrollees, we define power (ρ) as:

$$\mathrm{Power}\equiv \mathrm{\rho }=1-\frac{1}{\mathrm{N}}{\displaystyle {\sum }_{\mathrm{i}}\frac{{\mathrm{dp}}_{\mathrm{i}}}{{\mathrm{dx}}_{\mathrm{i}}}.}$$ (4)

Power in (4) is an inverse measure of the change in payments for a marginal change in costs. In some cases, power can be determined from the design of the payment system itself. For a pure mixed system, power is simply λ, the weight put on the prospective portion of payment. For a reinsurance-only scheme, power could in principle be computed analytically as a function of the reinsurance threshold if the empirical distribution of enrollee claims costs were known. In general, however, (4) will vary over types and ranges of spending and will need to be assessed empirically. We explain how we use simulation methods to do so in Section 3.2 below.

With explicit definitions of fit and power we can begin to characterize the tradeoff between the two. To illustrate the tradeoff, Figure 1 graphs the fit (as R²) and power of several types of payment systems. Point A is a cost-based payment system, with fit equal to 1 and power equal to 0. Point B is a fully prospective system with no risk adjustment, which pays average cost and generates fit equal to 0 and power equal to 1. A simple mixed system combines the two, and from above we know that both fit and power can be expressed as a function of the weight λ put on the realized costs. The combinations of fit and power achievable by a mixed system can be described by the solid curve in Figure 1, which traces Fit = 1 – (Power)².

Figure 1.

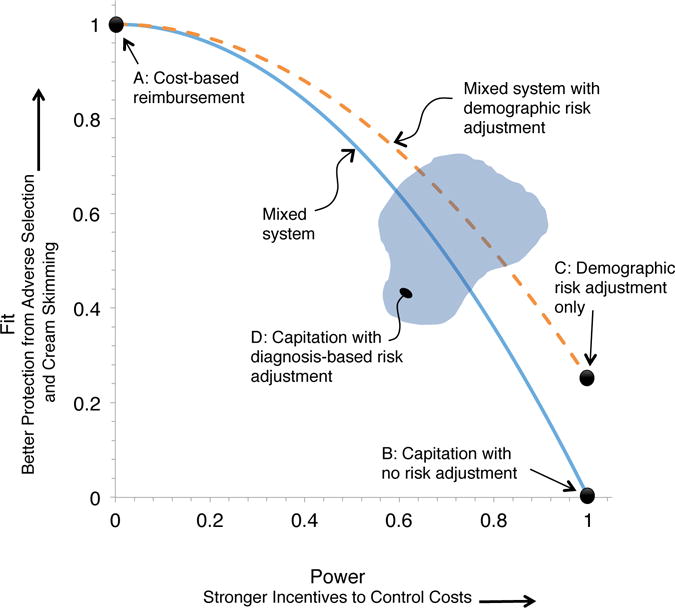
Fit-Power Tradeoff in Insurance Payment Systems

Notes: Figure illustrates the tradeoff between power and fit in insurance market payment systems. Fit, defined as the fraction of the variance of costs explained by payments as in Equation (1), is plotted along the vertical axis. Power, defined as the share of costs at the margin born by the health plan as in Equation (4), is plotted along the horizontal axis. Points in black illustrate the exact fit-power combination for several payment system types. The solid and dashed curves trace the fit-power tradeoff in mixed systems over a range of parameter values for the weight put on the prospective portion of payment, as in Equation (2). The cloud at D illustrates the theoretically ambiguous set of potential points representing the incentives under capitation with diagnostic-based risk adjustment.

Note that the terms of the tradeoff in a mixed system are the same for any distribution of cost (the x_i); in other words, independent of the population under study. Under the R² measure of fit, a small decrease in power away from power = 1, i.e., moving λ away from 0, buys a good deal of fit. Lowering power from 1.00 to .9 (putting a 10% weight on costs, x_i) lifts fit from 0 to 19%. Similarly, a small decrease in fit from 1 yields a large increase in power. Lowering fit from 100% to 90% lifts power from 0 to .32.

Other points can be added to Figure 1 after empirical analysis: A capitation system that uses only age and gender could improve fit with no sacrifice in power at a point like C. A mixed system with weight 1− λ on costs and weight λ on a hypothetical demographics-only risk adjustment system could produce the set of possibilities traced by the dotted line in Figure 1. Adding diagnoses from claims to the payment system would improve fit compared to point C but degrade power, and therefore lie above and to the left of C, in a region like D. Such points may or may not be outside the mixed system curves.

Before moving to balance, we note that more power in a payment system is not necessarily preferred. While a fully cost-based system (λ = 1) gives too much incentive to supply care, a fully prospective system, asking the provider/plan to bear all costs at the margin (λ = 0), may create the opposite problem and lead to underservice (Ellis and McGuire 1986; Newhouse 1996). This would be a problem in an imperfectly competitive setting in which plans were not fully incentivized to find the consumer-preferred optimal combination of service provision and price.

Our goal in this paper is to quantify the power, fit, and balance of payment systems, not to find the constrained optimal combination, which will vary across markets, and is always relative to a regulator’s objective function. Nonetheless, the focus in the current policy environment on more tightly constraining healthcare costs or cost growth suggests that the status quo power in the healthcare system lies below the desired level. Furthermore, optimal power on the supply side would depend on the demand-side incentives which aren’t the object of our analysis.

2.3 Balance

Payment systems partly based on costs may create incentives to distort the distribution of resources devoted to particular types of services, one of the efficiency concerns that risk adjustment was introduced to address. Research on health plan payment has investigated whether users of some services are systematically over or undercompensated by the payment system (Pope et al., 2011). Plans have an incentive to skimp on areas of care which tend to be used by “losers,” whereas the opposite incentive plays out for services used by those for whom payments exceed expected costs.

We address the issue of balance differently, focusing on marginal payment incentives. In our terms, a payment system with identical marginal reimbursement incentives across services is said to have balance. If costs across clinical areas are reimbursed differentially, then insurers may over-provide care in some areas and under-provide it in others. We propose to measure imbalance in the incentives in a payment system against the standard of equal marginal reimbursement incentives for all service areas.

From (4), we recognize that power could depend on the service, j:

$${\mathrm{\rho }}_{\mathrm{j}}=1-\frac{1}{\mathrm{N}}{\displaystyle {\sum }_{\mathrm{i}}\frac{{\mathrm{dp}}_{\mathrm{i}}}{{\mathrm{dx}}_{\mathrm{ji}}}}$$ (5)

For example, the power of the payment system could differ according to whether it was assessed with respect to spending on office-based care or hospital care or across various diagnostic categories. The relevant units j may be context-specific and could be chosen by the regulator.

We propose to measure imbalance by the weighted variance of power, which is the sum of squared deviations of power across services j, weighted by the share of spending on that service:

$$\mathrm{Imbalance}~{\displaystyle {\sum }_{\mathrm{j}}{\overline{\mathrm{S}}}_{\mathrm{j}}{\left({\mathrm{\rho }}_{\mathrm{j}}-\overline{\mathrm{\rho }}\right)}^2}$$ (6)

Where ${\overline{\mathrm{S}}}_{\mathrm{j}}$ is the share of spending on service j in the population and $\overline{\mathrm{\rho }}$ is the average power of the payment system. When the power is the same for every service area ( ${\mathrm{\rho }}_{\mathrm{j}}=\overline{\mathrm{\rho }}$ for all j), imbalance in (6) equals zero. Imbalance is increasing in the share of expenditures that deviate from the average power.

We propose the imbalance measure (6) as a rough-and-ready intuitive welfare metric. In Appendix A, however, we provide the theoretical grounding for the weighted squared deviation measure of imbalance, showing that under certain conditions, (6) is proportional to the loss generated by imbalance. Proportionality to the share of spending in an area has an obvious rationale. And efficiency problems proportional to the square of a distortion are also a common feature of “Harberger triangle” type measures. Most importantly, it is not necessary to know the optimal power, ${\overline{\mathrm{\rho }}}^{\prime }$, to derive the result in (6).¹⁴ Appendix A shows that the loss can be decomposed into a loss from the deviation of realized average power from the desired average power, plus the loss from the variation around this average. This implies that even if we do not know the desired power of the payment system overall we can still compute the loss from the variation around the realized average power.¹⁵

So far, we have assumed that there are no additional frictions (beyond the payment system incentives) that distort the allocation of resources across conditions or clinical areas. We return in Section 5 below to the issue of how other margins of distortion could affect the optimality of balanced incentives in a payment system. As we discuss in more detail there, imbalance could be second-best optimal if it specifically counteracted an unrelated distortion, like consumer moral hazard that differed across treatment types.

3. Data and Empirical Framework

In order to empirically assess fit, power, and balance in payment systems, we use claims from large, self-insured plans to compare the actual costs of insuring enrollees to the simulated payments that would be made to plans under each payment system.

We focus on illustrating the incentives embedded in the concurrent risk adjustment and reinsurance regulations governing the ACA Marketplaces. Concurrent risk adjustment links payments in a plan year to diagnoses entered in a patient’s claims records during that same year. In the Marketplaces it follows an algorithm designed by the department of Health and Human Services (HHS), which we discuss in detail below. Reinsurance in the ACA Marketplaces is slated to end in 2016. Under Marketplace reinsurance, insurers are required to pay a fee for reinsurance and will receive a reimbursement of 100% of the individual claims that exceed an attachment point of $45,000 and fall below a cap of $250,000. This reinsurance operates separately from, and in addition to, the risk adjustment payment.^16,17

3.1 Data

Our claims data come from the Truven Health Analytics MarketScan Commercial Claims and Encounters Database, which compiles health insurance claims from consumers insured by dozens of large employers across the US.¹⁸ Each claim lists the payment to the healthcare provider, and the portions of the bill paid by the insurer and by the consumer. Each claim also lists any associated procedures and diagnoses codes. Claims are linked to individuals, and individuals are linked across time. The same data source was used by US Department of Health and Human Services (HHS) for estimating the coefficients used in the risk adjustment model applied in the Marketplaces.¹⁹

We take claims from 2008 and 2009—the most recent years available to us—and restrict attention to individuals aged 21 to 64, who are observed in both years. The age range 21 to 64 corresponds to the definition of adult in the Marketplaces. Because our simulations require observing the actual cost to the plan of each claim, we keep only those individuals for whom care was paid for on a non-capitated basis. From this sampling frame, we take a random sample of 2 million covered lives as our analysis and simulation sample, which we use to evaluate fit, power and balance.

Concurrent risk adjustment in the Marketplace system is based on a Hierarchical Condition Categories (HCC) model. HCCs are comprised of indicators for particular conditions, with each condition determined by the presence of a diagnosis or diagnoses in the patient’s claims record.²⁰ The set of conditions that are represented in the HCCs were chosen by HHS. Risk adjustment coefficients, commonly called “risk adjustment weights,” are generated from a regression of costs on HCCs at the individual level, and reflect the dollar value association between a health condition and expected costs. A person with several HCC conditions would have a risk score equal to the sum of the coefficients (weights) associated with each condition.

The HHS HCC risk adjustment weights are scaled so that a person with mean expected costs would generate a risk score of 1.0. Actual payment for a person is the product of the risk score and the average cost in the population. For example, an enrollee with a risk score of 2.0 generates a net plan payment that is twice as large as the payment for an enrollee of average expected cost. Plans are compensated by the regulator averaging risk scores within plans and then transferring a risk adjustment payment from plans with lower than average risk enrollees to plans with higher than average risk enrollees.

3.2 Counterfactual Risk Adjustment

Below, we consider a hypothetical prospective risk adjustment scheme as an alternative to the ACA’s concurrent scheme. Prospective risk adjustment, in which prior period diagnoses determine current period risk scores is a more common alternative, used in Medicare Advantage, some state Medicaid programs, and public health systems across Europe. To evaluate this counterfactual we must first generate the parameters of the alternative hypothetical system (the prospective risk adjustment weights). For this we take advantage of the roughly 15 million individuals remaining in the sampling frame after drawing our analysis sample of 2 million. We use these out-of-sample observations to estimate the risk adjustment coefficients for this hypothetical payment mechanism, avoiding any overfitting problem caused by estimating and evaluating a payment system on the same sample.

We take two important steps to keep the counterfactual comparison to prospective risk adjustment as consistent as possible with the actual Marketplace system payment scheme. First, when estimating risk adjustment weights in the prospective model we use exactly the same set of conditions (HCCs) chosen by HHS for the concurrent model. Given the set of reimbursable conditions, calculating the risk adjustment weights consists of a straightforward individual-level regression of the realized payments in 2009 on a set of indicators corresponding to the HCCs in 2008.²¹ Second, in order to fairly compare the prospective and concurrent models, we re-estimate the weights for the concurrent model (2009 costs on 2009 conditions) on the same 15 million person sample used to estimate prospective weights, in all cases using the same mapping of diagnoses to HCCs defined by HHS. For consistency when comparing the two regimes, we use our estimated parameters for the concurrent system, rather than those dictated by HHS. Nonetheless, we show below that our main results are not sensitive to using the concurrent risk adjustment weights as estimated by HHS in place of those we estimate ourselves.

Further details about the risk adjustment system along with our empirical estimates of the parameters are reported in Appendix B. In all cases, the dependent variable in our risk adjustment regression is the total payments (insurer plus patient) in claims to service providers, a construction that removes any mechanical relationship between differences in cost sharing across plans (impacting net insurer costs) and sorting of different health types to different plans.²²

3.3 Measuring Fit, Power, and Balance

Applying the definition in Section 2, we measure fit of the payment system as the R² from a regression of payments to plans on plan costs at the person level.²³ The cost variable is the total cost of the claims filed by the person, and the payment is the net payment, inclusive of risk adjustment and reinsurance premiums and payouts. Reinsurance payouts are determined to the formula described above applied to the simulated sample of claims, and reinsurance premiums are simply the actuarially fair premium implied by the average reinsurance payout in the 100% sample.

Unlike fit, which is intended to describe how payments track costs in the cross-section and is conceptually aligned with a cross-sectional regression, power involves a different conceptual and therefore empirical exercise. Since power is related to how reimbursements change at the margin with utilization costs, we perform a simulation exercise that corresponds to a thought experiment of exogenously reducing utilization in order to trace the resulting change in payment for individual enrollees (dp_i/dx_i in Equation 4). We ask, for example: If a plan succeeds in randomly reducing outpatient medical events by 10%, by how much does the payment for that enrollee change? And, how does this average out over an entire population of enrollees?²⁴

We simulate changes in utilization by deleting, for our fixed population of enrollees, a random sample of the observed medical events. We define a medical event separately for outpatient and inpatient services, which both makes sense clinically and allows us to characterize power differently for these two major sectors of care. We define an outpatient event as all outpatient services during a single day and randomly eliminate all services that correspond to a particular patient-day pair. We define an inpatient event as a hospital stay, and we randomly eliminate hospital stays.²⁵ Thus, the variation used to measure power in this simulation is generated by reducing events within the medical histories of individual enrollees.

This random deletion approach regards the effect of incentives as working through the quantity of health care use rather than through prices paid by a plan.²⁶ It disregards plan response in the form of negotiating lower prices or seeking lower priced inputs in response to plan payment incentives. Power of the risk adjustment scheme is compromised by quantity responses, but not by price responses, whereas the power of reinsurance, based on dollars rather than codes coming in via quantity reports, is affected by either price or quantity responses. Our approach to measuring power may therefore overstate power reductions from risk adjustment in relation to reductions from reinsurance and other supply-side cost sharing.

To simulate reduced utilization we randomly sample without replacement medical events as defined above from individuals in our baseline sample of 2M adults. We remove 10% of events,²⁷ repeating the simulation five times and reporting mean payment and mean cost for the insured sample.²⁸ Each event removed decreases the plan’s costs by the dollar amount of the claims associated with the event. Each event removed also affects the risk score with some probability because the diagnoses on the claims associated with the event are also removed. Claims pivotal in establishing a diagnosis defining an HCC have a direct effect on payment. Claims containing no new information used in risk adjustment, for example, claims associated with the second visit to a doctor during a year for the same condition, have no effect on the risk adjustment score. If a person’s spending is in the range of reinsurance, removing an event will reduce payments for that person even if the risk score does not change.

For the final step of calculating power, for each individual we generate a counterfactual relative risk score based on diagnoses listed in the claims retained, and scale this score by the average cost in the original population.²⁹ We also take into account any change in reinsurance payments, evaluated at the simulated level of patient utilization, to calculate a new simulated payment for the individual. We then directly apply Equation (4) to summarize power for the entire population, substituting discrete changes for derivatives.

Finally, when evaluating the prospective risk adjustment payment system, we account for the fact that payments only impact utilization with a one-year lag and only for enrollees who remain in the same plan in the year after the diagnoses are recorded. Otherwise, a different insurer bears the payment response to a reduction in utilization. Comprehensive Marketplace data on turnover are not available, but recent research on non-group health insurance markets in the years 2008–2011 just preceding the ACA finds very high turnover rates (Sommers, 2014). In our Marketplace simulations, we characterize two cases, assuming 100% and then 50% of persons enrolled in a plan in one year stay in that plan the next.³⁰ This parameter could be made more precise when applying our framework to a setting like Medicare Advantage, where the retention of elderly beneficiaries in plans year-to-year has been well-measured.³¹ Here, we simply report results over a range of possibilities.

To characterize balance, we build on the power simulations, but divide events according to their primary diagnosis across the 25 Major Diagnostic Categories (MDCs), which are broad clinical groupings based on the five-digit ICD9 codes used in claims. For the 10 MDCs associated with the highest total dollar value of payments in our sample, plus the MDC for mental disorders, we replicate the simulation procedure we used to estimate power, but apply the sampling only to events associated with the MDC of interest. To illustrate, for MDC 5 (Diseases and Disorders of Circulatory System), we randomly remove 10% of events associated with that MDC and recalculate all risk scores. We also calculate the new cost of insuring the individual, and finally determine reinsurance payments. This yields a category-specific power. We show power for each clinical area and summarize balance by assessing squared deviations of power across categories from the system-level power, as called for in Equation (6).

In total, these 11 MDCs account for 23% and 56% of total inpatient and outpatient spending, respectively. A complete measure of balance would require a mutually exclusive set of categories covering all of spending. We could have created an “all-other” category here but we do not consider this to be meaningful and possibly misleading. The disaggregation by MDCs and by inpatient versus outpatient services is meant to illustrate the application of the balance metric; to go beyond an illustration would require an exhaustive classification. Most importantly, the particular lines across which balance was assessed could depend on the regulator’s specific objectives or concerns.

4. Results

4.1 Fit Results

Column (1) of Table 1 grades payment systems according to fit.³² Column (1) reports the standard R² measure. We consider several versions of the ACA payment system. The first row, which includes only concurrent risk adjustment, corresponds to the payment system planned for the Marketplaces for 2017 and beyond. The second row corresponds to a hypothetical Marketplace payment system that included only the temporary reinsurance feature of the Marketplace payment scheme. From 2014 to 2016, a transitional reinsurance program in the individual market will compensate plans for covering individuals with realized costs above an attachment point as described in Section 3. Row (3) corresponds closely to actual policy for 2014, including both concurrent risk adjustment and reinsurance, which consists of 100% reimbursement above the attachment point of $45,000.³³

Table 1.

Fit and Power Simulation Results

Simulated Payment Scheme	(1)	(2)	(3)	(4)
	Fit		Power
	R2	CPM	Inpatient Events	Outpatient Events
1 Concurrent RA (ACA Policy, 2017+)	0.37	0.25	0.62	0.77
2 Reinsurance	0.60	0.19	0.64	0.84
3 Concurrent RA + Reinsurance (ACA Policy, 2014–2016)	0.61	0.36	0.26	0.60
4 Prospective RA (100% Retention)	0.11	0.09	0.91	0.85
5 Prospective RA + Reinsurance (100% Retention)	0.61	0.26	0.57	0.69
6 Prospective RA (50% Retention)	0.11	0.09	0.96	0.92
7 Prospective RA + Reinsurance (50% Retention)	0.61	0.26	0.61	0.76

Concurrent risk adjustment in Row (1), nearly unique to ACA Marketplaces, achieves a fit of R²=0.37, substantially higher than what is typically achieved under prospective risk adjustment.³⁴ Fit under reinsurance alone reported in Row (2) is remarkably high. This is intentional – or at least implicit in the goal of shielding insurers from financial risk in the early years of the Marketplaces. Even though reinsurance activates for only about 1% of individuals in our simulations, more than half of the variance in insurer costs is eliminated by reinsurance. In contrast, hypothetical prospective risk adjustment in Row (4) yields a fit of R²=0.11, similar to estimates of fit in other prospectively adjusted payment systems, such as Medicare Advantage. Adding reinsurance in Row (5) closes the gap between the concurrent and prospective risk adjustment payment schemes.

The 2014–2016 ACA scheme that includes concurrent risk adjustment and reinsurance in Row (3) achieves high fit as measured by an R² of .61. This is not surprising. What is surprising is the small incremental contribution to R² (.01) of concurrent risk adjustment when added to ACA reinsurance. Also in contrast to the conventional wisdom, reinsurance with prospective risk adjustment (Row 5) fits as well as reinsurance with concurrent risk adjustment.³⁵ While the R² measure is just one of several potential operationalizations of fit, it is a standard measure in the literature for evaluating risk adjustment. By this metric, there appears to be little advantage in adding risk adjustment on top of reinsurance.

To explore the implications of using an alternative measure of fit, in column (2) of Table 1, we report the Cumming’s Prediction Measure (CPM), which is a function of absolute deviations, rather than squared deviations. This measure naturally weights small deviations from the predicted costs equally to large deviations.³⁶ The levels of these values in column (2) are not comparable to the R² levels in column (1), though the rank ordering can be compared. The notable difference in rankings between columns (1) and (2) is that concurrent risk adjustment performs relatively better. Reinsurance, which is more likely to be binding for larger deviations from expected costs, performs relatively worse.

4.2 Power Results

With regard to power, columns (3) and (4) in Table 1 characterize the power for inpatient and outpatient events for each of the five payment systems. Table 1 reports power for subtracting 10% of medical events at random in a simulation. Results for higher and lower shares of events deleted differed very little, implying that power of the payment systems was uniform over the range of 5–20% of events deleted.³⁷ Consistent with our discussion above about the de facto linking of expected and realized costs via healthcare events, power for concurrent risk adjustment shown in the first row deviates considerably away from 1.0. The .62 in the first row and third column means that for each dollar of cost removed when 10% of inpatient events are eliminated, payment falls on average by $0.38. The power of concurrent risk adjustment is greater for outpatient care, at .77, implying that the diagnoses lost as outpatient events are removed are less likely to be unique, i.e., appearing in other medical events, and thus having a smaller average effect on risk-adjusted payments.

Row (2) shows power for reinsurance only. Payments fall with reinsurance for medical events for persons whose total costs exceed the reinsurance threshold of $45,000. Persons with an inpatient event are more likely to be above this threshold so the power reduction from 1.0 is naturally greater for inpatient than for outpatient.

Combining concurrent risk adjustment and reinsurance degrades power considerably, as shown in Row (3). Looking first at inpatient, the power loss from concurrent risk adjustment of .38 plus the power loss from reinsurance of .36 sum to the power loss from their combination (1−.26 =) .74, implying that the margins on which these two payment features are reducing payments as events are removed are essentially independent. This “adding up” of power loss is also approximately true for events on the outpatient side where the power losses in the first two rows just sum to the power loss in the third row. An important takeaway emerges in comparing Rows (2) and (3): The power loss of adding concurrent risk adjustment to reinsurance is considerable.

Rows (4) through (7) show power for counterfactual prospective risk adjustment with and without reinsurance. Comparing Row (1) to (4) we see the unsurprising result that the power of prospective risk adjustment exceeds that of concurrent risk adjustment. This is because the diagnoses from the dropped events from the previous year tend to predict current cost less well than diagnoses from similar events drawn from the current year. Appendix B reports the risk adjustment model estimates for concurrent and prospective models and confirms this observation. Dropping an HCC designation generally but not always has a bigger impact in the concurrent than the prospective model as indicated by the generally larger estimated regression coefficients in the concurrent model.³⁸ Power of prospective risk adjustment with reinsurance, assuming 100% retention is also higher than with concurrent risk adjustment and reinsurance (compare Rows 5 and 3).

Lower, more realistic retention rates further elevate power of prospective risk adjustment by disconnecting plan spending in year 1 (when events are used to determine risk scores) from that plan’s revenues in year 2 for those members not continuing with the plan.³⁹ In the case of prospective risk adjustment and no reinsurance (Row 6), for the 50% of the population not retained, the power of the payment system is 1.0. Power with prospective risk adjustment and partial retention is a weighted average of the power for the share retained from Row (4) and 1.0 for the share not retained. We use this to figure the power estimates of .96 for inpatient and .92 for outpatient in Row (6).

Reinsurance effects on power are not affected by retention rates since reinsurance is based on current year spending and so reinsurance works the same whether or not a person was in the plan the previous year. We approximate the power of prospective risk adjustment with reinsurance and 50% retention by assuming the power gain observed between Rows (4) and (6) would be the same as between Rows (5) and (7).⁴⁰ This is reasonable in light of the independent margins on which risk adjustment and reinsurance largely appear to be operating. Clearly, reinsurance reduces power much more than does prospective risk adjustment.

4.3 Balance Results

We report results on balance in Table 2 for the same payment systems studied in Table 1. We list the 10 Major Diagnostic Categories (MDCs) associated with the largest total claims, as well as the MDC for Mental Health (MDC 19). We added the mental health category because it has been found previously to be subject to incentives to be underprovided in capitation-based managed care plans in both Medicare and Marketplace payment systems.⁴¹ Other diagnostic areas with similar characteristics are already included in the “top-ten” list. We chose MDCs for convenience with the purpose of highlighting the heterogeneity in how costs across different clinical areas are differentially reimbursed on the margin. One could evaluate balance by applying our Equation (5) across finer diagnostic categories; across places of service; or across primary, secondary, and tertiary care.

Table 2.

Balance of Power Across 11 Major Diagnostic Categories (MDCs)

	Power by MDC
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)	(14)
Simulated Payment Scheme	Musculoskeletal System and Connective Tissue (MDC 8)		Circulatory System (MDC 5)		Digestive System (MDC 6)		Factors Influencing Health Status (MDC 23)		Skin, Subcutaneous Tissue and Breast (MDC 9)		Nervous System (MDC 1)		Respiratory System (MDC 4)
	IP	OP	IP	OP	IP	OP	IP	OP	IP	OP	IP	OP	IP	OP
Share of Total Costs	5.64%	13.74%	5.10%	6.87%	2.75%	6.92%	0.57%	6.76%	0.62%	5.80%	1.83%	3.63%	1.78%	2.21%
Concurrent RA	0.92	0.91	0.64	0.53	0.54	0.81	0.70	0.89	0.67	0.81	0.62	0.62	0.33	0.11
ACA Reinsurance	0.65	0.90	0.58	0.85	0.64	0.84	0.45	0.91	0.60	0.74	0.52	0.79	0.60	0.77
Concurrent RA + Reinsurance	0.57	0.81	0.22	0.38	0.18	0.65	0.15	0.81	0.27	0.55	0.14	0.41	−0.06	−0.11
Prospective RA	0.96	0.94	0.90	0.78	0.84	0.89	0.91	0.94	0.83	0.88	0.90	0.78	0.84	0.35
Prospective RA + Reinsurance	0.62	0.84	0.47	0.63	0.50	0.73	0.36	0.86	0.43	0.63	0.42	0.57	0.44	0.12
	Power by MDC
	(15)	(16)	(17)	(18)	(19)	(20)	(21)	(22)		(23)	(24)		(25)	(26)
Simulated Payment Scheme	Pregnancy, Childbirth, and Puerperium (MDC 14)		Kidney and Urinary Tract (MDC 11)		Ear, Nose, Mouth, and Throat (MDC 3)		Mental Diseases and Disorders (MDC 19)			Range			Weigthed Average of Squared Deviations
	IP	OP	IP	OP	IP	OP	IP	OP		IP	OP		IP	OP
Share of Total Costs	3.31%	0.83%	0.89%	3.91%	0.21%	4.22%	0.40%	1.53%
Concurrent RA	0.18	0.68	0.70	0.86	0.70	0.91	0.76	0.63		0.18 – 0.92	0.11 – 0.91		0.057	0.034
ACA Reinsurance	0.95	0.97	0.54	0.72	0.72	0.92	0.73	0.94		0.45 – 0.95	0.72 – 0.97		0.017	0.005
Concurrent RA + Reinsurance	0.13	0.65	0.24	0.58	0.41	0.83	0.49	0.57		−0.06 – 0.57	−0.11 – 0.83		0.038	0.047
Prospective RA	1.02	0.81	0.89	0.90	0.87	0.93	0.87	0.69		0.83 – 1.02	0.35 – 0.94		0.003	0.015
Prospective RA + Reinsurance	0.96	0.76	0.42	0.61	0.51	0.86	0.63	0.63		0.36 – 0.96	0.12 – 0.86		0.031	0.025

Notes: Table lists power by Major Diagnostic Category (MDC) for each of the five payment systems listed in rows. Each cell in columns (1) through (22) reports the power determined by a separate simulation in which 10% of the events associated with the indicated MDC are removed at random. For each of these, we report the average from five replications. IP in odd columns indicates inpatient events and OP in even columns indicates outpatient events. Columns (23) and (24) in the bottom panel list the range of power across MDCs. Columns (25) and (26) display the weighted average of squared deviations of power across the 11 MDC categories shown. This weighted average is calculated according to Equation (6) using the shares listed at the top of each column.

Table 2 contains the power estimate for inpatient and outpatient services for each MDC, as well as the summary measure for imbalance from (6). Each entry in Table 2 is the result of a separate simulation. For example, for inpatient care associated with MDC 8 (Musculoskeletal System and Connective Tissue) under concurrent risk adjustment (in the upper left of the table), .92 is the average over simulations in which 10% of the inpatient admissions with MDC 8 are removed at random. Payments in this category are reduced by 0.8% on average, yielding a power estimate of 1 − .008/.100 = .92.

Row (1) corresponds to concurrent risk adjustment. Comparison across clinical areas reveals significant heterogeneity in the power of reimbursement incentives. Under concurrent risk adjustment, the category with the lowest power (Respiratory Systems; outpatient) reimburses insurers 89 cents on the dollar of their costs, whereas the category with the highest power (Musculosketal Systems; inpatient) pays insurers just 8 cents on the dollar. The balance criterion introduced above indicates that the marginal incentives to provide care should be equalized across clinical areas. For the concurrent risk adjustment-only payment scheme, this implies the optimal power within each MDC is equal to the overall average, which is 0.62 for inpatient and 0.77 for outpatient in Table 1, though even this inpatient/outpatient disparity is itself a margin of balance distortion.⁴² The summary measure of imbalance across clinical areas from Equation (6) is shown in the last columns of Table 2.

What leads to some conditions being reimbursed at a higher rate than others on the margin of utilization under risk adjustment? Conceptually, the marginal reimbursement of a claim is a function of two factors. First is the probability that a claim is pivotal in establishing a diagnosis—conditions generating many individual claims with identical diagnoses tend to be associated with higher power. Second is the relative generosity with which a diagnosis is reimbursed in relation to the cost of the condition. The estimated coefficient in a risk adjustment model picks up the additional total costs associated with the appearance of a diagnosis, not only the direct cost of actually treating that condition. When we eliminate an event, we lose the direct costs of treatment. How much reimbursement is affected depends on how predictive a particular condition is for total costs.

With reinsurance the power reduction from 1.0 for services in each clinical area is roughly proportional to the likelihood that the person with the medical event has annual spending over the cut-point (if not, reinsurance is not activated) times the share of spending covered by reinsurance (here 100%). Results for reinsurance alone are reported in Row (2). Under reinsurance, clinical areas that tend to be more frequently experienced by more expensive enrollees are the ones with greater power loss.⁴³ For example MDC 5, Circulatory System, is a category with low power under reinsurance because an expense in this MDC category is more highly correlated with the probability of individual spending exceeding the reinsurance threshold.

At the bottom right of the table, the summary measure of imbalance shows that for inpatient events, the loss under concurrent risk adjustment alone is about 3 times as large as under reinsurance alone. For outpatient events, the loss from imbalance is 5 times as large under concurrent risk adjustment. Row (3) shows that combining concurrent risk adjustment and reinsurance, as is done in the Marketplaces from 2014 to 2016, worsens imbalance compared to either mechanism separately.⁴⁴

Prospective risk adjustment, a standard alternative that we consider in Rows (4) and (5), represents a middle case. Compared to reinsurance alone, balance under prospective risk adjustment alone (Row 4) is worse for outpatient events, but better for inpatient events. Rows (4) and (5) calculate power for each clinical area assuming 100% retention. Power results for less than 100% retention could be figured as in Table 1 for power overall.

4.3 Summary of Tradeoffs

To visually summarize the many results in Tables 1 and 2, Figure 2 plots the three “grades” for each payment system, with the important caveat that these grades are a function of the particular metrics we have chosen to operationalize the concepts of fit, power and balance. The goal here is to demonstrate how payment systems could be compared given some set of preferred metrics, which we anticipate will vary from setting to setting.

Figure 2.

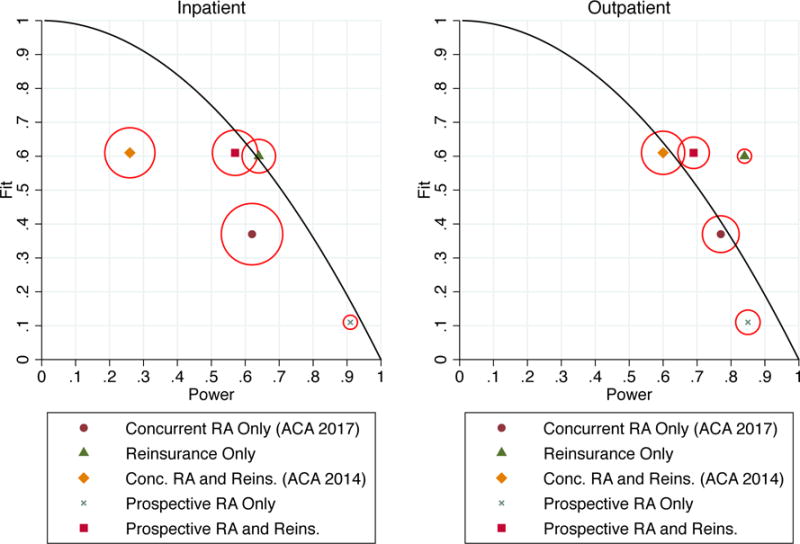
Fit, Power, and Balance under Risk Adjustment and Reinsurance in the Exchanges

Notes: Figure illustrates fit, power, and balance calculated for several actual and counterfactual payment systems. Vertical and horizontal positions indicate fit and power. The size of the circle around each marker indicates imbalance, with the diameter proportional to the weighted variance of power across the Major Diagnostic Categories (MDCs) examined. The solid curves trace, for reference, the theoretical fit-power tradeoff in a mixed system that reimburses a partial lump sum capitation payment plus a fraction of actual expenses.

Figure 2 plots power along the horizontal axis and fit as R² along the vertical axis. Balance is represented by the diameter of the circle around each marker, which is proportional to the weighted variance measure in (6). A wider circle indicates a larger loss from imbalance—our attempt to represent the 3 dimensions on the page. The mixed system curve, which pays a lump sum plus a fixed fraction of each healthcare dollar spent by the insurer, is plotted as a solid line with the parameter λ from Equation (2) ranging from zero to one. The mixed system has perfect balance by construction.

Focusing first on inpatient events in the left panel of Figure 2, the most striking results are for concurrent risk adjustment only and concurrent risk adjustment with reinsurance. These represent, respectively, the Marketplace payment policies planned for 2017 and beyond and in place for 2014–2016. Not only are these payment policies dominated in terms of fit, power and balance by other feasible policies, they are also dominated by a simple mixed system that reimburses insurers a fixed fraction of each claims cost, as they fall inside the solid curve. For outpatient events in the right panel, the concurrent risk adjustment policies also fare poorly. They have the worst balance and power of any scheme, and only marginally better fit than reinsurance alone. In sum, the chosen payment scheme for the Marketplaces is a dominated regulatory choice along these measures. This finding is significant and runs counter to the common intuition that risk adjustment is the best way to achieve fit without reimbursing actual realized costs on the margin. Nonetheless, as we discuss below, examining the less common CPM measure for fit reveals some advantage to concurrent risk adjustment, and points toward the need for additional investigation building on our findings.

Prospective risk adjustment alone sits near the mixed system curve in the lower right of both panels, and unlike concurrent risk adjustment, is not dominated by reinsurance alone. It is characterized by high power, low fit, and good balance. Nonetheless, a mixed system with a low weight of about .1 on realized costs beats prospective risk adjustment in terms of fit, approximately matches it in power, and dominates it in terms of balance. Adding reinsurance to prospective risk adjustment (rows 5 and 7 in Table 1) yields a payment system that grades similarly to reinsurance alone on fit (row 2), but with somewhat worse power and balance; for example, inpatient power for reinsurance alone is .72, whereas inpatient power for prospective risk adjustment plus reinsurance is .68.

One of the most relevant comparisons in Figure 2 is between what we label ACA 2017, concurrent risk adjustment only, and a feasible risk-adjusted alternative, prospective risk adjustment plus reinsurance. As the figure shows, concurrent risk adjustment is no better than prospective risk adjustment plus reinsurance on all metrics. In terms of “fit,” if the conventional R-squared metric is used, prospective risk adjustment plus reinsurance is far superior to concurrent risk adjustment. If the alternative CPM measure is used, (Table 1, Column 2) the two payment systems are essentially equivalent on fit. Movement to prospective risk adjustment, bringing risk adjustment in the Marketplaces in line with virtually all other individual health insurance markets is thus both feasible and desirable, as long as the payment scheme retains the reinsurance feature presently in place in the Marketplaces.

Traditional treatments of risk adjustment in the literature have ignored balance, and have either implicitly or explicitly assumed away what we call the power incentive. However, Figure 2 shows that the de facto power incentive, as well as imbalance across services, is a non-trivial concern in risk adjustment, and in particular in concurrent adjustment. To put the size of the power problem in context, consider that concurrent risk adjustment yields a fit of .37 and power of .62 for inpatient services, but a mixed system that simply pays insurers a fixed fraction for each enrollee dollar of healthcare utilization would achieve a power of .77 with the fit “set” to .4. The same also holds for the CPM measure of fit where power (for inpatient events) is .62 and fit is 0.25 compared to a mixed system where power is .70 with fit set at .30.⁴⁵ In other words, concurrent risk adjustment—which is aimed at reimbursing expected, not realized costs—reimburses insurers more generously on the margin of realized costs than a policy explicitly aimed at reimbursing insurers on this margin. This is the principle reason we argue that the de facto insurer incentives involved in risk adjustment have been misunderstood.

5. Discussion

Our most significant finding is that concurrent risk adjustment, the permanent feature of ACA Marketplace plan payment, fares poorly in relation to reinsurance, or even a simple mixed system, on all three performance metrics. Years of empirical research have focused on improving the statistical fit of prospective risk adjustment. Statistical fit is even higher when, as in Marketplaces, the risk adjustment is implemented concurrently. We introduce a broader fit measure, payment system fit, which allows us to assess reinsurance as well. We show that concurrent risk adjustment contributed little incrementally to fit when added on top of reinsurance under the conventional R² measure.

Turning to power, diagnostic risk adjustment systems are conditioned on health care events and therefore linked to realized costs. This is true even of prospective risk adjustment, which creates no direct tie between current period utilization and an enrollee’s risk score, as long as there is at least partial retention of enrollees in the same plan across years. Here we encounter another surprising result. Marketplace reinsurance dilutes power on average less than concurrent risk adjustment. Marketplace reinsurance also performs better than concurrent risk adjustment on our third measure of performance, the balance of incentives across clinical areas.

One reason why reinsurance may receive a better grading along fit than risk adjustment is that a large fraction of healthcare spending is generated by a small fraction of enrollees. Reinsurance activates in the upper tail of spending by design, while risk adjustment tends to systematically underpredict for persons with high predicted costs (Brown et al., 2014, Table 3), and it necessarily underpredicts for persons with high realized costs. Because the R² measure of fit disproportionately penalizes large deviations, reinsurance performs exceptionally well by this metric. In comparison, using the CPM to measure fit rates concurrent RA as superior to reinsurance (though reinsurance always compares favorably to concurrent risk adjustment on power and balance). To illustrate the importance of the squared property of R², Figure 3 demonstrates the extent to which healthcare spending is highly right-skewed. The figure bins the sample population into 3 groups defined by utilization percentiles: [0, 90), [90, 99), and [99, 100]. Each of these groups corresponds to roughly one third of total spending. Because of the squaring property of a variance measure, the contributions to the variance in spending are even more highly skewed than the contributions to the mean spending. Among the 2M enrollees included in the simulations, the top 1% of the distribution accounts for 27.7% of the spending but 85.4% of the variance. This remarkable property of health care spending distributions largely explains the effectiveness of a seemingly modest reinsurance policy in achieving major improvements in measured fit. Reinsurance by design targets the upper tail of the patient distribution in cost. At the same time, reinsurance provides little or no reimbursement at the margin for the vast majority of plan enrollees, retaining high power for the majority of enrollees.

Figure 3.

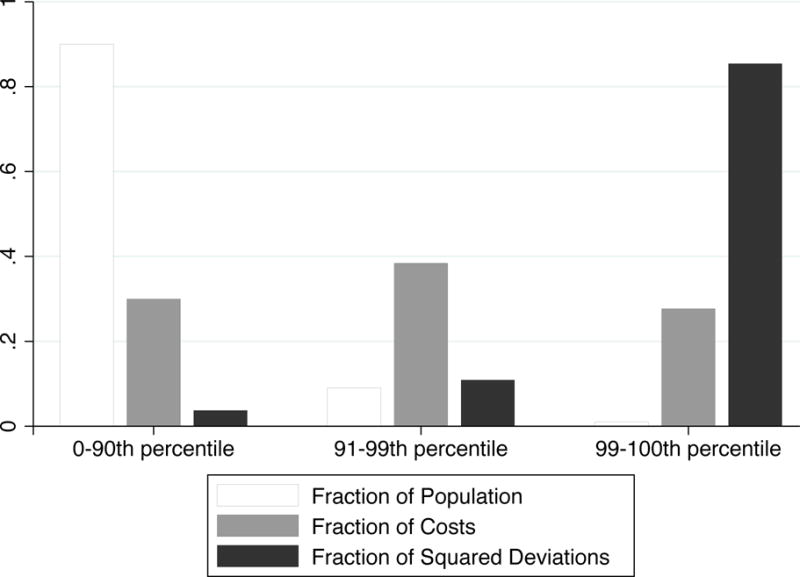
Skewness in Healthcare Spending

Notes: Figure shows distributions of costs and squared deviations of costs in the population, across groups defined by percentiles of individual costs: [0, 90), [90, 99), and [99, 100]. Vertical bars represent the fraction of the population within the percentile group, the fraction of total spending accounted for by the group, and the fraction of squared deviations accounted for by the group.

In 2017, when the payment system for Marketplaces moves out of its transition phase, regulators plan to drop reinsurance. Our results imply that from the perspective of our measures of power, fit, and balance this policy should be reconsidered. Pairing reinsurance with prospective risk adjustment is just as good as or outperforms (depending on the fit metric) plan payment based on concurrent risk adjustment alone.⁴⁶

We realize that this proposition strays from conventional wisdom about paying competing managed care plans, and more conceptual and empirical research is necessary to justify any radical change in policy direction. We identify a number of directions for future research to build on and confirm our initial findings. The first is to incorporate more features of Marketplace payment systems and to simulate on updated data. Marketplace payment systems include premiums, risk corridors (limiting gains and losses at plans) and plans with a higher or lower “actuarial value,” referring to the share of total costs paid for by the plans. Adding consideration of these features will affect our fit and power measures, though we have no reason to expect that the inferiority of concurrent risk adjustment relative to feasible alternatives will change. Updated data, including eventually data from the Marketplaces themselves, will enable a more accurate quantification of our performance metrics.

A second direction is to consider optimizing over the parameters of the payment systems features considered. Our paper takes the risk adjustment specification and the form of reinsurance as given in our simulations, but these could be modified and the effects studied on fit, power and balance. The cut point at which reinsurance activates and the reimbursement rate of reinsurance could be changed, for example, and the tradeoffs evaluated. Increasing the reinsurance share above the cut point improves fit and lowers power but has ambiguous effects on balance. Lowering the cut point improves fit and lowers power, again with ambiguous effects on balance.⁴⁷ Variables included in the risk adjustment formula could also be modified. Both exercises would require new empirical analysis. New combinations of risk adjustment and other forms of payment can be explored. A risk adjustment system with only demographic adjustors improves the R² measure of fit at no power loss or introduction of imbalance. Such a system could be combined with reinsurance, for example, and improve fit relative to reinsurance alone with no cost in terms of the other two metrics.

Third, most of our analysis has implicitly assumed that there are no other margins of distortion aside from those directly embedded in the payment system itself. In the presence of additional distortions, second-best policy might not correspond with our notions, especially for the case of balance. For example, plans might seek to attract or deter enrollees by channeling resources towards or away from clinical areas. Such “service-level selection” might be countered with some intentional imbalance in power.⁴⁸ Distortions arising from consumer behavior may also generate scope for welfare-improving imbalance. For example, if consumer moral hazard (i.e., sensitivity to consumer cost-sharing) differed across treatment areas and distorted utilization away from the first best level, this could in principle be undone by generating countervailing insurer incentives via imbalance in the payment system. Similarly, if care in certain areas was underutilized due to an information friction–for example, if consumers made systematic errors in assessing the value of a certain medical technology–then weaker power could be optimal for conditions subject to under-provision of care in order to counteract the information problem. We expect future empirical work to explore such additional complexities, including the interaction between the incentives created by imbalance and insurers’ differential ability across clinical areas to respond to those incentives.⁴⁹ Nonetheless, we note that this paper already advances the understanding of second-best policy in insurance markets by providing the first analysis of the simultaneous impacts of several of the most common payment system mechanisms in the presence of multiple information and incentive problems. In particular, we focus on those problems that are most commonly targeted by regulators.

Finally, as a fourth direction, each criterion we propose here may merit further development. While the concept of power is well-established in contract theory, it is infrequently applied to health plan contracting. The objective of balance also raises additional questions about the application of power-type measures to particular service areas.⁵⁰ Our payment systems R² measure of fit is the most standard of the three measures we propose, but the results with respect to fit were nonetheless the most striking and surprising. It was particularly notable to us how well reinsurance and mixed systems performed in terms of fit, since fit has been the metric of choice for proponents of risk adjustment. The finding implies that either the use of risk adjustment is correct and the fit objective that the risk adjustment literature seeks to maximize is the wrong target, or the fit objective is correct, and risk adjustment is simply inferior. Reinsurance and risk adjustment “explain” different parts of the distribution of costs, and it would be worth considering whether the square of the deviation from the mean captures in a single dimension all of the relevant incentives for cream-skimming and adverse selection distortions. Our empirical analyses are conducted in terms of realized costs, whereas a theme in the risk adjustment literature is that risk adjustment needs only to capture costs that are “predictable.” If reinsurance is explaining a larger share of the less predictable costs, as contended by Dow et al., (2010), the superiority of reinsurance in terms of fit may be mitigated.⁵¹ Operationalization of predictable costs, as was done by Layton et al (2015) is one way to go, but the form of a model of predictable costs, and taking account of whose predictions (consumers’? plans’?) is challenging. If a different metric for evaluating the cream-skimming and adverse selection incentives of risk adjustment is proposed, we hope our explicit accounting of the performance metrics can help illuminate such future research.

6. Conclusions

Delegation of responsibility for providing health care services to managed care plans which compete on price and quality is the foundation of health policy in many countries, making the design of the payment system for health plans the most important regulatory task in health care. In a nearly universal practice, regulators apply risk adjustment formula to transfer funds to plans enrolling individuals with higher expected costs. Other payment features such as enrollee-paid premiums and reinsurance also generally contribute to plan payments. Our paper proposes and implements a method to grade alternative plan payment schemes based on one measure related to selection incentives—fit—and two measures related to incentives to supply services—power, and balance. To our knowledge these incentives have not been previously measured. Our paper develops a method for quantifying these incentives and thus comparing payment system alternatives. We assess the two major components of the ACA payment system, concurrent risk adjustment and reinsurance, separately and when combined on these three dimensions of performance, and compare them to prospective risk adjustment.

Our analysis illustrates one way in which the incentives implicit in diagnosis-based risk adjustment have been misunderstood. Rather than being influenced only by enrollee characteristics, risk adjustment is influenced by utilization, and therefore affects incentives to provide services. Concurrent risk adjustment, which ties diagnoses to payments in the same plan period, performs particularly poorly in this regard. Surprisingly, we find that a simple reinsurance scheme rates favorably compared to the actual payment policy in the ACA Marketplaces in term of our measures of fit, power and balance.

The grading we outline formalizes and builds upon existing insights into payment systems incentives, capturing the main regulatory concerns in health insurance markets. Nonetheless, other criteria could be considered when assessing the relative merits of alternative payment schemes. Risk adjustment and reinsurance, for example, will differ in their incentives to “upcode” claims (Geruso and Layton 2015), in how well they respond to changing medical technology and practice patterns generally, and in costs of administration. Importantly, our work could be linked to other research on efficiency in health plan payment that focuses on the two adverse selection related issues of efficient sorting of individuals between plans (Einav, Finkelstein and Cullen, 2010), and on the incentives to plans to distort benefits to attract or deter enrollees based on their profitability (McGuire et al., 2014). A more comprehensive evaluation of risk adjustment in comparison to reinsurance and other payment options is necessary before making wholesale changes in the basis of payment to managed health care plans competing in markets for individual health insurance.

Appendix A: Balance and Efficiency

This appendix shows that the efficiency loss from imbalance in power can be approximated by expression (6) in the text.

Let ρ′ be the optimal power across all services. As we note in the text, the optimal power of a payment system might not be 1, and we show here that Equation (6) measures loss due to imbalance for any combination of observed average power $\overline{\mathrm{\rho }}$ and optimal average power ρ′. A ρ is optimal because it leads the plan to provide the optimal level of services, which we call ${\mathrm{x}}_1^{\prime }$ and ${\mathrm{x}}_2^{\prime }$ for services 1 and 2. Let ρ₁ and ρ₂ be the actual power for services 1 and 2, leading to service levels x₁(ρ₁) and x₂(ρ₂). We are interested in evaluating alternative payment systems in which the average power is held constant, i.e., where:

$$\overline{\mathrm{\rho }}=\frac{{\mathrm{\rho }}_1\overline{{\mathrm{x}}_1}+{\mathrm{\rho }}_2\overline{{\mathrm{x}}_2}}{\overline{{\mathrm{x}}_1}+\overline{{\mathrm{x}}_2}}.$$

The inefficiency loss as a function of ρ₁ and ρ₂ we call L(ρ₁, ρ₂). This loss can be approximated for one person (omitting i subscripts) with a Taylor series expansion of the function L(ρ₁,ρ₂). The second order Taylor approximation simplifies to:⁵²

$$\mathrm{L}({\mathrm{\rho }}_1,{\mathrm{\rho }}_2)~\frac{1}{2}\frac{\partial {\mathrm{x}}_1}{\partial {\mathrm{\rho }}_1}{({\mathrm{\rho }}_1-{\mathrm{\rho }}^{\prime })}^2+\frac{1}{2}\frac{\partial {\mathrm{x}}_2}{\partial {\mathrm{\rho }}_2}{({\mathrm{\rho }}_2-{\mathrm{\rho }}^{\prime })}^2.$$ (a.1)

Assume proportional responses to power so that $\frac{\frac{{\mathrm{dx}}_1}{{\mathrm{d}\mathrm{\rho }}_1}}{{\mathrm{x}}_1}=\frac{\frac{{\mathrm{dx}}_2}{{\mathrm{d}\mathrm{\rho }}_2}}{{\mathrm{x}}_2}=\mathrm{\alpha }$. Then, even though α is unknown, we can say:

$$\mathrm{L}({\mathrm{\rho }}_1,{\mathrm{\rho }}_2)~{\mathrm{x}}_1{({\mathrm{\rho }}_1-{\mathrm{\rho }}^{\prime })}^2+{\mathrm{x}}_2{({\mathrm{\rho }}_2-{\mathrm{\rho }}^{\prime })}^2$$

If we sum this for the entire population, we replace x₁ by ${\overline{\mathrm{x}}}_1$ and x₂ by ${\overline{\mathrm{x}}}_2$, and write the equivalent expression:

$$L({\mathrm{\rho }}_1,{\mathrm{\rho }}_2)~{\overline{\mathrm{x}}}_1{(({\mathrm{\rho }}_1-\overline{\mathrm{\rho }})-({\mathrm{\rho }}^{\prime }-\overline{\mathrm{\rho }}))}^2+{\overline{\mathrm{x}}}_2{(({\mathrm{\rho }}_2-\overline{\mathrm{\rho }})-({\mathrm{\rho }}^{\prime }-\overline{\mathrm{\rho }}))}^2$$

Expanding, we have three groups of terms:

$$\mathrm{L}({\mathrm{\rho }}_1,{\mathrm{\rho }}_2)~{\overline{\mathrm{x}}}_1{({\mathrm{\rho }}_1-\overline{\mathrm{\rho }})}^2+{\overline{\mathrm{x}}}_2{({\mathrm{\rho }}_2-\overline{\mathrm{\rho }})}^2(\text{loss from imbalance})$$

$$+{\overline{\mathrm{x}}}_1{({\mathrm{\rho }}^{\prime }-\overline{\mathrm{\rho }})}^2+{\overline{\mathrm{x}}}_2{({\mathrm{\rho }}^{\prime }-\overline{\mathrm{\rho }})}^2(\text{loss from how}\overline{\mathrm{\rho }}\text{deviates from}\mathrm{\rho }’)$$

$$-2({\mathrm{\rho }}^{\prime }-\overline{\mathrm{\rho }})[{\overline{\mathrm{x}}}_1({\mathrm{\rho }}_1-\overline{\mathrm{\rho }})+{\overline{\mathrm{x}}}_2({\mathrm{\rho }}_2-\overline{\mathrm{\rho }})](\text{zero by definition of }\overline{\mathrm{\rho }})$$

The last term is always zero. The middle term is the loss due to the gap between realized average power and optimal average power, and does not depend on ρ₁ and ρ₂. It is a constant when we compare payment systems with the same average power. Thus, only the first term varies as we change ρ₁ and ρ₂ keeping average power fixed. This first part, expression (6) in the text, is the contribution to inefficiency due to imbalance.

Appendix B: Risk Adjustment Payments and Coefficient Estimates

Risk Adjusted Payments

In the simulations of the payment systems including risk adjustment, the plan payment for individual i is assumed to be equal to the average cost in the sample (prior to randomly eliminating claims) multiplied by the individual’s relative risk score:

$${\mathrm{Pay}}_{\mathrm{i}}=\frac{{\mathrm{r}}_{\mathrm{i}}}{\overline{\mathrm{r}}}\overline{\mathrm{c}}.$$

This is motivated by the following risk adjustment transfer formula used in the Marketplaces:⁵³

$${\mathrm{t}}_{\mathrm{i}}=(\frac{{\mathrm{r}}_{\mathrm{i}}}{\overline{\mathrm{r}}}-1)\overline{\mathrm{P}}$$

where $\overline{\mathrm{P}}$ is the average premium in the market. If we assume that the market is perfectly competitive and that plan premiums equal average costs, then $\overline{\mathrm{P}}=\overline{\mathrm{c}}$. If we assume that all plans are identical, then the plan payment net of risk adjustment is equal to

$$\begin{array}{c}{\mathrm{Pay}}_{\mathrm{i}}=\overline{\mathrm{P}}+(\frac{{\mathrm{r}}_{\mathrm{i}}}{\overline{\mathrm{r}}}-1)\overline{\mathrm{P}}\\ =\frac{{\mathrm{r}}_{\mathrm{i}}}{\overline{\mathrm{r}}}\overline{\mathrm{c}}\end{array}$$

In other words, plan payment for individual i is the average cost in the market, multiplied by i’s relative risk score.

Coefficient Estimates

HHS provides a statutory set of risk adjustment coefficients—aka weights—for the concurrent model to be used in the Marketplaces. We estimate our own vector of prospective weights, β^P, and in order to ensure that the prospective and concurrent models we evaluate are comparable, we estimate our own vectors of concurrent weights β^C as well.

In all models, risk scores are calculated using the same vector of risk adjusters, Y_i, used in the HHS-HCC model, so that only the coefficients attached to the risk adjusters may differ. These risk adjusters consist of a set of age/sex cells, around 100 Hierarchical Condition Categories (HCCs), and a few interactions terms.⁵⁴ We use a program provided by HHS to generate these variables. The HCCs are generated using diagnoses from either the prior (prospective) or current (concurrent) year’s claims. For each model, risk scores are assigned by multiplying the vector of risk adjusters by a vector of risk adjustment weights: ${{\mathrm{r}}^{\mathrm{C}}}_{\mathrm{it}}={\mathrm{Y}}_{\mathrm{it}}{\mathrm{\beta }}^{\mathrm{C}}$.

$${\mathrm{r}}_{\mathrm{it}}^{\mathrm{P}}={\mathrm{Y}}_{\mathrm{i},\mathrm{t}-1}{\mathrm{\beta }}^{\mathrm{P}}$$

We estimate β^C and β^P using the portion of initial sample that was not selected as part of the random sample of 2,000,000 people we use in our simulations in order to avoid overfitting. This estimation sample consists of around 15 million individuals. We estimate β^C and β^P via the following linear regressions of total costs on Y_i:

$$\begin{array}{l}{\mathrm{c}}_{\mathrm{it}}={\mathrm{Y}}_{\mathrm{it}}{\mathrm{\beta }}^{\mathrm{C}}+{\mathrm{e}}_{\mathrm{it}}\\ {\mathrm{c}}_{\mathrm{it}}={\mathrm{Y}}_{\mathrm{i},\mathrm{t}-1}{\mathrm{\beta }}^{\mathrm{P}}+{\mathrm{e}}_{\mathrm{it}}\end{array}$$

The coefficient estimates, normalized by dividing by $\overline{\mathrm{c}}$, are found in Table B1. With the normalization, the coefficients indicate the contribution of each risk adjuster to the relative risk score. We use these weights combined with the risk adjusters, Y_i, to assign risk scores to individuals in our simulation sample.

Table B1.

Estimated Coefficients from Risk Adjustment Regressions

Variables	Concurrent Coefficient	Prospective Coefficient
Male, age 21–24	0.18	0.25
Male, age 25–29	0.22	0.28
Male, age 30–24	0.25	0.32
Male, age 35–39	0.28	0.37
Male, age 40–44	0.32	0.44
Male, age 45–49	0.38	0.57
Male, age 50–54	0.45	0.72
Male, age 55–59	0.52	0.91
Male, age > 60	0.59	1.11
Female, age 21–24	0.31	0.57
Female, age 25–29	0.38	0.78
Female, age 30–24	0.45	0.79
Female, age 35–39	0.49	0.70
Female, age 40–44	0.53	0.69
Female, age 45–49	0.56	0.76
Female, age 50–54	0.60	0.84
Female, age 55–59	0.62	0.93
Female, age > 60	0.66	1.06
HIV/AIDS	0.42	0.63
Septicemia, Sepsis, Systemic Inflammatory Response Syndrome/Shock	11.68	2.51
Central Nervous System Infections, Except Viral Meningitis	5.11	1.16
Viral or Unspecified Meningitis	2.45	0.68
Opportunistic Infections	3.61	1.74
Metastatic Cancer	14.95	11.35
Lung, Brain, and Other Severe Cancers, Including Pediatric Acute Lymphoid Leukemia	6.25	5.28
Non-Hodgkin’s Lymphomas and Other Cancers and Tumors	4.07	3.43
Colorectal, Breast (Age < 50), Kidney, and Other Cancers	3.91	2.70
Breast (Age 50+) and Prostate Cancer, Benign/Uncertain Brain Tumors, and Other Cancers and
Tumors	2.28	1.31
Thyroid Cancer, Melanoma, Neurofibromatosis, and Other Cancers and Tumors	1.11	0.71
Pancreas Transplant Status/Complications	4.99	3.81
Protein-Calorie Malnutrition	8.59	2.23
Liver Transplant Status/Complications	10.55	3.40
End-Stage Liver Disease	3.52	5.49
Cirrhosis of Liver	1.28	2.37
Chronic Hepatitis	0.69	0.67
Acute Liver Failure/Disease, Including Neonatal Hepatitis	2.04	1.03
Intestine Transplant Status/Complications	28.22	20.70
Peritonitis/Gastrointestinal Perforation/Necrotizing Enterocolitis	13.36	2.26
Intestinal Obstruction	5.03	1.63
Chronic Pancreatitis	4.23	3.09
Acute Pancreatitis/Other Pancreatic Disorders and Intestinal Malabsorption	2.41	1.27
Inflammatory Bowel Disease	1.39	1.44
Rheumatoid Arthritis and Specified Autoimmune Disorders	1.34	1.48
Systemic Lupus Erythematosus and Other Autoimmune Disorders	0.68	0.88
Cleft Lip/Cleft Palate	1.44	1.11
Hemophilia	28.28	30.83
Coagulation Defects and Other Specified Hematological Disorders	2.00	1.04
Schizophrenia	1.36	1.03
Major Depressive and Bipolar Disorders	0.90	0.86
Reactive and Unspecified Psychosis, Delusional Disorders	1.94	1.06
Personality Disorders	0.67	0.67
Anorexia/Bulimia Nervosa	1.40	1.17
Prader-Willi, Patau, Edwards, and Autosomal Deletion Syndromes	2.86	1.14
Down Syndrome, Fragile X, Other Chromosomal Anomalies, and Congenital Malformation Syndromes	1.16	0.74
Autistic Disorder	0.28	0.45
Pervasive Developmental Disorders, Except Autistic Disorder	0.44	0.10
Spinal Cord Disorders/Injuries	4.28	1.65
Amyotrophic Lateral Sclerosis and Other Anterior Horn Cell Disease	2.08	3.42
Quadriplegic Cerebral Palsy	1.07	2.97
Cerebral Palsy, Except Quadriplegic	0.23	0.84
Spina Bifida and Other Brain/Spinal/Nervous System Congenital Anomalies	0.96	1.03
Myasthenia Gravis/Myoneural Disorders and Guillain-Barre Syndrome/Inflammatory and Toxic
Neuropathy	2.97	2.47
Multiple Sclerosis	1.39	1.55
Seizure Disorders and Convulsions	6.63	1.13
Hydrocephalus	5.69	1.58
Non-Traumatic Coma, Brain Compression/Anoxic Damage	9.16	1.26
Respirator Dependence/Tracheostomy Status	25.91	4.06
Congestive Heart Failure	2.42	2.02
Acute Myocardial Infarction	8.29	1.06
Unstable Angina and Other Acute Ischemic Heart Disease	4.38	1.17
Heart Infection/Inflammation, Except Rheumatic	4.03	1.21
Specified Heart Arrhythmias	2.23	1.15
Intracranial Hemorrhage	6.50	1.15
Ischemic or Unspecified Stroke	2.98	1.06
Cerebral Aneurysm and Arteriovenous Malformation	3.67	1.27
Hemiplegia/Hemiparesis	4.17	1.75
Monoplegia, Other Paralytic Syndromes	2.55	1.29
Atherosclerosis of the Extremities with Ulceration or Gangrene	6.91	4.05
Vascular Disease with Complications	4.85	1.61
Pulmonary Embolism and Deep Vein Thrombosis	8.29	1.44
Lung Transplant Status/Complications	18.13	13.17
Cystic Fibrosis	2.59	4.27
Fibrosis of Lung and Other Lung Disorders	1.72	1.15
Aspiration and Specified Bacterial Pneumonias and Other Severe Lung Infections	3.39	1.06
Kidney Transplant Status	6.38	4.85
End Stage Renal Disease	24.95	29.00
Chronic Ulcer of Skin, Except Pressure	1.56	1.79
Hip Fractures and Pathological Vertebral or Humerus Fractures	6.08	2.49
Pathological Fractures, Except of Vertebrae, Hip, or Humerus	1.12	0.67
Stem Cell, Including Bone Marrow, Transplant Status/Complications	17.78	3.71
Artificial Openings for Feeding or Elimination	7.04	2.27
Amputation Status, Lower Limb/Amputation Complications	4.13	2.81
Group 01	0.58	0.72
Group 02A	1.55	1.13
Group 03	4.39	1.82
Group 04	2.67	1.55
Group 06	7.70	5.40
Group 07	5.08	3.83
Group 08	3.45	3.24
Group 09	2.49	1.78
Group 10	8.45	4.95
Group 11	6.77	4.43
Group 12	1.09	1.23
Group 13	12.02	1.72
Group 14	21.79	9.27
Group 15	0.68	0.66
Group 16	1.39	4.75
Group 17	0.95	1.20
Group 18	2.57	−0.14
Interaction Group M	−4.98	1.00
Interaction Group H	−3.00	1.31
Severe Illness Indicator	−6.05	−0.36
Severe X Opportunistic Infections	14.00	1.31
Severe X Metastatic Cancer	7.40	0.73
Severe X Lung, Brain, and Other Severe Cancers, Including Pediatric Acute Lymphoid Leukemia	6.44	0.33
Severe X Non-Hodgkin’s Lymphomas and Other Cancers and Tumors	7.55	1.16
Severe X Myasthenia Gravis/Myoneural Disorders and Guillain-Barre Syndrome/Inflammatory and
Toxic Neuropathy	7.13	0.42
Severe X Heart Infection/Inflammation, Except Rheumatic	7.94	0.53
Severe X Intracranial Hemorrhage	8.38	−1.78
Severe X Group 06	7.10	2.95
Severe X Group 08	5.28	1.16
Severe X End-Stage Liver Disease	3.33	0.03
Severe X Acute Liver Failure/Disease, Including Neonatal Hepatitis	6.47	−2.28
Severe X Atherosclerosis of the Extremities with Ulceration or Gangrene	7.51	2.78
Severe X Vascular Disease with Complications	7.56	−2.01
Severe X Aspiration and Specified Bacterial Pneumonias and Other Severe Lung Infections	8.44	−1.47
Severe X Artificial Openings for Feeding or Elimination	9.21	−0.59
Severe X Group 03	8.72	0.89

Table B2.

Group and Interaction Definitions

Group 01

Diabetes with Acute Complications

Diabetes with Chronic Complications

Diabetes without Complication

Group 02A

Mucopolysaccharidosis

Lipidoses and Glycogenosis

Amyloidosis, Porphyria, and Other Metabolic Disorders

Adrenal, Pituitary, and Other Significant Endocrine Disorders

Group 03

Necrotizing Fasciitis

Bone/Joint/Muscle Infections/Necrosis

Group 04

Osteogenesis Imperfecta and Other Osteodystrophies

Congenital/Developmental Skeletal and Connective Tissue Disorders

Group 06

Myelodysplastic Syndromes and Myelofibrosis

Aplastic Anemia

Group 07

Acquired Hemolytic Anemia, Including Hemolytic Disease of Newborn

Sickle Cell Anemia (Hb-SS)

Thalassemia Major

Group 08

Combined and Other Severe Immunodeficiencies

Disorders of the Immune Mechanism

Group 09

Drug Psychosis

Drug Dependence

Group 10

Traumatic Complete Lesion Cervical Spinal Cord

Quadriplegia

Group 11

Traumatic Complete Lesion Dorsal Spinal Cord

Paraplegia

Group 12

Quadriplegic Cerebral Palsy

Parkinson’s, Huntington’s, and Spinocerebellar Disease, and Other Neurodegenerative Disorders

Group 13

Respiratory Arrest

Cardio-Respiratory Failure and Shock, Including Respiratory Distress Syndromes

Group 14

Heart Assistive Device/Artificial Heart / Heart Transplant

Group 15

Chronic Obstructive Pulmonary Disease, Including Bronchiectasis

Asthma

Group 16

Chronic Kidney Disease, Stage 5

Chronic Kidney Disease, Severe (Stage 4)

Group 17

Ectopic and Molar Pregnancy, Except with Renal Failure, Shock, or Embolism

Miscarriage with Complications

Miscarriage with No or Minor Complications

Group 18

Completed Pregnancy With Major Complications

Completed Pregnancy With Complications

Completed Pregnancy with No or Minor Complications

Severe

Septicemia, Sepsis, Systemic Inflammatory Response Syndrome/Shock

Peritonitis/Gastrointestinal Perforation/Necrotizing Enterocolitis

Seizure Disorders and Convulsions

Respirator Dependence/Tracheostomy Status

Respiratory Arrest

Cardio-Respiratory Failure and Shock, Including Respiratory Distress Syndromes

Pulmonary Embolism and Deep Vein Thrombosis

Interaction Group H

Opportunistic Infections

Metastatic Cancer

Lung, Brain, and Other Severe Cancers, Including Pediatric Acute Lymphoid Leukemia

Non-Hodgkin’s Lymphomas and Other Cancers and Tumors

Myasthenia Gravis/Myoneural Disorders and Guillain-Barre

Syndrome/Inflammatory and Toxic Neuropathy

Heart Infection/Inflammation, Except Rheumatic

Intracranial Hemorrhage

Group 06

Group 08

Interaction Group M

End-Stage Liver Disease

Acute Liver Failure/Disease, Including Neonatal Hepatitis

Atherosclerosis of the Extremities with Ulceration or Gangrene

Vascular Disease with Complications

Aspiration and Specified Bacterial Pneumonias and Other Severe Lung Infections

Artificial Openings for Feeding or Elimination

Group 03

Appendix C: Simulation Results Using HHS Concurrent Weights

Here we show comparability of results between the concurrent weights we estimate and those estimated by HHS. In table C.1, we replicate our main results using the statutory HHS weights. To do so, we use the same software that will be used by Marketplace insurers to generate the risk scores that determine ex-post transfer payments across plans. For these simulations, the set of risk adjusters is the same as the set used in our prospective and concurrent models discussed above. Only the risk adjustment weights, β^C, differ.

Table C.1.

Fit and Power Simulation Results using HHS-HCC Statutory Coefficients

Simulated Payment Scheme	(1)	(2)	(3)	(4)
	Fit		Power
	R2	CPM	Inpatient Events	Outpatient Events
1 Concurrent RA (ACA Policy, 2017+)	0.35	0.24	0.59	0.72
2 Reinsurance	0.60	0.19	0.64	0.84
3 Concurrent RA + Reinsurance (ACA Policy, 2014–2016)	0.54	0.32	0.24	0.56

Notes: This table replicates results from Table 1 using the statutory risk adjustment coefficients (aka “weights”) developed by the Department of Health and Humans Services, in place of the risk adjustment model calibrated for this paper. Rows (1) and (3) correspond to the actual payment policy in the ACA Exchanges, based on concurrent risk adjustment (RA) and reinsurance. Fit in column (1) is measured as 1 – RSS/TSS in a regression of insurer payments on insurer costs. Fit in column (2) is calculated as the Cumming’s Prediction Measure (CPM). Power is calculated via a simulation in which healthcare events are randomly removed to determine the effect on insurer costs and payments at the individual level. Power for inpatient and outpatient events simulated separately. Reinsurance is simulated as 100% reimbursement after exceeding an attachment point of $45,000. Consult the text for full details