Multivariate analysis of the population representativeness of related clinical studies

Abstract

Objective

To develop a multivariate method for quantifying the population representativeness across related clinical studies and a computational method for identifying and characterizing underrepresented subgroups in clinical studies.

Methods

We extended a published metric named Generalizability Index for Study Traits (GIST) to include multiple study traits for quantifying the population representativeness of a set of related studies by assuming the independence and equal importance among all study traits. On this basis, we compared the effectiveness of GIST and multivariate GIST (mGIST) qualitatively. We further developed an algorithm called “Multivariate Underrepresented Subgroup Identification” (MAGIC) for constructing optimal combinations of distinct value intervals of multiple traits to define underrepresented subgroups in a set of related studies. Using Type 2 diabetes mellitus (T2DM) as an example, we identified and extracted frequently used quantitative eligibility criteria variables in a set of clinical studies. We profiled the T2DM target population using the National Health and Nutrition Examination Survey (NHANES) data.

Results

According to the mGIST scores for four example variables, i.e., age, HbA1c, BMI, and gender, the included observational T2DM studies had superior population representativeness than the interventional T2DM studies. For the interventional T2DM studies, Phase I trials had better population representativeness than Phase III trials. People at least 65 years old with HbA1c value between 5.7% and 7.2% were particularly underrepresented in the included T2DM trials. These results confirmed well-known knowledge and demonstrated the effectiveness of our methods in population representativeness assessment.

Conclusions

mGIST is effective at quantifying population representativeness of related clinical studies using multiple numeric study traits. MAGIC identifies underrepresented subgroups in clinical studies. Both data-driven methods can be used to improve the transparency of design bias in participation selection at the research community level.

Graphical Abstract

1. INTRODUCTION

Well-designed clinical studies play a vital role in generating evidence-based medical knowledge [1]. However, patient selection bias introduced during study design (e.g., use of overly-restrictive eligibility criteria) [2] and patient recruitment (e.g., patient self-selection [3] and cross-referral [4]) often compromise population representativeness and thus limit results generalizability [2–4]. This has been a concern of both the general public [5] as well as the scientific community [4]. Lack of population representativeness or inadequate sample size may lead to inaccurate estimate of treatment efficacy and safety problems [6]. As a consequence, some drugs have to be withdrawn from the market after serious adverse drug reactions (e.g., organ damage and toxicity) were reported when they were administered to a broader patient population [7].

To assess the representativeness of study populations in clinical studies, researchers typically compare the study sample derived from summary data in the literature and a convenience sample of real-world patients for the target medical condition [8–13]. These approaches often reveal the lack of a posteriori generalizability among clinical studies. For example, Schoenmaker et al. [13] reported a wide age gap between the demented patients enrolled in diagnostic/therapeutic studies and demented patients from the general population in Netherlands. However, such a posteriori generalizability assessment studies can be done only after study completion and results publication, thereby delaying detection of patient selection biases and missing the opportunity for preventing such biases during study design. In contrast, a priori generalizability, which focuses on the representativeness of eligible patients, can be assessed during the study design. As clinical research eligibility criteria subsume the characteristics of study sample, a posteriori generalizability is naturally lower than a priori generalizability [14]. At present, methods for analyzing a priori generalizability are scarce or laborious, and only itemize restrictive eligibility criteria [14, 15].

Hypothesizing that the population representativeness problem may exist not only at the individual study level but also across a whole body of studies for a clinical domain [16], Weng et al. proposed a metric for quantifying the population representativeness of a set of related studies. This metric, called Generalizability Index for Study Traits (GIST) [17], allows quantification of collective a priori generalizability of multiple studies using one study trait at a time. Since population representativeness is a multi-dimensional problem [18] involving multiple criteria, it is not informative to apply GIST on multiple variables linearly one after another for assessing multivariate population representativeness. Thus, we are motivated to extend GIST in a multivariate setting. Built upon our previous work [17, 19–22], this paper presents a framework for multivariate analysis of population representativeness of related clinical studies. The contribution of this work is two-fold: (1) a quantitative measure of a priori generalizability incorporating multiple numeric eligibility criteria variables (referred to as “mGIST” from this point on); and (2) a method called MAGIC for identifying and characterizing underrepresented population subgroups with combinations of value intervals across multiple eligibility criteria variables. This work has the potential to improve the transparency of population representativeness of related studies and enable clinical research stakeholders (e.g., policy makers, clinical researchers) to make informed patient selection decision during clinical study design. We illustrate this framework on example study traits of Type 2 diabetes mellitus (T2DM) studies.

2. MATERIALS AND METHODS

We first define the following:

• Target population: patients to whom the results of clinical studies are intended to be applied. The target population can be only approximated with available patient data.

• Study population: patients who are eligible for a clinical study (i.e., they satisfy the study inclusion and exclusion criteria).

• Underrepresented patient population: a subset of the target population rarely eligible for a set of clinical studies.

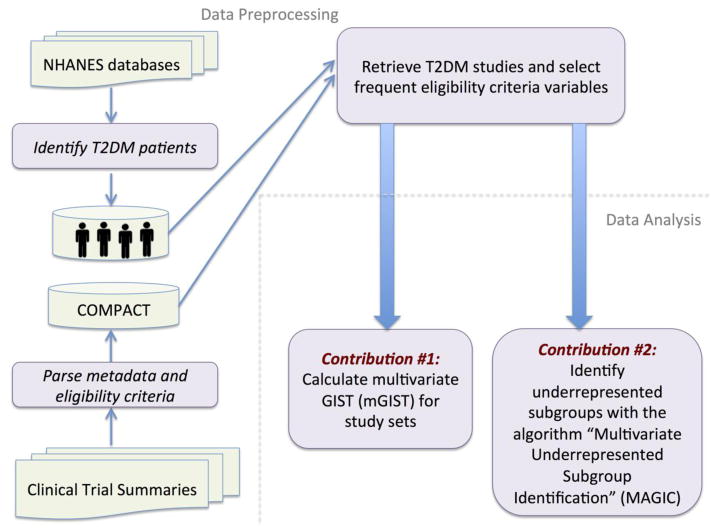
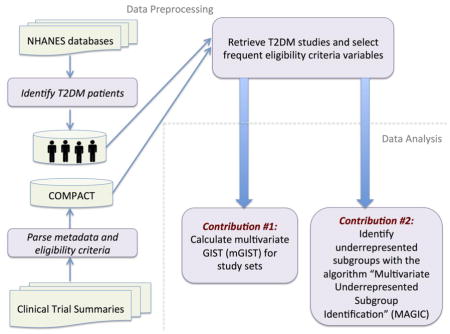
Figure 1 explains the overall workflow for multivariate analysis of population representativeness of related clinical studies, which includes two steps: data preprocessing and data analysis. In the data preprocessing step, we retrieve T2DM studies in ClinicalTrials.gov and select frequent eligibility criteria variables in these studies (Section 2.1.1). We identify real-world T2DM patients (target population) and extract their data from the database of National Health and Nutrition Examination Survey (NHANES) (Section 2.1.2), a continuous health survey conducted by the National Center for Health Statistics [23]. The data analysis step includes two components: (1) population representativeness quantification (Section 2.2); and (2) underrepresented population subgroup identification and characterization (Section 2.3).

Figure 1.

The workflow for multivariate analysis of population representativeness of related clinical studies.

2.1. Data Preprocessing

2.1.1. Retrieving T2DM Studies and Selecting Frequent Eligibility Criteria Variables

To facilitate aggregate analysis of clinical studies, we have previously built a database called COMPACT [19], which transformed all the study summaries in ClinicalTrials.gov into discrete study metadata and eligibility criteria variables. We have created a web-based visualization tool VITTA (http://is.gd/VITTA) to show how studies vary in their study populations with respect to study traits, one at a time [20]. Different trait names and measurement units were normalized by the Valx system [24] developed in house. Valx leveraged the Unified Medical Language System (UMLS) [25] and domain knowledge from Web resources such as MedLinePlus [26] to parse numeric expressions into a structured format. Quantitative variables (e.g., HbA1c and BMI) and their comparison statements in eligibility criteria, such as “HbA1c > 7.5%”, are therefore made readily analyzable.

The version of our COMPACT database used for this study stores parsed data of 162,586 clinical trial summaries downloaded from ClinicalTrials.gov as of 03/18/2014, out of which 3,897 were indexed as T2DM studies by ClinicalTrials.gov (i.e., condition = ‘Type 2 diabetes’). Note that ClinicalTrials.gov’s API may return T2DM studies for either treating or preventing T2DM. To match the year range for patient data retrieved from NHANES (described in Section 2.1.2), we included 3,158 T2DM studies with a start date between January 2003 and December 2012 for analysis in this study. We used the VITTA system [20] to find frequent quantitative variables in the eligible criteria of all the selected 3,158 T2DM studies. Age, HbA1c and BMI were identified as the most frequently used quantitative variables, appearing in 97.1% (3,066), 48.6% (1,534), and 42.8% (1,351) of the selected T2DM studies, respectively. We also included the categorical variable “gender”, which is a required field in the eligibility criteria section of each trial summary. In this work, we selected age, HbA1c, BMI, and gender for multivariate analysis of population representativeness.

2.1.2. Deriving Target Population Characteristics from NHANES

To ensure statistical power with sufficient patients, we combined NHANES data of five two-year survey cycles between 2003 and 2012. We extracted the interview results of demographic (i.e., age, gender, and ethnicity), medical conditions, body measures (i.e., BMI), as well as lab test results of Glycohemoglobin (HbA1c). After excluding Type 1 diabetes subjects using an existing method [27], we identified 3,082 subjects with T2DM. Out of these 3,082 subjects, 2,695 had no missing values for age, HbA1c, and BMI and were included for further analysis.

Given that the number of subjects with missing data exceeded 10% (387/3082 = 12.6%) of the total number of subjects, we used two categorical variables, gender and ethnicity, to assess the representativeness of these 2,695 subjects for all the 3,082 T2DM subjects. We employed chi-square test to assess the differences between any pair of three sets of samples: (1) all 3,082 subjects, (2) 2,695 subjects without missing values, and (3) 387 (3,082 - 2,695) subjects with some missing values. No statistically significant difference was observed for gender and ethnicity between any pair of samples (all p-value > 0.05). We also used t-test to assess the pairwise difference for age, HbA1c, and BMI among these three samples. No statistical significant differences were observed (all p-value > 0.05). Therefore, we concluded that the 2,695 subjects included for this analysis represented all the identified T2DM subjects in NHANES.

To account for complex survey design (e.g., oversampling of certain ethnic groups), non-response, and post-stratification, each sample in NHANES was assigned a two-year sample weight “WTMEC2YR”, the number of people in the U.S. national population that each sample can represent [28]. According to the analytic guideline of NHANES [29], we normalized the sample weight for each sample in the combined five survey cycles as WTMEC10YR (=1/5 * WTMEC2YR). After taking the normalized sample weight into account, these 2,695 subjects, who can represent 15,575,484 T2DM patients in the U.S. national population in the midpoint of the combined survey years, were used to profile T2DM target population in this study. All our analyses were performed after taking the sample weight into account.

2.2. Multivariate Generalizability Index for Study Traits (mGIST)

To assess the population representativeness of clinical studies, we extend GIST to accommodate multiple variables jointly. The GIST score is the sum of the products of the percentage of patients and the percentage of studies falling into each value interval across all the intervals of a single trait (e.g., age: (20, 21], (21, 22], ...) (“[]” refers to being inclusive, while “()” refers to being non-inclusive), whereas the multivariate GIST (mGIST) score is the sum of the products of the percentage of patients and the percentage of studies falling into each value interval combination for multiple study traits (e.g., age: (20, 21], BMI (kg/m²): (15, 16], HbA1c (%): (7, 8], gender: male) across all the combinations.

mGIST represents the percentage of patients in the target population (TP) that would have been eligible for a given set of studies (TS) when all the variables in the variable set (VS) are considered jointly. The formula of the mGIST is as follows,

$$\mathit{mGIST}(TS,TP,VS)={\sum }_{n=1}^{N={\prod }_{c=1}^C{N}_c}\frac{{\sum }_{j=1}^T{\prod }_{c=1}^C{\prod }_{i_c=1}^{N_c}I(i_{c,\mathit{low}}\le w_{j,c}<i_{c,\mathit{high}})}{T}\ast \frac{{\sum }_{k=1}^P{\prod }_{c=1}^C{\prod }_{i_c=1}^{N_c}I(i_{c,\mathit{low}}\le y_{k,c}<i_{c,\mathit{high}})}{P}$$ (1)

where C is the number of study criteria in VS, N_c is the number of distinct intervals within each study variable c, N is the total combination of distinct intervals across all study variables. T is the number of studies in TS, P is the number of patients in TP, w_j,c is the inclusion interval of variable c for the j^th study, such that an indicator I can be defined when the j^th study interval subsumes the i^th interval low and high boundary threshold for study variable c. For example, if a study’s permissible value interval for age is (25, 45], the indicator I for age of this study would be 1 for intervals (25, 26], (26, 27], … (44, 45], but would be 0 for intervals (45, 46], (46, 47], and thereafter. The product of Is will be 1 if and only if the indicators I for all the intervals in a combination are 1. y_k,c is the observed value of the variable c for the k^th patient such that an indicator I can be defined when the k^th patient’s value falls within the i^th interval of study variable c. For simple categorical variables, we construct value intervals with the category values of the variable. It does not yet process sophisticated categorical variables such as those with context information. We provide the algorithms of mGIST below. Algorithm 1 is the main algorithm for computing mGIST score. Algorithm 2 is applied for creating value intervals of the same width for each variable in Algorithm 1.

Algorithm 1.

mGIST

Input: study set T = {t1, t2,…, tN}, patient set P = {p1, p2, …, pM},

variable set V = {v1, v2, …, vL | vi (min, max, increment, category_values, intervals)}

Output: mGIST

Begin

for vi in V do

if vi is a quantitative variable

vi_intervals = create_value_intervals(vi _min, vi_max, vi_increment);

mGIST = 0;

//create all the combinations of value intervals

C = create_combinations (V);

for c in C do // for each combination of value intervals

//percentage of patients falling in a combination c

$\text{Percentage}\_\text{of}\_\text{patients}={\sum }_{i=1}^{M}I(p_i\subset c)/M$;

//percentage of studies considering a combination c

$\text{Percentage}\_\text{of}\_\text{studies}={\sum }_{i=1}^{N}I(t_i\subset c)/N$;

mGIST += Percentage_of_patients * Percentage_of_studies;

return mGIST

End

Algorithm 2.

create_value_intervals

Input: v_min, v_max, v_increment

Output: value_intervals

Begin

value_interval_borders = [];

cur_value = v_min;

while cur_value < v_max do

value_interval_borders.add(cur_value);

cur_value += v_increment;

//create value intervals using the border values

value_intervals = create_intervals (value_interval_borders);

return value_intervals

End

Note that value interval can also be created by sorting all the distinct threshold values of a variable in TS. For example, assume that we want to quantify the population representativeness of two studies with respect to age and BMI. Study A imposes a restriction on age 20–50 and BMI >= 25 kg/m², whereas Study B only imposes a restriction on age >=20. Thus, there are three value intervals for age: 0–20, 20–50, 50-inf. There are two value intervals for BMI: 0–25, 25-inf. Table 1 lists six possible combinations of the distinct value intervals of these two variables, the number of patients in each combination, percentage of studies recruiting patients in each combination, and the observed percentage of patients in each combination. Accordingly, mGIST = 0%*10% + 0%*10% + 50%*20% + 100%*40% + 50%*10% + 50%*10% = 0.60, indicating that 60% of the real-world patients would be represented in these two studies if age and BMI were considered jointly.

Table 1.

Six possible combinations of the distinct value intervals of age and BMI for two hypothetical studies and the observed patients in each combination.

Combinations of value intervals		Number of Patients	Percentage of studies recruiting patients with the characteristics	Percentage of patients eligible for the trials
Age	BMI (kg/m2)
0–20	0–25	10	0%	10%
0–20	25-inf	10	0%	10%
20–50	0–25	20	50% (Study B)	20%
20–50	25-inf	40	100% (Studies A and B)	40%
50-inf	0–25	10	50% (Study B)	10%
50-inf	25-inf	10	50% (Study B)	10%

The formula of mGIST can accommodate different numbers of value intervals for multiple quantitative variables. If a study does not specify a certain allowable value range for either inclusion or exclusion in the eligibility criteria, we consider that it accepts all possible values of that variable for patient selection. For example, the study NCT01741181 specifies the permissible value range for HbA1c (6.0% – 10.0%) and age (21 – 80), but does not specify an allowable range for BMI, so we assume all BMI values are acceptable for this study. As such, variables used by more studies with a narrow permissible value range play a more important role in mGIST than those used by fewer studies with a wide permissible value range. Also, variables in mGIST may be correlated and not have independent additive effects.

2.3. Multivariate Underrepresented Subgroup Identification (MAGIC)

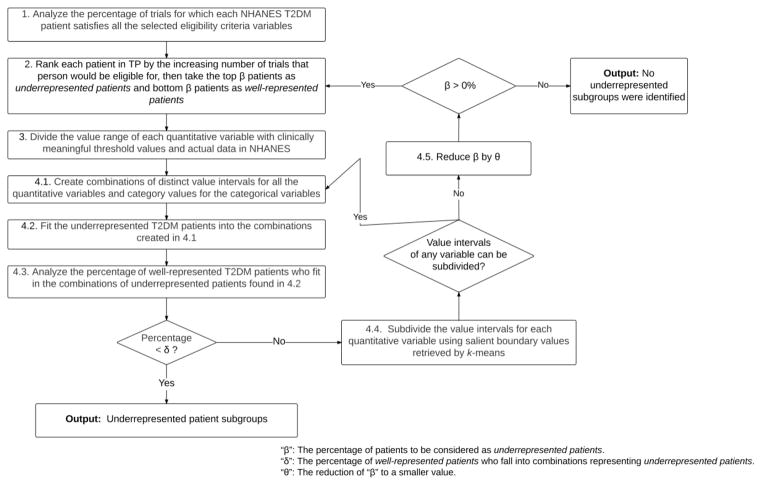
We now focus on identifying and characterizing underrepresented population subgroups in terms of combinations of value intervals of multiple variables in the eligibility criteria. We define the problem of identifying underrepresented population subgroups as follows: given a study set TS, a target population TP, and a variable set VS, the algorithm will return a list of combinations of distinct value intervals of all the variables in VS, each of which characterizes a subgroup of patients in TP that is underrepresented in the study population of studies in TS, i.e., satisfying all the criteria in a small proportion of studies in VS, or in other words, eligible for few studies. We propose an iterative algorithm named “Multivariate Underrepresented Subgroup Identification” (MAGIC), which identifies a set of rules that define subgroups underrepresented in the study population of studies. The algorithm explores combinations of value intervals for each study criterion to create composite rules, which can be evaluated to determine the proportion of patients and the proportion of studies for which the patients would be eligible. MAGIC aims to identify subpopulations that include large groups of the target population but are ineligible for most studies. We define the parameters in MAGIC, illustrate its flowchart in Figure 2, and describe the details of each step.

Figure 2.

Pipeline of Multivariate Underrepresented Subgroup Identification (MAGIC).

Definition of parameters

“β” (0% – 50%): The percentage of patients to be considered as underrepresented patients.

“δ” (0% – 20%): The percentage of well-represented patients who fall into combinations representing underrepresented patients. This parameter is used for evaluating the identified underrepresented subgroups in the current iteration.

“θ” (0% – 10%): The reduction of “β” to a smaller value.

“ω”: The minimum width of value intervals created by k-means clustering.

Step 1

Analyze the percentage of studies for which each patient satisfies the criteria of age, HbA1c, BMI, and gender simultaneously.

Step 2

Identify underrepresented patients and well-represented patients. We rank each patient in TP by the increasing number of studies that person would be eligible for, then take the top β patients as underrepresented patients and bottom β patients as well-represented patients.

Step 3

Divide each quantitative eligibility criterion variable’s value range in NHANES with the threshold values defined based on domain knowledge. For example, the minimum HbA1c value of NHANES subjects is 3.9% and the maximum 18.0%. According to MedlinePlus [30], HbA1c for normal people is less than 5.7%, for pre-diabetic is between 5.7% to 6.4%, and for diabetic is at least 6.5%. Therefore, we divide the value range of HbA1c (%) in NHANES (3.8, 18.0] into four intervals (3.8, 5.7], (5.7, 6.4], (6.4, 18.0]. Similarly, we divide the value range of age in NHANES (12, 85] into (12, 14] (children), (14, 24] (youth), (24, 64] (adults), and (64, 85] (seniors) according to [31]. We divide the value range of BMI (kg/m²) in NHANES (15, 82] into (15, 18.5] (underweight), (18.5, 25] (normal), (25, 30] (overweight), (30, 82] (obese) according to [32]. For the categorical variable "gender" with allowable values "male" and "female", we create value intervals [1,1], [2,2], and [1,2] to represent "male," "female," and "both gender," respectively.

Step 4.1

Create combinations of distinct value intervals for all the quantitative variables and category values for all the categorical variables. We start the iterative process, whose goal is to create the combinations of value intervals, such that bins representing underrepresented patients include as few well-represented patients as possible.

Step 4.2

Fit the underrepresented patients (identified in Step 2) into the combinations created in Step 4.1 and rank the combinations in a descending order of the number of patients.

Step 4.3

Analyze the percentage of well-represented patients (identified in Step 2) who fit in the combinations characterizing underrepresented patients analyzed in Step 4.2. If the percentage value is lower than δ, print out the combinations of underrepresented population subgroups and terminate the algorithm. Otherwise, execute Step 4.4.

Step 4.4

Subdivide the value intervals for quantitative variables, so that fewer well-represented patients are included in each one. In this step, we apply unsupervised discretization method to find boundary values in eligibility criteria and use them to subdivide the value intervals. K-means clustering, which takes the distribution of attribute values into account, is a popular unsupervised discretization method for quantizing one-dimensional continuous variables into non-uniform value intervals [33, 34]. We first retrieve all the occurrences of the boundary values of each quantitative variable in the eligibility criteria of T2DM studies. We apply k-means clustering with k = 2 on all the occurrences of these boundary values in each execution of this step. Note that k-means clustering may generate different clusters each time, we therefore run k-means multiple times until the same clusters are generated three times. We then retrieve four border values of the two clusters, sort them in ascending order, and discard border values that would create new intervals whose width is less than ω. Then we use the remaining border values to divide the current intervals into smaller intervals. If k-means clustering has been executed for the variable in the last iteration of this step, k-means will be executed separately for each cluster generated in the last k-means (divide-and-conquer). If any value intervals can be subdivided by the border values identified by k-means, create new value intervals and go to Step 4.1. Otherwise, go to Step 4.5.

Step 4.5

Reduce β by θ. The rationale is that if fully refined combinations of value intervals cannot represent underrepresented patients selected in Step 2, current β may not be small enough to define underrepresented patients. Therefore, we reduce β to exclude some patients who are eligible for relatively more studies in the current selection of underrepresented patients. As long as β is > 0%, go to Step 2 to identify underrepresented and well-represented patients using the current β value. Otherwise, terminate the algorithm with the note “no underrepresented patient subgroups were identified”. In Section I of the supplementary material, we give a hypothetical example to illustrate the algorithm of MAGIC.

3. RESULTS

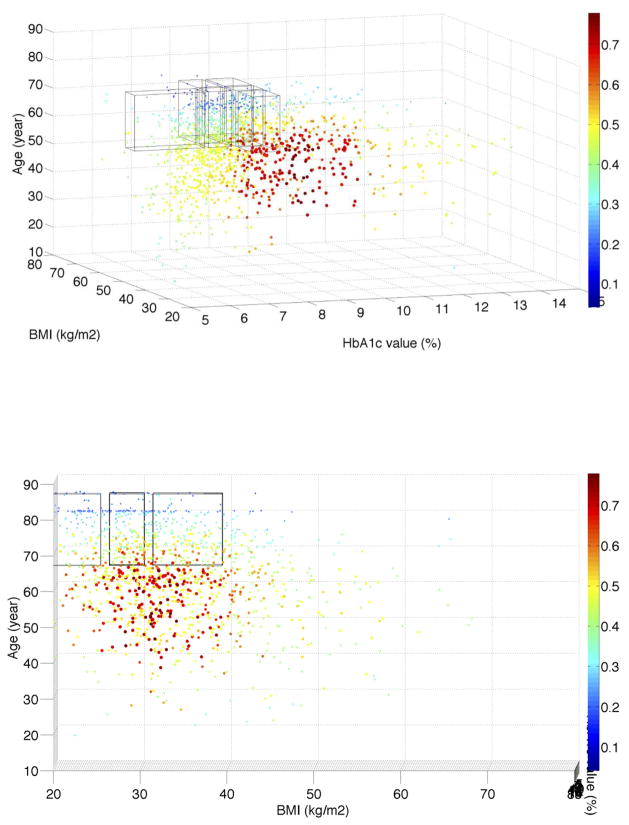
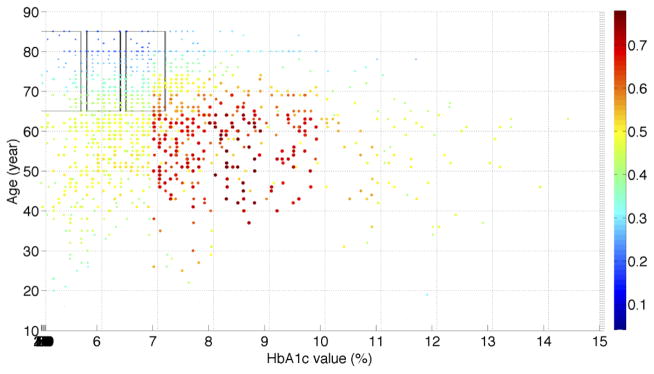
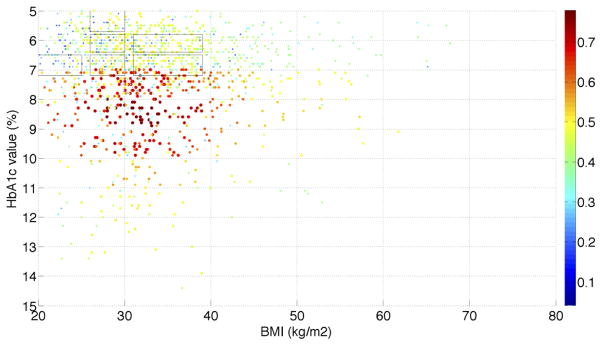
In the recently published paper of He et al. [21], we used the same T2DM patients from the NHANES data to assess the population representativeness of T2DM studies with respect to one variable at a time. We visualized the distributions of a single variable (i.e., age, HbA1c, and BMI) along with their distributions in the NHANES T2DM patients. With the univariate GIST metric, we observed that T2DM studies are the most representative of the population with respect to age, followed by BMI and then HbA1c. Figure S.1 in the supplementary material shows the univariate and bivariate distributions of patients with respect to age, HbA1c, and BMI. We analyzed the distribution of real-world T2DM patients with their eligibility for all the T2DM studies and visualized the distribution in MATLAB. Figure 3 illustrates the percentage of 3,158 T2DM studies for which T2DM patients satisfy the criteria of HbA1c, BMI, age, and gender simultaneously. Since at most three dimensions can be visualized in a figure, Figure 3 only shows the results for female patients. We found that a significant proportion of patients are eligible for fewer than 40% of studies (light blue and dark blue color). The dark blue area resided on the top, indicating that elderly patients (e.g., age > 70) are not eligible for most of the T2DM studies. Patients younger than 60 with HbA1c > 7.0% have better chances to be eligible for existing T2DM studies (red color). The distribution of studies for male patients is almost identical to that for female patients.

Figure 3.

(a) Visualization of the distribution of the real-world T2DM patients with their eligibility for 3,158 T2DM studies with respect to age, HbA1c, BMI, and gender jointly. The x-axis represents HbA1c value intervals. The y-axis represents BMI value intervals. The z-axis represents age value intervals. Each dot represents patients with the same set of characteristics. The size of every dot is proportional to the number of real-world patients (normalized sample weight “WTMEC10YR”) that each dot represents. The color of a dot represents the percentage of studies for which each sample satisfy all the variables, scaled such that red indicates the highest proportion of studies and blue indicates the lowest observed proportion of studies. Regions in blue highlight target populations that are systematically underrepresented across all the studies. The six transparent boxes represent the top six underrepresented female subgroups identified by the MAGIC algorithm; (b) A different orientation of the figure showing age and BMI; (c) A different orientation of the figure showing age and HbA1c; (d) A different orientation of the figure showing BMI and HbA1c. We provide the MATLAB figure file as a supplementary material. One can open the file in MATLAB and change the orientation of the figure and view it from different angles

3.1. mGIST Scores for Different Study Sets

Table 2 shows the mGIST scores of age, HbA1c, BMI, and gender as well as the GIST scores of age, HbA1c, and BMI. In the computation, we discretized the value range of the three quantitative variables (i.e., age, HbA1c, and BMI) into value intervals of size 1. We assumed that studies without any eligibility criterion on a certain variable accept participants with all the values of the variable. For example, if a study does not specify eligibility criteria about HbA1c, we assume this study recruits patients of any HbA1c value. The GIST scores for all three variables for observational studies are consistently higher than those of interventional studies.

Table 2.

GIST scores of age, HbA1c, BMI, gender, as well as mGIST scores of age, HbA1c, BMI, and gender of T2DM study sets that differ in study type, study phase, sponsor type, and start date.

Study characteristic	# of studies	GIST of age	GIST of HbA1c	GIST of BMI	GIST of gender	mGIST score
Study Type	--	--	--	--	--	--
Interventional	2731	0.77	0.70	0.86	0.97	0.43
Randomized	2338	0.77	0.66	0.84	0.97	0.43
Non-randomized	220	0.75	0.77	0.82	0.96	0.45
Observational	423	0.82	0.91	0.91	0.96	0.69
Study Phase	--	--	--	--	--	--
Phase I	374	0.61	0.83	0.81	0.95	0.35
Phase II	525	0.77	0.74	0.89	0.98	0.44
Phase III	779	0.87	0.65	0.87	0.99	0.47
Phase IV	499	0.80	0.64	0.88	0.95	0.43
Sponsor Type	--	--	--	--	--	--
NIH	50	0.63	0.87	0.89	0.94	0.48
Industry	1635	0.82	0.66	0.86	0.99	0.46
Other U.S. federal agency	29	0.82	0.85	0.93	1.00	0.65
Other	1444	0.74	0.80	0.86	0.94	0.48
Start Date	--	--	--	--	--	--
01/2003–12/2004	333	0.79	0.77	0.86	0.98	0.52
01/2005–12/2006	477	0.79	0.77	0.88	0.96	0.51
01/2007–12/2008	743	0.77	0.73	0.86	0.96	0.47
01/2009–12/2010	853	0.77	0.72	0.85	0.97	0.45
01/2011–12/2012	752	0.78	0.69	0.86	0.97	0.44

The GIST score of age increases from Phase I to Phase III, whereas the GIST score of HbA1c decreases from Phase I to Phase III. The mGIST score for all the 3,158 T2DM studies is 0.47. Observational studies have superior population representativeness than interventional studies (0.69 vs. 0.43), which is expected because interventional studies usually have stricter eligibility criteria than observational studies. The mGIST score increases from Phase I to Phase III, which is also to be expected because Phase I and II studies focus on safety and preliminary efficacy and are often conducted on relatively healthier individuals, while Phase III studies focus on efficacy so they try to include a population close to the target. The studies sponsored by other U.S. federal agencies have superior population representativeness than the studies sponsored by NIH, industry, other universities and organizations. In contrast, industry studies have the lowest mGIST score among all the studies, which is also expected because they are known to have relatively poor population representativeness [4]. Between 2003 and 2012, the declining mGIST score, primarily driven by stricter HbA1c limit, indicates that T2DM studies are focusing on a narrower segment of the clinical diabetes population. In order to investigate the reason for the issue of population representativeness, we applied MAGIC to characterize underrepresentation in the form of combinations of value intervals of multiple eligibility criteria variables.

3.2. Underrepresented Population Subgroups in T2DM Trials

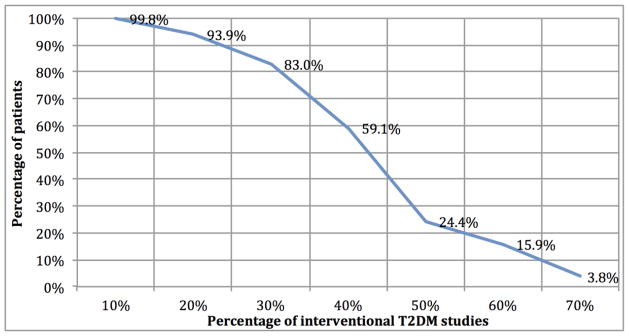
According to the mGIST scores, as expected, interventional studies are less representative and therefore less generalizable than observational studies. We focused on identifying underrepresented population subgroups in the 2,731 interventional T2DM studies (T2DM trials). For each T2DM patient, male or female, in NHANES, we analyzed the percentage of T2DM trials for which s/he satisfies the criteria of age, HbA1c, BMI, and gender simultaneously. Figure 4 shows the percentage of T2DM trials for which the percentage of patients satisfy the criteria. We found that 93.9% of patients would qualify for at least 20% of T2DM studies, but only 24.4% of patients would qualify for at least half of the studies. Only 15.9% of T2DM patients satisfy the criteria in >= 60% T2DM trials. Note that no patient is eligible for more than 80% of the trials, because some trials use restrictive eligibility criteria. For example, 45 T2DM trials between 2003 and 2012 recruited patients < 20 years old.

Figure 4.

Percentage of T2DM patients who satisfy four criteria of interventional T2DM studies.

To illustrate the feasibility and the results of the MAGIC algorithm, we applied it with empirical values of the parameters β = 20%, δ = 1%, θ = 5%, ω = 1/10 * value_range_in_NHANES to identify underrepresented population subgroups in the study set. Table 3 reports on the percentage of well-represented patients included in underrepresented subgroups in each iteration of MAGIC. When β was reduced to 10%, the percentage of well-represented patients included in underrepresented subgroups dropped below δ after value intervals were refined by the second k-means. See Table 4 for the value intervals for age, HbA1c, BMI, and gender for constructing combinations to represent underrepresented patients after the value intervals of numeric variables were refined by k-means twice. Of note divide-and-conquer k-means clustering in MAGIC also retrieved boundary values that were close to those in well-accepted domain knowledge, e.g., 25 kg/m² for BMI (lower limit for overweight), 25 (lower age limit for adults) and 65 (lower age limit for seniors) for age, demonstrating its effectiveness in identifying clinically meaningful boundary values from eligibility criteria. One may set a higher value of “δ” so that the combinations may consist of wider value intervals, or may include more patients deemed to be underrepresented by our algorithm.

Table 3.

The percentage of well-represented patients who are included in underrepresented subgroups in each step of the algorithm (β = 20%, δ = 1%, θ = 5%, ω = 1/10 * value_range_in_NHANES).

Iteration	Domain knowledge (DK)	DK + 1st k-means clustering	DK + 2nd k-means clustering
β
20%	96.0%	38.5%	32.2%
15%	65.4%	12.4%	6.2%
10%	1.5%	1.5%	0%

Table 4.

Value intervals for age, HbA1c, BMI, and gender after value intervals of numeric variables were refined by k-means (k = 2) clustering twice.

Variable	Value intervals
Age	(12, 14], (14, 24], (24, 44], (44, 64], (64, 85]
HbA1c	(3.8, 5.7], (5.7, 6.4], (6.4, 7.2], (7.2, 8.6], (8.6, 9.7], (9.7, 18.0]
BMI	(15, 18.5], (18.5, 25], (25, 30], (30, 39), (39, 60], (60, 82]
Gender	[1, 1], [2, 2]

After its termination, MAGIC identified 50 combinations as underrepresented population subgroups. See Section III of the supplementary material for all the 50 combinations. Table 5 lists the top 10 underrepresented subgroups in descending order of their proportion in underrepresented patients (10% of all the patients who are eligible for <= 22.5% of trials). These 10 subgroups represent 64.3% of all the underrepresented patients determined by MAGIC. We can see that all the top 10 underrepresented population subgroups include elderly (> 64 years old) patients with relatively low HbA1c (less than 7.2%) and a wide range of BMI (18.5 kg/m²–39 kg/m²). This finding is consistent with our population representativeness analysis using one variable at a time [17, 21]. Compared with underrepresented subgroups, the well-represented patients (eligible for >= 66.4% of trials) are younger (age between 44 and 64) and have higher HbA1c (> 7.2%).

Table 5.

The top 10 underrepresented subgroups of T2DM patients. Underrepresented patients were identified by MAGIC as those who satisfy eligibility criteria of age, BMI, HbA1c, and gender simultaneously in <= 22.5% T2DM trials.

Underrepresented Subgroups				Characteristics of subgroups	Percentage of patients in all the underrepresented patients
Age	HbA1c (%)	BMI (kg/m2)	Gender
(64, 85]	(5.7, 6.4]	(30, 39]	Female	Elderly obese pre-diabetic female	8.6%
(64, 85]	(5.7, 6.4]	(25, 30]	Female	Elderly overweight pre-diabetic female	8.3%
(64, 85]	(5.7, 6.4]	(25, 30]	Male	Elderly overweight pre-diabetic male	8.1%
(64, 85]	(6.4, 7.2]	(18.5, 25]	Female	Elderly normal weight diabetic female	6.5%
(64, 85]	(6.4, 7.2]	(30, 39]	Female	Elderly obese diabetic female	6.3%
(64, 85]	(6.4, 7.2]	(25, 30]	Male	Elderly overweight diabetic male	6.1%
(64, 85]	(5.7, 6.4]	(18.5, 25]	Male	Elderly normal weight pre-diabetic male	5.9%
(64, 85]	(3.8, 5.7]	(25, 30]	Female	Elderly overweight female with normal HbA1c	5.2%
(64, 85]	(6.4, 7.2]	(25, 30]	Female	Elderly overweight diabetic female	4.8%
(64, 85]	(6.4, 7.2]	(30, 39]	Male	Elderly obese diabetic male	4.6%

4. DISCUSSION

Many clinical studies are scientifically justified not to represent the real-world population broadly. The research presented in this paper does not aim to maximize the generalizability for clinical studies. Instead, it aims to improve the transparency of a priori generalizability of related clinical studies using a quantitative metric that considers multiple study traits. In this paper, we contribute a measure “mGIST” for quantifying population representativeness using multiple study traits as well as a method called MAGIC to identify underrepresented target population. Compared with the original GIST, mGIST is more effective and efficient in comparing the population representativeness of multiple study sets, i.e., if m variables and n study sets are considered, m*n GIST scores are needed while only n mGIST scores are needed. Yet, GIST can reveal the problem of population representativeness of a study set with respect to a specific variable. When determining permissible value intervals of a variable in the eligibility criteria, one can assess the global population representativeness using mGIST as well as the variable–specific population representativeness using GIST.

Using MAGIC, we were able to identify that it was elderly T2DM patients (> 64 years old) with HbA1c <= 7.2% who are underrepresented in T2DM trials. The under-representativeness of elderly patients was also reported for RCTs concerning other diseases such as cardiovascular diseases [35], cancer [36, 37], and Type 2 diabetes [38]. Relaxing the age limit in the eligibility criteria alone may not improve the representativeness of elderly due to other exclusion criteria [39]. Beers et al. [40] reported that older patients were underrepresented in Phase II and III trials of medical conditions characteristically associated with aging, partly because of age-sensitive exclusion criteria that are often not well justified.

We believe that our multivariate analysis method consisting of mGIST and MAGIC lays a foundation for improving the transparency of a priori generalizability in a scalable fashion. As demonstrated in the Results Section, mGIST can efficiently quantify the population representativeness of related studies, while MAGIC provides an automated and robust way to define and characterize underrepresented patients. MAGIC would be more informative than simply reporting whether or not the population median is present in the median inclusion intervals of each covariate, if normalized joint distributions were multi-modal in any of the covariates and the median inclusion interval only captured one of the peaks². In this framework, the variable set can include continuous variables (e.g., HbA1c, BMI, and age) and categorical variables (e.g., gender). This framework, which can be applied to studies on any condition with a representative sample of real-world patients, is significant in advancing data-driven clinical trial design by enabling future users of clinical evidence to have precise understanding of population subgroups that are systematically under-studied. The fact that the results generated by our method are consistent with the findings reported in literature proves the feasibility and effectiveness of developing computational methods for assessing population representativeness at scale and with efficiency.

4.1. Preliminary Evaluation of MAGIC

Previously, researchers have proposed methods for subgroup discovery aimed at finding patterns of subgroups with interesting properties in the data. Friedman and Fisher introduced the Patient Rule Induction Method (PRIM) [41], a technique from data mining for finding modal regions in datasets of continuous variables. Nannings et al. [42] later applied PRIM for selecting high-risk subgroups in elderly ICU patients. Breiman et al. [43] introduced Classification and Regression Trees (CART) for subgroup discovery. Tree-based methods, typically designed for classifying observations when the number of classes is fixed or known in advance, are expected to perform worse than PRIM for our problem as the number of subgroups is unknown. In this work, we performed a preliminary evaluation of MAGIC using PRIM as a baseline. We used the following two metrics to compare the accuracy of underrepresented patient subgroups discovered by MAGIC and PRIM:

1. The percentage of well-represented patients (patients eligible for >= 66.4% of T2DM trials) who can be characterized by the underrepresented subgroups discovered;

2. The percentage of neither well-represented nor underrepresented patients (patients eligible for > 22.5% and < 66.4% of T2DM trials) who can be characterized by the underrepresented subgroups discovered.

Lower percentages of metric (a) and (b) indicate more accurate characterization of underrepresented patients. In this preliminary evaluation, we used an R package of PRIM [44] with default parameters (peel.alpha = 0.05, paste.alpha = 0.01) and identified six underrepresented subgroups. Table 6 shows the six underrepresented subgroups identified by PRIM. Table 7 shows the results of the evaluation of MAGIC using PRIM as the baseline. As shown in the table, the accuracy of underrepresented subgroups identified by MAGIC is higher than those identified by PRIM (metric (a): 0% vs. 30.4%; metric (b): 31.2% vs. 58.7%) in this experiment. Note that the parameters of MAGIC are used for controlling the flow of the iterative algorithm while the parameters of PRIM are used for its pasting and peeling process. Thus, these native parameters of PRIM and those of MAGIC are not comparable. PRIM has limited capacity for characterizing underrepresented population subgroups with multiple variables, possibly because: (1) PRIM is not exhaustive in its search for subgroups; (2) PRIM will fail or perform poorly when variables are highly correlated [41]. Nevertheless, future work is warranted to evaluate the MAGIC algorithm for other medical conditions with other patient data. The results of this evaluation suggested that MAGIC is comparable to PRIM in identifying and characterizing underrepresented population subgroups in related studies.

Table 6.

Underrepresented population subgroups identified by PRIM with default parameters (peel.alpha = 0.05, paste.alpha = 0.01).

HbA1c (%)	BMI (kg/m2)	Age	Gender	Characteristics of Subgroups
[2.5, 19.4]	[45.0, 87.8]	[5.8, 92.2]	[0.9, 2.1]	Obese male and female
[2.5, 19.4]	[40.7, 44.8]	[5.8, 92.2]	[0.9, 2.1]	Obese male and female
[2.5, 8.0]	[38.1, 40.6]	[5.8, 92.2]	[0.9, 2.1]	Obese male and female with normal to diabetic HbA1c
[2.5, 6.9]	[9.3, 28.7]	[67.0, 92.2]	[0.9, 2.1]	Elderly male and female with normal to pre-diabetic HbA1c
[2.5, 19.4]	[34.7, 36.6]	[5.8, 92.2]	[0.9, 2.1]	Obese male and female
[2.5, 19.4]	[25.8, 33.5]	[60.0, 92.2]	[0.9, 2.1]	Elderly overweight male and female

Table 7.

Results of the preliminary evaluation of MAGIC using PRIM as the baseline.

Metric	(a)	(b)
Method
PRIM	30.4%	58.7%
MAGIC	0%	31.2%

4.2. Limitations and Future Work

Some limitations should be noted for this study.

Our method for assessing multivariate population representativeness has the following major limitations. First, all study traits were considered independently and the dependency among them was not accounted for. However, eligibility criteria variables have inherent dependency or correlations. For example, impaired fasting glucose is correlated with age [45]. Second, every trait was equally weighted, i.e. all traits were assumed to be of equal relevance. This is contrary to the clinical setting, where some traits may be more relevant than others. Consideration of the relevance of individual traits is currently lacking but should be accounted in the future. Third, it does not yet process sophisticated categorical variables such as those with contextual information. We only processed simple categorical variables such as gender. Moreover, MAGIC may yield a large number of subgroups when the number of variables and value intervals is large. Future work is needed to further aggregate the subgroups when necessary. In Step 3 of MAGIC, we used clinically relevant values to discretize the value range of a variable. The obstacles to this step include the acquisition and availability of domain knowledge. As the clinically relevant threshold values for some variables may be controversial or even unavailable, one may only identify important boundary values in clinical trial eligibility criteria to divide the value range or may create equal-sized intervals. Besides divide-and-conquer k-means clustering, future research is needed to test other methods for identifying important threshold values of a quantitative eligibility criterion. When only categorical variables are included in the analysis, one may skip the part of iterative optimization of value intervals of quantitative variables in the algorithm and optimize upon the percentage of patients being considered as underrepresented patients. Another limitation is the choice of empirical values of parameters (i.e., β, δ, θ, ω) in MAGIC. Overly restrictive parameters may lead to over-fitting [46] (i.e., when a model describes the features that arise from noise or variance in the data) and thus limit the capability of MAGIC for identifying underrepresented patient subgroups. Future methodological research opportunities also include automating the selection of parameters and evaluating other algorithms for subgroup identification.

A study design limitation is that NHANES uses self-reported medical condition that may not have been confirmed by laboratory tests; thus, there might be subjects that should not be included in our analysis. We used the method employed by Dodd et al. [27] to distinguish between Type 2 diabetes and Type 1 diabetes patients. There might be some misclassified samples using this method. Sample weights, which are post hoc adjustments based solely on demographic and socioeconomic characteristics of U.S. national Census, may not be sufficient to account for value difference between respondents and non-respondents of NHANES [47]. While the results are specific to NHANES, the approach is applicable to any real-world evidence source. Analyses could be performed using other observational data, e.g., patient registries, administrative claims, and electronic health records, to determine how clinical studies generalize to other populations of interest.

Another limitation is that we only used frequently used eligibility variables in this work. In the future, we plan to extend the method to ethnicity and fine-grained qualitative eligibility features. Additionally, location is an important factor for patient recruitment. In order to take the location of trial participants into account, we can extract study locations in ClinicalTrials.gov and combine them with geocoded census data. These will improve the accuracy of the representativeness assessment.

We believe it would be valuable to apply this method to a broader set of eligibility criteria and across multiple disease areas to evaluate a priori generalizability of clinical studies to the real-world populations. Beyond studying population representativeness across collections of studies, we also believe applying the method to individual studies will be valuable in supporting study design and results interpretation.

5. CONCLUSIONS

We contribute two data-driven computational methods, mGIST and MAGIC, for assessing the population representativeness for related clinical studies. We demonstrated how this framework may facilitate data-driven improvement of clinical trial design towards optimized generalizability. This methodology framework paves the way for transparent and population-representative clinical research design as well as more precise evidence-based medicine.

Highlights.

• We extend GIST for quantifying population representativeness of related studies

• We contribute a method for iteratively characterizing underrepresented patients

• We demonstrated the value of this method using Type 2 diabetes mellitus studies

• Our study confirms knowledge in literature and can generalize to other diseases