Biexponential Longitudinal Relaxation in White Matter: Characterization and Impact on T₁ Mapping with IR-FSE and MP2RAGE

Abstract

Purpose

Magnetization transfer in white matter (WM) causes biexponential relaxation, but most quantitative T₁ measurements fit data assuming monoexponential relaxation. The resulting monoexponential T₁ estimate varies based on scan parameters and represents a source of variation between studies, especially at high fields. In this study, we characterized WM T₁ relaxation and performed simulations to determine how to minimize this deviation.

Methods

To characterize biexponential relaxation, four volunteers were scanned at 3T and 7T using inversion recovery fast spin echo (IR-FSE) with 13 inversion times (TIs). Three volunteers were scanned with IR-FSE using TIs chosen by simulations to reduce T₁ deviation, and with MP2RAGE.

Results

At 3T, the biexponential relaxation has a short component of T₁ = 48 ms (9%) and a long component of T₁ = 939 ms. At 7T the short component is T₁ = 57 ms (11%) and the long component is 1349 ms (89%). For IR-FSE, acquiring four TIs with a minimum of 150 ms (3T) or 200 ms (7T) yielded monoexponential T₁ estimates that match the long component to within 10 ms. For MP2RAGE, significant differences (90 ms at 3T, 125 ms at 7T) remain at all parameter values.

Conclusion

Many T₁ mapping sequences yield robust estimates of the long T₁ component with suitable choice of TIs, allowing reproducible, sequence-independent T₁ values to be measured. However, this is not true of MP2RAGE in its current implementation.

INTRODUCTION

The primary goal of quantitative MRI is to obtain accurate, spatially resolved maps of tissue parameters and to relate these quantities to changes associated with disease. For such measurements to be reproducible and comparable across sites, platforms, and sequences, they must be independent of all contributions to the MRI signal aside from the parameter of interest. For example, a map of the longitudinal relaxation time T₁ must not be influenced by other relaxation effects (eg, T₂, T₂*), diffusion, or inhomogeneity in the B₀ and B₁ fields. It should also be independent of the specific scan parameters used during acquisition. Removing such influences is critical to enabling quantitative MRI for basic research and clinical applications.

In this study, we consider the application of T₁ mapping in the white matter (WM) of human brain, which may aid in the identification of pathologies caused by multiple sclerosis (1,2), Alzheimer disease (3), and other neurological diseases. A key prerequisite for the detection of diseased tissue is the accurate characterization of healthy, normal tissue. In the case of WM, however, there is no strong consensus in the literature about what constitutes a “baseline” healthy control T₁ value. For example, Table 1 lists a number of reported WM T₁ values at 7T. Significant variation is evident; a majority of values cluster around 1100–1200 ms, but some are much longer [eg, (4,12)], and one is much shorter (7).

Table 1.

Reported Measurements of T₁ in WM at 7T

Study	Reported WM T1 (ms)	Region	Sequence and Parameters
Li and Deoni (4)	1500 ± 100	Not stated	DESPOT1, flip angle = 5°/10°/20°
Rooney et al. (5)	1220 ± 36	Frontal	Look-Locker, 32 TIs, 20 ms to 10 s
Ikonomidou et al. (6)	1357 ± 22	Not stated	IR-EPI, TIs 30–8000 ms
Wright et al. (7)	1017 ± 86	Cortical	IR-FSE, 9 TIs, 120–2000 ms
Wright et al. (8)a	~1250?	Cortical	IR-EPI, 9 TIs, 120–4000 ms
Wright et al. (8)	1130 +/100	Cortical	MPRAGE, 8 TIs, 160–2100 ms
Grinstead and Rooney (9)	1180 ± 40	Not stated	IR-EPI, TI values not reported
Marques et al. (10)	1150 ± 60	Frontal	MP2RAGE, TI = 1000/3300 ms
Marques et al. (10)	1110 ± 60	Corpus callosum	MP2RAGE, TI = 1000/3300 ms
Dortch et al. (11)	1372	Global mean	Selective IR qMT, 15 TIs, 6 ms to 2s
Dieringer et al. (12)	1284 ± 22	Global mean	IR-FSE, 8 TIs, 60–5000 ms
Dieringer et al. (12)	1855 ± 141	Global mean	2D VFA, flip angle = 3°/8°/25°

Abbreviations: DESPOT1, driven equilibrium single point observation of T₁; IR-EPI, inversion recovery echo planar imaging; IR-FSE, inversion recovery fast spin echo; MPRAGE, magnetization prepared rapid acquisition of gradient echo; MP2RAGE, magnetization prepared 2 rapid acquisition gradient echoes; qMT, quantitative magnetization transfer; VFA, variable flip angle.

^aThe measurement using IR-EPI is not reported in the text but is inferred from Figure 5 in Wright et al. 2008.

Some of this variation is sequence-based. Stikov et al. (13) have shown that, at 3T, sequences based on variable flip angle acquisition such as DESPOT1 (4,14) tend to overestimate T₁ values compared with inversion recovery fast spin echo (IR-FSE) methods, whereas sequences based on the Look–Locker acquisition method (15) tend to underestimate T₁. It can be assumed that such deviations will only be larger at 7T, because one of their main causes is error in B₁ estimation (13), and that B₁ variations will begin to impact IR-FSE as well. Individual variation and changes due to aging or anatomical location (eg, frontal versus callosal WM) are also expected (16). Nevertheless, large differences in reported T₁ values obtained with similar sequences [eg, (6,9) or (8,12)] are concerning from the viewpoint of quantitative MRI and indicate that some variation in the T₁ measurement is not yet fully understood or accounted for.

We hypothesized that biexponential relaxation is a major source of variation in T₁ measurements in WM. Such biexponential relaxation is established in the literature, primarily in applications involving magnetization transfer (MT), but its impact on quantitative T₁ imaging has remained largely unexplored. We first quantified the relaxation time and signal fraction of the biexponential components in WM at both 3T and 7T using a 13-point IR-FSE series. However, because collecting sufficient data to allow such characterization is impractical for clinical applications, we sought methods to quickly and accurately estimate the long T₁ component, with minimal influence from the short component. We demonstrate that, for sequences that acquire multiple inversion times (TIs) to fit with a monoexponential model, the apparent T₁ value is shorter than the long T₁ component by an amount that depends mainly on the minimum TI, and this difference can be minimized by selecting an appropriate set of TIs. The resulting measurement of the long T₁ value should be consistent across sites and methods, and independent of scan parameters. However, the effect of the short T₁ component on other T₁ mapping methods such as MP2RAGE (10) cannot be mitigated as easily and will remain an important source of variation in such measurements.

THEORY

Biexponential T₁ Relaxation

The presence of biexponential T₁ relaxation in tissues such as muscle (17), cartilage (18), gray matter, and WM (19) has been acknowledged for some time. Although early studies of human WM at 1.5T (20) found that this biexponential T₁ relaxation did not contribute significantly to signal evolution, it is more easily detected and quantified at higher field strengths. Prantner et al. (21) tested several hypotheses that could explain the biexponential T₁ behavior observed in rat brains at 4.7T and 11.7T. These mechanisms included sequence or scanner artifact, blood flow, and multiple exchanging or nonexchanging compartments. It was concluded that MT between exchanging spin populations was the most likely mechanism for this biexponential behavior.

This is consistent with MT models such as that outlined by Dortch et al. (19), based on earlier work (22–24). The two spin populations in these models are often assumed to be hydrogen protons associated with free water and macromolecules, respectively, with rates of exchange k_fm and k_mf between pools. The evolution of the longitudinal magnetization following a radiofrequency (RF) pulse can be modeled with coupled Bloch equations:

$$\begin{array}{c}{\text{dM}}_{\mathrm{f}}/\text{dt}=-({\mathrm{M}}_{\mathrm{f}}-1)\times {\mathrm{R}}_{1\mathrm{f}}-{\mathrm{k}}_{\text{fm}}({\mathrm{M}}_{\mathrm{f}}-{\mathrm{M}}_{\mathrm{m}})\\ {\text{dM}}_{\mathrm{m}}/\text{dt}=-({\mathrm{M}}_{\mathrm{m}}-1)\times {\mathrm{R}}_{1\mathrm{m}}-{\mathrm{k}}_{\text{mf}}({\mathrm{M}}_{\mathrm{m}}-{\mathrm{M}}_{\mathrm{f}}).\end{array}$$ [1]

Here, M_f and M_m are the time-varying longitudinal magnetizations of the pools, normalized to their values at thermal equilibrium, and R₁ = 1/T₁. The solution of these equations (19) for the longitudinal magnetization M(t) of the visible protons (also normalized to its equilibrium value) now contains two relaxation rates, one with short T₁ (T_1S = 1/R_1S), the other with long T₁ (T_1L = 1/R_1L):

$$\mathrm{M}(\mathrm{t})=1+{\mathrm{b}}_{\mathrm{S}}\text{exp}(-\mathrm{t}\times {\mathrm{R}}_{1\mathrm{S}})+{\mathrm{b}}_{\mathrm{L}}\text{exp}(-\mathrm{t}\times {\mathrm{R}}_{1\mathrm{L}}),$$ [2]

where

$$\begin{array}{c}2{\mathrm{R}}_{1\mathrm{S}}={\mathrm{R}}_{1\mathrm{f}}+{\mathrm{R}}_{1\mathrm{m}}+{\mathrm{k}}_{\text{fm}}+{\mathrm{k}}_{\text{mf}}+\surd {({\mathrm{R}}_{1\mathrm{f}}-{\mathrm{R}}_{1\mathrm{m}}+{\mathrm{k}}_{\text{fm}}-{\mathrm{k}}_{\text{mf}})}^2+4{\mathrm{k}}_{\text{fm}}{\mathrm{k}}_{\text{mf}})\\ 2{\mathrm{R}}_{1\mathrm{L}}={\mathrm{R}}_{1\mathrm{f}}+{\mathrm{R}}_{1\mathrm{m}}+{\mathrm{k}}_{\text{fm}}+{\mathrm{k}}_{\text{mf}}+\surd ({({\mathrm{R}}_{1\mathrm{f}}-{\mathrm{R}}_{1\mathrm{m}}+{\mathrm{k}}_{\text{fm}}-{\mathrm{k}}_{\text{mf}})}^2+4{\mathrm{k}}_{\text{fm}}{\mathrm{k}}_{\text{mf}})\end{array}$$

and

$$\begin{array}{c}{\mathrm{b}}_{\mathrm{S}}=(({\mathrm{M}}_{\mathrm{f}}(0)-1)\times ({\mathrm{R}}_{1\mathrm{f}}-{\mathrm{R}}_{1\mathrm{L}})+({\mathrm{M}}_{\mathrm{f}}(0)-{\mathrm{M}}_{\mathrm{m}}(0))\times {\mathrm{k}}_{\text{fm}})/({\mathrm{R}}_{1\mathrm{S}}-{\mathrm{R}}_{1\mathrm{L}})\\ {\mathrm{b}}_{\mathrm{L}}=-(({\mathrm{M}}_{\mathrm{f}}(0)-1)\times ({\mathrm{R}}_{1\mathrm{f}}-{\mathrm{R}}_{1\mathrm{S}})+({\mathrm{M}}_{\mathrm{f}}(0)-{\mathrm{M}}_{\mathrm{m}}(0))\times {\mathrm{k}}_{\text{fm}})/({\mathrm{R}}_{1\mathrm{S}}-{\mathrm{R}}_{1\mathrm{L}}).\end{array}$$

For most common experimental parameters (ie, an RF pulse that fully or almost fully inverts the free pool), both coefficients b_S,L are negative and the normalized magnetization M(t) starts from a negative value and relaxes toward 1. For clarity when discussing the relative contributions of the two biexponential components, we may also refer to normalized weights w_S,L = b_S,L/(b_S + b_L).

The observed biexponential relaxation times T_1L and T_1S represent a mixture of the relaxation times of the underlying pools (T_1f and T_1m), as well as the exchange constants k_mf and k_fm. Reported values for these relaxation times in WM (11,19) indicate that the pools are in an intermediate exchange regime. The long component T_1L is weighted more heavily by T_1f and T_1m but also contains some contribution from exchange effects. In contrast, the short component T_1S is dominated by exchange effects, and in the intermediate exchange regime it is significantly shorter than T_1L while remaining observable with achievable TIs. As an example of typical values, Dortch et al. (11) found T_1L = 1370 ms (R_1L = 0.73 s⁻¹) at 7T. Based on their assumption R_1f = R_1m and their reported values of the pool size ratio (PSR = 17.6%) and exchange constants (k_mf = 14.5 s⁻¹, k_fm = PSR*k_mf = 2.55 s⁻¹), the short relaxation time they observed must have been T_1S ≈ 60 ms. The relative weights of the components w_S,L are also not identical to the population fractions of the two pools; for example, they are influenced by M_f(0) and M_m(0), the magnetizations of each pool immediately after the inversion pulse. Using the same assumptions as reported in Dortch et al. (11), we can infer an observed w_S = 0.09 and w_L = 0.91 such that w_S/w_L ≠ PSR.

Biexponential Relaxation and IR-FSE

Although the effects of exchange have been considered in the context of quantitative MT (qMT) sequences and others such as spoiled gradient echo imaging (25), this exchange model applies to even the common gold standard sequences for T₁ mapping, inversion recovery spin echo (IR-SE), or IR-FSE, and according to Equation [1], the T₁ relaxation observed by these sequences should be biexponential. However, this biexponential relaxation is typically neglected, and IR-FSE data are processed and analyzed assuming monoexponential recovery. This yields an apparent T₁, which we refer to as T₁*. For the simple case of a three-parameter fit to three acquired TIs (TI₁, TI₂, TI₃), and given certain assumptions about the values of T_1S and T_1L compared with these TIs (see Appendix), T₁* can be approximated as

$${\mathrm{T}}_1^{\ast }={\mathrm{T}}_{1\mathrm{L}}-[{{\mathrm{T}}_{1\mathrm{L}}}^2/({\text{TI}}_2-{\text{TI}}_1)]\times {\mathrm{b}}_{\mathrm{S}}/{\mathrm{b}}_{\mathrm{L}}\times [exp(-{\text{TI}}_1/{\mathrm{T}}_{1\mathrm{S}})/exp(-{\text{TI}}_1/{\mathrm{T}}_{1\mathrm{L}})]$$ [3]

T₁* will therefore be shorter than the long T₁ component by an amount that depends on T_1L, T_1S, the coefficients b_S and b_L, and the TIs at which the signal is sampled. Because the deviation from T_1L increases as T_1L², and the T_1L of most tissues increases with field strength, the absolute magnitude of the error term will also increase with field strength. The dependence of T₁* on the TIs can be reduced by choosing TI₁ ≫ T_1S. In that case, to good approximation, T₁* = T_1L and it becomes valid to use a monoexponential model such as

$${\mathrm{M}}_{\mathrm{z}}(\text{TI})={\mathrm{c}}_1+{\mathrm{c}}_{2}exp(-\text{TI}/{\mathrm{T}}_1^{\ast }).$$ [4]

As an alternative interpretation, once TI₁ ≫ T_1S, the short component no longer contributes to signal change during the acquisition and can be modeled as a constant that is subsumed into c₁ in Equation 4. Note that the magnetization of the exchanging pool that gives rise to T_1S is not necessarily fully relaxed after time TI₁, but because this pool’s signal is not observed directly, the single exponential model is still valid.

However, this choice of TI₁ is in opposition to the heuristic (26,27) of selecting the first TI to be as short as possible, which maximizes the dynamic range of the sampled signal intensity and improves the precision of the measurement. Reducing the difference between T₁* and T_1L will necessarily involve increasing the variance in the resulting measurement. For this reason, it is important to have accurate knowledge of T_1S values in WM, such that parameters can be chosen to balance gains in accuracy with loss of precision.

Biexponential Relaxation and MP2RAGE

An emerging method for fast three-dimensional (3D) T₁ mapping is MP2RAGE (10,28,29), which offers inherent robustness against M₀, T₂*, and most B₁ effects, making it a particularly promising candidate for high-field quantitative imaging. MP2RAGE acquires two images following a single inversion pulse, and instead of fitting a model to the acquired data, uses a lookup table computed from the signal equations to convert the intensity of a composite image into a T₁ value. This composite image is obtained from the acquired (complex) images using

$${\mathrm{S}}_{\text{MP}2}=\mathrm{S}({\text{TI}}_1)\times \mathrm{S}({\text{TI}}_2)/(\mathrm{S}{({\text{TI}}_1)}^2+\mathrm{S}{({\text{TI}}_2)}^2).$$ [5]

The image intensities S(TI₁) and S(TI₂) have a complicated dependence on T₁, α, repetition time (TR), and other parameters that can be computed based on the Bloch equations (10). This makes MP2RAGE sensitive to the choice of parameters but also allows T₁ map quality to be optimized for a desired range of T₁ values while minimizing B₁ sensitivity (29).

The MP2RAGE signal equations assume a single spin pool and monoexponential T₁ recovery. Including a second exchanging spin pool further complicates the signal equations and makes straightforward estimation of T₁ far more challenging. To conceptually explore the general mechanism by which biexponential relaxation impacts the estimated T₁ in MP2RAGE, consider an MP2RAGE signal consisting of independent (nonexchanging) contributions from long and short T₁ components:

$$\mathrm{S}({\text{TI}}_{\mathrm{n}})={\mathrm{b}}_{\mathrm{L}}\times \mathrm{S}({\text{TI}}_{\mathrm{n}},{\mathrm{T}}_{1\mathrm{L}})+{\mathrm{b}}_{\mathrm{S}}\times \mathrm{S}({\text{TI}}_{\mathrm{n}},{\mathrm{T}}_{1\mathrm{S}}).$$ [6]

This simplification assumes that the RF pulse train does not significantly modify the apparent relaxation due to exchange (ie, that T_1S,L and b_S,L have the same values as they would under free relaxation). In practice, exchange effects are likely to produce further deviations from this simplified behavior. However, even in this simple case of unperturbed relaxation during the RF pulse train, it can be shown that MP2RAGE will still yield an underestimation of T₁. If both TIs are long enough to ensure complete relaxation of the short component, but not long enough to allow full relaxation of the long component, then

$$\mathrm{S}({\text{TI}}_{\mathrm{n}})={\mathrm{b}}_{\mathrm{L}}\times \mathrm{S}({\text{TI}}_{\mathrm{n}},{\mathrm{T}}_{1\mathrm{L}})+{\mathrm{b}}_{\mathrm{S}}.$$ [7]

As with the IR-FSE case, the signal is that observed in the absence of any biexponential relaxation, plus a constant value to which the short T₁ component has relaxed. The expression for the MP2RAGE signal becomes

$${\mathrm{S}}_{\text{MP}2}=(\mathrm{S}({\text{TI}}_1)+{\mathrm{b}}_{\mathrm{S}})\times (\mathrm{S}({\text{TI}}_2)+{\mathrm{b}}_{\mathrm{S}})/({(\mathrm{S}({\text{TI}}_1)+{\mathrm{b}}_{\mathrm{S}})}^2+{(\mathrm{S}({\text{TI}}_2)+{\mathrm{b}}_{\mathrm{S}})}^2).$$ [8]

The constant but unknown contribution of the short T₁ component’s coefficient will not cancel from this expression, and though it may represent only a fraction of the desired signal, it can introduce significant errors into the computation of T₁. This can also be simulated once the biexponential relaxation has been characterized.

METHODS

Experiments

To better characterize relaxation behavior in WM, data were acquired from four healthy volunteers (male, n = 3; female, n = 1; mean age, 31 ± 1 y) at 7T and from four healthy volunteers (male, n = 2; female, n = 2; mean age, 30 ± 2 y) at 3T. Three of the volunteers were scanned at both field strengths. All scans were conducted after obtaining informed consent compliant with our institutional review board. 7T images were acquired on a GE Discovery MR950 scanner (GE Healthcare, Waukesha, Wisconsin, USA) using a 32-channel transmit/receive head coil (Nova Medical, Wilmington, Massachusetts, USA). 3T data were acquired on a GE MR750 (GE Healthcare) scanner with an eight-channel receive-only head coil (InVivo, Gainesville, Florida, USA).

In each volunteer, a series of 13 IR-FSE images was acquired with TI = 10, 20, 35, 55, 85, 125, 200, 350, 600, 1000, 1600, 2500, and 4000 ms. Each image was of a single 1.5-mm-thick axial slice centered on the thalamus and basal ganglia acquired using the following parameters: matrix = 128 × 128; field of view = 19.2 cm; echo train length = 8; TR = 6000 ms; bandwidth = 25 kHz. The inversion was performed with an adiabatic hyperbolic secant (HSn) pulse (30) using the following parameters: pulse width = 16 ms; bandwidth = 990 Hz; HSn = 1.0; β = 2.66; adiabatic threshold = 8.45 μT; peak B₁ = 14.1 μT (the same parameters were used at both field strengths). Echoes were collected in centric order to maximize T₁ contrast and reduce T₂ contrast. Acquisition time for each 2D image was 1:42 for a total of 22 min.

In three additional volunteers at 7T (male, n = 1; female, n = 2; mean age, 32 ± 2 y), a four-point IR-FSE time series (single 1-mm-thick slice; matrix = 192 × 192; TI = 200, 600, 1500, 4000 ms; TR = 6000 ms; scan time = 2:30 per image) was collected to compare with an MP2RAGE volume centered on the same slice. The MP2RAGE parameters [based on Marques et al. (10) but adjusted to improve robustness to flip angle errors] were as follows: MP2RAGETR = 7500 ms; TR = 7.4 ms; TI₁/TI₂ = 1000/3300 ms; α₁/α₂ = 5°/4°. A 180 × 180 × 180 matrix was collected at 1-mm isotropic resolution using a centrically ordered phase encoding scheme (31) that decouples the number of slices from the number of acquired phase encode lines per inversion, which was 200. The hyperbolic secant adiabatic inversion pulse was 16 ms, bandwidth of 913 Hz, HSn = 1.0, β = 4.5, adiabatic threshold = 8.35 μT, and peak B₁ = 20.9 μT. The scan time was 10 min with 2× acceleration via parallel imaging.

Analysis

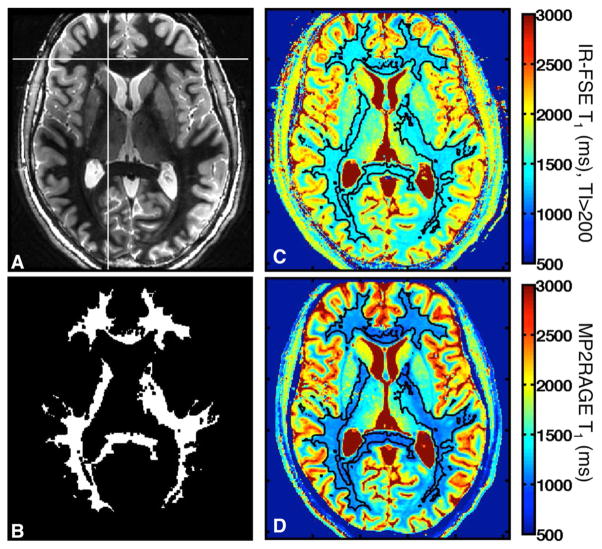
For each volunteer, a region of interest (ROI) that covers most of the WM in the acquired slice was defined using a region-growing algorithm in MATLAB (Mathworks, Natick, Massachusetts, USA), starting from seed pixels in WM of the IR-FSE image with TI = 600 (Fig. 1a). This image was used because the WM signal is approximately nulled and the white/gray contrast is highest. Seeds were manually chosen until most of the WM was included. The resulting ROI was eroded with a 3 × 3 filter to remove pixels on the white/gray boundary, giving a mask such as that shown in Figure 1b.

FIG. 1.

Generation of WM mask for T₁ analysis. (a) Example IR-FSE image with TI = 600 ms and one seed voxel used for ROI generation (crosshairs). (b) Resulting WM ROI after erosion. (c) Corresponding IR-FSE T₁ map (TI > 200 ms), with the ROI outlined in black. (d) Corresponding MP2RAGE T₁ map.

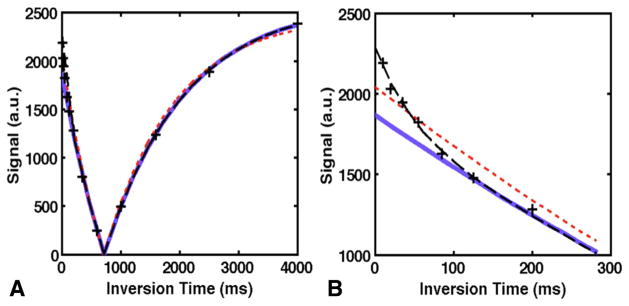
For the 13-point IR-FSE time series, T₁ was calculated at each pixel in the ROI by fitting a biexponential recovery model to the entire time series, as well as monoexponential fits to the entire series, and subsets of the data with 4–12 TIs at successively larger minimum TI values (eg, only the images with TI ≥ 200 ms, as shown in Fig. 1c). Examples of these fits are shown in Figure 2. Monoexponential fits were performed with a reduced-dimension nonlinear least squares fit (32) in MATLAB. This algorithm uses a four-parameter model that accounts for effects such as imperfect RF pulses and finite TR, so fitting only three TIs is generally not feasible. The biexponential fit uses a modified version of the model from (32) with separate parameters for the long and short components, and a standard Levenberg–Marquardt nonlinear least-squares fit.

FIG. 2.

Comparison of monoexponential and biexponential fits. (a) Fits to data at the voxel shown in Figure 1a; black dashed line = biexponential fit, red dotted line = monoexponential fit to all data, solid blue line = monoexponential fit to TI >200 ms. (b) Inset showing early TI values only.

Unless otherwise specified, parameter values obtained from the various fits are reported as the mean ± standard deviation of a Gaussian function fitted to the histogram of that parameter over the entire ROI. To quantify whether the biexponential fit represents a significant improvement over a monoexponential fit to the entire series, the F statistic was computed for each pixel in the ROI according to

$$\mathrm{F}=\frac{({\text{RSS}}_1-{\text{RSS}}_2)\times {\mathrm{f}}_2}{{\text{RSS}}_2\times ({\mathrm{f}}_1-{\mathrm{f}}_2)},$$ [9]

where RSS_i is the residual sum-of-squares of either the single-exponential (I = 1) or biexponential (I = 2) fit to all 13 TI values at that pixel, and f_i is the number of degrees of freedom in the fit. Using the associated cumulative distribution function, F can then be converted to a P value for evaluation of significance.

T₁ maps were created from MP2RAGE composite images (Eq. 6) using the signal equations given in Marques et al. (10), modified to account for the centric phase encode order. The same procedure as described above was used to delineate and compare ROIs with corresponding IR-FSE T₁ maps; an example is shown in Figure 1d.

Simulations

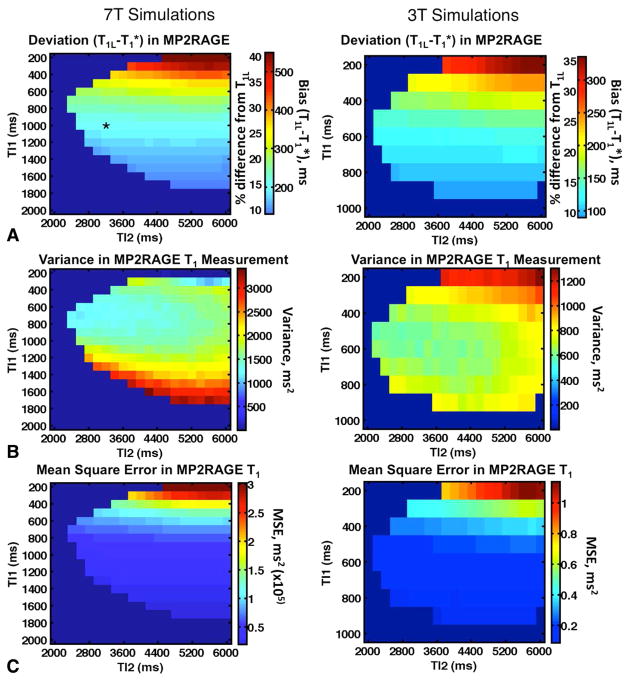
To assess the impact of a short T₁ component on a wide range of IR-FSE acquisition schemes, simulations were performed in which a biexponential T₁ recovery defined according to Equation [1] was sampled at various TIs and fitted with the monoexponential function in Equation [4] to obtain T₁* and the deviation T_1L−T₁*. Experimentally determined values for T_1L, T_1S, and w_S at 3T and 7T were used to define the biexponential recovery curve. TI values were geometrically spaced between a minimum and maximum TI. The maximum TI was set to 4000 ms to match experimental data, and the minimum TI varied between 10 and 600 ms. The number of TI values in each set varied between four and 12. This allowed direct comparison between simulated results and T₁ values from subsets of experimental data. Gaussian noise with a standard deviation of 2% or 1% of the equilibrium magnetization was added to the recovery curves to simulate images with signal-to-noise ratio (SNR) of 50 and 100, respectively. Five thousand repetitions were performed at each noise level and set of TI values, allowing the variance σ² to be computed. To evaluate the optimum combination, we used the figure of merit (T_1L − T₁*)² + σ², which is the mean squared error (MSE) of T₁* relative to T_1L.

T₁ mapping with MP2RAGE involves a lookup table based on the signal equations, which relates the intensity of the ratio image in Equation [5] to a T₁ value. However, if the signal behavior is modified by the presence of a short T₁ component, as in Equation [7], the lookup will generally be incorrect (Fig. 3). To assess the extent of this deviation, MP2RAGE signals were simulated for a range of TIs TI₁ (200–1000 ms at 3T and 200–1900 ms at 7T) and TI₂ (2000–6000 ms at 3T and 7T). Combinations where TI₂ − TI₁ was not large enough to accommodate the required number of TR intervals were disallowed, as were combinations in which the lookup table was non-monotonic over a range of interest centered on T_1L (400–1400 ms at 3T and 800–1800 ms at 7T). This ensures that the lookup yields a unique T₁ value for a given intensity. The following parameters were chosen to match experiments: TR = 7.4 ms; TS = 7500 ms between inversions; 200 phase encode lines per inversion; α₁/α₂ = 5°/4°.

FIG. 3.

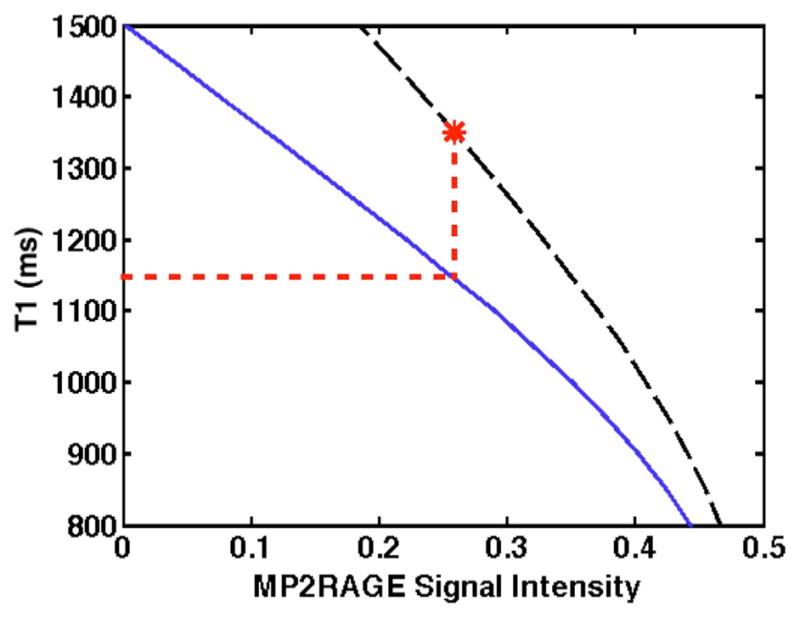
Example of an incorrect MP2RAGE T₁ lookup in the presence of a short T₁ component. The correct lookup table, based on biexponential relaxation for a range of T_1L values with T_1S and w_S constant, is indicated by the black dashed line, with a particular T₁ value of interest (T_1L = 1350 ms) marked by the asterisk. The lookup table assuming monoexponential relaxation is indicated by the blue solid line. If a lookup (red dotted line) is performed using the monoexponential table and the highlighted signal intensity, the resulting T₁* (1146 ms) is much less than T_1L.

For each combination of TI₁ and TI₂, the actual MP2RAGE signal in the presence of the short T₁ component was calculated using Equations [5] and [6]. The lookup table for all of the T₁ values in the range of interest is generated assuming monoexponential relaxation, and the resulting signal is converted into a T₁* using that lookup table (see Fig. 3 for an example). As with the IR-FSE simulations, 5000 repetitions were performed with 2% noise added to the biexponential S(TI_n), such that the variance and MSE of the lookup table result T₁* can be computed.

RESULTS

Experimental

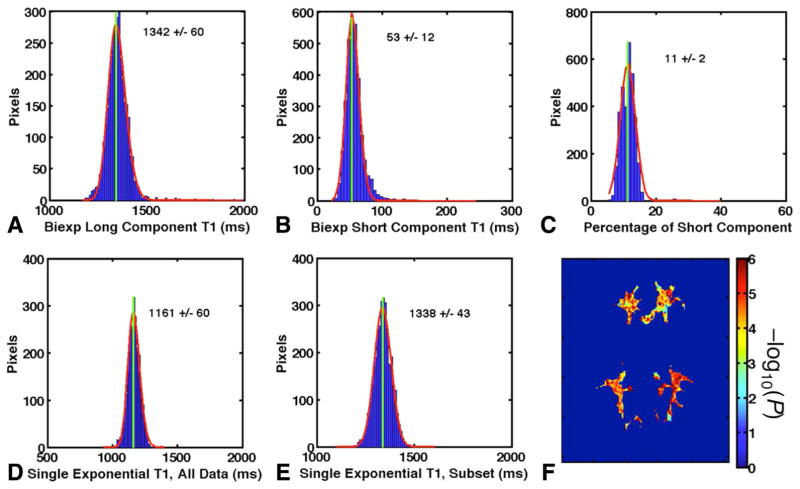
The various T₁ relaxation times and short T₁ component weight w_S obtained from the 13-point IR-FSE series in a typical volunteer at 7T are illustrated in Figure 4. There was clear evidence of biexponential relaxation, with a short component comprising approximately 11% of total signal. If all of the data from this biexponential recovery curve are fitted with a monoexponential model, as shown by the red dotted lines in Figure 2, the result is a fit that gives a T₁* significantly less than the true value of the long T₁ component. For the volunteer whose data are shown in Figure 4, the T₁* obtained from the monoexponential fit to all data (1161 ms, Fig. 4d) was shorter than T_1L (1342 ms, Fig. 4a) by 181 ms. Figure 4e shows that this can be remedied by fitting to only those data with sufficiently long TIs (TI > 200 ms in this case).

FIG. 4.

Results from a typical WM ROI (shown in Fig. 1b). (a) Gaussian fit to histogram of biexponential long component T_1L. (b) Biexponential short component T_1S. (c) Short component weight w_S. (d) Monoexponential T₁* using all data. (e) Monoexponential T₁* using only TI > 200 ms. (f) P value map of entire WM ROI. For ease of visualization, −log₁₀(P) is displayed such that P = 0.05 corresponds to a value of 1.3 and P = 0.01 corresponds to a value of 2.

All of the results from each of the volunteers at both field strengths are given in Table 2. In addition to those parameters illustrated in Figure 4, Table 2 also provides the percent difference in T₁ between monoexponential (T₁*) and biexponential (T_1L) fits to all data, and the percentage of voxels in the ROI for which the biexponential fit performed significantly better (P < 0.05 or P < 0.01) than the monoexponential fit. All volunteers at both field strengths consistently showed biexponential relaxation, with a larger effect at 7T (mean difference of 13% and significantly better biexponential than monoexponential fit in 96% of voxels at P = 0.05) than at 3T (mean difference of 6%, significantly better biexponential fit in 45% of voxels).

Table 2.

T₁ Relaxation in Volunteers at 7T and 3T Based on Biexponential and Monoexponential Fits to 13 IR-FSE Images

Volunteer	T1L (ms)	T1S (ms)	Short T1, Weight, wS	T1* (ms)	% Difference (T1*/T1L − 1)a	% Voxels
						P < 0.05	P < 0.01
7T
#1	1342 ± 60	53 ± 12	11% ± 2%	1161 ± 60	−13%	99.5%	98.8%
#2	1347 ± 64	51 ± 19	10% ± 2%	1173 ± 39	−13%	94.8%	80.0%
#3	1331 ± 77	61 ± 12	11% ± 2%	1106 ± 95	−17%	91.1%	86.9%
#4	1374 ± 46	64 ± 14	12% ± 2%	1162 ± 38	−18%	97.2%	93.3%
Meanb	1349 ± 18	57 ± 6	11% ± 1%	1151 ± 30	−15% ± 3%	96% ± 4%	90% ± 8%
3T
#1	949 ± 54	54 ± 40	7% ± 2%	906 ± 43	−4%	50.8%	27.5%
#2	928 ± 37	47 ± 48	10% ± 2%	864 ± 26	−7%	43.0%	14.8%
#3	926 ± 79	49 ± 64	9% ± 3%	869 ± 60	−6%	43.0%	19.3%
#4	952 ± 67	42 ± 43	8% ± 2%	887 ± 40	−7%	44.3%	20.2%
Meanb	939 ± 14	48 ± 5	9% ± 1%	882 ± 19	−6% ± 1%	45% ± 4%	20% ± 5%

Values are for an ROI encompassing all of the WM in an axial slice through the basal ganglia. Subjects #2–4 are the same volunteer at both field strengths.

^aGives the error in the fitted T₁* seen in monoexponential fits to all data compared with the biexponential long component T_1L.

^bMean ± standard deviation of the mean across all volunteers at that field strength.

The WM T₁ values determined by MP2RAGE in three volunteers at 7T are given in Table 3, along with the corresponding T₁ values calculated by a four-point IR-FSE sequence with TI_min = 200 ms, and the percent difference between them. Whereas the four-point IR-FSE measurement was consistent with the biexponential T_1L obtained from the 13-point series, MP2RAGE measurements showed an underestimation of T_1L of a degree similar to monoexponential IR-FSE fits with short minimum TIs (17% underestimation of T_1L).

Table 3.

Comparison of WM T₁ Values in MP2RAGE and IR-FSE at 7T

Subject	IR-FSE T1 (ms)	MP2RAGE T1 (ms)	% Difference
#5	1380 ± 66	1128 ± 69	−18%
#6	1354 ± 50	1125 ± 75	−17%
#7	1351 ± 66	1130 ± 56	−16%
Meana	1362 ± 16	1127 ± 3	−17% ± 1%

^aMean ± standard deviation of the data for all volunteers.

Simulations

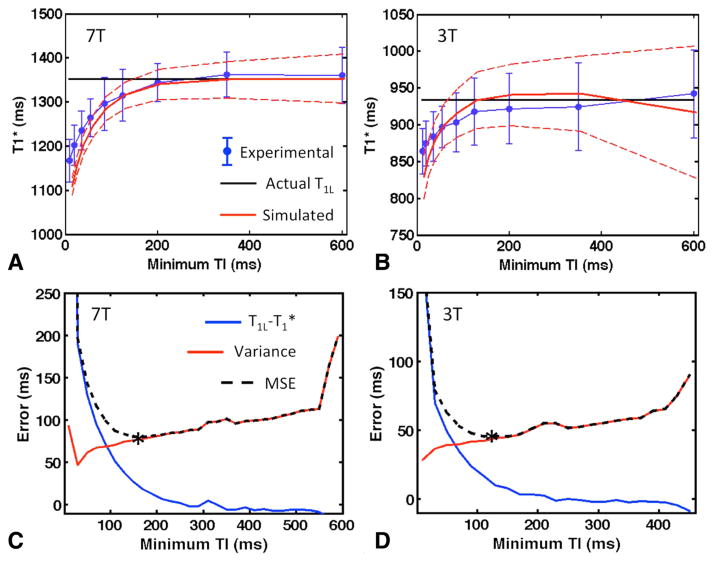
As shown graphically in Figure 2 and numerically in Figure 4, omitting the short TI values from the analysis of IR-FSE data resulted in a monoexponential T₁* fit that was in far better agreement with the long component T_1L. By comparing the results of fits with experimental data with increasingly longer minimum TI values, it can be seen that T₁* steadily approached T_1L, though the variance in the measurement also tended to increase (Fig. 5a,b). The corresponding simulated data show the same behavior at 3T and 7T.

FIG. 5.

Behavior of T₁* in IR-FSE acquisitions with increasing minimum TI. (a, b) Comparison of simulated and experimental data at 7T (a) and 3T (b). Blue dots are experimental results of monoexponential T₁* fits (mean ± standard deviation throughout ROI from subject #1 at 7T and subject #2 at 3T). The solid black line represents the T_1L used as input to the simulations, and the red dashed lines are T₁* fits to simulated data with the same minimum TI and number of TIs (mean ± standard deviation over 5000 repetitions). (c, d) Simulated mean deviation T_1L − T₁*, variance σ² in the fitted T₁* values, and MSE = (T_1L − T₁*)² + σ² as a function of minimum TI at 7T (c) and 3T (d). Mean and variance were measured over 5000 Monte Carlo repetitions with 2% noise added to the data. The optimal TI for each field strength is marked with an asterisk.

The simulations also demonstrated that acquiring more than four TIs has no significant impact on the deviation T_1L − T₁* except when the minimum TI was very short (data not shown). Additional TIs did result in decreased variance, but once this variance was normalized by the total scan time, this effect was also minimal, and the largest contribution to the variance was the minimum TI. Results for the entire range of simulated minimum TI values, with four TIs and 2% added noise, are shown in Fig. 5c and 5d (7T and 3T, respectively). As expected, the deviation diminished as TI_min increased, while the variance increased. The mean square error was lowest, with a minimum TI of 150 ms at 7T and 120 ms at 3T. If only 1% noise was added to simulated measurements instead (data not shown), the optimum TI_min values were 200 ms and 150 ms at 7T and 3T, respectively.

Corresponding results for the errors introduced in MP2RAGE T₁ measurements are shown in Figure 6. Unlike IR-FSE, the difference between T₁* and T_1L was never removed entirely. The difference decreased as both TIs increased, and though this increased the variance (Fig. 6b), the optimal MSE occurred when TI₁ and TI₂ were maximized. However, even at very long TIs, the difference at 3T could not be reduced below 90 ms with the parameters tested, and at 7T the minimum difference was 125 ms. Other image parameters, such as flip angle, TR, and TS, did not have a significant effect on these results (data not shown). With the parameters used experimentally at 7T (marked with an asterisk in Fig. 6a), the anticipated difference was approximately 200 ms, consistent with experimental observations (Table 3).

FIG. 6.

(a) Simulated deviation in MP2RAGE T₁ measurement (T_1L−T₁*) as a function of TIs TI₁ and TI₂, at 7T (top) and 3T (bottom). Values shown are the mean of 5000 Monte Carlo repetitions. The combination used for experimental comparison of MP2RAGE with IR-FSE is marked with an asterisk. Combinations that were disallowed due to ambiguous lookups or unfeasible parameters appear in dark blue. (b) Variance σ² in the T_1app values at 2% added noise. (c) MSE = (T_1L − T₁*)² + σ².

DISCUSSION

Biexponential T₁ relaxation is a known characteristic of many tissues, including WM, and the resulting short T₁ component is commonly measured in quantitative MT applications and used to compute parameters of interest. However, because the effect of T_1S at lower field strengths is on the order of a few percent, its impact on quantitative T₁ mapping has been largely ignored. Only now that T₁ mapping is becoming more common at very high field strengths is the true impact of biexponential relaxation becoming clear. Because accurate measurement of both biexponential components may be too time-consuming for most clinical applications, strategies to reduce the impact of T_1S are a more practical way to make T₁ measurements reproducible and independent of scan parameters.

It is worth emphasizing that T_1S does not correspond directly to the relaxation time of a particular population of protons, but is an apparent relaxation time constant whose value is governed by exchange effects. This may be one reason why the effects of biexponential T₁ behavior are not always recognized. For example, Kingsley et al. (33) noted that the quality of monoexponential fits to T₁ recovery data in WM would be greatly improved by the presence of a second T₁ component on the order of 50 ms that comprises approximately 10% of signal. The authors of that study believed a component having such properties was unlikely from a biological viewpoint, but these values are consistent with an interpretation of biexponential relaxation based on magnetization transfer, and in good agreement with both the present results and with previously reported qMT data (11,19).

At 7T, our IR-FSE data show the mean difference between T₁* and T_1L to be 13% when T₁* was calculated using a monoexponential fit to all available data. Because this data set had a minimum TI of 10 ms, this represents a near worst-case scenario in terms of deviation. If this T₁* of 1153 ms is compared with T₁ values in WM reported in the literature (Table 1), it is clear that many of those measurements may have been affected by this deviation to varying degrees. In addition, some of the variation in reported WM T₁ values may be due to differences in minimum TIs, the selection of which varies significantly from protocol to protocol. In contrast, our T_1L = 1349 ms agrees with the value reported by Dortch et al. (11), who also used a biexponential analysis that should yield results that are independent of the TIs acquired. It is our assertion that this is a more reliable estimate of the true T₁ of free water in WM.

The deviation from T_1L is also observable at 3T, albeit to a lesser degree. This is consistent with Equation [2], which predicts smaller deviations (T_1L − T₁*) as T_1L decreases. Rather than the 13% deviation in T₁ observed at 7T, the effect at 3T is on the order of 6%. Both T₁* and T_1L are within the range of accepted WM T₁ values at 3T [eg, (13)]. In addition, the proportion of WM voxels in which biexponential fits provide a significant benefit was much larger at 7T (90%–96%) compared with 3T (20%–45%). This finding is consistent with data at 1.5T (20) showing that biexponential fits provide little extra information at low fields and helps illustrate why short T₁ effects have not previously been considered significant for quantitative T₁ mapping.

The role of magnetic field inhomogeneity in the increased T₁* deviation at high fields cannot be ignored. As B₀ increases, flip angles become less uniform and inversion pulses become less efficient, though these effects can be accounted for with appropriate models (32), and we attempted to minimize these effects on our acquisition by using overdriven adiabatic inversion pulses and centric phase encoding strategies that acquired the center of k-space after as few RF excitations as possible. Nevertheless, some of the observed deviation will depend on RF pulse parameters. For instance, as illustrated in Equation [1], changes in the magnetization of the pools due to, for example, incomplete saturation of the macromolecular pool will affect the initial amplitude of the observed relaxation components b_S and b_L, and therefore the observed deviation in T₁*. For the pulses used in this study, we calculated that the saturation of the macromolecular pool [S_r in the notation of Pike (34), which is analogous to the value S_m reported by Dortch et al. (11)] varies from 0.16 to 0.31 (ie, macromolecular magnetization is reduced by 69%–84% after a single HSn pulse). This value depends on the pulse shape and power characteristics as well as the line shape (Gaussian, Lorentzian) and T₂ value (T_2m = 10–20 μs) used to model the macro-molecular pool. The saturation effect of the pulses is significant, and slight differences between the HSn pulses used will affect the observed b_S and b_L to some degree. Though we have calculated the impact of S_r variations to be secondary to variations in macromolecular PSR, the influence of the inversion pulse remains a source of variability to be studied and controlled. However, we contend that not all of the observed T₁* deviation can be attributed to RF inhomogeneity and pulse characteristics alone, because for a given value of w_S, our theoretical analysis shows a strong field strength dependence of T₁* independent of these RF pulse effects.

To reduce the influence of T_1S on IR-FSE measurements, the minimum TI can be increased, but this will necessarily increase the variance in the measurement. Although this trade-off can be optimized by minimizing the mean squared error, some deviation from T_1L may remain, depending on the SNR of the underlying data. For example, in the simulations with 2% noise, the remaining deviation at the optimal minimum TI is 20 ms at 3T, and >40 ms at 7T. If higher accuracy is desired, the minimum TI must be further increased (eg, to 150 ms at 3T and 200 ms at 7T) to reduce the deviation to acceptable levels (eg, <10 ms). Additional scan time may then be needed to compensate for the increased variance.

Although this strategy has been presented here in the context of IR-FSE, it applies to some other methods as well. For example, the 3-TI MPRAGE approach described by Liu et al. (35) acquires 3 MPRAGE images at different TIs, with a ratio of differences used to create a T₁ map free of B₀, B₁, and T₂ effects. This method is a promising candidate for fast 3D T₁ mapping and can be used to obtain T₁ maps with larger brain coverage and faster acquisition times than IR-FSE methods (36). If all TIs are long enough that the short component has fully relaxed, the resulting T₁ map will be unaffected by T_1S. Indeed, Liu et al. suggest a minimum TI of 150 ms for this reason, a value that is in agreement with our recommendations.

However, the influence of T_1S cannot be removed from all sequences in this way. In particular, the T₁* computed by MP2RAGE is significantly different from T_1L regardless of the TIs chosen. Although MP2RAGE T₁ values in WM were very consistent across the three volunteers imaged in this study, the T₁ given by MP2RAGE is significantly less than the T₁ obtained from a four-point IR-FSE series with optimized minimum TI, and the latter measurement is in good agreement with the biexponential T_1L value obtained using a 13-TI series. Although choosing very long TIs in MP2RAGE reduces this deviation somewhat, this comes at the cost of increased variance and scan time and will never eliminate the effect completely. This is a direct consequence of the lookup expression used for MP2RAGE, and only by exploring different approaches to ratio-based combination of images can this bias be potentially addressed. It is possible that this property of MP2RAGE has not been recognized previously because the T₁ values reported by MP2RAGE have often been in agreement with the T₁* obtained from IR-FSE and similar measurements made with typically minimum short TIs. Expansion of the MP2RAGE signal equation to include the effects of two-site exchange may provide methods for increasing the accuracy of MP2RAGE T₁ measurements, though the collection of only two TIs may still limit the extent to which the biexponential relaxation can be modeled.

The impact of biexponential relaxation on other quantitative MRI methods must also be considered. For example, MR fingerprinting with inversion recovery balanced steady state free precession (37) uses a database spanning a range of potential parameters to attempt to match the acquired signal. If this database does not properly model biexponential relaxation, the apparent T₁ may also not reflect the underlying signal behavior. T₁ quantification using variable flip angle methods like DESPOT1 (12,14) may also be susceptible to deviations, though in a different way than described here due to the lack of inversion preparation.

This study was performed with the assumption of biexponential relaxation caused by two-site exchange between a free and a macromolecular pool. It is possible that a more accurate model would include components corresponding to more pools of varying MR visibility in different exchange regimes (eg, myelin water). While studies of T₁ relaxation using multicomponent DESPOT analysis (38) indicate that the myelin pool is likely in fast exchange with the free water pool, implying that the myelin water would primarily contribute to T_1L, this hypothesis should be explored further. T₁ analysis of three or more components may be challenging with the methods presented herein. It has been shown (39) that five TIs are sufficient to determine qMT parameters assuming a two-pool model, but more points and higher SNR are likely necessary to reliably discriminate additional components.

Because T_1S arises from an exchange process between spin populations that may be modified by pathology, it is quite possible that T_1S contains information relevant to this pathophysiology and could itself be a desirable target for quantitative MRI. In this study, the goal was to reduce the influence of T_1S on the measurement of T_1L, but direct mapping of T_1S is also feasible. In addition to the method used in this study, MT methods have been used to estimate T_1S and w_S in 3D volumes with scan times on the order of 20 min (11), though this requires multiple TIs and provides limited spatial resolution (2–3 mm). It is possible that two consecutive T₁ mapping scans—one with parameters chosen to increase sensitivity to T_1S and one made insensitive to T_1S—could be combined to create simultaneous T_1S and T_1L maps with fewer total acquisitions. Correlations between T_1S and other measures of intercompartment exchange or macro-molecular content could then be explored more fully.

CONCLUSIONS

Variability between methods is a key obstacle to clinical implementations of quantitative T₁ mapping. The influence of biexponential T₁ relaxation on quantitative T₁ images has been overlooked because of its relative unimportance at low field strengths. However, as T₁ mapping at high field becomes common, it becomes critical to recognize these effects that, left unchecked, can introduce significant parameter-dependent variation in measurements of T₁. While differences between the long T₁ component and the apparent T₁ in WM are on the order of 6% at 3T, we have shown that this difference can be as large as 13% at 7T.

For sequences such as IR-FSE in which data are fitted to a monoexponential model, this deviation between T_1L and T₁* can be reduced through judicious selection of TIs. Optimal performance in terms of mean-squared error is obtained by acquiring four TIs with a minimum TI in the 100–150 ms range at 3T and 125–200 ms at 7T. The specific value of TI_min should be guided by the SNR of the underlying data to achieve a suitable balance of increased variance and reduced bias. This strategy can also be employed for some other T₁ mapping methods such as 3-TI MPRAGE (36). In contrast, the T_1L − T₁* deviation present in MP2RAGE cannot be mitigated in the same way, and remains a significant source of error even at very long TIs. This must be kept in mind when considering the application of this particular sequence to T₁ mapping of the brain, particularly at high fields.

APPENDIX A

Consider a monoexponential fit to three data points using, for example, an IR-FSE sequence with inversion times TI₁, TI₂ and TI₃. The most general model that can be fitted reliably to such data using a nonlinear least-squares method has three parameters:

$$\mathrm{S}(\text{TI})=\mathrm{a}+\mathrm{b}\times exp(-\text{TI}/{\mathrm{T}}_1).$$ [A1]

While analytically characterizing such a nonlinear fit is difficult in general, for the specific case of a three-parameter fit to three data points, the solution should be unique. Therefore, a solution found by alternative means should be identical, given the same input data. One alternate method for computing T₁ (35) is by forming the expression

$$\mathrm{L}=\frac{\mathrm{S}({\text{TI}}_3)-\mathrm{S}({\text{TI}}_1)}{\mathrm{S}({\text{TI}}_3)-\mathrm{S}({\text{TI}}_2)}=\frac{exp(-{\text{TI}}_3/{\mathrm{T}}_1)-exp(-{\text{TI}}_1/{\mathrm{T}}_1)}{exp(-{\text{TI}}_3/{\mathrm{T}}_1)-exp(-{\text{TI}}_2/{\mathrm{T}}_1)}.$$ [A2]

This expression depends only on T₁, and while it is generally not possible to solve directly for T₁ in terms of the TIs and signal intensities, a simple lookup can be performed based on the known TIs to compute T₁ for any given value of L.

Now consider the case in which the underlying relaxation is actually biexponential, of the form

$$\mathrm{S}(\text{TI})=\mathrm{a}+{\mathrm{b}}_{\mathrm{L}}\text{exp}(-\text{TI}/{\mathrm{T}}_{1\mathrm{L}})+{\mathrm{b}}_{\mathrm{S}}\text{exp}(-\text{TI}/{\mathrm{T}}_{1\mathrm{S}}).$$ [A3]

The relative contributions of the two T₁ components, T_1L and T_1S, are given by b_L and b_S, respectively. An expression analogous to Equation [A2] that includes this biexponential behavior is

$$\mathrm{L}=\frac{{\mathrm{b}}_{\mathrm{L}}\text{exp}(-{\text{TI}}_3/{\mathrm{T}}_{1\mathrm{L}})\pm {\mathrm{b}}_{\mathrm{S}}\text{exp}(-{\text{TI}}_3/{\mathrm{T}}_{1\mathrm{S}})-{\mathrm{b}}_{\mathrm{L}}\text{exp}(-{\text{TI}}_1/{\mathrm{T}}_{1\mathrm{L}})-{\mathrm{b}}_{\mathrm{S}}\text{exp}(-{\text{TI}}_1/{\mathrm{T}}_{1\mathrm{S}})}{{\mathrm{b}}_{\mathrm{L}}\text{exp}(-{\text{TI}}_3/{\mathrm{T}}_{1\mathrm{L}})+{\mathrm{b}}_{\mathrm{S}}\text{exp}(-{\text{TI}}_3/{\mathrm{T}}_{1\mathrm{S}})-{\mathrm{b}}_{\mathrm{L}}\text{exp}(-{\text{TI}}_2/{\mathrm{T}}_{1\mathrm{L}})-{\mathrm{b}}_{\mathrm{S}}\text{exp}(-{\text{TI}}_2/{\mathrm{T}}_{1\mathrm{S}})}.$$ [A4]

Two assumptions can be made to greatly simplify this expression. First, for most experimental parameters, TI₂ and TI₃ are much longer than T_1S, such that exp(−TI₃/T_1S) = exp(−TI₂/T_1S) ≈ 0. We will also assume that TI₃ is long compared with T_1L and exp(−TI₃/T_1L) ≈ 0. This is decreasingly justified at higher fields, but as a first-order approximation this assumption is worth considering. The lookup expression for biexponential relaxation is then approximately

$${\mathrm{L}}_{\text{bi}}=({\mathrm{b}}_{\mathrm{L}}\text{exp}(-{\text{TI}}_1/{\mathrm{T}}_{1\mathrm{L}})+{\mathrm{b}}_{\mathrm{S}}\text{exp}(-{\text{TI}}_1/{\mathrm{T}}_{1\mathrm{S}}))/{\mathrm{b}}_{\mathrm{L}}\text{exp}(-{\text{TI}}_2/{\mathrm{T}}_{1\mathrm{L}}).$$ [A5]

The corresponding expression for purely monoexponential relaxation has also been simplified to

$$\begin{array}{l}{\mathrm{L}}_{\text{mono}}=exp(-{\text{TI}}_1/{\mathrm{T}}_1)/exp(-{\text{TI}}_2/{\mathrm{T}}_1)\\ ={\mathrm{L}}_{\text{bi}}-{\mathrm{b}}_{\mathrm{S}}\text{exp}(-{\text{TI}}_1/{\mathrm{T}}_{1\mathrm{S}})/{\mathrm{b}}_{\mathrm{L}}\text{exp}(-{\text{TI}}_2/{\mathrm{T}}_{1\mathrm{L}}).\end{array}$$ [A6]

If the monoexponential lookup function L_mono is used to determine T₁ for data that actually exhibit biexponential relaxation, the lookup will be incorrect by an amount given by

$$\mathrm{\Delta }\mathrm{L}={\mathrm{b}}_{\mathrm{S}}\text{exp}(-{\text{TI}}_1/{\mathrm{T}}_{1\mathrm{S}})/{\mathrm{b}}_{\mathrm{L}}\text{exp}(-{\text{TI}}_2/{\mathrm{T}}_{1\mathrm{L}}).$$ [A7]

This can be converted to units of T₁ using ΔT₁ = ΔL dT₁/dL = ΔL/(dL/dT₁). Using L = L_mono and

$$\text{dL}/{\text{dT}}_1=\frac{({\text{TI}}_1-{\text{TI}}_2)\times exp(-{\text{TI}}_1/{\mathrm{T}}_1)}{{{\mathrm{T}}_1}^2\text{exp}(-{\text{TI}}_2/{\mathrm{T}}_1)}.$$ [A8]

we find the following expression for the change in T₁* introduced by the short component:

$$\mathrm{\Delta }{\mathrm{T}}_1^{\ast }=-[{{\mathrm{T}}_{1\mathrm{L}}}^2/({\text{TI}}_2-{\text{TI}}_1)]\times {\mathrm{b}}_{\mathrm{S}}/{\mathrm{b}}_{\mathrm{L}}\times [exp(-{\text{TI}}_1/{\mathrm{T}}_{1\mathrm{S}})/exp(-{\text{TI}}_1/{\mathrm{T}}_{1\mathrm{L}})].$$ [A9]

Though it is acknowledged that this expression relies on the validity of the assumptions concerning the magnitudes of TI₂ and TI₃ compared with T_1S and T_1L, this expression does give some intuition into the increased influence of biexponential relaxation at high field. In addition, the general behavior described by Equation [A9] should be extensible to larger numbers of TIs.