Abstract
We model the labor market impact of the key provisions of the national and Massachusetts “mandate-based” health reforms: individual mandates, employer mandates, and subsidies. We characterize the compensating differential for employer-sponsored health insurance (ESHI) and the welfare impact of reform in terms of “sufficient statistics.” We compare welfare under mandate-based reform to welfare in a counterfactual world where individuals do not value ESHI. Relying on the Massachusetts reform, we find that jobs with ESHI pay $2,812 less annually, somewhat less than the cost of ESHI to employers. Accordingly, the deadweight loss of mandate-based health reform was approximately 8 percent of its potential size.
Keywords: Affordable Care Act, Massachusetts health reform, welfare effects
The Affordable Care Act (ACA) of 2010 and the Massachusetts health reform of 2006 focus on expanding health insurance coverage to near-universal levels. These “mandate-based” reforms rely on three key provisions to expand coverage: 1) a mandate that individuals obtain coverage or pay a penalty, 2) a mandate that employers offer coverage or pay a penalty, and 3) expansions in publicly subsidized coverage. While regulatory policy has long relied on mandates (for example, command and control regulation of technologies to reduce pollution), public policies that mandate that individuals purchase privately supplied goods have little precedent. Such mandates are sufficiently unprecedented that uncertainty about whether the individual mandate was constitutional at the national level was not resolved until the Supreme Court upheld it in June 2012. Despite the resolution of legal questions around mandate-based policy, the question of economic efficiency remains.
We develop a simple model of mandate-based health reform. Our model incorporates the three key features of the national and Massachusetts health reforms. Using this model, we characterize the compensating differential for employee-sponsored health insurance (ESHI)—the causal change in wages associated with gaining ESHI—and we derive a set of sufficient statistics that capture the impact of the reforms on the labor market and on welfare. Although these sufficient statistics arise from difficult-to-measure structural parameters that determine individual health insurance and labor supply decisions, we can recover them from easily measured changes in labor market outcomes. Our model builds on the work of Summers (1989) who models a full-compliance employer mandate. We apply the model to current policy by allowing for a pay-or-play employer mandate and adding a pay-or-play individual mandate and expansions in subsidized coverage. The interaction between the employer and individual mandates changes the predictions of the Summers model. The central result that an employer mandate reduces deadweight loss relative to a tax does not hold if there is already an individual mandate in place. This theoretical result is relevant for policy, given that as of this writing, the ACA employer mandate has not yet been enforced.
Based on the structure implied by our theory, we then estimate the relationship between ESHI and the labor market, allowing us to empirically assess the impact of health reform on welfare. Using variation induced by the Massachusetts health reform—which mirrors the national reform in all of the elements of our model—we estimate the empirical analog of our model. We first estimate the compensating differential for health insurance. Our empirical strategy relies on exogenous shifts into and out of ESHI induced by reform. Using longitudinal data from the Survey of Income and Program Participation on wages, employment, and hours worked, we study changes in labor market outcomes for individuals who switch to and from ESHI over the reform period. We incorporate individual fixed effects to control for time-invariant attributes that determine an individual’s labor market outcomes, and we incorporate variation between Massachusetts and other states to control for national trends. We also incorporate variation in firm size to allow some firms to be exempt from the employer mandate and to control for variation in the Massachusetts labor market that is unrelated to the reform. Combining all of these sources of variation and the reform allows us to obtain causal estimates of the compensating differential associated with health insurance.
Adding a small amount of structure to the estimated compensating differential for health insurance, we estimate the sufficient statistics that determine the welfare impact of health reform. Once we demonstrate that these parameters are sufficient statistics for welfare analysis, we use our estimates to compute the deadweight loss associated with the mandate-based reform in Massachusetts. We also compare our estimated deadweight loss to the deadweight loss of a counterfactual tax-based insurance expansion that would involve levying a wage tax to pay for the provision of health insurance directly.
We find a compensating differential for ESHI that is of the expected theoretical sign though somewhat smaller in magnitude than the full cost of health insurance, suggesting high average valuation of the benefit among the newly insured. Consistent with the large compensating differential, we find a small hours differential between jobs with and without ESHI, also suggesting high average valuation of the benefit among the newly insured. Translating our estimated compensating and hours differentials into sufficient statistics for welfare analysis, we find that mandate-based reform is a relatively efficient way to expand coverage. We estimate that mandate-based coverage expansion in Massachusetts resulted in a deadweight loss due to distortion of the labor market that was only 7.7 percent of the distortion associated with instead providing health insurance through a tax on wages that workers do not link to receiving insurance. The relative efficiency of mandate-based reform follows from the high estimated valuation of the newly insured; because people were willing to work for ESHI as well as wages, the distortion to the labor market of mandating insurance was relatively small. We examine the robustness of our estimates to a variety of alternative specifications. Although our estimates vary, they always show that mandate-based reform is substantially more efficient than tax-based reform because our finding that individuals value ESHI is very robust.
Apart from our theoretical contributions, our findings contribute to the empirical literature on the incidence of fringe benefits, with health insurance as the largest of those benefits. Typically, the endogeneity of fringe benefits and labor market outcomes leads researchers to find wrong-signed compensating differentials for fringe benefits (see Gruber [2000] and Currie and Madrian [1999] for reviews); most studies find that individuals who receive more fringe benefits also receive higher wages. Existing studies that do not find wrong-signed compensating differentials for health insurance rely on incremental changes in the cost of health insurance, such as premium increases due to the addition of mandated maternity benefits (Gruber 1994) or increasing malpractice costs (Baicker and Chandra 2005). By using variation from the Massachusetts reform, we find a compensating differential for the full cost of health insurance; individuals who receive ESHI receive wages that are lower by approximately the amount their employer spends on ESHI.
In the next section, we discuss the provisions of Massachusetts and national reforms that are likely to affect the labor market. Section 2 incorporates these provisions into a theory of mandate-based health reform that we use to characterize the compensating differential for ESHI and the welfare impact of mandate-based health reform relative to tax-based health reform; Section 3 discusses identification and estimation. Section 4 introduces the data. Section 5 presents results and discusses robustness, and Section 6 concludes.
1 Massachusetts Health Reform, the Affordable Care Act, and the Labor Market
The Massachusetts health reform, passed in April 2006, and the federal Patient Protection and Affordable Care Act (the ACA), passed in March 2010, contain a number of similar provisions that are likely to affect the labor market. We provide a side-by-side comparison in Appendix A. The cornerstone of both reforms is the individual mandate to purchase health insurance. Unlike traditional full-compliance mandates, the individual mandate in both reforms is a “pay-or-play” mandate that allows individuals to pay a penalty if they choose not to comply. The penalty in Massachusetts for those who were unable to demonstrate they had coverage when they filed their taxes was initially $219 per person per year, and it increased to 50 percent of the cost of the least generous (“Bronze”) plan available in the Massachusetts health insurance exchange (“the Connector”) in 2008.1 The penalty associated with the ACA individual mandate is the higher of $695 per uninsured member of the household (up to three) or 2.5 percent of household income. Compliance with the individual mandate in Massachusetts has been high—over 97 percent of tax filers submitted the tax form to comply with the individual mandate in 2008, and less than 2 percent reported any spell of uninsurance (Massachusetts Health Connector and Department of Revenue 2010).2
Second, both reforms include a pay-or-play employer mandate, which requires employers to offer health insurance or pay a penalty. The Massachusetts reform requires employers with 11 or more full-time employees to offer their workers the option to purchase health insurance coverage. Health coverage options must include a plan that allows employees to purchase health insurance using pre-tax wages, and employers must contribute at least 33 percent of the value of the premium or they will be assessed a penalty of $295 per employee per year. The ACA incorporates a similar pay-or-play employer mandate, but it defines large employers as those with 50 or more full-time employees (Kaiser Family Foundation 2010b). The ACA also requires that coverage options be affordable, such that the insurance offered pays at least 60 percent of covered expenses and the employee is not required to pay more than 9.5 percent of family income for individual coverage (Burkhauser, Lyons, and Simon 2011). If the employer does not offer coverage, the penalty is $2,000 per full-time employee, excluding the first 30 employees. If the employer does not offer options that meet the definition of affordable, and employees enroll in subsidized coverage through an exchange, the employer must pay a penalty of $3,000 per employee who obtains subsidized coverage, up to a maximum of $2,000 times the total number of employees minus 30 (Kaiser Family Foundation 2010a). Despite the relatively low penalty, compliance in Massachusetts has been high.3
The third cornerstone of both reforms is the expansion of subsidized coverage: fully subsidized coverage through Medicaid and partially subsidized coverage through new programs for low-income individuals who do not qualify for Medicaid. The Massachusetts reform expanded traditional Medicaid (MassHealth) and new fully-subsidized “CommCare” plans to those earning less than 150 percent of the federal poverty level (FPL), (150 percent of FPL for a family of three was $29,685 in 2014).4 Individuals between 150 and 300 percent of the FPL can purchase CommCare plans with subsidies that decline with income. Similarly, the ACA expands Medicaid eligibility to all those with incomes below 133 percent of poverty, for states adopting the expansion.5 The ACA also extends subsidized coverage higher up the income distribution to 400 percent of poverty ($79,160 for a family of three). Even though the national reform extends subsidies to families with higher incomes, the Massachusetts subsidies (Commonwealth Connector 2011a, b) are more generous than the national subsidies (Kaiser Family Foundation 2010b) for almost all incomes and family sizes.
2 Model of Mandate-Based Health Reform and the Labor Market
2.1 The Model
We begin by considering labor demand. A representative firm sets wages to maximize profits, resulting in the following labor demand function:
Willingness to demand hours of work L in period t is a function or of the monetary hourly wage w, and other arguments, depending on an indicator for whether the firm provides health insurance ESHIt at time t.6 If the firm provides health insurance, labor demand depends solely on the cost of employing an individual in dollar terms—wages and the dollar cost to the employer of a standard health insurance benefit b. There are two periods: Before and After. The employer mandate is not in place before reform, so ρBefore = 0, but it is in place after reform, so ρAfter = ρ. If the firm does not provide health insurance, labor demand depends on the wage and the per-worker penalty ρtb for not complying with the employer mandate in place in period t (since b is a fixed dollar amount, we express the employer penalty as a fraction of b instead of a fixed dollar amount without loss of generality).
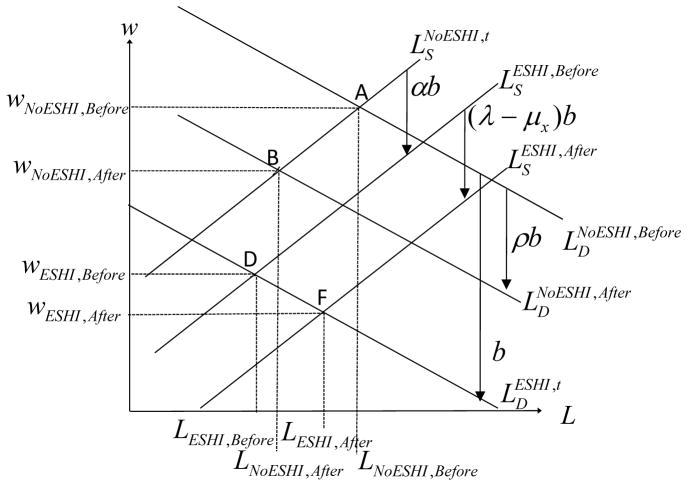
Figure 1 depicts labor demand graphically. Before reform, if the firm provides health insurance, labor demand is lower by b. After reform, if the firm does not provide health insurance, labor demand shifts down by the per-worker penalty for not complying with the employer mandate.
Figure 1.
Graphical Model
Next consider labor supply. A representative individual chooses how many hours to work to maximize utility, resulting in the following labor supply function:
Willingness to supply hours of work L in period t is a function or of the hourly wage w. For an individual with ESHI, given by the indicator ESHIt, which is exogenous for now, labor supply is also a function of factors beyond the wage. As shown, it is a function of the cost to the employer for a standard health insurance benefit b, scaled by the amount that an individual values a dollar of ESHI relative to a dollar of wages, α, and policy parameters in place at time t: the individual penalty for not having health insurance λt, and the subsidy μxt available on the individual health insurance market, which varies in generosity based on income group x. The individual mandate and the subsidies are not in place before reform, so the policy parameters are all equal to zero.
Figure 1 depicts labor supply graphically. Before the reform, if an individual moves from not having ESHI to having ESHI, labor supply shifts downward by αb because the individual is willing to work for lower wages in a job that provides ESHI. This shift results because ESHI is not merely a cost to the employer, it also has value to the employee. In the individual’s choice problem, several factors can affect the magnitude of the underlying valuation of ESHI relative to a dollar of wages: α. For example, canonical insurance theory demonstrates that willingness to pay for insurance is determined by an individual’s wealth, health risk, risk preferences, and the available insurance contract (see, e.g., Arrow [1963] and Rothschild and Stiglitz [1976]). Furthermore, there is a tax preference for ESHI, so we expect the tax preference to increase α as a function of the individual’s marginal tax rate. Rather than modeling these factors individually, we model only α, which we will demonstrate to be a sufficient statistic for welfare analysis in the spirit of Chetty (2009).
After the reform, labor supply also reflects the penalty associated with the individual mandate and any subsidy available to that individual for health insurance outside of employment. That is, the individual penalty augments the individual’s underlying valuation of ESHI, shifting his labor supply curve further downward for jobs offering ESHI—even if the individual does not value health insurance on its own merits, he will value it at least as much as the penalty that he must pay for not having it.7 A subsidy available outside of employment also affects the individual’s labor supply if he obtains health insurance through his employer because the outside coverage option has changed. He is more willing to work for ESHI instead of wages in the face of a penalty, and he is less willing to work for ESHI instead of wages in the face of a subsidy for health insurance outside of employment. After the reform, if the individual moves from not having ESHI to having ESHI, his labor supply shifts downward by α + λ − μx, which we call the “penalty-and-subsidy-inclusive valuation” of ESHI, multiplied by the cost of health insurance b. The penalty-and-subsidy-inclusive valuation incorporates underlying preferences for health insurance and the key policy features of mandate-based reform in a simple measure: the shift in labor supply. We will show that the penalty-and-subsidy-inclusive valuation is an important sufficient statistic for our welfare analysis.
Putting the two sides of the market together yields a labor market equilibrium (w, L) in period t that reflects the underlying parameters that determine labor supply and demand. As shown in Figure 1, there are two potential equilibria in each period t, conditional on whether the individual receives health insurance through the employer: D and A are the equilibria for individuals with and without ESHI before the reform, respectively; F and B are the equilibria for individuals with and without ESHI after the reform, respectively. Our remaining theoretical and empirical analysis relies on the distances between points A, B, D, and F. The remainder of this section focuses on translating these distances into parameters of interest that ultimately allow us to analyze welfare.
2.2 Characterization of the Compensating Differential for ESHI
We begin by demonstrating how the model allows us to identify the compensating differential for health insurance, defined as the causal difference in wages between jobs with ESHI and jobs without ESHI. We can also characterize the corresponding hours differential using hours in lieu of wages. To obtain compensating and hours differentials, we simply compare wages and hours in the equilibria with ESHI (equilibria D and F) to wages and hours in the equilibria without ESHI (equilibria A and B). The first column of Table 1 shows the four possible comparisons of equilibrium wages and hours that we can use to measure compensating and hours differentials. As shown in Figure 1, because health reform shifts labor supply and labor demand, the compensating and hours differentials are different depending on which equilibria we compare.
Table 1.
Compensating and Hours Differentials
| Compensating Differential | Sufficient Statistics | Coefficients | |
|---|---|---|---|
| wD − wA |
|
β8 [+ β8e] | |
| wF − wB |
|
β1 + β8 [+ β1e + β8e] | |
| wD − wB |
|
β8 − β11 [+ β8e] | |
| wF − wA |
|
β1 + β8 + β11 [+ β1e + β8e] |
| Hours Differential | Sufficient Statistics | Coefficients | |
|---|---|---|---|
| LD − LA |
|
γ8 [+ γ8e] | |
| LF − LB |
|
γ1 + γ8 [+ γ1e + γ8e] | |
| LD − LB |
|
γ8 − γ11 [+ γ8e] | |
| LF − LA |
|
γ1 + γ8 + γ11 [+ γ1e + γ8e] |
We can also use the compensating and hours differentials to learn about the valuation of ESHI and the other model parameters. In the second column of Table 1, we express each compensating or hours differential in terms of the sufficient statistics of the model. These expressions follow directly from the geometry of Figure 1. We represent the slope of the labor supply curve with s and the slope of the labor demand curve with d (these slopes are elasticities if we specify w as the logarithm of wages and h as the logarithm of hours).
In our empirical implementation, we will be particularly interested in the compensating and hours differentials for individuals who switch from not having ESHI before the reform (equilibrium A) to having it after the reform (equilibrium F). For these individuals, as shown in the expression in the last row of the each panel of Table 1, if the penalty-and-subsidy-inclusive valuation is full (α + λ − μx = 1), then the absolute value of the compensating differential is equal to the cost of ESHI (ESHI decreases wages by b), and the hours differential is zero (ESHI does not distort hours worked). Therefore, if the compensating differential is equal to the cost of the benefit b and the hours differential is zero, then we can infer that the penalty-and-subsidy-inclusive valuation is full.8
2.3 Characterization of the Welfare Impact of Mandate-Based Health Reform Using Sufficient Statistics
To this point, we have developed a simple model that allows us to express all of the key parameters of mandate-based reform as well as the set of preferences that determine an individual’s valuation of ESHI in terms of labor market equilibria. We are also interested in how the Massachusetts and national mandate-based reform affect welfare and how these policies compare to alternative approaches that could be taken to expand health insurance coverage. Our model allows us to conduct welfare analysis simply with sufficient statistics, building on our estimated compensating differential.
Mandate-based policy can reduce welfare in two ways. First, if it distorts the labor market such that workers are willing to work for wages lower than the market wage and employers are willing to hire workers for more than the market wage, but the transaction does not occur. Second, workers at firms not offering ESHI face a penalty cost. The combined deadweight loss of the policies of mandate-based health reform (denoted by the subscript m) is as follows:
| (1) |
If we know the values for all of the terms in this equation, we can calculate the welfare impact of mandate-based health reform on the labor market.
2.4 Characterization of the Welfare Impact of Mandate-Based to Tax-Based Health Reform
While the welfare impact of mandate-based reform is clearly of interest, we are also interested in comparing the welfare impact of mandate-based reform to the welfare impact of a counterfactual reform to inform policy decisions and to give us a sense of whether the welfare impacts that we find are large or small. Using Equation (1), we can compare the deadweight loss of mandate-based reform to the deadweight loss of an alternative policy. If we can express the key policy elements in terms of labor market equilibria, then we can compare different policies simply by taking the ratio of the deadweight losses. In the tradition of Summers (1989), we compare the welfare impact of mandate-based health reform to the welfare impact of an alternative tax-based health reform.9
As an alternative to the full-compliance mandate, Summers (1989) considers a single counterfactual policy, which he refers to as a “benefit tax”. Under this counterfactual policy, again there is a single equilibrium before its implementation at A – no jobs include ESHI. Upon the implementation of the policy, the government levies a tax τ on employers to provide health insurance. Suppose for now that the tax is equal to the cost of providing a standard health insurance benefit b. The deadweight loss of the tax-based reform is given by the triangle T′AT :
The key assumption about tax-based reform is that it does not induce a shift in labor supply. Taking the ratio of the deadweight loss of mandate-based reform to the deadweight loss of tax-based reform, allowing b ≠ τ gives
| (2) |
This equation characterizes the welfare of the combined features of mandate-based reform relative to a tax-based reform in terms of a small number of sufficient statistics: the cost b that employers pay for ESHI compared to the necessary tax revenue τ for the same benefit; the penalty-and-subsidy-inclusive valuation, α + λ − μx, for individuals who have ESHI after reform; the employer penalty ρ for individuals who do not have ESHI after reform; and the fraction of individuals with ESHI after reform, ESHIAfter. Since the same individuals would be covered by both mandate-based and tax-based reform, underlying health risk is invariant to the plan. Thus the ratio of b to τ is just the relative loading cost of ESHI and government-provided health insurance. We turn next to estimating the key sufficient statistics—the cost of the benefit b and the penalty-and-subsidy-inclusive valuation α + λ − μx— which are functions of the compensating and hours differentials from before to after the reform.
Our welfare ratio generalizes the ratio implied by Summers (1989) and offers some insights that are counter-intuitive. To see this, first consider the ratio implied by Summers (1989): the ratio of the deadweight loss of a full-compliance employer mandate given by the triangle D′AD″ to the deadweight loss of tax-based reform given by triangle T′AT. This ratio simplifies to (1 − α)2, yielding the theoretical contribution of Summers (1989): an employer mandate reduces deadweight loss relative to a tax.
However, our model demonstrates that an employer mandate does not always reduce deadweight loss relative to a tax. If there is already a pay-or-play individual mandate in place, then the addition of a full-compliance or a pay-or-play employer mandate weakly decreases welfare relative to a tax. Consider the case where there is already an individual pay-or-play mandate in place, and some firms provide ESHI while others do not, but there is no employer mandate of any kind. If the tax is equal to the cost of health insurance (t = b), then the deadweight loss of the individual mandate relative to a tax is given by Equation (2) with μx = ρ = 0, which simplifies to (1 − α)2ESHIAfter. We can see from this expression that if there is no employer penalty, then there is no distortion to the labor market for firms that do not provide ESHI. Adding a full-compliance employer mandate weakly increases the deadweight loss ratio because after its imposition, all firms must provide ESHI (ESHIAfter = 1); zero distortion without ESHI is no longer possible. Likewise, adding a pay-or-play mandate weakly increases the deadweight loss ratio, which becomes (1 − α)2ESHIAfter + ρ2(1 − ESHIAfter) because there is now a deadweight loss triangle for firms without ESHI. Intuitively, the individual mandate has a smaller deadweight loss than a tax because it makes individuals willing to work for lower wages if they receive ESHI. When the individual mandate is already in place, the employer mandate results in additional deadweight loss for individuals without ESHI.
3 Identifying and Estimating the Model
In this section, we develop the empirical analog of our theoretical model. We have shown that we can express the compensating differential for ESHI and the welfare impact of health reform in terms of differences between the four labor market equilibria. Thus, to estimate the model we must identify wages and hours at each equilibrium. To do so, we rely on the variation induced by the reform in Massachusetts. The simplest approach would require only eight pieces of data to estimate the four labor market equilibria in Figure 1: average wages and hours for jobs with and without ESHI before and after reform within Massachusetts. We could then calculate the compensating differential for ESHI and the sufficient statistics for the welfare impact of health reform. However, we need to incorporate additional sources of variation to account for factors outside of the model that would bias our estimates were we to merely compare means in Massachusetts over time across groups. In practice, we also calibrate the sufficient statistics that are the least well-identified by our empirical variation.
3.1 The Estimating Equation
To estimate all of the relevant differences between labor market equilibria, the compensating and hours differentials and the welfare impact of health reform, we specify and estimate wage and hours equations of the following form:
| (3) |
where Yit measures wages w or hours L for individual i in state s at time t. We specify wages and hours in levels.10 MA is an indicator for the state of Massachusetts relative to other states, ESHI is an indicator for ESHI relative to the absence of ESHI, After is an indicator for the period after the reform relative to the period before the reform, and Large is an indicator for large firms relative to firms of known small size that are exempt from the employer mandate. We represent the coefficients of the wage equation with subscripted β coefficients, and we represent the corresponding coefficients of the hours equation with subscripted γ coefficients. The numbers of the coefficients convey that they are a subset of the coefficients of the full equation that we use to separately identify different values of μx, which we present in the Online Appendix. We include state fixed effects ϕs with a state other than Massachusetts omitted to control for differences in wages across states, and we include individual fixed effects δi to control for time-invariant differences across individuals, allowing for individual-specific shocks at time t, εit. We include a time fixed effect, After, to control for changes in the labor market over time.11 We begin with a baseline specification that excludes all bracketed terms. This specification excludes variation between large and small (exempt) firms. We subsequently include the bracketed terms in our full specification.
Our approach incorporates three key sources of variation in addition to the changes in Massachusetts over time in labor market outcomes by ESHI status. First, we rely on variation within individuals over time by including individual fixed effects. The individual fixed effects are essential because they allow us to control for a myriad of worker characteristics that shift labor supply and demand for a given individual for reasons that are correlated with having ESHI. That is, individuals who have ESHI are likely to differ from those individuals who do not, and those differences also manifest in labor market outcomes. Unobserved differences between individuals with and without ESHI is the standard concern that has plagued the literature on the compensating differential for health insurance. A more subtle but critical reason to incorporate individual fixed effects is the need to address compositional change among those with ESHI in Massachusetts from before to after the reform. If mandate-based reform differentially increases ESHI rates among individuals with lower wages and/or work hours, without individual fixed effects, we could spuriously estimate a negative relationship between ESHI and wages after the reform.
Second, we incorporate variation between Massachusetts and other states to control for factors that shift labor supply and demand nationally for reasons that are unrelated to Massachusetts health reform. Incorporating this variation allows us to control for any aggregate trends in the relationship between ESHI and labor market outcomes.
Finally, in our full specification, we incorporate variation between small and large firms.12 This additional source of variation allows us to better identify the impact of the employer penalty by comparing firms that qualified relative to firms that were exempt. In contrast, because it does not include variation by firm size, our baseline specification assumes that all Massachusetts firms are subject to the employer penalty after reform. Incorporating variation by firm size also helps to control for Massachusetts-specific factors unrelated to health reform that could shift labor supply and demand.13
Our estimating equations are relatively straightforward, allowing us to estimate them with ordinary least squares. The simplicity of the estimating equations is an advantage of our model relative to alternative structural models because robustness analysis is easier to implement, and the results are more transparent. Furthermore, because the functional form of these equations is relatively simple, we can interpret the coefficients directly as well as the combinations of coefficients that make up the sufficient statistics.
3.2 Estimating Wages, Hours, and the Compensating Differential for ESHI
To identify the wage and hours associated with different equilibria, we focus on the linear combinations of coefficients that correspond to wage and hours at each equilibrium A, B, D and F, as opposed to focusing on a single coefficient as in a traditional difference-in-differences model. Accounting for differences with relevant control groups, we express the wages associated with each equilibrium in Table 2. The hours associated with each equilibrium are equivalent with γ in place of β. To ease interpretation, we normalize wA = 0 and LA = 0 so that all equilibria are relative to the equilibrium without ESHI before reform. The derivation of these expressions is straightforward. For example, the difference in wages between equilibrium B and A (the equilibrium without ESHI after the reform relative to the equilibrium without ESHI before the reform) is β11, the change in wages from after the reform to before the reform for individuals who remain without ESHI in Massachusetts, relative to individuals in other states who remain without ESHI.14
Table 2.
Wages in Terms of Coefficients
| wA | NoESHI, Before | 0 |
| wB | NoESHI, After | β11 |
| wD | ESHI, Before | β8 [+ β8e] |
| wF | ESHI, After | β1 + β8 + β11 [+ β1e + β8e] |
Using the expressions for the labor market equilibria in Table 2, we can then express the compensating and hours differentials in terms of regression coefficients in the last column of Table 1. Our preferred measure of the compensating differential, wF − wA, is the sum of several coefficients: β1 + β8 + β11 [+β1e + β8e]. These coefficients reflect the change in wages observed for individuals who switch from not having ESHI before the reform to having it after the reform, relative to individuals who have the same switch in ESHI status from before to after reform in other states. Because the most convincing identification comes from changes in ESHI status for a given individual induced by the reform, we focus on this comparison for our preferred estimates of the compensating and hours differentials. In contrast, the first two differentials in Table 1 rely on changes in ESHI status for a given individual within the period either before or after reform. The changes in ESHI status that identify these compensating differentials could be endogenous, even after including individual fixed effects, if individuals gain ESHI when they get a better job that includes health insurance.
3.3 Estimating the Welfare Impact of Mandate-Based Health Reform
To estimate the welfare impact of health reform given in Equations (1) and (2), we first estimate the underlying sufficient statistics. We can express most of the sufficient statistics in terms of differences in wages and hours between the four labor market equilibria depicted in Figure 1. Our derivation follows directly from the geometry of the figure. In the first two rows of Table 3, we express the supply and demand curve slopes in terms of wages and hours differences between equilibria. The last column gives equivalent expressions in terms of coefficients. In the subsequent rows of the table, we express other sufficient statistics in terms of the slope of the labor supply and demand curves as well as differences between other equilibria.
Table 3.
Sufficient Statistics
| Sufficient Statistics | Wages and Hours | Coefficients | ||
|---|---|---|---|---|
| s |
|
|
||
| d |
|
|
||
| b | d(LF − LA) − (wF − wA) | d (γ1+ γ8 + γ11 + [γ1e + γ 8e]) − (β1 + β8 + β11 [+β1e + β8e]) | ||
| ρ |
|
|
||
| α |
|
|
||
| λ − μx |
|
|
||
| α + λ − μx |
|
|
As discussed above, the differences between labor market equilibria that are identified by changes resulting from the Massachusetts reform are arguably best identified. Therefore, some sufficient statistics are identified more convincingly than others. Fortunately, these sufficient statistics are the most important for welfare analysis: the penalty-and-subsidy-inclusive valuation (α + λ − μx) and the cost of ESHI to employers (b).
The other sufficient statistics are identified in principle, but not as convincingly because they do not depend on changes in ESHI status induced by the reform.15 In practice, we estimate values for these parameters that do not accord well with values that we expect based on the literature and the empirical magnitude of the employer penalty. Given that these parameters are not identified by the Massachusetts reform and that their misspecification can affect the estimates of all the other sufficient statistics through the s and d terms in their derivations, we discard the empirical estimates and calibrate them. Reviewing the literature suggests that reasonable magnitudes for labor supply and demand elasticities are 0.1 and −0.2, respectively (Blundell and MaCurdy 1999, Hamermesh 1996).16 We also calibrate the employer penalty ρ such that the dollar value of the employer penalty ρb is equal to the statutory penalty of $295 per year.
Given that we calibrate some sufficient statistics, one might be tempted to calibrate most of our model using the statutory values of the policy parameters, rather than estimating any sufficient statistics. However, it is important to estimate the sufficient statistics for two main reasons. First, the individual’s underlying valuation α does not have a statutory value. Second, the behavioral response to the policy parameters might be smaller or larger than the statutory policy parameters because of interactions between them and the individual’s underlying valuation (see footnote 7), or if individuals over respond if they are averse to paying penalties on moral grounds.17 Therefore, we only calibrate values when we have reason to believe that identification is not convincing and the empirical results are not consistent with the model.
4 Data and Summary Statistics
4.1 The Survey of Income and Program Participation
For our main analysis, we use the Survey of Income and Program Participation (SIPP), a nationally representative longitudinal survey covering households in the civilian noninstitutionalized population. As we discuss in detail, the longitudinal nature of the SIPP is critical for identification. Individuals selected into the SIPP sample are interviewed once every four months over a four-year panel. Each interview covers information about the previous four-month period, resulting in person-month-level data. Interview months differ across individuals in the sample. Previous research has shown evidence of “seam bias” in the SIPP, whereby individuals tend to give the same responses during one interview for all four months associated with the interview period, but they do change responses from one interview to the next (see Chetty [2008]). To address seam bias, we restrict our data to the interview month in our regression specifications. We use weights in all summary statistics and regressions to account for the SIPP sampling and response unit design.18
We use the full 2004 SIPP panel, which covers October 2003 to December 2007. A potential limitation of this SIPP panel is that it does not extend for a long time after reform was fully implemented, and it will not be extended further because an entirely new SIPP cohort began in 2008. Despite this potential limitation, we believe the SIPP data are the best-suited to modeling the labor market impact of the Massachusetts reform for a number of reasons.
First and foremost, the SIPP is the largest longitudinal data set that we are aware of that includes labor market outcomes and insurance information. The Medical Expenditure Panel Survey (MEPS) is longitudinal, but it only extends for two and a half years, and the sample size is only approximately 15 percent of the size of the SIPP, with 160 individuals in Massachusetts.19 The Current Population Survey (CPS) and the American Community Survey (ACS) do not include longitudinal identifiers for health insurance. Although administrative data from Social Security are longitudinal, they do not include information on hours worked or insurance.
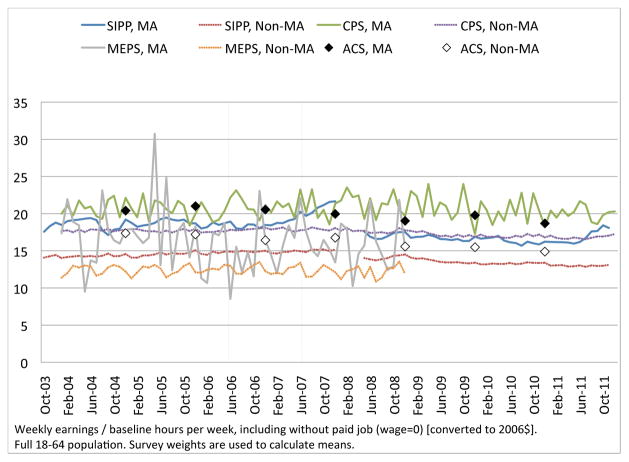
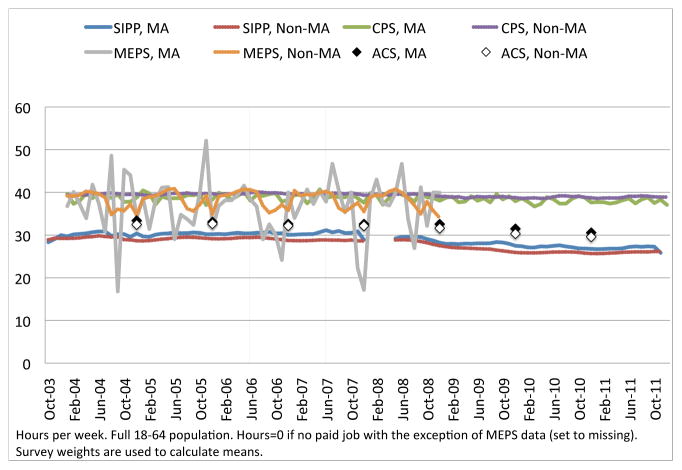
Second, while we cannot compare wage and hours trends conditional on individual fixed effects across data sets because of data availability, raw wage and hours trends are very similar in the SIPP to those in other data sets inside and outside of Massachusetts. We present these comparisons in Appendix B.
Third, although we observe a relatively short period of responses after the individual mandate went into effect on July 1, 2007, we also observe a full year of responses during the implementation of the reform. Thus, we are able to observe the response in wages and hours of all individuals who changed ESHI status in Massachusetts at any time after the reform was passed. This is particularly valuable because open-enrollment periods for ESHI are generally in November, with new coverage starting in January. Thus, to satisfy the individual mandate in July 2007 by taking up ESHI, many individuals would have to start coverage in January 2007, well before our data end at the end of December 2007.20 Using data from the CPS, we find that of the eventual increase in coverage among those 18–64 in Massachusetts by 2010, 87 percent had occurred by the end of 2007 (measured in the March 2008 CPS). The share of the eventual increase in those covered by ESHI by 2010 is even higher at 91 percent, suggesting that our sample period covers the time in which much of the expansion due to the reform had occurred despite our relatively short post-reform period.21
Despite all of the advantages of the 2004 SIPP panel, one limitation is that the sample size decreases over time, primarily because of interview reductions but also because of attrition. Our group of interest is the population between the ages of 18 and 64. In 2004, there are 72,057 unique individuals in this sample across states, of which 2,047 unique individuals are in Massachusetts. In 2007, there are 28,661 unique individuals in the sample, of which 685 unique individuals are in Massachusetts.
Using the SIPP, we construct our main dependent variables: hourly wages w and hours worked per week L. We convert all wages into 2006 dollars using the Consumer Price Index for all urban consumers (CPI-U) to adjust for inflation. The SIPP allows respondents to report wages and hours for up to two jobs, but our estimates rely on income and hours worked only in the primary job. Because the SIPP data only include monthly income, not monthly wages, we must divide income by a measure of hours worked to obtain monthly wages. However, because our model relies on separate movements in w and L, it would be problematic for both measures to reflect contemporaneous movements in L. To get around this issue, which is related to the division bias problem in the labor economics literature, we divide income by the average hours reported in the first four interviews (representing a 16-month period). Our regression estimates are robust to alternative wage measures because hours vary less than wages.
4.2 Summary Statistics
We report summary statistics in Table 4. We compare the full population, the Massachusetts population, and the non-Massachusetts population before reform and after reform. We exclude the during-reform period here for simplicity. The first row of the table shows our primary measure of w: weekly earnings divided by baseline hours per week, including zero wages for individuals without a paid job. Wages are higher in Massachusetts than they are in other states before and after reform. Netting out the change in wages in other states from before to after reform, as shown in the last column, hourly wages increased by $1.10 in Massachusetts after reform on a base of $17.90 before reform. This increase is statistically significant. Excluding individuals without a paid job in the second and third rows of the table, we see that wages increased by $0.05, or 0.1 percent among the employed, which is less than the wage increase that we see in the full sample, suggesting that part of the wage increase we observe is driven by an increase in the number of people with paid jobs. Indeed, the probability of reporting a paid job increased by 2.9 percentage points in Massachusetts after reform on a base of 81.8 percent before reform.
Table 4.
Summary Statistics
| Full Population | MA | Non-MA | MA-Non-MA | ||||
|---|---|---|---|---|---|---|---|
| Before | After | Before | After | Before | After | After-Before | |
| w: Weekly earnings / baseline hours per week | 13.998 | 14.189 | 17.895 | 19.164 | 13.909 | 14.077 | 1.101*** |
| w|paid job & w>0 | 20.247 | 20.757 | 24.707 | 25.259 | 20.141 | 20.644 | 0.049 |
| Log(w|paid job & w>0) | 2.736 | 2.773 | 2.930 | 2.973 | 2.732 | 2.768 | 0.007 |
| L: Hours per week | 29.237 | 28.803 | 30.257 | 31.053 | 29.214 | 28.752 | 1.258*** |
| L|paid job & L>0 | 39.055 | 38.848 | 38.288 | 37.817 | 39.074 | 38.874 | −0.271*** |
| Log(L|paid job & L>0) | 3.607 | 3.606 | 3.571 | 3.562 | 3.608 | 3.607 | −0.008** |
|
| |||||||
| Hours per week in all jobs | 39.896 | 39.471 | 39.452 | 38.313 | 39.906 | 39.499 | −0.732*** |
| Paid job | 0.783 | 0.777 | 0.818 | 0.841 | 0.782 | 0.775 | 0.029*** |
| Employed by Large Firm | 0.853 | 0.845 | 0.854 | 0.825 | 0.853 | 0.845 | −0.022*** |
|
| |||||||
| Any Health Insurance | 0.830 | 0.837 | 0.907 | 0.952 | 0.828 | 0.835 | 0.038*** |
| ESHI | 0.657 | 0.653 | 0.741 | 0.742 | 0.655 | 0.651 | 0.005 |
|
| |||||||
| <150%FPL† | 0.193 | 0.200 | 0.130 | 0.109 | 0.194 | 0.202 | −0.028*** |
| 150–300%FPL† | 0.283 | 0.288 | 0.207 | 0.171 | 0.285 | 0.291 | −0.042*** |
|
| |||||||
| Age | 39.996 | 40.265 | 40.499 | 40.785 | 39.985 | 40.254 | 0.018 |
| Married | 0.561 | 0.552 | 0.545 | 0.499 | 0.562 | 0.554 | −0.038*** |
| Female | 0.507 | 0.507 | 0.514 | 0.516 | 0.507 | 0.507 | 0.002* |
FPL category defined for each individual based on status in the Jan–June 2006 period.
2004 SIPP Panel. Monthly weights used.
Full 18–64 population. Only includes interview months.
Before: October 2003 – June 2006; After: July 2007 – December 2007. Statistics are averages over the relevant period.
MA-Non-MA After-Before is the coefficient on MA*After from a regression of the outcome on MA*After, MA, and After.
p<0.01,
p<0.05,
p<0.1, block bootstrapped by state.
w and L measures include individuals without a paid job with w=0 or L=0, respectively, unless noted otherwise.
Results in the fourth row suggest that hours increased by 1.3 hours per week in our preferred measure of L, which includes zero hours for individuals without a paid job. However, the increase in hours appears to entirely reflect an increase in employment. Among individuals with a paid job, hours decreased by 0.27 hours per week on a base of 38.3 hours per week before reform, or by 0.8 percent in the logarithmic specification. The next row shows that by focusing on the first job only in our primary measure of L, we account for approximately 95 percent of hours in all jobs.
Taken together, these statistics suggest that Massachusetts experienced increased wages and increased hours overall, with some of the increase in wages and all of the increase in hours operating through increased employment. The increases in wages and hours that we observe are consistent with our model, which predicts small but ambiguously signed impacts on the aggregate labor market, given small numbers of individuals who switch ESHI status. We will need to use our regression framework with individual fixed effects to focus on those individuals who changed coverage due to the reform, isolating the key empirical variation.
Individuals who changed ESHI status as a result of the reform are critical to our identification. In the middle rows of Table 4, we compare insurance coverage in Massachusetts and other states. Massachusetts has higher insurance coverage rates than other states; approximately 91 percent of individuals between the ages of 18 and 64 in Massachusetts had some type of health insurance before reform, increasing to 95 percent after reform. Outside of Massachusetts, health insurance coverage stayed flat at 83 percent. The simple difference-in-differences estimate for the increase in coverage in Massachusetts due to the reform is 3.8 percentage points—slightly lower but consistent with existing estimates (Long 2008; Kolstad and Kowalski 2012; Yelowitz and Cannon 2010). We also see an increase in the rate of ESHI coverage in Massachusetts of 0.5 percentage points; however, this increase is not statistically significant.
Table 5 presents summary statistics for those switching ESHI status from before reform to after reform in Massachusetts and control states. Our estimates likely give us a local average treatment effect for the individuals who are induced to switch ESHI status by the Massachusetts reform, but this local average treatment effect will be policy relevant if similar individuals are induced to switch by the ACA. We see that those who switched ESHI status following reform in Massachusetts had lower hourly wages, fewer working hours, and lower rates of employment before reform than the average Massachusetts resident. The differences between those who switched ESHI status and the rest of the population are relatively small, but they underscore the need for us to use individual fixed effects in our regression specifications to account for compositional change in the population with ESHI. We also see that those switching ESHI status were slightly younger, less likely to be married, and more likely to be male than the population that did not change ESHI status. Finally, the bottom panel shows that those changing ESHI status were roughly equally likely to change from a small to a large firm and vice versa from the period from before reform to after reform. Their rate of firm size switching was also no higher than it was nationally, suggesting that the population that identifies our main results does not systematically move between firms based on the applicability of the employer penalty.
Table 5.
Summary Statistics for Individuals Changing ESHI Status in MA vs. Non-MA
| All States | MA | |||
|---|---|---|---|---|
| All | ESHI Switchers | All | ESHI Switchers | |
| Unique Individuals observed Before and After Reform | 23,239 | 4,030 | 626 | 87 |
|
| ||||
| w: Weekly earnings / baseline hours per week | 14.040 | 8.487 | 18.175 | 9.151 |
| w|paid job & w>0 | 20.370 | 15.440 | 24.877 | 16.488 |
| Log(w|paid job & w>0) | 2.746 | 2.457 | 2.936 | 2.531 |
| L: Hours per week | 29.129 | 23.319 | 30.643 | 22.120 |
| L|paid job & L>0 | 39.008 | 36.737 | 38.366 | 33.162 |
| Log(L|paid job & L>0) | 3.607 | 3.526 | 3.571 | 3.344 |
|
| ||||
| Hours per week in all jobs | 39.786 | 38.104 | 39.377 | 34.280 |
| Paid job | 0.781 | 0.700 | 0.824 | 0.709 |
| Employed by Large Firm | 0.851 | 0.825 | 0.849 | 0.794 |
|
| ||||
| Any Health Insurance | 0.832 | 0.711 | 0.915 | 0.804 |
| ESHI | 0.656 | 0.357 | 0.736 | 0.314 |
|
| ||||
| <150%FPL† | 0.197 | 0.311 | 0.134 | 0.311 |
| 150–300%FPL† | 0.289 | 0.387 | 0.199 | 0.270 |
|
| ||||
| Age | 40.088 | 37.556 | 40.467 | 38.548 |
| Married | 0.559 | 0.452 | 0.533 | 0.303 |
| Female | 0.507 | 0.515 | 0.513 | 0.502 |
|
| ||||
| FIRM SIZE CHANGES (before to after): | ||||
| Large to small | 0.056 | 0.145 | 0.065 | 0.201 |
| Small to large | 0.077 | 0.198 | 0.065 | 0.171 |
Notes:
Sample includes 18–64 population, interview months only (4th-reference months).
ESHI switchers reports individuals who switched ESHI status between at least one inteview month before reform and at least one interview month after reform.
MA indicates in MA in at least one interview month.
5 Results and Discussion
5.1 Graphical Analysis
We begin by presenting a graphical version of our baseline specification that allows us to investigate trends over time, after incorporating individual fixed effects. To do so, we run a regression analogous to our baseline (no bracketed terms) specification given by Equation (3), where the only change is that we replace every instance of After with a vector of all two-month periods in our data, including those before reform, omitting only the last two-month period before reform (May–June 2006).22
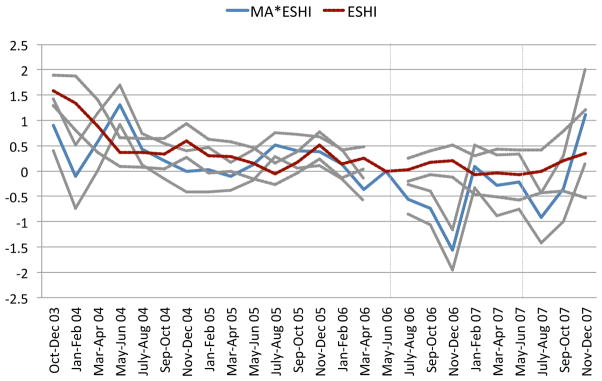
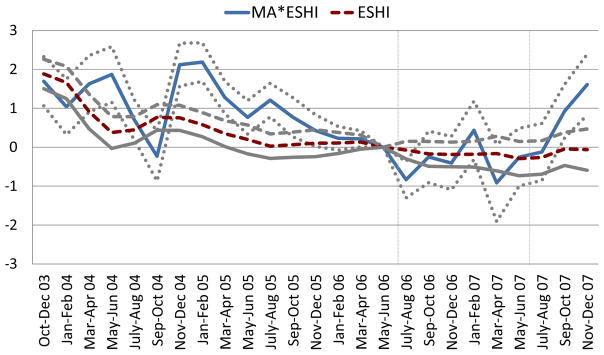
In Figure 2, we plot the vector of coefficients corresponding to β12 with the points connected by the dashed line labeled ESHI. This line gives the wage premium for jobs with ESHI relative to jobs without ESHI outside of Massachusetts—the empirical difference in wages between jobs with ESHI and jobs without ESHI. We also plot the vector of coefficients corresponding to β1 with the points connected by the solid line labeled MA * ESHI. This line gives the differential wage premium for ESHI jobs relative to jobs without ESHI in Massachusetts relative to other states. Because individual fixed effects are included in the regressions, the coefficients are identified by people who change ESHI status in the given period relative to the omitted period outside and inside of Massachusetts, respectively. We also show 95 percent confidence intervals for both lines, clustered by state. In Figure 3, we plot the corresponding γ coefficients from a regression with hours as the dependent variable.
Figure 2.
Wage Premium for ESHI, Controlling for Individual Fixed Effects, MA vs. Non-MA
Regression coefficients with w as dependent variable. See text for details.
Wages and ESHI are two-month indicators. May–June 2006 are normalized to zero.
Figure 3.
Hours Premium for ESHI, Controlling for Individual Fixed Effects, MA vs. Non-MA
Regression coefficients with h as dependent variable. See text for details.
Hours and ESHI are two-month indicators. May–June 2006 are normalized to zero.
Outside of Massachusetts, we see that the wage premium for ESHI jobs stays fairly constant over time in Figure 2. Within Massachusetts before reform, the wage premium appears more variable, likely given the smaller sample size. However, trends in the wage premium are broadly similar in Massachusetts and in the other states before reform, lending support to our identification strategy.
Following the passage of reform in Massachusetts, we see a striking shift in the relationship between ESHI and wages for individuals who switch ESHI status. There is a substantial drop in the wage premium for ESHI jobs relative to jobs without ESHI during and after the reform in Massachusetts relative to the period before the reform and relative to other states. We generally see a drop in the wage premium during each of the two-month periods after May–June 2006 except for the last two-month period, which shows a puzzling increase in both figures. The increase seems to be due to sizable attrition from the sample in the last two months and not to a real increase in the wage premium.23 Our regression specification, which pools all data within the before, during, and after periods separately, places little weight on the visible uptick in the very last two-month period because of the small sample size from which it is drawn.
The results in Figure 3 suggest that, while trends in the hours premium are somewhat noisy in Massachusetts, they do not change dramatically in Massachusetts after the reform. The uptick that we observe in the last period of observation appears to be due to sample attrition, as in Figure 2. The overall small impact that we observe on the hours premium is consistent with the relatively large observed decline in the wage premium; if wages for those with ESHI fell by roughly the full the cost of ESHI to the employer, we would not expect a change in hours worked. The timing of the shift in the wage premium coincides well with the reform.24
Although the regression results formalize the magnitude of the decline in the wage premium after reform, we can learn something about the magnitude by examining Figures 2 and 3, keeping in mind that the last point gets the smallest weight. We should also keep in mind that we expect wages for jobs with and without ESHI to fall in Massachusetts after reform, and by analyzing coefficients that correspond to β1 only, we are assuming that there is no employer penalty. The true compensating differential that takes the employer penalty into account will be larger than the effects we observe. In Figure 2, the magnitude of the decline in the wage premium for ESHI jobs in Massachusetts over the entire period during and after reform appears to be approximately $1.5/hour, which corresponds to a roughly 7.5 percent decline. These figures provide the first evidence that the Massachusetts reform affected jobs with ESHI, as we predict in our model. They also signal that we have found an exogenous source of variation that will be useful in identifying a compensating differential for ESHI.
The shift that we observe in the relationship between ESHI and wages from before to after reform in Massachusetts is particularly striking because it implies that individuals who switched into ESHI from before to after reform experienced declines in real wages that were larger than inflation, indicating that they experienced declines in nominal wages. The labor economics literature shows that it is very rare for workers who remain in the same job to accept declines in nominal wages. Since these figures do not condition on remaining in the same job, some of the decline could be due to workers who switch ESHI status at the same time that they switch jobs, and these workers could accept lower monetary wages if they receive health insurance. Alternatively, workers could have accepted lower nominal wages in the same job if the firm started providing health insurance. Because the reform in Massachusetts affected the universe of employers, it is plausible that it motivated compensation renegotiations, which allowed for nominal wage reductions. We know of no data on this, so we cannot say much about the detail of the mechanism. We do, however, return to these alternatives in a set of robustness checks that condition on remaining in the same job.
5.2 Regression Results
We report results from the baseline wage and hours equations in Table 6, and we begin our analysis by examining the coefficients directly. Recall that β1 gives the compensating differential and γ1 gives the hours differential if we assume that there is no employer penalty such that individuals without ESHI in Massachusetts after reform provide an additional control group for individuals with ESHI in Massachusetts after reform. That is, we do not allow for variation by firm size that distinguishes those who face the employer penalty in the group without ESHI. The estimated β1 tells us that hourly wages are $0.85 lower for the same individuals when they have ESHI relative to when they do not have ESHI, after the reform relative to before the reform, in Massachusetts relative to other states. This coefficient is statistically significant at the 99 percent level. Annualizing the decrease in hourly wages for a full-time worker, this coefficient implies that the compensating differential for ESHI is −$1, 759.68 (=−0.846 × 40 × 52) per year. This compensating differential is of the expected sign, standing in contrast to much of the literature.
Table 6.
Results from Baseline Specification
| (1) | (2) | |||
|---|---|---|---|---|
| w | L | |||
| Weekly earnings / baseline hours per week, including individuals without a paid job (wage=0) | Hours per week, including individuals without a paid job (hours=0) | |||
| MA* ESHI* After | β1 | −0.846*** | ϒ1 | −0.238 |
| [−1.321, −0.277] | [−0.917, 0.301] | |||
| MA* ESHI* During | β1d | −0.745*** | ϒ1d | −1.743*** |
| [−1.036, −0.346] | [−2.201, −1.331] | |||
| MA* ESHI | β8 | 1.128*** | ϒ8 | 1.053*** |
| [0.717, 1.418] | [0.404, 1.383] | |||
| MA* After | β11 | 1.728*** | ϒ11 | 1.559*** |
| [1.297, 1.993] | [1.085, 2.028] | |||
| MA* During | β11d | 1.191*** | ϒ11d | 2.433*** |
| [0.856, 1.360] | [2.092, 2.723] | |||
| ESHI* After | β12 | −0.298 | ϒ12 | −0.611** |
| [−0.790, 0.170] | [−0.942, −0.108] | |||
| ESHI* During | β12d | −0.380** | ϒ12d | −0.494*** |
| [−0.667, −0.098] | [−0.695, −0.231] | |||
| ESHI | β19 | 3.672*** | ϒ19 | 6.416*** |
| [3.286, 3.872] | [5.939, 6.703] | |||
| After | β22 | 0.629*** | ϒ22 | 0.314 |
| [0.226, 0.928] | [−0.189, 0.721] | |||
| During | β22d | 0.514*** | ϒ22d | 0.302** |
| [0.314, 0.722] | [0.045, 0.517] | |||
|
| ||||
| Observations | 543,630 | 499,828 | ||
| R-squared | 0.738 | 0.805 | ||
p<0.01,
p<0.05,
p<0.1, 95% confidence intervals reported; CIs block bootstrapped by state.
Including full 18–64 population.
Only includes interview months.
Individual and state fixed effects included. Monthly weights used.
In the second column of Table 6, our estimate of the hours differential using γ1 tells us that weekly hours are −0.238 lower for jobs with ESHI relative to jobs without ESHI in Massachusetts relative to other states, after reform relative to before reform. Recall that if the penalty-and-subsidy-inclusive valuation of the benefit is full, the hours differential will be zero. The estimated coefficient is not statistically different from zero, and the standard errors rule out large increases or decreases in hours, consistent with a relatively high valuation of the benefit.
To extend these results, we turn to estimating our full model that incorporates variation by firm size. As we discussed in Section 3, this additional source of variation allows us to separately estimate the employer penalty and to allow for changes in the Massachusetts labor market unrelated to health reform. We also find empirical support for the inclusion of this additional variation in our full specification.25
5.3 Estimates of the Compensating Differential for ESHI
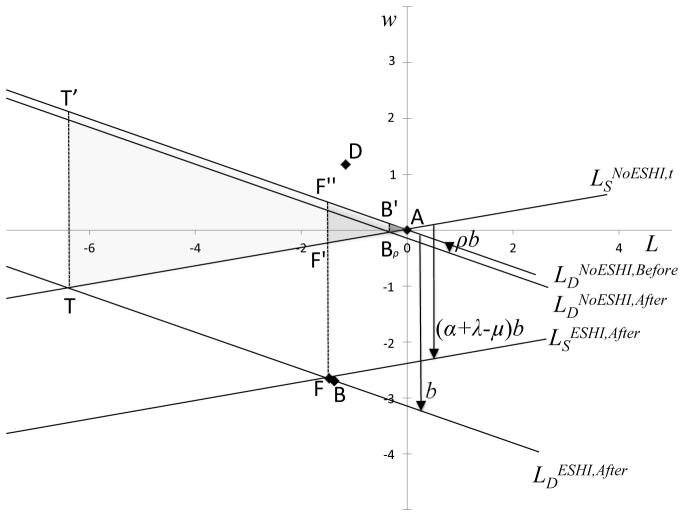
To obtain estimates of the compensating differential and hours differential for ESHI, we estimate our full specification with firm size interaction terms, and we report the results in Table 7. We plot the empirical analogs of the four theoretical equilibria shown in Figure 1 Figure 4. We plot all equilibria relative to equilibrium A (no ESHI before reform) at the origin.
Table 7.
Results from Full Specification
|
|
|||||||
|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | |||||
| w | L | ||||||
| Weekly earnings / baseline hours per week, including individuals without a paid job (wage=0) | Hours per week, including individuals without a paid job (hours=0) | Compensating and Hours Differentials, Sufficient Statistics, and Welfare Impact of Health Reform | |||||
| MA* ESHI* After* Large | β1 | −1.264* | Upsi;1 | −0.593 | wD−wA | 1.193*** | |
| [−2.328, 0.00400] | [−1.871, 0.425] | [0.801, 1.482] | |||||
| MA* ESHI* During* Large | β1d | −1.535*** | Upsi;1d | 0.433 | wF−wB | 0.136 | |
| [−2.485, −0.535] | [−0.197, 1.125] | [−0.409, 0.542] | |||||
| MA* ESHI* Large | β8 | 1.059*** | Upsi;8 | −2.001*** | wD−wB | 2.682*** | |
| [0.558, 1.515] | [−2.819, −1.332] | [1.987, 3.341] | |||||
| MA* After* Large | β11 | −1.488*** | Upsi;11 | −1.142** | wF−wA | −1.352*** | |
| [−2.156, −0.869] | [−2.010, −0.233] | [−2.447, −0.528] | |||||
| MA* During* Large | β11d | 1.107*** | Upsi;11d | −0.768*** | |||
| [0.318, 2.025] | [−1.438, −0.223] | ||||||
| ESHI* After* Large | β12 | 0.301 | Upsi;12 | −0.0484 | LD−LA | 0.42 | |
| [−0.787, 1.249] | [−1.083, 0.968] | [−0.293, 0.811] | |||||
| ESHI* During* Large | β12d | 0.561 | Upsi;12d | −0.414 | LF−LB | 0.185 | |
| [−0.322, 1.459] | [−0.896, 0.114] | [−0.939, 0.788] | |||||
| ESHI* Large | β19 | 1.844*** | Upsi;19 | 7.212*** | LD−LB | 1.563*** | |
| [1.365, 2.178] | [6.580, 7.800] | [0.341, 2.286] | |||||
| After* Large | β22 | −0.394 | Upsi;22 | −0.688** | LF−LA | −0.957** | |
| [−1.029, 0.165] | [−1.540, −0.00700] | [−2.279, −0.115] | |||||
| During* Large | β22d | −0.413 | Upsi;22d | −0.257 | |||
| [−1.300, 0.119] | [−0.837, 0.151] | ||||||
| Large | β23 | −2.458*** | Upsi;23 | −12.754** | |||
| [−4.593, −2.045] | [−14.515, −11.061] | ||||||
| MA* Large | β24 | −2.136 | Upsi;24 | 3.124** | |||
| [−2.414, 0.183] | [1.259, 5.140] | ||||||
| MA* ESHI* After | β1e | 0.207 | Upsi;1e | 0.358 | |||
| [−1.166, 1.497] | [−0.584, 1.255] | ||||||
| MA* ESHI* During | β1ed | 0.607 | Upsi;1ed | −1.853*** | s | 0.190 | |
| [−0.323, 1.716] | [−2.432, −1.211] | - | |||||
| MA* ESHI | β8e | 0.135 | Upsi;8e | 2.422*** | d | −0.380 | |
| [−0.442, 0.595] | [1.664, 2.885] | - | |||||
| MA* After | β11e | 2.895*** | Upsi;11e | 2.247*** | b | 1.715*** | |
| [2.152, 3.581] | [1.489, 2.963] | [0.684, 3.059] | |||||
| MA* During | β11ed | 0.189 | Upsi;11ed | 2.799*** | ρ | 0.083*** | |
| [−0.689, 0.812] | [2.182, 3.345] | [0.046, 0.208] | |||||
| ESHI* After | β12e | −0.528 | Upsi;12e | −0.512 | α + λ − μx | 0.682*** | |
| [−1.728, 0.747] | [−1.296, 0.297] | [0.405, 0.936] | |||||
| ESHI* During | β12ed | −0.843** | Upsi;12ed | −0.149 | ESHIAfter | 0.740 | |
| [−1.829, −0.0150] | [−0.559, 0.308] | - | |||||
| ESHI | β19e | 2.193*** | Upsi;19e | 0.589*** |
|
1.000 | |
| [1.682, 2.603] | [0.135, 0.952] | - | |||||
| After | β22e | 0.925*** | Upsi;22e | 0.829** | DWLm | 0.198*** | |
| [0.296, 1.546] | [0.261, 1.487] | [0.01, 1.1] | |||||
| During | β22ed | 0.842*** | Upsi;22ed | 0.523*** |
|
0.077*** | |
| [0.292, 1.632] | [0.105, 1.046] | [0.012, 0.265] | |||||
|
| |||||||
| Observations | 543,630 | 499,828 | |||||
| R-squared | 0.739 | 0.815 | |||||
p<0.01,
p<0.05,
p<0.1, 95% confidence intervals reported; CIs block bootstrapped by state.
Including full 18–64 population.
Only includes interview months.
Individual and state fixed effects included. Monthly weights used.
Figure 4.
Empirical Estimates of Wage and Hours Equilibria
The most important relationship to notice in Figure 4 is that equilibrium F (ESHI after reform) is to the lower left of equilibrium A (no ESHI before reform), as predicted by our theory. The relationship between A and F is the best identified relationship in the figure. The compensating differential for ESHI from Table 1 is the negative of the vertical distance between equilibrium A and equilibrium F. As depicted in Figure 4, the third column of Table 7 shows that wF − wA is equal to −$1.35 per hour. Annualizing the point estimate for a full-time worker, the implied compensating differential is −$2, 812 per year, which corresponds closely to the average cost of ESHI to employers. This suggests that the magnitude of our estimate is in a plausible range and that the penalty-and-subsidy-inclusive valuation is high. The annualized 95 percent confidence interval on the compensating differential is −$5, 090 to −$1, 098 per year.26 We obtain our preferred estimate of the hours differential for ESHI by taking the negative of the horizontal distance between equilibrium A and equilibrium F. As depicted in Figure 4, the third column of Table 7 shows that LF − LA is equal to −0.96 hours per week. While small in magnitude, this estimate is statistically different from zero at the 5 percent level.
We can also derive compensating and hours differentials by comparing other equilibria, as shown in Table 1. However, all of the other compensating differentials are of the wrong theoretical sign, which is not surprising because they are not identified by health reform. Because we cannot convincingly identify the location equilibrium D relative to equilibrium A, we are not able to separately identify the components of the penalty-and-subsidy-inclusive valuation of health insurance, α and λ − μ, and our separate estimates of these parameters are unreasonable. Although these parameters would be interesting to analyze, we do not need to separately identify them to identify the aggregate welfare impact of mandate-based health reform.
5.4 Estimates of the Welfare Impact of Health Reform
Up to this point, our results have come directly from the regression coefficients, and we have not made any calibrations. In theory, all of the sufficient statistics for the deadweight loss for health reform given by Equation (1) are identified. However, as we discuss above, we have reason to believe that the identification for equilibrium B and equilibrium D is not convincing, and plotting the empirical equilibria gives us further cause to doubt their identification. Therefore, we rely only on the difference between labor market equilibria that is identified by variation due to the Massachusetts reform (equilibrium F relative to equilibrium A), and we calibrate other sufficient statistics as shown in Table 8.27
Table 8.
Calibrated Sufficient Statistics
| Calibrated Sufficient Statistics | Calibrated Values with Wages and Hours | |
|---|---|---|
| s | 0.190 | |
| d | −0.380 | |
| b | d(LF − LA) − (wF − wA) | |
| ρ |
|
|
| α + λ − μx |
|
|
| ESHIAfter | 0.74 | |
| b/τ | 1 | |
| DWLm |
|
|
| DWLm/DWLτ |
|
The bottom portion of the third column of Table 7 gives the corresponding estimated values. As shown, we obtain a value of 1.72 for b, which translates into $3,566 annually for a full-time worker. This number is somewhat smaller than the rough cost of ESHI estimated from the Kaiser survey data of $6,105. We obtain an estimated value of 0.68 for the penalty-and-subsidy-inclusive valuation, which suggests that workers value health expenditures made by their employers at about $0.68 per $1.28 The magnitude of the penalty-and-subsidy-inclusive valuation is quite high. In fact, the 95 percent confidence interval for the penalty-and-subsidy-inclusive valuation ranges up to 0.94.
We find that the deadweight loss of mandate-based health reform is equal to $10 per year (= 0.198 × 12). Relative to tax-based health reform, mandate-based health reform is substantially more efficient: we calculate DWLm/DWLτ = 0.077; the distortions that mandate-based health reform induces are only 8 percent of the distortions induced by tax-based health reform.29 The confidence interval reported in Table 7 suggests that we are 95 percent certain that the deadweight loss of mandate-based health reform is between 1.2 percent and 26.5 percent of the deadweight loss of tax-based health reform. This substantial efficiency is perhaps not surprising as it follows directly from our estimate of a relatively high penalty-and-subsidy-inclusive valuation for ESHI.
5.5 Robustness of the Empirical Results
In Appendix C, we consider the robustness of the empirical results. In Appendix C.1, we examine the robustness of our empirical results to the calibrated values, and we show that our main finding that the deadweight loss of mandate-based health reform is substantially smaller than the deadweight loss of tax-based health reform is robust to a wide range of calibrated values. In Appendix C.2, we examine robustness to the estimation sample and show that the results are similar when we restrict our sample to individuals in New England and married individuals. When we restrict our sample to individuals in New England, we find that the ratio of the deadweight loss of mandate-based health reform to the ratio of the deadweight loss of tax-based health reform is 0.1 percent—which is smaller but qualitatively similar to our preferred estimate of 7.7 percent. In Appendix C.3, we examine continuous workers separately from workers who move into and out of employment, and we find that we still observe a compensating differential among continuous workers. Finally, in Appendix C.4, we show that our results are not robust to the exclusion of individual fixed effects—individual fixed effects are essential to identification.
5.6 Implications for National Reform
The impact of mandate-based reform in Massachusetts is interesting its own right. However, because the Massachusetts reform bore all of the same key features as national health reform, we can use our model and our estimates to reach some conclusions about the potential welfare impact of the ACA. While we do not model all of the underlying structure that would be required to fully predict the impact of national reform, because of the many similarities between both reforms, given our sufficient statistics approach, we expect the welfare impacts to be similar to the extent the policy parameters are equivalent in Massachusetts and under the ACA.30 Since the magnitudes of the individual penalty, employer penalty, and subsidies differ across the reforms, we can use our model to consider the robustness of our main conclusions. We can also use our model to consider the impact of other differences between Massachusetts and the rest of the nation.
The relatively larger individual penalty under the ACA suggests that the national reform could be even more efficient than the Massachusetts reform. The individual penalty increases the penalty-and-subsidy-inclusive valuation, decreasing distortion. Thus, while the labor market distortion of mandate-based health reform in Massachusetts was only 8 percent of the distortion of tax-based health reform, a larger individual penalty would decrease the ratio even further. On the other hand, the employer penalty is also larger under ACA than it is in Massachusetts, which increases distortion. In practice, the size of the employer penalty is unlikely to change our basic conclusions on the efficiency of mandate-based reform. As we show in Appendix C.1, our finding that mandate-based health reform is substantially more efficient than tax-based health reform is robust to the larger value of the penalty.
There could also be general equilibrium changes to health insurance markets under national reform that our analysis of the Massachusetts reform does not capture. For example, compliance with the reform in Massachusetts was high, mitigating adverse selection in the market for health insurance outside of employment (see Hackmann, Kolstad, and Kowalski [2012,2015] for evidence of adverse selection in Massachusetts prior to the reform). If compliance with national reform is not as high, adverse selection could remain high in the market for health insurance outside of employment, making the outside alternative to ESHI less attractive. In terms of our model, although adverse selection in the non-employer-sponsored market should not affect the cost of health insurance to employers b, it could affect the value of a dollar of ESHI relative to a dollar of wages α because employees will value ESHI more if their outside health insurance option is more expensive. In that case, more adverse selection in the market for health insurance outside of employment nationally could actually decrease the reform-induced distortion to the labor market relative to what we observed in Massachusetts.
6 Conclusion
The recent Massachusetts and national health reforms are the most profound changes to health policy in the United States since the introduction of Medicare and Medicaid in 1965. Since employers sponsor the majority of health insurance coverage for the nonelderly in the United States, changes to health policy can affect the labor market profoundly. To study the relationship between health reform and the labor market, we develop a model that incorporates the three key elements of mandate-based health reform: employer and individual pay-or-play mandates and expansions in subsidized coverage. Using our model, we characterize the compensating differential for ESHI. We also characterize the welfare impact of the labor market distortion induced by health reform in terms of a small number of sufficient statistics that can be recovered from labor market outcomes. By modeling all three elements at once, we show that if an individual mandate is already in place, then the addition of an employer mandate increases deadweight loss. This theoretical result has some relevance to the ACA employer mandate, which has not yet been enforced as of this writing.
Using variation from the Massachusetts reform—which includes the same mandate-based reform elements as the national reform—we estimate our model using longitudinal data from the Survey of Income and Program Participation. We find evidence of a substantial compensating differential for ESHI: full-time workers who gained coverage because of the Massachusetts reform earned lower wages than they would have had they not gained ESHI by $2,812 per year, a significant portion of the average cost of their health insurance to their employers. Our finding stands in stark contrast to the results from the extensive literature that searches for a compensating differential for ESHI but does not find one. Because of difficulties with identification, studies generally find that individuals with ESHI have higher wages than those without. A small number of studies do find evidence in favor of a compensating differential, showing that wages for workers with ESHI decrease as health insurance costs increase. However, these studies use variation in incremental changes in the cost of health insurance. We identify the compensating differential using variation in the entire cost of health insurance using reform-induced exogenous transitions into and out of ESHI.
Building on our estimated compensating differential, we estimate the welfare impact of the labor market distortion induced by health reform. Our large estimated compensating differential indicates that individuals who gained ESHI were willing to accept lower wages because they valued the coverage that they received. We estimate that individuals who gained coverage through their employers valued approximately $0.68 of every dollar that their employers spent on their coverage. Because individuals valued ESHI, mandate-based health reform in Massachusetts resulted in significantly less distortion to the labor market than it would have under alternative policies to expand insurance coverage. We estimate that if the government had instead increased insurance coverage by establishing a wage tax to pay for health insurance, the distortion to the labor market would have been roughly 13 times as large. Our results suggest that mandate-based reform has the potential to be a very efficient approach for expanding health insurance coverage nationally.
Finally, our results help to explain why ESHI coverage increased in Massachusetts relative to other states following reform, despite anticipation that other sources of coverage would crowd out ESHI (see Kolstad and Kowalski [2012]). Although it seemed plausible that employers would stop offering coverage, instead of electing to pay the small employer penalty, between 2005 and 2009, the rate of employers offering ESHI increased from 70 percent to 76 percent in Massachusetts while it remained flat nationally (Massachusetts DHCFP 2011a). Our model and results suggest that the individual mandate, combined with the large penalty-and-subsidy-inclusive valuation of ESHI, encouraged workers to demand ESHI from their employers, which they paid for out of decreased wages. If employers have a comparative advantage in offering health plans that their employees value, then we expect crowd-in to ESHI—precisely what we observed in Massachusetts. To the extent that ESHI is even more valuable relative to other coverage under national reform than it was in Massachusetts, perhaps because of the difference in the relative tax preference between reforms, we could see even greater crowd-in to employer-sponsored coverage under national reform than we did in Massachusetts.
Research Highlights.
We model the labor market impact of the Massachusetts and national health reforms.
Our approach identifies “sufficient statistics” for welfare analysis.
We estimate the model using the Massachusetts reform.
Jobs with health insurance pay $2,812 less annually, less than the cost to employers.
The deadweight loss of mandate-based reform was about 8% of its potential size.
Appendix A Massachusetts and National Reform Comparison
Table A1.
Summary of Labor Market Provisions in Massachusetts and National Reforms
| Massachusetts Health Care Reform, April 2006 | Patient Protection and Affordable Care Act (PPACA), March 2010 | |
|---|---|---|
| “Large” Employer | At least 11 employees1,2 | At least 50 full-time employees3 |
| Provisions Affecting Large Employers | Must either: In addition, employers: | Must either: Affordable coverage defined as: |
| “Small” Employer | Fewer than 11 employees | Fewer than 50 employees |
| Provisions Affecting Small Employers | May purchase coverage for employees via the Commonwealth Health Insurance Connector, which:1
|
Very small businesses (fewer than 25 employees) may: |
| Penalties (Large Employers) | Must pay a penalty of $295 per employee per year, if:
|
Two types of penalties:
|
| Provisions Affecting Individuals | Individuals are required either to: Individuals with incomes below 300% of poverty can access subsidized health insurance:7 | Individuals are required either to: Provides subsidies/access to coverage for low-income individuals: |
| Penalties (Individuals) | Individuals who do not purchase affordable coverage, but are in income brackets with affordable coverage available, face penalties:7
|
Individuals not purchasing coverage face a penalty of the greater of: These amounts phased in beginning in 20148 |
Notes:
Felland et al (2007),
Anonymous (2011),
Appendix B Comparison of SIPP to Alternative Survey Data
Figures B1 and B2 plot wages and hours in Massachusetts and non-Massachusetts states between 2004 and 2011 for three data sets in addition to the SIPP: the CPS, the MEPS, and the ACS. We also include data from the 2008 SIPP panel. It is clear that the 2004 SIPP panel captures the same trends as the other datasets, with the only deviation coming from an uptick in the last period of observation. As we discuss, the last period of observation is affected by attrition from the sample in the last survey month and though an uptick is visible, it does not impact our estimation substantially due to the weighting of the regression results. The 2008 SIPP panel continues with trends similar to the remainder of the country and to the 2004 SIPP panel.
We also note that the last period of the 2008 SIPP panel appears to have an uptick in wages, suggesting that the attrition from the sample we see in the 2004 panel is a general issue with the SIPP and does not reflect an unobserved change in Massachusetts the last two months of 2007. Taken together, these trends suggest that the 2004 SIPP is representative of Massachusetts and control states and does not obscure substantial change in Massachusetts in the period after our data ends (2008 onwards).
Figure B1.
Wage Levels in MA vs. Non-MA from Survey Data
Figure B2.
Hours Levels in MA vs. Non-MA from Survey Data
Appendix C Robustness of the Empirical Results
Appendix C.1 Robustness to Calibrated Values
Thus far, we have discussed point estimates for the welfare impact of health reform, but we are also interested in their robustness. Although the reported confidence intervals should be of the correct size for the compensating and hours differentials, the other confidence intervals should be too small because they reflect calibrated values, which were themselves estimated elsewhere. Therefore, it is instructive to consider robustness to alternative calibrated values.
First consider alternative values of ρ and ESHIAfter. These values have little impact on our overall conclusion that mandate-based health reform is substantially more efficient than tax-based health reform in Massachusetts. Our preferred calibrated ρ is 0.083, reflecting that the statutory employer penalty of $295 is approximately 8.3 percent of the estimated cost of ESHI b̂. If we increase ρ such that the penalty is instead 31.8 percent of the estimated cost of ESHI, the deadweight loss for individuals without ESHI after reform is equal to the deadweight loss for individuals with ESHI after reform, which is approximately 10 percent of the deadweight loss of mandate-based health reform. In this case, ESHIAfter has no impact because the size of both triangles is the same.
As discussed in Section 1, employer penalties under the ACA are substantially larger than those under the Massachusetts reform, up to a maximum of $3,000 per employee annually, approximately 84 percent of the estimated cost of ESHI. However, the deadweight loss for individuals without ESHI after mandate-based reform is only 7.7 percent of the deadweight loss of tax-based reform; this is because triangle BρAB′ grows with the square of the penalty, but triangle T AT′ grows with the square of the cost of ESHI. Taking into account the triangle F′AF″, the overall welfare cost of mandate-based reform is only 25.9 percent of the welfare cost of tax-based reform.
Next, consider alternative values for the loading cost of ESHI relative to the loading cost of government-provided health insurance, b/τ, keeping all other values the same as in our full specification. Suppose that ESHI costs 10 percent more to provide than government-provided health insurance because the government has economies of scale relative to employers, so b/τ=1.1. The deadweight loss of tax-based health reform decreases to $111 annually, but the deadweight loss of mandate-based health reform is still only 9.3 percent as large. Even if b/τ=1.50 such that ESHI costs 50 percent more to provide than government-provided health insurance, the deadweight loss of mandate-based health reform is still only 17.2 percent of the deadweight loss of tax-based health reform.
The last calibrated values to consider are the slope of the supply curve s and the slope of the demand curve d. To examine the effect of s and d on the ratio of the deadweight loss of mandate-based health reform to the deadweight loss of tax-based health reform, we see from Equation (2) that the ratio of the deadweight loss of mandate-based health reform to the deadweight loss of tax-based health reform grows with the square of the percentage of the cost of ESHI that workers do not value: ( ). Using the expressions in Table 3, we can express this percentage in terms of the compensating and hours differentials, the slope of the demand curve, and the slope of the supply curve. We find that the relative deadweight loss of mandate-based reform increases as the slope of the labor supply curve increases (becomes more inelastic) and increases as the slope of the labor demand curve decreases (becomes more elastic). Holding demand constant, if we increase the calibrated labor supply elasticity from 0.1 to 0.2 (from s = 0.19 to s = 0.38), the relative deadweight loss increases to 14.5 percent. If we increase it further to 0.3 (s = 0.57), the relative deadweight loss increases to 20.7 percent. Alternatively, holding supply constant, if we decrease the calibrated labor demand elasticity from −0.2 to −0.4 (from d = − 0.38 to d = −0.76), the relative deadweight loss increases to 14.3 percent. If we decrease it further to −1.2 (d = − 2.28), the relative deadweight loss increases to 33.1 percent. Thus, the finding that mandate-based health reform is efficient relative to tax-based health reform is robust to changes in calibrated labor supply and demand.
The slopes of the supply and demand curves do, however, fix the incidence of the deadweight loss of health reform on employees versus their employers. As we can see from Figure 4, as supply becomes less elastic, a larger fraction of each deadweight loss triangle is below the L axis, demonstrating that employees bear more of the burden of reform. Conversely, as demand becomes less elastic, a larger fraction of each deadweight loss triangle is above the L axis, demonstrating that employers bear more of the burden of reform.
Appendix C.2 Robustness to Different Estimation Samples
Thus far, our model has taken individual ESHI takeup decisions as exogenous. Therefore, individuals who switched into ESHI because of reform are representative of all individuals, and we have estimated the penalty-and-subsidy-inclusive valuation for the population. However, we can extend our model to make ESHI status endogenous by allowing underlying valuations, and thus penalty-and-subsidy-inclusive valuations, to vary across individuals. In this extended model, after allowing for some optimization error, individuals with a penalty-and-subsidy-inclusive valuation above a certain threshold purchase health insurance in each period. Individuals with the highest intrinsic valuation of health insurance α already have health insurance before reform. The reform will increase penalty-and-subsidy-inclusive valuations for some individuals, leading them to take up ESHI. Interpreted in light of the extended model, our estimates then reflect the average penalty-and-subsidy-inclusive valuation among individuals who take up ESHI. Therefore, our estimated valuation of 0.68 from our full specification suggests that individuals who take up ESHI because of reform value it at 68 cents on the dollar on average (after incorporating the individual penalty and taking the tax-preference for ESHI into account).
Under the extended model with endogenous takeup of ESHI, we can test whether the penalty-and-subsidy-inclusive valuation (and thus the incidence of reform among employees) varies across different populations by estimating our model on subsets of our estimation sample. Under our original model, the same specifications test the robustness of our estimates to alternative samples and control groups. We examine our baseline and full specifications on two subsets of the full population: individuals in New England and individuals who are married.
In the first column of Tables C1 and C2, we restrict our estimation sample to include only individuals in New England, on the grounds that Massachusetts might be more similar to other New England states than it is to the rest of the country. Table C1 reports results from the baseline specification on the New England sample. The estimates of β1 and γ1 (the compensating and hours differentials assuming that the employer penalty is zero, respectively), are slightly larger in magnitude than the corresponding estimates from the baseline specification. However, the compensating and hours differentials from the full specification are very similar to those from the full sample. In the sample that includes only New England, the annualized estimate of the cost of ESHI b is $10,997, much larger than our preferred estimate ($3,566), but the penalty-and-subsidy-inclusive valuation of 0.89 is also closer to 1 than our preferred estimate of 0.68. Furthermore, the ratio of the deadweight loss of mandate-based health reform to the ratio of the deadweight loss of tax-based health reform is 0.1 percent—which is smaller but qualitatively similar to our preferred estimate of 7.7 percent.
Table C1.
Results from Baseline Specification on Different Samples
| (1a) | (1b) | (2a) | (2b) | |||
|---|---|---|---|---|---|---|
| w | L | |||||
| Weekly earnings / baseline hours per week, including individuals without a paid job (wage=0) | Hours per week, including individuals without a paid job (hours=0) | |||||
|
| ||||||
| SAMPLE | New England | Married | New England | Married | ||
| MA* ESHI* After | β1 | −4.415*** | −0.232 | ϒ1 | −1.739** | 1.977*** |
| [−7.288, −2.776] | [−0.908, 0.459] | [−3.235, −0.111] | [1.282, 2.662] | |||
| MA* ESHI* During | β1d | −1.862** | 1.392*** | ϒ1d | −2.318** | −0.441** |
| [−4.124, −0.00600] | [0.941, 1.783] | [−4.508, −0.237] | [−1.040, −0.0510] | |||
| MA* ESHI | β8 | 2.148** | 0.762*** | ϒ8 | 2.149** | −0.912*** |
| [0.330, 6.524] | [0.310, 1.254] | [0.373, 3.995] | [−1.616, −0.498] | |||
| MA* After | β11 | 3.214*** | 1.280*** | ϒ11 | 1.171 | −1.077*** |
| [1.885, 4.442] | [0.750, 1.801] | [−0.368, 2.421] | [−1.662, −0.403] | |||
| MA* During | β11d | 1.405** | −0.820*** | ϒ11d | 2.497** | 0.844*** |
| [0.187, 3.277] | [−1.258, −0.386] | [0.459, 4.371] | [0.511, 1.445] | |||
| ESHI* After | β12 | 3.276*** | −0.623* | ϒ12 | 0.742 | −0.312 |
| [1.661, 6.114] | [−1.309, 0.061] | [−0.869, 2.373] | [−0.781, 0.407] | |||
| ESHI* During | β12d | 0.806 | −0.522*** | ϒ12d | −0.0560 | −0.291 |
| [−0.901, 3.097] | [−0.896, −0.132] | [−1.945, 2.164] | [−0.576, 0.285] | |||
| ESHI | β19 | 2.276 | 3.580*** | ϒ19 | 4.912*** | 5.383*** |
| [−1.403, 4.127] | [3.077, 3.823] | [2.901, 6.511] | [4.803, 5.780] | |||
| After | β22 | −1.107 | 0.231 | ϒ22 | 0.613 | −0.929*** |
| [−2.166, 0.174] | [−0.220, 0.681] | [−0.777, 2.121] | [−1.670, −0.435] | |||
| During | β22d | 0.120 | 0.311 | ϒ22d | 0.171 | −0.484*** |
| [−1.713, 1.314] | [−0.0690, 0.665] | [−1.754, 2.179] | [−1.071, −0.160] | |||
|
| ||||||
| Observations | 31,131 | 302,175 | 28,589 | 277,477 | ||
| R-squared | 0.670 | 0.760 | 0.814 | 0.834 | ||
p<0.01,
p<0.05,
p<0.1, 95% confidence intervals reported; CIs block bootstrapped by state.
Including full 18–64 population; only includes interview months.
Individual and state fixed effects included. Monthly weights used.
New England states include MA, CT, NH, VT, ME, RI.
Table C2.
Results from Full Specification on Different Samples
| (1a) | (1b) | (2a) | (2b) | (3a) | (3b) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| w | L | |||||||||
| Weekly earnings / baseline hours per week, including individuals without a paid job (wage=0) |
Hours per week, including individuals without a paid job (hours=0) |
Compensating and Hours Differentials, Sufficient Statistics, and Welfare Impact of Health Reform |
||||||||
|
| ||||||||||
| SAMPLE | New England | Married | New England | Married | New England | Married | ||||
| MA* ESHI* After* Large | β1 | −2.064 | −2.135*** | ϒ1 | −4.552 | 3.268*** | wD−wA | 1.792** | 0.244 | |
| [−5.701, 3.948] | [−4.271, −0.604] | [−10.591, 3.707] | [0.945, 4.444] | [0.337, 5.02] | [−0.143, 0.68] | |||||
| MA* ESHI* During* Large | β1d | −1.440 | −0.820 | ϒ1d | 0.109 | 2.078*** | wF−wB | −3.109 | −0.573** | |
| [−4.548, 3.210] | [−1.763, 0.463] | [−5.145, 4.501] | [0.767, 2.766] | [−6.794, 1.599] | [−1.277, −0.117] | |||||
| MA* ESHI* Large | β8 | 0.231 | −2.641*** | ϒ8 | −2.189 | −7.236*** | wD−wB | 3.58 | 5.718*** | |
| [−2.923, 2.564] | [−3.807, −1.869] | [−5.624, 1.584] | [−8.146, −6.311] | [−0.854, 11.208] | [4.279, 6.978] | |||||
| MA* After* Large | β11 | −1.788 | −5.473*** | ϒ11 | 0.997 | −6.723*** | wF−wA | −4.897** | −6.046*** | |
| [−6.598, 1.833] | [−6.556, −4.119] | [−5.149, 6.431] | [−7.756, −4.417] | [−8.274, −1.726] | [−7.458, −4.838] | |||||
| MA* During* Large | β11d | −0.0916 | −0.905** | ϒ11d | −1.576** | −2.644*** | ||||
| [−4.982, 2.871] | [−1.676, −0.0350] | [−3.195, −0.116] | [−3.191, −1.255] | |||||||
| ESHI* After* Large | β12 | 1.092 | 0.613 | ϒ12 | 3.777 | −0.294 | LD−LA | 1.025 | −2.293*** | |
| [−4.543, 4.444] | [−0.728, 2.164] | [−4.366, 9.645] | [−1.378, 1.737] | [−0.846, 2.314] | [−3.14, −1.867] | |||||
| ESHI* During* Large | β12d | 0.574 | 0.357 | ϒ12d | 0.0871 | −0.411 | LF−LB | −2.02** | 0.16 | |
| [−3.709, 3.352] | [−0.845, 1.217] | [−4.205, 4.488] | [−1.114, 0.775] | [−3.239, −1.011] | [−1.132, 1.02] | |||||
| ESHI* Large | β19 | 2.521** | 1.822*** | ϒ19 | 7.145*** | 6.663*** | LD−LB | 0.028 | 4.43*** | |
| [0.491, 5.487] | [1.045, 2.720] | [3.691, 10.522] | [5.728, 7.512] | [−5.781, 4.955] | [2.127, 5.673] | |||||
| After* Large | β22 | −0.358 | −0.138 | ϒ22 | −2.982 | −0.861 | LF−LA | −1.023 | −6.564*** | |
| [−3.577, 4.219] | [−1.500, 0.873] | [−8.119, 2.691] | [−2.938, 0.138] | [−6.464, 4.311] | [−7.554, −5.091] | |||||
| During* Large | β22d | 0.488 | −0.107 | ϒ22d | 0.162 | −0.199 | ||||
| [−2.085, 5.376] | [−0.871, 0.527] | [−0.966, 1.615] | [−1.463, 0.501] | |||||||
| Large | β23 | −9.536*** | −2.616*** | ϒ23 | −16.532** | −15.919** | ||||
| [−12.211, −2.407] | [−5.088, −1.644] | [−20.432, −10.877] | [−17.111, −6.294] | |||||||
| MA* Large | β24 | 5.094 | 1.146* | ϒ24 | 7.034*** | 14.250** | ||||
| [−2.004, 7.877] | [−0.0190, 3.646] | [1.269, 11.24] | [4.544, 15.502] | |||||||
| MA* ESHI* After | β1e | −2.838* | 1.318 | ϒ1e | 1.506 | −0.815 | ||||
| [−7.661, 0.267] | [−0.596, 3.581] | [−4.096, 7.407] | [−1.633, 0.788] | |||||||
| MA* ESHI* During | β1ed | −0.605 | 2.066*** | ϒ1ed | −2.442 | −2.000*** | s | 0.190 | 0.190 | |
| [−5.702, 1.446] | [0.876, 2.980] | [−6.461, 1.676] | [−2.543, −1.273] | - | - | |||||
| MA* ESHI | β8e | 1.561 | 2.886*** | ϒ8e | 3.214 | 4.943*** | d | −0.380 | −0.380 | |
| [−1.779, 7.743] | [2.053, 4.098] | [−1.795, 6.294] | [3.976, 5.604] | - | - | |||||
| MA* After | β11e | 4.770** | 6.231*** | ϒ11e | 0.737 | 4.735*** | b | 5.285** | 8.54*** | |
| [1.590, 9.243] | [4.948, 7.412] | [−4.736, 4.965] | [3.100, 5.494] | [0.605, 10.495] | [7.089, 9.969] | |||||
| MA* During | β11ed | 1.442 | −0.0845 | ϒ11ed | 3.874** | 2.859*** | ρ | 0.027** | 0.017*** | |
| [−1.125, 6.659] | [−0.958, 0.734] | [0.915, 6.152] | [1.977, 3.345] | [0.013, 0.157] | [0.014, 0.02] | |||||
| ESHI* After | β12e | 2.517* | −1.163 | ϒ12e | −1.721 | −0.0956 | α+λ−μx | 0.89** | 0.562*** | |
| [−0.262, 7.354] | [−3.114, 0.516] | [−7.306, 3.845] | [−1.306, 0.731] | [0.353, 3.012] | [0.474, 0.643] | |||||
| ESHI* During | β12ed | 0.333 | −0.825 | ϒ12ed | 0.128 | 0.0194 | ESHIAfter | 0.740 | 0.740 | |
| [−1.509, 5.335] | [−1.759, 0.247] | [−3.698, 4.330] | [−0.646, 0.570] | − | − | |||||
| ESHI | β19e | 0.507 | 2.119*** | ϒ19e | −0.442 | 0.0171 |
|
1.000 | 1.000 | |
| [−4.973, 3.708] | [1.065, 2.814] | [−3.416, 4.156] | [−0.658, 0.601] | - | - | |||||
| After | β22e | −0.980 | 0.343 | ϒ22e | 2.377 | −0.155 | DWLm | 0.225*** | 9.09*** | |
| [−5.060, 1.829] | [−0.697, 1.561] | [−1.625, 7.625] | [−0.876, 1.217] | [0.007, 9.272] | [5.471, 12.038] | |||||
| During | β22ed | −0.335 | 0.386 | ϒ22ed | −0.269 | −0.271 |
|
0.009*** | 0.142*** | |
| [−5.164, 2.076] | [−0.325, 1.224] | [−2.620, 2.289] | [−0.789, 0.524] | [0, 5.488] | [0.095, 0.205] | |||||
|
| ||||||||||
| Observations | 31,131 | 302,175 | 28,589 | 277,477 | ||||||
| R-squared | 0.671 | 0.761 | 0.823 | 0.841 | ||||||
p<0.01,
p<0.05,
p<0.1, 95% confidence intervals reported; CIs block bootstrapped by state.
Including full 18–64 population; only includes interview months.
All specifications include individual, state, and state*large firm fixed effects. Monthly weights used.
Large firm defined as >25 employees.
New England states include MA, CT, NH, VT, ME, RI.
In the second columns of Tables C1 and C2, we restrict our estimation sample to include only married individuals. Married individuals could value ESHI less than other individuals if they have health insurance options available through their spouses; alternatively, they could also value it more if their spouse relies on them for insurance. Empirically, we see in Table C2 that the valuation of ESHI for married individuals is approximately 0.56, with a 95 percent confidence interval of 0.47 to 0.64, slightly smaller than the valuation of ESHI for the full sample.
Appendix C.3 Robustness to Intensive Margin Only
Thus far, we have not distinguished the extensive margin decision of whether to work at all from the intensive margin decision to work a different number of hours in our measure of L. Instead, we have attempted to capture the broadest possible impact of reform by allowing for responses on the intensive and extensive margins. However, previous research, including Cutler and Madrian (1998), shows that ESHI could have different impacts on employment than it does on hours because ESHI has a fixed cost, regardless of hours worked. Furthermore, part-time employees often do not receive health insurance from their employers.
We now investigate whether we observe responses on the intensive margin and whether the distinction between the intensive and extensive margins affects our findings. Unfortunately, our model does not allow us to examine extensive margin decisions directly.31 Instead, we restrict our sample to individuals who worked; effectively limiting the response to the intensive margin. Comparing these estimates to our preferred results allows us to test whether the distinction between extensive and intensive margin effects drives our findings. We first include only individuals with a paid job and positive wages in a given period. We then further restrict our sample to include only individuals with a paid job and positive wages over the entire period, and then further to include only individuals with no job switch over the entire period. We adjust the calibrated values of s and d to reflect the higher average wages and hours. Because these three samples only include people with positive wages and hours, we can also estimate logarithmic specifications without losing any information. In the logarithmic specifications, our theoretical graph stays the same, the axes change from w to log(w) and from L to log(L). With the change in axes, the compensating differential and the cost of the benefit are percentages of wages instead of dollar amounts, and the hours differential is a percentage of hours. However, the units of the penalty-and-subsidy-inclusive valuation and the deadweight loss ratio do not change.
Table C3 presents results from the baseline specification on the three samples of workers, using levels and logarithms of the dependent variables. In all samples, our estimates of β1 give evidence of a compensating differential, assuming no employer penalty. The logarithmic specifications show a compensating differential from 6 percent to 10 percent of income, broadly consistent with our preferred results. The estimates of γ1, however, do not show any evidence of a negative hours differential. If anything, the effect is positive in the only specification with a coefficient estimate that is significant at the 95 percent confidence level. These results suggest that much of the small decline in hours that we observe in the full sample is driven by the extensive margin decision of whether to work.
Table C3.
Results from Baseline Specification to Investigate Intensive Margin
| (1a) | (1b) | (1c) | (1d) | (1e) | (1f) | ||
|---|---|---|---|---|---|---|---|
| w | Log(w) | w | Log(w) | w | Log(w) | ||
| Weekly earnings / baseline hours per week |
Weekly earnings / baseline hours per week |
Weekly earnings / baseline hours per week |
Weekly earnings / baseline hours per week |
Weekly earnings / baseline hours per week |
Weekly earnings / baseline hours per week |
||
|
| |||||||
| SAMPLE |
Workers with a paid job and wages>0 in the given period |
Workers with a paid job and wages>0 over the entire period |
Workers with a paid job and wages>0 and no job switch over the entire period |
||||
| MA* ESHI* After | β1 | −2.376*** | −0.100*** | −2.652*** | −0.0612*** | −3.729*** | −0.0729*** |
| [−2.811, −1.831] | [−0.124, −0.0630] | [−3.422, −2.283] | [−0.0850, −0.0280] | [−4.233, −3.031] | [−0.109, −0.0366] | ||
| MA* ESHI* During | β1d | −2.044*** | −0.182*** | −2.496*** | −0.206*** | −2.554*** | −0.206*** |
| [−2.426, −1.388] | [−0.202, −0.148] | [−2.917, −1.736] | [−0.233, −0.169] | [−3.084, −1.824] | [−0.243, −0.169] | ||
| MA* ESHI | β8 | 1.501*** | 0.108*** | 1.474*** | 0.100*** | 1.631*** | 0.106*** |
| [1.051, 1.688] | [0.0820, 0.121] | [0.815, 1.778] | [0.0710, 0.115] | [0.906, 1.959] | [0.0717, 0.141] | ||
| MA* After | β11 | 2.902*** | 0.126*** | 3.153*** | 0.0831*** | 3.720*** | 0.0788*** |
| [2.526, 3.179] | [0.0950, 0.144] | [2.887, 3.705] | [0.0510, 0.102] | [3.221, 4.070] | [0.0402, 0.117] | ||
| MA* During | β11d | 2.229*** | 0.190*** | 2.706*** | 0.212*** | 2.627*** | 0.215*** |
| [1.741, 2.457] | [0.161, 0.203] | [2.093, 3.008] | [0.175, 0.233] | [2.061, 3.001] | [0.183, 0.246] | ||
| ESHI* After | β12 | −0.441* | −0.0704*** | −0.319 | −0.0562*** | −0.273 | −0.0588*** |
| [−1.001, 0.005] | [−0.104, −0.0430] | [−0.828, 0.353] | [−0.0830, −0.0290] | [−0.855, 0.235] | [−0.0913, −0.0264] | ||
| ESHI* During | β12d | −0.551*** | −0.0421*** | −0.483** | −0.0361** | −0.533** | −0.0342** |
| [−0.999, −0.236] | [−0.0630, −0.0220] | [−1.033, −0.0370] | [−0.0560, −0.00300] | [−1.070, −0.0250] | [−0.0622, −0.00624] | ||
| ESHI | β19 | 1.827*** | 0.157*** | 1.786*** | 0.148*** | 1.753*** | 0.136*** |
| [1.527, 2.124] | [0.141, 0.166] | [1.491, 2.171] | [0.129, 0.163] | [1.381, 2.163] | [0.119, 0.152] | ||
| After | β22 | 1.452*** | 0.129*** | 1.251*** | 0.103*** | 0.955*** | 0.0933*** |
| [1.072, 1.743] | [0.0990, 0.155] | [0.739, 1.460] | [0.0720, 0.124] | [0.565, 1.245] | [0.0606, 0.126] | ||
| During | β22d | 1.058*** | 0.0801*** | 0.982*** | 0.0705*** | 0.865*** | 0.0583*** |
| [0.759, 1.430] | [0.0590, 0.100] | [0.618, 1.450] | [0.0360, 0.0900] | [0.447, 1.353] | [0.0293, 0.0873] | ||
|
| |||||||
| Observations | 370,996 | 370,996 | 307,438 | 307,438 | 281,624 | 281,624 | |
| R-squared | 0.792 | 0.749 | 0.790 | 0.762 | 0.794 | 0.771 | |
| (2a) | (2b) | (2c) | (2d) | (2e) | (2f) | ||
|---|---|---|---|---|---|---|---|
| L | Log(L) | L | Log(L) | L | Log(L) | ||
| Hours per week | Hours per week | Hours per week | Hours per week | Hours per week | Hours per week | ||
|
| |||||||
| SAMPLE |
Workers with a paid job and wages>0 in the given period |
Workers with a paid job and wages>0 over the entire period |
Workers with a paid job and wages>0 and no job switch over the entire period |
||||
| MA* ESHI* After | ϒ1 | −0.255 | −0.00409 | 0.734*** | 0.0346*** | −0.0480 | 0.0102 |
| [−0.594, 0.180] | [−0.0190, 0.0130] | [0.417, 1.286] | [0.0240, 0.0590] | [−0.489, 0.601] | [−0.0135, 0.0338] | ||
| MA* ESHI* During | ϒ1d | −1.694*** | −0.0304*** | −2.217*** | −0.0405*** | −2.397*** | −0.0461*** |
| [−1.955, −1.366] | [−0.0420, −0.0180] | [−2.431, −1.635] | [−0.0480, −0.0170] | [−2.864, −2.017] | [−0.0664, −0.0258] | ||
| MA* ESHI | ϒ8 | 1.659*** | 0.0433*** | 1.981*** | 0.0618*** | 2.191*** | 0.0690*** |
| [1.070, 1.960] | [0.0240, 0.0530] | [1.384, 2.348] | [0.0410, 0.0740] | [1.517, 2.557] | [0.0418, 0.0961] | ||
| MA* After | ϒ11 | 0.657*** | 0.0181** | −0.643*** | −0.0252*** | −0.0980 | −0.00888 |
| [0.156, 0.971] | [0.00100, 0.0300] | [−1.301, −0.378] | [−0.0490, −0.0160] | [−0.868, 0.329] | [−0.0336, 0.0159] | ||
| MA* During | ϒ11d | 2.137*** | 0.0439*** | 2.445*** | 0.0521*** | 2.798*** | 0.0636*** |
| [1.670, 2.371] | [0.0280, 0.0520] | [1.825, 2.556] | [0.0260, 0.0550] | [2.388, 3.153] | [0.0475, 0.0796] | ||
| ESHI* After | ϒ12 | −0.827*** | −0.0328*** | −0.687*** | −0.0267*** | −0.567** | −0.0248** |
| [−1.190, −0.493] | [−0.0460, −0.0180] | [−1.045, −0.229] | [−0.0370, −0.00900] | [−1.137, −0.193] | [−0.0435, −0.00615] | ||
| ESHI* During | ϒ12d | −0.614*** | −0.0235*** | −0.594*** | −0.0232*** | −0.520*** | −0.0201*** |
| [−0.805, −0.454] | [−0.0310, −0.0160] | [−0.810, −0.354] | [−0.0310, −0.0130] | [−0.783, −0.237] | [−0.0319, −0.00834] | ||
| ESHI | ϒ19 | 1.833*** | 0.0684*** | 1.763*** | 0.0642*** | 1.651*** | 0.0606*** |
| [1.593, 1.983] | [0.0600, 0.0740] | [1.431, 1.984] | [0.0530, 0.0720] | [1.343, 1.884] | [0.0498, 0.0714] | ||
| After | ϒ22 | 0.857*** | 0.0393*** | 0.580** | 0.0266*** | 0.361* | 0.0225** |
| [0.516, 1.223] | [0.0260, 0.0520] | [0.0850, 0.950] | [0.00800, 0.0360] | [−0.0550, 0.977] | [0.00423, 0.0408] | ||
| During | ϒ22d | 0.728*** | 0.0311*** | 0.660*** | 0.0286*** | 0.518*** | 0.0234*** |
| [0.540, 0.952] | [0.0220, 0.0400] | [0.376, 0.886] | [0.0170, 0.0370] | [0.223, 0.832] | [0.0107, 0.0361] | ||
|
| |||||||
| Observations | 344,315 | 344,315 | 287,144 | 287,144 | 263,033 | 263,033 | |
| R-squared | 0.720 | 0.697 | 0.707 | 0.678 | 0.718 | 0.691 | |
p<0.01,
p<0.05,
p<0.1, 95% confidence intervals reported; CIs block bootstrapped by state.
Including full 18–64 population; only includes interview months.
Individual and state fixed effects included. Monthly weights used.
In the results from the full specification restricted to workers, shown in Table C4, we continue to observe a compensating differential. Interestingly, our compensating differential findings do not appear to be driven exclusively by individuals who switch ESHI status by changing jobs—we still estimate a compensating differential when we only use variation from individuals who switch ESHI status within the same job. In all three samples, the penalty-and-subsidy-inclusive valuation is smaller in the level specifications and larger in the log specifications. The ratio of the deadweight loss of mandate-based health reform to the deadweight loss of tax-based health reform varies from 5.2 percent to 22.3 percent across all six specifications, and the largest upper bound of the 95 percent confidence interval is 36.1 percent. Overall, our results that include only the intensive margin decision are consistent with our preferred results, suggesting that the extensive margin decision of whether to work does not drive our key findings.
Table C4.
Results from Full Specification to Investigate Intensive Margin
| (1a) | (1b) | (1c) | (1d) | (1e) | (1f) | ||
|---|---|---|---|---|---|---|---|
| w | Log(w) | w | Log(w) | w | Log(w) | ||
| Weekly earnings / baseline hours per week |
Weekly earnings / baseline hours per week |
Weekly earnings / baseline hours per week |
Weekly earnings / baseline hours per week |
Weekly earnings / baseline hours per week |
Weekly earnings / baseline hours per week |
||
|
| |||||||
| SAMPLE |
Workers with a paid job and wages>0 in the given period |
Workers with a paid job and wages>0 over the entire period |
Workers with a paid job and wages>0 and no job switch over the entire period |
||||
| MA* ESHI* After* Large | β1 | 1.682*** | 0.358*** | 2.920*** | 0.615*** | 2.611*** | 0.656*** |
| [0.999, 2.756] | [0.320, 0.419] | [1.825, 3.971] | [0.570, 0.679] | [1.192, 3.823] | [0.581, 0.732] | ||
| MA* ESHI* During* Large | β1d | −0.532 | 0.0213 | −0.0587 | 0.0869** | 0.615 | 0.119*** |
| [−1.420, 0.619] | [−0.0160, 0.0720] | [−1.375, 1.120] | [0.0320, 0.133] | [−0.871, 1.745] | [0.0595, 0.178] | ||
| MA* ESHI* Large | β8 | 3.124*** | 0.118*** | 3.564*** | 0.113*** | 3.264*** | 0.104*** |
| [2.681, 3.610] | [0.0910, 0.141] | [3.043, 4.244] | [0.0890, 0.157] | [2.564, 3.876] | [0.0653, 0.143] | ||
| MA* After* Large | β11 | −2.635*** | −0.356*** | −4.742*** | −0.650*** | −4.363*** | −0.691*** |
| [−3.584, −1.615] | [−0.415, −0.309] | [−5.720, −3.166] | [−0.710, −0.597] | [−5.596, −2.736] | [−0.770, −0.612] | ||
| MA* During* Large | β11d | 0.518 | −0.000265 | −0.242 | −0.112*** | −0.679 | −0.140*** |
| [−0.307, 1.654] | [−0.0530, 0.0380] | [−1.228, 1.392] | [−0.159, −0.0590] | [−1.592, 1.071] | [−0.195, −0.0849] | ||
| ESHI* After* Large | β12 | −0.599 | −0.0695*** | −0.293 | −0.0681* | 0.186 | −0.0625* |
| [−1.487, 0.274] | [−0.119, −0.0150] | [−1.054, 0.912] | [−0.107, 0.00300] | [−0.891, 1.370] | [−0.136, 0.0113] | ||
| ESHI* During* Large | β12d | −0.00128 | −0.0539** | 0.420 | −0.0400 | 0.478 | −0.0367 |
| [−0.936, 0.958] | [−0.0950, −0.00800] | [−0.643, 1.671] | [−0.0810, 0.0180] | [−0.698, 1.792] | [−0.0920, 0.0185] | ||
| ESHI* Large | β19 | 0.677** | 0.0736*** | 0.617** | 0.0689*** | 0.616* | 0.0651*** |
| [0.190, 1.054] | [0.0510, 0.0950] | [0.033, 1.241] | [0.0390, 0.0990] | [−0.0500, 1.184] | [0.0349, 0.0952] | ||
| After* Large | β22 | 0.785 | 0.0507* | 0.814 | 0.0570 | 0.579 | 0.0579 |
| [−0.302, 1.678] | [−0.00700, 0.102] | [−0.757, 1.764] | [−0.00900, 0.0960] | [−0.789, 1.789] | [−0.0203, 0.136] | ||
| During* Large | β22d | 0.203 | 0.0344 | −0.123 | 0.0222 | 0.000 | 0.0271 |
| [−0.968, 0.967] | [−0.0130, 0.0750] | [−1.639, 0.822] | [−0.0350, 0.0580] | [−1.586, 1.004] | [−0.0275, 0.0817] | ||
| Large | β23 | 1.140 | 0.00659 | 0.738 | −0.0705 | 2.128 | −0.0133 |
| [−2.200, 1.807] | [−0.110, 0.0630] | [−2.727, 1.618] | [−0.135, 0.0350] | [−2.930, 2.768] | [−0.116, 0.0896] | ||
| MA* Large | β24 | −1.243 | −0.0222 | −1.865 | −0.0336 | −3.712 | −0.0804 |
| [−1.975, 2.199] | [−0.0880, 0.108] | [−2.739, 1.715] | [−0.155, 0.0320] | [−4.437, 1.479] | [−0.190, 0.0288] | ||
| MA* ESHI* After | β1e | −3.124*** | −0.321*** | −4.002*** | −0.454*** | −4.805*** | −0.486*** |
| [−4.075, −2.436] | [−0.365, −0.288] | [−5.176, −3.271] | [−0.506, −0.420] | [−5.881, −3.592] | [−0.545, −0.426] | ||
| MA* ESHI* During | β1ed | −1.672*** | −0.196*** | −2.285*** | −0.245*** | −2.755*** | −0.261*** |
| [−2.408, −0.763] | [−0.231, −0.151] | [−3.218, −1.152] | [−0.284, −0.193] | [−3.774, −1.680] | [−0.315, −0.207] | ||
| MA* ESHI | β8e | −0.873*** | 0.0167 | −1.234*** | 0.00925 | −0.749** | 0.0260 |
| [−1.444, −0.531] | [−0.0150, 0.0400] | [−2.051, −0.739] | [−0.0430, 0.0330] | [−1.571, −0.197] | [−0.0245, 0.0765] | ||
| MA* After | β11e | 4.489*** | 0.347*** | 6.086*** | 0.506*** | 6.300*** | 0.520*** |
| [3.625, 5.099] | [0.298, 0.381] | [5.306, 7.042] | [0.463, 0.545] | [5.240, 7.104] | [0.464, 0.576] | ||
| MA* During | β11ed | 1.879*** | 0.186*** | 2.774*** | 0.274*** | 2.916*** | 0.289*** |
| [0.693, 2.471] | [0.139, 0.222] | [1.276, 3.552] | [0.223, 0.310] | [1.450, 3.716] | [0.238, 0.340] | ||
| ESHI* After | β12e | −0.116 | −0.0240 | −0.276 | −0.0123 | −0.597 | −0.0214 |
| [−0.934, 0.688] | [−0.0670, 0.0120] | [−1.291, 0.579] | [−0.0650, 0.0190] | [−1.660, 0.393] | [−0.0710, 0.0281] | ||
| ESHI* During | β12ed | −0.587 | −0.00417 | −0.794 | −0.00678 | −0.929* | −0.00966 |
| [−1.424, 0.219] | [−0.0440, 0.0300] | [−1.797, 0.261] | [−0.0480, 0.0400] | [−1.956, 0.133] | [−0.0578, 0.0384] | ||
| ESHI | β19e | 1.317*** | 0.101*** | 1.327*** | 0.0960*** | 1.304*** | 0.0870*** |
| [0.907, 1.717] | [0.0810, 0.119] | [0.677, 1.861] | [0.0680, 0.123] | [0.655, 1.817] | [0.0600, 0.114] | ||
| After | β22e | 0.969*** | 0.0985*** | 0.760** | 0.0690*** | 0.630 | 0.0603*** |
| [0.390, 1.650] | [0.0660, 0.141] | [0.0610, 1.605] | [0.0410, 0.113] | [−0.201, 1.528] | [0.0158, 0.105] | ||
| During | β22ed | 0.928*** | 0.0589*** | 1.043*** | 0.0568*** | 0.859** | 0.0425* |
| [0.321, 1.983] | [0.0280, 0.100] | [0.293, 2.320] | [0.0190, 0.100] | [0.0400, 2.202] | [−0.00371, 0.0886] | ||
|
| |||||||
| Observations | 370,996 | 370,996 | 307,438 | 307,438 | 281,624 | 281,624 | |
| R-squared | 0.792 | 0.750 | 0.790 | 0.763 | 0.794 | 0.772 | |
| (2a) | (2b) | (2c) | (2d) | (2e) | (2f) | ||
|---|---|---|---|---|---|---|---|
| L | Log(L) | L | Log(L) | L | Log(L) | ||
| Hours per week | Hours per week | Hours per week | Hours per week | Hours per week | Hours per week | ||
|
| |||||||
| SAMPLE |
Workers with a paid job and wages>0 in the given period |
Workers with a paid job and wages>0 over the entire period |
Workers with a paid job and wages>0 and no job switch over the entire period |
||||
| MA* ESHI* After* Large | ϒ1 | 5.761*** | 0.215*** | 11.883*** | 0.480*** | 12.771*** | 0.498*** |
| [5.358, 6.567] | [0.204, 0.245] | [11.085, 13.147] | [0.454, 0.527] | [11.780, 13.719] | [0.462, 0.534] | ||
| MA* ESHI* During* Large | ϒ1d | 2.377*** | 0.0787*** | 5.711*** | 0.199*** | 5.638*** | 0.206*** |
| [1.755, 2.903] | [0.0540, 0.100] | [4.670, 6.083] | [0.154, 0.220] | [4.536, 6.233] | [0.162, 0.251] | ||
| MA* ESHI* Large | ϒ8 | 1.244*** | 0.0544*** | −0.134 | 0.0218 | 0.106 | 0.0248* |
| [0.665, 1.585] | [0.0350, 0.0650] | [−0.786, 0.372] | [−0.00400, 0.0370] | [−0.624, 0.720] | [−0.00241, 0.0519] | ||
| MA* After* Large | ϒ11 | −6.243*** | −0.260*** | −12.60*** | −0.544*** | −12.21*** | −0.541*** |
| [−7.000, −5.584] | [−0.288, −0.240] | [−13.544, −11.280] | [−0.580, −0.508] | [−13.201, −11.216] | [−0.578, −0.504] | ||
| MA* During* Large | ϒ11d | −2.557*** | −0.0885*** | −6.162*** | −0.231*** | −5.647*** | −0.220*** |
| [−3.209, −1.923] | [−0.114, −0.0660] | [−6.680, −5.331] | [−0.253, −0.199] | [−6.384, −4.731] | [−0.253, −0.187] | ||
| ESHI* After* Large | ϒ12 | −0.828*** | −0.0275*** | −0.766 | −0.0279 | −0.692* | −0.0307* |
| [−1.436, −0.256] | [−0.0510, −0.00900] | [−1.584, 0.199] | [−0.0560, 0.00300] | [−1.540, 0.0170] | [−0.0632, 0.00182] | ||
| ESHI* During* Large | ϒ12d | −0.833*** | −0.0288** | −0.779** | −0.0266* | −0.629* | −0.0246* |
| [−1.228, −0.294] | [−0.0460, −0.00800] | [−1.229, −0.152] | [−0.0470, 0.00200] | [−1.254, 0.0940] | [−0.0514, 0.00226] | ||
| ESHI* Large | ϒ19 | 0.794*** | 0.0240*** | 0.651*** | 0.0178*** | 0.452** | 0.0117 |
| [0.530, 1.121] | [0.0120, 0.0350] | [0.400, 1.096] | [0.00600, 0.0350] | [0.0400, 0.897] | [−0.00757, 0.0310] | ||
| After* Large | ϒ22 | 0.509 | 0.0110 | 0.586 | 0.0177 | 0.502 | 0.0185 |
| [−0.159, 1.110] | [−0.0100, 0.0320] | [−0.558, 1.366] | [−0.0210, 0.0440] | [−0.286, 1.255] | [−0.0147, 0.0518] | ||
| During* Large | ϒ22d | 0.544* | 0.0120 | 0.601* | 0.0151 | 0.550 | 0.0144 |
| [−0.0420, 0.977] | [−0.0140, 0.0330] | [−0.0310, 1.046] | [−0.0120, 0.0350] | [−0.285, 1.120] | [−0.0134, 0.0423] | ||
| Large | ϒ23 | −2.100 | −0.0621 | −1.527 | −0.0328 | −0.501 | −0.0143 |
| [−2.597, 4.995] | [−0.0760, 0.258] | [−2.015, 7.011] | [−0.0520, 0.392] | [−0.999, 6.232] | [−0.0492, 0.0206] | ||
| MA* Large | ϒ24 | 2.053 | 0.0565 | 2.330 | 0.0429 | 1.400 | 0.0336 |
| [−5.041, 2.853] | [−0.263, 0.0840] | [−6.070, 3.228] | [−0.375, 0.0800] | [−5.303, 2.368] | [−0.0123, 0.0794] | ||
| MA* ESHI* After | ϒ1e | −3.789*** | −0.131*** | −6.904*** | −0.268*** | −8.296*** | −0.303*** |
| [−4.529, −3.252] | [−0.160, −0.112] | [−8.162, −6.135] | [−0.311, −0.246] | [−9.240, −7.228] | [−0.342, −0.264] | ||
| MA* ESHI* During | ϒ1ed | −3.202*** | −0.0792*** | −5.816*** | −0.161*** | −5.896*** | −0.170*** |
| [−3.724, −2.629] | [−0.0970, −0.0590] | [−6.137, −4.876] | [−0.170, −0.125] | [−6.503, −5.110] | [−0.198, −0.142] | ||
| MA* ESHI | ϒ8e | 0.613** | −0.00170 | 1.913*** | 0.0380*** | 2.032*** | 0.0460** |
| [0.0220, 1.127] | [−0.0210, 0.0160] | [1.133, 2.608] | [0.0130, 0.0650] | [1.087, 2.836] | [0.00541, 0.0867] | ||
| MA* After | ϒ11e | 4.601*** | 0.182*** | 7.600*** | 0.331*** | 7.656*** | 0.340*** |
| [3.841, 5.159] | [0.159, 0.205] | [6.397, 8.355] | [0.295, 0.360] | [6.571, 8.542] | [0.302, 0.378] | ||
| MA* During | ϒ11ed | 3.796*** | 0.101*** | 6.437*** | 0.201*** | 6.321*** | 0.200*** |
| [3.102, 4.357] | [0.0780, 0.121] | [5.483, 6.824] | [0.166, 0.212] | [5.506, 6.995] | [0.172, 0.228] | ||
| ESHI* After | ϒ12e | −0.241 | −0.0122 | −0.177 | −0.00713 | −0.114 | −0.00333 |
| [−0.834, 0.356] | [−0.0300, 0.0100] | [−0.904, 0.647] | [−0.0290, 0.0220] | [−0.856, 0.604] | [−0.0319, 0.0252] | ||
| ESHI* During | ϒ12ed | −0.0257 | −0.00173 | −0.0786 | −0.00428 | −0.132 | −0.00297 |
| [−0.425, 0.286] | [−0.0150, 0.0110] | [−0.517, 0.326] | [−0.0220, 0.0110] | [−0.589, 0.326] | [−0.0192, 0.0133] | ||
| ESHI | ϒ19e | 1.218*** | 0.0491*** | 1.265*** | 0.0500*** | 1.296*** | 0.0507*** |
| [0.876, 1.427] | [0.0370, 0.0590] | [0.814, 1.499] | [0.0310, 0.0590] | [0.758, 1.656] | [0.0298, 0.0717] | ||
| After | ϒ22e | 0.542** | 0.0326*** | 0.225 | 0.0158 | 0.0720 | 0.0115 |
| [0.0140, 1.244] | [0.0130, 0.0530] | [−0.504, 0.949] | [−0.0100, 0.0380] | [−0.551, 1.023] | [−0.0145, 0.0375] | ||
| During | ϒ22ed | 0.385** | 0.0236*** | 0.298 | 0.0196** | 0.201 | 0.0151 |
| [0.00900, 0.844] | [0.0100, 0.0390] | [−0.107, 0.676] | [0.00400, 0.0330] | [−0.263, 0.691] | [−0.00387, 0.0341] | ||
|
| |||||||
| Observations | 344,315 | 344,315 | 287,144 | 287,144 | 263,033 | 263,033 | |
| R-squared | 0.720 | 0.698 | 0.708 | 0.679 | 0.718 | 0.691 | |
| (3a) | (3b) | (3c) | (3d) | (3e) | (3f) | ||
|---|---|---|---|---|---|---|---|
| w,L | Log(w),Log(L) | w,L | Log(w),Log(L) | w,L | Log(w),Log(L) | ||
| Compensating and Hours Differentials, Sufficient Statistics, and Welfare Impact of Health Reform | |||||||
|
| |||||||
|
Workers with a paid job and wages>0 in the given period |
Workers with a paid job and wages>0 over the entire period |
Workers with a paid job and wages>0 and no job switch over the entire period |
|||||
| wD−wA | 2.251*** | 0.135*** | 2.33*** | 0.123*** | 2.515*** | 0.130*** | |
| [1.797, 2.465] | [0.11, 0.146] | [1.775, 2.628] | [0.098, 0.138] | [1.789, 2.842] | [0.108, 0.156] | ||
| wF−wB | 0.809*** | 0.172*** | 1.248*** | 0.284*** | 0.321 | 0.300*** | |
| [0.418, 1.09] | [0.125, 0.217] | [0.266, 1.371] | [0.244, 0.312] | [−0.467, 0.725] | [0.253, 0.338] | ||
| wD−wB | 4.886*** | 0.49*** | 7.072*** | 0.773*** | 6.878*** | 0.821*** | |
| [3.655, 5.84] | [0.432, 0.557] | [4.968, 8.184] | [0.714, 0.839] | [4.802, 8.225] | [0.747, 0.903] | ||
| wF−wA | −1.826*** | −0.184*** | −3.494*** | −0.366*** | −4.042*** | −0.391*** | |
| [−2.779, −0.903] | [−0.234, −0.138] | [−4.675, −2.768] | [−0.425, −0.319] | [−5.132, −3.158] | [−0.488, −0.381] | ||
| LD−LA | 1.857*** | 0.053*** | 1.779*** | 0.06*** | 2.138*** | 0.071*** | |
| [1.264, 2.205] | [0.033, 0.063] | [1.215, 2.149] | [0.04, 0.073] | [1.551, 2.509] | [0.056, 0.093] | ||
| LF−LB | 3.829*** | 0.137*** | 6.758*** | 0.271*** | 6.613*** | 0.266*** | |
| [3.27, 4.293] | [0.117, 0.154] | [6.138, 7.214] | [0.247, 0.294] | [5.963, 7.122] | [0.247, 0.294] | ||
| LD−LB | 8.1*** | 0.313*** | 14.379*** | 0.604*** | 14.348*** | 0.612*** | |
| [7.198, 8.819] | [0.285, 0.341] | [12.895, 15.24] | [0.561, 0.64] | [13.063, 15.45] | [0.572, 0.665] | ||
| LF−LA | −2.414*** | −0.123*** | −5.842*** | −0.273*** | −5.598*** | −0.275*** | |
| [−3.197, −1.649] | [−0.153, −0.098] | [−6.664, −4.743] | [−0.308, −0.241] | [−6.601, −4.718] | [−0.303, −0.240] | ||
| s | 0.170 | 0.100 | 0.170 | 0.100 | 0.170 | 0.100 | |
| - | - | - | - | - | - | ||
| d | −0.350 | −0.200 | −0.350 | −0.200 | −0.350 | −0.200 | |
| - | - | - | - | - | - | ||
| b | 2.671*** | 0.209*** | 5.538*** | 0.421*** | 6.001*** | 0.446*** | |
| [1.523, 3.838] | [0.161, 0.262] | [4.629, 6.933] | [0.369, 0.484] | [4.992, 7.319] | [0.404, 0.519] | ||
| ρ | 0.053*** | 0.68*** | 0.026*** | 0.337*** | 0.024*** | 0.318*** | |
| [0.037, 0.094] | [0.542, 0.88] | [0.02, 0.031] | [0.293, 0.384] | [0.019, 0.028] | [0.287, 0.364] | ||
| α+λ−μx | 0.53*** | 0.823*** | 0.451*** | 0.806*** | 0.515*** | 0.815*** | |
| [0.304, 0.641] | [0.778, 0.846] | [0.379, 0.552] | [0.785, 0.824] | [0.436, 0.579] | [0.796, 0.829] | ||
| ESHIAfter | 0.740 | 0.740 | 0.740 | 0.740 | 0.740 | 0.740 | |
| - | - | - | - | - | - | ||
|
|
1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | |
| - | - | - | - | - | - | ||
| DWLm | 1.126*** | 0.01*** | 6.572*** | 0.017*** | 6.033*** | 0.017*** | |
| [0.529, 1.971] | [0.01, 0.011] | [4.333, 8.549] | [0.015, 0.019] | [4.291, 8.39] | [0.015, 0.018] | ||
|
|
0.164*** | 0.144*** | 0.223*** | 0.057*** | 0.174*** | 0.052*** | |
| [0.096, 0.361] | [0.096, 0.235] | [0.149, 0.285] | [0.047, 0.069] | [0.131, 0.236] | [0.045, 0.061] | ||
p<0.01,
p<0.05,
p<0.1, 95% confidence intervals reported; CIs block bootstrapped by state.
Including full 18–64 population; only includes interview months.
All specifications include individual, state, and state*large firm fixed effects. Monthly weights used.
Large firm defined as >25 employees.
Appendix C.4 Robustness to Elimination of Individual Fixed Effects
We have argued that individual fixed effects are essential to our identification. Indeed, empirically, we show that when we exclude individual fixed effects in the baseline and full specifications our estimate of the compensating differential becomes substantially smaller or loses statistical significance. We present these results in Appendix Tables C5 and C6. These tables also show that when we exclude individual fixed effects but instead control for age, gender, marital status, race, education, and industry, our estimated compensating differential is only slightly larger and is not statistically significant. These results demonstrate that even with a large set of demographic controls, there are still unobserved factors that bias the comparison of individuals with ESHI to those without before compared to after reform. Therefore, the longitudinal nature of the SIPP is very important to our analysis.
Table C5.
Results from Baseline Specification Without Individual Fixed Effects
| (1a) | (1b) | (2a) | (2b) | |||
|---|---|---|---|---|---|---|
| w | L | |||||
| Weekly earnings/baseline hours per week, including individuals without a paid job (wage=0) | Hours per week, including individuals without a paid job (hours=0) | |||||
| MA* ESHI* After | β1 | −0.132 | −0.660* | ϒ1 | 1.166*** | 3.600*** |
| [−0.646, 0.368] | [−1.345, 0.0470] | [0.484, 1.851] | [2.824, 4.109] | |||
| MA* ESHI* During | β1d | −0.424* | 0.200 | ϒ1d | −0.455** | 0.151 |
| [−0.872, 0.0430] | [−0.540, 1.112] | [−0.869, −0.0870] | [−0.276, 0.462] | |||
| MA* ESHI | β8 | 3.639*** | 2.323*** | ϒ8 | 1.956*** | 2.342*** |
| [2.899, 4.600] | [1.631, 3.255] | [1.347, 2.451] | [2.012, 2.626] | |||
| MA* After | β11 | 1.126*** | 1.238*** | ϒ11 | 0.214 | −3.024*** |
| [0.772, 1.470] | [0.612, 1.768] | [−0.471, 0.905] | [−3.552, −2.261] | |||
| MA* During | β11d | 0.326* | −0.464* | ϒ11d | 1.095*** | 0.363*** |
| [−0.0560, 0.598] | [−1.245, 0.0760] | [0.770, 1.534] | [0.0550, 0.729] | |||
| ESHI* After | β12 | −0.0148 | −0.904** | ϒ12 | 1.038*** | −0.197 |
| [−0.491, 0.468] | [−1.530, −0.252] | [0.371, 1.763] | [−0.692, 0.380] | |||
| ESHI* During | β12d | −0.0802 | −0.818*** | ϒ12d | 0.734*** | −0.166 |
| [−0.532, 0.347] | [−1.540, −0.254] | [0.361, 1.111] | [−0.429, 0.149] | |||
| ESHI | β19 | 12.131*** | 4.599*** | ϒ19 | 15.38*** | 3.195*** |
| [11.189, 12.879] | [3.993, 5.103] | [14.894, 16.009] | [2.960, 3.453] | |||
| After | β22 | 0.254 | 0.814*** | ϒ22 | −1.080*** | −0.103 |
| [−0.0870, 0.595] | [0.268, 1.325] | [−1.747, −0.445] | [−0.651, 0.414] | |||
| During | β22d | 0.193 | 0.660*** | ϒ22d | −0.669*** | 0.0140 |
| [−0.0570, 0.544] | [0.237, 1.348] | [−1.068, −0.344] | [−0.285, 0.244] | |||
|
| ||||||
| Controls? | No | Yes | No | Yes | ||
|
| ||||||
| Observations | 543,630 | 400,502 | 499,828 | 369,745 | ||
| R-squared | 0.076 | 0.169 | 0.15 | 0.164 | ||
p<0.01,
p<0.05,
p<0.1, 95% confidence intervals reported; CIs block bootstrapped by state.
Including full 18–64 population.
Only includes interview months.
State fixed effects included, no individual fixed effects. Monthly weights used.
Estimations with controls control for age, gender, marital status, race, education, and industry.
Table C6.
Results from Full Specification Without Individual Fixed Effects
| (1a) | (1b) | (2a) | (2b) | (3a) | (3b) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| w | L | |||||||||
| Weekly earnings/baseline hours per week, including individuals without a paid job (wage=0) |
Hours per week, including individuals without a paid job (hours=0) |
Compensating and Hours Differentials, Sufficient Statistics, and Welfare Impact of Health Reform |
||||||||
|
|
||||||||||
| MA* ESHI* After* Large | β1 | 0.912 | −1.452** | ϒ1 | −1.666** | 0.154 | wD−wA | 3.657*** | 1.977*** | |
| [−0.317, 2.147] | [−2.302, −0.244] | [−2.904, −0.570] | [−0.779, 1.288] | [2.854, 4.702] | [1.225, 3.067] | |||||
| MA* ESHI* During* Large | β1d | −2.418*** | −2.075*** | ϒ1d | −0.277 | 0.615* | wF−wB | 3.863*** | 1.313** | |
| [−3.527, −1.287] | [−3.415, −0.672] | [−0.789, 0.258] | [−0.0570, 1.190] | [2.763, 5.064] | [0.165, 2.724] | |||||
| MA* ESHI* Large | β8 | 0.710*** | −0.836* | ϒ8 | −0.340 | 0.829*** | wD−wB | 6.012*** | 2.67*** | |
| [0.320, 1.349] | [−1.361, 0.0250] | [−1.256, 0.406] | [0.284, 1.273] | [5.275, 6.934] | [1.695, 3.888] | |||||
| MA* After* Large | β11 | −2.355*** | −0.693 | ϒ11 | 1.626*** | −1.406*** | wF−wA | 1.508** | 0.62 | |
| [−3.019, −1.653] | [−1.732, 0.333] | [0.593, 2.819] | [−2.282, −0.530] | [0.396, 3.195] | [−0.781, 2.319] | |||||
| MA* During* Large | β11d | 1.198*** | −0.246 | ϒ11d | 0.596** | −0.993*** | ||||
| [0.632, 1.794] | [−1.243, 0.630] | [0.0520, 1.147] | [−1.484, −0.388] | |||||||
| ESHI* After* Large | β12 | 0.296 | −1.372*** | ϒ12 | 0.568 | −0.625 | LD−LA | 1.395*** | 2.43*** | |
| [−0.951, 1.457] | [−2.294, −0.450] | [−0.594, 1.651] | [−1.635, 0.379] | [0.78, 1.914] | [2.048, 2.725] | |||||
| ESHI* During* Large | β12d | 0.693 | −0.361 | ϒ12d | 0.411 | −0.550** | LF−LB | 2.708*** | 6.415*** | |
| [−0.410, 1.776] | [−1.663, 0.804] | [−0.152, 0.936] | [−1.057, −0.0530] | [1.793, 3.652] | [5.611, 6.91] | |||||
| ESHI* Large | β19 | 6.317*** | 2.230*** | ϒ19 | 16.770*** | 2.029*** | LD−LB | −0.231 | 3.836*** | |
| [5.685, 6.753] | [1.646, 2.635] | [16.024, 17.685] | [1.646, 2.512] | [−1.539, 0.941] | [2.877, 4.608] | |||||
| After* Large | β22 | −0.0896 | 1.348*** | ϒ22 | −0.844 | 0.258 | LF−LA | 4.334*** | 5.009*** | |
| [−0.815, 0.561] | [0.560, 1.971] | [−1.999, 0.242] | [−0.607, 1.009] | [3.272, 5.337] | [3.831, 5.79] | |||||
| During* Large | β22d | −0.383 | 0.575 | ϒ22d | −0.474* | 0.367 | ||||
| [−0.963, 0.246] | [−0.200, 1.576] | [−1.045, 0.0630] | [−0.226, 0.839] | |||||||
| Large | β23 | −4.987*** | 0.972 | ϒ23 | −19.596** | 1.755 | ||||
| [−9.625, −4.398] | [−2.351, 1.708] | [−26.838, −17.745] | [−0.408, 2.186] | |||||||
| MA* Large | β24 | −0.565 | 1.243* | ϒ24 | 1.634 | −0.954 | ||||
| [−1.389, 4.066] | [−0.0180, 4.564] | [−0.118, 8.972] | [−1.445, 1.168] | |||||||
| MA* ESHI* After | β1e | −0.706 | 0.788* | ϒ1e | 2.979*** | 3.832*** | ||||
| [−1.764, 0.264] | [−0.115, 1.706] | [1.843, 3.909] | [2.750, 4.684] | |||||||
| MA* ESHI* During | β1ed | 1.577*** | 2.124*** | ϒ1ed | −0.231 | −0.130 | s | 0.190 | 0.190 | |
| [0.638, 2.579] | [1.168, 3.366] | [−0.748, 0.289] | [−0.560, 0.351] | - | - | |||||
| MA* ESHI | β8e | 2.948*** | 2.813*** | ϒ8e | 1.735*** | 1.601*** | d | −0.380 | −0.380 | |
| [2.159, 3.845] | [2.079, 3.511] | [1.345, 2.232] | [1.202, 2.016] | - | - | |||||
| MA* After | β11e | 2.941*** | 1.608*** | ϒ11e | −1.615*** | −2.126*** | b | −3.155*** | −2.524*** | |
| [2.349, 3.490] | [0.833, 2.323] | [−2.519, −0.612] | [−2.834, −1.092] | [−4.926, −1.958] | [−4.123, −1.046] | |||||
| MA* During | β11ed | −0.618*** | −0.428* | ϒ11ed | 0.602** | 0.992*** | ρ | −0.045*** | −0.056*** | |
| [−1.078, −0.226] | [−1.127, 0.0400] | [0.0980, 1.071] | [0.536, 1.404] | [−0.072, −0.029] | [−0.136, −0.034] | |||||
| ESHI* After | β12e | −0.284 | −0.0596 | ϒ12e | 0.443 | 0.278 | α+λ−μx | 0.217 | −0.131 | |
| [−1.279, 0.757] | [−0.923, 0.740] | [−0.469, 1.604] | [−0.516, 1.347] | [−0.199, 0.498] | [−1.616, 0.394] | |||||
| ESHI* During | β12ed | −0.675 | −0.652 | ϒ12ed | 0.287 | 0.231 | ESHIAfter | 0.740 | 0.740 | |
| [−1.626, 0.249] | [−1.614, 0.146] | [−0.214, 0.797] | [−0.142, 0.675] | - | - | |||||
| ESHI | β19e | 7.036*** | 2.705*** | ϒ19e | 2.136*** | 1.506*** |
|
1.000 | 1.000 | |
| [6.152, 7.797] | [2.100, 3.411] | [1.642, 2.560] | [1.074, 1.878] | - | - | |||||
| After | β22e | 0.352 | 0.0193 | ϒ22e | −0.287 | −0.256 | DWLm | 3.966*** | 5.296*** | |
| [−0.204, 0.938] | [−0.561, 0.632] | [−1.182, 0.607] | [−1.076, 0.584] | [2.266, 6.012] | [3.1, 7.075] | |||||
| During | β22ed | 0.520** | 0.324 | ϒ22ed | −0.189 | −0.221 |
|
0.454*** | 0.948*** | |
| [0.0750, 0.968] | [−0.156, 0.766] | [−0.671, 0.313] | [−0.641, 0.227] | [0.187, 1.066] | [0.272, 5.071] | |||||
|
| ||||||||||
| Controls? | No | Yes | No | Yes | No | Yes | ||||
|
| ||||||||||
| Observations | 543,630 | 400,502 | 499,828 | 369,745 | ||||||
| R-squared | 0.081 | 0.172 | 0.214 | 0.171 | ||||||
p<0.01,
p<0.05,
p<0.1, 95% confidence intervals reported; CIs block bootstrapped by state.
Including full 18–64 population; only includes interview months.
All specifications include state and state*large firm fixed effects, no individual fixed effects. Monthly weights used.
Estimations with controls control for age, gender, marital status, race, education, and industry.
Large firm defined as >25 employees.
Footnotes
We thank Iris Chan, Toby Chaiken, Erin Taylor, and especially Michael Punzalan and Aditi Sen for excellent research assistance. Amitabh Chandra, John Friedman, Jonathan Gruber, Ben Handel, Samuel Kleiner, Lauren Nichols, Matt Notowidigdo, and Hugh Gravelle provided helpful conference discussions. This project has benefited greatly from comments from Joseph Altonji, Priyanka Anand, Bjoern Bruegemann, Tom Buchmueller, Marika Cabral, Joseph Doyle, Jesse Edgerton, Jason Fletcher, Bill Gale, Alex Gelber, Michael Grossman, Martin Hackmann, Lisa Kahn, Charles Kolstad, Kory Kroft, Ilyana Kuziemko, Fabian Lange, Anup Malani, Amanda Pallais, Mark Pauly, Vincent Pohl, Ebonya Washington, Heidi Williams, and Clifford Winston. We are also grateful for comments by seminar participants at Brookings, Brown, BU/Harvard/MIT Health Econ Workshop, the Bureau of Economic Analysis, FRB Richmond, Harvard, HEC Montreal, Olin, Penn, University of California–Berkeley, the Urban Institute, University of Texas–Austin, Stanford, Yale School of Public Health, the ASSA meetings, the Duke Empirical Microeconomics Jamboree, the European Econometrics and Health Economics Workshop, iHEA, the Mid-western Health Economics Conference, the National Tax Association annual meeting, the NBER Public Economics Program Meeting, the NBER Summer Institute, the New York Health Economics Workshop, and the Utah Winter Business Economics Conference. Funding from the National Institute on Aging grant #P30 AG012810, the Leonard Davis Institute for Health Economics, the Robert Wood Johnson Foundation, the W.E. Upjohn Institute for Employment Research, and the Wharton Dean’s Research Fund are gratefully acknowledged. During work on this project, Kowalski was the 2011–2012 Okun Model Early Career Fellow at the Brookings Institution.
According to the Massachusetts Connector website in 2010, in the zip code 02138 (Cambridge, MA), the cost of a Bronze plan for a family in Cambridge with two 40-year-old parents was $11,000 annually. For a couple with two individuals aged 35, the Bronze plan cost $6,600 annually. A 31-year-old purchasing a Bronze would expect to pay $2,868.
To satisfy the mandate, health insurance must meet or exceed a specific value (called “minimum creditable coverage”). See Kaiser Family Foundation (2009) and Raymond (2007). Individuals are automatically exempt from the individual mandate penalty in Massachusetts if they have a gap in creditable coverage of three months or less in a given calendar year, if they claim a religious exemption, or if their annual income is under 150 percent of the federal poverty level (effectively because the lowest cost Connector plan would be free for them). Other individuals can file for an exemption based on affordability using the Certificate of Exemption Application, which also provides details on the definition of “minimum creditable coverage.” (The application is available at https://www.mahealthconnector.org/portal/binary/com.epicentric.contentmanagement.servlet.ContentDeliveryServlet/FindInsurance/Individual/Affordability2520Calculator/2011CertificateofExemption.pdf, accessed December 1, 2011.)
Only approximately 4.6 percent of employers large enough to be subject to the penalty (12 percent of all Massachusetts employers) were required to pay it in 2010 (Massachusetts DHCFP 2011b). In addition, employers are subject to a separate “free rider surcharge” penalty if they do not offer a plan that allows employees to purchase health insurance using pre-tax wages and instead an employee receives care through the state’s uncompensated care pool. The compliance cost for employers to avoid this penalty is minimal. Accordingly, zero employers were liable for the free rider surcharge in fiscal years 2008 and 2009 (Massachusetts DHCFP 2011a).
In the 48 contiguous states and the District of Columbia, the 2014 poverty level is $11,670 for a single individual, and it grows by $4,060 for each additional family member (Federal Register 2014).
Effectively, eligibility will be extended to 138 percent of poverty because there is a special deduction of income under 5 percent of poverty (Kaiser Family Foundation 2010b).
We develop the model relying on the simplifying assumption that we can measure L in hours of work including nonworkers with zero hours, ignoring the potential difference between the extensive and intensive margin of employment. When we estimate the model, we relax this assumption in a series of specification checks that allow us to compare the intensive and extensive margin impacts in Massachusetts. We also note that we do not measure L as the probability of employment because only employed workers can have ESHI. We do not measure L as the number of employees because the goal of our model is to make predictions about labor market outcomes for individual workers that we observe in multiple periods.
In the first case, α is small, so λ takes on its statutory value, and the penalty-inclusive valuation, which we define as α + λ, is less than 1. In the second case, λ is large enough to augment α until the penalty-inclusive valuation is full. In the third case, the individual’s underlying valuation of health insurance is higher than the cost to the employer. Such a case could arise if an individual cannot access health insurance outside of employment, perhaps because of preexisting conditions that are excluded on the individual market. Such a case could also arise if health insurance through the employer is cheaper than other insurance, which is likely because of the tax-preference for employer-sponsored health insurance and because employers have more negotiating power than individuals. In this case, the penalty-inclusive valuation of health insurance is his underlying valuation, and the penalty has no impact. We define the subsidy similarly so that it cannot reduce an individual’s penalty-and-subsidy-inclusive valuation beyond zero.
Previous studies based on the Summers model have stopped at related inferences because they only have enough variation to identify the valuation if it is full. If the compensating differential is less than the cost of the benefit, and the hours differential is nonzero, then they cannot infer the magnitude of the penalty-and-subsidy-inclusive valuation beyond stating that it is not full. However, as we discuss in Section 3, the additional sources of variation in our model enrich the empirical content of the Summers model, allowing us to identify the penalty-and-subsidy-inclusive valuation, regardless of the true magnitude.
We note that the Summers model is a special case of our model
The level specification allows us to capture the impact of the reform on the intensive margin of how many hours to work and the extensive margin of whether to work because we can include unemployed workers in the sample, specifying that they have wages and hours of zero. The level specification also allows health insurance to have a realistic additive rather than multiplicative effect on wages, but we also investigate robustness to specifying wages and hours in logarithmic form.
In all specifications, we also allow for a “during” implementation period that is separate from the before and after periods. In our results tables, we represent the coefficients on during period terms with corresponding d superscripts.
We recognize that firm size can be endogenous in the sense that individuals can choose to work at small or large firms in response to health reform or firms that are near the firm size cutoff may endogenously change their size to avoid penalties. However, we want to allow for such behavior to capture the broadest possible impact of reform.
We extend the model to incorporate variation in subsidy amounts in the Online Appendix. This variation allows us to identify separate equilibria for individuals for different subsidy amounts. With these equilibria, we can separately identify λ from μx, and we can identify a different value of μx for each income eligibility group x. However, because using this variation requires us to divide the data into small groups based on income eligibility thresholds, we do not use this variation in our full specification.
In the full specification, which includes the bracketed terms in Equation (3), β11 also reflects the difference between individuals in large firms and individuals in small exempt firms, thus controlling for Massachusetts-specific factors after reform.
We can identify the slope of the demand curve d by comparing individuals with ESHI before and after the reform; we can identify the slope of the supply curve s by comparing individuals without ESHI before and after the reform; and we can also identify the employer penalty ρ by comparing individuals without ESHI before and after reform, using a value for d. We can also identify α, λ, and μx separately from their sum, which would allow us to analyze the welfare impact of the separate components of health reform independently. As shown in Table 3, identification of α requires a value for s and the comparison of people with and without ESHI before reform. The inclusion of individual fixed effects should help to identify α because we control for time-invariant factors that affect wages and benefits. However, any changes over time that affect both simultaneously will lead to bias. For example, if an individual without health insurance gets promoted to a job with higher wages and ESHI, we will estimate a negative value for α, even if the individual values the benefit such that the true value of α is positive. Such bias is precisely the problem that has hindered previous efforts to identify compensating differentials, which we overcome in identifying the penalty-and-subsidy-inclusive valuation but not in identifying α separately. We can also attempt to separately identify λ and μx. As shown in Table 3, identification of the difference λ − μx requires a value for s and the comparison of people with ESHI before and after reform. To separately identify μx from λ, and to identify different values of μx for people eligible for different subsidy amounts, we can incorporate variation in subsidy amounts across income eligibility thresholds as we discuss in the Online Appendix.
Because our specification is in levels (not logarithms), we convert these into slopes at the mean wage and hours.
The CBO considered a behavioral response to an individual mandate in their estimates of the impact of the ACA on coverage (Auerbach et al. 2010). They highlight the need to understand responses to the individual mandate in more detail, and our methodology could prove useful.
We use data from the core content of the SIPP. We construct our data by appending the 12 individual-wave files from the 2004 panel and merging longitudinal weights onto the full file by individual person identifiers. Longitudinal panel weights account for people who were in the sample in wave 1 of the panel and for whom data were obtained (either reported or imputed) for every month of the panel. There are four panel weights associated with the 2004 SIPP panel; the first covers people present in waves 1–4, the second covers people in waves 1–7, the third covers people in waves 1–10, and the fourth covers people who have data for the whole sample (waves 1–12). The panel weighting scheme does not assign weights to people who enter the sample universe after wave 1 (panel weight = 0 if the individual was not in the sample in wave 1, if they have missing data for one or more month(s), or both). In choosing the appropriate weights, there is a tradeoff between length of individual data and reductions in sample size associated with attrition. Our specification does not use panel weights and instead uses individual weights, therefore maximizing the number of respondents. In results not reported, we reestimate our regressions using each panel weight. Reassuringly, the coefficients of interest are relatively robust to these weight changes. Using weights 3 or 4 does lead to substantial loss of precision as the sample size falls when moving from longitudinal weight 1 to 4.
We have run our regressions in the restricted-access MEPS with state identifiers, but the sample size is not large enough for us to obtain reliable results.
We also note that even if we had data beyond December 2007, we would be reticent to rely on it to estimate our model because a recession began at that time. Dubay et al. (2012) present insurance coverage and employment measures in Massachusetts, a set of northeastern control states, and the remainder of the country over time. They show the impact of the recession in both Massachusetts and the various control groups beginning almost immediately in 2008. With 2008 data, we would thus be concerned that the recession could have had a differential impact on Massachusetts relative to other states.
We do, however, note that even though the CPS asks about coverage in the previous year, it is well known that responses also reflect current coverage. Thus, the responses from March of 2008 may reflect some share of people who gained coverage in 2008. Nevertheless, because the survey was very early in 2008, we would expect much of the change in coverage to have occurred in our sample period in 2007.
Because incorporating longitudinal variation through individual fixed effects places greater demands on the data, making the trend lines noisier, we combine each monthly response into mutually exclusive two-month periods, and we use all months available in the data instead of just interview months in these figures only.
If we examine the underlying data more closely, we see that there are approximately 3,000 observations (with multiple observations for approximately 1,600 unique individuals) in Massachusetts in each two-month period before reform, and approximately 1,000 observations (about 600 unique individuals) in Massachusetts in each two-month period after reform, with the exception of the last two-month period, Nov to Dec 2007, in which there are only 400 observations (273 unique individuals).
Chandra, Gruber, and McKnight (2011) examine enrollment in the individual health insurance market and find a spike in enrollment in December 2007. The decline in the wage premium that we observe begins before July 2007, but it does not contradict their results because enrollment in ESHI to comply with the individual mandate would have had to occur earlier than enrollment in the individual health insurance market to comply with the individual mandate. Although individuals were free to enroll in the individual health insurance market at any time—allowing them to carefully time enrollment to comply with the rules of the law—employers generally confine enrollment in ESHI to one particular “open season,” so individuals would need to enroll in ESHI earlier to satisfy the individual mandate in July 2007. In our data, we cannot observe open seasons, and it is difficult to verify enrollment timing, given issues with seam bias and reduced sample size after reform. Open enrollment frequently occurs on calendar or fiscal years. In either case, to comply by July 1, 2007, one would have had to sign up for ESHI in December 2006 or June 2007. Therefore, we would expect to see much of the impact of the reform prior to the precise implementation of the mandate, in the latter portion of 2006 or the first half of 2007.
If we do not assume that the employer penalty is zero, then the compensating differential from the baseline model is given by β1 + β8 + β11 = −0.846 + 1.128 + 1.728 = 2.010, which is of the wrong theoretical sign. Recall from Section 3.2 that if the employer penalty is small and there are no labor market changes in Massachusetts relative to other states after reform, we expect β11 to be small relative to β1 and negative. Similarly, if our individual fixed effects allow us to identify the compensating differential convincingly without using variation in ESHI induced by reform, we expect β8 to be small and negative relative to β1. However, both are positive and of the same order of magnitude as β1. Our estimated β11 suggests that something other than reform differentially affected the labor market in Massachusetts relative to other states (confirming our discussion of summary statistics), so we prefer the specification that incorporates variation by firm size. Our estimated β8 suggests that we need variation in ESHI induced by reform to estimate the compensating differential for ESHI. For these reasons, we focus on estimates that compare point A to equilibrium F incorporating variation by firm size in the full specification.
Confidence intervals are obtained by block-bootstrapping by state.
We discuss our choices of calibrated values in Section 3.3. The formulas in this table are drawn from the formulas in Table 3 and Equations (1) and (2). The formulas in the lower rows of the table reference values calibrated in the upper rows.
As discussed above, the estimate of $0.68 per $1 includes the tax preference for ESHI. Based on income, the vast majority of respondents in our sample fall in the 10 and 15 percent brackets (less than 20 percent fall in the other possible 25, 28, 33, and 35 percent brackets). However, these tax brackets overstate actual marginal tax rates because approximately 46 percent of households actually pay no federal income tax because of exemptions (Johnson et al. 2011). State and payroll taxes increase all marginal tax rates by approximately 10 percent. Therefore, most of our respondents have a penalty-and-subsidy-inclusive valuation of at least 48 cents on the dollar, excluding the tax preference, which is still quite high.
We find that the deadweight loss of tax-based health reform is $134 per year. A tax of size τ = b = $1.71 per hour, would raise $2,429 per person per year ($1.71 per hour × (30.26 hours per week in Massachusetts before reform − 3.01 hours per week after reform) × 52 weeks per year), which would not be large enough to finance the estimated average annual cost of ESHI per worker of $3,566. Even if we only require that tax-based reform insure as many individuals as mandate-based reform, 95 percent of individuals in the Massachusetts experience, the government would still need to collect $3,387 per worker ($3, 566 × 0.95). Therefore, we are conservative in setting τ = b. Under the tax, the ratio of the deadweight loss to revenue raised is 0.06, which is on the lower end of the range but consistent with prominent estimates from the literature such as Ballard, Shoven, and Whalley (1985) and Feldstein (1999).
Our work complements recent work by Aizawa and Fang (2013) that examines a richer interaction between the ACA and the labor market but requires additional structure.
Within our model, we cannot redefine L as an indicator variable for having a paid job, because all individuals with ESHI must have a paid job, so equilibrium D would always be above equilibrium F. Alternatively, if we instead aggregate our data, defining L as the fraction of individuals with a paid job, we cannot take advantage of longitudinal variation.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Jonathan T. Kolstad, Haas School, University of California, Berkeley and NBER
Amanda E. Kowalski, Department of Economics, Yale University and NBER
References
- Health Policy Brief: Employers and Health Care Reform. Health Affairs 2011 [Google Scholar]
- Aizawa Naoki, Fang Hanming. Equilibrium Labor Market Search and Health Reform. NBER Working Paper No. 18698 2013
- Arrow Kenneth J. Uncertainty and the Welfare Economics of Medical Care. American Economic Review. 1963;53(5):941–973. [Google Scholar]
- Auerbach David, Holtzblatt Janet, Jacobs Paul, Minicozzi Alexandra, Moomau Pamela, White Chapin. Will Health Insurance Mandates Increase Coverage? Synthesizing Perspectives from the Literature in Health Economics, Tax Compliance, and Behavioral Economics. 2010. (WP 2010-05) [Google Scholar]
- Baicker Katherine, Chandra Amitabh. Forum for Health Economics & Policy. Vol. 8. BE Press; 2005. The Effect of Malpractice Liability on the Delivery of Health Care; p. 4. [Google Scholar]
- Ballard Charles, Shoven John B, Whalley John. General Equilibrium Computations of the Marginal Welfare Costs of Taxes in the United States. American Economic Review. 1985;75(1):128–138. [Google Scholar]
- Blundell Richard, MaCurdy Thomas. Labor Supply: A Review of Alternative Approaches. Handbook of Labor Economics. 1999;3:1559–1695. [Google Scholar]
- Burkhauser Richard V, Lyons Sean, Simon Kosali I. NBER Working Paper 17279. 2011. The Importance of the Meaning and Measurement of “Affordable” in the Affordable Care Act. [Google Scholar]
- Chandra Amitabh, Gruber Jonathan, McKnight Robin. The Importance of the Individual Mandate — Evidence from Massachusetts. New England Journal of Medicine. 2011;(364):293–295. doi: 10.1056/NEJMp1013067. [DOI] [PubMed] [Google Scholar]
- Chetty Raj. Moral Hazard vs. Liquidity and Optimal Unemployment Insurance. Journal of Political Economy. 2008;1(2):173–234. [Google Scholar]
- Chetty Raj. Sufficient Statistics for Welfare Analysis: A Bridge Between Structural and Reduced-Form Methods. Annual Review of Economics. 2009;1:451–488. [Google Scholar]
- Commonwealth Connector. Helping Your Employees Connect to Good Health: Section 125 Plan Handbook for Employers. 2007 Available at < www.mahealthconnector.org>.
- Commonwealth Connector. [Accessed April 3, 2012];Affordability Information Sheet. 2011a Available at (link shortened for formatting): < http://tinyurl.com/connector2011-afforability>.
- Commonwealth Connector. [Accessed April 3, 2012];Frequently Asked Questions. 2011b Available at (link shortened for formatting): < http://tinyurl.com/connector2011-faq>.
- Currie Janet, Madrian Brigitte C. Health, Health Insurance and the Labor Market. Handbook of Labor Economics. 1999;3:3309–3416. [Google Scholar]
- Cutler David, Madrian Brigitte C. Labor Market Responses to Rising Health Insurance Costs: Evidence on Hours Worked. RAND Journal of Economics. 1998;29(3):509–530. [PubMed] [Google Scholar]
- Dubay Lisa, Long Sharon, Lawton Emily. [Accessed on July 3, 2012];Will Health Reform Lead to Job Loss? Evidence from Massachusetts Says No. 2012 Available at: < http://www.urban.org/publications/412583.html>.
- Federal Register. 2014;79(14):3593–3594. [Google Scholar]
- Feldstein Martin. Tax Avoidance and the Deadweight Loss of the Income Tax. The Review of Economics and Statistics. 1999;81(4):674–680. [Google Scholar]
- Gruber Jonathan. The Incidence of Mandated Maternity Benefits. American Economic Review. 1994;84(3):622–641. [PubMed] [Google Scholar]
- Gruber Jonathan. Health insurance and the labor market. Handbook of Health Economics. 2000;1:645–706. [Google Scholar]
- Hackmann Martin B, Kolstad Jonathan T, Kowalski Amanda E. Health Reform, Health Insurance, and Selection: Estimating Selection into Health Insurance Using the Massachusetts Health Reform. American Economic Review Papers and Proceedings. 2012;102(3):498–501. doi: 10.1257/aer.102.3.498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hackmann Martin B, Kolstad Jonathan T, Kowalski Amanda E. Adverse Selection and an Individual Mandate: When Theory Meets Practice. American Economic Review. 2015;105(3):1030–66. doi: 10.1257/aer.20130758. http://www.aeaweb.org/articles.php?doi=10.1257/aer.20130758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamermesh Daniel S. Labor Demand. Princeton University Press; 1996. [Google Scholar]
- Johnson Rachel, Nunns James, Rohaly Jeffrey, Toder Eric, Williams Roberton. Why Some Tax Units Pay No Income Tax. [Accessed on July 10, 2012];2011 Available at: < http://www.taxpolicycenter.org/UploadedPDF/1001547-Why-No-Income-Tax.pdf>.
- Kaiser Family Foundation. [Accessed on April 17, 2011];Massachusetts Health Care Reform Plan: An Update. 2007 Publication 7494-01. Available at: < http://www.kff.org/uninsured/7494.cfm>.
- Kaiser Family Foundation. Massachusetts Health Care Reform: Three Years Later. [Accessed on April 19, 2011];2009 Publication 7777-02. Available at: < http://www.kff.org/uninsured/upload/7777-02.pdf>.
- Kaiser Family Foundation. Explaining Health Care Reform: Questions about Health Insurance Exchanges. [Accessed April 2, 2012];2010a Available at: < http://www.kff.org/healthreform/upload/7908-02.pdf>.
- Kaiser Family Foundation. Focus on Health Reform: Summary of New Health Reform Law. [Accessed on April 19, 2011];2010b Available at: < http://www.kff.org/healthreform/upload/8061.pdf>.
- Kaiser Family Foundation. Medicaid and Children’s Health Insurance Program Provisions in the New Health Reform Law. [Accessed November 10, 2011];2010c Available at: < http://www.kff.org/healthreform/upload/7952-03.pdf>.
- Kaiser Family Foundation. Penalties for Employers Not Offering Affordable Coverage Under the Affordable Care Act Beginning in 2017. [Accessed on April 17, 2011];2010d Available at: < http://healthreform.kff.org/the-basics/~/media/Files/KHS/Flowcharts/employer__penalty_flowchart_1.pdf>.
- Kolstad Jonathan T, Kowalski Amanda E. The Impact of Health Care Reform On Hospital and Preventive Care: Evidence from Massachusetts. Journal of Public Economics. 2012;96(11–12):909–929. doi: 10.1016/j.jpubeco.2012.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long Sharon K. On the Road to Universal Coverage: Impacts of Reform in Massachusetts at One Year. Health Affairs. 2008;27(4):w270. doi: 10.1377/hlthaff.27.4.w270. [DOI] [PubMed] [Google Scholar]
- Massachusetts DHCFP. [Accessed on Feburary 22, 2012];The Employer Free Rider Surcharge: Policy Objectives, and Results. 2011a Available at: http://www.mass.gov/eohhs/docs/dhcfp/r/pubs/11/free-rider-2011.pdf.
- Massachusetts DHCFP. [Accessed on Feburary 22, 2012];Fair Share Contribution: Filing Year 2010 Results and Analyses. 2011b Available at: < http://www.mass.gov/eohhs/docs/dhcfp/r/pubs/11/fair-share-analyses-2010.pdf>.
- Massachusetts Health Connector and Department of Revenue. Data on the Individual Mandate: Tax Year 2008. 2010 Available at < www.mahealthconnector.org>.
- Raymond Alan G. The 2006 Massachusetts Health Care Reform Law: Progress and Challenges After One Year of Implementation. [Accessed on April 19, 2011];2007 Available at (link shortened for formatting): < http://masshealthpolicyforum.brandeis.edu/publications/all.html>.
- Rothschild Michael, Stiglitz Joseph. Equilibrium in Competitive Insurance Markets: An Essay on the Economics of Imperfect Information. The Quarterly Journal of Economics. 1976;90(4):629–649. [Google Scholar]
- Summers Lawrence H. Some Simple Economics of Mandated Benefits. American Economic Review. 1989;79(2):177–183. [Google Scholar]
- Yelowitz Aaron, Cannon Michael F. The Massachusetts Health Plan: Much Pain, Little Gain. Policy Analysis. 2010;(657) [Google Scholar]