Realistic Analytical Polyhedral MRI Phantoms

Abstract

Purpose

Analytical phantoms have closed form Fourier transform expressions and are used to simulate MRI acquisitions. Existing 3D analytical phantoms are unable to accurately model shapes of biomedical interest. It is demonstrated that polyhedral analytical phantoms have closed form Fourier transform expressions and can accurately represent 3D biomedical shapes.

Theory

The derivations of the Fourier transform of a polygon and polyhedron are presented.

Methods

The Fourier transform of a polyhedron was implemented and its accuracy in representing faceted and smooth surfaces was characterized. Realistic anthropomorphic polyhedral brain and torso phantoms were constructed and their use in simulated 3D/2D MRI acquisitions was described.

Results

Using polyhedra, the Fourier transform of faceted shapes can be computed to within machine precision. Smooth surfaces can be approximated with increasing accuracy by increasing the number of facets in the polyhedron; the additional accumulated numerical imprecision of the Fourier transform of polyhedra with many faces remained small. Simulations of 3D/2D brain and 2D torso cine acquisitions produced realistic reconstructions free of high frequency edge aliasing as compared to equivalent voxelized/rasterized phantoms.

Conclusion

Analytical polyhedral phantoms are easy to construct and can accurately simulate shapes of biomedical interest.

Introduction

In MRI acquisition and reconstruction development, it is useful to be able to quickly generate Fourier measurements of test objects. Physical test objects are referred to as physical MRI phantoms, or simply MRI phantoms. Realistic physical phantoms can be time consuming, cumbersome, and expensive to construct (1). In contrast, digital phantoms, sometimes referred to as computerized phantoms (2), are computer models. Digital phantoms are convenient because test data can be generated from simulated acquisitions but they currently have a number of shortcomings that limit their utility.

Digital phantoms can be divided into analytical or rasterized phantoms. Analytical phantoms are based on functions in the image domain which also have closed form Fourier transform (FT) expressions. These expressions allow the FT to be computed accurately at arbitrary spatial frequencies. An ideal analytical phantom for MRI development should accurately approximate the borders as well as the intensity profiles of shapes comprising biomedically relevant objects. However, existing 3D analytical phantoms are limited in the types of boundaries and intensity variations they can model. For instance, Koay’s implementation of the 3D Shepp-Logan head phantom (3,4) is constructed using ellipsoids with uniform intensity. Although Guerquin-Kern recently provided a closed form FT for 2D B-spline analytical phantoms with simulated coil sensitivity profiles (5) and Zhu used polygonal models to create an analytical vocal tract phantom (6), these phantoms are confined to 2D simulations.

In contrast to analytical phantoms, rasterized or voxelized phantoms (2,7–9) are based on voxels. They can be generated by discretely sampling continuous functions in the image domain but can also include simulations which evaluate the Bloch equation on a per voxel basis(10,11). Unlike the exact FT of analytical phantoms, rasterized phantoms can only provide an approximation of the FT of the original function by computing the discrete Fourier transform (DFT) of the image domain samples. The approximation accuracy is bounded by the rasterized phantom resolution. It can be made more accurate by oversampling, i.e. increasing the image domain sampling density, which in turn reduces high frequency aliasing in k-space. However, since the computational cost of the DFT increases with matrix size and keeping in mind that that all image space samples are required to compute a single k-space sample, motion simulations can be computational expensive. Separate image domain matrices are required to capture different motion states. Simulating motion between k-space samples requires computing the DFT of the matrix corresponding to the state of the object at sample time. Since the object may be moving continuously, the object may only spend a few k-space samples between state changes. Thus the DFT of many matrices must be computed to simulate even a few k-space samples, which can be time consuming. Additionally, non-Cartesian k-space trajectories are less straightforward to simulate since the DFT produces k-space points on a Cartesian grid.

Here we introduce 3D analytical phantoms constructed using polyhedra with uniform intensities, which although limited in their ability to model intensity variations, are able to accurately model the boundaries of many biomedically relevant shapes. A polyhedron is any closed surface comprised of polygonal faces and is general enough to accurately approximate the boundaries of many 3D objects. Additionally, since closed triangular meshes are also polyhedra, an analytical polyhedral phantom can be easily constructed using existing 3D computer graphics modeling tools that manipulate triangular meshes. Other 3D surface representations such as non-uniform rational B-splines (NURBS) can be converted to triangular meshes, which can then be used in an analytical polyhedral phantom.

We describe the theory and construction of analytical polyhedral phantoms, expanding on previously presented work (12). First, the closed form FT expressions for polyhedra are reviewed. Next, we describe an implementation of the FT of a polyhedron. Then we evaluate the accuracy of the FT computation for objects that can be exactly described using a polyhedra, e.g. a cube, and objects that can only be approximated, e.g. an ellipsoid. Finally, we describe the construction of analytical polyhedral phantoms that accurately model a brain and a torso and demonstrate their application in MRI simulations.

Theory

We review the analytical expressions for the FT of a polygon and polyhedron (13). A detailed derivation can be found in Appendix A. Vector quantities are in bold, scalars in plain typeface, and when both bold and plain typeface versions of a symbol exist, e.g. k and k, the plain typeface represents the magnitude of the corresponding vector.

Fourier transform of a polyhedron

A polyhedron is comprised of F polygonal faces. The boundary of the face f is composed of E_f vertices, ${\mathit{r}}^{(V_{f1})}\cdots {\mathit{r}}^{(V_{f{E}_f})}$ ordered in a counter-clockwise fashion when viewed with the face normal ${\widehat{\mathit{N}}}_f$ pointing at the observer. ${\mathit{L}}_{\mathit{fe}}={\mathit{r}}^{(V_{f(e+1)})}-{\mathit{r}}^{(V_{\mathit{fe}})}$ is a vector oriented in the direction of the e^th edge, pointing from vertex ${\mathit{r}}^{(V_{\mathit{fe}})}$ to ${\mathit{r}}^{(V_{f\left(e+1\right)})}$ with the same length as the edge. ${\widehat{\mathit{t}}}_{\mathit{fe}}={\mathit{L}}_{\mathit{fe}}/{\mathit{L}}_{\mathit{fe}}$ is the unit vector oriented in the direction of the e^th edge. ${\widehat{\mathit{n}}}_{\mathit{fe}}$ is a unit vector normal to the e^th edge and pointing outward from the interior of the polygon. Additionally, the first and last vertices are connected, thus ${\mathit{r}}^{(V_{f(E_f+1)})}={\mathit{r}}^{(V_{f1})}$.

$S_{3D}\left(\mathit{k}\right)$is the analytical expression for the FT of a unitary intensity polyhedron ρ(r) at spatial frequency k and is given in equation 1. If k=0, i.e. the DC offset, the FT is the volume polyhedron V. At non-zero k-space frequencies, $S_{3D}\left(\mathit{k}\right)$ is proportional to the sum of face contributions $S_f^{\ast }(\mathit{k})$, where $f\in [1,F]$. When a face f is normal to k, i.e. it’s normal vector ${\widehat{\mathit{N}}}_f$ is parallel to k, that face contribution is proportional to the area of the face, P_f modulated by a complex exponential whose argument is the dot product of k and the first vertex in the face ${\mathit{r}}^{(V_{f1})}$. Otherwise, when $\mathit{k}\ne k{\widehat{\mathit{N}}}_f$, the face contribution is proportional to the sum of contributions from each edge comprising the face. The contribution of edge e is proportional to the product of the length of the edge $L_{\mathit{fe}}$, a sinc and a complex exponential whose argument contains ${\mathit{r}}^{(C_{\mathit{fe}})}$, the midpoint of the edge. The number of terms in the overall sum for $S_{3D}\left(\mathit{k}\right)$ and thus the computational cost is proportional to the total number of edges in the polyhedron. Since the FT is linear, the expressions for non-unitary intensity polyhedra can be obtained by multiplying $S_{3D}\left(\mathit{k}\right)$ by the desired intensity. Figure 1 and Table 1 illustrate and define these quantities.

$$\begin{array}{l}{S}_{3D}\left(\mathit{k}\right)=\{\begin{array}{rr}\hfill -\frac{1}{{\left(2\pi k\right)}^2}{\displaystyle \sum }_{f=1}^F{S}_f^{\ast }\left(\mathit{k}\right),& \hfill \mathit{k}\ne 0\\ \hfill V,& \hfill \mathit{k}=0\end{array}\\ S_f^{\ast }\left(\mathit{k}\right)=\{\begin{array}{rr}\hfill \frac{\mathit{k}\cdot {\widehat{\mathit{N}}}_f}{k^2-{\left(\mathit{k}\cdot {\widehat{\mathit{N}}}_f\right)}^2}{\displaystyle \sum }_{e=1}^{E_f}{L}_{\mathit{fe}}\mathit{k}\cdot {\widehat{\mathit{n}}}_{\mathit{fe}}\frac{\sin \left(\pi \mathit{k}\cdot {\widehat{\mathit{t}}}_{\mathit{fe}}{L}_{\mathit{fe}}\right)}{\pi \mathit{k}\cdot {\widehat{\mathit{t}}}_{\mathit{fe}}{L}_{\mathit{fe}}}\mathit{exp}\left(-2\pi i\mathit{k}\cdot {\mathit{r}}^{(C_{\mathit{fe}})}\right),& \hfill \mathit{k}\ne k{\widehat{\mathit{N}}}_f\\ \hfill -2\pi i\mathit{k}\cdot {\widehat{\mathit{N}}}_f\mathit{exp}\left(-2\pi i\mathit{k}\cdot {\mathit{r}}^{(V_{f1})}\right)P_f,& \hfill \mathit{k}=k{\widehat{\mathit{N}}}_f\end{array}\\ P_f=\frac{1}{2}\left|{\widehat{\mathit{N}}}_f\cdot {\displaystyle \sum }_{e=1}^{E_f}\{{\mathit{r}}^{(V_{\mathit{fe}})}\times {\mathit{r}}^{(V_{fe+1})}\}\right|.\end{array}$$ (1)

Figure 1.

An illustration of a polygon A), a face of a polyhedron B) and their associated parameters. A) A unitary intensity 2D polygon comprised of four vertices V₁ … V₄ oriented in a counter-clockwise fashion. B) A single triangular face of a polyhedron comprised of vertices V_f1 … V_f3. The remaining parameters are described in Table 1.

Table 1.

Symbols

Symbol	Definition
S	Fourier Domain MR signal
k	k-space vector
2D polygon $\in {\mathbb{R}}^2$
$E$	Total number of vertices or edges
$e$	index of eth vertex or edge
$V_e$	eth vertex, first and last vectors connected, i.e. $V_{E+1}=V_1$ and $V_E=V_0$.
${\mathit{r}}^{(V_e)}$	position vector associated vertex $V_e$
${\mathit{L}}_e$	${\mathit{L}}_e={\mathit{r}}^{(V_{e+1})}-{\mathit{r}}^{(V_e)}$, vector oriented in the direction the eth edge, pointed from vertex $V_e$ to $V_{e+1}$ with the same length as the edge
${\widehat{\mathit{t}}}_e$	${\widehat{\mathit{t}}}_e={\mathit{L}}_e/L_e$, unit vector oriented in the direction of the eth edge
${\widehat{\mathit{n}}}_e$	is a unit vector normal to the eth edge and pointing outward from the polygon
${\mathit{r}}^{(C_e)}$	${\mathit{r}}^{(C_e)}={\mathit{r}}^{(V_e)}+{\widehat{\mathit{t}}}_e{L}_e/2$, position vector of the midpoint between vertices $V_e$ and $V_{e+1}$
P	Area of Polygon
3D polyhedron $\in {\mathbb{R}}^3$
$F$	total number of faces in the polyhedron
$f$	index of fth face
${\widehat{\mathit{N}}}_f$	outward normal of the fth face
$E_f$	total number of edges or vertices of the fth face
$V_{\mathit{fe}}$	eth vertex of fth face, first and last vectors connected, i.e. $V_{f,E_f+1}=V_{f1}$ and $V_{f{E}_f}=V_{f0}$
${\mathit{r}}^{(V_{\mathit{fe}})}$	position vector associated vertex $V_{\mathit{fe}}$
${\mathit{L}}_{\mathit{fe}}$	${\mathit{L}}_{\mathit{fe}}={\mathit{r}}^{(V_{f,e+1})}-{\mathit{r}}^{(V_{\mathit{fe}})}$, vector oriented in the direction the eth edge, pointed from vertex $V_{\mathit{fe}}$ to $V_{f,e+1}$ with the same length as the edge
${\widehat{\mathit{t}}}_{\mathit{fe}}$	${\widehat{\mathit{t}}}_{\mathit{fe}}={\mathit{L}}_{\mathit{fe}}/L_{\mathit{fe}}$, unit vector in the direction of the eth edge of the fth face
${\widehat{\mathit{n}}}_{\mathit{fe}}$	outward normal to the eth edge of the fth face and is in the plane of the face
${\mathit{r}}^{(C_{\mathit{fe}})}$	${\mathit{r}}^{(C_{\mathit{fe}})}={\mathit{r}}^{(V_{\mathit{fe}})}+{\widehat{\mathit{t}}}_{\mathit{fe}}{L}_{\mathit{fe}}/2$, position vector of the midpoint between vertices $V_{\mathit{fe}}$ and $V_{f,e+1}$
$P_f$	Area of fth face
V	Volume of Polyhedron

V is the volume of the polyhedron (14) which is given in terms of its vertices as:

$$\begin{array}{l}{S}_{3D}\left(\mathit{k}=0\right)=V\\ =\frac{1}{6}\left|\left[{\displaystyle \sum }_{f=1}^F\left({\mathit{r}}^{V_{f1}}\cdot {\widehat{\mathit{N}}}_f\right)\left|{\widehat{\mathit{N}}}_f\cdot \left\{{\displaystyle \sum }_{e=1}^{E_f}{\mathit{r}}^{(V_{\mathit{fe}})}\times {\mathit{r}}^{(V_{fe+1})}\right\}\right|\right]\right|\end{array}$$ (2)

Methods

Implementation

We implemented the FT of a polyhedron in two forms. First, a multi-threaded C++ MATLAB (15) plugin was created. Since the face contributions are independent they were computed in parallel using the available CPU threads. This strategy works well for motion simulations where the geometry of a polyhedral phantom with many faces changes every few k-space samples. Alternatively, if many k-space samples are needed for a single state of the object, e.g. in static simulations, an alternative efficient implementation can divide the computation among k-space samples instead of faces. Unless stated otherwise, this implementation was used for testing in this work. The second implementation is comprised of a set of MATLAB functions that take advantage of built-in parallelization and required no additional external libraries. This package is available to the MRI community though Mathworks. This implementation, apart from being platform-independent, is parallelized along both the faces and k-point dimensions, using either vectorization or innate multi-threading.

Multiple components comprising a polyhedral phantom can be modeled using separate polyhedra, similar to the multiple ellipsoids comprising the Shepp-Logan phantom. The FT of the composite phantom is obtained by computing the weighted sum of the individual FT of all component polyhedra, where the weights are the desired intensities of each component. Overlapping components will cause summation of intensities in the image domain.

Attention should be paid to the quality of polyhedra comprising a phantom. Polyhedra with undetected surface gaps, self-intersections, or incorrectly ordered vertices can produce unexpected results in the computed FT. The effect of a gap is proportional to its surface area. The gap can be interpreted as a missing face. Since the magnitude of the missing face contribution is proportional to the length of its edges, a larger gap has proportionately greater effect. Self-intersections cause reversal of internal and external regions, reversing the orientation of faces. The reversed orientation introduces a negative sign into the face contribution. As a result, a region of self-intersection can have the complex phase of its intensity reversed. The effect of a self-intersection is proportional to the volume of the regions involved. Finally, vertices that comprise a face are assumed to be ordered in a counterclockwise fashion with the face normal pointing toward the observer. Reverse ordering also reverses the face normal, again inverting inner and external regions similar to self-intersections. Again, artifacts associated with reverse ordering are proportional to the size of the faces involved. Since, these abnormalities affect the FT expression in a continuous fashion, the threshold at which they become noticeable will depend on machine numerical precision.

Validation

Accuracy

We compared the FT of a unit cube shaped polyhedron against the known gold standard FT of a unit cube. The unit cube, ${\rho }_{\mathit{gs}}$, has a closed form FT, $S_{\mathit{gs}}$, that is the product of sincs:

$$\begin{array}{c}\mathit{rect}\left(x\right)=\{\begin{array}{ll}0,\hfill & \text{if}|x|>\frac{1}{2}\hfill \\ \frac{1}{2},\hfill & \text{if}|x|=\frac{1}{2}\hfill \\ 1,\hfill & \text{if}|x|<\frac{1}{2}\hfill \end{array},ℱ\left(\mathit{rect}(x)\right)=\mathit{sinc}\left(k\right)=\frac{\sin \left(\pi k\right)}{\pi k}\\ {\rho }_{\mathit{gs}}\left(x,y,z\right)=\mathit{rect}\left(x\right)\cdot \mathit{rect}\left(y\right)\cdot \mathit{rect}\left(z\right)\\ S_{\mathit{gs}}\left(\mathit{k}\right)=ℱ\left({\rho }_{\mathit{gs}}\right)=W_x{W}_y{W}_z\cdot \mathit{sinc}\left(W_x{k}_x\right)\cdot \mathit{sinc}\left(W_y{k}_y\right)\cdot \mathit{sinc}\left(W_z{k}_z\right).\end{array}$$ (3)

$W_x,W_y,W_z$define the length of the $\mathit{rect}$ in the x, y, and z directions respectively and $k_x,k_y,k_z$ are elements of the k vector. The lengths were set to unity $(W_x=W_y=W_z=1)$ thus the function is a unit cube with unitary intensity centered at the origin. The unit cube can be exactly modeled using a triangular mesh thus the FT can also be computed with our implementation of the FT of a polyhedron. The unit cube shaped triangular mesh used in this validation had 12 triangular faces, two triangles defining each of the six square faces as illustrated in Figure 2. For the calculation of the FTs we used a field of view (FOV) of two corresponding to a k-space sampling density of $\mathrm{\Delta }k=1/\mathit{FOV}=0.5$ and a 64³ sampling matrix. These same parameters, unless otherwise specified, were used for all validation experiments.

Figure 2.

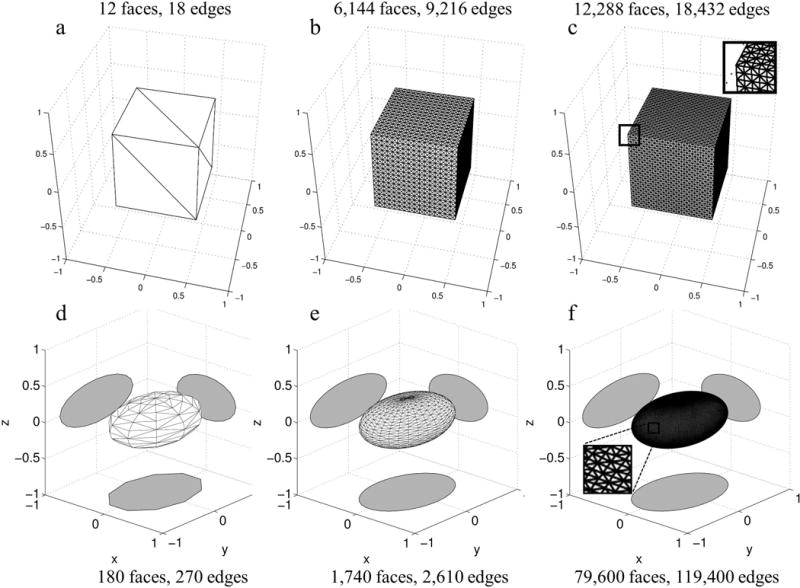
Examples of triangular meshes with varying number of faces used to model a unit cube a–c) and an ellipsoid d–f). Unit cube shaped triangular meshes containing varying number of faces were used to validate the implementation of the FT of a polyhedron against the gold standard of the FT of a 3D rect function. The magnified inset illustrates the small triangular faces comprising the mesh in c). Triangular meshes with varying number of faces d–f) were used to approximate the FT of an ellipsoid against the closed form FT. The grey shadows show cross sections of the mesh in the x=0, y=0 and z=0 planes. The magnified inset for the 79,600 face mesh illustrates dense triangles in the surface mesh.

Floating Point Precision

Edges are the basic unit in the computation of the FT of a polyhedron. Polyhedra with many faces, and thus many edges, are useful for modeling complex biomedically relevant geometry. Thus we assessed if the FT of a polyhedron accumulated prohibitively high floating point precision errors as the number of edges increased. The gold standard of the FT of a unit width 3D rect was compared with the FT of a unit cube shaped polyhedra containing 12 to 98,304 triangular faces or equivalently, 18 to 147,456 edges respectively (number of edges = 1.5 × number of faces for triangular meshes). Figure 2a–c illustrates example meshes containing 12, 6,144, and 12,288 triangular faces or 18, 9,216, and 18,432 edges, respectively. Additionally, the cube was shifted away from the origin by adding a random value between −0.5 and 0.5 to one or more of the x, y, and z components of the vertices and the gold standard k-space was multiplied by a corresponding linear phase.

Approximating smooth surfaces

To approximate smooth surfaces with a polyhedron, progressively smaller facets can be used until the desired approximation accuracy is obtained. We quantified the geometric approximation error incurred when modeling a smooth surface using a polyhedron. We examined how the error decreases when approximating an ideal ellipsoid with a polyhedron with increasing number of faces. We chose an ellipsoid because it is a smooth surface with a known closed form FT (3). The ellipsoidal triangular meshes were generated using Matlab in two steps. First points were generated on the surface of an ellipse (using ellipsoid). Then, a triangular mesh was generated from these points (using convhull). The meshes contained between 180 to 79,600 faces or 270 to 119,400 edges respectively. Figure 2d–f illustrate the meshes containing 180, 1,740 and 79,600 faces.

Brain phantom

3D MRI Simulation

Triangular meshes representing the outer and inner cortical brain surfaces were generated using anatomical data. The source data was a magnetization-prepared rapid gradient echo MRI volume from the Open Access Series of Imaging Studies (OASIS) dataset (16). The Topology Preserving Tissue Classification of Magnetic Resonance Brain Images (TOADS) algorithm (17) was used to segment the gray matter. The Cortical Reconstruction Using Implicit Surface Evolution (CRUISE) algorithm (18) was then applied to this segmentation to generate triangular meshes corresponding to the outer and inner cortical surfaces. The outer and inner cortical meshes contained 536,684 and 354,908 triangular faces respectively and are illustrated in Figure 3a–b. The number of faces was determined automatically by the TOADS and CRUISE algorithms and was dependent on factors such as the volume of the brain and the complexity of the cortical surface. Although subcortical structures such as ventricles were not included in this phantom there are no technical limitations that prohibit their inclusion.

Figure 3.

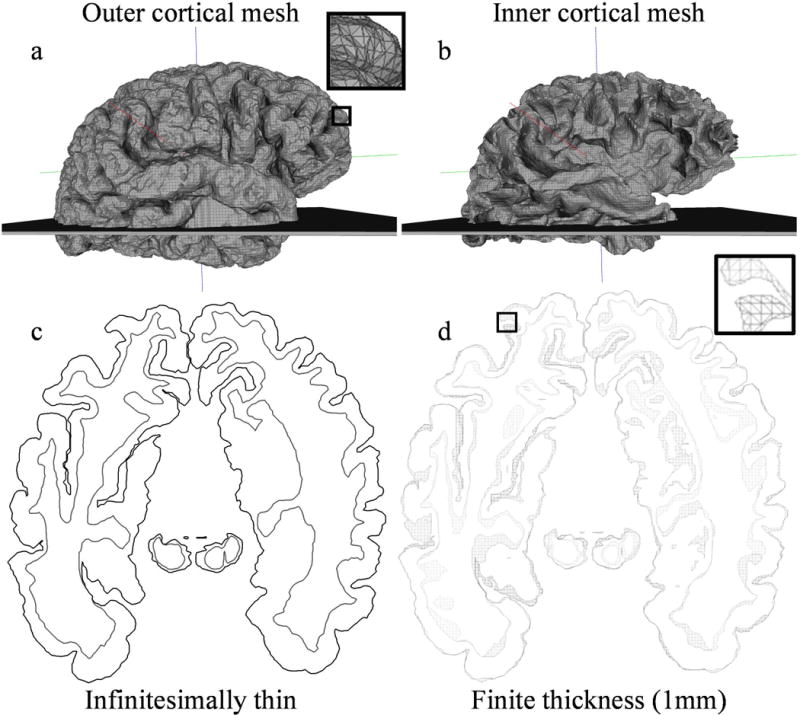
Triangular meshes comprising a 3D brain analytical polyhedral phantom used in 3D and 2D MRI simulations. The brain is oriented such that the x, y, z axes correspond to the right, anterior, superior anatomical axes. a) The outer cortical mesh with magnified inset illustrating triangles in the mesh, and b) inner cortical mesh with overlaid slab mesh used in 2D MRI simulation with finite slice thickness. Although not shown, the slice plane used to simulate idealized infinitesimally thin slice selection is centered in the slab mesh. c) The resulting 2D contours from the intersection of all meshes with the ideal slice plane. d) The resulting 3D sliced meshes from the intersection of all meshes with a 1mm thick slab mesh. The magnified inset illustrates triangles in the mesh.

We simulated a 3D MRI acquisition using these meshes. The k-space matrix size was 128³, and the FOV in right, anterior, superior directions were 137.35 mm, 170.15 mm, and 117.20 mm, respectively. The outer and inner cortical meshes were assigned intensities of 74 and 38, respectively, producing after summation due to overlap, intensities of 74 in the cortex and 112 in the subcortical regions. Finally, the volume was reconstructed using a 3D IDFT.

2D MRI simulation

We simulated a 2D MRI acquisition where a slice of the 3D object is selectively excited before k-space is acquired. To simulate ideal slice selection where an infinitesimally thin slice of the brain is excited by a slice selective radio-frequency pulse, a 2D plane perpendicular to the slice selection axis, the z-axis, was intersected with the meshes generating sets of 2D slice contours. The location of the slice plane lies midway between the top and bottom faces of the slab mesh in Figure 3a,b. We used the Computational Geometry Algorithms Library (CGAL) (19) to compute these intersections. CGAL is a C/C++ library containing peer validated, highly accurate geometry related functions. Figure 3c illustrates the resulting contours obtained through simulated ideal slice selection.

We also simulated slices with finite thickness as is typical in 2D MRI acquisitions. While real MRI slices usually have a Gaussian or sinc profile along the slice encoding direction, this can be approximated with a rect function which can be modeled as a slab mesh. Alternatively, one could compute the 3D FT of the slab and convolve it with the FT of the desired arbitrary slice profile. However, if a closed form solution does not exist for the convolution, it must be approximated by sampling the FTs, which would introduce approximation errors. Using CGAL’s Boolean surface operations, we computed the intersection between a 1-mm thick slab mesh, shown in Figure 3a,b, and the cortical meshes to generate a set of 1 mm thick sliced meshes for the inner and outer surfaces illustrated in Figure 3d. The slab mesh was perpendicular to the slice encoding z-axis and large enough in the x and y directions to encompass the brain. Since the intersection can disconnect sections of the original contiguous cortical mesh, creating “islands”, the result of the intersection between slab and cortical mesh is not a single closed sliced meshed but a set of closed meshes. Triangular faces in the original cortical mesh that are intersected by the top and bottom planes are converted to polygons with additional edges. The top and bottom surface of the sliced meshes are non-triangular polygons which outline the intersection of the top and bottom slab plane with the cortical mesh. The inner and outer cortical sliced mesh sets contained a total of 4,798, and 3,812 faces, respectively.

Using these contours and sliced meshes, we simulated a 2D MRI acquisition. We used the FT of polygons and polyhedra to compute the k-space of the infinitesimally thin slice 2D contours and finite thickness slice meshes respectively. The same acquisition parameters were used for both simulations. As in a real 2D MRI acquisition, we sampled k-space on a Cartesian grid of matrix sizes 64², 128², and 256² in the k_x−k_y plane, i.e. only the k_x=0 mm⁻¹ plane was sampled. Since the largest extent of the contours and sliced meshes was 122.78 mm in anterior-posterior dimension, the imaging FOV was set to 1.1 times larger at 135.06 mm to prevent image domain aliasing. Sampling only the k_x=0 mm⁻¹ plane integrates the finite slice in the z direction, which results in slice encoding related partial volume effects. The same tissue intensity assignments were used as in the 3D MRI simulation.

For comparison, we also generated a rasterized phantom by sampling the 2D contours in image space. The imaging parameters were equivalent to the analytical simulations. The image domain of each contour was sampled by assigning a value of one or zero for points inside or outside the contour respectively. Each rasterized contour was then scaled by the same tissue intensities used in the analytical simulations before summation in image space. We did not perform a finite thickness slice selection rasterized simulation because approximating through slice integration via image space sampling would introduce through-slice sampling density as another experimental parameter.

We used the IDFT to reconstruct images from the analytical phantom simulations. To compare the ideal slice and finite slice simulation images, the finite slice reconstruction was normalized by the slice thickness since the intensity is integrated through the slice. No image reconstruction was required for the rasterized phantom.

Torso phantom

We simulated the 2D MRI acquisition of a torso with cardio-respiratory motion to demonstrate the application of a polyhedral analytical phantom in cardiac MRI simulations. First, triangular meshes for the polyhedral torso phantom were generated with source geometry and motion derived from the eXtended Cardiac-Torso (XCAT) phantom (2,20,21). XCAT is a 4D NURBS and subdivision surface based anthropomorphic phantom. These NURBS and surfaces model anatomy from the high-resolution anatomical images of the Visible Male and Female National Library of Medicine datasets. XCAT also models cardiac motion based on 100 time frames over a cardiac cycle of high resolution (0.32 mm pixel size, 0.4 mm slice thickness) cardiac-gated multi-detector computed tomography (CT) data. Respiratory motion is also modeled based on respiratory-gated CT data. We used the male XCAT model for this simulation, extracting 90 sets of NURBS surfaces corresponding to uniformly spaced time points fully spanning a cardio-respiratory cycle.

The NURBS surfaces from the XCAT phantom were converted to triangular meshes using Rhinoceros (22), a computer graphics program specialized in manipulating NURBS. Each object in the XCAT phantom was represented by at least one mesh. Hollow objects such as the ventricles of the heart had separate meshes for inner and outer surfaces. The number of triangular faces per mesh varied. For instance, the left ventricular inner mesh contained 1,322 triangles, while the left lung mesh contained 4,086 faces. The total number of faces across all meshes for a single time point varied but was approximately 23,580. Figure 4a shows the resulting triangular mesh torso phantom at end-expiration/end-diastole. Conversion with Rhinoceros produced some self-intersecting meshes. As Rhinoceros is proprietary software, it is unclear why conversion from NURBS to triangular meshes would in some cases result in self-intersections, holes and other abnormalities. The CGAL library contains algorithms that detect self-intersections and using it we created a tool to determine which meshes were abnormal. We first attempted to repair these meshes using Polymender (23), a program that repairs defects in triangular meshes. After the attempted repair, we reran the self-intersection detection tool. If the repaired mesh was still self-intersecting, we used Meshlab (24), a program that specializes in manipulating triangular meshes, for a second attempt at repairing the mesh. Unfortunately, some meshes could not be repaired by either program and were excluded from all time points of the phantom.

Figure 4.

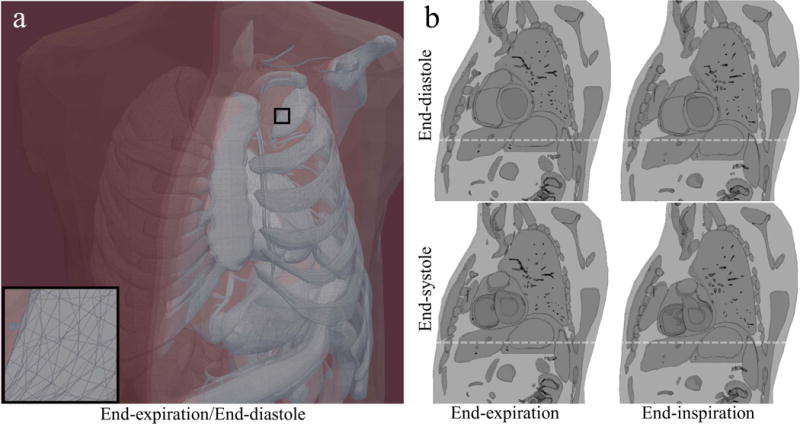
Rendering of triangular mesh torso phantom with intersecting slice plane and resulting sliced meshes for different time points in the cardio-respiratory cycle. a) 3D rendering of torso phantom mesh at end-expiration/end-diastole. Magnified inset illustrates triangular facets. The slice plane is highlighted in red. b) Resulting sliced meshes after mesh subtraction and intersection operations. Although meshes were generated for 90 time points throughout the cardio-respiratory cycle, only the extremes of the cardio-respiratory cycle are illustrated here. A video is included with this manuscript that illustrates all 90 times points. The white lines are present to aide in seeing relative motion of structures.

Some surfaces from XCAT overlapped during respiratory and cardiac motion, which caused undesired addition of intensities in the image domain. These overlapping regions were subtracted using mesh Boolean operations. As a consequence, meshes that contained other meshes were "hollowed" out. For instance, the left ventricular epicardial surface mesh derived from XCAT contained the endocardial surface mesh. The epicardial surface mesh, which describes a solid, was converted to a solid shell that had an outer and inner surface that precisely followed the endocardial surface and thus was able to accommodate the endocardial surface mesh without overlap.

Next, finite thickness slice selection was simulated for all time points. A 4 mm thick slab mesh representing the slice plane, positioned at the base of the heart in the short axis orientation was intersected with all meshes for each time point and is illustrated in Figure 4a. We used CGAL functions to compute this intersection resulting in 4 mm-thick sliced meshes. This process was repeated for all time points in the cardio-respiratory cycle. Figure 4b illustrates the resulting sliced meshes at the extremes of the cardio-respiratory cycles.

A 2D MRI acquisition was simulated individually for all time points. The k-space of the sliced meshes were sampled using a 128² Cartesian matrix and FOV=400 mm. The intensities of the polyhedra were chosen to simulate the relative intensity differences between tissues in a bright-blood gradient echo MRI sequence. Finally, the IDFT was used to reconstruct images for each time point.

Results

Validation

Accuracy

The FT of a unit cube triangular mesh with 12 faces (18 edges) computed using the proposed implementation closely matched the gold standard. To estimate differences between the proposed method and the gold standard, the magnitude of the error $|S_{\mathit{gs}}\left(\mathit{k}\right)-S_{3D}(\mathit{k})|$ and the normalized magnitude of the error $|S_{\mathit{gs}}\left(\mathit{k}\right)-S_{3D}(\mathit{k})|/|S_{\mathit{gs}}\left(\mathit{k}\right)|,|S_{\mathit{gs}}\left(\mathit{k}\right)|\ne 0$ were evaluated along the k_x-axis. As Figure 5a middle row illustrates, the magnitude of the error was small, below $3\times {10}^{-17}$ for all sample locations. Samples with larger coefficient magnitudes seemed correlated with higher magnitudes of error. The normalized magnitude of error was also very small, less than 3×10⁻¹⁸ as illustrated in Figure 5a bottom row. The normalized error was uncorrelated with the magnitude of the coefficient.

Figure 5.

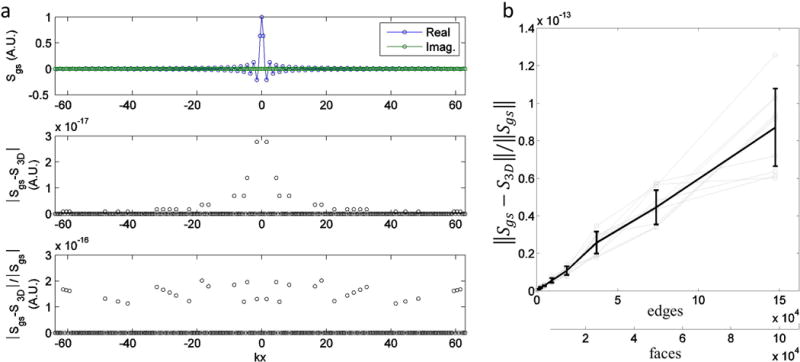
Evaluation of FT error with increasing edges in unit cube shaped triangular meshes. a) Sample-wise evaluation of the FT error. Top row) Plot of the gold standard computed using the product of sincs. Values are given in arbitrary units (A.U.) The real and imaginary components are displayed separately. Middle row) Graph of magnitude of error versus k_x-axis location. Bottom row) Graph of normalized magnitude of error versus k_x-axis location, excluding points where the gold standard coefficient magnitude is zero since this would result in an undefined value. b) Graph of the normalized l²-norm of the error versus the number of faces in the unit cube mesh. Gray lines indicate different shifts of the cube from the origin. The black line with error bars indicate the mean and standard deviation of the normalized error taken across all displacements.

Floating Point Precision

The error due to limited floating point precision was small, suggesting detailed meshes with many edges can be used to construct analytical polyhedral phantoms. We computed the l²-norm of the difference between the FT of the polyhedron and gold standard normalized by the l²-norm of the gold standard. Figure 5b shows that the normalized error increases approximately linearly with the number of edges with small variations between different displacements of the cube from the origin. Gray lines in the figure correspond to different displacements of the cube from the origin. The solid line with error bars indicates the mean and standard deviation of the error taken across all displacements. For the mesh with 147,456 edges, the mean normalized error is just 0.8717×10⁻¹³. These computations were performed on a quad core Intel Xeon 2.13 Ghz system. A five run average of the FT of the 12 face cube mesh (18 edges), over the 64³ k-space matrix using one, two, three, and four processor threads required and 7.78, 4.02, 2.84, 2.32 seconds or 1.65, 0.85, 0.60 and 0.49 μseconds per k-space sample per edge respectively. As run times were not recorded for all simulations, the computational rate corresponding to four threads will be used to estimate run times for other simulations. This is a reasonable estimate because the computational cost of the FT of a polyhedron is linear in the number edges and k-space samples.

Approximating Smooth Surfaces

We computed the l²-norm of the difference between the FT of the ellipsoidal polyhedron and ideal ellipsoid normalized by the l²-norm of the FT of the ideal ellipsoid. The normalized error decreased quickly with increasing number of faces. The log of the l²-norm of the error over the entire volume normalized by the l²-norm of the gold standard volume decreased rapidly with increasing face number as illustrated in Figure 6a. At 79,600 faces (119,400 edges) the normalized error is only 6.21×10⁻⁴. The geometric approximation error is magnitudes larger than the floating point precision error, suggesting the number of faces can be increased significantly although with an increase in computation time. Figure 6b top row shows the z=0 slice of the reconstructed FT of meshes containing 180, 760, 1,740, 79,600 faces and the corresponding error is indicated by arrows in Figure 6a. Gibbs ringing due to finite k-space sampling can be observed in the reconstructed images in Figure 6b top row. Figure 6c illustrates this artifact in more detail using an intensity profile corresponding to the dashed line in Figure 6b. In image space, the error as expected is concentrated at the edges and is shown in Figure 6b bottom row. In k-space, the largest absolute errors are concentrated at the lower frequencies, as shown in Figure 6d top row. However, when the absolute value of the error is normalized by the absolute value of the gold standard, higher frequencies tend to have more normalized error, shown in Figure 6d bottom row.

Figure 6.

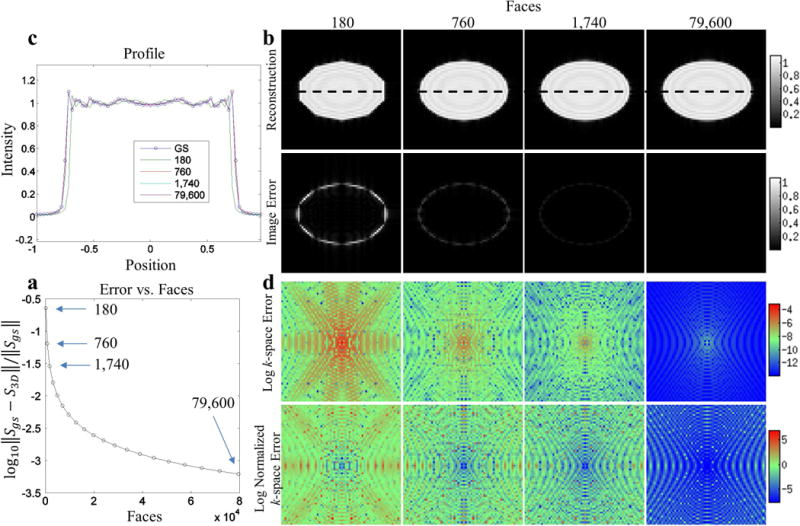
The behavior of the error incurred when approximating the smooth surface of an ideal ellipsoid using polyhedra with increasing number of faces. The gold standard is an ideal ellipsoid with a known closed form FT. a) The log of the l²-norm of the gold standard volume versus the number of faces in the triangular mesh. Arrows indicate error corresponding to meshes in Figure 2 and subfigures b and c show image space and k-space details respectively for these meshes. b top row) The z=0 slice of reconstructed 3D volume and image space error. c) The intensity profiles corresponding to the dotted lines on the slices. b bottom row) The magnitude of the image space error for the z=0 slice. d top row) The log of the absolute value of the k-space error corresponding to the k_z=0 plane. d bottom row) The log of the absolute value of the k-space error normalized by the absolute value of the gold standard.

Brain phantom

3D MRI simulation

The analytical polyhedral brain phantom was able to accurately model the gyri of the brain. Although, the surfaces were comprised of triangular facets, they were small enough to approximate the smooth curves of the brain at this resolution. Gibbs ringing from finite sampling of k-space can also be observed in the inhomogeneity of intensities near the edges, an artifact found in real MRI images. Figure 7 illustrates representative slices from the reconstructed volume. The estimated computational time for the FT of the 3D brain phantom was approximately 15.96 days. The exponential increase in the number of samples in the 3D 128³ sampling matrix compared to a 2D matrix and the large number of faces substantially increased computation time.

Figure 7.

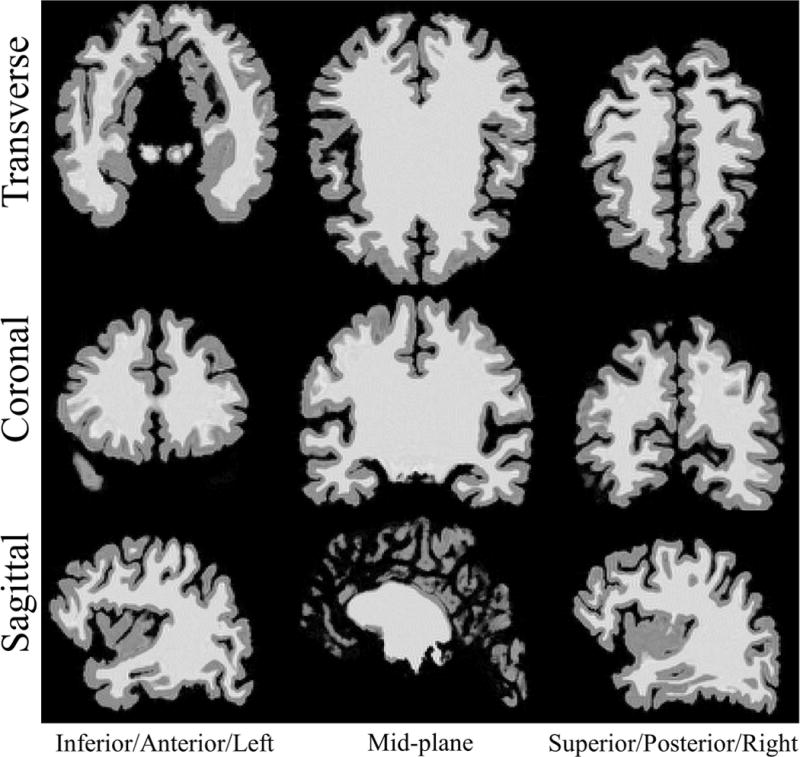
Representative slices of reconstructed volume from 3D MRI simulation using analytical polyhedral brain mesh phantom. Rows top to bottom: Transverse, coronal, sagittal planes. Columns left to right: Inferior, mid-plane, superior slices for the transverse plane. Anterior, mid-plane, posterior slices for coronal plane. Left, mid-plane, right slices for the sagittal plane.

2D MRI simulation

The results of the 2D MRI simulations using the 2D analytical infinitesimally thin and 3D finite slice thickness analytical phantoms were compared with a 2D rasterized phantom generated from the contours of the 2D infinitesimally thin slice phantom (Figure 8). Differences between the 2D analytical and the 2D rasterized phantoms were solely due to aliasing effects of image space sampling in the rasterized phantom. However, differences between the 3D finite slice analytical phantom and 2D rasterized phantom additionally include through-plane intensity variations that accurately reflect underlying mesh geometry. To demonstrate the effects of finite slice thickness, rasterized phantom must densely sample the through plane direction to approximate these variations (not shown). Using the C++-based MATLAB plugin, the time required to compute Fourier samples for the finite thickness slice selection 3D brain MRI simulation for 64², 128² and 256² matrix sizes was 0.43, 1.73 and 6.93 minutes, respectively. We omit the slice plane and slab intersection operations because they require a negligible amount of time compared to the FT computation.

Figure 8.

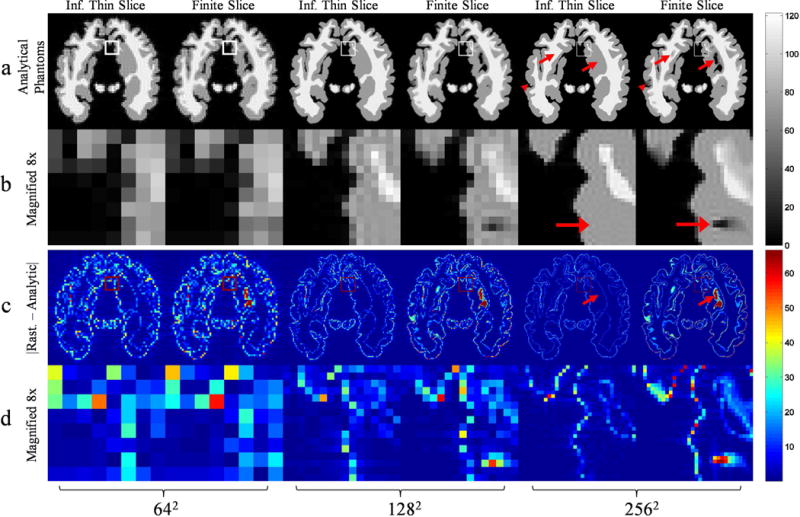
A comparison of a simulated 2D MRI brain acquisition using an analytical polyhedral phantom with infinitesimally thin and finite thickness slice selection for matrix sizes 64², 128², and 256². All images in the rows a, b have the same intensity scaling given by the color bar on the right and similarly with images in rows c, d. For each set of two columns, the left and right correspond to thin and finite thickness slice selection respectively. The arrowheads and full arrows highlight partial volume effects at the edges and in the interior respectively. Row a) IDFT reconstruction of ideal and finite slice simulations. Row b) A magnified section corresponding to the region outlined by boundary pixels in row a. The boundary pixels become proportionately smaller as a side effect of increasing matrix size. Row c) The magnitude of the difference between a rasterized simulation, not shown, generated from the infinitesimally thin slice selection contours and the analytical simulations. The rasterized simulation image matrix is the same size as the k-space matrix used for analytical phantoms. Row d) A magnified section corresponding to the region outlined by boundary pixels in row c, which is the same region outlined in row a) and magnified in row b).

The finite thickness slice selection 2D brain MRI simulation exhibited partial volume effects seen in real 2D MRI acquisitions. The arrowheads in Figure 8 highlight partial volume effects at the edges seen only in the finite thickness simulation. Oblique edges of the mesh caused changes in intensity along the slice encoding direction which was integrated simulating partial volume effects in the finite thickness slice selection simulation. Aside from the edges, regions of low intensity can be observed in the interior when using finite slices, illustrated by the full arrows in Figure 8. In the finite thickness simulation, normalizing the integrated intensity by the slice thickness produces the mean intensity through the slice plane. Thus, regions that were predominantly low intensity in the slice direction may have lower intensity than the infinitesimally thin slice simulation, which does not have intensity variation in the slice encoding direction.

Differences between the simulations using the rasterized phantom and the analytical phantoms were concentrated at the edges as illustrated in Figure 8, row c. The discrete image space samples of the rasterized phantom caused aliasing of high spatial frequencies of k-space. In the analytical phantom, regions of sudden intensity changes, such as edges, were accompanied by Gibb’s ringing and partial volume effects, both of which are not simulated by the rasterized phantom. The mean difference between the rasterized and analytical phantom decreased with matrix size. The spacing between image space samples of the rasterized phantom decreases for larger matrices, reducing high frequency aliasing and thus the DFT of the rasterized phantom more closely approximated the FT of the analytical phantoms. Edge differences were more pronounced in the finite slice simulation due to partial volume effects of oblique edges that were not modeled in the rasterized phantom.

The partial volume effect of finite thickness slice selection can be easily observed in Figure 8, row c. The full arrows illustrate a partial volume effect seen in the finite thickness simulation but was absent in the thin slice simulation. Since the rasterized phantom was based on the contours of the thin slice simulation it did not exhibit the partial volume effects seen in the finite thickness slice simulation and this can be observed in these difference images.

Torso phantom

The torso phantom demonstrates an analytical polyhedral phantom that incorporates motion. Using the C++-based MATLAB plugin, the FT for each time point required an estimated 4.75 minutes to compute and thus 7.12 hours for all 90 time points. Again, we omit the time required to convert, slice and fix the meshes because this was insignificant compared to the FT computation time. Figure 9 shows the reconstructed simulated acquisition of the phantom at the extremes of a cardio-respiratory cycle. Supporting Movie 1 shows the reconstructed simulated acquisition for 90 frames spanning a cardio-respiratory cycle. In-plane motion can be observed during the contraction of the heart between end-diastole and end-systole. The blood pool of the pulmonary artery seems to merge with the right ventricle due to their close vicinity in end-diastole but they separate in end-systole. Additionally, motion of objects through the spatially fixed slice plane can be observed. The arrowheads in Figure 9 illustrate a portion of a coronary artery that came into the slice plane at end-inspiration/end-systole which was out of plane at end-expiration/end-systole. The vessels and bronchioles of the lung also illustrate through-plane motion. The full arrows in Figure 9 illustrate a vessel in the lung that came into the slice plane at end-expiration/end-systole but was out of plane at end-inspiration/end-systole.

Figure 9.

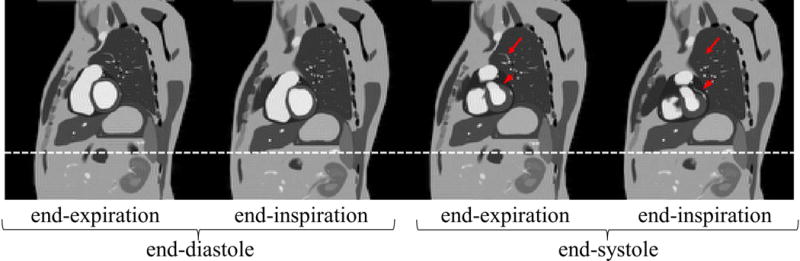
The IDFT reconstruction of a simulated 2D MRI acquisition using an analytical polyhedral phantom of the torso at the extremes of the cardio-respiratory cycle. The white line is a reference to aid in seeing relative motion between different time points. Arrowheads highlight through-plane movement of a coronary artery. Full arrows highlight through-plane movement of a vessel in the lungs.

The torso simulation also demonstrates that an analytical polyhedral phantom can be constructed using many meshes with greatly differing sizes. There were 180 meshes in each set of sliced torso meshes. They ranged from the large body surface mesh to small coronary artery meshes. A rasterized phantom would cause aliasing of the large high frequency components of small meshes, which does not occur using the closed form FT of the analytical polyhedral phantom.

Discussion

Analytical polyhedral phantoms are useful in a number of areas of MRI development as evidenced by the repeated use of the Shepp-Logan phantom and its derivatives based on ellipses or ellipsoids. Realistic 4D (3D space and 1D time) may be more accurately computed in comparison to using an oversampled, i.e. super-sampled rasterized, phantom. In some cases such as simulation of motion, the polyhedral phantoms may be more computationally efficient than super-sampled rasterized phantoms. For instance, with the torso phantom we only simulated motion between each complete 2D k-space matrix. However, we can also simulate motion between individual k-space samples. If motion information is available throughout the cardio-respiratory cycle, as it is in the XCAT phantom, every k-space sample can be computed using a set of meshes corresponding to the current sampling time, thereby modeling motion on an individual k-space sample resolution. To perform the equivalent motion simulation accurately using a rasterized phantom would require densely oversampling the entire 3D image space matrix for every k-space sample, which can be computationally intensive for 4D simulations. Consider such a motion simulation with a matrix size of 256³ using the outer cortical mesh in the 3D brain phantom and assuming two times oversampling factor for the rasterized phantom. The time required to compute a single k-space for a single motion state corresponds to the time required to compute the FFT of a 512³ matrix. This required our system approximately 4.44 seconds and one gigabyte of memory. In contrast, the time required to compute a single k-space point using the analytical phantom was 0.40 seconds and required 14.58 megabytes of memory. The number of operations required to compute N k-space points where every point is a different motion state using the FFT, ignoring oversampling, is $O\left(N^2\mathit{log}N\right)$ whereas computing the same points using a polyhedral phantom is O(N), linear with the number of k-space points. Note that though the polyhedral FT is significantly more computationally intensive than the standard FFT it does not have advantage of significant optimization as does the FFT via the fftw libraries. Further optimization in the implementation of the phantom, including efficient parallelization, should significantly reduce computation time.

Analytical polyhedral phantoms are also useful for developing motion compensation techniques. Periodically rotated overlapping parallel lines with enhanced reconstruction (PROPELLER) (25) and projection navigators (26–28) use non-Cartesian k-space trajectories and detect features shared between images or projections captured at different motion states. Using a polyhedral phantom these features can be realistically modeled and non-Cartesian k-space trajectories are readily simulated. In this paper we chose not to include examples of non-Cartesian trajectories such as 3D radial since that would introduce additional experimental factors such as the choice of non-Cartesian reconstruction algorithm. However, since the 2D torso phantom simulation samples 3D k-space along an oblique plane, this trajectory demonstrates the polyhedral phantom supports sampling of arbitrary k-space frequencies. Polyhedral phantoms may also have uses in computed tomography (CT) simulations through the relationship between the FT and the Radon transform via the Fourier slice theorem. Artifacts from using facets to approximate smooth surfaces can be alleviated by increasing the number of facets.

Any in vivo configuration that can be described in image space by altering the triangular mesh can be simulated using a polyhedral phantom. Hence, non-linear deformation of tissues is reduced to relocation of vertices before sampling of Fourier space. Other non-linear behavior such as eddy currents can also be simulated with this framework. Eddy currents, which introduce offsets in intended k-space sample locations, can be modeled by creating a mismatch between the k-space coordinates used to sample the phantom and the coordinates used to reconstruct the data. However, to simulate phase accrual due to flow as used in phase contrast imaging, is more difficult as it could require subdivision of the physiologically relevant polyhedral into significantly smaller polyhedrons as done in finite element methods. The position of each small element within a gradient at a given time point can then be used to weight the contribution of that element to the final Fourier transform, with the weight including both magnitude and phase, and the phase term being determined by the first moment of the experienced gradient. Though computationally intense, this approach could allow MR simulation of any finite element model–derived structure.

Limitations

As demonstrated in the 3D brain simulation, computation time can be an issue for large matrices and meshes with many edges. Using our basic C++-based plug-in, calculation of the polyhedral FT for a large number of faces (~50000) required on average 0.134 usec per kpoint per triangular face. Hence, calculation of a 256³ k-space matrix would take ~ 30 hrs. Further optimization of our C++-based implementation could certainly increase computation speed, especially if more efficient multi-threading is included. Additionally, the FT of a polyhedron is highly parallelizable since the computation of the contribution of each face is completely independent and therefore well suited for an optimized graphics processing unit implementation. Though not explored in this work, reusing any shared computations between edge and face contribution calculations may further increase performance (29).

Currently, this phantom and the associated framework are unable to model coil sensitivity profiles. The coil profile produces a modulation in image space and therefore a convolution of the FT of the phantom with the FT of the coil sensitivity profile. Though a solution for this problem has been presented by Guerquin-Kern (5) for a 2D analytical phantom, to our knowledge, no solution exists for 3D phantoms that results in a purely analytical expression. Another limitation of the current implementation of the polyhedral FT phantom involves tissue intensity gradients. More computationally intensive simulations are required as the presented equations assume piecewise constant regions of intensity. Nevertheless, we can approximate gradients by dividing objects into adjacent regions with gradually varying intensity. Furthermore, a simple reformulation of the polyhedral FT can be used to efficiently calculate these gradients (29).

Conclusions

In this paper, we reviewed the derivation of the FT of a polygon and polyhedron and described multi-threaded implementation for the later. We evaluated accumulated error due to limited floating point precision and determined that it remained small even for polyhedra with many faces. We determined that the k-space error of polyhedral approximations of smooth surfaces decreased rapidly with increasing number of faces. We used polyhedra to construct realistic 3D brain and 4D torso phantoms and demonstrated the application of these phantoms in simulated 2D and 3D MRI acquisitions. A MATLAB implementation of the phantom can be downloaded here: http://www.mathworks.com/matlabcentral/fileexchange/51911-realistic-analytical-polyhedral-mri-phantoms.

Supplementary Material

Supp MovieS1

Supporting Movie 1: Reconstruction of a simulated acquisition of the torso phantom over 90 points spanning a cardio-respiratory cycle. Jitter occurring at the body surface is due to the thin slice plane and large polygonal faces in the body surface mesh. This jitter can be reduced by increasing the number of faces during the body surface NURBs to mesh conversion or increasing the thickness of the slice plane. In contrast, jitter at the lungs is due to differences between repaired self-intersecting meshes produced by Polymender and Meshlab. Removing this jitter requires a NURBS to triangular mesh conversion that does not produce self-intersections or a tool that can correct meshes for all time frames with minimal differences.

A Appendix

A.1 Abbe transform theorem

For a function ϕ that satisfies the Helmhotz equation ${\nabla }^2\varphi +m^2\varphi =0$, the N-dimensional volume integral of ϕ can be expressed as an N-1 dimensional integral of the divergence of ϕ over the surface enclosing the integration volume.

$$\underset{V}{\overset{\left(N\right)}{{\displaystyle \int }}}\varphi d^{N}r=-\frac{1}{m^2}\underset{\partial V}{\overset{(N-1)}{{\displaystyle \int }}}\nabla \varphi \cdot \widehat{\mathit{n}}d\sigma$$ A.1

Proof

Let V be a finite region in a space of N dimensions, ∂V is the boundary of V, and dσ an infinitesimal element of ∂V. Also let ϕ(r), be a scalar valued function of the position vector r which satisfies the Helmholtz equation:

$${\nabla }^2\varphi +m^2\varphi =0$$ A.2

Where $m$ is some constant.

ϕ satisfies the Helmholtz equation, implying $\varphi =-{\nabla }^2\varphi /m^2$. By substitution, the integral of the function ϕ over the volume V can be expressed as

$$\underset{V}{\overset{(N)}{{\displaystyle \int }}}\varphi d^{N}r=-\frac{1}{m^2}\underset{V}{\overset{(N)}{{\displaystyle \int }}}{\nabla }^2\varphi d^{N}r$$ A.3

Additionally, according to Gauss’s theorem

$$\underset{V}{\overset{(N)}{{\displaystyle \int }}}\nabla \cdot A{d}^{N}r=\underset{\partial V}{\overset{(N-1)}{{\displaystyle \int }}}A\cdot \widehat{\mathit{n}}d\sigma$$ A.4

If we let $A=\nabla \varphi$ and $\nabla \cdot \mathrm{A}={\nabla }^2\varphi$ the above equation becomes

$$\underset{V}{\overset{(N)}{{\displaystyle \int }}}{\nabla }^2\varphi d^{N}r=\underset{\partial V}{\overset{(N-1)}{{\displaystyle \int }}}\nabla \varphi \cdot \widehat{\mathit{n}}d\sigma$$ A.5

Substituting this result into the right side of A.3 produces the general case of the Abbe Transform:

$$\underset{V}{\overset{\left(N\right)}{{\displaystyle \int }}}\varphi d^{N}r=-\frac{1}{m^2}\underset{\partial V}{\overset{(N-1)}{{\displaystyle \int }}}\nabla \varphi \cdot \widehat{\mathit{n}}d\sigma$$ A.6

A.2 Applying the Abbe transform to the Fourier transform

To apply the Abbe Transform to the Fourier integral, let $\varphi \left(\mathit{r}\right)=\text{exp}(-2\pi i\mathit{k}\cdot \mathbf{r})$ be the kernel of the Fourier transform (FT) so the integral on the left of 0 is the N dimensional FT of the constant valued volume V. ϕ(r) satisfies the Helmholtz equation (k is a considered a constant) with $m^2={(2\pi k)}^2$, where k is the magnitude of the k space vector:

$$\nabla \varphi =\nabla \mathit{exp}\left(-2\pi i\mathit{k}\cdot \mathbf{r}\right)=-2\pi i\mathit{exp}\left(-2\pi i\mathit{k}\cdot \mathbf{r}\right)\mathit{k}$$ A.7

$$\begin{array}{l}{\nabla }^2\varphi =\nabla \cdot \left[-2\pi i\mathit{exp}\left(-2\pi i\mathit{k}\cdot \mathbf{r}\right)\mathit{k}\right]\\ =-{\left(2\pi k\right)}^2\exp \left(-2\pi i\mathit{k}\cdot \mathbf{r}\right)\end{array}$$ A.8

$${\nabla }^2\varphi +m^2\varphi =-{\left(2\pi k\right)}^2\mathit{exp}\left(-2\pi i\mathit{k}\cdot \mathbf{r}\right)+{\left(2\pi k\right)}^2\mathit{exp}\left(-2\pi i\mathit{k}\cdot \mathbf{r}\right)=0.$$ A.9

Thus we can apply the Abbe transform to convert the N-dimensional Fourier volume integral of a constant valued region V to an equivalent N-1 dimensional surface integral.

$$\begin{array}{l}S\left(\mathit{k}\right)=\underset{V}{\overset{\left(N\right)}{{\displaystyle \int }}}\mathit{exp}\left(-2\pi \mathit{k}\cdot \mathit{r}\right)d^{N}r\\ =\frac{i}{2\pi k^2}\underset{\partial V}{\overset{(N-1)}{{\displaystyle \int }}}\mathit{exp}\left(-2\pi i\mathit{k}\cdot \mathbf{r}\right)\mathit{k}\cdot \widehat{\mathit{n}}d\sigma \end{array}$$ A.10

A.3 Derivation of the Fourier transform of a polygon

First we will derive the closed form expression for the FT of a plane polygon. This expression will be used in the face contribution of the polyhedron to its overall transform.

In 2D, we wish to find the FT S_2D(k)of a polygon ρ(r) whose boundary is composed of E vertices V₁ ⋯ V_E oriented in a counter-clockwise fashion, where $\rho \left(\mathit{r}\right)=1if\mathit{r}\mathit{\in }P,\mathit{else}\rho \left(\mathit{r}\right)=0$. The Abbe transform expresses the FT ρ(r) as a line integral along the boundary L where dl is a small segment of that boundary:

$$\begin{array}{l}{S}_{2D}\left(\mathit{k}\right)=\underset{P}{\overset{\left(2\right)}{{\displaystyle \int }}}\mathit{exp}\left(-2\pi i\mathit{k}\cdot \mathit{r}\right)d^2\mathit{r}\\ =\frac{i}{2\pi k^2}\underset{L}{\overset{(1)}{{\displaystyle \int }}}\mathit{exp}\left(-2\pi i\mathit{k}\cdot \mathit{r}\right)\mathit{k}\cdot \widehat{\mathit{n}}dl.\end{array}$$ A.11

Notice that $\widehat{\mathit{n}}$, the outward pointing normal to the edge of the polygon, and r are implicitly functions of the position on the boundary.

Let ${\mathit{L}}_e={\mathit{r}}^{(V_{e+1})}-{\mathit{r}}^{(V_e)}$ be the vector oriented in the direction of the e^th edge, pointing from vertex V_e to V_e+1with the same length as the edge, where ${\mathit{r}}^{(V_e)}$, ${\mathit{r}}^{(V_{e+1})}$ are the position vectors associated with the V_e and V_e+1 vertices of the polygon respectively. ${\widehat{\mathit{t}}}_e={\mathit{L}}_e/L_e$ is the unit vector oriented in the direction of the e^th edge. ${\widehat{\mathit{n}}}_e$ is a unit vector normal to the e^th edge and pointing outward from the interior of the polygon. Additionally, the first and last vertices are connected, thus $V_{E+1}=V_1$ and likewise $V_E=V_0$.

A polygon’s boundary can be broken up into edges and the line integral can be expressed as the sum of the contributions $S_e\left(\mathit{k}\right)$ from each of the edges.

$$S_{2D}\left(\mathit{k}\right)={\displaystyle \sum }_{v=1}^E{S}_e\left(\mathit{k}\right)$$ A.12

$$S_e\left(\mathit{k}\right)=\frac{i}{2\pi k^2}\underset{0}{\overset{{\mathit{L}}_e}{{\displaystyle \int }}}\mathit{exp}\left(-2\pi i\mathit{k}\cdot \mathit{r}\right)k\cdot {\widehat{\mathit{n}}}_{e}dl$$ A.13

Here, ${\widehat{\mathit{n}}}_e$ has replaced $\widehat{\mathit{n}}$ and is constant along a given edge.

A point on the e^th edge can be parameterized by setting $\mathit{r}={\mathit{r}}^{(V_e)}+{\mathit{t}}_{e}l$, where lis the distance from the vertex V_e, which makes explicit the dependence of the position ron the boundary to the scalar variable l. The contribution from the right edge can be rewritten as

$$S_e\left(\mathit{k}\right)=\frac{i}{2\pi k^2}k\cdot {\widehat{\mathit{n}}}_e\mathit{exp}\left(-2\pi i\mathit{k}\cdot {\mathit{r}}^{(V_e)}\right)\underset{0}{\overset{L_e}{{\displaystyle \int }}}\mathit{exp}\left(-2\pi i\mathit{k}\cdot {\widehat{\mathit{t}}}_{e}l\right)dl$$ A.14

$$S_e\left(\mathit{k}\right)=\frac{1}{{\left(2\pi k\right)}^2}\frac{\mathit{k}\cdot {\widehat{\mathit{n}}}_e}{\mathit{k}\cdot {\widehat{\mathit{t}}}_e}\mathit{exp}\left(-2\pi i\mathit{k}\cdot {\mathit{r}}^{(V_e)}\right)\left(1-\mathit{exp}\left(-2\pi i\mathit{k}\cdot {\widehat{\mathit{t}}}_e{L}_e\right)\right).$$ A.15

Let ${\mathit{r}}^{(C_e)}={\mathit{r}}^{(V_e)}+{\widehat{\mathit{t}}}_e{L}_{듒}/2$ to rewrite S^e in terms of phasors related to the midpoint of the edge.

$$S_e\left(\mathit{k}\right)=\frac{1}{{\left(2\pi k\right)}^2}\frac{\mathit{k}\cdot {\widehat{\mathit{n}}}_e}{\mathit{k}\cdot {\widehat{\mathit{t}}}_e}\mathit{exp}\left(-2\pi i\mathit{k}\cdot \left({\mathit{r}}^{(C_e)}-\frac{{\widehat{\mathit{t}}}_e{L}_e}{2}\right)\right)\left(1-\mathit{exp}\left(-2\pi i\mathit{k}\cdot {\widehat{\mathit{t}}}_e{L}_e\right)\right)$$ A.16

$$S_e\left(\mathit{k}\right)=\frac{1}{{\left(2\pi k\right)}^2}\frac{\mathit{k}\cdot {\widehat{\mathit{n}}}_e}{\mathit{k}\cdot {\widehat{\mathit{t}}}_e}\mathit{exp}\left(-2\pi i\mathit{k}\cdot {\mathit{r}}^{(C_e)}\right)\left(\mathit{exp}\left(\pi i\mathit{k}\cdot {\widehat{\mathit{t}}}_e{L}_e\right)-\mathit{exp}\left(-\pi i\mathit{k}\cdot {\widehat{\mathit{t}}}_e{L}_e\right)\right)$$ A.17

$$S_e\left(\mathit{k}\right)=\frac{i}{2\pi k^2}{L}_e\mathit{k}\cdot {\widehat{\mathit{n}}}_e\frac{\sin (\pi \mathit{k}\cdot {\widehat{\mathit{t}}}_e{L}_e)}{\pi \mathit{k}\cdot {\widehat{\mathit{t}}}_e{L}_e}\mathit{exp}\left(-2\pi i\mathit{k}\cdot {\mathit{r}}^{(C_e)}\right)$$ A.18

Summing over all edge contributions $S_e\left(\mathit{k}\right)$ we obtain the final form for the expression for the FT of a polygon:

$$S_{2D}\left(k\right)=\frac{i}{2\pi k^2}{\displaystyle \sum }_{e=1}^E{L}_e\mathit{k}\cdot {\widehat{\mathit{n}}}_e\frac{\sin \left(\pi \mathit{k}\cdot {\widehat{\mathit{t}}}_e{L}_e\right)}{\pi \mathit{k}\cdot {\widehat{\mathit{t}}}_e{L}_e}\mathit{exp}\left(-2\pi i\mathit{k}\cdot {\mathit{r}}^{(C_e)}\right),k\ne 0$$ A.19

The above expression is finite as long as $\mathit{k}\ne \mathbf{0}$, i.e. the center of k-space. The value at k=0 is equal to the area of the polygon. The area of a 2D planar polygon in terms of its vertices is

$$S_{2D}\left(\mathit{k}=\mathbf{0}\right)=\frac{1}{2}\left|{\displaystyle \sum }_{e=1}^E{r}_x^{(V_e)}{r}_y^{(V_{e+1})}-r_x^{(V_{e+1})}{r}_y^{(V_e)}\right|.$$ A.20

A.4 Derivation of the Fourier transform of a polyhedron

We wish to find an analytical solution for the FT of a polyhedron ρ(r)

$$S\left(\mathit{k}\right)={\displaystyle \iiint }\rho (\mathit{r})\mathit{exp}\left(-2\pi i\mathit{k}\cdot \mathit{r}\right)d^3\mathit{r}$$ A.21

where $\rho \left(\mathit{r}\right)=1if\mathit{r}\mathit{\in }V,\mathit{else}\rho \left(\mathit{r}\right)=0$.

Using the Abbe transform, the volume integral in the FT of a polyhedron can be expressed as an integral over the surface ∂V.

$$\begin{array}{l}{S}_{3D}\left(\mathit{k}\right)=\underset{V}{\overset{3}{{\displaystyle \iiint \mathit{exp}\left(-2\pi \mathit{k}\cdot \mathit{r}\right)d^3\mathit{r}}}}\\ =\frac{i}{2\pi k^2}\underset{\partial V}{\overset{(2)}{{\displaystyle ∯}}}\mathit{exp}\left(-2<i\mathit{k}\cdot \mathit{r}\right)\mathit{k}\cdot \widehat{\mathit{n}}d\sigma \end{array}$$ A.22

We wish to express the surface integral as the sum of the contributions of the faces of the polyhedron $S_f(\mathit{k})$. Let $\mathit{r}={\mathit{r}}^{0f}+{\mathit{r}}_f$ where ${\mathit{r}}_f$ is a vector in the plane of the face of P_f whose origin is at r^0f and r^0f is the position vector of an arbitrarily chosen point 0f in the face P_f. Additionally, let ${\widehat{\mathit{N}}}_f$ be the outward normal of the f^th face and F be the total number of faces in the polyhedron.

Similar to the FT of a polygon, we can express the FT of a polyhedron as the sum of the contributions from each of its individual faces.

$$S_{3D}\left(\mathit{k}\right)={\displaystyle \sum }_{f=1}^F{S}_f\left(\mathit{k}\right)$$ A.23

$$S_f\left(k\right)=\frac{i}{2\pi }\frac{\mathit{k}\cdot {\widehat{\mathit{N}}}_f}{k^2}\mathit{exp}\left(-2\pi i\mathit{k}\cdot {\mathit{r}}^{0f}\right)I_f(\mathit{k})$$ A.24

$$I_f\left(\mathit{k}\right)=\underset{P_f}{\overset{(2)}{∯}}\mathit{exp}\left(-2\pi i\mathit{k}\cdot {\mathit{r}}_f\right)d^{2}r$$ A.25

The integral $I_f\left(\mathit{k}\right)$ over the surface P_f of the f^th polygonal face can be evaluated using the formula for the FT of a polygon if k_f is substituted for k, the projection of k onto the plane P_f or the component of k that exists purely in the plane of P_f. Since $\mathit{k}\cdot {\mathit{r}}_f=({\mathit{k}}_f+{\mathit{k}}_{f\mathit{perp}})\cdot {\mathit{r}}_f={\mathit{k}}_f\cdot {\mathit{r}}_f,I_f\left({\mathit{k}}_f\right)=I_f\left(\mathit{k}\right)$ and k_f exists purely in the plane of the face (the plane of integration) we can apply the formula for the FT of a polygon. Additionally, let E_f be the number of edges of the f^th face, ${\mathit{r}}^{(C_{\mathit{fe}})}$ is the position vector of the midpoint of the e^th edge on the f^th face, ${\widehat{\mathit{t}}}_{\mathit{fe}}$ be the unit vector in the direction of the e^th edge of the f^th face, ${\mathit{L}}_{\mathit{fe}}$ be the length of the e^th edge of the f^th face, ${\widehat{\mathit{n}}}_{\mathit{fe}}$ is the outward normal to the eth edge of the f^th face and is in the plane of the face.

$$\begin{array}{l}{I}_f\left(\mathit{k}\right)=I_f\left({\mathit{k}}_f\right)\\ =\frac{i}{2\pi {k_f}^2}{\displaystyle \sum }_{e=1}^{E_f}{L}_{\mathit{fe}}{\mathit{k}}_f\cdot {\widehat{\mathit{n}}}_{\mathit{fe}}\frac{\sin \left(\pi i{\mathit{k}}_f\cdot {\widehat{\mathit{t}}}_{\mathit{fe}}{L}_{\mathit{fe}}\right)}{{\mathit{k}}_f\cdot {\widehat{\mathit{t}}}_{\mathit{fe}}}\mathit{exp}\left(-2\pi i{\mathit{k}}_f\cdot {{\mathit{r}}_f}^{(C_{\mathit{fe}})}\right)\end{array}$$ A.26

This expression has a singularity when k_f=0. In this case I_f is the area of the f^th face, P^f. The following equalities can be used to rewrite the above equation in terms of k and ${\mathit{r}}^{(C_e)}$. in the global coordinate system: ${k_f}^2=k^2-{(\mathit{k}\cdot {\widehat{\mathit{N}}}_f)}^2$, ${\mathit{k}}_f\cdot {\widehat{\mathit{n}}}_{\mathit{fe}}=\mathit{k}\cdot {\widehat{\mathit{n}}}_{\mathit{fe}}$, ${\mathit{k}}_f\cdot {\widehat{\mathit{t}}}_{\mathit{fe}}=k\cdot {\widehat{\mathit{t}}}_{\mathit{fe}}$, ${\mathit{k}}_f\cdot {{\mathit{r}}_f}^{(C_{\mathit{fe}})}=\mathit{k}\cdot {{\mathit{r}}_f}^{(C_{\mathit{fe}})}$, and ${{\mathit{r}}_f}^{(C_{\mathit{fe}})}={\mathit{r}}^{(C_e)}-{\mathit{r}}^{0f}$.

$$I_f\left(\mathit{k}\right)=\frac{i}{2\pi [k^2-{\left(\mathit{k}\cdot {\widehat{\mathit{N}}}_f\right)}^2]}{\displaystyle \sum }_{e=1}^{E_f}{L}_{\mathit{fe}}k\cdot {\widehat{\mathit{n}}}_{\mathit{fe}}\frac{\sin \left(\pi i\mathit{k}\cdot {\widehat{\mathit{t}}}_{\mathit{fe}}{L}_{\mathit{fe}}\right)}{\mathit{k}\cdot {\widehat{\mathit{t}}}_{\mathit{fe}}}\mathit{exp}\left(-2\pi i\mathit{k}\cdot {\mathit{r}}^{(C_{\mathit{fe}})}\right)$$ A.27

The singularity at k_f=0 becomes a singularity at $\mathit{k}=k{\widehat{\mathit{N}}}_f$ because k perpendicular to the f^th face implies k_f=0. In this case $I_f\left(k{\widehat{\mathit{N}}}_f\right)$ is the surface area P_f of the polygonal face f given in the global coordinate system as

$$\begin{array}{l}{I}_f\left(\mathit{k}=k{\widehat{\mathit{N}}}_f\right)=P_f\\ =\frac{1}{2}\left|{\widehat{\mathit{N}}}_f\cdot {\displaystyle \sum }_{e=1}^E\{{\mathit{r}}^{(V_{\mathit{fe}})}\times {\mathit{r}}^{(V_{fe+1})}\}\right|.\end{array}$$ A.28

Substituting I_f into S_f produces

$$\begin{array}{l}{S}_f\left(\mathit{k}\ne 0,k{\widehat{\mathit{N}}}_f\right)=-\frac{1}{{\left(2\pi k\right)}^2}\frac{\mathit{k}\cdot {\widehat{\mathit{N}}}_f}{k^2-{\left(\mathit{k}\cdot {\widehat{\mathit{N}}}_f\right)}^2}{\displaystyle \sum }_{e=1}^{E_f}{L}_{\mathit{fe}}\mathit{k}\cdot {\widehat{\mathit{n}}}_{\mathit{fe}}\frac{\sin \left(\pi \mathit{k}\cdot {\widehat{\mathit{t}}}_{\mathit{fe}}{L}_{\mathit{fe}}\right)}{\pi \mathit{k}\cdot {\widehat{\mathit{t}}}_{\mathit{fe}}{L}_{\mathit{fe}}}\mathit{exp}\left(-2\pi i\mathit{k}\cdot {\mathit{r}}^{(C_{\mathit{fe}})}\right)\\ S_f\left(\mathit{k}=k{\widehat{\mathit{N}}}_f\right)=\frac{i}{2\pi }\frac{\mathit{k}\cdot {\widehat{\mathit{N}}}_f}{k^2}\mathit{exp}\left(-2\pi i\mathit{k}\cdot {\mathit{r}}^{0f}\right)P_f\end{array}$$ A.29

r^0f can be any arbitrary point in the plane of the face. For instance it can be set to the first vertex ${\mathit{r}}^{(V_{f1})}$.

Thus, summing over the appropriate contribution of each face, factoring out $-1/{\left(2\pi k\right)}^2$ from S_f. to produce $S_f^{\ast }$ and substituting ${\mathit{r}}^{(V_{f1})}$ for r^0f, the final simplified expression for the FT of a polyhedron is:

$$\begin{array}{l}{S}_{3D}\left(k\right)=\{\begin{array}{rr}\hfill -\frac{1}{{\left(2\pi k\right)}^2}{\displaystyle \sum }_{f=1}^F{S}_f^{\ast }(\mathit{k}),& \hfill \mathit{k}\ne 0\\ \hfill V,& \hfill \mathit{k}=0\end{array}\\ S_f^{\ast }\left(\mathit{k}\ne k{\widehat{\mathit{N}}}_f\right)=\frac{\mathit{k}\cdot {\widehat{\mathit{N}}}_f}{k^2-{\left(\mathit{k}\cdot {\widehat{\mathit{N}}}_f\right)}^2}{\displaystyle \sum }_{e=1}^{E_f}{L}_{\mathit{fe}}\mathit{k}\cdot {\widehat{\mathit{n}}}_{\mathit{fe}}\frac{\sin \left(\pi \mathit{k}\cdot {\widehat{\mathit{t}}}_{\mathit{fe}}{L}_{\mathit{fe}}\right)}{\pi \mathit{k}\cdot {\widehat{\mathit{t}}}_{\mathit{fe}}{L}_{\mathit{fe}}}\mathit{exp}\left(-2\pi i\mathit{k}\cdot {\mathit{r}}^{(C_{\mathit{fe}})}\right)\\ S_f^{\ast }\left(\mathit{k}=k{\widehat{\mathit{N}}}_f\right)=\{\begin{array}{c},\\ -2\pi i\mathit{k}\cdot {\widehat{\mathit{N}}}_f\mathit{exp}\left(-2\pi i\mathit{k}\cdot {\mathit{r}}^{(V_{f1})}\right)P_f\end{array}\\ P_f=\frac{1}{2}\left|{\widehat{\mathit{N}}}_f\cdot {\displaystyle \sum }_{e=1}^{E_f}\{{\mathit{r}}^{(V_{\mathit{fe}})}\times {\mathit{r}}^{(V_{fe+1})}\}\right|.\end{array}$$ A.30

where V is the volume of a polyhedron (14) which is given in terms of its vertices as

$$\begin{array}{l}{S}_{3D}\left(\mathit{k}=\mathbf{0}\right)=V\\ =\frac{1}{6}\left|\left[{\displaystyle \sum }_{f=1}^F\left({\mathit{r}}^{V_{f1}}\cdot {\widehat{\mathit{N}}}_f\right)\left|{\widehat{\mathit{N}}}_f\cdot \left\{{\displaystyle \sum }_{e=1}^{E_f}{\mathit{r}}^{(V_{\mathit{fe}})}\times {\mathit{r}}^{(V_{fe+1})}\right\}\right|\right]\right|.\end{array}$$ A.31