Abstract
Background
For physicians dealing with patients with a limited life expectancy, knowing the time to benefit (TTB) of preventive medication is essential to support treatment decisions.
Objective
The aim of this study was to investigate the usefulness of statistical process control (SPC) for determining the TTB in relation to fracture risk with alendronate versus placebo in postmenopausal women.
Methods
We performed a post hoc analysis of the Fracture Intervention Trial (FIT), a randomized, controlled trial that investigated the effect of alendronate versus placebo on fracture risk in postmenopausal women. We used SPC, a statistical method used for monitoring processes for quality control, to determine if and when the intervention group benefited significantly more than the control group. SPC discriminated between the normal variations over time in the numbers of fractures in both groups and the variations that were attributable to alendronate. The TTB was defined as the time point from which the cumulative difference in the number of clinical fractures remained greater than the upper control limit on the SPC chart.
Results
For the total group, the TTB was defined as 11 months. For patients aged ≥70 years, the TTB was 8 months [absolute risk reduction (ARR) = 1.4 %]; for patients aged <70 years, it was 19 months (ARR = 0.7 %).
Conclusion
SPC is a clear and understandable graphical method to determine the TTB. Its main advantage is that there is no need to define a prespecified time point, as is the case in traditional survival analyses. Prescribing alendronate to patients who are aged ≥70 years is useful because the TTB shows that they will benefit after 8 months. Investigators should report the TTB to simplify clinical decision making.
Key Points for Decision Makers
| Statistical process control is a clear and understandable method to determine the time to benefit of preventive drugs. |
| We showed that in the Fracture Intervention Trial (FIT), the time to benefit of alendronate for prevention of fractures was 11 months. |
| Clinical decision making for an individual patient with a limited life expectancy can be simplified by applying the time to benefit. |
Introduction
The number of drug prescriptions in older patients is large [1] because the number of diseases increases with age. Consequently, older patients are prone to possible side effects of medication because of altered pharmacodynamics and pharmacokinetics [2]. Therefore, medication should be prescribed only to patients who are likely to benefit. For physicians dealing with older patients with multiple conditions, it is important to take the life expectancy of the patient into account, as it is possible that patients will not live long enough to benefit from preventive medication. Therefore, knowing the time to benefit (TTB) supports treatment decisions. The TTB can be defined as an estimate of the time needed until a treatment becomes significantly effective in a group of patients [3]. Although it seems clear that it is important to take the TTB into account when prescribing medication [4, 5], the concept is seldom mentioned in trial results and is even more rarely calculated for the subpopulation of elderly patients [4, 5]. Answers to these questions cannot readily be provided by other traditional techniques, such as survival analysis, because there a pre-fixed analysis point is used.
Osteoporosis is highly prevalent at older ages; it has been estimated to affect 55 % of the US population ≥50 years of age [6]. There is sufficient evidence from randomized clinical trials that the current pharmacological therapies for osteoporosis are effective in preventing new fractures in older patients as well [6]. Bisphosphonates are frequently prescribed [7]; therefore, it is important to know the TTB of this medication.
The aim of this study was to use statistical process control (SPC) to determine the TTB of alendronate for fracture risk in postmenopausal women with osteoporosis. SPC is a statistical method that is used in research for health care improvements but not often in other branches of medicine [8]. It is an innovative and easy-to-interpret method to identify significant variations in clinical outcomes in a range of health care settings. Usefulness was assessed by inspecting whether SPC could provide an answer to the following question: if and when patients receiving alendronate benefited significantly more than those receiving placebo. We aimed to calculate the TTB especially for older adults (aged ≥70 years) because the oldest individuals are at highest risk of side effects and a limited life expectancy.
Methods
Original Data from the FIT Study
Original data from the Fracture Intervention Trial (FIT) were used to determine the TTB [9, 10]. FIT was a randomized, placebo-controlled trial investigating the effect of alendronate versus placebo on the risks of morphometric vertebral fractures, as well as clinically evident fractures at all sites in postmenopausal women (aged 55–80 years). Full details of the study are described elsewhere [9, 11]. The present analysis was performed in all patients (n = 3658) with confirmed osteoporosis [either a femoral neck bone mineral density (BMD) T score ≤−2.5 (n = 1631) or at least one morphometric vertebral fracture (n = 2027)]. The outcome of interest was any new clinical fracture (either vertebral or non-vertebral). A clinical fracture was defined as a fracture diagnosed by a physician and confirmed by written reports or radiographs. We chose the outcome of clinical fracture instead of morphometric vertebral fracture because for clinical fracture it was clear at which time point it had developed, whereas a nonclinical vertebral fracture became visible only when a radiograph was performed. The analysis was limited to the first fracture. Patients who did not complete follow-up were censored when they left the study. Formal consent or approval was not necessary for this post hoc analysis.
Analysis: Statistical Process Control
We assessed the longitudinal effect of alendronate on the incidence of clinical fractures in postmenopausal women with osteoporosis, using SPC [12–14].
SPC relies on statistical methods to monitor a series of measurements (process) to indicate when a structural change in the measurements, i.e. not due to chance, has occurred [12–14]. When this happens, it is said that the process goes from ‘in control’ (stable) to ‘out of control’ [15]. Out of control is determined by analysis of the variability of the measurements over time. An important tool used in SPC to show the results is a graphical chart, called a ‘control chart’, which plots the measurements (e.g. a proportion or a mean) over time and uses the observed variability of these measurements to calculate the limits of the expected variation [8]. Several types of control chart are available, depending on the nature of the measurement and the purpose of the study. Generally, the limits of variation are three adjusted standard deviations (called ‘three sigmas’) from the mean of the measurements. When measurements cross these limits, then the process is out of control, otherwise it is stable. The limit of three sigmas was chosen because SPC implicitly uses multiple tests—one for every measurement. When the significance level is set at three sigmas, 99.7 % of values are in the specified range. In this way, SPC also accounts for multiple testing [16].
In the FIT data, the cumulative difference in the numbers of new clinical fractures in the placebo group versus the treatment group was measured per month and, in a second analysis, every 2 weeks. These intervals were chosen because we considered 2 weeks a relevant clinical interval to see a change. For these time points, the absolute risk reduction (ARR) was calculated. These intervals were chosen to define the TTB as precisely as possible. We used the measurements in the first 6 months to calculate the control limits. This period was chosen because we hypothesized that it takes 6 months for the medication to become effective in improving bone strength; variation within this period can be seen as physiological fluctuation not related to the pharmacological effect of bisphosphonates [17]. The rate of suppression of bone resorption by bisphosphonates increases until a limit is reached after about 3 months; thereafter it remains at a constant level. Paradoxically, bone formation decreases after commencement of bisphosphonates, as a result of the coupling of bone formation and resorption in the basic molecular units. Biochemical markers have shown that the decrease in bone formation is smaller and lags behind the suppression of bone resorption [18]. Eventually, a balance between formation and suppression is reached in 3–6 months [19]. For this study, we used an XmR SPC chart (‘X’ stands for individual measurements, and ‘mR’ stands for ‘moving range’). The XmR chart is popular for its ability to visually depict variation when only one observation exist in each time period—in our case, the cumulative difference in the number of fractures per month [16]. This chart has a distinctive pattern marked by three horizontal reference lines. The centre line is the average value of the measurements when the process is in control; the other two reference lines are the upper and lower control limits, corresponding to the boundaries beyond which the process will be considered out of control. The upper and lower control limits are three sigmas away from the centre line, in order to adjust for multiple testing.
There are several rules that indicate when a relevant variation has occurred on a process control chart. Most of them are designed to identify a trend in the effect rather than an absolute effect [16]. Because we were interested in a sustained effect of time (the TTB), we limited the SPC analysis to one rule: the process being out of control at one point beyond three sigmas when the next points also remain beyond three sigmas. Thus, a successful intervention causes the process to go out of control in the direction of improvement. The TTB—the estimate of time needed until the treatment group and the placebo group start to differ in terms of the effect—was defined in this study as the first month at which the cumulative difference in the percentages of any clinical fractures between the two study arms remained greater than three sigmas. In this regard, the time point that we called the TTB occurred when the difference in the ARR between the two groups exceeded and remained greater than three sigmas.
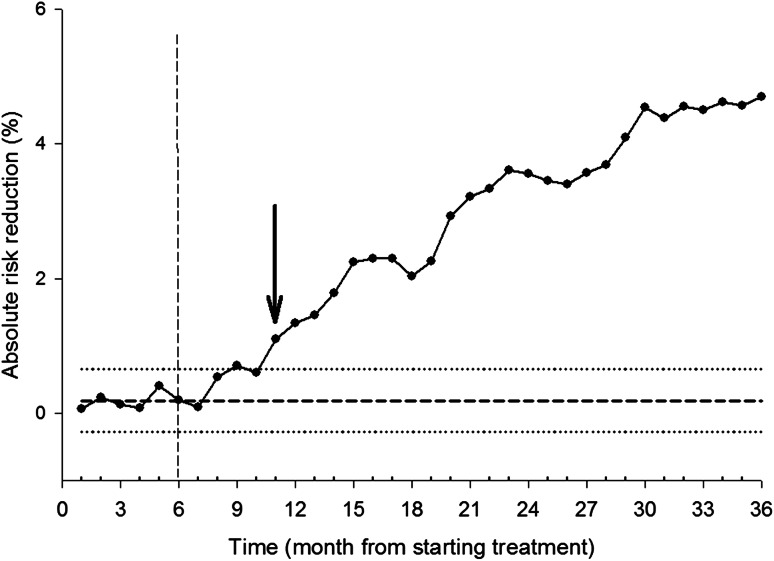
The SPC chart and the ARR calculation are illustrated in Fig. 1. At time point 6, which corresponded to month 6 of the study, there were, in total, 1834 patients remaining under observation in the treatment group and 1813 patients in the placebo group. Among these patients (at time point 6) there were nine patients with fractures in the treatment group and five patients with fractures in the placebo group. Therefore, the percentages of new patients with fractures were 0.49 % (9/1834) in the treatment group and 0.28 % (5/1813) in the placebo group. Thus, the difference amounted to −0.21 (0.28 − 0.49). The cumulative difference at month 5 was 0.40; therefore, the new cumulative difference was 0.40 + (−0.21) = 0.19.
Fig. 1.
Statistical process control chart of the cumulative absolute risk reduction (ARR) in clinical fractures in the total group of patients in the Fracture Intervention Trial (FIT) (n = 3658). The down arrow at 11 months is the time to benefit, i.e. the first point at which the difference is greater than the upper control limit (ARR = 1.1 %). The centre line (dashed horizontal line), upper control limit (upper dotted horizontal line) and lower control limit (lower dotted horizontal line) were calculated on the basis of the data from the first 6 months (indicated by the dashed vertical line)
Subgroup Analysis
Because the incidence of fractures increases with age [20], older patients in trials are likely to have an increased risk of fracture in comparison with younger patients. Therefore, we hypothesized that older patients might have a shorter TTB than younger patients. We performed a predefined subgroup analysis for age groups (aged <70 and ≥70 years). We performed a subgroup analysis for specific fractures as well.
Results
Patient Characteristics
In FIT, 3658 patients with osteoporosis were included: 1841 in the alendronate group and 1817 in the placebo group (Table 1). During the study period, there were 511 primary fractures; 190 patients had two or more reported fractures. Seventy-six patients died, of whom 20 had a fracture.
Table 1.
Characteristics of the participants in the Fracture Intervention Trial (FIT): postmenopausal women (n = 3658) aged 55–80 years with confirmed osteoporosis [either a femoral neck bone mineral density (BMD) T score ≤−2.5 (n = 1631) or at least one morphometric vertebral fracture (n = 2027)]. The main study outcome is also reported
| Characteristic | Alendronate group, n = 1841 | Placebo group, n = 1817 | P value |
|---|---|---|---|
| Age [years; mean (SD)] | 69.3 (6.0) | 69.5 (5.9) | |
| Clinical fracture after the age of 45 years [n (%)] | 935 (51) | 907 (49) | |
| Femoral neck BMD T-score [mean (SD)] | −2.74 (0.55) | −2.76 (0.55) | |
| Clinical fracture during 36-month follow-up [n (%)] | 215 (12) | 296 (16) | <0.001 |
| Death during follow-up [n (%)] | 40 (2) | 36 (2) | 0.69 |
SD standard deviation
Statistical Process Control
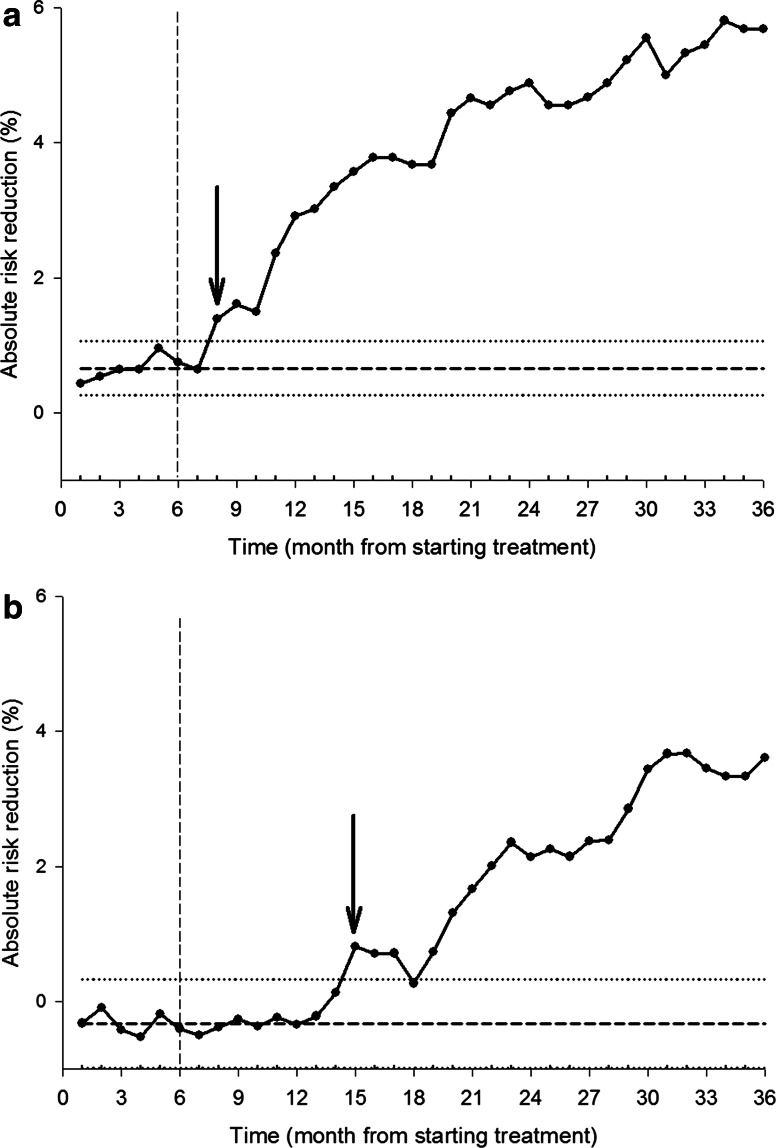
SPC analysis of the total group showed that the process went out of control and remained so after 11 months (Fig. 1), when the cumulative ARR was 1.1 %. This corresponded to a number needed to treat (NNT) of 100. The TTB was shorter for patients aged ≥70 years (n = 1870; after 8 months, ARR = 1.4 %, NNT = 71) than for younger patients (after 19 months, ARR = 0.7 %, NNT = 143) (Fig. 2a, b). The results were similar when two measure points per month were used (data not shown). At 3 years (the end of follow-up), the ARR in FIT was 4 %, corresponding to an NNT of 25.
Fig. 2.
Statistical process control chart of the cumulative absolute risk reduction (ARR) in clinical fractures in a patients aged ≥70 years (n = 1870) and b patients aged <70 years (n = 1788) in the Fracture Intervention Trial (FIT). In a, the down arrow at 8 months indicates where the process is out of control (the time to benefit), i.e. the first point at which the difference is greater than the upper control limit (ARR = 1.4 %). In b, the down arrow is at 19 months (ARR = 0.7 %). The centre line (dashed horizontal line), upper control limit (upper dotted horizontal line) and lower control limit (lower dotted horizontal line) were calculated on the basis of the data from the first 6 months (indicated by the dashed vertical line)
Discussion
Statistical process control is a graphical method with a clear and understandable chart for calculating the TTB on data from a randomized, controlled trial. With this method, we calculated that the TTB of alendronate for prevention of osteoporotic clinical fractures was 11 months in a population of postmenopausal women with osteoporosis. In the subgroup analysis of older participants (aged ≥70 years), the TTB was 8 months.
Although much literature on osteoporosis therapy is available, few authors have reported an analysis before the end of follow-up, and even fewer have reported a time-to-event analysis of clinical fractures. Six studies reported the outcome before the end of follow-up, within 1 year [4, 5, 10, 21, 22], by means of a survival analysis. In all of these cases, a predefined point was used to perform a log rank test. One study used a post hoc analysis at 3 and 6 months to determine an early effect [22]. In all seven studies, the absolute effect at the time of significance was small.
The advantage of SPC in comparison with the most frequently used survival analysis is that the measure point at which the difference is greater than three sigmas is directly visible in the graph and can therefore be detected at a glance, while in the survival analysis, multiple analyses have to be done. Moreover, for a logistic regression model, it is necessary to check the assumptions of the model; when there is a U-shaped response, this will not become clear in a logistic regression model, whereas in a SPC graph, it will immediately become clear whether it is a sustained effect. In short, logistic regression and SPC are two useful and complementary tools to be considered by the modeller. SPC is less versatile in terms of modelling covariates but, in doing so, it does not impose distributional restrictions on the monitored quantities over time, and it does provide an intuitive machinery geared towards detecting changes over time. Other tools, such as logistic regression, allow for more versatile modelling and interpretation of the coefficients but require assumptions and various modelling choices. In addition, such models, if sound, allow for interpolation and extrapolation. Knowing the TTB allows for an informed prediction on when (and how large) a benefit is expected to be observed in a patient, and hence it informs decision making. In addition, such answers may inform the economical follow-up time in clinical trials. SPC is convenient to use; there are simple tools available for creating the plots, and learning the method does not require a lot of training.
At the TTB—the time point at which the numbers of fractures in the placebo group and the alendronate group started to differ significantly—the reported ARRs were small. In the follow-up after this point, the ARR in clinical fractures increased to 4.5 % after 3 years because of the ongoing effect of alendronate on bone. The clinical decision to start a treatment depends on the patient’s and physician’s preferences and the patient’s clinical condition [23]. With knowledge of the TTB, a treatment can be better adjusted to patients with a limited life expectancy, although estimating this has proven to be difficult [24]. The SPC graph could also be presented as the number needed to treat (NNT = 1/ARR) over time. Taking into account a patient’s life expectancy, the TTB and the NNT could help in clinical decision making [25]. Therefore, we suggest that the authors of randomized, controlled trials report these data as well. Furthermore, it is known that the medication adherence to bisphosphonates is low [26]. This could possibly lead to underestimation of the TTB, as the number of fractures in the intervention groups would be decreased.
The age range of the participants in FIT was 55–80 years [29]. Our predefined subgroup of patients aged ≥70 years was therefore not older than 81 years during the first year of follow-up. Because the TTB was dependent on the a priori chance of having a (vertebral) fracture, and the chance of a (vertebral) fracture increases with age (with the highest a priori chance existing in patients aged >80 years), we can assume that the TTB for alendronate may be even shorter for the oldest old and in an older geriatric population with high risks of falls and fractures. As a result, we conclude that not discussing use of bisphosphonates in older patients with a life expectancy of >8 months is not evidence-based clinical practice when reducing the risk of additional fractures is the patient’s preferred clinical goal. Fractures are associated with significant mortality and morbidity, and represent a substantial economic burden to society [27].
SPC is a statistical method that was originally designed for quality control to monitor and control a process; it provides a signal when abnormal variation in the process is detected. There are several rules that indicate when a process is out of control. Apart from the rule we used to indicate when the process was out of control (i.e. one point being greater than three sigmas), there are frequently used rules that are able to detect a trend over time. This shows the versatility of SPC. In our application, we used only the rule that we felt was relevant to this specific application. If one wants to detect the first point of change (regardless of magnitude), then one may use other rules. If we had used these trend rules, we would have found an earlier effect. Using SPC in this way could help in defining the time period when any effect is lacking for certain. However, this early effect would correspond with a very small absolute effect, which might not be clinically relevant. In cohort studies, one could think of many alternative ways to use SPC—for example, to measure treatment and side effects over time, or it could be used in the decision to stop a trial early because an effect has already been achieved.
A limitation of applying SPC for defining the TTB is that when the first measurements in the study reflect an unstable process, it is impossible to define the upper and lower limits. If an early effect of treatment is expected, one should find an alternative way to define the central line and its limits—for example, by using different time intervals between measurements, or preferably by using data before the start of the treatment. Because we performed a post hoc analysis, we had to define a period to define the limits, which, although well considered, could be debated. For instance, in the subgroup analysis, the centre line lay above zero for the group aged ≥70 years and below zero for the younger group, suggesting minimal differences in fracture risks between the treatment and placebo groups. We assume that these differences were caused by coincidence rather than by real differences between the groups, because we checked both groups’ patient characteristics, such as age and number of falls (data not shown). Ideally, the limit should be at zero and should be calculated before the start of treatment.
Conclusion
Statistical process control is a novel method to define the TTB for medication used to treat and prevent clinical outcomes. Its main advantages are that it becomes clear at a glance when the effect occurs, and no predefined endpoints are necessary to define the TTB. We would encourage scientists to report the TTB, especially in studies of preventive medication in older patients. Clinical decision making can be made more evidence based by applying the TTB and ARR, so that the pros and cons of initiating or stopping medication can be weighed for an individual patient with a limited life expectancy.
Acknowledgments
The authors thank the Fracture Intervention Trial (FIT) Research Group and Steering Committee for use of their data and for reviewing the manuscript prior to journal submission.
Author contributions
This study was conceived and designed by Ameen Abu-Hanna, Sophia de Rooij and Barbara van Munster. The data acquisition and statistical analysis were performed by Esther van de Glind, Hanna Willems, Saeid Eslami Hassanabadi and Ameen Abu-Hanna. The manuscript was prepared by Esther van de Glind and Hanna Willems. Critical revision of the manuscript was performed by all authors. This study was performed as part of a PhD project for Esther van de Glind and Hanna Willems.
Compliance with Ethical Standards
Funding
Agrant for this project was provided by the National Care for the Elderly Programme. The Fracture Intervention Trial (FIT) was sponsored by Merck.
Conflicts of interest
Esther van de Glind, Hanna Willems, Saeid Eslami Hassanabadi, Ameen Abu-Hanna, Lotty Hooft, Sophia de Rooij and Barbara van Munster declare that they have no conflicts of interest that are relevant to the content of this review. Willem Lems has earned speaker’s fees from the following companies: Merck, Eli Lilly, Amgen, Novartis, Servier, Procter and Gamble, and Warner Chilcott. Dennis Black has received consulting fees from Amgen and Radius, has received a lecture honorarium from Novartis and is a Data Safety Monitoring Board member for Eli Lilly.
Ethical approval
Formal consent or ethical approval was not required for this type of study.
Footnotes
E. M. M. van de Glind and H. C. Willems should be considered joint first authors of this work.
D. M. Black and B. C. van Munster should be considered joint last authors of this work.
References
- 1.Slabaugh SL, Maio V, Templin M, Abouzaid S. Prevalence and risk of polypharmacy among the elderly in an outpatient setting: a retrospective cohort study in the Emilia-Romagna region, Italy. Drugs Aging. 2010;27(12):1019–1028. doi: 10.2165/11584990-000000000-00000. [DOI] [PubMed] [Google Scholar]
- 2.Bowie MW, Slattum PW. Pharmacodynamics in older adults: a review. Am J Geriatr Pharmacother. 2007;5(3):263–303. doi: 10.1016/j.amjopharm.2007.10.001. [DOI] [PubMed] [Google Scholar]
- 3.Holmes HM, Min LC, Yee M, Varadhan R, Basran J, Dale W, et al. Rationalizing prescribing for older patients with multimorbidity: considering time to benefit. Drugs Aging. 2013;30(9):655–666. doi: 10.1007/s40266-013-0095-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Lindsay R, Miller P, Pohl G, Glass EV, Chen P, Krege JH. Relationship between duration of teriparatide therapy and clinical outcomes in postmenopausal women with osteoporosis. Osteoporos Int. 2009;20(6):943–948. doi: 10.1007/s00198-008-0766-0. [DOI] [PubMed] [Google Scholar]
- 5.Adachi JD, Rizzoli R, Boonen S, Li Z, Meredith MP, Chesnut CH., III Vertebral fracture risk reduction with risedronate in post-menopausal women with osteoporosis: a meta-analysis of individual patient data. Aging Clin Exp Res. 2005;17(2):150–156. doi: 10.1007/BF03324588. [DOI] [PubMed] [Google Scholar]
- 6.Gates BJ, Sonnett TE, Duvall CA, Dobbins EK. Review of osteoporosis pharmacotherapy for geriatric patients. Am J Geriatr Pharmacother. 2009;7(6):293–323. doi: 10.1016/j.amjopharm.2009.12.004. [DOI] [PubMed] [Google Scholar]
- 7.Wysowski DK, Greene P. Trends in osteoporosis treatment with oral and intravenous bisphosphonates in the United States, 2002–2012. Bone. 2013;57(2):423–428. doi: 10.1016/j.bone.2013.09.008. [DOI] [PubMed] [Google Scholar]
- 8.Benneyan JC, Lloyd RC, Plsek PE. Statistical process control as a tool for research and healthcare improvement. Qual Saf Health Care. 2003;12(6):458–464. doi: 10.1136/qhc.12.6.458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Black DM, Cummings SR, Karpf DB, Cauley JA, Thompson DE, Nevitt MC, et al. Randomised trial of effect of alendronate on risk of fracture in women with existing vertebral fractures. Fracture Intervention Trial Research Group. Lancet. 1996;348(9041):1535–1541. doi: 10.1016/S0140-6736(96)07088-2. [DOI] [PubMed] [Google Scholar]
- 10.Black DM, Thompson DE, Bauer DC, Ensrud K, Musliner T, Hochberg MC, et al. Fracture risk reduction with alendronate in women with osteoporosis: the Fracture Intervention Trial. FIT Research Group. J Clin Endocrinol Metab. 2000;85(11):4118–4124. doi: 10.1210/jcem.85.11.6953. [DOI] [PubMed] [Google Scholar]
- 11.Cummings SR, Black DM, Thompson DE, Applegate WB, Barrett-Connor E, Musliner TA, et al. Effect of alendronate on risk of fracture in women with low bone density but without vertebral fractures: results from the Fracture Intervention Trial. JAMA. 1998;280(24):2077–2082. doi: 10.1001/jama.280.24.2077. [DOI] [PubMed] [Google Scholar]
- 12.Eslami S, Abu-Hanna A, de Keizer NF, Bosman RJ, Spronk PE, de Jonge E, et al. Implementing glucose control in intensive care: a multicenter trial using statistical process control. Intensive Care Med. 2010;36(9):1556–1565. doi: 10.1007/s00134-010-1924-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Eslami S, de Keizer NF, Dongelmans DA, de Jonge E, Schultz MJ, Abu-Hanna A. Effects of two different levels of computerized decision support on blood glucose regulation in critically ill patients. Int J Med Inform. 2012;81(1):53–60. doi: 10.1016/j.ijmedinf.2011.10.004. [DOI] [PubMed] [Google Scholar]
- 14.Medlock S, Eslami S, Askari M, van Lieshout EJ, Dongelmans DA, Abu-Hanna A. Improved communication in post-ICU care by improving writing of ICU discharge letters: a longitudinal before–after study. BMJ Qual Saf. 2011;20(11):967–973. doi: 10.1136/bmjqs-2011-000074. [DOI] [PubMed] [Google Scholar]
- 15.Cher DJ, Deubner DC, Kelsh MA, Chapman PS, Ray RM. Assessment of the beryllium lymphocyte proliferation test using statistical process control. Inhal Toxicol. 2006;18(11):901–910. doi: 10.1080/08958370600822631. [DOI] [PubMed] [Google Scholar]
- 16.Mohammed MA, Worthington P, Woodall WH. Plotting basic control charts: tutorial notes for healthcare practitioners. Qual Saf Health Care. 2008;17(2):137–145. doi: 10.1136/qshc.2004.012047. [DOI] [PubMed] [Google Scholar]
- 17.Manolagas SC. Birth and death of bone cells: basic regulatory mechanisms and implications for the pathogenesis and treatment of osteoporosis. Endocr Rev. 2000;21(2):115–137. doi: 10.1210/edrv.21.2.0395. [DOI] [PubMed] [Google Scholar]
- 18.Cremers SC, Pillai G, Papapoulos SE. Pharmacokinetics/pharmacodynamics of bisphosphonates: use for optimisation of intermittent therapy for osteoporosis. Clin Pharmacokinet. 2005;44(6):551–570. doi: 10.2165/00003088-200544060-00001. [DOI] [PubMed] [Google Scholar]
- 19.Papapoulos SE. Use of bisphosphonates in the management of postmenopausal osteoporosis. Ann N Y Acad Sci. 2011;1218:15–32. doi: 10.1111/j.1749-6632.2010.05767.x. [DOI] [PubMed] [Google Scholar]
- 20.Sambrook P, Cooper C. Osteoporosis. Lancet. 2006;367(9527):2010–2018. doi: 10.1016/S0140-6736(06)68891-0. [DOI] [PubMed] [Google Scholar]
- 21.Harrington JT, Ste-Marie LG, Brandi ML, Civitelli R, Fardellone P, Grauer A, et al. Risedronate rapidly reduces the risk for nonvertebral fractures in women with postmenopausal osteoporosis. Calcif Tissue Int. 2004;74(2):129–135. doi: 10.1007/s00223-003-0042-4. [DOI] [PubMed] [Google Scholar]
- 22.Qu Y, Wong M, Thiebaud D, Stock JL. The effect of raloxifene therapy on the risk of new clinical vertebral fractures at three and six months: a secondary analysis of the MORE trial. Curr Med Res Opin. 2005;21(12):1955–1959. doi: 10.1185/030079905X75032. [DOI] [PubMed] [Google Scholar]
- 23.Americans Geriatrics Society Expert Panel on the Care of Older Adults with Multimorbidity. Patient-centered care for older adults with multiple chronic conditions: a stepwise approach from the American Geriatrics Society: American Geriatrics Society Expert Panel on the Care of Older Adults with Multimorbidity. J Am Geriatr Soc. 2012;60(10):1957–68. [DOI] [PMC free article] [PubMed]
- 24.Welch HG, Albertsen PC, Nease RF, Bubolz TA, Wasson JH. Estimating treatment benefits for the elderly: the effect of competing risks. Ann Intern Med. 1996;124(6):577–584. doi: 10.7326/0003-4819-124-6-199603150-00007. [DOI] [PubMed] [Google Scholar]
- 25.Pines A, Shapiro S, Suissa S. NNT, number needed to treat: does it have any real value? Climacteric. 2012;15(2):139–142. doi: 10.3109/13697137.2012.656004. [DOI] [PubMed] [Google Scholar]
- 26.Hiligsmann M, Bours SP, Boonen A. A review of patient preferences for osteoporosis drug treatment. Curr Rheumatol Rep. 2015;17(9):61. doi: 10.1007/s11926-015-0533-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Fleurence RL, Iglesias CP, Johnson JM. The cost effectiveness of bisphosphonates for the prevention and treatment of osteoporosis: a structured review of the literature. Pharmacoeconomics. 2007;25(11):913–933. doi: 10.2165/00019053-200725110-00003. [DOI] [PubMed] [Google Scholar]