Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Apr 20;6:24850. doi: 10.1038/srep24850

Theoretical Investigations of Optical Origins of Fluorescent Graphene Quantum Dots

Jingang Wang 1,2,3,*, Shuo Cao 1,*, Yong Ding 1,*, Fengcai Ma 1,a, Wengang Lu 2, Mengtao Sun 1,2,b
PMCID: PMC4837401  PMID: 27094439

Abstract

The optical properties of graphene quantum dots (GQDs) were investigated theoretically. We focused on the photoinduced charge transfer and electron-hole coherence of single-layer graphene in the electronic transitions in the visible regions. Surface functionalization with donor or acceptor groups produced a red shift in the absorption spectrum, and electrons and holes were highly delocalized. The recombination of excited, well-separated electron-hole (e–h) pairs can result in enhanced fluorescence. This fluorescence enhancement by surface functionalization occurs because of the decreased symmetry of the graphene resulting from the roughened structure of the surface-functionalized GQDs.

Graphene is a single atomic layer that consists of a two-dimensional honeycomb lattice of carbon atoms. Because of its fundamental physics and excellent optical, thermal and electrical properties, it has been widely investigated, both experimentally and theoretically1,2,3,4. Graphene has been widely applied in quantum information processing5, fuel cells6, photovoltaic materials7, water purification8, controlling reactions9, and optical modulation10.

Because the fragments of graphene are limited in size or domains, graphene quantum dots (GQDs) are emerging as an advanced material with multiple functionalities because of their unique optical, electronic11, spin12, and photoelectric properties induced by edge effects and quantum confinement effects. There are many important applications for GQDs in fluorescent materials13, photocatalysis14, bioimaging15 and organic photovoltaic (OPV) solar cells16. To apply GQDs to optoelectronic nano devices, elucidating and understanding the mechanisms underlying their novel light-absorption/emission properties is of critical importance. The influence of edge structure on the electronic properties of GQDs with 2–20-nm lateral dimensions has been investigated11. When the size of a GQD is less than 10 nm, quantum confinement and edge effects can induce photoluminescence (PL)17,18. Many efforts have been directed at increasing the quantum yield of GQDs, for example, by surface functionalization of the GQDs (SF-GQDs) with organic molecules19 or surface oxidation20. The PL of GQDs can be tuned based on the charge-transfer effect of electron-withdrawing or electron-donating functional groups21. The PL mechanism of GQDs has been interpreted as the minimization of thermalization resulting from electron-phonon scattering22, or the formation of an excited-state relaxation channel, which causes inelastic light scattering by electric doping23. Kim attributed this behavior to fast carrier–carrier scattering24, which encourages the direct recombination of the excited electron–hole (e–h) pairs that produce this PL before the carriers are thermalized in the lattice.

In this paper, we investigated the effects of surface functionalization on the optical properties of GQDs with a lateral dimension of approximately 2 nm, mainly focusing on the charge-transfer and e–h coherence in the electronic transition of GQDs. We also evaluated the influence of the geometrical roughness resulting from surface functionalization with organic molecules on the GQDs’ optical properties. Our results can facilitate a deeper understanding of the origin of the optical properties of GQDs.

Results

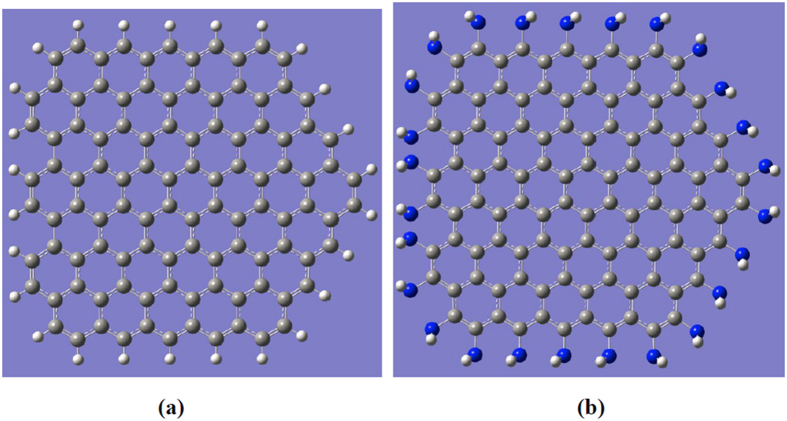
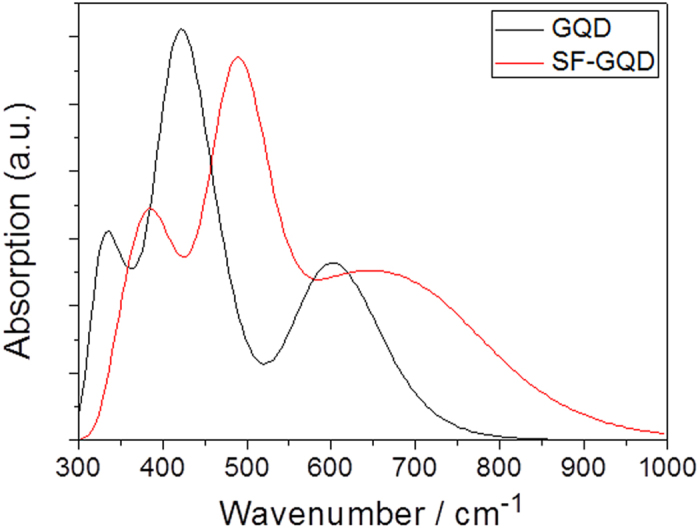
The models used for the calculations can be seen in Fig. 1(a,b), which show a GQD and an SF-GQD with -NH2, respectively. In mode (a), there are four zigzag edges and one armchair edge. The calculated absorption spectra of both GQDs in the visible region are presented in Fig. 2 and demonstrate that the optical absorption peaks of SF-GQD with -NH2 groups are significantly red shifted. This finding indicated that the fluorescence peaks of SF-GQD with -NH2 should also be significantly red shifted. These red-shift phenomena are consistent with the experimental findings13,19,21.

Figure 1. The models used for the calculations.

Figure 1

Open in a new tab

(a) GQD and (b) SF-GQD with -NH2.

Figure 2. The calculated absorption spectra of the GQD and SF-GQD with -NH2.

Figure 2

Open in a new tab

To reveal the nature of the optical origins of fluorescent GQDs, it is important to observe the e–h coherence and electron transfer in electronic transitions in the visible region. The degree of electron transfer determines the degree of fluorescence because the direct recombination of excited e–h pairs produces fluorescence24. We first demonstrate the degree and orientation of charge transfer for GQDs for strong electronic transitions. The charge difference densities (CDDs) in Fig. 3 reveal that the electrons and holes were locally excited and that the electrons transferred from the adjacent holes. Therefore, the electrons and holes were not significantly separated, and the degree of electron transfer from holes is weak because of the strong interaction between holes and electrons in the electronic transitions in the visible region. Note that electrons seem to significantly transfer from holes in the near-ultraviolet region (see CDD at 327.9 nm) but cannot contribute to the fluorescence in the visible region.

Figure 3. Charge-transfer densities for the strong electronic transitions in the GQD, where the holes and electrons are represented in green and red, respectively.

Figure 3

Open in a new tab

The three-dimensional CDDs in Fig. 3 demonstrate the qualitative visualization analysis of photoinduced charge transfer. To quantitatively analyze the charge transfer, Δr is introduced to measure the charge-transfer length25,

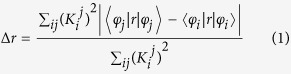graphic file with name srep24850-m1.jpg

where i and j traverse all of the occupied and virtual molecular orbitals, respectively, and φ is the orbital wave function. When Δr > 2, the electronic state transition is considered in the charge-transfer excited state, whereas when Δr < 2.0, it is considered to be in an excited state with a different charge25. The calculated results are summarized in Table 1, where the electronic transition states of GQDs are localized excited states, and the electronic state transitions of SF-GQD are the charge-transfer excited states.

Table 1. Charge-transfer lengths for the GQD and SF-GQD.

GQD
 SF-GQD
nm f ΔL(A) nm f ΔL(A)
612 0.4266 1.08 803 0.0729 2.10
591 0.3629 1.26 724 0.3547 2.95
436 0.3762 1.78 611 0.3565 3.44
415 0.5205 1.41 488 0.3192 3.59
411 0.6472 0.26. 487 0.6787 3.00
328 0.2868 1.64 392 0.1431 4.35
Open in a new tab

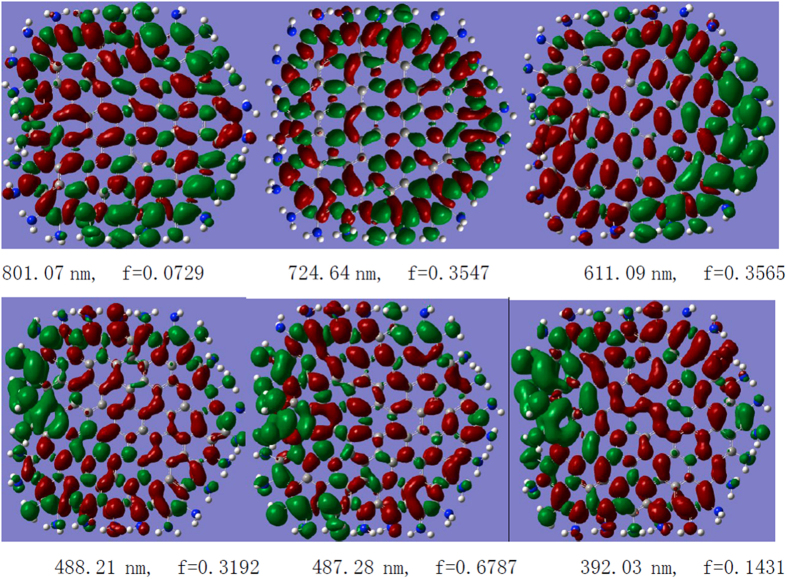
Therefore, all of the strong electronic transitions of-GQDs are charge-transfer excited states because the charge-transfer lengths of these excited states all exceed 2.0 Å. The CDDs of these excited states confirm this phenomenon; the holes and electrons are well separated, and the degree and orientation of the electron transfer are well visualized (Fig. 4). For example, for the electronic transition at 801 nm, almost all holes are localized on the edge, whereas the electrons are localized on the center. For the electronic transition at 611 nm, the holes are localized on the right edges, and the electrons are delocalized to the center of graphene and the left edges. This behavior means that in this excited state, the optical excitation occurs at the right edge, and then the electrons excited at this edge are delocalized to the other parts, indicating strong electron transfer in the excited state.

Figure 4. Charge-transfer densities for the strong electronic transitions in the SF-GQD with -NH2, where the holes and electrons are represented in green and red, respectively.

Figure 4

Open in a new tab

Discussion

The surface functionalization of GQDs can result in a red shift in the absorption spectrum and a corresponding red shift in the fluorescence spectrum. Our theoretical calculations are consistent with the experimental results. The CDDs in Fig. 4 reveal that the mechanism of fluorescence enhancement is not, as expected, mainly attributable to the functionalized donor or acceptor groups because both electrons and holes exist on the functionalized -NH2. To further reveal the mechanism of fluorescence enhancement by surface functionalization, we also obtained the optimized molecular geometries of GQDs and SF-GQDs with -NH2 (see Fig. 5). The optimized GQD geometry was found to be flat, whereas the optimized F-GQD geometry was not highly flattened, thereby decreasing the symmetry of the graphene. Therefore, the holes can be localized on the edge of the SF-GQD, and the electrons can transfer to other parts.

Figure 5. Optimized molecular structures.

Figure 5

Open in a new tab

(a) GQD and (b) SF-GQD with -NH2.

We visualized the theoretical mechanism of fluorescence enhancement in surface-functionalized GQDs using CDD. This surface functionalization can result in a red shift in the absorption spectrum and roughness in the graphene structure. The decrease in the GQD’s symmetry by surface functionalization also causes the electrons to delocalize along the graphene. The large electron transfer and well-separated e–h pairs can significantly enhance the fluorescence because the direct recombination of excited e–h pairs produces strong fluorescence. Our results can promote a deeper understanding of the origin of the optical properties of GQDs. It should be noted that the doping, size and edge are also important for the fluorescence enhancement. They will be studied in our further theoretical work.

Methods

The models used in the calculations are shown in Fig. 1(a,b): graphene and surface-functionalized graphene with -NH2, respectively. In mode (a), there are four zigzag edges and one armchair edge. All the calculations were performed with Gaussian 09 software26. The ground-state geometries of both GQDs were optimized with density functional theory (DFT)27 using the B3LYP functional28 and 6-31g(d) basis set. Their optical absorption spectra in the visible region were calculated with time-dependent DFT (TD-DFT)29 using the CAM-B3LYP functional30 and 6-31g(d) basis set. Note that the long-range-corrected functional (CAM-B3LYP) was employed for the non-Coulomb part of the exchange functional. The charge transfer in the electronic transition was visualized using CDDs31.

Additional Information

How to cite this article: Wang, J. et al. Theoretical Investigations of Optical Origins of Fluorescent Graphene Quantum Dots. Sci. Rep. 6, 24850; doi: 10.1038/srep24850 (2016).

Acknowledgments

This work was supported by the National Science Foundation of China (Grant Nos 11274149, 91436102, 11374353, and 11544015) and the Program of Liaoning Key Laboratory of Semiconductor Light Emitting and Photocatalytic Materials.

Footnotes

Author Contributions F.M. and M.S. supervised the project, and J.W. and M.S. performed the calculations. M.S., J.W., S.C., Y.D., F.M. and W.L. analyzed the data. M.S. wrote the paper. All authors were involved in the discussion.

References

  1. Novoselov S. et al. Electric field effect in atomically thin carbon film. Science. 306, 666 (2004). [DOI] [PubMed] [Google Scholar]
  2. Zhang Y. B., Tan Y. W., Stormer H. L. & Kim P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature. 438, 201–204 (2005). [DOI] [PubMed] [Google Scholar]
  3. Geim A. K. & Novoselov K. S. The Rise of Graphene. Nature Materials. 6, 183–191 (2007). [DOI] [PubMed] [Google Scholar]
  4. Novoselov K. S. et al. Two-dimensional gas of massless Dirac fermions in graphene. Nature. 438, 197–200 (2005). [DOI] [PubMed] [Google Scholar]
  5. Wang C. et al. Concentration and distribution of entanglement based on valley qubits system in graphene. Sci. Bulletin, 60, 2016–2021 (2015). [Google Scholar]
  6. Seselj N., Engelbrekt C. & Zhang J. Graphene-supported platinum catalysts for fuel cells. Sci. Bulletin 60, 864–876 (2015). [Google Scholar]
  7. Zhang J. et al. Two-dimensional silicon-carbon hybrids with a honeycomb lattice: New family for two-dimensional photovoltaic materials. Sci. China. Phys. Mech. Astron. 58, 106801 (2015). [Google Scholar]
  8. Sun C., Wen B. & Bai B. Recent advances in nanoporous graphene membrane for gas separation and water purification. Sci. Bulletin. 60, 1807–1823 (2015). [Google Scholar]
  9. Dai Z. et al. Plasmon-driven reaction controlled by the number of graphene layers and localized surface plasmon distribution during optical excitation. Light: Sci. Appl. 4, e342 (2015). [Google Scholar]
  10. Chen J. H. et al. An all-optical modulator based on a stereo graphene-microfiber structure. Light: Sci. Appl. 4, e360 (2015). [Google Scholar]
  11. Ritter K. A. & Lyding J. W. The influence of edge structure on the electronic properties of graphene quantum dots and nanoribbons. Nature Mater. 8, 235–242 (2009). [DOI] [PubMed] [Google Scholar]
  12. Güclü A. D., Potasz P. & Hawrylak P. Electric-field controlled spin in bilayer triangular graphene quantum dots. Phys. Rev. B 84, 945–949 (2011). [Google Scholar]
  13. Luk C. M. et al. An efficient and stable fluorescent graphene quantum dot–agar composite as a converting material in white light emitting diodes. J. Mater. Chem. 22, 22378–22381 (2012). [Google Scholar]
  14. Zhuo S., Shao M. & Lee S. T. Upconversion and Downconversion Fluorescent Graphene Quantum Dots: Ultrasonic Preparation and Photocatalysis. ACS Nano. 6, 1059–1064 (2012). [DOI] [PubMed] [Google Scholar]
  15. Zhu S. et al. Surface Chemistry Routes to Modulate the Photoluminescence of Graphene Quantum Dots: From Fluorescence Mechanism to Up-Conversion Bioimaging Applications. Adv. Func. Mater. 22, 4732–4740 (2012). [Google Scholar]
  16. Gupta V. et al. Luminescent Graphene Quantum Dots for Organic Photovoltaic Devices. J. Am. Chem. Soc. 133, 9960–9963 (2011). [DOI] [PubMed] [Google Scholar]
  17. Li X. L., Wang X., Zhang L., Lee S. & Dai H. Chemically derived, ultrasmooth graphene nanoribbon semiconductors. Science. 319, 1229–1232 (2008). [DOI] [PubMed] [Google Scholar]
  18. Ponomarenko L. A. et al. Chaotic Dirac Billiard in Graphene Quantum Dots. Science. 320, 356–358 (2008). [DOI] [PubMed] [Google Scholar]
  19. Wang X. et al. Bandgap-Like Strong Fluorescence in Functionalized Carbon Nanoparticles. Angew. Chem. Int. Ed. 49, 5310–5314 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Zhu S. J. et al. Surface chemistry routes to modulate the photoluminescence of graphene quantum dots: from fluorescence mechanism to up-conversion bioimaging applications. Adv. Funct. Mater. 22, 4732–4740 (2012). [Google Scholar]
  21. Jin S. H., Kim D. H., Jun G. H., Hong S. H. & Jeon S. Tuning the Photoluminescence of Graphene Quantum Dots through the Charge Transfer Effect of Functional Groups. ACS Nano. 7, 1239–1245 (2013). [DOI] [PubMed] [Google Scholar]
  22. Lui C. H., Mak K. F., Shan J. & Heinz T. F. Ultrafast Photoluminescence from Graphene. Phys. Rev. Lett. 105, 127404 (2010). [DOI] [PubMed] [Google Scholar]
  23. Chen C. F. et al. Controlling Inelastic Light Scattering Quantum Pathways in Graphene. Nature 471, 617–620 (2011). [DOI] [PubMed] [Google Scholar]
  24. Kim S. et al. Anomalous Behaviors of Visible Luminescence from Graphene Quantum Dots: Interplay between Size and Shape. ACS Nano. 6, 8203–8208 (2012). [DOI] [PubMed] [Google Scholar]
  25. Guido C. A., Cortona P., Mennucci B. & Adamo C. On the Metric of Charge Transfer Molecular Excitations: A Simple Chemical Descriptor. J. Chem. Theory Comput. 9, 3118–3126 (2013). [DOI] [PubMed] [Google Scholar]
  26. M. Frisch Team, R: Gaussian 09, Wallingford CT, USA. URL http://www.gaussian.com/g_prod/g09.htm.(2009).
  27. Hohenberg P. & Kohn W. Inhomogeneous electron gas. Phys. Rev. 136, B864 (1964). [Google Scholar]
  28. Becke A. D. Density-functional exchange-energy approximation with correct asymptotic behaviour. Phys. Rev. A 38, 3098 (1988). [DOI] [PubMed] [Google Scholar]
  29. Gross E. K. U. & Kohn W. Local density-functional theory of frequency-dependent linear response. Phys. Rev. Lett. 55, 2850 (1985). [DOI] [PubMed] [Google Scholar]
  30. Yanai T., Tew D. P. & Handy N. C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 393, 51–57 (2004). [Google Scholar]
  31. Sun M. T. Control of structure and photophysical properties by protonation and subsequent intramolecular hydrogen bonding. J. Chem. Phys. 124, 054903 (2006). [DOI] [PubMed] [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES