Nonlinear Statistical Reconstruction for Flat-Panel Cone-Beam CT with Blur and Correlated Noise Models

Abstract

Flat-panel cone-beam CT (FP-CBCT) is a promising imaging modality, partly due to its potential for high spatial resolution reconstructions in relatively compact scanners. Despite this potential, FP-CBCT can face difficulty resolving important fine scale structures (e.g, trabecular details in dedicated extremities scanners and microcalcifications in dedicated CBCT mammography). Model-based methods offer one opportunity to improve high-resolution performance without any hardware changes. Previous work, based on a linearized forward model, demonstrated improved performance when both system blur and spatial correlations characteristics of FP-CBCT systems are modeled. Unfortunately, the linearized model relies on a staged processing approach that complicates tuning parameter selection and can limit the finest achievable spatial resolution. In this work, we present an alternative scheme that leverages a full nonlinear forward model with both system blur and spatially correlated noise. A likelihood-based objective function is derived from this forward model and we derive an iterative optimization algorithm for its solution. The proposed approach is evaluated in simulation studies using a digital extremities phantom and resolution-noise trade-offs are quantitatively evaluated. The correlated nonlinear model outperformed both the uncorrelated nonlinear model and the staged linearized technique with up to a 86% reduction in variance at matched spatial resolution. Additionally, the nonlinear models could achieve finer spatial resolution (correlated: 0.10 mm, uncorrelated: 0.11 mm) than the linear correlated model (0.15 mm), and traditional FDK (0.40 mm). This suggests the proposed nonlinear approach may be an important tool in improving performance for high-resolution clinical applications.

1. Introduction

Flat-panel cone-beam CT (FP-CBCT) has found application in a number of dedicated CT systems due to its ability to provide high-spatial-resolution reconstructions in a relatively compact device. Specific clinical applications include extremities imaging¹ and mammography.² Such systems are often capable of higher resolution reconstructions than diagnostic multidetector CT. Despite the improved high-resolution capability, some imaging tasks demand even higher spatial resolution including microcalcification detection in mammography, trabecular bone visualization in extremities imaging, and plaque detection and classification in CT angiography. While hardware improvements might increase high-resolution capabilities, a software approach can improve currently available systems and may also provide increased design freedom in future designs. Conventional reconstruction methods are limited by system blur which may also impart spatial correlations in the measurements. These effects, especially spatial correlations in projection data, are often ignored in reconstruction. Accounting for both of these phenomena should improve high-resolution performance and enable more widespread application of FP-CBCT.

There are a number of examples in previous work that have attempted to improve high-resolution performance through improved system models. For example, system blur without spatial correlation has been integrated in likelihood based approaches,^{3, 4} while others have accounted for system blur⁵ and noise correlations⁶ in a sinogram restoration step. While these methods have the potential to extend the high-resolution capability over approaches that do not model blur and/or correlation, we have found previously that proper handling of both the mean blur model as well as the spatial correlations are important to maximize imaging performance. We have previously presented a multistage reconstruction algorithm, consisting of a preprocessing step and a linear least-squares objective function, which accounts for both system blur and noise correlations.^7,8 While this linearized approach performs well, there are a few drawbacks that complicate its use. In particular, the initial deconvolution step adds a number of complications including 1) the need to apply some form of regularization in the preprocessing step which adds an additional tuning parameter to the reconstruction; 2) difficulties with deconvolution when the system blur has a null space (zeros in the frequency response); and 3) potential problems surrounding negative projection values after deblurring (and prior to log transformation). Similarly, because the initial deconvolution step must be regularized in practice for real systems, we have found that this preprocessing can limit the finest spatial resolution that may be achieved.

In this work, we develop a full nonlinear forward model and a likelihood-based objective function that uses the measured data directly, eliminating the need for a deblurring step, and permitting the use of a single regularization term (i.e. a single tuning parameter). Both the system blur and spatial noise correlations are modeled. We presume normally distributed measurement noise with a covariance that may be computed from the measurements themselves. This results in a nonlinear generalized weighted least-squares objective function which we solved using a custom iterative reconstruction algorithm which is discussed in detail below. The proposed nonlinear algorithm is evaluated using a digital extremities phantom and two noise models, an uncorrelated and a correlated noise model. The two noise models and the previously reported linearized approach are compared quantitatively by analyzing their resolution-variance trade-offs as well as in qualitative comparisons of noise- and resolution-matched reconstructions.

2. Methods

2.1 Objective Function

We consider a generic FP-CBCT system with a generic linear blur and gain with the following vector-form forward model:

$$\overline{y}=\mathbf{B}exp(-\mathbf{A}\mu )$$ (1)

where A is the forward projection operator (system matrix), μ is a vector of attenuation values, and B is a linear transformation that applies system blurs and any gain terms (associated with fluence levels and detector sensitivities). We assume the measurements follow a Gaussian distribution about this mean with a covariance given by K_Y:

$$y~\mathcal{N}(\overline{y},{\mathbf{K}}_Y)$$ (2)

Under these conditions, we may form the penalized-likelihood objective function:

$$\psi =\varphi +\beta R(\mu )=1/2{[y-\mathbf{B}f(\mathbf{A}\mu )]}^T\mathbf{W}[y-\mathbf{B}f(\mathbf{A}\mu )]+\beta R(\mu )$$ (3)

which is a penalized nonlinear generalized least-squares objective where R is a penalty function, $\mathbf{W}={\mathbf{K}}_Y^{-1}$, and f(x) = e^−x.

2.2 General Solving Strategy

A steepest descent algorithm accelerated by Nesterov's method^9,10 (Algorithm 1) was used to minimize (3). Gradient and curvature information was required to pick a search direction (p) and step length (α). The gradient and curvature of the penalty term were approximated using a separable surrogate method.¹¹ The gradient and Hessian of ϕ is given by:

$$\nabla \varphi ={\mathbf{A}}^T\mathbf{D}\{exp(-A\mu )\}{\mathbf{B}}^T\mathbf{W}[y-\mathbf{B}exp(-\mathbf{A}\mu )]$$ (4)

$${\nabla }^2\varphi ={\mathbf{A}}^T\mathbf{D}\{exp(-\mathbf{A}\mu )\}{\mathbf{B}}^T\mathbf{\text{WBD}}\{exp(-\mathbf{A}\mu )\}\mathbf{A}+{\mathbf{A}}^T\mathbf{D}\{exp(-\mathbf{A}\mu )\}\mathbf{D}\{{\mathbf{B}}^T\mathbf{W}[\mathbf{B}exp(-\mathbf{A}\mu )-y]\}\}\mathbf{A}$$ (5)

The search direction was set equal to the negative gradient of ψ. The step length was determined by finding the approximate minimum of (3) along this direction. In this work, a line search based on Newton's method was used. Using (4,5), the slope and curvature of the objective with respect to α can be obtained. Defining q ≜ Ap_n and l ≜ Aμ_n:

$$\frac{d\psi }{d\alpha }=q^T\mathbf{D}\{exp(-l-\alpha q)\}{\mathbf{B}}^T\mathbf{W}[y-\mathbf{B}exp(-l-\alpha q)]+\beta p^T\nabla R(\mu +\alpha p)$$ (6)

Algorithm 1.

Basic outline of algorithm focusing on the line search and acceleration.

μ0 ← deblur and FDK recon

n ← 0, t0 ← 1, z0 ← μ0

while n < N do

pn ← − Δψ|μn, αi ← 0, i ← 0

while i < I do

$c\leftarrow \frac{d^2\psi }{d{\alpha }^2}{|}_{{\alpha }_i}$

if c < 0 then

c ← cub

end if

${\alpha }_{i+1}\leftarrow {\alpha }_i-c^{-1}\frac{d\psi }{d\alpha }{|}_{{\alpha }_i}$, i ← i + 1

end while

$t_{n+1}\leftarrow (1+\sqrt{1+4t_n^2})/2$, μn+1 ← [zn + αIp]+

$z_{n+1}\leftarrow {\mu }_{n+1}+\frac{t_{n-1}}{t_{n+1}}({\mu }_{n+1}-{\mu }_n)$, n ← n + 1

end while

$$\frac{d^2\psi }{d{\alpha }^2}=q^T\mathbf{D}\{exp(-l-\alpha q)\}{\mathbf{B}}^T\mathbf{\text{WBD}}\{exp(-l-\alpha q)\}q+q^T\mathbf{D}\{exp(-l-\alpha q)\}\mathbf{D}\{{\mathbf{B}}^T\mathbf{W}[\mathbf{B}exp(-l-\alpha q)-y]\}\}q+\beta p^T{\mathbf{D}}_{R}p$$ (7)

where D_R is the diagonal Hessian approximation given by the surrogate penalty function. The step length was found using multiple iterations of Newton's method. An upper bound on the curvature (c_ub) was found and used if (7) was negative.

2.3 Simplifying Approximations

We used the above framework to model two system blurs. Specifically, we modeled source blur associated with the finite size x-ray focal spot (B_s) and detector blur resulting from light spread in the detector scintillator (B_d), such that:

$$\mathbf{B}={\mathbf{B}}_d{\mathbf{B}}_s{I}_0$$ (8)

Where I₀ is a scalar gain term (presuming uniform x-ray fluence and detector sensitivity). We note that the source and detector blurs are intentionally separated since source blur does not lead to noise correlation, while detector blur induces noise correlation due to the indirect conversion of single x-ray photons to many light photons. That is, the signal incident on the detector exhibits source blur but has independent quantum noise (variance is equal to the mean, given by B_sI₀ exp(−Aμ)), and the noise is correlated in the detector due to scintillator blur. Combined with additive readout noise, this yields the following covariance matrix:

$${\mathbf{K}}_Y={\mathbf{B}}_d\mathbf{D}\{{\mathbf{B}}_s{I}_{0}exp(-\mathbf{A}\mu )\}{\mathbf{B}}_d^T+{\mathbf{K}}_{\mathit{\text{ro}}}\approx {\mathbf{B}}_d\mathbf{D}\{y\}{\mathbf{B}}_d^T+{\mathbf{K}}_{\mathit{\text{ro}}}$$ (9)

We can simplify the above equations by assuming readout noise is negligible, allowing the B_d terms to cancel.

$${\mathbf{B}}^T\mathbf{\text{WB}}\approx I_0{\mathbf{B}}_s^T{\mathbf{B}}_d^T{[{\mathbf{B}}_d\mathbf{D}\{y\}{\mathbf{B}}_d^T]}^{-1}{\mathbf{B}}_d{\mathbf{B}}_s{I}_0=I_0^2{\mathbf{B}}_s^T\mathbf{D}\{1/y\}{\mathbf{B}}_s$$ (10)

Substituting (10) into the above equations eliminates the explicit use of W in every iteration. The full form of W was used to calculate the constant vector B^TWy used in gradient and curvature calculations. Because of the inversion in W, Wy was solved iteratively using the conjugate gradient method.

The same approximation allows for a simple expression for an upper bound on the curvature (c_ub).

$$c_{ub}={|q|}^2{I}_0^{2}max(1/y)+|q||{\mathbf{B}}^T\mathbf{W}\mathbf{B}q|+|q||{\mathbf{B}}^T\mathbf{W}y|+\beta p^T{\mathbf{D}}_{R}p\ge \frac{d^2\psi }{d{\alpha }^2}$$ (11)

2.4 Simulation Studies

Simulation studies to assess the relative performance of the proposed approach were conducted using the phantom in Figure 1. Data were generated by projecting the 4000×4000 voxel digital phantom (0.025 mm voxels) onto a 1D 7000 pixel detector (0.035 mm pixels). A C-Arm geometry was used, with a source-axis distance of 60 cm and a source-detector distance of 120 cm. The line integrals were downsampled by a factor of four to generate simulated noiseless data, which were blurred with both source and detector kernels as in (1). Both source and detector blur were Gaussian, with a FWHM of 0.34 mm and 0.70 mm, respectively. Blurs used for data generation and reconstruction were matched. Uncorrelated Gaussian noise with variance equal to the mean incident on the detector was generated and blurred by B_d to form correlated measurement noise. The correlated noise and additional uncorrelated readout noise was added to the mean measurement data. The system gain was 1e6 (unattenuated) photons/detector element, and readout standard deviation (σ_ro) was 1.9 photons. This readout noise is small enough to justify the assumption of negligible readout noise in (10). All data were reconstructed onto a 1000×1000 voxel grid with 0.1 mm voxels.

Figure 1.

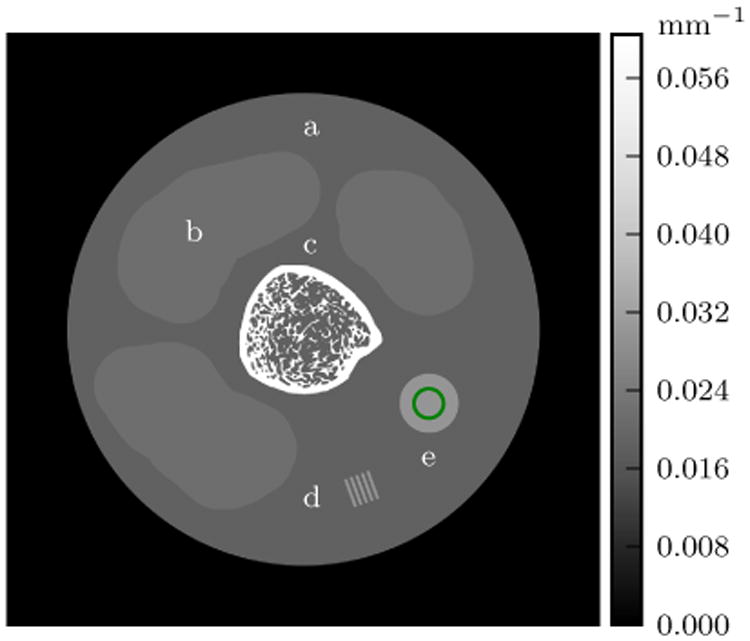
Extremities Phantom. This phantom contains (a) fat, (b) muscle, (c) cortical and trabecular bone, (d) line pairs, and (e) a uniform disk.

Two noise models were studied for nonlinear model reconstructions: a correlated noise model (12) that closely matches the data generation model and an uncorrelated noise model (13) as is traditionally used.

$${\mathbf{K}}_Y={\mathbf{B}}_d\mathbf{D}\{y\}{\mathbf{B}}_d^T+{\mathbf{K}}_{\mathit{\text{ro}}},{\mathbf{B}}^T\mathbf{\text{WB}}\approx I_0^2{\mathbf{B}}_s^T\mathbf{D}\{1/y\}{\mathbf{B}}_s$$ (12)

$${\mathbf{K}}_Y=\mathbf{D}\{y\}+{\mathbf{K}}_{\mathit{\text{ro}}},{\mathbf{B}}^T\mathbf{\text{WB}}=I_0^2{\mathbf{B}}^T\mathbf{D}\{1/(y+{\sigma }_{\mathit{\text{ro}}}^2)\}\mathbf{B}$$ (13)

Algorithm 1 was implemented with I = 5 (Newton line search iterations) and N = 2000 (steepest descent iterations). In addition to the proposed nonlinear approach, we applied the linearized approach⁸ using 100 conjugate gradient iterations and a correlated noise model.

Performance of different noise models was compared by plotting the resolution-variance trade-off - formed by sweeping the regularization strength (β) over a range of values. Spatial resolution was measured as the width (based on an error function fit) of the edge response of the disc (Figure 1e) in reconstructions of noiseless data. Variance was estimated as the sample variance over voxels inside the green circle in Figure 1e in noisy data reconstructions.

3. Results

Figure 2 summarizes the simulation study results and includes resolution-noise plots, as well as noise- and resolution-matched reconstructions (shown in Figure 2A,B,C and indicated with squares in the resolution-noise plot). We note that all model-based approaches investigated performed in a much higher resolution regime than traditional Feldkamp reconstruction (FDK) which was limited in resolution in these studies to 0.40 mm. The noise-resolution operating point for ramp-filtered FDK lies to the right of the curves shown in Figure 2. At coarser resolutions, all three model-based methods were roughly equivalent, following essentially the same resolution-noise curve. At finer resolutions, the correlated noise model had a superior resolution-variance trade-off to the uncorrelated model. We find that the linearized approach encountered a high-resolution limit of around 0.15 mm (smaller regularization values did not improve spatial resolution), whereas the proposed correlated nonlinear model could achieve spatial resolutions down to 0.10 mm.

Figure 2.

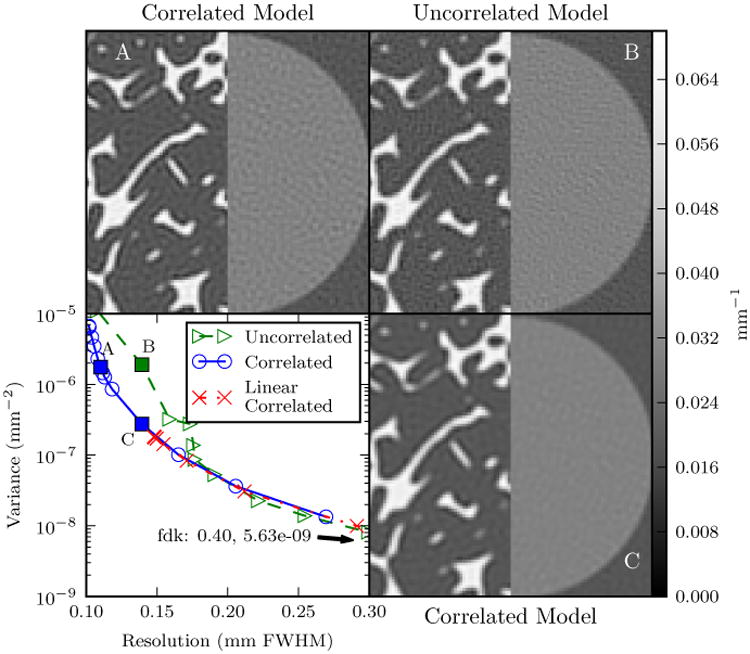
Resolution-Variance Plot and Reconstructions. The images correspond to the square data points in the resolution-variance plot. The horizontally aligned images (A and B) are noise matched, and the vertically aligned images (B and C) are resolution matched. Each image shows a section of the disc (Figure 1e) used for resolution and variance measurements and trabecular bone (Figure 1c).

At matched (high) resolution, the correlated noise model resulted in a reconstruction with less noise, which is evident in the disc portion of the phantom when comparing 2B and 2C. At matched variance, the correlated noise model was able to achieve a higher resolution, which can be appreciated in the sharpness of the disc and trabecular structure edges when comparing 2A and 2B.

4. Discussion and Conclusion

We have presented a novel nonlinear forward model and reconstruction scheme that accounts for both the system blur and spatial correlations found in FP-CBCT projection data. Accounting for these correlations resulted in a better resolution-variance trade-off (particularly at high resolutions).

In ongoing work we seek to apply the nonlinear approach to physical FP-CBCT data and evaluate its high-resolution performance. We note that the nonlinear forward model and reconstruction framework presented is very general - Equation (3) only constrains A and B to be linear operators. Thus, in future research, one may adapt the methodology to encompass additional flat-panel physics including detector lag, aliasing effects, and shift-variant system blurs, for additional potential performance gains. While the proposed iterative approach was successful in optimizing the nonlinear objective, we also seek faster algorithms to decrease the required number of iterations and time required.

Even without these additional refinements to the methodology we have seen significant potential improvements in high-resolution performance. Not only do these findings suggest that current FP-CBCT systems can be pushed to higher resolutions, but the availability of these kinds of model-based approaches may have additional impact on the design of future systems. Thus, the proposed techniques offer great potential to extend one of the main advantages of FP-CBCT, facilitating improved performance in high-resolution clinical applications where current FP-CBCT spatial resolution is insufficient.