A Neural Basis of Facial Action Recognition in Humans

Abstract

By combining different facial muscle actions, called action units, humans can produce an extraordinarily large number of facial expressions. Computational models and studies in cognitive science and social psychology have long hypothesized that the brain needs to visually interpret these action units to understand other people's actions and intentions. Surprisingly, no studies have identified the neural basis of the visual recognition of these action units. Here, using functional magnetic resonance imaging and an innovative machine learning analysis approach, we identify a consistent and differential coding of action units in the brain. Crucially, in a brain region thought to be responsible for the processing of changeable aspects of the face, multivoxel pattern analysis could decode the presence of specific action units in an image. This coding was found to be consistent across people, facilitating the estimation of the perceived action units on participants not used to train the multivoxel decoder. Furthermore, this coding of action units was identified when participants attended to the emotion category of the facial expression, suggesting an interaction between the visual analysis of action units and emotion categorization as predicted by the computational models mentioned above. These results provide the first evidence for a representation of action units in the brain and suggest a mechanism for the analysis of large numbers of facial actions and a loss of this capacity in psychopathologies.

SIGNIFICANCE STATEMENT Computational models and studies in cognitive and social psychology propound that visual recognition of facial expressions requires an intermediate step to identify visible facial changes caused by the movement of specific facial muscles. Because facial expressions are indeed created by moving one's facial muscles, it is logical to assume that our visual system solves this inverse problem. Here, using an innovative machine learning method and neuroimaging data, we identify for the first time a brain region responsible for the recognition of actions associated with specific facial muscles. Furthermore, this representation is preserved across subjects. Our machine learning analysis does not require mapping the data to a standard brain and may serve as an alternative to hyperalignment.

Introduction

Faces are used to express action and intent and, thus, visual analysis of facial behavior is of fundamental importance to us (Darwin, 1965; Ekman et al., 1969; Bruce and Young, 2012; Emmorey and Lane, 2013). This is achieved seemingly effortlessly, typically without conscious awareness. This visual recognition is also highly accurate, although the number of facial expressions we encounter in daily life is very large (Ekman and Friesen, 1977; Russell and Fernández-Dols, 1997; Emmorey and Lane, 2013; Du et al., 2014). This large variety of facial expressions is achieved by differentially moving our facial muscles (Duchenne, 1862). Muscle articulations resulting in distinctive visible featural changes are called action units (AUs; Ekman and Friesen, 1977). For example, AU 1 defines a medial contraction of the frontalis muscle, resulting in the raising of the inner section of the eyebrows (Fig. 1a). Computational models (Martinez and Du, 2012; Cohn and De la Torre, 2014) and studies in cognitive and social psychology (Oosterhof and Todorov, 2009) posit that visual recognition of these AUs is essential to interpret facial behavior and a necessary intermediate step to achieve categorization of emotions. Surprisingly, neuroimaging studies to identify the neural basis of the recognition of AUs are missing. A major reason for the lack of these studies is the difficulty of identifying patterns of neural responses associated with the small image changes observed when only a few facial muscles move, e.g., AU 1 results in a small visible image change (Fig. 1a).

Figure 1.

a, AUs. Sample images with AUs 2 and 12 and AUs 1 and 20 present. We study the hypothesis that visual recognition of AUs is performed in pSTS. To study this hypothesis, participants saw blocks of images with these AUs present or not present. b, Sample block. Each block starts with a 4 s blank screen and a 6 s fixation cross. This is followed by six sample images of a facial expression of emotion with the same AUs present in each image but expressed by different individuals. Each sample image is shown for 1.5 s and followed by a random noise mask that is shown for 0.5 s. The block concludes with a categorization task. Participants are given 2 s to indicate which of two alternative semantic categories (e.g., disgusted/happily disgusted) best describes the emotion of the images in the block. Participants watch a total of 168 blocks.

Here, using functional magnetic resonance imaging (fMRI) and an innovative analysis using machine learning algorithms, we identify for the first time a neural basis for visual recognition of AUs. In particular, we hypothesize that these computations are housed in the posterior superior temporal sulcus (pSTS), a brain region thought to play a crucial role in the analysis of changeable aspects of the face (Allison et al., 2000; Haxby et al., 2000). Single-cell recordings in nonhuman primates and fMRI studies with humans show strong activation of the pSTS when observing some facial movements, such as eye direction (Adolphs, 2003; Fox et al., 2009; Vytal and Hamann, 2010; Harris et al., 2012; Johnston et al., 2013).

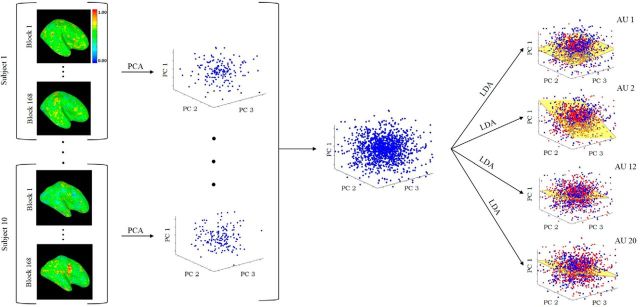
We define a multivoxel analysis approach to identify neural patterns consistent when observing images with the same AU present but differential between AUs. To do this, we first define a machine learning approach to learn to detect when subjects in the scanner are looking at images of a specific AU. Then, we test this decoder with a set of independent subjects (i.e., subjects not used to train the decoder). The results show that we can decode the presence of AUs in an image even across subjects. To be able to work across subjects, the pattern of neural activity of each subject is defined in a feature space given by a small number of linear combinations of all voxels. That is, the d voxels of each subject's brain [or region of interest (ROI)] are described by the p linear combinations of voxels that best describe the original neural activity in the least-squares sense. Although d is generally different in each subject, p can be kept constant, allowing for easy comparison of data across subjects. This approach eliminates the need to map the data to a standard brain and may offer a less data-intensive alternative to “hyperalignment” (Haxby et al., 2011) by defining a common subject-independent feature representation instead.

We use this approach to first test our hypothesis that visual recognition of AUs is processed by a set of voxels in pSTS. Then, we apply a discovery-search analysis to the whole brain to identify the most discriminant cluster of voxels for classifying AUs. This information-based approach yields consistent results, identifying a small number of voxels in the pSTS as the most discriminant in the brain. In conjunction, these results provide the first evidence for a specialized region in the brain dedicated to the visual recognition of AUs.

Materials and Methods

Stimuli.

One thousand eight images of facial expressions were selected from the database of Du et al. (2014). Images corresponded to one of seven emotion categories: (1) disgusted; (2) happily surprised; (3) happily disgusted; (4) angrily surprised; (5) fearfully surprised; (6) sadly fearful; or (7) fearfully disgusted. Thus, there were 144 images for each emotion category as expressed by different people. These are color images downsized to 472 × 429 pixels, yielding a visual angle of 7.86° × 7.17°. The images were normalized for intensity and contrast. The fixation cross had a visual angle of 1.2° × 1.2°. All images were shown centrally. Stimulus presentation was controlled using MATLAB running on a desktop personal computer and projected onto a rear-projection screen located at the back of the scanner bore, viewed through a mirror mounted on the head coil.

Experimental design.

The experiment design and protocol were approved by the Office of Responsible Research Practices at Ohio State University (OSU). Ten right-handed subjects (eight women; mean age, 25.3 years) with normal or corrected-to-normal vision participated in the present experiment. The experiment lasted ∼1.5 h. Anatomical and functional data were captured in the same session. To collect functional data, we used a block design. The experiment was divided into 12 runs. Each run included 14 blocks. In each block, six images of a facial expression of emotion were shown (Fig. 1b). Images showed expressions with one, two, or three of the selected AUs present (i.e., AU 1, AU 2, AU 12, and AU 20; Fig. 1a). The six images in a block showed the same expression of emotion and had the same AUs present. At the end of the block, subjects saw two semantic labels on the screen (left and right of center) and were asked to quickly indicate which label best described the category of the six facial expressions in that block by key press. The correct category name was on the left or right with 50% probability. Subjects responded with a hand-held button box and were given 2 s to respond. Then, the screen was blank for 4 s, followed by a fixation cross, which was shown for 6 additional seconds, for a total of 12 s between blocks (Fig. 1b). At the end of each run, subjects saw two face images (left and right of center) and were instructed to indicate which image had been seen in that run by a key press. The position of the previously seen image was chosen randomly (50% chance of being left or right of center).

MRI parameters.

The fMRI experiment was conducted at the Center for Cognitive and Behavioral Brain Imaging at OSU. A Siemens 3 T Trio MRI total imaging matrix system was used to obtain the structural and functional imaging data. A 32-channel phase array receiver head coil was used. For the anatomical scan, a T1-weighted scan was obtained with the following: TR, 1950 ms; TE, 4.44 ms; field of view, 176 × 232 mm; slice thickness, 1 mm, yielding 256 axial slices. For functional data, the following were used: TR, 2 s; TE, 28 ms; field of view, 222 × 222 mm; flip angle, 72°; 3 × 3 × 3.3 mm voxels scanned. This yielded a total of 37 contiguous axial slices.

Data preprocessing.

The functional data were registered to the T1 anatomical scan for each subject. Motion correction to align acquisitions and temporal high-pass filtering (cutoff, 0.0128 Hz) to eliminate scanner noise were used. Acquisitions were shifted two positions to account for the delay of the hemodynamic function. Intensity normalization was done by dividing the value of each voxel at each time point by its maximum value in the run; this normalizes changes of magnitude typically seen between runs. This was followed by a baseline adjustment by subtracting the average normalized value of the two TRs preceding the block, which normalizes changes attributable to the short interblock delay (i.e., by subtracting the value of the TRs preceding the block, we obtained a better representation of the pattern of changes within the block regardless of small changes of neural activation at the beginning of each block). We also analyzed our data using another standard normalization approach in which first the mean is subtracted and the resulting vectors divided by the SD, yielding zero-mean, unit-variance feature vectors. The results reported in the present study were statistically identical when using either of these two normalizing methods. Finally, we averaged the resulting fMRI blood oxygenation level-dependent (BOLD) responses of all acquisitions in the block, which yielded one response sample per voxel per block for each subject.

The bilateral pSTS was defined anatomically using the Harvard–Oxford atlas (Desikan et al., 2006). This was done by mapping the atlas from MNI to each subject's anatomical scan. The early visual cortex (EVC) was functionally defined based on the BOLD contrast comparing all images > fixation. For each subject, this contrast was used to identify the most visually responsive areas, and then anatomical landmarks were used to guide selection of bilateral ROIs covering approximately V1–V3.

Data analysis (multivoxel pattern analysis).

Let d be the number of voxels of a subject. (For the whole-brain scan, d varied from a low of ∼40,000 to a maximum of ∼60,000. For pSTS, d was between 682 and 927.) Each normalized sample feature vector x̂_i (one per block) is defined in a d-dimensional feature space, x̂_i ∈ R^d. We have 168 feature vectors (samples) per subject (i.e., 14 blocks × 12 runs). This can be written in matrix form as X̂ = (x̂₁, …, x̂₁₆₈). Principal component analysis (PCA; Jolliffe, 2002) was applied to reduce the dimensionality of these vectors to keep >95% of the data variance (∼100 PCs). Formally, V^TΣ_XV = Λ, where Σ_X = ${\displaystyle {\sum }_{i=1}^{168}{\left({\widehat{x}}_i-\widehat{\mu }\right)}^T}$, μ̂ is the sample mean, V = (v₁, …, v_d) is a matrix whose columns are the eigenvectors of Σ_X and Λ = diag(λ₁, …, λ_d) are the corresponding eigenvalues, λ₁ ≥ … ≥ λ_d ≥ 0. The feature vectors projected onto the PCA space are defined by the matrix X^T = V̂^TX̂, with V̂ = (v₁, …, v_p), and p is the number of PCs. The dimensions of this space define the linear combination of all voxels that keep most of the variance of the BOLD signal and thus maintain most of the original data structure in the least-squares sense. Applying this dimensionality reduction procedure to the block-averaged data of each subject allowed us to define these feature vectors in a common p-dimensional feature space (Fig. 2). In this space, the first PC (v₁) defines the linear combination of voxels that accounts for the largest variance of each subject's neural responses; the ith PC defines the linear combination of voxels with ith largest variance.

Figure 2.

Subjects observed images of facial expressions with AU 1, AU 2, AU 12, and AU 20 either present or not present. Images were shown in blocks of six images each. Subjects saw a total of 168 blocks. The fMRI BOLD responses (see Materials and Methods) for each of these blocks are shown on the left column. The 168 responses of each subject are used to compute the covariance matrix (Σ_X) of the data, from which the PCs are obtained (middle column). This yields a common PCA feature representation for all subjects. Classification of each AU (present versus not present) is computed in this common PCA space. LDA is used as a classifier. Each LDA (i.e., to determine the presence of each AU) is a hyperplane dividing the PCA space into two regions: one region corresponds to the samples with that specific AU present and the other region to samples of this AU not present (right-most column). This figure illustrates the approach as it applies to a whole-brain analysis. When studying the hypothesis that the computations of visual recognition of AUs is in the pSTS, only those voxels in the pSTS region were used.

Linear discriminant analysis (LDA; Fisher, 1938) was then used to classify samples of AU present versus samples of AU not present in this PCA space (Fig. 2). LDA computes the between-conditions scatter matrix S_B, which is the covariance matrix of the class means, and the within-class scatter matrix S_W, which is the covariance matrix of the samples in each condition. The unit vector w that maximizes the ratio of these two matrices |w^TS_Bw|/|w^TS_Ww|, provides the Bayes optimal hyperplane separating the sample feature vectors of the two conditions (i.e., AU present versus not present; Hamsici and Martinez, 2008). We defined four such classifiers, one for each of the conditions (AU 1, AU 2, AU 12, and AU 20 present/not present; Fig. 2). The hyperplanes in this figure are defined by the norm vector w.

Advantages of the PCA-alignment approach.

The data analysis method defined in the preceding paragraph is innovative because it does not require anatomical alignment of the voxels across subjects. To clarify this, note that voxels from different subjects cannot be compared directly in native space because a one-to-one matching does not exist (i.e., the brain of each subject is defined by a different number of voxels d). The classical solution to circumvent this problem is to map each subject's data to a standard brain (e.g., MNI) using a linear or nonlinear anatomical mapping. However, mapping each subject's brain to a standard brain still does not guarantee that corresponding voxels exhibit the same functional response in the same voxels. For example, imagine that we map the data of two subjects to MNI and assume that the functional pattern of activation in these two subjects is identical. However, after mapping, the pattern of BOLD activation of the first subject is shifted a few voxels to the left of the pattern of BOLD activation of the second subject. Thus, these two representations are not identical in MNI, and a between-subject classifier would fail in this standard brain space. Nonetheless, if the two patterns of neural activation are indeed functionally the same, they also share the same data variance. This directly suggests a representation based on a linear combination of voxels that maximizes the data variance of all acquisitions. PCA is a technique used to achieve this, and certain existing decoding techniques have taken advantage of it by including a PCA step after MNI transformation (O'Toole et al., 2005; Misaki et al., 2010; Coutanche and Thompson-Schill, 2012). This PCA step aligns the data of different subjects functionally, facilitating across-subject classification.

Our key methodological contribution is to note that, if the PCA functionally aligns the data in MNI space, then it also aligns the data in the subject's space. This means that the data variance (PCA) approach can be applied directly to the data in the original subject's space, and, hence, the mapping to a standard brain is redundant and unnecessary.

Recall that the reason one generally maps the data to a standard brain is to test whether the neural activation across subjects is the same. Our PCA-alignment method also tests whether the neural activation is similar across people, but we do not require the signal to be located physically in the exact same voxels. If the neural responses in each subject are functionally the same, their variance will also be the same and the p PCs used to define the feature representation will be common across subjects, resulting in successful decoding. Note that the ordering of the PCs needs not be identical across subjects because we apply a subsequent LDA step; as long as the transformation between subject representations is linear, the PCA–LDA analysis will be able to decode across subjects (Martinez and Zhu, 2005). If the neural computations responsible for the visual recognition of AUs are not the same across subjects, then our approach will fail to find a common PCA representation, and we will not be able to decode AUs across subjects. This is the hypothesis we test in the current experiments.

We compare our PCA-alignment approach to the one in which we first map all acquisitions of every subject to MNI and then apply PCA and LDA to this anatomically aligned data. The same PCA and LDA approach and the same ROIs defined above were used. As shown in Results, this anatomical alignment and our PCA alignment yield the same decoding results, further demonstrating the unnecessary anatomical alignment step.

Because our approach is less data intensive than hyperalignment techniques, we suggest that it can also provide practical advantages over these techniques and may be worth attempting before considering hyperalignment. However, if the data transformation between subjects is nonlinear, our approach will not uncover a common between-subject representation, and nonlinear methods such as hyperalignment will need to be used. Note that kernel PCA could also be used to attempt to solve this nonlinear mapping, but this would only work if the kernel function that provides the between-subject functional correspondences was known or could be estimated from independent data, as is the case in hyperalignment.

Downsampling to avoid classification biases.

When working with classifiers, such as LDA, the number of samples per condition must be identical; otherwise, the classifier generally learns to always select the condition (AU present/not present) with the largest number of samples, yielding high classification accuracies and giving the false impression that it learned the underlying distribution of the data. To address this problem, we use the following downsampling approach. Let n₁ be the number of samples in condition 1 (AU present) and n₂ the number of samples in condition 2 (AU not present). If n_i > n_j, we reduce the number of samples in condition i by randomly selecting n_j samples from the pool of n_i samples. Care is taken to select the same number of samples from each emotion category, to prevent classification biases attributable to emotion rather than AUs. This process is repeated m times, each time yielding a slightly different LDA classifier. We then compute the average classification accuracy (and SE) on the data of the subject left out using these m classifiers. We used m = 1000.

Between-subject data analysis.

For testing, we used the leave-one-subject-out cross-validation procedure. This means that the feature vectors of nine subjects were used to train the LDA classifiers, whereas the feature vectors of the remaining subject were used for testing it. There were 10 subjects, so we iterated across all 10 combinations of leaving one subject out and computed the average classification accuracies and SEs. To compute statistical significance, we first estimated the distribution of the test statistics (i.e., classification accuracy) under the null hypothesis (i.e., classification is at chance). This null hypothesis states that the labels of the samples (i.e., which AUs are present in each image) can be randomized without affecting the classification accuracy. To estimate this underlying but unknown distribution, we sampled 1000 values by randomly permuting the labels of the images in each block. These accuracies plus that obtained using the true labels were rank ordered. The rank order of the correctly labeled sample was divided by the number of permutation tests (i.e., 1000) to yield the p value (Kriegeskorte et al., 2006). We also collapsed the data of all AUs and ran a t test to check for statistical significance of the overall decoding of AUs (with chance at 50%).

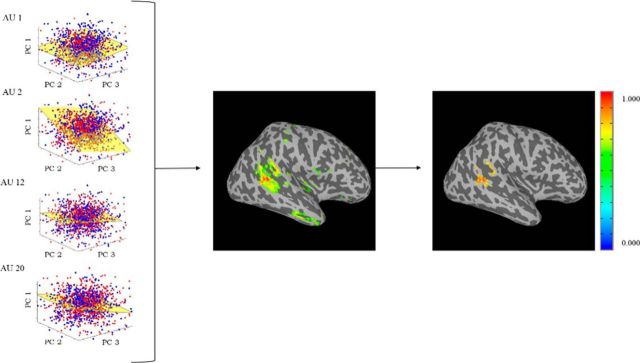
The above procedure was first applied to the pSTS to determine whether the presence of AUs could be decoded in this a priori hypothesized ROI. Then, the same procedure was applied to the whole brain, with the goal to identify which voxels were most discriminant. One advantage of using PCA plus LDA to derive our classifiers is that the process can be reversed to determine how much each voxel contributed to the classification of each AU. These values are given by the coefficient vectors of PCA and LDA described above. As shown in Figure 3, we can map the coefficients of LDA into each of the subjects' brains using the inverse projection of the PCs obtained previously, V̂. This yielded five maps, showing the most significant voxels for all AUs for each subject. Only the voxels with the 2% largest coefficients were kept. These results were mapped into MNI and smoothed with a 6 mm Gaussian, from which the average discriminant map across subjects was computed. The cluster with the highest discriminant coefficient was then identified (Fig. 3).

Figure 3.

Finding the most discriminant voxels. The four LDA spaces are defined by the coefficients of the basis vector w. This vector can be mapped to the d-dimensional space defining each subject's brain using the inverse transform given by PCA. These results are then mapped into MNI and the average across subjects is computed. The voxels with the top 2% weights are kept (middle image). The cluster with the largest weights is then selected (right image).

Within-subject data analysis.

We also used the same methodology defined above—PCA alignment plus LDA—to measure how well AUs could be decoded within individual subjects. Here, we used a leave-one-run out cross-validation approach. This means that, for each subject, we used the data of 11 runs for training the classifier and the data of the left-out run to test the decoding of AUs. Because there are 12 ways of leaving one run out, we tested each possibility. This yields 10 sets of decoding accuracies (one per subject) for each of the four AUs. We then calculated the mean and SE of these 10 values for each of the AUs and computed statistical significance using the permutation test described earlier. We also collapsed the data of all AUs and ran a t test to check for an overall statistical significance of these results (with chance at 50%).

Results

To test our hypothesis, we used the selected 1008 images of facial expressions of Du et al. (2014). These images include typically observed AUs. These were AU 1, AU 2, AU 12, and AU 20 (Fig. 1a). Whereas AU 1 corresponds to facial muscle actions that raise the inner corners of the eyebrows, AU 2 defines facial muscle activation yielding an upper movement of their outer corners. These two AUs are thus part of the upper face. AU 12 and AU 20 are in the lower face instead, with AU 12 defining the upper–outer pulling of the corners of the mouth and AU 20 the lateral stretching of the lips. Each of these AUs was present in only some of the selected images. Specifically, AU 1 was present in 55.5%, AU 2 in 42.3%, AU 12 in 38.5%, and AU 20 in 39.7% of the images. As a result, each image had either none of these AUs or had one, two, or three of them present. All four were never present at the same time because no facial expression of emotion is produced with all four of these AUs. For example, when showing a facial expression of disgust, none of these AUs is present, whereas when showing a facial expression of happily surprised, AU 1, AU 2, and AU 12 are present. It is important to note here that the same AU is present in several facial expressions. For instance, AU 1 is present when expressing happily surprised, fearfully surprised, sadly fearful, and fearfully disgusted. Thus, our goal is to decode AU regardless of emotion category.

Participants saw the 1008 facial expressions in blocks of six images while in the MRI scanner. Each block started with a blank screen (4 s), followed by a fixation cross (6 s). The six images were then presented for 1.5 s each and masked (0.5 s each), for a total of 12 s (Fig. 1b). The images in each block were of different individuals but displayed the exact same AUs.

Does the pSTS code for AUs?

Pattern analysis was used to define a multivoxel decoder for each of the AUs. That is, we defined a classifier to detect the presence or absence of AU 1 in the image, another classifier to detect AU 2, another for AU 12, and a final one for AU 20. To test whether AU representations are consistent across subjects, we used an across-subject decoding method that tests whether the neural activation pattern is functionally similar across people, without requiring the signal to be physically located in the exact same voxels (as described in detail in Materials and Methods). We did this by first anatomically segmenting the pSTS region in each subject's brain using an atlas (Desikan et al., 2006). Only the voxels in this segmented region were subsequently used. The neural response for each block was computed as the average neural signal across the 12 s stimulation period (time shifted by 4 s) for each pSTS voxel for each subject. The neural response for each block was then projected onto a common feature space using PCA. Each subject's data were written in matrix form (voxels × blocks), which allowed us to compute the PCs of this data matrix that kept most of its variance (>95%). Keeping the number of PCs identical in each subject yielded a common (subject-independent) feature space (Fig. 2), within which the four AU classifiers were computed with LDA (Martinez and Kak, 2001). This approach tests the hypothesis that the neural responses in each subject are functionally the same (in which case, their variance will also be the same and the PCs used to define the feature space will be common across subjects, resulting in successful decoding).

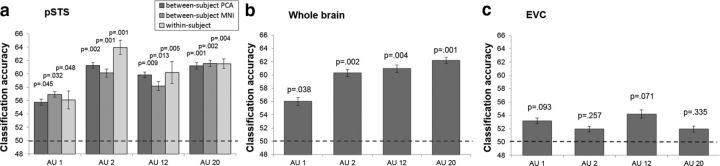
To determine the AU decoding efficacy of these voxels in the pSTS, we used a leave-one-subject-out cross-validation test. This means that the fMRI data of all but one of the subjects were used to train the four AU classifiers described above, whereas the data of the subject left out was used for testing them. Because there were 10 subjects that could be left out, we tested each option and computed the average classification accuracy and SE (Fig. 4a).

Figure 4.

Decoding results. Classification accuracy for an MVPA decoding the presence of AU 1, AU 2, AU 12, and AU 20 in images of facial expression. a, Classification accuracy in the pSTS, an anatomically defined region thought to process changeable and dynamic aspects of the face. Results are shown for the between-subjects PCA approach, between-subjects MNI approach, and within-subjects approach. Decoding accuracies are based on leave-one-out cross-validation tests computed using LDA. Error bars are SE. p values are calculated based on a permutation test comparing classification with chance (dotted line). All AUs could be decoded significantly above chance in all cases, and the results were not statistically different across methods. b, Classification accuracy across the whole brain, using the between-subjects PCA approach. All AUs could be decoded significantly above chance, and whole-brain decoding was not statistically better than pSTS alone. c, Classification accuracy in the EVC, using the between-subjects PCA approach. The EVC was functionally defined by finding the voxels in anatomical regions of the EVC that had a larger BOLD signal in all images compared with fixation. Classification in the EVC was not significantly greater than chance.

The results revealed significant decoding across subjects in the pSTS for each of the four AUs (Fig. 4a). Notably, the image changes in the stimuli were extremely small. For example, AU 2 corresponds to the upper movement of the outer corners of the eyebrows and AU 20 specifies the lateral stretching of the lips (Fig. 1a). Furthermore, univariate analysis did not uncover significant differences in mean activation responses across AUs. However, our results indicate that the pSTS response pattern [multivoxel pattern analysis (MVPA)] is sensitive to these small image changes. Also note the small SE in the plot. These small differences indicate that the results are similar regardless of which subject is left out for testing, further demonstrating the consistent representation of AUs in the pSTS across subjects. Moreover, collapsing these classification accuracies over all AUs yielded a statistically significant (t = 7.349, p = 0.002) average decoding of 59.52%.

Computational models of the perception of facial expressions have long speculated that high-level categorizations (e.g., emotions) are based on the recognition of AUs (Martinez and Du, 2012; Cohn and De la Torre, 2014). Studies in cognitive science and social psychology also support this view (Oosterhof and Todorov, 2009; Bartlett et al., 2014). However, to our knowledge, until now, no studies had yet confirmed or identified the neural basis of the visual recognition of AUs.

Decoding in MNI

The above decoding results were compared with those obtained by a more classical approach—mapping the data of each subject's brain to a standard brain (MNI) and performing between-subjects classification with PCA plus LDA in this standard-brain space. As can be seen in Figure 4a, this approach also revealed significant decoding for each AU. These results are statistically identical (t = 0.4840, p = 0.6615) to those obtained with our proposed PCA-aligned approach.

Within-subject decoding

The above between-subjects decoding results were comparable with those obtained when doing a within-subject analysis (Fig. 4a). For our within-subject analysis, we used a leave-one-run-out cross-validation approach within each subject independently and then computed the mean classification accuracy and SE for each AU across subjects. Collapsing the results over all AUs also yields a statistically significant (t = 6.3424, p = 0.004) average decoding of 60.44%. There was no significant decoding change when going from a within-subject to a between-subject analysis (t = 1.577, p = 0.212). This suggests that, not only does the pSTS contain information about AUs, but the coding of AUs in the pSTS is consistent across people; otherwise, a within-subject analysis would yield significantly better decoding than the between-subjects analysis described above.

Whole-brain analysis

To further investigate whether the pSTS is indeed the main brain region in which this visual analysis occurs or whether other brain areas might be as or more discriminant, we repeated the MVPA used above but applied it to the whole brain (Fig. 4b). These results can be thought of as the maximum neural decoding accuracies for these data, because they include contributions from the whole brain. These whole-brain accuracies are statistically comparable with those obtained in the pSTS alone (t = 0.957, p = 0.515), suggesting that the discriminant information is indeed coded in that brain region. Moreover, when the same MVPA was performed in the EVC, the AU classifiers were at chance (Fig. 4c), suggesting that the pSTS decoding was not driven by low-level visual differences in the images but rather a higher-level visual analysis of facial AUs. A qualitative analysis of the results in Figure 4 also shows a distinctive pattern of decoding in the pSTS versus EVC, and these patterns were statistically different (t = 4.135, p < 0.02).

Is the pSTS the primary brain region coding AUs?

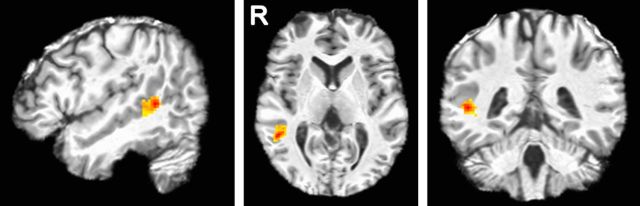
Finally, to more explicitly test our hypothesis, we inverted the whole-brain classification process to identify the most discriminant voxels in the brain. Note that both the PCA + LDA transformations are linear. This means that we can invert the procedure described above (i.e., compute the inverse linear transformation) to see which voxels are most discriminative for the classification of these four AUs in the brain. Because the PCA projection is subject specific, we mapped the coefficients (i.e., discriminant coefficients) of LDA to each of the subjects by inverting the PCA projection (see Materials and Methods; Fig. 3). This approach identified the most discriminant cluster of voxels. This corresponded to a cluster in the right pSTS (MNI coordinates, x = 50, y = −39, z = 4; Fig. 5). Hence, an information-based search yielded the same conclusion as the hypothesis-based analysis reported previously, reinforcing the significant and specific role of the pSTS in the visual analysis of facial actions.

Figure 5.

Most discriminant region. Sagittal, axial, and coronal views of the most discriminant region of the MVPA for AU decoding from the whole-brain analysis. This cluster is given by the voxels with the largest LDA coefficients.

Does the pSTS also code emotion categories?

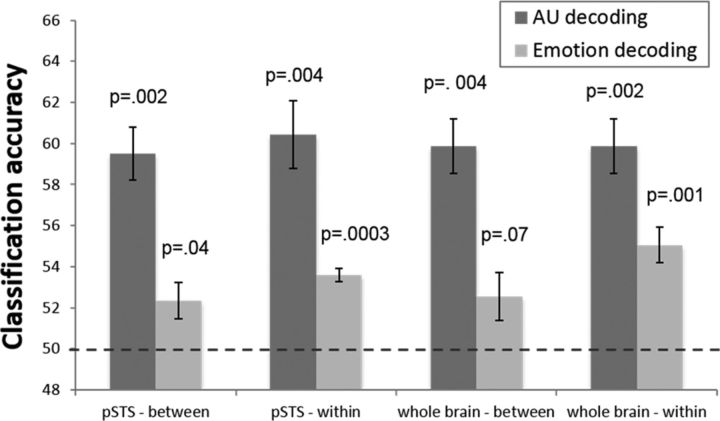
Our results strongly suggest that pSTS codes AUs. One may wonder whether it also codes emotion categories. Using the approach described previously in this paper, we asked whether emotion categories could be decoded in the pSTS and the whole brain (Fig. 6). As seen in this figure, although we can consistently decode AUs across subjects, decoding of emotion categories was much less reliable. Collapsing across emotion categories, between-subject decoding was significantly above chance (t = 2.622, p = 0.04 in the pSTS and t = 2.164, p = 0.07 in the whole brain), but the effect size was very small. Furthermore, attempting to decode specific emotion categories yielded null results, i.e., our algorithm was unable to decode any of the seven emotion categories in the PCA-aligned space or in MNI.

Figure 6.

Decoding emotion categories. Decoding results (average and SE) of AU and emotion categories in the pSTS and whole brain with a between-subject and within-subject analysis. Average results over all AUs and all emotion categories. Here, p values are given by the corresponding t test computed after collapsing the results over all AUs or emotion categories.

We also performed a within-subject analysis for emotion category (Fig. 6). Here, we were able to decode emotion category overall (p = 0.00003 in the pSTS, p = 0.001 in the whole brain), although the effect size was once more very small. Additionally, the decoding results of specific emotion categories were much less reliable than those of AUs; using our MVPA approach, we were only able to decode three of the seven emotions with a p < 0.05 in the whole brain and only one of seven in the pSTS. Our limited ability to decode emotion categories in pSTS could be attributable to the low spatiotemporal resolution of fMRI; it is possible that emotion categories are simply coded at a finer scale. Moreover, recall that our method is specifically designed to detect consistent neural representations that vary linearly between subjects. Therefore, our inability to find a consistent common representation across subjects does not mean that such a representation of emotion categories does not exist in the pSTS, but rather that there is possibly greater variability across participants in how emotions are encoded by pSTS patterns than in how AUs are encoded.

Discussion

A longstanding debate has endured on how facial expressions of emotion are recognized by our visual system. The debate has typically focused on whether neural representations of facial expression are categorical or continuous. The categorical model propounds the existence of neurons tuned to fire exclusively when a single emotion category is recognized in a facial expression (Darwin, 1965; Ekman et al., 1969). The continuous model argues for a group of cells to respond to continuous features of the expression, such as valance and arousal (Woodworth and Schlosberg, 1954; Russell, 1980). Computational models have suggested the coexistence of both representations (Dailey et al., 2002; Martinez and Du, 2012), and case studies and fMRI studies and single-cell recordings in humans have found evidence for these two representations in the brain (Harris et al., 2012; Sieger et al., 2015). However, computational models also suggest the existence of a third type of representation based on AU analysis, which is thought to precede the other representations (Cohn and De la Torre, 2014; Du et al., 2014). However, this AU level representation had not been identified previously in the brain.

Using fMRI, we identified a brain region responsible for the recognition of these facial actions. First, a hypothesis-based analysis showed that we could decode AUs in the pSTS, both within and across subjects. Then, a whole-brain exploratory analysis showed that the most discriminant voxels to decode AUs are in fact located in the pSTS. Furthermore, these results were different from decoding in the EVC, suggesting that this classification is not based on low-level image features. Critically, this coding was found to be consistent across people, such that we could decode the perceived facial action in participants not used to train the decoder. These results thus support the coexistence of this third AU-based representation for the visual analysis of facial expressions in humans.

The existence of these three distinct types of representation demonstrates the complexity and importance of emotion processing for human behavior. They further suggest that atypical processing of facial expressions of emotion may be attributable to a variety of causes, potentially explaining the variety of distinct behavioral changes seen in psychopathologies. The coexistence of these three representations of emotion should not be taken to mean that one is more important than the others or that they are independent. It is most likely that the three representations interact with one another. It is also believed that the recognition of AUs is a necessary step for the categorization of emotion and the decoding of valance and arousal in faces (Cohn and De la Torre, 2014; Du et al., 2014). However, although these are reasonable hypotheses, additional research is needed to define the specific mechanisms of recognition of emotion in the brain. It is also possible that the pSTS encodes information at an even finer scale than AUs as, for example, configural (i.e., second-order) features, which are known to play a major role in the visual recognition of emotion (Neth and Martinez, 2009).

Previous studies had shown that the pSTS is active when observing changes of eye gaze and other biologically salient features (Allison et al., 2000; Haxby et al., 2000; Harris et al., 2012). Cognitive studies of facial expressions of emotion also suggest that the pSTS is involved in the analysis of changeable aspects of the face (Adolphs, 2002, 2003). However, these studies did not address the question of which changeable aspects are represented in the pSTS. The present study provides evidence for the hypothesis that the pSTS is involved in the recognition of AUs in a facial expression. This neural mechanism suggests that the pSTS is involved in the recognition of faces at an intermediate level of abstraction, i.e., higher level of abstraction than similarity based on image features, but less abstract than a high-level semantic description of the whole image (e.g., emotion category). A neural mechanism for the representation of AUs has been theorized (but never localized), because it provides a highly efficient way to interpret a large number of facial expressions of emotion (Du et al., 2014) by reducing later categorization tasks to a simple check of present (active) AUs rather than having to categorize each emotion independently. This system is also consistent with computational models of the visual system (Riesenhuber and Poggio, 1999; Serre et al., 2007) and image categorization (Grill-Spector and Weiner, 2014), which assume a hierarchy of specialized areas with descriptors at several levels of abstraction.

Importantly, we found that we could decode AU activation in the pSTS but could not decode emotion category reliably across subjects in this ROI. Although this may seem surprising given that AU information could technically be used to classify emotions, it is notable that the pSTS does not seem to be performing this computation in a consistent way across subjects at the spatio-resolution scanned. Previous attempts to decode emotion categories from fMRI have yet to yield robust findings, with no positive results for between-subject decoding (Lindquist et al., 2012). Two studies have been able to decode a small number of emotion categories in a within-subject analysis in the pSTS (Said et al., 2010; Wegrzyn et al., 2015), and Peelen et al. (2010) and Skerry and Saxe (2014) found emotion-specific activation in other areas of the STS. We also found some weak within-subject emotion decoding in the pSTS, but emotion decoding was stronger in the whole-brain analysis, suggesting that decoding of emotional categories may be performed in combination with other ROIs as suggested by computational models (Martinez and Du, 2012) and fMRI studies (Harris et al., 2012; Lindquist et al., 2012).

To obtain the results described above, we defined an innovative machine learning analysis approach. Many MVPA methods used in fMRI studies use a within-subject analysis (Cox and Savoy, 2003; Nestor et al., 2011; Huth et al., 2012). This means that a percentage of the acquisitions of a specific subject are used to train the classifier, whereas the other acquisitions of the same subject are used to test it. Thus, each subject provides training and testing data. When decoding is achieved, the results suggest we have identified a consistent and differential pattern of activation within each subject. However, we do not know whether these results generalize to other subjects, i.e., would we be able to decode from data of additional subjects? This is problematic, because, if an ROI is believed to specifically code for AUs, decoding should be achieved even in subjects not used to train the decoder. The present study shows that this is indeed the case by training the decoder with data of nine subjects and testing it with the data of an independent subject.

The use of our new approach applying classifiers in subject-aligned feature space enables us to access a common functional space across subjects without having to rely on anatomical normalization. It is important to note here that the innovation of the present approach is in the definition of the PCA-alignment approach, not in the use of PCA and LDA themselves, which have been used previously in within-subject analyses and in anatomically aligned data before (O'Toole et al., 2005; Misaki et al., 2010; Coutanche and Thompson-Schill, 2012). Our approach also provides an alternative way of functionally aligning data across subjects without requiring separate hyperalignment steps (Haxby et al., 2011) and does not require the ranking of the PCs of each subject's normalized BOLD response to be identical. Because our approach does not require independent datasets for estimating the mapping across subjects and for classification, the method can be applied to smaller amounts of data than hyperalignment. However, our method will only work when the linear combination of all voxels given by PCA is functionally the same across subjects (i.e., the PCs are aligned across subjects up to a linear transformation). If between-subject functional correspondences require nonlinear transformations, then our method would not be able to find it, and in these cases hyperalignment would be more applicable.

As a final note, it is worth mentioning the relevance of our theoretical findings in the abnormal perception of faces. Specifically, the seemingly effortless, nonconscious recognition of facial expressions is believed to be disrupted in certain psychopathologies. For example, in autism spectrum disorders, there is a lack of neural activation in the pSTS compared with neurotypicals (Harms et al., 2010). This difficulty interpreting faces and facial actions may be attributable, in part, to a lack of the AU decoding in the pSTS defined in the present study. Atypical functioning of this neural system for AU decoding could explain these individuals' difficulties analyzing other facial actions and intentions, e.g., speech and social cues (Redcay et al., 2013).

In summary, the results reported herein support the view of a specialized, dedicated neural mechanism for the analysis of facial actions. This would explain how humans can recognize a large number of facial expressions seemingly effortlessly and interpret other people's actions and intentions. A loss or disruption of this system or its connections to other processing areas may underlie the difficulty that some people have in interpreting facial constructs.