Commissural Gain Control Enhances the Midbrain Representation of Sound Location

Abstract

Accurate localization of sound sources is essential for survival behavior in many species. The inferior colliculi (ICs) are the first point in the auditory pathway where cues used to locate sounds, ie, interaural time differences (ITDs), interaural level differences (ILDs), and pinna spectral cues, are all represented in the same location. These cues are first extracted separately on each side of the midline in brainstem nuclei that project to the ICs. Because of this segregation, each IC predominantly represents stimuli in the contralateral hemifield. We tested the hypothesis that commissural connections between the ICs mediate gain control that enhances sound localization acuity. We recorded IC neurons sensitive to either ITDs or ILDs in anesthetized guinea pig, before, during, and following recovery from deactivation of the contralateral IC by cryoloop cooling or microdialysis of procaine. During deactivation, responses were rescaled by divisive gain change and additive shifts, which reduced the dynamic range of ITD and ILD response functions and the ability of neurons to signal changes in sound location. These data suggest that each IC exerts multiplicative gain control and subtractive shifts over the other IC that enhances the neural representation of sound location. Furthermore, this gain control operates in a similar manner on both ITD- and ILD-sensitive neurons, suggesting a shared mechanism operates across localization cues. Our findings reveal a novel dependence of sound localization on commissural processing.

SIGNIFICANCE STATEMENT Sound localization, a fundamental process in hearing, is dependent on bilateral computations in the brainstem. How this information is transmitted from the brainstem to the auditory cortex, through several stages of processing, without loss of signal fidelity, is not clear. We show that the ability of neurons in the auditory midbrain to encode azimuthal sound location is dependent on gain control mediated by the commissure of the inferior colliculi. This finding demonstrates that commissural processing between homologous auditory nuclei, on either side of the midline, enhances the precision of sound localization.

Introduction

An important challenge for many animals is to locate where sounds originate in their environment. To localize sounds in the horizontal plane, the mammalian auditory system uses two cues: interaural time differences (ITDs) and interaural level differences (ILDs; Strutt, 1907; Grothe et al., 2010). These cues are first processed in the medial (Masterton et al., 1967; Goldberg and Brown, 1969) and lateral (Boudreau and Tsuchitani, 1968) superior olivary nuclei in the brainstem. Afferent projections from these and other auditory brainstem nuclei converge in the final subthalamic nuclei of the auditory system, the inferior colliculi (IC; Beyerl, 1978; Aitkin and Schuck, 1985; Saint Marie and Baker, 1990; Oliver et al., 1995; Schofield, 2002). Each IC is essential for accurate sound localization; lesions of one IC lead to localization deficits in the contralateral hemifield in animals (Jenkins and Masterton, 1982; Kelly and Kavanagh, 1994) including humans (Litovsky et al., 2002).

The ICs do not operate in isolation from each other; indeed the largest afferent source to each IC is the contralateral IC (Moore, 1988). Intercollicular projections via the commissure of the inferior colliculi (CoIC) have been found in all mammals examined, suggesting a fundamental role in auditory processing (Adams, 1980; González-Hernández et al., 1986; Saldaña and Merchán, 1992; Malmierca et al., 1995, 2009). Most CoIC fibers are thought to be glutamatergic, although a significant minority are GABAergic (González-Hernández et al., 1996; Hernández et al., 2006; Nakamoto et al., 2013). Stimulation of the CoIC produces both excitatory and inhibitory effects on IC neurons in vitro (Smith, 1992; Moore et al., 1998; Li et al., 1999; Reetz and Ehret, 1999). Changes in IC responses to sounds, consequent to deactivation of the IC contralateral to recording, suggest that the CoIC mediates gain control between the ICs (Malmierca et al., 2003, 2005; Orton and Rees, 2014). Such findings raise the possibility that interaction between the ICs plays a role in sound localization.

We tested the hypothesis that intercollicular gain control influences the representation of sound localization cues in the IC. We reversibly blocked neural activity in one IC and observed divisive gain change and additive shifts in the firing of neurons encoding ITDs and ILDs in the contralateral IC. Without CoIC input, IC neurons were less able to signal changes in sound location. Similar changes observed for responses to both ITDs and ILDs demonstrate a general mechanism of gain control operating between the ICs that enhances the neural representation of sound localization cues in the azimuthal plane.

Materials and Methods

We report the findings of experiments performed in accordance with the terms and conditions of a license (PPL 60/3934) issued by the UK Home Office under the Animals (Scientific Procedures) Act 1986, and with the approval of the Local Ethical Review committee of Newcastle University. Experiments were performed using methods similar to those reported previously (Orton et al., 2012; Orton and Rees, 2014).

Animals.

We performed experiments on 20 (12 male, 8 female) outbred, pigmented guinea pigs (Cavia porcellus). Animals had a median age of 4 months [interquartile range (IQR) = 4–6] and a median weight of 746 g (IQR = 654–862).

Anesthetic protocol.

Guinea pigs were anesthetized with urethane (Sigma-Aldrich; 0.7–1 g/kg as 20% solution, intraperitoneal injection) and Hypnorm (VetaPharma; fentanyl citrate 0.315 mg/ml and fluanisone 10 mg/ml; 0.5–1 ml/kg, intramuscular injection). Atropine sulfate monohydrate (BDH Chemicals; 0.05 mg/kg, subcutaneous injection) was given to suppress bronchial secretions. Anesthesia was maintained with further doses of Hypnorm as required.

Surgical procedure.

The trachea was cannulated to ensure a clear airway and to facilitate artificial respiration if required. If necessary, animals were artificially respired with medical air or oxygen via a modified small animal ventilator (Harvard Apparatus), which maintained end-tidal CO₂ at ∼5%. Core temperature was measured via a rectal probe and maintained at 38 ± 1°C with a thermostatically controlled electric blanket (Harvard Apparatus).

Experiments were conducted inside a single walled, sound attenuating room (IAC). Animals were placed in a stereotaxic frame (Kopf) in which the standard ear bars were replaced by custom-made hollow polymethyl methacrylate conical speculae. These held the head stable throughout the experiment and allowed sound stimuli to be delivered to the animal. Correct positioning of the speculae in the auditory meatuses was checked by visualization of the tympanic membranes using a surgical microscope (OpMi 99, Zeiss). The ear canal and eardrum were clean and healthy in all animals.

A midsagittal incision was made along the scalp. The skin was reflected and the tissues overlying the skull were abraded. Two holes were trephined on either side of the midline with a drill bit to expose the occipital lobe covering the left and right IC. Each pilot hole was extended with rongeurs. The dura mater was retracted bilaterally. The cortex overlying the left IC was aspirated. The aspirated region of the cortex was restricted to the caudal part of the occipital lobe in all experiments, and thus well away from the auditory cortex, to avoid the possibility that the surgery damaged corticofugal fibers to the IC from the auditory cortex.

Neural deactivation of the left IC.

The deactivation techniques of cooling or reverse microdialysis of procaine used in this study have been reported and validated previously (Orton et al., 2012; Orton and Rees, 2014) but are briefly described here.

Cooling.

A cryoloop (Lomber et al., 1999) was constructed from stainless steel tubing. A Type-T (copper-constantan) thermocouple was secured to the cryoloop tip to allow monitoring of the cryoloop temperature with a digital thermometer (HH506RA, Omega). A peristaltic pump (MINIPULS 3, Gilson) pumped ethanol cooled to −80°C around a hydraulic system. Regulating the flow rate enabled control of the temperature of the cryoloop. The cryoloop was curved to maximize contact with the dorsolateral surface of the IC. Cooling cycles were kept as brief as possible to optimize the chance of holding the unit throughout recovery and to minimize spread of cooling outside the IC. Median cooling duration was 14 min (minimum 6, maximum 25). The cryoloop was never allowed to fall <2°C. The median of minimum cryoloop temperatures achieved during all cooling cycles was 4.1°C (minimum 1.9, maximum 7.2).

We have previously verified the use of this method as a reliable means by which to induce neural deactivation in the dorsal half of the cooled IC. We found that cryoloop cooling deactivated firing of IC neurons in response to pure-tone stimuli in the central nucleus of the IC in frequency-band laminae with characteristic frequencies (CFs) <8 kHz, which is approximately halfway through the dorsoventral extent of the IC. More ventral areas were less affected by deactivation. We also found that deactivation did not have a pronounced effect on the ascending afferent volley to the IC contralateral to cooling, but did modulate responses consistent with commissural processing (Orton et al., 2012). Thus, cooling leads to diminished commissural input from the dorsal IC to the uncooled IC.

Although we have validated our cooling technique, it does not deactivate the more ventral, high-frequency regions of the IC. In this study, we investigated both low-frequency ITD and high-frequency ILD-sensitive neurons. We therefore used a complementary technique, microdialysis of procaine (MDP), to verify our cooling method and provide a means of deactivating the entire dorsoventral extent of the IC.

Microdialysis probes were constructed (Gartside et al., 1996). The probe was implanted vertically into the exposed IC with a stereotaxic manipulator. The probe was continuously perfused (2 μl/min) with artificial CSF (aCSF) composed of the following (in mm): 140 NaCl, 3 KCl, 0.27 Na₂H₂PO₄, 1.2 Na₂HPO₄, 2.4 CaCl₂, 1 MgCl₂, and 7.2 glucose, pH 7.4.

The sodium channel-blocker procaine (Sigma-Aldrich) was dissolved in aCSF. Switches from aCSF alone to aCSF plus procaine, or vice versa, were made at a securely clamped junction positioned 4 cm from the probe. This avoided mechanical disturbance of the probe during the changeover, which was essential for holding single units throughout control, MDP, and recovery phases of recording. Because of a time lag of ∼10 min from the point of changing the microdialysis solution, MDP deactivations were longer than cooling deactivations. Every effort was made to keep MDP deactivation times to a minimum to increase the likelihood of obtaining recordings after recovery from the drug. The median deactivation time using MDP was 23 min (minimum 12, maximum 48).

Microdialysis confers advantages over cooling and local iontophoretic application of drugs, which are effective over much smaller area. A benefit of microdialysis is that one is not constrained to neural deactivation, but a range of drugs can be applied via the same probe and their effects measured both electrophysiologically and neurochemically (by analysis of the dialysate).

Stimulus generation.

Stimuli were generated by TDT2 hardware (Tucker-Davis Technologies) controlled by software running on a PC. The software allowed the frequency and level of the stimulus to be varied in real time while searching for units. Stimulus waveforms were digitally generated and pure tones were cosine² ramped for 5 ms at the onset and offset.

Stimulus presentation.

Stimuli were delivered through Sony MDR 464 earphones, each housed in an alloy enclosure that fitted into the speculae (Rees et al., 1997). The output of the system was calibrated using an ⅛ inch Bruel and Kjaer 4138 microphone, a Type 2639 preamplifier, and Type 2610 measuring amplifier. The microphone was seated in a small coupler made from silicon tubing that sealed the narrow end of the speculum. The maximum output of the system was approximately flat from 0.1 to 9 kHz (100 ± 8 dB SPL) and then fell with a slope of ∼20 dB/octave so that the maximum output of the system at 16 kHz was 78 dB SPL from both the left and right speakers.

Electrophysiological recordings.

Recordings were made using borosilicate glass-coated tungsten microelectrodes (Merrill and Ainsworth, 1972). Electrode position was controlled by a custom-made stepper-motor microdrive activated by remote control outside the sound attenuating room. Vertical electrode penetrations were made in the right IC through the cortex in a mirror opposite position to the center of the exposed IC. Extracellular action potentials were amplified (×10,000) and bandpass filtered (0.1–3 kHz) by an amplifier (Dam-80, World Precision Instruments). Spikes were further high-pass filtered (300 Hz) via TDT2 hardware before being discriminated online, converted to logic pulses, and time stamped with an accuracy of 10 μs via TDT2 hardware.

Search stimuli were pure tones of 50 ms duration that were roved between 0.1 and 20 kHz and between 0 and 99 dB attenuation, presented at a repetition rate of 4 Hz. On isolation of a single unit, the CF and threshold were estimated from the frequency response area of the unit (LeBeau et al., 2001).

Following initial characterization, each unit response to stimuli of varying ITD and ILD was measured. All responses reported here were taken in response to 75 ms pure tones, presented at a repetition rate of 4 Hz. Spike times were saved over a 150 ms count window starting 10 ms before each stimulus onset. Each stimulus in an ITD or ILD was presented from 25 to 100 times.

ILDs were generated by holding the stimulus at the contralateral (left) ear to the recorded IC at a fixed level (median = 20 dB above threshold, range 6–50) at CF, while the level of the stimulus in the ipsilateral (right) ear was varied. ILD values represent the sound level in the ipsilateral ear relative to the fixed sound level in the contralateral ear. The fixed level for each unit was selected in an arbitrary manner after collection of a frequency response area to ensure the selected level was suprathreshold. Thirty-seven units were presented with ILDs before, during deactivation, and after recovery. Because of the heterogeneous nature of IC responses, the range the ILDs we presented varied between units from ±16 to ±40 dB. The increments of ILD within these ranges also varied between units from 2 to 10 dB. The variable nature of the ILD functions meant that we optimized the stimuli to increase the chances of recovering the unit while getting the most information we could from each individual unit.

ITDs were presented at a fixed suprathreshold level for each unit, also chosen pseudorandomly (median = 25 dB above threshold, range = 10–45), at CF. ITDs were generated by delaying or advancing the waveform of the sound in one ear relative to the other. Positive ITDs correspond to the waveform in the ear contralateral to the recorded colliculus leading that in the ipsilateral ear. Fifteen units were presented with ITD stimuli. Responses to ITDs were generated for 12 units across at least an entire cycle of interaural phase disparity. Three further units were recorded in small increments of ITD spanning the center of the physiological range of ITDs experienced by guinea pigs so that only the steeply sloping portion of the response was detected (Palmer et al., 1990). One of these units was also studied with ILD stimuli.

For individual units, identical stimuli were presented before, during and after deactivation of the contralateral (left) IC. Units were held for a median time of 60 min (IQR = 54–81 min; range 28–193). Units were allowed as long as was needed to recover from deactivation, but the majority recovered within 30 min.

Termination of experiments.

At the conclusion of each experiment, an intraperitoneal injection of sodium pentobarbital (Euthanal, Merial; 200 mg/ml, 2 ml) was given. After 5 min, the pedal withdrawal and blink reflexes were assessed to confirm a deep plane of anesthesia. The animal was then perfused transcardially with paraformaldehyde to fix the brain tissue for histologic analysis.

Data analysis.

The goal of this study was to assess what influence intercollicular processing has on the ability of IC neurons to represent changes in ITD and ILD with changes in their firing rate. Responses recorded before deactivation were characterized as “control” to which all subsequent responses of that unit were compared. In this respect, each neuron served as its own control. It was important that changes during contralateral IC deactivation recovered after cessation of cooling or MDP to demonstrate the causal effects of our deactivation protocols. Of the 51 units in our dataset, recovery recordings were obtained from 46. The other five units were held as single units throughout deactivation, but were lost before recovery recordings could be made. These units changed on deactivation in a manner similar to those for which recovery was obtained so have been included in our dataset.

Data were analyzed using MATLAB. To make the figures, the firing rate of each unit as a function of ITD or ILD was plotted. A color scheme was created that is suitable for colorblind people (http://jfly.iam.u-tokyo.ac.jp/color/index.html). Responses were three point smoothed for figures, however, all calculations were made on the raw data.

We calculated the spiking dynamic range as the minimum firing rate subtracted from the maximum firing rate in each function. We also calculated the median firing rate in each response function in each condition. For these measures, we calculated an Index of Change during deactivation using the equation:

This provides a measure of difference in firing rate between the two conditions, with no change indicated by a value of 0, with increases being positive and decreases, negative. This value is a continuous variable that scales in proportion to the magnitude of the control and deactivated measures. Thus, the measure facilitated comparisons of change across the population of units.

Analysis of gain modulation.

Firing rates at each ITD or ILD in the deactivated and recovery conditions were plotted as a function of firing rates in the control condition. Each of these plots was fitted with a linear regression of the form y = mx + c; where x is the control firing rate, y is the firing rate in the deactivated or recovery condition, m is the slope, and c is the intercept. These gain functions quantified the change in rate along the ILD or ITD axis and produced a measure of the divisive or multiplicative gain change (by the value of m), and a measure of the subtractive or additive shift (by the value of c).

Bootstrap analyses.

We used bootstrap resampling with replacement to test for changes in the slopes and intercepts of each unit. To do this we extracted the mean spike counts of each unit to each ILD/ITD in the control and deactivated conditions. Considering that each control value has a corresponding value in the deactivated condition, we can define for each unit a set of points on a line (see Fig. 4B). This set of points was bootstrapped 50,000 times to produce bootstrapped distributions of slope and intercept after fitting a linear model on each resample (using linear regression). The 95% two-sided confidence interval was calculated for both distributions using the MATLAB function bootci, which applies bias correction. The values of 1 for slope and 0 for intercept (which represent the control case) were tested to determine whether they were within the confidence intervals of the corresponding bootstrapped distributions of deactivated values. Control values of slope or intercept falling outside the confidence interval indicated a change in the corresponding measure. This procedure therefore tested the null hypotheses that there were no systematic changes in either intercept or slope due to deactivation.

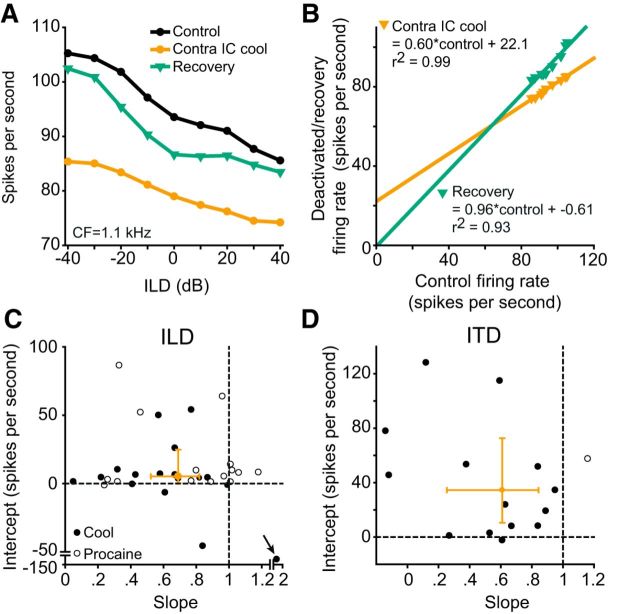
Figure 4.

Gain functions characterized changes in ITD and ILD response functions. A, An ILD-sensitive unit (black circles) whose firing was suppressed by contralateral deactivation (orange circles) and recovered to near control levels (green triangles). B, We plotted the deactivated (orange triangles) and recovered (green triangles) firing rates as a function of control firing rates and fitted linear regressions to each. Each regression characterized the additive/subtractive and multiplicative/divisive components of change. For this unit the change on deactivation was additive (22.1 spikes/s) and divisive (slope 0.60) relative to control. On recovery the slope (0.96) and intercept (−0.61) were almost unchanged relative to control. C, Intercept plotted as a function of slope for all ILD units. Almost all units had additive and divisive changes on deactivation. Orange bars indicate 99% CI. D, Intercept plotted as a function of slope for all ITD units. The same pattern of additive and divisive gain changes on deactivation was seen for ITD units. The median and 99% CI for intercept and slope were contained within the additive and divisive quadrant for both ITD and ILD units.

ROC analyses.

We performed ROC analyses using signal detection theory to investigate the effect of deactivating the contralateral IC on the discriminability of changes in ITD and ILD due to changes in firing rate (Green and Swets, 1966). An advantage of ROC analysis is that it makes no assumptions about the distribution of the data. A similar method has been used previously to investigate the ITD discrimination thresholds of IC neurons in guinea pig (Shackleton et al., 2003).

The 75% criterion is commonly used in psychophysical studies as a measure of just noticeable difference (JND); i.e., the minimum change in a parameter required for an observer to detect that change at least half the time. We used this measure as a criterion of neural discrimination of ITD and ILD change because of differences in firing rate along the ITD or ILD axis. The number of times each spike count occurred was constructed for each ILD or ITD in each condition (Bradley et al., 1987, their Fig. 3). We then set one spike count distribution as a reference and calculated for all other responses, in that condition, the ROC area relative to the reference. This was done for each ILD or ITD, in each condition. From these we constructed neurometric functions at each ILD or ITD (Bradley et al., 1987). From each neurometric function, we interpolated the minimum deviation from the reference that would produce a discrimination of 75 or 25% (whichever was smaller). This produced an array of JND values from each position in the ILD/ITD function, in each condition. We then found the minimum JND in the control condition. This JND was compared with the JND at this ILD/ITD value in the deactivated and recovery conditions. This analysis produced an estimate of the how well changes in ILD or ITD could be discriminated based on the spike rate output of IC neurons, and what effect removing CoIC input had on the discrimination threshold of each unit.

Figure 3.

The ITD and ILD values at half-maximum of most units were unchanged by deactivation. A, An example ILD unit (black circles) that increased its firing rate on deactivation (orange circles) before returning to near control levels on recovery (green triangles). B, To compare the position of the function in ITD or ILD space, the minimum firing rate in each condition was subtracted and the responses were then normalized. The slopes of the normalized ILD functions in A overlapped. The position of half-maximum firing rate was almost unchanged between conditions, as shown by the dashed lines. C, The location of half-maximum firing rates for ILD (solid lines) and ITD (dashed lines) units in the control condition varied across ILD/ITD space for the population (black line). The distribution of ITD units was constrained to the midline and contralateral hemifield, while ILD units spanned both positive and negative ILDs. The distribution of half-maximum firing rates on contralateral IC deactivation (orange line) and recovery (green line) were almost unchanged relative to control. D, Data for the individual units represented in (C) showing their half-maximal ILD or ITD values in the control and deactivated conditions. Most units were unchanged by deactivation. ILD units (black filled circles) showed greater variance about the line of identity than ITD units (blue open circles).

As the location of the minimum JND in the control condition was subject to the potentially noisy output of neurometric functions, we further analyzed these data by sorting the array of JNDs in each condition from minimum to maximum. We then found the upper quartile of JND values and then calculated their mean. These values were then compared between conditions in the same manner as the minimum JNDs. This produced a measure of how well each neuron encoded ILD/ITD over the sloping portion of its response function, rather than just at the steepest point.

Half-maximal firing rate analyses.

The position of the sloping portion of the ITD or ILD function on the ITD or ILD axis was also determined by deriving the stimulus value giving rise to half-maximal firing. The minimum firing rate in each response function was subtracted from the function and the function was then normalized to the maximum firing rate (Rees and Palmer, 1988). A vertical line dropped from the point on the normalized curve representing half-maximal firing was used to interpolate the corresponding ITD or ILD value that would give rise to the response.

Statistical analyses.

Nonparametric statistical tests have been used in all analyses performed in this study. All reported P values are exact and two tailed. A between groups comparison of the effects of cooling and MDP on firing rate was performed using a Mann–Whitney test. For paired analyses with three groups, we performed Friedman's repeated-measures ANOVA on ranks. Post hoc analyses were performed using two Wilcoxon signed-rank tests: one between the control group and the deactivated group, the other between the control group and the recovery group. The α was set to 3 σ: p = 0.0027 (Berger and Sellke, 1987; Colquhoun, 2014). For post hoc analyses the α was Šidák corrected. A one sample Wilcoxon signed-rank test was used to compare changes on deactivation re control to a hypothetical distribution with no change. All statistical tests were performed in MATLAB.

Results

Data were collected from 51 single units recorded in the right IC of 20 guinea pigs (12 cooling experiments and 8 MDP experiments); other data not reported here were also collected in these experiments. Thirty-seven units were studied with ILD stimuli, and 15 were studied with ITD stimuli; one unit was included in both groups as it was studied with both ITD and ILD stimuli. Thirty-two units were recorded throughout cooling deactivation of the left IC (Orton et al., 2012); the other 19 were recorded throughout deactivation of the left IC by MDP (Orton and Rees, 2014).

Cooling and MDP could produce reversible increases or decreases in firing rate

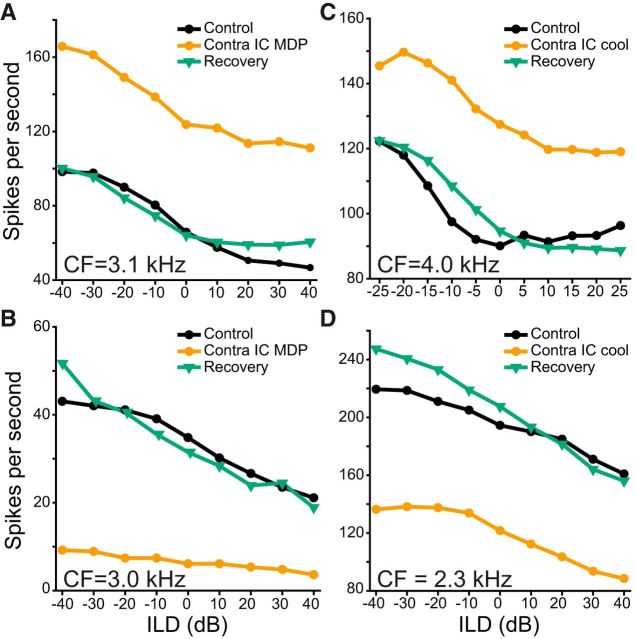
Both deactivation techniques applied to one IC caused large increases or decreases in the responses of some neurons in the other IC. Figure 1A shows a unit which increased its firing rate during MDP (Friedman test: χ²₍₂₎ = 26.96; p = 1.40 × 10⁻⁶; post hoc Wilcoxon signed-rank test control vs deactivated: Z = −3.62; p = 2.93 × 10⁻⁴) and recovered to control firing rate (control vs recovery: Z = −0.67; p = 0.501). MDP could also lead to a reduction in firing rate, as in in Figure 1B (χ²₍₂₎ = 13.56; p = 0.001; post hoc control vs deactivated: Z = −2.67; p = 0.004). The firing rate of this unit recovered after termination of contralateral deactivation (Z = 0.06; p = 0.977). Cooling increased the firing of the unit in Figure 1C (χ²₍₂₎ = 16.55; p = 3.0 × 10⁻⁴; post hoc control vs deactivated: Z = 2.93; p = 9.77 × 10⁻⁴) but decreased the firing rate of the unit in Figure 1D (χ²₍₂₎ = 14.0; p = 9.0 × 10⁻⁴; post hoc control vs deactivated: Z = −2.67; p = 0.004). Both of these changes reversed after cooling was stopped (Fig. 1C, post hoc: Z = 0.311; p = 0.781; Fig. 1D, post hoc: Z = 1.72; p = 0.098).

Figure 1.

Cooling or MDP could induce large, reversible increases or decreases in firing rate. A, Responses of an ILD-sensitive unit (black circles) which increased its firing rate during MDP (orange circles) and recovered after MDP was stopped (green triangles). B, Responses of a single unit for which MDP caused a reversible reduction in firing. C, Responses of a single unit for which cooling led to a reversible increase in firing. D, Responses of a single unit for which cooling caused a reversible decrease in firing. In this and remaining figures, ILD represents the sound level in the ear ipsilateral to the recorded IC, relative to that in the contralateral ear.

Median firing rate of the population was unchanged by deactivation

To analyze the magnitude and proportion of facilitatory and suppressive effects of contralateral IC deactivation on the population, we calculated an index of change for the median firing rate between the deactivated and control conditions (see Materials and Methods) for each interaural cue. The majority of units whose firing rate was modulated on deactivation decreased their firing rate (Fig. 2). This was true for unit responses to ILD (Fig. 2A) or ITD (Fig. 2B) stimuli. For ILD stimuli, where a similar number of units were recorded in response to cooling (Fig. 2A, black bars) and MDP (Fig. 2A, white bars), the distribution of changes in median firing rate was similar using either method (Mann–Whitney test: U₍₃₅₎ = 141; p = 0.37). We pooled median firing rates from both ITD and ILD responses from units in which recovery recordings were achieved. The distribution of median firing rates was similar in the control [median = 15.80 spikes/s; 99% confidence interval (CI) = 9.45–26.80], deactivated (median = 14.95; 99% CI = 7.45–23.50), and recovery (median = 14.80; 99% CI = 8.90–23.70) conditions (χ²₍₂₎ = 3.55; p = 0.17). Thus, although the median firing rate of some units changed, at the population level no trend was observed, indicating similar levels of net facilitatory and suppressive effects.

Figure 2.

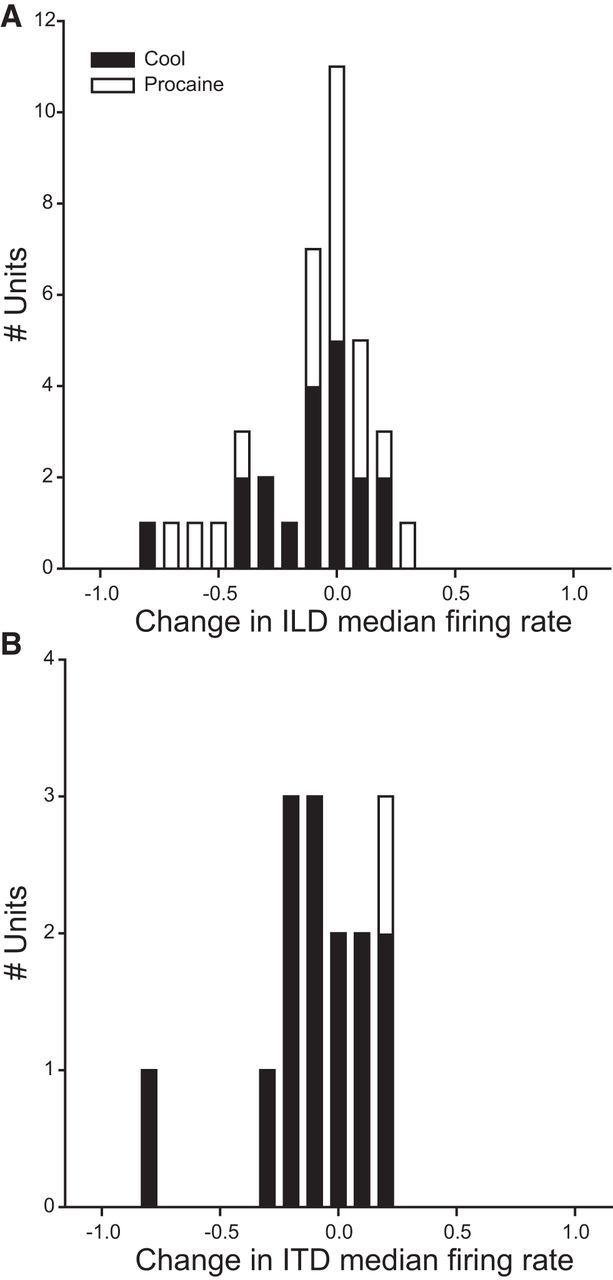
Index of change in median firing rate on contralateral IC deactivation. A, Index of change in median firing rates in ILD response functions. The distribution peaked at zero change. Similar changes were observed in response to cooling (black bars) and MDP (white bars). B, The majority of ITD units had a decreased median firing rate; however, this distribution was also centered close to zero change.

To ensure that an increase or decrease in firing rate at the population level was not obscured by the presence of units that showed no change in median firing rate on deactivation, we assessed the effect of deactivation on the population comprising only those units that changed firing rate on deactivation under strict criteria (p < 0.0027; Berger and Sellke, 1987; Colquhoun, 2014). In total, 34/52 units were determined to have changed firing rate by deactivation: 23/37 for ILD (12/19 cooling, 11/18 MDP) and 11/15 for ITD (10/14 cooling, 1/1 MDP). The median firing rate for these units in the control condition was 47.2 spikes/s. On deactivation, it was 40.6 spikes/s, whereas on recovery it was 39.2 spikes/s. As for the entire dataset, the variation in firing rates between conditions for this subpopulation did not follow any consistent pattern of change (Z = −1.84; p = 0.067). Thus, even for units whose firing rate was modulated by deactivation, there were similar degrees of net facilitation and suppression.

Positions of ITD and ILD functions in azimuthal space were unchanged by deactivation

In almost all units, we found little change in the position of the sloping portion of the response in ILD or ITD space. To quantify this we measured the half-maximal firing rate in ITD and ILD space for each condition. The half-maximum firing rates for ILD responses of an example unit are shown for each condition in Figure 3A. Derivation of the half-maximal position in each function for this unit showed that, while there was a reversible increase in firing rate, the position of the ILD response function in ILD space was unchanged throughout (Fig. 3B). For the population of units, ITD and ILD were assessed separately. Plotting the cumulative distributions of half-maximal ILD (Fig. 3C, solid lines) and ITD (Fig. 3C, dashed lines) populations of units showed no change. For some units the slight changes in position caused the sign of the ITD or ILD at half-maximum firing to change from negative to positive (or vice versa). To account for this we analyzed these data with a two-sample Wilcoxon signed-rank test. The distribution of ILD (Z = 0.84; p = 0.41) and ITD (Z = −1.02; p = 0.33) half-maximum firing rates did not change between control and deactivated conditions. Figure 3D shows the individual unit data of all units in Figure 3C. The spread of values for ILD units (Fig. 3D, black filled circles) from the line of unity was greater than for ITD units (Fig. 3D, blue open circles). We found 29/37 ILD units changed by <10 dB during deactivation, whereas 14/15 ILD units changed by <20 μs, suggesting that that the contralateral IC exerts little influence on the position of interaural functions in azimuthal space.

Gain functions show divisive and additive changes

To describe and quantify the impact of removing CoIC input on the representation of ITDs and ILDs we constructed gain functions for each unit by plotting the change in firing rate during deactivation and recovery against the control firing rate (see Materials and Methods). Figure 4A shows data from an ILD-sensitive unit for the three stages of experimental manipulation. During deactivation, there was a reduction in firing rate and the slope of the ILD function decreased (Fig. 4A, orange circles). On recovery, the firing rate approached control levels (Fig. 4A, green triangles). The gain functions for this unit are shown in Figure 4B. The change in firing on deactivation (Fig. 4B, orange circles) was well described by the linear regression (r² = 0.99). This regression had a divisive gain change (slope = 0.60) and an additive shift (intercept = 22.1 spikes/s) on deactivation. The gain function on recovery was similar to the control condition (slope = 0.96; intercept = −0.61 spikes/s, r² = 0.93).

We calculated the multiplicative/divisive gain change and the additive/subtractive shifts during deactivation for all units by plotting the intercept of each linear regression as a function of the slope (Fig. 4C). The variances of five of the 37 ILD units were not well described by the linear regression (r² < 0.20) and were excluded from this analysis. For ILD units the intercept and slope were not correlated (Spearman's rank correlation: r₍₂₉₎ = −0.008; p = 0.96). The linear regressions of the majority of units (21/32) displayed a combination of divisive gain change and additive shifts during deactivation. The median slope was 0.69 (99% CI = 0.52–0.82) and the median intercept was 5.25 spikes/s (99% CI = 0.30–24.66). To estimate the reliability of this measure, we used bootstrap resampling to investigate each unit's slope and intercept statistically (see Materials and Methods). For ILD units, the intercept value of 0 and the slope value of 1 (which represent the respective null hypotheses) fell outside the 95% confidence intervals of their respective bootstrapped distributions for 11/32 and 16/32 units, respectively.

The 15 ITD units showed a similar trend to that seen for ILD units (Fig. 4D) with the majority (13/15) exhibiting divisive and additive changes on deactivation. The median slope for these units was 0.63 (99% CI = 0.26–0.84) and the median intercept was 39.96 spikes/s (99% CI = 10.53–72.53). Bootstrap resampling of the intercepts and slopes of the gain functions in the deactivated condition for ITD units, shows that the intercept value of 0 and the slope value of 1 fell outside the 95% CI of their respective bootstrapped distributions for 10/15 and 12/15 units, respectively.

The median and 99% confidence intervals were confined within the quadrant representing divisive and additive gain change for units studied with either method of deactivation (Figs. 4C,D). The median slope of the total population of ITD and ILD-sensitive units was 0.67 (99% CI = 0.53–0.87). The distribution of this population was centered below a hypothetical distribution with a median of 1, demonstrating that deactivating the contralateral IC caused a divisive gain change (Z = −4.32; p = 1.54 × 10⁻⁵). The median intercept was 7.98 (99% CI = 4.48–45.46), greater than that of a hypothetical distribution with a median of 0 (Z = 4.57; p = 4.82 × 10⁻⁶), demonstrating additive shifts in the population. Thus, the main effects of removing intercollicular input on the population of IC neurons were an additive shift and divisive gain change.

One possible explanation for the gain changes we observed may be that the responses in the control condition were at the steepest point of the contralateral rate-level function, and any change from that position on deactivation would lead to a reduction in gain. Although we did not specifically select the steepest point of the contralateral rate-level function for the stimulus level, we have used the available data to investigate this possibility. We limited the number of stimuli presented in each condition to maximize the probability of obtaining full recovery; therefore, our dataset contained only eight ILD units for which contralateral rate-level functions were measured throughout recovery. For these units, neither contralateral rate threshold (r₍₈₎ = −0.50; p = 0.18), nor half-maximum firing rate (r₍₈₎ = −0.38; p = 0.32) were correlated with gain change. To assess how robust changes in gain were to the choice of contralateral fixed level, we analyzed the five units in our dataset that were presented with ILDs at fixed contralateral levels 20 dB above and below the one used in our population data. A decrease in gain occurred for all but one of these 15 stimulus levels, demonstrating that the changes in gain we observed were consistent and robust at different contralateral levels.

The response dynamic range of ITD and ILD units reversibly decreased

Divisive gain changes are consistent with a reduction in the spiking dynamic range of ITD or ILD functions during deactivation. Figure 5A shows the responses of an ILD-sensitive unit in which there was a reversible reduction in firing rate on deactivation. Figure 5B shows the response of this unit after subtraction of the minimum firing rate and highlights the reduction of the spiking dynamic range on deactivation of the contralateral IC. This trend was consistent across the majority of units in our sample (Fig. 5C,D). With a criterion index of change ±0.1, we found that the responses of 19/37 units tested with ILD fell below this criterion, whereas just 4/37 increased. For ITD responses, the dynamic ranges of 9/15 units fell by more than the criterion, and one increased.

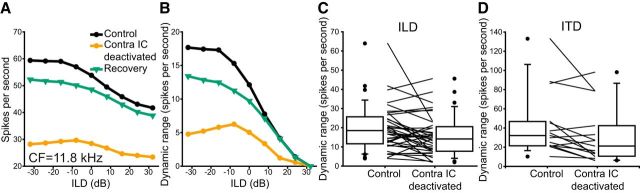
Figure 5.

Divisive gain change reduced the dynamic range of ITD and ILD response functions. A, An example single unit that was ILD-sensitive in the control condition (black circles). Deactivation of the contralateral IC suppressed firing (orange circles). Firing rate recovered to near control levels on cessation of deactivation (green triangles). B, Subtraction of the minimum firing rate in each condition showed that the dynamic spiking range over which ILD was encoded was reversibly reduced by deactivation. C, The dynamic ranges of the populations of ILD units and (D) ITD units were reduced by deactivation.

The change in dynamic range for pooled ITD and ILD responses was less than a hypothetical distribution with a median of 0 (median = −0.11; 99% CI = −0.22 to −0.01; Z = −3.73; 1.89 × 10⁻⁴). This reduction in dynamic range led us to hypothesize that blocking intercollicular connections reduced the ability of IC neurons to discriminate changes in ITD or ILD by changes in firing rate.

Discriminability of ITDs and ILDs in IC is improved by intercollicular interaction

To assess whether intercollicular interactions improved the discriminability of sound localization cues in our sample, we performed ROC analyses (see Materials and Methods). To illustrate this method, we took each ITD or ILD response function, such as the ILD function in Figure 6A, determined the number of spikes elicited to each stimulus presentation and plotted the distribution of these responses (Fig. 6B). For each ILD value, we plotted the frequency distribution of the number of spikes per stimulus (Fig. 6C). These data were used to perform an ROC analysis using each point in the ITD or ILD as a reference, with all responses to all other stimuli in that function designated as targets. For example, the responses to an ILD of 25 dB were used as a reference to compare the responses at other ILDs (Fig. 6D). These data were used to construct neurometric functions at each ILD or ITD value. The data in Figure 6D were used to construct the neurometric function shown in Figure 6E, using 25 dB ILD as the reference. From this, we calculated the distance from the reference ILD to the ILD value that intersected the neurometric function at 0.75 or 0.25—equivalent to the minimum ILD required to distinguish the spatial location of two pure tones at least half the time in a two alternative forced choice task (Fig. 6E). For this reference ILD, the JND was 12.73 dB. The JND at each ILD (or ITD where appropriate) in each response function was plotted and the minimum JND in the control condition was derived (Fig. 6F). For the ILD responses of this unit, the minimum JND was 8.66 dB located at +10 dB ILD. The minimum JND was then compared at this ILD between experimental conditions.

Figure 6.

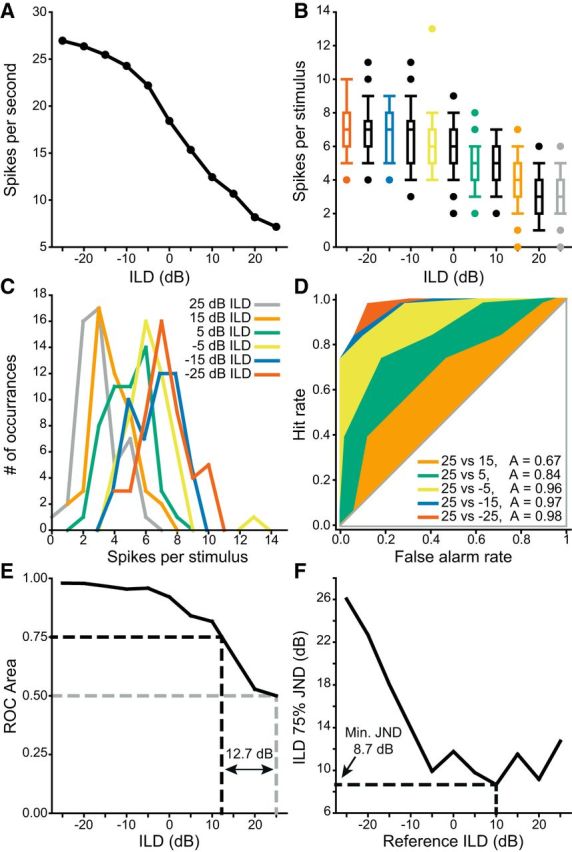
Illustration of the ROC analysis used to find the minimum JND. A, An example ILD-sensitive unit. B, Replotting this unit as the distribution of spikes fired per stimulus shows the variance is similar across all responses. C, Representing the responses of every other ILD value as histograms shows that the overlap in the responses decreased as a function of increasing separation of ILD. D, ROC analysis using the +25 dB ILD (gray) responses in B, C as a reference with each of the other colored examples as a target. As ILD separation between the reference and the target increased, the distributions of firing rates overlapped less and the ROC area thus increased from 0.5 toward 1. E, Neurometric function formed from the output of the analyses in D. JND was defined as the distance from reference ILD where the neurometric function intersected with 0.75 (or 0.25). For this example the JND at +25 dB ILD was 12.73 dB. F, JND as a function of all ILDs for this unit. The minimum JND was 8.7 dB at +10 dB ILD.

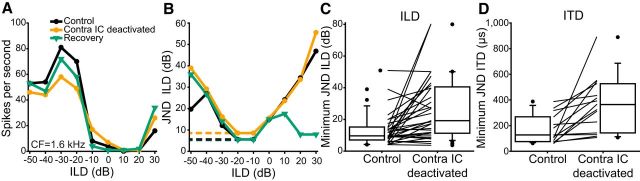
The implementation of this method is illustrated for an example unit in Figure 7. An ILD-sensitive unit was recorded in the control condition (Fig. 7A, black line). On deactivation, the maximum firing rate decreased and the dynamic range consequently decreased (Fig. 7A orange line). On recovery, these changes reversed (Fig. 7A, green line). The minimum JND in the control condition was 4.38 dB using −20 dB ILD as a reference (Fig. 7B, black line). The reduction in dynamic range and concomitant decrease in slope between ILDs caused the JNDs to increase on deactivation (Fig. 7B, orange line) giving a minimum JND of 8.44 dB. On recovery, the distribution of JNDs returned to near control levels (Fig. 7B, green line) and the minimum JND decreased to 5.25 dB at −20 dB ILD.

Figure 7.

The minimum JND increased for the population of both ITD and ILD units. A, An example ILD-sensitive unit (black circles) that reduced in dynamic range on deactivation (orange circles) and recovered (green triangles). B, The minimum JND in the control condition was found next to the steepest slope in the ILD response function in each condition. In the control condition, the JND was 4.38 dB. Deactivation of the contralateral IC caused the JND at the same ILD to increase to 8.44 dB. On recovery, the JND at this ILD decreased to 5.25 dB. C, The minimum JND of the population of ILD units was increased by contralateral IC deactivation. D, The distribution of minimum JND in the deactivated condition was also higher than in the control condition for ITD units.

We conducted this analysis for all units in our dataset. A similar pattern was observed for both ITD and ILD responses. (4/37 ILD units did not discriminate ILDs <50 dB and were therefore excluded from further analysis.) Of the 33 ILD-sensitive units included for analysis, the minimum discrimination threshold of 27 units increased during deactivation (Fig. 7C). The minimum discrimination threshold of all 15 ITD units increased during deactivation (Fig. 7D). We pooled these units and calculated the Index of Change in sound localization discriminability for all units. The trend toward an increase in minimum discrimination threshold was shown by the index of change, which had a median of 0.27 (99% CI = 0.14–0.48). This effect on the population demonstrates that commissural gain control enhances the ability of IC neurons to discriminate changes in sound location through changes in their spike-rate response functions (one-sample Wilcoxon signed-rank tests against a hypothetical population with a median of 0: Z = 5.40, p = 6.55 × 10⁻⁸).

Although this method is highly sensitive to changes in JND, neurometric functions can be noisy. To assess the influence of our experimental protocol on the response of each unit across a range of ILDs or ITDs we found the mean of the top quartile (most sensitive) of JNDs for each unit in each condition, regardless of their ILD or ITD, and compared these values between conditions for the population of units. For ILD, the median of the averaged upper quartile of JNDs in the control condition was 12.3 dB (IQR = 9.1–19.7). This increased in the deactivated condition to 20.0 dB (IQR = 8.4–41.9). A signed ranks test showed that this change was likely to be a real effect (Z = 2.1, p = 0.038). Recovery values returned toward control values with the median being 17.7 dB (IQR = 10.3–32.1). A signed-rank test between control and recovery values demonstrated the partial recovery of the ILD population (Z = 2.6; p = 0.011).

For ITD, the median of the averaged upper quartile of JNDs in the control condition was 137 μs (IQR = 101–197). This increased in the deactivated condition to 323 μs (IQR = 188–389). A signed-rank test showed that this change was also likely to be a real effect (Z = 2.9; p = 0.002). The recovery values also tended to return toward control values with the median being 178 μs (IQR = 131–230). A signed-rank test between control and recovery values demonstrated the partial recovery of the ITD population (Z = 2.1; p = 0.032).

These data show that the effect of removing CoIC input was to reduce the precision with which IC neurons encode JND.

Discussion

Our main findings are first, that ITD and ILD responses of most IC neurons are influenced by intercollicular interactions. Second, for the majority of IC neurons, intercollicular modulation of ITD or ILD manifests as divisive gain changes accompanied by additive shifts (Fig. 4C,D), implying that when intact, commissural influences produce multiplicative gain changes and subtractive shifts. Third, divisive gain changes produced by deactivation of commissural input reduces the ability of IC neurons to represent changes in ITD or ILD by changes in firing rate (Fig. 7C,D). This suggests that CoIC input improves the discriminability of azimuthal sound location in the IC. Finally, similar effects on both ITD and ILD responses suggest a general mechanism of multiplicative gain control between the IC that generates a congruent representation of interaural cues in the IC.

We observed divisive gain change and additive shifts in 74% (34/46) of ILD and ITD responses. The effect was larger and more prevalent for ITD (Fig. 4D) than ILD (Fig. 4C) -sensitive units. We have demonstrated that cooling is effective in dorsal, low-frequency regions of IC (Orton et al., 2012). As the CoIC is organized tonotopically (Saldaña and Merchán, 1992; Malmierca et al., 1995, 2009), one would expect the largest effect of deactivation to be in dorsal, low-frequency regions where ITD-sensitive units are most abundant (Fig. 2B; McAlpine et al., 1996). The similar effects seen in our sample of ILD-sensitive units with cooling or MDP (Figs. 1, 2A) demonstrate these effects were because of attenuation reduction of intercollicular input.

Technical limitations

Other methods of determining ILD thresholds have been reported (Tollin et al., 2008) using the standard separation metric (Sakitt, 1973). We attempted to replicate these methods; however, due to the heterogeneity of IC responses, many were not described by sigmoidal functions. We therefore used ROC analysis that is independent of model fitting.

To capture minimum discrimination thresholds using ROC analysis, stimulus increments need to be small (Shackleton et al., 2003). To minimize recording time, we did not present stimuli with sufficiently fine resolution to estimate each neuron's true minimum JND. Therefore, the JNDs we report may underestimate the best performance of IC neurons. However, although the minimum ROC threshold may be underestimated, this limitation is identical in each condition, making comparison between conditions valid.

Experiments were performed under urethane anesthesia, which might modify the balance of excitation and inhibition, particularly in auditory cortex which projects extensively to the IC. Evidence suggests that neural discrimination in the auditory midbrain is not altered by urethane (Schumacher et al., 2011), but we cannot discount possible differences between the anesthetized and awake state.

Functional significance

The ICs are the first structures where all three sound localization cues, ITDs, ILDs, and pinna cues, converge (Palmer and Kuwada, 2005; Grothe et al., 2010). Studies on ILD encoding in the midbrain are consistent with a model in which each IC is dominated by sounds in the contralateral hemifield and responses change inversely between the ICs as a sound moves in azimuth. In such a model, if each IC operates independently, changes in response due to a change in sound position might not be distinguishable from a change in sound level. Comparing the activity profiles between the ICs, however, could disambiguate the two: for shifts in position, firing rate changes would be opposite, whereas with changes in level, they would be correlated. The mechanisms of ITD coding remain controversial (see discussions in Goodman et al., 2013 and Franken et al., 2015), but nevertheless interactions between the ICs could provide additional information to enhance the representation of sound source location.

Unilateral IC lesions produce deficits in azimuthal localization mainly in the hemifield contralateral to the lesion in cat (Jenkins and Masterton, 1982), ferret (Kelly and Kavanagh, 1994) and human (Litovsky et al., 2002). The absence of major deficits in the hemifield ipsilateral to the lesion might be taken to indicate the ICs operate independently in this regard, but some indications of ipsilateral deficits are apparent and the nature of the stimuli and limited testing conditions may be factors that influence the degree of interaction between the ICs.

Some reports suggest ILD responses are generated de novo at the level of the midbrain (Li and Kelly, 1992; Park and Pollak, 1994; Burger and Pollak, 2001). CoIC projections may contribute to this process, with ipsilateral excitation to one IC originating from excitatory CoIC neurons in the other (Li and Pollak, 2013). We found little evidence for this in our dataset. One unit (Fig. 7A) exhibited facilitation in all conditions. However, this facilitation was reduced during deactivation, suggesting the CoIC contributed to this response. No other units in our dataset showed such facilitation, suggesting it is not a common property of ILD units.

The CoIC mediates both facilitatory and suppressive effects on IC responses to sound. This was first demonstrated by chemical deactivation of the IC in rat (Malmierca et al., 2003, 2005) and subsequently elaborated using cooling and MDP in guinea pig (Orton et al., 2012; Orton and Rees, 2014). The heterogeneity of effects observed also concurs with previous work in vitro, where electrical stimulation of the CoIC in IC slices produces both monosynaptic and polysynaptic inhibition, and monosynaptic excitation in rat (Smith, 1992; Li et al., 1999) and gerbil (Moore et al., 1998). These effects are consistent with studies showing between 10 and 20% of CoIC neurons in rat (González-Hernández et al., 1996; Hernández et al., 2006) and guinea pig (Nakamoto et al., 2013) IC are GABAergic.

The auditory pathway must process and encode information representing stimulus parameters over several orders of magnitude. A mechanism used by neural systems for this task is gain control (Silver, 2010). Gain control has been observed at each stage of the auditory pathway, from the periphery (Wen et al., 2009) to cortex (Phillips and Hall, 1986). In the IC, gain control aids the representation of sound level (Rees and Palmer, 1988; Dean et al., 2005), stimulus-specific adaptation (Pérez-González et al., 2012), frequency modulation (Gittelman et al., 2012), ITDs (Ingham and McAlpine, 2005), and ILDs (Xiong et al., 2013). A contributing factor to gain control in the IC is the action of local inhibition (LeBeau et al., 2001).

Gain control has been postulated as a mechanism by which the CoIC could influence auditory processing (Malmierca et al., 2003, 2005; Ono and Oliver, 2014). We found that the discriminability of azimuthal sound location cues in the IC is diminished on blockade of intercollicular processing. This influence manifests as multiplicative gain change (Fig. 4), but does not alter the position of ITD or ILD response functions in auditory space (Fig. 3), which is dependent on processing in the superior olive (Li and Pollak, 2013). Although our experiments demonstrate the CoIC enhances the discriminability of sound location cues in the midbrain, we cannot distinguish whether it leads to their absolute enhancement, or whether it maintains the representation it receives from the brainstem in the face of other factors.

Each IC provides additional information to the other about the azimuthal location of sound sources. The divisive gain changes we observed resulted in a reduction in response dynamic range in ILDs (Fig. 5C) and ITDs (Fig. 5D). This reduction in dynamic range diminished the ability of the population of IC neurons to signal changes in sound position due to a change in ILD (Fig. 7C) or ITD (Fig. 7D). Multiplicative gain control exerted via the CoIC increases the dynamic range of neural outputs and so may lead to improved discrimination under different listening conditions, such as in background noise.

Modifying the balance of inhibition and excitation can induce changes in gain (Chance et al., 2002). Multiplicative gain control could be produced by excitation or inhibition alone or in combination (Murphy and Miller, 2003), or via synaptic depression (Rothman et al., 2009). In the current data, we cannot determine the contribution that excitation or inhibition makes to gain control, but both are likely important.

The additive shifts observed in ITD or ILD response functions of many units during deactivation (Fig. 4) indicate that the CoIC mediates subtractive shifts in the ITD and ILD response functions, possibly due to a reduction in inhibition (Holt and Koch, 1997). Subtractive shifts can increase spike selectivity by removing spontaneous activity (Gittelman et al., 2012), thus reducing noise entropy, as less bandwidth is occupied by spikes at null responses. Such changes may increase the information content of the response (Dayan and Abbott, 2001; Bale and Petersen, 2009), and reduce the energy required to encode ITDs and ILDs (Attwell and Laughlin, 2001).

In conclusion, our data show that the representation of binaural cues, first extracted in the superior olive, are not simply directed upward through the bilateral limbs of the brainstem pathways, but are further influenced by sideward connections that are important for the representation of ITDs and ILDs. By enabling the ICs to act in concert, rather than independently, the gain control mediated by the CoIC enhances the discriminability of azimuthal cues in the midbrain.