Abstract
Spatial variation in biodiversity is the result of complex interactions between evolutionary history and ecological factors. Methods in historical biogeography combine phylogenetic information with current species locations to infer the evolutionary history of a clade through space and time. A major limitation of most methods for historical biogeographic inference is the requirement of single locations for terminal lineages, reducing contemporary species geographical ranges to a point in two-dimensional space. In reality, geographic ranges usually show complex geographic patterns, irregular shapes, or discontinuities. In this article, we describe a method for phylogeographic analysis using polygonal species geographic ranges of arbitrary complexity. By integrating the geographic diversification process across species ranges, we provide a method to infer the geographic location of ancestors in a Bayesian framework. By modeling migration conditioned on a phylogenetic tree, this approach permits reconstructing the geographic location of ancestors through time. We apply this new method to the diversification of two neotropical bird genera, Trumpeters (Psophia) and Cinclodes ovenbirds. We demonstrate the usefulness of our method (called rase) in phylogeographic reconstruction of species ancestral locations and contrast our results with previous methods that compel researchers to reduce the distribution of species to one point in space. We discuss model extensions to enable a more general, spatially explicit framework for historical biogeographic analysis.
Keywords: Bayesian inference, continuous trait evolution, diversification, historical biogeography, phylogeography, species distributions
Understanding the mechanisms that drive spatial variation in biodiversity is one of the main goals in evolutionary biology. Ultimately, two distinct processes give rise to differences between species-rich and depauperate regions: diversification (the net outcome of species origination and loss) and migration (Wiens and Donoghue 2004; Ricklefs 2007). In turn, these processes are likely influenced by contrasting temporal and spatial dynamics, making it crucial to consider both when assaying the causes of biodiversity. For instance, relevant ecological processes such as facilitation and competitive exclusion can largely determine migration rates among regions (Wiens and Donoghue 2004). Still, inferring the evolutionary history of most lineages remains a challenge. The fossil record can be a powerful tool for geographic localization of ancestral species, but its incompleteness hinders its application to most clades and regions (Silver and Schultz 1982; Jablonski et al. 2006). Instead, phylogenetic inference has become the main tool to analyze processes and patterns in evolutionary history.
Historical biogeographic methods are based on the premise that combining a lineage's phylogenetic and spatial information can reveal a richer picture of evolutionary history (Lemmon and Lemmon 2008; Bloomquist et al. 2010; Lemey et al. 2010). Specifically, historical biogeography combines the current geographic location of species with evolutionary relationships to infer their evolutionary history through space and time (Ronquist and Sanmartín 2011). In recent years, model-based methods that estimate parameters using maximum likelihood or Bayesian estimation of posterior distributions by Markov Chain Monte Carlo (MCMC) have been favored over non-model-based approaches (Beaumont et al. 2010; Bloomquist et al. 2010). These parametric methods treat geographic range data either as discrete (Ree et al. 2005; Ree and Smith 2008; Landis et al. 2013) or as continuous variables (Lemmon and Lemmon 2008; Lemey et al. 2010; Nylinder et al. 2014). Although dividing geographical space into discrete domains allows efficient computation of likelihoods, enables tractable feedback between diversification and range dynamics, and may be appropriate for analyses of inherently discrete regions (e.g., islands), most geographical distributions cannot be easily categorized into discrete bins (Ree et al. 2005; Ree and Smith 2008; Goldberg et al. 2011; Landis et al. 2013). In contrast, continuous historical biogeographic methods do not need an a priori geographic discretization (Lemmon and Lemmon 2008). These methods typically model migration as a continuous spatial diffusion or random walk process over evolutionary timescales (Avise et al. 1987; Neigel et al. 1991) and, when a speciation event occurs, the daughter species inherit their ancestor's spatial location and subsequently diffuse independently (Lemmon and Lemmon 2008; Lemey et al. 2010).
Continuous methods in phylogeography and historical biogeography have seen significant advancement in recent years with the development of more computationally efficient and robust methods (Lemmon and Lemmon 2008; Lemey et al. 2010; Bielejec et al. 2011; Bartoszek et al. 2012; Nylinder et al. 2014). However, these methods are limited by the need to specify a single geographic location for each taxon, despite the fact that species ranges can be large, spatially diffuse, or irregularly shaped (Camargo et al. 2013; Nylinder et al. 2014). Lemey et al. (2010, p. 1884) acknowledge:
We have, for example, not taken into account the geographical uncertainty […] and only considered the centroid of the county as location point estimates. To achieve more realism, tip locations could be integrated across geographical regions, which would also be of particular interest for speciation studies to incorporate species ranges.
Indeed, use of point estimates instead of bounded continuous domains has been a limitation not only for phylogeography and historical biogeography, but for all phylogenetic inference using continuous-valued traits or characters (Martins and Hansen 1997; Garamszegi 2014).
In this article, we develop a statistical method for inference of the geographic location of ancestors, given contemporary species geographic ranges and a phylogenetic tree. We take the standard Brownian motion (BM) model as the generative process for spatial diffusion, but instead of constraining contemporary species locations to a single point, we allow specification of polygons of arbitrary complexity at the tips. Our method is a significant improvement over recently proposed approaches (i.e., Bouckaert et al. 2012; Nylinder et al. 2014), namely: (i) it integrates the likelihood over the relevant range, bypassing the need for data augmentation in the tips, (ii) it dramatically increases computational efficiency enabling extension to more complex models, (iii) it eliminates error associated with Monte Carlo approximation of the polygonal likelihood, (iv) it is not limited to phylogeography and historical biogeography, generalizing previous methods for ancestral state estimation under Brownian motion. Moreover, we provide a rigorous description of our model, and make explicit its assumptions. We validate the method using simulated data, and demonstrate the technique for the diversification of the bird genus Psophia (Trumpeters) in the Amazon and Cinclodes (a genus of ovenbirds) in South America as empirical examples. Finally, we empirically demonstrate that taking into account species geographic ranges can substantially affect the estimates for ancestral states and rates of evolution.
Background
Given a model of species migration, the statistical problem of inferring the geographic location of ancestral species is equivalent to ancestral character estimation on a phylogeny (Schluter et al. 1997), where species location is treated as an evolutionary character (Lemmon and Lemmon 2008; Lemey et al. 2010). Homogeneous diffusion (Brownian motion) is a flexible, simple, and analytically tractable model for species migration over evolutionary timescales (Felsenstein 1985; Lemey et al. 2010). Despite the simplicity of the BM model, empirical observations of range expansion of invasive species may often be consistent with its use in phylogeographic reconstruction (Andow et al. 1990). A lineage evolving under BM behaves as an individual particle moving randomly on a plane. Specifically, under univariate BM, the trait change from ancestral value after some time follows a normal distribution with mean and variance , where is a constant evolutionary rate (Felsenstein 1985; Butler and King 2004). If is the starting value, then the value evolving under BM with constant rate after time has a normal probability density (Felsenstein 1985; Schluter et al. 1997; Revell et al. 2008):
| (1) |
In continuous historical biogeography, two-dimensional (longitudinal/latitudinal) processes follow a bivariate BM, where a value of a bivariate BM process beginning at and evolving for time has a bivariate normal probability density
| (2) |
where the symmetric Brownian covariance matrix is
The longitudinal and latitudinal processes can be independent (i.e., when the off-diagonal elements of are zero) or correlated (Lemey et al. 2010). If independent, the likelihood function of a BM diffusion process given a phylogeny is the product of each of the one-dimensional processes.
Currently available comparative methods that model continuous trait evolution (Paradis et al. 2004; Drummond and Rambaut 2007; Harmon et al. 2008; Lemey et al. 2010; Butler and King 2004; Garamszegi 2014) compel researchers to reduce the natural range of trait values for each tip into one value (usually the midpoint). Specifically, in continuous phylogeographic inference, the geographic distributions of taxa are reduced to latitudinal and longitudinal centroids (Blackburn and Measey 2009; Bloomquist et al. 2010; Lemey et al. 2010; Rebernig et al. 2010; Escobar García et al. 2012; Lynch Alfaro et al. 2012; Surget-Groba and Thorpe 2013), which are then treated as the outcomes (“traits”) that have evolved through a BM process.
Polygonal Domains Instead of Points
Here, we develop a general model that permits analyses of historical biogeography using geographic ranges in their entirety instead of points. We are aware of only two studies that attempted this (Bouckaert et al. 2012; Nylinder et al. 2014), but the algorithms used there randomly sampled points inside polygons within the MCMC sampling procedure to approximate the likelihood. In contrast, here we use a numerical method to compute the likelihood exactly, bypassing the need for data augmentation of tip states and obviating costly simulation. In the Online Appendix in the Supplementary Material (available on Dryad at http://dx.doi.org/10.5061/dryad.16nt8), we demonstrate why using Monte Carlo techniques to approximate the true likelihood over a polygon is computationally inefficient and less precise than exact integration over the polygon.
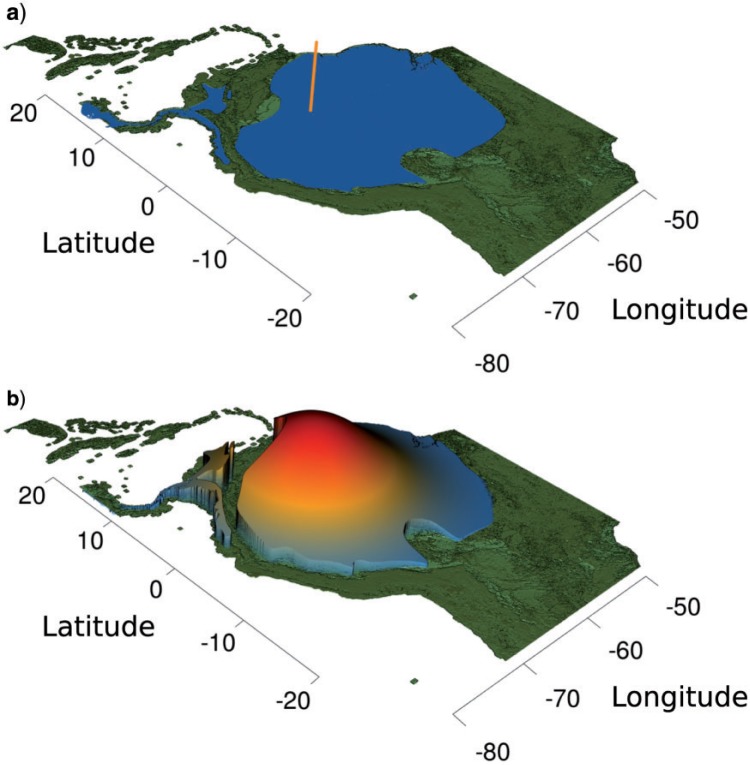
Our likelihood function for the ancestors of interior branches (branches that do not connect directly with tips) is identical to Equation (2), but the likelihood function for terminal branches (branches connecting an ancestor node with a tip) is modified to incorporate polygonal domains instead of single values (e.g., midpoints). The latter likelihood function constrains the BM process on terminal branches to end within the tip domains. This is achieved by integrating the BM likelihood over the polygonal domain (Fig. 1).
Figure 1.
Illustration of two different interpretations of species ranges in phylogeographic analyses. a) To date, continuous phylogeographic methods limit researchers to using only the midpoint of a species range (homogeneously colored polygon), disregarding its two-dimensional nature and irregular shape. b) The approach proposed here, implemented through the rase algorithm, uses the whole species range to estimate ancestral states. The multivariate normal density function over the polygon corresponds to the probability density of species location, where the species is constrained to lie within the blue shape, conditional on the location of an ancestor. Integrating over this density gives the likelihood.
We use a particle-based viewpoint to interpret estimates of ancestral location using polygonal domains under BM. As stated above, BM is a continuous stochastic process describing the random diffusion of particles across some -dimensional space. When modeling over a fixed phylogenetic tree, one initial particle (the common ancestor) diffuses through space at some dispersal rate until a branching event, where it instantly becomes two independent particles that start at the same location. Subsequently, these particles diffuse independently thereafter. When the current position of each species is represented as one spatial point in continuous phylogeography, the model handles each species as the independent history of a single particle (Fig. 2a). In this new approach, integrating over the whole geographic range, we aim at jointly inferring the history of the entirety of particles that make up the geographic range of a species (Fig. 2b). That is, we are jointly estimating all the histories of the infinitesimal number of diffusing particles that result, upon observation, within the species polygonal domain (Fig. 2b).
Figure 2.

Representation of diffusing particles through space and time according to BM. a) Hitherto, continuous phylogeographic methods model the most probable diffusing path of a particle observed at a point in space, given common ancestry with another particle. b) Our model integrates all diffusing particles ending within the polygonal domains assuming they are normally distributed.
To illustrate, let be a species geographical range represented as one or more non-self-intersecting polygons (the domain), each with vertices where the last edge encloses the polygon. For clarity, if the domain is described by more than one polygon, there are several edges within that enclose more than one polygon. Suppose an ancestral species separated by time from its next descendant has a value . For any particular point , the likelihood of observing the descendant species with value is given by (Equation (2)). To find the likelihood for a descendant species in domain that has an ancestral species with value a, we must integrate over and divide by the area of ,
| (3) |
where is the area of . When is a single polygon, this is given by
| (4) |
Computing Equation (3) over arbitrary domains can pose analytic and numerical difficulties. However, when is composed of one or more polygons, we can take advantage of two principles: first, any polygon can be decomposed into a set of disjoint triangles, and efficient software exists to perform this operation (e.g., tristrip from R package gpclib; (Murta 2013)). Second, numerical integration of bivariate Gaussian functions over triangular domains is stable and robust (Abramowitz and Stegun 1964), implemented in the polyCub package for R (Meyer and Held 2014).
A further simplification of Equation (3) arises when is a rectangle and migration rates are independent,
Then the likelihood factorizes as
| (5) |
where and are the lower horizontal and vertical boundaries of the rectangle, and and are the upper horizontal and vertical boundaries. We note that the diffusion process described above also occurs on a plane and not on the surface of a sphere. In our applications below we use an equal-area projection, with less distortion on distances than, say, the Mercator projection. However, modeling the diffusion of particles over a sphere can be extended in future work with a recently proposed approach (Bouckaert 2015).
A final simplification worth mentioning is when the trait under consideration is one-dimensional. Here, is a one-dimensional domain (i.e., , is reduced to , and the likelihood simplifies to
| (6) |
Efficient and accurate methods for numerically computing definite integrals of the univariate Gaussian density are available (e.g., pnorm in R). This is particularly useful when analyzing evolution of characters that are described by a range; including species niche axes (e.g., physiological tolerance range), intra-tip variation, and measurement error, among others (see section “Discussion”).
Inference Algorithm for Ancestral Species Locations Using a Phylogenetic Tree
First, we establish some notation to ease exposition. Consider a fixed, binary phylogenetic tree with tips and hence internal nodes corresponding to ancestral taxa as the one represented in Figure 3. Let be the trait values of the daughter nodes of a particular internal node , and let denote the trait value of the ancestor of . If is the most recent common ancestor (MRCA) of all taxa, let be the empty set . We observe domains at the tips of the tree and we wish to estimate the ancestral values and variance terms under a bivariate BM process with covariance matrix . Let be a prior distribution for the location of the MRCA in the tree. In the next section, we present a MCMC algorithm for sampling from the joint posterior distribution of the ancestral node value and the Brownian variance parameters .
Figure 3.
Illustration of the four different conditional likelihoods used by the MCMC sampling of the rase algorithm following the notation in the main text. Conditional likelihood for BM using points is represented as (•) while conditional likelihood that requires integration over a bounded domain is represented by (R | •). On each panel, the posterior density is being evaluated at ancestor x (marked with a black dot). a) When x is connected by internal branches only (, and ) and is not the MRCA, its conditional distribution depends on regular point BM with its ancestor a and daughters d1 and d2. b) When x is connected with two terminal branches and and one internal branch , its conditional distribution depends on the integration of the bounded domains and , and regular BM with its ancestor a. c) When x is connected with two internal branches and and one terminal branch , its conditional distribution depends on the integration of the bounded domain and regular BM process with d2 and a. d) When x is the MRCA, its conditional distribution depends on its prior (x), and regular BM process with d1 and d2.
MCMC Sampling of the Internal Node Values
Consider a particular internal node in the tree whose value we would like to sample, conditional on all other values in the tree. Let be the value of the ancestor of , and let and be the values of the daughter species , which may be either a domain or a point. Suppose the branch connecting the ancestor and the node of interest has length and the branches connecting the node to and have lengths and , respectively. To sample the value conditional on , , and , we consider four cases, illustrated in Figure 3:
(I) If both daughter species are internal nodes, then and are points (Fig. 3). The conditional density of , given , , and is:
| (7) |
where is given by Equation (2) and we have suppressed dependence of on , ,, and for clarity. To sample the bivariate value of the current node, conditional on , , and their respective branch lengths and , the ancestral value and associated branch length , we draw from the product density, which also has the Gaussian form:
| (8) |
where the mean is a weighted average of the adjacent node values:
| (9) |
and the variance–covariance matrix is scaled as follows:
| (10) |
In this case, exact Gibbs sampling of is possible because is a normal density.
(II) If, instead of points, we know that both daughter species values are domains, that is, and , then the conditional distribution of is:
| (11) |
(III) If one daughter species (say , for concreteness) is an internal node and is in a domain, that is, , then the conditional distribution is:
| (12) |
Sampling in cases (II) and (III) requires a Metropolis–Hastings step because we cannot draw from the exact conditional distribution for . Instead, we take an approximate draw from the conditional distribution by replacing polygons by their centroids and drawing from Equation (8). The proposal distribution is given by Equation (8), where and are the polygon centroids of and . Call the proposed value and the current value . The proposed value is accepted with probability:
| (13) |
(IV) Finally, if has no ancestor (it is the root of the tree, i.e., MRCA), then we replace by a prior distribution on the location of the ancestor (Fig. 3). In our analyses, we use a flat prior for the ancestral value, so its conditional distribution depends only on its daughter values and and daughter branch lengths and . The conditional density can be obtained by setting in Equations (8), (9), and (10). We call this algorithm “rase,” which stands for “Range Ancestral State Estimation.”
Validation
To validate the proposed methodology, we contrasted estimated values from rase with maximum likelihood inference using range centroids. We simulated one-dimensional trait evolution according to a BM process on simulated phylogenetic trees under a constant birth–death process (Nee 2006). For every tip point value simulated under BM, we increased and decreased the range width (see below) from the point to obtain an enclosing symmetrical range to be used by rase. If the domain becomes infinitely small, the parameter estimates from rase should converge to the estimates based on domain centroids. We used two different values for the rate parameter ( and ) as well as six different domain widths but held constant the mean of the BM process (), the birth–death process parameters, and the number of taxa on each simulation. For clarity, we considered a total of 12 different simulation scenarios: six different domain widths, each with the two different rate parameters. For each combination of and width, we performed 1000 random simulations where tree topology, age, and outcome of the BM process varied. In total, we performed 12,000 simulations. For each simulation, we estimated the ancestral state () and rate () of the BM process using point likelihood and rase. The point likelihood function was extracted from the ace function in ape package (Paradis et al. 2004) for R, while tree simulation under birth–death process was performed using the phytools package (Revell 2013).
We calculated residual sum of squares (RSS) from linear regression between rase and point likelihood estimates for mean () and rate () for each of the 12 simulation scenarios. We expect that for small range widths, RSS will be small, and that it would increase with broader range widths. Overall, we found consistent results with our expectations (Table 1, Fig. 4). The rate () parameter estimates from rase are generally lower than the estimates using points as tip-data. This difference increases with range width (Fig. 4). This is consistent with our method since we are constraining the BM process to fall within the range; thus, tip values that fall within the range but that are closer to the overall mean of the BM process will increase the likelihood of lower rates ().
Table 1.
Validation results for likelihood estimates of ranges
| Width size | RSS | RSS | |
|---|---|---|---|
| 1 | 0.05 | 0.062 | 0.214 |
| 0.1 | 0.066 | 0.084 | |
| 0.2 | 0.056 | 14.765 | |
| 0.4 | 0.095 | 23.508 | |
| 0.6 | 0.193 | 36.460 | |
| 0.8 | 0.295 | 54.313 | |
| 2 | 0.05 | 0.034 | 0.046 |
| 0.1 | 0.075 | 0.411 | |
| 0.2 | 0.082 | 1.002 | |
| 0.4 | 0.527 | 1.510 | |
| 0.6 | 0.162 | 100.223 | |
| 0.8 | 0.430 | 157.813 |
Notes: Results from the validation procedure for rase for each of the 12 simulation scenarios were varied between two different rate parameters () to simulate the BM process and between different width sizes to input in rase as ranges. RSS is the residual sum of squares between the estimates of point likelihood against the estimates of rase for the BM process mean and the rate .
Figure 4.
Validation results for the likelihood estimates using rase versus point likelihood. The parameter corresponds to the ancestral state of the root, while the parameter corresponds to the rate of change in both the horizontal and the vertical dimension, according to a BM. The point likelihood is evaluated using the centroids of enclosing squares of 0.1 (first two columns) and 0.6 range widths (last two columns), while the rase estimate is evaluated with the squares as input. For each square width, the distribution of 1000 simulations of BM among random phylogenetic trees is given. The upper row displays the maximum likelihood estimates (MLE) returned by rase across all simulations for both parameters; dotted vertical lines correspond to the true parameters used to simulate the data (i.e., the state value of the root () = 0 and the rate of change (). The lower row displays the MLE of point likelihood against the MLE of rase; dashed gray line is a 1:1 correspondence. For additional simulation results, see Table 1.
Case Studies
Trumpeters (Psophia) in the Amazon
We use rase to analyze a paleogeographic model describing the diversification of trumpeters (Aves: Gruiformes: Psophiidae, Psophia) in the Amazonian rainforest. Ribas et al. (2012) use a time-calibrated phylogenetic tree and species distributions to infer the evolutionary history of this genus. The phylogeny revealed distinct monophyletic groups, currently not categorized as species, which the authors identify as “phylogenetic” species (Cracraft 1989). The authors use current knowledge of the geological history of the Amazonian rivers and conclude that there is a qualitative temporal correspondence between emergence of major Amazonian rivers and the phylogeography of Psophia, assuming a vicariance scenario of speciation. Here, we extract the phylogenetic and distributional information of Psophia from Ribas et al. (2012), and apply rase to infer the taxon's evolutionary history in time and space. We contrast our results, which are model-based, with the qualitative inference outlined in Ribas et al. (2012). Our method integrates the wide range of sizes and shapes of Psophia spatial distributions to reconstruct its evolutionary history.
The phylogenetic tree of Psophia was constructed using a Bayesian method using two mitochondrial DNA (mtDNA) sequences (cytb + ND2; further details in Ribas et al. 2012). Here, we assume that this phylogenetic tree reflects the true species tree, but we note that phylogenetic inference based only on mtDNA can be problematic (Rubinoff and Holland 2005). Particularly, for closely related species, mtDNA can distort the true historical relationships among individuals because of introgression, hybridization, non-neutrality, and idiosyncratic behavior across different clades (Ballard and Whitlock 2004). Geographical distributions of the phylogenetic species of Psophia introduced in the study were extracted manually by overlaying Figure 1 in Ribas et al. using ArcGIS 10 (ESRI 2011). We used rase to infer the location of the ancestral nodes and assumed no correlation between rates of dispersal in longitude and latitude. We ran rase for 12,000 iterations, discarded the first 2000 as burn-in, and logged every 10th iteration, obtaining posterior distributions of ancestral nodes and rates ( of 1000 samples each (Fig. 5). We evaluated the MCMC results by plotting the trace, sampling time autocorrelation, running mean and posterior densities for each of the estimated parameters, and confirmed that the algorithm converged to the posterior distribution.
Figure 5.
a) Three-dimensional graph with space in the horizontal plane and time as the vertical axis, displaying the reconstruction of the phylogeographic history the Psophia genus as given by rase. The current distribution of each of the phylogenetic species is given in different colors where (i) P. leucoptera, (ii) P. viridis, (iii) P. napensis, (iv) P. ochroptera, (v) P. crepitans, (vi) P. obscura, (vii) P. interjecta, and (viii) P. dextralis. In each ancestral node of the overlaid phylogeny, the 95% CI of the posterior distribution is mapped. b) Posterior distributions of the dispersal rate parameter () given as histograms and kernel-smoothed densities for longitude in dark cyan and latitude in orange.
Figure 5a displays the results of rase in a three-dimensional graph where space is illustrated in longitudinal and latitudinal coordinates and time as the vertical axis, oldest being toward the upper part. Variance parameters ( and represent the dispersal rate in each of the spatial axes as longitudinal/latitudinal degrees2 over Myr. During Psophia's evolutionary history, there was low latitudinal migration, as evinced by the latitudinal dispersal rate (), with a mean of 3.801 degrees2/Myr (95% credible interval (CI) = [2.836, 5.524]). Thus, almost all movement happened along the longitudinal axis, with a longitudinal dispersal rate () mean of 31.213 degrees2/Myr (CI = [21.469, 53.907]; Fig. 5b).
Figure 6 reconstructs the evolutionary history of Psophia as given by rase, using evenly spaced time slices (ca. every 0.391 Myr). Overall, our results suggest an evolutionary history similar to that outlined in Ribas et al. (compare Fig. 6 to Fig. 3 in Ribas et al.). According to rase, the first split, ca. 2.74 Ma, occurred very close to where the Amazon River is now, at a mean longitude of −61.154 (CI = [−71.368, −50.585]) and mean latitude of −4.48 (CI = [−7.692, −1.286]; Fig. 6a). In concordance with Ribas et al. (2012), this result suggests that the Amazon River was the main barrier that caused this speciation event at about 2.74 Ma. Whether this was vicariance or a long-distance founder event depends on which paleogeographic model one follows (Ribas et al. 2012). Vicariance is consistent with the paleogeographic model followed by Ribas et al., where the transcontinental Amazon River is established in the Pliocene (Campbell Jr. et al. 2006; Latrubesse et al. 2010; Ribas et al. 2012). Conversely, the Amazon River might had been established around 10–12 Ma, with increased drainage toward the present and, possibly, a drainage reversal (Figueiredo et al. 2009; Hoorn et al. 2010; Sacek 2014). The latter would suggest long-distance dispersal causing the initial split in the Psophia phylogeny, where according to our results, some individuals on the southern side of the Amazon River would have dispersed toward the north.
Figure 6.
Ancestral estimation according to rase at eight evenly spaced time slices, from 2.74 Ma to the current distribution of the Psophia genus. a)–g) The 25%, 50%, and 75% highest posterior density is plotted for each extant branch (25% with the more color intensity). h) 100% of the distribution is plotted (i.e., its current distribution). The branches of the phylogenetic tree are color coded as in (a)–(h) to identify its position in the map. Major Amazonian rivers are sequentially added—in their contemporary arrangement—according to the hypothesis outlined in Ribas et al. (2012). For further discussion, see main text.
Around 1.79 Ma, there was a second split that is linked to where the Rio Madeira currently is (Fig. 6d), giving rise to Psophia leucoptera. The mean longitude and latitude of the posterior distribution of this ancestral node is −59.128 (CI = [−67.239, −51.384]) and −6.435 (CI = [−8.582, −4.199]), which falls to the east of the contemporary Rio Madeira (although the river is within the 95% CI of the posterior distribution, Fig. 6d). At approximately 1.25 Ma, there was a split of the southern ancestor (longitudinal mean = −55.529, CI = [−62.311, −48.505]; latitudinal mean = −6.68, CI = [−8.826, −4.77]) that gave rise to P. viridis, associated with the current location of the Rio Tapajós (Ribas et al. 2012). Again, rase placed this ancestor east of the Tapajós River, although it is within the 95% range of the posterior distribution (Fig. 6e). Following is a split in the northern species that gave rise to P. napensis, ca. 1.21 Ma (longitudinal mean = −64.293, CI = [−70.661, −58.321]; latitudinal mean = −1.379, CI = [−3.259, 0.553]; Fig. 6e). Subsequently, around 1.04 Ma, there was a split that has been associated with the Rio Negro, which gave rise to P. ochroptera and P. crepitans (Fig. 6f). Rase estimated the highest posterior density of the ancestor west of the Rio Negro, at a mean longitude of −63.95, CI = [−69.95, −57.48] and latitude of −1.131, CI = [−2.771, 0.752]; again, however, the 95% range of the posterior distribution contains the river.
About 0.76 Ma, P. obscura arose, presumably as the Rio Tocantins emerged (Fig. 6g). Rase estimated the ancestral node to be at −51.946 longitude (CI = [−57.286, −46.813]) and −6.224 latitude (CI = [−7.812, −4.659]), west of the Rio Tocantins River with no overlapping 95% range of the posterior distribution. And finally, ca. 0.48 Ma, a split associated with the Rio Xingu gave rise to P. interjecta and P. dextralis (Fig. 6g). The mean density of the posterior distribution locates this ancestor at −52.787 longitude (CI = [−57.507, −48.034]) and −7.165 latitude (CI = [−8.677, −5.661]), very close to the eastern edge of the Rio Xingu. Although latitudinal rates were smaller when taking into account the whole geographical range of the species, our estimates are largely congruent with a BM model using the midpoints as tip values (Appendix 1). This is probably due to the fact that the geographical distributions across species are similarly shaped and sized. This contrasts with our second application, where differently shaped and sized polygonal domains dramatically affect the parameter estimates (see below and Appendix 1).
We have applied and demonstrated rase to infer patterns of diversification in the Amazon. As described above, our results are largely congruent with the movements inferred qualitatively by Ribas et al. (2012) in their Figure 3. Without including knowledge of the paleogeographical models, we were able to recover a similar evolutionary history of Psophia with a clear, explicit, and quantitative model. Moreover, we identified contrasting dispersal rates across longitude and latitude (Fig. 5). The slow dispersal rates in latitude suggests that the trumpeters have been largely restricted to inhabiting tropical Amazonian forest, instead, they have been moving across similar available habitats along the longitudinal axis; a reflection that “it is easier to move than to evolve” (Donoghue 2008).
Intriguingly, although the inferred ancestors and corresponding river barriers are largely congruent with that of Ribas et al., our model allows other interpretations about the underlying mechanisms during the speciation processes. Some of the estimated locations of ancestors are not completely congruent with river barriers, but instead are located fairly far from them (Fig. 6). This could suggest that long-distance dispersal might have had some role in the initial fragmentation, instead of strict vicariance, during the diversification of the Amazonian trumpeters. Recent evidence suggests that indeed dispersal might be a key driver in the Neotropics (Smith et al. 2014). Novel discrete historical biogeographic algorithms have also suggested that founder effects might be more important than previously acknowledged (Matzke 2014). However, our results would also be congruent with the strict vicariant view of Ribas et al., and the lack of past distributional information makes such distinction impossible.
Cinclodes Radiation across South America
There are 15 currently recognized species of Cinclodes (Aves: Passeriformes, Furnariidae) that occur from Northern Colombia to Tierra del Fuego, Argentina (Fig. 7h; Chesser 2004). These species are the result of a recent radiation (ca. 7 Ma) and exhibit different habitat specialization, including exclusively coastal species and Polylepis woodlands in the high Andes. The latter are of pressing conservation concern, categorized as Critically Endangered as a result of habitat destruction and degradation (IUCN 2014). Two biogeographic hypotheses exist that aim to explain the evolutionary history of the genus. First, the genus Cinclodes might have a southern origin, in the temperate zone, and then colonized northern highland regions (Chapman 1917; Fjeldså 1992; Sanín et al. 2009). Alternatively, colonization of lowland and southern areas may postdate a mountainous origin (Sanín et al. 2009). Chesser (2004) and Sanín et al. (2009) used discrete reconstruction methods and found some limited support for the second hypothesis. Here, we use rase to infer the geographic location of ancestors using a time-calibrated phylogenetic tree of the Furnariids, inferred using both nuclear and mitochondrial sequence data (Derryberry et al. 2011), and the geographic distribution of the Cinclodes species, which vary greatly in size, complexity, and distribution (Fig. 7h; Jetz et al. 2012). Geographical distributions based on expert range maps are only accurate to ca. 1°resolution longitude/latitude (Hurlbert and Jetz 2007); to attain more accurate geographical distributions, we refined them according to the species altitudinal ranges provided by experts (Chesser 2004). Specifically, we converted each range polygon into a 2.5 arc-minute binary raster (1 for presence, 0 for absence) and we set to 0 all pixels that lay above or under the altitudes that the species is known to occupy. We then converted the resulting raster back to a polygon. We used the SRTM dataset in WorldClim (Hijmans et al. 2005) to get the per-pixel mean elevations.
Figure 7.
Ancestral estimation according to rase at eight evenly spaced time slices, from ca. 7 Ma to the current distribution of the Cinclodes genus. a)–g) The 10%, 15%, and 20% highest posterior density is plotted for each extant branch (10% with highest color intensity). h) 100% of the geographical distribution is plotted (i.e., its current distribution, note that many geographical ranges overlap). The branches of the phylogenetic tree are color coded as in (a)–(h) to identify its position in the map. i) Posterior distribution of the dispersal rate parameter (*sigma2*) given histograms and kernel-smoothed densities for longitude in dark cyan and latitude in orange. For further discussion, see main text.
We ran rase for 100,000 iterations, discarded the first 10,000 as burn-in, and logged every 20, obtaining posterior distributions of ancestral nodes and rates () of 4500 samples each. In contrast to our Psophia results, Cinclodes exhibited high dispersal rates across latitude (), with an average of of 178.86 degrees2/Myr (CI = [122.93, 308.27]; Fig. 7i). Intriguingly, longitudinal dispersal rates were even higher, with a mean of 199.93 degrees2/Myr (CI = [119.45, 386.21]; Fig. 7i). This elevated longitudinal dispersal rate is the direct result of incorporating the whole geographical range of the species instead of using the midpoint, as evinced by comparing the estimates when using only point values in the tips (Appendix 2). Figure 7 reconstructs the evolutionary history of Cinclodes according to rase by estimating the location of ancestral branches in slices of time every ca. 1 Myr. Because of the high posterior variance in estimates, we show the 20%, 15%, and 10% of the highest posterior density to visually present the results. The first branching event estimate at ca. 6.99 Ma was uncertain but most likely to have occurred in central South America, on the eastern Andean slopes (longitudinal mean = −55.87, CI = [−96.3, −15.98]; latitudinal mean = −19.59, CI = [−48.49, 11.97]), resulting in the geographical isolation of Cinclodes pabsti (Fig. 7a). This is parallel to the results obtained by Chesser (2004) and Sanín et al. (2009), where, with great ambiguity, the Central Andes appeared as the most likely ancestral area when using the dispersal–extinction–cladogenesis model (DEC; Ree and Smith 2008)—with one topological difference between our phylogenetic trees.
At ca. 5.3 Ma, the second split occurred, probably at a very similar location as the initial one (longitudinal mean = −59.49, CI = [−90.77, −26.45]; latitudinal mean = −18.62, CI = [−45.51, 11.05]), leading to two main clades: Clade I and Clade II (Fig 7c; as in Chesser 2004). The ancestor of Clade I (longitudinal mean = −58.97, CI = [−94.32, −24.37]; latitudinal mean = −20.65, CI = [−47.9, 9.46]) was estimated to be more southern than the ancestor of Clade II (longitudinal mean = −64.45, CI = [−87.81, −41.21]; latitudinal mean = −15.36, CI = [−35.97, 4.77]; Fig. 7c,d). This is also congruent with ancestral reconstructions presented before (Chesser 2004; Sanín et al. 2009). Our main results suggest that, in accordance with the second biogeographic hypothesis, the Cinclodes genus originated in central South America, possibly linked with the eastern slopes of the Central Andes. Thus, it is most likely that colonization of southern Patagonia and eastern Brazilian highlands results from diversification in South American western mountains. However, the high dispersal rates of Cinclodes results in large uncertainty around the ancestral geographical location estimates. Importantly, the high longitudinal rate was appreciated only when taking into account the species' contrasting geographical ranges (Appendix 2).
Discussion
Phylogenetic methods have increased in complexity and flexibility over the last decade. Here, we overcome a common limitation of continuous inference of the geographic location of ancestors by incorporating the full range of characters defined by a bounded domain. Our novel BM, rase, uses MCMC parameter estimation that yields a posterior distribution for each ancestral state, which allows propagation of the uncertainty of tip trait domains. We demonstrated the usefulness of rase in phylogeographic reconstruction of species ancestral locations and contrasted our results with previous methods that compel researchers to reduce the distribution of species to one point in space—a comparison that was further facilitated by providing rase as a readily usable R package (see Software). Importantly, we show that using rase can considerably influence the parameter estimates in ancestral states and rates of evolution, as evinced in the Cinclodes example (Appendix 2). This contrasts with the subtler differences found in the trumpeters example (Appendix 1). This is probably caused by the dramatic among-species differences in geographic range shape and sizes of the former (Fig 7h) compared to the latter (Fig. 6h).
Expert range maps are routinely used in ecology to describe patterns of species richness (Jetz and Rahbek 2002; Ruggiero and Hawkins 2008; Storch et al. 2013). However, over the past decades, there has been an increased awareness of the importance of historical factors for our understanding of current biodiversity, which triggered the integration of phylogenetic information (Wiens and Donoghue 2004; Ree et al. 2005; Kozak and Wiens 2007; Lemmon and Lemmon 2008; Jetz et al. 2012; Quintero and Wiens 2013a). Historical biogeographic methods attempt to reconstruct a clade's history of diversification by combining current species distributions and their evolutionary relationships. In the last decade, the rise of methods that demand discrete areas defined a priori has hindered assaying the evolutionary biogeographic history of several clades for which such preliminary discretization of ancestral regions is untenable (Ree et al. 2005; Lemmon and Lemmon 2008; Goldberg et al. 2011; Landis et al. 2013). Meanwhile, implementations of continuous historical biogeographic inference have not been as common, presumably, because current statistical methods require some unrealistic model assumptions (e.g., geographical ranges are reduced to points). Previous phylogenetic methods have either not considered the whole extent of the tip values (e.g., the geographic ranges; Lemey et al. 2010) or iteratively sampled from the range using point tip values for inference (Bouckaert et al. 2012; Nylinder et al. 2014). Here, we propose that species' whole geographic distributions can be utilized directly in historical biogeography under an efficient inference algorithm.
Our model makes simplifying assumptions about relevant biological processes acting on the evolution of geographic ranges. Models dealing with historical biogeography require different assumptions in order to remain tractable (Lemmon and Lemmon 2008). For instance, the diffusion process of a group of particles is conditionally independent of other contemporaneously diffusing particles, given the state of their MRCA. This perspective necessarily omits interspecific dynamics (e.g., facilitation, competition) during their evolutionary history. These might only be indirectly inferred by observing the movement history of the ancestors. Moreover, in accordance with the traditional BM model of migration, at the moment of speciation both daughter species inherit their ancestor's range and evolve independently thereafter. This disregards the intricacies of geographical speciation, in particularly of the allopatric and parapatric modes. This can be especially problematic in certain empirical applications such as islands, where colonization is a rare and improbable event that does not conform to a diffusion-based model of migration. However, the BM model of range inheritance should prove useful in several other applications, such as sympatric speciation scenarios or where allopatry and parapatry has occurred over narrow barriers (e.g., rivers, valleys, straight mountain chains).
Inference of evolutionary outcomes in the distant past carries greater uncertainty than inference of more recent events, and this is no less true when applying rase. Indeed, the uncertainty of ancestral states increases toward the past. BM as a model for migration might be ill suited for certain evolutionary scenarios, particularly those involving large timescales. Similarly, large spatial scales (e.g., cross-continental), or archipelagos might prove unsuitable for a migration model based on BM. Additional sources of information and increased model complexity, discussed below, would broaden the applicability of rase. Finally, our model disregards any interactions between the distribution and shape of geographical ranges with the evolutionary history of the clade (e.g., lower probability of extinction in larger ranges, higher probability of speciation in fragmented ranges) or with abiotic changes in the environment. Although these restrictive assumptions are shared by all continuous phylogeographic methods, we expand on a critical issue lacking in previous implementation (Lemmon and Lemmon 2008; Lemey et al. 2010; Nylinder et al. 2014). These are exciting avenues for future research that can be built into our new technique, attaining increased realism, while accounting for geographically varying domains of species geographic ranges. An alternative that has gained popularity for dealing with complex phylogeographic and demographic scenarios uses Approximate Bayesian Computation, where the posterior distribution is approximated, bypassing the evaluation of the likelihood function (Beaumont et al. 2010; Csilléry et al. 2010). These techniques are most useful when the likelihood is intractable and represent a promising avenue for tackling more intricate evolutionary histories (Bloomquist et al. 2010; Marin et al. 2011).
Our methodology can be extended to incorporate greater complexity and attain increased realism. One limitation of rase is a shared diffusion rate among all branches of the BM process, which may be unrealistic. A natural extension to rase is the implementation of uncorrelated rates on each branch, similar to the relaxed random walk (RRW) from Lemey et al. (2010). Further, when fossil or other geological evidence provides information about the location of ancestral species, the proposed approach could be modified to accommodate this information by constraining ancestral values to be at certain location, as well as tip values. Finally, hard geographic or environmental boundaries (i.e., continental border, other natural barriers to dispersal) could be incorporated within our model framework to enhance the realism of the model and prevent unreasonable results, such as inferring the ancestral location of a terrestrial species within a large body of water. If available, a series of maps representing changes through time in the configuration of landmasses and habitat could be used to constrain the geographic location or traits of ancestors.
The application of rase is not limited to historical biogeographic inference. Continuous-valued traits are often intrinsically constrained. Constraints on continuous traits include the impossibility of negative values in size, weight, etc., physiological limits, and limited trait space to adapt to, among others (Garland et al. 1992). For instance, ancestral estimation of continuous niche axes (Graham et al. 2004; Yesson and Culham 2006; Vieites et al. 2009; Kozak and Wiens 2010; Quintero and Wiens 2013a, 2013b), which are usually observed as a range, can now be inferred using the whole uncertainty of the range and not midpoints. In addition, it allows simultaneous phylogenetic inference of several variables in multidimensional niche space. To illustrate, one could replace longitude and latitude by temperature and precipitation as the dimensions and “map” an estimate of the realized niche distribution of species. Importantly, this does not only affect analyses of ancestral state estimation but any phylogenetic comparative analysis that attempts to account for the effect of phylogeny in a given character (e.g., phylogenetic generalized least squares; Martins and Hansen 1997; Revell 2010). Given that using rase can considerably influence parameter estimates, we recommend that researchers consider the availability of species ranges instead of points when performing comparative evolutionary analyses.
An exciting avenue for future research using our model is the spatial configuration of diversification through geological time. Diversification is defined as species accumulation through time (Ricklefs 2007; Rabosky 2009; Morlon 2014), and, as such, is time-dimensional by nature. Indeed, most methodologies dealing with the study of diversification ignore the spatial setting where they have occurred (Nee et al. 1994; Morlon 2014). Our method can be used to create model-based geographic maps of the diversification process across time, as it produces spatially explicit maps of the relative probability of origination of each node in the phylogeny. These maps can be overlaid and summed to identify areas with high probability of lineage origination and maintenance (similar to figure 8f in Nylinder et al. 2014). So far, the few attempts to gauge a continuous geographic representation of diversification rates have been limited by relying on current-day species distributions to geographically ascribe rates (Jetz et al. 2012; Hutter et al. 2013; Kennedy et al. 2014; but see Nylinder et al. 2014). This complicates interpretation of the resulting spatial diversification rates since they do not account for historical range changes and past geographical barriers that have contributed to present-day biodiversity. Our method helps to address this by enabling the identification of probability density peaks of origination while taking into account all the information and uncertainty for all species.
Software
We implemented rase in R language. The package is called “rase” and is available for download from CRAN: cran.r-project.org/web/packages/rase/ and at https://bitbucket.org/ignacioq/rase (last accessed 20 August, 2015).
Acknowledgments
We thank Sebastian Meyer for providing help with the polyCub code. We thank Frank E. Anderson, Richard Glor, and two anonymous reviewers for providing helpful comments on earlier versions of the manuscript.
Appendix 1
Posterior density estimates for the parameters of the Psophia application. Ancestral location estimated of the nodes in longitude are denoted by “n_x”, and in latitude by “n_y”. Estimates of dispersal rates () are labeled “sigma2x” for longitudinal dispersal () and “sigma2y” for latitudinal dispersal (). Red densities are the parameter estimates using rase, while blue densities are the parameter estimates when using the domain midpoints as tip values.
Appendix 2
Posterior density estimates for the parameters of the Cinclodes application. Ancestral location estimated of the nodes in longitude are denoted by “n_x”, and in latitude by “n_y”. Estimates of dispersal rates () are labeled “sigma2x” for longitudinal dispersal () and “sigma2y” for latitudinal dispersal (). Red densities are the parameter estimates using rase, while blue densities are the parameter estimates when using the domain midpoints as tip values.
Supplementary Material
Data available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.16nt8.
Funding
This work was supported by the Graduate Student Research Award from the Society of Systematic Biologists to I.Q.; the People Programme (Marie Curie Actions) of the European Union's Seventh Framework Programme (FP7/2007-2013) under REA Grant agreement no. 302868 to P.K.; and the NASA Biodiversity Grant NNX11AP72G and National Science Foundation grants DBI 0960550, DEB 1026764 to W.J. F.W.C. was supported by CTSA Grant Number UL1 TR000142 and KL2 TR000140 from the National Center for Advancing Translational Science (NCATS), components of the National Institutes of Health (NIH), and NIH roadmap for Medical Research.
References
- Abramowitz M., Stegun I.A. 1964. Handbook of mathematical functions: with formulas, graphs, and mathematical tables. New York: Dover Publications , Inc. [Google Scholar]
- Andow D.A., Kareiva P.M., Levin S.A., Okubo A. 1990. Spread of invading organisms. Landsc. Ecol. 4:177–188. [Google Scholar]
- Avise J.C., Arnold J., Ball R.M., Bermingham E., Lamb T., Neigel J.E., Reeb C.A., Saunders N.C. 1987. Intraspecific phylogeography: the mitochondrial DNA bridge between population genetics and systematics. Annu. Rev. Ecol. Syst. 18:489–522. [Google Scholar]
- Ballard J.W.O., Whitlock M.C. 2004. The incomplete natural history of mitochondria. Mol. Ecol. 13:729–744. [DOI] [PubMed] [Google Scholar]
- Bartoszek K., Pienaar J., Mostad P., Andersson S., Hansen T.F. 2012. A phylogenetic comparative method for studying multivariate adaptation. J. Theor. Biol. 314:204–215. [DOI] [PubMed] [Google Scholar]
- Beaumont M.A., Nielsen R., Robert C., Hey J., Gaggiotti O., Knowles L., Estoup A., Panchal M., Corander J., Hickerson M., Sisson S.A., Fagundes N., Chikhi L., Beerli P., Vitalis R., Cornuet J.-M., Huelsenbeck J., Foll M., Yang Z., Rousset F., Balding D., Excoffier L. 2010. In defence of model-based inference in phylogeography. Mol. Ecol. 19:436–446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bielejec F., Rambaut A., Suchard M.A., Lemey P. 2011. SPREAD: spatial phylogenetic reconstruction of evolutionary dynamics. Bioinformatics. 27:2910–2912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blackburn D.C., Measey G.J. 2009. Dispersal to or from an African biodiversity hotspot? Mol. Ecol. 18:1904–1915. [DOI] [PubMed] [Google Scholar]
- Bloomquist E.W., Lemey P., Suchard M.A. 2010. Three roads diverged? Routes to phylogeographic inference. Trends Ecol. Evol. 25:626–632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bouckaert R. 2015. Phylogeography by diffusion on a sphere. bioRxiv.:016311. [DOI] [PMC free article] [PubMed]
- Bouckaert R., Lemey P., Dunn M., Greenhill S.J., Alekseyenko A.V., Drummond A.J., Gray R.D., Suchard M.A., Atkinson Q.D. 2012. Mapping the origins and expansion of the Indo-European language family. Science 337:957–960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butler M.A., King A.A. 2004. Phylogenetic comparative analysis: a modeling approach for adaptive evolution. Am. Nat. 164:683–695. [DOI] [PubMed] [Google Scholar]
- Camargo A., Werneck F.P., Morando M., Sites J.W., Avila L.J. 2013. Quaternary range and demographic expansion of Liolaemus darwinii (Squamata: Liolaemidae) in the Monte Desert of Central Argentina using Bayesian phylogeography and ecological niche modelling. Mol. Ecol. 22:4038–4054. [DOI] [PubMed] [Google Scholar]
- Campbell K.E., Jr., Frailey C.D., Romero-Pittman L. 2006. The Pan-Amazonian Ucayali Peneplain, late Neogene sedimentation in Amazonia, and the birth of the modern Amazon River system. Palaeogeogr. Palaeoclimatol. Palaeoecol. 239:166–219. [Google Scholar]
- Chapman F.M. 1917. The Distribution of Bird-life in Colombia: A Contribution to a Biological Survey of South America. Bull. Am. Mus. Nat. Hist. 36:1–729. [Google Scholar]
- Chesser R.T. 2004. Systematics, evolution, and biogeography of the South American ovenbird genus Cinclodes. The Auk. 121:752–766. [Google Scholar]
- Coyne J.A., Orr H.A. 2004. Speciation. Sunderland, MA: Sinauer Associates. [Google Scholar]
- Cracraft J.Otte D., Endler D. J. A. 1989. Speciation and its ontology: the empirical consequences of alternative species concepts for understanding patterns and processes of differentiation. Speciation and its Consequences. Sunderland, MA: Sinauer; p. 28–59. [Google Scholar]
- Csilléry K., Blum M.G.B., Gaggiotti O.E., François O. 2010. Approximate Bayesian Computation (ABC) in practice. Trends Ecol. Evol. 25:410–418. [DOI] [PubMed] [Google Scholar]
- Derryberry E.P., Claramunt S., Derryberry G., Chesser R.T., Cracraft J., Aleixo A., Perez-Eman J., Remsen J.V., Brumfield R.T. 2011. Lineage diversification and morphological evolution in a large-scale continental radiation: the Neotropical ovenbirds and woodcreepers (Aves: Furnariidae). Evolution. 65:2973–2986. [DOI] [PubMed] [Google Scholar]
- Donoghue M.J. 2008. A phylogenetic perspective on the distribution of plant diversity. Proc. Natl. Acad. Sci. 105:11549–11555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drummond A.J., Rambaut A. 2007. BEAST: Bayesian evolutionary analysis by sampling trees. BMC Evol. Biol. 7:214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Escobar García P., Winkler M., Flatscher R., Sonnleitner M., Krejčíková J., Suda J., Hülber K., Schneeweiss G.M., Schönswetter P. 2012. Extensive range persistence in peripheral and interior refugia characterizes Pleistocene range dynamics in a widespread Alpine plant species (Senecio carniolicus, Asteraceae). Mol. Ecol. 21:1255–1270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- ArcGIS Desktop: Release 10. Redlands, CA: Environmental Systems Research Institute.
- Felsenstein J. 1985. Phylogenies and the comparative method. Am. Nat. 125:1–15. [Google Scholar]
- Figueiredo J., Hoorn C., Ven P. van der, Soares E. 2009. Late Miocene onset of the Amazon River and the Amazon deep-sea fan: Evidence from the Foz do Amazonas Basin. Geology 37:619–622. [Google Scholar]
- Fjeldså J. 1992. Biogeographic patterns and evolution of the avifauna of relict high-attitude woodlands of the Andes. Steenstrupia:9–62. [Google Scholar]
- Garamszegi L.Z. 2014. Modern phylogenetic comparative methods and their application in Evolutionary Biology: concepts and practice. New York: Springer. [Google Scholar]
- Garland T., Harvey P.H., Ives A.R. 1992. Procedures for the analysis of Comparative Data using phylogenetically independent contrasts. Syst. Biol. 41:18–32. [Google Scholar]
- Goldberg E.E., Lancaster L.T., Ree R.H. 2011. Phylogenetic inference of reciprocal effects between geographic range evolution and diversification. Syst. Biol. 60:451–465. [DOI] [PubMed] [Google Scholar]
- Graham C.H., Ron S.R., Santos J.C., Schneider C.J., Moritz C. 2004. Integrating phylogenetics and environmental niche models to explore speciation mechanisms in Dendrobatid frogs. Evolution 58:1781–1793. [DOI] [PubMed] [Google Scholar]
- Harmon L.J., Weir J.T., Brock C.D., Glor R.E., Challenger W. 2008. GEIGER: investigating evolutionary radiations. Bioinformatics 24:129–131. [DOI] [PubMed] [Google Scholar]
- Hijmans R.J., Cameron S.E., Parra J.L., Jones P.G., Jarvis A. 2005. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. 25:1965–1978. [Google Scholar]
- Hoorn C., Wesselingh F.P., Steege H. ter, Bermudez M.A., Mora A., Sevink J., Sanmartín I., Sanchez-Meseguer A., Anderson C.L., Figueiredo J.P., Jaramillo C., Riff D., Negri F.R., Hooghiemstra H., Lundberg J., Stadler T., Särkinen T., Antonelli A. 2010. Amazonia through time: Andean uplift, climate change, landscape evolution, and biodiversity. Science 330:927–931. [DOI] [PubMed] [Google Scholar]
- Hurlbert A.H., Jetz W. 2007. Species richness, hotspots, and the scale dependence of range maps in ecology and conservation. Proc. Natl. Acad. Sci. 104:13384–13389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutter C.R., Guayasamin J.M., Wiens J.J. 2013. Explaining Andean megadiversity: the evolutionary and ecological causes of glassfrog elevational richness patterns. Ecol. Lett. 16:1135–1144. [DOI] [PubMed] [Google Scholar]
- IUCN. 2014. IUCN Red List of Threatened Species. Version 2014.3. Available from: URL http://www.iucnredlist.org last accessed 20 August, 2015.
- Jablonski D., Roy K., Valentine J.W. 2006. Out of the tropics: evolutionary dynamics of the latitudinal diversity gradient. Science 314:102–106. [DOI] [PubMed] [Google Scholar]
- Jetz W., Rahbek C. 2002. Geographic range size and determinants of avian species richness. Science 297:1548–1551. [DOI] [PubMed] [Google Scholar]
- Jetz W., Thomas G.H., Joy J.B., Hartmann K., Mooers A.O. 2012. The global diversity of birds in space and time. Nature 491:444–448. [DOI] [PubMed] [Google Scholar]
- Kennedy J.D., Wang Z., Weir J.T., Rahbek C., Fjeldså J., Price T.D. 2014. Into and out of the tropics: the generation of the latitudinal gradient among New World passerine birds. J. Biogeogr. 41:1746–1757. [Google Scholar]
- Kozak K.H., Wiens J.J. 2007. Climatic zonation drives latitudinal variation in speciation mechanisms. Proc. R. Soc. B Biol. Sci. 274:2995–3003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kozak K.H., Wiens J.J. 2010. Niche conservatism drives elevational diversity patterns in Appalachian salamanders. Am. Nat. 176:40–54. [DOI] [PubMed] [Google Scholar]
- Landis M.J., Matzke N.J., Moore B.R., Huelsenbeck J.P. 2013. Bayesian analysis of biogeography when the number of areas is large. Syst. Biol. 62:789–804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latrubesse E.M., Cozzuol M., da Silva-Caminha S.A.F., Rigsby C.A., Absy M.L., Jaramillo C. 2010. The Late Miocene paleogeography of the Amazon Basin and the evolution of the Amazon River system. Earth Sci. Rev. 99:99–124. [Google Scholar]
- Lemey P., Rambaut A., Welch J.J., Suchard M.A. 2010. Phylogeography takes a relaxed random walk in continuous space and time. Mol. Biol. Evol. 27:1877–1885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemmon A.R., Lemmon E.M. 2008. A likelihood framework for estimating phylogeographic history on a continuous landscape. Syst. Biol. 57:544–561. [DOI] [PubMed] [Google Scholar]
- Lynch Alfaro J.W., Boubli J.P., Olson L.E., Di Fiore A., Wilson B., Gutiérrez-Espeleta G.A., Chiou K.L., Schulte M., Neitzel S., Ross V., Schwochow D., Nguyen M.T.T., Farias I., Janson C.H., Alfaro M.E. 2012. Explosive Pleistocene range expansion leads to widespread Amazonian sympatry between robust and gracile capuchin monkeys. J. Biogeogr. 39:272–288. [Google Scholar]
- Marin J.-M., Pudlo P., Robert C.P., Ryder R.J. 2011. Approximate Bayesian computational methods. Stat. Comput. 22:1167–1180. [Google Scholar]
- Martins E.P., Hansen T.F. 1997. Phylogenies and the Comparative Method: a general approach to incorporating phylogenetic information into the analysis of interspecific data. Am. Nat. 149:646–667. [Google Scholar]
- Matzke N.J. 2014. Model selection in historical biogeography reveals that founder-event speciation is a crucial process in island clades. Syst. Biol. 63:951–970. [DOI] [PubMed] [Google Scholar]
- Meyer S., Held L. 2014. Power-law models for infectious disease spread. Ann. Appl. Stat. 8:1612–1639. [Google Scholar]
- Morlon H. 2014. Phylogenetic approaches for studying diversification. Ecol. Lett. 17:508–525. [DOI] [PubMed] [Google Scholar]
- Murta R.D.P. with contributions from D.M. and B.R.G. library by A. 2013. gpclib: General Polygon Clipping Library for R.
- Nee S. 2006. Birth-Death models in macroevolution. Annu. Rev. Ecol. Evol. Syst. 37:1–17. [Google Scholar]
- Nee S., May R.M., Harvey P.H. 1994. The reconstructed evolutionary process. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 344:305–311. [DOI] [PubMed] [Google Scholar]
- Neigel J.E., Ball R.M., Jr., Avise J.C. 1991. Estimation of single generation migration distances from geographic variation in animal mitochondrial DNA. Evolution 45:423–432. [DOI] [PubMed] [Google Scholar]
- Nylinder S., Lemey P., Bruyn M.D., Suchard M.A., Pfeil B.E., Walsh N., Anderberg A.A. 2014. On the biogeography of Centipeda: a species-tree diffusion approach. Syst. Biol. 63:178–191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paradis E., Claude J., Strimmer K. 2004. APE: analyses of phylogenetics and evolution in R language. Bioinformatics 20:289–290. [DOI] [PubMed] [Google Scholar]
- Quintero I., Wiens J.J. 2013a. What determines the climatic niche width of species? The role of spatial and temporal climatic variation in three vertebrate clades. Glob. Ecol. Biogeogr. 22:422–432. [Google Scholar]
- Quintero I., Wiens J.J. 2013b. Rates of projected climate change dramatically exceed past rates of climatic niche evolution among vertebrate species. Ecol. Lett. 16:1095–1103. [DOI] [PubMed] [Google Scholar]
- Rabosky D.L. 2009. Ecological limits and diversification rate: alternative paradigms to explain the variation in species richness among clades and regions. Ecol. Lett. 12:735–743. [DOI] [PubMed] [Google Scholar]
- Rebernig C.A., Schneeweiss G.M., Bardy K.E., Schönswetter P., Villaseñor J.L., Obermayer R., Stuessy T.F., Weiss-Schneeweiss H. 2010. Multiple Pleistocene refugia and Holocene range expansion of an abundant southwestern American desert plant species (Melampodium leucanthum, Asteraceae). Mol. Ecol. 19:3421–3443. [DOI] [PubMed] [Google Scholar]
- Ree R.H., Moore B.R., Webb C.O., Donoghue M.J. 2005. A likelihood framework for inferring the evolution of geographic range on phylogenetic trees. Evolution 59:2299–2311. [PubMed] [Google Scholar]
- Ree R.H., Smith S.A. 2008. Maximum Likelihood inference of geographic range evolution by dispersal, local extinction, and cladogenesis. Syst. Biol. 57:4–14. [DOI] [PubMed] [Google Scholar]
- Revell L., Harmon L.J., Collar D. 2008. Phylogenetic signal, evolutionary process, and rate. Syst. Biol. 57:591–601. [DOI] [PubMed] [Google Scholar]
- Revell L.J. 2010. Phylogenetic signal and linear regression on species data. Methods Ecol. Evol. 1:319–329. [Google Scholar]
- Revell L.J. 2013. phytools: Phylogenetic Tools for comparative biology (and other things). .
- Ribas C.C., Aleixo A., Nogueira A.C.R., Miyaki C.Y., Cracraft J. 2012. A palaeobiogeographic model for biotic diversification within Amazonia over the past three million years. Proc. R. Soc. B Biol. Sci. 279:681–689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ricklefs R.E. 2007. Estimating diversification rates from phylogenetic information. Trends Ecol. Evol. 22:601–610. [DOI] [PubMed] [Google Scholar]
- Ronquist F., Sanmartín I. 2011. Phylogenetic methods in Biogeography. Annu. Rev. Ecol. Evol. Syst. 42:441–464. [Google Scholar]
- Rubinoff D., Holland B.S. 2005. Between Two Extremes: Mitochondrial DNA is neither the panacea nor the nemesis of phylogenetic and taxonomic inference. Syst. Biol. 54:952–961. [DOI] [PubMed] [Google Scholar]
- Ruggiero A., Hawkins B.A. 2008. Why do mountains support so many species of birds? Ecography 31:306–315. [Google Scholar]
- Sacek V. 2014. Drainage reversal of the Amazon River due to the coupling of surface and lithospheric processes. Earth Planet. Sci. Lett. 401:301–312. [Google Scholar]
- Sanín C., Cadena C.D., Maley J.M., Lijtmaer D.A., Tubaro P.L., Chesser R.T. 2009. Paraphyly of Cinclodes fuscus (Aves: Passeriformes: Furnariidae): Implications for taxonomy and biogeography. Mol. Phylogenet. Evol. 53:547–555. [DOI] [PubMed] [Google Scholar]
- Schluter D., Price T., Mooers A.Ø., Ludwig D. 1997. Likelihood of ancestor states in adaptive radiation. Evolution 51:1699–1711. [DOI] [PubMed] [Google Scholar]
- Silver L.T., Schultz P.H. 1982. Geological implications of impacts of large asteroids and comets on the Earth. Geological Society of America.
- Smith B.T., McCormack J.E., Cuervo A.M., Hickerson M.J., Aleixo A., Cadena C.D., Perez-Eman J., Burney C.W., Xie X., Harvey M.G., Faircloth B.C., Glenn T.C., Derryberry E.P., Prejean J., Fields S., Brumfield R.T. 2014. The drivers of tropical speciation. Nature 515:406–409. [DOI] [PubMed] [Google Scholar]
- Storch D., Keil P., Jetz W. 2013. Universal species-area and endemics-area relationships at continental scales. Nature 488:78–81. [DOI] [PubMed] [Google Scholar]
- Surget-Groba Y., Thorpe R.S. 2013. A likelihood framework analysis of an island radiation: phylogeography of the Lesser Antillean gecko Sphaerodactylus vincenti, in comparison with the anole Anolis roquet. J. Biogeogr. 40:105–116. [Google Scholar]
- Vieites D.R., Nieto-Roman S., Wake D.B. 2009. Reconstruction of the climate envelopes of salamanders and their evolution through time. Proc. Natl. Acad. Sci. 106:19715–19722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiens J.J., Donoghue M.J. 2004. Historical biogeography, ecology and species richness. Trends Ecol. Evol. 19:639–644. [DOI] [PubMed] [Google Scholar]
- Yesson C., Culham A. 2006. Phyloclimatic modeling: Combining phylogenetics and bioclimatic modeling. Syst. Biol. 55:785–802. [DOI] [PubMed] [Google Scholar]