Fluence-Field Modulated X-ray CT using Multiple Aperture Devices

Abstract

We introduce a novel strategy for fluence field modulation (FFM) in x-ray CT using multiple aperture devices (MADs). MAD filters permit FFM by blocking or transmitting the x-ray beam on a fine (0.1–1 mm) scale. The filters have a number of potential advantages over other beam modulation strategies including the potential for a highly compact design, modest actuation speed and acceleration requirements, and spectrally neutral filtration due to their essentially binary action. In this work, we present the underlying MAD filtration concept including a design process to achieve a specific class of FFM patterns. A set of MAD filters is fabricated using a tungsten laser sintering process and integrated into an x-ray CT test bench. A characterization of the MAD filters is conducted and compared to traditional attenuating bowtie filters and the ability to flatten the fluence profile for a 32 cm acrylic phantom is demonstrated. MAD-filtered tomographic data was acquired on the CT test bench and reconstructed without artifacts associated with the MAD filter. These initial studies suggest that MAD-based FFM is appropriate for integration in clinical CT system to create patient-specific fluence field profile and reduce radiation exposures.

INTRODUCTION

Current clinical CT systems have a few options that allow data acquisitions to be tailored to the specific patient and imaging task. Options include specification of the x-ray technique (kVp, mAs), tube current modulation, and selection of a static bowtie filter (usually only a couple choices). All of these methods can be used to improve imaging performance or minimize radiation exposure. Fluence field modulation (FFM), which permits dynamic customization of the x-ray beam profile, has been proposed as a potential strategy for dose reduction in x-ray CT^1,2. Various strategies for FFM have been proposed including inverse geometry CT¹ and dynamic beam filtration^3–6. Beam filtering methods include actuated double-wedge systems³, piecewise-linear attenuators⁴, and fluid-filled bowties^5,6. All of the latter methods rely on the variable attenuation of the beam filter. One exception to this strategy is digital beam attenuation using multi-leaf collimation⁷, where modulation is achieved by using many pulsed exposures with a (essentially) binary filter at different locations. There are challenges associated with all of these approaches that make their integration into modern clinical CT scanners difficult. In particular, there is very little room for complex motion systems and actuation within CT systems. Similarly, with newer CT systems scanning 360 degrees in under 300 ms, both the actuation speeds and accelerations required can pose substantial engineering challenges.

In this work, we propose and develop a new strategy for FFM using a dynamic filtering scheme. The proposed filter uses a set of fine-scale binary filters which we call multiple aperture devices (MADs). These devices either block or pass x-rays on a fine scale to create a spatial modulation of the fluence profile. Small relative motions in the position of the MADs allow for different modulation patterns. In this paper we introduce the MAD-based FFM concept and a design process that permits specification of different classes of modulation patterns. Moreover, we have fabricated a MAD filter and conducted an initial characterization study on a flat-panel-based CT test bench. These studies include initial reconstructions of physical phantom data using a MAD filter.

METHODS

Traditional bowtie filters modify the beam profile through variable attenuation of x-rays across the face of the CT detector. This is typically achieved using a homogeneous material and varying the thickness of the bowtie as a function of position. We propose a novel modulation scheme using a binary filter. Consider the simplified x-ray projection illustrated in Figure 1A. Like traditional bowtie filters, we choose to place a filter close to the x-ray source to customize the x-ray beam before it reaches the patient. However, instead of achieving modulation through variable material thickness, we choose to either entirely block or entirely pass the x-ray beam. This can be achieved by using a relatively thin slab of a high atomic number material (e.g., tungsten) which has been fabricated with through-hole apertures (e.g., slots). A multiple aperture device (MAD) permits a spatial modulation of the x-ray beam through the design of variably sized apertures (see zoomed detail in Figure 1B). Appropriate design of these apertures is important to ensure x-rays reach all detector elements. That is, the apertures must be small enough to ensure there are no significant gaps in x-ray illumination (to avoid a “missing data” problem).

Figure 1.

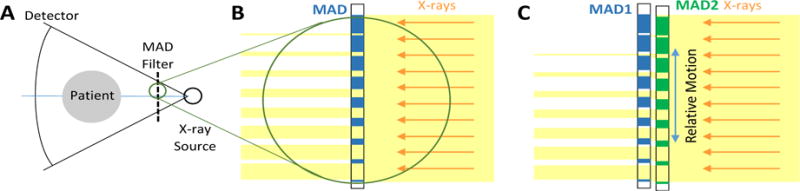
Illustration of the MAD-based FFM concept: A) Simplified CT diagram where the MAD is placed in front of the x-ray source. B) On a fine scale the MAD filter selectively entirely blocks or entirely permits x-ray transmission, so that (in this example) there is more x-ray fluence at the center of the field than at the edge. C) With the use of two MAD filters one can create an entire class of modulation patterns using small relative motions between the MADs. In this case, two identical MAD filters create a fluence pattern identical to the single MAD scenario when perfectly aligned, and, when displaced, the fluence pattern exhibits a relative concentration of fluence in the center as compared with the edge detector elements.

MAD filters offer an interesting possibility for dynamic spatial modulation of x-rays when two MAD filters are used in series (Figure 1C). In this scenario, relatively small displacements between the two filters can result in a significant change in the shape of the modulation. There are a number of potential advantages of MAD-based FFM: 1) The small displacements required for modulation translate to smaller required motions and accelerations in a clinical CT system. 2) A MAD filter module is relatively thin (e.g., the MADs themselves need only be a few mm thick) permitting a very compact design that could fit into current CT gantries. 3) The MAD filters should be spectrally neutral due to the binary attenuation which means beam hardening (and correction) is only associated with the patient anatomy. 4) There is potentially less scatter from MAD filters than compared to a traditional low atomic number attenuating bowtie since the photoelectric attenuation will dominate for higher atomic number filters.

There are a number of challenges associated with using MAD filters as well. In particular, there are significant design trade-offs associated with the specification and fabrication of the MADs, especially with regard to the size of the MAD apertures. For example, one might presume that to achieve relatively smooth fluence profiles that are detected without gaps, extremely fine apertures would be required (e.g., one aperture per detector element) leading to infeasible fabrication specifications (e.g., features << 100 μm). Fortunately, this is not the case and one can take advantage of other system features – specifically, the extended focal spot to achieve smooth profiles with reasonable aperture sizes. Consider the idealized thin-plane, perfectly attenuating MAD in Figure 2A. In this simple system, we have a rectangular x-ray focal spot and a flat detector. If one seeks uniform fluence at the detector, (ignoring 1/r² falloff) every triangle connecting the edges of the focal spot to points on the detector must intersect the same fractional transmission based on the amount of MAD blockage. Using geometrical arguments, we find that the optimal MAD pitch (spacing between adjacent apertures) that achieves a uniform fluence is a function of the source-to-MAD distance (SMD), source-to-detector distance (SDD), and focal spot size (FS). This optimal pitch is essentially a demagnification of the focal spot size and is given as FS*(1-SMD/SDD). (The same relation can be derived using Fourier analysis where one seeks the first null in the blur function associated with the focal spot. We also note that MADs may be designed for curved detector systems; however, the optimal pitch will vary as a function of position.) Non-uniform but smooth fluence profiles may be induced by maintaining the optimal pitch and smoothly varying the aperture size with position. See Figure 2B for a sample MAD where aperture area (slot width) was varied linearly from center to edge to achieve a triangular profile (in simulation).

Figure 2.

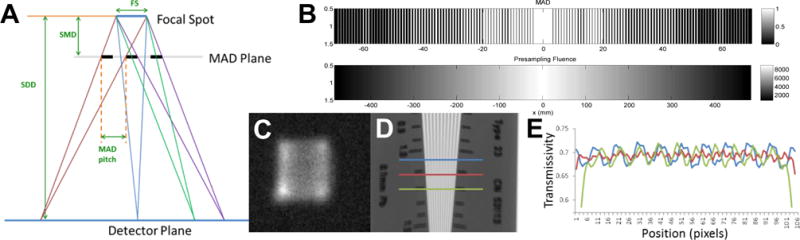
MAD system model: A) Geometric interpretation for optimal MAD pitch in a flat-detector system with an idealized rectangular x-ray focal spot. Note that all triangles formed by the edges of the focal spot and a point on the detector intersect exactly one MAD period to achieve the same transmission value (e.g., ½ each of 2 blockers for the green triangle, exactly one for other identified triangles). B) Smooth but non-uniform fluence patterns may be induced using a MAD with constant pitch but variable aperture size as shown in theoretical simulations. Pinhole images of actual focal spots (C) are rarely true rectangles; however, one can empirically determine an optimal pitch using a variable line pair phantom (D) and finding the lowest frequency where the line pair profiles (E) have a minimum in the modulation.

While the idealized system model in Figure 2A is helpful for understanding basic system tradeoffs, physical systems rarely have truly rectangular focal spots (see Figure 2C). However, we may determine the optimal pitch empirical in real system using a straightforward measure using a variable line pair pattern. Specifically, we may form projection images (Figure 2D) and profiles (Figure 2E) of variable line pairs to identify the line pair frequency (corresponding to the optical pitch) for which the modulation achieves a minimum.

Multiple MAD filters are required to achieve varying profiles. We have formulated a basic design process for dual MAD designs presuming two desired fluence patterns. The basic concept is illustrated in Figure 3 where the MAD pitch (P) has previously been determined and we seek to design the blocking functions, b₁(x) and b₂(x), for each MAD. Presuming b₁(x) < b₂(x) for all x (i.e., only b₁(x) contributes to the blocking function for zero displacement, Δx=0), we may find b₁(x) as a function (Figure 3B) of a desired fluence pattern, q₁(x), up to a scale factor, g₁, which can be controlled via tube current modulation. Presuming a sufficient Δx displacement (less than P) where b₂(x) does not lie in the shadow of b₁(x), blockage is additive, and we may write a second relation relating a second desired fluence pattern, q₂(x), again, within a scale factor, g₂. A sample set of target fluence patterns, blocking functions, and resultant patterns are shown in Figure 3C–E, respectively, using this minimum and maximum displacement design process. Moreover, transition fluence profiles for intermediate Δx displacements are shown in Figure 3F.

Figure 3.

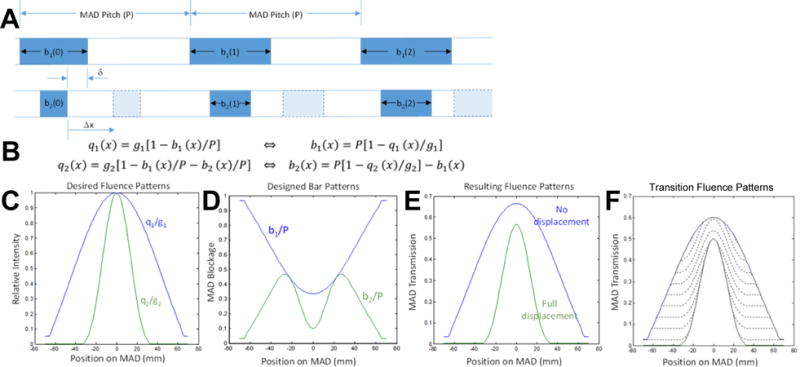
A) Parameterization of a dual MAD design including the blocking functions, b₁(x) and b₂(x), for each MAD, the relative displacement, Δx, and a justification parameter, δ. B) Design rules based on minimum and maximum displacement conditions that relate the blocking functions to desired fluence patterns. The design process is applied to two desired fluence patterns (C) to achieve the blocking functions in (D). The resulting fluence patterns (E) from this set of MADs matches up to a scale factor. Moreover, transition patterns for intermediate values of Δx are also shown (F) for the case of δ = [b₁(x) + b₂(x)]/2.

RESULTS

Based on estimated focal spot size measurements indicating a focal spot size of 1.19 mm, we estimated an optimal MAD pitch of P=0.909 mm for our test bench setup (SDD=1040 mm, SMD = 341 mm). This setup is shown in Figure 4B and 4C with single and dual MAD capabilities permitting independent motion of each MAD to allow for both relative and joint displacement of MADs permitting both dynamic modulation and centering of the x-ray beam profile. An initial set of MAD filters (Figure 4A) was constructed using a tungsten laser sintering process (similar to 3D printing). The MADs were constructed to be 140 mm wide and 1.5 mm thick and contained slot-type apertures that are focused (like a 1D antiscatter grid) to the x-ray tube with a variable inclination angle (with a maximum 11.6° tilt at the edges). Apertures were designed in an initial single MAD to flatten the detected fluence profile for a 32 cm water phantom. Due to fabrication limitations, a minimum slot width of 100 μm and a minimum bar width of 150 μm was employed. An photograph of a dual MAD setup is shown in Figure 4D where the relative displacement of the MADs has been changed by approximately P/2 ≈ 0.5 mm. This illustrates the significant change in fluence (beam width) for a small relative motion.

Figure 4.

A) Partially fabricated MAD on support substrate and a backlit photograph of a completed MAD. B) The flat-panel-based x-ray CT bench with Varian 4343CB detector and Varian Rad-94 x-ray tube. C) Closeup of the dual MAD actuation system that permits both relative and absolute translations of the MADs to achieve dynamic modulations and centering of fluence profiles. D) Backlit photographs of a dual MAD setup for two relative translations illustrating modulation of beam width.

The fluence profile associated with a single MAD setup was investigated and compared to three different traditional bowtie filters (using Teflon, titanium, and aluminum – all designed to flatten fluence for a 32 cm acrylic phantom). The resulting fluence field patterns in air and behind a 32 cm acrylic phantom are shown in Figure 5A and 5B, respectively. Note that the fluence profile shape is essentially the same across each method with slight variations in scale, and all filters achieve a reasonable flattening of the field in the central portion of the field of view. The Teflon and aluminum bow-ties, as well as the MAD, exhibit plateaus at the outer edge due to maximum bowtie thickness limitations (5 cm) and minimum MAD slot size allowances. There is significant high frequency modulation remaining in the MAD fluence pattern of around 10–20%. The modulation is variable as a function of position. We believe that this is due, in part, to variations in the apparent focal spot size as a function of angular position. Subsequent designs will include this variation as part of the MAD design to further eliminate the high frequency content.

Figure 5.

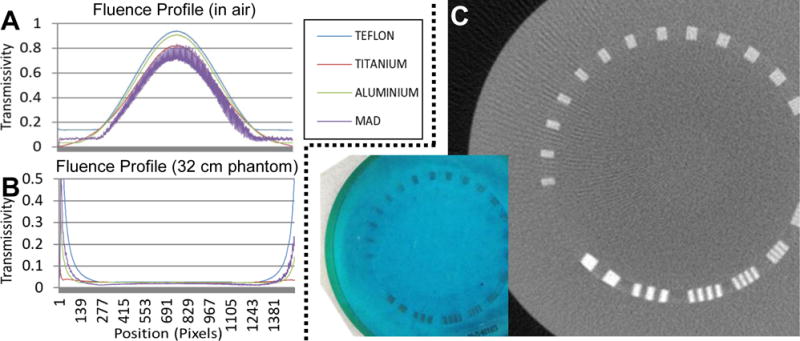
Initial MAD characterization: A) Illustration of fluence field profiles produced by the MAD filter versus traditional attenuating bowtie filters constructed from Teflon, titanium, and aluminum. While all filters produce a similar fluence field modulation and similarly flatten the central region for a 32 cm acrylic phantom (B), the MAD filter exhibits from residual high-spatial-frequency modulations. The magnitude of these variations differs as a function of angular position on the detector and we conjecture that this is due to a changing apparent focal spot shape as a function of position. Future MAD designs can accommodate this variation. Despite the high frequency modulations in this initial design, C) reconstruction of projection data acquired on a resolution phantom with the MAD filter in place do not exhibit significant artifacts associated with the MAD device.

Phantom data was also collected with the MAD filter in place. Reconstruction of this data is shown in Figure 5C. We note that the reconstruction is typical for a flat-panel system and, with proper gain correction, the residual high frequency modulations present in the projection data do not adversely affect the reconstruction. That is, there are no ring artifacts or other defects observed that are attributable to the MAD filter in this reconstruction.

CONCLUSION

We have introduced a new concept for FFM in x-ray imaging using MAD filters. The basic operating theory, a design process, initial fabrication, integration, and characterization of the technology have been performed. Initial studies suggest that this novel modulation strategy is feasible in realistic CT configurations, and the compact designs and modest actuation requirements allow for potential inclusion in current clinical CT systems. Ongoing studies include the fabrication and development of optimized dual MAD designs. Future work will investigate the potential for this methodology to customize CT acquisitions to the patient and specific imaging tasks for reduced radiation exposures.