Abstract
Motivation: Protein contact prediction is important for protein structure and functional study. Both evolutionary coupling (EC) analysis and supervised machine learning methods have been developed, making use of different information sources. However, contact prediction is still challenging especially for proteins without a large number of sequence homologs.
Results: This article presents a group graphical lasso (GGL) method for contact prediction that integrates joint multi-family EC analysis and supervised learning to improve accuracy on proteins without many sequence homologs. Different from existing single-family EC analysis that uses residue coevolution information in only the target protein family, our joint EC analysis uses residue coevolution in both the target family and its related families, which may have divergent sequences but similar folds. To implement this, we model a set of related protein families using Gaussian graphical models and then coestimate their parameters by maximum-likelihood, subject to the constraint that these parameters shall be similar to some degree. Our GGL method can also integrate supervised learning methods to further improve accuracy. Experiments show that our method outperforms existing methods on proteins without thousands of sequence homologs, and that our method performs better on both conserved and family-specific contacts.
Availability and implementation: See http://raptorx.uchicago.edu/ContactMap/ for a web server implementing the method.
Contact: j3xu@ttic.edu
Supplementary information: Supplementary data are available at Bioinformatics online.
1 Introduction
Protein contacts contain important information for protein folding and recent works indicate that one correct long-range contact for every 12 residues may allow accurate topology-level modeling (Kim et al., 2014). Thanks to high-throughput sequencing and better statistical and optimization techniques, evolutionary coupling (EC) analysis for contact prediction has made good progress, which makes de novo prediction of some large proteins possible (Hopf et al., 2012; Marks et al., 2011; Nugent and Jones, 2012; Skwark et al., 2013). For example, the Baker group successfully predicted the fold of a CASP11 target T0806 with 256 amino acids using predicted contacts. Nevertheless, contact prediction accuracy is still low even if only the top L/10 (L is the sequence length) predicted contacts are evaluated.
Existing contact prediction methods belong to roughly two categories: (i) EC analysis methods, such as (Burger and van Nimwegen, 2010; Di Lena et al., 2011; Marks et al., 2011), that make use of multiple sequence alignment; and (ii) supervised machine learning methods, such as SVMSEQ (Wu and Zhang, 2008), NNcon (Tegge et al., 2009), SVMcon (Cheng and Baldi, 2007), CMAPpro (Di Lena et al., 2012), that predict contacts from a variety of information including mutual information and sequence profiles. In addition, a couple of methods also use physical constraints, such as PhyCMAP (Wang and Xu, 2013) and Astro-Fold (Klepeis and Floudas, 2003). MetaPSICOV (Jones et al., 2015) is a recent supervised learning method that predicts contacts by integrating four EC analysis methods and lots of non-coevolutionary information.
Residue EC analysis is a pure sequence-based, unsupervised method that predicts contacts by detecting coevolved residues from the multiple sequence alignment (MSA) of a single protein family. This is based upon an observation that a pair of coevolved residues is often found to be spatially close in the three-dimensional structure. Mutual information (MI) is a local statistical method used to measure residue coevolution strength, but it cannot tell apart direct and indirect residue interaction and thus, has low prediction accuracy. Along with many more sequences are available, global statistical methods such as maximum entropy and probabilistic graphical models are developed to infer residue coevolution from MSA (Balakrishnan et al., 2011; Cocco et al., 2013; Jones et al., 2012; Lapedes et al., 1999, 2012; Marks et al., 2011; Thomas et al., 2008, 2009; Weigt et al., 2009). These global methods can differentiate direct from indirect residue couplings and thus, are more accurate than MI. See (de Juan et al., 2013) for an excellent review of EC analysis. Representative tools of EC analysis include Evfold (Marks et al., 2011), PSICOV (Jones et al., 2012), GREMLIN (Kamisetty et al., 2013), and plmDCA (Ekeberg et al., 2013).
Supervised machine learning methods (Cheng and Baldi, 2007; Shackelford and Karplus, 2007; Wang and Xu, 2013) make use of MI, sequence profile and other protein features, as opposed to EC analysis that makes use of only residue co-evolution. Experiments show that due to use of more information, supervised learning may outperform EC methods for proteins with few sequence homologs (Wang and Xu, 2013). Recently, a few groups such as DNcon (Eickholt and Cheng, 2012), CMAPpro (Di Lena et al., 2012) and PConsC2 (Skwark et al., 2014) have applied deep learning to contact prediction and reported performance improvement.
In this article, we present a new method CoinDCA (coestimation of inverse matrices for direct-coupling analysis) for contact prediction that conducts joint multifamily EC analysis through group graphical lasso (GGL) (Danaher et al., 2014), which is an extension of the graphical lasso formulation employed by PSICOV (Jones et al., 2012). The underlying intuition for joint EC analysis is that distantly related families with divergent sequences may share similar contact maps and we can leverage this by enforcing contact map consistency to improve accuracy. Supervised learning uses different information sources than EC analysis, so their combination should also lead to better prediction accuracy.
The experiments presented here show that our method outperforms existing EC or supervised machine learning methods regardless of the number of non-redundant sequence homologs available for a target protein under prediction, and that our method not only performs better on conserved contacts, but also on family-specific contacts. We also find out that contact prediction may be worsened by merging multiple related families into a single one followed by single-family EC analysis, or by consensus of single-family EC analysis results.
2 Methods
Overview. Our joint multifamily EC analysis predicts contacts of a target family not only using its own residue co-evolution information, but also those in its related families, which may share similar contact maps. It may not be the best to model all these related families using a single Gaussian graphical model (GGM) since their sequences may not be very similar. In contrast, we employ group graphical lasso (GGL) to estimate their joint probability distribution, in which each family is modeled by a separate but correlated GGM. The correlation of two GGMs depends on the evolutionary distance of their corresponding families. We use Random Forests, a popular supervised learning method, to predict the probability of two residues forming a contact from a variety of protein features. Then we integrate the predicted probability as a prior into our GGL to further improve the accuracy of joint EC analysis.
2.1 Probabilistic model of a single protein family
Modeling a single protein family using a probabilistic graphical model has been described in a few papers (Balakrishnan et al., 2011; Jones et al., 2012; Ma et al., 2014; Marks et al., 2011). Here, we briefly introduce GGM used by PSICOV since it is needed to understand our joint graphical model. In this article, we use k to index one protein family under study and K the total number of related protein families, respectively. Given a protein family k and the MSA (MSA) of its sequences, let X denote this MSA where is a 21-dimension binary vector indicating the amino acid type (or gap) at row r (of this MSA) and column i and is equal to 1 if the amino acid at row r (of this MSA) and column i is a. Let denote the mean vector of across all the rows (i.e. proteins). Let L denote the sequence length of this family and Nk the number of sequences. Assuming this MSA has a Gaussian distribution where is the mean vector with 21 L elements and the covariance matrix of size 21 L21 L. The covariance matrix consists of L2 submatrices, each having size 2121 and corresponding to two columns in the MSA. Let denote the submatrix for columns i and j. For any two amino acids (or gap) a and b, their corresponding entry can be calculated as follows.
| (1) |
The calculated by (1) is an empirical covariance matrix, which can be treated as an estimation of the true covariance matrix. Let denote the inverse covariance matrix (also called precision matrix), which indicates the residue or column interaction (or co-evolution) pattern in this protein family. The precision submatrix indicates the interaction strength (or inter-dependency) between two columns i and j, which are totally independent (given all the other columns) if and only if is zero.
Due to matrix singularity, we cannot directly calculate as the inverse of . Instead, can be estimated by maximum-likelihood with a regularization factor as follows.
Where is the L1 norm of , which is used to make sparse and avoid overfitting. Since we assume P to be Gaussian, the above optimization problem is equivalent to the following.
Where is the empirical covariance matrix calculated from the MSA.
2.2 Probabilistic model of multiple related protein families by GGL
Above we have introduced how to model a single protein family using a GGM. Here we present our probabilistic model for a set of K related protein families using a set of correlated GGMs. We still assume that each protein family has a Gaussian distribution with a precision matrix (k = 1, 2,…,K). Let denote the set {,,…, }, and = {,,…,} denote the set of MSAs. If we assume that the K families are independent of each other, we can estimate their precision matrices by maximizing their joint log-likelihood as follows.
| (2) |
We model the correlation of these families through their precision matrices. The correlation of the precision matrices is estimated through the alignment of the related protein families. We build a MSA of these K protein families using a sequence alignment method. Each column in this MSA may consist of columns from several families. If column pair (j1, j3) in family k1 is aligned to column pair (j2, j4), the interaction strength between two columns j1 and j3 in family k1 shall be similar to that between columns j2 and j4 in family k2. That is, if there is one contact between two columns j1 and j3, then it is very likely there is also a contact between two columns j2 and j4.
Accordingly, the precision submatrix for the two columns j1 and j3 in the family k1 shall be related to the submatrix for the two columns j2 and j4 in the family k2 (i.e. ). The correlation strength between and depends on the conservation level of these two column pairs. That is, if these two column pairs are highly conserved, and shall also be highly correlated. Otherwise, they may be only weakly related.
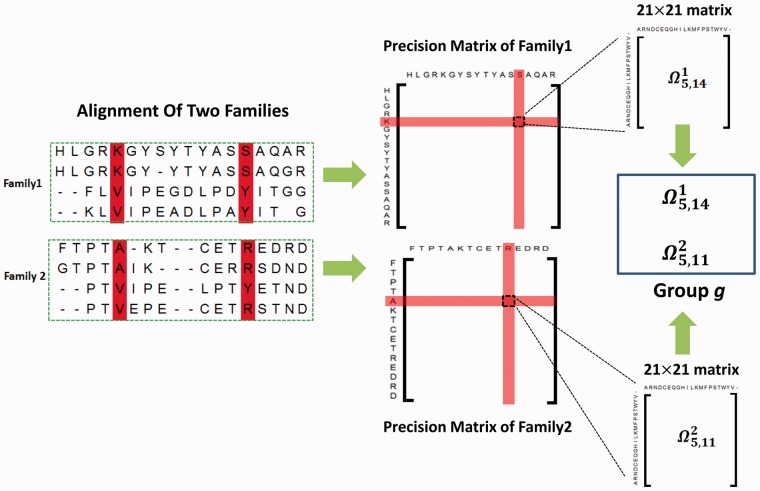
Based upon this observation, we divide all the column pairs into groups so that any two aligned column pairs belong to the same group, as shown in Figure 1. Therefore, if a target family has L columns aligned to at least one auxiliary family, then there are in total L(L − 1)/2 groups.
Fig. 1.
Illustration of column pair and precision submatrix grouping. Columns 5 and 14 in the first family are aligned to columns 5 and 11 in the second family, respectively, so column pair (5,14) in the first family and the pair (5,11) in the second family are assigned to the same group. Accordingly, the two precision submatrices and belong to the same group
Let G denote the number of groups and K the number of involved families. We estimate the K precision matrices by taking into account their correlation using GGL as follows.
| (3) |
Where g represents one group and . Meanwhile, is the square of the entry-wise L2 norm of the precision submatrix . By using this penalty item, we ensure that the column pairs in the same group have similar interaction strength. That is, if one column pair in a particular group has a relatively strong interaction (i.e. is large), the other column pairs in this group shall also have a larger interaction strength. Conversely, if one column pair in a particular group has a relatively weak interaction (i.e. is small), the other column pairs in this group shall also have a smaller interaction strength.
The parameter is used to enforce residue co-evolution consistency in the same group. It is proportional to the conservation level in group g. We measure the conservation level using both the square root of the number of aligned families in a group and also the alignment quality. In particular, is defined as follows.
| (4) |
Where is a constant (=0.001), N is the number of column pairs in group g and Pn is the alignment score (or probability) between the target family and the nth related family at the two aligned columns belonging to group g. Meanwhile, Pn is calculated as Pn = PiPj where Pi and Pj are the marginal alignment probabilities at the two aligned columns. That is, when the two aligned column pairs are conserved, both Pi and Pj are large, so is Pn. Consequently, is large and thus the interaction strength consistency among the column pairs in group g is strongly enforced. In the opposite, if the marginal alignment probability is relatively small, is small. In this case, we shall not strongly enforce the interaction strength consistency among column pairs in this group. By using the conservation level (or alignment quality) to control the consistency of interaction strength, our method is robust to bad alignments and thus, can deal with protein families similar at different levels.
Note that our formulation (3) differs from PSICOV only in the last term, which is used to enforce co-evolution pattern consistency among multiple families. Without this term, our formulation is exactly the same as PSICOV when the same is used. We use an ADMM (Hestenes, 1969) algorithm to solve formulation (3), which is described in the Supplementary Material.
2.3 Including supervised prediction as prior information
Compared to single-family EC analysis, our joint EC analysis uses residue coevolution information from auxiliary families to improve contact prediction. In addition to coevolution information, sequence profile and some non-evolutionary information are also useful for contact prediction. To make use of them, we first use a supervised machine learning method Random Forests to predict the probability of two residues forming a contact and then integrate this predicted probability as prior into our GGL framework. In particular, our Random Forests model predicts the probability of two residues forming a contact using the following information.
PSI-BLAST sequence profile. To predict the contact probability of two residues, we use their position-specific mutation scores and those of the sequentially adjacent residues.
MI and its power series. When residue A has strong interaction with B and B has strong interaction with residue C, it is likely that residue A also has interaction with C. We use the MI power series to account for this kind of chaining effect. In particular, we use MIk where k ranges from 2 to 11 where MI is the mutual information matrix.When there are many sequence homologs, the MI power series are very helpful for medium- and long-range contact prediction.
Non-evolutionary information such as residue contact potential described in (Tan et al., 2006).
EPAD: a context-specific distance-dependent statistical potential (Zhao and Xu, 2012), derived from protein evolutionary information. The Cα and Cβ atomic interaction potentials at all the distance bins are used. The atomic distance is discretized into bins by 1Å and all the distance>15Å is grouped into a single bin.
Homologous pairwise contact score. This score quantify the probability of a residue pair forming a contact between two secondary structure types. See paper (Wang and Xu, 2013) for more details.
Amino acid physic-chemical properties.
Some features are calculated on the residues in a local window of size 5 centered at the residues under consideration. In total there are ∼300 features for each residue pair. We trained and selected the model parameters of our Random Forests model by 5-fold cross validation. In total we used about 850 training proteins, all of which have <25% sequence identity with our test proteins. All of these proteins were selected before CASP10 started in May 2012. See article (Wang and Xu, 2013) for the description of the training proteins.
Finally, our GGL formulation with predicted contact probability as prior is as follows.
| (5) |
Where is the predicted contact probability by Random Forests and is used to reduce the impact of very small predicted probability. Meanwhile, the last term in (5) can be interpreted as the prior probability of , which is used to promote the similarity between the precision matrix and the predicted contact probability. Formulations (3) and (5) differ only in the last term. From computational perspective, the last term of (5) is similar to , so we can use almost the same computational method to optimize both formulations.
2.4 Computational complexity
When no auxiliary family is found, our method becomes a graphical lasso problem with prior and has exactly the same theoretical computational complexity as PSICOV. When multiple auxiliary families are available, theoretically our method is slower than PSICOV. We have parallelized our method using OpenMP to speed up, so empirically the running time of our method depends on the number of available CPUs and the number of related families and their lengths. Overall, it may still take our server (4–5 CPUs) a few hours to predict the contact map of one protein. We are still optimizing our algorithm and code to further reduce the running time. For example, we are implementing a GPU-based version of our algorithm.
2.5 Alignment of multiple protein families
To build the alignment of multiple protein families, we employ a probabilistic consistency method in (Doet al., 2006; Peng and Xu, 2011). To employ this consistency method, we need to calculate the probabilistic alignment matrix between any two protein families. Each matrix entry is the marginal alignment probability (MAP) of two columns, each in one family. By using this consistency method, we ensure that when column i in family 1 is aligned to both column j in family 2 and column k in family 3 with a large probability, then column j and k will also be aligned with a good probability. The consistent alignment among the related families is important for our method to enforce contact map consistency. In addition to this probability method, we also tested MCoffee (Wallace et al., 2006) for generating alignment of multiple related families, which does not show explicit advantage over the probabilistic consistency method.
2.6 Majority voting method for contact prediction
Majority voting is a simple way of utilizing auxiliary protein families for contact prediction. Here, we implemented this method simply for comparison. We first build an alignment of multiple protein families using the methods mentioned above. Then we use PSICOV to predict contact map for each of the related protein families. To determine if there is a contact between any two columns i and j in the target protein family, we use a majority voting based upon the predicted contacts for all the column pairs aligned to the pair (i, j). In addition, we also assign a weight to each family proportional to the number of non-redundant sequence homologs in it. The more sequence homologs, the more weight this family carries since usually such a family has higher contact prediction accuracy. In this experiment, we use PSICOV to predict contacts for each related family separately.
2.7 Pre-processing and Post-processing
We employ the same pre- and post-processing procedures as PSICOV to ensure our comparison with PSICOV is fair. Briefly, to reduce the impact of redundant sequences, we apply the same sequence weighting method as PSICOV. In particular, duplicate sequences are removed and columns containing more than 90% of gaps are also deleted. The sequence is weighted using a threshold of 62% sequence identity. We add a small constant (=0.1) to the diagonal of the empirical covariance matrix to ensure it is not singular. Similar to PSICOV and plmDCA (Ekeberg et al., 2013), average-product correction (APC) (Dunn et al., 2008) is applied to post-process predicted contacts.
3 Results
We use three datasets to evaluate the performance of our method. One is a subset of the benchmark used in the PSICOV paper, consisting of 98 Pfam families, each of which has at least one auxiliary family. As shown in (4), when no auxiliary families are available, our method becomes normal graphical lasso with supervised prediction as prior. By considering only the Pfam families with auxiliary families, we can evaluate the impact of auxiliary families. The CASP10 and CASP11 targets form another two test sets, but many targets have no auxiliary families. See the Supplementary Material for more results.
3.1 PSICOV dataset
It is selected from the 150 Pfam (Bateman et al., 2004; Finn et al., 2014) families used by PSICOV as benchmark, all of which have solved structures in PDB. To make a fair comparison, we use the same solved structures as PSICOV to calculate native contacts. Only contact prediction results are presented. Similar performance trend is observed for contacts. We denote these Pfam families, for which we would like to predict contacts, as the target families. For each target family, we find its related families in Pfam, also called auxiliary families, using HHpred (Söding, 2005) with E-value = 10−6 as cutoff. As a result, 98 families have at least one auxiliary family and are used as our test data. We can also relax the E-value cutoff to obtain more distantly-related auxiliary families, but this does not lead to significant accuracy improvement. Among the 98 target families, the average TM-score (Zhang and Skolnick, 2005) between the representative solved structures of a target family and of its auxiliary families is ∼0.7. That is, the target and auxiliary families are not very close, although they may have similar folds. Even using E-value ≤ 10−17 as cutoff, some target and auxiliary families are only similar at the SCOP fold level.
To ensure that the Pfam database does not miss important sequence homologs, we generate an MSA for each target family by PSI-BLAST (five iterations and E-value = 0.001) and then apply PSICOV to this MSA. Such a method is denoted as PSICOV_b. Since HHblits (Remmert et al., 2012) sometimes may detect sequence homologs of higher quality than PSI-BLAST, we also run HHblits to build an MSA for a target sequence and then examine if this MSA can lead to better prediction or not.
3.2 Methods to be compared
We compare our method with a few popular EC methods such as PSICOV, Evfold, plmDCA and GREMLIN and a few supervised learning methods such that NNcon and CMAPpro. We chose their parameter settings suggested in their respective papers (Di Lena et al., 2012; Ekeberg et al., 2013; Jones et al., 2012; Kamisetty et al., 2013; Marks et al., 2011; Tegge et al., 2009). Since both plmDCA and GREMLIN use the pseudo-likelihood methods, we run Evfold with the mean field solution instead of the pseudo-likelihood solution to diversify the set of methods to be compared. The parameters of Evfold are set as indicated in (Marks et al., 2011). We tested both the old and new version of PSICOV, but did not see much difference. We also tested different parameter settings of PSICOV and Evfold, but could not systematically improve their accuracy.
There are two alternative strategies to use information in auxiliary families. One is that we can merge a target and its auxiliary families into a single MSA and then apply single-family EC analysis. To test this strategy, we align and merge a target and its auxiliary families into a single MSA using a probabilistic consistency method and MCoffee, respectively, and denote them as Merge_p and Merge_m. The other strategy, denoted as Voting, is that we apply the single-family EC method PSICOV to each of the target and auxiliary families and then apply a majority voting method to predict the contacts in the target family.
We evaluate the top L/10, L/5 and L/2 predicted contacts where L is the sequence length of a protein (family) under prediction. The prediction accuracy is defined as the percentage of native contacts among the top predicted contacts. Contacts are short-, medium- and long-range when the sequence distance between the two residues in a contact falls into three intervals [6, 12], (12, 24], and >24, respectively. Generally speaking, medium- and long-range contacts are more important, but more challenging to predict.
3.3 Overall performance on the PSICOV testset
As shown in Table 1, tested on all the 98 Pfam families with auxiliary families, our method CoinDCA outperforms the others when the top L/10, L/5 and L/2 predicted contacts are evaluated, no matter whether the contacts are short, medium and long range. When neither auxiliary families nor supervised learning is used, CoinDCA is exactly the same as PSICOV. Therefore, the results in Table 1 indicate that combining joint EC analysis and supervised learning indeed can improve contact prediction accuracy over single-family EC analysis. We have the following observations.
In terms of contact prediction, the MSAs generated by PSIBLAST or HHblits are not better than those in Pfam.
A simple majority voting scheme performs worse than the single-family EC methods. This may be due to a couple of reasons. When a single family is considered, PSICOV may wrongly predict contacts in each family in very different ways, so consensus of single-family results can only identify those highly conserved contacts, but not those specific to one or few families. In addition, majority voting may suffer from alignment errors.
It does not work well by merging the target and auxiliary families together into a single MSA and then applying single-family EC analysis. There are two possible reasons. One is that the resultant MSA may contain alignment errors, especially when the auxiliary families are not very close to the target family. The other is that we cannot use a single Gaussian distribution to model the related but different families due to sequence divergence (at some positions). Since Merge_p performs better than Merge_m, we will consider only Merge_p in the following sections.
Table 1.
Contact prediction accuracy on all the 98 test Pfam families. plmDCA and GREMLIN use the MSAs in the Pfam database while plmDCA_h and GREMLIN_h use the MSAs generated by HHblits
| Short range |
Medium range |
Long range |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| L/10 | L/5 | L/2 | L/10 | L/5 | L/2 | L/10 | L/5 | L/2 | |
| CoinDCA | 0.528 | 0.446 | 0.316 | 0.496 | 0.435 | 0.312 | 0.561 | 0.502 | 0.391 |
| PSICOV | 0.369 | 0.299 | 0.205 | 0.375 | 0.312 | 0.213 | 0.446 | 0.400 | 0.311 |
| PISCOV_h | 0.382 | 0.306 | 0.204 | 0.418 | 0.334 | 0.218 | 0.466 | 0.421 | 0.310 |
| PSICOV_b | 0.356 | 0.286 | 0.199 | 0.388 | 0.306 | 0.199 | 0.462 | 0.400 | 0.294 |
| Merge_p | 0.316 | 0.265 | 0.183 | 0.303 | 0.246 | 0.178 | 0.370 | 0.328 | 0.253 |
| Merge_m | 0.298 | 0.237 | 0.172 | 0.276 | 0.223 | 0.169 | 0.355 | 0.309 | 0.232 |
| Voting | 0.343 | 0.232 | 0.184 | 0.405 | 0.280 | 0.168 | 0.337 | 0.353 | 0.275 |
| plmDCA | 0.422 | 0.327 | 0.203 | 0.433 | 0.354 | 0.233 | 0.484 | 0.443 | 0.343 |
| plmDCA_h | 0.387 | 0.300 | 0.186 | 0.433 | 0.339 | 0.211 | 0.480 | 0.413 | 0.292 |
| plmDCA_b | 0.381 | 0.301 | 0.184 | 0.431 | 0.338 | 0.210 | 0.478 | 0.421 | 0.289 |
| GREMLIN | 0.410 | 0.312 | 0.220 | 0.401 | 0.332 | 0.225 | 0.447 | 0.423 | 0.329 |
| GREMLIN_h | 0.387 | 0.291 | 0.188 | 0.391 | 0.316 | 0.204 | 0.428 | 0.400 | 0.301 |
| GREMLIN_b | 0.379 | 0.289 | 0.187 | 0.390 | 0.314 | 0.203 | 0.426 | 0.398 | 0.303 |
| Evfold | 0.340 | 0.274 | 0.191 | 0.364 | 0.298 | 0.209 | 0.400 | 0.361 | 0.281 |
| Evfold_h | 0.326 | 0.250 | 0.171 | 0.345 | 0.279 | 0.189 | 0.381 | 0.333 | 0.262 |
| Evfold_b | 0.324 | 0.252 | 0.169 | 0.344 | 0.275 | 0.190 | 0.382 | 0.332 | 0.261 |
See the Supplementary Material for statistical significance (i.e. P value).
PSICOV models the MSA of a protein family using a multivariate Gaussian distribution. This Gaussian assumption holds only when the family contains a large number of sequence homologs. plmDCA and GREMLIN do not use the Gaussian assumption and are reported to outperform PSICOV on some Pfam families. Our method CoinDCA still uses the Gaussian assumption. This test result indicates that when EC information in multiple related families is used, even with Gaussian assumption, we can still outperform the single-family EC methods without using Gaussian assumption.
3.4 Dependency on the number of sequence homologs
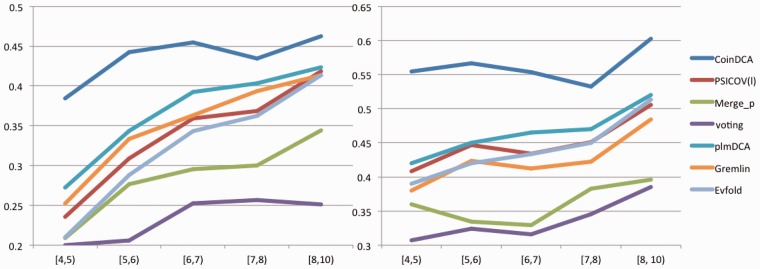
Our method outperforms the others regardless of the size of a protein family. Similar to (Marks et al., 2011; Wang and Xu, 2013), we calculate the number of non-redundant sequence homologs in a family (or MSA) by where i and j are sequence indexes and si,j is a binary variable indicating if two sequences are similar or not. It is equal to 1 if the normalized hamming distance between two sequences is less than 0.3; otherwise, 0. The reason why we use Meff instead of the number of sequences to quantify the information content in an MSA is that there may exist many highly similar homologs in the MSA. Highly similar homologs do not provide more information for coevolution detection than a single one, so we can only count the number of non-redundant sequence homologs. We divide the 98 test families into five groups by lnMeff : [4,5), [5,6), [6,7), [7,8), [8,10), and calculate the average L/10 prediction accuracy in each group. Figure 2 shows that our method outperforms the others regardless of lnMeff. In particular, the advantage of our method over the others is even larger when lnMeff is small. In the Supplementary Figures S1 and S2, we also show the relationship between accuracy and relatively large Meff (>300).
Fig. 2.
(A) Medium-range and (B) Long-range L/10 prediction accuracy with respect to lnMeff
3.5 Performance and contact conservation level
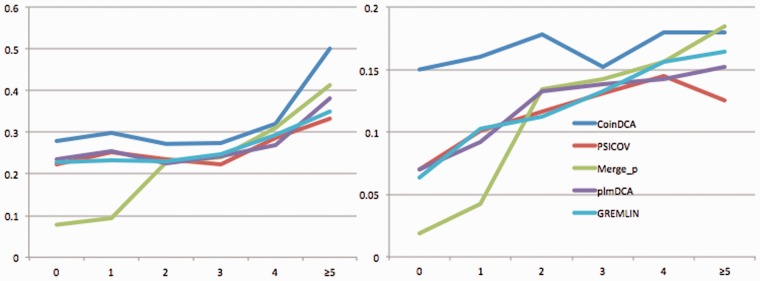
For a native contact in the target family, we measure its conservation level by the number of auxiliary families with a contact alignable to this target contact. The 98 test families have conservation levels ranging from 0 to 8, corresponding to non-conserved and highly conserved, respectively. In particular, a native contact with a conservation level of 0 is target family-specific since it has no support from any auxiliary families. Correct prediction of family-specific contacts is important since they may be very useful to the refinement of a template-based protein model.
Supplementary Figure S3 shows the distribution of the contact conservation level in our test set and that a large number of native contacts are not conserved. Figure 3(A) and (B) shows the ratio of medium- and long-range native contacts ranked among top L/10 predictions with respect to contact conservation level. Our method CoinDCA ranks many more native long-range contacts among top L/10 than the single-family EC methods PSICOV, plmDCA and GREMLIN regardless of conservation level. CoinDCA has similar performance as the family merging method Merge_p for long-range contacts with conservation level ≥5, but significantly outperforms Merge_p for family-specific contacts. This may be because when the target and auxiliary families are merged together, the signal for highly conserved contacts is reinforced but that for family-specific contacts is diluted. By contrast, our joint EC analysis method can reinforce the signal for highly conserved contacts without losing family-specific information.
Fig. 3.
The ratio (Y-axis) of native contacts ranked by a prediction method among top L/10 with respect to contact conservation level (X-axis) for (A) medium range and (B) long range
3.6 Performance on the CASP10 targets
In this test we run NNcon, PSICOV, plmDCA, GREMLIN and EVfold locally with default parameters, and CMAPpro through its web server. Again, we run HHpred to search the Pfam database for auxiliary families for each test target. Meanwhile, 75 of 123 targets have at least one auxiliary family. For those targets without any auxiliary families, our method actually becomes the combination of single-family EC analysis and supervised learning. As shown in Table 2, on the whole CASP10 set, our method CoinDCA again outperforms the others in terms of the accuracy of the top L/10, L/5 and L/2 predicted contacts.
Table 2.
Contact prediction accuracy on all the 123 CASP10 targets
| Short range |
Medium range |
Long range |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| L/10 | L/5 | L/2 | L/10 | L/5 | L/2 | L/10 | L/5 | L/2 | |
| CoinDCA | 0.517 | 0.435 | 0.311 | 0.500 | 0.440 | 0.340 | 0.412 | 0.351 | 0.279 |
| PSICOV | 0.234 | 0.191 | 0.140 | 0.310 | 0.259 | 0.192 | 0.276 | 0.225 | 0.168 |
| plmDCA | 0.264 | 0.218 | 0.152 | 0.344 | 0.289 | 0.214 | 0.326 | 0.280 | 0.213 |
| NNcon | 0.499 | 0.399 | 0.275 | 0.393 | 0.334 | 0.226 | 0.239 | 0.188 | 0.001 |
| GREMLIN | 0.256 | 0.212 | 0.161 | 0.343 | 0.280 | 0.229 | 0.320 | 0.278 | 0.159 |
| CMAPpro | 0.437 | 0.368 | 0.253 | 0.414 | 0.363 | 0.276 | 0.336 | 0.297 | 0.227 |
| EVfold | 0.193 | 0.165 | 0.130 | 0.294 | 0.249 | 0.188 | 0.257 | 0.225 | 0.171 |
See the Supplementary Material for statistical significance (i.e. P value).
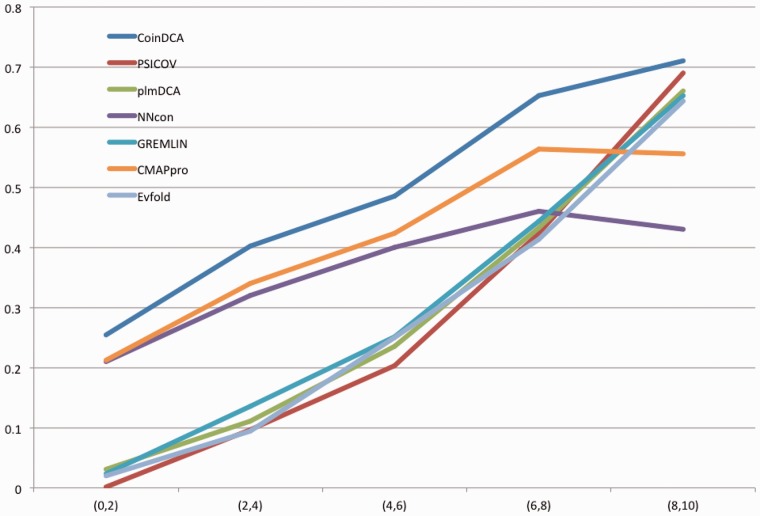
We also divide the 123 CASP10 targets into five groups according to lnMeff : (0,2), (2,4), (4,6), (6,8), (8,10), which contain 19, 17, 25, 36 and 26 targets, respectively. Meanwhile, Meff measures the number of non-redundant sequence homologs available for a target protein under prediction. We then calculate the average medium- and long-range contact prediction accuracy in each group. Figure 4 clearly shows that the prediction accuracy increases with respect to lnMeff and that our method outperforms the others on all the five intervals of lnMeff. In particular, our method works much better than the single-family EC analysis methods when lnMeff < 8.
Fig. 4.
The relationship between prediction accuracy and lnMeff. X-axis is the lnMeff value and Y-axis is the mean accuracy of top L/10 predicted contacts in the corresponding CASP10 target group. Only medium- and long-range contacts are considered
We also show the results of our method on the CASP10 hard targets and the CASP11 targets in the Supplementary Material. Our method outperforms the others on these datasets in terms of both medium- and long-range accuracy. On the hard targets, all the tested methods have low long-range accuracy because these targets have very few sequence homologs, so it is unclear if the predicted long-range contacts will be useful or not. However, our method has reasonable medium-range accuracy (∼0.4 for top L/10 predictions), which may be useful to ab initio folding and other applications.
3.7 More Results in the Supplementary Material
Results in the Supplementary Material. (i) performance on all the 150 Pfam families in the PSICOV test set; (ii) performance on the CASP10 hard targets; (iii) performance on the whole CASP11 set and the CASP11 hard targets; (iv) P values between our method and the others on the PSICOV, CASP10 and CASP11 sets; (v) performance on the 98 test Pfam families with respect to the number of non-redundant sequence homologs divided into 11 intervals; (vi) distribution of contact conservation level and (vii) comparison with MetaPSICOV.
4 Discussion
This article has presented a GGL method to predict contacts by exploring joint multi-family EC analysis and supervised machine learning. EC analysis and supervised learning are currently two major methods for contact prediction, but they use different information sources. Our joint EC analysis predicts contacts in a target family by analyzing residue co-evolution information in a set of related protein families which may share similar contact maps. In order to effectively integrate information across multiple families, we use GGL to estimate the joint probability distribution of multiple related families by a set of correlated Gaussian models. Experiments show that the combination of joint EC analysis with supervised machine learning can significantly improve contact prediction, and that our method even outperforms single-family EC analysis on protein families with a large number of sequence homologs. We have also shown that contact prediction cannot be improved by a simple method, such as family merging and majority voting of single-family EC analysis results. These simple methods may improve prediction for highly conserved contacts at the cost of family-specific contacts.
Our method can be further improved. For example, similar to GREMLIN and plmDCA, we may relax the Gaussian assumption to improve prediction accuracy. This article uses an entry-wise L2 norm to penalize contact map inconsistency among related protein families. There may be other penalty functions that can more accurately quantify contact map similarity between two families as a function of sequence similarity and thus, further improve contact prediction. It may further improve contact prediction by integrating other supervised learning methods such as CMAPpro, NNcon and DNcon or even other EC methods into our GGL framework.
In this paper we use Pfam to define a protein family because it is manually curated and very accurate. There are also other criteria to define a protein family. For example, SCOP defines a protein family based upon structure information and thus, classifies protein domains into much fewer families than Pfam. In our experiment, the average structure similarity, measured by TMscore (Zhang and Skolnick, 2004), between a target (Pfam) family and its auxiliary (Pfam) families is only around 0.7. That is, many auxiliary families are not highly similar to its target families even by the SCOP definition. Indeed, some auxiliary families are only similar to the target family at the SCOP fold level. That is, even a remotely-related protein family may provide information useful for contact prediction.
We can further extend our method to predict contacts of all the protein families simultaneously, instead of one-by-one, by joint EC analysis across the whole protein family universe. First we can use a graph to model the whole Pfam database, each vertex representing one Pfam family and an edge indicating that two families may be related. Then we can use a graph of correlated GGMs to model the whole Pfam graph, each GGM for one vertex. The GGMs of two vertices in an edge are correlated together through the alignment of their respective protein families. By this way, the residue co-evolution information in one family can be passed onto any family that is connected through a path. As such, we may predict the contacts of one family by making use of information in all the path-connected families. By enforcing this global consistency, we should be able to further improve EC analysis for contact prediction. However, to simultaneously estimate the parameters of all the GGMs, a large amount of computational power will be needed. Such an idea is similar (in spirit) to the global trace graph method described by (Heger et al., 2007).
Supplementary Material
Acknowledgments
Funding
National Institutes of Health (R01GM0897532); National Science Foundation (DBI-0960390, CAREER award CCF-1149811); Alfred P. Sloan Research Fellowship; UChicago RCC allocation.
Conflict of Interest: none declared.
References
- Balakrishnan S., et al. (2011) Learning generative models for protein fold families. Proteins Struct Funct Bioinform., 79, 1061–1078. [DOI] [PubMed] [Google Scholar]
- Bateman A., et al. (2004) The Pfam protein families database. Nucleic Acids Res., 32(Suppl. 1), D138–D141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burger L., van Nimwegen E. (2010) Disentangling direct from indirect co-evolution of residues in protein alignments. PLoS Comput. Biol., 6, e1000633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng J., Baldi P. (2007) Improved residue contact prediction using support vector machines and a large feature set. BMC Bioinformatics, 8, 113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cocco S., et al. (2013) From principal component to direct coupling analysis of coevolution in proteins: Low-eigenvalue modes are needed for structure prediction. PLoS Comput. Biol., 9, e1003176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danaher P., et al. (2014) The joint graphical lasso for inverse covariance estimation across multiple classes. J. Roy. Stat. Soc. B, 76, 373–397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Juan D., et al. (2013) Emerging methods in protein co-evolution. Nat. Rev. Genet., 14, 249–261. [DOI] [PubMed] [Google Scholar]
- Di Lena P., et al. (2011) Is there an optimal substitution matrix for contact prediction with correlated mutations? IEEE/ACM Trans Comput . Biol. Bioinformatics, 8, 1017–1028. [DOI] [PubMed] [Google Scholar]
- Di Lena P., et al. (2012) Deep architectures for protein contact map prediction. Bioinformatics, 28, 2449–2457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Do C.B., et al. (2006) CONTRAlign: discriminative training for protein sequence alignment. In: Research in Computational Molecular Biology. Springer, pp. 160–174. [Google Scholar]
- Dunn S.D., et al. (2008) Mutual information without the influence of phylogeny or entropy dramatically improves residue contact prediction. Bioinformatics, 24, 333–340. [DOI] [PubMed] [Google Scholar]
- Eickholt J., Cheng J. (2012) Predicting protein residue–residue contacts using deep networks and boosting. Bioinformatics, 28, 3066–3072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ekeberg M., et al. (2013) Improved contact prediction in proteins: Using pseudolikelihoods to infer Potts models. Phys. Rev. E, 87, 012707. [DOI] [PubMed] [Google Scholar]
- Finn R.D., et al. (2014) Pfam: the protein families database. Nucleic Acids Res., 42, D222–D230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heger A., et al. (2007) The global trace graph, a novel paradigm for searching protein sequence databases. Bioinformatics, 23, 2361–2367. [DOI] [PubMed] [Google Scholar]
- Hestenes M.R. (1969) Multiplier and gradient methods. J. Optim. Theory Appl., 4, 303–320. [Google Scholar]
- Hopf T.A., et al. (2012) Three-dimensional structures of membrane proteins from genomic sequencing. Cell, 149, 1607–1621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones D.T., et al. (2012) PSICOV: precise structural contact prediction using sparse inverse covariance estimation on large multiple sequence alignments. Bioinformatics, 28, 184–190. [DOI] [PubMed] [Google Scholar]
- Jones D.T., et al. (2015) MetaPSICOV: combining coevolution methods for accurate prediction of contacts and long range hydrogen bonding in proteins. Bioinformatics, 31, 999–1006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kamisetty H., et al. (2013) Assessing the utility of coevolution-based residue–residue contact predictions in a sequence-and structure-rich era. Proc. Natl Acad. Sci. USA, 110, 15674–15679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim D.E., et al. (2014) One contact for every twelve residues allows robust and accurate topology‐level protein structure modeling. Proteins, 82, 208–218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klepeis J., Floudas C. (2003) ASTRO-FOLD: a combinatorial and global optimization framework for ab initio prediction of three-dimensional structures of proteins from the amino acid sequence. Biophys. J., 85, 2119–2146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lapedes A., et al. Using sequence alignments to predict protein structure and stability with high accuracy. arXiv preprint arXiv:1207.2484 2012. [Google Scholar]
- Lapedes A.S., et al. (1999) Correlated mutations in models of protein sequences: phylogenetic and structural effects. Lecture Notes Monograph Series, 236–256. [Google Scholar]
- Ma J., et al. (2014) MRFalign: Protein Homology Detection through Alignment of Markov Random Fields. arXiv:1401.2668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marks D.S., et al. (2011) Protein 3D structure computed from evolutionary sequence variation. PLoS One, 6, e28766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nugent T., Jones D.T. (2012) Accurate de novo structure prediction of large transmembrane protein domains using fragment-assembly and correlated mutation analysis. Proc. Natl Acad. Sci. USA, 109, E1540–E1547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng J., Xu J.A. (2011) multiple‐template approach to protein threading. Proteins Struct. Funct. Bioinformatics, 79, 1930–1939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Remmert M., et al. (2012) HHblits: lightning-fast iterative protein sequence searching by HMM-HMM alignment. Nat. Methods, 9, 173–175. [DOI] [PubMed] [Google Scholar]
- Shackelford G., Karplus K. (2007) Contact prediction using mutual information and neural nets. Proteins Struct. Funct. Bioinformatics, 69, 159–164. [DOI] [PubMed] [Google Scholar]
- Skwark M.J., et al. (2013) PconsC: combination of direct information methods and alignments improves contact prediction. Bioinformatics, 29, 1815–1816. [DOI] [PubMed] [Google Scholar]
- Skwark M.J., et al. (2014) Improved contact predictions using the recognition of protein like contact patterns. PLoS Comput. Biol., 10, e1003889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Söding J. (2005) Protein homology detection by HMM–HMM comparison. Bioinformatics, 21, 951–960. [DOI] [PubMed] [Google Scholar]
- Tan Y.H., et al. (2006) Statistical potential‐based amino acid similarity matrices for aligning distantly related protein sequences. Proteins Struct. Funct. Bioinformatics, 64, 587–600. [DOI] [PubMed] [Google Scholar]
- Tegge A.N., et al. (2009) NNcon: improved protein contact map prediction using 2D-recursive neural networks. Nucleic Acids Res., 37(Suppl. 2), W515–W518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas J., et al. (2008) Graphical models of residue coupling in protein families. IEEE/ACM Trans. Comput. Biol. Bioinformatics (TCBB), 5, 183–197. [DOI] [PubMed] [Google Scholar]
- Thomas J., et al. (2009) Graphical models of protein–protein interaction specificity from correlated mutations and interaction data. Proteins Struct. Funct. Bioinformatics, 76, 911–929. [DOI] [PubMed] [Google Scholar]
- Wallace I.M., et al. (2006) M-Coffee: combining multiple sequence alignment methods with T-Coffee. Nucleic Acids Res., 34, 1692–1699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Z., Xu J. (2013) Predicting protein contact map using evolutionary and physical constraints by integer programming. Bioinformatics, 29, i266–i273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weigt M., et al. (2009) Identification of direct residue contacts in protein–protein interaction by message passing. Proc. Natl Acad. Sci. USA, 106, 67–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu S., Zhang Y. (2008) A comprehensive assessment of sequence-based and template-based methods for protein contact prediction. Bioinformatics, 24, 924–931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y., Skolnick J. (2004) Scoring function for automated assessment of protein structure template quality. Proteins Struct. Funct. Bioinformatics, 57, 702–710. [DOI] [PubMed] [Google Scholar]
- Zhang Y., Skolnick J. (2005) TM-align: a protein structure alignment algorithm based on the TM-score. Nucleic Acids Res., 33, 2302–2309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao F., Xu J. (2012) A position-specific distance-dependent statistical potential for protein structure and functional study. Structure, 20, 1118–1126. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.