The intrinsic mechanics of B-DNA in solution characterized by NMR

Abstract

Experimental characterization of the structural couplings in free B-DNA in solution has been elusive, because of subtle effects that are challenging to tackle. Here, the exploitation of the NMR measurements collected on four dodecamers containing a substantial set of dinucleotide sequences provides new, consistent correlations revealing the DNA intrinsic mechanics. The difference between two successive residual dipolar couplings (ΔRDCs) involving C6/8-H6/8, C3′-H3′ and C4′-H4′ vectors are correlated to the ³¹P chemical shifts (δP), which reflect the populations of the BI and BII backbone states. The δPs are also correlated to the internucleotide distances (D_inter) involving H6/8, H2′ and H2″ protons. Calculations of NMR quantities on high resolution X-ray structures and controlled models of DNA enable to interpret these couplings: the studied ΔRDCs depend mostly on roll, while D_inter are mainly sensitive to twist or slide. Overall, these relations demonstrate how δP measurements inform on key inter base parameters, in addition to probe the BI↔BII backbone equilibrium, and shed new light into coordinated motions of phosphate groups and bases in free B-DNA in solution. Inspection of the 5′ and 3′ ends of the dodecamers also supplies new information on the fraying events, otherwise neglected.

INTRODUCTION

Characterizing the relationships between the different structural parameters describing the B-DNA is crucial to understand DNA behavior and interactions with other molecules. That is especially relevant for indirect readout mechanisms, modulated by the sequence-dependent DNA intrinsic mechanical properties (1–4). An earlier analysis of a large data set of X-ray structures showed that in both free and bound DNA the slide, roll and twist are correlated to various degrees, depending on the dinucleotidic sequence (5). Several other studies, based on high resolution X-ray structures, revealed intimate structural couplings between the phosphate group states, sugar conformations, inter base pair parameters, base pair displacement (X-disp) and groove dimensions (6–13). The backbone conformations in free B-DNA consist of two states, BI and BII, originally defined by the conformations of the torsion angles ε and ζ trans/g- in BI (ε − ζ ∼ −90°) and g-/trans in BII (ε − ζ ∼ +90°) (14) (Figure 1). Analysis of these states enabled us to define two structural profiles at the dinucleotide level: BI linkages correspond to negative slide, null or positive roll and low or moderate twist (BI profile), while BII linkages are associated with positive slide, negative roll and high twist (BII profile) (6,7). The minor and major groove dimensions are also intrinsically coupled to the BII density (8,15). However, although several molecular modeling studies have supported this view (7,16–19), experimental evidence of DNA intrinsic structural couplings is still lacking.

Figure 1.

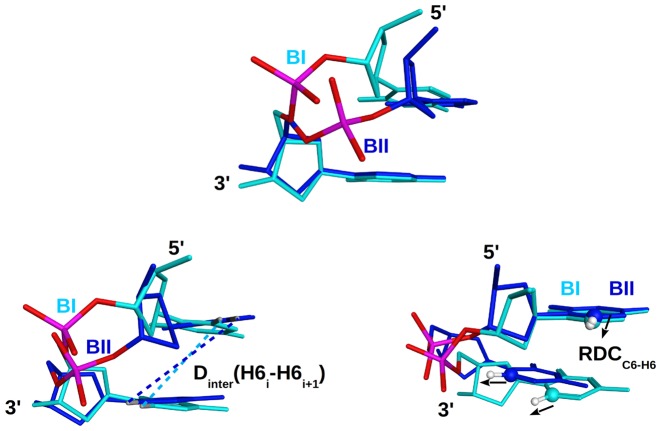
Structural basis for the relation between BI and BII states and two types of NMR observables. In each panel, the BI and BII states are compared by superposition of a CpC dinucleotide in these two backbone conformations (X-ray structure, PDB ID: 3U89). CpC in BI (sugars and bases in cyan) is characterized by a roll of +9° and a twist of 37°, while CpC in BII (sugars and bases in dark blue) has a roll of −2° and a twist of 45°. Note that these values were calculated for a single strand, and not combining the two strands. Top: comparison of the BI and BII phosphate linkage conformations resulting from changes in the ε and ζ torsions. Bottom left: dependence of the internucleotide distances on the phosphate state, illustrated with a H6–H6 internucleotide distances which is longer in a BII (dark blue dashed lines) than in a BI step (cyan dashed lines). Bottom right: influence of the backbone conformation on the relative orientation between internucleotides RDCs, illustrated with C6–H6 vectors (RDC_C6–H6) indicated by black arrows.

This knowledge could progress by considering DNA structures derived from nuclear magnetic resonance spectroscopy (NMR), taking advantage of residual dipolar couplings (RDC) that substantially improve the accuracy of refined DNA structures (20–23). RDCs are collected in partially oriented media and result from an incomplete averaging of anisotropic magnetic interactions between proximal active spins of nuclei, typically carbon and hydrogen in C–H bonds in DNA. RDCs inform about the angle between specific C–H vectors and the alignment tensor, which is roughly parallel to the external applied magnetic field B0 when Pf1 phages are used to orientate the DNA (24,25). RDCs thus complement the other NMR data, essentially internucleotide distances from nuclear overhauser effect (NOE) connectivities, useful in providing constrains to the relative position of two successive nucleosides, and scalar couplings to investigate the behavior of sugars and phosphodiester linkages. Thus, the recent DNA structural models obtained from NMR are expected to be more reliable to explore the B-DNA mechanics than those, more loosely restrained, which did not benefit from the RDC observations.

As of today, the DNA structures obtained from RDC and NOE restraints (20,22,26–32) remain scarce and suffer from several limitations. The sequences are dominated by A-tracts (21,27,28,32) and the Drew–Dickerson dodecamer (29–31). This redundancy has revealed inconsistencies between the refined structures of oligomers of identical or similar sequences. For instance, TpA in T₃A₃ or T₄A₄ had either a negative (21) or a marked positive roll (32); the structures of the Drew–Dickerson dodecamer show substantial differences when refined from the same NMR data set but with different NMR-based backbone restraints (29–31). More generally, even if the restraints are expected to contain the impact of varying refinement protocols, the use of different force fields and representations of solvent (implicit or explicit) raise the question of the protocol-dependent outcomes and thus of the reliability of the details for those DNA NMR structures. The very short restrained molecular dynamics, 1 ns or less, and the recurrent use of artificial restraints on the backbone angles (21,27,30–32) could also introduce biases on the final DNA representation. In sum, the lack of sequence variety combined with limitations of the refinement protocols have not yet delivered a data set of structures with consistent information on the intrinsic mechanics of free B-DNA in solution.

Here, we approach this intrinsic mechanics by exploiting directly the NMR measurements instead of the derived refined structural models. In addition to RDCs and distances, ³¹P chemical shift (δP) measurements were also taken into account. The structural significance of δP was deciphered earlier, mainly from correlations between δP and coupling constants (33,34), and more recently from quantum chemistry calculations (35,36). Thus, the dispersion of δP in B-DNA is attributed to the variable propensity of phosphate groups to undergo the BI↔BII conformational exchange. In solution, high-field shifted δP indicate BI-rich linkages while down-field shifted δP are typical of BII-rich linkages (33,34,36). In practice, the translation of δP in terms of BI/BII ratios is now possible using two different approaches (37,38).

The δPs can be used to probe the backbone behavior and its strong sequence dependence (15,29,37–39). Taking advantage of the accuracy of δP measurements, it has emerged that specific δP values, and hence specific BI/BII ratios, characterize the 16 unique dinucleotides (NpN). These specific δP values led to conceive an experimental scale in which the 10 complementary dinucleotides (NpN•NpN) are characterized by individual scores that represent their BII propensities (40). This scale is called TRX in reference to the relationship between the BI and BII states, Twist, Roll and base pair displacement (X-disp), with reference to the BI and BII profiles from X-ray data, as explained above. This view is supported by consistent NMR data collected in solution on a 14 bp DNA, in which internucleotide distances were found to be correlated to δPs (37).

The aim of the present study is to further develop this strategy, using a large variety of NMR data, comprising δPs, distances and RDCs, collected on four non-palindromic dodecamers that offer a substantial set of dinucleotide sequences. These oligomers, once juxtaposed, correspond to a fragment of the ‘sequence 601’, known for its strong ability to form nucleosomes (41). Recently, the fresh δPs from the four dodecamers were used as a test set, which validated the TRX scale, thereby demonstrating that the BII propensities are predictable based on the DNA sequence (15).

To broaden and deepen the previous analyses, here we uncover and interpret relationships between δPs on one hand, and ΔRDCs and internucleotide distances on the other hand. Data from the terminal dinucleotides are excluded because of end effects. ΔRDCs are the differences between two RDCs of successive bases on the same strand, directly related to the angles between two dipolar vectors. The advantage is to avoid the calculation of the alignment tensor. Similar techniques are used in protein refinement protocols (42,43). The combination of ΔRDCs, δPs and internucleotide distances provides a consistent data package which is used to characterize the behavior of the dinucleotides in free DNA in solution. Meanwhile we determine which helical parameters of DNA influence the ΔRDCs and internucleotide distances, using ultrahigh resolution X-ray structures as experimental templates, and additional models where the helicoidal parameters were controlled. Combining those two analyses leads to a coherent reconstitution of the couplings between NMR observables in terms of the intrinsic DNA mechanics. These results are used in the last part of our study to scrutinize the 3′- and 5′-terminal dinucleotides and to determine whether the fraying events, still experimentally poorly characterized, do perturb the double helix as severely as suggested by recent Molecular Dynamics (MD) simulations (16,44,45).

Overall, the issue is a new characterization of the B-DNA intrinsic mechanics in solution. Our results show that combining various directly observed NMR measurements on DNA offers a practical strategy to uncover the heterogeneous sequence-dependent structural couplings underlying the B-form double-helix. As a consequence, the local helicoidal parameters can be estimated from a readout of δPs, which is advantageous considering that the δPs can be accessed with relative ease.

MATERIALS AND METHODS

DNA sequences

Four oligodeoxyribonucleotides of 12 base pairs (bp) (sequences in Table 1) were studied by NMR. These sequences, placed end to end after discarding the terminal base pairs, span a continuous 39 bp segment corresponding to the 5′ part of the non-palindromic sequence 601, selected from SELEX experiments for its very high-affinity to associate with the histone octamers (41).

Table 1. Sequences of the four studied DNA dodecamers constituents of the sequence 601.

Oligo 1	5′-TpCpGpTpApGpCpApApGpCpT-3′•5′-ApGpCpTpTpGpCpTpApCpGpA-3′
Oligo 2	5′-GpCpTpCpTpApGpCpApCpCpG-3′•5′-CpGpGpTpGpCpTpApGpApGpC-3′
Oligo 3	5′-CpCpGpCpTpTpApApApCpGpC-3′•5′-GpCpGpTpTpTpApApGpCpGpG-3′
Oligo 4	5′-CpGpCpApCpGpTpApCpGpCpG-3′•5′-CpGpCpGpTpApCpGpTpGpCpG-3′

Sample preparation

Oligomers were synthesized by Eurogentec Inc. (Belgium). The sample was dissolved in an aqueous sodium-phosphate buffer corresponding to an ionic strength of 0.1 (mol/l) with 0.1 mM EDTA, at pH 6.5. The duplexes were prepared by mixing the two complementary strands in a 1:1 ratio in 450 μl H₂O and 50 μl D₂O for studies of exchangeable protons. For studies of non-exchangeable protons, the duplexes were lyophilized three times and dissolved in 500 μl of 99.9% D₂O. The final concentration of double strand oligomers is 1–1.5 mM.

NMR spectroscopy

³¹P chemical shifts and distances

All NMR spectra were recorded on a Bruker Avance spectrometer operating at a proton frequency of 500 MHz and at a phosphorus frequency of 202 MHz with a 5 mm gradient indirect probe. All spectra were processed with NMRpipe (46) or Topspin softwares (Bruker) and analyzed with Sparky (T. D. Goddard and D. G. Kneller, SPARKY 3, University of California, San Francisco, USA).

One-dimensional ¹H spectra collected from 5 to 60°C with a 5°C step enabled us to check the stability of the duplexes over this range of temperature. All the imino protons were clearly observable until 40°C, except those of the terminal base pairs.

The aromatic (H6, H8, H2, H5 and CH3) and ribose (H1′, H2′, H2″, H3′, H4′) protons of the four oligonucleotides were assigned using classical 2D homonuclear NMR (NOESY, TOCSY, COSY). 2D ¹H-¹³C HSQC and TROSY experiments were also performed to observe the ribose and aromatic correlations, respectively. The assignment of H3′ and H4′ protons enabled in a second step to assign the ³¹P signals through the ³J ¹H3′_i-1–³¹P_i (inter-residue connectivity) and ⁴J ¹H4′_i-³¹P_i (intraresidue connectivity) cross peaks in HETCOR experiments. Therefore, two independent types of correlations were used to guarantee safe phosphorus assignments.

¹H NMR studies were performed at 10, 20 and 30°C. 2D NOESY spectra were recorded using mixing times of 100, 200, 300 ms for exchangeable protons and 80, 100, 200, 300 and 400 ms for non exchangeable protons. MLEV-17 TOCSY experiments were run using mixing time of 120 ms. The 2D NOESY and MLEV-17 TOCSY were recorded under the following experimental conditions: 2048 data points and 512 t1 increments with spectral widths of 10 000 Hz for exchangeable protons and 5000 Hz for non exchangeable protons. The water signal was suppressed with a WATERGATE sequence (47). NOE distances were extracted with particular care from cross-peaks after visual inspection of the build-up rates and using the distance extrapolation method to correct the spin-diffusion effects (48). However, some large distances (typically > 5 Å) were only observable in NOESY spectra recorded with a mixing time of 300 ms and were thus less accurately measured than shorter distances. Distances were normalized using the cytosine H5–H6 proton pairs (r = 2.5 Å) apart from those involving the CH₃ group, for which the reference was the average H6–CH₃ distance (r = 2.9 Å). The experimental error was estimated to 10% of the measured distances.

¹H-³¹P HETCOR (49) experiments were run at 20, 30, 40°C. The spectra width was 2500 Hz in the ¹H dimension and 810 Hz in the ³¹P dimension. Data were recorded with 2048 points in the ¹H dimension and 256 increments in the ³¹P dimension. ³¹P chemical shifts (δP) were referenced relative to internal trimethyl phosphate. A previous study of δPs as a function of temperature (15) showed that the phosphate group behavior in the present dodecamers is consistent with that was previously observed on other oligomers (38,50). Only one particular case of strong δP change was observed on a BI-rich step, A₇pA₈ in Oligo 3, which is suspected to undergo transient excursions toward unknown low-populated conformations (15). Uncertainty of δPs measured in solution was estimated to ±0.02 ppm. Note that in case of correlations between δP and ΔRDCs, the uncertainty on δPs was estimated to ±0.05 ppm to take account of the slight variations that could be induced by the oriented medium (51).

All δPs and distances presented here were collected at 20°C.

Sugar conformations

The sugar conformation was estimated by inspecting the intensities of TOCSY H1′–H4′ cross-peaks. These intensities are related to the values of the successive scalar couplings involved in the TOCSY H1′–H4′ transfer, J_H1′-H2′, J_H1′-H2″, J_H2′-H3′, J_H2″-H3′ and J_H3′-H4′. Among these scalar couplings, J_H3′-H4′ is strongly sensitive to the sugar conformation (52,53). Its value, quasi null for South (C2′-endo) sugars, increases with North (C3′-endo) or East (O4′-endo) populations and allows the H1′–H4′ transfer. In practice, observable TOCSY H1′–H4′ cross-peaks thus sign the presence of North or East conformers. That TOCSY H1-H3′ cross-peaks of all the residues in the four dodecamers are observed while several TOCSY H1′-H4′ cross-peaks are missing confirms the role of bottleneck played by J_H3′-H4′, as postulated before (54).

Conformation of the backbone angles β and γ

The conformation of the backbone angles β and γ was deduced from the observation of ⁴J_H4′-P coupling constants. These couplings appear in the spectra only if β/γ is in the trans/g+ region (33,52), typical of B-DNA.

Residual Dipolar Coupling constants

With DNA oligomers, low concentrations (few mg/ml) of Pf1 phages are adequate for forming an ordered medium in which the long axis of the phages aligns parallel to the magnetic field B0 (55,56). These oriented phages promote the DNA alignment, which is considered to be nearly parallel to B0 (23,55).

Oriented solutions were obtained by adding 12 mg/ml Pf1 phage to oligonucleotide solutions. The phage concentration was chosen to obtain a homogeneous liquid crystal phase and to preserve the spectrum quality, i.e. well-defined peaks. The solution homogeneity and the extent of orientation were checked with ²H detection of HDO peak (57).

The measurements were performed at ¹³C natural-abundance conditions. The water resonance was suppressed using pre-saturation methods. The ¹³C–¹H direct RDC constants were determined using different strategies for anomeric (C1′, C3′, C4′) and aromatic (C8, C6, C2) carbons. For the anomeric carbons, ¹³C–¹H RDC were determined by comparing the in-phase ¹³C–¹H splittings in the direct dimension of non-decoupled 2D HSQC spectra acquired in isotropic and oriented solutions (30). For the aromatic carbons improved sensitivity and resolution was obtained using TROSY experiments (58–60). Accurate RDC measurements were carried out by recording pairs of complementary Hα and Hβ-TROSY experiments on isotropic and oriented solutions.

TROSY and HSQC experiments were performed at 500 MHz at 25°C. The spectral range was 5000 Hz for proton dimension and 5030 Hz for the carbon dimension. A total of 512 experiments of 2048 complex points were recorded with an accumulation of 256 scans per experiment.

A total of 291 RDCs were collected. The experimental error on RDCs linked to recording conditions and data processing is estimated to 2.5 Hz, in accordance with previous evaluations (20). The estimated error on ΔRDC, which is the difference between two RDCs, is then 5 Hz.

NMR data

The NMR data are available in the Biological Magnetic Resonance Bank (BMRB), entry 19222.

B-DNA structural models

The data set of crystal structures included 9 B-DNA decamers (PDB IDs: 3GGI 1EN8 1D8G 1ENE 3U89 3GGK 1EN9 1EN3 1ZF5) from data strictly limited to 1.0 Å resolution or better. The stringent resolution cut-off was chosen to calculate RDCs and internucleotide distances that must be as precise as possible. The protons were added with Amber tools (D.A. Case et al., 2006, AMBER 9, University of California, San Francisco, USA), known to position hydrogen reliably on DNA molecules. All the considered X-ray oligomers correspond to palindromic sequences and their structures are symmetric; this was done on purpose to avoid redundancy. The backbone, sugar and base pair positional heterogeneities in 3U89, 3GGI and 3GGK were considered and analyzed. The final X-ray data set contained 108 dinucleotide steps.

D_inter(H6/8_i-H6/8_i+1), D_inter(H2′_i-H6/8_i+1), D_inter(H2″_i-H6/8_i+1) were directly inferred from the added protons. RDCs involving C6/8-H6/8, C3′-H3′, C4′-H4′ vectors were calculated on X-ray structures with PALES (61), using a concentration of Pf1 phage of 10 mg/ml.

In addition to the X-ray structures, a series of DNA models were generated with 3DNA (62). They are based on canonical B-DNA structures (called ‘generic’ in 3DNA) with C2′-endo sugars, BI phosphates, twist of 36° and rise of 3.4Å. We considered two sequences, (CpG)₂₀•(CpG)₂₀ and (GpG)₂₀•(CpC)₂₀, to get a representative collection of different purine-pyrimidine types (CpG, GpC, GpG and CpC). In these DNAs, the slide, roll and twist were successively and independently scanned over the range of values observed in X-ray structures on only one dinucleotide, i.e. either CpG, GpC, GpG or CpC. For instance, twist was constrained from 20 to 50° by interval of 5° on one given dinucleotide, keeping the other inter base parameters (shift, slide, rise, tilt and roll) of this step at their canonical values. The 5′- and 3′ flanking nucleotides spontaneously adjusted in response to the changes in the central step, thus maintaining a reasonable steric environment around the central base-step where the systematic variation takes place. RDCs and D_inter were then calculated only on the step where the helical parameter of interest (e.g. the twist) was geometrically constrained, and not on the 5′- and 3′-nearest neighbors. These simplified models were not used to obtain precise detailed geometries, since the systematic variation of a helicoidal parameter is clearly an artificial situation. However, such artificial models did help explore systematically the respective roles of the slide, roll and twist on DRDC and D_inter.

Structural analyses

Analyses of DNA X-ray structures were carried out using Curves5 (63), which calculates the optimal helical axis and a complete set of conformational and helicoidal parameters. Inter base parameters were calculated separately for dinucleotides NpN in each DNA strand and not for complementary dinucleotides NpN•NpN which combine the two strands. This is the most advisable choice compatible with the fact that all the NMR data examined here, δPs, ΔRDCs and internucleotide distances, pertain to one strand (in the double stranded DNAs).

RESULTS

Correlations between NMR observables

The four dodecamers studied by NMR (Table 1) offer a large representation of YpR, RpY, YpY and RpR (Y:pyrimidine; R: purine) steps. A total of 72 ³¹P chemical shifts (δPs), 194 internucleotide distances (D_inter) and 291 RDCs (86 RDC_C6/8-H6/8, 33 RDC_C3′-H3′, 61 RDC_C4′-H4′ and 111 RDC_C1′-H1′) were collected on the four dodecamers, discarding the first and last steps of each oligomer. This section examines the relations between the backbone linkage conformation and the relative orientations and distances between consecutive bases, using NMR data collected at 20°C.

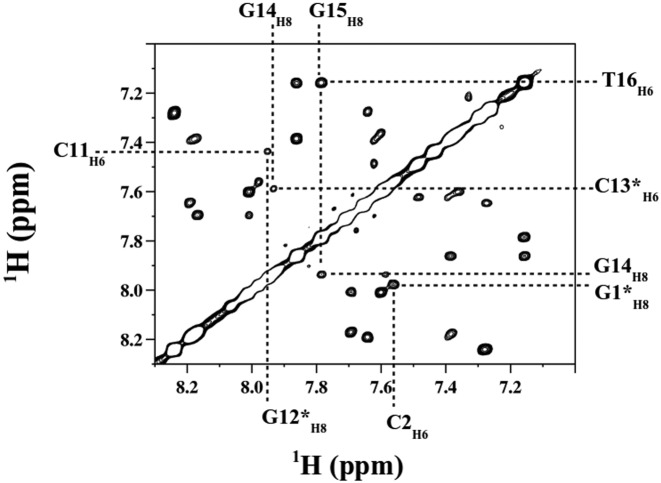
The δP values were extracted from well resolved ¹H-³¹P HETCOR spectra (Figure 2). They reflect the phosphate group dynamics that, in B-DNA, is dominated by the BI ↔ BII equilibrium that involves ε and ζ (Figure 1). Also, the presence of intense, well defined ⁴J_H4′-P coupling constants testifies that β/γ angles remain in the trans/g+ region (see Materials and Methods), consistent with energy profiles (64,65).

Figure 2.

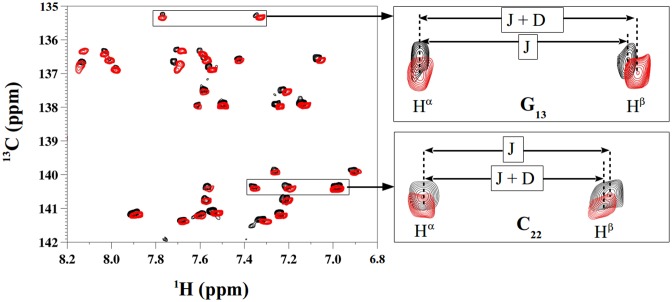
Representative ¹H-³¹P HETCOR spectrum at 500 Mhz for δP determination. The ¹H -³¹P HETCOR spectrum, used to determine δPs of pN residues (N for any base), shows a section of the H4′-³¹P region collected with Oligo 2 at 20°C. The positive and negative cross-peaks are in black and red, respectively. The blue arrows indicate the cross-peak centers for specific bases. The terminal residues are indicated by stars.

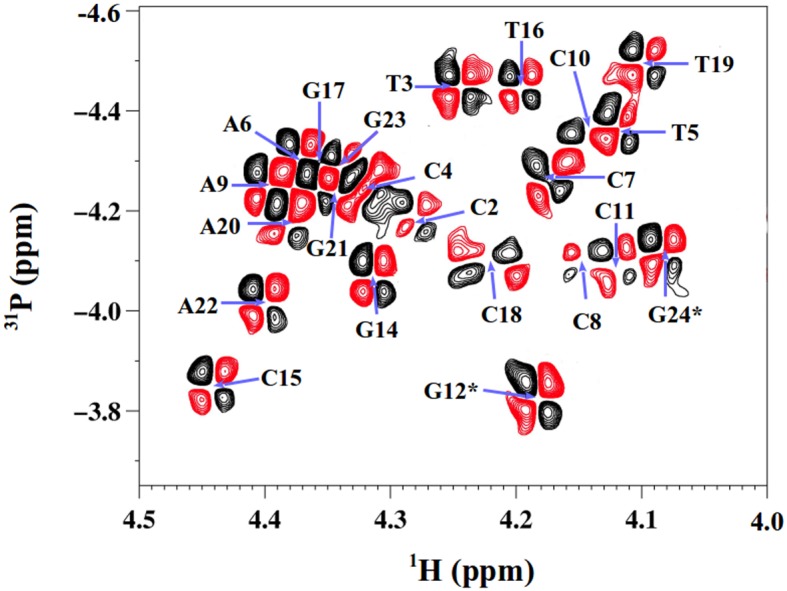
For each type of RDC vector (see Figure 1), we examined ΔRDC, defined as the difference between the RDC values of two consecutive vectors on the same DNA strand, measured on residues i and i+1 (ΔRDC = RDC_{residue i+1} − RDC_{residue i}). ΔRDC quantities contain information on the relative orientations of two successive vectors and therefore about the internal structure of a dinucleotide step, thus supplement the information provided by δP and D_inter. Due to the global regularity of the double helix, a given family of RDC (examples in Figure 3) covers a restricted range, which causes overlaps (66,67). This is particularly striking in the case of RDC_C3′-H3′ and RDC_C4′-H4′ that are in addition affected by the suppression of the water signal. This latter phenomenon is enhanced for pyrimidines belonging to YpR steps with down-field shifted δP, which are associated to strongly high field shifted H3′ protons especially close to the water signal. The RDCs are thus all at once less numerous and less precisely measured on DNA than on proteins or RNA (20). To evaluate the quality of our measurements, RDCs involving two types of C–H vectors belonging to a same base were compared. The vectors C6/8–H6/8 are coplanar with the C2–H2 vectors in adenines and C5–H5 in cytosines. Hence, the corresponding RDCs are expected to be very similar and may be used to test the quality of the measured RDCs. The correlation coefficients between RDC_C6/8-H6/8 and RDC_C2-H2 on one hand, and RDC_C6/8-H6/8 and RDC_C5-H5 on the other hand, are 0.95 and 0.89, respectively. This good agreement is reassuring, at least for the quality of RDCs involving these base atoms.

Figure 3.

Representative ¹H-¹³C TROSY spectra for RDC determination. H^α H^β TROSY spectra obtained for Oligo 3 in isotropic solution (black peaks) and anisotropic medium (red peaks) were superimposed in the three panels presented here. The left panel represents a region of C6/8-H6/8 vectors. The right panels focus on two representative TROSY peaks involving G13 (top) and C22 (bottom). The splitting between H^α and H^β is indicated by arrows showing ¹J(C–H) coupling in isotropic solution (J) and the sum of ¹J(C–H) and RDC in oriented medium (J + D). RDC is positive for G13 and negative for C22.

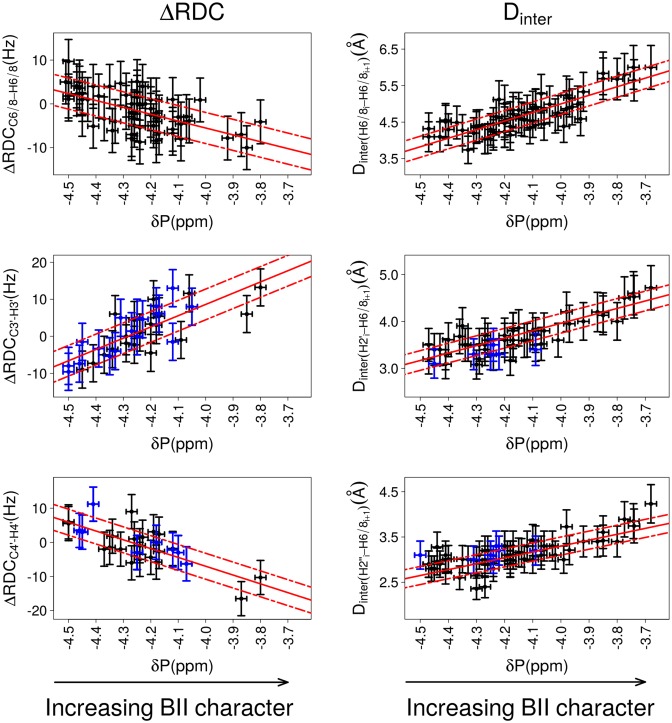
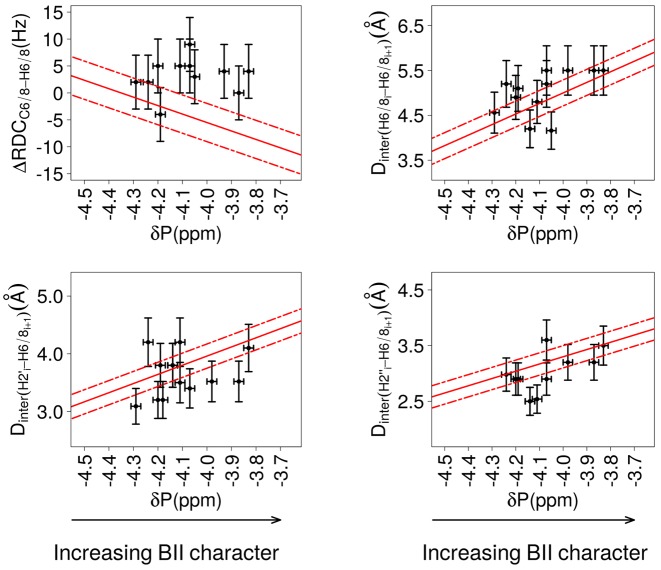
Notable correlations are found between three ΔRDCs (ΔRDC_C6/8-H6/8, ΔRDC_C3′-H3′ and ΔRDC_C4′-H4′) and δPs (Figure 4 and Table 2; details per dodecamer in Table S1 in Supplementary data). On the plots reporting ΔRDC_C3′-H3′ and ΔRDC_C4′-H4′ as a function of δP in Figure 4, the lack of data for δP between −4.1 and −3.7 ppm reflects the difficulty of the associated RDC measurements, as explained above. The correlation coefficients (Table 2) provide evidence that those ΔRDCs are significantly coupled to the δPs. By comparison, the very low correlation coefficient of 0.2 between ΔRDC_C1′-H1′ and δP shows that these quantities are essentially not correlated (Figure S1 in Supplementary data). Distinctive trends characterize the couplings between ΔRDCs and δPs: ΔRDC_C6/8-H6/8 and ΔRDC_C4′-H4′ tend to be positive for high-field shifted δP (BI-rich step) and negative for down-field shifted δP (increased BII character), while the inverse is observed for ΔRDC_C3′-H3′ (Figure 4).

Figure 4.

Correlations between δP and ΔRDCs or internucleotide distances. The relative orientation of bases of the same strand in a base step is characterized either by ΔRDCs (left panels) or by internucleotide distances (right panels). The backbone conformation is represented by ³¹P chemical shifts (δP). ΔRDCs were calculated from RDCs measured at 25°C; δP and D_inter were collected at 20°C. The data exclude the terminal steps, which are shown in Figure 7. Left: Correlations between δPs and ΔRDC_C6/8-H6/8, ΔRDC_C3′-H3′ and ΔRDC_C4′-H4′., with ΔRDC = RDC_{residue i+1} – RDC_{residue i}. Right: Correlations between δPs and the internucleotide distances D_inter(H6/8_i-H6/8_i+1), D_inter(H2′_i-H6/8_i+1) and D_inter(H2″_i-H6/8_i+1). This data set also contains measurements previously collected on the Jun-Fos oligomer (37,68). Note that D_inter(H6/8_i-H6/8_i+1) > 5 Å are extracted from NOESY spectra recorded with a mixing time of 300 ms and are thus less precisely measured than shorter distances. The points in blue in panels involving ΔRDC_C3′-H3′, ΔRDC_C4′-H4′, D_inter(H2′_i-H6/8_i+1) and D_inter(H2″_i-H6/8_i+1) correspond to dinucleotides with detectable populations of East or North sugars. The vertical bars are the estimated experimental errors on ΔRDC and D_inter (see Materials and Methods). The experimental error on δPs (horizontal bars) is estimated to ±0.05 ppm for the left panel plots and to ±0.02 ppm for the right panel plots (see Materials and Methods). The best linear fits are represented with red lines; the residual standard deviations are depicted by dashed red lines. The characteristics of the correlations are reported in Table 2.

Table 2. Relationships between δPs, ΔRDCs and internucleotide distances.

	N	CC	Linear fit	SDres	P-value
ΔRDCC6/8-H6/8	60	−0.60	ΔRDCC6/8-H6/8 = -15.7 δP – 68.3	3.55	5.44 10−7
ΔRDCC3′-H3′	37	0.76	ΔRDCC3′-H3′ = 30.4 δP + 130.2	4.15	5.38 10−8
ΔRDCC4′-H4′	29	−0.75	ΔRDCC4′-H4′ = -25.8 δP – 110.2	3.8	3.42 10−6
Dinter(H6/8i-H6/8i+1)	64	0.81	Dinter(H6/8i-H6/8i+1) = 2.3 δP + 14.3	0.29	<2.2 10−16
Dinter(H2′i-H6/8i+1)	50	0.84	Dinter(H2′i-H6/8i+1) = 1.6 δP + 10.2	0.22	6.20 10−15
Dinter(H2″i-H6/8i+1)	70	0.76	Dinter(H2″i-H6/8i+1) = 1.3 δP + 7.9	0.21	2.78 10−14

This table reports the characteristics of the correlations shown in Figure 4 between δPs and (i) ΔRDCs or (ii) internucleotide distances (D_inter), based on NMR measurements at 25°C (ΔRDCs) or 20°C (D_inter) and excluding the terminal dinucleotides. The number of experimental data (N) and correlation coefficient (CC) are given for each type of ΔRDCs or D_inter. The equations correspond to linear fits of the data by least square fit, the root mean square residual deviation on ΔRDCs or D_inter given in (SD_res) and P-values. The data set of D_inter contains additional measurements previously collected on the Jun-Fos oligomer (37,68). ΔRDCs are in Hz, δP in ppm and D_inter in Å.

The internucleotide distances D_inter(H6/8_i-H6/8_i+1), D_inter(H2′_i-H6/8_i+1) and D_inter(H2″_i-H6/8_i+1) are strongly correlated with δP (Figure 4, Table 2; details per dodecamer in Table S2 in Supplementary data). No coupling with δP is observed for D_inter(H1′_i-H6/8_i+1), an echo of the lack of correlation between δP and ΔRDC_C1′-H1′. D_inter(H6/8_i-H6/8_i+1), D_inter(H2′_i-H6/8_i+1) and D_inter(H2″_i-H6/8_i+1) increase when δP is shifted down-field, that is, when the BII population increases (Figure 4). This behavior is consistent with the sequential distances involving H6/8 and the methyl group of thymines in NpT steps being always short (2.9 ± 0.2 Å on average) and their δP being high-field shifted (4.4 ± 0.1 ppm, BI-rich steps). The correlations between δPs and the three internucleotide distances, D_inter(H6/8_i-H6/8_i+1), D_inter(H2′_i-H6/8_i+1) and D_inter(H2″_i-H6/8_i+1), were previously observed on a 14 bp DNA (37,68). That they are retrieved with different systems and a much larger data set considerably strengthens the notion that such couplings represent a general property of free DNA in solution.

Four correlations involve NMR data on sugar protons, either 5′ and 3′ (ΔRDC_C3′-H3′ and ΔRDC_C4′-H4′), or only 5′ (D_inter(H2′_i-H6/8_i+1) and D_inter(H2″_i-H6/8_i+1)), of the phosphate linkage and could be sensitive to the sugar behavior. Investigations on sugar conformation (see Material and Methods) show that South conformers largely prevail in purine nucleotides of the dodecamers, but observable TOCSY H1′-H4′ cross-peaks indicate the presence of North or East conformers on 17 sugars of pyrimidine nucleotides (C7, C15 and C19 in Oligo 1; C2, C4, T5, C8, C10 and T16 in Oligo 2; C4, T6, C10 and T16 in Oligo 3; C9, C11, C15 and C23 in Oligo 4). Such a feature is thus typically seen on cytosine sugars, in line with previous ab initio quantum mechanical predictions (69) and subsequent observations (13,29,46,70–73). Nevertheless, steps with sugars undergoing South ↔ North or East transitions do not stand out in the correlations shown in Figure 4.

The next section examines further the structural significance of the relations highlighted here, to better understand how they can be related to the intrinsic DNA mechanics.

ΔRDCs and internucleotide distances versus phosphate and sugar conformations

This section and the next aim to interpret structurally ΔRDCs and D_inter, using molecular models of the B-DNA helix. Ultrahigh resolution X-ray DNA structures (see Materials and Methods) were chosen as probably the best available templates to calculate RDC_C6/8-H6/8, RDC_C3′-H3′, RDC_C4′-H4′, the corresponding ΔRDCs values and D_inter(H6/8_i-H6/8_i+1), D_inter(H2′_i-H6/8_i+1) and D_inter(H2″_i-H6/8_i+1) and to examine their relationship with the phosphate and sugar conformations, before considering the helical parameters in the next section.

In the X-ray structures the phosphate groups adopt two discrete states (BI or BII), defined from (ε-ζ) values instead of a continuous variable (δP) representing populations arising from the BI↔BII equilibrium. In our data set containing 120 nucleotides, the sugars are overwhelmingly in the South conformation, and a minority of 24 nucleotides have East sugars, all associated to BI linkages, as previously reported (6,74). We first categorized the calculated ΔRDCs and D_inter according to BI and BII (Table 3). Then, the BI dinucleotides were divided in two sub-categories according to the South and East sugars. The average values of ΔRDCs and D_inter undoubtedly depend on BI and BII. 5′-East sugars do not significantly influence D_inter(H2′_i-H6/8_i+1) or D_inter(H2″_i-H6/8_i+1). ΔRDC_C3′-H3′ and ΔRDC_C4′-H4′ appear more sensitive to 5′ or 3′-East sugars, but the large standard deviations preclude firm conclusions about this effect. Importantly, these results show a strong dependence of ΔRDCs and D_inter on the backbone state, BI or BII, qualitatively consistent with the relations shown in Figure 4.

Table 3. Values of ΔRDCs and internucleotide distances in BI and BII steps from X-ray structures.

Phosphates	All	BI	BII	BI	BI
Sugars	all	all	all	5′ & 3′ South	5′ or 3′ East
N	108	70	38	48	22
ΔRDCC6/8-H6/8	1.8 (5.9)	4.7 (4.1)	−3.7 (4.7)	-	-
ΔRDCC3′-H3′	−0.7 (6.5)	−3.2 (4.1)	3.9 (4.7)	−4.2 (5.9)	−1.3 (5.3)
ΔRDCC4′-H4′	1.4 (7.1)	5.4 (4.8)	−5.9 (4.2)	5.0 (4.6)	6.2 (5.2)
Phosphates	All	BI	BII	BI	BI
Sugars	all	all	all	5′ South	5′ East
N	108	70	38	59	11
Dinter(H6/8i-H6/8i+1)	5.2 (1.1)	4.6 (0.7)	6.3 (0.6)	-	-
Dinter(H2′i-H6/8i+1)	3.8 (1.1)	3.1 (0.4)	5.1 (0.4)	3.1 (0.4)	2.9 (0.2)
Dinter(H2″i-H6/8i+1)	2.9 (0.6)	2.6 (0.4)	3.5 (0.4)	2.6 (0.4)	3.0 (0.4)

Calculated ΔRDC (Hz) and internucleotide distances D_inter (Å) were obtained from 108 dinucleotide steps of the high resolution X-ray B-DNA structures listed in Materials and Methods. The average values of ΔRDC and D_inter are reported for all steps and then selecting either BI or BII steps. A second categorization was applied to the BI steps, according to the sugar conformation. Such partitioning is not applicable to the BII steps, which are exclusively surrounded by South sugars. N is the occurrence of each category. The standard deviations are in brackets.

Relations between DNA helicoidal parameters, ΔRDCs and internucleotide distances

The relationship between the inter base parameters and either ΔRDCs or D_inter were then investigated, focusing on slide, roll and twist. These parameters are the most variable inter base parameters in our high-resolution X-ray data set as well as in much larger data sets (5,6). Thus, they are especially good candidates when seeking meaningful couplings. In this section, the inter base parameter values are given for NpN dinucleotides, i.e. within one strand of the double helix, to be compatible with the derived-NMR ΔRDCs and D_inter.

The characteristics of the linear bivariate fits involving either ΔRDC or D_inter versus a single helical parameter, slide, roll or twist, are summarized in Table 4. In addition, multiple linear regressions were performed, which enable to find the equations optimized to express ΔRDC or D_inter as functions of the three combined parameters of slide, roll and twist (Table 5). In the latter approach, one should keep in mind that the slide variations cover ∼2.5 Å while those of roll and twist correspond to ∼35° (Figure 5); therefore only the coefficients associated to roll and twist can be directly compared. As expected, the correlation coefficients are higher with multiple linear regressions (Tables 4 and 5). However, the characteristics of the best fits of pairs of variables are also excellent (Table 4), suggesting that this simpler view provides relevant information. Indeed, both approaches lead to coherent results.

Table 4. Correlations between ΔRDCs or internucleotide distances and each inter base parameters of slide, roll and twist, from X-ray structures.

	Slide			Roll			Twist
	CC	SDres	P-value	CC	SDres	P-value	CC	SDres	P-value
ΔRDCC6/8-H6/8	−0.62	4.65	5.6 10−13	0.70	4.26	<2.2 10−16	−0.64	4.60	1.5 10−13
ΔRDCC3′-H3′	0.40	5.97	1.8 10−05	−0.54	5.49	2.1 10−09	0.35	6.10	1.9 10−04
ΔRDCC4′-H4′	−0.53	6.03	2.5 10−09	0.76	4.67	<2.2 10−16	−0.62	5.63	1.4 10−12
Dinter(H6/8i-H6/8i+1)	0.62	0.83	1.2 10−15	−0.82	0.60	<2.2 10−16	0.84	0.58	<2.2 10−16
Dinter(H2′i-H6/8i+1)	0.68	0.78	1.7 10−15	−0.89	0.48	<2.2 10−16	0.88	0.49	<2.2 10−16
Dinter(H2″i-H6/8i+1)	0.84	0.29	<2.2 10−16	−0.69	0.40	<2.2 10−16	0.46	0.48	4.8 10−07

Calculated ΔRDC (Hz), internucleotide distances D_inter (Å), slide (Å), roll (°) and twist (°) were obtained from the high resolution X-ray B-DNA structures listed in Materials and Methods. The data set contains a total of 108 dinucleotide steps.

The correlation coefficients (CC), standard residual deviations on ΔRDCs or D_inter (SD_res) and P-values characterize the linear fits between either ΔRDC or D_inter and each of the three parameters of slide, roll and twist (see Figure 5). Slide, roll and twist were calculated for each strand of the DNA double helix, to be consistent with ΔRDCs and D_inter.

Table 5. Relationships between ΔRDCs or internucleotide distances and the combined inter base parameters of slide, roll and twist, from X-ray structures.

	CC	SDres	P-value
ΔRDCC6/8-H6/8 = −2.6 Slide + 0.2 Roll − 0.15 Twist + 5.7	0.91	2.4	<2.2 10−16
ΔRDCC3′-H3′ = −0.06 Slide − 0.53 Roll − 0.12 Twist + 5.1	0.56	3.2	3.6 10−8
ΔRDCC4′-H4′ = 0.41 Slide + 0.62 Roll − 0.03 Twist + 0.34	0.75	2.7	<2.2 10−16
Dinter(H6/8i-H6/8i+1) = 0.2 Slide − 0.04 Roll + 0.05 Twist + 3.5	0.87	0.3	<2.2 10−16
Dinter(H2′i-H6/8i+1) = 0.2 Slide − 0.05 Roll + 0.05 Twist + 2.3	0.93	0.2	<2.2 10−16
Dinter(H2″i-H6/8i+1) = 0.6 Slide − 0.02 Roll + 0.005 Twist + 3.2	0.84	0.2	<2.2 10−16

This table reports the equations expressing either ΔRDCs (Hz) or internucleotide distances (D_inter, Å) as function of the inter base parameters of slide (Å), roll (°) and twist (°); the equations were obtained from multiple linear regressions on data from high resolution X-ray structures. They are characterized by the CC, the standard residual deviations on ΔRDCs or D_inter (SD_res) and the P-values.

Figure 5.

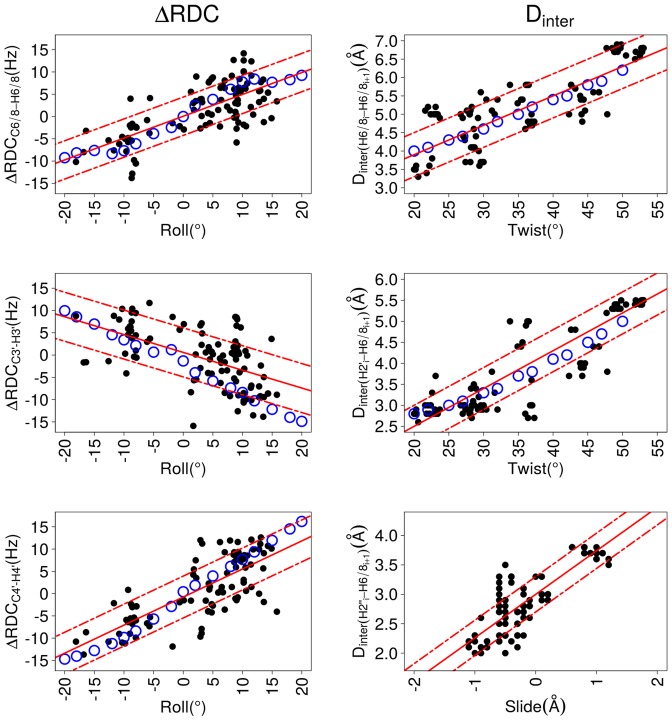
Dependence of inter base parameters on ΔRDCs and D_inter. These plots illustrate correlations between inter base parameters of roll, slide and twist versus residual dipolar coupling differences (ΔRDCs) or internucleotide distances (D_inter). ΔRDC, D_inter, slide, roll and twist were obtained from the high resolution X-ray B-DNA structures (black points, characteristics in Table 4) or from 3DNA molecular models (blue circles). The best linear fits calculated for the X-ray structures (equations in Table 6) are represented by red lines; the standard deviations of the residuals are traced by dashed red lines. The inter-base parameters were calculated for each strand of the DNA double helix, to be consistent with ΔRDCs and D_inter.

ΔRDC_C6/8-H6/8, ΔRDC_C3′-H3′ and ΔRDC_C4′-H4′ are more strongly coupled to roll than to twist or slide. In agreement with an earlier modeling study (75), D_inter(H6/8_i-H6/8_i+1) and D_inter(H2′_i-H6/8_i+1) are especially sensitive to roll and twist (Tables 4 and 5). D_inter(H2″_i-H6/8_i+1) appears as a good indicator of the slide value (Tables 4 and 5). Examples of the strongest couplings are illustrated in Figure 5. Despite their convincing characteristics, these correlations suffer from notable deviations that may just represent the natural variability in the present sample. They might also indicate biases which could affect the details of the X-ray DNA structures, such as lateral inter-molecular interactions (76–78) or underestimated structural heterogeneities (79).

However, because of the couplings existing between roll and twist in B-DNA X-ray structures (present data set: correlation coefficient of 0.8), and between roll and slide (present data set: correlation coefficient of 0.75), it is difficult to interpret the relations in terms of the specific influence arising from each helicoidal parameter. To gain a better idea of the respective roles of these parameters, we built a series of simplified, but structurally controlled, models of B-DNA generated with 3DNA (62) (see Materials and Methods). These models contain one dinucleotide step in which the roll and twist were independently constrained (one parameter at a time) over the range of values observed in X-ray structures, keeping the other helical parameters at their canonical values. ΔRDCs and D_inter were then monitored on the constrained dinucleotide steps.

This approach reveals that neither twist nor slide variations affect ΔRDCs. Conversely, changes in roll generate ΔRDC variations that account for the ΔRDC versus roll correlations inferred from the X-ray structures (Figure 5). On the other hand, variations in roll or slide only produce minor changes in D_inter(H6/8_i-H6/8_i+1) and D_inter(H2′_i-H6/8_i+1), compared to the increase of more than 2Å when incrementing the twist from 20 to 55°. There is a remarkable agreement between the twist/D_inter correlations obtained from the 3DNA models and the X-ray structures (Figure 5). Thus, ΔRDCs are primarily sensitive to the roll, while D_inter(H6/8_i-H6/8_i+1) and D_inter(H2′_i-H6/8_i+1) are mainly modulated by the twist. The controlled models indicate that the correlations reported in Tables 4 and 5 also reflect the slide/roll and roll/twist couplings, as expected (see above).

Overall, the relationships highlighted here establish that both ΔRDCs and D_inter inform about inter base helicoidal parameters. Positive and negative values of ΔRDC_C6/8-H6/8 and ΔRDC_C4′-H4′ indicate positive and negative rolls, respectively, while the inverse is found for ΔRDC_C3′-H3′. Both D_inter(H6/8_i-H6/8_i+1) and D_inter(H2′_i-H6/8_i+1) increase with the twist value; small and large values of D_inter(H2′_i-H6/8_i+1) reveal negative and positive slides, respectively. To estimate helical parameters from NMR measurements, we propose to use the equations derived from the correlations involving two variables (Table 6). We emphasize that such derived helical parameters correspond to average values, the oligomers being obviously dynamical in solution, the deviations around the values are also of importance. The values should not be taken without the error bars given by the uncertainty in the underlying relations, in particular those involving ΔRDCs. Nevertheless, exploiting these equations supplies a very simple way to glean key structural characteristics without building a structural model of the studied DNA.

Table 6. Relationships between helical parameters and ΔRDCs or internucleotide distances, from bivariate correlations based on X-ray structures.

	CC	SDres	P-value
Roll = 1.0 ΔRDCC6/8-H6/8 + 1.7	0.70	6.1	<2.2 10−16
Roll = −0.7 ΔRDCC3′-H3′ + 2.9	−0.54	7.2	2.12 10−9
Roll = 0.9 ΔRDCC4′-H4′ + 2.2	0.76	5.6	<2.2 10−16
Twist = 8.5 Dinter(H6/8i-H6/8i+1) − 8.8	0.84	5.9	<2.2 10−16
Twist = 9.0 Dinter(H2′i-H6/8i+1) + 1.3	0.88	5.1	<2.2 10−16
Slide = 0.94 Dinter(H2″i-H6/8i+1) − 2.8	0.84	0.35	<2.2 10−16

This table reports the equations expressing roll (°), twist (°) and slide (°) as function of ΔRDCs (Hz) or internucleotide distances (D_inter, Å). The equations were obtained from linear regressions involving either ΔRDC or D_inter versus a single helical parameter, slide, roll or twist (bivariate correlations) from high resolution X-ray structures (see Table 4 and Figure 5). They are characterized by the CC, the standard residual deviations on the helical parameters (SD_res) and the P-values.

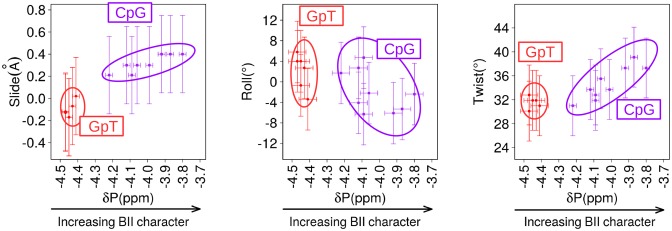
To illustrate this practical point together with the DNA mechanics, we used the NMR data collected on the GpT and CpG steps of the four dodecamers (Figure 6). The 6 GpT steps are all BI-rich, with consistent high-field shifted δPs (−4.47 to −4.41 ppm). In contrast, the 10 CpG steps are mainly BII-rich, however their δPs are more variable (−4.22 to −3.8 ppm) because of the effect of the tetrameric environment (15,40). Importantly for our purpose, a large collection of ΔRDC_C6/8-H6/8, D_inter(H2′_i-H6/8_i+1) and D_inter(H2″_i-H6/8_i+1) were measured on these steps, which represents a rare opportunity given the numerous overlaps otherwise occurring in DNA spectra. The slide, roll and twist values were inferred from the equations in Table 6, which express slide versus D_interH2″_i-H6/8_i+1, roll versus ΔRDC_C6/8-H6/8 and twist versus D_interH2′_i-H6/8_i+1. It clearly emerges that the average structures of the BI-rich GpT correspond to negative slides, positive or slightly negative rolls and low twists (Figure 6). The characteristics of CpG steps depends on the BII population, reflected in the δPs, with the most down-field shifted δPs associated with strong positive slides, negative rolls and high twists (Figure 6).

Figure 6.

Structural characteristics of CpG and GpT steps in the four oligomers. These plots illustrate the relationship between experimental δPs and three helical parameters, roll, twist and slide, on two types of dinucleotides present in several copies in the four dodecamers, CpG (10 copies, violet) and GpT (6 copies, red). The experimental D_inter(H2″i-H6/8i+1), ΔRDC_C6/8-H6/8, D_inter(H2′i-H6/8i+1) values were used to calculate the helical parameters according the equations in Table 6. The horizontal bars are the experimental errors on δPs. The vertical bars are the standard residual deviations reported Table 6.

In sum, the couplings between δPs, ΔRDCs and D_inter (Figure 4) can now be coherently combined to reconstitute the intrinsic B-DNA mechanics, in which increasing BII populations are associated with more positive slide, more negative roll and higher twist.

Behavior of 3′ and 5′ terminal dinucleotides

In the above sections, only internal steps were considered. Indeed, the terminal dinucleotides are usually discarded from studies of DNA oligomers in solution because of the fraying of the terminal base pairs that occurs on the pico and nanosecond time scales (72,80). Recent molecular dynamics represented such fraying as large motions involving not only the terminal base pairs but also their neighbors (16,44,45). However, the presence of such motions is difficult to assess since fraying events are poorly documented by experiments. The characterization of the intrinsic mechanics of the internal part of the four oligomers, provides an interesting context for comparison with the terminal nucleotides. Thus, we turn to the NMR data collected on the outermost nucleotides and dinucleotides to appreciate to what extent they differ from the internal counterparts.

In NMR, monitoring the imino proton resonances in one-dimensional ¹H spectra is usually used to probe the stability of base pairing. More precisely, the absence of imino proton resonances reveals dynamic base pairs, weakly protected from proton exchange. For the four dodecamers, one-dimensional ¹H spectra show that the imino proton resonances are lost in N₁:N₂₄, and N₁₂:N₁₃ (N standing for any base type) from 20°C, while they are clearly observable in all the other, internal base pairs, comprising N₂:N₂₃ and N₁₁:N₁₄. This is consistent with earlier NMR experiments (81,82) which indicated that the penultimate base pairs are much less subjected to long-lived opening events than the terminal base pairs. Despite the loss of Watson–Crick base pairing signature in N₁:N₂₄ and N₁₂:N₁₃, numerous NMR observables were collected on the outermost individual nucleotides, N₁, N₁₂, N₁₃ and N₂₄ or dinucleotides, N₁pN₂, N₁₁pN₁₂, N₁₃pN₁₄ and N₂₃pN₂₄, for each oligomer.

At the nucleotide level, the intranucleotide distances H1′_i-H6/8_i for the terminal nucleotides are on average 4.08 ± 0.25 Å (values given in Table S3 in Supplementary data), typical of glycosidic torsion χ in the usual (52) and energetically most stable (83) anti-orientation. The terminal sugars are flexible since their H1′–H4′ TROSY cross-peaks show signs of the of East or North conformers, except in T1 in Oligo 1 and G13 in Oligo 3 (Table S3 in Supplementary data).

Concerning the dinucleotides, the intense ⁴J_H4′-P couplings seen in all 3′-terminal phosphates unambiguously testify of β/γ in trans/g+ (these couplings cannot be observed on the 5′ terminal step since they lack the corresponding phosphate). The δPs of both 3′- and 5′-ends are very similar to those of internal phosphates, from 20° (Table 7; examples on Figure 2) to 40°C. The only exception was the terminal CpT of Oligo 1, down-field shifted by 0.25 ppm compared to their internal counterparts. It is intriguing that the sequence effect on δPs in B-DNAs, established from internal dinucleotides (15,39), appears to hold for these eight terminal steps (Table 7).

Table 7. Comparison between δP values of internal and terminal phosphates.

	δP of 5′ or 3′ ends	δP of internal steps	Predicted δP
CpT	−4.18	−4.43 (0.07)	−4.38 (0.12)
TpC	−4.24	−4.25	−4.26 (0.12)
ApG	−4.20	−4.22 (0.03)	−4.21 (0.09)
GpC	−4.15 (0.11)	−4.14 (0.07)	−4.13 (0.08)
CpC	−4.11	−4.12	−4.07 (0.06)
GpA	−4.11	−4.02	−4.10 (0.09)
CpG	−4.01 (0.13)	−4.02 (0.13)	−4.02 (0.12)
GpG	−3.93	−3.85	−4.02 (0.09)

The δP values (in ppm) collected at 20°C are given for the first and last dinucleotide steps of the four dodecamers and for their internal counterparts. For dinucleotides present in several copies, δP is the average value, with the standard deviations in brackets. The last column reports δPs predicted depending on the dinucleotidic sequence (40).

We collected 14 RDC_C6/8-H6/8 (out of a total of 16, see Table S3 in Supplementary data) on N₁, N₂₄, N₁₂ and N₁₃. ΔRDC_C6/8-H6/8 involving either one terminal base and one internal base, or two internal bases, are in the same range. This strongly suggests that no extreme, stable roll distortions occur in the terminal region. However, terminal ΔRDC_C6/8-H6/8, in particular those associated to down-field shifted δPs, appear to depart from the correlation existing for the internal observables (Figure 7).

Figure 7.

Behavior of terminal dinucleotides regarding δP versus ΔRDCs or internucleotide distances. ³¹P δP, ΔRDC_C6/8-H6/8, D_inter(H6/8_i-H6/8_i+1), D_inter(H2′_i-H6/8_i+1) and D_inter(H2″_i-H6/8_i+1) were collected on the first and last dinucleotides of the four dodecamers, at 20°C. They are compared to the correlations obtained for the internal dinucleotides (see Figure 4), which are depicted here by the best linear fits (red lines) and the standard deviations of the normal distribution of the residuals (dashed red lines). The bars are the estimated experimental errors on ΔRDC and D_inter (vertical bars) and δP (horizontal bars).

Finally, the internucleotide distances were subjected to close examination (Table S4 in Supplementary data). D_inter(H2′_i-H6/8_i+1) and D_inter(H2″_i-H6/8_i+1) were observed for all the terminal dinucleotides, in addition to 13 D_inter(H6/8_i-H6/8_i+1) (see examples in Figure 8). Most of them were accurately measured from connectivities without overlaps. That all these distances are observable reinforces the idea that, on average, there is no dramatic disruption in the double helix. In addition, these distances tend to increase with down-field shifted δPs (Figure 7), but that may be coincidental rather than true correlations, considering the small sample sizes (10 to 12 points) and their variability. If these are weak correlations, they are much less convincing than those obtained with internal steps (Figure 4).

Figure 8.

Representative H8/6_i-H8/6_i+1 intrastrand connectivities on terminal and internal steps, from ¹H-¹H NOESY spectrum. The NOESY spectrum shows a section of a region of base-base protons collected with Oligo 2 at 20°C, using a mixing time of 300 ms. The crossing of dashed lines correspond to proton–proton connectivities. The terminal residues are indicated by stars. The connectivities involving terminal bases are as well observed as those involving internal bases.

Thus, despite the absence of Watson–Crick hydrogen bonds at the oligonucleotide termini, the outermost dinucleotides maintain some characteristics of the double helix. RDC, ΔRDC and D_inter values indicate that the DNA does not fray into long-lived structures with large changes in the orientation of the terminal bases. These results are in line with those obtained with an experimental approach of ultrafast DNA dynamics that reported only modest changes at the end of the double helix (84). Nevertheless, the correlations highlighted here for internal base pairs are significantly weakened or even lost. This supports the intuitive perception that the terminal dinucleotides do not firmly adhere to the mechanics of a regular B-DNA helix, as characterized in the above sections.

DISCUSSION

To build on previous studies (8,15,37,39), we explored here the dynamical structure of free B-DNA by NMR in solution. Our approach exploits data gathered on four B-DNA dodecamers, which contain a large variety of dinucleotide steps. We collected a consistent data set including δPs, internucleotide distances and RDCs. Then, ΔRDCs were compiled as the difference between two sequentially consecutive RDCs on the same DNA strand.

First, this work highlights a series of couplings between NMR observables, some of them for the first time. The strong correlations between δP and the internucleotide distances D_inter(H6/8_i-H6/8_i+1), D_inter(H2′_i-H6/8_i+1) and D_inter(H2″_i-H6/8_i+1), strengthen and generalize initial insights in this area reported for the 14 bp Jun-Fos oligomer (37,68). New additional couplings are uncovered between δP and three ΔRDCs, ΔRDC_C6/8-H6/8, ΔRDC_C3′-H3′ and ΔRDC_C4′-H4′. This shows that the RDCs can be exploited to gain a deeper understanding of the couplings between backbone states and orientation of the bases. In addition, our data suggest that the correlations involving either ΔRDCs or D_inter are not significantly affected by the sugar dynamics, presumably because the populations of North or East sugars remain modest. Incidentally, flexibility of the sugar was mainly discernible on cytosine residues, consistent with quantum mechanical calculations (69). In addition to their structural significance, these correlations support the consistency of the NMR data, keeping in mind that they only concern B-DNA oligomers.

The mechanistic interpretation of the NMR-derived correlations was expanded by calculating ΔRDCs and D_inter on ultrahigh resolution X-ray structures and 3DNA controlled models, which enabled to relate these quantities to the structural descriptors of dinucleotides. In the X-ray structures, different ranges of ΔRDCs and D_inter are indeed associated to the backbone BI and BII states. ΔRDC_C6/8-H6/8 and D_inter do not seem influenced much by the discrete South and East sugar categories, accessible in the X-ray structures. That corroborates and strengthens the couplings observed from the NMR data. Our approach also uncovers that the three helical parameters, slide, roll and twist, each affect ΔRDCs and D_inter to various degree. Such redundancy should actually help when using the NMR observables for structure determination, making the refinement protocols more robust. A detailed analysis reveals that (i) ΔRDCs are especially sensitive to roll (ii) D_inter(H6/8_i-H6/8_i+1) and D_inter(H2′_i-H6/8_i+1) mostly depend on twist and (iii) D_inter(H2″_i-H6/8_i+1) relate to slide. Therefore, using the derived equations, ΔRDCs and D_inter collected by NMR can provide an estimate of slide, roll and twist. Such estimates must be taken in the probabilistic sense, including the uncertainty margins. Noise comes from the experimental precision, but also and probably mostly from the mechanical origin of the correlation, involving a significant range of variations. Also one must keep in mind that, in solution, the DNA is dynamic and thus the measured average values of ΔRDCs and D_inter inform about average values of the helical parameters. Moreover, as quantities pertaining to one strand, ΔRDCs and D_inter refer to inter base—but not inter base pair—parameters. Yet, because they are measured on double stranded DNAs, the experimental ΔRDCs and D_inter and therefore the inter base parameters include all the potential interstrand effects.

The overall emerging trends offer a general framework to untangle the sequence-dependent intrinsic mechanics of DNA free in solution, generalizing and extending the earlier findings gleaned from X-ray data (6,7). Thus, BI-rich dinucleotides (high-field shifted δP) correlate with an average structure with negative slide (short D_inter(H2″_i-H6/8_i+1)), null or positive roll (positive ΔRDC_C6/8-H6/8 and ΔRDC_C4′-H4′; negative ΔRDC_C3′-H3′) and low twist (short D_inter(H6/8_i-H6/8_i+1) and D_inter(H2′_i-H6/8_i+1)); an increasing BII population (down-field shifted δP) is associated to shifts toward positive slide (large D_inter(H2″_i-H6/8_i+1)), negative roll (negative ΔRDC_C6/8-H6/8, and ΔRDC_C4′-H4′; positive ΔRDC_C3′-H3′) and high twist (large D_inter(H6/8_i-H6/8_i+1) and D_inter(H2′_i-H6/8_i+1)).

We recall that δP and the associated BII propensities are primarily controlled at the dinucleotide level (40), as confirmed by the four dodecamers studied here (15): CpG, CpA, TpG, GpC, GpG and CpC are characterized by BII percentages markedly higher than average; ApN (N: any base), NpT and TpA are globally BI-rich; GpA•TpC is an intermediate case, with BII percentage close to the average. According to our analysis, slide, roll and twist should follow the same type of sequence dependence, as illustrated here with CpG and GpT steps (Figure 6).

Our findings established in solution have biological relevance regarding the free sequence 601 and its ability to form nucleosome. Previous studies showed that this sequence contains alternations of regions enriched in A:T and G:C base pairs (41) corresponding to dinucleotide steps of low and high BII propensities (15,40), with a periodicity of ∼10 bp. This alternation can now be firmly interpreted in term of predisposition to adopt positive and negative rolls, echoing the periodic roll profile observed in the X-ray structures of nucleosome (85,86). Performing molecular dynamics under NMR restraints will ultimately be required to precisely describe the curvature in the free dodecamers studied here, which is expected to be related to the instantaneous distribution of BI and BII steps along the sequences and thus to be dynamic. However, one can already infer that the free sequence 601 shows local structural properties that are compatible with the global characteristics of the nucleosome, such as the curvature or the groove dimensions (15). Indeed, recent work (15) has shown that alternation of intrinsic low and high BII propensities, coupled to intrinsic narrow and wide minor grooves, largely coincides with the sinusoidal variations of the DNA minor groove width observed in crystallographic structures of the nucleosome.

Finally, examining the NMR data collected on the oligomer termini shows that the correlations between δPs, ΔRDCs and D_inter are notably weakened or even lost for the 3′ and 5′ terminal steps. Nevertheless, the values of the NMR observables are in the same range for external and internal steps. This indicates that, on average, the outermost dinucleotides maintain some structural characteristics of the B-double helix and that the DNA fraying does not imply long-lived severe alteration of the orientation of the terminal bases.

Overall, this work provides new information on the structural significance of a range of NMR observables for DNA. In addition, it offers suitable reference data against which MD-simulated DNA structures may be compared, with or without NMR restraints. The number of long unrestrained MD simulations of DNA has grown quickly in recent years (87–91), however the development and tests of the underlying force-fields are hampered by the dearth of detailed experimental structural information for DNA in solution. An illustration of one probable MD shortcoming is the behavior of the DNA termini. In recent simulations (44,45,91), the stacking between terminal bases and neighbors was disrupted, with dramatic changes of χ and backbone angles and occurrence of various interactions involving the bases, including contacts with internal phosphate group, insertion into the minor groove or mispairing with internal base. Such motions and interactions, which incidentally compromise the convergence of the simulations, can be suspected of being artifacts (45) in view of the present NMR data. In such context, the present results help to assess and improve the representation of DNA by force-fields.

It is now widely accepted that the sequence introduces structural and dynamical heterogeneity along the free B-DNA double helix. This heterogeneity has historically been difficult to detect and characterize in solution because it involves only limited departures from the overall helical pattern. The couplings documented here provide new evidence of the intrinsic DNA mechanics, which involves a tight relationship between backbone and base behavior. Importantly, each type of dinucleotide populates the BI and BII profiles differently, resulting in variable deformability along the double helix. Using the phosphorus NMR as an efficient reporter of the DNA dynamics enabled to decode much of the mechanism underlying the interaction of DNA with either the transcription factors NF-κB (92–95) and Jun-Fos (96) or the non-specific enzyme DNase I (39). TRX, which summarizes the sequence dependence of the BI versus BII propensities, helped to begin to decipher the intrinsic DNA properties favoring the nucleosome formation (15,40). Combined with this background, the present results reinforce the idea that the intrinsic structural characteristics of the free sequence 601 minimize the cost of the distortions required for wrapping around the histone core. Overall, the work presented here strengthens the notion that the TRX scale provides a fundamental guide to understand more completely the heterogeneity in B-DNA, and how it modulates the recognition by proteins.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Funding for open access charge: Laboratoire de Biologie et Pharmacologie Appliquée, ENS Cachan, CNRS.

Conflict of interest statement. None declared.