Abstract
Child chronic malnutrition is endemic in low- and middle-income countries and deleterious for child development. Studies investigating the relationship between nutrition at different periods of childhood, as measured by growth in these periods (growth trajectories), and cognitive development have produced mixed evidence. Although an explanation of this has been that different studies use different approaches to model growth trajectories, the differences across approaches are not well understood. Furthermore, little is known about the pathways linking growth trajectories and cognitive achievement. In this paper, we develop and estimate a general path model of the relationship between growth trajectories and cognitive achievement using data on four cohorts from Ethiopia, India, Peru, and Vietnam. The model is used to: (a) compare two of the most common approaches to modelling growth trajectories in the literature, namely the lifecourse plot and the conditional body size model, and (b) investigate the potential channels via which the association between growth in each period and cognitive achievement manifests. We show that the two approaches are expected to produce systematically different results that have distinct interpretations. Results suggest that growth from conception through age 1 year, between age 1 and 5 years, and between 5 and 8 years, are each positively and significantly associated with cognitive achievement at age 8 years and that this may be partly explained by the fact that faster-growing children start school earlier. We also find that a significant share of the association between early growth and later cognitive achievement is mediated through growth in interim periods.
Keywords: Nutrition, Cognitive achievement, Path analysis, Cohort study, Ethiopia, India, Peru, Vietnam
Highlights
-
•
Different models of growth trajectories and cognition have distinct interpretations.
-
•
Growth through and after infancy is positively associated with childhood cognition.
-
•
Early school enrolment explains the link between growth trajectories and cognition.
-
•
Early growth predicts later growth that in turns predicts cognition.
Introduction
Child undernutrition, as measured by stunting (low-height for age), is endemic in low- and middle-income contexts and poses a threat to child survival, health, and development. In 2011, there were 165 million stunted children worldwide, with undernutrition accounting for 45% of deaths among children under 5 years and resulting in a loss of individual developmental potential reflected by poorer cognitive, psychosocial, and schooling outcomes (Black, Victora & Walker, 2013).
Although there is mixed evidence on the impact of stunting on cognitive development (Sudfeld, Charles McCoy & Danaei, 2015), a number of studies from low- and middle- income countries have identified the period from conception to the age of 2 years as critical, during which child growth and cognitive development are particularly susceptible to nutritional insults (Victora et al., 2008, Victora et al., 2010). There is some evidence of improvements in nutrition beyond infancy (Adair, 1999; Mani, 2012; Schott, Crookston, Lundeen, Stein & Behrman, 2013; Prentice et al., 2013) that raises the question of whether this is accompanied by an improvement in cognitive development as well. Indeed, there is some evidence that nutrition beyond infancy may also matter for cognitive development (Gandhi et al., 2011, Crookston et al., 2013), but studies investigating the relationship between nutrition at different periods of early life, as measured by growth in these periods (growth trajectories), and human capital outcomes produce different estimates of the relative magnitudes of the associations between outcomes and growth at different periods (see Table 1 for a summary of these studies).
Table 1.
Review of studies investigating the relationship between growth trajectories and human capital outcomes in low- and middle-income contexts.
| Authors | Data Set | Periods of Growth Considered | Growth Measures | Human Capital Outcomes | Approach to Modelling Growth Trajectories | Periods when growth exhibits the strongest association with the outcomes (in descending order) |
|---|---|---|---|---|---|---|
| Glewwe and King (2001) | CLHNS, Cebu, Philippines | Gestation | Birth weight, height | IQ test score | Regression with change in body size | Gestation |
| 0–1 y | 1–2 y | |||||
| 0–1 y | ||||||
| 2–8 y | ||||||
| 1–2 y | ||||||
| 2–8 y | ||||||
| Martorell et al. (2010) | Pelotas Birth cohort, Brazil | Gestation | Weight | Highest grade attained, ever failed a grade, age of starting school | Conditional body size model | 0–2 y |
| 0–2 y | gestation | |||||
| INCTS, Guatemala | 2–4 y | 2–4 y | ||||
| New Delhi Birth Cohort, India | ||||||
| CLHNS, Cebu, Philippines | ||||||
| Birth to Twenty cohort, South Africa | ||||||
| Cheung and Ashorn (2010) | CLHNS, Cebu, Philippines | Conception to 6 months | Height-for-age Z score (HAZ) | IQ test score, English reading comprehension test score,mathematics test score | Regression with change in body size | Conception to 6 months |
| 6–24 months | 6–24 months | |||||
| 24 months-11 y | ||||||
| 24 months–11 y | ||||||
| Gandhi et al. (2011) | LCSS, cohort study, Malawi | Conception to 1 month | Height-for-age Z score (HAZ) | School attendance, highest grade completed, number of times repeating a grade, percentage of correct answers in a mathematics test | Conditional body size model | 18 months-5 y, associations of growth in all other periods are statistically insignificant |
| 1–6 months | ||||||
| 6–18 months | ||||||
| 18 months–5 y | ||||||
| Crookston et al. (2011) | Young Lives study, Peru | Conception to 1 y | Height-for-age Z score (HAZ) | Verbal test score, quantitative test score | Lifecourse plot | 1–5 y |
| Conception to 1 y | ||||||
| 1–5 y | ||||||
| Crookston et al (2013) | Young Lives study, Ethiopia, India, Peru, Vietnam | Conception to 1 y | Height-for-age Z score (HAZ) | Age-for-grade, reading comprehension test score, verbal test score, mathematics test score | Conditional body size model | Conception to 1 y |
| 1-8 y | 1–8 y | |||||
| Adair et al. (2013) | Pelotas Birth cohort, Brazil | Gestation | Birth weight, birth length, weight, height | Completion of secondary school | Conditional body size model | 0–2 y |
| gestation | ||||||
| INCTS, Guatemala | ||||||
| 0–2 y | 2–4 y | |||||
| New Delhi Birth Cohort, India | ||||||
| 2–4 y | ||||||
| CLHNS, Cebu, Philippines | ||||||
| Birth to Twenty cohort, South Africa | ||||||
| Fink and Rockers (2014) | Young Lives study, Ethiopia, India, Peru, Vietnam | Conception to 8 y | Height-for-age Z score (HAZ) | Highest grade completed, verbal test score, mathematics test score | Lifecourse plot | 8–12 y |
| 12–15 y | ||||||
| 8–12 y | conception to 8 y | |||||
| 12–15 y |
The discordant results across studies are likely to have derived, at least partly, from differences in the approaches used to model the relationship between growth trajectories and human capital, that include, inter alia, the lifecourse plot approach (Crookston et al., 2011, Fink and Rockers, 2014) and the conditional body-size model (Martorell et al., 2010, Gandhi et al., 2011, Adair et al., 2013, Crookston et al., 2013). The difference between the lifecourse plot and the conditional body size model is that the former is based on a regression of the outcome on body size measures at different ages, whereas the latter entails a regression of the outcome on a measure of body size in the initial period and conditional body size measures in subsequent periods that are residuals from a regression of body size in each period on body size measures in all previous periods (Tu, Tilling, Sterne & Gilthorpe, 2013). Although, a few methodological studies (De Stavola et al., 2006, Tu et al., 2013) have been engaged with clarifying the similarities and differences across approaches, these are not yet well understood. In particular, Tu et al. (2013) use a path model to show that the lifecourse plot estimates direct relationships and argue that the results of the lifecourse plot and conditional body size models are to be interpreted in a similar way, but they do not show this in the context of the path model. An advantage of path analysis compared to the lifecourse plot is that it produces estimates of both direct and indirect paths simultaneously, yielding the overall effect and thus allowing the identification of the channels via which the total effects manifest. Nevertheless, despite this advantage, to our knowledge, no study to date has employed this method to estimate the relationship between growth trajectories and cognitive development.
In this paper, we develop and estimate a general path model of the relationship between growth trajectories and cognitive outcomes using longitudinal data from Ethiopia, India, Peru, and Vietnam. We have two goals: (1) to show whether there are differences in the interpretation of estimates from lifecourse plot and conditional body size models and (2) to investigate some of the putative pathways linking growth in each period with cognitive development.
Methods
Study population
Study children were participants in the Young Lives study, an international cohort study of childhood poverty in Ethiopia, India (the states of Andhra Pradesh and Telangana), Peru, and Vietnam. Details of the study methods, sampling, and information collected are in included several published studies (Petrou and Kupek, 2010, Barnett et al., 2013, Crookston et al., 2013, Lundeen et al., 2014). The Young Lives protocol was reviewed by the Central University Ethics Committee of the University of Oxford and the Instituto de Investigación Nutricional Peru. Collective consent was obtained within communities and informed consent was obtained from children and caregivers. For our analysis we use data from the first three rounds of the study, collected from children at ages 1, 5, and 8 years.
Nutritional status measures
Nutritional status was measured using length and height measures. Length at age 1 y and height at ages 5 and 8 y were measured using standard techniques (Petrou and Kupek, 2010, Crookston et al., 2013). We calculated height-for-age z scores (HAZ) using the 2006 WHO standard (WHO, 2006) for children younger than 5 years and the 2007 WHO reference (de Onis et al., 2007) for children older than 5 years. Children with implausible values (absolute values of HAZ greater than 5 in any round; n=89, 50, 25, and 30 in Ethiopia, India, Peru, and Vietnam respectively) were dropped from the analysis.
Cognitive achievement measures
Cognitive development was assessed at age 8 years using the Peabody Picture Vocabulary Test (PPVT) and a mathematics achievement test. The PPVT is a widely-used test of receptive vocabulary and includes items consisting of a stimulus word and a set of pictures and requires that the child selects the picture that best represents the meaning of the stimulus word presented orally by the examiner. In Peru, the 125 item Spanish version of PPVT (PPVT-R) was used, whereas for the other three countries the 204-item PPVT-III was adapted and standardised in each country (Cueto & Leon, 2012). PPVT scores are not comparable across countries or within countries across different languages. The mathematics test (we refer to this as MATH henceforth) includes 29 items on counting, number discrimination, knowledge of numbers, and basic operations with numbers. Extensive analysis of the psychometric characteristics of both tests (Cueto & Leon, 2012), indicated high reliability and validity of test items. Both tests were administered in different languages within each country to allow children to respond in the language they felt most comfortable.
In the statistical analysis, we used the number of correct answers in each test standardised by age in months as our measures of cognitive achievement.
Indicators of behavioural responses to child nutrition
We employed a number of variables that may indicate behavioural mechanisms linking growth at any given period with growth in subsequent periods and cognitive achievement (see the following section for details). In the case of the link between early and later growth, these variables included the dietary diversity score of the child at age 5 and 8 years, i.e. the number of different food groups consumed over the last 24 h, that is a well-validated measure of the macro- and micro-nutrient adequacy of the diet (Ruel, 2002, FAO, 2007). Overall, 11 food groups were considered for children at age 5 and 15 food groups for children at age 8, except for Ethiopia where 14 and 17 food groups were considered for children at ages 5 and 8 respectively. The variable used to explore a behavioural link between nutrition and cognitive achievement was the age at which the child started primary school.
Control variables
We controlled for potential confounders using child gender and birth order, parental socio-demographic characteristics, including caregiver’s characteristics (96%, 99%, 98%, and 98% of caregivers are biological mothers in Ethiopia, India, Peru, and Vietnam respectively), such as ethnicity, schooling, age when the child was 8 years, and height, father’s schooling, and logarithm of real monthly per capita household consumption expenditure at age 8 years. We also control for the language in which the test was administered and whether the language the test was administered is the child’s native language and for locality characteristics by including a set of dummies for the site in which the household was residing when the child was 1, 5, and 8 years. In order to maximise the estimation sample, we imputed missing values of these covariates (prevalence 0.1% to 8%) with their sample means.
A path model of the relationship between nutrition at different periods of childhood and cognitive achievement
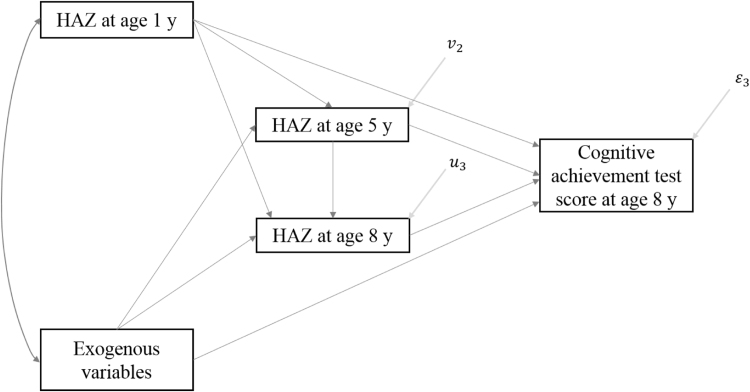
We consider the path model of the relationship between a child’s growth trajectory from conception to age 8 years, as measured by height-for-age Z-score (HAZ) at age 1, 5, and 8 years (we refer to this as HAZ 1 y, HAZ 5 y, and HAZ 8 y henceforth) and cognitive achievement at age 8 years, measured by achievement test scores, that is presented in Fig. 1. The model can be viewed partly as an operationalisation of a general conceptual framework presented in Pollitt, Golub, and Gorman (1996) laying out the mechanisms through which malnutrition at different stages of childhood impacts cognitive development. The framework in Pollitt et al. (1996) identifies two types of mechanisms linking nutrition and cognitive development, namely a biological mechanism manifesting through the impact of malnutrition on brain development processes, such as myelination and synaptogenesis (Levitksy and Strupp, 1995, Thompson and Nelson, 2001) and behavioural mechanisms that operate through the impact of malnutrition on the behaviour of the child but also the behaviour of others, such as parents and peers, that in turn impacts cognitive development. For example, malnutrition may impact the child’s cognitive development through its influence on the child’s exploratory behaviour, social interactions, and responsiveness to environmental stimulation (Brown & Pollitt, 1996) as well as on parents, who may adjust their time and attention spent on the child as well as decisions related to the child’s schooling in response to the child’s malnutrition (Glewwe & Jacoby, 1995).
Fig. 1.
A path model of the relationship between growth trajectories through age 8 years and cognitive achievement at age 8 years.
The model allows for nutrition in periods before age 5 y to impact cognitive achievement at age 8 y directly, that is over and above the effect of nutrition in interim periods but also indirectly through nutrition in these periods. Direct effects can manifest through a biological channel, as nutrition at a given period impacts cognitive achievement at a later period, independently of nutrition in other periods, through its impact on brain processes that are initiated or reach their peak during this period (Pollitt et al., 1996). In this way, nutrition at a given period impacts cognitive development in another period through its impact on cognitive development in the same period (Pollitt et al., 1996). Alternatively, direct effects can also be the result of behavioural responses to nutrition at a given period that persist beyond this period (Galler et al., 1983). Indirect effects manifest through the impact of nutrition at a given period on nutrition in subsequent periods that in turn affect cognitive achievement through the same biological and behavioural channels postulated for direct effects. Similar to the link between nutrition and cognition, the effect of nutrition at a given period on nutrition in subsequent periods may manifest through biological and behavioural mechanisms. A putative biological mechanism has been that malnutrition in early life may induce adaptations in organ function or size, and metabolism, and through that affect nutritional status in later stages (Barker et al., 1989, Komlos, 1994). Behavioural mechanisms postulate that child malnutrition may trigger reactions by parents who may change resources allocated to the child’s care and nutrition that in turn may impact nutrition in subsequent periods. Nevertheless, it is ambiguous whether parental responses to child malnutrition at a given period attenuate or exacerbate child malnutrition in following periods (Griliches, 1979, Behrman et al., 1994).
The path model is more general than the one postulated by Tu et al. (2013), as it allows HAZ 1 y to impact HAZ 8 y over and above the effect of HAZ 5 y on HAZ 8 y. As discussed in the case of the relationship between HAZ 1 y and cognitive achievement, this effect can hold if the biological and behavioural mechanisms through which HAZ 1 y impacts HAZ 8 y persist beyond age 5 y (Strauss & Thomas, 2008, pp. 3387). For example, parental resources allocated to child health after age 5 y might respond to child malnutrition from conception to age 1 y, independently of child nutritional status at age 5 y. Moreover, even if this mechanism is ruled out a priori, it can be shown (see appendix for proof) that the effect of HAZ 1 y on HAZ 8 y, conditional on HAZ 5 y, is zero if HAZ 5 y is a sufficient statistic for nutritional history up to age 5 y. The latter condition, however, will not hold if there is catch-up or lag-down growth (Prader, 1978) between age 1 and 5 y that cannot be ruled out based on evidence from studies using Young Lives data (Outes-Leon and Porter, 2013, Singh et al., 2014) but also from other studies (Adair, 1999, Victora et al., 2010;).
The diagrammatic model in Fig. 1 can be expressed in terms of the following system of equations:
| (1) |
| (2) |
| (3) |
where is cognitive achievement at age 8 y, , , and are HAZ scores at age 1, 5, and 8 y respectively, and , , and are error terms that capture all factors, other than HAZ scores across periods, that determine , , and respectively. We also assume that the error term in each equation is orthogonal to the body-size measures included in the right-hand side of that equation and that errors across equations are uncorrelated. Coefficients , , and estimate the direct effect of growth from conception to age 1 y, from age 1 to 5 y, and from age 5 to 8 y respectively on cognitive achievement at age 8 y. Moreover, coefficients and capture the direct effect of growth from conception to age 1 y and from age 1 to 5 y respectively on HAZ 8 y, whereas coefficient expresses the direct effect of growth from conception to age 1 y on HAZ 5 y. Other exogenous variables have been excluded from the equations to simplify the exposition.
Eq. (1) indicates the lifecourse plot approach to modelling the relationship between early growth trajectories and an outcome later in life (Tu et al., 2013) that, by construction, is expected to produce identical estimates of direct effects of growth in each period on cognitive achievement at age 8 y with those produced by path analysis of the model expressed by Eqs. (1), (2), (3).
Using (3) to substitute for in (2), Eq. (2) becomes as follows:
| (4) |
where, , , and . Coefficients in (4) express total effects of growth in period 1 and 2 respectively on HAZ score at age 8 y. The total effect of on in (4) is the sum of the direct effect, , and the indirect effect, manifesting through , , whereas the total effect of on is equal to the direct effect, .
Substituting (4) for and (3) for in (1), Eq. (1) becomes as follows:
| (5) |
where , , , and +. Coefficients in (5) express total effects of growth in each period on cognitive achievement at age 8 y, including both direct effects from (1) and indirect effects manifesting through growth in subsequent periods. Using the fact that from (2) and that , where , , , and are least squares estimates of , , and respectively, can be expressed in terms of as follows:
| (6) |
Similarly, using the fact that from (3), and that , can be re-written as:
| (7) |
Substituting and in (5) using (6), (7) respectively, (5) can be written as follows:
| (8) |
where is given by the following equation:
| (9) |
Eq. (8) denotes the conditional body size approach to modelling the relationship between growth trajectories and outcomes (Tu et al., 2013). As coefficients in (8) are the same as those in (5), this derivation shows that the coefficients from the conditional body size model can be interpreted as the total effects of growth in each period on cognitive achievement at age 8 years.
We estimated independently the following models:
-
a)
the path model in Fig. 1, expressed by Eqs. (1), (2), (3) for PPVT and MATH,
-
b)
a variant of Eq. (3), where the outcome variable was the child’s dietary diversity at age 5 y that assumes that dietary diversity at age 5 y summarises dietary diversity before this age and thus it is determined prior to HAZ 5 y,
-
c)
a variant of the path model consisting of Eqs. (2), (3), where the outcome variable in (2) was the child’s dietary diversity at age 8 y that assumes that dietary diversity at age 8 y is determined prior to HAZ 8 y as in (b)
-
d)
a variant of the path model consisting of Eqs. (1), (2), (3), where the outcome in (1) was the child’s school starting age.
All models were estimated by Full-Information Maximum Likelihood using the ‘sem’ command in STATA software (StataCorp. 2015. Stata Statistical Software: Release 14 College Station, TX: StataCorp LP).
Results
Table 2, Table 3 report summary statistics of cognitive achievement and growth measures and covariates. Mean height-for-age was at least one standard deviation below that of the reference child at all ages, and there are changes in mean HAZ as children age.
Table 2.
Descriptive Statistics of Cognitive Achievement and Growth Measures across Countries.
| Variable | Ethiopia | India | Peru | Vietnam |
|---|---|---|---|---|
| PPVT score | 79.16 | 58.49 | 58.93 | 93.98 |
| (44.22) | (30.45) | (17.65) | (28.56) | |
| MATH score | 6.58 | 12.03 | 14.20 | 18.43 |
| (5.39) | (6.42) | (5.82) | (5.84) | |
| Height-for-age z score (HAZ) at age 1 y | −1.45 | −1.27 | −1.27 | −1.07 |
| (1.71) | (1.44) | (1.26) | (1.18) | |
| HAZ at age 5 y | −1.45 | −1.65 | −1.53 | −1.34 |
| (1.11) | (0.96) | (1.09) | (1.03) | |
| HAZ at age 8 y | −1.21 | −1.44 | −1.16 | −1.10 |
| (1.10) | (1.02) | (1.04) | (1.06) | |
| Language of administration of tests | ||||
| Amharic | 0.41 | |||
| Oromifa | 0.20 | |||
| Tigrigna | 0.19 | |||
| Telugu | 0.84 | |||
| English | 0.14 | |||
| Spanish | 0.93 | |||
| Quechua | 0.03 | |||
| Vietnamese | 0.99 | |||
| Other | 0.20 | 0.03 | 0.04 | 0.01 |
| Test administered in native language | 0.99 | 0.81 | 0.91 | 0.81 |
| Number of observations | 1876 | 1918 | 1889 | 1949 |
Notes: The table reports means with standard deviations in parentheses. The sample is restricted to children with no missing observations in PPVT or MATH in round 3. Other languages at which tests were administered include Hadiyigna, Sidamigna, Siltigna, and Welayitegna in Ethiopia, Urdu, Kannada, and Oriya in India, a mix of Spanish and Quechua, and Nomatsiguenga in Peru, and H’roi in Vietnam.
Table 3.
Descriptive statistics of indicators of behavioural responses to child nutrition and control variables across countries.
| Variable | Ethiopia | India | Peru | Vietnam |
|---|---|---|---|---|
| Dietary diversity score at age 5 y | 4.82 | 5.78 | 7.85 | 6.87 |
| (1.59) | (1.55) | (1.59) | (2.03) | |
| Dietary diversity score at age 8 y | 5.09 | 6.44 | 8.99 | 7.76 |
| (1.81) | (1.63) | (1.85) | (2.31) | |
| School starting age (in months) | 91.32 | 68.25 | 74.09 | 73.32 |
| (18.54) | (12.09) | (5.32) | (7.01) | |
| Male | 0.53 | 0.53 | 0.50 | 0.51 |
| First-born | 0.23 | 0.39 | 0.37 | 0.46 |
| Second-born | 0.20 | 0.39 | 0.26 | 0.36 |
| Third or higher-born | 0.58 | 0.22 | 0.37 | 0.18 |
| Caregiver’s age when child was 8 y (years) | 36.40 | 31.58 | 35.17 | 36.36 |
| (9.31) | (6.85) | (8.46) | (9.25) | |
| Caregiver’s education (years) | 2.87 | 3.66 | 7.65 | 6.85 |
| (3.73) | (4.44) | (4.47) | (4.02) | |
| Caregiver’s height (cm) | 158.66 | 151.48 | 149.98 | 152.17 |
| (5.87) | (6.02) | (5.38) | (5.85) | |
| Caregiver’s ethnicity | 0.08 | |||
| Amhara | 0.29 | |||
| Gurage | 0.08 | |||
| Hadia | 0.05 | |||
| Oromo | 0.20 | |||
| Sidama | 0.05 | |||
| Tigrian | 0.22 | |||
| Wolayta | 0.06 | |||
| Scheduled castes | 0.18 | |||
| Scheduled tribes | 0.13 | |||
| Backward castes | 0.48 | |||
| White | 0.04 | |||
| Quechua | 0.19 | |||
| Mixed | 0.72 | |||
| Kinh | 0.86 | |||
| H’mong | 0.05 | |||
| Other | 0.04 | 0.21 | 0.05 | 0.08 |
| Father’s education (years) | 4.87 | 5.58 | 9.04 | 7.66 |
| (4.24) | (5.03) | (3.82) | (3.99) | |
| Logarithm of real monthly per capita household consumption expenditure at age 8 y | 4.82 | 6.71 | 5.20 | 6.03 |
| (0.59) | (0.53) | (0.59) | (0.60) | |
| Urban community at age 1 y | 0.35 | 0.24 | 0.68 | 0.20 |
| Number of observations | 1876 | 1918 | 1889 | 1949 |
Notes: The table reports means with standard deviations in parentheses. The sample is restricted to children with no missing observations in PPVT or MATH tests in round 3. Other ethnic groups include Mixed, Agew, and Kambata in Ethiopia, Other castes in India, Black, Asian, Aymara, and Amazonian Indian in Peru, and Chinese, Tay, Nung, Tan, and Giay in Vietnam.
Table 4, Table 5 present estimates of direct, indirect, and total associations between HAZ at each age and cognitive achievement scores at age 8 y. The results presented in Table 4 suggest that the total association between HAZ 1 y and PPVT at age 8 y (PPVT 8 y) is positive and significant in Ethiopia, India, and Peru, whereas it is positive though insignificant in Vietnam. A comparison of the direct and indirect associations of HAZ 1 y with PPVT 8 y indicate that the share of the total association between HAZ 1 y and PPVT 8 y that is mediated though HAZ in subsequent periods is 40% in Ethiopia and 75% in India. In Peru and Vietnam, direct associations are negative whereas indirect associations are positive and larger in absolute value than the direct associations, suggesting that the positive total association between HAZ 1 y with PPVT 8 y is fully mediated through HAZ at later ages in these two countries.
Table 4.
Path analysis results for PPVT scores across countries.
| Ethiopia | |||||||
|---|---|---|---|---|---|---|---|
| Direct associations |
Indirect associations |
Total associations |
|||||
| PPVT age 8 y | HAZ age 8 y | HAZ age 5 y | PPVT age 8 y | HAZ age 8 y | PPVT age 8 y | HAZ age 8 y | |
| HAZ 1 y | 0.026b | 0.102c | 0.234c | 0.017c | 0.136c | 0.043c | 0.238c |
| (0.012) | (0.012) | (0.013) | (0.005) | (0.008) | (0.010) | (0.013) | |
| HAZ 5 y | 0.034 | 0.584c | 0.022c | 0.056b | 0.584c | ||
| (0.024) | (0.020) | (0.0007) | (0.023) | (0.020) | |||
| HAZ 8 y | 0.039a | 0.039a | |||||
| (0.023) | (0.023) | ||||||
| Observations | 1729 | 1729 | 1729 | 1729 | 1729 | 1729 | 1729 |
| India | |||||||
| HAZ 1 y | 0.013 | 0.065c | 0.289c | 0.038c | 0.205c | 0.051c | 0.270c |
| (0.017) | (0.011) | (0.013) | (0.008) | (0.010) | (0.014) | (0.013) | |
| HAZ 5 y | −0.003 | 0.71c | 0.105c | 0.102c | 0.711c | ||
| (0.035) | (0.018) | (0.002) | (0.035) | (0.018) | |||
| HAZ 8 y | 0.148c | 0.148c | |||||
| (0.034) | (0.033) | ||||||
| Observations | 1833 | 1833 | 1833 | 1833 | 1833 | 1833 | 1833 |
| Peru | |||||||
| HAZ 1 y | −0.034a | 0.117b | 0.324c | 0.065c | 0.205b | 0.031b | 0.322b |
| (0.018) | (0.013) | (0.016) | (0.008) | (0.011) | (0.016) | (0.015) | |
| HAZ 5 y | 0.086c | 0.633c | 0.075c | 0.161c | 0.633*** | ||
| (0.030) | (0.017) | (0.002) | (0.030) | (0.017) | |||
| HAZ 8 y | 0.119c | 0.119*** | |||||
| (0.031) | (0.031) | ||||||
| Observations | 1784 | 1784 | 1784 | 1784 | 1784 | 1784 | 1784 |
| Vietnam | |||||||
| HAZ 1 y | −0.012 | 0.012 | 0.439c | 0.041c | 0.366c | 0.029 | 0.378c |
| (0.022) | (0.015) | (0.015) | (0.012) | (0.015) | (0.018) | (0.017) | |
| HAZ 5 y | −0.038 | 0.835c | 0.127c | 0.089b | 0.835c | ||
| (0.041) | (0.019) | (0.002) | (0.041) | (0.019) | |||
| HAZ 8 y | 0.153c | 0.153c | |||||
| (0.036) | (0.036) | ||||||
| Observations | 1783 | 1783 | 1783 | 1783 | 1783 | 1783 | 1783 |
Notes: Standard errors in parentheses, HAZ stands for Height for age Z score. PPVT is standardised by age in months. Controls include child gender and birth order, caregiver’s ethnicity, education, height, and age when the child was 8 y, father’s education, log of real monthly per capita household consumption expenditure at age 8 y, dummies for site at age 1, 5, and 8 y, language in which the test was administered, and whether the language in which the test was administered is the child’s native language. Estimates of the errors in Eqs. (1), (2), (3) are not reported, as well as estimates of indirect and total associations for the path model component for HAZ 5 y, as the former are zero and the latter are equal to the corresponding estimates of direct associations.
significant at 10%.
significant at 5%.
significant at 1%.
Table 5.
Path analysis results for MATH scores across countries.
| Ethiopia | |||||||
|---|---|---|---|---|---|---|---|
| Direct Associations |
Indirect Associations |
Total Associations |
|||||
| MATH age 8 y | HAZ age 8 y | HAZ age 5 y | MATH age 8 y | HAZ age 8 y | MATH age 8 y | HAZ age 8 y | |
| HAZ 1 y | 0.025** | 0.107*** | 0.234*** | 0.024*** | 0.138*** | 0.049*** | 0.245*** |
| (0.012) | (0.012) | (0.013) | (0.005) | (0.009) | (0.010) | (0.013) | |
| HAZ 5 y | 0.037 | 0.592*** | 0.036*** | 0.073*** | 0.592*** | ||
| (0.024) | (0.021) | (0.001) | (0.024) | (0.021) | |||
| HAZ 8 y | 0.062*** | 0.062*** | |||||
| (0.024) | (0.024) | ||||||
| Observations | 1683 | 1683 | 1683 | 1683 | 1683 | 1683 | 1683 |
| India | |||||||
| HAZ 1 y | 0.037** | 0.065*** | 0.287*** | 0.049*** | 0.203*** | 0.086*** | 0.268*** |
| (0.016) | (0.011) | (0.013) | (0.007) | (0.010) | (0.014) | (0.013) | |
| HAZ 5 y | 0.068** | 0.709*** | 0.078*** | 0.146*** | 0.709*** | ||
| (0.034) | (0.018) | (0.001) | (0.034) | (0.018) | |||
| HAZ 8 y | 0.111*** | 0.111*** | |||||
| (0.033) | (0.033) | ||||||
| Observations | 1837 | 1837 | 1837 | 1837 | 1837 | 1837 | 1837 |
| Peru | |||||||
| HAZ 1 y | −0.037* | 0.120*** | 0.326*** | 0.066* | 0.205*** | 0.029* | 0.325*** |
| (0.019) | (0.013) | (0.016) | (0.009) | (0.011) | (0.017) | (0.015) | |
| HAZ 5 y | 0.076** | 0.631*** | 0.081*** | 0.157*** | 0.631*** | ||
| (0.033) | (0.017) | (0.002) | (0.032) | (0.017) | |||
| HAZ 8 y | 0.129*** | 0.129*** | |||||
| (0.034) | (0.034) | ||||||
| Observations | 1826 | 1826 | 1826 | 1826 | 1826 | 1826 | 1826 |
| Vietnam | |||||||
| HAZ 1 y | 0.039* | 0.011 | 0.450*** | 0.044*** | 0.377*** | 0.083*** | 0.388*** |
| (0.022) | (0.014) | (0.015) | (0.013) | (0.014) | (0.018) | (0.016) | |
| HAZ 5 y | 0.0002 | 0.838*** | 0.095** | 0.095** | 0.838*** | ||
| (0.042) | (0.019) | (0.002) | (0.041) | (0.019) | |||
| HAZ 8 y | 0.114*** | 0.114*** | |||||
| (0.036) | (0.036) | ||||||
| Observations | 1858 | 1858 | 1858 | 1858 | 1858 | 1858 | 1858 |
Notes: Standard errors in parentheses, HAZ stands for Height for age Z score. MATH is standardised by age in months. Controls include child gender and birth order, caregiver’s ethnicity, education, height, and age when the child was 8 y, father’s education, log of real monthly per capita household consumption expenditure at age 8 y, dummies for site at age 1, 5, and 8 y, language in which the test was administered, and whether the language in which the test was administered is the child’s native language. Estimates of the errors in Eqs. (1), (2), (3) are not reported, as well as estimates of indirect and total associations for the path model component for HAZ 5 y, as the former are zero and the latter are equal to the corresponding estimates of direct associations.
significant at 10%.
significant at 5%.
significant at 1%.
The total associations of HAZ 5 y and 8 y and PPVT 8 y are positive and significant in all countries. In particular, in Ethiopia and Peru the share of the total association between HAZ 5 y and PPVT 8 y mediated through HAZ 8 y is 40 and 47% respectively, whereas in India and Vietnam direct and indirect associations are counteracting, with the latter being much larger in absolute value than the former.
Path analysis results for MATH presented in Table 5 suggest positive and significant associations between HAZ at all ages and MATH scores at age 8 years in all countries. Indirect associations account for around 50% of the total association between HAZ 1 y and MATH 8 y in Ethiopia and Vietnam and around 60% in India, whereas direct and indirect associations are of opposite sign in Peru with the latter dominating the former. In the case of HAZ 5 y in Ethiopia, India, and Peru around 50% of the total association is mediated through HAZ 8 y, whereas in Vietnam the total association is almost completely indirect. Overall, in almost all cases, the magnitudes of the associations between HAZ at different ages and cognitive achievement measures at age 8 years suggest that growth in earlier periods of life is not more strongly associated with cognitive achievement at age 8 years than growth in later periods.
Table 6 presents estimates of direct, indirect, and total associations of growth trajectories and dietary diversity at age 5 and 8 y and primary school starting age. Table 6 does not report associations between early HAZ and later HAZ that were estimated in the case of dietary diversity at age 8 y and school starting age because these are the same as those reported in Table 4, Table 5. Results suggest that HAZ 1 y is positively and significantly associated with dietary diversity at age 5 y in India and Peru. This implies that the positive association between HAZ 1 y and HAZ 5 y can be partly explained by the fact that HAZ 1 y predicts dietary diversity between age 1 and 5 y that in turn may be a predictor of HAZ 5 y. The positive and significant association between HAZ 1 y and dietary diversity persists through age 8 y in Peru but the same is not the case in India, where only HAZ 5 y has a weakly significant and positive association with dietary diversity at age 8 y. This suggests that the link between HAZ 5 y and HAZ 8 y cannot be explained by the link between HAZ 5 y and dietary diversity between age 5 and 8 y. Moreover, results suggest a negative association between HAZ at each age and school starting age but the association is not significant in all cases. In particular, although the association between HAZ 1 y and school starting age is significant in all countries, HAZ 5 y is significantly associated with school starting age in Ethiopia and Peru, and HAZ 8 y only in Peru.
Table 6.
Path Analysis Results for Dietary Diversity at Age 5 and 8 Years and School Starting Age across Countries.
| Ethiopia | |||||||
|---|---|---|---|---|---|---|---|
| Direct Associations |
Indirect Associations |
Total Associations |
|||||
| Dietary Diversity age 5 y | Dietary Diversity age 8 y | School Starting Age | Dietary Diversity age 8 y | School Starting Age | Dietary Diversity age 8 y | School Starting Age | |
| HAZ 1 y | −0.020 | 0.002 | −0.946*** | −0.014 | −0.548*** | −0.012 | −1.494*** |
| (0.018) | (0.022) | (0.237) | (0.009) | (0.106) | (0.020) | (0.214) | |
| HAZ 5 y | −0.061 | −2.013*** | −0.268*** | −0.061 | −2.281*** | ||
| (0.039) | (0.504) | (0.009) | (0.039) | (0.504) | |||
| HAZ 8 y | −0.453 | −0.453 | |||||
| (0.481) | (0.481) | ||||||
| Observations | 1838 | 1808 | 1773 | 1808 | 1773 | 1808 | 1773 |
| India | |||||||
| HAZ 1 y | 0.086*** | −0.026 | −1.120*** | 0.024* | −0.157 | -0.002 | −1.277*** |
| (0.023) | (0.028) | (0.220) | (0.012) | (0.104) | (0.024) | (0.194) | |
| HAZ 5 y | 0.084* | −0.463 | −0.061 | 0.084* | −0.524 | ||
| (0.044) | (0.459) | (0.001) | (0.044) | (0.458) | |||
| HAZ 8 y | −0.091 | −0.091 | |||||
| (0.442) | (0.442) | ||||||
| Observations | 1912 | 1879 | 1854 | 1879 | 1854 | 1879 | 1854 |
| Peru | |||||||
| HAZ 1 y | 0.108*** | 0.085** | 0.087 | −0.020 | −0.341*** | 0.065* | −0.254*** |
| (0.027) | (0.037) | (0.124) | (0.016) | (0.058) | (0.033) | (0.015) | |
| HAZ 5 y | −0.062 | −0.328 | −0.469*** | −0.062 | 0.797*** | ||
| (0.049) | (0.211) | (0.012) | (0.049) | (0.211) | |||
| HAZ 8 y | −0.738*** | −0.738*** | |||||
| (0.221) | (0.221) | ||||||
| Observations | 1939 | 1935 | 1879 | 1935 | 1879 | 1935 | 1879 |
| Vietnam | |||||||
| HAZ 1 y | 0.042 | 0.036 | −0.299* | 0.002 | −0.143 | 0.038 | −0.442*** |
| (0.032) | (0.045) | (0.175) | (0.025) | (0.098) | (0.037) | (0.144) | |
| HAZ 5 y | 0.007 | −0.270 | −0.074*** | 0.007 | −0.344 | ||
| (0.062) | (0.340) | (0.001) | (0.062) | (0.339) | |||
| HAZ 8 y | −0.089 | −0.089 | |||||
| (0.289) | (0.289) | ||||||
| Observations | 1954 | 1923 | 1893 | 1923 | 1893 | 1923 | 1893 |
Notes: Standard errors in parentheses, HAZ stands for Height for age Z score. Controls in all specifications include child gender and birth order, caregiver’s ethnicity, education, height, and father’s education. Additional controls in specifications for dietary diversity at age 5 y include caregiver’s age, log of real monthly per capita household consumption expenditure at age 5 y, and dummies for site at age 1 and 5 y, whereas additional controls in specifications for dietary diversity at age 8 y and school start age include caregiver’s age, log real monthly per capita household consumption expenditure at age 8 y, and dummies for site at age 1, 5, and 8 y. Estimates of the errors of the path model estimated for each of the outcomes, for the path model component of HAZ 5 y for dietary diversity at age 8 y and school starting age, and the path model component of HAZ 8 y for school starting age are not reported.
significant at 10%.
significant at 5%.
significant at 1%.
Discussion
Although child chronic malnutrition has been identified as a key threat to child development in low- and middle-income countries, there is mixed evidence on the relative importance of nutrition in different periods of childhood for cognitive development. A potential explanation of this, the implications of which have not been investigated exhaustively, is that studies investigating the relationship between nutrition measures, such as growth, at different periods of childhood, also known as growth trajectories, and cognitive development rely on different approaches to model growth trajectories. Moreover, to our knowledge, no study to date, examining the relationship between growth trajectories and cognitive development in low- and middle-income countries has investigated the potential pathways linking growth trajectories and cognition. In this paper, we develop and estimate a general path model of the relationship between growth trajectories and cognitive achievement using data on four cohorts from Ethiopia, India, Peru, and Vietnam. Our model: a) compares two of the most common approaches used for modelling growth trajectories in the literature, namely the lifecourse plot and the conditional body size models, and b) investigates some of the potential channels via which the association between growth in each period and cognitive achievement manifests.
We show that the conditional body size model estimates total effects that, combined with the result of Tu et al. (2013) that the lifecourse plot estimates direct effects, implies that the two approaches are expected to produce systematically different results that have distinct interpretations. This supports that differences in the approach used to model growth trajectories could provide a partial explanation of the differences in the results across studies. Moreover, this result is in contrast to previous empirical and methodological studies that treat lifecourse plot and conditional models as alternatives to testing a given relationship and suggest that the latter should be preferred on statistical grounds. In particular, this result implies that the two approaches are not substitutes but complements and thus combining them may yield better insights. We also show that the combination of the two approaches provides a way to explore direct and indirect pathways linking growth trajectories and cognitive development, as it is equivalent to path analysis of a general model. This is in line with Tu et al. (2013) who argue that “it is likely that a combination of approaches will be required to unravel the complexity in lifecourse research”.
Our results reinforce findings from previous studies supporting a link between growth through age 1 year and cognitive achievement in childhood (Crookston et al., 2013). Nevertheless, a limitation of our study is that we do not have anthropometric measures at age 2 years and thus our results are not completely comparable with studies documenting a significant association between growth from conception through age 2 years and cognitive development (Martorell et al., 2010, Adair et al., 2013). Another limitation of the Young Lives data is the lack of complete information on birth weight and length that does not allow us to estimate separately the association between intrauterine growth and cognition and post-natal infancy growth and cognition.
We also find that post-infancy growth is significantly and positively associated with cognitive achievement, consistent with previous studies (Gandhi et al., 2011, Crookston et al., 2013). Overall, our results are not consistent with the hypothesis that cognitive development is more strongly associated with growth in earlier periods of life than in later periods. In particular, we find that growth in later periods in many cases is more strongly associated with cognitive development than growth in early periods. A key new finding of our study is that the association between early growth and cognitive achievement is mediated, to a great extent, through growth in subsequent periods. This seems to highlight the importance of both pre- and post-infancy growth, as on the one hand this mechanism is likely to lead to accumulation of disadvantage as children age and on the other hand it suggests that part of the link between early growth and later cognitive development may be due to biological and behavioural mechanisms linking later growth with cognitive development.
Moreover, we find evidence that children experiencing slower growth during infancy and in some cases after infancy are more likely to be enroled in primary school at an older age. This is consistent with existing studies producing evidence that malnutrition during the pre-school years leads to delays in primary school enrolment (Glewwe and Jacoby, 1995, Glewwe et al., 2001) and could be suggestive of a behavioural mechanism linking growth and cognitive achievement through parental choice to delay primary school enrolment of slower growing children. In fact, there is evidence providing support to such a mechanism, as Glewwe et al. (2001) find that better nourished children perform significantly better in school, partly because they enter school earlier and thus have more time to learn. Nevertheless, as also suggested by Glewwe et al. (2001), the association of delayed primary school enrolment with cognitive achievement is expected to be ambiguous in general, as on the one hand children who are enroled in school at an older age and have spent less time in school and thus have less time to learn but on the other hand may be more mature and better prepared for learning.
We also find no systematic differences in the sign, significance, and magnitude of total associations between HAZ at each age with PPVT and MATH scores across countries. The only exceptions were the total association between HAZ 5 y and PPVT and MATH scores in Peru that was significantly larger than the other three countries and the total association between HAZ 1 y and PPVT in Ethiopia that was significantly smaller than the other three countries (results on hypotheses tests regarding differences in the magnitudes of coefficients of HAZ at each age are available from the authors on request). Therefore, this evidence does not seem to suggest systematic differences in the association between growth and development across contexts. Given that results persist across countries, one can be more confident about their generalisability to other similar contexts compared to results from studies focusing on a single context.
Our estimates could partly reflect bias arising from confounders that is expected to lead to violation of the assumption that the errors of the equations of the path model are uncorrelated with HAZ. Another source of bias stems from measurement error in HAZ, as linear growth is determined by factors not related to nutrition such as genes, gene-environment interaction, and health-seeking behaviour and thus it is not expected to be a perfect indicator of nutritional status. If height does not have an effect on cognitive development, over and above the effect of nutrition on cognition, as suggested by Martorell et al. (2010), then the measurement error will lead to attenuation bias (Griliches, 1986, Glewwe and King, 2001). If the latter does not hold, then estimated coefficients of HAZ would reflect both the effect of nutrition and of factors other than nutrition determining height on cognition. Because of the different sources of bias, we interpret our results as reflecting associations and not causal effects. Nevertheless, we expect that controlling in estimation for a range of characteristics and period/locality fixed effects ameliorates somewhat these concerns. We also tested whether our results are affected by sample selection bias arising from attrition and missing information (see Table A1, Table A2 for the results) or whether our results are sensitive to the method used to impute missing covariate values (results are available from the authors on request) but we find no evidence to suggest that either of these might be a concern in our study.
Overall, the evidence is suggestive that: (a) growth-promoting interventions that start in utero and in infancy and are sustained through childhood may benefit child development, and (b) that the design of these interventions should take into account behavioural responses to child growth that, in some cases, may mitigate the desired impact of the intervention. Clearly, more and causal evidence is needed to identify critical periods during which cognitive development is particularly susceptible to nutritional insults.
Acknowledgements
This work was supported by the Bill and Melinda Gates Foundation [OPP10327313]; Eunice Shriver Kennedy National Institute of Child Health and Development [R01 HD070993]; and Grand Challenges Canada [Grant 0072-03]. The data used in this study come from Young Lives, an international study of childhood poverty, following the lives of 12,000 children in four countries – Ethiopia, India, Peru and Vietnam – over 15 years (www.younglives.org.uk). Young Lives is core-funded by UK aid from the Department for International Development (DFID) and co-funded from 2010–2014 by the Netherlands Ministry of Foreign Affairs, and by Irish Aid from 2014 to 2015. Findings and conclusions in this article are those of the authors and do not necessarily reflect positions or policies of the Bill and Melinda Gates Foundation, the Eunice Kennedy Shriver National Institute of Child Health and Human Development, Grand Challenges Canada, Young Lives, DFID or other funders. The funders had no involvement in the study design, in the collection, analysis, and interpretation of data, in the writing of this study, and in the decision to submit it for publication.
Appendix A. The effect of HAZ 1 y on HAZ 8 y Conditional HAZ 5 y
Consider the following simple model of the determination of HAZ 8 y and 5 y:
| (A1) |
| (A2) |
where , , and is HAZ at age 1, 5, and 8 y respectively, is a random error, , is the change in HAZ between age 1 and 5 y, and equation (A2) is an identity expressing that HAZ 5 y is the sum of HAZ 1 y and the change in HAZ between age 1 and 5 y. Eq. (A1) does not impose a priori the restriction that , as discussed in the section presenting the path model.
Using (A2) to substitute for in (A1), Eq. (A1) becomes as follows:
| (A3) |
Moreover, consider the following simple model of the determination of :
| (A4) |
where is a random error. Substituting (A4) into (A3), Eq. (A3) becomes as follows:
| (A5) |
If , then from (A4), (A2), is a sufficient statistic for , as it summarises up to a random error, and, from (A5), will have no effect on , conditional on . If , that is the condition for catch-up growth, or that is the condition for lag-down growth, then, from (A5), will have an effect on , over and above the effect of on . The effect of on in (A5) is a combination of the effect of 1on from (A1) that, as discussed in the section presenting the path model manifests through both behavioural and biological channels and of on from (A4) that may also operates through biological and behavioural channels (see Godoy, Nyberg & Eisenberg, 2010 for a detailed discussion on this).
Table A1.
Coefficients estimates of the path model for PPVT using Heckman’s two-step sample selection correction method.
| Ethiopia |
India |
|||||
|---|---|---|---|---|---|---|
| PPVT age 8 y | HAZ age 8 y | HAZ age 5 y | PPVT age 8 y | HAZ age 8 y | HAZ age 5 y | |
| HAZ 1 y | 0.027b | 0.103c | 0.235c | 0.013 | 0.065c | 0.288c |
| (0.012) | (0.016) | (0.015) | (0.017) | (0.011) | (0.013) | |
| HAZ 5 y | 0.034 | 0.582c | −0.004 | 0.709c | ||
| (0.024) | (0.028) | (0.035) | (0.018) | |||
| HAZ 8 y | 0.039a | 0.146c | ||||
| (0.023) | (0.034) | |||||
| Inverse Mills ratio | 0.116 | 1.246 | 1.272 | 0.545 | 0.558a | 0.793a |
| (0.603) | (0.960) | (0.979) | (0.448) | (0.316) | (0.411) | |
| Censored observations | 270 | 270 | 270 | 178 | 178 | 178 |
| Uncensored Observations | 1729 | 1729 | 1729 | 1833 | 1833 | 1833 |
| Observations | 1999 | 1999 | 1999 | 2011 | 2011 | 2011 |
| Peru | Vietnam | |||||
| HAZ 1 y | −0.034a | 0.117c | 0.324c | −0.010 | 0.013 | 0.440c |
| (0.018) | (0.013) | (0.016) | (0.022) | (0.015) | (0.015) | |
| HAZ 5 y | 0.086c | 0.633c | −0.038 | 0.834c | ||
| (0.030) | (0.017) | (0.041) | (0.019) | |||
| HAZ 8 y | 0.118c | 0.152c | ||||
| (0.031) | (0.035) | |||||
| Inverse Mills ratio | −0.551 | −0.496 | 0.430 | −0.429 | −0.349 | −0.529a |
| (0.684) | (0.529) | (0.693) | (0.367) | (0.247) | (0.310) | |
| Censored observations | 268 | 268 | 268 | 217 | 217 | 217 |
| Uncensored Observations | 1784 | 1784 | 1784 | 1783 | 1783 | 1783 |
| Observations | 2052 | 2052 | 2052 | 2000 | 2000 | 2000 |
Notes: Standard errors in parentheses, HAZ stands for Height for age Z score. PPVT is standardised by age in months. The path model also includes controls for child gender and birth order, caregiver’s ethnicity, education, height, and age when the child was 8 y, father’s education, log of real monthly per capita household consumption expenditure at age 8 y, dummies for site at age 1, 5, and 8 y, language in which the test was administered, and whether the language the test was administered is the child’s native language. The sample selection equation includes variables for child gender and birth order, caregiver’s ethnicity, education, height, and age when the child was 8 y, father’s education, wealth index at age 1 y, dummies for site at age 1 y, and dummies for the month of the interview at age 1 y. Estimates of the errors and of coefficients in Eqs. (2), (3), and the sample selection equation are not reported.
significant at 10%.
significant at 5%.
significant at 1%.
Table A2.
Coefficients estimates of the path model for MATH using Heckman’s two-step sample selection correction method.
| Ethiopia |
India |
|||||
|---|---|---|---|---|---|---|
| MATH age 8 y | HAZ age 8 y | HAZ age 5 y | MATH age 8 y | HAZ age 8 y | HAZ age 5 y | |
| HAZ 1 y | 0.026b | 0.109c | 0.236c | 0.037b | 0.065c | 0.288c |
| (0.012) | (0.020) | (0.019) | (0.016) | (0.011) | (0.013) | |
| HAZ 5 y | 0.037 | 0.588c | 0.069b | 0.708c | ||
| (0.025) | (0.034) | (0.034) | (0.018) | |||
| HAZ 8 y | 0.060b | 0.112c | ||||
| (0.024) | (0.033) | |||||
| Inverse Mills ratio | 0.587 | 1.232a | 1.356a | 0.097 | −0.260 | 0.780b |
| (0.494) | (0.724) | (0.796) | (0.349) | (0.253) | (0.344) | |
| Censored observations | 316 | 316 | 316 | 174 | 174 | 174 |
| Uncensored Observations | 1683 | 1683 | 1683 | 1837 | 1837 | 1837 |
| Observations | 1999 | 1999 | 1999 | 2011 | 2011 | 2011 |
| Peru | Vietnam | |||||
| HAZ 1 y | −0.036a | 0.121c | 0.326c | 0.041a | 0.012 | 0.451c |
| (0.019) | (0.013) | (0.016) | (0.022) | (0.014) | (0.021) | |
| HAZ 5 y | 0.077b | 0.630c | −0.001 | 0.837c | ||
| (0.033) | (0.017) | (0.041) | (0.019) | |||
| HAZ 8 y | 0.127c | 0.113c | ||||
| (0.034) | (0.036) | |||||
| Inverse Mills ratio | −0.715 | −0.657a | −1.121a | −0.363 | −0.306 | −0.485 |
| (0.518) | (0.372) | (0.624) | (0.457) | (0.298) | (0.371) | |
| Censored observations | 226 | 226 | 226 | 142 | 142 | 142 |
| Uncensored Observations | 1826 | 1826 | 1826 | 1858 | 1858 | 1858 |
| Observations | 2052 | 2052 | 2052 | 2000 | 2000 | 2000 |
Notes: Standard errors in parentheses, HAZ stands for Height for age Z score. MATH is standardised by age in months. The path model also includes controls for child gender and birth order, caregiver’s ethnicity, education, height, and age when the child was 8 y, father’s education, log of real monthly per capita household consumption expenditure at age 8 y, dummies for site at age 1, 5, and 8 y, language in which the test was administered, and whether the language the test was administered is the child’s native language. The sample selection equation includes variables for child gender and birth order, caregiver’s ethnicity, education, height, and age when the child was 8 y, father’s education, wealth index at age 1 y, dummies for site at age 1 y, and dummies for the month of the interview at age 1 y. Estimates of the errors and of coefficients in Eqs. (2), (3), and the sample selection equation are not reported.
significant at 10%.
significant at 5%.
significant at 1%.
References
- Adair L.S. Filipino children exhibit catch-up growth from age 2 to 12 years. The Journal of Nutrition. 1999;129:1140–1148. doi: 10.1093/jn/129.6.1140. [DOI] [PubMed] [Google Scholar]
- Adair L.S., Fall C.H.D., Osmond C. Associations of linear growth and relative weight gain during early life with adult health and human capital in countries of low and middle income: findings from five birth cohort studies. The Lancet. 2013;382:525–534. doi: 10.1016/S0140-6736(13)60103-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barker D.J.P., Winter P.D., Osmond C. Weight in infancy and death from ischaemic hear disease. The Lancet. 1989;2:577–580. doi: 10.1016/s0140-6736(89)90710-1. [DOI] [PubMed] [Google Scholar]
- Barnett I., Ariana P., Petrou S. Cohort profile: the young lives study. International Journal of Epidemiology. 2013;42:701–708. doi: 10.1093/ije/dys082. [DOI] [PubMed] [Google Scholar]
- Behrman J.R., Rosenzweig M.R., Taubman P. Endowments and the allocation of schooling in the family and in the marriage market: the twins experiment. Journal of Political Economy. 1994;102:1131–1174. [Google Scholar]
- Black R.E., Victora C.G., Walker S.P. Maternal and child undernutrition and overweight in low-income and middle-Income countries. The Lancet Maternal and Child Nutrition. 2013;6:15–39. doi: 10.1016/S0140-6736(13)60937-X. [DOI] [PubMed] [Google Scholar]
- Brown L.J., Pollitt E. Malnutrition, poverty, and intellectual development. Scientific American. 1996:38–43. doi: 10.1038/scientificamerican0296-38. [DOI] [PubMed] [Google Scholar]
- Cheung Y.B., Ashorn P. Continuation of linear growth failure and its association with cognitive ability are not dependent on initial length-for-age: a longitudinal study from 6 months to 11 years of age. Acta Pædiatrica. 2010;99 doi: 10.1111/j.1651-2227.2009.01593.x. 179-23. [DOI] [PubMed] [Google Scholar]
- Crookston B.T., Dearden K.A., Alder S.C. Impact of early and concurrent stunting on cognition. Maternal Child Nutrition. 2011;7:397–409. doi: 10.1111/j.1740-8709.2010.00255.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crookston B.T., Schott W., Cueto S. Postinfancy growth, schooling, and cognitive achievement: Young Lives. The American Journal of Clinical Nutrition. 2013;98:1555–1563. doi: 10.3945/ajcn.113.067561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cueto S., Leon J. Psychometric characteristics of cognitive development and achievement instruments in Round 3 of Young Lives. Young Lives Technical Note. 2012;25 [Google Scholar]
- De Stavola B.L., Nitsch D., dos Santos Silva I. Statistical Issues in Life Course Epidemiology. American Journal of Epidemiology. 2006;163:84–96. doi: 10.1093/aje/kwj003. [DOI] [PubMed] [Google Scholar]
- FAO . FAO; Rome: 2007. Guidelines for measuring household and individual dietary diversity- version 3. [Google Scholar]
- Fink G., Rockers P.C. Childhood growth, schooling, and cognitive development: further evidence from the Young Lives study. The American Journal of Clinical Nutrition. 2014;100:182–188. doi: 10.3945/ajcn.113.080960. [DOI] [PubMed] [Google Scholar]
- Galler J.R., Ramsey F., Solimano G. The influence of early malnutrition on subsequent behavioural development. II. Classroom behaviour. Journal of the American Academy of Child Psychiatry. 1983;22:16–22. doi: 10.1097/00004583-198301000-00003. [DOI] [PubMed] [Google Scholar]
- Gandhi M., Ashorn P., Maleta K., Teivaanmäki T., Duan X., Cheung Y.B. Height gain during early childhood is an important predictor of schooling and mathematics ability outcomes. Acta Paediatrica. 2011;100:1113–1118. doi: 10.1111/j.1651-2227.2011.02254.x. [DOI] [PubMed] [Google Scholar]
- Glewwe P., Jacoby H. An economic analysis of delayed primary school enrollment in a low income country: the role of childhood nutrition. Review of Economics and Statistics. 1995;1:156–199. [Google Scholar]
- Glewwe P., King E.M. The Impact of Early Childhood Nutritional Status on Cognitive Development: Does the Timing of Malnutrition Matter? The World Bank Economic Review. 2001;15:81–113. [Google Scholar]
- Glewwe P., Jacoby H., King E. Early childhood nutrition and academic achievement: a longitudinal analysis. Journal of Public Economics. 2001;81:345–368. [Google Scholar]
- Godoy R., Nyberg C., Eisenberg D.T. Short but catching up: statural growth among native Amazonian Bolivian children. American Journal of Human Biology. 2010;22:336–347. doi: 10.1002/ajhb.20996. [DOI] [PubMed] [Google Scholar]
- Griliches Z. Sibling models and data in economics: beginnings of a survey. Journal of Political Economy. 1979;87:S37–S64. [Google Scholar]
- Griliches Z. Economic data issues. In: Griliches Zvi, Intriligator Michael D., editors. Vol. 3. Elsevier B.V; Amsterdam: 1986. pp. 1465–1513. (Handbook of econometrics). [Google Scholar]
- Komlos J. Univ. of Chicago Press; Chicago: 1994. Stature, living standards and economic development: essays in anthropometric history. [Google Scholar]
- Levitksy D.A., Strupp B.J. Malnutrition and the brain: changing concepts, changing concerns. Journal of Nutrition Supplement. 1995;125:2212S–2220SS. doi: 10.1093/jn/125.suppl_8.2212S. [DOI] [PubMed] [Google Scholar]
- Lundeen E.A., Behrman J.R., Crookston B.T. Growth faltering and recovery in children aged 1–8 years in four low- and middle-income countries: Young Lives. Public Health Nutrition. 2014;17:2131–2137. doi: 10.1017/S1368980013003017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mani S. Is there complete, partial, or no recovery from childhood malnutrition? Empirical evidence from Indonesia. Oxford Bulletin of Economics and Statistics. 2012;74:691–715. [Google Scholar]
- Martorell R., Horta B.L., Adair L.S. Weight gain in the first two years of life is an important predictor of schooling outcomes in pooled analyses from five birth cohorts from low- and middle-income countries. The Journal of Nutrition. 2010;140:348–354. doi: 10.3945/jn.109.112300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Onis M., Onyango A.W., Borghi E., Siyam A., Nishida C., Siekmann J. Development of a WHO growth reference for school-aged children and adolescents. Bulletin of the World Health Organization. 2007;85:660–667. doi: 10.2471/BLT.07.043497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Outes-Leon I., Porter C. Catching-up from early nutritional deficits. Economics and Human Biology. 2013;11:148–163. doi: 10.1016/j.ehb.2012.03.001. [DOI] [PubMed] [Google Scholar]
- Petrou S., Kupek E. Poverty and childhood undernutrition in developing countries: A multi-national cohort study. Social Science Medicine. 2010;71:1366–1373. doi: 10.1016/j.socscimed.2010.06.038. [DOI] [PubMed] [Google Scholar]
- Pollitt E., Golub M., Gorman K. A reconceptualization of the effects of undernutrition on children’s biological, psychosocial, and behavioural development. Social Policy Report Society for Research in Child Development. 1996;10:1–22. [Google Scholar]
- Prader A. Catch-up growth. Postgraduate Medical Journal. 1978;1:133–146. [PubMed] [Google Scholar]
- Prentice A.M., Ward K.A., Goldberg G.R. Critical windows for nutritional interventions against stunting. The American Journal of Clinical Nutrition. 2013;97:911–918. doi: 10.3945/ajcn.112.052332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruel M.T. Operationalizing dietary diversity: a review of measurement issues and research priorities. Journal of Nutrition. 2002;133:3911S–3926S. doi: 10.1093/jn/133.11.3911S. [DOI] [PubMed] [Google Scholar]
- Schott W.B., Crookston B.T., Lundeen E.A., Stein A.D., Behrman J.R. Periods of child growth up to age 8 years in Ethiopia, India, Peru and Vietnam: key distal household and community factors. Social Science Medicine. 2013;97:278–287. doi: 10.1016/j.socscimed.2013.05.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh A., Park A., Dercon S. School meals as a safety net: an evaluation of the midday meal scheme in India. Economic Development and Cultural Change. 2014;62:275–306. [Google Scholar]
- Strauss J., Thomas D. Health over the life course. In: Schultz Paul, Strauss John., editors. Vol. 4. Elsevier B.V; Amsterdam: 2008. pp. 3562–3606. (Handbook of development economics). [Google Scholar]
- Sudfeld R., Charles McCoy D., Danaei G. Linear growth and child development in low- and middle-income countries: a meta-analysis. Pediatrics. 2015;135:1–12. doi: 10.1542/peds.2014-3111. [DOI] [PubMed] [Google Scholar]
- Thompson R.A., Nelson C.A. Developmental science and the media: early brain development. American Psychologist. 2001;56:5–15. doi: 10.1037/0003-066x.56.1.5. [DOI] [PubMed] [Google Scholar]
- Tu Y.-K., Tilling K., Sterne J.A., Gilthorpe M.S. A critical evaluation of statistical approaches to examining the role of growth trajectories in the developmental origins of health and disease. International Journal of Epidemiology. 2013;42:1327–1339. doi: 10.1093/ije/dyt157. [DOI] [PubMed] [Google Scholar]
- Victora C.G., Adair L., Fall C. Maternal and child undernutrition: consequences for adult health and human capital. The Lancet. 2008;371:340–357. doi: 10.1016/S0140-6736(07)61692-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Victora C.G., de Onis M., Hallal P.C., Blössner M., Shrimpton R. Worldwide timing of growth faltering: revisiting implications for interventions. Pediatrics. 2010;125:e473–e480. doi: 10.1542/peds.2009-1519. [DOI] [PubMed] [Google Scholar]
- WHO Multicentre Growth Reference Study Group WHO child growth standards based on length/height, weight and age. Acta Paediatrica Supplement. 2006;450:76–85. doi: 10.1111/j.1651-2227.2006.tb02378.x. [DOI] [PubMed] [Google Scholar]