Sojourn time and lead time projection in lung cancer screening

Abstract

Objectives

We investigate screening sensitivity, transition probability and sojourn time in lung cancer screening for male heavy smokers using the Mayo Lung Project data. We also estimate the lead time distribution, its property, and the projected effect of taking regular chest X-rays for lung cancer detection.

Methods

We apply the statistical method developed by Wu et al. [1] using the Mayo Lung Project (MLP) data, to make Bayesian inference for the screening test sensitivity, the age-dependent transition probability from disease-free to preclinical state, and the sojourn time distribution, for male heavy smokers in a periodic screening program. We then apply the statistical method developed by Wu et al. [2] using the Bayesian posterior samples from the MLP data to make inference for the lead time, the time of diagnosis advanced by screening for male heavy smokers. The lead time is distributed as a mixture of a point mass at zero and a piecewise continuous distribution, which corresponds to the probability of no-early-detection, and the probability distribution of the early diagnosis time. We present estimates of these two measures for male heavy smokers by simulations.

Results

The posterior sensitivity is almost symmetric, with posterior mean 0.89, and posterior median 0.91; the 95% highest posterior density (HPD) interval is (0.72, 0.98). The posterior mean sojourn time is 2.24 years, with a posterior median of 2.20 years for male heavy smokers. The 95% HPD interval for the mean sojourn time is (1.57, 3.35) years. The age-dependent transition probability is not a monotone function of age; it has a single maximum at age 68. The mean lead time increases as the screening time interval decreases. The standard error of the lead time also increases as the screening time interval decreases.

Conclusion

Although the mean sojourn time for male heavy smokers is longer than expected, the predictive estimation of the lead time is much shorter. This may provide policy makers important information on the effectiveness of the chest X-rays and sputum cytology in lung cancer early detection. Published by Elsevier Ireland Ltd.

1. Introduction

Lung cancer is the most common cancer in terms of both incidence and mortality with 1.35 million new cases per year and 1.18 million deaths, with the highest rates in Europe and North America [3]. It is estimated that 219,440 men and women (116,090 men and 103,350 women) were diagnosed with the lung and bronchus cancer in 2009 [4]; and 159,390 men and women died in 2009 [4]. The age-specific lung cancer risk rises continuously with advancing age and reaches its peak between 75 and 80 [5].

The most common cause of lung cancer is long term exposure to tobacco smoking. Many people do not have symptoms, or have only vague symptoms, until the disease has progressed significantly. As a result, only 15% of lung cancers are discovered in early stages, when the possibility of curative treatment is greatest. However, there is no evidence of reduction in lung cancer mortality due to early detection so far [6]. Therefore, there is no recommendation of screening for lung cancer, even for those at high risk. After all, survival depends not only on early detection, but also on effective treatment that follows. We will evaluate lung cancer screening from another point of view in this paper. We want to investigate whether screening can detect the lung cancer early and how early could it be, though early detection may not lead to effective treatment and hence longer survival.

The Mayo Lung Project was started in August 1971, with a purpose to determine whether the death rate from bronchogenic carcinoma can be reduced significantly by vigorous application of modern detecting techniques and aggressive treatment [6]. Between 1971 and 1983, 9309 candidates for the Mayo Lung Project had been enrolled in the study. They are male heavy smokers. As a group, 85% were smoking between 1 and 2.5 packs of cigarettes per day. More than 97% had smoked at least 20 years. More than 90% of the participants were still smoking regardless the warnings that they received. Each participant took a screening test every 4 months, with 19 tests altogether. Each screening test includes a chest X-ray and a three-day pooled sputum cytology sampling. If any of the tests was positive, then the screen was considered positive and a definitive work-up exam, such as biopsy, was done.

We assume that the disease develops by progressing through three states, denoted by S₀ → S_p → S_c, corresponding, respectively, to the disease-free state; the preclinical disease state, in which an asymptomatic individual unknowingly has disease that a screening exam can detect; and the clinical state when the disease manifests itself in clinical symptoms. If a person enters the preclinical state (S_p) at age t₁, and his (or her) clinical symptoms present later at age t₂, then (t₂ − t₁) is the sojourn time in the preclinical state. If he (or she) is offered a screening exam at time t within the interval (t₁, t₂), and cancer is diagnosed, then the length of the time (t₂ − t) is the lead time (see Fig. 1).

Fig. 1.

Illustration of sojourn time and lead time in disease development.

The goal of screening is to detect lung cancer in the preclinical state, that is, when a person has tumor but there is no symptoms. There are two other key parameters involved in the screening program: sensitivity of the diagnosis technique and transition probability from disease-free to preclinical state. The sensitivity is the probability that the screening exam is positive given that the individual is in the preclinical stage. The transition probability into the preclinical stage is the probability density function of making a transition from the disease-free state to the preclinical state.

Knowledge of these parameters is valuable to policy makers. As we know that the goal of screening is to detect the disease before the clinical symptom appears, and usually a case with a longer sojourn time will be easier to detect than the one with a shorter sojourn time. The natural history of the disease progress makes it impossible to observe the exact onset of the preclinical state. Also, once a tumor is diagnosed, it is removed through medical intervention, so the observation of the onset of the clinical state is impossible. The sensitivity of a screening exam cannot be estimated directly from simple data analysis, because it is impossible and unethical to give all participants a definitive diagnostic test. However, by statistical modeling, we can estimate these key parameters using screening data in an effective way. Wu et al. [1] developed new statistical methods to estimate the sensitivity, the sojourn time distribution and the age-dependent transition probability from cancer screening data. We will apply it to the Mayo Lung Project data.

For a particular tumor case detected by screening, the lead time is unobservable. Wu et al. [2] derived the probability distribution for the lead time for the whole cohort who takes part in the screening, including both the screen-detected cases and the interval incident cases. The distribution is a mixture with a point mass at zero, and a piecewise continuous probability density function (PDF). Based on this research, the proportion of patients whose lead time is zero (those diagnosed through clinical symptoms) could be estimated, and the proportion of those whose lead time is positive (that would be detected by regular screening) could be estimated in the long term. We apply this method to the Mayo Lung Project data and the result may provide insights to policy makers regarding lung cancer screening to male heavy smokers.

2. Methods

Our statistical methods [1] for estimating sojourn time, age-dependent sensitivity and transition probability were applied to the Mayo Lung Project data. The data that we used includes the total number of participants in each screening exam, the number of detected and confirmed cancer cases in each screening exam, and the number of interval cases. These data were stratified by age at entry. The age at entry ranges from 44 to 76 years old in the Mayo Lung Project. However, we only used the data from age 45 to age 69, because the other age groups have too few participants, and may cause large variation in our estimation. In particular, consider a cohort of male heavy smokers who are all aged t₀ at study entry, and K (=19) ordered screening examinations occurring at ages t₀ < t₁ < … < t_K−1, where t_i = t₀ + Δ × i, with Δ = 4 months or 1/3 year. Define the i-th screening interval as the time interval between the i-th and the (i + 1)-th screening exams (t_i−1, t_i), i = 1, 2, …, K − 1. We let t₋₁ ≡ 0. For each screening exam, let n_i,t0 be the total number of individuals in this cohort examined at the i-th screening, s_i,t0 is the number of cases detected at the i-th screening exam, and r_i,t0 is the number of cases diagnosed in the clinical state S_c within the interval (t_i−1, t_i), the interval cases.

The likelihood function is

$$L=\prod _{t_0=45}^{69}\prod _{k=1}^{19}{D}_{k,t_0}^{s_{k,t_0}}{I}_{k,t_0}^{r_{k,t_0}}{(1-D_{k,t_0}^{s_{k,t_0}}-I_{k,t_0}^{r_{k,t_0}})}^{n_{k,t_0}-s_{k,t_0}-r_{k,t_0}},$$ (1)

where D_k,t0 is the probability that an individual will be diagnosed at the k-th scheduled exam given that he is in the preclinical state S_p; and I_k,t0 is the probability of being incident in the k-th screening interval. These two probabilities were derived in [1]:

$$D_{k,t_0}=\beta (t_{k-1})\{\sum _{i=0}^{k-2}[1-\beta (t_i)]\cdots [1-\beta (t_{k-2})]{\int }_{t_{i-1}}^{t_i}w(x)Q(t_{k-1}-x)dx+{\int }_{t_{k-2}}^{t_{k-1}}w(x)Q(t_{k-1}-x)dx\};$$

$$I_{k,t_0}=\sum _{i=0}^{k-1}[1-\beta (t_i)]\cdots [1-\beta (t_{k-1})]{\int }_{t_{i-1}}^{t_i}w(x)[Q(t_{k-1}-x)-Q(t_k-x)]dx+{\int }_{t_{k-1}}^{t_k}w(x)[1-Q(t_k-x)]dx.$$

where β(t) is the sensitivity at age t; w(t)dt is the probability of a transition from S₀ to S_p during (t, t + dt); q(t) is the probability density function of the sojourn time in S_p. And $Q(z)={\int }_z^{\infty }q(x)dx$, is the survivor function of the sojourn time in the preclinical state S_p.

The original method was designed for breast cancer screening, where the sensitivity was a logistic function of age, however, after consulting with lung cancer radiologists and oncologists, there seems no obvious age effect connected with sensitivity in practice in lung cancer screening. Hence in this study, the model is simplified as β(t) = β = 1/(1 + exp(−b₀)).

The transition probability density function is a sub-density:

$$w(t)=\frac{0.3}{\sigma t\sqrt{2\pi }}\text{exp }\{-\frac{{(\text{log }t-\mu )}^2}{2{\sigma }^2}\}.$$

As according to the NCI’s “SEER Fast Fact Stats” database [6], the lifetime risk of being diagnosed with lung and bronchus cancer is about 6.94% for both genders. According to Wikipedia [12], the lifetime risk for male smokers is 17.2%. Since the Mayo Lung Project participants were male heavy smokers, the risk should be much higher than that. Therefore we picked 30% as a reasonable upper limit. μ and σ² are parameters to be estimated from the likelihood.

We adopted the log logistic distribution to model the sojourn time in the preclinical state,

$$q(x)=\frac{\kappa x^{\kappa -1}{\rho }^{\kappa }}{{[1+{(x\rho )}^{\kappa }]}^2},\hspace{1em}x>0,$$

where x is the sojourn time, and κ and ρ are positive parameters to be estimated. For justifications on how these age effect functions are chosen, see Wu et al. [1].

The lead time distribution is a conditional distribution given that someone will develop clinical disease before death. We define D as a Bernoulli random variable, with D = 1 indicating the development of clinical disease and D = 0 indicating the absence of the clinical disease before death. We use L to denote the lead time. We consider the lead time to be zero for individuals whose disease is not detected by the screening exam but who develop clinical symptoms. The distribution of the lead time is a mixture of the conditional probability P(L = 0|D = 1) and the conditional probability density function f_L(z|D = 1), for any 0 < z ≤ T − t₀. Here, T represents human life span, which is a fixed upper bound, and t₀ is the individual’s age at his/her initial screening exam.

The distribution for the lead time was derived in Wu et al. [2] as follows:

$$P(L=0|D=1)=\frac{P(L=0,D=1)}{P(D=1)}\text{and}{f}_L(z|D=1)=\frac{f_L(z,D=1)}{P(D=1)}.$$ (2)

where $P(D=1)={\int }_{t_0}^T{\int }_0^{t}w(x)q(t-x)dxdt$, is the probability of developing lung cancer in one’s lifetime after age t₀.

The lead time is zero if and only if the individual is an interval case, therefore the joint probability P(L = 0, D = 1) = I_K,1 + I_K,2 + ⋯ + I_K,K, where I_K,j is the probability of an interval case within the interval (t_j−1, t_j), and it was derived as follows:

$$I_{K,j}=\sum _{i=0}^{j-1}(1-{\beta }_i)\cdots (1-{\beta }_{j-1}){\int }_{t_{i-1}}^{t_i}w(x)[Q(t_{j-1}-x)-Q(t_j-x)]dx+{\int }_{t_{j-1}}^{t_j}w(x)[1-Q(t_j-x)]dx$$

for all j = 1, 2, …, K, with β_i = β(t_i), the sensitivity at age t_i.

The joint PDF f_L(z, D = 1) in Eq. (2) was derived as follows:

$$f_L(z,D=1)=\sum _{i=1}^{j-1}{\beta }_i\{\sum _{r=0}^{i-1}(1-{\beta }_r)\cdots (1-{\beta }_{i-1}){\int }_{t_{r-1}}^{t_r}w(x)q(t_i+z-x)dx+{\int }_{t_{i-1}}^{t_i}w(x)q(t_i+z-x)dx\}+{\beta }_0{\int }_0^{t_0}w(x)q(t_0+z-x)dx.$$

where z ∈ (T − t_j, T − t_j−1), j = 2, ⋯ K. And when j = 1, it is simplified as follows:

$$f_L(z,D=1)={\beta }_0{\int }_0^{t_0}w(x)q(t_0+z-x)dx,\text{ if}z\in (T-t_1,T-t_0).$$

From the formulae, we can see that the lead time is a function of the sensitivity, the sojourn time and the transition probability.

3. Results

We now describe our analysis of the Mayo data based on the likelihood function and lead time distribution derived. In our likelihood function, there are five parameters need to be estimated, that is, θ = (b₀, μ, σ², κ, ρ). Theoretically, the parameters have a domain of either (− ∞, ∞) or (0, ∞). The practical meaning of these parameters will limit them to a finite range. The range for each of them was identified as: 0 < b₀ < 5, 3.5 < μ < 4.5, 0 < σ² < 1, 0.1 < ρ < 2.0, and 1 < κ < 5. Please see [1] for detailed reason why these intervals were chosen.

Markov Chain Monte Carlo (MCMC) was used to generate a random sample from the joint posterior distribution of the parameters for a Bayesian inference. The posterior simulation was partitioned into 3 sub-chains, then we used Gibbs sampling to sample the posteriors for b₀, (μ, σ²), (κ, ρ) separately.

We picked non-informative priors for all the parameters: b₀ follows Uniform (0, 5), and μ follows Uniform (3.5, 4.5). The prior for σ² was Uniform (0, 1), and the prior distributions for κ and ρ were Uniform (1, 5) and Uniform (0.1, 2), respectively. The integrals in D_k,t0 and I_k,t0 do not have an analytical form. We used the trapezoidal rule to evaluate them when calculating the likelihood.

Each Markov Chain Monte Carlo simulation was run for 30,000 steps, with a burn-in of 5000 steps. After the burn-in time, the posteriors were sampled every 100 steps, giving 250 posterior samples for the parameter vector θ. Four chains were simulated, each with different starting values that are over dispersed with respect to the target distribution. The 250 posterior samples from each of the 4 chains were pooled for the analysis; giving a total of 1000 posterior samples ${\theta }_i^{*}$, i = 1, …, 1000. The posterior estimates for parameters θ and the standard errors are listed in Table 1.

Table 1.

Bayesian posterior estimates for the 5 parameters in Mayo Lung Project.

Parameters	Median	Mean	S.E.
b0	2.357	2.395	0.845
μ	4.252	4.252	0.017
σ2	0.034	0.035	0.005
κ	1.531	1.545	0.043
ρ	1.040	1.054	0.189

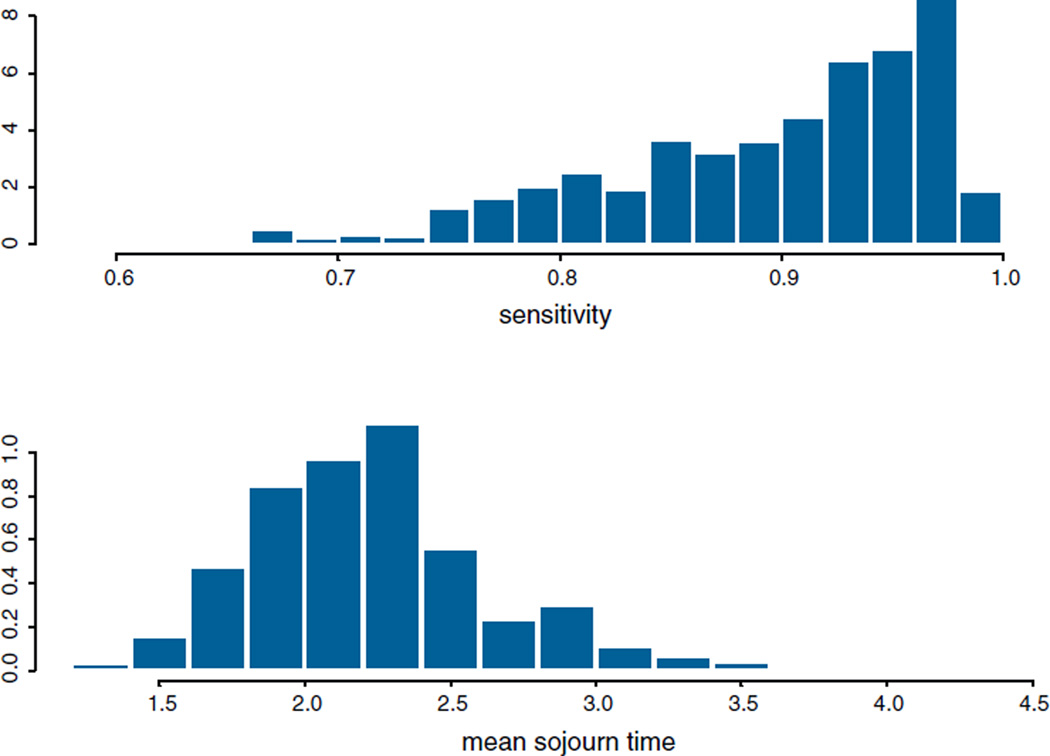
The posterior sensitivity is skewed to the left, see Fig. 2. The posterior mean sensitivity for the lung cancer screening is 89.40%, and the posterior median is 91.35%, with the 95% highest posterior density (HPD) interval (71.84%, 98.07%). The posterior mean sojourn time is 2.24 years, with a posterior median of 2.20 years for male heavy smokers. The 95% HPD interval is (1.57, 3.35) years for the sojourn time, which means 95% of the lung cancer cases have a sojourn time between 1.57 and 3.35 years before symptoms present.

Fig. 2.

Histogram and density estimation for the sensitivity and the sojourn time.

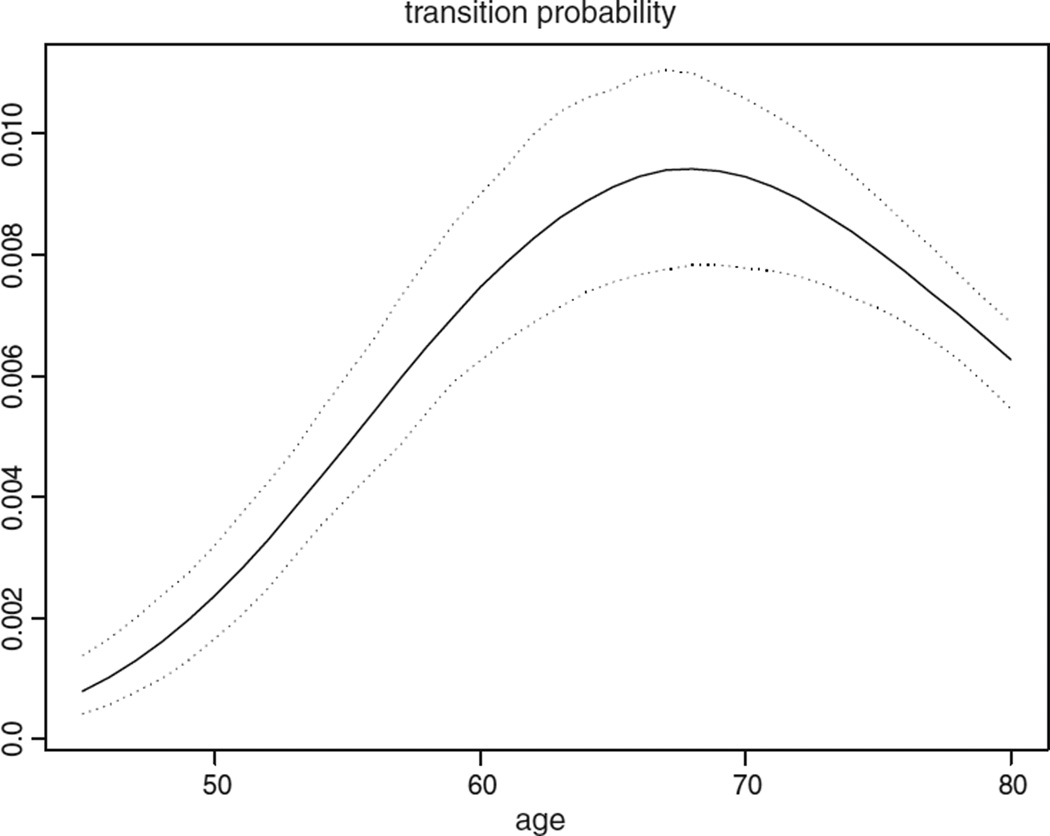
The posterior density curve of the transition probability can be seen from Fig. 3. The posterior mean transition probability varies from 0.814 × 10⁻³ to 9.361 × 10⁻³ for males aged 45–69. This means, in every 1000 people, there will be 0.814–9.361 people making a transition from disease free to preclinical lung cancer per year, depending on their age. The transition probability is not a monotone function of age, having a single maximum at age 68 for male heavy smokers.

Fig. 3.

Posterior quantiles (2.5%, 50%, and 97.5%) of transition probability for male heavy smokers.

We then use the posterior samples ${\theta }_i^{*}$ to estimate the lead time distribution. Given the Mayo data, the posterior predictive distribution of the lead time z can be estimated by the Monte Carlo simulation as follows [8]:

$$f(z|\text{Data})=\int f(z,\theta |\text{Data})d\theta =\int f(z|\theta ,\text{ Data})f(\theta |\text{Data})d\theta \approx \frac{1}{n}\sum _{i}f(z|{\theta }_i^{*}).$$

where $f(z|{\theta }_i^{*})$ represents the mixture distribution in Eq. (2), and ${\theta }_i^{*}$ is the 1000 posterior samples from the MCMC simulation.

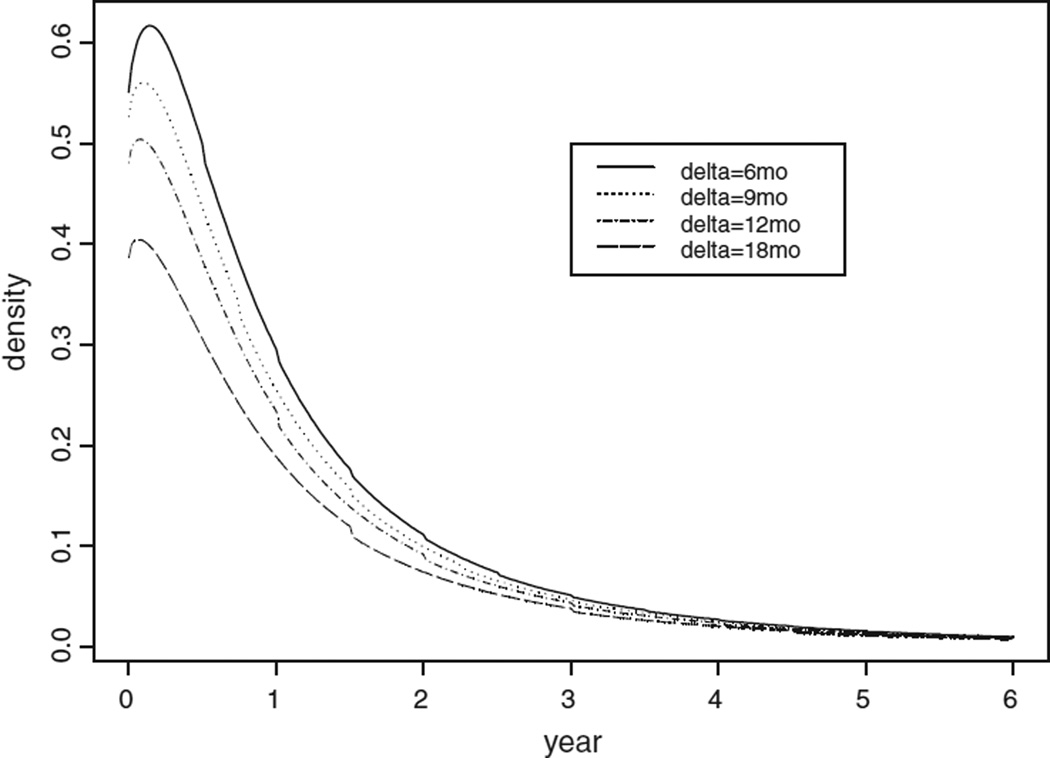
We applied our method to make predictive inference in the case of a screening program consisting of periodic lung screening tests for male heavy smokers aged 45–75 years. We estimated what the results would be if people were screened at different screening intervals starting at age 45. The results are summarized in Table 2. The time interval Δ between these hypothetical screens was 6, 9, 12 and 18 months, starting at age 45 (t₀) and continuing until age 75 (T). The density curves for the lead time are shown in Fig. 4 for different screening intervals.

Table 2.

Lead time estimation for male heavy smokers using Mayo Lung Project data.

Δ	Number of screens	P1 (%)	1−P1 (%)	Mode (months)	Mean (years)	S.E. (years)
6 mo	60	16.79	83.21	1.68	1.18	1.79
9 mo	40	25.30	74.70	1.20	1.07	1.77
12 mo	30	32.74	67.26	0.96	0.98	1.74
18 mo	20	44.65	55.35	0.72	0.84	1.69

Δ = t_i − t_i−1 is the time interval between two screens. P₁ = P(L = 0|D = 1) is the probability of lead time equals to zero, i.e. “no-early-detection.” The columns of P₁ and (1 − P₁) are in percentages.

Fig. 4.

The probability density curve of the lead time for male heavy smokers.

From these results, we see that if a male heavy smoker begins screening when he is 45 years old with an annual screening interval (i.e. Δ = 12 months), and continues until he reaches 75, then there is a 25.30% chance that he will not be detected early by the regular screening program if he develops lung cancer during those thirty years. His chance of no-early-detection from the screening program decreases to 16.79% if the exams are twice a year.

The mean and the mode of the lead time increases as the screening time interval decreases in Table 2. This is compatible with our intuition. For example, with infrequent screening, those with short sojourn times (hence short lead time) will tend to be missed, therefore, the percentage of no-early-detection will be bigger for this group; it is about 45% in the 18-month-interval group. However, it will be more likely that those with short sojourn times to be detected with more frequent screening; hence the probability of no-early-detection will be smaller. Since the lead time is a mixture of point mass at zero and a piecewise continuous density, the mean of the lead time equals to: $EX=0*P(L=0|D=1)+{\int }_0^{T-t_0}{f}_L(z|D=1)dz={\int }_0^{T-t_0}{f}_L(z|D=1)dz$. A large percentage of no-early-detection in the infrequently screened group will dramatically decrease the mean lead time. In other words, more frequent screening exams will contribute to a longer average lead time, which would translate to treatment of the disease at an earlier stage and, potentially improved prognosis. The standard error of the lead time decreases as the time between screening exams increases. In the table, the largest mode is 0.14 years or 1.68 months, corresponding to screening exams every 6 months. With annual exams, the mode value for the lead time is 0.1 years or 1.20 months.

4. Discussion

We applied the likelihood and Bayesian method in Wu et al. [1] to the Mayo Lung Project study and obtained some useful information for lung cancer. The mean sojourn time for male heavy smokers is about 2.2 years, with a 95% credible interval (1.57, 3.35) years. The sensitivity for the combined X-rays and sputum cytology is 0.89. The transition probability from disease-free to preclinical state has a peak around age 68 for male heavy smokers. We compared this result with the SEER database. The “SEER Fast Fact Stats” [5] show that the probability of developing lung cancer has a single maximum between age 70 and 74 for males. Our results agree with that fact, but the age was slightly earlier; since our study population is male heavy smokers, without females, that is probably why the peak age is a few years earlier. Chien et al. [10] estimated the mean sojourn time for lung cancer was 5.51 months, with a 95% credible interval (4.04, 7.12) months, which was much shorter than our estimation. Chien and Chen [11] also estimated that the sensitivity of computed tomography (CT) for lung cancer was 0.97.

As suggested by an anonymous referee, we studied how the parameter estimation would change when the upper limit for the transition probability w(t) changes from 10% to 30%. The estimates do change a bit. With a higher upper limit, the sensitivity of the screening is slightly increased, while the sojourn time for the preclinical state is decreased. We know that the sensitivity and the sojourn time are negatively correlated from other studies and literatures. The transition probability density function does not change very much. The reason might be that w(t) has a domain from zero to infinity; when we increase the upper limit, we just forced the w(t) to have a fatter tail, while we can only make inferences from age 45 to age 69 based on the Mayo data. However, we can only present what we think the most appropriate estimates from this study.

We applied the lead time distribution model in Wu et al. [2] to the Mayo data and get some valuable information on the early-detection of taking chest X-ray and the three-day “pooled” sputum cytology for lung cancer. Our model characterizes two aspects of a screening program’s long-term effects. One aspect is the proportion of clinical (interval) cases among the program’s participant; this is the same as the probability of no-early-detection. The second aspect is the length of time by which screening advances the age of diagnosis of cancer. This length of time will hopefully lead to treatment of disease in earlier stages of development and a better prognosis. The ultimate goal of a screening program in cancer is to reduce cancer mortality. Reduction in cancer mortality is discussed in Fontana et al. [6]. However, no reduction in lung cancer mortality has been demonstrated from screening. Our model contributes to the study of a screening program in other ways. One can use our model to evaluate and compare the characteristics of different possible lung cancer screening programs. For example, the model can provide answers to questions, such as what may be the outcomes of screening exams for a male heavy smoker in his 50 s or 60 s? How do these outcomes change as the frequency of screening exams changes (e.g., screening every 6, 9, or 12 months)? What is the probability that one’s cancer will be detected early if he has lung cancer? How does changing the screening program affect the lead time distribution?

Our results showed that: although the mean sojourn time of lung cancer is much longer than we had expected, the lead time is more skewed to the right. That is, the mode of the lead time is much shorter than we had expected; the mean lead time is also shorter in lung cancer screening, which translates to much shorter early-detection time. The reason might be that the distribution of the sojourn time is very skewed to the right. We noticed from previous research that usually the lead time density curve would be very similar to that of the sojourn time. In this project, even though the posterior mean sojourn time has a 95% Bayesian credible interval of (1.57, 3.35) years, the (individual) posterior sojourn time distribution could still be very skewed. The mean lead time increases as the interval between screening exams decreases. Although the chest X-ray has undergone changes since the Mayo screening study was done, the methods presented in this paper can still be applied to evaluate screening trials.