Measuring and modeling diffuse scattering in protein X-ray crystallography

Significance

The structural details of protein motions are critical to understanding many biological processes, but they are often hidden to conventional biophysical techniques. Diffuse X-ray scattering can reveal details of the correlated movements between atoms; however, the data collection historically has required extra effort and dedicated experimental protocols. We have measured 3D diffuse intensities in X-ray diffraction from CypA and trypsin crystals using standard crystallographic data collection techniques. Analysis of the resulting data is consistent with the protein motions resembling diffusion in a liquid or vibrations of a soft solid. Our results show that using diffuse scattering to model protein motions can become a component of routine crystallographic analysis through the extension of commonplace methods.

Abstract

X-ray diffraction has the potential to provide rich information about the structural dynamics of macromolecules. To realize this potential, both Bragg scattering, which is currently used to derive macromolecular structures, and diffuse scattering, which reports on correlations in charge density variations, must be measured. Until now, measurement of diffuse scattering from protein crystals has been scarce because of the extra effort of collecting diffuse data. Here, we present 3D measurements of diffuse intensity collected from crystals of the enzymes cyclophilin A and trypsin. The measurements were obtained from the same X-ray diffraction images as the Bragg data, using best practices for standard data collection. To model the underlying dynamics in a practical way that could be used during structure refinement, we tested translation–libration–screw (TLS), liquid-like motions (LLM), and coarse-grained normal-modes (NM) models of protein motions. The LLM model provides a global picture of motions and was refined against the diffuse data, whereas the TLS and NM models provide more detailed and distinct descriptions of atom displacements, and only used information from the Bragg data. Whereas different TLS groupings yielded similar Bragg intensities, they yielded different diffuse intensities, none of which agreed well with the data. In contrast, both the LLM and NM models agreed substantially with the diffuse data. These results demonstrate a realistic path to increase the number of diffuse datasets available to the wider biosciences community and indicate that dynamics-inspired NM structural models can simultaneously agree with both Bragg and diffuse scattering.

X-ray crystallography can be a key tool for elucidating the structural basis of protein motions that play critical roles in enzymatic reactions, protein–protein interactions, and signaling cascades (1). X-ray diffraction yields an ensemble-averaged picture of the protein structure: each photon simultaneously probes multiple unit cells that can vary because of internal rearrangements or changes to the crystal lattice. Bragg analysis of X-ray diffraction only yields the mean charge density of the unit cell, however, which fundamentally limits the information that can be obtained about protein dynamics (2, 3).

An inherent limitation in Bragg analysis is that models with different concerted motions can yield the same mean charge density (4). The traditional approach assumes a single structural model with individual atomic displacement parameters (B factors). Given enough data, anisotropic displacement parameters can be modeled. When the data are more limited, translation–libration–screw (TLS) refinement, which models rigid-body motions of subdomains (5), is often used [22% of Protein Data Bank (PDB) depositions (6, 7)]. Variations in the TLS domains can predict very different motions that agree equally well with the Bragg data (8, 9).

Bragg analysis can be combined with additional information to model coupled motions in proteins. Patterns of steric clashes between alternative local conformations (10) can suggest certain modes of concerted motion, but the atomistic details may only be reliably (yet indirectly) identified at high resolution. Time-averaged ensemble refinement (11) is another possibility, but it is complicated by the use of a TLS model to account for crystal packing variations (11). Solid-state NMR experiments (12) and long-timescale molecular dynamics (MD) simulations (13–15) can be used to probe the structural basis of crystal packing variations and internal protein motions.

Extra information about protein motions can also be obtained in the X-ray crystallography experiment itself by analysis of diffuse scattering. Diffuse scattering arises when crystal imperfections cause X-rays to be diffracted away from Bragg reflections. When the deviations are due to crystal vibrations, they can be described using textbook temperature diffuse scattering theory (see, e.g., ref. 16). When each unit cell varies independently, the diffuse intensity is proportional to the variance in the unit cell structure factor (17), which describes correlations in the charge density variations. This assumption is appropriate when analyzing the broadly distributed diffuse intensity that corresponds to small correlation lengths (18–21), as the contribution of inter-unit cell atom pairs in this case is a small fraction of the total signal.

Several approaches have been used to connect macromolecular diffuse scattering data to models of protein motion and lattice disorder. Peter Moore (22) has emphasized the need to validate TLS models using diffuse scattering, as has been performed in a limited number of cases (8, 23, 24). Good agreement with the data has previously been observed for liquid-like motions (LLM) models (18–21), which provide a softer model of the protein than the TLS model. In the LLM model, the atoms in the protein are assumed to move randomly, like in a homogeneous medium; the motions were termed “liquid-like” by Caspar et al. (19) because the correlations in the displacements were assumed to fall off exponentially with the distance between atoms.

Normal-modes (NM) models also treat the protein as a softer substance than the TLS model, but treat it as a solid. Normal-mode analysis (NMA) provides a more detailed picture of the conformational ensemble than the LLM model, enabling a direct connection to putative mechanisms of protein function (25). The NM refinement methods that have been developed for Bragg analysis use few additional parameters (26–30); however, these methods are not currently available in the standard builds of the major refinement software. Reasonable qualitative agreement previously has been seen using NM to model diffuse intensity in individual diffraction images (31, 32). More recently, the fit of alternative coarse-grained elastic network models to diffuse scattering data of staphylococcal nuclease has been investigated (33).

There is also a long-standing interest both in using diffuse scattering to validate improvements in MD simulations and in using MD to derive a structural basis for the protein motions that give rise to diffuse scattering (13, 31, 34–39). Recent advances in computing now enable microsecond duration simulations (13) that can overcome past barriers to accurate calculations seen using 10-ns or shorter MD trajectories (35, 38).

Despite the fact that diffuse scattering analysis is relatively well developed in small-molecule crystallography (40) and materials science (3), it has been underused in protein crystallography. There are relatively few examples of diffuse data analyzed using individual diffraction images from protein crystallography experiments, including studies of tropomyosin (41, 42), 6-phosphogluconate dehydrogenase (43), yeast initiator tRNA (44), insulin (19), lysozyme (20, 23, 24, 31, 32), myoglobin (38), Gag protein (45), and the 70s ribosome subunit (46). Moreover, there are an even smaller number of examples involving complete 3D diffuse datasets; these include studies of staphylococcal nuclease (21) and calmodulin (18).

To exploit diffuse scattering for modeling protein motions, there is a pressing need to increase the number of proteins for which complete 3D diffuse datasets have been experimentally measured. Conventional data collection procedures use oscillation exposures to estimate the full Bragg intensities. In contrast, the complete 3D datasets measured by Wall et al. (18, 21) used specialized methods for integrating 3D diffuse data from still diffraction images. Similar methods now can be generalized and applied to other systems using modern beamlines and X-ray detectors. In particular, the recent commercial development of pixel-array detectors (PADs), which possess tight point-spread functions and single-photon sensitivity (47), have created opportunities for measuring diffuse scattering as a routine tool in protein crystallography experiments using more conventional data collection protocols.

Here, we present diffuse scattering datasets for the human proline isomerase cyclophilin A (CypA) and the bovine serine protease trypsin. These datasets substantially increase the amount of experimental 3D diffuse scattering data available to the macromolecular crystallography community, providing a necessary foundation for further advancement of the field (48). To assess the potential for routine collection of diffuse datasets in crystallography, rather than expending a great deal of effort in optimizing the diffuse data and collecting still images (18, 21), we used oscillation images obtained using best practices for high-quality Bragg data collection. The resulting datasets yield 3D diffuse data that can discriminate among alternative TLS refinements (8), LLM models (19, 20), and NM models (32–34). Moreover, the agreement of the NM models with both Bragg and diffuse scattering data suggests a path forward for using both data sources simultaneously with a small number of variables. Our results demonstrate that diffuse intensity can, and should, be measured in a typical X-ray crystallography experiment and indicate that diffuse scattering can be applied broadly as a tool to understand protein motions.

Results

Experimental Diffuse Data Show Crystallographic Symmetry.

We obtained nearly complete 3D anisotropic diffuse datasets D′ for CypA and trypsin using a PAD detector with synchrotron radiation (Methods, Fig. 1, and SI Appendix, Fig. S1), and used the Friedel and Laue group symmetry to quantify the level of crystallographic symmetry. We averaged intensities between Friedel pairs to create a symmetrized map D′_F and calculated the linear correlation CC_F between D′ and D′_F. For CypA and trypsin, CC_F = 0.90 and 0.95, respectively. We averaged P222-related reflections (corresponding to the P2₁2₁2₁ space group of both CypA and trypsin) to produce the Laue symmetrized intensities, D′_L. The linear correlation CC_L was then computed between D′ and D′_F, yielding CC_L = 0.70 for CypA and CC_L = 0.69 for trypsin. These correlations indicate the experimental diffuse intensity follows the Bragg peak symmetry.

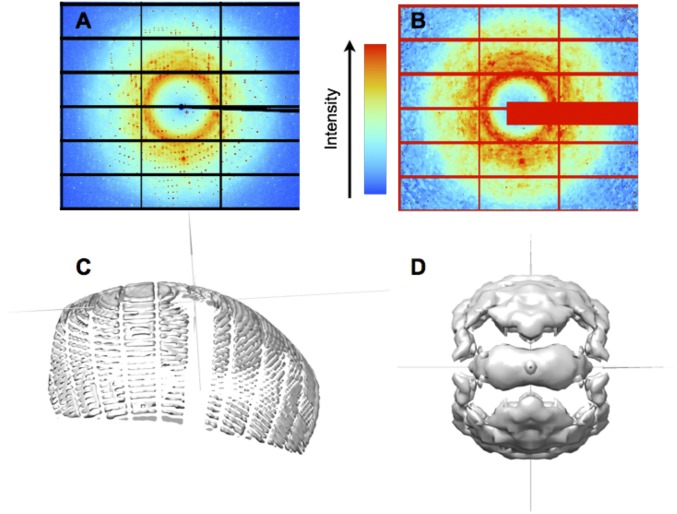
Fig. 1.

Steps in diffuse data integration. (A) Raw CypA diffraction images are processed (B) to remove Bragg peaks and enable direct comparisons of pixel values to models. (C) Pixels in diffraction images are mapped to reciprocal space and values of diffuse intensity are accumulated on a 3D lattice; each diffraction image produces measurements of diffuse intensity on the surface of an Ewald sphere. (D) The data from individual images are combined and symmetrized to yield a nearly complete dataset (isosurface at a value of 65 photon counts in the total intensity, before subtracting the isotropic component).

TLS Models Yield Low Correlation with Diffuse Scattering Data.

To investigate how well TLS models agree with the molecular motions in the CypA crystal, we compared the experimental diffuse data to intensities calculated from three alternative TLS models: “Phenix,” “TLSMD,” and “whole-molecule” (SI Appendix, Fig. S2 A–D). Although all three models predict different motions, the R factors are very similar: R,R-free = 16.4%, 18.1% for the whole-molecule and Phenix models; and 16.2%, 18.1% for the TLSMD model. The correlations between the calculated diffuse intensity for these models and the anisotropic experimental data are low: 0.03 for the phenix model; 0.04 for the TLSMD model; and 0.14 for the whole-molecule model. In addition, the pairwise correlations of the calculated diffuse intensities are low: 0.066 for whole-molecule/TLSMD; 0.116 for whole-molecule/Phenix; and 0.220 for Phenix/TLSMD.

Like CypA, the three trypsin TLS models (SI Appendix, Fig. S2 E–H) yielded very similar R,R-free values: 15.1%, 16.7% for the whole-molecule model; 15.3%, 16.6% for the Phenix model; and 15.2%, 16.6% for the TLSMD model. Correlations between the calculated and experimental diffuse intensities are again low: 0.02 for the Phenix and TLSMD models, and 0.08 for the whole-molecule model. Comparisons of the calculated anisotropic diffuse intensity show that the whole-molecule motion is dissimilar to both the Phenix and TLSMD predictions (CC = 0.03 and 0.05, respectively). In contrast, the Phenix and TLSMD models yield much more similar diffuse intensities (CC = 0.515). The relatively high correlation between these models is consistent with the similarity in the TLS groups (SI Appendix, Fig. S2 F–H). The low correlation of the CypA and trypsin TLS models with the diffuse data suggests that the protein motions might be correlated on a shorter length scale than provided by these models.

LLM Models Yield Substantial Correlation with Diffuse Scattering Data.

One model that accounts for short-range correlations is LLM (19, 20). The LLM model assumes that atomic displacements are uncorrelated between different unit cells, but are correlated within the unit cells. The correlation in the displacements is assumed to decay exponentially as $e^{-x/\gamma }$, where x is the separation of the atoms, and γ is the length scale of the correlation. The displacements of all atoms are assigned a SD of σ. The LLM model previously has been refined against 3D diffuse intensities obtained from crystalline staphylococcal nuclease (21) and calmodulin (18), yielding insights into correlated motions.

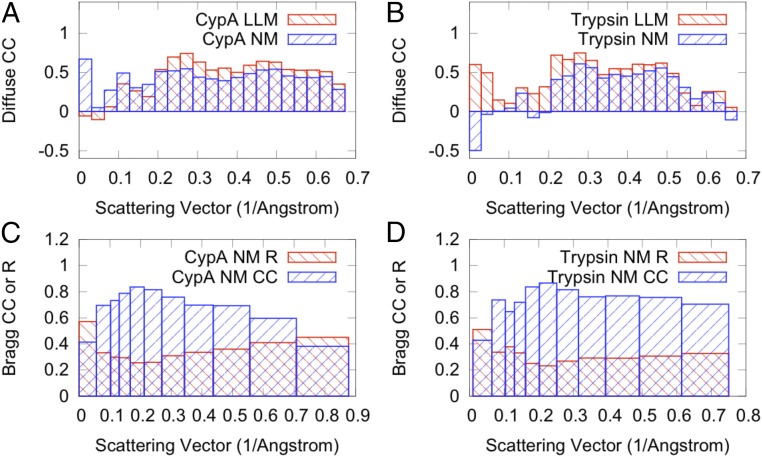
We refined isotropic LLM models of motions in CypA and trypsin against the experimental diffuse intensities (Methods). The CypA model was refined using data in the resolution range of 31.2–1.45 Å, and the trypsin model using 68- to 1.46-Å data. For CypA, the refinement yielded γ = 7.1 Å and σ = 0.38 Å with a correlation of 0.518 between the calculated and experimental anisotropic intensities. The highest correlation between data and experiment occurs in the range of 3.67–3.28 Å, where the value is 0.74 (Fig. 2A). For the trypsin dataset, the refinement yielded γ = 8.35 Å and σ = 0.32 Å with a correlation of 0.44, which is lower than for CypA. The peak value is 0.72 in the resolution range of 4.53–4.00 Å (Fig. 2B).

Fig. 2.

Agreement of models of protein motions with diffuse and Bragg data. (A and B) Linear correlation coefficients (CCs) between diffuse data and LLM (red bars) or NM models (blue bars) computed by resolution shell for (A) CypA and (B) trypsin. (C and D) Correlations and R factors between Bragg data and NM models computed by resolution shell for (C) CypA and (D) trypsin. Agreement factors for the diffuse and Bragg data were computed using LUNUS (60) and Phenix (67), respectively.

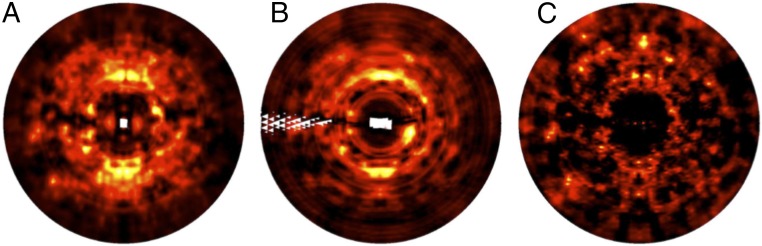
The refined LLM models also were compared with the data using simulated diffraction images. Images corresponding to frame number 67 of the CypA data were obtained using the LLM model (Fig. 3A) and the 3D diffuse data (Fig. 3B). The main bright features above and below the origin are similar between the two. Many of the weaker features also appear to be similar, both at high and low resolution. The similarity is diminished but still apparent for images obtained for frame number 45 of trypsin (SI Appendix, Fig. S3). These simulations provide a visual confirmation of the substantial correlations obtained for the 3D diffuse intensity (see SI Appendix, Fig. S1, for visualization comparisons of the LLM model to the diffuse data in 3D).

Fig. 3.

Simulated diffraction images for CypA frame 67 obtained using the following: (A) LLM model; (B) integrated 3D diffuse data; (C) elastic network NM model. Lighter colors correspond to stronger intensity. White regions correspond to pixel values where there are missing values in the corresponding 3D lattice (Methods).

Normal Modes Can Model Both Diffuse and Bragg Scattering Data.

To assess the potential of NMA to be developed for diffuse scattering studies, we developed coarse-grained elastic network models of the CypA and trypsin unit cells. The C_α coordinates and B factors for the NM models of diffuse scattering are by definition identical to those derived from the Bragg data (Methods). To assess the agreement of specific NM-derived conformational variations with the Bragg data, we eliminated the B factor constraint and generated 50-member ensembles from the 10 lowest-frequency nonzero modes (Methods). To more accurately model the Bragg data, we adjusted the overall spring constant and applied an additional uniform isotropic B factor to all atoms (Methods and SI Appendix, Fig. S4). The correlations were high across resolution shells (Fig. 2 C and D), yielding overall R factors of 38% (CypA) and 31% (trypsin) (SI Appendix, Tables S1 and S2). We also calculated the predicted diffuse intensity from the NM models: the correlation of the CypA model with the data is 0.41 in the resolution range of 31.2–1.45 Å, and the correlation of the trypsin model with the data is 0.38 in the resolution range of 68–1.46 Å. The agreement with the data is substantial within individual resolution shells (Fig. 2). The NM simulated diffraction image for CypA (Fig. 3C) shows bright features that are found in the data (Fig. 3B). The relative strength at high versus low resolution is greater than in the data, however, suggesting that this NM model is too rigid; this discrepancy might be addressed by softening the intraresidue interactions and optimizing the model against the diffuse scattering data directly. The comparisons of simulated diffraction images for trypsin are consistent with the findings for CypA (SI Appendix, Fig. S3).

Discussion

Diffuse X-ray scattering is a potentially valuable yet little exploited source of information about macromolecular dynamics. Diffuse intensities can double the total number of measured data points in the crystallographic experiment while providing a parallel dataset against which structural dynamical models can be refined or validated. Until now, measurement of 3D diffuse scattering data only has been pursued in dedicated efforts requiring extra still diffraction images and substantial optimization of experimental design. The present collection of two datasets obtained using oscillation images using best current practices in room temperature protein crystallography (49), and the use of the data in evaluating TLS, LLM, and NM models, illustrates the potential for using diffuse scattering to increase understanding of protein structure variations in any X-ray crystallography experiment, representing a significant step toward moving diffuse scattering analysis into the mainstream of structural biology.

Diffuse data obtained for CypA and trypsin can distinguish among the TLS, LLM, and NM models of motions. However, the agreement with the data are somewhat lower than in previous LLM models of 3D diffuse scattering (18, 21). In this study, the correlation of the LLM model with the data was 0.518 in the range of 31.2–1.45 Å for CypA, and 0.44 in the range of 68–1.46 Å for trypsin; in comparison, the correlation was 0.595 in the range of 10–2.5 Å for staphylococcal nuclease (21) and 0.55 in the range of 7.5–2.1 Å for calmodulin (18). Some possible explanations for the lower agreement for CypA and trypsin include the following: the use of higher-resolution data in the present studies; that LLM might be a better description of motions in staphylococcal nuclease and calmodulin than in CypA and trypsin; and that the measurements might have been more accurate in the past experiments, as the data collection was tailored for diffuse scattering. An apparent alignment of the residual intensity distribution with the unit cell axes (SI Appendix, Fig. S2 C and F) suggests that an anisotropic LLM model might be more appropriate than an isotropic LLM model for CypA and trypsin.

The low correlation of the present TLS models with the diffuse intensity for CypA and trypsin suggests that the variations in the protein crystal might involve motions that are correlated on a shorter length scale than accounted for by these models. TLS models with large rigid domains might be more appropriate for interpreting small-scale diffuse features in the immediate neighborhood of Bragg peaks, similar to the rigid-body motions model of Doucet and Benoit (23). Methods to integrate the small-scale features in protein crystallography onto a finer 3D reciprocal space grid than used here do exist (18) and could be used to investigate this possibility.

The agreement of the LLM models with 3D experimental diffuse data across multiple systems warrants further consideration for using diffuse scattering in model refinement and validation. A key finding is that the agreement of the LLM models with the diffuse data are higher than the TLS models, which currently are used widely in protein crystallography. The LLM model implies that the motions of atoms separated by more than 7–8 Å are relatively independent, and that atoms that are closer to each other move in a more concerted way. Interestingly, this length scale of the correlations is comparable to the size of the TLS domains; however, compared with the sharp domains of the TLS model, the exponential form of the correlations indicates that there is a smooth spatial transition between the correlated and uncorrelated atoms in the LLM. The smooth transition might be key to the increased agreement of the LLM with the diffuse data compared with the rigidly defined regions of the TLS model.

The agreement of the NM models with the data assessed using either correlations across complete datasets (Fig. 2) or simulated diffraction images (Fig. 3 and SI Appendix, Fig. S3) is substantial but slightly less than for the LLM models. However, it is important to interpret this comparison in light of the fact that the covariance matrices of the NM models were normalized to agree with the Bragg data and not parameterized against the diffuse data (Methods), whereas the LLM model is parameterized against the diffuse data. In addition, in the coarse-grained NM model, the residues are treated as rigid; relaxing this approximation should lead to more accurate models. The agreement with the Bragg data is currently limited by the fact that the parameter optimization used only the refined C_α positions and B factors to agree with the Bragg data and that heteroatoms, such as solvent, were not included in the calculations. Collectively, these results point to the potential for normal modes to be refined jointly against Bragg and diffuse scattering data as an alternative atomic displacement model, replacing TLS or individual B factors.

Overall, the 3D diffuse scattering data obtained here for CypA and trypsin, and previously for staphylococcal nuclease (21) and calmodulin (18), suggest that the protein structure varies more like a soft material than like a collection of independent rigid domains. An important consideration in developing these future refinement methods is to maintain a key advantage of TLS refinement at lower resolutions: the introduction of relatively few additional parameters for refinement. This requirement also would be satisfied by NMA, which can have a low computational cost and general applicability, making it a promising model for integrating diffuse scattering into crystallographic model building and refinement (48). Whether this pursuit is well-motivated hinges on whether new biological insights can be gained from atomic displacements generated by NM models refined against Bragg and diffuse data. Indeed, although use of TLS in model refinement is now widespread, it scarcely has been used to generate biological hypotheses (for exceptions, see refs. 50 and 51). In contrast to TLS models, elastic network NM models have been widely used to draw functional inferences (52). Both the encouraging agreement of the NM models with the diffuse scattering and the potential for NM models to yield insights about the importance of conformational dynamics in protein function provide a strong motivation for further developing NM models for protein X-ray crystallography.

Diffuse scattering also can be used to validate models of molecular motions other than those considered here, including models produced by ensemble refinement (11); multiconformer modeling performed by discrete (53, 54) or continuous (18, 55, 56) conformational sampling; and MD simulations (13–15, 31, 35–39, 57). In particular, MD simulations now provide sufficient sampling to yield robust calculations of diffuse intensity (13), and these can be used to consider a myriad of intramolecular motions (e.g., loop openings and side-chain flips) (58) and lattice dynamics. Polikanov and Moore (46) recently have demonstrated the importance of lattice vibrations in explaining experimental diffuse scattering measurements of ribosome crystals, which indicates that models should simultaneously account for correlations that are coupled both within and across unit cell boundaries (18, 20); accounting for lattice vibrations more accurately also might yield improved Bragg integration (48). Moreover, comparisons of crystal simulations and diffuse scattering can provide an additional observable for benchmarking improvements in energy functions and sampling schemes (14).

Although the initial successes of dynamics-based models of diffuse scattering indicate that crystal defects can play a secondary role in contributing to the diffuse signal, at least in some cases, consideration of crystal defects might become important to achieve the highest model accuracy and most general applicability of diffuse scattering in crystallography. Additionally, as more X-ray data from both brighter conventional and X-ray free-electron laser light sources, accounting for all sources of Bragg and diffuse scattering will be necessary to model the total scattering needed for innovative phasing applications (59). In summary, the datasets presented here demonstrate that diffuse scattering can now be routinely collected and that using these data will help us obtain an increasingly realistic picture of motion in protein crystals, including integrated descriptions of intramolecular motions, lattice vibrations, and crystal defects.

Methods

Diffuse Data Integration.

After conventional crystallization, data collection, and processing (SI Appendix, Supplementary Text: Methods), image processing was performed, using the LUNUS collection of diffuse scattering tools (60), to transform raw images (Fig. 1A) into ones in which the pixel values could be used to integrate 3D datasets (Fig. 1B). The beam stop and image edges were masked, as were pixel values outside of the range 1–10,000 photon counts. A beam polarization correction and solid-angle normalization were applied (60). Bragg peaks were removed using mode filtering with a mask width of 20 pixels and a histogram bin of one photon count.

Diffuse data integration was performed using a python script that calls DIALS methods within the Computational Crystallography Toolbox (CCTBX) (61, 62). The script obtains an indexing solution and uses the results to map each pixel in each diffraction image to fractional Miller indices h′k′l′ in reciprocal space. It sums the intensities from pixels in the neighborhood of each integer Miller index hkl and tracks the corresponding pixel counts, while ignoring pixels that fall within a 1/2 × 1/2 × 1/2 region about hkl. It writes the intensity sums and pixel counts for each frame on a grid, populated on an Ewald sphere that varies according to the crystal orientation for each image (Fig. 1C). Lunus methods were used to obtain a radial scattering vector intensity profile for each frame, which was used for scaling. The mean diffuse intensity was calculated at each grid point using the scaled sums and pixel counts from all of the frames. The integration yielded a CypA dataset with 438,627 measurements that is 98% complete to a resolution of 1.4 Å, and a trypsin dataset with 233,381 measurements that is 95% complete to 1.25-Å resolution.

Experimental and model diffuse intensities were compared using just the anisotropic component of the signal, which is primarily due to the protein (13). Lunus methods were used to subtract the radial average and obtain the anisotropic signal. Intensities were symmetrized by averaging P222-equivalent points. The comparable degree of symmetry in the CypA and trypsin data suggests that the measurement of diffuse intensity is robust with respect to the difference in the phi angle oscillation during data collection (0.5° for CypA vs. 1° for trypsin).

All images are available on SBGrid Data Grid (https://data.sbgrid.org/dataset/68/ for CypA; https://data.sbgrid.org/dataset/201/ for trypsin), and the symmetrized datasets are available in Datasets S1 and S2.

Simulated Diffraction Images.

Diffuse scattering images were simulated using methods similar to those for data integration. A template frame was used to map each pixel to a fractional Miller index. The new value of each pixel was obtained by linear interpolation between the nearest-neighbor integer points hkl in the 3D diffuse model or data. In the case of the 3D data, the images greatly enhanced the diffuse features compared with the raw images (SI Appendix, Figs. S5 and S6) because of statistical averaging in data integration. For visualization of simulated images, the minimum pixel value was computed within each pixel-width annulus about the beam center, and was subtracted from each pixel value within the annulus. Images were displayed using Adxv version 1.9.10 (63), with display parameters selected for meaningful comparison of the diffuse features.

TLS Structure Refinement and Diffuse Scattering Model.

Three independent TLS refinements were performed for CypA (SI Appendix, Fig. S2 A–D). The whole-molecule selection consists of the entire molecule as a single TLS group. The Phenix selection consists of the eight groups (residues 2–14, 15–41, 42–64, 65–84, 85–122, 123–135, 136–145, and 146–165) identified by phenix.find_tls_groups. The TLSMD selection consists of eight groups (residues 2–15, 16–55, 56–80, 81–85, 86–91, 92–124, 125–143, and 144–165) identified by the TLS Motion Determination web server (6, 7). All TLS refinement was performed within phenix.refine through five macrocycles. Aside from the inclusion of TLS refinement, these macrocycles were identical to the initial structure refinement described above.

Similarly, for trypsin, we selected whole-molecule, Phenix, and TLSMD TLS refinement strategies as described above (SI Appendix, Fig. S2 E–H). The Phenix selection consists of seven TLS groups: residues 16–54, 55–103, 104–123, 124–140, 141–155, 156–225, and 226–245. The TLSMD selection consists of nine groups: residues 16–52, 53–98, 99–115, 116–144, 145–171, 172–220, 221–224, 225–237, and 238–245.

Structural ensembles were generated using the phenix.tls_as_xyz method (9). One thousand random samples were drawn assuming independent distributions for each domain. Diffuse intensities were calculated using phenix.diffuse (8). CypA and trypsin models were generated to a final resolution of 1.2 and 1.4 Å, respectively.

LLM Model.

LLM models of diffuse scattering were calculated using PDB entries 5F66 (CypA) and 5F6M (trypsin). Temperature factors were set to zero and squared calculated structure factors I₀(hkl) were computed using the structure_factors, as_intensity_array, and expand_to_p1 methods in CCTBX (61, 62). The Lunus symlt method was used to complete the grid using the P222 Laue group.

Given a correlation length γ and amplitude of motion σ, the diffuse intensity at scattering vector $\mathbf{s}$ was calculated as $D_{LLM}\left(\mathbf{s}\right)=4{\pi }^2{s}^2{\sigma }^2{e}^{-4{\pi }^2{s}^2{\sigma }^2}{I}_0\left(\mathbf{s}\right)*{\mathrm{\Gamma }}_{\gamma }\left(\mathbf{s}\right)$, with ${\mathrm{\Gamma }}_{\gamma }\left(\mathbf{s}\right)=8\pi {\gamma }^3/\left(1+4{\pi }^2{s}^2{\gamma }^2\right)$. Fourier methods in Lunus (fftlt) were used for the convolution. The linear correlation of the anisotropic intensities with the data was used as a target function for refinement. Optimization of the target with respect to γ and σ was performed using the Powell minimization method.

NM Model.

The NM model followed methods similar to those of Riccardi et al. (33). Atomic coordinates and isotropic displacement parameters were obtained from PDB entries 5F66 (CypA) and 5F6M (trypsin), and were expanded to the P1 unit cell using the iotbx.pdb methods in CCTBX (62). The Hessian matrix H was defined using a modified anisotropic elastic network model (64), with springs between C_α atoms (i, j) within a cutoff radius of 25 Å. The spring force constants were computed as $k{e}^{-r_{ij}/\lambda }$, where $r_{ij}$ is the closest distance between atoms i and j, either in the same unit cell or in neighboring unit cells; $\lambda$ = 10.5 Å; and k = 1 for $r_{ij}<$ 25 Å and k = 0 otherwise (the nonzero value of k is arbitrary due to the normalization used below). Covariances of atom pair displacements $v_{ij}=\langle {\mathbf{r}}_i\cdot {\mathbf{r}}_j\rangle$ were obtained using the pseudoinverse of H as described in ref. 64. The values of $v_{ij}$ were renormalized to ${\varphi }_{ij}=v_{ij}{\sigma }_i{\sigma }_j/{\left(v_{ii}{v}_{jj}\right)}^{1/2}$ using the isotropic displacement parameters σ_i of the ith C_α atom from the Bragg refinement; the model was thus consistent with the refined crystal structure.

The diffuse intensity was computed as $D_{NM}\left(\mathbf{s}\right)={\displaystyle {\sum }_i{\displaystyle {\sum }_j{f}_i{f}_j^{\ast }{e}^{-4{\pi }^2\left({\sigma }_i^2+{\sigma }_j^2\right)s^2}\left(e^{-4{\pi }^2{s}^2{\varphi }_{ij}}-1\right)}}$, where $f_i$ is the structure factor of the combined atoms in the residue associated with the ith C_α atom. Structure factors were computed using a two-Gaussian approximation of atomic form factors; the parameters were obtained using the eltbx.X-ray_scattering methods in CCTBX (62); phase factors were applied using the atomic coordinates.

The Bragg intensities were computed from ensembles generated by using the first 10 nonzero eigenvectors of H with corresponding inverse eigenvalues as their weights. Because the overall scale of the spring constant was arbitrary in the NM model (see above), the amplitudes of motion were too large using the absolute eigenvalues; they were therefore scaled to maintain the connectivity of the backbones. Fifty member ensemble models were generated by Normal Mode Wizard (NMWiz) (65), which is a VMD (66) plugin. A single B factor of 10 Ų was applied to all atoms in the ensemble. Structure factors were generated using phenix.fmodel and compared with the experimental data using phenix.reflection_statistics (67).