State selection in Markov models for panel data with application to psoriatic arthritis

Abstract

Markov multistate models in continuous-time are commonly used to understand the progression over time of disease or the effect of treatments and covariates on patient outcomes. The states in multistate models are related to categorizations of the disease status but there is often uncertainty about the number of categories to use and how to define them. Many categorizations, and therefore multistate models with different states, may be possible. Different multistate models can show differences in the effects of covariates or in the time to events, such as death, hospitalization or disease progression. Furthermore, different categorizations contain different quantities of information, so that the corresponding likelihoods are on different scales, and standard, likelihood-based model comparison is not applicable.

We adapt a recently-developed modification of Akaike’s criterion, and a cross-validatory criterion, to compare the predictive ability of multistate models on the information which they share. All the models we consider are fitted to data consisting of observations of the process at arbitrary times, often called “panel” data. We develop an implementation of these criteria through Hidden Markov models and apply them to the comparison of multistate models for the Health Assessment Questionnaire score in Psoriatic Arthritis. This procedure is straightforward to implement in the R package ’msm’.

1. Introduction

Markov multistate models in continuous-time are commonly used to understand the progression over time of disease or the effect of treatments and covariates on patient outcomes [1]. The states of a multistate model can represent a particular patient outcome, such as the extent of disease or whether or not the patient has been hospitalised. However, the choice of the most appropriate outcomes to represent with states is not always clear and multistate models with different state spaces can disagree in their estimates of the effects of covariates or median time to events.

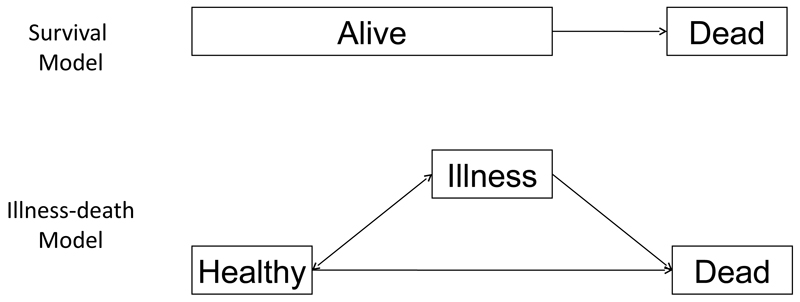
Figure 1 illustrates the choice between a simple 2-state model for survival and a 3-state illness-death model [2]. This choice may arise if our outcome of interest is death but where we know that illness can increase the risk of death and should be accounted for in our model. The illness-death model splits the ‘Alive’ state of the survival model into separate ‘Healthy’ and ‘Illness’ states. The traditional likelihood approach to model selection would compare the fit of these models to their data based on the likelihood function. For example, the likelihood ratio test uses

$$-2\Delta \text{log-likelihood}=-2\left(\text{log}\left(f\left(\text{x}|M_1\right)\right)-\text{log}\left(f\left(\text{x}|M_2\right)\right)\right)$$

which is approximately Chi-squared distributed under the null hypothesis that model M₁ is true. However, this is only appropriate if both models are fitted to the same dataset x.

Figure 1.

Illustration of 2-state survival model and 3-state illness-death model.

Table 1 illustrates the dataset corresponding to a patient who was observed to die at time 4. The observations are recorded at arbitrary, not necessarily common time-points, so we have “panel” data. From the perspective of the simple survival model, the patient was simply alive at time points 1, 2, and 3 before transitting to death. From the perspective of the illness-death model, the patient made an extra transition between time point 1 and 2 from ‘Healthy’ to ‘Illness’. The outcomes in the illness-death model are two-dimensional, namely time to reach ’Illness’ and time to reach ’Death’, while those of the survival model are one-dimensional, namely time to reach ’Death’. The dataset for the illness-death model therefore contains more information than that for the survival model. Standard likelihood-based model comparison methods, as well as the Akaike Information Criterion (AIC) [3] or Bayesian Information Criterion (BIC) [4], are therefore not applicable. Goodness-of-fit statistics have been developed for multistate models [5, 6] but these assess the absolute goodness-of-fit to a particular dataset and cannot be used to compare models across datasets. The error in parameter estimation introduced by state aggregation, or lumping, has been considered [7] and could be used to guide state-selection. However, this makes the questionable assumption that the maximum likelihood estimates from the largest model are the truth. We avoid making this assumption with an alternative approach based on comparisons of the predictive ability of multistate models with different state structures.

Table 1.

Comparison of datasets underlying simple survival model and illness-death models for a patient’s history.

	Time 1	Time 2	Time 3	Time 4
Simple survival	Alive	Alive	Alive	Dead
Illness-death	Healthy	Ill	Ill	Dead

Liquet and Commenges [2] have recently developed a modification of the AIC, and a leave-one-out likelihood cross validation criterion (LCV), for comparing estimators fit to differently aggregated, or coarsened datasets on the basis of the data they have in common. We use the terminology that if one dataset is completely determined by the another, it is nested within it. If two datasets have a common sub-dataset that is nested in both, then they are overlapping. The previous work considered only a comparison of the 3-state illness-death multistate model for survival with the 2-state survival model discussed above and was thus limited to the case of nested datasets. We extend their applicability to the comparison of general multistate models for panel data, with arbitrary numbers of states, which are fitted to overlapping datasets. We develop a simple method for evaluating these criteria through Hidden Markov models (HMMs) [8] in a similar manner to the use of HMMs for representing semi-Markov models suggested by Titman and Sharples [9].

We consider the application of multistate models to the understanding of disability progression, and its relation with covariates, in Psoriatic Arthritis (PsA) patients. Extent of functional disability associated with PsA is measured by the Health Assessment Questionnaire (HAQ) score of quality of life. The HAQ score is defined by 20 questions, on 8 topics, measuring severity on a four point scale, from 0 to 3, thus giving a total of 32 possible values. The scores across these 8 topics are averaged to give a single score ranging from 0 (no disability) to 3 (severe disability) [10]. Our data come from 790 PsA patients followed at the University of Toronto (UoT) Psoriatic Arthritis Clinic since June 1993 [11]. State spaces for possible multistate models correspond to different categorizations of the HAQ score but the choice of categorization is uncertain. We will show that different models give different results. We will then apply the modified AIC and LCV criteria to choose between models on the basis of their ability to predict disability progression in patients.

2. Application: Markov multistate models for quality of life of psoriatic arthritis patients

We are interested in choosing the best Markov multistate model, with transition intensities defined as rates per day, for predicting and understanding changes over time in patients’ functional disability associated with PsA. Data on 790 PsA patients followed at the UoT PsA clinic since June 1993, with follow-up to almost 30 years is available. Functional disability was assessed by the HAQ quality of life score, measured at approximately 6-month intervals and HAQ scores were recorded at an average of 5.09 time points per patient, although 193 patients had only one recorded HAQ score and so will not contribute to our multistate models. In addition to the HAQ score, explanatory variables, including gender and the total number of damaged joints at follow-up, were also recorded. The unit of time in our models is days since randomization. Our database did not record patient death so we could not distinguish between those who died and those who were lost to follow-up for other reasons. If a patient had died, their HAQ score histories were simply treated as right-censored. This is the approach taken by previous multistate model analyses of PsA [11, 12], although it may bias our analyses. This potential bias is expected to be small as PsA is not associated with substantially increased risk of death [?, ?] and the mean age at visit of patients at the UoT PsA clinic was 50.8 years with 95% range (26.7, 76.1) so death was likely to be a rare event.

Clinical interest is in the pattern of progression of disability, such as the time since first visit to the UoT PsA clinic to progress to severe disability (HAQ> 1.5) or from mild (HAQ< 0.5) to moderate (0.5 ≤HAQ≤ 1.5) disability. We will commonly refer to this outcome as the time to progression from a lower to higher disease state. There is also interest in finding relations between the explanatory variables and the progression in HAQ score. We focus on discrete-state multistate models rather than treating HAQ as a continuous outcome as discrete-state models most directly address our clinical questions. Although discretizing the outcome loses information, our aim is to choose the degree of discretization which gives the best estimates, on the basis of available information, of progression between categories of disability and their relationship with covariates. The method we develop could in principle be used to compare discrete and continuous outcome models [2], although this is not something we explore. Note also that while HAQ represents an underlying continuous process, the measurement itself is discrete. To understand progression and its relation with covariates, we therefore categorised HAQ score into 3 to 6 possible ranges and used a multistate model approach with states corresponding to these ranges [11, 12]. Treatments were recorded at the UoT PsA clinic, but it was not practical to model their effects as the treatment changed frequently between visits in response to severity of symptoms and was strongly correlated with explanatory variables, such as the number of actively inflamed joints. The total number of damaged joints also changed from visit to visit but could be more reasonably assumed to be piecewise-constant and included as a covariate in our multistate models.

We give details of multistate models for panel data in general, and of our five possible models, and show how their results differ. All our analyses were conducted in the ‘R’ statistical software [13] using the ‘msm’ package for multistate models [14]. This implements maximum likelihood estimation, with standard errors obtained from the asymptotic normal distribution of the maximum likelihood estimates. The BFGS method [?] was used to numerically maximise the likelihood with the aid of analytic gradients, as presented in Kalbfleisch and Lawless [15]. Convergence of multistate models for panel data can be adversely affected by identifiability problems if too many transitions and covariates are included [15], however we found good convergence for all the models we present.

2.1. Markov multistate models

A multistate process X(t) at time t on R states is defined by its transition intensity matrix Q(t), with entries

$$q_{rs}(t)=\underset{\delta t\to 0}{\lim }\frac{P(X(t+\delta t)=s|X(t)=r)}{\delta t},r\ne s,r,s=1,\dots ,R$$

and diagonal entries

$$q_{rr}(t)=-{\displaystyle \sum _{r\ne s}{q}_{rs}(t)}$$

so that rows sum to zero. Our models are assumed to satisfy the Markov assumption, which is that future evolution only depends on the current state. Formally, we assume q_rs(t, ℱ_t) is independent of ℱ_t, where ℱ_t is the observation history of the process up to the time preceding t. A time-homogeneous Markov process has intensities q_rs that are constant and independent of time t. If the process is in state r at time u then the probability that it will be in state s at time u + t is

$$p_{rs}\left(t,u\right)=P\left(X\left(u+t\right)=s|X\left(u\right)=r\right)$$

If the process is time-homogeneous, these probabilities depend only on the length t of the time interval and are p_rs(t). These are elements of the transition probability matrix P (t) which is related to the intensity matrix, under the assumption that Q is time-homogeneous, by taking a matrix exponential

$$P\left(t\right)=\text{exp}\left(tQ\right)$$

which gives the forward Kolmogorov equations [1].

We fit these models to observations of the process X(t) for a patient i, which consist of m_i observations x_ij, j = 1, …, m_i at times t_ij, j = 1, …, m_i. Under the Markov assumption, the likelihood contribution of patient i is

$$L_i=P\left(X\left(t_{i2}\right)=x_{i2}|X\left(t_{i1}\right)=x_{i1}\right)\dots P\left(X\left(t_{i,mi}=x_{i,m_i}\right)|X\left(t_{i,m_i-1}\right)=x_{i,mi-1}\right).$$

Note that the initial state x_i1 is assumed fixed and known and is only used to define the conditional distribution of the second observation through the Markov assumption and its marginal distribution is not estimated. The likelihood is therefore conditional on the initial state, analogously to a covariate. Each of the terms above are

$$P\left(X\left(t_{i,j+1}\right)=x_{i,j+1}|X\left(t_{ij}\right)=x_{ij}\right)=P_{x_{ij},x_{i,j+1}}\left(t_{i,j+1}-t_{ij}\right)$$

which are elements of the transition probability matrix. The product of the L_i gives the standard likelihood for a multistate model fit to panel observed data [15].

The effect of a set of U covariates are typically included through proportional hazards adjustments on the transition rates

$$q_{rs}({\mathbf{v}}_{ij})=q_{rs}\exp ({\beta }_{rs}^T{\mathbf{v}}_{ij})$$

where v_ij is the covariate vector of length U for patient i at time t_ij, β_rs is the vector of covariate effect parameters, and q_rs are the baseline rates which are assumed time-homogeneous. In this paper, we assume the covariates v_ij to be piecewise-constant (i.e. constant between observation times t_ij) or simply constant across all observations (eg. gender of a patient). It is therefore possible to use P(t) = exp(tQ) for each interval. In the next section we will see an application of these multistate modelling methods to the understanding of psoriatic arthritis.

2.2. Markov multistate models for HAQ in PsA patients

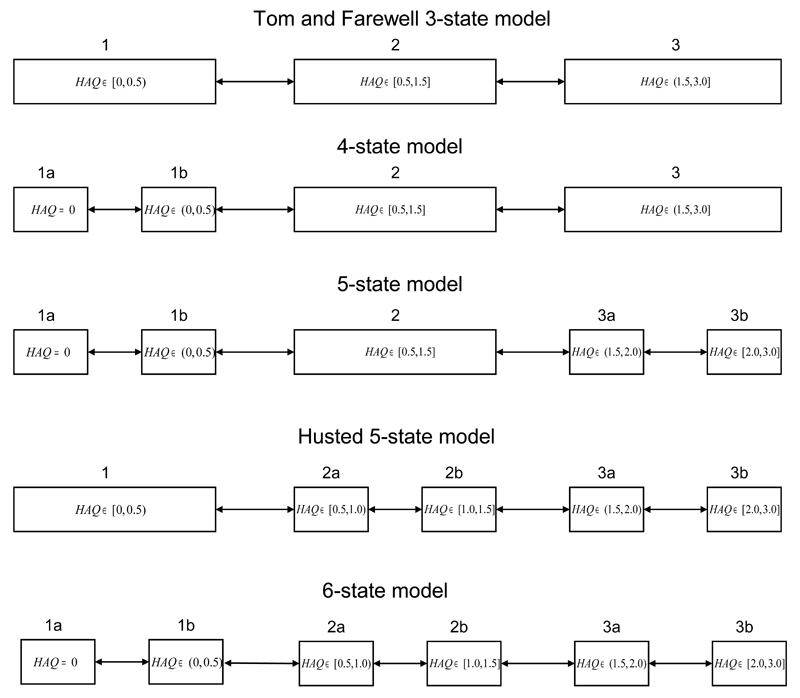
The basecase, and simplest, multistate model we fitted to the PsA HAQ data was a 3-state model with the categories [0, 0.5), [0.5, 1.5] and (1.5, 3.0] described in Tom and Farewell [12] and illustrated in Figure 2. On this categorisation, there were a total of 766 observed transitions across the 790 patients, of which 356 were progressions in disease severity while 410 were regressions, or reductions, in severity. This 3-state categorisation has been used extensively for the analysis and interpretation of HAQ scores in the literature [16, 10, 17, 18] and explicitly models progression between the mild, moderate and severe categories of HAQ. Note that transitions directly from mild to severe, or vice-versa, are not included. If a patient is observed to make such a transition, it is assumed that the patient passed through the intermediary state but that the path was not completely observed. The interest was in estimating the median time to these progressions and the effect of covariates. We included covariate adjustments for patient sex (transition rate in males compared to females) and for the total number of damaged joints at the most recent previous visit, which is assumed to be piecewise-constant. As the number of damaged joints varies with time, the multistate models are not time-homogeneous. 59.1% of patients included in the study at the UoT PsA clinic were male and the mean number of damaged joints at baseline was 5.06. Standard AIC and likelihood ratio tests indicated that these covariates had a significant effect on progression and regression in the 3-state model and also in the more complex models we considered. In this example, we assume for simplicity that these two covariates are all that are of interest. However, the criteria we will use in our method can be used for covariate selection as well and a more complete investigation would consider all models with all possible covariates.

Figure 2.

Multistate models for PsA HAQ based on different categorizations of HAQ score. Each model includes covariate adjustments for sex and total number of damaged joints.

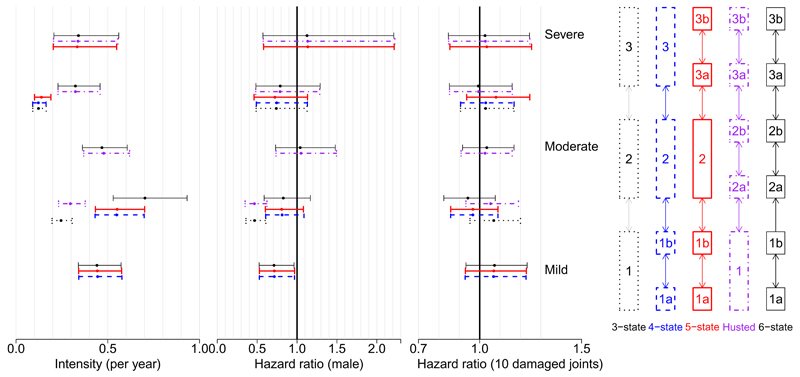
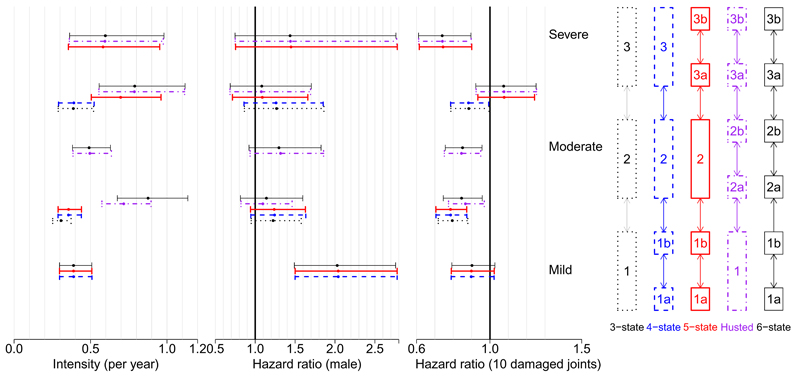
Estimated baseline transition rates per day and the hazard ratios corresponding to the covariate effects in this 3-state model are illustrated in Figure 3, for disease progression, and 4, for recovery, with full results provided in Appendix A. There is evidence that males are less likely to progress to higher disease levels and more likely to recover, although the width of the confidence intervals indicates that these relations are generally weak. There is also evidence that patients with more damaged joints are less likely to recover, perhaps because the damage is permanent and acts as a bound on improvement in quality of life. This effect, and that number of damaged joints has no significant effect on rate of deterioration in HAQ, is in line with that found in Husted et al. [11].

Figure 3.

Progression to the next state of severity. Estimates and 95% confidence intervals for baseline rates (female, 0 damaged joints) per day and hazard ratios under five different state structures. Each interval is aligned horizontally with the corresponding transition in the model structure on the right with the same colour and line type

Figure 4.

Regression to the previous state of severity. Estimates and 95% confidence intervals for baseline rates (female, 0 damaged joints) per day and hazard ratios under five different state structures. Each interval is aligned horizontally with the corresponding transition in the model structure on the right with the same colour and line type

An alternative 5-state categorisation for HAQ was proposed in Husted et al. [11] and is illustrated in Figure 2. This splits the HAQ score into 5 categories: [0, 0.5), [0.5, 1.0), [1.0, 1.5], (1.5, 2.0) and [2.0, 3.0]. The motivation for using this alternative is that the extra detail in modelling of HAQ may give better estimates of the median time to progression to severe disability associated with PsA (HAQ > 1.5). Covariate adjustments for sex and the total number of damaged joints were included as in the 3-state model. This model can be used to estimate the time to progression between mild, moderate and severe categories of HAQ as they are simply aggregations of some of the 5 states, as can be seen from Figure 2. The estimated effects of covariates on disease progression and recovery in PsA patients are illustrated for this ‘Husted’ model in Figures 3 and 4. A similar pattern emerges as in the 3-state model, with males being less likely to progress and patients with more damaged joints less likely to recover. However there is now mixed evidence about the effect of gender on progression, as some point estimates of the hazard ratio are greater than 1 while others are less than 1, although most of the confidence intervals include the possibility that there is no effect. Note the similarity between the baseline transition rate 1 → 2a in the Husted model and 1 → 2 in the 3-state model, illustrating that these models are not completely inconsistent. Also note that the baseline recovery rate 2a → 1 in Husted is much higher than the rate 2 → 1 in the 3-state model, indicating that patients progress slowly but recover quickly in Husted but both progress and recover slowly in the 3-state model. This may lead to differences in the predictions of the models.

In order to improve the estimates of time to progression from mild disability associated with PsA to moderate and/or severe disability, we used a 4-state categorization for HAQ which included a specific zero state. The motivation for this was to account for potential violation of the Markov assumption in the progression from mild to moderate/severe HAQ. This categorisation was [0], (0, 0.5), [0.5, 1.5] and (1.5, 3.0] and is included in Figure 2. This is similar to a two part model where patients have a probability of having a non-zero level of disability (eg. HAQ> 0) and, if it is non-zero, the extent of disability is modelled separately [19]. We also tried a 5-state model with a finer division of higher HAQ states with the categorization [0], (0, 0.5), [0.5, 1.5], (1.5, 2.0) and [2.0, 3.0], as a compromise between the 4-state model and the Husted model, and finally a 6-state model which included all the HAQ categories considered so far. Both of these models are illustrated in Figure 2. Estimated covariate adjustments for sex and total number of damaged joints were included and the estimates are illustrated in Figures 3 and 4. Under these models, males are again less likely to progress and patients with more damaged joints are less likely to recover. The 3-state model weakly indicated that patients with more damaged joints were more likely to progress but this pattern is not apparent in the more complex models. This shows that the choice of categorization can affect covariate effects. However, it should also raise a concern that we may not have enough data to correctly specify the covariate effects in the more complex models and that we are potentially overfitting. More complex categorizations were investigated but convergence became more and more difficult to achieve, as did clinical interpretation and justification.

Baseline transition rates between states are also illustrated in Figures 3 and 4. Estimated transition rates between similar categories are similar across models, for example the rates from 2 → 1, 2 → 1b, and 2 → 1b in the 3-state, 4-state and 5-state models, respectively, are very similar. This is not always the case, as these do not match the 2a → 1 rate in the Husted model, perhaps because this excludes transitions from the 2b state which is merged with the 2a state in the 3-state, 4-state and 5-state models. Where the categories are identical and there are no alternative state paths along which patients can travel, as in the 1a → 1b transition rate for the 4-state, 5-state and 6-state models, the estimated transition rates and 95% intervals are almost identical. The confidence intervals of baseline hazards in the 3-state model are narrower than those of the more complex models by an approximate factor of $\frac{1}{5}$, confirming that the larger number of parameters have weaker data to inform them, which may be a reason to use the simpler model.

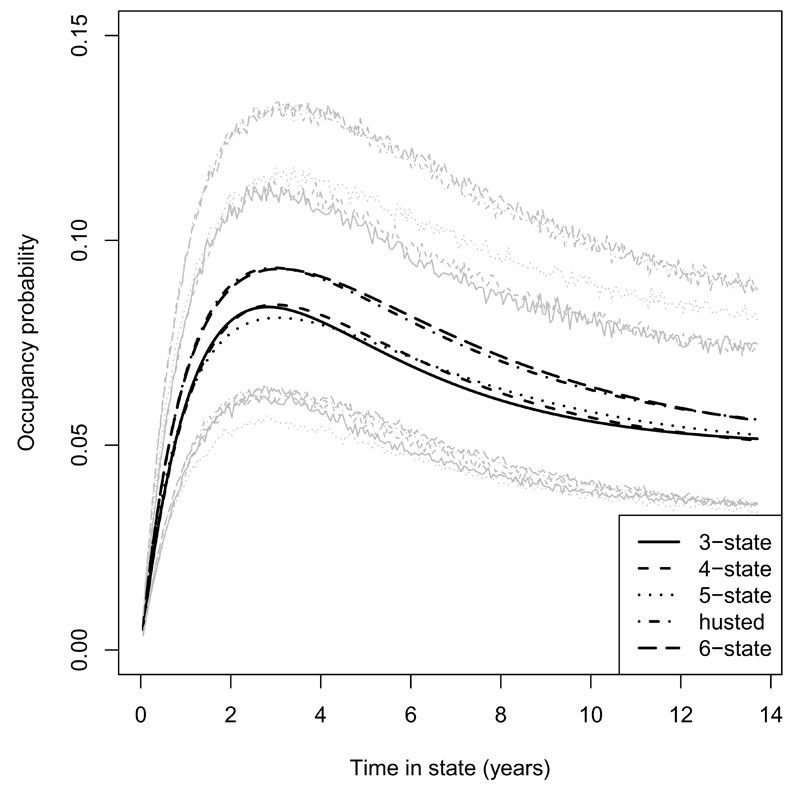
Figure 5 illustrates the multistate model estimates of the probability that a patient who was in the moderate (0.5 ≤ HAQ≤ 1.5) category of disability at time 0 would be in the severe (HAQ> 1.5) category at a later time. For models where the moderate category corresponds to more than one state, such as the 6-state model, the probability was a weighted average over the constitutent states using the initial prevalence, conditional on occupying the moderate category, as weights. There are only small differences in the estimates and their 95% confidence intervals overlap.

Figure 5.

Probability estimates of occupying HAQ > 1.5 states at different times assuming at 0.5 ≤ HAQ ≤ 1.5 initially with 95% confidence intervals, simulated from the assumed asymptotic Normal distributions of the parameter estimates, in grey. Estimated by the 3-state, 4-state, 5-state, Husted et al., and 6-state models. Estimates are for a female patient with total number of damaged joints set to the mean over all patients at baseline (5.06).

As the models are reversible, patients could transit to moderate disability and then recover to mild disability. In order to characterise the onset of more severe disability associated with PsA, we estimated the median first passage time t to state r by finding the time such that the probability of having ever entered state r by time t is 0.5. These probabilities are obtained by setting all transition intensities out of state r to zero, while keeping all others unchanged, and calculating the transition probabilities P*(t) = exp (tQ*) for the simplified intensity matrix Q*. The median first passage time from, say, state 1 to state r is then the solution of P*(t)_1,r = 0.5, obtained by numerical methods

The median first time, in years, with 95% confidence intervals found using the upper and lower limits of the transition probabilities, to progress from one set of HAQ disability categories to another are summarized in Table 2. The Husted and 6-state models disagree considerably with the 3-state, 4-state and 5-state models about the median time to progress from mild to moderate/severe disability associated with PsA, although the confidence intervals overlap. There is also disagreement in the median time to progress from mild to severe disability, although the confidence intervals are much wider so the difference is of less concern. Note that the median times for the first progressions are longer than the length of follow-up at the UoT clinic because they are based on all patients, including those who did not reach severe disability during the study, who we found made up approximately 90% of the sample. We also calculated the mean first passage times using the method of Harrison et al. [20] and found a similar pattern to that found for the medians.

Table 2.

Median time, in years, with 95% confidence intervals, to first progress from mild to moderate/severe PsA (HAQ [0, 0.5) to HAQ [0.5, 3.0]) and from mild to severe PsA (HAQ [0, 0.5) to HAQ (1.5, 3.0]), based on different multistate models. Initial distributions are assumed to be those observed in the UoT HAQ data and time to progression is averaged over this distribution of initial states.

Model	[0, 0.5) to [0.5, 3.0]	[0, 0.5) to (1.5, 3.0]
3-state	4.16 (3.67, 4.65)	22.44 (18.65, 27.15)
4-state	4.18 (3.70, 4.83)	22.50 (18.61, 27.49)
5-state	4.18 (3.63, 4.80)	19.94 (16.43, 24.34)
Husted	3.50 (3.05, 4.01)	23.47 (19.72, 28.34)
6-state	3.42 (2.97, 4.03)	23.46 (19.81, 28.35)

Table 3 reports the number of observed transitions between the states, defined as observed changes in HAQ category between consecutive visits, of the 6-state model. As the total numbers in each row are similar to, but not exactly the same as, the number of experiments for multinomial outcomes, they suggest the quantity of information available to estimate the baseline transition rates in the 6-state model, as well as in the other models formed by aggregating table rows. For example, only 211 transitions were observed from 3a while 1038 were observed from 1a, greater than the total number of transitions from 3 (615), so estimation of rates for the latter transitions is informed by a greater quantity of evidence. We may therefore judge that there is too little evidence to estimate the transition rates from 3a and that we should not separate this state from 3b. Note however that this is only an informal assessment. Also, the state transition table does not give all the evidence as it ignores the time that patients spent in each of the states as well as any covariate effects. The model comparison methods we develop include this information through the likelihood functions.

Table 3.

Number of transitions, state changes between consecutive visit dates, between categories of HAQ in the 6-state model

from\to	1a	1b	2a	2b	3a	3b
1a	776	196	51	13	2	0
1b	230	296	136	46	4	2
2a	57	156	213	120	10	4
2b	14	55	114	280	74	14
3a	7	4	7	88	70	35
3b	1	3	2	16	31	107

These investigations illustrate the uncertainty about time to progression and the relation between covariates and transition rates, all of which casts doubt on inferences about the progression of disability associated with PsA. Model choice is often informal and based on judgements about the extent to which the model reflects the perceived disease progression. We cannot choose the models on the basis of state transition tables or, as will be explained more formally, by direct comparison of the likelihoods. We will now introduce criteria that can be used to choose between these multistate models on the basis of their predictive ability on the common data, the 3-state categorization of HAQ.

3. Modified AIC and Likelihood Cross-Validation for state-selection

It is not possible to use standard likelihood-based methods to compare two multistate models with different states, labelled $M_1(\widehat{\mathit{\theta }}(\text{x}))$ and $M_2(\widehat{\gamma }({\mathbf{x}}^{\prime }\text{))}$ with parameters θ and γ and densities g(·) and h(·), respectively, as the information contained in the datasets x and x′ may be different. In Section 1, we explained why this application of likelihood methods was inappropriate for the example of simple survival and illness-death models. An example related to models for observed HAQ score over time is described by Table 4. In this table, the HAQ score and the state into which it is categorised are presented. From the perspective of the 3-state model, there is no transition between time 1 and time 2, while there is a transition from the perspective of the 4-state and 5-state models. This illustrates the issue that the data to which the more complex models are fitted contains more information than that to which the 3-state model is fitted, a similar situation to the comparison of survival and illness-death models discussed in Section 1.

Table 4.

Observed HAQ score for a patient at 5, not necessarily regularly spaced, time-points and the categorised states into which they fall in four different multistate models. There are varying levels of information contained in the datasets and the 3-state data is determined by the 4-state, 5-state and Husted data, so is nested within them.

	Time 1	Time 2	Time 3	Time 4	Time 5
HAQ	0	0.4	0.7	1.7	2.6
3-state model	1	1	2	3	3
4-state model	1a	1b	2	3	3
5-state model	1a	1b	2	3a	3b
Husted model	1	1	2a	3a	3b

However, if there is a dataset x″ such that x″ ⊂ x and x″ ⊂ x′, so it is a subset common to both datasets, we can follow Liquet et al. [2] and estimate the difference in predictive ability of the multistate models on a replicate of x″. The common dataset in the example of Table 4 is that on which the 3-state model is estimated as it is completely determined by the datasets to which any of the other models are fitted and is therefore nested within them. In the information theoretic setting ([21]), predictive ability is measured by the Kullback-Leibler (KL) risk. The KL risk of using g at its maximum likelihood estimator $\widehat{\mathit{\theta }}(\mathbf{\text{x}})$, labelled ${\widehat{\mathit{\theta }}}_n$ where n is the number of independent and identically distributed observations in the dataset x, in our examples the number of patients, in place of the true, or data-generating, f on a replicate $x_{n+1}^{″}$ of a dataset x″ is

$$\text{KL}\left({\widehat{\mathit{\theta }}}_n|X_{n+1}^{″}\right)={\mathbf{\text{E}}}_{X_{n+1}^{″}}\left[\text{log}\frac{f\left(X_{n+1}^{″}\right)}{g\left(X_{n+1}^{″}|{\widehat{\mathit{\theta }}}_n\right)}\right]$$ (1)

If there are covariates, the densities f and g are those of the conditional distributions given the covariates. As KL risk above depends, through the estimator ${\widehat{\mathit{\theta }}}_n$, on a particular sample x, it is subject to random variation. Commenges et al. [22] proposed to remove this variation by taking the expectation over the sample x with respect to the truth f and obtain the Expected Kullback-Leibler risk (EKL)

$$\text{EKL}\left({\widehat{\mathit{\theta }}}_n|X_{n+1}^{″}\right)={\mathbf{\text{E}}}_f\left[\text{log}\frac{f\left(X_{n+1}^{″}\right)}{g\left(X_{n+1}^{″}|{\widehat{\mathit{\theta }}}_n\right)}\right].$$ (2)

where E_f is the expectation with respect to f, with a similar EKL for ${\widehat{\mathit{\gamma }}}_n$. The choice between $M_1(\widehat{\mathit{\theta }}(\mathbf{x}))$ and $M_2(\widehat{\mathit{\gamma }}({\mathbf{x}}^{\prime }))$ is then guided by estimation of

$$\Delta \left({\widehat{\mathit{\theta }}}_n,{\widehat{\gamma }}_n|X_{n+1}^{″}\right)=\text{EKL}\hspace{0.17em}\left({\widehat{\theta }}_n|X_{n+1}^{″}\right)-\text{EKL}\hspace{0.17em}\left({\widehat{\gamma }}_n|X_{n+1}^{″}\right)$$ (3)

a difference which we will denote by Δ_n.

If x″ = x or x′ = x, then Taylor approximations, dropping terms constant in θ or γ, and multiplying by the conventional 2n, would yield a difference in the standard Akaike Information Criterion (AIC) [3] and the model with the smallest AIC, or estimated EKL, would then be chosen. In the nonstandard case where x″ is nested in x′ and x, Liquet et al. [2] extended the standard asymptotic approximations to estimate $\Delta \left({\widehat{\mathit{\theta }}}_n,{\widehat{\gamma }}_n|X_{n+1}^{″}\right)$ with

$$D_{RAIC}=\frac{1}{n}\left(l\left({\widehat{\mathit{\gamma }}}_n|x^{″}\right)-l\left({\widehat{\mathit{\theta }}}_n|x^{″}\right)+trace\left(J\left({\widehat{\mathit{\theta }}}_n|x^{″}\right)J{\left({\widehat{\mathit{\theta }}}_n|\text{x}\right)}^{-1}-J\left({\widehat{\mathit{\gamma }}}_n|x^{″}\right)J{\left({\widehat{\mathit{\gamma }}}_n|x^{\prime }\right)}^{-1}\right)\right)$$

where n is the number of observations. $l\left({\widehat{\mathit{\gamma }}}_n|{\text{x}}^{″}\right)$ and $l\left({\widehat{\mathit{\theta }}}_n|{\text{x}}^{″}\right)$ are the log-likelihoods of the models on the common data x″, or the log-likelihoods of models for x″ implied by M₁ and M₂, using parameter values which are estimated from the bigger data x′ and x″, respectively. Section 3.1 will give an example of these implied models. The estimators of the information matrices are

$$\begin{array}{c}J\left({\widehat{\mathit{\theta }}}_n|\text{x}\right)=-\nabla {\nabla }^{T}l\left(\mathit{\theta }|\text{x}\right){|}_{\widehat{\mathit{\theta }}n},\\ J\left({\widehat{\mathit{\theta }}}_n|x^{″}\right)=-\nabla {\nabla }^{T}l\left(\mathit{\theta }|x^{″}\right){|}_{\widehat{\mathit{\theta }}n},\\ J\left({\widehat{\mathit{\gamma }}}_n|x^{\prime }\right)=-\nabla {\nabla }^{T}l\left(\mathit{\gamma }|x^{\prime }\right){|}_{\widehat{\mathit{\gamma }}n},\end{array}$$

and

$$J\left({\widehat{\mathit{\gamma }}}_n|x^{″}\right)=-\nabla {\nabla }^{T}l\left(\mathit{\gamma }|x^{″}\right){|}_{\widehat{\mathit{\gamma }}n},$$

which gives a general criterion comparing models fit to overlapping datasets. The difference in log-likelihood terms can be interpreted as a comparison of the fit to the common data while the trace terms compare the complexity of the models on this common dataset. Note that in the standard case (x″ = x′ = x) the trace term becomes

$$trace\hspace{0.17em}\left(J({\widehat{\mathit{\theta }}}_n|\text{x})J{({\widehat{\mathit{\theta }}}_n|\text{x})}^{-1}\right)-trace\hspace{0.17em}\left(J\left({\widehat{\mathit{\gamma }}}_n|\text{x}\right)J{\left({\widehat{\mathit{\gamma }}}_n|\text{x}\right)}^{-1}\right)=dim(\mathit{\theta })-dim(\mathit{\gamma })$$

the difference in the number of parameters, which is the complexity penalty term of the AIC.

An alternative to the above procedure is to use leave-one-out Likelihood Cross Validation (LCV) to estimate EKL on replicates of the common data x″ [23]. The LCV is defined as

$$LCV\left({\widehat{\mathit{\gamma }}}_n|{\text{x}}^{″}\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^n\text{log}\frac{f^0\left(x_i^{″}\right)}{h_{{\mathbf{\text{X}}}^{\mathbf{″}}}\left(x_i^{″}|\widehat{\mathit{\gamma }}-i\right)}}$$

where ${\widehat{\mathit{\gamma }}}_{-i}$ is the maximum likelihood estimator for γ based on all but the i^th observation, and similarly for ${\widehat{\mathit{\theta }}}_{-i}$. f⁰ is a reference density which will cancel out when differences of LCVs are taken. Liquet et al. [2] demonstrated that

$${\text{E}}_f\hspace{0.17em}\left[LCV({\widehat{\mathit{\theta }}}_n|{\mathbf{\text{X}}}^{″})-LCV({\widehat{\gamma }}_n|{\mathbf{\text{X}}}^{″})\right]=\Delta ({\widehat{\mathbf{\theta }}}_n,{\widehat{\gamma }}_n|X_{n+1}^{″})+o(n^{-1})$$ (4)

so that the criterion

$$D_{RLCV}=LCV({\widehat{\mathit{\theta }}}_n|{\text{x}}^{″})-LCV({\widehat{\gamma }}_n|{\text{x}}^{″})=\frac{1}{n}{\displaystyle \sum _{i=1}^n\text{log}\frac{h_{{\mathbf{\text{X}}}^{″}}\left(x_i^{″}|{\widehat{\gamma }}_{-i}\right)}{g_{{\mathbf{\text{X}}}^{″}}\left(x_i^{″}|{\widehat{\mathit{\theta }}}_{-i}\right)}}$$

is asymptotically equivalent to $\Delta ({\widehat{\mathit{\theta }}}_n,{\widehat{\mathit{\gamma }}}_n|X_{n+1}^{″})$ with bias o(n⁻¹). Liquet et al. [2] gave limited evidence that the D_RLCV is a more accurate estimator of differences in EKL than the D_RAIC and the justification for cross-validation as an assessment of predictive ability is perhaps clearer than the asymptotic arguments leading to D_RAIC. However, it is computationally intensive and so unattractive for complicated models. Also, D_RAIC is an estimator of the D_RLCV in the standard case of x″ = x′ = x where D_RAIC is a difference of standard AIC divided by 2n [24].

Commenges et al. [22] used results from Vuong [25] to develop a “tracking interval” for a normalized difference of AIC; Liquet and Commenges [2] noted that the same approach could be applied to D_RAIC and D_RLCV. These provide intervals with 95% coverage for Δ_n and will be presented in our application. We extended these ideas to find the coverage of the widest interval for Δ_n that does not include 0. This coverage can be interpreted in a frequentist manner as the probability that a resample of size n will yield a negative difference in EKL. We refer to these as the P_RAIC and P_RLCV, for the coverage based on D_RAIC and D_RLCV, respectively. Details of the tracking intervals and probabilities are provided in Appendix B.

3.1. Hidden Markov models to evaluate D_RAIC and D_RLCV

The difficulty in using the D_RAIC and D_RLCV is in calculating terms such as $l\left({\widehat{\mathit{\theta }}}_n|{\mathbf{x}}^{″}\right)$, the likelihood of a model fitted to a dataset x but evaluated on an aggregated version x″ of this data. Recall the multistate models described in Section 2.1 with transition rates Q, defined by θ and γ, but consider the case where we have only observations x″ ⊊ x of a restricted process X″(t). For patient i with restricted observations with restricted observations ${\mathbf{x}}_i^{″}$ at times t_i, the likelihood contribution to model $M_1(\widehat{\mathit{\theta }}(x))$ is determined by a sum over all possible observations x_i which are consistent with ${\mathbf{x}}_i^{″}$. These are the possible paths x_i1, …, $x_{i,m_i}$. The likelihood contribution of the restricted observation ${\mathbf{x}}_i^{″}$ is

$$\begin{array}{l}{L}_i={\displaystyle \sum _{x_{i1}}\text{e}(x_{i1}^{″}|x_{i1})\mathbf{\text{P}}(x_{i1}|x_{i1}^{″})}\\ \times {\displaystyle \sum _{x_{i2}}\text{e}(x_{i2}^{″}|x_{i2})P_{x_{i1},x_{i2}}(t_{i2}-t_{i1})}\\ \cdots {\displaystyle \sum _{x_i,m_i}\text{e}(x_{i,m_i}^{″}|x_{i,m_i})P{x}_{i,m_i-1,}}{x}_{i,m_i}(t_{i,mi}-t_{i,mi-1})\end{array}$$

where $P_{x_{ij},x_{i,j+1}}(t_{i,j+1}-t_{ij})$ are terms of the transition probability matrix of the more complex underlying model.

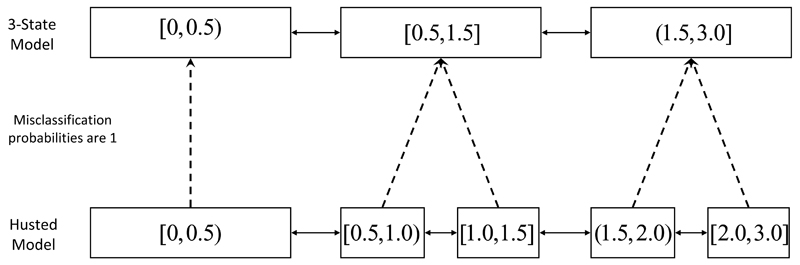
The terms $\text{e}\left(x_{ij}^{″}|x_{ij}\right)$ are 1 or 0, the emission probabilities that $x_i^{″}$ will be observed given the more complex model is in state x_ij, and are elements of some coarsening matrix mapping observations from x to x″. For the 3-state and Husted models illustrated in Figure 6, for example, the mapping from the states of the Husted to those of the 3-state models are

$$\left(\begin{array}{l}\begin{array}{ccc}1& 0& 0\end{array}\\ \begin{array}{ccc}0& 1& 0\end{array}\\ \begin{array}{ccc}0& 1& 0\end{array}\\ \begin{array}{ccc}0& 0& 1\end{array}\\ \begin{array}{ccc}0& 0& 1\end{array}\end{array}\right)$$

So the probability $\mathbf{\text{E}}\left(x_{ij}^{″}=1|x_{ij}=2\right)=0$ is read from the first column of the second row of this coarsening matrix.

Figure 6.

Fit the full and restricted models to the full and restricted datasets, respectively. Likelihood of full model on restricted dataset is calculated by ‘msm’ using the illustrated misclassification model. Illustrated for the Husted 5-state model evaluated on the 3-state data.

Note that the above likelihood contribution is the same as that of a Hidden Markov model [8], except that the initial state x_i1 has a distribution conditional on the observed $x_{i1}^{″}$, which is fixed and known. The unconditional distribution of x_i1 is estimated from the observations x_,1 to which the model $M_1\left(\widehat{\mathit{\theta }}\right(\mathbf{x}\left)\right)$ was fit and these can be used to define

$$\mathbf{\text{P}}\left(x_{i1}|x_{i1}^{″}\right)=\frac{\mathbf{\text{E}}\left(x_{i1}^{″}|x_{i1}\right)\mathbf{\text{P}}\left(x_{i1}\right)}{{\displaystyle {\sum }_{x_{j1}}\mathbf{\text{E}}\left(x_{j1}^{″}|x_{j1}\right)\mathbf{\text{P}}\left(x_{j1}\right)}}$$

where the $\text{E}\left(x_{i1}^{″}|x_{i1}\right)$ are again elements of the coarsening matrix. In our models for HAQ, for example, if a patient was initially observed to be in the mild category, then they could be in either of the first two states of the 5-state model and the initial conditional distribution above would be over these two states. This allows the above likelihood component to be evaluated in a similar manner to that of Hidden Markov models and gives $l({\widehat{\mathit{\theta }}}_n|{\mathbf{x}}^{″})$ and, similarly, $l({\widehat{\gamma }}_n|{\mathbf{x}}^{″})$. This procedure is similar to the use of Hidden Markov models to evaluate the likelihoods of phase-type semi-Markov models [9] except that we estimate the model on the basis of observations of the ‘underlying’, more complex, multistate model rather than of the ‘observed’, simpler, multistate model.

We implemented this Hidden Markov model scheme for the evaluation of the D_RAIC and D_RLCV criteria in the ‘R’ statistical software [13] using the ‘msm’ package for multistate models [14]. This required several modifications to the base code of ‘msm’, such as evaluating the likelihood contribution of individual patients and allowing initial state distributions in Hidden Markov models to be specified, which have been included in the latest version. Specific functions for evaluating the criteria for the comparison of suitable multistate models will also be included in future releases of ‘msm’. These functions are currently computationally intensive and further optimisation work will be required.

4. Application of D_RAIC and D_RLCV to Markov multistate model comparison

We compared the possible multistate models discussed in the previous section using the D_RAIC and D_RLCV criteria on the basis of the data to which we fit the 3-state model. This compares their ability to predict transitions between [0, 0.5) and [0.5, 1.5] and between [0.5, 1.5] and (1.5, 3.0], which is what was of clinical interest. If there was interest in the best model for predicting transitions from [0.5, 1.0) to [1.0, 1.5], say, then the comparison on the basis of this 3-state data would not be relevant and we should use either the Husted or 6-state models. The implementation of the D_RAIC and D_RLCV uses the Hidden Markov model scheme outlined in Section 3. This scheme is illustrated for the evaluation of the Husted model on the 3-state data in Figure 6.

The results of this model comparison are presented in Table 5 and on the basis of the likelihood terms, the 6-state model gives the best fit to the 3-state data. Including the penalty for complexity and normalizing by the number of observations (n = 597) give D_RAIC that favour the more complex models, with strongest preference for the 6-state model. The D_RLCV are very close to the D_RAIC and their 95% tracking intervals overlap. As mentioned in Section 3, the D_RAIC is an approximation to the D_RLCV and these results illustrate how good an approximation it is in this example. The P_RAIC and P_RLCV, the coverage of the largest tracking interval for Δ_n which does not include 0, interpreted in a sampling framework as the probability that the models will have a lower estimated EKL on a resample of the data, are all close to 100%. This indicates that there is little uncertainty in the preference for the more complex models.

Table 5.

Comparison of multistate models to 3-state model on the basis of common data. D_RAIC includes complexity terms assessing statistical risk while likelihood terms only consider fit to x′. P_RAIC and P_RLCV are one-sided coverage of largest tracking interval for difference in EKL on common data not including 0. Complexity is D_RAIC trace term while fit is $\frac{1}{n}\left(l({\widehat{\gamma }}_n|{\text{x}}^{″})-l({\widehat{\mathit{\theta }}}_n|{\text{x}}^{″})\right)$ with log-likelihood of 3-state model $l({\widehat{\gamma }}_n|{\text{x}}^{″})=-1975.7$ and n = 597. *These coverage probabilities were > 99.9999%

Model	4-state	5-state	Husted	6-state
$l({\widehat{\mathit{\theta }}}_n|{\text{x}}^{″})$	−1943.0	−1929.2	−1916.4	−1884.1
Complexity	−0.003	−0.002	−0.001	−0.001
Fit	−0.055	−0.078	−0.099	−0.153
DRAIC (95% ti)	−0.057 (−0.073, −0.041)	−0.080 (−0.101, −0.058)	−0.100 (−0.130, −0.071)	−0.154 (−0.186, −0.123)
PRAIC	100.00%	100.00 %	100.00%	100.00%*
DRLCV (95% ti)	−0.056 (−0.072, −0.040)	−0.080 (−0.102, −0.058)	−0.100 (−0.129, −0.071)	−0.156 (−0.187, −0.124)
PRLCV	100.00%	100.00%	100.00%	100.00%

On the basis of the 3-state data, we should choose the 6-state model over the 4-state, 5-state and Husted model. These criteria provide guidance on how to interpret the results of Table 2 on the median time to initial onset of more severe disability symptoms. We may conclude that the Husted and 6-state models give better predictions of these median times and that 50% of patients willl take less than about 3.5 years to first show functional disability (moderate or severe category of disability assessed by HAQ), rather than the 4.2 years and above estimated by other models. The median time to progress to severe functional disability is expected to be about 23.5 years but this does not vary widely between models. The criteria, and their indication that the 6-state model is better for predictions on the 3-state data, provide a useful insight into the epidemiology of disability associated with PsA that was not previously available.

5. Discussion

In this paper we have considered possible Markov multistate models for the progression of functional disability associated with PsA and assessed by the HAQ quality of life score. We showed that models with different states corresponding to different categorizations of the HAQ score lead to different conclusions about the median first time to suffer disability and the relation between progression and covariates. We also explained the unsuitability of standard likelihood based approaches to choosing between these models due to their underlying datasets being different. We reviewed the D_RAIC and D_RLCV criteria [2] for comparing estimators fit to different overlapping datasets and developed a novel Hidden Markov model scheme for their evaluation and use in the comparison of general multistate models. An application to the comparison of models for HAQ assessed disability in PsA patients suggested the use of a 6-state model as it gave the best predictions on the basis of the common 3-state categorization of HAQ. This guidance aided interpretation of the conflicting predictions of the various possible multistate models.

There are several outstanding issues in the use and interpretation of the D_RAIC and D_RLCV criteria for the comparison of multistate models and other more general classes of estimators. An important problem is that it is difficult to understand why the 6-state model, for example, is superior to the 3-state model for the prediction of the 3-state data. The inclusion of the extra disease progression data in the larger models appears to improve efficiency of the estimates (as in Gray et al. [26]), but it is unclear whether it is, for example, a failure of the Markov assumption or a mis-specified relationship with covariates that is driving the preference between the models. We compared the different multistate models without covariates and found the same ordering of the D_RAICs as in the covariate adjusted case. However, the Husted and 6-state models were much more similar, perhaps indicating that the covariates are required to get the full benefit from the finer categorisation of HAQ. The Markov assumption might be tested more formally by using our criteria to compare against semi-Markov models, which are challenging to implement for panel data, but a promising solution involving phase-type distributions has been proposed [9].

As our aim was primarily to illustrate the method of comparing state structures, we did not conduct an exhaustive investigation and comparison of all possible multistate models. We did investigate more complex 7, 8, 9, and 10-state multistate models and found that the D_RAIC was lower than that of the 6-state model and that the D_RAIC of the 8-state model was the lowest. However, the differences became increasingly small and it became much more difficult to achieve convergence of maximum likelihood estimation.

Due to the division by 2n, the criteria are, in theory, measuring the difference in predictive ability, assessed by EKL, on a single observation and are therefore on a common scale which could be qualified. Commenges et al. [22] estimated the difference in Kullback-Leibler loss when using alternatives to a true Normal distribution. They qualified (10⁻¹, 10⁻², 10⁻³, 10⁻⁴) as (“large”, ”moderate”, “small”, “negligible”), respectively. However, there is uncertainty about the number of independent observations to use in normalizing the criteria. Throughout our work, complete patient histories were assumed to be a single observation, rather than every observation of a patient’s state, or every transition, contributing a separate observation. This issue of the correct normalizing constant requires further research and, until this is completed, we recommend simply choosing the model with the lowest D_RAIC or D_RLCV, as in our application. The coverage of the widest tracking intervals not including 0, our P_RAIC and P_RLCV described in Appendix B, provide guidance as to how strong the results of the pairwise comparisons are.

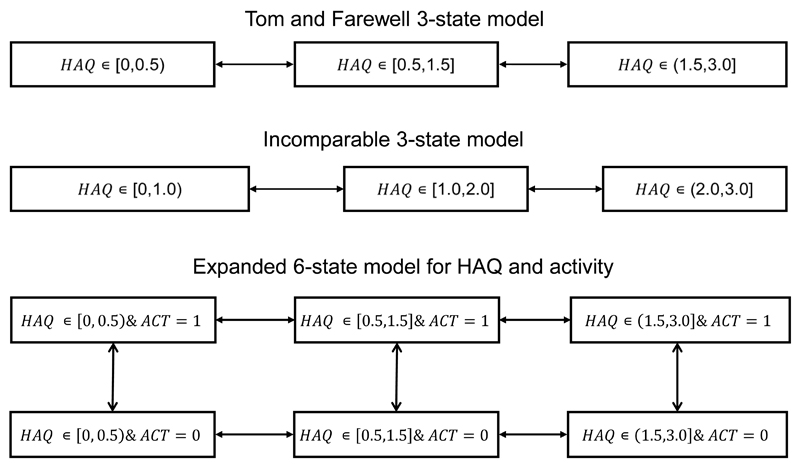
When incorporating covariates into multistate models for panel data, it is commonly assumed that they remain constant between observation times [14]. However, if covariates were to fluctuate rapidly between observation times then this assumption would not hold. An example of this is the number of actively inflamed joints in PsA patients, which can change on a daily basis. Tom et al. [12] suggested expanding the HAQ states into extra states accounting for different categories of number of actively inflamed joints and thus jointly modelling this as a second outcome. An example of a 6-state version of this model is illustrated in Figure 7 where each state of the 3-state model has been expanded into two separate states for two different categories of number of actively inflamed joints (indicated by ACT=0 or ACT=1). In theory, the D_RAIC and D_RLCV could be used to compare the expanded and 3-state models on the basis of the 3-state data. However, further work is required to evaluate the criteria for these types of expanded models given their computational complexity, and requirement for more extensive data.

Figure 7.

Multistate models for PsA HAQ based on different categorizations of HAQ score. The two 3-state models are not comparable with D_RAIC or D_RLCV as their datasets do not overlap. The 3-state and 6-state model, which includes a binary categorization for number of actively inflamed joints, are in theory comparable on the basis of the 3-state data.

The D_RAIC and D_RLCV can only be used to compare multistate models for HAQ if the models have some data in common, i.e. give predictions for common outcomes. An example of a model which is incomparable to our standard 3-state model for HAQ would be a 3-state model based on the categorisation [0, 1.0), [1.0, 2.0] and (2.0, 3.0], illustrated in Figure 7. This model cannot predict the outcomes of the 3-state model, and vice versa, and the D_RAIC and D_RLCV would not be suitable for their comparison. However, the clinical question of interest should guide the choice of model in this case. If the interest was in modelling patient progression to HAQ > 2.0 then the incomparable 3-state model should be used. It is important when using these criteria to keep the clinical questions in mind. If it had been of interest to estimate the mean or median time to progress from HAQ= 0 to HAQ≥ 0 then we should have only considered the 4-state, 5-state and 6-state models as the Husted and 3-state models give us no information about this transition. Once the clinical question is specified we believe the D_RAIC and D_RLCV criteria, and the Hidden Markov model implementation we have proposed, provide helpful guidance for model development.

A. Baseline transition rates and covariate effects for fitted multistate models

In this appendix we present Table 6 which reports the baseline transition rates and covariate effects which are illustrated in Figures 3 and 4.

Table 6.

Estimated baseline transition rates per day and covariate effects, as hazard ratios, with 95% confidence intervals, for 3-state, 4-state, 5-state, Husted and 6-state models. The baseline patient is female with zero damaged joints. Conventionally significant covariate effects, with confidence intervals excluding 1, are highlighted in grey.

	Transition	Baseline	Male	Number of damaged joints*
3-state	1 → 2 2 → 3 2 → 1 3 → 2	0.00067 (0.00054, 0.00084 ) 0.00034 (0.00025, 0.00045 ) 0.00084 (0.00069, 0.0010 ) 0.0011 (0.00079, 0.0014 )	0.47 (0.36, 0.61 ) 0.74 (0.49, 1.13 ) 1.22 (0.95, 1.58 ) 1.27 (0.87, 1.86 )	1.07 (0.95, 1.20 ) 1.03 (0.91, 1.17 ) 0.80 (0.72, 0.88 ) 0.89 (0.79, 0.99 )
4-state	1a → 1b 1b → 2 2 → 3 1b → 1a 2 → 1b 3 → 2	0.0012 (0.0009, 0.0016 ) 0.0015 (0.0012, 0.0019 ) 0.00033 (0.00025, 0.00045 ) 0.00107 (0.00081, 0.0014 ) 0.00097 (0.00079, 0.0012 ) 0.0011 (0.0008, 0.0014 )	0.72 (0.53, 0.97 ) 0.81 (0.61, 1.09 ) 0.74 (0.49, 1.13 )  2.04 (1.50, 2.78 ) 1.24 (0.94, 1.63 ) 1.26 (0.86, 1.85 )	1.07 (0.93, 1.23 ) 0.97 (0.86, 1.09 ) 1.03 (0.907, 1.17 ) 0.90 (0.79, 1.02 )  0.79 (0.71, 0.87 )  0.88 (0.79, 0.99 )
5-state	1a → 1b 1b → 2 2 → 3a 3a → 3b 1b → 1a 2 → 1b 3a → 2 3b → 3a	0.0012 (0.00094, 0.0016 ) 0.0015 (0.0012, 0.0019 ) 0.00038 (0.00028, 0.00052 ) 0.00091 (0.00056, 0.0015 ) 0.0011 (0.0008, 0.0014 ) 0.00098 (0.00079, 0.0012 ) 0.0019 (0.0014, 0.0026 ) 0.0016 (0.00097, 0.0026 )	0.72 (0.53, 0.97 ) 0.81 (0.60, 1.08 ) 0.72 (0.46, 1.13 ) 1.13 (0.58, 2.22 ) 2.04 (1.50, 2.78 ) 1.24 (0.94, 1.63 ) 1.09 (0.71, 1.66 ) 1.45 (0.75, 2.78 )	1.07 (0.93, 1.23 ) 0.97 (0.86, 1.09 ) 1.08 (0.94, 1.25 ) 1.04 (0.85, 1.25 ) 0.90 (0.79, 1.02 ) 0.78 (0.71, 0.87 ) 1.08 (0.93, 1.24 ) 0.74 (0.61, 0.90 )
Husted	1 → 2a 2a → 2b 2b → 3a 3a → 3b 2a → 1 2b → 2a 3a → 2b 3b → 3a	0.00081 (0.00064, 0.00103 ) 0.0013 (0.0010, 0.0017 ) 0.00089 (0.00063, 0.0013) 0.00092 (0.00056, 0.0015 ) 0.002 (0.0016, 0.0025 ) 0.0014 (0.0011, 0.0017 ) 0.0022 (0.0015, 0.0031 ) 0.0016 (0.00099, 0.0027 )	0.47 (0.35, 0.62 ) 1.05 (0.74, 1.49 ) 0.79 (0.48, 1.28 ) 1.13 (0.58, 2.23 ) 1.10 (0.82, 1.46 ) 1.32 (0.94, 1.86 ) 1.08 (0.68, 1.69 ) 1.44 (0.75, 2.77 )	1.05 (0.93, 1.19 ) 1.03 (0.909, 1.16 ) 0.99 (0.85, 1.16 ) 1.03 (0.85, 1.25 ) 0.87 (0.77, 0.97 ) 0.84 (0.75, 0.95 ) 1.08 (0.92, 1.25 ) 0.74 (0.61, 0.90 )
6-state	1a → 1b 1b → 2a 2a → 2b 2b → 3a 3a → 3b 1b → 1a 2a → 1a 2b → 2a 3a → 2b 3b → 3a	0.0012 (0.00093, 0.0016 ) 0.0019 (0.0015, 0.0026 ) 0.0013 (0.00099, 0.0017 ) 0.00089 (0.00063, 0.0013 ) 0.00093 (0.00057, 0.0015 ) 0.0011 (0.00081, 0.0014 ) 0.0024 (0.0018, 0.0031) 0.0013 (0.0011, 0.0017 ) 0.0022 (0.0015, 0.0031 ) 0.0016 (0.00099, 0.0027 )	0.71 (0.53, 0.96) 0.83 (0.59, 1.17 ) 1.04 (0.73, 1.48 ) 0.79 (0.48, 1.29 ) 1.13 (0.57, 2.21 ) 2.03 (1.49, 2.76 ) 1.14 (0.82, 1.60 ) 1.30 (0.92, 1.83 ) 1.08 (0.69, 1.70 ) 1.44 (0.75, 2.76 )	1.07 (0.93, 1.23 ) 0.94 (0.82, 1.08 ) 1.03 (0.92, 1.17 ) 0.99 (0.85, 1.16 ) 1.03 (0.85, 1.24 ) 0.90 (0.79, 1.03 ) 0.85 (0.75, 0.96 ) 0.85 (0.76, 0.96 ) 1.07 (0.92, 1.25 ) 0.74 (0.61, 0.90 )

^*Effect of 10 extra damaged joint on transition rate.

B. Tracking intervals and probabilities for difference in EKL

The aim of the D_RAIC and D_RLCV criteria is to estimate a difference in EKL, defined in Equation 3, between models $M_1(\widehat{\mathit{\theta }}(\text{x}))$ and $M_2(\widehat{\gamma }({\text{x}}^{\prime }))$ on a replicate $X_{n+1}^{\mathrm{″}}$ of a common restricted dataset. If the estimate of either of these quantities is negative, then $M_1(\widehat{\mathit{\theta }}(\text{x}))$ would be chosen as the EKL minimizing model, and vice-versa for $M_2(\widehat{\gamma }({\text{x}}^{\prime }))$. It is desirable to express sampling uncertainty about these estimates and this choice, as they are dependent on the particular sample x. Commenges et al. [22] used Theorem 3.3 of Vuong [25] to show that, for the case of non-nested models where $M_1({\mathit{\theta }}_0)\ne M_2({\gamma }_0)$, where θ₀ and γ₀ are the Kullback-Leibler risk minimizing parameter values,

$$n^{1/2}\left(D({\widehat{\mathit{\theta }}}_n,{\widehat{\gamma }}_n|\text{x}")-\Delta ({\widehat{\mathit{\theta }}}_n,{\widehat{\gamma }}_n|X_{n+1}^{"})\right)\stackrel{D}{\to }N\left(0,{\omega }_f^2\right)$$ (5)

where $D(\widehat{\mathit{\theta }},\widehat{\gamma }|{\text{x}}^{″})$ is a normalized difference of AIC and

$${\omega }_f^2={\mathbf{V}}_f\left[\log \frac{g(X_{n+1}^{"}|{\widehat{\mathit{\theta }}}_n)}{h(X_{n+1}^{"}|{\widehat{\gamma }}_n)}\right]$$

is the variance under the true distribution of the log-likelihood ratio, which is estimated by

$$\widehat{\omega }\begin{array}{c}2\\ n\end{array}\hspace{0.17em}=n^{-1}{{\displaystyle \sum _{i=1}^n\left[\log \frac{g\left(x_i^{"}|{\widehat{\mathit{\theta }}}_n\right)}{h\left(x_i^{"}|{\widehat{\gamma }}_n\right)}\right]}}^2-{\left[n^{-1}{\displaystyle \sum _{i=1}^n\log \frac{g\left(x_i^{"}|{\widehat{\mathit{\theta }}}_n\right)}{h\left(x_i^{"}|{\widehat{\gamma }}_n\right)}}\right]}^2$$ (6)

Commenges et al. then constructed a so-called tracking interval (A_n, B_n) for the difference in EKL, with

$$A_n=D({\widehat{\mathit{\theta }}}_n,{\widehat{\gamma }}_n{|x}^{\prime \prime })-z_{\alpha /2}{n}^{-1/2}{\widehat{\omega }}_n$$

and

$$B_n=D\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathit{\gamma }}}_n|x^{″}\right)+z_{\alpha /2}{n}^{-1/2}{\widehat{\omega }}_n$$

where 1 − Φ(z_α/2) = α/2 and Φ is the cdf of a standard normal random variable. This interval obeys

$${\mathbf{\text{P}}}_f\left(A_n<\Delta \left({\widehat{\mathit{\theta }}}_n,{\widehat{\gamma }}_n|X_{n+1}^{″}\right)<B_n\right)\to 1-\alpha$$

where probability is with respect to the true distribution f. Liquet and Commenges [2] noted that the above results could be applied to either the D_RAIC or D_RLCV and thus are used to form 95% intervals in our analyses. All of our model comparisons are between non-nested statistical models (M₁(θ₀) ≠ M₂(γ₀)). Vuong [25] showed that the distribution of the log-likelihood ratio statistic for nested, mis-specified, models is distributed as a weighted sum of χ²-distributions, but this could not be used to find distributions for the true EKL difference. Even in this case of nested models, Equation 6 is an estimator of the variance of $D\left(\widehat{\mathit{\theta }},\widehat{\Upsilon }|{\text{x}}^{\mathbf{″}}\right)$. However, it is an underestimate of the variance as it neglects the complexity terms its focus is only the fit to observed data rather than prediction.

Note the difference between the above tracking interval and a standard confidence interval. A confidence interval is an interval around an estimator ${\widehat{\mathit{\theta }}}_n\left(\text{x}\right)$ for some fixed truth θ₀. The estimator and the interval will depend on both the size n and values x of the data, but the truth remains fixed. The tracking interval is defined to contain the estimated Δ_n, the difference in EKL for two models fit to the data by maximum likelihood estimation, for a certain proportion of resamples but this target for estimation depends on n, hence the difference from a confidence interval.

It may be useful to construct a test of the hypothesis that $M_1\left(\widehat{\mathit{\theta }}(x)\right)$, say, is the EKL minimizing model on a replicate $X_n^{″}$ under resamples of x. We do this by estimating the coverage of the largest tracking interval for ∆_n which does not include 0. This coverage is similar to a p-value for the hypothesis that $M_1\left(\widehat{\mathit{\theta }}(x)\right)$ will have a lower EKL than $M_2\left(\widehat{\mathit{\gamma }}\left(x^{\prime }\right)\right)$ on $X_{n+1}^{″}$ if x were to be resampled from f and is found by rearranging Equation 5 to obtain

$$\Phi \left(-\frac{D\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathit{\gamma }}}_n|\mathbf{\text{x}}\mathbf{″}\right)n^{1/2}}{{\omega }_f}\right)$$

which can be estimated by $\Phi \left(-\frac{D\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathit{\gamma }}}_n|{\mathbf{\text{x}}}^{\mathbf{″}}\right)n^{1/2}}{{\widehat{\omega }}_n}\right)$. This can be interpreted as the probability, under resampling of x and x^′, that the difference in EKL on the replicate $X_{n+1}^{″}$ will be negative and thus favour $M_1\left(\widehat{\mathit{\theta }}(x)\right)$. This coverage, or probability, is actually 2-sided as it includes a negative limit. It can therefore be increased from the two-sided 1 − α to the one-sided $1-\frac{\alpha }{2}$, where $\alpha =\Phi \left(-\frac{D\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathit{\gamma }}}_n|{\mathbf{\text{x}}}^{\mathbf{″}}\right)n^{1/2}}{{\widehat{\omega }}_n}\right)$. If $D\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathit{\gamma }}}_n|x^{\mathbf{″}}\right)$ is the D_RAIC, we label this one-sided asymptotic probability the P_RAIC and we label it P_RLCV if it is the D_RLCV. These one-sided probabilities are what we reported in Table 5. In the case of more than 2 models, it would be necessary to generalise Theorem 3.3 of Vuong to the multivariate case and use a standard multivariate normal distribution to find the coverage of higher dimensional tracking intervals.