The Anatomy of High-Performance 2D Similarity Calculations

Abstract

Similarity measures based on the comparison of dense bit-vectors of two-dimensional chemical features are a dominant method in chemical informatics. For large-scale problems, including compound selection and machine learning, computing the intersection between two dense bit-vectors is the overwhelming bottleneck. We describe efficient implementations of this primitive, as well as example applications, using features of modern CPUs that allow 20-40x performance increases relative to typical code. Specifically, we describe fast methods for population count on modern x86 processors and cache-efficient matrix traversal and leader clustering algorithms that alleviate memory bandwidth bottlenecks in similarity matrix construction and clustering. The speed of our 2D comparison primitives is within a small factor of that obtained on GPUs, and does not require specialized hardware.

Introduction

A large variety of methods in chemical informatics, including compound selection,^1,2 clustering, and ligand-based virtual screening, depend on pairwise compound similarities as a critical subroutine. Continuing increases in the size of chemical databases (e.g., 35 million nominally-purchasable compounds in ZINC³ or nearly one billion possible compounds under 13 heavy atoms in GDB-13⁴) create immense demands on computer power to run these algorithms. Consequently, there has been significant interest in the development of fast methods to compute chemical similarity. Previous work has focused on the use of specialized hardware,^5–7 clever data structures,⁸ or approximation techniques⁹ to accelerate large-scale pairwise similarity comparison using a variety of similarity methods.

So-called “two-dimensional” bit-vector Tanimoto similarities are particularly interesting by virtue of their dominant position in terms of similarity metrics used in the field. These similarity measures represent molecules by long (hundreds to thousands of bits long) binary vectors representing the presence or absence of chemical features and compute pairwise compound similarity as a similarity coefficient between pairs of such vectors.

Past work has examined high-level algorithmic strategies to perform large-scale searches in sublinear time, using complex data structures or bounds on the similarity measure to eliminate many comparisons.^8,10–12 However, in some cases these algorithms must still evaluate the underlying similarity measure a large number of times, motivating fast direct calculation of the 2D Tanimoto. Liao, Wang, and Watson recently reported that graphics processing units (GPUs), a type of massively-parallel specialized hardware, achieved 73-143× speedup on common 2D Tanimoto-based compound selection algorithms, relative to the same methods running on a conventional CPU.⁵ However, the reference CPU method used in their work was not properly optimized.

In this paper, we discuss methods for the optimal implementation of 2D similarity computations on modern CPUs. We combine architecture-specific fast implementations of the population count primitive and architecture-agnostic algorithms for reducing memory traffic that enable 20-40× speedup relative to traditional CPU methods and achieve 65% of the theoretical peak machine performance. We demonstrate the performance of our methods on two model problems, similarity matrix construction and leader clustering. Without using specialized hardware, we achieve performance that is, at worst, within 5× that of GPU-based code, and that at best beats the GPU. We include implementations of our high-speed algorithms under a permissive open-source license.

Overview of 2D Similarity

“Two-dimensional” chemical similarity measures define the similarity between a pair of compounds in terms of substructural similarities in their chemical graphs. Typical similarity measures of this type (e.g., MDL keys and path-based fingerprints like Daylight fingerprints)^13,14) represent molecules as binary vectors of a user-defined length. In simple fingerprints, such as MDL keys,¹³ each bit represents the presence or absence of a particular chemical feature. Hashed fingerprints, such as the ECFP family,¹⁴ first compute a large number of features (such as circular paths around each atom), hash these features, and then “fold” the (potentially-large) hashed values into a fixed-length fingerprint by binary OR¹⁵ (sparse fingerprints like ECFP may be represented as a list of integers rather than a bit-vector). The same fingerprint approach can also be used for 3D similarity measures; Haigh and colleagues have described a “shape fingerprint” approach in which bits represent similarity to particular reference shapes, allowing the machinery of 2D fingerprint comparison to be used for shape comparison.¹⁶

Given fingerprint representations of a pair of molecules A and B, a number of different similarity measures can be computed; popular examples include the Tanimoto, cosine, and Dice similarity coefficients.¹⁷ Typically, the terms involved in the computation of such similarity coefficients are the number of 1-bits set in either fingerprint, the number of 1-bits in common between the two fingerprints, and the number of 1-bits present in either fingerprint. In this paper we will specifically consider the computation of the bit-vector Tanimoto, defined by the following equation:

$$T_{A,B}=\frac{\left|A\cap B\right|}{\left|A\cup B\right|}=\frac{\left|A\cap B\right|}{\left|A\right|+\left|B\right|-\left|A\cap B\right|}$$ (1)

However, the techniques described here are applicable to all of the typical similarity coefficients used on bit-vectors. In the next section we discuss two strategies that dramatically improve performance on 2D similarity computation relative to typical existing code, without the use of GPUs or other specialized hardware.

Fast Computation of the 2D Tanimoto

We describe two techniques for accelerating 2D Tanimoto calculations. The first method is to accelerate the population count primitive (the |A∩B| term in equation 1), which is the computational bottleneck in 2D similarity code) using features of modern CPUs; this is useful even for single Tanimoto computations. Secondly, we show that careful optimization of memory access patterns is necessary to achieve maximum performance.

Fast Population Count

Most of the computational expense of 2D similarity comparison comes from the need to count the number of 1-bits set in a given bit-vector, the so called population count, popc, or Hamming weight function. In the Tanimoto equation, this appears in two forms: |x|, the number of 1s set in vector x (where x is A or B), and |A∩B|, the number of 1s set in the binary-AND of vectors A and B.

A common way of computing the population count of a long bit-vector is to use a small lookup table (LUT) to “compute” the population count of short subsections of the full vector (e.g., 8 bits for a 256-entry table or 16 bits for a 65,536 entry table) and then sum all of these values. The LUT contains at address i the population count of i represented in binary. This method is conceptually simple, but a poor choice on modern hardware, especially for large bit-vectors such as those encountered in 2D chemical fingerprints. The LUT lookup requires one memory access for every table lookup; even if serviced from cache, these are an inefficient use of CPU resources.

Modern CPUs have multiple parallel instruction pipelines per core, allowing them to evaluate multiple independent logic instructions simultaneously, but usually only dedicate one pipeline to memory reads (e.g., the Intel Nehalem architecture has 3 instruction issue ports for logic, but only one for memory reads).¹⁸ Therefore, only one memory read instruction can be processed per cycle (implying a peak population-count throughput of 8 or 16 bits per cycle, depending on LUT size). Furthermore, these LUT lookups must contend for pipeline resources with reads of the actual fingerprints, meaning that throughput must be lower than this upper bound. Thus, a memory-lookup-based algorithm will become quickly bottlenecked by memory access, and will perform poorly; logic-based solutions are preferable.

Very recent x86 CPUs (Intel processors since Nehalem; AMD processors since K10) support a population count instruction (PoPCNT) in hardware with single-cycle throughput. This allows computation of a population count on an entire 32- or 64-bit word in one instruction: a clear win over a small lookup table, which would require 4-8 lookups to process 64 bits. However, a significant installed base of processors lack such an instruction, motivating other fast population count algorithms. The two logic-based methods presented below rely on the SSE (Streaming Single-instruction, multiple-data Extensions) vector extensions to x86, implemented by both Intel and AMD. SSE exposes a set of 128-bit registers, which can be interpreted (for our purposes) as vectors of four 32-bit, eight 16-bit, or sixteen 8-bit integers; as well as vector arithmetic and logic instructions operating on these registers. We present fast implementations of population count based on the SSE2 (SSE version 2) and SSSE3 (Supplemental SSE 3) versions of SSE, at least one of which is available on essentially any x86 processor manufactured in the last decade.

Vectorized Lookup Table Method

Many processors that do not support the PoPCNT instruction support the SSSE3 instruction set, including Intel CPUs since the Core 2 generation (still in widespread use in clusters). SSSE3 supports a byte-shuffle instruction which selects bytes from one vector register based on half-bytes (4-bit nibbles) from another. This instruction (PSHUFB, packed shuffle bytes) can be used to implement a 16-element lookup table, where each table element is at most one byte. This can be used to implement a parallel 4-bit population count in logic: 4 bits are sufficient to index into a sixteen-element LUT, and each LUT element stores the number of set bits for that element's LUT index. This leads to a parallel population count method.¹⁹ The input bit-vector to be counted is read in 128-bit chunks into a vector register, interpreted as a set of sixteen bytes. This is then split into two registers: one containing the low nibble of each byte, and one containing the high nibble, shifted to the right. These nibbles are then used as indices into a 16-byte register containing a population count lookup table, using PSHUFB. Finally, adding the two shuffled results produces a population count for each byte in the input chunk. This can be accumulated over multiple input chunks, with some bookkeeping to avoid overflow of the individual byte counters by occasionally accumulating byte counters into wider 16- or 32-bit counters. Conceptually, this method is similar to the lookup-table based approach; however, it is able to count sixteen bytes in parallel and is able to do so with no memory accesses in the inner loop except the unavoidable loads of the input string.

Vectorized Parallel Reduction Method

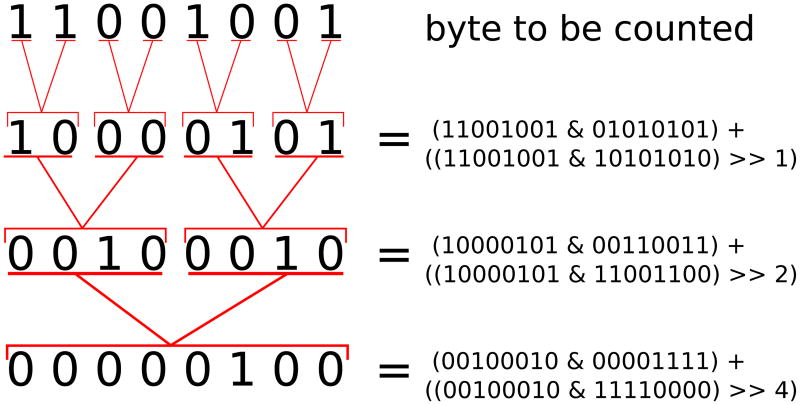
If hardware or compiler support for SSE4 PoPCNT or SSSE3 PSHUFB are not available or are slow, it is possible to implement a fast vectorized population count using a parallel bit reduction technique.²⁰ Given instructions that are atomic on N-bit words (i.e., up to 32- or 64-bit words on typical modern integer hardware), this algorithm is able to count the number of set bits in an N-bit word in o(log N) steps using a divide-and-conquer strategy. At each stage in the recurrence, the algorithm sums up the population counts for two half-size chunks into one larger chunk. Figure 1 shows the operation of the algorithm on an 8-bit byte. The base case for the recurrence is a single bit, which is its own population count. The first reduction step takes adjacent bits and sums them to get a 2-bit population count for a set of two bits. Next, adjacent 2-bit chunks are summed into a 4-bit result; finally, the same is done on each 4-bit half to get the population count for the entire byte. While CPUs do not typically have sub-byte arithmetic operations, these can be emulated using bit masks and shifts, as shown in the figure. To achieve maximum performance, we implement this parallel reduction algorithm at the byte-level, vectorized over sixteen simultaneous bytes in an SSE register. This reduces the operation count per SSE register (3 reduction stages for an 8-bit PoPCNT, versus 4 or 5 for 16/32-bit), at the expense of requiring occasional external reduction stages to avoid overflowing individual byte counters.

Figure 1.

Parallel reduction population count of a byte in three stages. We wish to count the number of 1-bits in the byte 11001001 (base-2). In the first reduction stage, pairs of adjacent bits are summed to form counts of the number of bits set in each two-bit chunk. Pairs of 2-bit chunks are then summed into 4-bit chunks, and the 4-bit halves are then summed into the final 8-bit population count 00000100 = 4 bits set (base 10). These sub-byte operations can be implemented in software using shifts, masks, and bytewise addition, as shown in the equations in the right column.

Cache-Efficient Methods for Large Similarity Matrices

The previous section discussed logic-efficient techniques for the population count operation itself, to accelerate individual Tanimoto computations. However, large-scale similarity problems often have memory bandwidth as a bottleneck, rather than logic performance. As an example, consider the problem of taking the population count of a 2048-bit fingerprint (typical in size for Daylight fingerprints) using the SSE4 hardware PoPCNT instruction. Ignoring loop overhead, this would take 3 instructions (1 load, 1 PoPCNT, and 1 add into an accumulator) per 64-bit chunk. However, assuming perfect superscalar instruction scheduling by the CPU based on logic pipeline availability, these instructions can be issued in parallel, for a total latency of 32 clock cycles. A four-core, 2.5GHz CPU (a typical mid-range CPU of today) could thus compute over 312 million such population counts per second (4×2.5 ×10⁹/32) if arithmetic-limited. However, CPUs typically have memory bandwidth only on the order of 20GB/s per socket; only 78 million fingerprints per second could be read from memory at this rate. Thus, in the absence of data reuse, Tanimoto computation will be memory-bound. Note that this applies even more strongly for GPUs: while GPUs typically feature peak arithmetic performance 30-fold or more higher than the peak performance of a CPU, their memory bandwidth advantage is typically only on the order of 5-10×. Thus, on both CPUs and GPUs, making efficient use of caches to reuse data is essential to high-performance Tanimoto computation. We describe methods of data reuse in two algorithms to illustrate this principle.

Speculative computation in the leader algorithm

The leader clustering algorithm,²¹ given a set of molecules, a similarity distance, and a threshold, clusters the data set according to the following procedure:

1. Choose an unassigned molecule to be a cluster center

2. Compare all remaining unassigned molecules to the new center chosen in step 1

3. Assign to that center any molecules above the threshold similarity

4. If any molecules are still unassigned, return to step 1

Note that in the second step of the algorithm, all unassigned molecules must be streamed from memory through the processor to be compared against the current cluster center. If the similarity threshold is very high, then on most iterations, very few molecules will be removed from the active data set (most molecules will not be assigned). For large data sets (those which do not fit entirely within the cache) this means that almost the entire set of fingerprints will have to be streamed from memory into the processor on every iteration, making the caches useless and making memory bandwidth the limiting factor. In this case, a strategy which we call speculation can produce a significant speedup. The speculative leader clustering algorithm is parameterized by a degree of speculation D; for D = 1, it reduces to the standard leader method described above:

1. Choose at most D unassigned molecules as candidate cluster centers

2. Compute all pairwise similarities among the ≤ D candidates; if any candidates are within threshold similarity to another candidate, assign them to the first candidate to which they are within threshold and remove them from the current pool of centers

3. Compare all unassigned molecules to the pool of centers chosen in step 2

4. For each molecule, if it is above the similarity threshold to any center in the pool, assign it to the first center for which it is above threshold

5. If any molecules remain unassigned, return to step 1

The speculative leader algorithm is optimized for the case in which most clusters will be small, so that on average, most molecules will end up being compared to many centers. It guesses (speculates) that given two centers, the database will have to be compared to both anyway. Thus, in step 3, when each database molecule is read in from memory, it is compared to all candidate centers in the pool. Because (given a reasonable size for D) the candidates can be stored in cache over the entire iteration, the cost of loading database fingerprints from memory is effectively amortized over the pool size. We have implemented and benchmarked the speculative leader algorithm for D = 2 to illustrate the performance benefit from reduced memory traffic relative to non-speculative (D = 1) leader clustering.

Cache-oblivious algorithms for similarity matrix construction

Large similarity matrix construction faces the same bandwidth limitation as the leader algorithm, but the greater regularity of its computational structure admits a more elegant solution to optimizing cache utilization. The family of methods known as cache-oblivious algorithms rely on recursive subdivision of a large problem into a hierarchy of smaller problems such that, at some level in the recursion, each small problem will fit completely into the processor cache. Careful design of the recursion order can then optimize cache usage between recursive subproblems (to prevent or delay eviction between subproblem evaluations). These algorithms are described as cache-oblivious because they are intended to reduce hardware-specific parametrization: rather than having to be reoptimized for processors with 4MB vs 2MB caches, the cache-oblivious method will naturally take advantage of a differing cache size through its recursive structure.

The computational structure of fingerprint matrix construction is similar to that of standard (cubic-complexity) matrix multiplication. Specifically, multiplication of M×K and K × N matrices takes o(MNK) time: one o(K) dot product must be computed for each of the M × N output elements. Similarly, computing an M × N similarity matrix on fingerprints of length K also takes o(MNK) time: o(K) work must be done for each output location to compute the Tanimoto on K words of fingerprint. Since K ≪ M and K ≪ N for typical large-scale similarity computations, similarity matrix construction is analogous to the multiplication of rectangular matrices.

Certain self-similar space-filling curves provide a natural hierarchy and iteration order to optimize locality in a cache-oblivious algorithm. In particular, Morton ordering, based on the hierarchical Z-order curve, has been previously used to optimize cache locality in matrix multiplication,²² suggesting that it may also be useful for similarity matrices. Figure 2 contrasts the order in which similarity matrix elements are computed in Morton order versus standard row-major order. The Z-shaped order in which each sub-block is computed ensures that at some level of recursion, the fingerprints for an entire tile will fit in memory. Other space-filling curves, such as the Hilbert curve, also have excellent cache-locality properties; however, the calculations required to implement the Z-order curve are particularly simple. Given a linear index i along the curve, the X and Y coordinates of the point are given by, respectively, the odd and even bits of the binary representation of i.

Figure 2.

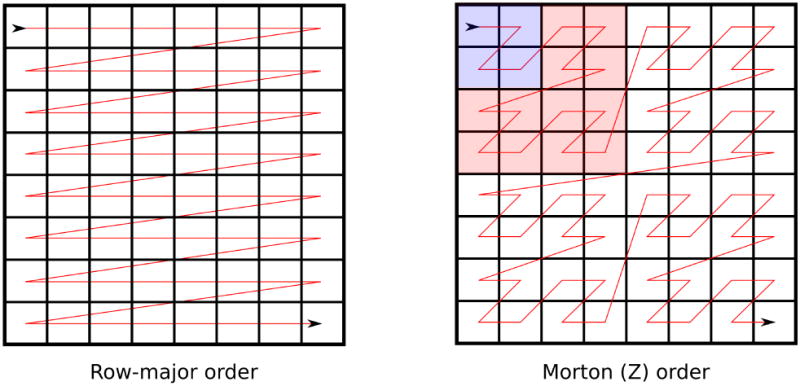
Row-major-order versus Morton order for similarity matrix construction

To understand the memory bandwidth impact of Morton ordering, consider Figure 2 and a hypothetical machine with enough cache space to store eight fingerprints (in actual usage, the cache would be much larger, but the similarity matrix would also be larger than 8×8). In row-major order, the machine would achieve no benefit from its cache between rows of the matrix: one cache slot would be used to store the row fingerprint; additional slots would be allocated for each column fingerprint in order, but since there are eight of these and only seven free slots in the cache, they will evict each other before they are reused in the next row. In contrast, in Morton order, each 4×4 block (e.g., the highlighted red block) could be processed entirely within the cache. Furthermore, this ordering is cache-oblivious. If the algorithm were instead run on a machine with half the cache size, 2×2 blocks would still benefit from having their fingerprints entirely within cache (e.g., the blue block). We have implemented a Morton/Z-ordered method to compute a similarity matrix and demonstrate its performance in the results.

Results

To demonstrate our high-performance CPU 2D similarity methods, we have implemented serial and parallel versions of similarity matrix construction and leader clustering.²¹ our similarity matrix code is derived from internal code developed at Vertex. Both our serial and parallel leader clustering programs are based on the serial leader code written by Liao and colleagues.⁵ We diverge from Liao et al. by using openMP, a multi-vendor standard for language-level parallelism in C and FoRTRAN, to parallelize the similarity matrix and leader methods, rather than Intel's Threading Building Blocks. Additionally, we have changed the representation of fingerprints in memory by coalescing all fingerprints into one large memory allocation and keeping counts of number of bits set in arrays separate from the fingerprint array to enhance memory locality. We tested the original Liao et al. serial CPU code on selected examples and found no significant performance difference versus our code using one thread with their 8-bit lookup table population count; thus, our results using the “LUT” method without the speculative algorithm stand in for comparison with the earlier CPU code.

Benchmarking Methodology

To compare performance between the CPU and GPU, we have also measured the performance of the Liao et al. GPU leader code on a pair of GPUs: an NVIDIA GeForce GTX 480 and a GeForce GTX 260. We made one change to the Liao code: standard CUDA floating-point division (the ‘/’ operator) was replaced with IEEE 754-compliant round-to-nearest floating-point division (__fdiv_rn). This change resolves the slight discrepancy between CPU and GPU Tanimotos noted by Liao and colleagues and had negligible performance impact in informal benchmarks.

Our test data for leader clustering are 100,000, 500,000, and 1,000,000-molecule subsets of the PubChem compound database,²³ drawn uniformly at random. We generated 2048-bit path fingerprints using the oEGraphSim toolkit version 1.7.2.4 from openEye Scientific Software (Santa Fe, NM) using a maximum path distance of 5 and default atom and bond typing. For similarity matrix construction, we drew random sets of 32,768 and 131,072 molecules from PubChem and used 1024-bit path fingerprints generated using the same settings as for the leader clustering.

Our benchmark machine was equipped with an Intel Core i7-920 CPU (2.66-2.93 GHz, 4 cores, Nehalem architecture), 12 GB of DDR3-1066 memory, and two GPUs: an Nvidia GeForce GTX 480 (480 SP @ 1.40GHz, GF100/Fermi architecture) and a GeForce GTX 260 (192 SP @ 1.08 GHz, GT200 architecture). CPU code was compiled using gcc and g++ 4.3 with the following performance-relevant compiler options: -fno-strict-aliasing -fopenmp -o3 -ffast-math. We built GPU code using CUDA toolkit version 4.0 release candidate 2 and Thrust 1.3.0, using NVIDIA driver version 270.40.

Similarity Matrix Construction

To measure raw Tanimoto throughput, we benchmarked the performance of similarity matrix construction on 1024-bit fingerprints on the GPU vs the CPU, using the SSE4 algorithm both with and without Morton-order-based cache blocking. The benchmark program, modeling a compound selection exercise, took two sets of molecules: the “database” and “vendor” sets. It computes the database × vendor Tanimoto matrix and counts for each vendor molecule how many database molecules are within a threshold Tanimoto similarity. The threshold has a negligible effect on runtime; calculation of the Tanimotos dominates the computational expense. For the GPU code, only the count of molecules-within-threshold is transferred back to the CPU, not the entire Tanimoto matrix. We used the same set of molecules for both vendor and database sets in this benchmark.

Table 1 shows the result of the Tanimoto matrix benchmark. The GPU code, processing over one billion 1024-bit Tanimotos per second, is only around five times faster than the best CPU code, which uses SSE4 64-bit population count and Morton ordering on the matrix blocks.

Table 1.

Similarity matrix construction throughput for CPU (SSE4 population count algorithm with row-major and Morton-order) vs GPU (GeForce GTX 480), 1024-bit fingerprints. Similarity matrix for N molecules had shape N×N.

# molecules	Method	Time (s)	Throughput (Tan/s * 106)
	SSE4	6.36	174.3
32,768	SSE4-Morton	5.2	214.8
	GPU	1.19	1088
	SSE4	124.1	139.4
131,072	SSE4-Morton	79.98	217.0
	GPU	15.6	1157

The theoretical limit for the CPU, assuming perfect superscalar instruction scheduling to parallelize population counts, adds, and loads, is bound by the memory read pipeline. Every 64 bits of fingerprint requires two memory reads (one for each fingerprint), and only one read may be issued per clock cycle.¹⁸ Thus, the theoretical limit (estimated using the method described in the section on cache optimization) is approximately 330 million Tanimotos/sec; we reach 65% of this limit.

To estimate the GPU theoretical peak, we assume the inner block of the fingerprint calculation requires two load instructions (one for each fingerprint, because the GPU is a load-store architecture), a bitwise AND, a population count, and an integer add; these steps must be repeated 32 times for a 1024-bit fingerprint since the GPU has a 32-bit native word length. Based on GPU microbenchmarks,²⁴ we estimate each operation as 1 clock cycle, except for population count, which takes 2 clock cycles; no operations overlap since the shader processor in the GTX 480 is not superscalar. The GTX 480 has 480 shader processors running at 1.401 GHz; the theoretical throughput is thus $\frac{1.401\times {10}^9\times 480}{32\times (1+1+1+2+1)}$≈ 3500 million Tanimotos/sec. Therefore, the Liao GPU code (1157 million Tanimoto/sec) runs around 33% of theoretical peak.

Leader Clustering

To measure application-level performance of our fast Tanimoto methods, we modified the leader clustering code of Liao et al.⁵ to use openMP multithreading, several fast population count methods, and the speculative leader algorithm to optimize memory bandwidth.

Figure 3 shows the results of the leader clustering benchmark on representative database sizes and threshold values. Note that the plots show throughput (inverse runtime), normalized to the performance of the fastest GPU. The leftmost black bar, labeled “LUT (NS)”, represents the performance of the original leader algorithm reported by Liao et al., using the 8-bit lookup table population count and no speculation. Black and red bars show the performance of various CPU methods using one and four threads, respectively. The blue bars show the performance of the Liao GPU code on our two test GPUs.

Figure 3.

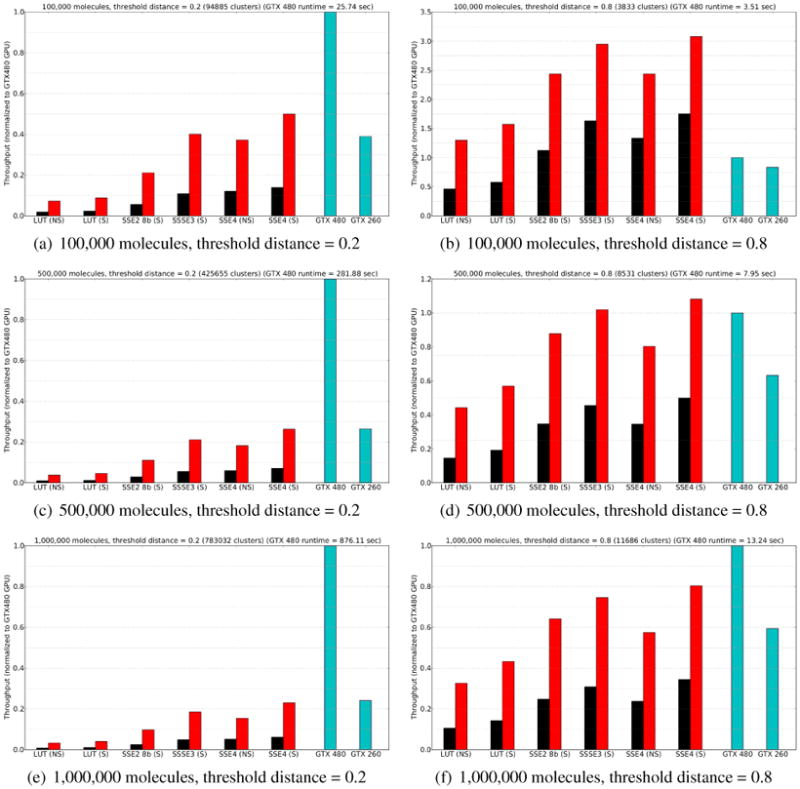
Leader clustering benchmark: throughput (1/runtime) normalized to performance of GeForce GTX480 GPU. Black bars are single-threaded CPU methods; red bars are CPU methods with 4 threads; blue bars are the Liao et al. GPU code run on a GeForce GTX 480 or GTX 260 GPU. CPU methods suffixed with (NS) use the standard leader algorithm; those suffixed with (S) use the speculative leader algorithm. Key to CPU methods: LUT = Liao et al. 8-bit lookup table; SSE2 8b = Bytewise parallel reduction using SSE2; SSSE3 = Vectorized 4-bit lookup table using SSSE3; SSE4 = SSE4 hardware PoPCNT instruction.

Perhaps the most striking result is that on the small distance threshold cases (many clusters), the best CPU code is a factor of 20 to 40 faster than naïve single-threaded CPU code. Consequently, even on the faster of our GPUs, the GPU advantage in this problem versus a properly optimized CPU code is only a factor of two to four. This indicates that prior reports of over a hundredfold speedup do not accurately measure the GPU's true relative advantage. Indeed, on small problems (100k-500k molecules and large distance thresholds), the CPU methods are actually faster, as they have less overhead in GPU initialization and transfer.

The other interesting aspect of the plots in Figure 3 is the performance comparison among the high-speed CPU techniques. All of the methods are much faster than the LUT technique; the SSSE3 vectorized lookup table is competitive with the SSE4 hardware population count. Furthermore, the speculative leader algorithm significantly boosts performance, both for fast algorithms (SSE4 (S) vs SSE4 (NS)) and for slow ones (LUT (S) vs LUT (NS)): the performance increase for the SSE4 population count method is approximately 30-40%.

Conclusion

We have described a collection of techniques to enable high-performance 2D Tanimoto computation on conventional CPUs. Extensions to the x86 instruction set allow the computation of bit-vector Tanimotos 20-40x faster than with architecture-neutral CPU code used for this purpose. Additionally, we have described two algorithmic schemes to reduce memory bandwidth, which is often the limiting factor (rather than logic performance) in large-scale similarity matrix and clustering applications. The combination of these methods is able to bring the 2D Tanimoto performance of a modern four-core CPU to within a factor of two to five of a high-end GPU for large-scale problems, and faster than a GPU for smaller problems. Indeed, the ready availability of six- and eight-core CPUs (rather than the relatively old four-core CPU used in this test) implies that GPUs and CPUs are near parity on this problem; perhaps within a factor of two. We have included the code used in this paper in the hopes that it will enable more efficient use of existing hardware for these industrially-significant calculations.

Our results suggest a performance/labor tradeoff in high-performance algorithms. Simple CPU methods (here exemplified by the lookup table-based population count) are very simple to code, but may have correspondingly low performance. Two possible paths for optimization are the use of better CPU methods or full-scale ports to the GPU, using CUDA or openCL. Historically, CPU optimization (in particular, parallelization) has been an arduous task. However, recent language-level constructs (in particular, OpenMP for language-level parallelism) make it much easier to exploit the performance of modern multicore processors.

Of course, as demonstrated in the population count section, reaching maximum performance on a CPU requires careful consideration of deep architecture-level details and significant work. Thus, for many problems, GPU coding is useful as a middle ground: GPUs require some architecture-awareness and knowledge of parallelism, but relatively simple ports can achieve large speedups relative to simple CPU code. GPU codes can serve as middle ground not only symbolically in terms of performance/labor tradeoff, but literally as well. Once a program has been ported to run well on the GPU (using many independent cores, coherent memory access, good use of shared memory caches, etc.), a direct execution of that program on the CPU will typically also perform better than the naïve CPU version. Language features make this simple: the biggest change in our parallel leader code from the Liao et al. serial code was a change in the memory layout of fingerprints, very similar to that used in their GPU code. Once this was done, making the program run over multiple cores was a single-line change: the addition of an openMP parallel-for pragma. For GPU programs written in openCL, the situation is even simpler, as openCL runtimes for the CPU are widely available.

In a nutshell: GPU coding requires one to think of the hardware, but high speed CPU programming is the same; spending time optimizing CPU code at the same level of architectural complexity that would be used on the GPU often allows one to do quite well.

Algorithmic strategies based on bounding the range of possible similarity coefficients have been used to implement search primitives that are, in some cases, asymptotically more efficient than the methods implemented here (e.g., sublinear for query-vs-database search).^10–12 This prior work does not negate the value of the methods we have presented here: we, like GPU implementors, focus on improvements in the constant factor hidden in Big-o notation. Our fast population count primitives are directly usable by codes implementing sublinear search (and should offer a speedup). Making sublinear search cache-oblivious is an interesting direction for future research.

We have included the code used in this paper in the hopes that it will enable more efficient use of existing hardware for the industrially-significant 2D Tanimoto calculation and serve as a demonstration for CPU optimization techniques.