New insights from cluster analysis methods for RNA secondary structure prediction

Abstract

A widening gap exists between the best practices for RNA secondary structure prediction developed by computational researchers and the methods used in practice by experimentalists. Minimum free energy (MFE) predictions, although broadly used, are outperformed by methods which sample from the Boltzmann distribution and data mine the results. In particular, moving beyond the single structure prediction paradigm yields substantial gains in accuracy. Furthermore, the largest improvements in accuracy and precision come from viewing secondary structures not at the base pair level but at lower granularity/higher abstraction. This suggests that random errors affecting precision and systematic ones affecting accuracy are both reduced by this “fuzzier” view of secondary structures. Thus experimentalists who are willing to adopt a more rigorous, multilayered approach to secondary structure prediction by iterating through these levels of granularity will be much better able to capture fundamental aspects of RNA base pairing.

2 Introduction

Computational methods for RNA secondary structure prediction have been an important resource for experimentalists since the early 1980’s [1, 2, 3]. Prediction of a single minimum free energy (MFE) structure as the native was one of the first approaches [2, 3] and remains the most popular. MFE prediction has enjoyed this remarkable longevity due to its degree of accuracy, especially for shorter sequences [4, 5], and the simplicity of dealing with a single structural prediction.

However, in the past three decades the RNA computational community has moved beyond the single MFE secondary structure prediction paradigm, yielding improvements to prediction accuracy [6, 7, 8]. Moreover, mounting experimental evidence indicates that many critical cellular processes are mediated by changes in RNA (secondary) structure [9, 10, 11, 12]. Hence, there are now strong biological, as well as computational, reasons for considering an ensemble of possible structures instead of just one.

In addition to new methods for generating possible secondary structures [13, 14, 15, 16, 17], significant advances have been made in refining approaches grounded in thermodyanmic optimization. Two critical enhancements to MFE predictions have included considering characteristics of individual base pairs [4, 18, 19, 20, 21, 22, 23, 24, 25] and of other low-energy alternatives to the MFE prediction known as suboptimal structures [26, 27, 28]. Importantly, these two approaches are now unified by the methodology of sampling structures from the Boltzmann distribution for a given sequence [29] according to base pair probabilities [18].

Yet, despite the demonstrated improvements in prediction accuracy from Boltzmann sampling [30, 31, 32], in practice MFE prediction programs like Mfold [33] still dominate among experimentalists¹. The purpose of this paper is to convince the reader that this gap can and should be bridged.

The power of the Boltzmann sampling approach rests on the ability to extract key structural information from a representative set (typically of size 1000) of suboptimal structures. This is achieved by a data mining technique known as cluster analysis [34] in which similar structures are grouped together to reveal underlying patterns. Currently, there are three programs, Sfold [35], RNAShapes [36], and RNA profiling [37], which implement different approaches to secondary structure cluster analysis. The crucial differences in methodology rest on how each defines “similar” structures. This, in turn, is fundamentally a function of the granularity of the given method. Thus, in the next section, we first summarize each of the three methods, along with a related deterministic approach (RNAHeliCes [38]), through the lens of structural granularity.

Next, we compare and contrast these methods with each other and with the MFE prediction based on accuracy, precision, size of results, and efficiency. We show that at the level of secondary structure prediction the differences between Boltzmann clustering programs are not significant. Moreover, the representative structure for the most probable cluster for any of the three programs is at least as good as the MFE prediction. Hence, experimentalists who wish to retain the simplicity of a single structural prediction should simply replace the MFE one with the most probable representative structure to achieve better accuracy on average.

Our analysis goes well beyond this, however. We show that there are significant gains in prediction accuracy to be obtained by moving beyond the single structure paradigm. In particular, there frequently exists a representative structure with markedly better accuracy among the other probable clusters. Hence, experimentalists who view secondary structure predictions as generating a small set of possible configurations, to be vetted by further computational analysis, experimental testing, and/or biological insight, will be well-rewarded for their efforts.

Finally, we demonstrate that the largest improvements in accuracy and precision come from viewing secondary structures not at the base pair level but at lower granularity/higher abstraction. Along with a representative structure, methods which employ abstraction assign to each cluster a signature which captures the structural similarities at the chosen level of granularity. It is these signatures which truly harness the power of the Boltzmann sampling approach. Hence, experimentalists who are willing to begin with a “fuzzier” approach to understanding secondary structures will be much better able to capture fundamental aspects of RNA base pairing.

Because of the different granularity levels at which each method operates, from the fine-grained base pairs of Sfold through the higher level helices of profiling to the most abstract “topologies” of RNAshapes, these cluster analyses are not merely competitors which each other in improving over the MFE prediction. Rather, they offer complementary approaches to representing, grouping, and comparing structures which can be used in conjunction to great advantage.

To illustrate the advantages offered by a more iterative approach to RNA structure prediction via the power of Boltzmann sampling and cluster analysis, we discuss the challenge of aptamer design. In this way, we show that ad-hoc comparisons of single MFE structure predictions can yield to a more rigorous, multilayered approach which draws on a wealth of computational advances.

3 Methods

While the cluster analysis methods all vary in their details, the critical difference is their level of structural granularity. The granularity used by each method informs its clustering approach, illuminates the differences between the methods, and highlights the utility of each method for different applications.

Hence, granularity is the organizing principle of this paper. In particular for this section, we describe the granularity of each method, and its ramifications for (1) structure representation, (2) clustering method, (3) representative structure, and (4) cluster signature. (Granularity also has ramifications for the type of scenario most appropriate for each method, which will be addressed in the Discussion section.) We use the example sequence given by each method to illustrate both their granularity choice and the original issue it was designed to address.

3.1 Sfold: at the base pair level

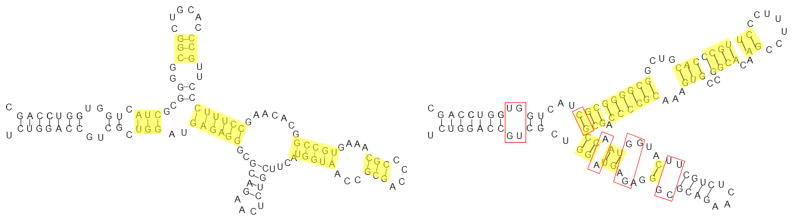
Having pioneered Boltzmann sampling for RNA secondary structures, Sfold was the first to tackle the challenge of data mining a set of suboptimal structures. Sfold recognized that the sample contains important information beyond the MFE structure, particularly when the native structure is not the MFE structure. One example is the A. tumefaciens 5S sequence, whose native conformation is markedly different from the predicted MFE (Figure 1). Accordingly, Sfold [35] identifies different viable low energy structures from a Boltzmann sample.

Figure 1.

The two Sfold cluster centroids for A. tumefaciens 5S. The first is the MFE structure, the second very close to the native; they respectively represent clusters with probabilities 62.1% and 37.9%. Base pairs in the symmetric difference are shown in yellow and total 47. Base pairs separating the second from the native are shown in red; many are noncanonical. Note that single stranded bases do not count toward the symmetric difference.

Sfold represents one end of the granularity spectrum by operating at the finest level of resolution: the base pair level. This fine-grained approach is reflected in its representation of structures as a set of base pairs (i.e. a set of canonical pairs of nucleotides according to the allowed pairings A ↔ U, C ↔ G or G ↔ U). Sfold also compares structures in these terms, defining the distance between two structures as the number of base pairs in either one but not in both (the symmetric difference of the two sets of base pairs).

With this well-defined metric, classic clustering algorithms can now be employed to group suboptimal structures together [39]. Sfold uses a divisive hierarchical clustering algorithm [34], beginning with all elements in a single cluster. Successive steps divide the cluster with largest diameter (maximum base pair distance between any two elements). Sfold computes twenty clusters before determining which division is optimal.

At each step, the quality of clustering is assessed with the Calinski-Harabasz (CH) index [40], a data mining metric previously used to good effect in microarray analysis [41]. The CH index calculates the ratio of distances between clusters over distances within clusters; the higher the ratio, the better the clustering. Sfold selects the clustering division between two and twenty with the highest CH index as the optimum.

These clusters capture critical information about the Boltzmann ensemble, namely that there may be more than one significant energy well present. This information is embodied in the structure chosen to represent each cluster, called the centroid structure. The centroid by definition minimizes the total base pair distance to all structures in the cluster [30]. Qualitatively, centroids reflect the high frequency base pairs of the sample, which have been shown to have higher positive predictive value (PPV) [25]. Quantitatively, centroids show improvements in sensitivity and PPV over the MFE when compared against the native [30].

This is the case with the A. tumefaciens 5S sequence, whose native structure is not the MFE but a low energy alternative. Thus, its Boltzmann sample yields two centroids (Figure 1), one for the MFE energy well and the other for the native one. By broadening the search beyond a single MFE structure, Sfold’s analysis identifies a major structural group with almost the same frequency as the MFE cluster, and substantially more accuracy.

3.2 RNAshapes: at the branching pattern level

Developed around the same time as Sfold, RNAshapes operates at the other end of the granularity spectrum. While Sfold represents and clusters its structures at a base pair resolution, RNAshapes does so with respect to gross morphology. Its high level of abstraction serves as an intuitive way to cluster and manage a large number of low-energy suboptimal structures [32].

RNAshapes represents structures in terms of their topology, or shape, by abstracting away internal loops, bulges, and the location and length of helices. Nesting and adjacency information are preserved, and embodied in its abstract shape, as denoted by pairs of well-formed brackets. By representing structures with their abstract shapes, RNAshapes then clusters structures with the same shape together.

Each cluster has the common shape as its signature, and the number of constituent structures as its frequency. To enable structure prediction, each group is also represented by the structure with the lowest free energy of the group, known as its shrep.

Like Sfold’s clustering, shape analysis reveals patterns in a sample about which nothing is known. Additionally, this abstraction is particularly useful when a general topology is suspected a priori concerning the sequence, e.g. when the sequence is related to other characterized sequences by homology or experimental data. By grouping structures with a common shape, RNAshapes enables researchers to zero in on a topology of interest [32].

An example of this discussed by RNAshapes and reprised here is the sequence N. pharaonis tRNA-ala [32], whose native structure is the well-known tRNA cloverleaf. However, the MFE has a markedly different topology of one long extended helix. Identifying low energy candidates for the native possessing the appropriate shape is difficult, without organizing structures based on topology.

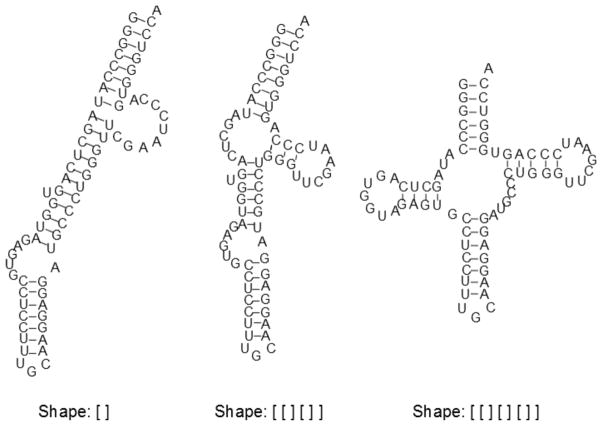
RNAshapes’ analysis of N. pharaonis yields three distinct shape groups, seen in Figure 2. The MFE structure belongs to the most frequent (incorrect) shape, which dominates the sample at a frequency of 99%. Without the benefit of shape analysis, many structures would have to be sifted through in search of one with the desired cloverleaf topology. With shape analysis, the native structure is easily located as the shrep of the third shape [42].

Figure 2.

The three shapes present in a N. pharaonis tRNA-ala sample, with their shreps; their probabilities from left to right are 99.0%, 0.7% and 0.3%. The MFE is the shrep for the first, most populous shape, while the native is the shrep for the last.

Thus, RNAshapes enables very quick perusal of the different topologies present in a set of suboptimal structures. This view of the sample at a low level of structural granularity gives one important way to summarize the structural information of the sample. This is useful when first exploring the characteristics of a sequence, but especially useful if a known topology is suspected.

3.3 RNAHeliCes: a refinement of RNAshapes

Developed as an extension of RNAshapes, RNAHeliCes [38] operates at a granularity between the fine gained Sfold and the abstract RNAshapes, and hence is included in this review for its interesting abstraction scheme. However, in contrast to the other methods discussed here, RNAHeliCes does not stochastically sample from the Boltzmann distribution. Rather, it deterministically enumerates all low energy structures, beginning with the lowest ones, until by default three hishapes are identified. While its abstraction scheme is of interest, this abbreviated analysis of suboptimal space limits its practical use. Nevertheless, we discuss RNAHeliCes for its unique granularity level, and as a general contrast to the more preferred Boltzmann sampling methods.

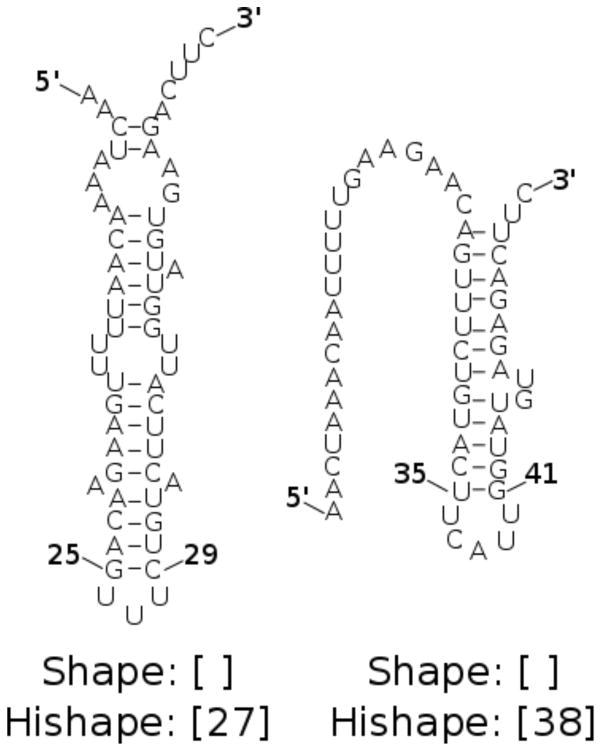
RNAHeliCes’ intermediate level of granularity is appropriate in scenarios when multiple structures of interest have the same shape and must be differentiated. Such is the case for the spliced leader RNA from Leptomonas collosoma [43], their test sequence [38]. Since its two structures (seen in Figure 3) both have the shape [ ], using shape abstraction would identify at most one of them. Thus, a finer grained abstraction is needed.

Figure 3.

The two alternating native structures for the spliced leader RNA from Leptomonas collosoma. Both have the same shape [ ], but different hishapes. The first structure has the innermost base pair (25, 29) and thus an index of $\frac{25+29}{2}=27$; its hishape is [27]. The second structure has a helix midpoint of $38=\frac{35+41}{2}$ and a hishape of [38].

Specifically, RNAHeliCes adds an index to every bracket pair in the shape abstraction to form a helix index shape, or hishape. The index is calculated as the average of the indices of the closing base pair and serves to differentiate helices located at different nucleotide positions, unless they are centered at the same position.

Like RNAshapes, RNAHeliCes uses abstraction as its organizing principle, clustering structures with the same hishape together. Allowable differences within a hishape group include exact helix composition, length and location of stack extensions, and internal loops and bulges. While each group has the hishape signature common to all its structures, it is also characterized by a representative structure (called a hishrep) that is the minimum free energy structure in the group.

RNAHeliCes can be used to view common hishapes but also to predict structure, as with L. collosoma. By distinguishing between stems centered around different midpoints, it identifies two hishapes within the common shape. For L. collosoma, the shreps for each hishape approximate the two alternate structures for the sequence. Thus, this level of abstraction is more appropriate to the L. collosoma sequence than RNAshapes.

3.4 Profiling: at the helix level

Like RNAHeliCes, profiling operates at an intermediate granularity, disregarding certain low frequency base pairs to consider only common helices. Developed to take a more modular approach to clustering structures, profiling enables the structural behavior of a subsequence or region of interest to be investigated [37]. Such regions include known functional domains and any new regions of interest discovered through experimental or computational means [44].

We consider the Vibrio cholerae quorum regulatory sequence VcQrr3 example used by profiling [37]. No native structure is known, although a large portion of it is evolutionarily conserved with other quorum sensing sequences [45]. With sequence conservation pointing to functional and hence structural importance, the structural patterns of the given region need to be determined.

Profiling addresses this scenario by taking a helix-centric approach to representing and clustering structures. By focusing on high frequency helices known as features, profiling represents structures by their particular combination of features, known as its profile. Structures with the same profile are clustered together, and the most frequent profiles are selected as clusters of particular interest. The clusters with their profile signatures thus summarize the helical information in a Boltzmann sample. By abstracting away low frequency helices, common patterns involving the key helices and thus key regions can emerge.

In addition to highlighting regional and helical trends, profiling can be used for simple structure prediction. Thus in addition to a signature profile, a representative structure is given for each cluster. This is the consensus structure, which is composed of all the base pairs present in a majority of structures in the profile. Profiles provide a more abstract way of viewing the salient information in a cluster, while the consensus structures give a base-pair resolution view of the information.

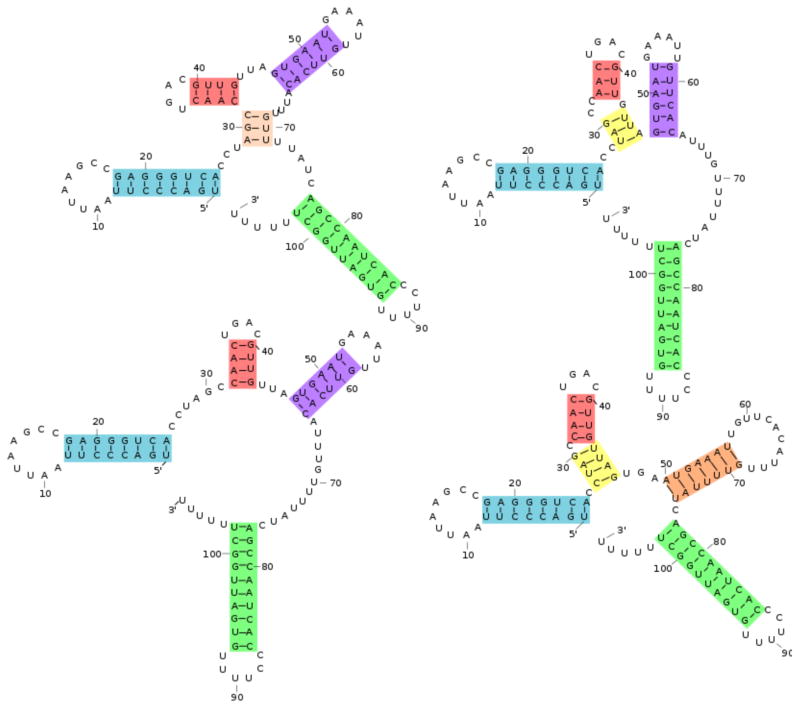
The consensus structures for the four VcQrr3 selected profiles are seen in Figure 4. Previously, these profiles were shown to contain four distinct structural patterns in the conserved region [37], with the variations centering around nucleotides known as key to functionality [46, 47, 48]. Thus, for extracting information at the regional level, profiling clears away lower level details and presents major helical patterns.

Figure 4.

Four VcQrr3 consensus structures, with colors indicating different features. Their probabilities are, clockwise from top left, 6.8%, 56.4%, 7.0% and 20.5% Each structure as a combination of colors illustrates profiling’s representation of a structure as a set of features. The MFE structure is the lower left.

4 Evaluation criteria

As illustrated, each cluster analysis method extracts important information from sets of suboptimal structures at complementary levels of granularity. In addition to these individual proof-of-principle results, in this section we compare the methods in four key measures: accuracy, precision, result size and runtime.

Accuracy is always a factor when choosing a method, as is the practical issue of runtime. Precision, or the repeatability of results, is an issue due to the stochasticity of Boltzmann sampling. Finally, since we are moving beyond considering just one MFE structure to multiple suboptimal ones, the typical number of clusters returned is an important characteristic of the analysis method.

As described, the methods associate both a representative structure and a signature to each cluster. To investigate the effect of abstraction, we evaluate the performance of the signatures as well as the more commonly assessed structures. It will be shown that although representative structures across methods have comparable accuracy, increased abstraction typically yields increased accuracy as well as increased precision.

We evaluate these measures using ten Rfam [49] families with sequence length less than 200, the range of best performance for thermodynamic optimization [5]. From each Rfam family alignment, ten seed sequences were chosen to give a median and average MFE F-measure score of approximately 0.5. For the accuracy comparisons, the native base pairings for each sequence were obtained by aligning it with the Rfam consensus structure.

For the computations, we use GTfold, a parallel implementation of the MFE algorithm [50], Sfold 2.2, RNAshapes 2.1.6, RNAHeLiCes 2.0.14 and profiling 1.0.

4.1 Accuracy

There are several options when measuring accuracy, the first and most important assessment of a method. Unlike the MFE optimization, the cluster analysis methods return multiple clusters, each represented by both a structure and a signature. Thus, there is the option of measuring the accuracy of one structure or of the aggregate of multiple ones, and of doing so for signatures as well. As we shall see, there are reasons for exploring all these options.

As others have done [30], we report the accuracy of the best representative structure, i.e. the structure with the highest accuracy. This gives a sense of the best the methods can do, and of the fundamental limitations to accuracy each method is bound by. However, when the native is not known, the best structure cannot be identified. Instead, the highest frequency or most probable structure, is always apparent; hence, we also calculate its accuracy.

Moreover, in addition to considering the accuracy of a single structure, we will argue that considering multiple structures is worth the improvement to accuracy. As some researchers may be able to systematically investigate all structures, we calculate the overall average accuracy of all structures, both unweighted and weighted by the frequency of the cluster. Comparing unweighted versus weighted indicates the general frequency of more accurate structures; if accurate structures are of lower frequency, then the unweighted accuracy will be greater, and vice versa.

Representative structures, however, are not the only structural information produced about the clusters. These methods also give information at higher abstraction levels in the form of cluster signatures. We will show that structural predictions on a broader scale than base pairs have a better accuracy than the representative structure, and hence are also evaluated in addition to the more traditional structure level.

For each method including the MFE prediction, we calculate its accuracy as the F-measure, which is the harmonic mean of positive predictive value and sensitivity. We summarize results for each family by reporting the median most probable, best, average and weighted accuracy over all sequences in the family.

More precisely, positive predictive value is calculated as

$$\mathit{PPV}=\frac{TP}{TP+FP}$$

and sensitivity as

$$S=\frac{TP}{TP+FN}$$

where TP denotes a true positive, FP a false positive, and FN a false negative. The F-measure is defined as

$$F=2·\frac{\mathit{PPV}·S}{\mathit{PPV}+S}$$

We compare the base pairs of the native against the predicted structure to determine accuracy. Base pairs common to both structures are counted as true positives; base pairs occurring only in the native but not the predicted as false negatives; and base pairs only in the predicted but not the native as false positives.

A more general definition of true positive, false positive and false negative involving edit distance is needed to calculate signature accuracy. The edit distance details the transformation of the native into the predicted by a series of either insertions or deletions. Any insertions to the native signature is considered a false positive, and any deletion a false negative. Any element of the native signature not deleted in the edit distance is a true positive. The shortest edit distance gives us the necessary terms to calculate the F-measure. Recall that Sfold’s clusters have the centroid as both signature as well as representative structure.

For profiling, each group has its profile (a set of features) as its signature. We calculate the F-measure of selected profiles against the profile representation of the native structure, with helices that are not features omitted from the profile by definition. Common features are true positives, features found only in the profile representation of the native are false negatives, and features found only in the selected profile are false positives. For simplicity we consider only features of length greater than two base pairs. Because very low frequency profiles are not selected, the weighted accuracies of the selected profiles are calculated using normalized frequencies.

The RNAHeliCes signature is its hishape. Each hishape is a set of indices with associated loop type. To calculate accuracy, we use their convert function to translate the native structure into a hishape, comparing it against the predicted hishapes with their tree edit program. A true positive is a loop type and index found in both the native and predicted hishape, with false positives and negatives found only in the predicted or native respectively. Because RNAHeliCes gives free energies and not frequencies for its hishapes, we approximate hishape frequency in calculating the weighted average accuracy. An abbreviated partition function from the given free energies is used as a normalizing factor to determine the probability of each hishape.

We use a similar tree edit approach to calculating the accuracy of RNAshapes signatures. For simplicity and consistency, we use the RNAHeliCes tree edit program to determine the edit distance between the native and predicted shapes. Both the native and the representative structure are translated into hishapes by the RNAHeliCes convert function before being input into the tree edit program. The additional index of hishape is disregarded by ignoring any relabeling edits. Insertions and deletions as before provide counts for true positives, false positives and false negatives.

4.2 Precision

The deterministic MFE and RNAHeliCes algorithms always return the same result for a given sequence. However, there is no such guarantee with methods analyzing a stochastically generated Boltzmann sample. Thus, not only the accuracy but also the precision (or repeatability) of results is an issue.

We measure precision by running each stochastic method ten times. The precision score for each cluster representation (structure or signature) is the observed fraction of runs in which it represents a cluster. For example, if a structure appears as an Sfold centroid in eight runs out of ten, it receives a precision score of 0.8. The precision of the cluster representatives can thus be calculated for all methods.

Like accuracy, we report precision in four ways: the score of the most frequent element, of the best element, of the average of all the elements, and of the average of all the elements weighted by their frequencies. The most probable element is always apparent and can be used if only one element is desired, while the best element demonstrates the advantages of using multiple structures. Finally, comparing the weighted with the unweighted average reveals that precision increases when the higher frequency elements are weighted accordingly.

4.3 Size of results

Although accuracy results will demonstrate the viability of using cluster analysis methods even when only one structure is processed, results will also show that there is almost always a more accurate representative structure. Results size thus quantifies how many representative structures are produced. This result, in combination with others, demonstrates that using only a handful more structures pays a significant dividend in accuracy.

For Sfold, we report the number of clusters; for profiling, the number of selected profiles; and for RNAshapes, the number of shapes. We show results for RNAHeliCes as a reference only, as the default setting for this deterministic method always produces the three lowest energy hishapes.

4.4 Runtimes

The expediency of computational prediction methods is a significant motivator for their use. Accordingly, we quantify the efficiency of each method by its runtime.

By now, MFE methods are well-optimized, resulting in efficient runtimes. Although these cluster analysis methods have been developed more recently, we show that their run times do not suffer much in comparison. We use the runtime of GTfold [50], a parallelized implementation of the MFE method, for comparison. We measure the time it takes to generate and analyze a Boltzmann sample for a given sequence using a high resolution timer. We report the median run time across all sequences in a family.

5 Results

Results confirm the superiority of using cluster analysis methods instead of the MFE prediction. First, if only one possible structure will be considered, the most probable structure should be used since its accuracy is often better, and unlikely to be worse, than the MFE prediction. Second, considering just a few alternative structures confers real improvements in accuracy, so researchers are strongly urged to broaden their methodology beyond single-structure predictions. Finally, the most significant gains in accuracy, as well as precision, are achieved by viewing structures more abstractly as cluster signatures. This suggests that random errors affecting precision and systematic ones affecting accuracy are both reduced by this “fuzzier” view of secondary structures. As discussed in the next section, the implication for researchers is that the most accurate structure predictions will be achieved by iterating through the levels of granularity. Furthermore, this benefit will be maximized by coupling the computational analyses with experimental hypothesis testing.

5.1 Accuracy

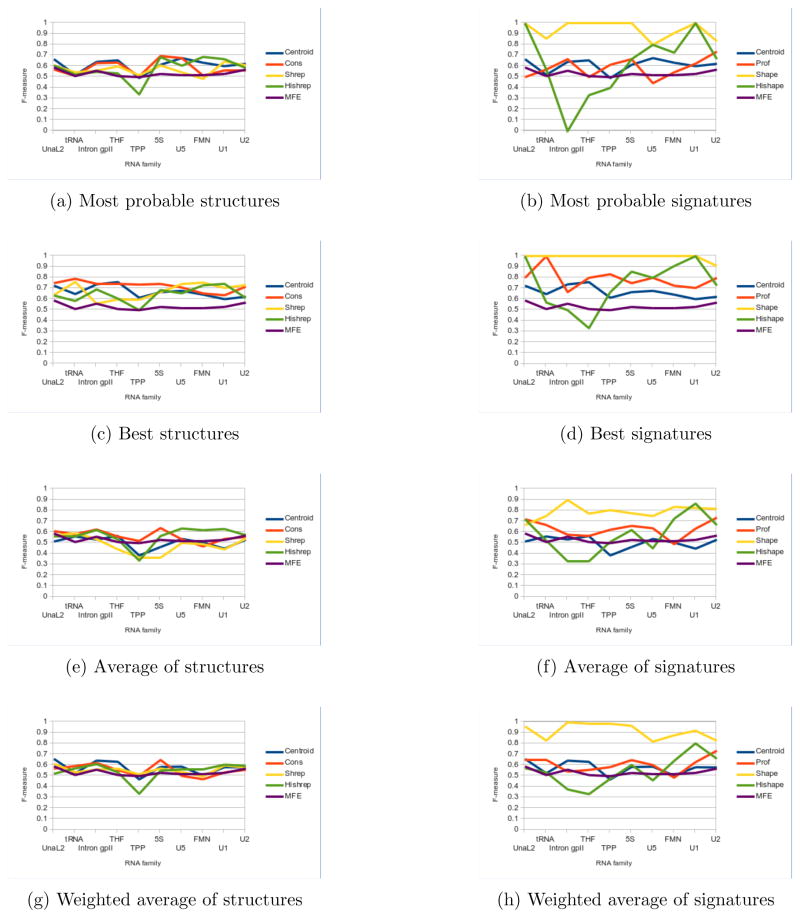
Results confirm the preferred approach of Boltzmann sampling. Because Sfold, profiling and RNAshapes summarize the structural information from a larger, more representative group of structures, accuracy results as a whole are more reliable. Boltzmann sampling methods in general either perform at or above the level of MFE structures, while RNA-HeliCes can dip significantly below (Figure 5a). Furthermore, while Boltzmann signatures (e.g. Figure 5b and Figure 5d) perform reliably better than their associated representative structures (e.g. Figure 5a and Figure 5c), this relation is not seen in RNAHeliCes. Thus, while we consider RNAHeliCes for its unique abstraction scheme, we focus primarily on the three Boltzmann sampling methods.

Figure 5.

Accuracy comparisons for representative structures (left) and signatures (right). Median scores are reported for each family. Sfold centroids are used for both. The median MFE F-measure is also reported for comparison. Note the significant improvement in accuracy for signatures versus structures.

Within the sampling methods, the best accuracies achieved by Sfold, profiling and RNAshapes for their representative structures are close to each other (Figure 5c). No one method sustains a clear advantage, with all methods producing the best accuracy for at least one RNA family. Similarly, the top accuracy score among most probable structures does not uniformly belong to one method, but shifts between methods depending on RNA family (Figure 5a). Thus at the base pair level of accuracy, there is little difference between these three methods. Consequently, we now compare all the methods’ representative structures collectively against the MFE structure.

Figure 5a illustrates that using the most probable structure is a better strategy than using the MFE. For each method, only RNAHeliCes had one family (TPP) with accuracy below 95% of the MFE accuracy. Moreover, on average, the accuracy is usually 6% above.

However, in nearly all the cases, the accuracy of the most probable representative (Figure 5a) structure is not the best (Figure 5c). Every method has a representative structure with accuracy better than the MFE, for every RNA family. Even adding only two additional suboptimal structures for RNAHeliCes, which always produces just three structures by default, significantly improves the best accuracy in a substantial number of cases. (The improved scores of the most probable and best structures have previously been shown with Sfold [30], but we demonstrate that these results are not tied to Sfold’s methodology but are a general result of clustering suboptimal structures.) Thus, while considering only one structure is the simplest, expanding the scope of investigation even a little carries significant benefits.

If resources allow for only a few more suboptimal structures to be processed, then the higher frequency ones should be considered first. This is implied by comparing the unweighted average accuracies (Figure 5e) against the weighted average (Figure 5g). For Sfold and RNAshapes, the weighted accuracy is higher than the unweighted because the very low frequency structures are unlikely to be the native pairings. In contrast, profiling already removes these structures from consideration. Hence, the lower frequency selected profiles are exactly those shown to be more accurate by the other two methods. Accordingly, for profiling the unweighted has higher accuracy than the weighted. Thus, if only a few but not all of the structures can be considered, selecting the more frequent ones is the best strategy.

Although the methods are largely interchangeable at the base pair level, this is not the case as abstraction is introduced. In a majority of the cases (e.g. Figure 5c vs. Figure 5d), the signature has a higher accuracy than its representative structure, indicating that broader structural predictions are more correct than specific ones.

Additionally, the degree of abstraction is related with the degree of accuracy. Especially for the best and averaged accuracies (Figures 5d and 5f), shapes is clearly better than profiles, which is clearly better than centroids. The improvement in accuracy is especially significant for RNAshapes; the most probable shape is the correct one in most families (Figure 5b). This agrees with an intuitive sense that computational prediction, while not completely accurate in all the base pair details, nevertheless is sophisticated enough to predict the broad outlines of structure correctly at this length scale.

Thus, accuracy results confirm the superiority of using structures from a Boltzmann sample, preferably more than one. They also confirm the strategy of using abstraction when possible.

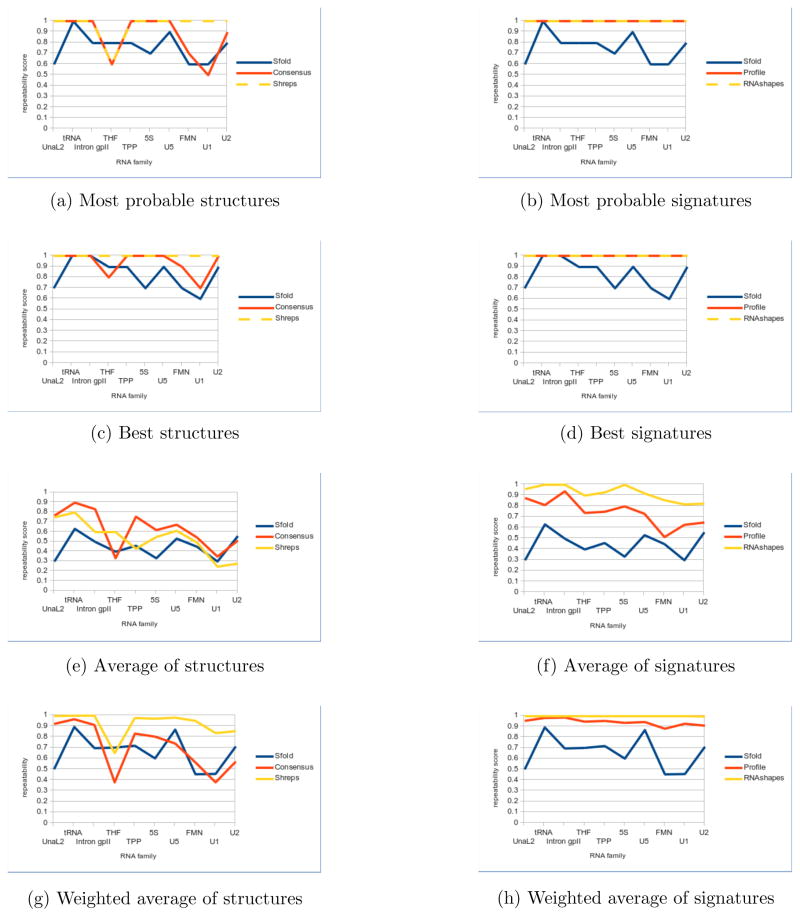
5.2 Precision

Precision increases as abstraction increases. Because a lack of precision often indicates the presence of random errors, this indicates that there is significant stochastic noise at the base pair level in Boltzmann sampling. The best scores (Figure 6c) indicate that despite stochastic noise, the Boltzmann sample has a clear signal that the methods are consistently picking up. The precision of the most probable structure (Figure 6a) is usually among the best scores of each run (Figure 6c). Hence the more frequent elements are consistently present in runs with high repeatability, with stochastic noise affecting the low frequency elements more. This is further confirmed by precision scores significantly increasing when average scores (Figure 6e) are weighted according to their frequencies (Figure 6g). Thus, considering the most probable structure, and preferably two to five other high frequency structures, as the native is advantageous not only with respect to accuracy but also to precision.

Figure 6.

Precision comparisons for representative structures (left) and signatures (right). Median scores are reported for each family. Sfold centroids are used for both. Neither RNAHeliCes nor the MFE prediction are included, since both are deterministic with perfect precision. Note the improvement in precision for signatures versus structures.

The stochastic noise is further reduced by lowering the granularity from structures to signatures. Both profiling and RNAshapes have their best and most probable precision scores boosted to perfect repeatability for all families when considering signatures (Figures 6d and 6b). Even between signatures, there is a clear inverse relation between level of granularity and precision. According to the average precision scores (Figure 6f), Sfold’s fine-grained centroids perform worse than profiling’s more abstract helix centric view, which in turn is worse than RNAshapes’ more abstract shapes. This again is consistent with accuracy results, which strongly encourage the use of signatures under the principle that the lower granularity, the better.

Taken together with the accuracy scores, we see that both accuracy and precision typically increase with higher frequency structures, and even more so with signatures. This indicates that abstraction alleviates both random stochastic errors that affect precision, and potentially more systematic ones affecting accuracy. Precision results also confirm the strategy of always considering the most probable structures, additional high frequency structures when resources allow, and abstract signatures when feasible.

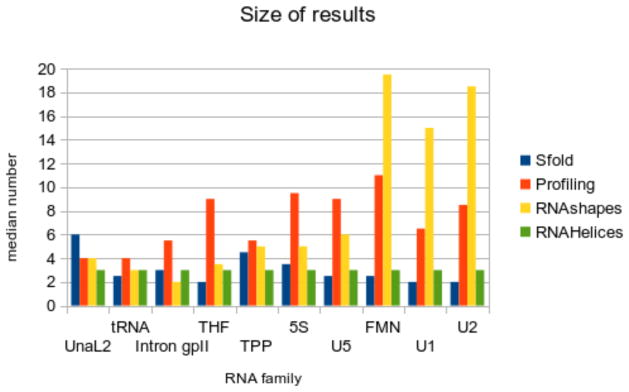
5.3 Size of results

For researchers partial to the one structure simplicity of the MFE method, any of the Boltzmann methods’ most probable structure is a better choice than the MFE. However, analyzing additional high frequency structures pays dividends in accuracy, as seen by the fact that the most probable structure is usually not the most accurate. Results size confirm that the number of additional structures to be analyzed is typically small.

Sfold consistently gives some of the smallest number of clusters, i.e. between two to six clusters. For Sfold, the number of clusters does not noticeably differ as sequence length increases. Thus, the best accuracies of Sfold are accessible by considering only a handful of additional structures, which covers all the clusters.

The median number of selected profiles is slightly larger but always under a dozen, and generally correlated to sequence length. Considering all the selected profiles is still feasible, as is focusing on the most frequent two to five profiles.

RNAshapes reports a median number of shapes ranging from two to 19, with the number of shapes increasing more significantly with longer sequence lengths. However, the growing number of shapes is populated in large part by very low frequency clusters, which have been shown to have relatively poor accuracy and precision. Hence, using a few of the most frequent structures is again encouraged. If signatures are used, employing just the most probable is a valid strategy, given the most probable signatures’ very high accuracy and perfect precision.

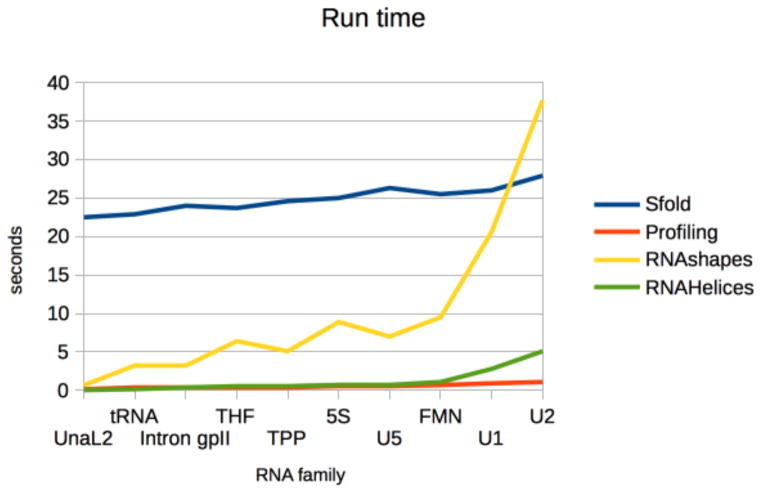
5.4 Runtime

Compared to GTfold, the cluster analysis methods are slower, though to human perception there is little difference between the runtimes of GTfold, profiling and RNAHeliCes. Hence, runtime is not a discriminating factor under normal conditions (e.g. no massive number of runs).

Sfold was fairly consistent in generating and analyzing Boltzmann samples, averaging around 25 seconds, with the most time spent in its computationally intensive clustering algorithm. Both profiling and RNAHeliCes ran in usually under a second, though RNA-HeliCes’ run time went up for longer families. RNAshapes’ run time was inbetween Sfold and profiling, and was the most variable. Run time increased with sequence length for all methods, as expected.

Thus, while high volume studies may preclude using slower methods, single runs can be made by any method in reasonable time.

6 Discussion

Results demonstrate that at the base pair level, the Boltzmann cluster analysis methods are indistinguishable, most notably in terms of accuracy. Hence, whether selecting one structure to use or employing the more preferred multiple structures, any of the methods is sufficient to show improvements over the MFE prediction. Real differences, however, appear when considering signatures with their differing granularity levels. Specifically, lowered granularity translates to higher accuracy and precision, indicating that errors both systematic and random are addressed at least in part by structural abstraction.

These results taken together present a clear strategy for employing cluster analysis methods: use the most probable structure instead of the MFE prediction, consider multiple structures when resources allow, and begin with signatures instead of structures when feasible. While the methods are largely indistinguishable at the base pair level, careful consideration is needed if abstract signatures are used, as each method operates at a different granularity level.

Use of the appropriate method yields information at the given granularity, which in turn should motivate further investigation. By iterating between computation and experimentation, the granularity of exploration can progress from very low to very high. Thus, while their representative structures make these methods competitors at the base pair level, their signatures make them complementary tools from a granularity perspective.

If nothing but the broadest knowledge concerning a sequence is known, then the broadest and most abstract method (RNAshapes) is the place to begin. For example, a group of related sequences (identified through evolutionary homology, sequence alignment, or experimental results) may need to be characterized. Such a scenario occurs with aptamers, which are sequences that bind to a ligand of interest and are typically of length 100 nucleotides or less. Of increasing interest in therapeutic use [51, 52], aptamers can be found experimentally from a large random pool of sequences [53, 54, 55]. The nature of aptamer-ligand binding, however, is not well understood, nor is it always clear what the key similarity is that causes a group of sequences to all bind to the same ligand [56].

The secondary structure of the sequence is thought to be crucial to its binding, and structural features common to all the sequences are of high interest. Since little is known about the sequence(s) of interest, a very high level, shapes-oriented approach is a good starting point to identifying common branching motifs. Sampled shapes are highly accurate and precise at this level, and can be directly compared between sequences of differing lengths. If a branching pattern of interest is identified (such as the linear or slightly branched topologies known to be favored [57, 58, 59]), then only aptamers with the predicted branching pattern, for example, can be included in a experimental selection pool. This early weeding out of potentially unviable sequences could alleviate the low yield and high cost of aptamer synthesis [55], thus increasing the effectiveness of experimentation. Using shape predictions could also preclude the not uncommon scenario of generating random sequence pools with low structural diversity [59] or with characteristics different from functional molecules.

Results from aptamer selection usually produce a smaller subset of sequences with the desired binding affinity. Thus, while all sequences may have the same branching configuration, a higher granularity level is now needed to investigate details that enable some sequences to bind while others do not. The wide gap between shape and shrep accuracies in Figures 5c and 5d indicate that much accuracy is lost by jumping from a shape to the MFE structure with that shape.

By considering different helix combinations with the same shape, the focus can be narrowed further without moving directly to base pairs. Helix-centric methods like profiling give the location and length of helices within a topology, enabling the search for common regional motifs and domains, like the bulge-hairpin [55] or the stem-loop motif [60] known to be functionally important in many characterized aptamers.

Regional analysis afforded by profiling is needed when computational or experimental data points to a particular area of interest. Computationally, sequence alignment tools can determine that a conserved subsequence exists. Experimentally, subregions of interest are found in sequences from partially structured libraries [60, 61]. Shown to improve aptamer selection, these sequences typically contain a conserved subsequence flanked by two randomized subsequences. High performing sequences require regional analysis to determine the structural behavior of their randomized subsequences. Profiling a sequence gives the major combinations of helices possible for the region, enabling common motifs to emerge.

A proposed motif can be verified by screening additional sequences predicted to form similar substructures in the key region. Once a motif or domain is identified as the potential key to binding, granularity can be increased to a nucleotide level. Mutation experiments predicted to disrupt key domains can verify computational predictions or necessitate alternate hypotheses. Successful knockout mutations pinpoint specific nucleotides of interest, which can be tracked by the cluster analysis methods’ representative structures. Sfold in particular can process a set of structures with only a few key base pair differences among them. Because mutagenesis experiments at this level are resource-intensive, such a fine-grained level of analysis should only be performed after iterating through coarser grained signature analysis.

Researchers can thus iterate between experimentation and computation, using one to inform the other. By employing a more nuanced use of these complementary signatures, brute force experiments can give way to faster and more informed techniques. Furthermore, ad-hoc comparisons of structures can yield to a more rigorous, multilayered approach that draws on a wealth of computational research.

Finally, given the benefits of this multilayered approach, it would be interesting to incorporate other abstractions, such as trees [62, 63, 64] or graphs [65, 66, 67, 68] into the cluster analysis of Boltzman samples. Expanding the number and granularity of tools can only strengthen the computational benefits to experimentalists.

7 Conclusion

The RNA computational community has long known the advantages of considering information in addition to the MFE prediction, investigating the use of base pairs and suboptimal structures to improve accuracy. Yet, the single MFE prediction paradigm still dominates among experimentalists, although increasing biological evidence indicates that multiple secondary structures have functional significance in nature. The purpose of this paper has been to convince the reader that this gap can and should be bridged.

First, the gap should be bridged because cluster analysis of Boltzmann samples outperforms MFE predictions, even at sequence lengths where thermodynamic optimization is the most accurate. To begin, picking the representative structure associated with the highest frequency cluster from any Boltzmann sampling method is more accurate on average than the MFE. Moreover, whenever additional information (experimental, computational or otherwise) is available to discriminate between potential alternatives, multiple structures should be considered, since an even more accurate structure can almost always be found. Furthermore, the more accurate structures are likely to be the higher frequency ones, so low frequency structures need be considered only when resources allow. This, in conjunction with the relatively small numbers of clusters, typically a dozen or less, ensure that only a handful of additional structures need to be processed to improve accuracy.

Second, the gap should be bridged because the cluster analysis methods offer a more powerful function than mere structure prediction. Namely, these methods also represent clusters with abstract signatures. The signatures’ different granularities provide alternative ways to view and compare structures that confer better accuracy and precision. These improved results imply that signatures help reduce systematic errors (potentially present in the thermodynamic model) and random ones introduced by stochastic sampling.

Signatures also provide complementary ways of mining the important structural information of a Boltzmann sample. These include the trends and motifs in the sample concerning branching, helical and base pair patterns. The appropriate level of cluster analysis depends on the level of information known or desired concerning a structure, i.e. very broad or general hypotheses are well suited for RNAshapes analysis and testing, more specific regional ones for profiling, and very specific base pair ones for Sfold.

The different granularity levels also indicate the viability of iterating back and forth between computation and experimentation. Computation helps guide experimentation, which generates more fine-grained hypotheses to be verified by higher granularity methods, and so forth. Because lower granularity signatures are in general more accurate, employing this graduated approach to analysis should funnel researchers toward more accurate results than leaping straight to the base pair resolution of an MFE structure.

As shown, cluster analysis methods have much to offer the experimental community, from a superior single structure prediction strategy to a more sophisticated one of iterating between computation and experimentation. These methods reflect the wealth of research relevant to real world problems developed in the last decades to turn RNA structural data into actionable information. Their adoption by the experimental RNA community will only improve current analysis and speed up the rate of important discovery and applications.

Figure 7.

Median number of groups for each RNA family. RNAHeliCes always by design returns three groups, and is included here for reference.

Figure 8.

Median run time of Sfold, profiling, RNAshapes and RNAHelices.

Table 1.

Information for the ten test families, each having ten test sequences. MFE accuracies are calculated with F-measures using the GTmfe package of GTfold and the native structure from the Rfam consensus alignment. The median score is reported in the table. Sequence length reflect average family length as reported by Rfam, which were used in selecting the ten families.

ID	Description	Length	MFE acc.
UnaL2	UnaL2 LINE 3′ element	54.1	0.59
tRNA	transfer RNA	73.4	0.51
Intron group II	Group II catalytic intron	87.2	0.56
THF	THF riboswitch	99.6	0.51
TPP	TPP riboswitch	111.6	0.5
5S	5S ribosomal RNA	116.6	0.53
U5	U5 spliceosomal RNA	117.2	0.52
FMN	FMN riboswitch	136.6	0.52
U1	U1 spliceosomal RNA	162	0.53
U2	U2 spliceosomal RNA	190	0.57