Co-expression network-based analysis of hippocampal expression data associated with Alzheimer's disease using a novel algorithm

Abstract

Recent progress in bioinformatics has facilitated the clarification of biological processes associated with complex diseases. Numerous methods of co-expression analysis have been proposed for use in the study of pairwise relationships among genes. In the present study, a combined network based on gene pairs was constructed following the conversion and combination of gene pair score values using a novel algorithm across multiple approaches. Three hippocampal expression profiles of patients with Alzheimer's disease (AD) and normal controls were extracted from the ArrayExpress database, and a total of 144 differentially expressed (DE) genes across multiple studies were identified by a rank product (RP) method. Five groups of co-expression gene pairs and five networks were identified and constructed using four existing methods [weighted gene co-expression network analysis (WGCNA), empirical Bayesian (EB), differentially co-expressed genes and links (DCGL), search tool for the retrieval of interacting genes/proteins database (STRING)] and a novel rank-based algorithm with combined score, respectively. Topological analysis indicated that the co-expression network constructed by the WGCNA method had the tendency to exhibit small-world characteristics, and the combined co-expression network was confirmed to be a scale-free network. Functional analysis of the co-expression gene pairs was conducted by Kyoto Encyclopedia of Genes and Genomes (KEGG) pathway enrichment analysis. The co-expression gene pairs were mostly enriched in five pathways, namely proteasome, oxidative phosphorylation, Parkinson's disease, Huntington's disease and AD. This study provides a new perspective to co-expression analysis. Since different methods of analysis often present varying abilities, the novel combination algorithm may provide a more credible and robust outcome, and could be used to complement to traditional co-expression analysis.

Introduction

Generally, complex diseases result from a combination of genetic perturbations and their interactions (1). During the past few decades, a considerable number of gene biomarkers have been successfully identified to be associated with complex diseases through genome-wide analysis of gene expression profiles (2,3). However, biomolecules in living organisms rarely act individually but interact to achieve biological functions (4). Network-based approaches have been developed as powerful and informative tools to identify candidate biomarkers or therapeutic targets based on transcript data (5–7). These methods generally utilize the knowledge of physical or functional interactions between molecules, and have been successfully applied in various diseases, such as cancer.

Various types of intermolecular interactions have been disclosed, including protein-protein interactions, protein phosphorylation networks, DNA methylation networks and gene co-expression. These interactions can be represented as networks with nodes that denote molecules, and edges that denote interactions between them. Genes in the same pathways or functional complex often exhibit similar expression patterns across multiple experiments and various organisms (8). Thus, the creation of a co-expression network from high-throughput data has become a popular alternative to the conventional methods of analysis, as it allows researchers to study the whole spectrum of pairwise associations of genes (9). By constructing a co-expression network, the regulatory relationships underlying different conditions can be estimated (10).

Co-expression networks can have small-world (11) and scale-free properties (12). A scale-free network is a network in which the node degree distribution follows a power law, and is characterized by a small number of highly connected nodes, the majority of which interact with only a few neighbors, and a high robustness to withstand random failure. A small-world network is considered to be efficient, in that it enables the rapid integration of information (13). It has two independent structural features, comprising a low average shortest path length and a high clustering coefficient.

With the development of bioinformatics analysis, a variety of algorithms have been developed to evaluate these biological networks (14,15), both in terms of experimental measurements and computational prediction techniques. Correlation-based methods are perceived as being the most straightforward for exploration of gene co-expression networks (15). Weighted gene co-expression network analysis (WGCNA), as a statistical approach based on correlations, has been widely used to analyze transcriptional profiles, and has been demonstrated to be an informative approach for the functional annotation of uncharacterized genes (16). In a recent study conducted by Allen et al (15), WGCNA was one of the best-performing methods for the construction of global co-expression networks. Moreover, an empirical Bayesian (EB) approach aims to identify differential co-expression by examining correlations among gene pairs (17). It effectively avoids the problem of inconsistent co-expression between different studies by producing a false discovery rate (FDR)-controlled list of differential co-expression pairs without sacrificing power. This approach is applicable within a single study and across multiple studies. Differentially Co-expressed Genes and Links (DCGL) is an R-package for the identification of differentially co-expressed genes and links from gene expression microarray data (18). It examines gene expression correlation using exact co-expression changes of gene pairs between two conditions, and thus can differentiate significant co-expression changes from relatively trivial ones (19). In addition, the database Search Tool for the Retrieval of Interacting Genes/Proteins (STRING) provides a comprehensive, quality-controlled collection of protein-protein associations for a large number of organisms (20). It integrates and ranks associations derived from high-throughput experimental data, database and literature mining, and predictions based on genomic context analysis, respectively. STRING has an integrated scoring scheme for the interactions, and provides a high level of confidence.

The aforementioned co-expression-based methods have been used in a number of studies and have shown their usefulness in the interpretation of biological results and identification of important gene modules (17,21,22). Each method has certain advantages. However, different approaches often produce different co-expression data for the same experiment (15). Thus, in the present study, a novel algorithm was applied to combine four existing methods to identify co-expression gene pairs and networks. Topological features, including clustering coefficient, average shortest path length and degree distribution were investigated and compared to evaluate whether each network tended to be a scale-free or small-world network. The study initially focused on identifying differentially expressed (DE) genes between Alzheimer's disease (AD) patients and normal controls on the basis of hippocampal transcript profiles. To compare the approaches, the related scores of gene pairs were obtained using the STRING database, DCGL package, EB analysis and WGCNA algorithm, respectively. Considering the non-uniform outcomes from different approaches, all scores from the four methods were converted and united using a rank-based model and a combined score of each gene pairs was obtained. Then, gene co-expression networks obtained from the four approaches respectively and a combined network were constructed, and topological properties were further analyzed. The aim was to provide a novel tool for the analysis of gene interactions with a higher credibility and rapid transmission of information, concentrating on the scores of each gene pair across multiple approaches.

Materials and methods

Data recruitment and preprocessing

In the present study, three hippocampal transcript profiles of AD patients and normal controls deposited in ArrayExpress (http://www.ebi.ac.uk/arrayexpress/) were examined: E-GEOD-1297 (23), E-GEOD-28146 (24), and E-GEOD-5281 (3,25). These datasets contained data for 54 patients with AD and 30 normal controls. The characteristics of the studies are shown in Table I.

Table I.

Characteristics of the individual datasets included in this study.

Accession number	Year	Sample size (cases/controls)	Platform
E-GEOD-1297	2004	31 (22/9)	Affymetrix HG-U133A
E-GEOD-28146	2011	30 (22/8)	Affymetrix HG-U133Plus2
E-GEOD-5281	2007	23 (10/13)	Affymetrix HG-U133Plus2

Prior to analysis, the original expression information from all conditions was subjected to data preprocessing. For each dataset, in order to eliminate the influence of nonspecific hybridization, background correction and normalization were carried out by the robust multichip average (RMA) method (26) and quantile-based algorithm (27), respectively. Perfect match and mismatch values were revised using the Micro Array Suite 5.0 algorithm (28), the value of which was selected via the median method. The gene expression values of all data were transformed to a comparable level. The data were then screened using the feature filter method of the genefilter package (version 1.52.0; bioconductor.org/packages/genefilter). Each probe is mapped to one gene, where the probe is discarded if it does not match any genes.

Detection of DE genes

Since the three sets of AD data had different origins, a rank product (RP) algorithm was implemented to integrate the array datasets (RankProd; Version 2.42.0; bioconductor.org/packages/RankProd/). This method can determine how significant changes are and how many of the selected genes are likely to be truly differentially expressed. It also allows for the flexible control of the FDR and family-wise error rate in the multiple testing situation of a microarray experiment (29). Considering a situation of the microarray experiment with two replicates (A and B), RP for a certain gene g will be as follows:

$$R{P}_g=\left(\mathit{\text{ran}}{k}_g^{\mathit{\text{replicateA}}}{/}_n\right)\text{x}\left(\mathit{\text{ran}}{k}_g^{\mathit{\text{replicateB}}}{/}_n\right)$$

where rank is the position of gene g in the list of genes in the replicate A. RPg can be taken as a P-value when all ranks are equally likely, but cannot be used directly to assess the significance of an observed change in. Therefore, a simple permutation-based estimation procedure is used to determine how likely it is to observe a given RP value or better in a random experiment, thus converting the RP value to an E value (30). Subsequently, for each gene g, a conservative estimate of the percentage of false-positive (pfp) is calculated if this gene is considered as significantly differentially expressed:

$$q_g{=}^{E(\mathit{\text{RPg}})}{/}_{\mathit{\text{rank}}(g)}$$

Rank (g) denotes the position of gene g in a list of all genes sorted by increasing RP value. This method can decide how large a pfp will be accepted and extend the list of accepted genes up to the gene with this q_g value. In the present study, a pfp cut-off value of <0.01 was used.

Construction of gene co-expression network for DE genes

Scoring of gene co-expression using STRING database

Gene and protein interactions have been annotated at various levels of detail ranging from raw data repositories to highly formalized pathway databases in online resources. In the present study, the possible functional associations of DE genes were investigated using STRING (http://string-db.org/), which provides a comprehensive, quality-controlled collection of protein-protein associations for a large number of organisms with a global perspective (31). In the STRING database, most of the available information on genes (proteins) can be aggregated, scored and weighted with known and predicted associations. A scored association between two proteins could be transferred between organisms. Following assignment of association scores and transfer between species, a final combined score between any pair of proteins was computed, which increased confidence with a higher score than the individual sub-scores. The combined score took into account the prediction and known scores obtained from each protein interaction. Subsequently, a graphical protein-protein network was constructed and the topological features of the network were further analyzed.

Identifying differential co-expression by DCGL

Biological functions result from numerous gene products acting together, and highly co-expressed genes take part in similar biological processes and pathways. The DCGL 2.0 package was applied to identify differentially co-expressed (DC) genes and links. DCGL (version 2.0; lifecenter.sgst.cn/main/en/dcgl.jsp) is a R Package for revealing differential regulation from differential co-expression. It contains four modules: Gene filtration, link filtration, differential co-expression analysis (DCEA) and differential regulation analysis (DRA) modules. Differential co-expression profile (DCp) and differential co-expression enrichment (DCe) are involved in the DCEA module for extracting DC genes and DC links. DCp operated on the filtered set of gene co-expression value pairs, where each pair comprised two co-expression values determined under two different conditions separately. The subset of co-expression value pairs associated with a particular gene, in two groups for the two conditions separately, was written as vectors X and Y (n is number of co-expression neighbors).

$$X=(x_{i1},x_{i2},\dots ,x_{\mathit{\text{in}}})$$

$$Y=(y_{i1},y_{i2},\dots ,y_{\mathit{\text{in}}})$$

A length-normalized Euclidean distance was used to measure the differential co-expression (dC) of this gene.

$$d_{C_n}(i)=\sqrt{\frac{{(x_{i1}–y_{i1})}^2+{(x_{i2}–y_{i2})}^2+\cdot \cdot \cdot +{(x_{\mathit{\text{in}}}–y_{\mathit{\text{in}}})}^2}{n}}$$

A permutation test was performed to assess the significance of dC. In this test, the disease samples and normal controls were randomly permuted, new Pearson correlation co-efficient (PCC) was calculated, gene pairs were filtered based on the new PCC, and new dC statistics were calculated. The sample permutation was repeated N times, and a large number of permutation dC statistics formed an empirical null distribution. The P-value for each gene could then be estimated.

DCe was also used to identify DC genes and DC links, which based on the ‘Limit Fold Change’ (LFC) model. First, correlation pairs were divided into three sets according to the pairing of signs of co-expression values and the multitude of co-expression values: Pairs with same signs (N1), pairs with different signs (N2) and pairs with differently-signed high co-expression values (N3). The first two sets were processed with the ‘LFC’ model separately to produce two subsets of DC links (K1, K2), while the third set (N3) was added to the set of DC links directly. Therefore, K = N3 + K1 + K2 DC links were determined from N gene links. For a gene (g_i), the total number of links (n_i) and DC links in particular (k_i) associated with it were counted. Binomial probability model was used to estimate the significance of the gene being a DC gene.

$$p(g_i)=\sum _{x=k_i}^{n_i}{C}_{n_i}^x{\left(\frac{K}{N}\right)}^x{\left(1–\frac{K}{N}\right)}^{n_i–x}$$

Differentially co-expression summarization (DCsum) was implemented to combine the results from the DCp and DCe methods.

Identification of differential co-expression by EB

Several approaches have been developed for differential regulation analysis by the identification of DC gene pairs. However, these methods are frequently underpowered, prone to false discoveries or computationally intractable under the conditions of large cardinality of the space to be interrogated and influential outliers (32). To address this limitation, Dawson and Kendziorski (17) presented an effective EB approach that provided a FDR controlled list of notable pairs along with pair-specific posterior probabilities to identify DC gene pairs without sacrificing power; the EB approach is suitable for use within and across experiments, has exhibited improved runtimes and may be a useful complement to existing DE methods by simulations and case studies respectively. In the present study, the identification of DC gene pairs was conducted using the following steps: Three inputs of matrix X, the conditions array and the pattern object were required. The expression values in an m-by-n matrix of X (where m is the number of genes/probes under consideration, and n is the total number of microarrays over all conditions) were normalized with background normalization and median correction and were represented on the log2 scale. The members of the conditions array with length n took values 1-K (where K indicated the total number of conditions). It was used to define the equal co-expression/differential co-expression classes with an ebarraysPatterns object based on the unique values in the conditions array. Intra-group correlations for all p=m*(m-1)/2 gene pairs from X and the conditions array were calculated using bi-weight mid-correlation. A p-by-K of D matrix with correlations was obtained. The mclust algorithm (33) was used to initialize the hyper-parameters to find the component normal mixture model that could best fit the empirical distribution of correlations. The values of the component in the normal mixture model with component means, standard deviations and weights would be used to initialize the Expectation-maximization (EM) algorithm. In this step, the initial estimates of the hyper-parameters were used to generate posterior probabilities of differential co-expression. Finally, a soft threshold was provided by controlling the posterior probabilities of differential co-expression to identify particular types of DC gene pairs. DC genes were distinguished from gene pairs having invariant expression by controlling the posterior expected FDR at 0.05 and a co-expression network was constructed to represent the correlation between each pair of genes.

Identifying differential co-expression by WGCNA

Gene co-expression networks, which represent a major application of correlation network methodology, are instrumental for describing the pairwise relationships among gene transcripts (34,35) and facilitate the understanding of their function and identification of their key players. In the present study, WGCNA (36), a systems biology method for performing a correlation network analysis of large and high-dimensional data sets, was used to describe correlation patterns among gene expression profiles. Also, co-expression network construction as a function in the WGCNA package was demonstrated. Genes were denoted as nodes of a gene co-expression network which were labeled by indices i, j=1,2,……n, and correlations between gene pairs were presented as edges. The network can be illustrated with its adjacency matrix A, a symmetric n × n matrix with entries a_ij in (0,1) which encodes the strength of the network link between genes i and j. An intermediate quantity of co-expression similarity is first defined to calculate the adjacency A of an unsigned network (value between 0 and 1), in which positive and negative correlations are treated equally. However, the use of an absolute value for the correlation may obscure biologically relevant information of the distinction between gene activation and repression. A signed co-expression measure between x_i and x_j is used to preserve the sign of the correlation, which is defined with a simple transformation of the correlation:

$$S_{\mathit{\text{ij}}}=\frac{1+\mathit{\text{cor}}(x_i,x_j)}{2}$$

The difference between signed and unsigned similarities lies in how they treated negatively correlated genes. There will be a high similarity in an unsigned network of genes with a high negative correlation compared with a low similarity in a signed network (37).

Then, A=[a_ij] is defined using a thresholding procedure of the co-expression similarity. For an unweighted network, the adjacency is defined to be 1 (a_ij=1) and 0 otherwise if the absolute correlation between expression profiles is above a pre-defined threshold τ and deemed separated otherwise, as described in the following formula:

$$a_{\mathit{\text{ij}}}=\mathit{\text{signum}}(s_{\mathit{\text{ij}}},\tau )=\{\begin{array}{ll}1\hfill & \mathit{\text{if}}\hspace{0.17em}{S}_{\mathit{\text{ij}}}\ge \tau \hfill \\ 0\hfill & \mathit{\text{otherwise}}\hfill \end{array}$$

The hard thresholding of unweighted networks may lose the continuous nature of the underlying co-expression information (36). By contrast, a weighted network adjacency can be defined by raising the co-expression similarity s_ij to a power β≥1, which is referred to as soft thresholding. It can allow the adjacency to take on values in succession between 0 and 1 to preserve the continuous nature of the co-expression information. The continuous measure for the assessment of gene connection strength is as follows:

$$a_{\mathit{\text{ij}}}=S_{i{j}^{\beta }}$$

This formula implies that the weighted adjacency a_ij between two genes is proportional to their similarity in the form of log (a_ij) = β × log(s_ij).

Conversion and combination of gene association scores of the four methods

Following analysis of the gene interactions using the above four methods, the score of each gene pair was obtained. Since the results differed because of the various approaches taken, all score values of gene pairs were processed further to make them uniform at the same standard and converted to the form of rank/(total number of gene pairs). A novel algorithm was implemented to convert the scores of all gene pairs in this study. Four matrices were presented in three columns comprising gene pairs and the new score of each pair. By multiplication of the four matrices, a new matrix with a combined score of each gene pair was produced and sorting was conducted using a rank-based method similar to the application used in DE gene detection. Gene pairs were obtained ultimately following the management of all scores with a q-value package of FDR<0.1. A combined gene interaction network was then constructed by linking gene pairs.

Topological analysis

Following the calculation of scores using the four existing methods and the novel algorithm, and the construction of five networks, the clustering coefficient and short average path length of each were obtained and compared to investigate whether or not the networks had the classic small-world network property. Furthermore, considering that protein/gene interaction networks in general are scale-free (38), which means that they have power-law (or scale-free) degree distributions, the fitting coefficient R² of the power-law y=ax^b of the five networks was also compared. The evaluation of topological parameters was conducted using the Network Analyzer Version 2.7 (39) plugin in Cytoscape Version 3.1.0 (40).

Functional enrichment analysis

Highly co-expressed genes generally participate in similar biological processes and pathways. To further investigate the biological functional enrichment of the co-expression gene pairs that were identified, a signaling pathway analysis was performed to assess the functional relevance of selected genes based on Kyoto Encyclopedia of Genes and Genomes (KEGG) database (www.genome.jp/kegg/), a widely used comprehensive resource for the pathway mapping of genes. DE genes identified by RP were first imported to the online tool Database for Annotation, Visualization and Integrated Discovery (DAVID; http://david.abcc.ncifcrf.gov/tools.jsp), and all pathways these genes were enriched in was obtained. Then, on the basis of the DE genes in each pathway, the number of enriched co-expression gene pairs identified by the four existing methods and the new combined approach, respectively, were calculated and compared.

Results

Integrated analysis of DE genes in multiple studies

In the present study, three sets of hippocampal expression data associated with AD were integrated to identify DE genes using the RP method. After data preprocessing of three different datasets, the number of genes in E-GEOD-1297, E-GEOD-28146 and E-GEOD-5281 were 12,493, 20,109 and 20,109, respectively. Finally, a total of 144 DE genes were detected, including 8 upregulated genes and 136 downregulated genes, under an estimated pfp<0.01.

Co-expression analysis of four existing methods

Co-expression networks of DE genes were constructed using STRING, DCGL, EB and WGCNA analysis, respectively, and the co-expression relationships between gene and gene or co-expressed gene pairs were determined.

Scoring of gene associations based on STRING

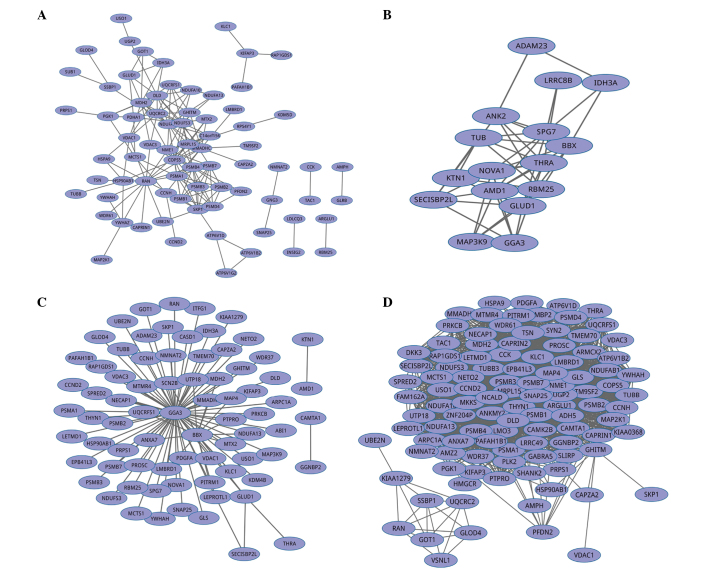
A combined score was computed using the known and predicted associations, considering that various sources of association data are benchmarked independently in the STRING database. The combined score indicates a higher confidence level when more than one type of information supports a given association. A graphical protein-protein interaction network was constructed with 74 nodes and 166 edges (Fig. 1A). Also, all scores of gene pairs were obtained in the context of inputting 144 DE genes. A clustering coefficient of 0.300 and mean shortest path of 2.925 were computed. After conducting degree distribution by nonlinear curve fitting according to the power law (y=ax^b), a fitting coefficient (R²=0.786) was produced.

Figure 1.

Graphical representation of co-expression networks identified by four existing method. Genes are denoted as nodes and interactions between gene pairs are presented as edges. (A) Search tool for the retrieval of interacting genes/proteins database, (B) differentially co-expressed genes and links, (C) empirical Bayesian and (D) weighted gene co-expression network analysis.

Construction of a gene co-expression network using DCGL

The DCGL 2.0 package in R was applied to identify DC genes and DC links, in which DCp and DCe methods involved in the DCEA module were employed. A total of 43 co-expression gene pairs were identified, and the two genes in each gene pair were DC genes. Finally, a co-expression network with 16 nodes and 43 edges was built using Cytoscape (Fig. 1B). A clustering coefficient of 0.178 and mean shortest path of 1.783 were computed. Likewise, the degrees of all nodes were determined and a fitting coefficient (R²=0.037) of their degree distribution was obtained, which indicated that this network was not a scale-free network.

Construction of a gene co-expression network using EB methods

The EB approach was used to identify DC gene pairs based on 144 DE genes. A total of 88 protein pairs with FDR≤0.05 were produced and the relational values of all pairs were yielded following the analysis of gene expression relationships using meta-analysis. A gene interaction network containing 76 nodes and 88 edges was constructed using the 88 protein pairs in this analysis (Fig. 1C). The network was binary, with all interactions being unweighted and undirected. In addition, a clustering coefficient of 0.0 and mean shortest path of 2.038 were obtained. The degrees of all proteins were determined and a fitting coefficient of R²=0.477 for their degree distribution was obtained following nonlinear regression according to the power law.

Construction of gene co-expression network using WGCNA

Using the WGCNA package, a total of 2,271 protein pairs were produced, and a co-expression network with 107 nodes and 2,271 edges was built using Cytoscape (Fig. 1D). The degrees of all nodes were determined and a fitting coefficient (R²=0.071) of their degree distribution was obtained following nonlinear regression, which also presented a non scale-free property.

Combination of all gene pairs and construction of a co-expression network

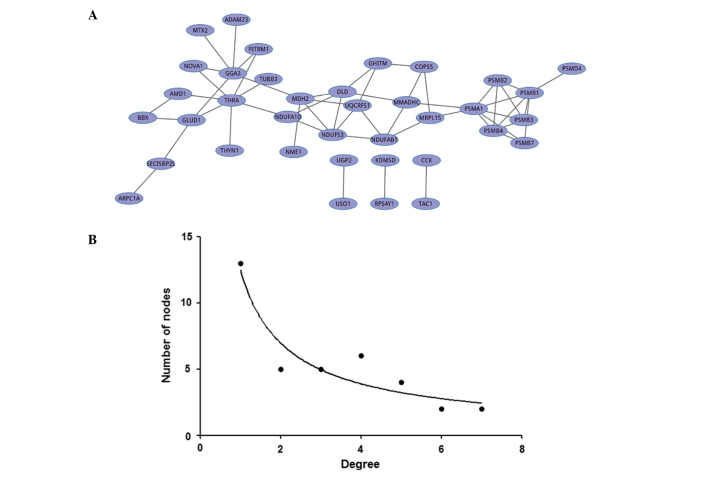
In the present study, a novel algorithm was implemented to convert the score values of all gene pairs obtained from the four existing approaches in the form of rank/(total number of gene pairs). Multiplication of the four matrices produced a new matrix containing a combined score for each gene pair, and a simple rank-based permutation procedure was conducted. Then, a combined gene co-expression network was constructed that comprised 37 nodes linked by a total of 57 connections (Fig. 2A). The distribution of the number of links per node was scale free with R²=0.881. Thus, the results conformed to a scale-free network whose degree distribution followed the power law (y=ax^b, a=12.464, b=−0.840; Fig. 2B).

Figure 2.

Combined co-expression network using the novel algorithm and its degree distribution. (A) Combined co-expression network based on the novel scores of each gene pair across four methods. A total of 37 nodes and 57 edges composed this combined network. (B) Scatter-gram of gene degree in this co-expression network. The combined co-expression network was a scale-free network whose degree distribution followed a power law (y=ax^b, where a=12.464, b=−0.840, R²=0.881).

Topological analysis of the five networks

Topological parameters of the five networks were compared, including the clustering coefficient, mean shortest path length and the fitting coefficient R² (Table II). The results showed that the network constructed by the WGCNA method had the greatest tendency to display small-world characteristics, as it had the smallest mean shortest path length and the largest clustering coefficient. However, the combined network showed a higher fitting coefficient R² than the other four networks, indicating its scale-free property.

Table II.

Topological parameters of co-expression networks constructed using four existing approaches and the new algorithm.

Measure	STRING	DCGL	EB	WGCNA	Combined
R2	0.786	0.037	0.477	0.071	0.810
Clustering coefficient	0.300	0.178	0.0	0.820	0.172
Mean shortest path length	2.925	1.783	2.038	1.578	3.618

STRING, search tool for the retrieval of interacting genes/proteins database; DCGL, differentially expressed genes and links; EB, empirical Bayesian; WGCNA, weighted gene co-expression network analysis.

Functional enrichment analysis

Firstly, all pathways that DE genes enriched were identified as background. To investigate the biological functional enrichment of the co-expression gene pairs identified by the different methods, the number of gene pairs enriched in each pathway was calculated and compared. The top five pathways were shown in Fig. 3. Co-expression gene pairs obtained using the EB and DCGL methods could not be enriched in any of the pathways that were identified, while co-expression gene pairs identified by STRING, WGCNA and the novel method were enriched in similar pathways. Following combination of the four existing methods, the co-expression gene pairs were found to be mostly enriched in proteasome, oxidative phosphorylation, Parkinson's disease, Huntington's disease, and AD pathways.

Figure 3.

Five most enriched pathways of co-expression gene pairs identified by four existing methods and the novel algorithm. Co-expression gene pairs identified by EB and DCGL methods could not be enriched in any of the identified pathways. The five pathways were proteasome, oxidative phosphorylation, Parkinson's disease, Huntington's disease and Alzheimer's disease. EB, empirical Bayesian; STRING, search tool for the retrieval of interacting genes/proteins database; WGCNA, weighted gene co-expression network analysis; DCGL, differentially co-expressed genes and links.

Discussion

Co-expression network-based approaches are powerful tools for the systematic identification of molecular mechanisms underlying biological processes, and a variety of algorithms have been developed to study these biological networks. Co-expression networks present binary relationships between individual genes, and also encode obscure higher level forms of cellular communication. In the present study, a co-expression network was constructed using a list of gene pairs with combined scores across multiple approaches. Three sets of hippocampal data associated with AD were employed and a total of 144 DE genes were identified using the RP package. From these DE genes, co-expression gene pairs were extracted by STRING, DCGL, EB and WGCNA approaches respectively, and the score value of each gene pair was computed. Different approaches often give different results. To achieve a more reliable result, a novel algorithm was presented to produce a new score for each gene pair by combining the above four methods. Then, five networks were constructed, and their degree distribution and network topological properties (clustering coefficient and mean shortest path length) were compared.

Previous studies have analyzed the topological properties of gene co-expression networks, and have indicated that co-expression networks have small-world and scale-free properties (41,42). Such properties are typical of biological networks in which the nodes are connected when they are involved in the same biological process. Featherstone and Broadie (43) demonstrated that the uneven distribution of gene degrees in a network, that is, a scale-free organization, helped organisms to resist the deleterious effects of mutation. A similar architecture was also found in the gene co-expression network of gastric cancer, which exhibited a hierarchical scale-free architecture (44). Furthermore, previous studies have confirmed the small-world property of biological networks with multiple data sources (45,46). However, a study conducted by Arita (47) indicated that the mean shortest path length of the biological network of Escherichia coli was much longer than previously thought, and the topology of this organism was not small. In the present study, co-expression networks for AD were built using four existing approaches and a novel algorithm, respectively. The results showed that the co-expression network constructed using the WGCNA method exhibited greater small-world network properties than the other four networks did, as it had the smallest mean shortest path length and the largest clustering coefficient. When analyzing the degree distributions of these co-expression networks, the combined gene interaction networks whose node degree distributions followed a power law with a high fitting coefficient clearly exhibited scale-free network characteristics.

Gene interactions are considered to be highly effective for use in the determination of gene functions and the identification of groups of genes that encode proteins in the same pathway. Previous studies have investigated the pathway enrichments associated with AD. Karim et al (48) demonstrated using an Ingenuity Pathway Analysis tool that synapse-associated pathways in neurons were tightly associated with the development and progression of AD. A more recent study highlighted cell adhesion molecules and purine metabolism pathways in AD by integrating genome-wide association study and brain expression data (49). In the present study, the co-expression gene pairs identified by the novel algorithm were mostly enriched in proteasome, oxidative phosphorylation, Parkinson's disease, Huntington's disease and AD. Consistent with this, Zabel et al (50) confirmed that proteasome and oxidative phosphorylation changes were closely associated with neurodegenerative disorders, such as AD, Parkinson's disease and Huntington's disease. Furthermore, in the present study, it was found that co-expression gene pairs identified by the EB and DCGL methods could not be enriched in any pathways that were identified, which was in contrast to the STRING and WGCNA analysis, and the novel method of the present study. Different methods for conducting co-expression network-based analysis often present varying abilities; thus, careful consideration is required when selecting synthetic methods, dependent on the nature of the research being undertaken.

In this study, a novel merged approach was used to identify co-expression gene pairs and enriched pathways, and this approach was compared with various network construction methods. Network analysis showed that the co-expression network constructed by the WGCNA method was most inclined to exhibit small-world properties, and the combined co-expression network exhibited scale-free network features. Moreover, the co-expression gene pairs were mostly enriched in proteasome, oxidative phosphorylation, Parkinson's disease, Huntington's disease and AD pathways. Each method of analysis has certain advantages and disadvantages. Considering the applications and limitations of each co-expression method, the novel algorithm developed in the present study may provide a new method for the analysis of gene interactions with a greater credibility and strength.