Multiobjective Optimization for Model Selection in Kernel Methods in Regression

Abstract

Regression plays a major role in many scientific and engineering problems. The goal of regression is to learn the unknown underlying function from a set of sample vectors with known outcomes. In recent years, kernel methods in regression have facilitated the estimation of nonlinear functions. However, two major (interconnected) problems remain open. The first problem is given by the bias-vs-variance trade-off. If the model used to estimate the underlying function is too flexible (i.e., high model complexity), the variance will be very large. If the model is fixed (i.e., low complexity), the bias will be large. The second problem is to define an approach for selecting the appropriate parameters of the kernel function. To address these two problems, this paper derives a new smoothing kernel criterion, which measures the roughness of the estimated function as a measure of model complexity. Then, we use multiobjective optimization to derive a criterion for selecting the parameters of that kernel. The goal of this criterion is to find a trade-off between the bias and the variance of the learned function. That is, the goal is to increase the model fit while keeping the model complexity in check. We provide extensive experimental evaluations using a variety of problems in machine learning, pattern recognition and computer vision. The results demonstrate that the proposed approach yields smaller estimation errors as compared to methods in the state of the art.

I. Introduction

Regression analysis has been a very active topic in machine learning and pattern recognition, with applications in many problems in science and engineering. In a standard regression problem, a linear or nonlinear model is estimated from the data such that the functional relationship between the dependent variables and the independent variables can be established. Of late, regression with kernel methods [39, 33] has become popular. The success of the kernel methods in regression comes from the fact that they facilitate the estimation of nonlinear function using well-defined and - tested approaches in, for example, computer vision [40], signal processing [38, 7], and bioinformatics [28].

The underlying idea in kernel methods is to map the data samples from an original space to a space of (intrinsically) much higher (or infinite) dimensionality. We refer to the resulting space as the kernel space. The goal is to find a mapping that converts the original nonlinear problem (defined in the original space) into a linear one (in the kernel space) [32]. In practise, this mapping is done using a pre-determined nonlinear function. Given this function, the main challenge is to fine those parameters of the function that convert a nonlinear problem into a linear one. Thus, the selection of these kernel parameters is a type of model selection. This is the problem we consider in this paper – to define a criterion for the selection of the appropriate parameters of this kernel function.

The selection of the appropriate parameters of a kernel is a challenging one [47]. If the parameters were chosen to minimize the model fit, we would generally have an over-fitting to the training data. As a consequence, the regressed function would not be able to estimate the testing data correctly. A classical solution is to find a good fit, while keeping the complexity of the function low, e.g., using a polynomial of lower order [16]. However, if the parameters are selected to keep the complexity too low, then we will under-fit the data. In both these cases, the regressed function will have a poor generalization, i.e., a high prediction error to the testing data. In general, the kernel parameters should be selected to achieve an appropriate trade-off between the model fit and model complexity.

To date, the most widely employed technique to do this selection of the kernel parameters is k-fold cross-validation (or CV, for short) [16]. In this approach, the performance of the prediction models is evaluated by setting aside a validation set within the training set. The model which produces the smallest validation error is selected. Unfortunately, this method has three known major drawbacks. First, it is computational expensive. Second, only part of the training data is used to estimate the model parameters. When doing model selection, one wants to employ the largest possible number of training samples, since this is known to yield better generalizations [24]. Third, the value of k as a parameter plays a major role in the process. Note that the value of k affects the trade-off between the fitting error and the model complexity, yet general methods for selecting an appropriate value do not exist.

An alternative to CV is Generalized CV (GCV) [39], an approach originally defined to select the ridge parameter in ridge regression. GCV can be directly extended to do model selection in regression with kernel approaches, as long as the hat matrix [39], which projects the original response vector to the estimated one, can be obtained. However, since this criterion is an approximation of the leave-one-out CV (i.e., n-fold CV, n is the number of training samples), the estimated result generally has a large variance and small bias, i.e., the regressed function is highly variant and dependent of the training data.

Another alternative is to minimize the structural risk [37], which is a function of the model fit and the Vapnik-Chervonenkis (VC) dimension of the regressed function. Unfortunately, the VC dimension is infinite in regularized Kernel regression approaches with an induced infinite dimensional space (e.g, Radial Basis Function), limiting the applicability of such approaches [11, 12].

While a single kernel may not be sufficient to describe the data, Multiple Kernel Learning (MKL) [21, 34] has attracted much attention recently as a potential alternative. In [28], MKL is applied to Support Vector Regression (SVR). The coefficients that determine the combination of kernels are learned using a constrained quadratic programming problem. This method was shown to outperform CV in some applications. Unfortunately, the selection of its parameters is generally problem specific [6, 46, 28], and while the general problem remains unsolved, this is an active area of research. In yet another approach, the kernel parameters are selected by maximizing the marginal data likelihood after reformulating the regression problem as probabilistic models using Bayesian inference. This approach has been used to define the well-known Relevance Vector Machine (RVM) [36] and Gaussian processes for regression [45]. It has been shown [30] that the marginal likelihood has the nice property of automatically incorporating a trade-off between model fit and model complexity. However, since the Bayesian learning generally leads to analytically intractable posteriors, approximations are necessary, and, the results are generally computationally very expensive. Furthermore, the determination of the priors for the parameters is an intrinsic problem in Bayesian learning with no clear solution.

In this paper, we resolve the kernel optimization problem using a completely novel approach. In our proposed approach, the two measures of model fitness and model complexity are simultaneously minimized using a multiobjective optimization (MOP) framework through the study of Pareto-optimal solutions. MOP and Pareto-optimality are specifically defined to find the global minima of several combined criteria. To this end, we will first derive a new criterion for model complexity which can be employed in kernel methods in regression. We then define a method using MOP and derive a new approach called modified ε-constraint. We show that this newly derived approach achieves the lowest mean square error. We provide extensive comparisons with the state of the art in kernel methods for regression and on approaches for model selection. The results show that the proposed framework leads to better generalizations for the (unseen) testing samples.

The remainder of this paper is organized as follows. In Section II we derive the two new measures of model fitness and model complexity. Then, in Section III, we derive a new MOP approach to do model selection. In Section IV, the proposed framework is applied to two typical kernel methods in regression. Experimental results are provided in Section V. We conclude in Section VI.

II. Regression Models

We start with an analysis of the generalization error of a regression model. Given a training set ${\left\{({\mathbf{x}}_i,{\mathbf{y}}_i)\right\}}_{i=1}^n$, where ${\mathbf{x}}_i\in {\mathbb{R}}^p$, ${\mathbf{y}}_i\in {\mathbb{R}}^q$, with the training samples (x_i, y_i), i = 1, ..., n generated from a joint distribution g(x, y), one wants to find the regression model f(x) that minimizes the generalization error

$$E=\int L(\mathbf{y},\mathbf{f}\left(\mathbf{x}\right))g(\mathbf{x},\mathbf{y})d\mathbf{x}d\mathbf{y},$$ (1)

where f(x) is the regression function, $\mathbf{f}\left(\mathbf{x}\right)={(f_1\left(\mathbf{x}\right),\dots ,f_q\left(\mathbf{x}\right))}^T,f_i(.):{\mathbb{R}}^p\to \mathbb{R}$ is the i^th regression function, and L(y, f(x)) is a given loss function, for instance, the quadratic loss $L(\mathbf{y},\mathbf{f}\left(\mathbf{x}\right))=\frac{1}{2}{\Vert \mathbf{y}-\mathbf{f}\left(\mathbf{x}\right)\Vert }_2^2=\frac{1}{2}{\sum }_{i=1}^q{(y_i-f_i\left(\mathbf{x}\right))}^2$.

A. Generalization error

Holmstrom and Koistinen [18] show that by adding noise to the training samples (both x and y), the estimation of the generalization error is asymptotically consistent, i.e., as the number of training examples approaches infinity, the estimated generalization error is equivalent to the true one. The addition of noise can be interpreted as generating additional training samples. This means that we can estimate the generalization error by adding the noise to the training samples.

For convenience, denote the training set that consists of n pairs of observation vectors and prediction vectors by ${\mathbf{z}}_i=({\mathbf{x}}_i,{\mathbf{y}}_i),i=1,\dots ,n,{\mathbf{z}}_i\in {\mathbb{R}}^m,m=p+q$. Then the generalization error can be rewritten as

$$E=\int L\left(\mathbf{z}\right)g\left(\mathbf{z}\right)d\mathbf{z}.$$ (2)

Assume that the training samples z_i are corrupted by the noise ξ. Suppose the distribution of ξ is ψ(ξ). The noise distribution is generally chosen to have zero mean and to be uncorrelated, i.e.,

$$\int {\xi }_i\psi \left(\xi \right)d\xi =0,$$ (3)

$$\int {\xi }_i{\xi }_j\psi \left(\xi \right)d\xi =\nu {\delta }_{ij},$$ (4)

where ν is the variance of the noise distribution, and δ_ij is the delta function with δ_ij = 1 when i = j and δ_ij = 0 otherwise.

We consider the following steps for generating new training samples by introducing additive noise:

• 1)Select a a training sample z_i randomly from the training set.
• 2)Draw a sample noise vector ξ_i from ψ(ξ).
• 3)Set z = z_i + ξ_i.

Thus, the distribution of a particular sample z generated from the training sample z_i is given by ψ(ξ_i) = ψ(z – z_i). Then the distribution of z generated from the entire training set is

$$\widehat{g}\left(\mathbf{z}\right)=\frac{1}{n}\sum _{i=1}^n\psi (\mathbf{z}-{\mathbf{z}}_i).$$ (5)

The above result can be viewed as a kernel density estimator of the true distribution of the data g(z) [18]. The distribution of the noise ψ(.) is the kernel function used in the estimator.

Substituting (5) into (2), we have

$$\begin{array}{cc}\hfill E=& \int L\left(\mathbf{z}\right)\widehat{g}\left(\mathbf{z}\right)d\mathbf{z}\hfill \\ \hfill =& \frac{1}{n}\sum _{i=1}^n\int L\left(\mathbf{z}\right)\psi (\mathbf{z}-{\mathbf{z}}_i)d\mathbf{z}.\hfill \end{array}$$ (6)

The result shown above in (6) can also be derived from a known convolution smoothing function ψ(.) [9, 35]. This is achieved by approximating the cost function iteratively. While this provides further justification for the proposed measure, note that the difference between our derivations and those presented in [9, 35] is that we do not require to work with a known density or specific regression function.

We now reformulate (6) by approximating the loss function L(., .).

Let z – z_i = ξ_i, then (6) is reformulated as

$$E=\frac{1}{n}\sum _{i=1}^n\int L({\mathbf{z}}_i+{\xi }_i)\psi \left({\xi }_i\right)d{\xi }_i.$$ (7)

We expand L(z + ξ) as a Taylor series in powers of ξ, i.e.,

$$L(\mathbf{z}+\xi )=L\left(\mathbf{z}\right)+\sum _{i=1}^m\frac{\partial L\left(\mathbf{z}\right)}{\partial z_i}{\xi }_i+\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m\frac{{\partial }^{2}L\left(\mathbf{z}\right)}{\partial z_i\partial z_j}{\xi }_i{\xi }_j+\mathcal{O}\left({\xi }^3\right).$$ (8)

Assuming that the noise amplitude is small, the higher order term $\mathcal{O}\left({\xi }^3\right)$ can be neglected. Combining (8) with (7), (3) and (4), we obtain

$$\begin{array}{cc}\hfill E=& \frac{1}{n}\sum _{i=1}^n\left(L\left({\mathbf{z}}_i\right)+\frac{1}{2}\nu \sum _{j=1}^m\frac{{\partial }^{2}L\left({\mathbf{z}}_i\right)}{\partial z_j^2}\right)\hfill \\ \hfill =& \frac{1}{n}\sum _{i=1}^{n}L\left({\mathbf{z}}_i\right)+\frac{1}{2n}\nu \sum _{i=1}^n\sum _{j=1}^m\frac{{\partial }^{2}L\left({\mathbf{z}}_i\right)}{\partial z_j^2}.\hfill \end{array}$$ (9)

Let L(z) be the quadratic loss, i.e., $L\left(\mathbf{z}\right)=\frac{1}{2}{\sum }_{i=1}^q{(y_i-f_i\left(\mathbf{x}\right))}^2$ Then, as shown in Appendix A, we have

$$\sum _{j=1}^m\frac{{\partial }^{2}L\left({\mathbf{z}}_i\right)}{\partial z_j^2}=\sum _{k=1}^q\sum _{j=1}^p\left({\left(\frac{\partial f_k\left({\mathbf{x}}_i\right)}{\partial x_{ij}}\right)}^2+(f_k\left({\mathbf{x}}_i\right)-y_{ik})\frac{{\partial }^2{f}_k\left({\mathbf{x}}_i\right)}{\partial x_{ij}^2}\right)+q,$$ (10)

where y_ij is the j^th entry of vector y_i and x_ij is the j^th entry of vector x_i. Substituting (10) into (9), we have

$$E=E_f+\nu E_c,$$ (11)

with

$$E_f=\frac{1}{2n}\sum _{i=1}^n{\Vert {\mathbf{y}}_i-\mathbf{f}\left({\mathbf{x}}_i\right)\Vert }_2^2$$ (12)

and

$$E_c=\frac{1}{2n}\sum _{i=1}^n\sum _{k=1}^q\sum _{j=1}^p\left({\left(\frac{\partial f_k\left({\mathbf{x}}_i\right)}{\partial x_{ij}}\right)}^2+(f_k\left({\mathbf{x}}_i\right)-y_{ik})\frac{{\partial }^2{f}_k\left({\mathbf{x}}_i\right)}{\partial x_{ij}^2}+q\right).$$ (13)

Therefore, the generalization error consists of two terms. The first term E_f measures the discrepancy between the training data and the estimated model, i.e., the model fit. The second term E_c measures the roughness of the estimated function provided by the first and second derivatives of the function, i.e., the model complexity. It controls the smoothness of the function to prevent it from overfitting. The parameter ν controls the trade-off between the model fit and model complexity.

In order to minimize the generalization error E, we need to minimize both E_f and E_c. However, due to the bias and variance trade-off [16], a decrease in the model fit may result in an increase in the model complexity and vice-versa. The regularization parameter ν may achieve a balance between the model fit and complexity to some extent, however, there are two limitations for selecting ν to do model selection. First, a good ν should be chosen beforehand. A common way is to use cross-validation, but this suffers from several drawbacks as we discussed earlier. Second, note that our goal is to simultaneously minimize model fit and model complexity. An ideal solution is that we cannot further decrease one without increasing the other. This means that even when the appropriate ν is selected, minimizing E is not directly related to our goal. To solve these problems, we derive a multiobjective optimization approach in Section III. We first derive the kernel models for model fit E_f and model complexity E_c.

B. Model fit

We start by considering the standard linear regression model, f(x) = W^Tx, where W = (w₁, ..., w_q) is a p × q weight matrix, with ${\mathbf{w}}_i\in {\mathbb{R}}^p$. And, we assume all the vectors are standardized.

We can rewrite the above model as $f_i\left(\mathbf{x}\right)={\mathbf{w}}_i^T\mathbf{x},i=1,\dots ,q$. In kernel methods for regression, each sample x is mapped to ϕ(x) in a reproducing kernel Hilbert space as $\varphi (.):{\mathbb{R}}^p\to \mathcal{F}$. With this, we can write $f_i\left(\mathbf{x}\right)={\mathbf{w}}_i^{{\varphi }^T}\varphi \left(\mathbf{x}\right),i=1,\dots ,q$ . The Representer's Theorem [39] enables us to use ${\mathbf{w}}_i^{\varphi }=\Phi \left(\mathbf{X}\right){\alpha }_i$, where Φ(X) = (ϕ(x₁), ..., ϕ(x_n)) and α_i is an n × 1 coefficient vector. Putting everything together, we get

$$\begin{array}{cc}\hfill f_i\left(\mathbf{x}\right)=& {\alpha }_i^T\Phi {\left(\mathbf{X}\right)}^T\varphi \left(\mathbf{x}\right)={\alpha }_i^T\mathbf{k}\left(\mathbf{x}\right)\hfill \\ \hfill =& \sum _{j=1}^n{\alpha }_i^j\kappa \langle {\mathbf{x}}_j,\mathbf{x}\rangle ,i=1,\dots ,q,\hfill \end{array}$$ (14)

where ${\alpha }_i^j$ is the j^th element in α_i, and κ〈x_j, x〉 is a kernel function on x_j and x.

Using the results derived thus far, we can write E_f as

$$E_f=\sum _{i=1}^q{({\tilde{\mathbf{y}}}_i-\mathbf{K}{\alpha }_i)}^T({\tilde{\mathbf{y}}}_i-\mathbf{K}{\alpha }_i),$$ (15)

where K = Φ(X)^TΦ(X) is the n × n kernel matrix, ${\tilde{y}}_i={(y_{1i},\dots ,y_{ni})}^T$ is an n × 1 vector, and y_ji is the i^th entry of y_j.

C. Roughness penalty in RBF

We now derive solutions of E_c for two of the most used kernel functions, the Radial Basis Function (RBF) and the polynomial kernels.

The RBF kernel is given by $\kappa \langle {\mathbf{x}}_i,{\mathbf{x}}_j\rangle =\exp (-\frac{{\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert }^2}{2{\sigma }^2})$, where σ is the kernel parameter. Since $f_l\left(\mathbf{x}\right)={\sum }_{m=1}^n{\alpha }_l^m\kappa \langle {\mathbf{x}}_m,\mathbf{x}\rangle$, the partial derivatives are given by

$$\frac{\partial f_l\left({\mathbf{x}}_i\right)}{\partial x_{ij}}=\frac{1}{{\sigma }^2}\sum _{m=1}^n{\alpha }_l^m\exp \left(-\frac{{\Vert {\mathbf{x}}_m-{\mathbf{x}}_i\Vert }^2}{2{\sigma }^2}\right)(x_{mj}-x_{ij}).$$

Writing this result in matrix form,

$$\sum _{j=1}^p{\left(\frac{\partial f_l\left({\mathbf{x}}_i\right)}{\partial x_{ij}}\right)}^2={\alpha }_l^R{\mathbf{R}}_i{\alpha }_l,$$

where ${\mathrm{R}}_i=\frac{1}{{\sigma }^4}{\mathbf{W}}_i{\mathbf{W}}_i^T$, W_i is a n × p matrix with the j^th column equal to ${(\exp (-\frac{{\Vert {\mathbf{x}}_1-{\mathbf{x}}_i\Vert }^2}{2{\sigma }^2})(x_{1j}-x_{ij}),\dots ,\exp (-\frac{{\Vert {\mathbf{x}}_n-{\mathbf{x}}_i\Vert }^2}{2{\sigma }^2})(x_{nj}-x_{ij}))}^T$.

And, the second partial derivatives (see Appendix B-A) are given by

$$\frac{{\partial }^2{f}_l\left({\mathbf{x}}_i\right)}{\partial x_{ij}^2}={\alpha }_l^T{\mathbf{p}}_{ij},$$

where p_ij is an n × 1 vector whose m^th (m ≠ i) entry is $\frac{1}{{\sigma }^2}\exp (-\frac{{\Vert {\mathbf{x}}_m-{\mathbf{x}}_i\Vert }^2}{2{\sigma }^2})(\frac{{(x_{mj}-x_{ij})}^2}{{\sigma }^2}-1)$ and i^th entry is 0. Then ${\sum }_{j=1}^p\frac{{\partial }^2{f}_l\left({\mathbf{x}}_i\right)}{\partial x_{ij}^2}={\alpha }_l^T{\mathbf{p}}_i$ where ${\mathbf{p}}_i={\sum }_{j=1}^p{\mathbf{p}}_{ij}$. Thus,

$$\begin{array}{cc}\hfill (f_l\left({\mathbf{x}}_i\right)-y_{il})\sum _{j=1}^p\frac{{\partial }^2{f}_l\left({\mathbf{x}}_i\right)}{\partial x_{ij}^2}=& ({\alpha }_l^T{\mathbf{k}}_i-y_{il}){\alpha }_l^T{\mathbf{p}}_i\hfill \\ \hfill =& {\alpha }_l^T\left({\mathbf{k}}_i{\mathbf{p}}_i^T\right){\alpha }_l-y_{il}{\mathbf{p}}_i^T{\alpha }_l,\hfill \end{array}$$

where ${\mathbf{k}}_i={(\kappa \langle {\mathbf{x}}_1,{\mathbf{x}}_i\rangle ,\dots ,\kappa \langle {\mathbf{x}}_n,{\mathbf{x}}_i\rangle )}^T$.

Using the above results, we can define the roughness penalty function in the RBF kernel space as

$$E_c=\sum _{l=1}^q({\alpha }_l^T\mathbf{M}{\alpha }_l-{\mathbf{q}}_l^T{\alpha }_l+n),$$ (16)

where $\mathbf{M}=\frac{1}{2n}{\sum }_{i=1}^n({\mathbf{R}}_i+{\mathbf{k}}_i{\mathbf{p}}_i^T)$, and ${\mathbf{q}}_l=\frac{1}{2n}{\sum }_{i=1}^n{y}_{il}{\mathbf{p}}_i$.

D. Polynomial kernel

A polynomial kernel of degree d is given by $\kappa \langle {\mathbf{x}}_i,{\mathbf{x}}_j\rangle ={({\mathbf{x}}_i^T{\mathbf{x}}_j+1)}^d$. Its partial derivatives are,

$$\frac{\partial f_l\left({\mathbf{x}}_i\right)}{\partial x_{ij}}=\sum _{m=1,m\ne i}^n{\alpha }_l^{m}d{({\mathbf{x}}_m^T{\mathbf{x}}_i+1)}^{d-1}{x}_{mj}+2{\alpha }_l^{i}d{({\mathbf{x}}_i^T{\mathbf{x}}_i+1)}^{d-1}{x}_{ij}.$$

We can write the above result in matrix form as

$$\sum _{j=1}^p{\left(\frac{\partial f_l\left({\mathbf{x}}_i\right)}{\partial x_{ij}}\right)}^2={\alpha }_l^T{\mathbf{B}}_i{\alpha }_l,$$

where ${\mathbf{B}}_i=d{\mathbf{C}}_i{\mathbf{C}}_i^T$, C_i is a n × p matrix with j^th column equal to ${({({\mathbf{x}}_1^T{\mathbf{x}}_i+1)}^{d-1}{x}_{1j},\dots ,2{({\mathbf{x}}_i^T{\mathbf{x}}_i+1)}^{d-1}{x}_{ij},\dots ,{({\mathbf{x}}_n^T{\mathbf{x}}_i+1)}^{d-1}{x}_{nj})}^T$.

The second partial derivatives (see Appendix B-B) are

$$\frac{{\partial }^2{f}_l\left({\mathbf{x}}_i\right)}{\partial x_{ij}^2}={\alpha }_l^T{\mathbf{g}}_{ij},$$

where g_ij is a n × 1 vector whose m^th (m ≠ i) entry is $d(d-1)({\mathbf{x}}_m^T{\mathbf{x}}_i+1)(d-2)x_{mj}^2$ and the i^th entry is $d{({\mathbf{x}}_m^T{\mathbf{x}}_i+1)}^{d-2}(3(d-1)x_{ij}^2+2({\mathbf{x}}_i^T{\mathbf{x}}_i+1))$. Then, ${\sum }_{j=1}^p\frac{{\partial }^2{f}_l\left({\mathbf{x}}_i\right)}{\partial x_{ij}^2}={\alpha }_l^T{\mathbf{g}}_i$, where ${\mathbf{g}}_i={\sum }_{j=1}^p{\mathbf{g}}_{ij}$.

Thus,

$$\begin{array}{cc}\hfill (f_l\left({\mathbf{x}}_i\right)-y_{il})\sum _{j=1}^p\frac{{\partial }^2{f}_l\left({\mathbf{x}}_i\right)}{\partial x_{ij}^2}=& ({\alpha }_l^T{\mathbf{k}}_i-y_{il}){\alpha }_l^T{\mathbf{g}}_i\hfill \\ \hfill =& {\alpha }_l^T\left({\mathbf{k}}_i{\mathbf{g}}_i^T\right){\alpha }_l-y_{il}{\mathbf{g}}_i^T{\alpha }_l,\hfill \end{array}$$

Using the derivations above, the roughness function for the polynomial kernel can be written as

$$E_c=\sum _{l=1}^q({\alpha }_l^T\mathbf{N}{\alpha }_l-{\mathbf{u}}_l^T{\alpha }_l+n),$$ (17)

where $\mathbf{N}=\frac{1}{2n}{\sum }_{i=1}^n({\mathbf{B}}_i+{\mathbf{k}}_i{\mathbf{g}}_i^T)$, and ${\mathbf{u}}_l=\frac{1}{2n}{\sum }_{i=1}^n{y}_{il}{\mathbf{g}}_i$.

E. Comparison with other complexity measure

Thus far, we have introduced a new model complexity measure E_c. E_c is related to the derivatives of the regressed function f(x). A commonly seen alternative in the literature is the norm of the regression function instead. The L₂ norm in the kernel Hilbert space being the most common of norms used in this approach [39]. This section provides a theoretical comparison between the approach derived in this paper and this classical L₂ norm alternative. In particular, we show that the L₂ norm does not penalize the high frequencies of the regression function, whereas the proposed criterion emphasizes smoothness by penalizing the high frequency components of this function.

To formally prove the above result, we write generalized Fourier series of f(x),

$$f\left(x\right)=\sum _{k=0}^{\infty }{a}_k{\phi }_k\left(x\right),$$

where ${\left\{{\phi }_k\left(x\right)\right\}}_{k=0}^{\infty }$ forms a complete orthonormal basis and a_k are the corresponding coefficients. A commonly used complete orthonormal basis is ${\{\sin kx,\cos kx\}}_{k=0}^{\infty }$ in [−π, π], with k the index of the frequency component. Using this basis set, f(x) can be written as

$$f\left(x\right)=a_0+\sum _{k=1}^{\infty }(a_k\sin kx+b_k\cos kx),$$ (18)

where a_k and b_k are the coefficients of each frequency components.

Let ∥f∥₂ be the L₂ norm in the reproducing kernel Hilbert space, then

$$\begin{array}{cc}\hfill {\Vert f\Vert }_2^2=& \int {\mid f\left(x\right)\mid }^{2}dx\hfill \\ \hfill =& {\int }_{-\pi }^{\pi }{\left(a_0+\sum _{k=1}^{\infty }(a_k\sin kx+b_k\cos kx)\right)}^{2}dx\hfill \\ \hfill =& 2\pi a_0+\pi \sum _{k=1}^{\infty }(a_k^2+b_k^2).\hfill \end{array}$$ (19)

Note that in this case, all the coefficient are equal, regardless of the frequency component.

The complexity measure derived in the present paper and given in (13) can be reformulated as

$$E_c=\int \left({\left(\frac{\partial f\left(x\right)}{\partial x}\right)}^2+(f\left(x\right)-y)\frac{{\partial }^{2}f\left(x\right)}{\partial x^2}\right)dx,$$ (20)

where we have neglected the constant p⁻¹.

Moreover, remember for (11) that the generalization error E can be expressed as $f\left(x\right)=y+\mathcal{O}\left(\nu \right)$ [4]. Hence, substituting (18) into (20), yields

$$\begin{array}{cc}\hfill E_c=& \int {\left(\sum _{k=1}^{\infty }k(-a_k\sin kx+b_k\cos kx)\right)}^{2}dx\hfill \\ \hfill =& \pi \sum _{k=1}^{\infty }{k}^2(a_k^2+b_k^2).\hfill \end{array}$$ (21)

Compared to the L₂ norm result shown in (19), the complexity measure (21) of the proposed approach penalizes the higher frequency components of the regressed function. This is due to the squared of the index of the frequency component seen in (21). By emphasizing lower frequencies, the proposed criterion will generally select smoother functions than those selected by the L₂ norm method.

A numerical comparison is provided in Section V. To do this, we will need the explicit equation of the L₂ norm of the regression function f in the kernel space. This is given by,

$$\begin{array}{cc}\hfill {\Vert \mathbf{f}\Vert }_2^2=& \sum _{i=1}^q{\Vert f_i\Vert }_2^2=\sum _{i=1}^q\sum _{j=1}^n\sum _{k=1}^n{\alpha }_i^j{\alpha }_i^k\kappa \langle \cdot ,{\mathbf{x}}_j\rangle \kappa \langle \cdot ,{\mathbf{x}}_k\rangle \hfill \\ \hfill =& \sum _{i=1}^q\sum _{j=1}^n\sum _{k=1}^n{\alpha }_i^j{\alpha }_i^k\kappa \langle {\mathbf{x}}_j,{\mathbf{x}}_k\rangle \hfill \\ \hfill =& \sum _{i=1}^q{\alpha }_i^T\mathbf{K}{\alpha }_i.\hfill \end{array}$$ (22)

III. Multiobjective Optimization

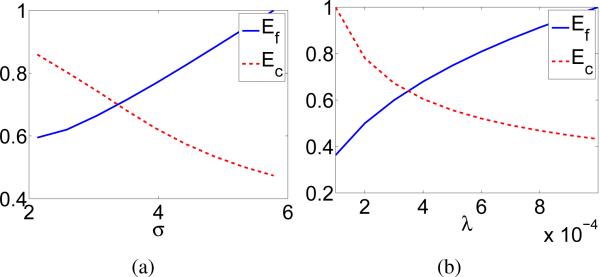
The parameters in kernel approaches in regression can now be optimized by simultaneously minimizing E_f and E_c of the corresponding fitting function described in the preceding section. Of course, in general, the global minima of these two functions are not the same. For instance, a decrease in the fitting error may lead to an increase in the roughness of the function, and vice-versa. This trade-off is depicted in Figure 1. In the plots in this figure, we show the performance of the two criteria with respect to the their corresponding parameters, i.e., the kernel parameter σ and the regularization parameter λ in the case of Kernel Ridge Regression (KRR)[16] with an RBF kernel. As can be observed in the figure, the criteria do not share a common global minimum. To resolve this problem, we now derive a multiobjective optimization approach.

Fig. 1.

The two plots in this figure show the contradiction between the RSS and the curvature measure with respect to: (a) the kernel parameter σ, and (b) the regularization parameter λ in Kernel Ridge Regression. The Boston Housing data-set [5] is used in this example. Note that in both cases, while one criterion increases, the other decreases. Thus, a compromise between the two criteria ought to be determined.

A. Pareto-Optimality

As its name implies, multiobjective optimization (MOP) is concerned with the simultaneous optimization of more than one objective function. More formally, MOP can be stated as follows,

$$\begin{array}{cc}\underset{\theta }{\text{minimize}}\hfill & u_1\left(\theta \right),u_2\left(\theta \right),\dots ,u_k\left(\theta \right)\hfill \\ \text{subject to}\hfill & \theta \in S,\hfill \end{array}$$ (23)

where we have k objective functions $u_i:{\mathbb{R}}^p\to \mathbb{R}$, and $S\subset {\mathbb{R}}^p$ is the set of possible vectors. Denote the vector of objective functions by z = u(θ) = (u₁(θ), u₂(θ), ..., u_k(θ))^T, and the decision vectors as θ = (θ₁, θ₂, ...,θ_p)^T.

The goal of MOP is to find that θ* which simultaneously minimizes all u_j(.). If all functions shared a common minimum, the problem would be trivial. In general, however, the objective functions contradict one another. This means that minimizing one function can increase the value of the others. Hence, a compromise solution is needed to attain a maximal agreement of all the objective functions [25]. The solutions of the MOP problem are called Pareto-optimal solutions. To provide a formal definition, let us first state another important concept.

Definition 1

A decision vector θ₁ is said to dominate θ₂ if u_i(θ₁) ≤ u_i(θ₂) for all i = 1, ..., k and u_j(θ₁) < u_j(θ₂) for at least one index j.

This definition now allows us to give the following formal presentation of Pareto-optimality.

Definition 2

A decision vector θ* ∈ S is Pareto-optimal if there does not exist another decision vector θ ∈ S for which u_i(θ) ≤ u_i(θ*) for all i = 1, ..., k and u_j(θ) < u_j(θ*) for at least one index j.

In other words, a Pareto-optimal solution is not dominated by any other decision vector. Similarly, an objective vector z* ∈ Z(= u(S)) is called Pareto-optimal if the decision vector corresponding to it is Pareto-optimal. We can see that such a vector is the one where none of the components can be improved without deteriorating one or more of the others. In most problems, there will be many Pareto-optimal solutions. This set of Pareto-optimal solutions is called the Pareto-optimal set or Pareto-frontier.

B. The ε-constraint approach

One classical method to find the Pareto-optimal solutions is the ε-constraint approach [15]. In this case, one of the objective functions is optimized while the others are considered as constraints. This is done by defining constraints as upper-bounds of their objective functions. Therefore, the problem to be solved can be formulated as follows,

$$\begin{array}{cc}\arg \underset{\theta }{\min }\hfill & u_l\left(\theta \right)\hfill \\ \text{subject to}\hfill & u_j\left(\theta \right)\le {\epsilon }_j,\text{for all}j=1,\dots ,k,j\ne l,\theta \in S,\hfill \end{array}$$ (24)

where l ∈ {1, ..., k}.

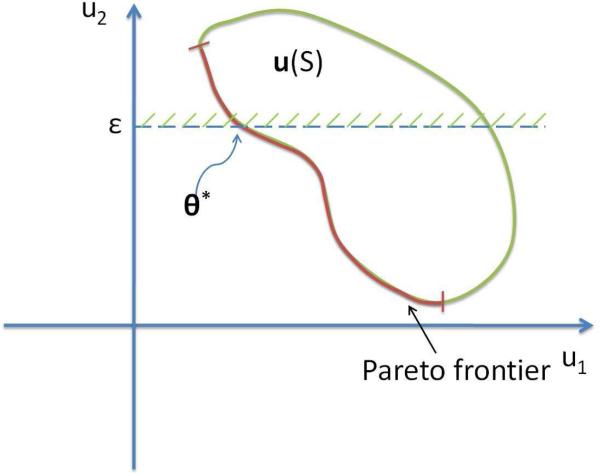
Figure 2 demonstrates the idea behind this approach. In this figure, we show a bi-objective example, k = 2. The Pareto-optimal solution θ is determined by minimizing u₁ provided that that u₂ is upper-bounded by ε.

Fig. 2.

Here we show a case of two objective functions. u(S) represents the set of all the objective vectors with the Pareto frontier colored in red. The Pareto-optimal solution θ can be determined by minimizing u₁ given that u₂ is upper-bounded by ε.

Before exploring the Pareto-optimality of the ε-constraint method, let us look at a weaker definition of the term.

Definition 3

A decision vector θ* ∈ S is weakly Pareto-optimal if there does not exist another decision vector θ ∈ S such that u_i(θ) < u_i(θ*) for all i = 1, ..., k.

From the above definition, we can see that the Pareto-optimal set is a subset of the weakly Pareto-optimal set and that a weakly Pareto-optimal solution may be dominated by any Pareto-optimal solution.

It has been shown [25] that the solution of the ε-constraint method defined in (24) is weakly Pareto-optimal. This means that the solution to (24) cannot be guaranteed to be Pareto-optimal. Although the solution is determined by the prespecified upper-bounds ε_j's and some ε_j's may lead to Pareto-optimal solutions, in practice, we do not know how to choose ε_j's to achieve the Pareto-optimal solutions. In the following, we propose a modified version of this method and prove that the solution to this modified approach is guaranteed to be Pareto-optimal.

C. The modified ε-constraint

The main idea of our approach is to reformulate the constraints in (24) as equalities. This can be achieved if these equalities are multiplied by a scaler smaller than or equal to s on the right. Formally, u_j(θ) = h_jε_j, h_j ∈ [0, s], for all j = 1, ..., k, j ≠ l. Let h = (h₁, ..., h_l–1, h_l+1, ..., h_l)^T. Then, the modified ε-constraint method is given by

$$\begin{array}{cc}\arg \underset{\theta ,\mathbf{h}}{\min }\hfill & u_l\left(\theta \right)+s\sum _{j=1,j\ne l}^k{h}_j\hfill \\ \text{subject to}\hfill & u_j\left(\theta \right)=h_j{\epsilon }_j,\text{for all}j=1,\dots ,k,j\ne l,0\le h_j\le s,\text{for all}j=1,\dots ,k,j\ne l,\theta \in S,\hfill \end{array}$$ (25)

where s is a positive constant. We can now prove the Pareto-optimality of (25).

Theorem 4

Select a small scalar s satisfying $s{\sum }_{j=1,j\ne l}^k{h}_j^{\ast }\le u_l\left(\mathbf{x}\right)-u_l\left({\mathbf{x}}^{\ast }\right)$, where θ* ∈ S and h* are the solutions of (25). Then, θ* is Pareto-optimal for any given upper-bound vector ε = (ε₁, ..., ε_l–1, ε_l+1, ..., ε_k)^T.

Proof

Let θ* ∈ S and h* be a solution of (25). Since $s{\sum }_{j=1,j\ne l}^k{h}_j^{\ast }\le u_l\left(\theta \right)-u_l\left({\theta }^{\ast }\right)$, we have u_l(θ*) ≤ u_l(θ) for all θ ∈ S when u_j(θ*) = h_jε_j, for every j = 1,..., k, j ≠ l. Let us assume that θ* is not Pareto-optimal. In this case, there exists a vector θ^o ∈ S such that u_i(θ^o) ≤ u_i(θ*) for all i = 1, ..., k and u_j(θ^o) < u_j(θ*) for at least one index j.

If j = l, this means that u_l(θ^o) < u_l(θ*). Here we have a contradiction with the fact that u_l(θ*) ≤ u_l(θ) for all θ ∈ S.

If j ≠ l, then u_l(θ^o) ≤ u_l(θ*), u_j(θ^o) < u_j(θ*) = h_jε_j and u_i(θ^o) ≤ u_i(θ*) = h_iε_i for all i ≠ j and i ≠ l. Denote $u_i\left({\theta }^o\right)=h_i^o{\epsilon }^i$for all i ≠ l. Then, we have l – 1 inequalities $h_i^o{\epsilon }_i\le h_i{\epsilon }_i$ with at least one strict inequality $h_j^o{\epsilon }_j<h_j{\epsilon }_j$. Canceling out ε_i on each of the inequality and taking their sum, yields ${\sum }_{j=1,j\ne l}^k{h}_j^o<{\sum }_{j=1,j\ne l}^k{h}_j$. This contradicts the fact that the solution to (25) minimizes ${\sum }_{j=1,j\ne l}^k{h}_j$.

We can demonstrate the utility of this modified ε-constraint method in the following two examples. In our first example, the objective functions are given by

$$u_1\left(x\right)=\{\begin{array}{cc}1\hfill & x\le 1\hfill \\ x^2\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$

and u₂(x) = (x – 5)². In our second example, the two functions are given by $u_1^{\prime }\left(x\right)=1-e^{-{(x+1)}^2}$ and

$$u_2^{\prime }\left(x\right)=\{\begin{array}{cc}1-e^{-{(x-2)}^2}\hfill & x\le 0.5\hfill \\ 1-e^{-2.25}\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$

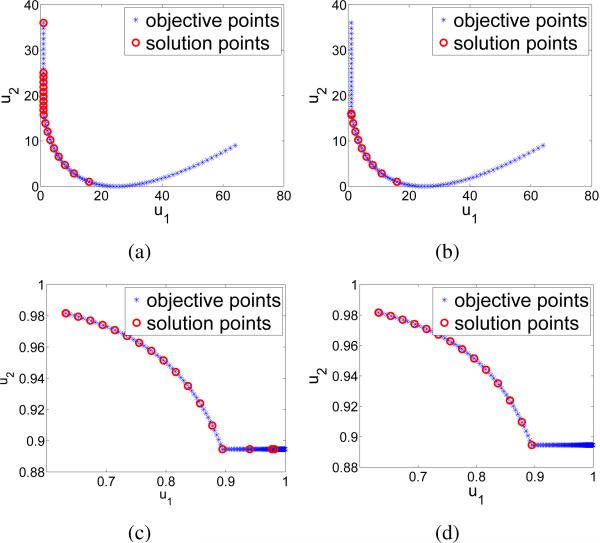
In both these examples, we compare the performance of the proposed modified ε-constraint approach and the ε-constraint method. This is illustrated in Figure 3. In these figures, the blue stars denote the objective vectors and the red circles represent the solution vectors given by each of the two methods. We see that in Figure 3a and 3c, the original ε-constraint method includes the weakly Pareto-optimal solutions, whereas in Figure 3b and 3d the proposed modified approach provides the Pareto-optimal solutions.

Fig. 3.

Comparison between the proposed modified and the original ε-constraint methods. We have used ‘*’ to indicate the objective vector and ‘o’ to specify the solution vector. Solutions given by (a) the ε-constraint method and (b) the proposed modified ε-constraint approach on the first example, and (c) the ε-constraint method and (d) the modified ε-constraint approach on the second example. Note that the proposed approach identifies the Pareto-frontier, while the original algorithm identifies weakly Pareto-solutions, since the solution vectors go beyond the Pareto-frontier.

Using the solution defined above, we can formulate the parameter optimization problem as follows,

$$\begin{array}{cc}\arg \underset{\theta ,\mathbf{h}}{\min }\hfill & E_f\left(\theta \right)+sh\hfill \\ \text{subject to}\hfill & E_c\left(\theta \right)=h\epsilon \hfill \\ \hfill & 0\le h\le s.\hfill \end{array}$$ (26)

Note that given different ε's, we may have different Pareto-optimal solutions. In our parameter optimization problem, we only need one Pareto-optimal solution. Hence, our next goal is to define a mechanism to determine an appropriate value for ε.

To resolve this problem, we select ε such that the corresponding Pareto-optimal objective vector is as close to the ideal point as possible. Specifically, let θ_ε be a Pareto-optimal solution given ε, then the optimal ε is

$${\epsilon }^{\ast }=\arg \underset{\epsilon }{\min }\left[w_f{(E_f\left({\theta }_{\epsilon }\right)-z_f^{\ast })}^2+w_c{(E_c\left({\theta }_{\epsilon }\right)-z_c^{\ast })}^2\right],$$ (27)

where $z_f^{\ast }$ and $z_c^{\ast }$ are the ideal vectors of E_f(θ) and E_c(θ), respectively, and w_f, w_c are the weights associated to each of the objective functions. The incorporation of these weights can drive the optimization to favor one objective function over the other. If E_f(θ_ε) (or E_c(θ_ε)) is close to its ideal value $z_f^{\ast }\left(z_c^{\ast }\right)$, then w_f (w_c) should be relatively small. But if E_f(θ_ε) (E_c(θ_ε)) is far apart from it ideal value $z_f^{\ast }\left(z_c^{\ast }\right)$, then w_f (w_c) should be large. This can be formally stated as follows,

$$\begin{array}{cc}\hfill w_f=& {\mid E_f\left({\theta }_{{\epsilon }_0}\right)-z_f^{\ast }\mid }^2,\hfill \\ \hfill w_c=& {\mid E_c\left({\theta }_{{\epsilon }_0}\right)-z_c^{\ast }\mid }^2,\hfill \end{array}$$ (28)

where ε₀ is the initialization for ε. The proposed modified ε-constraint approach is summarized in Algorithm 1.

Algorithm 1.

Modified ε-constraint algorithm

Input: Training set {(x1, y1), ..., (xn, yn)}, θ0, h0, ε0, s.

1. Calculate the ideal vector point $(z_f^{\ast },z_c^{\ast })$.

2. Specify the weights wf and wc using (28).

3. Obtain ε* using (27).

4. Obtain θ* using (26).

Return: The optimal model parameter θ*.

D. Alternative Optimization Approaches

Thus far, we have derived a MOP approach for model selection based on Pareto-optimality. The most pressing question for us is to show that this derived solution yields lower prediction errors than simpler, more straight forward approaches. Two such criteria are the sum and product of the two terms to be minimized [47], given by

$$Q^{sum}\left(\theta \right)=E_f\left(\theta \right)+\nu E_c\left(\theta \right).$$ (29)

and

$$Q^{pro}\left(\theta \right)=E_f\left(\theta \right)E_c{\left(\theta \right)}^{\gamma },$$ (30)

where ν and γ are regularization parameters needed to be selected. Note that minimizing (30) is equivalent to minimizing

$$\lg Q^{pro}\left(\theta \right)=\lg E_f\left(\theta \right)+\gamma \lg E_c\left(\theta \right).$$ (31)

which is the logarithm of (30). We could use cross-validation to select the regularization parameters ν and γ. Experimental results comparing these two alternative optimization approaches with the proposed approach will be given in the experiments section.

IV. Applications to Regression

Let us derive two kernel-based regression approaches using the kernels and MOP criteria derived above. In particular, we use our derived results in Kernel Ridge Regression (KRR) [16] and Kernel Principal Component Regression (KPCR) [31].

A. Kernel Ridge Regression

Ridge regression (RR) is a penalized version of the ordinary least squares (OLS) solution. More specifically, RR regularizes the OLS solution with a penalty on the norm of the weight factor. This regularization is used to avoid overfitting. Formally, RR is defined as

$${\mathbf{w}}_i={({\mathbf{XX}}^T+\lambda {\mathbf{I}}_p)}^{-1}\mathbf{X}{\tilde{y}}_i,i=1,\dots ,q,$$ (32)

where X = (x₁, ..., x_n), I_p is the p × p identity matrix, ${\tilde{y}}_i={(y_{1i},\dots ,y_{ni})}^T$, and λ is the regularization parameter.

We can now extend the above solution using the kernel trick. The resulting method is know as Kernel Ridge Regression (KRR), and is given by

$${\alpha }_i={(\mathbf{K}+\lambda {\mathbf{I}}_n)}^{-1}{\tilde{y}}_i,i=1,\dots ,q,$$ (33)

where, as above, K is the kernel matrix.

In KRR, there are two parameters to optimize: the kernel parameter (e.g., σ in the RBF kernel) and the regularization parameter λ. In the following, we derive a gradient descent method to simultaneously optimize the two.

Since both, the residual sum of squares term E_R and the curvature term E_C, are involved in our parameter optimization problem, we need to derive the gradient of these terms with respect to their parameters.

We start with the derivations of the RBF kernel. In this case, we have

$$\begin{array}{cc}\hfill \frac{\partial E_c}{\partial \sigma }=& \frac{\partial {\sum }_{i=1}^q{({\tilde{y}}_i-\mathbf{K}{\alpha }_i)}^T({\tilde{y}}_i-\mathbf{K}{\alpha }_i)}{\partial \sigma }\hfill \\ \hfill =& 2\sum _{i=1}^q{({\tilde{y}}_i-\mathbf{K}{\alpha }_i)}^T\frac{\partial ({\tilde{y}}_i-\mathbf{K}{\alpha }_i)}{\partial \sigma }\hfill \\ \hfill =& -2\sum _{i=1}^q{({\tilde{y}}_i-\mathbf{K}{\alpha }_i)}^T\left(\frac{\partial \mathbf{K}}{\partial \sigma }{\alpha }_i+\mathbf{K}\frac{\partial {\alpha }_i}{\partial \sigma }\right),\hfill \end{array}$$

where $\frac{\partial \mathbf{K}}{\partial \sigma }=\frac{1}{{\sigma }^3}\mathbf{K}\circ \mathbf{D}$, ○ defines the Hadamard product of two matrices of the same dimensions, i.e., ${(\mathbf{A}\circ \mathbf{B})}_{ij}={\mathbf{A}}_{ij}{\mathbf{B}}_{ij}$, with A_ij denoting the (i, j)^th entry of matrix A. $\mathbf{D}={\left[{\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert }^2\right]}_{i,j=1,\dots ,n}$ is the matrix of pairwise sample distances, and $\frac{\partial {\alpha }_i}{\partial \sigma }=\frac{\partial {(\mathbf{K}+\lambda {\mathbf{I}}_n)}^{-1}}{\partial \sigma }{\tilde{y}}_i=-{(\mathbf{K}+\lambda {\mathbf{I}}_n)}^{-1}\frac{\partial \mathbf{K}}{\partial \sigma }{(\mathbf{K}+\lambda {\mathbf{I}}_n)}^{-1}{\tilde{y}}_i=-{(\mathbf{K}+\lambda {\mathbf{I}}_n)}^{-1}\frac{\partial \mathbf{K}}{\partial \sigma }{\alpha }_i$. And,

$$\begin{array}{cc}\hfill \frac{\partial E_c}{\partial \sigma }=& \sum _{l=1}^q\frac{\partial ({\alpha }_l^T\mathbf{M}{\alpha }_l-{\mathbf{q}}_l^T{\alpha }_l+n)}{\partial \sigma }\hfill \\ \hfill =& \frac{1}{2n}\sum _{i=1}^n\sum _{l=1}^q\left(\frac{\partial \left({\alpha }_l^T{\mathbf{R}}_i{\alpha }_l\right)}{\partial \sigma }+\frac{\partial \left({\mathbf{k}}_i^T{\alpha }_l\right)}{\partial \sigma }{\mathbf{p}}_i^T{\alpha }_l({\mathbf{k}}_i^T{\alpha }_l-y_{il})\frac{\partial \left({\mathbf{p}}_i^T{\alpha }_l\right)}{\partial \sigma }\right),\hfill \end{array}$$

where

$$\frac{\partial \left({\alpha }_l^T{\mathbf{R}}_i{\alpha }_l\right)}{\partial \sigma }=\frac{2{\alpha }_l^T{\mathbf{W}}_i\left(\frac{\partial {\mathbf{W}}_i^T}{\partial \sigma }{\alpha }_l+{\mathbf{W}}_i^T\frac{\partial {\alpha }_l}{\partial \sigma }\right)-4{\sigma }^3{\alpha }_l^T{\mathbf{R}}_i{\alpha }_l}{{\sigma }^4},$$

$\frac{\partial {\mathbf{W}}_i^T}{\partial \sigma }$ is a n × p matrix whose (j, k)^th entry is $\frac{{\Vert {\mathbf{x}}_j-{\mathbf{x}}_i\Vert }^2}{{\sigma }^3}\exp (-\frac{{\Vert {\mathbf{x}}_j-{\mathbf{x}}_i\Vert }^2}{2{\sigma }^2})(x_{jk}-x_{ik})$, and

$$\begin{array}{cc}\hfill \frac{\partial \left({\mathbf{k}}_i^T{\alpha }_l\right)}{\partial \sigma }=& \frac{\partial {\mathbf{k}}_i^T}{\partial \sigma }{\alpha }_l+{\mathbf{k}}_i^T\frac{\partial {\alpha }_l}{\partial \sigma },\hfill \\ \hfill \frac{\partial \left({\mathbf{p}}_i^T{\alpha }_l\right)}{\partial \sigma }=& \frac{\partial {\mathbf{p}}_i^T}{\partial \sigma }{\alpha }_l+{\mathbf{p}}_i^T\frac{\partial {\alpha }_l}{\partial \sigma },\hfill \end{array}$$

$\frac{\partial {\mathbf{k}}_i}{\partial \sigma }$ is the i^th column of $\frac{\partial \mathbf{K}}{\partial \sigma }$, $\frac{\partial {\mathbf{p}}_i^T}{\partial \sigma }={\sum }_{j=1}^p\frac{\partial {\mathbf{p}}_{ij}^T}{\partial \sigma }$, $\frac{\partial {\mathbf{p}}_{ij}^T}{\partial \sigma }$ is a n × 1 vector whose m^th (m ≠ i) entry is $\frac{1}{{\sigma }^3}\exp (-\frac{{\Vert {\mathbf{x}}_m-{\mathbf{x}}_i\Vert }^2}{2{\sigma }^2})[\left(\frac{1}{{\sigma }^2}{\Vert {\mathbf{x}}_m-{\mathbf{x}}_i\Vert }^2\right)(\frac{{(x_{mj}-x_{ij})}^2}{{\sigma }^2}-1)-\frac{2}{{\sigma }^2}{(x_{mj}-x_{ij})}^2]$ and i^th entry is 0.

Seemingly, deriving with respect to the regularization parameter λ, yields

$$\begin{array}{cc}\hfill \frac{\partial E_R}{\partial \lambda }=& 2\sum _{i=1}^q{({\tilde{y}}_i-\mathbf{K}{\alpha }_i)}^T\frac{\partial ({\tilde{y}}_i-\mathbf{K}{\alpha }_i)}{\partial \lambda }\hfill \\ \hfill =& -2\sum _{i=1}^q{({\tilde{y}}_i-\mathbf{K}{\alpha }_i)}^T\mathbf{K}\frac{\partial {\alpha }_i}{\partial \lambda },\hfill \end{array}$$

where $\frac{\partial {\alpha }_i}{\partial \lambda }=\frac{\partial {(\mathbf{K}+\lambda {\mathbf{I}}_n)}^{-1}}{\partial \lambda }{\tilde{y}}_i=-{(\mathbf{K}+\lambda {\mathbf{I}}_n)}^{-1}{(\mathbf{K}+\lambda {\mathbf{I}}_n)}^{-1}{\tilde{y}}_i=-{(\mathbf{K}+\lambda {\mathbf{I}}_n)}^{-1}{\alpha }_i$ And,

$$\begin{array}{cc}\hfill \frac{\partial E_c}{\partial \lambda }=& \sum _{l=1}^q\frac{\partial ({\alpha }_l^T\mathbf{M}{\alpha }_l-{\mathbf{q}}_l^T{\alpha }_l+n)}{\partial \lambda }\hfill \\ \hfill =& \sum _{l=1}^q\left(2{\alpha }_l^T\mathbf{M}\frac{\partial {\alpha }_l}{\partial \lambda }-{\mathbf{q}}_l^T\frac{\partial {\alpha }_l}{\partial \lambda }\right)\hfill \end{array}$$

When using the polynomial kernel, we cannot employ a gradient descent technique for finding the optimal value of d, because this is discrete. Thus, we will have to try all possible discrete values of d (within a given range) and select the degree yielding the smallest error. The derivations of E_f with respect to λ are the same for any kernel, and $\frac{\partial E_c}{\partial \lambda }={\sum }_{l=1}^q(2{\alpha }_l^T\mathbf{N}\frac{\partial {\alpha }_l}{\partial \lambda }-{\mathbf{u}}_l^T\frac{\partial {\alpha }_l}{\partial \lambda })$.

B. Kernel Principal Component Regression

Solving an overdetermined set of equations is a general problem in pattern recognition. The problem is well studied when there are no collinearities (i.e., close to linear relationships among variables), but special algorithms are needed to deal with them. Principal Component Regression (PCR) is a regression approach designed to deal with collinearities in the exploratory variables. Instead of using the original predictor variables, a subset of principal components of these are selected. By deleting the principal components with small variances, a more stable estimate of the coefficient {w_i}_i=1...,q, can be obtained. In this way, the large variances of {w_i}i=1,...,q, which were caused by multicollinearities, will be greatly reduced. More formally,

$${\mathbf{w}}_i=\sum _{j=1}^m\frac{1}{l_j}{\mathbf{a}}_j{\mathbf{a}}_j^T\mathbf{X}{\tilde{y}}_i,i=1,\dots ,q,$$ (34)

where a_i is the eigenvector of the covariance matrix associated to the i^th largest eigenvalue.

The above formulation can once again be calculated in the kernel space as,

$${\alpha }_i=\sum _{j=1}^m\frac{1}{{\lambda }_j}{\mathbf{v}}_j{\mathbf{v}}_j^T{\tilde{y}}_i,i=1,\dots ,q,$$ (35)

where v_i is the eigenvector of the centered kernel matrix $\tilde{\mathbf{K}}$ associated to the i^th largest eigenvalue λ_i. This algorithm is known as Kernel Principal Component Regression (KPCR).

In KPCR, we need to optimize two parameters – the kernel parameter and the number of eigenvectors m we want to keep. Since m is discrete, the cost function with respect to m is non-differentiable. But testing all possible value for m is computationally expensive, because the range of m is dependent on the size of the training set. Here, we present an alternative approach to select the optimal subset. The basic idea is to use the percentage of the variance $r=\frac{{\sum }_{i=1}^m{\lambda }_i}{{\sum }_{i=1}^t{\lambda }_i}$, t is the rank of $\tilde{\mathbf{K}}$. Note that r can now change continuously (from 0 to 1) and can thus be incorporated in a gradient descent framework.

Since KPCR differs from KRR in the solution vector {α_i}i=1,...,q, we need to derive α_i. The derivative with respect to σ is given by,

$$\begin{array}{cc}\hfill \frac{\partial {\alpha }_i}{\partial \sigma }=& \sum _{j=1}^m\frac{\partial \frac{1}{{\lambda }_j}{\mathbf{v}}_j{\mathbf{v}}_j^T}{\partial \sigma }{\tilde{y}}_i\hfill \\ \hfill =& \sum _{j=1}^m\left(-\frac{1}{{\lambda }_i^2}\frac{\partial {\lambda }_i}{\partial \sigma }{\mathbf{v}}_i{\mathbf{v}}_i^T+\frac{1}{{\lambda }_j}\frac{\partial {\mathbf{v}}_i}{\partial \sigma }{\mathbf{v}}_i^T+\frac{1}{{\lambda }_j}{\mathbf{v}}_i\frac{\partial {\mathbf{v}}_i^T}{\partial \sigma }\right){\tilde{y}}_i,\hfill \end{array}$$

where $\frac{\partial {\lambda }_i}{\partial \sigma }={\mathbf{v}}_i^T\frac{\partial \mathbf{K}}{\partial \sigma }{\mathbf{v}}_i$, $\frac{\partial {\mathbf{v}}_i}{\partial \sigma }=-{(\mathbf{K}-{\lambda }_i{\mathbf{I}}_d)}^{+}\frac{\partial \mathbf{K}}{\partial \sigma }{\mathbf{v}}_i$ [22], and A⁺ is the pseudoinverse of the matrix A.

The partial derivative with respect to r cannot be given, because an explicit definition of α_i as a function of r does not exist. We resolve this issue by deriving an approximation to $\frac{\partial {\alpha }_i}{\partial r}$ using a Taylor expansion. That is,

$$\begin{array}{cc}\hfill {\alpha }_i(r+\Delta r)=& {\alpha }_i\left(r\right)+\Delta r{\alpha }_i^{\prime }\left(r\right)+\frac{\Delta r^2}{2!}{\alpha }_i^{″}\left(r\right)+\frac{\Delta r^3}{3!}{\alpha }_i^{″\prime }\left(r\right)+\mathcal{O}\left(\Delta r^4\right),\hfill \\ \hfill {\alpha }_i(r-\Delta r)=& {\alpha }_i\left(r\right)-\Delta r{\alpha }_i^{\prime }\left(r\right)+\frac{\Delta r^2}{2!}{\alpha }_i^{″}\left(r\right)-\frac{\Delta r^3}{3!}{\alpha }_i^{″\prime }\left(r\right)+\mathcal{O}\left(\Delta r^4\right).\hfill \end{array}$$

Combining the two equations above, we have

$${\alpha }_i^{\prime }\left(r\right)=\frac{{\alpha }_i(r+\Delta r)-{\alpha }_i(r-\Delta r)}{2\Delta r}+\mathcal{O}\left(\Delta r^2\right).$$

Therefore, we can write

$$\frac{\partial {\alpha }_i}{\partial r}\approx \frac{{\alpha }_i(r+\Delta r)-{\alpha }_i(r-\Delta r)}{2\Delta r}=\frac{{\sum }_{j=m_1+1}^{m_2}\frac{1}{{\lambda }_j}{\mathbf{v}}_j{\mathbf{v}}_j^T{\tilde{y}}_i}{2\Delta r},$$

where m₁ and m₂ are selected such that ${\sum }_{i=1}^{m_1}{\lambda }_i∕{\sum }_{i=1}^t{\lambda }_i\le r-\Delta r<{\sum }_{i=1}^{m_1+1}{\lambda }_i{\sum }_{i=1}^t{\lambda }_i$ and ${\sum }_{i=1}^{m_2}{\lambda }_i∕{\sum }_{i=1}^t{\lambda }_i\le r+\Delta r<{\sum }_{i=1}^{m_2+1}{\lambda }_i∕{\sum }_{i=1}^t{\lambda }_i$.

V. Experimental Results

In this section, we will use the Pareto-optimal criterion derived in this paper to select the appropriate kernel parameters of KRR and KPCR. Comparisons with the state of the art as well as the alternative criteria (i.e., sum and product) defined in the preceding section are provided.

A. Standard data-sets

We select fifteen data-sets from the UCI machine learning databases [5] and the DELVE collections [1]. Specifically, these databases include the following sets (in parenthesis we show the number of samples/number of dimensions): Boston housing (506/14), auto mpg (398/8), slump(103/8), price(159/16), diabetes(43/3), wdbc(194/33), servo(167/5), puma-8nm (8192/9), puma-8nh (8192/9), puma-8fm (8192/9), puma-8fh (8192/9), kin-8nm (8192/9), kin-8nh (8192/9), kin-8fm (8192/9) and kin-8fh (8192/9). The Boston housing data-set was collected by the U.S. Census Service and describes the housing information in Boston, MA. The task is to predict the median value of a home. The auto mpg set details fuel consumption predicted in terms of 3 discrete and 4 continuous attributes. In the slump set, the concrete slump is predicted by 7 different ingredients. The price data-set requires predicting the price of a car based on 15 attributes. In the diabetes set, the goal is to predict the level of the serum C-peptide. In the Wisconsin Diagnostic Breast Cancer (wdbc) set, the time of the recurrence of breast cancer is predicted based on 32 measurements of the patients. The servo set concerns a robot control problem. The rise time of a servomechanism is predicted based on two gain settings and two choices of mechanical linkages. The task in the Pumadyn is to predict angular accreditation from a simulation of the dynamics of a robot arm. And, the Kin set requires us to predict the distance of the end-effector from a target in a simulation of the forward dynamics of an 8 link all-revolute robot arm. There are different scenarios in both Pumadyn and Kin data-sets according to the degree of non-linearity (fairly-linear or nonlinear) and the amount of noise (moderate or high).

When using the ε-constraint criterion, we employ the interior-point method of [19]. Recall that in our proposed modified ε-constraint criterion, we also need to select a small scalar s. We tested for values of s = {10⁻¹, 10⁻², 10⁻³} obtaining the same results regardless of the value of this parameter. The results reported in the present paper are for s = 10⁻³.

We compare our model selection approaches to the two typical criteria used in the literature, Cross-Validation (CV) and Generalized Cross-Validation (GCV) [39]. In particular, we employ a 10-fold CV. The kernel parameter in the RBF is searched in the range [μ – 2δ, μ + 2δ], where μ and δ are the mean and standard deviation of the distances between all pairwise training samples. In the polynomial kernel, its degree is tested in the range of 1 to 6. The regularization parameter in KRR is selected among the set {10⁻⁵, . . . ,10⁴}, and the percentage of variance r in KPCR is searched in the range [0.8, 1]. Moreover, we compare our modified ε-constraint approach with the original ε-constraint method.

To test all the different algorithms, for each data-set, we generate five random permutations and conduct 10-fold cross-validation on each one. This yields a total of 50 estimated errors. Herein, we report their means and the standard deviations (stdv). Unless otherwise noted, in the experiments below, we report the Root Mean Squared Error (RMSE) as our measure of the deviation between the true response y_i and the predicted response ŷ , i.e., $RMSE={\left[n^{-1}{\sum }_{i=1}^n{({\mathbf{y}}_i-{\widehat{\mathbf{y}}}_i)}^2\right]}^{1∕2}$. It is important to that the random permutations utilized at this testing stage is different from the one employed for parameter selection. Note also that in order to provide a fair comparison, we tested all the algorithms using the same sets. In addition, the Bonferroni-Dunns test and a two-sided paired Wilcoxon signed rank test [44, 17, 20] are used to check for statistical significance. Errors in bold mean that they were significantly smaller than the others with significance level of .05.

Table I shows the regression results of KRR using both the RBF and the polynomial kernels. We see that regardless of the kernel used, the proposed modified ε-constraint approaches consistently provide the smallest RMSE. We also note that the modified ε-constraint approach obtains smaller RMSE than the ε-constraint method.

TABLE I.

Results for KRR. Mean RMSE and standard deviation (in parentheses).

Kernel	RBF				Polynomial
Data set/Method	Modified ε-constraint	ε-constraint	CV	GCV	Modified ε-constraint	ε-constraint	CV	GCV
Housing	2.89*(0.77)	3.01(0.78)	3.25(0.84)	4.01(1.01)	3.71(0.87)	4.38(0.99)	4.24(1.03)	8.67(6.78)
Mpg	2.51*(0.52)	2.59*(0.57)	2.72*(0.40)	2.61(0.52)	2.82(0.45)	3.25(0.58)	3.24(0.57)	3.21(0.80)
Slump	6.62*(1.49)	7.36(2.29)	6.70(1.53)	22.1(8.95)	7.09(1.22)	8.85(2.05)	9.86(1.53)	7.20(1.77)
Price	2.21*(0.90)	2.73(1.54)	2.42(0.90)	8.88(5.43)	3.08(1.20)	3.29(1.50)	4.01(1.48)	3.41(1.5)
Diabetes	0.55*(0.23)	0.72(0.33)	0.57(0.19)	0.88(0.31)	0.52*(0.17)	0.60(0.20)	2.31(0.87)	0.62(0.33)
Wdbc	31.46*(1.59)	32.15*(4.86)	31.50*(4.37)	50.30(9.13)	34.11(4.23)	35.12(5.21)	46.61(6.89)	32.04*(4.35)
Servo	0.51*(0.29)	0.56(0.30)	0.59(0.32)	0.81(0.52)	0.70(0.25)	0.70(0.25)	0.75(0.25)	0.65(0.27)
Puma-8nm	1.44*(0.02)	1.51(0.03)	2.42(0.05)	1.44*(0.03)	1.42*(0.02)	1.89(0.04)	1.89(0.04)	1.46(0.02)
Puma-8nh	3.65(0.03)	3.64(0.03)	3.98(0.06)	3.56*(0.04)	5.08(1.26)	5.28(0.19)	4.11(0.14)	3.61*(0.06)
Puma-8fm	1.13*(0.01)	1.19(0.02)	1.19(0.01)	1.14*(0.02)	1.27(0.01)	1.37(0.09)	1.29(0.005)	1.27(0.01)
Puma-8fh	3.23*(0.01)	3.45(0.02)	3.23*(0.01)	3.23*(0.01)	3.78(0.16)	4.86(0.14)	3.23(0.01)	3.24*(0.02)
Kin-8nm	0.11*(0.002)	0.15(0.003)	0.16(0.002)	0.19(0.02)	0.18(0.0008)	0.24(0.03)	0.22(0.002)	0.19(0.01)
Kin-8nh	0.18*(0.001)	0.18(0.002)	0.19(0.002)	0.18(0.002)	0.20(0.002)	0.29(0.006)	0.24(0.003)	0.22(0.003)
Kin-8fm	0.016(0.002)	0.016(0.03)	0.013*(0.0001)	0.339(0.202)	0.013*(0.0001)	0.02(0.0001)	0.16(0.003)	0.015(0.0001)
Kin-8fh	0.07(0.002)	0.061(0.002)	0.043*(0.0002)	0.043*(0.0002)	0.046(0.0002)	0.046(0.0002)	0.16(0.003)	0.050(0.0003)

In each kernel, the best result is in bold.

^*The symbol is used to indicate the top result over all methods and kernels.

Table II shows the regression results of KPCR using the RBF and polynomial kernels. Once more, the proposed approach generally outperforms the others. Additionally, as in KRR, the modified ε-constraint approach generally yields the best results.

TABLE II.

Results for KPCR. Mean RMSE and standard deviation (in parentheses).

Kernel	RBF				Polynomial
Data set/Method	Modified ε-constraint	ε-constraint	CV	GCV	Modified ε-constraint	ε-constraint	CV	GCV
Housing	4.04*(0.88)	4.56(0.67)	9.14(1.10)	11.99(6.89)	8.45(1.72)	9.12(2.30)	6.05(0.95)	9.37(1.77)
Mpg	3.00*(0.58)	4.64(0.82)	7.71(0.90)	3.64(1.63)	7.30(0.81)	7.82(1.54)	5.92(1.00)	8.16(1.78)
Slump	6.39*(1.53)	7.55(1.68)	9.28(1.94)	7.64(1.42)	7.68(1.88)	8.15(2.11)	8.48(2.80)	9.49(3.00)
Price	3.90*(2.16)	4.67(2.15)	12.62(2.02)	9.78(2.98)	6.06(1.93)	6.27(2.29)	5.79(1.49)	6.61(1.61)
Diabetes	0.76*(0.33)	0.96(0.43)	0.99(0.53)	0.74*(0.34)	1.01(1.47)	0.73*(0.80)	1.85(1.92)	1.23(1.31)
Wdbc	30.66*(4.71)	35.32(5.87)	33.5(4.53)	43.53(7.05)	34.47(10.27)	56.68(7.71)	47.21(13.44)	41.13(14.89)
Servo	0.71*(0.30)	1.35(0.33)	1.41(0.34)	1.29(0.40)	1.13(0.25)	1.11(0.25)	0.74(0.24)	0.81(0.24)
Puma-8nm	3.69(0.02)	3.66(0.02)	2.42(0.05)	1.75*(0.07)	3.71(0.32)	4.12(0.25)	4.13(0.53)	4.15(0.70)
Puma-8nh	4.39(0.04)	4.39(0.02)	4.56(0.13)	3.65*(0.08)	4.58(0.29)	4.84(0.22)	4.56(0.16)	5.59(0.58)
Puma-8fm	1.28*(0.05)	1.73(0.77)	4.04(1.13)	1.26*(0.01)	1.29*(0.005)	1.46(0.36)	1.56(0.61)	1.81(0.44)
Puma-8fh	3.22*(0.01)	3.33*(0.28)	3.49(0.08)	3.26*(0.07)	3.75(0.24)	3.92(0.41)	3.99(0.39)	5.04(0.74)
Kin-8nm	0.19*(0.01)	0.19*(0.01)	0.22(0.02)	0.22(0.01)	0.22(0.04)	0.21(0.03)	0.26(0.05)	0.30(0.07)
Kin-8nh	0.21*(0.007)	0.21*(0.01)	0.23(0.01)	0.24(0.01)	0.25*(0.05)	0.30(0.09)	0.27(0.05)	0.33(0.07)
Kin-8fm	0.05(0.01)	0.06(0.04)	0.03(0.007)	0.04(0.01)	0.02*(0.0001)	0.05(0.08)	0.08(0.11)	0.10(0.13)
Kin-8fh	0.06*(0.01)	0.07(0.02)	0.05(0.006)	0.06*(0.01)	0.07*(0.07)	0.07*(0.07)	0.12(0.12)	0.12(0.12)

A major advantage of the proposed approach over CV is that it uses all the training data for training. In contrast, CV needs to use part of the training data for verification purposes. This limits the amount of training data used to fit the function to the data.

B. Comparison with the state of the art

We now provide a comparison with the methods available in the literature and typically employed in the above databases. Specifically, we compare our results with Support Vector Regression (SVR) [37] with the RBF and polynomial kernels, Multiple Kernel Learning in SVR (MKL-SVR) [28], and Gaussian Processes for Regression (GPR) [45]. In SVR, the parameters are selected using CV. In MKL-SVR, we employ three kernel functions: the RBF, the polynomial and the Laplacian defined as $k({\mathbf{x}}_i,{\mathbf{x}}_j)=\exp (-\frac{\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert }{\beta })$. The RBF kernel parameter is set to be the mean of the distances between all pairwise training samples; the degree of the polynomial kernel is set to 2; and β in the Laplacian kernel is set as $\beta =\frac{2}{n(n+1)}{\sum }_{i=1}^n{\sum }_{j=i}^n\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert$, where n is the number of training samples. MOSEK [3] is used to solve the quadratically constrained programming problems to get the combinational coefficients of the kernel matrices. In GPR, the hyperparameters of the mean and covariance functions are determined by minimizing the negative log marginal likelihood of the data.

We compare the results given by the above algorithms with those obtained by our approach applied to KRR and using the RBF kernel, because this method tends to yield more favorable results. The comparisons are shown in Table III. Note that our approach generally yields smaller RMSE.

TABLE III.

Mean and standard deviation of RMSE of different methods.

Data set/Method	Modified ε-constraint	SVRrbf	SVRpol	MKL-SVR	GPR
Housing	2.89(0.77)	3.45(1.04)	5.66(1.88)	3.34(0.70)	3.05(0.82)
Mpg	2.51(0.52)	2.69(0.60)	4.03(0.96)	2.67(0.61)	2.64(0.50)
Slump	6.62(1.49)	6.77(1.90)	8.37(2.86)	6.90(1.41)	6.88(1.51)
Price	2.21(0.90)	2.40(0.84)	3.72(1.55)	2.51(0.91)	11.2(2.26)
Diabetes	0.55(0.23)	0.68(0.31)	0.78(0.39)	0.65(0.35)	0.59(0.20)
Wdbc	31.46(1.59)	32.08(4.76)	44.1(9.87)	32.20(4.65)	31.60(4.3)
Servo	0.51(0.29)	0.61(0.35)	1.37(0.41)	0.60(0.36)	0.57(0.30)
Puma-8nm	1.44(0.02)	1.44(0.03)	3.35(0.11)	1.51(0.02)	1.47(0.03)
Puma-8nh	3.65(0.03)	3.67(0.06)	4.55(0.07)	3.78(0.05)	3.65(0.03)
Puma-8fm	1.13(0.01)	1.17(0.02)	2.04(0.05)	1.21(0.03)	1.17(0.02)
Puma-8fh	3.23(0.01)	3.24(0.02)	3.84(0.06)	3.35(0.05)	3.23(0.01)
Kin-8nm	0.11(0.002)	0.12(0.002)	0.21(0.003)	0.16(0.03)	0.12(0.002)
Kin-8nh	0.18(0.001)	0.19(0.003)	0.23(0.01)	0.20(0.002)	0.18(0.002)
Kin-8fm	0.016(0.002)	0.043(0.002)	0.048(0.001)	0.045(0.002)	0.013(0.00009)
Kin-8fh	0.07(0.002)	0.047(0.0009)	0.06(0.006)	0.05(0.001)	0.043(0.0007)

Furthermore, for each of the data-sets described above, we provide a comparison between our results and the best results found in the literature. For the Boston housing data-set, [36] reports the best fits with Relevance Vector Machine (RVM); for the Auto mpg data-set, the best result is obtained by MKL-SVR [28]; for the Slump data, [8] proposes a k nearest neighbor based regression method and shows its superiority over others; for the price data-set, [41] reports the best result with pace regression; Diabetes data-set is used in [10] and the best results is obtained using Least Angle Regression; for the servo data-set, [13] shows that regression with random forests gets best results; and for the last eight data-sets, Gaussian processes for regression trained with a maximum-a-posteriori approach is generally considered to provide state of the art results [43]. The comparison across all the data-sets is given in Table IV. We see that our approaches provide better or comparable results to the top results described in the literature but with the main advantage that a single algorithm is employed in all data-sets.

TABLE IV.

Comparison of our results with the state of the art.

	Housing	Mpg	Slump	Price	Diabetes	servo	Puma-8nm
Best	3.46(0.93)	2.67(0.61)	6.79(1.89)	2.62(0.87)	0.68(0.25)	0.59(0.30)	1.47(0.03)
Ours	2.89(0.77)	2.51(0.50)	6.62(1.49)	2.21(0.90)	0.55(0.23)	0.51(0.29)	1.44(0.02)

	Puma-8nh	Puma-8fm	Puma-8fh	Kin-8nm	Kin-8nh	Kin-8fm	Kin-8fh
Best	3.65(0.03)	1.17(0.02)	3.23(0.01)	0.12(0.002)	0.18(0.002)	0.013(0.00009)	0.043(0.0007)
Ours	3.65(0.03)	1.13(0.01)	3.23(0.01)	0.11(0.002)	0.18(0.002)	0.016(0.002)	0.07(0.002)

C. Alternative Optimizations

In Section III-D, we presented two alternatives for combining different objective functions – the sum and the product criteria. Here we provide a comparison of these criteria and the approach derived in this paper. In particular, we combine model fit E_f and model complexity E_c via the summation and product in KRR and KPCR. The regularization term in (29) and in (31) is selected by 5-fold CV. Table V shows the corresponding regression results. In this table, ${\mathcal{A}}_R$ and ${\mathcal{A}}_P$ denote the method $\mathcal{A}$ with a RBF and a polynomial kernel, respectively. We see that these two alternative criteria generally perform worse than the Pareto-optimal based approach.

TABLE V.

Regression performance with alternative optimization criteria.

Method	KRRR			KRRP			PCRR			PCRF
Data set	Ours	Sum	Product	Ours	Sum	Product	Ours	Sum	Product	Ours	Sum	Product
Housing	2.89(0.77)	3.06(0.78)	3.30(0.85)	3.71(0.87)	4.75(0.89)	4.66(1.75)	4.04(0.88)	9.46(5.73)	6.48(3.85)	8.45(1.72)	5.56(6.77)	4.97(3.98)
Mpg	2.51(0.52)	2.63(0.50)	2.64(0.49)	2.82(0.45)	4.34(2.51)	18.04(2.59)	3.00(0.58)	4.56(0.83)	4.25(0.69)	7.30(0.81)	5.48(6.04)	4.29(3.21)
Slump	6.62(1.49)	6.87(1.51)	6.85(1.51)	7.09(1.22)	8.03(1.78)	13.17(2.84)	6.39(1.53)	7.65(1.86)	7.64(1.87)	7.68(1.88)	14.70(9.04)	16.79(9.10)
Price	2.21(0.90)	2.73(1.45)	2.76(1.46)	3.08(1.20)	2.72(1.11)	3.10(1.11)	3.90(2.16)	4.17(2.85)	4.17(2.86)	6.06(1.93)	8.76(1.99)	13.43(20.9)
Diabetes	0.55(0.23)	0.66(0.29)	0.75(0.33)	0.52(0.17)	0.60(0.21)	3.47(2.15)	0.76(0.33)	0.86(0.45)	0.86(0.43)	1.01(1.47)	1.09(1.56)	0.65(0.22)
Wdbc	31.46(1.59)	47.99(7.01)	48.60(8.98)	34.11(4.23)	51.31(16.98)	64.29(73.02)	30.66(4.71)	34.01(4.86)	38.91(5.31)	34.47(10.27)	56.61(19.90)	56.58(32.64)
Servo	0.51(0.29)	0.60(0.31)	0.57(0.30)	0.70(0.25)	0.94(0.36)	1.33(0.40)	0.71(0.30)	0.83(0.50)	0.86(0.49)	1.13(0.25)	0.70(0.27)	0.91(0.33)
Puma-8nm	1.44(0.02)	1.50(0.03)	1.50(0.03)	1.42(0.02)	3.40(0.59)	3.89(0.04)	3.69(0.02)	2.25(0.38)	2.37(0.53)	3.71(0.32)	8.50(0.87)	6.96(3.00)
Puma-8nh	3.65(0.03)	3.80(0.03)	3.86(0.04)	5.08(1.26)	4.36(0.29)	4.54(0.03)	4.39(0.04)	3.90(0.64)	3.97(0.65)	4.58(0.29)	13.82(3.81)	11.27(5.41)
Puma-8fm	1.13(0.01)	1.18(0.01)	1.18(0.01)	1.27(0.01)	1.52(0.48)	2.79(0.12)	1.28(0.05)	2.58(0.97)	2.09(0.84)	1.29(0.005)	6.98(1.23)	3.88(2.81)
Puma-8fh	3.23(0.01)	3.28(0.02)	3.28(0.02)	3.78(0.16)	3.81(0.38)	3.79(0.08)	3.22(0.01)	3.40(0.38)	3.30(0.12)	3.75(0.24)	9.78(5.64)	7.82(5.44)
Kin-8nm	0.11(0.002)	0.12(0.008)	0.13(0.01)	0.18(0.0008)	0.21(0.02)	0.68(0.35)	0.19(0.01)	0.21(0.02)	0.22(0.02)	0.22(0.04)	0.27(0.24)	0.26(0.25)
Kin-8nh	0.18(0.001)	0.19(0.002)	0.19(0.002)	0.20(0.002)	0.22(0.005)	0.42(0.27)	0.21(0.007)	0.22(0.002)	0.23(0.01)	0.25(0.005)	0.50(0.47)	0.29(0.01)
Kin-8fm	0.016(0.002)	0.020(0.0005)	0.020(0.0005)	0.013(0.0001)	0.020(0.0001)	0.57(0.22)	0.05(0.01)	0.07(0.03)	0.06(0.01)	0.02(0.0001)	0.11(0.29)	0.03(0.01)
Kin-8fh	0.07(0.002)	0.05(0.0007)	0.046(0.0005)	0.046(0.0002)	0.05(0.0001)	0.75(0.30)	0.06(0.01)	0.08(0.03)	0.08(0.02)	0.07(0.07)	0.13(0.25)	0.06(0.02)

D. Comparison with the L₂ norm

We provide a comparison between our complexity measure E_c and the commonly used L₂ norm. This was done by plugging in the L₂ norm as the constraint in the modified ε-constraint algorithm. The RMSE results are shown in Table VI. We see that the proposed complexity measure generally outperforms the L₂ norm in penalizing the regression function.

TABLE VI.

Comparison with L₂ norm.

Method	KRRR		KRRP		PCRR		PCRP
Data set	Ours	L2 norm	Ours	L2 norm	Ours	L2 norm	Ours	L2 norm
Housing	2.89(0.77)	3.45(0.95)	3.71(0.87)	4.96(0.92)	4.04(0.88)	4.36(0.96)	8.45(1.72)	7.40(1.72)
Mpg	2.51(0.52)	3.09(0.51)	2.82(0.45)	4.19(2.23)	3.00(0.58)	3.45(0.75)	7.30(0.81)	7.42(1.29)
Slump	6.62(1.49)	6.98(1.48)	7.09(1.22)	14.97(2.23)	6.39(1.53)	6.43(1.47)	7.68(1.88)	8.12(2.08)
Price	2.21(0.90)	2.81(1.21)	3.08(1.20)	2.45(3.77)	2.35(1.04)	2.73(1.31)	6.06(1.93)	5.88(1.73)
Diabetes	0.55(0.23)	0.68(0.25)	0.52(0.17)	0.78(0.20)	0.76(0.33)	0.87(0.43)	1.01(1.47)	0.94(1.40)
Wdbc	31.46(1.59)	32.10(4.56)	34.11(4.23)	42.69(13.41)	30.66(4.71)	30.69(4.66)	34.47(10.27)	45.79(15.69)
Servo	0.51(0.29)	0.90(0.31)	0.70(0.25)	0.96(0.34)	0.71(0.30)	0.73(0.31)	1.13(0.25)	1.03(0.25)
Puma-8nm	1.44(0.02)	1.47(0.03)	1.42(0.02)	3.84(0.04)	3.69(0.02)	3.37(0.04)	3.71(0.32)	4.21(0.16)
Puma-8nh	3.65(0.03)	3.75(0.03)	5.08(1.26)	4.66(0.06)	4.39(0.04)	4.19(0.14)	4.58(0.29)	4.61(0.31)
Puma-8fm	1.13(0.01)	1.23(0.01)	1.27(0.01)	1.63(0.49)	1.28(0.05)	1.26(0.003)	1.29(0.005)	1.58(0.64)
Puma-8fh	3.23(0.01)	3.23(0.01)	3.78(0.16)	4.06(0.03)	3.22(0.01)	3.30(0.12)	3.75(0.24)	3.97(0.52)
Kin-8nm	0.11(0.002)	0.17(0.001)	0.18(0.0008)	0.21(0.03)	0.19(0.01)	0.16(0.03)	0.22(0.04)	0.22(0.03)
Kin-8nh	0.18(0.001)	0.20(0.001)	0.20(0.002)	0.26(0.007)	0.21(0.007)	0.21(0.002)	0.25(0.005)	0.29(0.09)
Kin-8fm	0.016(0.002)	0.020(0.0003)	0.013(0.0001)	0.024(0.0005)	0.05(0.01)	0.03(0.003)	0.02(0.0001)	0.05(0.08)
Kin-8fh	0.07(0.002)	0.06(0.0007)	0.046(0.0002)	0.067(0.0005)	0.06(0.01)	0.06(0.004)	0.07(0.07)	0.05(0.003)

E. Age estimation

In the last two sections we want to test the derived approach on two classical applications – age estimation from faces and weather prediction.

The process of aging can cause significant changes in human facial appearances. We used the FG-NET aging database described in [2] to model these changes. This data-set contains 1,002 face images of 82 subjects at different ages. The age ranges from 0 to 69. Face images include changes in illumination, pose, expression and occlusion (e.g., glasses and beards). We warp all images to a standard size and constant position for mouth and eyes as in [23]. All the pictures are warped to a common size of 60 × 60 pixels and converted to 8-bit graylevel images. Warped images of one individual are shown in Figure 4. We represent each image as a vector concatenating all the pixels of the image, i.e., the appearance-based feature representation.

Fig. 4.

Sample images showing the same person at different ages.

We generate five random divisions of the data, each with 800 images for training and 202 for testing. Results in Table VII are presented using the Mean Absolute Errors (MAE). Here, we report the MAE rather than the RMSE because it is the common measure reported in the literature in age estimation [14] and thus facilitates comparison with the state of the art. We can see that the modified ε-constraint method outperforms the other algorithms. In [48], the authors represent the images using a set of highly redundant Haar-like features and select relevant features using a boosting method. We implemented this method using the same five divisions of the data. Our approach is slightly better using a simpler appearance-based representation.

TABLE VII.

MAE of the proposed approach and the state of the art in age estimation.

	Modified ε-constraint	CV	GCV	SVRrbf	SVRpol	MKL-SVR	GPR	[48]
MAE	5.85	6.59	13.83	6.46	6.95	7.18	15.46	5.97

F. Weather prediction

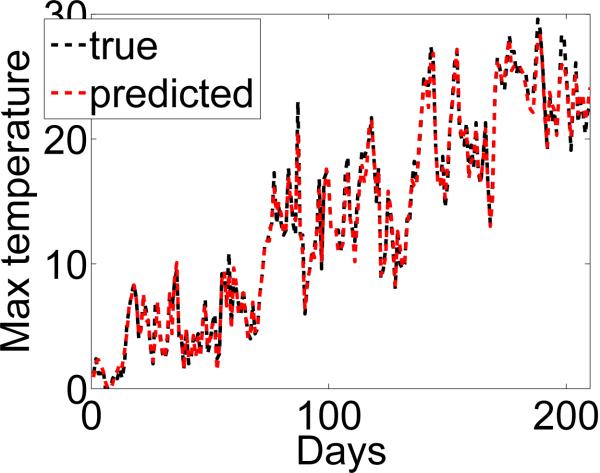
The weather data of the University of Cambridge [42] is used in this experiment. The maximum temperature of a day is predicted based on several parameters measured every hour during the day. These parameters include pressure, humanity, dew point (i.e., the temperature at which a parcel of humid air must be cooled for it to condense), wind knots, sunshine hours and rainfall. We use the data in a period of five years (2005-2009) for training and the data between January and July of the year 2010 for testing. This corresponds to 1,701 training samples and 210 testing samples. The results are in Table VIII. In [29], the authors employed support vector regression and report state of the art results. Our experiment shows that our approach performs better than their algorithm. The predictions obtained from the modified ε-constraint approach are also plotted in Figure 5. We observe that our approach can provide the prediction of the daily maximum temperature with high accuracy.

TABLE VIII.

RMSE of several approaches applied to weather prediction.

	Modified ε-constraint	CV	GCV	SVRrbf	SVRpol	MKL-SVR	GPR
RMSE	0.81	0.83	0.90	0.87	0.95	1.07	2.53

Fig. 5.

This figure plots the estimated (lighter dashed curve) and actual (darker dashed curve) maximum daily temperature for a period of more than 200 days. The estimated results are given by the algorithm proposed in this paper.

VI. Conclusions

Non-linear regression is a fundamental problem in machine learning and pattern recognition with multiple applications in science and engineering. Many approaches have been proposed for linear regressions, but their non-linear extensions are known to present several limitations. A major limitation is the lack of regularization of the regressor. Without proper regularization, the complexity of the estimated function (e.g., the degree of the polynomial describing the function) increases very rapidly, yielding poor generalizations on the unseen testing set [27]. To resolve this problem, we have derived a roughness penalty that measures the degree of change (of the regressed function) in the kernel space. This measure can then be used to obtain estimates that (in general) generalize better to the unseen testing set. However, to achieve this, the newly derived objective function needs to be combined with the classical one measuring its fitness (i.e., how well the function estimates the sample vectors). Classical solutions would be to use the sum or product of the two objective functions [47]. However, we have shown that these solutions do not generally yield desirable results in kernel methods in regression. To resolve this issue, we have proposed a multiple optimization approach based on the idea of Pareto-optimality. In this MOP framework, we have derived a novel method: the modified ε-constraint approach. While the original ε-constraint method cannot guarantee Pareto-optimal solutions, we have proven that the derived modified version does. Extensive evaluations with a large variety of databases has shown that this proposed modified ε-constraint approach yields better generalizations than previously proposed algorithms. Although the proposed method was applied to classical non-linear regression methods such as KRR and KPCR, our methodology is general enough that can be applicable to other regularized regression approaches methods such as [26].

The other major contribution of the paper has been to show how we can use the derived approach for optimizing the kernel parameters. In any kernel method, one always has to optimize the parameters of the kernel mapping function. The classical approach for this task is CV. This technique suffers from two main problems. First, it is computationally expensive. Second, and arguably most important, it cannot use the entire sample set for training, because part of it is employed as a validation set. But, we know that (in general) the larger the training set, the better. Our proposed MOP framework is ideal for optimizing the kernel parameters, because it yields nice objective functions that can be minimized with standard gradient descent techniques.

We have provided extensive comparisons of the proposed approach against CV and GCV and the other state of the art techniques in kernel methods in regression. We have also compared our results to those obtained with the sum and product criteria. And, we have compared our results to the best fits found in the literature for each of the databases. In all cases, these comparisons demonstrate that the proposed approach yields fits that generalize better to the unseen testing sets.

Appendix A

Partial Derivatives of the quadratic loss function

Let $L\left(\mathbf{z}\right)=\frac{1}{2}{\sum }_{i=1}^q{(y_i-f_i\left(\mathbf{x}\right))}^2$ be the quadratic loss then (10) is given by

$$\begin{array}{cc}\hfill \sum _{j=1}^m\frac{{\partial }^{2}L\left({\mathbf{z}}_i\right)}{\partial z_j^2}=& \frac{1}{2}\sum _{j=1}^m\sum _{k=1}^q\frac{{\partial }^2{(y_{ik}-f_k\left({\mathbf{x}}_i\right))}^2}{\partial z_j^2}\hfill \\ \hfill =& \frac{1}{2}\sum _{k=1}^q\left(\sum _{j=1}^p\frac{{\partial }^2{(y_{ik}-f_k\left({\mathbf{x}}_i\right))}^2}{\partial x_{ij}^2}+\sum _{j=1}^q\frac{{\partial }^2{(y_{ik}-f_k\left({\mathbf{x}}_i\right))}^2}{\partial y_{ij}^2}\right)\hfill \\ \hfill =& \sum _{k=1}^q\left(\sum _{j=1}^p{\left(\frac{\partial f_k\left({\mathbf{x}}_i\right)}{\partial x_{ij}}\right)}^2+\sum _{j=1}^p(f_k\left({\mathbf{x}}_i\right)-y_{ik})\frac{{\partial }^2{f}_k\left({\mathbf{x}}_i\right)}{\partial x_{ij}^2}+1\right)\hfill \\ \hfill =& \sum _{k=1}^q\sum _{j=1}^p\left({\left(\frac{\partial f_k\left({\mathbf{x}}_i\right)}{\partial x_{ij}}\right)}^2+(f_k\left({\mathbf{x}}_i\right)-y_{ik})\frac{{\partial }^2{f}_k\left({\mathbf{x}}_i\right)}{\partial x_{ij}^2}\right)+q.\hfill \end{array}$$

Appendix B

Partial derivatives of the roughness function

Sections B-A and B-B show the derivations to obtain the second partial derivatives for the RBF and polynomial kernels. Note that this is a key component for the roughness function Ec. To do so, recall that the regression function is defined as $f_l\left(\mathbf{x}\right)={\sum }_{m=1}^n{\alpha }_l^m\kappa \langle {\mathbf{x}}_m,\mathbf{x}\rangle$

A. RBF Kernel

The RBF kernel is given by $\kappa \langle {\mathbf{x}}_i,{\mathbf{x}}_j\rangle =\exp (-\frac{{\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert }^2}{2{\sigma }^2})$, where σ is the kernel parameter. Then the second partial derivative of f_l with respect to x_ij is

$$\begin{array}{cc}\hfill \frac{{\partial }^2{f}_l\left({\mathbf{x}}_i\right)}{\partial x_{ij}^2}=& \frac{1}{{\sigma }^2}\frac{\partial \left[{\sum }_{m=1}^n{\alpha }_l^m\exp \left(-\frac{{\Vert {\mathbf{x}}_m-{\mathbf{x}}_i\Vert }^2}{2{\sigma }^2}\right)(x_{mj}-x_{ij})\right]}{\partial x_{ij}}\hfill \\ \hfill =& \frac{1}{{\sigma }^2}\left[\sum _{m=1}^n{\alpha }_l^m\exp \left(-\frac{{\Vert {\mathbf{x}}_m-{\mathbf{x}}_i\Vert }^2}{2{\sigma }^2}\right)\frac{{(x_{mj}-x_{ij})}^2}{{\sigma }^2}-\sum _{m=1,m\ne i}^n{\alpha }_l^m\exp \left(-\frac{{\Vert {\mathbf{x}}_m-{\mathbf{x}}_i\Vert }^2}{2{\sigma }^2}\right)\right]\hfill \\ \hfill =& \frac{1}{{\sigma }^2}\left[{\alpha }_l^i+\sum _{m=1}^n{\alpha }_l^m\exp \left(-\frac{{\Vert {\mathbf{x}}_m-{\mathbf{x}}_i\Vert }^2}{2{\sigma }^2}\right)\left(\frac{{(x_{mj}-x_{ij})}^2}{{\sigma }^2}-1\right)\right]\hfill \\ \hfill =& {\alpha }_l^T{\mathbf{p}}_{ij}.\hfill \end{array}$$

B. Polynomial kernel

The polynomial kernel is given by $\kappa \langle {\mathbf{x}}_i,{\mathbf{x}}_j\rangle ={({\mathbf{x}}_i^T{\mathbf{x}}_j+1)}^d$, where d is the kernel parameter. The second partial derivative of f_l(.) with respect to x_ij is

$$\begin{array}{cc}\hfill \frac{{\partial }^2{f}_l\left({\mathbf{x}}_i\right)}{\partial x_{ij}^2}=& \sum _{m=1,m\ne i}^n{\alpha }_l^{m}d{x}_{mj}\frac{\partial {({\mathbf{x}}_m^T{\mathbf{x}}_i+1)}^{d-1}}{\partial x_{ij}}+2{\alpha }_l^{i}d\frac{\partial \left[{({\mathbf{x}}_i^T{\mathbf{x}}_i+1)}^{d-1}{x}_{ij}\right]}{\partial x_{ij}}\hfill \\ \hfill =& d\left[{\alpha }_l^i{({\mathbf{x}}_i^T{\mathbf{x}}_i+1)}^{d-2}(3(d-1)x_{ij}^2+2({\mathbf{x}}_i^T{\mathbf{x}}_i+1))+(d-1)\sum _{m=1}^n{\alpha }_l^m{({\mathbf{x}}_m^T{\mathbf{x}}_i+1)}^{d-2}{x}_{mj}^2\right]\hfill \\ \hfill =& {\alpha }_l^T{\mathbf{g}}_{ij}.\hfill \end{array}$$

Appendix C

Running Time

Table C.1 presents the running time for four different model selection algorithms: Modified ε-constraint, ε-constraint, CV and GCV. These values correspond to the execution time for KRR with an RBF Kernel using the cross-validation testing procedure described in Section V.

TABLE C.1.

Running time for KRR with a Gaussian Kernel in Seconds

Data set	Modified ε-constraint	ε-constraint	CV	GCV
Housing	1562.1	10502.3	1282.3	757.7
Mpg	878.1	3083.9	1233.7	904.2
Slump	412.7	935.6	37.8	29.9
Price	573.7	4064.2	71.8	20.2
Diabetes	24.3	203.3	4.7	10.4
Wbdc	1735.3	20689.2	88.7	248.3