Coupling all-atom molecular dynamics simulations of ions in water with Brownian dynamics

Abstract

Molecular dynamics (MD) simulations of ions (K⁺, Na⁺, Ca²⁺ and Cl⁻) in aqueous solutions are investigated. Water is described using the SPC/E model. A stochastic coarse-grained description for ion behaviour is presented and parametrized using MD simulations. It is given as a system of coupled stochastic and ordinary differential equations, describing the ion position, velocity and acceleration. The stochastic coarse-grained model provides an intermediate description between all-atom MD simulations and Brownian dynamics (BD) models. It is used to develop a multiscale method which uses all-atom MD simulations in parts of the computational domain and (less detailed) BD simulations in the remainder of the domain.

1. Introduction

Molecular dynamics (MD) simulations of ions in aqueous solutions are limited to modelling processes in relatively small domains containing (only) several thousands of water molecules [1,2]. Ions play important physiological functions in living cells which typically consist of 10¹⁰ to 10¹² water molecules. In particular, processes which include transport of ions between different parts of a cell cannot be simulated using standard all-atom MD approaches. Coarser models are instead used in applications. Examples include Brownian dynamics (BD) simulations [3] and mean-field Poisson–Nernst–Planck equations [4]. In BD methods, individual trajectories of ions are described using

$$\mathrm{d}{X}_i=\sqrt{2D}\hspace{0.17em}\mathrm{d}{W}_i,i=1,2,3,$$ 1.1

where X=(X₁,X₂,X₃) is the position of the ion, D is its diffusion constant and W_i, i=1,2,3, are three independent Wiener processes [5]. BD description (1.1) does not explicitly include solvent molecules in the simulation. Moreover, in applications, equation (1.1) can be discretized using a (nanosecond) timestep which is much larger than the typical timestep of MD simulations (femtosecond) [6]. This makes BD less computationally intensive than the corresponding MD simulations.

Longer timesteps of BD simulations enable efficient simulations of ion transport between different parts of the cell, but they limit the level of detail which can be incorporated into the model. For example, intracellular calcium is regulated by the release of Ca²⁺ ions from the endoplasmic reticulum via inositol-4,5-triphosphate receptor (IP₃R) channels. BD models in the literature use equation (1.1) to describe trajectories of calcium ions [3,7]. The conformational changes between the open and closed states of IP₃R channels are controlled by the binding of Ca²⁺ to activating and inhibitory binding sites. BD models postulate that binding of an ion occurs with some probability whenever the distance between the ion and an empty site is less than the specific distance, the so-called reaction radius [8,9]. Although details of the binding process are known [10,11], they cannot be incorporated into coarse BD models of calcium dynamics, because equation (1.1) does not correctly describe short-time behaviour of ion dynamics.

The calcium-induced calcium release through IP₃R channels is an example of a multiscale dynamical problem where MD simulations are important only in certain parts of the computational domain (close to an IP₃R channel), while in the remainder of the domain a coarser, less detailed, BD method could be used (to describe trajectories of ions). Such multiscale problems cannot be simulated using MD methods, but there is potential to design multiscale computational methods which compute the desired information with an MD-level of resolution by using MD and BD models in different parts of the computational domain [12].

In [12], three relatively simple and analytically tractable MD models are studied (describing heat bath molecules as point particles) with the aim of developing and analysing multiscale methods which use MD simulations in parts of the computational domain and less detailed BD simulations in the remainder of the domain. In this follow-up paper, the same question is investigated in all-atom MD simulations which use the SPC/E model of water molecules. In order to couple MD and BD simulations, we need to first show that the MD model is in a suitable limit described by a stochastic model which does not explicitly take into account heat bath (water) molecules. In [12], this coarser description was given in terms of Langevin dynamics. Considering all-atom MD simulations, the coarser stochastic model of an ion is more complicated than Langevin dynamics. In this paper, it will be given by

$$\begin{array}{rl}\mathrm{d}{X}_i& =V_i\hspace{0.17em}\mathrm{d}t,\end{array}$$ 1.2

$$\begin{array}{rl}\mathrm{d}{V}_i& =U_i\hspace{0.17em}\mathrm{d}t,\end{array}$$ 1.3

$$\begin{array}{rl}\mathrm{d}{U}_i& =(-{\eta }_1{V}_i+Z_i)\hspace{0.17em}\mathrm{d}t\end{array}$$ 1.4

$$\begin{array}{rl}\text{and}\mathrm{d}{Z}_i& =-({\eta }_2{Z}_i+{\eta }_3{U}_i)\hspace{0.17em}\mathrm{d}t+{\eta }_4\hspace{0.17em}\mathrm{d}{W}_i,i=1,2,3,\end{array}$$ 1.5

where X≡(X₁,X₂,X₃) is the position of the ion, V≡(V ₁,V ₂,V ₃) is its velocity, U≡(U₁,U₂,U₃) is its acceleration, Z≡(Z₁,Z₂,Z₃) is an auxiliary variable, dW≡(dW₁,dW₂,dW₃) is white noise and η_j, j=1,2,3,4, are parameters. These parameters will be chosen according to all-atom MD simulations as discussed in §3. In §4, we show that (1.2)–(1.5) provides a good approximation of ion behaviour. In §5, we further analyse the system (1.2)–(1.5) and show how parameters η_j, j=1,2,3,4, can be connected with diffusion constant D used in the BD model (1.1).

The coarse-grained model (1.2)–(1.5) is used as an intermediate model between the all-atom MD model and BD description (1.1). In §5, we show how it can be coupled with the BD model which uses a much larger timestep than the MD model. In §6, the coarse-grained model (1.2)–(1.5) is coupled with all-atom MD simulations. We then show that all-atom MD models of ions can be coupled with BD description (1.1) using the intermediate coarse-grained model (1.2)–(1.5). In §7, we introduce a hierarchy of stochastic coarse-grained models which generalize the coarse-grained model (1.2)–(1.5) and can be used to fit additional properties of all-atom MD. This generalization is formulated in terms of fictitious particle models [13] which are themselves based on earlier work in non-equilibrium statistical physics [14–17]. In particular, we show that the dynamics of the intermediate coarse-grained model (1.2)–(1.5) can be equivalently described by an appropriately formulated fictitious particle model [13]. We conclude by discussing related methods developed in the literature in §8.

2. Molecular dynamics simulations of ions in SPC/E water

There have been several MD models of liquid water developed in the literature. The simplest models (e.g., SPC [18], SPC/E [19] and TIP3P [20]) include three sites in total, two hydrogen atoms and an oxygen atom. More complicated water models include four, five or six sites [21,22]. In this paper, we use the three-site SPC/E model of water which was previously used for MD simulations of ions in aqueous solutions [23,1]. In the SPC/E model, the charges (q_h =0.4238 e) on hydrogen sites are at 1 Å from the Lennard–Jones centre at the oxygen site which has negative charge q_o=−0.8476 e. The HOH angle is 109.47°. We use the RATTLE algorithm [24] to satisfy constraints between atoms of the same water molecule.

We investigate four ions (K⁺, Na⁺, Ca²⁺ and Cl⁻) at 25°C using MD parameters presented in [23]. Let us consider a water molecule and let us denote by r_i0 (respectively, r_i1 and r_i2) the distance between the ion and the oxygen site (respectively, the first and second hydrogen sites). The pair potential between the water molecule and the ion is then given by [1,23],

$$A_{\mathrm{io}}{\left(\frac{1}{r_{\mathrm{io}}}\right)}^{12}-B_{\mathrm{io}}{\left(\frac{1}{r_{\mathrm{io}}}\right)}^6+k_e\frac{q_{\mathrm{i}}{q}_{\mathrm{o}}}{r_{\mathrm{i}0}}+k_e\frac{q_{\mathrm{i}}{q}_{\mathrm{h}}}{r_{\mathrm{i}1}}+k_e\frac{q_{\mathrm{i}}{q}_{\mathrm{h}}}{r_{\mathrm{i}2}},$$ 2.1

where A_io and B_io are Lennard–Jones parameters between the oxygen on the water molecule and the ion, k_e is Coulomb's constant and q_i is the charge on the ion. The values of parameters are given for four ions considered in table 1. We express mass in daltons (Da), length in ångströms (Å) and time in picoseconds (ps), consistently in the whole paper. Using these units, the parameters of the Lennard–Jones potential between the oxygen sites on two SPC/E water molecules are A_oo=2.6334×10⁸ Da Ź⁴ ps⁻² and B_oo=2.6171×10⁵ Da Å⁸ ps⁻².

Table 1.

Parameters of all-atom MD simulations of ions.

ion	Aio [Da Å14 ps−2]	Bio [Da Å8 ps−2]	qi [e]	M [Da]
K+	2.8973×108	2.4587×105	+1	39.0983
Na+	6.6813×107	1.1807×105	+1	22.9898
Ca2+	1.1961×108	1.5797×105	+2	40.078
Cl−	1.8038×109	6.1347×105	−1	35.453

We consider a cube of side L=24.83 Å containing 511 water molecules and 1 ion, i.e. we have 8³=512 molecules in our simulation box. In the following section, we use standard NVT simulations where the temperature is controlled using Nosé–Hoover thermostat [25,26] and the number of particles is kept constant by implementing periodic boundary conditions. In particular, we assume that our simulation box is surrounded by periodic copies of itself. Then the long-range (Coulombic) interactions can be computed using several different approaches, including the Ewald summation or the reaction field method [27,28]. We use the cut-off sphere of radius L/2 and the reaction field correction as implemented in [1]. This approach is more suitable for multiscale methods (studied later in §6) than the Ewald summation technique. The MD timestep is for all MD simulations in this paper chosen as Δt=10⁻³ ps =1 fs.

3. Parametrization of the coarse-grained model of ion

In MD simulations, an ion is described by its position X≡(X₁,X₂,X₃) and velocity V≡(V ₁,V ₂,V ₃) which evolve according to

$$\mathrm{d}{X}_i=V_i\hspace{0.17em}\mathrm{d}t$$ 3.1

and

$$M\hspace{0.17em}\mathrm{d}{V}_i=F_i\hspace{0.17em}\mathrm{d}t,i=1,2,3,$$ 3.2

where M is the mass of the ion (given in table 1) and F≡(F₁,F₂,F₃) is the force acting on the ion. We use all-atom MD simulations as described in §2 to estimate diffusion coefficient D and second moments of V _i and U_i=F_i/M, i=1,2,3. They are given for four ions considered in table 2. To estimate $⟨U_i^2⟩,$ we calculate the average force in the ith direction $⟨F_i^2⟩,$ where 〈⋅〉 denotes an average over sufficiently large time interval (nanosecond) of MD simulations. Taking into account the symmetry of the problem, we estimate $⟨U_i^2⟩=⟨F_i^2⟩/M^2$ as the average over all three dimensions

$$\frac{⟨U_1^2⟩+⟨U_2^2⟩+⟨U_3^2⟩}{3}.$$

This value is reported in table 2. In the same way, the reported values of $⟨V_i^2⟩$ are computed as averages over all three dimensions. Diffusion constant D can be estimated by calculating mean square displacements or velocity autocorrelation functions. In table 2, we report the values of D which were estimated in [1] by calculating mean square displacements.

Table 2.

Average values obtained by all-atom MD simulations of ions.

ion	D [ Å2 ps−1]	$⟨V_i^2⟩$ [ Å2 ps−2]	$⟨U_i^2⟩$ [ Å2 ps−4]	$⟨Z_i^2⟩$ [ Å2 ps−6]
K+	0.183	6.32	4.86×103	1.65×107
Na+	0.128	10.8	2.21×104	8.88×107
Ca2+	0.053	6.18	1.87×104	9.23×107
Cl−	0.177	6.98	6.56×103	2.97×107

Let us consider the coarse-grained model (1.2)–(1.5) and let 〈⋅〉 denotes an average over many realizations of a stochastic process. Multiplying equations (1.3) and (1.4) by V _i and U_i, respectively, we obtain the following ordinary differential equations (ODEs) for second moments:

$$\frac{\mathrm{d}}{\mathrm{d}t}⟨V_i^2⟩=2⟨U_i{V}_i⟩$$ 3.3

and

$$\frac{\mathrm{d}}{\mathrm{d}t}⟨U_i^2⟩=-2{\eta }_1⟨U_i{V}_i⟩+2⟨U_i{Z}_i⟩.$$ 3.4

Consequently, we obtain that 〈U_iV _i〉=0 and 〈U_iZ_i〉=0 at steady state. Multiplying equations (1.3)–(1.5) by V _i, U_i and Z_i, respectively, and taking averages, we obtain

$$\frac{\mathrm{d}}{\mathrm{d}t}⟨U_i{V}_i⟩=⟨U_i^2⟩-{\eta }_1⟨V_i^2⟩+⟨V_i{Z}_i⟩$$ 3.5

and

$$\frac{\mathrm{d}}{\mathrm{d}t}⟨V_i{Z}_i⟩=⟨U_i{Z}_i⟩-{\eta }_2⟨V_i{Z}_i⟩-{\eta }_3⟨U_i{V}_i⟩.$$ 3.6

Using 〈U_iV _i〉=0 and 〈U_iZ_i〉=0, we obtain that 〈V _iZ_i〉=0 at steady state and

$${\eta }_1=\frac{⟨U_i^2⟩}{⟨V_i^2⟩}.$$ 3.7

This equation is used in table 3 to estimate η₁ using the MD averages $⟨U_i^2⟩$ and $⟨V_i^2⟩$ which are given in table 2. Since we know the value of η₁, we can also estimate the value of $⟨Z_i^2⟩$ by calculating the second moment of

$$⟨Z_i^2⟩\approx ⟨{(\frac{U_i(t+\mathrm{\Delta }t)-U_i(t)}{\mathrm{\Delta }t}+{\eta }_1{V}_i)}^2⟩.$$ 3.8

This value is reported in the last column of table 2. Multiplying equation (1.4) by Z_i and equation (1.5) by U_i, we obtain

$$\frac{\mathrm{d}}{\mathrm{d}t}⟨U_i{Z}_i⟩=⟨Z_i^2⟩-{\eta }_1⟨V_i{Z}_i⟩-{\eta }_2⟨U_i{Z}_i⟩-{\eta }_3⟨U_i^2⟩.$$ 3.9

Using 〈U_iZ_i〉=0 and 〈V _iZ_i〉=0, we obtain at steady state

$${\eta }_3=\frac{⟨Z_i^2⟩}{⟨U_i^2⟩}.$$ 3.10

Table 3.

Values of η_j, j=1,2,3,4, estimated by (3.7), (3.10), (3.15) and (3.17) using theresults of all-atom MD simulations reported in table 2.

ion	η1 [ps−2]	η2 [ps−1]	η3 [ps−2]	η4 [ Å ps−7/2]
K+	768.7	152.5	3.393×103	7.094×104
Na+	2.044×103	166.1	4.020×103	1.717×105
Ca2+	3.026×103	190.2	4.933×103	1.874×105
Cl−	940.0	189.7	4.524×103	1.061×105

Multiplying equation (1.2) by X_i, V _i, U_i and Z_i and equations (1.3)–(1.5) by X_i and taking averages, we obtain the following system of ODEs for second moments:

$$\begin{array}{rl}\frac{\mathrm{d}}{\mathrm{d}t}⟨X_i^2⟩& =2⟨X_i{V}_i⟩,\end{array}$$ 3.11

$$\begin{array}{rl}\frac{\mathrm{d}}{\mathrm{d}t}⟨X_i{V}_i⟩& =⟨V_i^2⟩+⟨X_i{U}_i⟩,\end{array}$$ 3.12

$$\begin{array}{rl}\frac{\mathrm{d}}{\mathrm{d}t}⟨X_i{U}_i⟩& =⟨U_i{V}_i⟩-{\eta }_1⟨X_i{V}_i⟩+⟨X_i{Z}_i⟩\end{array}$$ 3.13

$$\begin{array}{rl}\text{and}\frac{\mathrm{d}}{\mathrm{d}t}⟨X_i{Z}_i⟩& =⟨V_i{Z}_i⟩-{\eta }_2⟨X_i{Z}_i⟩-{\eta }_3⟨X_i{U}_i⟩.\end{array}$$ 3.14

Consequently, at equilibrium, we obtain 〈X_iV _i〉=D, $⟨X_i{U}_i⟩=-⟨V_i^2⟩,$ 〈X_iZ_i〉=η₁D and

$${\eta }_2=-\frac{{\eta }_3⟨X_i{U}_i⟩}{⟨X_i{Z}_i⟩}=\frac{{\eta }_3⟨V_i^2⟩}{{\eta }_{1}D}.$$

Using (3.7) and (3.10), we have

$${\eta }_2=\frac{⟨Z_i^2⟩}{D}{\left(\frac{⟨V_i^2⟩}{⟨U_i^2⟩}\right)}^2.$$ 3.15

Finally, multiplying equation (1.5) by Z_i, we obtain

$$\frac{\mathrm{d}}{\mathrm{d}t}⟨Z_i^2⟩=-2{\eta }_2⟨Z_i^2⟩-2{\eta }_3⟨U_i{Z}_i⟩+{\eta }_4^2.$$ 3.16

Consequently, we obtain at steady state

$${\eta }_4^2=2{\eta }_2⟨Z_i^2⟩.$$

Using (3.15), we get

$${\eta }_4=\sqrt{\frac{2}{D}}\frac{⟨V_i^2⟩⟨Z_i^2⟩}{⟨U_i^2⟩}.$$ 3.17

The values calculated by (3.10), (3.15) and (3.17) are presented in table 3.

4. Accuracy of the coarse-grained model of ion

The coarse-grained model (1.2)–(1.5) has four parameters η_j, j=1,2,3,4. To parametrize this model, we have used four quantities estimated from detailed MD simulations, diffusion constant D and steady-state values of $⟨V_i^2⟩,$ $⟨U_i^2⟩$ and $⟨Z_i^2⟩$. In particular, the coarse-grained model (1.2)–(1.5) will give the same values of these four quantities, including the value of diffusion constant D which is the sole parameter of the BD model (1.1). In this section, we explain why the coarse-grained description given by (1.2)–(1.5) can be used as an intermediate model to couple BD and MD models.

We begin by illustrating why Langevin dynamics (which is used in [12] for a similar multiscale problem) is not suitable for all-atom MD simulations studied in this paper. In [12], a few (heavy) particles with mass M and radius R are considered in the heat bath consisting of a large number of light point particles with masses m≪M. The collisions of particles are without friction, which means that post-collision velocities can be computed using the conservation of momentum and energy. In this case, it can be shown that the description of heavy particles converges in an appropriate limit to Brownian motion given by equation (1.1). One can also show that the model converges to Langevin dynamics (in the limit m/M→0) [29–31]:

$$\mathrm{d}{X}_i=V_i\hspace{0.17em}\mathrm{d}t$$ 4.1

and

$$\mathrm{d}{V}_i=-\gamma V_i\hspace{0.17em}\mathrm{d}t+\gamma \sqrt{2D}\hspace{0.17em}\mathrm{d}{W}_i,i=1,2,3,$$ 4.2

where X≡(X₁,X₂,X₃) is the position of a diffusing molecule, V≡(V ₁,V ₂,V ₃) is its velocity, D is the diffusion coefficient and γ is the friction coefficient. In [12], Langevin dynamics (4.1)–(4.2) is used as an intermediate model which enables the implementation of BD description (1.1) and the original detailed model in different parts of the computational domain.

Langevin dynamics (4.1)–(4.2) describes a diffusing particle in terms of its position and velocity, i.e. it uses the same independent variables for the description of an ion as the MD model (3.1)–(3.2). Langevin dynamics can be further reduced to BD model (1.1) in the overdamped limit $\gamma \to \mathrm{\infty }$. However, it cannot be used as an intermediate model between BD and all-atom MD simulations considered in this paper, because it does not correctly describe the ion behaviour at times comparable with the MD timestep Δt. To illustrate this, let us parametrize Langevin dynamics (4.1)–(4.2) using diffusion constant D and the second velocity moment $⟨V_i^2⟩$ estimated from all-atom MD simulations. To get the same second moment of velocity, Langevin dynamics requires that we choose

$$\gamma =\frac{⟨V_i^2⟩}{D}.$$ 4.3

Discretizing equation (4.2), the ion acceleration during one timestep is

$$\frac{V_i(t+\mathrm{\Delta }t)-V_i(t)}{\mathrm{\Delta }t}=-\gamma V_i(t)+\gamma \sqrt{\frac{2D}{\mathrm{\Delta }t}}\hspace{0.17em}{\xi }_i,$$ 4.4

where (ξ₁,ξ₂,ξ₃) is a vector of normally distributed random numbers with zero mean and unit variance. Using (4.3), the second moment of the right-hand side of (4.4) is

$${\gamma }^2(⟨V_i^2⟩+\frac{2D}{\mathrm{\Delta }t})=\frac{{(⟨V_i^2⟩)}^3}{D^2}+\frac{2{(⟨V_i^2⟩)}^2}{D\hspace{0.17em}\mathrm{\Delta }t}.$$ 4.5

Using the MD values of D and $⟨V_i^2⟩$ for K⁺ which are given in table 2 and using MD timestep Δt=10⁻³ ps, we obtain that the second moment (4.5) is equal to 4.44×10⁵ Ų ps⁻⁴. On the other hand, $⟨U_i^2⟩$ estimated from all-atom MD simulations and given in table 2 is 4.86×10³ Ų ps⁻⁴ which is one hundred times smaller. The main reason for this discrepancy is that Langevin dynamics postulates that the random force in equation (4.2) acting on the particle at time t is not correlated to the random force acting on the particle at time t+Δt. However, this is not true for all-atom MD simulations where random force terms at subsequent timesteps are highly correlated.

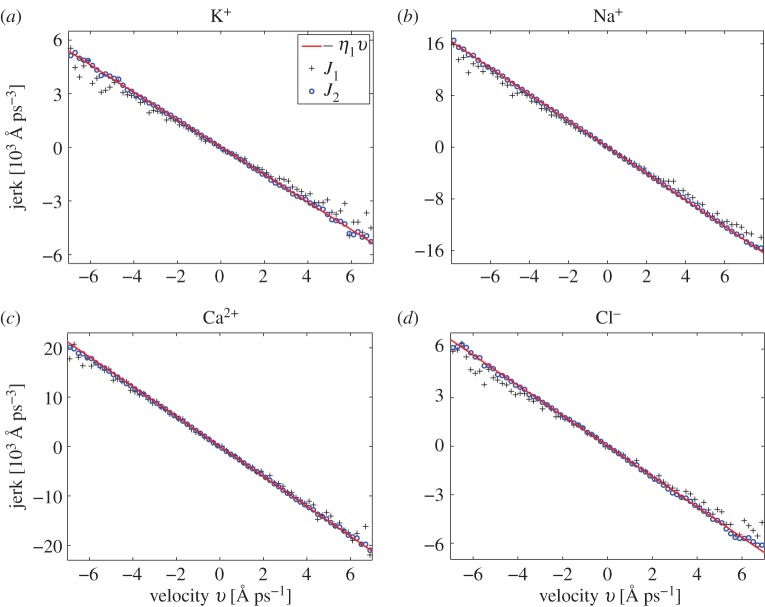
Since Langevin dynamics is not suitable for coupling MD and BD models, we need to introduce a stochastic model of ion behaviour which is more complicated than Langevin dynamics. The coarse-grained model (1.2)–(1.5) studied in this paper is a relatively simple example of such a model. Its parametrization, discussed in §3, guarantees that the coarse-grained model (1.2)–(1.5) well approximates all-atom MD simulations at equilibrium. They both have the same value of diffusion constant D and steady-state values of $⟨V_i^2⟩,$ $⟨U_i^2⟩$ and $⟨Z_i^2⟩$. Next, we show that the coarse-grained model (1.2)–(1.5) also compares well with all-atom MD simulations at shorter timescales. We consider the rate of change of acceleration (jerk or the scaled derivative of force). We define the average jerk as a function of current velocity and acceleration of the ion:

$$J(v,u)=\underset{\tau \to 0}{lim}\frac{⟨U_i(t+\tau )-u\hspace{0.17em}|\hspace{0.17em}{V}_i(t)=v,U_i(t)=u⟩}{\tau }.$$ 4.6

To estimate J(v,u) from all-atom MD simulations, we calculate the rate of change of acceleration during each MD timestep

$$J(v,u)\approx \frac{⟨U_i(t+\mathrm{\Delta }t)-u\hspace{0.17em}|\hspace{0.17em}{V}_i(t)=v,U_i(t)=u⟩}{\mathrm{\Delta }t},$$ 4.7

i.e. we run a long (nanosecond) MD simulation, calculate the values of (U_i(t+Δt)−U_i(t))/Δt during every timestep and record their average in two-variable array J(v,u) indexed by binned values of V _i(t)=v and U_i(t)=u. Since the estimated J(v,u) only weakly depends on u, we visualize our results in figure 1 using two functions of one variable, v, namely

$$J_1(v)=J(v,0)\mathrm{and}{J}_2(v)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}J(v,u)\hspace{0.17em}{p}_u(u)\hspace{0.17em}\mathrm{d}u,$$ 4.8

where p_u(u) is the steady-state distribution of U_i estimated from the same long-time MD trajectory. As before, we use all three dimensions to calculate the averages J(v,u) and p_u(u). Function J₁(v) (which gives jerk at the most likely value of U_i) is plotted using crosses and function J₂(v), the average over U_i variable, is plotted using circles in figure 1. In order to compare all-atom MD simulations with the coarse-grained model (1.2)–(1.5), we calculate the corresponding jerk matrix J(v,u) for the coarse-grained model. We denote by p(v,u,z) the stationary distribution of the stochastic processes (1.3)–(1.5), i.e. p(v,u,z) dv du dz is the probability that V _i(t)∈[v,v+dv), U_i(t)∈[u,u+du) and Z_i(t)∈[z,z+dz). Then the jerk matrix (4.6) of the coarse-grained model (1.2)–(1.5) is

$$J(v,u)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\underset{\tau \to 0}{lim}\frac{⟨U_i(t+\tau )-u\hspace{0.17em}|\hspace{0.17em}{V}_i(t)=v,U_i(t)=u,Z_i(t)=z⟩}{\tau }\hspace{0.17em}p(v,u,z)\hspace{0.17em}\mathrm{d}z.$$

Figure 1.

Comparison of the rate of change of acceleration (jerk) computed by all-atom MD simulations and by the coarse-grained model (1.2)–(1.5). MD results are visualized using functions J₁(v) (black crosses) and J₂(v) (blue circles) defined by equation (4.8). The coarse-grained model result is given by formula (4.10) (red solid line). We consider (a) K⁺ ion; (b) Na⁺ ion; (c) Ca²⁺ ion and (d) Cl⁻ ion. Parameters are given in tables 1 and 3.

Using (1.4), we rewrite it as

$$J(v,u)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}(-{\eta }_{1}v+z)\hspace{0.17em}p(v,u,z)\hspace{0.17em}\mathrm{d}z.$$ 4.9

The stationary distribution p(v,u,z) of (1.3)–(1.5) is Gaussian with mean (0,0,0) and stationary covariance matrix:

$$\frac{1}{2{\eta }_1{\eta }_2{\eta }_3}\left(\begin{array}{ccc}{\eta }_4^2& 0& 0\\ 0& {\eta }_1{\eta }_4^2& 0\\ 0& 0& {\eta }_1{\eta }_3{\eta }_4^2\end{array}\right).$$

Consequently, equation (4.9) implies

$$J(v,u)=-{\eta }_{1}v.$$ 4.10

In figure 1, we plot (4.10) using the red solid line. The comparison with all-atom MD results (circles and squares) is excellent for all four ions considered in this paper. In particular, we have shown that the coarse-grained model (1.2)–(1.5) provides a good description of the rate of change of acceleration (jerk) at the MD timescale. We make use of this property in §6, where we use the same time step (Δt=10⁻³ ps) for both the coarse-grained model (1.2)–(1.5) and all-atom MD simulations. The coarse-grained model (1.2)–(1.5) can also be coupled with BD description (1.1), which uses much larger timesteps, as we show in the next section.

5. From the coarse-grained model to Brownian dynamics

Let us consider the three-variable subsystem (1.3)–(1.5) of the coarse-grained model. Denoting y_i=(V _i,U_i,Z_i)^T, where T stands for transpose, equations (1.3)–(1.5) can be written in vector notation as follows:

$$\mathrm{d}{\mathbf{\text{y}}}_i=B{\mathbf{\text{y}}}_i\hspace{0.17em}\mathrm{d}t+\mathbf{\text{b}}\hspace{0.17em}\mathrm{d}{W}_i,$$ 5.1

where matrix $B\in {\mathbb{R}}^{3\times 3}$ and vector $\mathbf{\text{b}}\in {\mathbb{R}}^3$ are given as

$$B=\left(\begin{array}{ccc}0& 1& 0\\ -{\eta }_1& 0& 1\\ 0& -{\eta }_3& -{\eta }_2\end{array}\right)\mathrm{and}\mathbf{\text{b}}=\left(\begin{array}{c}0\\ 0\\ {\eta }_4\end{array}\right).$$ 5.2

Let us denote the eigenvalues and eigenvectors of B as λ_j and ν_j=(ν_1j,ν_2j,ν_3j)^T, j=1,2,3, respectively. The eigenvalues of B are the solutions of the characteristic polynomial

$${\lambda }^3+{\eta }_2\hspace{0.17em}{\lambda }^2+({\eta }_1+{\eta }_3)\hspace{0.17em}\lambda +{\eta }_1{\eta }_2=0.$$

Since η₁, η₂ and η₃ are positive parameters, we conclude that real parts of all three eigenvalues are negative and lie in interval (−η₂,0). Using the values of η_j, j=1,2,3, given in table 3, we present the values of eigenvalues λ_j, j=1,2,3, in table 4. The eigenvalues λ_j, j=1,2,3, are distinct. The general solution of the SDE system (5.1) can be written as follows [32]:

$${\mathbf{\text{y}}}_i(t)=\mathrm{\Phi }(t)\hspace{0.17em}\mathbf{\text{c}}+\mathrm{\Phi }(t){\int }_0^t{\mathrm{\Phi }}^{-1}(s)\hspace{0.17em}\mathbf{\text{b}}\hspace{0.17em}\mathrm{d}{W}_i,$$ 5.3

where $\mathbf{\text{c}}\in {\mathbb{R}}^3$ is a constant vector determined by initial conditions and matrix $\mathrm{\Phi }(t)\in {\mathbb{R}}^{3\times 3}$ is given as $\mathrm{\Phi }(t)=(\exp ({\lambda }_{1}t){\mathit{\nu }}_1\hspace{0.17em}|\hspace{0.17em}\exp ({\lambda }_{2}t){\mathit{\nu }}_2\hspace{0.17em}|\hspace{0.17em}\exp ({\lambda }_{3}t){\mathit{\nu }}_3),$ i.e. each column is a solution of the ODE system dy_i=By_i dt. Considering deterministic initial conditions, equation (5.3) implies that the process is Gaussian at any time t>0. Equations for means, variances and covariances then uniquely determine the distribution of y_i(t) for t>0. Equations for means can be written in the vector form as d〈y_i〉=B〈y_i〉 dt. Equations for variances and covariances are given in §3 as equations (3.3)–(3.6), (3.9) and (3.16).

Table 4.

Eigenvalues λ_j, j=1,2,3, of matrix B defined by (5.2) and time shifts $t_1^{\ast }$ and $t_2^{\ast }.$ Symbol $\mathbb{i}$ denotes the imaginary unit.

ion	λ1 [ps−1]	λ2 [ps−1]	λ3 [ps−1]	$t_1^{\ast }$ [ps]	$t_2^{\ast }$ [ps]
K+	−127.0	$-12.75+27.58\hspace{0.17em}\mathbb{i}$	$-12.75-27.58\hspace{0.17em}\mathbb{i}$	3.08×10−2	−9.39×10−3
Na+	−140.1	$-12.99+47.47\hspace{0.17em}\mathbb{i}$	$-12.99-47.47\hspace{0.17em}\mathbb{i}$	6.15×10−3	−2.35×10−2
Ca2+	−163.1	$-13.58+57.84\hspace{0.17em}\mathbb{i}$	$-13.58-57.84\hspace{0.17em}\mathbb{i}$	1.47×10−3	−2.48×10−2
Cl−	−162.9	$-13.41+30.25\hspace{0.17em}\mathbb{i}$	$-13.41-30.25\hspace{0.17em}\mathbb{i}$	2.50×10−2	−1.13×10−2

There are two important conclusions of the above analysis. First of all, eigenvalues λ_j, j=1,2,3, given in table 4 satisfy

$${\lambda }_1<\mathrm{Re}\hspace{0.17em}{\lambda }_2=\mathrm{Re}\hspace{0.17em}{\lambda }_3<0,$$

where Re denotes the real part of a complex number. There is a spectral gap between the first eigenvalue and the complex conjugate pair of eigenvalues. If we used this spectral gap, we could reduce the system to two evolution equations for times t≫1/|λ₁|. However, there is no spectral gap to reduce the system to Langevin dynamics (4.1)–(4.2). In particular, we again confirm our conclusion that a coarse-grained approximation of ion behaviour is not given in terms of Langevin dynamics. Our second conclusion is that on a picosecond time scale, we can assume stationarity in (5.1) to get

$$\mathrm{d}{X}_i=\frac{{\eta }_4}{{\eta }_1{\eta }_2}\hspace{0.17em}\mathrm{d}{W}_i,i=1,2,3.$$ 5.4

Using (3.7), (3.15) and (3.17), we have

$$\frac{{\eta }_4}{{\eta }_1{\eta }_2}=\sqrt{2D}.$$

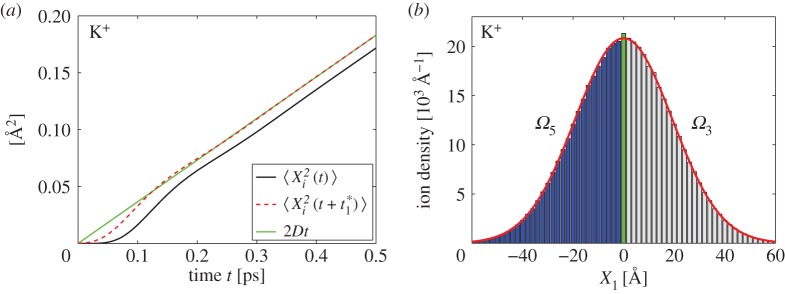
Consequently, equation (5.4) is equivalent to BD description (1.1). The convergence of (1.2)–(1.5) to the BD model is illustrated in figure 2a. We solve the system of 10 ODEs for variances and covariances given as equations (3.3)–(3.6), (3.9), (3.11)–(3.14) and (3.16). We consider (deterministic) zero initial conditions, i.e. X_i(0)=V _i(0)=U_i(0)=Z_i(0)=0. All moments are then initially equal to zero. We plot the mean square displacement $⟨X_i^2⟩$ as a function of time. We compare it with the mean square displacement of BD model (1.1) which is given as 2Dt. We observe that there is an approximately constant shift, denoted $t_1^{\ast },$ between both solutions for times t>0.2 ps. We illustrate this further by plotting $⟨X_i^2(t+t_1^{\ast })⟩$ in figure 2a. The values of shift $t_1^{\ast }$ for different ions estimated by solving the ODEs for second moments with zero initial conditions are given in table 4.

Figure 2.

(a) Comparison of the coarse-grained model (1.2)–(1.5) and BD description (1.1) for K⁺ ion. The mean square displacement computed by solving 10 ODEs (3.3)–(3.6), (3.9), (3.11)–(3.14) and (3.16) with zero initial conditions (black solid line). The same curve shifted by the value of $t_1^{\ast }$ is plotted as a red dashed line. (b) Test of accuracy of the multiscale approach in Ω₃∪Ω₄∪Ω₅ for K⁺ ion. Histogram obtained by simulating 10⁶ ions over time 10³ ps is compared with the analytical result (5.6) (red solid line). Grey bars show the ion density in Ω₃, the green bar shows the ion density in Ω₄ and blue bars show the ion density in Ω₅. Parameters are given in tables 1 and 3.

Next, we show how the BD model (1.1) and the coarse-grained model (1.2)–(1.5) can be used in different parts of the computational domain. This coupling will form one component of multiscale methodology developed in §6. BD algorithms based on equation (1.1) have been implemented in a number of methods designed for spatio-temporal modelling of intracellular processes, including Smoldyn [33], MCell [34] and Green's-function reaction dynamics [35]. Smoldyn discretizes (1.1) using a fixed BD timestep ΔT, i.e. it computes the time evolution of the position X≡X(t) of each molecule by

$$X_i(t+\mathrm{\Delta }T)=X_i(t)+\sqrt{2D\mathrm{\Delta }T}\hspace{0.17em}{\xi }_i,i=1,2,3,$$ 5.5

where (ξ₁,ξ₂,ξ₃) is a vector of normally distributed random numbers with zero mean and unit variance. We use discretization (5.5) of BD model (1.1) in this paper. BD time step ΔT has to be chosen much larger than the MD timestep Δt. We use ΔT=0.5 ps, but any larger timestep would also work well. We could also use a variable timestep, as implemented in the Green's-function reaction dynamics [35].

In §6, we consider all-atom MD simulations in domain $\mathrm{\Omega }\subset {\mathbb{R}}^3$. Our main goal is to design a multiscale approach which can compute spatio-temporal statistics with the MD-level of detail in relatively small subdomain Ω₁⊂Ω by using BD model (5.5) in the most of the rest of the computational domain. This is achieved by decomposing domain Ω into five subdomains Ω_j, j=1,2,3,4,5 (see equation (6.1) and discussion in §6). We use MD in Ω₁, the coarse-grained model (1.2)–(1.5) in Ω₃ and the BD model (5.5) in Ω₅. The remaining two subdomains, Ω₂ and Ω₄, are two overlap (hand-shaking) regions where two different simulation approaches can be used at the same time [12,36]. In the rest of this section, we focus on simulations in region Ω₃∪Ω₄∪Ω₅ which concerns coupling the coarse-grained model (1.2)–(1.5) with the BD model (5.5). We use the coarse-grained model in Ω₃∪Ω₄ and the BD model (5.5) in Ω₄∪Ω₅. In particular, we use both models in the overlap region Ω₄. Each particle which is initially in Ω₃ is simulated according to (1.2)–(1.5) (discretized using timestep Δt) until it enters Ω₅. Then we use (5.5) to evolve the position of a particle (over BD timesteps of length ΔT) until it again enters Ω₃ when we switch the description back from the BD model to the coarse-grained model. In order to do this, we have to initialize variables V _i, U_i and Z_i, i=1,2,3. We use deterministic initial conditions, V _i(0)=U_i(0)=Z_i(0)=0, discussed above.

In figure 2b, we present an illustrative simulation where ${\mathrm{\Omega }}_3\cup {\mathrm{\Omega }}_4\cup {\mathrm{\Omega }}_5={\mathbb{R}}^3$ for simplicity. We use ${\mathrm{\Omega }}_3=[h,\mathrm{\infty })\times {\mathbb{R}}^2,$ ${\mathrm{\Omega }}_4=(-h,h)\times {\mathbb{R}}^2$ and ${\mathrm{\Omega }}_5=(-\mathrm{\infty },-h]\times {\mathbb{R}}^2,$ where h=1 Å. We report averages over 10⁶ simulations of ions, half of them are initiated at X(0)=(h,0,0), i.e. they initially follow the coarse-grained model (1.2)–(1.5) with zero initial condition for other variables (V _i(0)=U_i(0)=Z_i(0)=0). The second half of ions are initiated at X(0)=(−h,0,0), i.e. they initially follow BD description (5.5). We plot the (marginal) distribution of ions along the first coordinate (X₁) at time 10³ ps in figure 2b. The computed histogram is plotted using bins of length 2 Å, i.e. the overlap region Ω₄ is equal to one bin (visualized as a green bar). Grey (respectively, blue) bars show the density of ions in Ω₃ (respectively, Ω₅). We compare our results with the analytical distribution computed for BD description (1.1) at time t=10³ ps given by

$$\varrho (x_1)=\frac{{10}^6}{4\sqrt{\pi Dt}}(\exp [-\frac{{(x_1-h)}^2}{4Dt}]+\exp [-\frac{{(x_1+h)}^2}{4Dt}]).$$ 5.6

The computed histogram compares well with (5.6), although we can observe a small error: the green bar is slightly taller than the corresponding value of (5.6). If we wanted to further improve the accuracy, we could take into account that there is time shift $t_1^{\ast },$ discussed above, introduced to the multiscale approach by using the deterministic initial conditions, V _i(0)=U_i(0)=Z_i(0)=0, for ions entering domain Ω₃. Another possibility is to sample the initial condition for V _i, U_i and Z_i from a suitable distribution. If we use the stationary distribution of subsystem (1.3)–(1.5), then $⟨V_i^2⟩$ does not evolve and is equal to

$$⟨V_i^2⟩=\frac{{\eta }_4^2}{2{\eta }_1{\eta }_2{\eta }_3}.$$

Substituting this constant for $⟨V_i^2⟩$ into (3.12), the system of 10 ODEs for second moments of (1.2)–(1.5) simplifies to four ODEs (3.11)–(3.14). Solving system (3.11)–(3.14) with zero initial conditions (assuming X_i(0)=0), we can again compute the mean square displacement. As in figure 2a, it can be shifted in time to better match with the BD result, 2Dt. We denote this time shift as $t_2^{\ast }$. Its values are given in table 4. We observe that $t_2^{\ast }$ is negative and $t_1^{\ast }$ is positive for all four ions considered in table 4. Both time shifts $t_1^{\ast }$ and $t_2^{\ast }$ (together with optimizing size h of the overlap region) could be used to further improve the accuracy of multiscale simulations in Ω₃∪Ω₄∪Ω₅ [12]. However, our main goal is to introduce a multiscale approach which can use all-atom MD simulations in Ω₁. Since MD simulations are computationally intensive, we will only consider 100 realizations of the multiscale method in §6. In particular, the Monte Carlo error will be larger than the error observed in figure 2b. Thus, we can use the above approach in Ω₃∪Ω₄∪Ω₅ without introducing observable errors in the multiscale method developed in the next section.

6. Coupling all-atom MD and BD

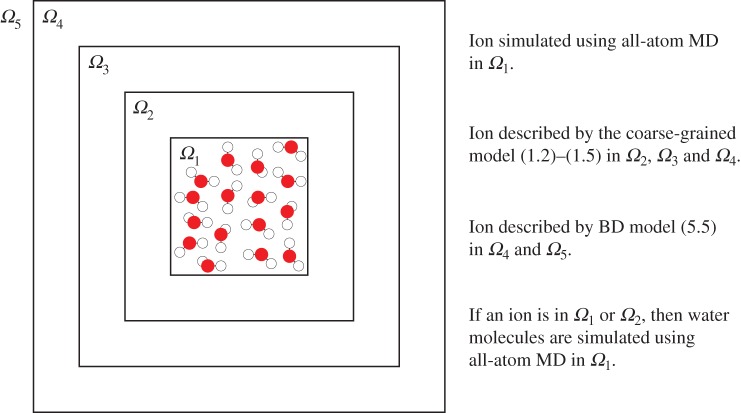
Let us consider all-atom MD in domain $\mathrm{\Omega }\subset {\mathbb{R}}^3$ which is so large that direct MD simulations would be too computationally expensive. Let us assume that a modeller only needs to consider the MD-level of detail in a relatively small subdomain Ω₁⊂Ω, while, in the rest of the computational domain, ions are transported by diffusion and BD description (1.1) is applicable. For example, domain Ω₁ could include binding sites for ions or (parts of) ion channels. In this paper, we do not focus on a specific application. Our goal is to show that the coarse-grained model (1.2)–(1.5) is an intermediate model between all-atom MD and BD which enables the use of both methods during the same dynamic simulation. To achieve this, we decompose domain Ω into five subdomains, denoted as Ω_j, j=1,2,3,4,5 (as it is schematically illustrated in figure 3). These sets are considered pairwise disjoint (i.e. Ω_i∩Ω_j=∅ for i≠j) and

$$\mathrm{\Omega }={\mathrm{\Omega }}_1\cup {\mathrm{\Omega }}_2\cup {\mathrm{\Omega }}_3\cup {\mathrm{\Omega }}_4\cup {\mathrm{\Omega }}_5.$$ 6.1

In our illustrative simulations, we consider the behaviour of one ion. If the ion is in Ω₁, then we use all-atom MD simulations as described in §2. In particular, the force between the ion and a water molecule is obtained by differentiating potential (2.1), provided that the distance between the ion and the water molecule is less than the cut-off distance (L/2). Let us denote the force exerted by the ion on the water molecule by F_iw(r_i0,r_i1,r_i2), where r_i0 (respectively, r_i1 and r_i2) is the distance between the ion and the oxygen site (respectively, the first and second hydrogen sites) on the water molecule. We use periodic boundary conditions for water molecules in Ω₁.

Figure 3.

Schematic of multiscale set-up. Note that the schematic is drawn in two spatial dimensions to enable better visualization, but all models are formulated and simulated in three spatial dimensions. (Online version in colour.)

Whenever the ion leaves Ω₁, it enters Ω₂ where we simulate its behaviour using the coarse-grained model (1.2)–(1.5). We still simulate water molecules in Ω₁ and we allow them to experience additional forces exerted by the ion which is present in Ω₂. These forces have the same functional form, F_iw, as in MD, but they have modified arguments as follows:

$${\mathbf{\text{F}}}_{\mathrm{iw}}(r_{\mathrm{i}0}+\omega \hspace{0.17em}\mathrm{dist}(\mathbf{\text{X}},{\mathrm{\Omega }}_1),r_{\mathrm{i}1}+\omega \hspace{0.17em}\mathrm{dist}(\mathbf{\text{X}},{\mathrm{\Omega }}_1),r_{\mathrm{i}2}+\omega \hspace{0.17em}\mathrm{dist}(\mathbf{\text{X}},{\mathrm{\Omega }}_1)),$$ 6.2

where ω≥0 is a parameter and dist(X,Ω₁) is the (closest) distance between the ion at position X and subdomain Ω₁. If the ion is in region Ω₃∪Ω₄∪Ω₅, then water molecules in Ω₁ are no longer simulated. We use the coarse-grained model (1.2)–(1.5) to simulate the ion behaviour in Ω₃ and the BD model (5.5) in Ω₅. Overlap region Ω₄ is used to couple these simulation methods as explained in §5.

In §5, we have already presented illustrative simulations to validate the multiscale modelling strategy chosen in region Ω₃∪Ω₄∪Ω₅. Next, we focus on testing and explaining the multiscale approach chosen to couple region Ω₁ with Ω₂. The key idea is given by force term (6.2) which is used for MD simulations of water molecules in Ω₁ when an ion is in Ω₂. This force term has two important properties:

• (i) If an ion is on the boundary of Ω₁, i.e. X∈∂Ω₁, then dist(X,Ω₁)=0 and force (6.2) is equal to force term F_iw(r_i0,r_i1,r_i2) used in Ω₁.

• (ii) If ω dist(X,Ω₁)≥L/2, then force (6.2) is equal to zero.

Property (i) implies that formula (6.2) continuously extends the force term used in MD. In particular, water molecules do not experience abrupt changes of forces when the ion crosses boundary ∂Ω₁. Property (ii) is a consequence of the cut-off distance used (together with the reaction field correction [1]) to treat long-range interactions. In our illustrative simulations, we use

$${\mathrm{\Omega }}_1={[-\frac{L}{2},\frac{L}{2}]}^3\mathrm{and}{\mathrm{\Omega }}_2={[-\frac{L}{2}-\frac{L}{2\omega },\frac{L}{2}+\frac{L}{2\omega }]}^3\mathrm{\setminus }\hspace{0.17em}{\mathrm{\Omega }}_1.$$ 6.3

Property (ii) implies that extra force (6.2) is equal to zero on boundary ∂Ω₂∖∂Ω₁ which is the boundary between regions Ω₂ and Ω₃. This is consistent with the assumption that ions in region Ω₃∪Ω₄∪Ω₅ do not interact with water molecules in region Ω₁.

If an ion is in Ω₁, we use all-atom MD as formulated in §2. Periodic boundary conditions are implemented in MD simulations. Water molecules are subject to forces exerted not only by the ion at its real position X in Ω₁, but also by its copies at periodic locations X+(iL,jL,kL), where $i,j,k\in \mathbb{Z}.$ When the ion moves to Ω₂, one of its copies is in Ω₁. Force term (6.2) is designed in such a way that the strength of interaction decreases (for every copy of the ion) with the distance, dist(X,Ω₁), between the real position of the ion and Ω₁. In particular, force term (6.2) ensures that there are continuous changes of all forces when the ion moves between regions Ω₁, Ω₂ and Ω₃.

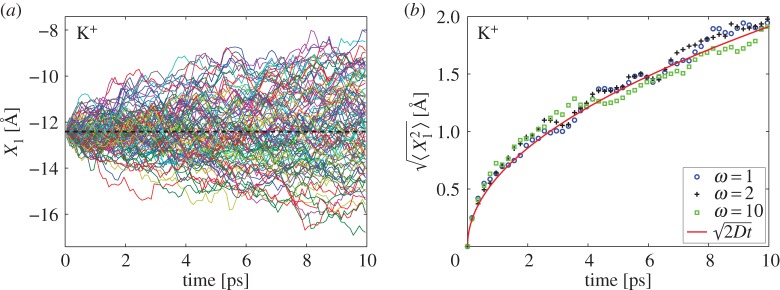
In figure 4, we present results of simulations of K⁺ ion in region Ω₁∪Ω₂. We consider 100 realizations of a multiscale simulation with one ion. Its initial position is X(0)=(−L/2,0,0) which lies on boundary ∂Ω₁. We simulate each realization for time 10 ps which is short enough that all trajectories stay inside the ball of radius L/2 centred at X(0). Then X₁-coordinate of the trajectory determines whether the ion is in Ω₁ or Ω₂. If X₁(t)≥−L/2, then the ion is in Ω₁ and it is simulated using all-atom MD. If X₂(t)<−L/2, then the ion is in Ω₂ and evolves according to the coarse-grained model (1.2)–(1.5). In figure 4a, we use (6.2) with ω=1 and plot X₁ coordinates of all 100 realizations. We observe that the computed trajectories spread on both sides of boundary ∂Ω₁ (dashed line) without any significant bias. The mean square displacement is presented in figure 4b for three different values of ω. The results compare well with (2Dt)^1/2 which is the mean square displacement of one coordinate of the diffusion process.

Figure 4.

(a) One hundred realizations of a multiscale simulation of K⁺ ion initiated at (−L/2,0,0). We plot X₁ coordinate as a function of time. Ion is described by all-atom MD for X₁≥−L/2 and by the coarse-grained model (1.2)–(1.5) for X₁<−L/2. The boundary between Ω₁ and Ω₂ is visualized using the black dashed line. We use ω=1 in (6.2). (b) The mean square displacement in the first coordinate of K⁺ ion simulated in Ω₁∪Ω₂ and computed as the average of 100 realizations for ω=1 (blue circles), ω=2 (black crosses) and ω=10 (green squares).

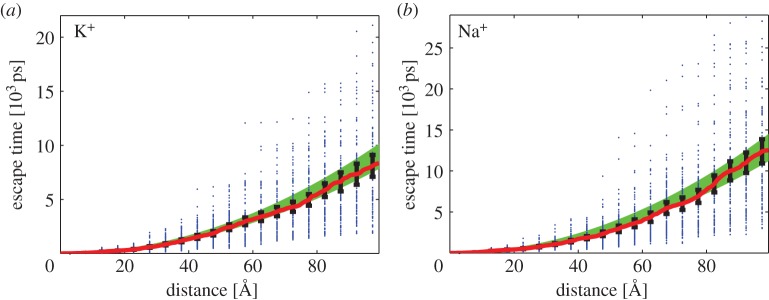
We conclude with illustrative simulations which are coupling all-atom MD with BD. We use domain $\mathrm{\Omega }\in {\mathbb{R}}^3$ decomposed into five regions as in equation (6.1), where Ω₁ and Ω₂ are given by (6.3), and

$$\begin{array}{rl}{\mathrm{\Omega }}_3& ={[-\frac{L}{2}-\frac{L}{2\omega }-h_1,\frac{L}{2}+\frac{L}{2\omega }+h_1]}^3\mathrm{\setminus }\hspace{0.17em}({\mathrm{\Omega }}_1\cup {\mathrm{\Omega }}_2),\\ {\mathrm{\Omega }}_4& ={[-\frac{L}{2}-\frac{L}{2\omega }-h_1-h_2,\frac{L}{2}+\frac{L}{2\omega }+h_1+h_2]}^3\mathrm{\setminus }\hspace{0.17em}({\mathrm{\Omega }}_1\cup {\mathrm{\Omega }}_2\cup {\mathrm{\Omega }}_3),\\ {\mathrm{\Omega }}_5& ={\mathbb{R}}^3\setminus ({\mathrm{\Omega }}_1\cup {\mathrm{\Omega }}_2\cup {\mathrm{\Omega }}_3\cup {\mathrm{\Omega }}_4),\end{array}$$

where ω=10, h₁=L/20 and h₂=L/10. Then the BD domain is ${\mathrm{\Omega }}_5={\mathbb{R}}^3\setminus {[-7L/10,7L/10]}^3$. We place an ion at the origin (centre of MD domain Ω₁), i.e. X(0)=(0,0,0), and we simulate each trajectory until it reaches the distance 4L=99.32 Åfrom the origin. Let $\mathcal{T}(r)$ be the time when a trajectory first reaches distance r from the origin. In figure 5, we plot escape time $\mathcal{T}(r)$ as a function of distance r. We plot the value of $\mathcal{T}(r)$ for each realization as a blue point. The largest computed escape times (for r=4L) are 38 506 ps for K⁺ and 47 212 ps for Na⁺. They are outside the range of panels in figure 5, but the majority of data points are included in this figure. We also plot average $⟨\mathcal{T}(r)⟩$ (red solid line) together with 95% confidence intervals. They are compared with theoretical results obtained for the BD model (1.1). The escape time distribution for the BD model (1.1) has mean equal to $⟨\mathcal{T}(r)⟩=r^2/(6D)$ and standard deviation $r^2/(3\sqrt{10}\hspace{0.17em}D).$ The corresponding theoretical 95% confidence interval (for 100 samples) is

$$(\frac{r^2}{6D}-1.96\frac{r^2}{30D},\hspace{0.17em}\frac{r^2}{6D}+1.96\frac{r^2}{30D}).$$ 6.4

This interval is visualized as the green area in figure 5. We note that it would be relatively straightforward to continue the presented multiscale computation and simulate ion diffusion in domains covering the whole cell. The most computationally intensive part is all-atom MD simulation in Ω₁∪Ω₂. However, once the ion enters Ω₅, we can compute its trajectory very efficiently. We could further increase the BD timestep in parts of Ω₅ which are far away from Ω₄, or we could use event-based algorithms, like Green's-function reaction dynamics [35] or First-passage kinetic Monte Carlo method [37], to compute the ion trajectory in region Ω₅.

Figure 5.

Escape time $\mathcal{T}(r)$ to reach distance r from the origin computed by the multiscale method. We consider (a) K⁺ ion; and (b) Na⁺ ion. We plot escape times for individual realizations (blue points), the mean escape time estimated from 100 realizations (red solid line) and the theoretical 95% confidence interval (6.4) (green area). We use ω=10 in (6.2).

7. A hierarchy of stochastic coarse-grained models

In §6, the coarse-grained model (1.2)–(1.5) has been used in intermediate regions (denoted Ω₂, Ω₃ and Ω₄ in figure 3) to couple all-atom MD and BD. It is a simple model which has all the necessary properties for this task. The developed multiscale algorithm enables the use of MD together with modern spatio-temporal simulation algorithms for intracellular processes. The coarse-grained model (1.2)–(1.5) (parametrized by four constants η₁, η₂, η₃ and η₄) provides a better description of ion dynamics than BD (parametrized by one constant D). However, it does not capture all the details of MD. In this section, we introduce a hierarchy of coarse-grained models which generalize (1.2)–(1.5) and include an increasing number of parameters. We illustrate that these models can be used to fit additional characteristics of all-atom MD simulations.

There has been a lot of approaches in the literature to develop coarse-grained models at equilibrium by constructing suitable coarse-grained potential energy functions with fewer degrees of freedom [38–40]. However, the same coarse-grained potential energy function can correspond to many different dynamic coarse-grained models. In particular, the conservative Hamiltonian dynamics of coarse-grained variables on a coarse-grained potential surface is usually a poor approximation of the real dynamics of all-atom MD models [41,42]. In recent work, Davtyan et al. [13] use fictitious particles with harmonic interactions with coarse-grained degrees of freedom (i.e. they add quadratic terms to the potential function of the system) to improve the fit between an MD model and the dynamics on a coarse-grained potential surface. Each fictitious particle is also subject to a friction force and noise. We will apply the fictitious particle approach to develop a hierarchy of coarse-grained models which generalize (1.2)–(1.5).

Let us consider N fictitious particles interacting with an ion at position $\mathbf{X}\equiv (X_1,X_2,X_3)$ with velocity $\mathbf{V}\equiv (V_1,V_2,V_3)$. Let ${\tilde{\mathbf{X}}}_j\equiv ({\tilde{X}}_{j,1},{\tilde{X}}_{j,2},{\tilde{X}}_{j,3})$ be the position of the jth fictitious particle, $j=1,2,\dots ,N$. Let ${\tilde{\mathbf{V}}}_j\equiv ({\tilde{V}}_{j,1},{\tilde{V}}_{j,2},{\tilde{V}}_{j,3})$ be its velocity. Then the fictitious particle model [13] of an ion can be written as the following set of 6(N+1) equations (for i=1,2,3 and $j=1,2,\dots ,N$)

$$\begin{array}{rl}\mathrm{d}{X}_i& =V_i\hspace{0.17em}\mathrm{d}t,\end{array}$$ 7.1

$$\begin{array}{rl}\mathrm{d}{V}_i& =\sum _{j=1}^N{\alpha }_{j,1}({\tilde{X}}_{j,i}-X_i)\hspace{0.17em}\mathrm{d}t,\end{array}$$ 7.2

$$\begin{array}{rl}\mathrm{d}{\tilde{X}}_{j,i}& ={\tilde{V}}_{j,i}\hspace{0.17em}\mathrm{d}t\end{array}$$ 7.3

$$\begin{array}{rl}\text{and}\mathrm{d}{\tilde{V}}_{j,i}& =-({\alpha }_{j,2}{\tilde{V}}_{j,i}+{\alpha }_{j,3}({\tilde{X}}_{j,i}-X_i))\hspace{0.17em}\mathrm{d}t+{\alpha }_{j,4}\hspace{0.17em}\mathrm{d}{W}_{j,i},\end{array}$$ 7.4

where white noise vectors dW_j≡(dW_j,1,dW_j,2,dW_j,3) are mutually independent. Each fictitious particle can be characterized by four constants: three of them correspond to three force terms on the right-hand side of (7.4) and the fourth one is the fictitious particle mass. In order to write the fictitious particle model in a similar way as other models in this paper, we adsorbed the masses of the ion and fictitious particles into the constants on the right-hand sides of equations (7.2) and (7.4). In particular, the jth fictitious particle is characterized by four positive constants α_j,1, α_j,2, α_j,3 and α_j,4. To connect the hierarchy of the stochastic fictitious particle models (7.1)–(7.4) with the coarse-grained model (1.2)–(1.5), we introduce new variables ${\tilde{U}}_{j,i}={\alpha }_{j,1}({\tilde{X}}_{j,i}-X_i)$ and ${\tilde{Z}}_{j,i}={\alpha }_{j,1}{\tilde{V}}_{j,i}$. Then equations (7.2)–(7.4) read as follows:

$$\begin{array}{rl}\mathrm{d}{V}_i& =\sum _{j=1}^N{\tilde{U}}_{j,i}\hspace{0.17em}\mathrm{d}t,\end{array}$$ 7.5

$$\begin{array}{rl}\mathrm{d}{\tilde{U}}_{j,i}& =({\tilde{Z}}_{j,i}-{\alpha }_{j,1}{V}_i)\hspace{0.17em}\mathrm{d}t\end{array}$$ 7.6

$$\begin{array}{rl}\text{and}\mathrm{d}{\tilde{Z}}_{j,i}& =-({\alpha }_{j,2}{\tilde{Z}}_{j,i}+{\alpha }_{j,3}{\tilde{U}}_{j,i})\hspace{0.17em}\mathrm{d}t+{\alpha }_{j,1}{\alpha }_{j,4}\hspace{0.17em}\mathrm{d}{W}_{j,i}.\end{array}$$ 7.7

Using N=1 and denoting $U_i={\tilde{U}}_{1,i}$ and $Z_i={\tilde{Z}}_{1,i},$ we obtain the coarse-grained model (1.2)–(1.5) where η₁=α_1,1, η₂=α_1,2, η₃=α_1,3 and η₄=α_1,1α_1,4. Thus, the coarse-grained model (1.2)–(1.5) is equivalent to the fictitious particle model (7.1)–(7.4) for N=1. Moreover, stochastic coarse-grained models in the hierarchy (7.1)–(7.4) provide generalizations of the coarse-grained model (1.2)–(1.5) for N≥2 and can be used to fit additional details of MD simulations.

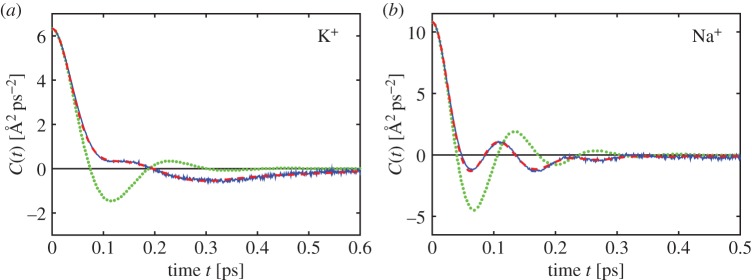
One commonly used MD characteristic is the velocity autocorrelation function

$$C(t)=⟨V_i(t)V_i(0)⟩.$$ 7.8

In figure 6, we plot the velocity autocorrelation function estimated from MD simulations of K⁺ and Na⁺ ions. Using (5.3), we can find an analytical expression for the velocity autocorrelation function of the coarse-grained model (1.2)–(1.5) as follows:

$$C(t)=(1,0,0)\hspace{0.17em}\mathrm{\Phi }(t)\hspace{0.17em}{\mathrm{\Phi }}^{-1}(0)\left(\begin{array}{c}⟨V_i^2⟩\\ 0\\ 0\end{array}\right),$$ 7.9

Figure 6.

(a) Velocity autocorrelation function (7.8) calculated by the all-atom MD model of K⁺ ion (blue solid line), by the coarse-grained model (1.2)–(1.5) (green dotted line) and by the fictitious particle model (7.1)–(7.4) for N=3 (red dashed line), where the parameters of (7.1)–(7.4) are α_1,1=5.64×10² ps⁻², α_1,2=73.8 ps⁻¹, α_1,3=3.42×10³ ps⁻², α_1,4=80.9 Å ps^−3/2, α_2,1=1.26× 10² ps⁻², α_2,2=21.3 ps⁻¹, α_2,3=7.27×10² ps⁻², α_2,4= 3.43×10⁻¹ Å ps^−3/2, α_3,1=72.1 ps⁻², α_3,2=2.02×10² ps⁻¹, α_3,3=3.26×10⁻¹ ps⁻² and α_3,4=1.22× 10² Å ps^−3/2. The parameters of the coarse-grained model (1.2)–(1.5) are given in table 3. (b) The same computations for Na⁺ ion, where the parameters of the fictitious particle model (7.1)–(7.4) are α_1,1=3.05×10³ ps⁻², α_1,2=3.08×10² ps⁻¹, α_1,3=8.99× 10³ ps⁻², α_1,4=98.7 Å ps^−3/2, α_2,1= 96.5 ps⁻², α_2,2=2.48×10² ps⁻¹, α_2,3=4.62×10² ps⁻², α_2,4=15.8 Å ps^−3/2, α_3,1=23.5 ps⁻², α_3,2=25.5 ps⁻¹, α_3,3=3.82×10² ps⁻² and α_3,4=1.18×10³ Å ps^−3/2.

where matrix $\mathrm{\Phi }(t)\in {\mathbb{R}}^{3\times 3}$ is given as $\mathrm{\Phi }(t)=(\exp ({\lambda }_{1}t){\mathit{\nu }}_1\hspace{0.17em}|\hspace{0.17em}\exp ({\lambda }_{2}t){\mathit{\nu }}_2\hspace{0.17em}|\hspace{0.17em}\exp ({\lambda }_{3}t){\mathit{\nu }}_3),$ where λ_j, j=1,2,3, are eigenvalues of matrix B given by (5.2) and ν_j=(ν_1j,ν_2j,ν_3j)^T are the corresponding eigenvectors. In figure 6, we plot velocity autocorrelation functions (7.9) as green dotted lines for K⁺ and Na⁺ ions.

Using t=0 in (7.9), we obtain $C(0)=⟨V_i^2⟩$. Since we have parametrized the coarse-grained model (1.2)–(1.5) to give the same value of $⟨V_i^2⟩$ as obtained by the corresponding MD model, the velocity autocorrelation function of the coarse-grained model agrees with MD simulations for t=0. In figure 6, we observe that the coarse-grained model approximates C(t) well for t between 0 and 30 fs. It is also a good approximation for large values of t, because C(t)→0 as $t\to \mathrm{\infty },$ but we can clearly see a difference for intermediate values of t. Since we have parametrized the coarse-grained model (1.2)–(1.5) by fitting the diffusion constant D, the coarse-grained model also approximates well the integral of C(t), because of the Green–Kubo formula

$$D={\int }_0^{\mathrm{\infty }}⟨V_i(t)V_i(0)⟩\hspace{0.17em}\mathrm{d}t={\int }_0^{\mathrm{\infty }}C(t)\hspace{0.17em}\mathrm{d}t.$$

If a modeller wants to improve the approximation of C(t) for intermediate values of t, the fictitious particle model (7.1)–(7.4) can be used for N>1 as a generalization of the coarse-grained model (1.2)–(1.5). We will illustrate this by using N=3. Equations (7.5)–(7.7) can then be rewritten in vector notation as follows (cf. (5.1)):

$$\mathrm{d}{\widetilde{\mathbf{\text{y}}}}_i=\tilde{B}\hspace{0.17em}{\widetilde{\mathbf{\text{y}}}}_i\hspace{0.17em}\mathrm{d}t+{\tilde{b}}^{\mathrm{T}}\hspace{0.17em}\mathrm{d}\stackrel{~}{{\mathbf{\text{W}}}_i},$$ 7.10

where ${\widetilde{\mathbf{\text{y}}}}_i={(V_i,{\tilde{U}}_{1,i},{\tilde{Z}}_{1,i},{\tilde{U}}_{2,i},{\tilde{Z}}_{2,i},{\tilde{U}}_{3,i},{\tilde{Z}}_{3,i})}^{\mathrm{T}}$,

$$\tilde{b}=\left(\begin{array}{ccccccc}0& 0& {\alpha }_{1,1}{\alpha }_{1,4}& 0& 0& 0& 0\\ 0& 0& 0& 0& {\alpha }_{2,1}{\alpha }_{2,4}& 0& 0\\ 0& 0& 0& 0& 0& 0& {\alpha }_{3,1}{\alpha }_{3,4}\end{array}\right),\mathrm{d}\stackrel{~}{{\mathbf{\text{W}}}_i}=\left(\begin{array}{c}\mathrm{d}{W}_{1,i}\\ \mathrm{d}{W}_{2,i}\\ \mathrm{d}{W}_{3,i}\end{array}\right),$$

and matrix $\tilde{B}\in {\mathbb{R}}^{7\times 7}$ is given as (cf. (5.2))

$$\tilde{B}=\left(\begin{array}{ccccccc}0& 1& 0& 1& 0& 1& 0\\ -{\alpha }_{1,1}& 0& 1& 0& 0& 0& 0\\ 0& -{\alpha }_{1,3}& -{\alpha }_{1,2}& 0& 0& 0& 0\\ -{\alpha }_{2,1}& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& -{\alpha }_{2,3}& -{\alpha }_{2,2}& 0& 0\\ -{\alpha }_{3,1}& 0& 0& 0& 0& 0& 1\\ 0& 0& 0& 0& 0& -{\alpha }_{3,3}& -{\alpha }_{3,2}\end{array}\right).$$

Let us denote the eigenvalues and eigenvectors of $\tilde{B}$ as ${\tilde{\lambda }}_j$ and ${\tilde{\mathit{\nu }}}_j,$ $j=1,2,\dots ,7,$ respectively. In what follows, we will assume that coefficients α_j,k are chosen so that the eigenvalues of $\tilde{B}$ are distinct and have negative real parts. Then the velocity autocorrelation function of the fictitious particle model (7.10) can be computed as follows (cf. (7.9))

$$C(t)=(1,0,0,0,0,0,0)\hspace{0.17em}\tilde{\mathrm{\Phi }}(t)\hspace{0.17em}{\tilde{\mathrm{\Phi }}}^{-1}(0)\hspace{0.17em}⟨V_i{\widetilde{\mathbf{\text{y}}}}_i⟩,$$ 7.11

where matrix $\tilde{\mathrm{\Phi }}(t)\in {\mathbb{R}}^{7\times 7}$ is given as $\tilde{\mathrm{\Phi }}(t)=(\exp ({\tilde{\lambda }}_{1}t){\tilde{\mathit{\nu }}}_1|\exp ({\tilde{\lambda }}_{2}t){\tilde{\mathit{\nu }}}_2\hspace{0.17em}|\hspace{0.17em}\cdots \hspace{0.17em}|\hspace{0.17em}\exp ({\tilde{\lambda }}_{7}t){\tilde{\mathit{\nu }}}_7),$ i.e. each column is a solution of the ODE system $\mathrm{d}{\widetilde{\mathbf{\text{y}}}}_i=\tilde{B}{\widetilde{\mathbf{\text{y}}}}_i\hspace{0.17em}\mathrm{d}t$. Vector $⟨V_i{\widetilde{\mathbf{\text{y}}}}_i⟩$ is the first column of the equilibrium covariance matrix $⟨{\widetilde{\mathbf{\text{y}}}}_i{\widetilde{\mathbf{\text{y}}}}_i^{\mathrm{T}}⟩$ which can be obtained as the solution of the linear system

$$\tilde{B}⟨{\widetilde{\mathbf{\text{y}}}}_i{\widetilde{\mathbf{\text{y}}}}_i^{\mathrm{T}}⟩+⟨{\widetilde{\mathbf{\text{y}}}}_i{\widetilde{\mathbf{\text{y}}}}_i^{\mathrm{T}}⟩{\tilde{B}}^{\mathrm{T}}=-{\tilde{b}}^{\mathrm{T}}\tilde{b}.$$ 7.12

Since we want the fictitious particle model (7.1)–(7.4) to be a generalization of the coarse-grained models (1.2)–(1.5), we select its parameters so that the model (7.1)–(7.4) has the same diffusion constant D and moments $⟨V_i^2⟩$ and $⟨U_i^2⟩$ as calculated by all-atom MD simulations in table 2. This yields three conditions between 12 parameters α_j,k, j=1,2,3, k=1,2,3,4, of the fictitious particle model (7.1)–(7.4). In particular, we have a lot of freedom to choose the 12 model parameters. In figure 6, we plot the velocity autocorrelation function (7.11) for specific choices of parameters α_j,k, illustrating that we can select these parameters to approximate velocity autocorrelation functions obtained by all-atom MD. To obtain these results, we use a simple acceptance–rejection algorithm based on equations (7.11)–(7.12). We start with an initial guess of 12 parameters α_j,k and calculate the L¹-error between the velocity autocorrelation function (7.11) and the MD result (blue solid line in figure 6). Then we perturb the parameters α_j,k in a way that the resulting model still has the same D, $⟨V_i^2⟩$ and $⟨U_i^2⟩$ and we use the new set of parameters α_j,k to recalculate the L¹-error between the velocity autocorrelation function (7.11) and the MD result. If the error decreases, then we accept the new set of parameters. We iterate these steps until the desired level of error.

In figure 6, we observe that the velocity autocorrelation function computed by (7.11) for N=3 (red dashed line) approximates well the MD result. In a similar way, we could fit other autocorrelation functions (if required) by coarse-grained models in the hierarchy (7.1)–(7.4) for sufficiently large N. However, as we have seen in §6, coupling all-atom MD and BD can be achieved by the coarse-grained model (1.2)–(1.5), i.e. by using N=1.

8. Discussion

In this paper, we have introduced and studied the coarse-grained model (1.2)–(1.5) of an ion in aqueous solution. We have parametrized this model using all-atom MD simulations for four ions (K⁺, Na⁺, Ca²⁺ and Cl⁻) and showed that this model provides an intermediate description between all-atom MD and BD simulations. It can be used both with MD timestep Δt (to couple it with all-atom MD simulations) and BD time step ΔT (to couple it with BD description (1.1)). In particular, the coarse-grained model enables multiscale simulations which use all-atom MD and BD in different parts of the computational domain.

In §6, we have illustrated this multiscale methodology using a first passage type problem where we have reported the time taken by an ion to reach a specific distance. Possible applications of this multiscale methodogy include problems where a modeller considers all-atom MD in several different parts of the cell (e.g. close to binding sites or ion channels) and wants to use efficient BD simulations to transport ions by diffusion between regions where MD is used. The proposed approach thus enables the inclusion of MD-level of detail in computational domains which are much larger than would be possible to study by direct MD simulations.

Although the illustrative simulations in §6 are reported over distances of the order of 10² Å, this is not a restriction of the method. Most of the computational time is spent by considering all-atom MD in Ω₁∪Ω₂. BD uses a much larger timestep which enables us to further extend the BD region Ω₅ (and consequently, the original domain Ω). Moreover, if we are far away from the MD domain Ω₁, we can further increase the efficiency of BD simulations by using different BD timesteps in different parts of the BD subdomain Ω₅ [12], or by using event-based BD algorithms [35,37]. The computational intensity of BD simulations can be further decreased by using multiscale methods which efficiently and accurately combine BD models with lattice-based (compartment-based) models [43,44]. Such a strategy has been previously used for modelling intracellular calcium dynamics [3,7] or actin dynamics in filopodia [45], and enables us to extend both temporal and spatial extents of the simulation.

In §7, we have presented a systematic procedure for including additional auxiliary variables and parameters to the coarse-grained model (1.2)–(1.5). We have illustrated that the generalized models can be used to fit additional details of all-atom MD simulations. The generalization of the coarse-grained model (1.2)–(1.5) is based on the fictitious particle approach [13] which introduces fictitious particles with harmonic interactions with coarse-grained degrees of freedom. Such special heat baths have been previously studied in the context of the generalized Langevin equation [14–17]. In §7, we have shown that an appropriately formulated fictitious particle model which uses one fictitious particle per ion [13] has the same dynamics as the coarse-grained model (1.2)–(1.5).

In the literature, MD methods have been used to estimate parameters of BD simulations of ions [46]. There has also been a lot of progress in systematic coarse-graining of MD simulations [40,47]. The approach presented in this paper not only uses all-atom MD simulations to estimate parameters of a coarser description, but it also designs a multiscale approach where both methods are used during the same simulation. Methods which adaptively change the resolution of MD on demand have been previously reported in [48,49]. They include algorithms which couple all-atom MD with coarse-grained MD. The coarse-grained model studied in this work does not include any water molecules and has different application areas. One of them is modelling of calcium induced calcium release through IP₃R channels [3] which is discussed as a motivating example in §1. MD simulations in this paper use the three-site SPC/E model of water. An open question is to extend our observations and analysis to other MD models of water, which include both more detailed water models with additional sites [21,22] and coarse-grained MD models of water [50].

Competing interests

I have no competing interests.

Funding

I thank the Royal Society for a University Research Fellowship and the Leverhulme Trust for a Philip Leverhulme Prize.