Dynamic interfacial trapping of flexural waves in structured plates

Abstract

The paper presents new results on the localization and transmission of flexural waves in a structured plate containing a semi-infinite two-dimensional array of rigid pins. In particular, localized waves are identified and studied at the interface boundary between the homogeneous part of the flexural plate and the part occupied by rigid pins. A formal connection has been made with the dispersion properties of flexural Bloch waves in an infinite doubly periodic array of rigid pins. Special attention is given to regimes corresponding to standing waves of different types as well as Dirac-like points that may occur on the dispersion surfaces. A single half-grating problem, hitherto unreported in the literature, is also shown to bring interesting solutions.

1. Introduction

The advent of designer materials such as metamaterials, photonic crystals and micro-structured media that are able to generate effects unobtainable by natural media, such as Pendry's flat lens [1], is driving a revolution in materials science. Many of these ideas originate in electromagnetism and optics, but are now percolating into other wave systems such as those of elasticity, acoustics or the idealized Kirchhoff–Love plate equations for flexural waves, with this analogue of photonic crystals being labelled as platonics [2]. Many of the effects from photonics also appear in the flexural wave context, albeit with some changes due to the biharmonic nature of the Kirchhoff–Love equation: ultra-refraction and negative refraction [3–5], Dirac-like cones, Dirac-cone cloaking and related effects [6–8] among others.

The Kirchhoff–Love equations are good approximations within their realm of applicability (for instance with h, λ as plate thickness and typical wavelength, respectively, then h/λ≪1 is required) and capture much of the essence of the wave physics, hence their emergent popularity. The system is relatively simple so analytic results for infinite periodic structured plates pinned, say, at regular points readily emerge [9], with much of this earlier work reviewed in Mead [10]; more recently multipole methods [11], extending pins to cylinders or high-frequency homogenization approaches [12] to obtain effective continuum equations that encapsulate the microstructure, have emerged. For finite pinned regions of a plate, a Green's function approach [13] leads to rapid numerical solutions, or for an infinite grating one may employ an elegant methodology for exploring Rayleigh–Bloch modes. This includes extensions to stacks of gratings and the trapping and filtering of waves [14–16] which further exemplify this approach. Problems such as these start to pose questions about semi-infinite gratings, or edge states in semi-infinite lattices, and our aim is to generate the relevant exact solutions.

For semi-infinite cracks, and other situations where the change in the boundary condition along a line is of interest, the classical Wiener–Hopf technique [17] for solving integral equations is highly developed and often used for mixed boundary-value problems in continuum mechanics; indeed, the seminal Wiener–Hopf treatise by Noble [18] covers this aspect almost exclusively. However, lesser known [19] and presented only as an exercise in Noble [18], 4.10, pp. 173–174 is its application to continuum discrete problems such as gratings. As such, it has seen notable application to the fracture of discrete lattice systems as reviewed by Slepyan [20], to antenna design [21] and to various semi-infinite grating and lattice scattering problems in acoustics [22,23], where the early work of Hills & Karp [24] (hereafter referred to as HK), motivated by Karp [25], provides a wealth of useful information.

The corresponding exact solutions for the platonic system are not available and, given the current interest in platonics and the versatility of these in, say, asymptotic schemes and the key insight given into the physics and results, we aim to provide these here. Of particular interest are regimes for which one observes the interplay between grating modes and Floquet–Bloch waves in a full doubly periodic infinite structure. In particular, these include frequencies and wavevector components corresponding to stationary points on the dispersion surfaces as well as neighbourhoods of the Dirac-like points. Additionally, we address a fundamental question as to whether a simple, yet surprisingly physically rich, structure such as a half-plane of rigid pins in a plate supports flexural interfacial modes; by which we mean waves that propagate along the interface of the platonic crystal and the homogeneous part of the biharmonic plate.

Since the underlying mathematical structure of a semi-infinite linear grating and that of a semi-infinite lattice are very similar, we choose to treat both examples within this paper. For clarity, we shall refer to a grating when we have a single half-line of scatterers (figure 1a) and to a lattice when there is a lattice of scatterers in a half-plane (figure 1b); throughout this paper, we shall assume that we have point-clamped scatterers although the analysis is readily extended to more complicated conditions holding at a point. In §2, we formulate the problem, drawing upon the discrete Wiener–Hopf technique used by HK for the semi-infinite diffraction grating governed by a Helmholtz operator; much is directly applicable provided we replace the point source Green's function for the two-dimensional Helmholtz operator with that for the biharmonic operator. In some regards, difficulties associated with the Helmholtz Green's function's logarithmic singularity are bypassed for the biharmonic case, where there is no singularity. We turn our attention to the linear grating first, in §2a, and follow that with an analysis of the lattice, in §2b. As noted above this is a parametrically and physically rich problem displaying a surprisingly wide range of behaviours and we outline methodologies for both interpreting and designing specific behaviours; we consider these in §3a,b for the semi-infinite grating and lattice, respectively. Concluding remarks are drawn together in §4.

Figure 1.

(a) A single semi-infinite grating of rigid pins in a biharmonic plate with spacing s. The pins are represented by the large black discs. The forces/intensities are represented by the coefficients A_i, and displacements, used in the Wiener–Hopf approach, by b_i. (b) The semi-infinite lattice of pins, consisting of an array of infinite gratings with period d_y in the vertical direction and horizontal spacing d_x.

2. Formulation

The methodology primarily adopted here, at least for the exact solution, is that of discrete Wiener–Hopf drawing upon the treatment of the Helmholtz semi-infinite grating by HK, which we briefly review here. To avoid issues with singularities in their problem, HK consider cylinders of finite radius, small compared with wavelength and widely spaced. The diffracted field consists of a cylindrical wave plus a set of plane waves that possess amplitudes and directions of propagation identical to those for an infinite grating, but for the semi-infinite case they do not exist everywhere. Instead the end-effects lead to shadow boundaries defined by lines drawn from the end of the grating to infinity along propagation directions of various plane waves. The cylindrical wave has sharp zeros followed by a maximum for certain directions; these zeros occur in the directions that would be shadow boundaries if the incident wave travels directly into the end of the grating—a class of resonant cases characterized by a diffracted wave that travels parallel to the grating. HK note that, for the wave that travels parallel and out of the grating, the cylindrical wave and all the other plane waves vanish.

Assuming isotropic scatterers HK (see also Linton & Martin [22]) pose the solution in the form

$$U(r,\theta )=\sum _{n=0}^{\mathrm{\infty }}{A}_n{H}_0^{(1)}(\beta r_n),$$ 2.1

for some coefficients A_n to be determined and $H_0^{(1)}(z)$ being the usual Hankel function of the first kind with wavenumber β, and r_n representing the distance between the observation point (r,θ) and the nth scattering element on the x-axis; for an infinite array these just differ by a phase factor and the analysis is simpler. The assumption that the grating's elements are small, and therefore scatter isotropically, is not formally required for the pinned biharmonic plate as this is exactly true.

In HK, the spacing between the scatterers is assumed to be large compared with the wavelength, and it must not be an integral or half-integral multiple of the wavelength. These assumptions are required by the mathematical analysis employed. The reason for the limitation on the integral or half-integral multiples of wavelength is to ensure that branch cuts for $z=\exp (\mathrm{i}\beta s)$ and $z=\exp (-\mathrm{i}\beta s)$ are distinct (see the electronic supplementary material, appendix B, for a discussion of branch cuts for the biharmonic plate), where s is the spacing of the pins.

To determine the scattered wave coefficients A_n in (2.1), the boundary conditions generate an infinite system of linear equations solvable using discrete Wiener–Hopf. In the neighbourhood of the nth scatterer, the field consists of the incident plane wave, the sum of waves scattered to the nth element by the other elements and the wave scattered by the nth element itself,

$${\mathrm{e}}^{\mathrm{i}ns\beta \cos \psi }+\sum _{\begin{array}{c}m=0\\ m\ne n\end{array}}^{\mathrm{\infty }}{A}_m{H}_0^{(1)}(\beta |n-m|s)+H_0^{(1)}(\beta a)=0,n=0,1,2,\dots .$$ 2.2

Here a is the radius of the individual elements. The term $H_0^{(1)}(\beta a)$ is treated separately because of the logarithmic singularity arising for the Hankel function at the origin. Although a small radius a is assumed by HK, the singularity poses problems as a→0 and much of HK involves dealing with this; for the biharmonic case we discuss in this article, the Green's function is finite at the source point rather than diverging logarithmically.

(a). Semi-infinite grating of rigid pins in a biharmonic plate

The Green's function G(β,|r−r′|) for an infinite Kirchhoff–Love plate is given by

$$G(\beta ,|\mathbf{\text{r}}-{\mathbf{\text{r}}}^{\prime }|)=\frac{\mathrm{i}}{8{\beta }^2}[H_0^{(1)}(\beta |\mathbf{\text{r}}-{\mathbf{\text{r}}}^{\prime }|)+\frac{2\mathrm{i}}{\pi }{K}_0(\beta |\mathbf{\text{r}}-{\mathbf{\text{r}}}^{\prime }|)].$$ 2.3

This function describes an outgoing flexural wave in an isotropic homogeneous thin plate generated by a point source at r=r′, and it satisfies the equation

$${\mathrm{\Delta }}^{2}G(\beta ,|\mathbf{\text{r}}-{\mathbf{\text{r}}}^{\prime }|)-{\beta }^{4}G(\beta ,|\mathbf{\text{r}}-{\mathbf{\text{r}}}^{\prime }|)=\delta (\mathbf{\text{r}}-{\mathbf{\text{r}}}^{\prime }).$$ 2.4

As in (2.1) the Green's function (2.3) contains $H_0^{(1)}$, but there is now an additional term containing the modified Bessel function K₀ [26]; this Green's function is bounded at r=r′.

For a semi-infinite array of rigid pins located at points r′_n=(ns,0) for spacing s and non-negative integer n, the amplitude of the scattered field is given by

$$U(r,\theta )=\sum _{n=0}^{\mathrm{\infty }}{A}_{n}G(\beta ,|\mathbf{\text{r}}-{\mathbf{\text{r}}}_n^{\prime }|),$$ 2.5

where the coefficients A_n are to be determined. To set up the system of equations, we introduce displacements b_n at (ns,0) for all n, imposing zero displacements at the pins, b_n=0 for n≥0; b_n are unknown for n<0. For the intensities, we define A_n=0 for all n<0.

The analogue of (2.2) is

$${\mathrm{e}}^{\mathrm{i}ns\beta \cos \psi }+\sum _{m=0}^{\mathrm{\infty }}{A}_{m}G(\beta ,|n-m|s)=b_n,n\in \mathbb{Z}.$$ 2.6

We now employ the z-transform, multiply (2.6) by zⁿ for the z complex, and sum over all n,

$$\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{z}^n\hspace{0.17em}{\mathrm{e}}^{\mathrm{i}ns\beta \cos \psi }+\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}\sum _{m=0}^{\mathrm{\infty }}{z}^n{A}_{m}G(\beta ,|n-m|s)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{z}^n{b}_n.$$ 2.7

To transform (2.7) into a single functional equation of the Wiener–Hopf type, it is convenient to define A(z) and a kernel function $\mathcal{K}(z)$ as

$$A(z)=\sum _{m=0}^{\mathrm{\infty }}{A}_m{z}^m$$ 2.8

and

$$\mathcal{K}(z)=\frac{\mathrm{i}}{8{\beta }^2}\sum _{j=-\mathrm{\infty }}^{\mathrm{\infty }}[H_0^{(1)}(\beta s|j|)+\frac{2\mathrm{i}}{\pi }{K}_0(\beta s|j|)]z^j.$$ 2.9

Notably, for $\mathcal{K}(z)$, the j=0 term is constant, i/8β², which replaces the awkward $H_0^{(1)}(\beta a)$ term of (2.2). Using these functions, (2.7) becomes

$$F(z)+A(z)\mathcal{K}(z)=B(z),\mathrm{where}\hspace{0.17em}B(z)=\sum _{n=1}^{\mathrm{\infty }}{b}_{-n}{z}^{-n},$$ 2.10

and the forcing function, in this case, is

$$F(z)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{(z\hspace{0.17em}{\mathrm{e}}^{\mathrm{i}s\beta \cos \psi })}^n$$ 2.11

but could take different forms if the forcing were altered.

Equation (2.10) is the starting point for the Wiener–Hopf technique with key steps being the product factorization of the kernel function $\mathcal{K}(z)$ into two factors which are analytic in given but different regions, and factorization of the forcing function. Before proceeding we turn to the semi-infinite lattice as the formulation is almost identical.

(b). Semi-infinite lattice of rigid pins in a biharmonic plate

We now replace each pin in the semi-infinite grating with an infinite grating in the vertical direction, as illustrated in figure 1b. The properties of the infinite grating are well known (e.g. [27]), and the quasi-periodic grating Green's function,

$$G_0^q(\beta ,x;{\kappa }_y,d_y)=\frac{\mathrm{i}}{8{\beta }^2}\sum _{j=-\mathrm{\infty }}^{\mathrm{\infty }}[H_0^{(1)}(\beta \sqrt{{(j{d}_y)}^2+x^2})+\frac{2\mathrm{i}}{\pi }{K}_0(\beta \sqrt{{(j{d}_y)}^2+x^2})]{\mathrm{e}}^{\mathrm{i}{\kappa }_{y}j{d}_y},$$ 2.12

plays an important role. Here d_y is the vertical period (in §2a we used s to denote the period for the single grating) and κ_y is the corresponding Bloch parameter. The gratings are separated by integer multiples of spacing d_x and the semi-infinite lattice is created from columns of infinite gratings (or rows of semi-infinite gratings). The analogue of (2.6) emerges as

$${\mathrm{e}}^{\mathrm{i}n{d}_x\beta \cos \psi }+\sum _{m=0}^{\mathrm{\infty }}{A}_m{G}_m^q(\beta ,|n-m|d_x;{\kappa }_y,d_y)=b_n,n\in \mathbb{Z}.$$ 2.13

We repeat the procedure used for the semi-infinite grating with the only difference being that the kernel function is now connected with the doubly quasi-periodic Green's function,

$$A(z)\mathcal{K}(z)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}\sum _{m=0}^{\mathrm{\infty }}{A}_m{G}_{n-m}^q(\beta ,|n-m|d_x;{\kappa }_y,d_y)z^n,$$ 2.14

when z=e^iκ_xd_x with ${\kappa }_x=\beta \cos \psi$.

(c). Wiener–Hopf factorization

The crux of the Wiener–Hopf methodology is to unravel (2.10) using the analyticity properties of the unknown functions A(z),B(z) and the known functions $\mathcal{K}(z)$, F(z).

Here, a regularization of the kernel function $\mathcal{K}$ (2.9) uses complex β_ϵ=β+iϵ instead of the real β, where 0<ϵ≪1 is a small positive imaginary part. As a result of such a regularization, one creates a ring of analyticity bounded by circles γ_± (as shown by the shaded region in figure 2), containing the unit circle. Inside this annulus of analyticity, the regularized kernel function does not have any poles. As ϵ→0, the circles γ_± tend to the unit circle, of course.

Figure 2.

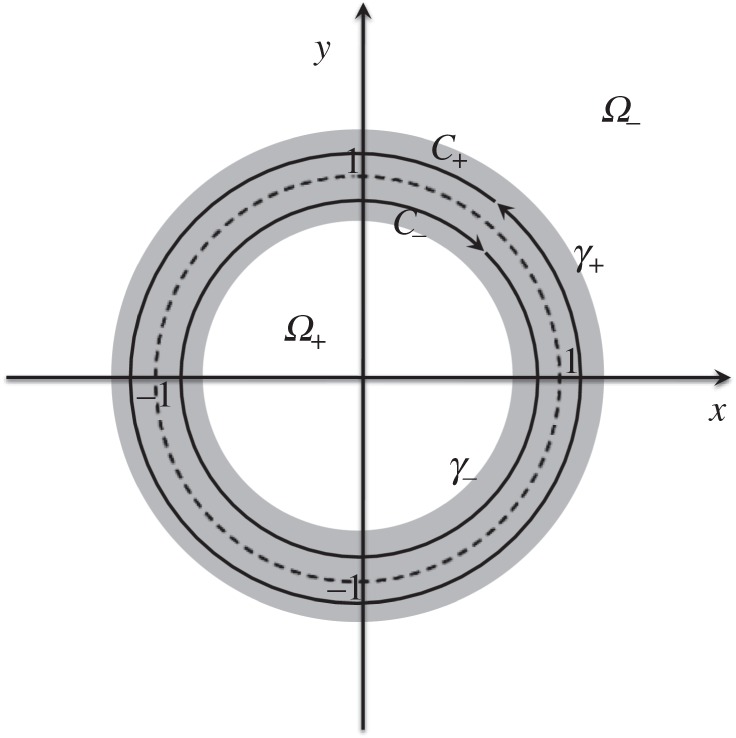
The unit circle (dashed curve), circles γ_±, which define the bounds for the ring of analyticity (shaded region), Ω₊, Ω₋ and contours C₊ and C₋. The integrals on C₊ and C₋ are evaluated counter-clockwise and clockwise, respectively.

To proceed we define domains Ω₊ and Ω₋ such that

$${\mathrm{\Omega }}_{+}=\{z:|z|\le c_{+}\}\mathrm{and}{\mathrm{\Omega }}_{-}=\{z:|z|\ge c_{-}\},$$ 2.15

where C₊ is a circle of radius c₊=1+δ, inside γ₊, and C₋ is a circle of radius c₋=1−δ, outside γ₋, for 0<δ≪1 (see figure 2 and the electronic supplementary material, appendix A, for more details); the intersection Ω₊∩Ω₋ belongs to an annulus of analyticity in the neighbourhood of the unit circle, and γ_± are bounds for the circles C_±.

From the definitions of A(z) (2.8) and B(z) (2.10), and assuming appropriate decay at infinity, we identify them as + and − functions analytic in Ω₊ and Ω₋, respectively. We then attempt to separate (2.10) into sides entirely analytic in Ω_±; the only way both can be equal, given an overlapping region of analyticity, is for them both to equal the same entire function—thus identifying A₊(z) and B₋(z). The outcome is

$${\mathcal{F}}_{+}(z)+A_{+}(z){\mathcal{K}}_{+}(z)=\frac{B_{-}(z)}{{\mathcal{K}}_{-}(z)}-{\mathcal{F}}_{-}(z)=0,$$ 2.16

which requires the product factorization $\mathcal{K}(z)={\mathcal{K}}_{+}(z){\mathcal{K}}_{-}(z)$ and sum factorization $\mathcal{F}(z)={\mathcal{F}}_{+}(z)+{\mathcal{F}}_{-}(z)$, where $\mathcal{F}(z)=F(z)/{\mathcal{K}}_{-}(z)$; the product factorization is highly technical so we give a brief outline here with more details in the electronic supplementary material, appendix A—the sum factorization is straightforward by inspection. The product factorization is

$$\mathcal{K}(z)=\exp \{\frac{1}{2\pi \mathrm{i}}{\int }_{C_{+}}\frac{\log \mathcal{K}(\varrho )}{\varrho -z}\hspace{0.17em}\mathrm{d}\varrho \}\exp \{\frac{-1}{2\pi \mathrm{i}}{\int }_{C_{-}}\frac{\log \mathcal{K}(\varrho )}{\varrho -z}\hspace{0.17em}\mathrm{d}\varrho \}={\mathcal{K}}_{+}(z){\mathcal{K}}_{-}(z).$$ 2.17

We note here that ϱ is of the form e^i(θ±iδ) for C_∓, with z=e^iθ. It is also assumed that C_± are chosen so that $\log \mathcal{K}$ is well defined.

After some algebra, we obtain

$$\begin{array}{rl}& A_{+}(z){\mathcal{K}}_{+}(z)+\frac{1}{{\mathcal{K}}_{-}({\mathrm{e}}^{-\mathrm{i}{\beta }_{ϵ}s\cos \psi })[1-z\hspace{0.17em}{\mathrm{e}}^{\mathrm{i}{\beta }_{ϵ}s\cos \psi }]}\\ & =\frac{1}{(1-z\hspace{0.17em}{\mathrm{e}}^{\mathrm{i}{\beta }_{ϵ}s\cos \psi })}[\frac{1}{{\mathcal{K}}_{-}({\mathrm{e}}^{-\mathrm{i}{\beta }_{ϵ}s\cos \psi })}-\frac{1}{{\mathcal{K}}_{-}(z)}]+\frac{B_{-}(z)}{{\mathcal{K}}_{-}(z)}=0,\end{array}$$ 2.18

except for different definitions of A₊(z), B₋(z) and ${\mathcal{K}}_{+}(z)$, ${\mathcal{K}}_{-}(z)$ this mirrors HK. The common entire function is identified, after using Liouville's theorem to extend to the whole complex plane, as zero. Thus

$$A_{+}(z)=-\frac{{\mathcal{F}}_{+}(z)}{{\mathcal{K}}_{+}(z)}=-\frac{1}{{\mathcal{K}}_{+}(z){\mathcal{K}}_{-}({\mathrm{e}}^{-\mathrm{i}{\beta }_{ϵ}s\cos \psi })[1-z\hspace{0.17em}{\mathrm{e}}^{\mathrm{i}{\beta }_{ϵ}s\cos \psi }]},$$ 2.19

and the z-transform for the displacement coefficients B₋(z) also follows.

Technical details of the discrete Wiener–Hopf method used here are given in the electronic supplementary material, appendices. The kernel function $\mathcal{K}(z)$ is the sum of an infinite series of Hankel and modified Bessel functions, and its factorization is discussed in the electronic supplementary material, appendix A, together with details about the evaluation of the integrals for ${\mathcal{K}}_{+}(z),\hspace{0.17em}{\mathcal{K}}_{-}(z)$. We also note that the regularization using complex β_ϵ, with a small imaginary part, instead of real β, ensures that the right-hand side of (2.19) is analytic for all z inside Ω₊. The electronic supplementary material, appendix B, provides explanations and formulae required to accelerate the extremely slow convergence of the kernel's series, owing to the highly oscillatory nature of the Hankel function terms and the presence of branch cuts. We also suggest some alternative approaches to accelerate numerical evaluation of the series besides the regularization method primarily implemented here.

3. Results

We present the results and illustrative examples for the displacement fields associated with the two types of array: the single semi-infinite pinned platonic grating characterized by spacing s in §3a and the two-dimensional lattice defined by d_x and d_y in §3b. We use the discrete Wiener–Hopf method described above and compare the results with those for a truncated semi-infinite array analysed with a method attributable to Foldy [28], which we outline in §3a for a single grating.

(a). The semi-infinite grating of rigid pins

For a plane wave incident at an angle ψ as in figure 1a, we determine the coefficients A_k for a truncated grating by solving the algebraic system of linear equations,

$$\sum _{k=0}^N{A}_{k}G(\beta ,|m-k|s)=-u_i(ms),m=1,2,\dots ,N,$$ 3.1

with s being the spacing of the grating's pinned points and u_i the incident wave as defined in equation (2.5). This is the standard Foldy scattering equation [28], and is used among others by Linton & Martin [22] for the Helmholtz problem and Evans & Porter [13] for the biharmonic plate. It is solved for N pinned points, and the displacements are plotted using

$$u(\mathbf{\text{r}})=u_i(\mathbf{\text{r}})+\sum _{k=0}^N{A}_{k}G(\beta ,|\mathbf{\text{r}}-(ks,0)|).$$ 3.2

We compare the results with those obtained from the discrete Wiener–Hopf technique for the semi-infinite grating, which gives us the exact solution. The expressions for ${\mathcal{K}}_{+}(z),{\mathcal{K}}_{-}(z)$ (2.17) are substituted into equation (2.19) to determine A₊(z), bearing in mind the contribution arising from the $1-z\hspace{0.17em}{\mathrm{e}}^{\mathrm{i}{\beta }_{ϵ}s\cos \psi }$ term in the denominator. Referring to the expansion (2.8), we take the inverse of the z-transform to determine the coefficients A_m. Multiplying (2.8) through by z^−k and integrating with respect to z=e^iθ, we obtain

$${\int }_0^{2\pi }{z}^{-k}{A}_{+}(z)\hspace{0.17em}\mathrm{d}\theta ={\int }_0^{2\pi }\sum _{m=0}^{\mathrm{\infty }}{A}_m{z}^m{z}^{-k}\hspace{0.17em}\mathrm{d}\theta =A_{k}2\pi .$$ 3.3

The final result for the coefficients is the integral

$$A_k=\frac{1}{2\pi }{\int }_0^{2\pi }\hspace{0.17em}{\mathrm{e}}^{-\mathrm{i}k\theta }{A}_{+}({\mathrm{e}}^{\mathrm{i}\theta })\hspace{0.17em}\mathrm{d}\hspace{0.17em}\theta ,$$ 3.4

for which the singularities and the branch cuts of the electronic supplementary material, appendix B, have to be taken into account. The results compare well with a truncated version (at least 2000 pins) treated with the Foldy scattering approach. In the examples that follow we use both real parts and moduli of the displacement field defined by these complex coefficients, since they give us insight into the propagation tendencies of the scattered waves.

For the far-field behaviour of the coefficients A_k, we deduce a relation of the form

$$A_{k+1}\approx \mathrm{\lambda }{A}_k,|\mathrm{\lambda }|\le 1.$$ 3.5

The case |λ|=1 denotes the propagating Bloch wave and for |λ|<1 we observe localization linked with the exponential decay of the coefficients. The ratio λ is determined by

$$\mathrm{\lambda }=\underset{k\to \mathrm{\infty }}{lim}\frac{{\int }_C{A}_{+}(z)z^{-(k+1)}\hspace{0.17em}\mathrm{d}z}{{\int }_C{A}_{+}(z)z^{-k}\hspace{0.17em}\mathrm{d}z},$$ 3.6

where the kernel in its present form is evaluated numerically.

(i). Resonant cases

We consider some of the frequency regimes mentioned by Evans & Porter [13] for a finite array of pinned points and an infinite grating, as well as those referred to by HK for a semi-infinite grating, including the case they define as a resonance. This is where the incident wave travels directly into the end of the grating and then the diffracted wave travels parallel to the grating, either into (inward resonance) or away from (outward resonance) the grating.

Spectral orders of diffraction ϕ_p are defined according to the equation (see for instance [29])

$$\cos {\varphi }_p(\psi )=\cos \psi +\frac{2\pi p}{s\beta }p\in \mathbb{Z},$$ 3.7

with only a finite number of the ϕ_p(ψ) being real and representing propagating waves. The remaining orders are complex and represent evanescent waves. According to HK, the resonant cases arise when one of the spectral directions is zero (inward resonance) or π, the case of outward resonance. Thus, resonances coincide with additional diffraction orders becoming propagating. For outward resonance

$$s\beta \cos \psi +2\pi p=-s\beta ,\text{for some }p=0,\pm 1,\pm 2,\dots ,$$ 3.8

thus for ψ=0, sβ=−πp and outward resonances occur for frequencies corresponding to β being a multiple of π.

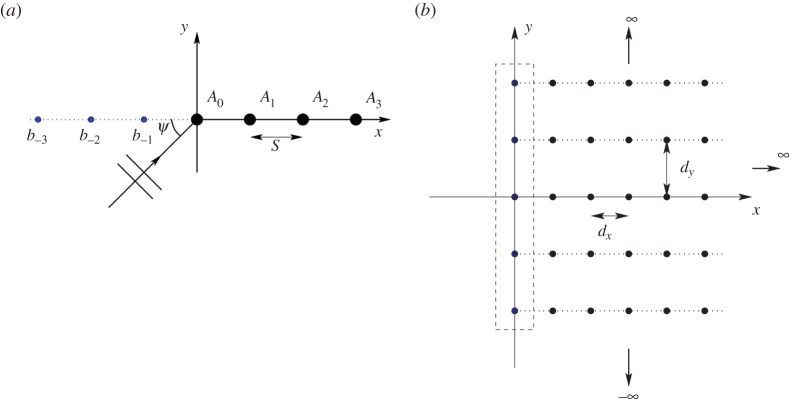
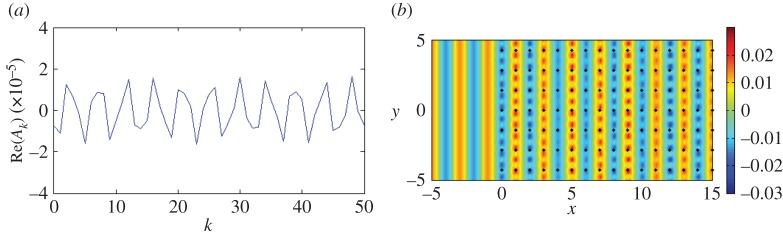
We observe some evidence of this effect for the case p=−1 in figure 3a–c, where we plot the scattered displacement fields for values of β=3.1,π,3.3 for angle of incidence ψ=0 and period s=1.0. In figure 3, we use both Foldy, truncated to 2000 pins, and the results from Wiener–Hopf, and they are visually indistinguishable for the first several gratings, as shown in figure 3d, which compares the moduli of the coefficients |A_k| in both cases for β=3.1 (i.e. the solid line and dots for Foldy and Wiener–Hopf, respectively). The high reflected energy for β=3.1 shown in figure 3a is illustrative of the outward resonance described by HK for the resonant value β=π.

Figure 3.

Plane wave incident on a semi-infinite grating with spacing s=1.0 at ψ=0. (a–c) Real part of the scattered displacement u−u_i, for β=3.1,π,3.3. (d) Comparison of the moduli of the coefficients |A_k| using the Wiener–Hopf (dots for β=3.1) and Foldy methods (shown for all). (Online version in colour.)

We contrast this with β=3.3 in figure 3c for which an additional diffraction order p=−1 has become propagating. For diffraction orders p<0 to pass off, $\beta s(1+\cos \psi )=-2\pi p$. Thus for ψ=0, the order p=−1 becomes propagating along with p=0 for the resonant value β=π, and the presence of two distinct propagating orders is clearly illustrated for β=3.3. The two examples either side of β=π show strong evidence of the circular wave that is typical for the end-effects of a semi-infinite scatterer.

The resonant frequency case of β=π is shown in figure 3b and there are relatively lower amplitudes of displacement (with a maximum of approx. 0.3) with most of the scattering occurring along the grating, contrasting with the effects illustrated in figure 3a,c. The localization and reduction of the maximum amplitudes to 0.3 is consistent with HK's observation that, for outward resonance, the cylindrical wave and all but one of the plane waves vanish. Indeed, the real part of the total displacement field (not shown) closely resembles that of the incident wave, except for the region surrounding the grating itself. Comparing the coefficients A_k, as we do in figure 3d, further emphasizes the difference between this resonant case, for which |A_k| rapidly saturates to a low value, and those for β=3.1,3.3, which take much longer to saturate and then do so to a larger value.

(ii). Shadow boundaries

HK refer to non-resonant cases where the diffracted field for a Helmholtz-governed semi-infinite grating consists of a set of plane waves and a cylindrical wave. The plane waves are consistent with those arising for the infinite grating, but do not exist everywhere. We obtain similar results for the biharmonic case, for which the propagating waves are due to the Hankel functions arising from the Helmholtz part of the Green's function in equation (2.3). The coefficients for the scattered field are defined by equations (2.19) and (3.4), leading to the expression

$$A_k=-\frac{1}{2\pi {\mathcal{K}}_{-}({\mathrm{e}}^{-\mathrm{i}\beta s\cos \psi })}{\int }_0^{2\pi }\frac{{\mathrm{e}}^{-\mathrm{i}k\theta }\hspace{0.17em}\mathrm{d}\theta }{{\mathcal{K}}_{+}({\mathrm{e}}^{\mathrm{i}\theta })[1-{\mathrm{e}}^{\mathrm{i}\theta }\hspace{0.17em}{\mathrm{e}}^{\mathrm{i}\beta s\cos \psi }]}.$$ 3.9

Furthermore, the representation (2.5) for the displacement leads to the following approximate expression for large values of |r−r′_n|:

$$u(r,\varphi )\simeq \frac{\mathrm{i}}{8{\beta }^2}\sum _{n=0}^{\mathrm{\infty }}{A}_n{H}_0(\beta |\mathbf{\text{r}}-{\mathbf{\text{r}}}_n^{\prime }|).$$

HK have proved in their paper that the shadow boundaries correspond to singularities of the z-transform A₊(z) (2.19), when z is a point on the unit circle defined in the form $z={\text{e}}^{-\mathrm{i}\beta s\cos {\varphi }_p}$. We note that the regularized kernel $\mathcal{K}(z)$ does not have roots and poles on the unit circle, and hence the shadow boundaries are defined by equation (3.7) and coincide with those discussed by HK in [24].

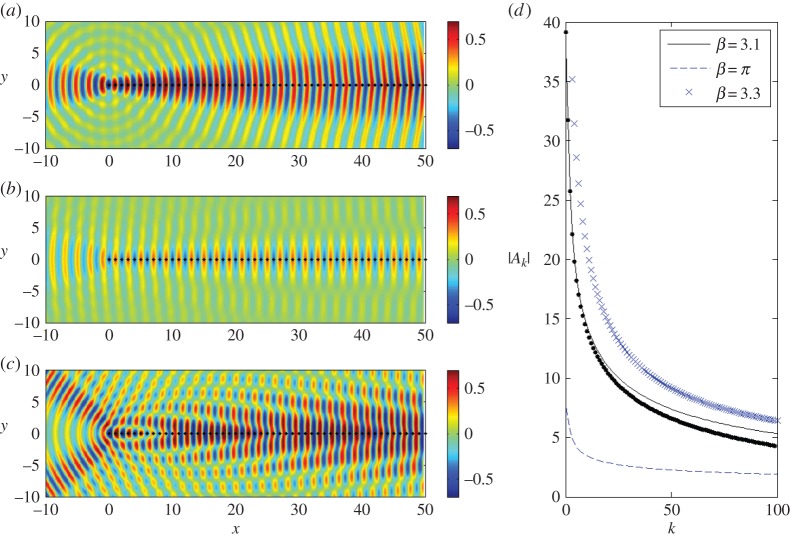
The lines θ=ϕ_p(ψ) act as shadow boundaries and this is illustrated in figure 4 where β=4.0, s=1.0 and ψ=π/4. For ψ=π/4, the diffraction order p=−1 becomes propagating for $\beta =2\pi /(1+1/\sqrt{2})\approx 3.6806$, so for β=4.0 both p=0 and −1 are propagating. We observe the two shadow boundaries for ϕ₀(π/4)=π/4 and ${\varphi }_{-1}(\pi /4)=\arccos (\sqrt{2}-\pi )/2$, and the field consisting of two propagating diffracted waves, as well as the reflected wave. Figure 4b complements figure 4a by showing a comparison of the moduli of the coefficients |A_k| with the Foldy method represented by the solid line, the Wiener–Hopf by the dots; for oblique incidence, the two methods match well and for the Wiener–Hopf we set ϵ=0.005, δ=0.0025 and take 1200 intervals for the trapezoidal integration (see the electronic supplementary material, appendices A and B). Increasing the number of intervals leads to closer convergence to the Foldy coefficients.

Figure 4.

The scattering of a plane wave ψ=π/4 by a grating with s=1.0, for β=4.0. (a) Real part of the displacement field u. The shadow boundaries for ϕ₀ and ϕ₋₁ are marked using dashed black lines. (b) Comparison of the Wiener–Hopf (dots) and Foldy (solid line) coefficients |A_k|. (Online version in colour.)

(iii). Reflection and transmission

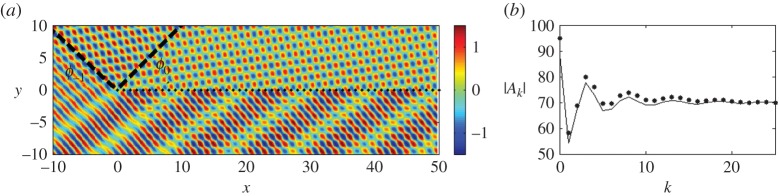
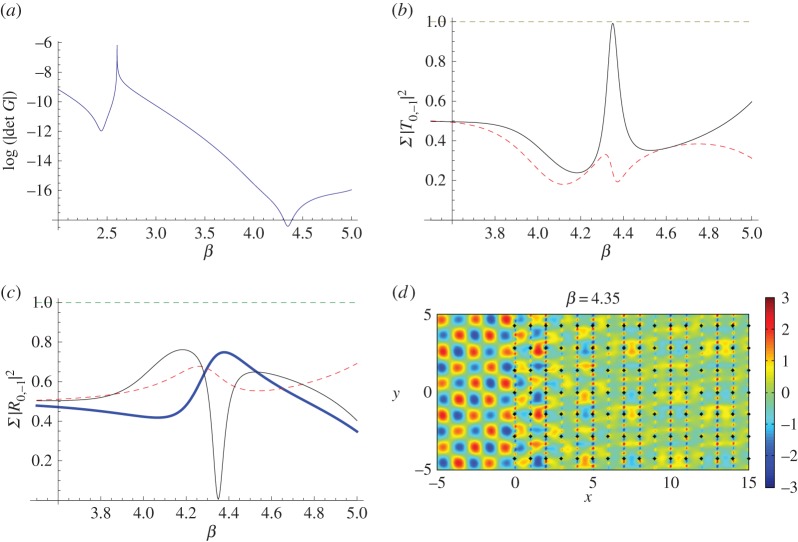
Frequency regimes associated with total reflection and total transmission by an infinite grating, as identified by Evans & Porter [13] and Movchan et al. [14], are interesting cases. For an infinite pinned grating (period s=1.0, ψ=π/4), the normalized reflected and transmitted energies are plotted against β in figure 5a. Three important values of β = 3.2; 3.55; 3.68, which are total reflection, equipartition of energy and total transmission, respectively, are labelled b–d and we show the real part of the total displacement field for the corresponding semi-infinite gratings in figure 5b–d.

Figure 5.

Plane wave incident on a semi-infinite grating with spacing s=1.0 at an angle ψ=π/4. (a) The normalized reflected, R, (solid curve) and transmitted, T, (dashed) energy versus β for scattering by an infinite pinned grating. The real part of the displacement field for the semi-infinite grating is shown for (b) β=3.2, (c) β=3.55 and (d) β=3.68. Fields for parts (b–d) are plotted using Wiener–Hopf coefficients. (Online version in colour.)

Figure 5a shows that the maximum reflected energy (solid curve) for the zeroth propagating order arises for β=3.2. The Wood anomaly at β=3.6806 signifies the passing off of the order p=−1, explaining the multiple orders illustrated in figure 4 for β=4.0. The real part of the total displacement field for the semi-infinite grating for the same parameter values ψ=π/4 and β=3.2 shows strong reflection to the right of the vertex, consistent with that observed for the full grating for the single propagating plane wave. This contrasts sharply with the results observed for the frequency associated with β=4.0 in figure 4. Note that there is only one shadow boundary in figure 5b (for the shadow region behind the grating), whereas figure 4a shows evidence of two distinct shadow lines.

In figure 5c, we highlight β=3.55, which supports a mixture of reflected and transmitted energy for both the infinite and semi-infinite gratings; the dashed line in figure 5a represents the transmitted energy. The real part of the displacement field in figure 5c is consistent with the information provided by the energy diagrams for the corresponding infinite grating; both reflection and transmission are visible, with the shadow region above the grating now admitting transmittance. This transmission effect dilutes the reflection of figure 5b, and total reflectance is converted to total transmission by adjusting the β parameter appropriately. This is illustrated in figure 5a where β=3.68 leads to full transmission for the infinite grating, and produces a similar effect for the semi-infinite grating whose total displacement field is shown in figure 5d. This transmission resonance is an example of the outward resonant effect for oblique incidence. The scattered field (not shown) is reminiscent of figure 3b; evidence of the outward-travelling wave close to the vertex is visible in figure 5c for β=3.55.

(b). Semi-infinite lattice of rigid pins

For an incident plane wave characterized by ψ as in figure 1a, we determine the coefficients A_k for a truncated half-plane by solving the algebraic system of linear equations (3.1) but replacing each pin with a grating in the vertical direction. We compare results with those obtained using discrete Wiener–Hopf. We clarify that, whenever the figure caption gives a finite number of gratings, the computation has been performed using Foldy's method.

(i). Zeros of the kernel function

Recall from equations (2.12), (2.14) that, for $z=\exp \{\mathrm{i}{\kappa }_x{d}_x\}$ lying on the unit circle, the function $\mathcal{K}(z)$ is precisely the doubly quasi-periodic Green's function. Therefore, its zeros represent points on the dispersion surfaces for Bloch waves in the infinite doubly periodic structure. This direct connection between the kernel and the doubly periodic medium enables us to analyse wave phenomena using dispersion surfaces, band diagrams and slowness contours.

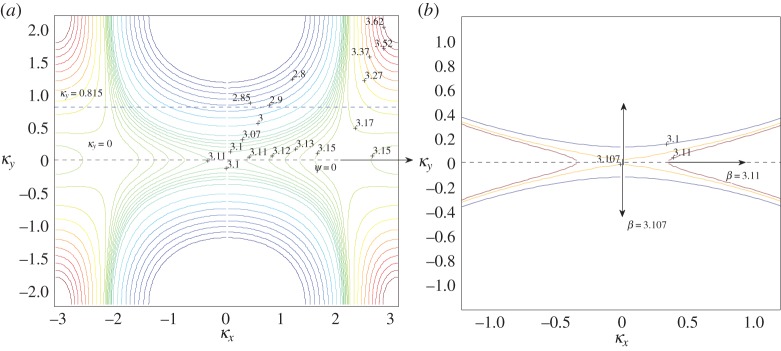
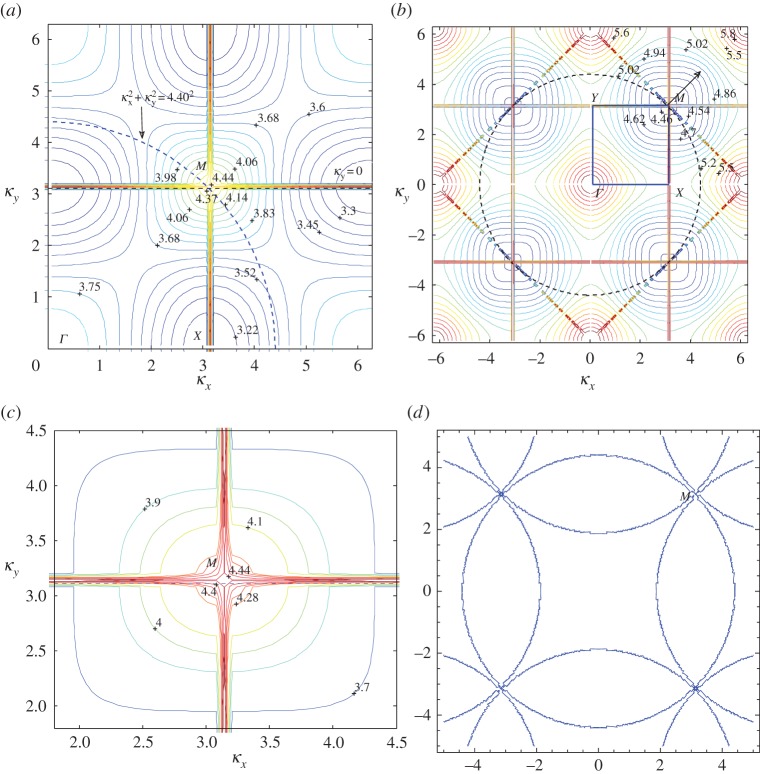
We determine the coefficients A_k and b_k using the discrete Wiener–Hopf method. A good approximation to these results is obtained by applying Foldy's method to a large enough array. For systems of at least 2000 gratings, we demonstrate several interesting wave phenomena. McPhedran et al. [8] highlight the potential for varying the aspect ratio of rectangular lattices of pins, linking Dirac-like points with parabolic profiles in their neighbourhood. The characteristic of this parabolic profile determines the direction of propagation of localized waves. We consider first a semi-infinite rectangular lattice with aspect ratio $\eta =d_y/d_x=\sqrt{2}$. The band diagram for the doubly periodic rectangular array is shown in fig. 7 of McPhedran et al. [8]. Here we represent the dispersion surfaces with isofrequency contour diagrams.

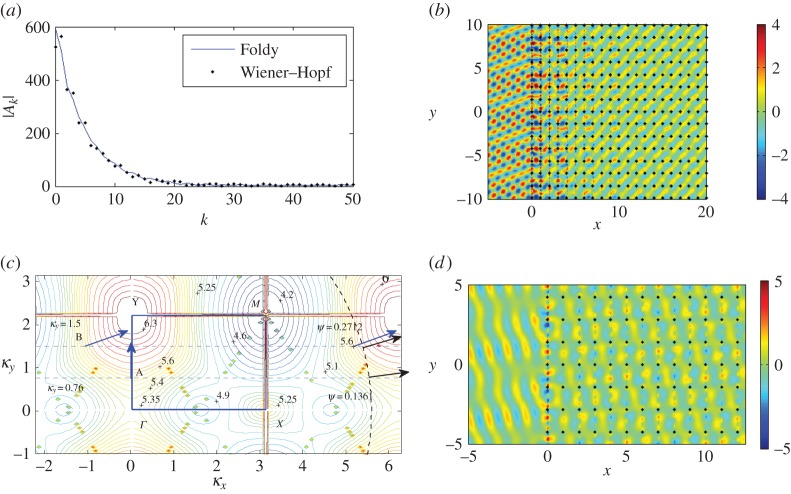
For our initial investigations, we focus on the first three dispersion surfaces. In figure 6, we illustrate the third surface for the rectangular lattice with d_x=1.0 and $d_y=\sqrt{2}$ with the boundary of the irreducible Brillouin zone labelled by ΓXMY , where $M=(\pi ,\pi /\sqrt{2})$. The rectangular grid k_x=±πn/d_x, k_y=±πn/d_y is due to singularities in the dispersion equation. The distortions near the grid should be disregarded. We observe a parabolic cylinder profile along ΓX with an inflection at Γ where the contours change direction for β≈5.365 and a Dirac-like point for β≈5.45 at X.

Figure 6.

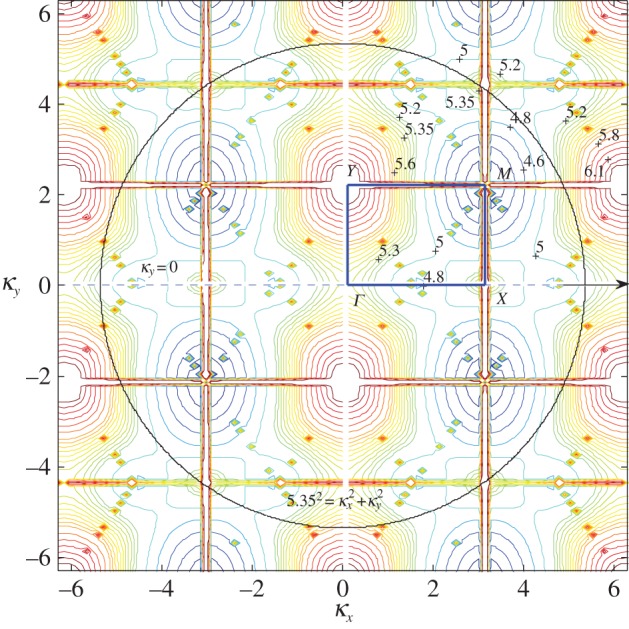
Isofrequency contours (a selection of β values are labelled) for the third dispersion surface of the rectangular lattice with d_x=1, $d_y=\sqrt{2}$. The boundary of the irreducible Brillouin zone ΓXMY is marked by the solid rectangle, with $M=(\pi ,\pi /\sqrt{2})$. (Online version in colour.)

The notion of ‘light surfaces’ and ‘light lines’ is well known in the modelling of Bloch waves. The term originally came from electromagnetism, but is now well used in problems of acoustics and elasticity. In particular, in §4 of their article, McPhedran et al. [8] give an accurate account of ‘light cones’ for flexural waves in Kirchhoff plates. In this context, the ‘light cones’ are defined as surfaces in the space (k_x,k_y,β) given by the equations

$$\begin{array}{rl}{\eta }^2{(n_1+\frac{{\kappa }_x{d}_x}{2\pi })}^2+{(m_1+\frac{{\kappa }_y{d}_y}{2\pi })}^2& ={\left(\frac{\beta d_y}{2\pi }\right)}^2\\ \text{and}{\eta }^2{(n_2+\frac{{\kappa }_x{d}_x}{2\pi })}^2+{(m_2+\frac{{\kappa }_y{d}_y}{2\pi })}^2& ={\left(\frac{\beta d_y}{2\pi }\right)}^2.\end{array}\}$$ 3.10

We also note that the concentration of points in figure 6 tending towards the straight lines

$${\kappa }_y\pm \left(\frac{\pi +2\pi d_y}{2\pi d_y}\right){\kappa }_x=\pm \frac{\pi }{d_y}$$

and periodic shifts by π/d_y are projections (onto the κ_x,κ_y-plane) of intersections of two light cones, which are given by (3.10).

The remaining surfaces are presented together with displacement fields in the examples that follow. Both β=3.1538 for the first surface and β=4.40 for the second surface are mentioned by McPhedran et al. [8]. This immediately gives us some frequency regimes to investigate for finding wave phenomena including neutrality and interfacial waves. Recall from the Introduction that we define interfacial waves to be exponentially localized within the structure of pins and propagating parallel to the interface of the platonic crystal and the homogeneous part of the biharmonic plate. We also demonstrate blocking and resonant behaviour.

(ii). Wavevector diagrams

Zengerle [30] demonstrated an elegant strategy using wavevector diagrams to investigate wave phenomena in planar waveguides; the technique was also outlined by Joannopoulos et al. [31] for photonic crystals in their ch. 10. Zengerle [30] was able to illustrate negative refraction, focusing and interference effects, having predicted them with careful analysis of the wavevector diagrams. We adopt an analogous approach for this platonic crystal system.

The underlying principle is a corollary of Bloch's theorem; in a linear system with discrete translational symmetry the Bloch wavevector k=(κ_x,κ_y) is conserved as waves propagate, up to the addition of reciprocal lattice vectors. Since there is only translational symmetry along directions parallel to the interface, only the wavevector parallel to the interface, k_∥, is conserved. In our case, this is precisely the direction κ_y. Thus for any incident plane wave defined by β and k=(κ_x,κ_y), any reflected or refracted (transmitted) wave must also possess the same frequency β²=ω and wavevector (κ′_x,κ_y+2πl/d_y) for any integer l and some κ′_x. Therefore, wavevector diagrams may be used to analyse the reflection and refraction of waves within the pinned system.

These isofrequency diagrams (also called slowness contour plots) consist of dispersion curves for constant β (characterizing the platonic crystal) and the contour for the ambient medium (the homogeneous biharmonic plate) on the same κ_x, κ_y diagram (figure 6). The incident wavevector (whose group velocity direction is characterized by ψ) is appended to the ambient medium's contour (the circle ${\beta }^2={5.35}^2={\kappa }_x^2+{\kappa }_y^2$ in figure 6), and a dashed line perpendicular to the interface of the platonic crystal and the homogeneous part of the biharmonic plate (κ_x=0 or ΓY direction here) is drawn through this point. The dashed line κ_y=0 and ψ=0 has been added to figure 6. The places where this dashed line intersects the platonic crystal contours determine the refracted waves and their directions, such that their group velocity is perpendicular to the β contours, and points in the direction of increasing β.

Additional information relating to the coefficients A_k is obtained from the Wiener–Hopf method. Exponential decay of form (3.5) with λ<1 would indicate the possibility of interfacial waveguide modes, with verification supported by the prediction of the refracted waves' directions using wavevector diagrams. We illustrate the technique with an introductory example demonstrating a localized mode along the edge of the crystal for the first dispersion surface, as well as reflection and transmission which are predicted from the isofrequency diagram.

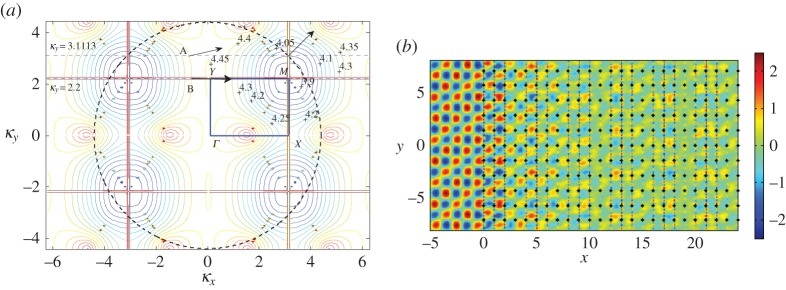
(iii). Reflection, transmission and interfacial waves for the first dispersion surface

In figure 7a, we show a collection of isofrequency contours for constant β for the first dispersion surface for the rectangular lattice with aspect ratio $\eta =d_y/d_x=\sqrt{2}$. This range of frequencies is notable for its flat bands and the parabolic profile mentioned by McPhedran et al. [8] at β=3.1538 in the vicinity of a Dirac-like point. For normal incidence ψ=0, indicated by the direction of the arrow in figure 7a, the dashed line intersecting the ambient medium's contour and normal to the interface (κ_x=0) corresponds to κ_y=0, as shown in figure 7a. We seek the intersections of this line with the isofrequency contour for a specific choice of β. Since the direction of the group velocity of the refracted waves is perpendicular to these β=const. contours, for an interfacial mode we would require the contour to be tangent to the line κ_y=0.

Figure 7.

(a) Isofrequency contours β= constant for the first dispersion surface for the rectangular lattice with d_x=1.0, $d_y=\sqrt{2}$. (b) Isofrequency contours β=3.10, 3.107, 3.11. (Online version in colour.)

(iv). Interfacial waves

It is clear from figure 7a that the contours tend towards tangency as β increases to β≈3.1 but then their behaviour in the vicinity of β=π is less predictable. This is connected both with the resonant case β=π for the single semi-infinite grating (see §3a(i)) and with the parabolic profiles associated with Dirac-like points to which McPhedran et al. [8] alluded for β≈3.1538. This observation is supported by the discontinuous nature of the contours for 3.11≤β≤3.15 when they intersect the line κ_y=0 in figure 7a, and in particular the two distinct contour curves labelled by β=3.15 on the right. The contours change direction at Γ=(0,0) for 3.10<β<3.11, as shown clearly in figure 7b; this corresponds to a point of inflection on the band diagram, a case that exhibits interesting wave phenomena that we illustrate in figure 8 for the semi-infinite lattice.

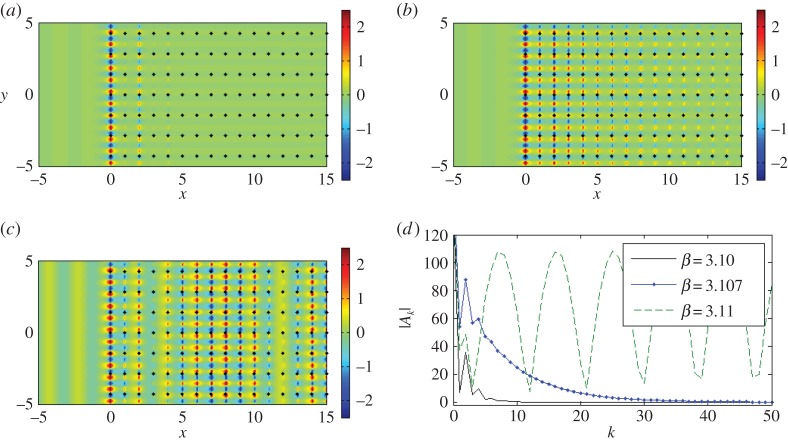
Figure 8.

A plane wave is incident at ψ=0 on a lattice of 2000 gratings with d_x=1.0, $d_y=\sqrt{2}$. (a–c) Real part of the total displacement field for β=3.10, β=3.107, β=3.11. (d) Comparison of the moduli of coefficients |A_k|. Computations performed using the Foldy method. (Online version in colour.)

In figure 7b, we show isofrequency contours for β=3.10, 3.107 and 3.11 to emphasize the transition of the contours through this narrow frequency window. The curve for β=3.10 is consistent with preceding values of β but it does not touch the κ_y=0 line, whereas β=3.107 is extremely close to touching, with the origin of a point of discontinuity clearly observable. This point of inflection for some 3.107<β<3.11 is the limit as the contours tend to κ_y=0 and occurs at Γ. For this value of β, the refracted wave would travel along the interface, but there would be no preferential direction of propagation since the upper contour would indicate a ‘downward’ direction (increasing β), whereas the lower contour would indicate the opposite direction. This suggests the presence of a standing wave, localized within the first few gratings of the half-plane of pins.

Figure 8a–d gives an interesting illustration of the scattering patterns near the edge of the stop band for a doubly periodic ‘platonic crystal’. The parameters of the lattice and the frequencies are chosen according to figure 7, and correspond to a ‘parabolic regime’, which supports a unidirectional propagation. This choice has been refined, and it is not just an arbitrary example of stop-pass-band excitation. In particular, figure 8a shows a very sharp localization, evidence for which is provided by the accompanying graph of the coefficients in figure 8d. It is also demonstrated that a small perturbation of the frequency, as in figure 8c, leads to a propagating oscillatory pattern inside the structured half-plane.

We see evidence of some localization and some propagation when we plot the real part of the displacement field for β=3.107 in figure 8b, with the predicted preferential direction of propagation indicated in figure 7b. The moduli of the coefficients |A_k| are plotted versus the x-position of the grating in figure 8d, for the three values of β featured in figure 7b. Both β=3.10 and β=3.107 show exponential decay of the coefficients, suggesting localization of waves, whereas the steady oscillation of the coefficients for β=3.11 predicts transmission of the waves through the system. Figure 8b clearly illustrates the localization of waves within the first five gratings, and a clearer example of an interfacial wave is illustrated in figure 8a for β=3.10, although comparison with lower values of β shows similar results, but with more striking reflection action.

(v). Transmission

Figure 7b predicts that, for β=3.11, the preferred direction of propagation of the refracted waves is normal to that for β=3.107, in the form of transmission through the system. Note that the opposite direction (θ=π rather than 0) is ruled out since any intersections corresponding to the group velocity directed towards the interface from the crystal would violate the boundary conditions. The coefficients' behaviour in figure 8d also supports the hypothesis of propagating waves. This is demonstrated in figure 8c, where we observe transmission as the wave propagates through the system without any change in direction, with the period of the wave's envelope function consistent with the period for the coefficients in figure 8d.

(vi). Coupling with finite grating stacks

The spikes in figure 8d for β=3.10 and β=3.107 seem to indicate resonant interaction with the first few gratings of the semi-infinite array, as does the localization evident in figure 8a,b. There is a connection with the finite grating stacks analysed by Haslinger et al. [27]; resonances associated with the Bloch modes for the finite systems are linked to the neighbourhood of the Dirac-like point illustrated in figure 7a,b.

For the pinned waveguide consisting of an odd number of gratings of period d_y, a quasi-periodic Green's function (2.12) is used to derive the dispersion equation for Bloch modes within the system. At each pin, the boundary conditions are u=0. Therefore, for a system of aligned gratings with spacing d_x,

$$u({\mathit{\text{a}}}^m)=\sum _{j=-M}^M{S}_j{G}_j^q(\beta ,m{d}_x;{\kappa }_y,d_y)=0;{\mathit{\text{a}}}^m=(m{d}_x,0)\text{for }m\in [-M,M],$$ 3.11

where u is the displacement, S_j are coefficients to be determined for each Green's function $G_j^q$ and 2M+1 is the number of gratings in the finite stack. This is equivalent to the matrix equation

$$\mathbf{\text{G}}\mathbf{\text{S}}=\mathbf{\text{0}},$$ 3.12

where S is the column vector of coefficients S_j and the Green's function matrix G is complex and symmetric Toeplitz. The accompanying dispersion equation is

$$\text{Det}(\mathbf{\text{G}})=0,$$ 3.13

the solutions of which characterize the system's Bloch modes.

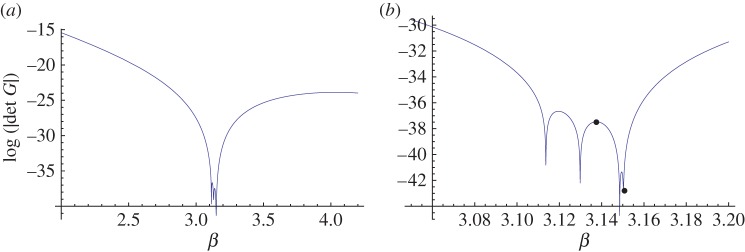
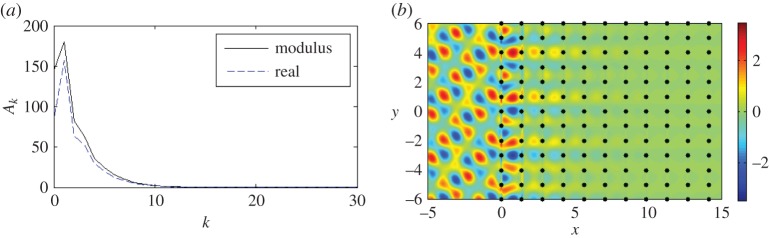
Figure 8b features localized waves within the first five gratings so we solve the eigenvalue problem for a system of five gratings with period $d_y=\sqrt{2}$ and separation d_x=1.0 in figure 9a. The frequencies for the 5-grating system's Bloch modes coincide with the frequency window for the Dirac-like point of the doubly periodic rectangular array. Similar results have been obtained for all 2M+1-grating stacks with M≤6, with localized modes always confined to the range 3.10<β<3.17. This is consistent with figure 7a,b, where the contours are well behaved for β≤3.10 and ≥3.17 but exhibit discontinuities in the neighbourhood of the Dirac-like point.

Figure 9.

(a) Solutions of the eigenvalue problem for a system of five gratings with period $d_y=\sqrt{2}$ and separation d_x=1.0. (b) Close-up of the frequency window for Bloch mode frequencies; local maximum β=3.1375 and root β=3.151 are marked. (Online version in colour.)

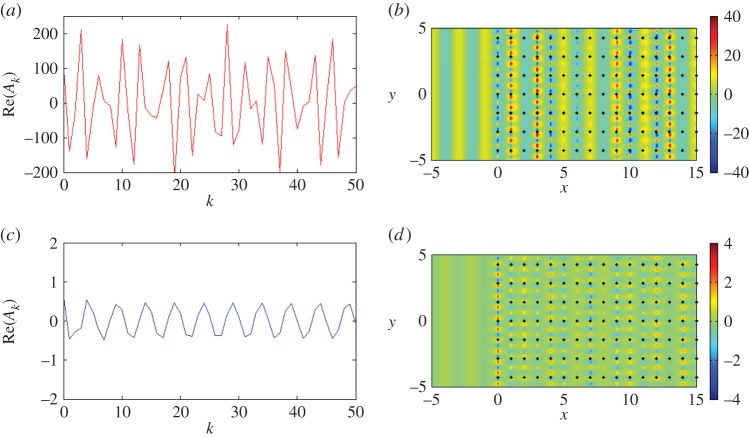
It has been shown that a finite system's resonant Bloch modes may be coupled to appropriately chosen incident plane waves to generate transmission action [27]. We observe the same phenomenon for the half-plane in figure 8c as well as evidence of similar localization for β=3.10, β=3.107 in figure 8a,b. Figure 9b adds further insight when we select two specific values of β marked on the diagram: the local maximum for β≈3.1375 and the root β=3.151, which is close to the Dirac-like point value β=3.1538. In figure 10a, the real parts of the coefficients A_k for β=3.1538 are of order 10² (the accompanying total displacement field is shown in figure 10b), whereas for β=3.1375 in figure 10c,d they are <1. One should take note of the scaling bars when comparing the total displacement fields in figure 10b,d. Both β values in the vicinity of the Dirac-like point support propagation, but the intensities of the transmitted waves are linked to the turning points and roots for the finite grating stack structures, illustrated in figure 9.

Figure 10.

A plane wave is incident at ψ=0 on a lattice of 2000 gratings with d_x=1.0, $d_y=\sqrt{2}$. (a) Real part of the coefficients A_k for β=3.15138. (b) Real part of the total displacement field for β=3.15138. (c) Real part of the coefficients A_k for β=3.1375. (d) Real part of the total displacement field for β=3.1375. (Online version in colour.)

This coupling can be switched off by altering the period and/or separation of the gratings or the incoming angle of incidence. It should be noted that these examples for the lowest frequency band involve the zeroth propagating order only. Higher frequencies introduce additional diffraction orders and their coupling facilitates more exotic wave phenomena including negative refraction, similar to those recorded by Zengerle [30] for optical waveguides.

(vii). Neutrality in the vicinity of Dirac-like cones

We now consider neutrality effects that arise for parabolic profiles in the vicinity of Dirac-like cones. It is well known that, close to Dirac points, waves may propagate as in free space, unaffected by any interaction with the microstructure within the crystal medium. These directions of neutral propagation around the Dirac point engender cloaking properties within the crystal, meaning that there is potential for ‘hiding’ objects within the appropriate frequency regime. This property of neutrality for platonic crystals was mentioned by McPhedran et al. [2] and was explained in a simple way in terms of the singular directions of the Green's functions for the biharmonic equation. More recently, Farhat et al. [32] have discussed neutrality when studying the scattering cancellation technique for flexural waves in elastically uniform thin plates.

The first dispersion surface for the rectangular lattice with d_x=1.0, $d_y=\sqrt{2}$ in figure 7 possesses such a parabolic profile near β=π. It is the horizontal spacing of d_x=1.0 that governs the special behaviour for normal incidence ψ=0 at β=π, illustrated in figure 11 (see equation (3.8)). For the vertical period $d_y=\sqrt{2}$, we observe neutral propagation of the incident plane wave, similar to that observed for the single grating in figure 3b, and we also see this for ψ=0 for the square lattice. Since the total displacement and incident fields are visually indistinguishable, we provide the real parts of the coefficients A_k in figure 11a and the real part of the scattered field in figure 11b. It is clear that for this choice of β=π the wave does not ‘see’ this specific lattice with d_x=1.0, $d_y=\sqrt{2}$.

Figure 11.

A plane wave is incident at ψ=0 on a lattice of 4000 gratings with d_x=1.0, $d_y=\sqrt{2}$ for β=π. (a) Real parts of the coefficients A_k. (b) Real part of the scattered field. (Online version in colour.)

(viii). Neutrality for oblique incidence

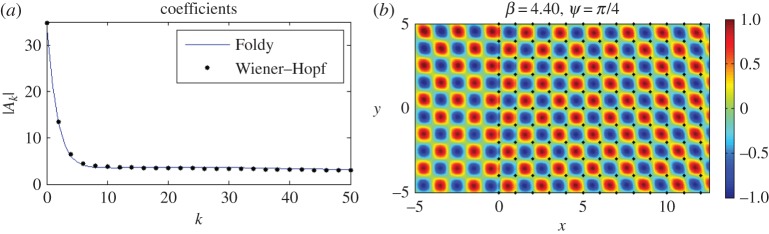
For illustrative purposes, we consider a square lattice of pins with aspect ratio η=d_y/d_x=1 before moving back to the rectangular lattice with $\eta =\sqrt{2}$. In figure 12, a plane wave is incident at ψ=π/4 with the Bloch parameter in the y-direction set to ${\kappa }_y=\beta \sin (\psi )=3.1113$.

Figure 12.

A plane wave is incident at ψ=π/4 on a lattice of 2000 gratings with d_x=1.0, d_y=1.0 for β=4.40, κ_y=3.1113. (a) Modulus of the coefficients |A_k| for both Wiener–Hopf (dots) with δ=0.005 and Foldy (solid line). The first 50 are shown. (b) Real part of the total displacement field. (Online version in colour.)

The real part of the total displacement field is shown in figure 12b, and it appears that the direction of the incident field is virtually unchanged as it passes through the array of pins. Another notable feature is that the stripes of the incident plane wave are replaced by spots of positive and negative intensity; this pattern is due to the individual scatterers and is linked to the neutrality arising from the Dirac-like point. Figure 12a illustrates the moduli of the scattering coefficients |A_k| obtained using both the Wiener–Hopf (dots) and Foldy (solid line) methods. The agreement is very good, virtually indistinguishable for the first 50 gratings, and for both approaches the coefficients decay to a non-zero constant supporting the neutral propagation that we observe in figure 12b. One other interesting feature is that this propagation is not the only wave action; the appearance of ‘spots’ to the left of the crystal indicates that some reflection action is also present.

In figure 13, we use isofrequency diagrams to aid our interpretation of this neutrality effect. In figure 13a, we show the isofrequency contours for the first surface for the square lattice, and in figure 13b the second surface since β=4.40 is in the vicinity of Dirac-like cones for both. The contours surrounding the point M=(κ_x,κ_y)=(3.1113,3.1113) in the Brillouin zone in both figure 13a,b indicate that M is a Dirac-like point. The lowest value β contour near M in figure 13a is β=4.37, and in figure 13b for the second surface is β=4.46. Figure 13c shows a magnified picture of the neighbourhood of M, for which the β=4.40 contour is more visible. We also illustrate an alternative derivation of the β=4.40 contours in figure 13d, where they take the form of star-like features at the Dirac points. Figure 13d also displays the high degree of degeneracy of the light lines at Dirac-like points such as M, where we observe multiple intersections. Note that figure 13b features the projections of light cone intersections onto the κ_x,κ_y-plane in the form of lines | |κ_x|−|κ_y| |=2π for the square lattice defined by η=1, similar to equation (3.10) in §3b(i).

Figure 13.

(a) Isofrequency contours for the first surface for the square lattice with d_x=1.0, d_y=1.0. The ambient medium's contour for β=4.40 is the dashed circle ${\beta }^2={\kappa }_x^2+{\kappa }_y^2$. (b) Isofrequency curves for the second surface. The dashed line κ_y=3.1113 has been drawn to correspond with Bloch waves in the vertical direction for β=4.40, ψ=π/4. The boundary of the irreducible Brillouin zone ΓXMY is also shown. (c) Close-up of isofrequency contours around β=4.40. (d) Star-like features of the dispersion curves for β=4.40 at M and collection of light circles for the square lattice (note the multiple intersections of the light lines at Dirac-like points). (Online version in colour.)

The dashed line κ_y=κ_x=3.1113 intersects both the ambient medium's contour ${\beta }^2={\kappa }_x^2+{\kappa }_y^2$ and these platonic crystal isofrequency contours β=4.40 precisely at the point M. Recalling that the group velocity should be perpendicular to these slowness contours, and in the direction of increasing β, we would expect to see refracted and reflected waves at an angle of π/4 as illustrated in figure 12b.

(ix). Interfacial waves for the second dispersion surface

Now we change the aspect ratio to $\eta =\sqrt{2}$ to obtain a rectangular lattice as in §3b(iii), but keeping all other parameter values the same. In figure 14a, we plot the isofrequency contours for the second dispersion surface, ranging from around 3.9 to 4.65. We also add the incident wave arrow for ψ=π/4 and the dashed line ${\kappa }_y=\beta \sin (\psi )$ = 3.1113. The intersecting line at κ_y=3.1113 cuts the β=4.40 contour in multiple places, meaning that it is more difficult to predict the behaviour of the system, although intersections corresponding to the group velocity being directed towards the interface from the crystal can be ruled out since the only incoming energy is from the incident medium [31].

Figure 14.

(a) Isofrequency curves for the second surface for a rectangular lattice with d_x=1, $d_y=\sqrt{2}$. The angle of incidence ψ=π/4, the dashed line κ_y=3.1113 and the ambient medium's contour ${\beta }^2={4.4}^2={\kappa }_x^2+{\kappa }_y^2$ are also shown. The predicted directions of propagation for scattered waves are shown by the arrows at A and B for ψ=0,β=4.40,κ_y=3.1113 and ψ=π/6,β=4.45,κ_y=2.225, respectively. (b) Real part of the displacement field for β=4.40, ψ=π/4, κ_y=3.1113 for the rectangular lattice. The Foldy method was used for 2000 gratings. (Online version in colour.)

The intersection at A indicates that the system supports transmission action in the form of refracted waves at an oblique angle less than π/4. This transmission action is visible in figure 14b, although at an apparently lower intensity than the reflection observed. Another interesting feature of the real part of the displacement field plotted in figure 14b is a wave that appears to be localized within the first three gratings of the half-plane discrete system of pins, which can also be considered as a superposition of several evanescent waves that interfere constructively in the neighbourhood of the structured interface. There is also evidence of coupling between the reflection pattern in the homogeneous plate and the interfacial mode.

It appears that this mode is odd, so that in effect the central grating of the triplet of pinned gratings is not seen, and this demonstrates again the connection with finite-grating stacks discussed in §3b(iii), although here we have coupling between the diffraction orders 0 and −1. We explain this coupling using figure 15, where we show the solutions to the eigenvalue problem for a set of three gratings with period $d_y=\sqrt{2}$, separation d_x=1.0 and ${\kappa }_y=\beta \sin (\pi /4)$.

Figure 15.

(a) Solutions of the eigenvalue problem for a system of three gratings with $d_y=\sqrt{2}$ and separation d_x=1 for ${\kappa }_y=\beta \sin (\pi /4)$. (b) Normalized transmitted energy versus β for the triplet's −1 diffraction order (thin solid curve) and the triplet's 0 order (dashed curve) for ψ=π/4. (c) Normalized reflected energy versus β for the triplet's −1 diffraction order (thin solid curve) and the first pair's 0 (dashed curve) and −1 (thick solid) orders for ψ=π/4. (d) Real part of displacement for β=4.35, ψ=π/4, κ_y=3.0759. The Foldy method was used for 2000 gratings. (Online version in colour.)

Referring to figure 15a, the first solution at β≈2.5 is due to the zeroth order only, whereas the solution at β≈4.35 arises for a mixture of 0 and −1 orders. This value of β is very close to β=4.40; this explains the localization we observe in figure 14b, an effect we optimize by setting the frequency of the system with β=4.35.

We show transmitted and reflected energy profiles for the corresponding transmission problem for the first two and three gratings in figure 15b,c. In figure 15b, the solid curve denotes the transmitted energy due to the −1 order for the triplet, explaining how the localized mode helps to support transmission through the rest of the half-plane system. The dashed curve in figure 15b represents the transmitted energy for the 0 order, emphasizing that the −1 order dominates. This means that the first pair has to be able to facilitate transmission of the −1 order to reach the third grating. This is illustrated in figure 15c, where reflected energy is plotted versus β. The thick solid curve shows that the reflection due to the pair's −1 order is around 75%, meaning that there is at least 25% transmission to feed the third grating, which in turn helps to feed the rest of the system.

Figure 15a–c shows that the maxima for the triplets arise for β=4.35 rather than β=4.40. Therefore in figure 15d, we plot the real part of the displacement field for the same rectangular lattice for ψ=π/4, but with β=4.35 and the corresponding value of κ_y to support Bloch waves along the vertical gratings. The results are similar to those observed in figure 14b except that the transmission pattern within the pinned system is slightly more intense than that observed for β=4.40.

A similar but more intense effect is observed for β=4.45 at Y with ψ=π/6 and κ_y=2.225. The resultant propagation parallel to κ_y=0 is illustrative of the uni-directional localized modes associated with such parabolic profiles, and can be rotated through π/2 by swapping the horizontal and vertical periods of the lattice. Thus for a lattice of 4000 gratings with period d_y=1.0 and spacing $d_x=\sqrt{2}$, we show an interfacial wave in figure 16b propagating in the vertical direction parallel to κ_x=0, as predicted by the corresponding isofrequency contour, and very little wave action inside the pins, as predicted by the decay of the coefficients in figure 16a.

Figure 16.

(a) Moduli (solid line) and real parts (dashed) of the coefficients A_k for 4000 gratings with β=4.45, ψ=π/6, κ_y=2.225. The first 30 of 4000 gratings with $d_x=\sqrt{2}$, d_y=1.0 are shown. (b) Real part of the total displacement field. (Online version in colour.)

(x). Higher frequencies—interfacial waves

It is clear that, as the frequency ω=β² increases, a more complicated picture emerges. We illustrate this with an example for β=5.6 in figure 17a,b. The third surface illustrated in figure 6 and magnified here in figure 17c possesses many important features. At the point Γ, the contours change direction by π/2 for β≈5.365 and there is a Dirac-like point at X for β≈5.45. This narrow frequency window supports an array of interesting wave phenomena, similar to those discussed for the first surface in §3b(iii).

Figure 17.

A plane wave is incident at ψ=0.1361 on a lattice of 2000 gratings with d_x=1.0, $d_y=\sqrt{2}$ for β=5.6, κ_y=0.76. (a) Moduli of the coefficients |A_k| with the first 50 shown for both Foldy (solid curve) and Wiener–Hopf (dots). (b) Real part of the total displacement field. (c) Magnification of the third dispersion surface. (d) Real part of the total displacement field for β=5.6, ψ=0.2712, κ_y=1.5. (Online version in colour.)

In figure 17c, we show a collection of isofrequency contours for the platonic crystal's third dispersion surface, as well as the contour for the homogeneous biharmonic plate medium—an arc of the dashed circle defined by ${\beta }^2={\kappa }_x^2+{\kappa }_y^2$ for the case β=5.6. We also refer again to equation (3.10) to explain the appearance of the light cone projections on the isofrequency diagram.

We seek an interfacial wave so we choose ψ such that ${\kappa }_y=\beta \sin (\psi )$ is tangent to the β=5.6 contour for the third surface (point A in figure 17c). The vertical arrow predicts the propagation direction of the refracted waves for this κ_y=0.76 and corresponding ψ=0.1361. In this way, we predict that some refracted waves will propagate perpendicularly to this contour, i.e. in a vertical direction parallel to the interface. We plot the real part of the displacement field for these parameter settings in figure 17b, along with the moduli for the coefficients |A_k| in figure 17a generated by both the Foldy and Wiener–Hopf methods.

Figure 17b shows low propagation within the pinned structure, and relatively low reflection, compared with figure 15b for example. However, there is clearly a travelling wave localized within the first few gratings, albeit with a relatively long wavelength. The exponential decay of the moduli of the scattering coefficients |A_k| is illustrated in figure 17a. In figure 17d, we consider an example for an arbitrary value of κ_y to highlight the contrast in behaviour for various ψ and κ_y. For κ_y=1.5 and ψ=0.2712, we show the real part of the total displacement field in figure 17d. Although there is increased intensity at the interface, as one would expect, the dominant behaviour is propagation and in almost the same direction as the incident wave. This is predicted by the direction of the arrows at B and on the β=5.6 contour close to the incident wave's arrow ψ=0.2712 in figure 17c.

Finally, we consider the case ψ=0, κ_y=0. At the point Γ in figure 17c, the contours for β=5.35 support propagation in a direction normal to those of β=5.40, which support propagation parallel to the interface similar to A for β=5.6 for ψ=0.1361 in figure 17b,c. Thus, there is a point of inflection for 5.35<β<5.40 and it occurs for β≈5.365. For β≤5.365, the refracted waves propagate through the pinned system rather than along its edge, which is what happens for 5.365<β<5.45. However at the Dirac-like point X; β≈5.45, the waves exhibit a mixture of edge localization and propagation through the system. This is because we have the third, fourth and fifth dispersion surfaces meeting at this frequency, leading to a combination of behaviours. The third surface (figure 17c) predicts propagation along the edge for β=5.45 contours while the fourth and fifth surfaces predict propagation parallel to κ_y=0, into the pinned lattice.

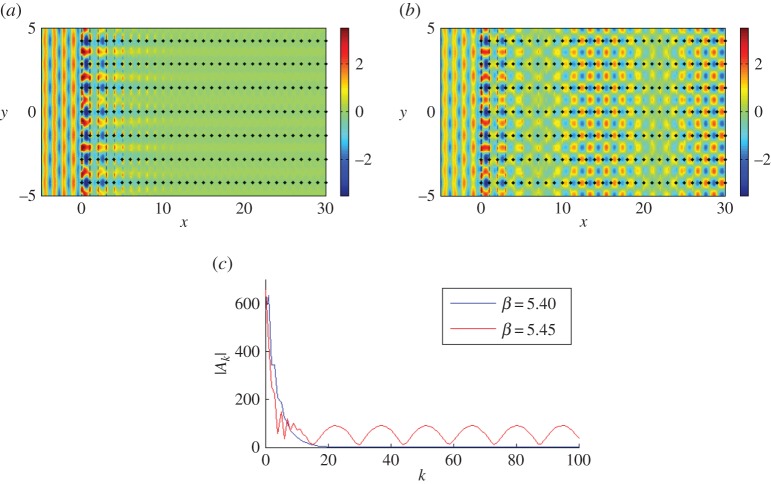
We observe these properties in figure 18, where parts figure 18a,b shows the real part of the total displacement field for β=5.40 and 5.45, respectively. The amplitudes are extraordinarily large for β=5.365, where the isofrequency contours are about to change direction to support interfacial waves rather than propagation through the pinned system (see Γ in figure 17c). This transition has occurred in figure 18a for β=5.40, where the localized interface mode clearly dominates any action inside the pinned region. The comparison of the coefficients A_k in figure 18c also demonstrates the decay of the coefficients to zero inside the crystal for β=5.40. However β=5.45 close to a Dirac-like point supports both edge localization and wave propagation as illustrated in figure 18b,c, where a wave is seen to propagate through the pinned lattice with the wavelength of the envelope function matching that of the coefficients.

Figure 18.

A plane wave is incident at ψ=0 on a lattice of 4000 gratings with d_x=1.0, $d_y=\sqrt{2}$. (a,b) Real part of the total displacement field for β=5.40, β=5.45. (c) Comparison of the moduli of coefficients |A_k|. (Online version in colour.)

4. Concluding remarks: interfacial waves and dynamic localization

The theory and examples presented in this paper have identified novel regimes, typical of flexural waves in structured Kirchhoff–Love plates, for the case of a semi-infinite structured array of rigid pins in an otherwise homogeneous plate. The interface waveguide modes have been identified and studied here.

For a half-plane occupied by periodically distributed rigid pins, we have demonstrated an interplay between the transmission/reflection properties at the interface and dispersion properties of Floquet–Bloch waves in an infinite doubly periodic constrained plate. Specifically, we have analysed regimes corresponding to frequencies and wavevectors that determine stationary points on the dispersion surfaces, as well as Dirac-like points. For such regimes, we have demonstrated that the structure supports localized interfacial waves, among other dynamic effects.

The localization was predicted by an analytical solution, and a formal connection has been shown here between the doubly quasi-periodic Green's function for an infinite plane and the system of equations required to obtain the intensities of sources at the rigid pins, which occupy the half-plane.

Data accessibility

The work does not include any experimental data. All computational results presented in the examples of the paper are reproducible using the analytical methods detailed in the article and the appendices of the electronic supplementary material.

Authors' contributions

All of the authors have provided substantial contributions to the conception and design of the model, analysis and interpretation of the results, writing the article and revising it following the helpful comments and suggestions of the anonymous referees. All authors have given their final approval of the version to be published. Figures for the illustrative examples were produced by S.G.H. and R.V.C.

Competing interests

The authors of the paper have no competing interests.

Funding

All of the authors thank the EPSRC (UK) for its support through Programme grant no. EP/L024926/1.