Multi-shell model of ion-induced nucleic acid condensation

Abstract

We present a semi-quantitative model of condensation of short nucleic acid (NA) duplexes induced by trivalent cobalt(iii) hexammine (CoHex) ions. The model is based on partitioning of bound counterion distribution around single NA duplex into “external” and “internal” ion binding shells distinguished by the proximity to duplex helical axis. In the aggregated phase the shells overlap, which leads to significantly increased attraction of CoHex ions in these overlaps with the neighboring duplexes. The duplex aggregation free energy is decomposed into attractive and repulsive components in such a way that they can be represented by simple analytical expressions with parameters derived from molecular dynamic simulations and numerical solutions of Poisson equation. The attractive term depends on the fractions of bound ions in the overlapping shells and affinity of CoHex to the “external” shell of nearly neutralized duplex. The repulsive components of the free energy are duplex configurational entropy loss upon the aggregation and the electrostatic repulsion of the duplexes that remains after neutralization by bound CoHex ions. The estimates of the aggregation free energy are consistent with the experimental range of NA duplex condensation propensities, including the unusually poor condensation of RNA structures and subtle sequence effects upon DNA condensation. The model predicts that, in contrast to DNA, RNA duplexes may condense into tighter packed aggregates with a higher degree of duplex neutralization. An appreciable CoHex mediated RNA-RNA attraction requires closer inter-duplex separation to engage CoHex ions (bound mostly in the “internal” shell of RNA) into short-range attractive interactions. The model also predicts that longer NA fragments will condense more readily than shorter ones. The ability of this model to explain experimentally observed trends in NA condensation lends support to proposed NA condensation picture based on the multivalent “ion binding shells.”

I. INTRODUCTION

Condensation of highly charged DNA and RNA molecules by cationic agents is biologically important for processes such as packaging of genetic material inside living cells and viruses,^1–5 compactization and delivery of small interfering RNA molecules for gene silencing,⁶ and gene therapy.⁷ In aqueous solution, DNA condensation requires cations with charges of +3e or higher,^8–10 e.g., trivalent cobalt(iii) hexammine (CoHex), trivalent spermidine, or tetravalent spermine can generally condense DNA at room temperatures, while divalent cations cannot.

Several decades of experimental and theoretical studies of DNA condensation have resulted in a general physical picture wherein the major contribution to the effective attraction is due to electrostatic interactions.^11–29 Theoretical models have previously been developed to clarify the details of nucleic acid (NA) interactions, starting from the models of interacting uniformly charged cylinders immersed in an implicit ionic bath,^30–33 to nucleic acid models with more realistic helical geometries of molecular charge distributions.^26,34–40 Counterion electrostatic treatments range from simple mean-field descriptions to strong coupling models^{18,29,33,40–43} with the more sophisticated strong coupling models able to reproduce NA-NA attraction. It has been shown that mean-field description of the counterion atmosphere always leads to repulsion between the oppositely charged cylinders^14,29 – correlations between counterions is a necessary condition for the attraction.^30,42–44 All-atom explicit solvent molecular dynamics (MD) simulations of short DNA fragments demonstrated the existence of short-range attractive forces between B-form DNA duplexes at sufficient degree of duplex neutralization by multivalent ions.^45–47,87

Despite progress in understanding NA-NA interactions, an atomic-level mechanism of multivalent ion-induced nucleic acid condensation has not yet been fully established and some recent experimental data are difficult to rationalize within the accepted models. For example, the condensation propensity of double-stranded (ds) RNA in the presence of trivalent CoHex ion was recently found to be much smaller than for the equivalent sequence of dsDNA.^48,49 In other words, dsRNA helices resist CoHex-induced condensation under conditions where the DNA duplexes readily condense. The unexpected findings are still very recent, with only a limited number of theoretical models attempting to rationalize it so far. For example, a recent extension⁵⁰ of an earlier model²² of DNA condensation suggests that the striking difference between RNA and DNA condensation stems from the differences in intrinsic helical parameters of the duplexes. However, it has recently been shown experimentally that significant differences in condensation propensity can arise in some NA duplexes without significant differences in their helical parameters.⁴⁹ Nevertheless, the model⁵⁰ emphasizes critical role of counterion distributions in NA condensation; some of the distributions of bound trivalent counterions assumed by the model are consistent with the latest all-atom molecular dynamics (MD) simulations,⁴⁹ but some are very different, pointing to the critical need to take these atomistic details into account for quantitative and even qualitative agreement with recent condensation experiments.

Although it is possible to count the number of excess ions around nucleic acids, using techniques like buffer equilibration and atomic emission spectroscopy (BE-AES)⁵¹ or an indicator dye,⁵² only absolutely calibrated small angle X-ray scattering (SAXS) experiments can both count the number of ions⁵³ and reveal their locations.^54,55 Even so, only the ensemble average distribution can be detected. At this point, only atomistic simulations that treat the solvent (water and ions) explicitly can provide several key details of counterion binding and distributions around nucleic acids, which are otherwise near impossible to obtain experimentally. Among these critical details is thermodynamic characterization of CoHex binding to different regions of NA, which, as we shall see, is necessary for a quantitative description of condensation. However, at this point experiment can only provide average, aggregate binding affinity to NA, but this is not the key quantity of interest for condensation.⁴⁹ Atomistic simulations can bridge the gap with experiment in that respect and provide estimates of the counterion distributions and affinities to various loci in the NA duplexes. In what follows we show that such estimates become valuable in building a quantitative picture of NA condensation—picture that can be verified experimentally.

A. The “shells” model of CoHex distributions around NA duplexes

Recent all-atom MD simulations⁴⁹ of short (25-bp) DNA, RNA, and DNA:RNA hybrid duplexes with CoHex counterions show that, under near neutralization conditions necessary for NA condensation (∼90% of NA charge neutralized by bound counterions), the majority (∼2/3) of neutralizing CoHex ions bound to B-form DNA are localized at the external surface of the phosphate groups in the cylindrical layer 12–16 Å from the helical axis, Fig. 1. This layer is defined as the “external” ion binding shell.⁴⁹ The smaller fraction of bound CoHex ions around B-DNA (∼1/3) are localized in the major groove at distances 7–12 Å from the helical axis—the corresponding cylindrical layer is defined as the “internal” ion binding shell.⁴⁹ In contrast to B-DNA, the majority of CoHex ions (∼2/3) bound to A-form RNA are localized within the RNA major groove, in the “internal” ion binding shell, Fig. 1. This substantial difference in CoHex distributions is explained by the major difference in the electrostatic potential of B-DNA and A-RNA.^49,56 The potential in the major groove of A-RNA is about 10 (kcal/mol)/|e| lower than on the rest of the RNA surface accessible to CoHex, or anywhere on the surface of B-DNA. The resulting much stronger attraction of trivalent CoHex ions overwhelms the ion-ion repulsion, leading to the qualitatively different pictures in CoHex binding.

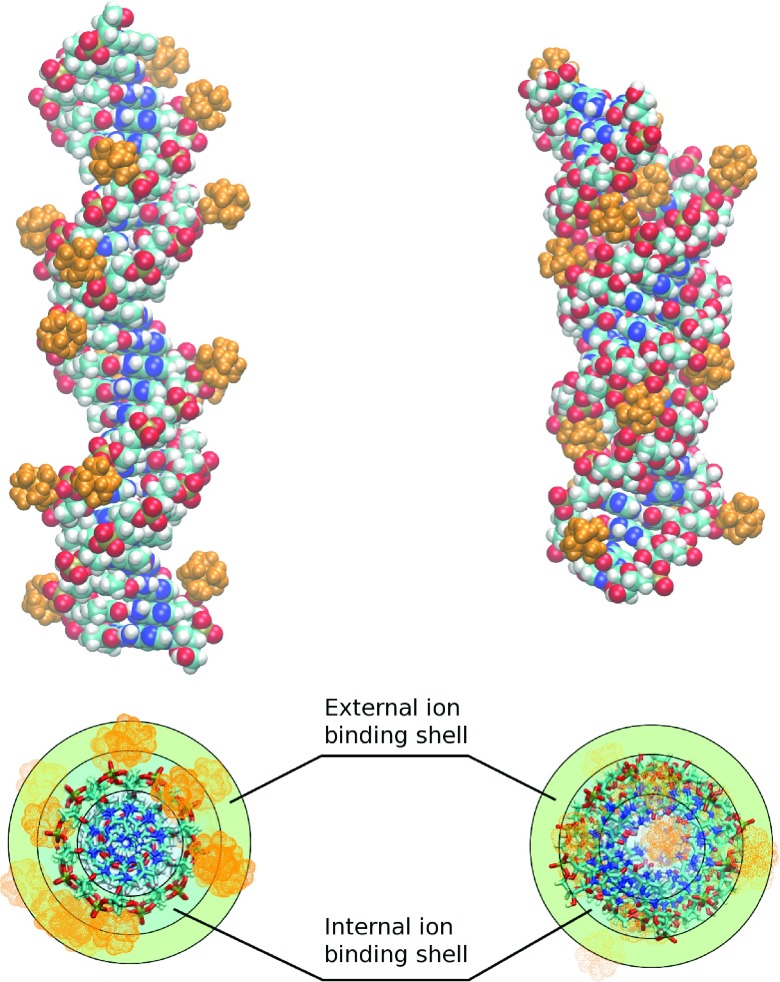
FIG. 1.

The “shells” of counterion distribution around nucleic acids duplexes.⁴⁹ Upper panel: representative snapshots of B-form dsDNA (left) and A-form dsRNA (right) structures with bound CoHex ions (orange). Lower panel: the “external” and “internal” cylindrical ion binding shells around B-DNA (left) and A-RNA (right). Most of the ions (∼2/3) shown in the upper panel are bound in the “external” shell of the B-DNA and the “internal” shell of the A-RNA.

An analysis of the simulated CoHex ion distributions around 25-bp DNA, RNA, and DNA:RNA hybrid duplexes of the equivalent mixed sequence⁵⁷ and around homopolymeric poly(dA):poly(dT) DNA led to the following two observations.⁴⁹ First, at the near-neutralizing conditions necessary for NA condensation, the fractions of CoHex ions in the “external” ion binding shells of the four NA duplexes correlate with measured condensation propensities of these duplexes.⁴⁹ Second, the “external” CoHex binding shells of NA molecules are the only shells that overlap substantially at the inter-axial duplex separation corresponding to the separations observed in CoHex condensed (aggregated) DNA phases (about 28 Å ^16,58).

These two observations constitute a basis for the “overlapping ion binding shell” mechanism of NA condensation which was proposed in our previous paper.⁴⁹ According to the mechanism, the fraction of neutralizing multivalent ions bound in the NA “external” ion binding shell (and not the total number of bound ions) is a key parameter for understanding multivalent ion-induced nucleic acid condensation. This fraction reflects a complex interplay between various structural and sequence features of NA helices, and its ions are responsible for most of the attractive interaction between the helices. The proposed mechanism was rationalized by simple and robust electrostatic arguments and is in excellent qualitative agreement with experimental condensation propensities of various NA duplexes. The mechanism was later illustrated by explicit calculations of the potential of mean force (PMF) between two adjacent NA duplexes.⁴⁷ However, no quantitative model of the duplex condensation phenomenon has been presented so far; such a model would be the best illustration for the proposed new mechanism and could lead to novel predictions.

In this work, we develop a semi-quantitative model of CoHex-induced NA duplex condensation that is based on the “overlapping ion binding shell” mechanism. The model provides a quantitative relationship between key characteristics of bound multivalent counterion distributions around NA molecules and the free energy changes upon NA duplex aggregation. We show that the estimated free energy changes for different NA duplexes correlate well with the experimental condensation propensities of these duplexes and explain observed differences in DNA and RNA condensation and make several predictions.

II. THE MULTI-SHELL MODEL OF ION-MEDIATED NA-NA INTERACTION

We consider a transition between a dilute aqueous solution of relatively short nucleic acid duplexes (compared to the DNA persistence length of ∼150-bp) and their condensed (aggregated) phase represented by a bundle of parallel, hexagonally packed NA molecules⁵⁸ with a distance between neighbors smaller than their length. The solution phase contains a certain amount of trivalent CoHex counterions sufficient to neutralize all the duplexes. Part of these ions is bound to the duplexes due to Manning-Oosawa condensation.^59–62 The fraction of NA duplex charge neutralized by bound CoHex ions, Θ, in the solution and aggregated phases is considered to be the same, although the aggregated phase as a whole is assumed to be neutral.

The aggregated phase is stabilized by short-range attractive forces between the duplexes that originate mostly from the electrostatic interactions of multivalent counterions bound to one duplex with the “correlation holes”^{21,24,41,42,62} on the charged surface of another duplex covered by a layer of bound multivalent counterions, i.e., these interactions have a significant non-mean-field component^28–30,33 due to correlations between multivalent counterions bound to different neighboring duplexes in the aggregate.

Our goal is to estimate the free energy difference between the aggregated and solution phases of NA duplexes, ΔG_aggr, as a function of Θ. The latter can be used as a convenient proxy for bulk CoHex concentration in the solution phase.

The multivalent ion-induced aggregation free energy can be represented as a sum of three additive components,

$${\displaystyle \mathrm{\Delta }{G}_{\mathit{aggr}}=\mathrm{\Delta }{G}_{\mathit{attr}}+\mathrm{\Delta }{G}_{\mathit{el}-\mathit{rep}}-T\mathrm{\Delta }{S}_{\mathit{conf}}.}$$ (1)

The first two terms in Eq. (1) describe the changes in the electrostatic interactions upon the transition between the solution and aggregated phases. These interactions are decomposed into the short-range net attractive term, ΔG_attr, and the net repulsive term, ΔG_el−rep that describes the (residual) repulsion between the duplexes almost neutralized by bound counterions. The last term, TΔS_conf, represents the loss of duplex configurational entropy (translational and rotational) upon the aggregation.

The decomposition of the electrostatic contributions to ΔG_aggr in Eq. (1) into net attractive and net repulsive terms is not unique. Both terms include contributions from the interactions of multivalent ions bound to one duplex with the bare charges of adjacent duplex, which are favourable for the aggregation, and contributions from the interactions of these same ions with the ions bound to the adjacent duplex, which oppose the aggregation. Due to ion-ion correlations this latter type of the interactions between bound multivalent ions is difficult to estimate. However, grouping these interactions between bound multivalent ions into the contributions where the ion-ion correlations play a substantial role and where they can be neglected allows us to estimate the net attractive ΔG_attr and net repulsive ΔG_el−rep electrostatic terms through simple analytical expressions.

The last term in Eq. (1), −TΔS_conf, can be estimated using a simple coarse-grained approach. This term is usually neglected for long DNA molecules,²⁴ but, as we shall see later, it can contribute appreciably to the destabilization of the aggregated phase in the case of relatively short 25-bp NA duplexes.

Additional underlying assumptions of our model for the aggregation free energy, physical considerations that justify them, and details of how each term in Eq. (1) is calculated are presented in Sec. IV. Derivations of the components of Eq. (1) are described below.

A. Short-range attractive component, ΔG_attr, of the ion-mediated duplex-duplex interactions

The multivalent ion-mediated short-range attractive forces between the duplexes in the aggregated phase arise from the interactions of the multivalent counterions bound to the surface of one duplex with all the charges on the neighboring duplex (including its bound counterions). These are the same interactions that determine the distribution of counterions around NA duplexes in the solution phase. They are strong when the counterion is inside the duplex ion binding shell and relatively weak when outside^38,63 and can be characterized by the ion binding affinity to nearly neutralized duplex. In the case of multivalent counterions these interactions can have a significant non-mean-field component^28,29,33 due to ion-ion correlations which reduce the ion-ion repulsion.

In our decomposition of the aggregation free energy, Eq. (1), we consider that these attractive interactions contribute to ΔG_attr when CoHex ion bound to one duplex enters the “external” ion binding shell of another duplex,⁶⁴ i.e., when the “external” binding shells of the two duplexes overlap upon aggregation. When the bound CoHex ion is outside the ion binding shell of a neighboring duplex we no longer consider its interaction with the duplex contributing to ΔG_attr. In this case the bound ion can be treated as part of the averaged neutralizing background^63,65–67 that screens the bare duplex charge and reduces the mutual electrostatic repulsion between the duplexes described by ΔG_el−rep. The proposed decomposition assumes that the non-mean-field component of the ion interactions with the counterions bound to the neighboring duplex can be significant and accounted for in ΔG_attr when the ion enters the “external” ion binding shell of the neighboring duplex but is small and can be neglected when the ion is outside the ion binding shell.

Once the duplexes approach each other upon aggregation, CoHex ions bound in the “external” ion binding shell of one duplex enter the “external” shell of another duplex. The additional interaction energy of each of these ions in the “external” ion binding shell of the neighboring duplex is essentially the binding energy for the additional CoHex ions in the “external” shell of the duplex. Assuming that minimal changes in the CoHex distributions occur when the two duplexes approach each other, this binding energy averaged over the volume the shell can be approximated by CoHex binding affinity, μ_a, to the “external” ion binding shell of an isolated NA duplex. This quantity varies with the degree of duplex neutralization Θ, but for a narrow range of Θ (at near neutralizing conditions, 0.9 ≤ Θ ≤ 1.0) that is of interest to us here, this dependence is small and can be neglected. Ion affinity μ_a reflects the balance between the attraction to the bare NA duplex charges and the repulsion from all other bound ions around the duplex and, therefore, depends on the ion charge, Ze. It also absorbs the contribution from the ion-ion correlations which increases with the ion valency Z.

The above assumptions about the contributions to ΔG_attr result in a short-range attractive component of the interactions between the two neighboring NA duplexes that is proportional to two quantities: (1) the average number of CoHex ions in the overlapping region of the ion binding shells of these duplexes, ΔN_s, and (2) the binding affinity μ_a of CoHex ion in the “external” ion binding shell of NA duplex at near neutralizing conditions.

For the hexagonal packing of the duplexes in the aggregated phase,⁵⁸ the total short-range attractive term in the decomposition of the aggregation free energy, Eq. (1), per duplex can therefore be estimated as

$${\displaystyle \mathrm{\Delta }{G}_{\mathit{attr}}=3{\mu }_a\times \mathrm{\Delta }{N}_s,}$$ (2)

where the factor of 3 accounts for the half of the attractive interactions with the six nearest neighbors in the hexagonally packed aggregate.

To estimate μ_a and ΔN_s we will use the equilibrium properties of CoHex distribution around a single NA duplex in the solution phase obtained from the MD simulation.

1. CoHex binding affinity μ_a

The binding affinity of an ion to the ion binding shell of a polymer can be defined as a difference of the excess chemical potentials of this ion in the binding shell and in the bulk. In the case of the “external” ion binding shell of NA duplex where the excluded volume effects for CoHex ions are negligible this difference can be estimated as

$${\displaystyle {\mu }_a=-k_{B}Tln\left({\rho }_s/{\rho }_b\right),}$$ (3)

where ρ_b and ρ_s are the number densities of CoHex ions in the bulk and in the “external” ion binding shell of the NA duplex, respectively. A more detailed derivation of this equation is presented in Sec. IV.

Because of the finite size of the simulation box used in all-atom MD simulations⁴⁹ and the absence of a monovalent salt screening in the simulations, the CoHex concentration at the simulation box boundary, ρ_B, is not equal to the bulk value ρ_b required in Eq. (3) for estimating μ_a. To account for the difference, we introduce a long-range correction to μ_a,

$${\displaystyle {\mu }_a=-k_{B}Tln\left({\rho }_s/{\rho }_B\right)+Ze\phi \left(r_B\right),}$$ (4)

where Zeφ(r_B) is the energy of the CoHex ion charge, Ze, in the electrostatic potential of the NA duplex and its bound ions, φ(r_B), at the system boundary (r_B = 31 Å). Without monovalent ions present, φ(r) can be estimated as the electrostatic potential of a uniformly charged non-conducting rod of length H with a linear charge density λ in a solvent with dielectric constant ε,

$${\displaystyle \phi \left(r\right)=\frac{2\lambda }{\epsilon }ln\left(\frac{H/2+\sqrt{{(H/2)}^2+r^2}}{r}\right).}$$ (5)

Here λ corresponds to the linear charge density of 25-bp NA duplex (charge Q_na = − 48e, length H⁶⁹) re-normalized (scaled down) by the charge of all bound CoHex ions (N₀Ze) within the outer boundary of the “external” ion binding shell, λ = (Q_na + N₀Ze)/H = Q_na(1 − Θ₀)/H, where Θ₀ = N₀Ze/|Q_na| is a degree of duplex neutralization by all (N₀) bound CoHex ions determined from the results of MD simulations.⁴⁹ The potential φ(r) is zero at infinity. The values of the potential estimated for the NA duplexes of interest at r_B = 31 Å and dielectric constant ε = 78.5 are relatively small, ranging from −0.7 to −1.1 k_BT/e.

2. Number of bound CoHex ions, ΔN_s, in the overlapping volume of ion binding shells

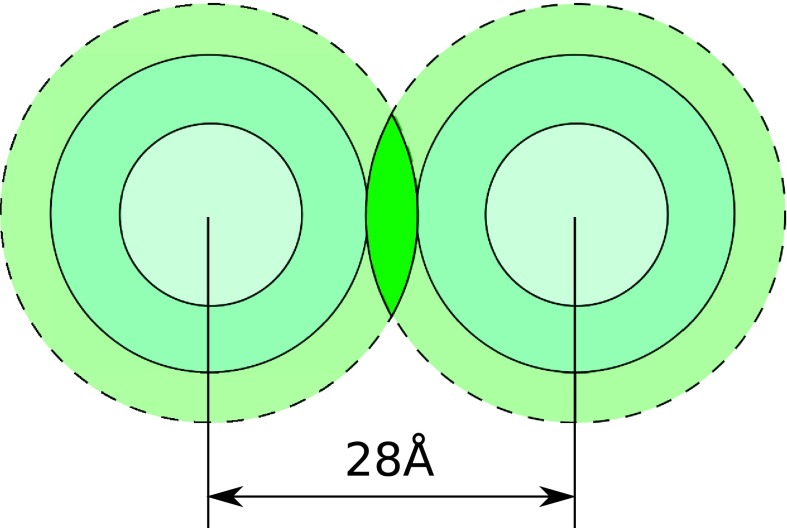
Fig. 2 shows a schematic of the “internal” and “external” ion binding shells around two parallel duplexes at the typical duplex-duplex separation of 28 Å in the DNA aggregate.^16,58,68 The shells overlap volume is completely defined by geometries of the shells and mutual orientation of the duplexes. In the hexagonal packing of the duplexes in the aggregated phase⁵⁸ considered in our model, the duplexes are parallel to each other and their ends are assumed at the same height.

FIG. 2.

Horizontal cross section of the overlap of the “external” CoHex ion binding shells of two NA duplexes at the inter-axial separation d = 28 Å. The overlap region (volume) is indicated by dark green color. CoHex ions in this volume element, which is about 80 Å high (length of the NA duplex), strongly interact with both duplexes creating the effective short-range attraction between NA molecules. These ions are excluded from the estimation of the effective duplex-duplex electrostatic repulsion in Eq. (10).

Under the assumption of minimal changes in the CoHex distributions when the duplexes approach each other the number of ions ΔN_s in the overlap volume of the two “external” ion binding shells ΔV_s⁶⁹ can be estimated as

$${\displaystyle \mathrm{\Delta }{N}_s=2{\rho }_s\mathrm{\Delta }{V}_s=2\hspace{0.17em}\frac{N_s}{V_s}\mathrm{\Delta }{V}_s,}$$ (6)

where V_s and N_s are the volume and the average number of CoHex ions bound in the “external” ion binding shell, respectively.

Since we are interested in exploring the dependence of the aggregation free energy ΔG_aggr on the degree of NA duplex neutralization Θ at near neutralizing conditions when Θ is close to its value Θ₀ observed in MD simulations, we need to estimate how N_s changes with Θ. Assuming the fractions of the bound CoHex ions in each of the ion binding shell are insensitive to the small changes in the total number of bound CoHex ions, N, we can write

$${\displaystyle N_s=f_{s}N=f_s\frac{\left|Q_{\mathit{na}}\right|}{Ze}\mathrm{\Theta },}$$ (7)

where $f_s=N_s^0/N_0$ is the fraction of CoHex ions bound in the “external” shell, $N_s^0$ and N₀ are the simulation results values.⁴⁹

The above results allow one to rewrite Eq. (2) as

$${\displaystyle \mathrm{\Delta }{G}_{\mathit{attr}}\left(\mathrm{\Theta }\right)=6{\mu }_a\frac{\mathrm{\Delta }{V}_s}{V_s}\frac{\left|Q_{\mathit{na}}\right|}{Ze}{f}_s\mathrm{\Theta }.}$$ (8)

Note that for long duplexes, μ_a is independent of the duplex length H, and so ΔG_attr in Eq. (8) depends on H only through the bare duplex charge Q_na = λ_naH, where λ_na is the (constant) linear charge density of the unscreened NA duplex.

B. Repulsive electrostatic component ΔG_el−rep of the ion-mediated duplex-duplex interactions

Our decomposition of the electrostatic interactions between two NA duplexes upon ion-mediated duplex aggregation onto the attractive and repulsive parts is based on the separation of the bound CoHex ions into those which are in the ion binding shell overlap volume ΔV_s, Fig. 2, and the rest of the bound ions. The interactions of the former ones with the neighboring duplex and all of its bound counterions have a significant ion-ion correlation contribution and constitute the attractive part of the aggregation energy ΔG_attr described above. The interactions of rest of the bound ions with the neighboring duplexes and their bound counterions can be treated at the mean-field level. In this case these counterions can be considered as a neutralizing background which uniformly reduces the bare charge of each duplex. This approximation allows us to use continuum electrostatics in estimating ΔG_el−rep.

As discussed above, the NA duplex neutralization by bound CoHex is described by a degree of neutralization Θ which, according to Manning counterion condensation theory⁶¹ applied to NA molecules interacting with trivalent counterions, reaches ∼0.92 level. Approximately the same level of duplex neutralization by CoHex ions (Θ₀ ∼ 0.88–0.92) is observed in all-atom MD simulations.⁴⁹

As in the case of ΔG_attr, we consider the repulsive interactions between the duplexes at zero monovalent salt condition, neglecting a small monovalent ion screening in the NA duplex condensation experiments.^48,49 Indeed, for spermine⁴⁺, which is similar to CoHex in its condensing power, condensation of 150-bp DNA fragments was shown to be unaffected by monovalent ion concentrations of 20 mM and lower if DNA monomer concentration ([P]) is higher than 0.4 mM.⁷⁰ In the condensation experiments we discuss,^48,49 NA monomer concentration is about 2 mM.

Additional considerations of why the influence of 20 mM of NaCl on CoHex induced duplex condensation can be neglected here include: (1) the interactions of bound CoHex ions with NA molecules are virtually unaffected by monovalent salt concentration below 40 mM¹⁵ and (2) CoHex affinity μ_a to NA duplex is affected by a small amount of monovalent salt through the change of long-range potential in much the same way as the long-range repulsive duplex-duplex interactions. Since each of these two monovalent salt screening effects on ΔG_attr ∼ μ_a and ΔG_el−rep are small and opposite, we assume that the combined salt screening effect on the duplex-duplex attractive and repulsive terms is negligibly small and estimate these terms without considering the monovalent screening. However, at physiological monovalent salt concentrations (∼100 mM), the difference could increase; the drop in the attraction due to reduction of CoHex affinity may be substantially larger than the drop in the repulsive term, contributing to the onset of NA duplex aggregation by monovalent ions.⁷⁰

The above approximations (no ion-ion correlations and zero monovalent salt condition) allow us to estimate the duplex-duplex repulsion as interaction between the neighboring NA duplexes with their charges uniformly re-normalized by bound counterions, with the duplexes being in continuum dielectric without free ions. The interactions beyond the nearest neighbors in the hexagonal packing are neglected (assumed to be screened out by monovalent ions or by unbound CoHex ions in the net neutral duplex aggregated phase).

Within the linear response electrostatics in a continuum dielectric, the interaction between two duplexes with the charges re-normalized uniformly by a factor ξ is equivalent to scaling the interaction between bare duplexes, ΔG_el−na, by ξ².

To estimate ξ we notice that according to the specific way we decompose the electrostatic interactions, all CoHex ions bound to one NA duplex (N ∼ Θ), except those (ΔN_s/2) in the shell overlapping volume, participate in the duplex charge re-normalization. Taking into account Eqs. (6) and (7), the charge fraction of these ΔN_s/2 ions that has to be excluded from the re-normalization is

$${\displaystyle \mathrm{\Lambda }=\frac{\mathrm{\Delta }{N}_s}{2}\frac{Ze}{\left|Q_{\mathit{na}}\right|}=\frac{\mathrm{\Delta }{V}_s}{V_s}{f}_s\mathrm{\Theta }.}$$ (9)

This fraction reduces the duplex screening and changes the duplex charge re-normalization coefficient from ξ = 1 − Θ to ξ = 1 − Θ + Λ. The resulting estimate for the duplex repulsive contribution to the aggregation free energy at the hexagonal packing of the aggregated phase can be written as

$${\displaystyle \mathrm{\Delta }{G}_{\mathit{el}-\mathit{rep}}\left(\mathrm{\Theta }\right)=3\mathrm{\Delta }{G}_{\mathit{el}-\mathit{na}}{(1-\mathrm{\Theta }+\mathrm{\Lambda })}^2=3\mathrm{\Delta }{G}_{\mathit{el}-\mathit{na}}{\left(1-\mathrm{\Theta }\left[1-\frac{\mathrm{\Delta }{V}_s}{V_s}{f}_s\right]\right)}^2,}$$ (10)

where ΔG_el−na is the electrostatic interaction between the two bare duplexes in a dielectric continuum which can be estimated numerically, within the Poisson framework. Here we neglect the interactions with more distant neighbors in the hexagonal packing taking into account that they should be scaled by a much smaller factor (ξ² = (1 − Θ)² at Λ = 0) and assuming the overall neutrality of the aggregated phase due to unbound diffuse ions.

Note that the re-normalization coefficient ξ is independent of the duplex length H and so the repulsion term ΔG_el−rep in Eq. (10) depends on H only through the bare duplexes repulsion ΔG_el−na. For long duplexes $\mathrm{\Delta }{G}_{\mathit{el}-\mathit{na}}\sim {\lambda }_{\mathit{na}}^{2}H$ leading to ΔG_el−rep linear with H, similar to ΔG_attr.

We estimate ΔG_el−na by solving the Poisson equation (PE) for the two parallel unscreened duplexes and averaging the interaction energies over 12 different mutual duplex orientations. The details of this estimation are presented in Sec. IV.

C. Configurational entropy loss upon duplex association

The change in the NA duplex configuration entropy upon duplex aggregation, ΔS_conf, is caused by restrictions of the duplex translational and rotational motion in the aggregated phase compared to a free motion in a dilute solution phase. For long NA molecules this entropic contribution to the aggregation free energy is usually neglected compared to other repulsive and attractive contributions.²⁴ For short 25 base pair NA duplexes, however, the contribution of TΔS_conf can be substantial and, as we will see, comparable with the electrostatic repulsion between the duplexes in the aggregated phase.

Short NA duplexes of the length smaller than the NA persistence length (∼150-bp for dsDNA) can be considered as rigid rods. We estimate their configuration entropy change, ΔS_conf = ΔS_tran + ΔS_rot, by following the approach described in Ref. 71,

$${\displaystyle \mathrm{\Delta }{S}_{\mathit{conf}}=k_{B}ln\left(c\mathrm{\Delta }X\mathrm{\Delta }Y\mathrm{\Delta }Z\right)+k_{B}ln(\mathrm{\Delta }X\mathrm{\Delta }Y/\pi H^2).}$$ (11)

Here, the first term corresponds to the change in the duplex translational entropy S_tran due to reduction of volume available for translational motion of the duplex center of mass from 1/c in the solution phase to ΔXΔYΔZ in the aggregated phase, where c is a NA duplex concentration in the solution. The second term reflects the loss of the rotational entropy ΔS_rot in two of the three duplex rotational degrees of freedom upon aggregation; the corresponding reduction of the available rotational phase space being Δθ₁Δθ₂/4π where Δθ₁₍₂₎ ≈ ΔX(Y)/(H/2), Fig. 3. In our estimations we use ΔX = ΔY = (d − 2a)/2 where d is inter-axial duplex separation and a is the radius of the NA duplex estimated as a = 11 Å. At d = 28 Å corresponding to duplex separation observed in CoHex condensed DNA phases,^16,58 ΔX = ΔY = 3 Å—a half-width of the nucleic acid effective attraction energy well⁵⁰ at 5k_BT above the minimum. For simplicity we use the same value for ΔZ (ΔZ = 3 Å), which describes the vertical misalignment of the ends of parallel duplexes in the hexagonal bundle.

FIG. 3.

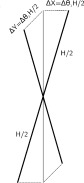
Schematic of a rigid rod rotation about the two axes used in the estimate of the rotational entropy change upon aggregation.

From Eq. (11) it follows that only ΔS_rot part of the duplex configuration entropy chanwge depends on the duplex length H—this part scales logarithmically with H, increasing its contribution to the aggregation energy for longer duplexes.

D. Attractive and repulsive interactions at the “internal-external” ion binding shell overlaps

So far, we considered the simplest case of two parallel NA duplexes at such separations in the aggregated phase that only their “external” ion binding shells overlap; we approximated the additional binding free energy for the CoHex ion bound in the “external” ion binding shell of one duplex and entering the “external” ion binding shell of the neighboring duplex by the CoHex binding affinity μ_a to the “external” shell. This affinity, defined as a difference of the CoHex excess chemical potentials, Eq. (16), reflects only the change of CoHex ion interactions with its environment and does not depend on CoHex configurational entropy. Since this entropy in either of the two “external” ion binding shells of the two neighboring duplexes is same, the above approximation is reasonable.

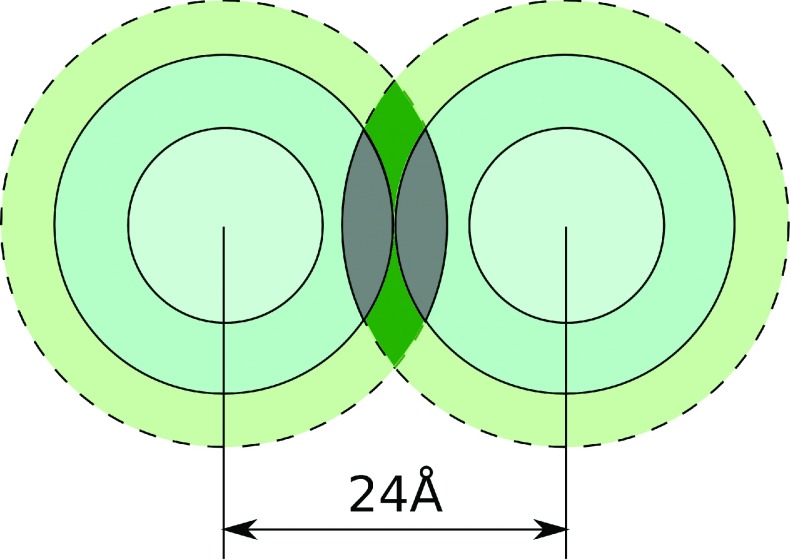
If the duplex-duplex separations in the aggregated phase are smaller than 28 Å, in addition to the “external-external” shell overlaps the overlaps of the “external” and “internal” ion binding shells of the adjacent duplexes occur, Fig. 4. Below we will argue that the attractive contribution ΔG_attr to the aggregation energy can still be estimated by Eq. (2) where the quantity ΔN_s is replaced by ΔN, the sum of the numbers of bound CoHex ions in both overlaps.

FIG. 4.

Schematic of the overlaps of the “external” and “internal” ion binding shells of two NA duplexes at the inter-axial separation d = 24 Å. The regions of the “external-internal” shells overlap are gray. Dark green indicates “external-external” shells overlap as in Fig. 2.

In equilibrium, the chemical potential of CoHex ions in the “external” and “internal” ion binding shells is the same. Any difference in the excess chemical potentials of the ions in these shells (and, thus, in the ion binding affinities) is compensated by the difference in ion configurational entropies within these shell. The same consideration can be applied to the estimation of the free energy gain for the CoHex ion bound in the “external” shell of one duplex once entering the “internal” shell of adjacent duplex when these shells overlap. Whatever correction to μ_a might be applied due to the difference in the CoHex excess chemical potentials in these shells, it should be compensated by the original difference in the ion configurational entropies in these shells. Therefore, the contribution of each CoHex ion in the “external-internal” shell overlaps to ΔG_attr can still be approximated by the same value of μ_a as in the case of the CoHex ions in the “external-external” shell overlaps. This approximation allows us to use Eq. (2) for the close inter-duplex separation, Fig. 4, as well, but now ΔN_s becomes ΔN, the sum of the numbers of ions in two overlapping shell regions, “external-external” and “external-internal” (combined gray and dark green regions in Fig. 4). This quantity can be estimated as

$${\displaystyle \mathrm{\Delta }N=2{\rho }_s\mathrm{\Delta }{V}_s+({\rho }_i+{\rho }_s)\mathrm{\Delta }{V}_{is}=\left[\frac{f_i}{V_i}\mathrm{\Delta }{V}_{is}+\frac{f_s}{V_s}(\mathrm{\Delta }{V}_{is}+2\mathrm{\Delta }{V}_s)\right]\frac{\left|Q_{\mathit{na}}\right|}{Ze}\mathrm{\Theta },}$$ (12)

where ΔV_is is the volume of the “external-internal” overlap, ρ_i and f_i are the number density and the fraction of CoHex ions bound in the “internal” ion binding shell of the volume V_i. Similar to f_s, the fraction f_i is defined as $f_i=N_i^0/N_0$ where $N_i^0$ is the number of CoHex ions in the “internal” shell determined from the all-atom MD simulations.⁴⁹ Estimations of $N_i^0$, N₀ are in Table II, while ΔV_is and ΔV_s are presented in the supplementary material.⁶⁹

TABLE II.

Average numbers of bound CoHex ions in the “external” and “internal” ion binding shells around the four NA duplexes estimated from the MD simulations.⁴⁹

	DNA(dA:dT)	DNA	HYB	RNA
“External” shell ions, $N_s^0$	9.8	8.5	3.3	2.0
“Internal” shell ions, $N_i^0$	4.6	4.2	7.7	9.4
All bound CoHex ions, N0	14.5	14.4	14.1	14.7

Using Eq. (12), the attractive contribution to the aggregation free energy, Eq. (8), can be rewritten as

$${\displaystyle \mathrm{\Delta }{G}_{\mathit{attr}}\left(\mathrm{\Theta }\right)=3{\mu }_a\left[\frac{f_i}{V_i}\mathrm{\Delta }{V}_{is}+\frac{f_s}{V_s}(\mathrm{\Delta }{V}_{is}+2\mathrm{\Delta }{V}_s)\right]\frac{\left|Q_{\mathit{na}}\right|}{Ze}\mathrm{\Theta }.}$$ (13)

We do not consider the “internal-internal” shell overlaps, as these could only occur at such short inter-duplex separations where steric repulsion would become prohibitively large.

In the case of “external-internal” ion binding shell overlap, the quantity ΔN, Eq. (12), has to be used instead of ΔN_s in determining the correction Λ, Eq. (9), to the duplex charge re-normalization coefficient ξ = 1 − Θ + Λ. The latter one can now be written as

$${\displaystyle \xi =1-\mathrm{\Theta }+\frac{1}{2}\left[\frac{f_i}{V_i}\mathrm{\Delta }{V}_{is}+\frac{f_s}{V_s}(\mathrm{\Delta }{V}_{is}+2\mathrm{\Delta }{V}_s)\right]\mathrm{\Theta },}$$ (14)

resulting in the following duplex-duplex repulsive term in the aggregation free energy:

$${\displaystyle \mathrm{\Delta }{G}_{\mathit{el}-\mathit{rep}}\left(\mathrm{\Theta }\right)=3\mathrm{\Delta }{G}_{\mathit{el}-\mathit{na}}{\left(1-\mathrm{\Theta }\left[1-\frac{1}{2}\left(\frac{f_i}{V_i}\mathrm{\Delta }{V}_{is}+\frac{f_s}{V_s}(\mathrm{\Delta }{V}_{is}+2\mathrm{\Delta }{V}_s)\right)\right]\right)}^2.}$$ (15)

As in the case of the duplex separations in the aggregated phase when only the “external” ion binding shells overlap, for long duplexes the attractive and repulsive contributions, Eqs. (13) and (15), depend linearly on the duplex length H through the bare duplex charge, Q_na = λ_naH, and bare duplexes repulsion, $\mathrm{\Delta }{G}_{\mathit{el}-\mathit{na}}\sim {\lambda }_{\mathit{na}}^{2}H$, respectively. The entropic contribution, Eq. (11), remains unchanged and scales logarithmically with H.

Note that Eqs. (13) and (15) reduce to simpler Eqs. (8) and (10) when the “external-internal” overlap volume ΔV_is vanishes for the inter-axial duplex separations d ≥ r_i + r_s = 28 Å (r_i + r_s is the sum of the outer radii of the “internal” and “external” ion binding shells). Since the typical inter-axial duplex separation in the CoHex induced DNA aggregates is 28 Å,^16,58,68 for this and larger separations we can use more simple Eqs. (8) and (10).

III. APPLICATION OF THE MODEL AND DISCUSSION

A. The stability of nucleic acid aggregates

We apply our semi-quantitative model, Eq. (1), where the terms are determined by Eqs. (13), (15), and (11), to characterize CoHex induced aggregation of four 25-bp long nucleic acid duplexes previously simulated and studied experimentally in Ref. 49; these are DNA, RNA, and DNA:RNA hybrid duplexes of the equivalent mixed sequence^57,72 and homopolymeric poly(dA):poly(dT) DNA duplex.

The model presented here allows us to estimate the aggregation free energies of these duplexes, ΔG_aggr, as functions of the degree of duplex neutralization by bound CoHex ions, Θ, and compare them with the duplex condensation propensities observed in Ref. 49. The aggregation begins when Θ, which depends on the bulk CoHex concentration in the solution phase, reaches the level at which the NA aggregated phase is more stable than the solution phase, i.e., when ΔG_aggr < 0.

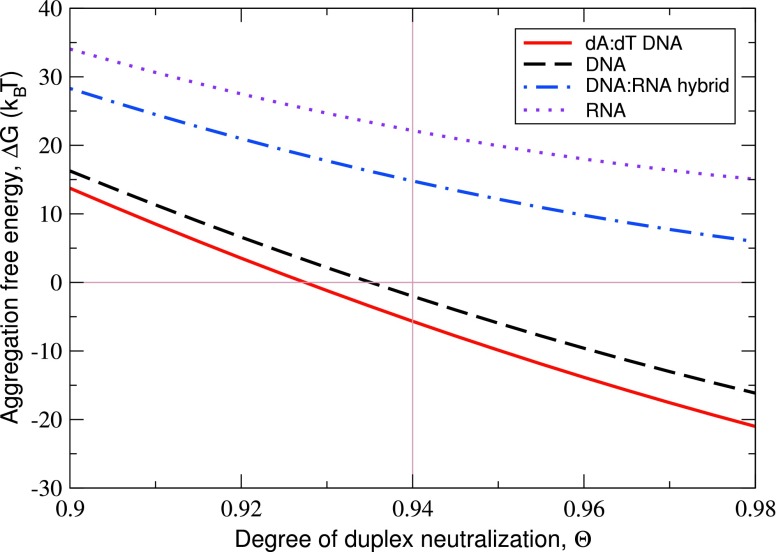
Our main results for ΔG_aggr and its components at the typical 28 Å inter-axial duplex separation in the hexagonal aggregated phase are summarized in Table I and Fig. 5. The latter shows ΔG_aggr as a function of Θ. In Table I, the attractive, repulsive, and configurational entropy components of ΔG_aggr for the four NA duplexes are compared for the same degree of duplex neutralization Θ = 0.94, at which the aggregated phase for the two considered DNA duplexes is more stable than the solution phase, ΔG_aggr < 0. The main factors determining the CoHex ion-mediated duplex attraction, CoHex binding affinity to the “external” ion binding shell μ_a, and the fraction of bound CoHex ions in this shell f_s are presented as well.

TABLE I.

Estimated changes of the free energy, ΔG_aggr = ΔG_attr + ΔG_el−rep − TΔS_conf, upon CoHex induced 25-bp NA duplex aggregation under experimentally relevant conditions (CoHex concentration corresponds to 94% of duplex charge neutralization, NA duplex concentrations in the solution phase is 40 μM). All energy components are in k_BT units per one duplex, T = 300 K. The calculations assume 28 Å inter-axial duplex separation^16,58 in the hexagonal aggregated phase that corresponds to “external-external” CoHex binding shells overlap shown in Fig. 2.

	dA:dT	DNA	HYB	RNA
CoHex binding affinity, μa	−7.66	−7.57	−7.34	−5.79
Fraction of “externally” bound ions, fs	0.67	0.59	0.24	0.14
Number of ions in single overlap, ΔNs	2.41	2.12	0.88	0.49
ΔGattr	−55.5	−48.2	−18.6	−8.4
ΔGel−rep	27.6	24.0	11.5	8.7
−TΔSconf	22.2	22.2	21.9	21.9
ΔGaggr	−5.7	−2.0	14.8	22.2

FIG. 5.

Predicted aggregation free energy ΔG_aggr for the four 25-bp NA duplexes as a function of the degree of duplex charge neutralization Θ by bound CoHex ions. The calculations assume 28 Å inter-axial duplex separation in the hexagonal aggregated phase and 40 μM duplex concentration in the solution phase. The data in Table I correspond to Θ = 0.94 (thin vertical line).

The predicted aggregation free energies suggest that at the same degree of duplex neutralization the DNA aggregates are more stable than the DNA:RNA hybrid or RNA aggregates (see Fig. 5). Among the two DNA molecules, the mixed sequence DNA duplex requires higher degree of neutralization by CoHex ions for the beginning of the aggregation, ΔG_aggr < 0. Provided that the CoHex affinities μ_a for both DNA duplexes are roughly the same (see Table I), the higher Θ at ΔG_aggr = 0 for the mixed sequence DNA translates into the higher bulk CoHex concentration in the solution phase at which mixed sequence DNA duplexes condense. At roughly the same μ_a for both DNA duplexes, the major difference in the values of the attractive components stems from the difference in the fractions of bound CoHex ions in the “external” ion binding shells f_s of these duplexes, 0.67 for the homopolymeric DNA and 0.59 for the mixed sequence DNA, leading to different values of the number of CoHex ions ΔN_s in the overlaps of these shells for two adjacent NA duplexes in the aggregated phase.

Comparing the DNA:RNA hybrid and RNA duplexes, the differences in both μ_a and f_s (and, therefore, ΔN_s) contribute to a smaller value of the attractive component in ΔG_aggr for the RNA duplex. The same conclusion is valid when comparing DNA and RNA duplexes. However, the major part of the difference in ΔG_attr for DNA and RNA duplexes arises from a drastic difference in f_s, 0.59 and 0.14, respectively (see Table I), leading to fourfold difference in the number of CoHex ions ΔN_s in the shell overlaps.

B. Dependence of the NA aggregation free energy on inter-axial duplex separation

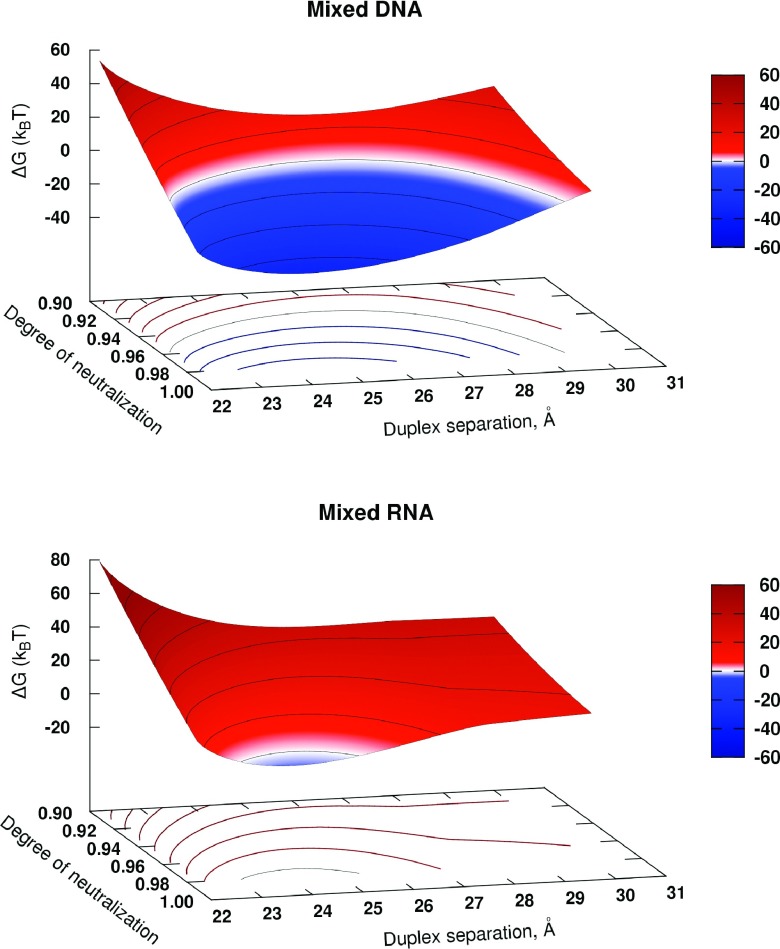
A more detailed investigation of the model predictions over a range of duplex-duplex separation distances and degrees of duplex neutralization is presented in Fig. 6; the trends are exemplified for the mixed sequence DNA and RNA molecules. The aggregation free energy values are estimated using Eqs. (11), (13), and (15). Several conclusions can be made that further support the validity of our approach.

FIG. 6.

Predicted aggregation free energy ΔG_aggr of 25-bp long DNA and RNA duplexes as a function of the degree of duplex neutralization Θ and the inter-axial duplex separation, d. Condensation conditions, ΔG_aggr < 0, correspond to blue regions of the parameter space, while the white band designates ΔG_aggr ≈ 0. Lines of equal ΔG_aggr are projected onto the d − Θ plane.

For both DNA and RNA, a region of ΔG_aggr < 0 as a function of inter-duplex separation d in the aggregated phase exists at large enough degrees of duplex neutralization Θ by CoHex ions. For the mixed DNA duplex, the region of the favorable condensation conditions begins at Θ > 0.92 with a minimum of ΔG_aggr(d) at the inter-duplex separation d = 26 Å. This minimum is not too different from the known experimental value d = 28 Å measured for long DNA strands.^16,58 With the increase of Θ, the minimum slightly shifts toward the smaller separations.

The existence of the minimum of ΔG_aggr(d) can be rationalized by considering differences in scaling behavior of the attractive and repulsive components of ΔG_aggr within our model. The attractive part ΔG_attr scales linearly with the number of CoHex ions in the shells overlap ΔN_s (Eq. (2)), which increases as the inter-duplex separation d decreases. At the same time, the repulsive contribution ΔG_el−rep is quadratic in ΔN_s, Eqs. (9) and (10).

Also, it is reassuring that at typical DNA condensation conditions, the predicted value of ΔG_aggr per base pair is a fraction of k_BT, in agreement with the experimental estimates.²⁰

Relative to the DNA, the region of the parameter space (d,Θ) where the RNA duplexes may be expected to aggregate is very narrow, suggesting that almost complete neutralization of the RNA duplex by bound CoHex ions is required prior to aggregation. This result is consistent with the notion that RNA is generally harder to condense than the equivalent in sequence DNA,^48,49 requiring a much larger CoHex concentrations in the solution phase.

Several testable predictions can be made directly from Fig. 6. A close examination reveals that, compared to the DNA, the aggregated phase of RNA is expected to have shorter inter-duplex distances, ∼1.5 Å shorter than for the aggregated DNA phase. Physically, this is because even if the RNA neutralization were 100%, where ΔG_el−rep ≈ 0, a relatively weak attractive force at 28 Å of inter-duplex separation would not be enough to overcome the entropic cost of aggregation of short 25-bp RNA duplexes, ∼22 k_BT per duplex. At inter-duplex distances shorter than 28 Å, an additional attractive contribution comes into play, the one resulting from the counterions in the more populated “internal” ion binding shell of the RNA. These shells begin to overlap with the “external” ion binding shells of the opposite duplexes at the separation d < 28 Å, Fig. 4. That additional attractive force tips the total attraction-repulsion balance towards RNA condensation at 25 Å inter-duplex separation and near 100% (Θ = 0.99) duplex neutralization. However, as the duplex-duplex separation decreases further in the already tightly packed aggregate, both the configurational entropy loss and the electrostatic repulsion increase, quickly driving the RNA out of the condensation regime.

Another specific prediction that follows directly from the free energy balance within our model is that longer duplexes are expected to condense better than shorter ones. The explanation, based on Eqs. (1), (2), (10), and (11), is as follows. All of the contributions to ΔG_aggr, except the configurational entropy loss, Eq. (11), are proportional to the duplex length H (if one neglect the end effects, which is a reasonable approximation for the number of base pairs in a duplex ≫1). In contrast, the unfavorable configurational entropy change scales logarithmically with H, Eq. (11). Thus, as H increases, the relative (per unit length) contribution of the entropic term to ΔG_aggr diminishes. Since the entropic term resists condensation, we expect longer duplexes to condense better.

C. Over-all model performance compared to experiment

It is reassuring that our estimations based on MD simulation results for CoHex ion distributions produce CoHex binding affinities of the same magnitude as earlier estimates of CoHex-DNA binding free energies based on equilibrium dialysis and single-molecule magnetic tweezers study⁷³ (−14.5 k_BT), isothermal titration calorimetry data²⁵ (−13.7 k_BT), and ⁵⁹Co chemical shift NMR measurements¹⁵ (−8.6 k_BT). The predicted CoHex affinities to the “external” ion binding shells of the nearly neutralized DNA duplexes are smaller than the above experimental estimates, which makes sense since the latter were derived from the apparent binding constants in the limit of zero binding, i.e., in the absence of the mutual repulsion between bound CoHex ions that decreases the effective affinity in our calculations.

More importantly, the values in Table I correctly predict the aggregation propensity of different nucleic acid duplexes, ranging from the favorable aggregation energies for the poly(dA):poly(dT) and mixed sequence DNA constructs to the unfavorable energies for the DNA:RNA hybrid and RNA duplex at the same degree of duplex neutralization. The fact that the order of the condensation propensities observed in the condensation experiments⁴⁹ is captured by our semi-quantitative model, last line in Table I, provides further support for the robustness of the conceptual picture that we have developed.

We have verified that the results for the aggregation free energy and its components presented above are robust with respect to simulation details: water model used for simulations, initial conditions and details of the RNA duplex simulation protocol (see supplementary material, “Robustness to force-field details and initial conditions”⁶⁹).

IV. METHODOLOGICAL DETAILS

A. Additional assumptions and considerations

• 1.Since the condensation experiments⁴⁹ we are trying to explain have been conducted at low (20 mM) concentrations of monovalent ions in solution, when they produce a negligible effect on the bound CoHex ions,¹⁵ the effects of monovalent salt are omitted from our semi-quantitative model. Whenever appropriate, we will discuss the consequences of neglecting the presence of small amount of monovalent salt.
• 2.The fractions of NA duplex charge neutralized by bound CoHex ions, Θ, in the solution and aggregated phases are considered to be the same. That is the aggregation energy we estimate does not include the contributions related the changes of CoHex concentration (and Θ) when CoHex ions are added to the solution phase prior to the aggregation and replace the monovalent counterion atmosphere around the NA duplexes.
• 3.The aggregated phase as a whole is assumed to be net neutral. In addition to bound CoHex ions, a small amount of unbound ions between the duplexes in a bundle or between the layers of duplex bundles is assumed in the aggregated phase. This assumption of the overall neutrality of the aggregated phase allows one to neglect the interactions between the duplexes beyond the nearest neighbors.
• 4.We use the degree of NA duplex neutralization Θ as a convenient proxy for bulk CoHex concentration. Even though CoHex concentration in the bulk is the quantity most relevant for the thermodynamics analysis presented, it is not easily accessible experimentally. Typically, NA condensation experiments simply report the total CoHex concentration in the solution prior to the condensation, which does not equal the bulk CoHex concentration. The relationship between the two and Θ is complex,^24,62 but it is monotonic, which justifies the use of Θ for our purposes: we are interested in the relative NA condensation propensities, not their absolute values. The relation between Θ and the bulk multivalent ion concentration has some non-trivial form^24,62 different from the original Manning predictions^59,61 and predictions based on the Poisson-Boltzmann (PB) model^63,65–67 due to correlations between bound multivalent ion at the surface of NA molecules. We do not need to consider the exact relation here. The only general property of the layer of bound (condensed) trivalent counterions at the NA duplex surface we will use is that the degree of NA duplex charge neutralization by these counterions, Θ, weakly depends on the bulk ion concentration and monotonically increases with the increase of the latter.^24,62 At low (mM) trivalent ion bulk concentration the value of Θ is close to the Manning theory prediction for the double-stranded DNA, Θ ≈ 0.9.

B. Estimation of CoHex binding affinity μ_a

We approximate the average binding energy that a CoHex ion bound in the “external” binding shell of NA duplex 1 gains when it enters the “external” binding shell of the (neighboring) NA duplex 2, by the CoHex binding affinity μ_a to the “external” ion binding shell of an isolated duplex in the solution phase at near neutralizing conditions. This approximation is based on the assumption that minimal changes in the CoHex distributions occur when the two NA duplexes approach each other at the inter-duplex distances relevant to NA condensation.

The above assumption was tested in Ref. 49 for homopolymeric poly(dA):poly(dT) DNA and mixed sequence RNA duplexes. By comparing the superposition of two independent single duplex CoHex distributions with CoHex distribution around a pair of NA duplexes separated by 26 Å, no changes in the number of “internally” bound (inside 12 Å from the helical axis) CoHex ions were observed. A small increase (1.1 ions) in the “external” ion binding shell (12–16 Å from the helical axis) of a duplex in both DNA and RNA duplex pairs was seen. The latter was suggested to be due to some redistribution of the bound ions in the external shell toward the shell overlapping region of the pair, which can be neglected in the case of six neighbors of the hexagonal packing considered in this work.

CoHex binding affinity μ_a to the “external” ion binding shell of NA duplex can defined as a difference of the excess chemical potentials of CoHex ion in the “external” shell of the duplex, ${\mu }_{\mathit{excess}}^s$, and in the bulk, ${\mu }_{\mathit{excess}}^b$,

$${\displaystyle {\mu }_a={\mu }_{\mathit{excess}}^s-{\mu }_{\mathit{excess}}^b.}$$ (16)

The quantity reflects the change of the ion interaction with its environment as the ion moves from the bulk towards the surface of charged NA molecule.

The chemical potential of CoHex ion, μ, can be written as

$${\displaystyle \mu ={\mu }_{\mathit{excess}}+{\mu }_{\mathit{ideal}},}$$ (17)

where

$${\displaystyle {\mu }_{\mathit{ideal}}=k_{B}T\ln \left({\rho }_{n}C\right)}$$ (18)

is a portion of the potential that can be treated as a chemical potential of an ideal gas with a particle number density ρ_n corresponding to the CoHex density,⁷⁴ C is a constant which does not depend on ρ_n. At equilibrium between the bulk (b) and the layer of bound CoHex ions in the “external” ion binding shell (s), μ is constant throughout the system,

$${\displaystyle {\mu }_{\mathit{excess}}^s+{\mu }_{\mathit{ideal}}^s={\mu }_{\mathit{excess}}^b+{\mu }_{\mathit{ideal}}^b.}$$ (19)

From Eqs. (18) and (19) and the definition of the ion binding affinity, Eq. (16), we arrive at Eq. (3), i.e., ${\mu }_a=-k_{B}Tln\left({\rho }_s/{\rho }_b\right)$.

CoHex number density in the “external” ion binding shell ${\rho }_s=N_s^0/V_s$ is estimated using the average number of CoHex ions in this shell $N_s^0$ determined from the MD simulations⁴⁹ and presented in Table II. With the height H = 88 Å for the two DNA duplexes and H = 76 Å for the DNA:RNA hybrid and RNA duplexes, the “external” shell volume, $V_s=\pi (r_s^2-r_i^2)H$, constitutes 30 964 and 26 741 ų, respectively.

C. Estimation of repulsive interaction ΔG_el−na between the two unscreened NA duplexes

We define ΔG_el−na(d) as the difference of the electrostatic free energy of the two duplexes in water, ΔG_el, at the separations d and ∞. The ΔG_el is estimated as⁷⁵

$${\displaystyle \mathrm{\Delta }{G}_{\mathit{el}}=\mathrm{\Delta }{G}_{\mathit{solv}}+E_{\mathit{Coul}}.}$$ (20)

Here ΔG_solv is the solvation energy of the two duplexes, estimated from the solution of the PE, and E_Coul is the Coulomb charge-charge interactions in the system computed with AMBER12.⁷⁶ Both terms in Eq. (20) are computed using charge distributions on NA duplexes determined from the AMBER ff99bsc0 nucleic acid force-field.^77,78 The ΔG_el for the two infinitely separated duplexes is calculated as the sum of the electrostatic free energies of the two isolated molecules.

We estimate ΔG_el by solving the Poisson equation (PE) for the two parallel unscreened duplexes and averaging the interaction energies over 12 different mutual duplex orientations. The interactions are computed at two different inter-axial separations, d = 24 and 28 Å. The orientations were changed by rotating one of the duplexes around its helical axis with 30° increment. The interactions at other inter-axial duplex separations were estimated using an interpolation, see below.

The PE was solved using MEAD solver⁷⁹ with three levels of focusing and with 281 grid points in each dimension: the coarsest grid spacing was 5.0 Å, and the finest 0.5 Å. The internal (NA duplex) and the external (water) dielectric constants were 4.0 and 78.5, respectively.^80,81

The interaction ΔG_el−na(d) between the two parallel NA duplexes in water is then estimated as the difference of the orientationally averaged ΔG_el at a separation d and ∞,

$${\displaystyle \mathrm{\Delta }{G}_{\mathit{el}-\mathit{na}}\left(d\right)=〈\mathrm{\Delta }{G}_{\mathit{el}}\left(d\right)〉-\mathrm{\Delta }{G}_{\mathit{el}}\left(\infty \right).}$$ (21)

The value of ΔG_el−na(d) at the inter-duplex separations different from the two distances (d₁ = 24 Å and d₂ = 28 Å) for which it was directly calculated⁶⁹ is then estimated using the logarithmic interpolation,

$${\displaystyle \mathrm{\Delta }{G}_{\mathit{el}-\mathit{na}}\left(d\right)=\mathrm{\Delta }{G}_{\mathit{el}-\mathit{na}}\left(d_1\right)+(\mathrm{\Delta }{G}_{\mathit{el}-\mathit{na}}\left(d_2\right)-\mathrm{\Delta }{G}_{\mathit{el}-\mathit{na}}\left(d_1\right))\frac{ln(d_1/d)}{ln(d_1/d_2)}.}$$ (22)

At high degree of duplex neutralization, ∼90%, the variation of the scaled ΔG_el−na(d₂) with one of the duplex rotating about its helical axis does not exceed 0.3 k_BT, consistent with an earlier estimate of ∼0.5 k_BT per 25-bp based on a different model.⁵⁰ The insignificance of the variation justifies the use of the simple averaging for ΔG_el−na. Small (ΔZ/H ≪ 1) axial translations of one duplex with respect to another reduce the repulsive contribution mostly through the reduction of Λ which is proportional to the shell overlapping volume (Λ ∼ ΔN_s ∼ ΔV_s). At the same time, the change in ΔN_s leads to a reduction of the attractive contribution to the aggregation energy resulting in a destabilization of the duplex bundle.

D. Atomistic simulations

The details of CoHex ion distributions and its chemical potential were extracted from recently published MD simulations⁴⁹ of the same four NA duplexes considered here. A brief description of the protocols used is presented below. Other details of the duplex structure preparations and simulations are described in Ref. 49.

All-atom MD simulations were used to generate CoHex ions distributions around four 25-bp NA duplexes: homopolymeric poly(dA):poly(dT) DNA, mixed sequence DNA, DNA:RNA hybrid, and RNA. Each system contained one 25-bp NA duplex, a neutralizing amount of 16 CoHex ions and 16 880 TIP3P⁸² water molecules. To avoid uncertainties associated with monovalent ions force field parameters,⁸³ no monovalent salt was added to the simulated systems. The simulated trajectories were 300-380 ns long, generated at 300 K temperature in the canonical (NVT) ensemble. The simulations were performed using AMBER12 package.⁸⁴ and ff99bsc0 force-field.^77,78 Since no measurable effects of CoHex on the DNA duplex structures were experimentally observed,⁴⁹ the homopolymeric and mixed sequence DNA duplexes were restrained to their B′ ⁸⁵ and canonical B-form, respectively, during the simulations. These restraints minimized possible structure bias due to the use of imperfect modern force-fields.⁸⁶ On the other hand, the addition of CoHex has lead to the experimentally observed changes in RNA helical structure.⁴⁹ Therefore, the RNA and DNA:RNA hybrid duplexes were simulated unrestrained allowing the duplex structures to relax when CoHex ions bind to these molecules. The CoHex ion distributions were analyzed using 28 000, 30 000, and 34 000 snapshots extracted from DNAs, DNA:RNA hybrid, and RNA duplex trajectories, respectively.

V. CONCLUSIONS

Counterion-induced condensation of nucleic acids (NAs) is a complex phenomenon that attracted experimental and theoretical attention for several decades. Recent experiments in which trivalent CoHex ions failed to condense short 25-bp double-stranded (ds) RNA fragments, in contrast to equivalent dsDNA fragments, demonstrated that our understanding of the process needs further refinement. The fact that dsRNA resists condensation at the same conditions where dsDNA readily condenses is counter-intuitive: indeed, the binding of CoHex ions to dsRNA is stronger than to the DNA, and the two highly charged molecules are virtually the same at the level of “charged rods” model. As it turns out, however, details of counterion distributions around dsDNA and dsRNA are very different with respect to proximity of bound CoHex to the helical axis. Namely, the NA-NA attraction, and, as a consequence, condensation propensity, is determined mainly by the fraction of counterions bound to the external (outermost) surface of the double-helix.

Here, we have developed the first semi-quantitative model of nucleic acid aggregation (condensation) induced by trivalent CoHex ($\mathrm{Co}{\left({\mathrm{NH}}_3\right)}_6^{+3}$) counterions in which the radial distribution of the bound counterions is the key ingredient. Namely, the counterions bound to a NA duplex are partitioned into an “external” and “internal” ion binding shells; the fraction of ions in each shell, and their affinity to the nearly neutralized duplex can be accurately quantified from converged ion distributions obtained from all-atom molecular dynamics simulations in explicit solvent. Within the model, the source of the short-range attraction between two approaching NA duplexes is the oppositely charged CoHex ions from the overlapping region of the ion binding shells of these duplexes. Basic thermodynamic arguments are then used to estimate the aggregation free energy components corresponding to CoHex-mediated attraction between the duplexes and the opposing residual repulsion of the nearly neutralized duplexes and configurational entropy loss upon aggregation of the short duplexes. Importantly, robustness of the model estimates to simulation details has been thoroughly verified.

The key conclusion from this study is that our semi-quantitative model based on the “ion binding shells” framework is able to reproduce the correct order of condensation propensities seen in experiment for various NA duplexes, some of which differ in fairly subtle way, e.g., poly(dA):poly(dT) DNA vs. mixed sequence DNA. The key role of the fraction of multivalent ions bound in the “external” ion binding shell of NA duplexes in nucleic acid condensation is clarified. The larger the fraction of the externally bound multivalent ions, the larger the condensation propensity of a nucleic acid molecule.

Another conclusion is a relatively small value of the attractive interactions between the RNA duplexes at the inter-axial distances and degree of neutralization at which DNA duplexes begin to aggregate. To overcome the relatively large entropic cost of the aggregation of short RNA duplexes it is necessary both to increase the attractive component and to minimize the electrostatic repulsive contribution by a more complete duplex neutralization compare to the case of the DNA. We therefore predict that RNA condensation occurs at inter-helical distances smaller than ones experimentally found in DNA aggregates. Consistent with experiment, the model predicts that higher degree of RNA neutralization is needed as well (in experiment, RNA condensation starts at considerably higher CoHex concentrations than for the equivalent DNA molecules).

We look forward to experimental testing of these predictions through anomalous small-angle X-ray scattering and related approaches.

In contrast to some of the available models of counterion-induced NA condensation, ours is simple enough to allow for analytical estimates and analyses of trends. For example, we show why longer NA fragments are expected to condense easier than shorter ones. At the same time, the apparent simplicity of the model does not come at the expense of its physical realism: the key component of the model—counterion affinity to the “external” ion binding shell and the fraction of ions in this shell are computed from explicit solvent atomistic simulations, which is arguably the most accurate practical approach to such estimates to-date. The details of the NA duplex geometry and sequence are implicitly included in the values of these parameters. The atomistic level of details “built into” the basics physics model greatly enhances versatility of the latter. In particular, in the future we are interested in exploring a wider range of multivalent ion types and look more closely into sequence dependence of NA condensation.