Regulatory inhibition of biological tissue mineralization by calcium phosphate through post-nucleation shielding by fetuin-A

Abstract

In vertebrates, insufficient availability of calcium and inorganic phosphate ions in extracellular fluids leads to loss of bone density and neuronal hyper-excitability. To counteract this problem, calcium ions are usually present at high concentrations throughout bodily fluids—at concentrations exceeding the saturation point. This condition leads to the opposite situation where unwanted mineral sedimentation may occur. Remarkably, ectopic or out-of-place sedimentation into soft tissues is rare, in spite of the thermodynamic driving factors. This fortunate fact is due to the presence of auto-regulatory proteins that are found in abundance in bodily fluids. Yet, many important inflammatory disorders such as atherosclerosis and osteoarthritis are associated with this undesired calcification. Hence, it is important to gain an understanding of the regulatory process and the conditions under which it can go awry. In this manuscript, we extend mean-field continuum classical nucleation theory of the growth of clusters to encompass surface shielding. We use this formulation to study the regulation of sedimentation of calcium phosphate salts in biological tissues through the mechanism of post-nuclear shielding of nascent mineral particles by binding proteins. We develop a mathematical description of this phenomenon using a countable system of hyperbolic partial differential equations. A critical concentration of regulatory protein is identified as a function of the physical parameters that describe the system.

I. INTRODUCTION

In biology, ionic calcium (Ca²⁺) plays many diverse roles including acting as a secondary messenger in biochemical cascades and modulating neuronal excitability.¹ Structurally, Ca²⁺ and inorganic phosphate ions (${\mathrm{PO}}_4^{-}$) are also the main constituents of bones in vertebrates. For these reasons, it is important for organisms to obtain adequate amounts of calcium from the environment.

In normal circumstances, Ca²⁺ is plentiful throughout extracellular spaces and in the circulatory system, stably existing at concentrations exceeding the saturation point, whereby sedimentation is favored.² Even under the dangerous condition of hypocalcemia, Ca²⁺ may still be supersaturated relative to the most thermodynamically stable phase of calcium phosphate, hydroxyapatite (HAP), which is the building block of teeth and bones.

Yet, while the deposition of calcium into bones is desirable, ectopic calcification into soft tissues is pathological and either causes or exacerbates a variety of inflammatory disorders including arteriosclerosis, heart disease, and arthritis.^3–5 So, the regulation of ectopic calcium sedimentation is important in maintaining the health of soft tissues.

When calcium-phosphate solutions are supersaturated, HAP is formed in a multi-step process traversing through several intermediate crystalline or pseudo-crystalline states. The first step in this process is thought to be formation of pre-nucleation clusters,^6–8 which are small calcium-phosphate complexes.⁹ Although some debate exists,^7,8,10 these small complexes are thought to be Posner’s clusters (PCs), with composition Ca₉(PO₄)₆.¹¹ A combination of experimental and theoretical analyses have confirmed the stability of PCs,^12,13 their presence in physiological solutions,¹¹ and their consistency with the unit-cell structure of calcium-phosphate precipitates.^6,14 For the purposes of this manuscript, we will assume that PCs are the fundamental building blocks of larger-scale calcium-phosphate clusters and refer to them as monomers.

These monomers aggregate whereby they nucleate into amorphous spherical post-nucleation clusters composed of amorphous calcium phosphate (ACP),^15–18 having a calcium to phosphate ratio of approximately three to two.¹⁹ As long as supersaturation persists, and in the absence of regulation, ACP clusters continue to grow by absorbing additional monomers into their structure. When ACP clusters become sufficiently large, they sediment into the tissue while simultaneously undergoing several phase transitions before eventually transforming into HAP.

This situation is seemingly incompatible with life as the persistent supersaturation of calcium and phosphate in biological fluids dictates unyielding sedimentation, at least in the absence of regulatory inhibition. Fortunately a regulatory mechanism does exist. The main machinery for preventing calcium phosphate sedimentation is the plasma protein fetuin-A (FA).^5,20–23 FA is an acidic protein that is found abundantly in blood as well as throughout all extracellular compartments. Maintenance of adequate levels of FA protein has been shown to be necessary for inhibition of calcification in relation to many disorders.^24,25

FA interacts with the calcium phosphate mineralization process in several different ways. It can directly bind calcium, with each molecule able to weakly and reversibly bind approximately 12–15 ions.²⁶ Yet, this direct binding of calcium cannot be the main regulatory mechanism of FA as it would effectively reduce the supersaturation. There is also evidence that FA binds to pre-nucleation clusters,²² a possibility that has been analyzed,²⁷ although somewhat contradictory evidence has also shown that the presence of FA does not affect the rate of nucleation of calcium phosphate clusters.²⁸ Primarily, FA binds strongly to post-nuclear calcium-rich calcium-phosphate clusters, shielding them from further growth and imparting upon them enhanced colloidal stability so that they do not sediment.

In this manuscript, we adapt mean-field classical nucleation theory (CNT) to look at the inhibition of mineral cluster growth by FA. We provide a quantitative description of the overall regulatory process and examine conditions necessary for stability.

II. QUANTITATIVE METHODS

The problem of understanding the combined process of mineralization and FA-induced inhibition is an example of a nucleation problem. Our approach to this problem is to use ideas from mean-field classical nucleation theory (CNT). In particular, we utilize a continuum approximation to the kinetic theory whereby we frame our problem using a series of serially coupled partial differential equations (PDEs). It is notable, however, that theoretical treatments of the inherently high-dimensional stochastic problem of nucleation and aggregation also exist.^29–31 The mean-field theoretic CNT approach is ultimately motivated by the behavior of such stochastic treatments.

Our overarching goal in this section is to understand the kinetics of the concentration profile for mineral clusters as a function of size and interactions with FA. To this end, in Section II A, we first solve for the nucleation rate (formation rate of critically sized clusters), which provides a boundary condition for our PDE problem. Then, in Section II B, we derive an effective growth rate (v_n(s)) for the mineral portion of formed mineral and protein-mineral clusters as a function of their fixed mineral surface area s and number of bound FA proteins n. Then, in Section II C, for a fixed cluster configuration, we derive the shielding rate under the assumption that it is governed by diffusion-limited kinetics. Finally, in Section II D, we tie together the various components of our theory (nucleation, growth, shielding) into an overarching continuum model.

For the reader’s convenience, we have compiled a list of the mathematical symbols that we use throughout this manuscript into Table I.

TABLE I.

List of mathematical symbols used in the manuscript for easy reference.

Symbol	Description
s	Surface area of mineral phase of cluster
m	Number of mineral monomers in a cluster, where
	monomer refers to Posner’s cluster Ca9(PO4)6
r	Radius
V	Volume
n	Number of shielding proteins attached to surface of cluster
γ	Interfacial free energy per unit surface area in units kBT per squared meter
f	Geometric correction for surface free energy for non-spherical pre-critical states
ρ∞	Concentration of mineral monomers
ρs	Saturation concentration
Δμ	−log(ρ∞/ρs), chemical free energy per mineral monomerin units kBT
ΔG	Gibbs free energy in units kBT
cn(s, t)	Concentration of mineral clusters of surface area s shielded
	by n FA monomers
$c_n^{\infty }\left(s\right)$	Steady-state concentration
s′	Shielded surface area
sn	Amount of surface shielded (s′) when n
	FA monomers are bound
δsn	sn − sn−1 for n ≥ 1
s∗, m∗	Critical cluster size at nucleation
sp, mp	Critical cluster surface area and monomer number at sedimentation
D	Diffusivity of mineral monomers
DFA	Diffusivity of FA monomers
k−	Dissociation rate per unit surface area for mineral
ϕ∞	Concentration of FA monomers
$\overline{r},\overline{s},\overline{v}$	Mineral monomer radius, surface area, volume
ω	$D\sqrt{4\pi }{\rho }_s/k_{-}$
α	$8\overline{v}D\pi {\rho }_{\infty }$
β	$-\mathrm{\Delta }\mu \sqrt{s_{\ast }}/f$
ε	Thickness of shielding layer (of FA protein)
λ	$\sqrt{4\pi }{D}_{\mathrm{FA}}{\varphi }_{\infty }$

A. Nucleation

CNT explains the emergence and evolution of colloidal phases in solutions through the development of a simple thermodynamical picture. The key element of CNT is the assumption that the emergence of a new phase carries an energetic cost due to the creation of an interfacial surface.

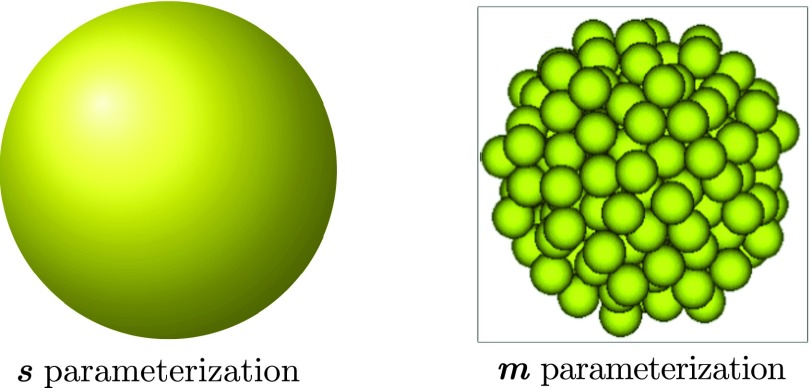
Consider a mineral particle consisting of an integer number m mineral subunits, hereby termed an “m-cluster.” We say that this particle has volume $V=m\overline{v}$, where $\overline{v}$ is the effective volume of each subunit “monomer.” Assuming that this particle is spherical, it has surface area $s={\left(36{\overline{v}}^2\pi \right)}^{1/3}{m}^{2/3}$, and radius $r=\sqrt{s/4\pi }$. In this manuscript, we use both m and s to parameterize the size of mineral clusters (see Fig. 1). We also will refer to the conversion between these two parameterizations as m(s) and s(m).

FIG. 1.

Cluster size parameterizations. Surface area (s) and monomer count (m) parameterizations are used interchangeably for expressing the size of mineral clusters. Clusters are assumed to be spherical and composed of an integer number m of monomers (Posner’s clusters). The cluster as a whole has surface area s. To denote the conversion between these two parameterizations, we use functions m(s) : s → m and s(m) : m → s.

For an m-cluster, CNT assigns as per the capillary approximation the free energy,

$${\displaystyle \mathrm{\Delta }G=\stackrel{\mathrm{\Delta }{G}_{\gamma }}{\overbrace{\gamma fs}}+\stackrel{\mathrm{\Delta }{G}_{\mu }}{\overbrace{m\mathrm{\Delta }\mu }}=\stackrel{\mathrm{spherical}}{\overbrace{\gamma fs+\frac{\mathrm{\Delta }\mu }{6\overline{v}\sqrt{\pi }}{s}^{3/2}}},}$$ (1)

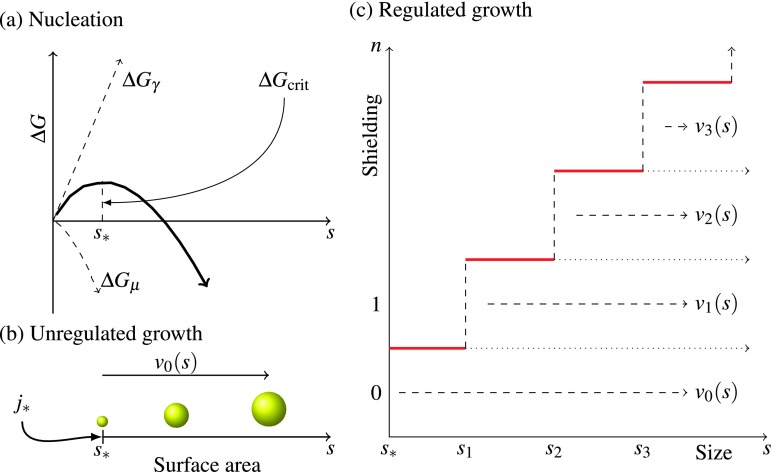
where Δμ is the molecular free energy per monomer in the cluster relative to in the solution (in units k_BT), $\overline{v}$ is the volume per monomer, γ > 0 is the interfacial surface energy per unit area (in units k_BT per square meter), and f is a geometric factor than can be adjusted to account for non-spherical growth in the pre-nucleation stage as well as size-dependent variations in the surface free energy.³⁹ For constant supersaturation, Δμ < 0 so that ΔG → −∞ as s → ∞, thereby thermodynamically favoring the existence of large clusters. Yet, as shown in Fig. 2(a), the state of pure-monomers (s = 0) is also a local minimum of this free energy. The emergence of clusters is governed by kinetic rather than thermodynamic considerations as an energy barrier of ΔG_crit corresponding to the free energy of a critical cluster with size s_∗ must be overcome. This barrier is overcome when a cluster reaches a size m = m_∗, s = s_∗. The steady-state mean-field rate at which clusters reach this size is exponential in the magnitude of the energy gap and is known as the Zeldovich rate,

$${\displaystyle j_{\ast }=\kappa exp\left(-\mathrm{\Delta }{G}_{\mathrm{crit}}\right),}$$ (2)

where κ is a constant with units of concentration per time.³² While the presence of pre-nucleation clusters in the calcium phosphate system violates the assumptions of CNT, Habraken et al.⁸ showed that CNT is still applicable with the use of some minor modifications that result in the reduction of the effective energy gap. Hence, we will assume for the purposes of this manuscript that critically sized clusters of size s_∗ are forming spontaneously at some rate in the form of Eq. (2).

FIG. 2.

Nucleation, growth, and shielding. (a) Classical nucleation of an initial critically sized spherical mineral cluster of surface area s_∗ (≈3 nm²). The activation energy ΔG_crit (units of k_BT) corresponds to the energy of the cluster of critical size (of units surface area). A flux j_∗ of nucleating particles is generated by the system under the condition of supersaturation. (b) Unregulated growth. Upon nucleation, particles grow uncontrollably at a size dependent rate v₀(s) as defined in Eq. (22). (c) The attachment of proteins (shielding) alters the growth rate. The growth rate of the mineral v_n(s) depends on the size s of the mineral phase as well as the number of attached FA monomers n. The attachment of an additional protein to a cluster shielded by n proteins shields an additional surface area of size s_n+1 − s_n. Completely shielded particles, where the surface area s is less than the shielding capacity s_n, do not grow.

In the blood and extracellular compartments, fluid is under constant exchange. For this reason, we will also assume that the supersaturation is constant, and hence that j_∗ and s_∗ are fixed, and study the growth of clusters after their nucleation.

B. Growth of the mineral phase

An m-cluster (of surface area s(m)) may find itself caked by a number of proteins, which effectively shield a surface area s′ ≤ s(m). Our immediate goal is to compute an effective growth rate for this particle assuming that its shielding is fixed. We will assume that each successive protein shields a maximal surface area δs_n = s_n − s_n−1. In other words, if n proteins are attached, then a total surface area of size s′ = s_n is shielded from further free monomer adsorption.

Due to surface reactions, this particle experiences an instantaneous net flux of monomers into its structure,

$${\displaystyle J=\underset{\mathrm{absorption}}{\underbrace{k_{+}(s,s^{\prime }){\rho }_r}}-\underset{\mathrm{dissociation}}{\underbrace{k_{-}\times (s-s^{\prime })}},}$$ (3)

where ρ_r is the concentration of free monomers at the surface, k₋ is the dissociation rate per unit surface area, and k₊(s, s′) is the absorption rate which is dependent on m as well as the free surface area.

To begin, we will eliminate the unknown physical parameter function k₊(s, s′) by using equilibrium considerations to relate it to the other physical parameter k₋. There exists a critical monomer concentration ρ_m at which an m-cluster is at equilibrium with its surroundings so that

$${\displaystyle k_{+}{\rho }_m-k_{-}(s-s^{\prime })=0.}$$ (4)

At the equilibrium concentration, the free energy gap between clusters of size m and m + 1 also disappears so that

$${\displaystyle \delta G=\mathrm{\Delta }\mu +{\left(36{\overline{v}}^2\pi \right)}^{1/3}\gamma ({(m+1)}^{2/3}-m^{2/3})=0,}$$ (5)

where Δμ = log(ρ_s/ρ_m) is the chemical potential, and ρ_s is the free monomer concentration at saturation (where the solution is in equilibrium with an infinitely large cluster). Eq. (5) implies that

$${\displaystyle {\rho }_m={\rho }_{s}exp\left[{\left(36{\overline{v}}^2\pi \right)}^{1/3}\gamma ({(m+1)}^{2/3}-m^{2/3})\right]={\rho }_{s}exp\left[-\frac{\mathrm{\Delta }\mu }{f}{\left(\frac{m_{\ast }}{m}\right)}^{1/3}\left(1-\frac{1}{6m}+\mathcal{O}\left(m^{-2}\right)\right)\right]={\rho }_{\infty }exp\left\{\mathrm{\Delta }\mu \left[1-\frac{1}{f}{\left(\frac{m_{\ast }}{m}\right)}^{1/3}\right]\right\}\times exp\left\{\frac{\mathrm{\Delta }\mu }{f}{\left(\frac{m_{\ast }}{m}\right)}^{1/3}\left[\frac{1}{6m}+\mathcal{O}\left(m^{-2}\right)\right]\right\}.}$$ (6)

Substitution of ρ_m from Eq. (6) into Eq. (4) yields the expression for k₊,

$${\displaystyle k_{+}=\frac{k_{-}(s-s^{\prime })}{{\rho }_{s}exp[-\mathrm{\Delta }\mu \sqrt{(s_{\ast }/s)}/f]}\left(1+\mathcal{O}\left(m^{-4/3}\right)\right).}$$ (7)

Eq. (7), substituted into Eq. (3), allows us to write the flux of monomers into the mineral cluster,

$${\displaystyle J\approx k_{-}(s-s^{\prime })\left[\frac{{\rho }_r-{\rho }_{s}exp\left(\frac{\beta }{\sqrt{s}}\right)}{{\rho }_{s}exp\left(\frac{\beta }{\sqrt{s}}\right)}\right],}$$ (8)

as a function of the physical dissociation constant k₋, the free monomer saturation concentration at saturation ρ_s, the free monomer concentration at the surface of the mineral ρ_r, and

$${\displaystyle \beta =-\frac{\mathrm{\Delta }\mu \sqrt{s_{\ast }}}{f}.}$$ (9)

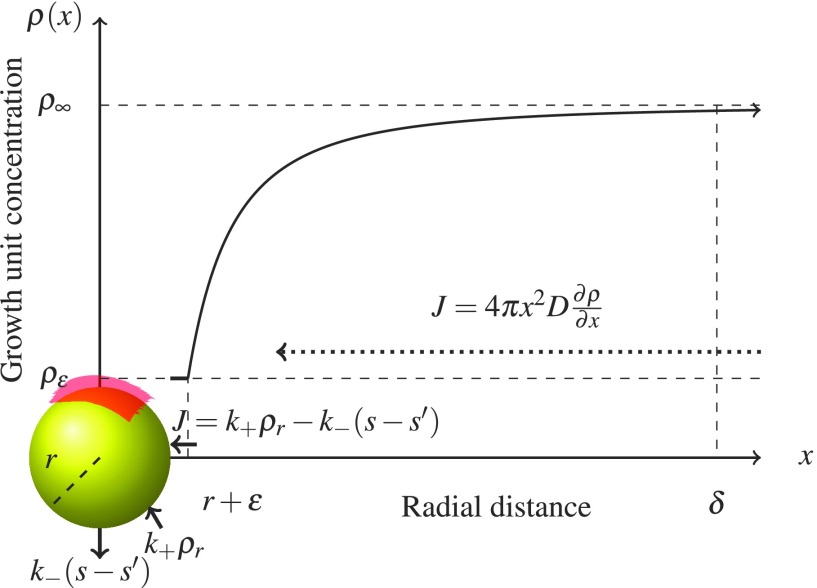
The concentration ρ_r is found through conservation of monomer mass by flux matching as in Fig. 3 in the quasi-steady diffusive limit, where the FA protein forms a shielding layer around the mineral of thickness ε. At a distance x from the center of the mineral, outside of the shielding layer (x > r + ε), the free monomer flux obeys Fick’s law

$${\displaystyle J=4\pi x^{2}D{\partial }_x\rho =4\pi D\frac{(r+\delta )(r+\epsilon )}{\delta -\epsilon }({\rho }_{\infty }-{\rho }_{\epsilon })=4\pi D(r+\epsilon )({\rho }_{\infty }-{\rho }_{\epsilon })+\mathcal{O}\left(\frac{r+\epsilon }{\delta -\epsilon }\right),}$$ (10)

where the second equality is obtained by integration of the concentration from x = r + ε to x = r + δ, where δ ≫ r is the thickness of the diffusion layer. At the surface, the flux is given by Eq. (8). Invoking free monomer conservation, by equating Eq. (8) with Eq. (10), while also assuming that ε is small relative to the characteristic diffusion length (ρ_r ≈ ρ_ε), allows us to solve for the monomer concentration at the mineral surface,

$${\displaystyle {\rho }_r\approx {\rho }_s\frac{4\pi D(r+\epsilon ){\rho }_{\infty }+k_{-}(s-s^{\prime })}{4\pi D(r+\epsilon ){\rho }_{s}exp\left(\frac{\beta }{\sqrt{s}}\right)+k_{-}(s-s^{\prime })}exp\left(\frac{\beta }{\sqrt{s}}\right).}$$ (11)

In Eq. (11), one sees that as D → ∞, the concentration at r goes to ρ_∞, as expected. Plugging the concentration from Eq. (11) into Eq. (8) yields the growth rate

$${\displaystyle \dot{V}=\overline{v}J\approx k_{-}(s-s^{\prime })\left[\frac{4\pi \overline{v}D(r+\epsilon )({\rho }_{\infty }-{\rho }_s{e}^{\beta /\sqrt{s}})}{4\pi D(r+\epsilon ){\rho }_s{e}^{\beta /\sqrt{s}}+k_{-}(s-s^{\prime })}\right].}$$ (12)

While clusters of any size can be shielded, entirely shielded clusters below the size s = s₁ are not of our concern because they are inert (recall that the first protein shields a maximal surface area of size s₁). Hence, we only wish to find the shielded growth rate when s > s₁. Making the assumption that ε is small relative to r, for $r=\sqrt{s/4\pi }>\sqrt{s_1/4\pi }$, yields the volume growth rate in terms of s,

$${\displaystyle \dot{V}\approx \frac{1}{\sqrt{16\pi }}\frac{\alpha s^{1/2}(s-s^{\prime })(1-{\rho }_s{e}^{\beta /\sqrt{s}}/{\rho }_{\infty })}{\omega s^{1/2}{e}^{\beta /\sqrt{s}}+(s-s^{\prime })},}$$

with constants

$${\displaystyle \omega =D\sqrt{4\pi }{\rho }_s/k_{-}}$$ (13)

and

$${\displaystyle \alpha =8\overline{v}D\pi {\rho }_{\infty }.}$$ (14)

FIG. 3.

Shielded diffusion-limited growth. FA protein forms a diffusion barrier of height ε and surface area s′ = s_n, where n is the number of associated proteins, around the mineral cluster. The absorption rate k₊ρ_r per unit surface area of the growth units depends on the local concentration ρ_r of growth units at the surface of the particle. Dissociation also occurs at rate k₋ per unit surface area. Neither absorption nor dissociation occurs in the shielded region (red). For ε sufficiently small, ρ_r ≈ ρ_ε. The concentration ρ_r is then determined through conservation of flux. Outside of the diffusion layer (of thickness δ ≫ r), the concentration of growth units approaches ρ_∞.

Note that in the limit as $s-s^{\prime }\ll \omega s^{1/2}{e}^{\beta /\sqrt{s}}$, this growth rate is surface-limited, whereas in the limit as $s-s^{\prime }\gg \omega s^{1/2}{e}^{\beta /\sqrt{s}}$, growth is diffusion limited. The parameters ω and β define the length-scale under which surface-limited effects are significant. Typically, in nucleation problems, the surface-limited regime is ignored as it is usually only important when the particle is small. For the purposes of our system, we take a cue from the study of Treboux et al.,¹³ which showed that aggregation of PCs is highly favorable energetically and assume that aggregation of post-nuclear PCs is diffusion limited. However, the surface-limited effects can become significant at larger particle sizes for clusters that are nearly completely shielded. In this regime, we note that $e^{\beta /\sqrt{s}}\approx 1$, allowing us to use the simplified growth rate,

$${\displaystyle \dot{V}\approx \frac{1}{\sqrt{16\pi }}\frac{\alpha s^{1/2}(s-s^{\prime })}{\omega s^{1/2}+(s-s^{\prime })}.}$$ (15)

The surface area growth rate is related to the volume growth rate through the chain rule,

$${\displaystyle v_n\left(s\right)=\sqrt{\frac{16\pi }{s}}\dot{V}\approx \frac{\alpha (s-s_n)}{\omega s^{1/2}+(s-s_n)}.}$$ (16)

C. Shielding by the protein phase

In this section, we compute the FA shielding rate for a fixed cluster configuration. The shielding of the mineral phase by FA can be understood in a manner similar to the growth of the mineral phase. The overall adsorption rate of FA monomers onto the surface results from a balance between the diffusive supply and the surface reactions. Assuming first that mineral clusters have less mobility than FA, and denoting the diffusivity of FA by D_FA, one may use similar reasoning as in Sec. II B to find the overall attachment rate of FA. As before, we may express the flux into the surface as a balance between two competing reactions through a conservation law

$${\displaystyle J_{\mathrm{FA}}=k_{\mathrm{on}}{\varphi }_r(s-s^{\prime })-k_{\mathrm{off}}{s}^{\prime },}$$ (17)

where k_on is the binding rate of FA to the mineral per unit free surface area per unit concentration, k_off is the dissociation rate of FA, ϕ_∞ is the far-field heat bath concentration of FA, and ϕ_r is the concentration of FA at the surface. By Eq. (10), we may also write the diffusive flux

$${\displaystyle J_{\mathrm{FA}}\approx D_{\mathrm{FA}}\sqrt{4\pi s}({\varphi }_{\infty }-{\varphi }_r),}$$ (18)

which, through conservation, matches the reaction flux of Eq. (17). Equating Eq. (17) and Eq. (18) allows us to solve for the surface concentration of FA,

$${\displaystyle {\varphi }_r\approx \frac{D_{\mathrm{FA}}\sqrt{4\pi s}{\varphi }_{\infty }+k_{\mathrm{off}}{s}^{\prime }}{k_{\mathrm{on}}(s-s^{\prime })+D_{\mathrm{FA}}\sqrt{4\pi s}}.}$$ (19)

Back-substituting Eq. (19) into Eq. (17) yields the overall rate,

$${\displaystyle J_{\mathrm{FA}}\approx k_{\mathrm{on}}(s-s^{\prime })\frac{D_{\mathrm{FA}}{\varphi }_{\infty }\sqrt{4\pi s}+k_{\mathrm{off}}{s}^{\prime }}{k_{\mathrm{on}}(s-s^{\prime })+D_{\mathrm{FA}}\sqrt{4\pi s}}-k_{\mathrm{off}}{s}^{\prime }.}$$ (20)

At this stage we make a few simplifying assumptions—namely, that the overall shielding process is diffusion-limited in the regime of most interest (where 0 ≤ s′ < s < s_p). First we remind the reader that our continuous formulation is an approximation of an underlying discrete system. For this reason, we note that the unshielded area s − s′ cannot become infinitesimal. This fact allows us to make the assumption that the binding reaction is always sufficiently fast such that $k_{\mathrm{on}}(s-s^{\prime })\gg D_{\mathrm{FA}}\sqrt{4\pi s}$, for s ≤ s_p.

Finally, we will assume that the rate of detachments is negligible (irreversible binding of FA to mineral clusters). Altogether, these assumptions allow us to write the simpler diffusion-limited shielding rate rule,

$${\displaystyle J_{\mathrm{FA}}\approx D_{\mathrm{FA}}\sqrt{4\pi s}{\varphi }_{\infty }.}$$ (21)

Strictly speaking, the parameters ϕ_∞ and ρ_∞ contained in these expressions are themselves dynamical variables. Their evolution can be determined through mass conservation, as all changes are due to the balance between supply and consumption. We are interested however in the biologically relevant situation where calcification is a local phenomenon coupled to global auto-regulatory processes that maintain supersaturation. For instance, fluid present in a knee joint is continually replenished through interstitial flow. That is to say, we set ϕ_∞ and ρ_∞ constant and examine the conditions for the regulation of sedimentation in this regime.

D. Overall continuum model

Classical work by Landau and Lifshitz³³ defined an advection problem to quantitatively describe the evolution of the cluster concentrations as clusters grow due to monomer absorption. This work has been extended throughout the years,³⁴ and recently united with nucleation,^35,36 which was introduced as an effective boundary condition. We further extend this prior work by incorporating the effects of shielding. In this continuum approach, one may describe the evolution in size of the concentration profile of clusters using an advection equation, where the cluster growth rate provides an effective “velocity” or drift. Overall, the dynamic concentration c_n(s, t) of clusters of mineral surface area s associated with n FA monomers is described for all non-negative integers n ≥ 0 for s > s_n by the partial differential equations indexed by n,

$${\displaystyle \frac{\partial c_n(s,t)}{\partial t}+\frac{\partial }{\partial s}\left[\stackrel{v_n\left(s\right)}{\overbrace{\frac{\alpha (s-s_n)}{\omega s^{1/2}+(s-s_n)}}}{c}_n(s,t)\right]=\underset{\mathrm{diffusion\; limited}}{\underbrace{-\mathrm{\lambda }{s}^{1/2}\left(c_n(s,t)-c_{n-1}(s,t)\right)}},}$$ (22)

where v_n(s) is surface growth rate dependent on the number of bound FA monomers, s′ = s_n for n ≥ 1 and s′ = 0 for n = 0,

$${\displaystyle \mathrm{\lambda }=\sqrt{4\pi }{D}_{\mathrm{FA}}{\varphi }_{\infty },}$$ (23)

and for notational convenience we set c₋₁(s, t) ≡ 0. The right-hand-side describes diffusion-limited shielding of the mineral particles by FA protein, which is assumed to have high affinity for the mineral phase. The solution domain for Eq. (22) is shown in Fig. 2(c). For our purposes, we will assume that the system starts at a reference time t = t₀ at the initial state

$${\displaystyle c_n(s,t_0)=\{\begin{array}{ll}0\hfill & s>s_{\ast }\hfill \\ c_0^{\infty }\left(s_{\ast }\right)\hfill & s=s_{\ast }\hfill \end{array},}$$ (24)

where $c_0^{\infty }\left(s_{\ast }\right)$ is an equilibrium concentration set by the nucleation process.

Critically sized clusters (of size s_∗) are assumed to be created at the Zeldovich rate j_∗ of Eq. (2). This creation rate is balanced with consumption due to growth and shielding. As in the work of Farjoun and Neu,³⁵ this growth flux is expressed in terms of the non-dimensional rate of number-growth, $\dot{V}/\overline{v}$ of Eq. (15). Invoking their balance argument leads to the constraint

$${\displaystyle j_{\ast }=\underset{s\searrow \underset{\ast }{s}}{lim}\left[(D_{\mathrm{FA}}{\varphi }_{\infty }\sqrt{4\pi s}+\frac{\sqrt{4\pi }D{\rho }_{\infty }{s}^{3/2}}{\omega s^{1/2}+s})c_0(s,t)\right].}$$ (25)

Hence, the combined effects of nucleation and shielding impose an effective Dirichlet boundary condition

$${\displaystyle c_0^{\infty }\left(s_{\ast }\right)\equiv c_0(s_{\ast },t)=j_{\ast }{\left[\mathrm{\lambda }\sqrt{s_{\ast }}+\frac{\sqrt{4\pi }D{\rho }_{\infty }{s}_{\ast }^{3/2}}{\omega s_{\ast }^{1/2}+s_{\ast }}\right]}^{-1}.}$$ (26)

III. RESULTS

In this section we construct a solution to the system of partial differential equations defined in Eq. (22) and the boundary conditions defined in Eqs. (24)–(26). We proceed first by non-dimensionalization of the problem formulation. Then, using the method of characteristics, we derive a sequential relationship between the solutions of the system. Approximating the solution of the system of equations, we analyze the steady-state behavior of the system in the limit where inhibition is sufficiently strong, from which we compute the overall rate of protein consumption and propose a criterion for effective inhibition of calcification. Finally, we parameterize our equations using experimentally measured values found in the literature.

A. Nondimensionalization

We seek a convenient non-dimensionalization of our serial system of PDEs describing the shielded growth problem. We begin by normalizing the surface area s, which ranges between the critical nucleation surface area s_∗ and another critical surface area s_p which represents the surface area at sedimentation. Using these constants, we write the non-dimensionalized size variable,

$${\displaystyle \hat{s}=\frac{s-s_{\ast }}{s_p-s_{\ast }},}$$ (27)

critical cluster size s_∗,

$${\displaystyle {\hat{s}}_{\ast }=\frac{s_{\ast }}{s_p-s_{\ast }},}$$ (28)

shielded surface area,

$${\displaystyle {\hat{s}}^{\prime }=\frac{s^{\prime }}{s_p-s_{\ast }},}$$ (29)

shielding levels s′ = s_n,

$${\displaystyle {\hat{s}}_n=\frac{s_n}{s_p-s_{\ast }},}$$ (30)

and surface-limiting parameter ω,

$${\displaystyle \hat{\omega }=\frac{\omega }{\sqrt{s_p-s_{\ast }}}.}$$ (31)

Rescaling time

$${\displaystyle \hat{t}=\frac{\alpha (t-t_0)}{s_p-s_{\ast }}}$$ (32)

results in the series of non-dimensional advection equations of asymptotically unit speed,

$${\displaystyle \frac{\partial {\hat{c}}_n}{\partial \hat{t}}+\frac{\partial }{\partial \hat{s}}\left[\frac{(\hat{s}+{\hat{s}}_{\ast }-{\hat{s}}_n){\hat{c}}_n(\hat{s},\hat{t})}{\hat{\omega }{(\hat{s}+{\hat{s}}_{\ast })}^{1/2}+(\hat{s}+{\hat{s}}_{\ast }-{\hat{s}}_n)}\right]=-\hat{\mathrm{\lambda }}\sqrt{\hat{s}+{\hat{s}}_{\ast }}\left({\hat{c}}_n(\hat{s},\hat{t})-{\hat{c}}_{n-1}(\hat{s},\hat{t})\right)}$$ (33)

with non-dimensional shielding constant

$${\displaystyle \hat{\mathrm{\lambda }}=\frac{\mathrm{\lambda }{(s_p-s_{\ast })}^{3/2}}{\alpha },}$$ (34)

where the concentrations have been scaled by the nucleation boundary condition

$${\displaystyle {\hat{c}}_n(\hat{s},\hat{t})=\frac{c_n(s\left(\hat{s}\right),t\left(\hat{t}\right))}{c_0^{\infty }\left(s_{\ast }\right)},}$$ (35)

so that the concentration of critical clusters is fixed

$${\displaystyle {\hat{c}}_0(0,\hat{t})=1.}$$ (36)

B. Characteristics of the PDE system

The non-dimensionalized partial differential equations of Eq. (33) can be solved by invoking the method of characteristics sequentially for each PDE. The solutions to the PDEs contain the characteristic curves described by the equations,

$${\displaystyle \frac{\mathrm{d}\hat{s}}{\mathrm{d}\hat{t}}=\frac{(\hat{s}+{\hat{s}}_{\ast }-{\hat{s}}^{\prime })}{\hat{\omega }{(\hat{s}+{\hat{s}}_{\ast })}^{1/2}+(\hat{s}+{\hat{s}}_{\ast }-{\hat{s}}^{\prime })}.}$$ (37)

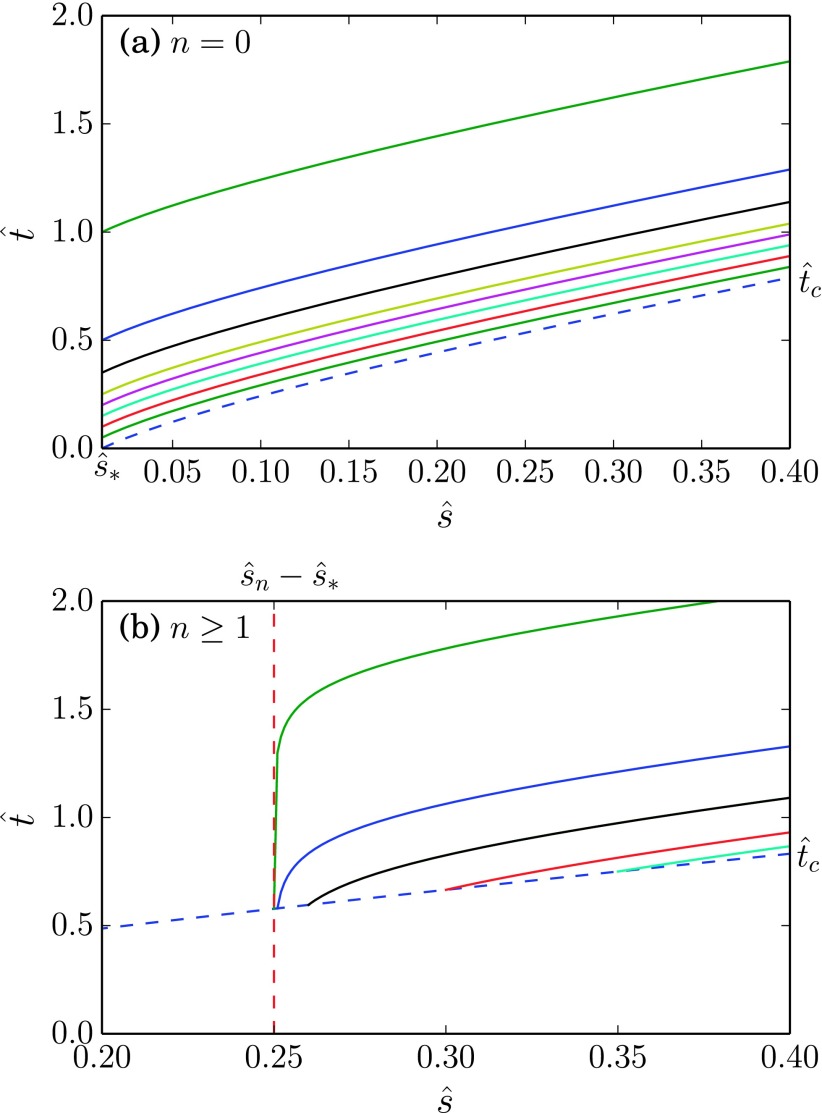
The $\hat{s}-\hat{t}$ characteristics, as shown in Fig. 4, originate from points $({\hat{t}}_0,\hat{s}\left({\hat{t}}_0\right))$. They follow the relationship

$${\displaystyle \hat{t}-{\hat{t}}_0=\hat{s}-\hat{s}\left({\hat{t}}_0\right)+2\hat{\omega }\left[\sqrt{\hat{s}+{\hat{s}}_{\ast }}-\sqrt{\hat{s}\left({\hat{t}}_0\right)+{\hat{s}}_{\ast }}\right]+\hat{\omega }{\hat{s}}^{\prime }log\left(\frac{\sqrt{\hat{s}+{\hat{s}}_{\ast }}-\sqrt{{\hat{s}}^{\prime }}}{\sqrt{\hat{s}+{\hat{s}}_{\ast }}+\sqrt{{\hat{s}}^{\prime }}}\frac{\sqrt{\hat{s}\left({\hat{t}}_0\right)+{\hat{s}}_{\ast }}+\sqrt{{\hat{s}}^{\prime }}}{\sqrt{\hat{s}\left({\hat{t}}_0\right)+{\hat{s}}_{\ast }}-\sqrt{{\hat{s}}^{\prime }}}\right).}$$ (38)

Particularly, for unshielded clusters (where ${\hat{s}}^{\prime }=0$), the last line of Eq. (38) is zero.

FIG. 4.

Characteristics for advection problem. Some sample $\hat{s}-\hat{t}$ characteristics for the nondimensionalized PDE problem with ${\hat{s}}_n-{\hat{s}}_{\ast }=0.25$. For (a) n = 0, and characteristics emerge from $\hat{s}={\hat{s}}_{\ast }$. For (b) n ≥ 1, the characteristics emerge from the curve $\left\{(\hat{s},{\hat{t}}_c\left(\hat{s}\right))\right\}$, where ${\hat{t}}_c$ is given in Eq. (47).

Along these curves, the concentration varies as

$${\displaystyle \frac{\mathrm{d}{\hat{c}}_n}{\mathrm{d}\hat{t}}=-\frac{\hat{\omega }}{2\sqrt{\hat{s}+{\hat{s}}_{\ast }}}\frac{\hat{s}+{\hat{s}}_{\ast }+{\hat{s}}^{\prime }}{{\left[\hat{\omega }\sqrt{\hat{s}+{\hat{s}}_{\ast }}+\hat{s}+{\hat{s}}_{\ast }-{\hat{s}}^{\prime }\right]}^2}{\hat{c}}_n\left(\hat{t}\right)-\hat{\mathrm{\lambda }}\sqrt{\hat{s}+{\hat{s}}_{\ast }}\left({\hat{c}}_n\left(\hat{t}\right)-{\hat{c}}_{n-1}(\hat{s},\hat{t})\right).}$$ (39)

For the purpose of solving these equations, it is advantageous to invoke the change-of-variables,

$${\displaystyle u\equiv \sqrt{\hat{s}+{\hat{s}}_{\ast }}}$$ (40)

$${\displaystyle {\hat{s}}^{\prime }\equiv {\hat{s}}_n}$$ (41)

$${\displaystyle \mathrm{d}s=2u\mathrm{d}u,}$$ (42)

to reparameterize the curves as

$${\displaystyle \frac{\mathrm{d}\hat{t}}{\mathrm{d}u}=2u\left[\frac{\hat{\omega }u}{u^2-{\hat{s}}_n}+1\right]\ge 0\forall u>\sqrt{{\hat{s}}_n},}$$ (43)

from where it is evident that the relationship between $\hat{t}$ and u is bijective. Hence, we may use u as a proxy for $\hat{t}$, finding that the concentration profiles along these curves vary with u as

$${\displaystyle \frac{\mathrm{d}{\hat{c}}_n}{\mathrm{d}u}=-\left[\frac{\hat{\omega }}{u^2-{\hat{s}}_n}\frac{u^2+{\hat{s}}_n}{\hat{\omega }u+u^2-{\hat{s}}_n}+2\hat{\mathrm{\lambda }}{u}^2\frac{u^2+\hat{\omega }u-{\hat{s}}_n}{u^2-{\hat{s}}_n}\right]{\hat{c}}_n+2\hat{\mathrm{\lambda }}{u}^2\frac{u^2+\hat{\omega }u-{\hat{s}}_n}{u^2-{\hat{s}}_n}{\hat{c}}_{n-1}(\hat{s}\left(u\right),\hat{t}\left(u\right)).}$$ (44)

With the aid of an integrating factor, Eq. (44) can be written in the exact differential form,

$${\displaystyle \mathrm{d}\left\{\frac{{(u^2-{\hat{s}}_n)}^{\hat{\mathrm{\lambda }}\hat{\omega }{\hat{s}}_n+1}}{u^2+\hat{\omega }u-{\hat{s}}_n}exp\left[\hat{\mathrm{\lambda }}{u}^2\left(\hat{\omega }+\frac{2}{3}u\right)\right]{\hat{c}}_n\right\}=2\hat{\mathrm{\lambda }}{u}^2{(u^2-{\hat{s}}_n)}^{\hat{\mathrm{\lambda }}\hat{\omega }{\hat{s}}_n}exp\left[\hat{\mathrm{\lambda }}{u}^2\left(\hat{\omega }+\frac{2}{3}u\right)\right]{\hat{c}}_{n-1}(u,\hat{t}\left(u\right)).}$$ (45)

The equation for the unshielded particle concentration ${\hat{c}}_0$ corresponds to the homogeneous problem $({\hat{s}}_0\equiv 0;{\hat{c}}_{-1}\equiv 0)$. Respecting the boundary condition invoked by nucleation, as well as the initial Cauchy data, yields the solution

$${\displaystyle {\hat{c}}_0(\hat{s},\hat{t})=H\left(\hat{t}-{\hat{t}}_c\left(\hat{s}\right)\right)\frac{\hat{\omega }+\sqrt{\hat{s}+{\hat{s}}_{\ast }}}{\sqrt{\hat{s}+{\hat{s}}_{\ast }}}\frac{\sqrt{{\hat{s}}_{\ast }}}{\hat{\omega }+\sqrt{{\hat{s}}_{\ast }}}\times \frac{exp\left[\hat{\mathrm{\lambda }}{\hat{s}}_{\ast }\left(\hat{\omega }+\frac{2}{3}\sqrt{{\hat{s}}_{\ast }}\right)\right]}{exp\left[\hat{\mathrm{\lambda }}(\hat{s}+{\hat{s}}_{\ast })\left(\hat{\omega }+\frac{2}{3}\sqrt{\hat{s}+{\hat{s}}_{\ast }}\right)\right]},}$$ (46)

where H is the unit step function and

$${\displaystyle {\hat{t}}_c\left(\hat{s}\right)=\hat{s}+2\hat{\omega }\left(\sqrt{\hat{s}+{\hat{s}}_{\ast }}-\sqrt{{\hat{s}}_{\ast }}\right)}$$ (47)

is analogous to a “first-passage-time” for the formation of size-$\hat{s}$ clusters.

To solve for the subsequent concentrations, we take advantage of the Cauchy data by initializing all characteristic curves along the curve $({\hat{t}}_c\left(\hat{s}\right),\hat{s})$ given by Eq. (47), thereby setting ${\hat{c}}_n=0$ at the left endpoint. Hence, each point $(\hat{s},\hat{t})$ such that $\hat{s}\ge {\hat{s}}^{\prime }={\hat{s}}_n$, and $\hat{t}\ge {\hat{t}}_c\left(\hat{s}\right)$ lies uniquely on a single curve originating from

$${\displaystyle \sqrt{\hat{s}\left({\hat{t}}_0\right)+{\hat{s}}_{\ast }}=\sqrt{{\hat{s}}^{\prime }}\frac{\frac{\sqrt{\hat{s}+{\hat{s}}_{\ast }}+\sqrt{{\hat{s}}^{\prime }}}{\sqrt{\hat{s}+{\hat{s}}_{\ast }}-\sqrt{{\hat{s}}^{\prime }}}exp\left[\frac{\hat{t}-\hat{s}-2\hat{\omega }(\sqrt{\hat{s}+{\hat{s}}_{\ast }}-\sqrt{{\hat{s}}_{\ast }})}{\hat{\omega }{\hat{s}}^{\prime }}\right]+1}{\frac{\sqrt{\hat{s}+{\hat{s}}_{\ast }}+\sqrt{{\hat{s}}^{\prime }}}{\sqrt{\hat{s}+{\hat{s}}_{\ast }}-\sqrt{{\hat{s}}^{\prime }}}exp\left[\frac{\hat{t}-\hat{s}-2\hat{\omega }(\sqrt{\hat{s}+{\hat{s}}_{\ast }}-\sqrt{{\hat{s}}_{\ast }})}{\hat{\omega }{\hat{s}}^{\prime }}\right]-1}.}$$ (48)

As growth of the mineral phase occurs more quickly in the unshielded clusters than in the shielded clusters, the $\hat{s}-\hat{t}$ characteristics propagate quickest in the unshielded clusters. Hence, the hierarchy $\mathrm{supp}\left({\hat{c}}_n\right)\subseteq \mathrm{supp}\left({\hat{c}}_{n-1}\right)\subseteq \cdots \subseteq \mathrm{supp}\left({\hat{c}}_0\right)$ holds. In fact, the supports of all functions ${\hat{c}}_n$ are equal, as necessitated by the coupling defined by the right-hand-side of Eq. (33). The creation of size-$\hat{s}$ clusters of shielding n is driven more by the shielding of “n − 1 clusters” rather than the growth of “n clusters.” We use this fact along with the presence of an exponential term within the exact differential of the right hand side of Eq. (45) to formulate the ansatz,

$${\displaystyle {\hat{c}}_n(\hat{s},\hat{t})=H\left(\hat{t}-{\hat{t}}_c\left(\hat{s}\right)\right)g_n(\hat{s},\hat{t})exp\left[-\hat{\mathrm{\lambda }}(\hat{s}+{\hat{s}}_{\ast })\left(\hat{\omega }+\frac{2}{3}\sqrt{\hat{s}+{\hat{s}}_{\ast }}\right)\right]exp\left[\hat{\mathrm{\lambda }}{\hat{s}}_{\ast }\left(\hat{\omega }+\frac{2}{3}\sqrt{{\hat{s}}_{\ast }}\right)\right],}$$ (49)

where

$${\displaystyle g_n\left(u\right)=2\hat{\mathrm{\lambda }}\frac{u^2+\hat{\omega }u-{\hat{s}}_n}{{(u^2-{\hat{s}}_n)}^{\hat{\mathrm{\lambda }}\hat{\omega }{\hat{s}}_n+1}}\times {\int }_{\sqrt{\hat{s}\left({\hat{t}}_0\right)+{\hat{s}}_{\ast }}}^u{q}^2{(q^2-{\hat{s}}_n)}^{\hat{\mathrm{\lambda }}\hat{\omega }{\hat{s}}_n}{g}_{n-1}\left(q\right)\mathrm{d}q.}$$ (50)

According to Eq. (46),

$${\displaystyle g_0\left(u\right)=\frac{\hat{\omega }+u}{u}\frac{\sqrt{{\hat{s}}_{\ast }}}{\hat{\omega }+\sqrt{{\hat{s}}_{\ast }}}.}$$ (51)

For solving $g_n(\hat{s},\hat{t})$, the lower bound for the integral in Eq. (50) is taken from Eq. (48). For solving the next equation $g_{n+1}(\hat{s},\hat{t})$, all instances of $\hat{s},\hat{t}$ reparameterized by the variable u using Eq. (48).

The iterated integrals of Eq. (50) can be solved numerically through standard quadrature methods. Here we find some properties of the solutions to these equations before exploring their steady-state behavior, which is of the most interest to us.

First, there is the question of whether these equations are well-posed. For u near $\sqrt{{\hat{s}}_n}$, one can invoke L’Hospital’s rule on Eq. (50) to find that

$${\displaystyle \underset{u\searrow \sqrt{\underset{n}{\hat{s}}}}{lim}{g}_n\left(u\right)=\frac{\hat{\mathrm{\lambda }}\hat{\omega }\sqrt{{\hat{s}}_n}}{\hat{\mathrm{\lambda }}\hat{\omega }{\hat{s}}_n+1}=\mathcal{O}\left(1\right).}$$

So, the solutions are bounded on the left. Now, we seek to find pointwise bounds for the solution away from the left boundary (for $u>\sqrt{{\hat{s}}_n}$). We note that the lower bound of the integral term in Eq. (50), given by Eq. (48), approaches $\sqrt{{\hat{s}}_n}$ as t → ∞. Since the integrand is non-negative, the solution is bounded from above by the steady state solution,

$${\displaystyle g_n\left(u\right)=2\hat{\mathrm{\lambda }}\frac{u^2+\hat{\omega }u-{\hat{s}}_n}{{(u^2-{\hat{s}}_n)}^{\hat{\mathrm{\lambda }}\hat{\omega }{\hat{s}}_n+1}}\times {\int }_{\sqrt{\hat{s}\left({\hat{t}}_0\right)+{\hat{s}}_{\ast }}}^u{q}^2{(q^2-{\hat{s}}_n)}^{\hat{\mathrm{\lambda }}\hat{\omega }{\hat{s}}_n}{g}_{n-1}\left(q\right)\mathrm{d}q\le 2\hat{\mathrm{\lambda }}\frac{u^2+\hat{\omega }u-{\hat{s}}_n}{{(u^2-{\hat{s}}_n)}^{\hat{\mathrm{\lambda }}\hat{\omega }{\hat{s}}_n+1}}{\int }_{\sqrt{{\hat{s}}_n}}^u{q}^2{(q^2-{\hat{s}}_n)}^{\hat{\mathrm{\lambda }}\hat{\omega }{\hat{s}}_n}{g}_{n-1}\left(q\right)\mathrm{d}q\equiv g_n^{\infty }\left(u\right).}$$ (52)

By repeated applications of the Cauchy-Schwarz inequality, one sees that the integral term in Eq. (52) satisfies the inequalities,

$${\displaystyle {\int }_{\sqrt{{\hat{s}}_n}}^u{q}^2{(q^2-{\hat{s}}_n)}^{\hat{\mathrm{\lambda }}\hat{\omega }{\hat{s}}_n}{g}_{n-1}\left(q\right)\mathrm{d}q\le {\left[{\int }_{\sqrt{{\hat{s}}_n}}^u{q}^4{(q^2-{\hat{s}}_n)}^{2\hat{\mathrm{\lambda }}\hat{\omega }{\hat{s}}_n}\mathrm{d}q\right]}^{1/2}\Vert g_{n-1}^{\infty }{\Vert }_{L^2(\sqrt{{\hat{s}}_n},u)}\le {\left[\frac{{(u^2-s_n)}^{4\hat{\mathrm{\lambda }}\hat{\omega }{\hat{s}}_n+1}}{4\hat{\mathrm{\lambda }}\hat{\omega }{\hat{s}}_n+1}\right]}^{1/4}{\left[\frac{u^8-s_n^4}{8}\right]}^{1/4}\Vert g_{n-1}{\Vert }_{L^2(\sqrt{{\hat{s}}_n},u)}.}$$

This computation gives us the pointwise bound on $g_n^{\infty }$,

$${\displaystyle g_n^{\infty }\left(u\right)\le \frac{2\hat{\mathrm{\lambda }}}{{(4\hat{\mathrm{\lambda }}\hat{\omega }{\hat{s}}_n+1)}^{1/4}}\frac{u^2+\hat{\omega }u-{\hat{s}}_n}{{(u^2-{\hat{s}}_n)}^{3/4}}\times {\left[\frac{u^8-{\hat{s}}_n^4}{8}\right]}^{1/4}\Vert g_{n-1}{\Vert }_{L^2(\sqrt{{\hat{s}}_n},u)}.}$$

Using the fact that $g_0^{\infty }\left(u\right)=\mathcal{O}\left(1\right)$, it is easy to see by induction that g_n(u) is bounded and smooth (behaving locally like a polynomial with order controlled by n) for $u>\sqrt{{\hat{s}}_n}$, where it is of note that $g_n^{\infty }$ is bounded also in the vicinity of $\sqrt{{\hat{s}}_n}$. Hence, by Eq. (49), each solution of c_n(s, t) is Schwartz-class, for all t ≥ 0.

C. Steady-state behavior

Our interest is in long-term behavior of the system. Observe that the solutions of Eq. (49) contain an exponential multiplicative factor that represents regulatory shielding (Fig. 5). This shielding is strong provided that the term in the exponential is large, which is the case when

$${\displaystyle \hat{\mathrm{\lambda }}{(1+{\hat{s}}_{\ast })}^{3/2}\gg 1.}$$ (53)

In physical units, this criterion can be expressed succinctly in terms of the concentration of FA protein needed,

$${\displaystyle {\varphi }_{\infty }\gg \frac{D}{D_{FA}}\frac{{\rho }_{\infty }-{\rho }_s}{m_p},}$$ (54)

where m_p is critical number of Posner clusters in a pure-mineral cluster at sedimentation. Note that if this condition were not to hold, then a significant number of clusters of sedimentation size would form. Sedimentation would then occur until exhaustion of supersaturated species. In our subsequent analysis, we will assume that this condition holds.

FIG. 5.

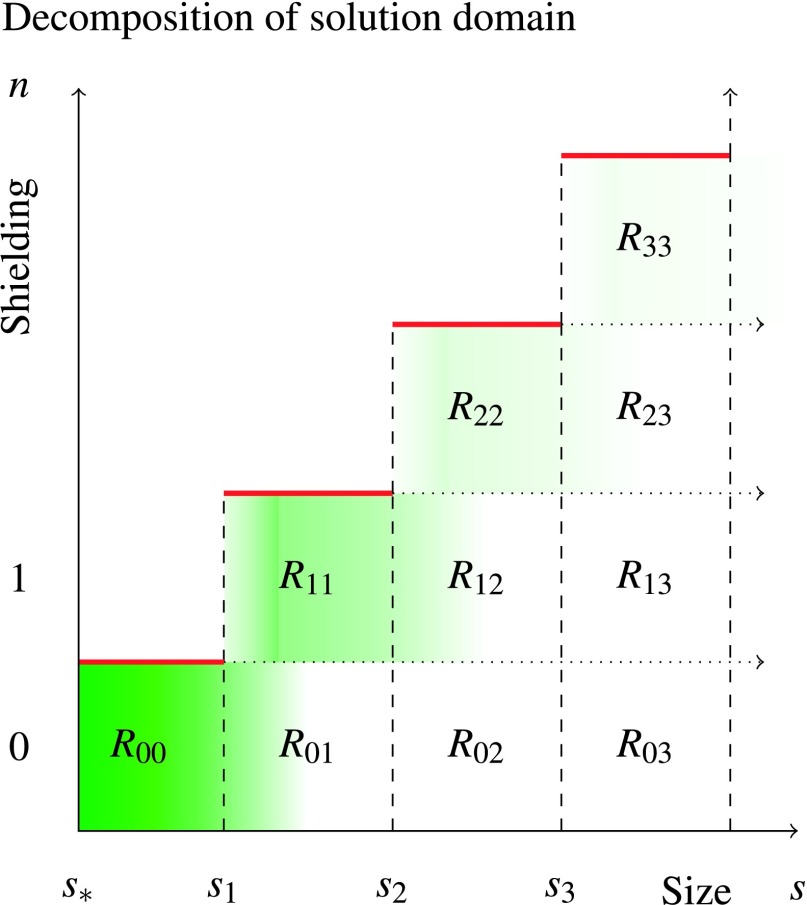
Steady-state cluster concentration $c_n^{\infty }\left(s\right)$ and domain decomposition for computing the protein consumption rate. Green shading (darker is more concentrated) corresponds to increased steady-state concentration of mineral clusters of the particular size (given by horizontal axis) with the given number of attached FA proteins (given by the vertical axis). In the asymptotic case of strong shielding (Eq. (54)), an exponential decay of concentration is seen according to size. From this solution, an overall consumption rate of FA protein can be computed by summing over the attachment rates R_nj, where R_nj refers to the rate of protein consumption by clusters of n bound proteins of size s_j to s_j+1.

Since the overall solution is tapered by the exponential term which goes as s^3/2, or as the volume, we are most interested in the behavior of $g_n^{\infty }\left(u\right)$ in the vicinity of $\sqrt{s_n}$. In this limit, we use the binomial theorem to approximate the integrals of the general form, for a, b ∈ ℝ,

$${\displaystyle {\int }_{\sqrt{{\hat{s}}_n}}^u{q}^2{(q^2-{\hat{s}}_n)}^{\hat{\mathrm{\lambda }}\hat{\omega }{\hat{s}}_n}{q}^a{(q^2-{\hat{s}}_n)}^b\mathrm{d}q=\frac{\sqrt{{\hat{s}}_n^{a+1}}}{2}{\int }_0^{u^2-{\hat{s}}_n}{x}^{\hat{\mathrm{\lambda }}\hat{\omega }{\hat{s}}_n+b}{\left(1+\frac{x}{s_n}\right)}^{(a+1)/2}\mathrm{d}x=\frac{\sqrt{{\hat{s}}_n^{a+1}}}{2}\left[\frac{{(u^2-{\hat{s}}_n)}^{\hat{\mathrm{\lambda }}\hat{\omega }{\hat{s}}_n+b+1}}{\hat{\mathrm{\lambda }}\hat{\omega }{\hat{s}}_n+b+1}+\mathcal{O}\left({(u^2-{\hat{s}}_n)}^{\hat{\mathrm{\lambda }}\hat{\omega }{\hat{s}}_n+b+2}\right)\right].}$$ (55)

Eq. (55) allows us to evaluate $g_1^{\infty }$ to the leading order,

$${\displaystyle g_1^{\infty }\left(u\right)\approx \frac{\sqrt{{\hat{s}}_{\ast }}}{\hat{\omega }+\sqrt{{\hat{s}}_{\ast }}}\frac{\hat{\mathrm{\lambda }}(\sqrt{{\hat{s}}_1}+\hat{\omega })}{\hat{\mathrm{\lambda }}\hat{\omega }{\hat{s}}_1+1}\left[(u^2-{\hat{s}}_1)+\hat{\omega }u\right].}$$ (56)

Through an inductive argument, one finds that for n ≥ 1,

$${\displaystyle g_n^{\infty }\left(u\right)\approx (u^2-{\hat{s}}_n+\hat{\omega }u)\frac{\sqrt{{\hat{s}}_{\ast }}}{\hat{\omega }+\sqrt{{\hat{s}}_{\ast }}}\times \frac{1}{{\hat{s}}_1}\prod _{j=1}^n\frac{\hat{\mathrm{\lambda }}(({\hat{s}}_j-{\hat{s}}_{j-1})\sqrt{{\hat{s}}_j}+{\hat{s}}_j\hat{\omega })}{\hat{\mathrm{\lambda }}\hat{\omega }{\hat{s}}_j+1}.}$$ (57)

We retain both u² − s_n and $\hat{\omega }u$ in this expression because it is unclear which term is large. As n increases however, the $\hat{\omega }u$ term will begin to dominate. This fact implies that surface-limited effects arise for large clusters, contrary to the situation for most other nucleation problems.

D. Rate of FA consumption

Since we know the rate of protein association as a function of n (the number of bound proteins) and s (the surface area of the mineral phase), we can compute the total rate of FA consumption. Denote R_jk (Fig. 5) as the cumulative rate of mineral consumption in shielding particles of j FA monomers with size s ∈ (s_k, s_k+1). We derive this rate first for the shielding of unshielded clusters of size at most s₁, R₀₀. Returning back to an integer parameterization of the size, it is clear that the total rate of consumption of FA for these clusters follows

$${\displaystyle R_{00}=\sum _{m=m\left(s_{\ast }\right)}^{m\left(s_1\right)}\mathrm{\lambda }\sqrt{s\left(m\right)}{c}_0^{\infty }\left(s\left(m\right)\right),}$$ (58)

where $c_0^{\infty }$ is the steady state concentration depicted in Fig. 5. The sum in Eq. (58) can be approximated by a left-Riemann integral so that

$${\displaystyle \sum _{m=m\left(s_{\ast }\right)}^{m\left(s_1\right)}\mathrm{\lambda }\sqrt{s\left(m\right)}{c}_0^{\infty }\left(s\left(m\right)\right)\approx {\int }_{m\left(s_{\ast }\right)}^{m\left(s_1\right)}\mathrm{\lambda }\sqrt{s\left(m\right)}{c}_0^{\infty }\left(s\left(m\right)\right)\mathrm{d}m.}$$ (59)

After transformation from m back to s, one finds that

$${\displaystyle R_{00}\approx \frac{\mathrm{\lambda }}{\sqrt{16{\overline{v}}^2\pi }}{\int }_{s_{\ast }}^{s_1}s{c}_0^{\infty }\left(s\right)\mathrm{d}s.}$$ (60)

Generalizing this result, it is easy to see that

$${\displaystyle R_{nj}\approx \frac{\mathrm{\lambda }}{\sqrt{16{\overline{v}}^2\pi }}{\int }_{s_j}^{s_{j+1}}s{c}_n^{\infty }\left(s\right)\mathrm{d}s.}$$ (61)

The total consumption rate of FA protein follows

$${\displaystyle R\approx \stackrel{\mathrm{at\; nucleation}}{\overbrace{\mathrm{\lambda }\sqrt{s_{\ast }}{c}_0^{\infty }\left(s_{\ast }\right)}}+\sum _{n=0}^{\infty }\sum _{j=n}^{\infty }{R}_{nj}}$$ (62)

where the first term represents FA consumed in the instantaneous shielding of critical clusters. Substituting Eq. (49) yields

$${\displaystyle R\approx \mathrm{\lambda }\sqrt{s_{\ast }}{c}_0^{\infty }\left(s_{\ast }\right)\{1+exp\left[\frac{\mathrm{\lambda }{s}_{\ast }}{\alpha }\left(\omega +\frac{2}{3}\sqrt{s_{\ast }}\right)\right]\times \sum _{n=0}^{\infty }{\int }_{s_n}^{\infty }\frac{s{g}_n^{\infty }\left(u\left(s\right)\right)}{\sqrt{16{\overline{v}}^2{s}_{\ast }\pi }}exp\left[-\frac{\mathrm{\lambda }s}{\alpha }\left(\omega +\frac{2}{3}\sqrt{s}\right)\right]\mathrm{d}s\},}$$ (63)

where $u\left(s\right)=\sqrt{s/(s_p-s_{\ast })}$. We approximate the integrals in Eq. (63) using the change of variables

$${\displaystyle \begin{array}{cc}\hfill \xi & =\frac{\mathrm{\lambda }s}{\alpha }\left(\omega +\frac{2}{3}\sqrt{s}\right),\hfill \end{array}}$$

which we invert to find that

$${\displaystyle \begin{array}{rcl}\hfill s& \hfill =\hfill & {\left(\frac{3\alpha }{2\mathrm{\lambda }}\xi \right)}^{2/3}-\omega {\left(\frac{3\alpha }{2\mathrm{\lambda }}\xi \right)}^{1/3}+\mathcal{O}\left({\omega }^2\right)\hfill \\ \hfill \mathrm{d}\xi & \hfill =\hfill & \frac{\mathrm{\lambda }}{\alpha }\left(\omega +\sqrt{s}\right)\mathrm{d}s\hfill \\ \hfill & \hfill =\hfill & \frac{\mathrm{\lambda }}{\alpha }\left[{\left(\frac{3\alpha }{2\mathrm{\lambda }}\xi \right)}^{1/3}+\frac{\omega }{2}+\mathcal{O}\left({\omega }^2\right)\right]\mathrm{d}s.\hfill \end{array}}$$ (64)

For n ≥ 1, we evaluate the integrals in Eq. (63),

$${\displaystyle {\int }_{s_n}^{\infty }\frac{s{g}_n^{\infty }\left(u\left(s\right)\right)}{\sqrt{16{\overline{v}}^2{s}_{\ast }\pi }}exp\left[-\frac{\mathrm{\lambda }s}{\alpha }\left(\omega +\frac{2}{3}\sqrt{s}\right)\right]\mathrm{d}s=\frac{1}{\sqrt{16{\overline{v}}^2{s}_{\ast }\pi }}\frac{\sqrt{s_{\ast }}}{\omega +\sqrt{s_{\ast }}}\frac{1}{s_1}\prod _{j=1}^n\frac{\mathrm{\lambda }((s_j-s_{j-1})\sqrt{s_j}+s_j\omega )}{\mathrm{\lambda }\omega s_j+\alpha }\times {\int }_{\frac{\mathrm{\lambda }{s}_n}{\alpha }\left(\omega +\frac{2}{3}\sqrt{s_n}\right)}^{\infty }\frac{s(s-s_n+\omega \sqrt{s})}{\frac{\mathrm{\lambda }}{\alpha }\left({\left(\frac{3\alpha }{2\mathrm{\lambda }}\xi \right)}^{1/3}+\frac{\omega }{2}+\mathcal{O}\left({\omega }^2\right)\right)}{e}^{-\xi }\mathrm{d}\xi .}$$ (65)

We approximate the integral in Eq. (65) by a sum of incomplete Gamma functions Γ(a, x),

$${\displaystyle {\int }_{\frac{\mathrm{\lambda }{s}_n}{\alpha }\left(\omega +\frac{2}{3}\sqrt{s_n}\right)}^{\infty }\frac{s(s-s_n+\omega \sqrt{s})}{\frac{\mathrm{\lambda }}{\alpha }\left({\left(\frac{3\alpha }{2\mathrm{\lambda }}\xi \right)}^{1/3}+\frac{\omega }{2}+\mathcal{O}\left({\omega }^2\right)\right)}{e}^{-\xi }\mathrm{d}\xi =\frac{\alpha }{\mathrm{\lambda }}{\int }_{\frac{\mathrm{\lambda }{s}_n}{\alpha }\left(\omega +\frac{2}{3}\sqrt{s_n}\right)}^{\infty }\{\left(\frac{3\alpha }{2\mathrm{\lambda }}\xi \right)+s_n{\left(\frac{3\alpha }{2\mathrm{\lambda }}\xi \right)}^{1/3}-\omega \left[\frac{5}{2}{\left(\frac{3\alpha }{2\mathrm{\lambda }}\xi \right)}^{2/3}-\frac{s_n}{2}\right]+\mathcal{O}\left({\omega }^2\right)\}{e}^{-\xi }\mathrm{d}\xi \sim \frac{3{\alpha }^2}{2{\mathrm{\lambda }}^2}\mathrm{\Gamma }\left(2,\frac{\mathrm{\lambda }{s}_n}{\alpha }\left(\omega +\frac{2}{3}\sqrt{s_n}\right)\right)+s_n{\left(\frac{3{\alpha }^4}{2{\mathrm{\lambda }}^4}\right)}^{1/3}\mathrm{\Gamma }\left(\frac{4}{3},\frac{\mathrm{\lambda }{s}_n}{\alpha }\left(\omega +\frac{2}{3}\sqrt{s_n}\right)\right)-\frac{5s_n\alpha \omega }{2\mathrm{\lambda }}{\left(\frac{3\alpha }{2\mathrm{\lambda }}\right)}^{2/3}\mathrm{\Gamma }\left(\frac{5}{3},\frac{\mathrm{\lambda }{s}_n}{\alpha }\left(\omega +\frac{2}{3}\sqrt{s_n}\right)\right)+\frac{\alpha s_n\omega }{2\mathrm{\lambda }}\mathrm{\Gamma }\left(1,\frac{\mathrm{\lambda }{s}_n}{\alpha }\left(\omega +\frac{2}{3}\sqrt{s_n}\right)\right),}$$ (66)

where the remainder term is exponentially small by rationale of Watson’s Lemma. For n = 0, we have

$${\displaystyle {\int }_{s_{\ast }}^{\infty }\frac{s{g}_0^{\infty }\left(u\left(s\right)\right)}{\sqrt{16{\overline{v}}^2{s}_{\ast }\pi }}exp\left[-\frac{\mathrm{\lambda }s}{\alpha }\left(\omega +\frac{2}{3}\sqrt{s}\right)\right]\mathrm{d}s=\frac{1}{\sqrt{16{\overline{v}}^2{s}_{\ast }\pi }}\frac{\sqrt{s_{\ast }}}{\omega +\sqrt{s_{\ast }}}{\int }_{s_{\ast }}^{\infty }\left(s+\omega \sqrt{s}\right)exp\left[-\frac{\mathrm{\lambda }s}{\alpha }\left(\omega +\frac{2}{3}\sqrt{s}\right)\right]\mathrm{d}s}$$ (67)

$${\displaystyle =\frac{1}{\sqrt{16{\overline{v}}^2{s}_{\ast }\pi }}\frac{\sqrt{s_{\ast }}}{\omega +\sqrt{s_{\ast }}}\frac{\alpha }{\mathrm{\lambda }}{\int }_{\frac{\mathrm{\lambda }{s}_{\ast }}{\alpha }\left(\omega +\frac{2\sqrt{s_{\ast }}}{3}\right)}^{\infty }\left[{\left(\frac{3\alpha }{2\mathrm{\lambda }}\xi \right)}^{1/3}-\frac{\omega }{2}+\mathcal{O}\left({\omega }^2\right)\right]e^{-\xi }\mathrm{d}\xi \sim \frac{\alpha }{\mathrm{\lambda }\sqrt{16{\overline{v}}^2{s}_{\ast }\pi }}\frac{\sqrt{s_{\ast }}}{\omega +\sqrt{s_{\ast }}}\{{\left(\frac{3\alpha }{2\mathrm{\lambda }}\right)}^{1/3}\mathrm{\Gamma }\left(\frac{4}{3},\frac{\mathrm{\lambda }{s}_{\ast }}{\alpha }\left(\omega +\frac{2\sqrt{s_{\ast }}}{3}\right)\right)-\frac{\omega }{2}\mathrm{\Gamma }\left(1,\frac{\mathrm{\lambda }{s}_{\ast }}{\alpha }\left(\omega +\frac{2\sqrt{s_{\ast }}}{3}\right)\right)\}.}$$ (68)

In the regime where λ/α → ∞, no clusters of size greater than s_∗ form, and the rate of FA consumption matches the nucleation rate for ACP. Conversely, if clusters of size greater than s₁ form, the FA consumption rate is strictly greater than the ACP nucleation rate.

E. Parameterization

As we have mentioned, normal physiological calcium concentrations exceed supersaturation relative to the most thermodynamically stable phase of calcium phosphate. In fact, as we shall see, they also exceed supersaturation relative to ACP.

Normal serum free ionic Ca²⁺ concentration varies between 1.2 mM and 1.3 mM,³⁷ and normal total serum phosphate concentration varies between 1.12 mM and 1.45 mM. At pH = 7.4, one finds using the Henderson-Hasselbalch equation that the concentration of free ${\mathrm{PO}}_4^{3-}$ lies between 3.7 and 4.9 nM. Various studies have explored the solubility of ACP relative to concentrations of its constituent ions (Ca²⁺, ${\mathrm{PO}}_4^{3-}$). By empirical formula, ACP has the negative-log₁₀-solubility pK_s = 3pCa + 2pPO₄ ≈ 26 at 310 K and pH = 7.4.³⁸ Using this calculation, one may compute the supersaturation relative to ACP,

$${\displaystyle S^{\left(0\right)}={\left(\frac{{\left[{\mathrm{Ca}}^{2+}\right]}^3{\left[{\mathrm{PO}}_4^{3-}\right]}^2}{10^{-26}}\right)}^{1/5}.}$$ (69)

Hence, the supersaturation ratio is approximately S⁽⁰⁾ ≈ 1.3 in normal conditions.

Estimates for the molecular weight of FA range from 51 to 67 kDa, while the usual serum concentrations of FA range from 0.5 to 1.0 g/L. Thus, FA ranges in concentration between 7 μM and 19 μM in normal situations. We assume that $m_p=\mathcal{O}\left(10^2\right)$, where it notable that a single FA protein shields approximately 10² Posner clusters.²² For context, a cluster of size m = 100 corresponds to a diameter of approximately 4 nm, assuming hexagonal close packing and using $\overline{v}=0.3{\mathrm{nm}}^3$.²² A diameter of 4 nm is similar in extent to the size of FA, which has been measured to have a hydrodynamical radius of 4.3 nm.⁴² We also note here that the radius of a PC is approximately 0.4 nm, so the ratio of the diffusivities between a PC monomer and FA molecule (D/D_FA) is approximately 10.

To estimate the concentration of PC monomers (ρ_∞), we rely on indirect evidence as precise quantification of these clusters does not appear to have been performed in the literature. We note that a study by Chughtai et al.⁴⁰ found that in physiological conditions, approximately 6% of solution Ca²⁺ is present in calcium-phosphate complexes. A separate study has found that approximately 50% of calcium phosphate complexes have size consistent with Posner’s cluster.⁴¹ An ACP nucleation study using 2.5 mM free Ca²⁺ and 1 mM K₂HPO₄ found spherical clusters of approximately 30–80 nm in diameter after 1 h.⁶ Assuming that the 80 nm size corresponds to a cluster that nucleated soon after t = 0, one finds that the concentration of PCs is at least 2 nM in their preparation. Using this value, we estimate an equilibrium constant for the formation of PCs,

$${\displaystyle k_{\mathrm{eq}}=\frac{{\rho }_{\infty }}{{\left[{\mathrm{Ca}}^{2+}\right]}^3{\left[{\mathrm{PO}}_4^{3-}\right]}^2},}$$ (70)

finding that pk_eq ≈ − 16. This computation estimates nanomolar-range concentrations for PCs in the physiological range that we defined above.

With these rough estimates in mind, we may approximate an “inhibition-ratio” from Eq. (53) as

$${\displaystyle I=\frac{m_p{D}_{\mathrm{FA}}{\varphi }_{\infty }}{D{\rho }_{\infty }}\approx \mathcal{O}\left(10^3\right).}$$ (71)

The concentration of post-nuclear clusters is exponential in this ratio, suggesting that large values for I would inhibit calcification. We turn now to assays of calcification inhibition in order to validate this computation.

Heiss et al.⁴³ assessed the inhibition of sedimentation in a highly supersaturated solution of 20 mM Ca²⁺ and 6 mM Na₂HPO₄ in a closed system. For this system, Eq. (70) provides an estimate of ρ_∞ = 2.5 × 10⁻⁵ M. At 20 μM, corresponding to $I=\mathcal{O}\left(10^2\right)$, FA was shown to inhibit sedimentation fully over a time interval of days. At 1.5 μM, corresponding to $I=\mathcal{O}\left(10^1\right)$, FA was seen to initially inhibit sedimentation, but only for a period of 2 h. In the latter case, we expect two things to be occurring. First, because the experiments are conducted in closed systems, exhaustion of FA is occurring over the long time span. Second, inhibition is exponentially weaker than it is in physiological settings implying a proportionally quicker rate of sedimentation.

IV. DISCUSSION

A. Protein consumption rate and implications

The quantity R sets a minimum replenishment rate for new FA protein in order to maintain a steady concentration of FA, and hence colloidal stability. As seen in Eq. (26), the parameter λ is present in the denominator of $c_0^{\infty }\left(s_{\ast }\right)$. As a result, to the leading order, R increases as λ decreases. Failure to maintain this replenishment rate leads to decrease in ϕ_∞, the concentration of FA. A drop in ϕ_∞ further decreases λ, thereby further exacerbating the situation (the less FA available, the more that is needed). Effectively, in the regime where calcium and phosphate concentrations remain supersaturated, the number of FA molecules required to buffer each nucleating mineral particle increases as the concentration of FA decreases.

Thus, even a small destabilization in FA replenishment can feed-forward to avalanche into catastrophic calcium phosphate sedimentation. This observation explains the experimental finding that serum FA is often significantly depressed in systems exhibiting ectopic calcification, yet plentiful in the sedimented plaques.⁴⁴

B. Assumptions, limitations, and extensions

In our theoretical treatment of this topic, we have made some key simplifying assumptions. Correspondingly, we have also limited the scope of our formulation and results. We reiterate that we are primarily interested in the earliest stages of the mineralization process, immediately after nascent nuclei have overcome the kinetic barrier and progression is governed by thermodynamic considerations. For this reason, we do not consider later phases of calcium phosphates, as well as their nucleation through heterogeneous nucleation involving ACP precursors.¹⁹ It is notable, however, that the transformations of calcium phosphate from ACP to HA have been a rich topic of research, and FA protein is known to interact with these phases as well, just as it interacts with ACP.⁴²

Biologically, we also assume that the specific structure of FA is important in two ways. First, its hydrodynamical mobility determines the rate at which it is able to interact with mineral clusters. Second, its precise biochemical structure determines its propensity for strong interactions with post-nuclear clusters. We have assumed this mechanism to be the primary mechanism for FA-based inhibition for several reasons.

Mainly, this mechanism has been suggested in the experimental literature.²⁸ Alternatively, FA has been reported to be able to bind calcium ions directly,²⁶ and hypothesized to bind pre-nucleation clusters (Posner’s clusters) directly.²² Yet, binding free calcium ions directly would not inhibit nucleation without decreasing supersaturation. Binding of pre-nucleation clusters would decrease the nucleation rate for calcium phosphates, running counter to experimental evidence.²⁸

Aside from the experimental evidence, there are apparent advantages to the solubilizing of post-nuclear particles as both an effective and efficient strategy for controlling sedimentation in super-saturated systems. While binding of pre-nucleation clusters would inhibit nucleation by increasing the energy barrier, it would require more inhibitory proteins to work because pre-nucleation clusters form at quicker rates than post-nucleation clusters. Experimental and theoretical evidence has confirmed the presence and stability of Posner’s clusters in biological solutions. In our formulation, we assume that pre-nucleation clusters exist in quasi-steady equilibrium with free calcium and phosphate. We also assume that FA–free calcium and FA–pre-nucleation cluster interactions are weak and reversible so that we may ignore them.

It is this specificity of mechanism that makes FA a potent calcification inhibitor. Uniquely, experiments have shown that FA is the crucial protein for in vivo mineralization inhibition. While other macromolecules such as albumin are known to interact with calcium phosphates, their physical attributes make them insufficient for this task.

Albumin acts as a buffering agent for calcium in blood, helping to maintain Ca²⁺ concentration in an analogous manner to maintenance of free H⁺ ion concentration by pH buffers. For purposes of this study, the main effect of albumin is in setting the far-field equilibrium concentration of Ca²⁺ and hence mineral monomers. We are ignoring interactions between the regulatory FA protein and other plasma proteins such as albumin. Although lacking in intrinsic capability, albumin has been shown to enhance the inhibitory properties of FA protein;⁴⁵ however, their main effect is in later-stage stabilization of complexes containing multiple protein-mineral clusters.⁴³

In this manuscript, we have also ignored other possible contributing factors to the overall mineralization process including interactions with other ions such as sodium, chloride, magnesium, zinc, or H⁺/OH⁻. While these ions have been shown to influence mineralization, their importance in the early stages of nucleation is unclear.

We also have not considered secondary interactions between mineral-FA hybrids, or the formation of calciprotein polymers. One of the goals of the present study has been to determine the content of the individual calciprotein monomers (the protein-mineral hybrid complexes we study in this manuscript). Observations by Wald et al.⁴⁶ have shown that the stability and size of these secondary structures varies with the concentration of FA present in the system. A possible cause for this effect is the variations in the mineral to protein ratio in the clusters that we form in our model. The understanding of these calciprotein monomers gained from this study should prove useful in better-understanding the kinetics behind the formation of calciprotein polymers as well as subsequent phase transitions.

Finally, while we have made an attempt to parameterize our model based on quantitative results from the past literature, our numerical estimates remain rough guides and further experimentation is likely needed to more-accurately parameterize our model. In particular, as the precise mechanism for calcium phosphate nucleation becomes better known, it will become easier to characterize the precise nucleation barrier and nucleation rate of calcium phosphate in order to better-understand the FA consumption rate. We have assumed for instance that the Posner cluster is the pre-nucleation cluster for this system, but recent literature has been mixed with respect to this hypothesis. We would like to emphasize, however, that our formulation is independent of the precise nature of these clusters as the bulk of our analyses focus on post-nucleation events.

Looking more broadly at our work, the methodology that we have developed in this manuscript has potential in explaining a variety of solubility problems throughout biology. As an example, the system of stabilization, transport, and clearance of lipid molecules by high-density lipoprotein (HDL) and low-density lipoprotein (LDL) bears striking resemblance to the calcium-phosphate-FA system that we have analyzed in this manuscript. The formation of protein-non-protein complexes or colloids is a widespread feature of the homeostasis of solutions in biology.

V. SUMMARY

In this manuscript we have utilized classical nucleation theory to provide a quantitative description of the growth of calcium phosphate nanoparticles interacting with a shielding protein. In contrast with other theoretical work on similar systems, we have not neglected possible surface-limiting regimes of the process. Our quantitative description of the process provides an estimate of the critical concentration of shielding protein necessary for stable long-term inhibition of calcification, as well as an estimate of the total rate that the protein is consumed.

Critically, we have found that disruptions of the ability to maintain the concentration of FA leads to increased overall consumption of the protein, and hence, exhaustion and sedimentation.