Universal equation for estimating ideal body weight and body weight at any BMI

Abstract

Background: Ideal body weight (IBW) equations and body mass index (BMI) ranges have both been used to delineate healthy or normal weight ranges, although these 2 different approaches are at odds with each other. In particular, past IBW equations are misaligned with BMI values, and unlike BMI, the equations have failed to recognize that there is a range of ideal or target body weights.

Objective: For the first time, to our knowledge, we merged the concepts of a linear IBW equation and of defining target body weights in terms of BMI.

Design: With the use of calculus and approximations, we derived an easy-to-use linear equation that clinicians can use to calculate both IBW and body weight at any target BMI value. We measured the empirical accuracy of the equation with the use of NHANES data and performed a comparative analysis with past IBW equations.

Results: Our linear equation allowed us to calculate body weights for any BMI and height with a mean empirical accuracy of 0.5–0.7% on the basis of NHANES data. Moreover, we showed that our body weight equation directly aligns with BMI values for both men and women, which avoids the overestimation and underestimation problems at the upper and lower ends of the height spectrum that have plagued past IBW equations.

Conclusions: Our linear equation increases the sophistication of IBW equations by replacing them with a single universal equation that calculates both IBW and body weight at any target BMI and height. Therefore, our equation is compatible with BMI and can be applied with the use of mental math or a calculator without the need for an app, which makes it a useful tool for both health practitioners and the general public.

See corresponding editorial on page 1193.

INTRODUCTION

How to accurately determine desirable or target body weights for nutritional and health assessments has been an important challenge for more than a century (1, 2). Many of the first attempts were based on actuarial data and defined ideal or desirable body weights with the use of height-weight tables. Because these tables are cumbersome to use, ideal body weight (IBW) equations for predicting weight as a linear function of height were developed starting in the late 1800s (2). Later, the popularity of IBW equations increased after Hamwi (3) and Devine (4) published their seminal equations (4). A decade later, motivated by applications to drug dosing, Robinson et al. (5) and Miller et al. (6) formulated IBW equations on the basis of the 1959 and 1983 Metropolitan Life Insurance Company height-weight tables, respectively. More recently, Hammond (7) created a metric version of the Hamwi equation. Although not as popular as they once were, IBW equations are still being used by clinicians to calculate drug dosing, to estimate overweight and underweight statuses, and to calculate nutrient intakes (2).

The advantage of IBW equations is that they predict weight (variable: Wt) as a linear function of height (variable: Ht) as

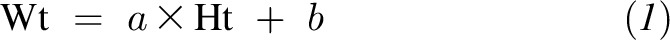where a is the slope and b is the intercept. Often, the height term is expressed as the difference from a reference value such as height in inches in excess of 5 ft. For example, the sex-specific equations of Hamwi (3), which were developed for the US system, estimate IBW for men as

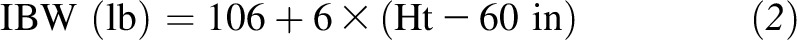and for women as

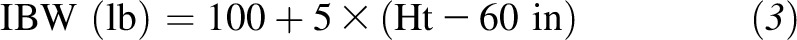whereas the sex-specific equations of Devine (4), which were developed for the metric system, estimate IBW for men as

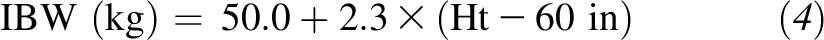and for women as

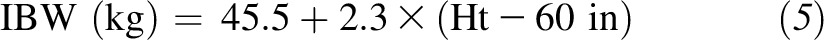where Ht is in inches and Ht is ≥60 in. The simple linear structure of these equations makes them easy to calculate with the use of mental math or a calculator.

However, despite the advantage of simplicity, the IBW approach has 3 important limitations. First, although IBW or desirable weight was originally defined as the weight associated with the greatest life expectancy at each height, there is no single ideal weight that applies universally to all comorbidities and mortality-specific causes, and there is no single ideal weight that is applicable across all demographic factors, including age and ethnicity (8). Second, IBW equations predict a single target body weight, whereas most clinicians favor, and the empirical data support, a range of target body weights. Third, Shah et al. (2) analyzed IBW equations and showed that they were incompatible with BMI and, instead, that IBW equations underestimated body weight at shorter heights and overestimated body weights at taller heights (2). For these reasons, IBW equations have largely been replaced by BMI ranges.

In contrast, BMI, which is defined as body weight divided by height squared (kg/m²), is now more widely used in clinical settings to diagnose excess adiposity and underweight status (9–11). BMI has the following 2 important advantages: it quantifies adiposity in a height-independent manner, and clinicians can use BMI to prescribe a range of target weights. The BMI range of 18.5–24.9 is often viewed as the range of ideal or healthy body weights [although more recent data, such as provided by Flegal et al. (12), have suggested that somewhat higher BMIs are associated with lower mortality], whereas the BMI ranges for overweight status (25.0–29.9), class 1 obesity (30–34.9; low risk), class 2 obesity (35.0–39.9; moderate risk), and class 3 obesity (≥40.0; high risk) are used to delineate the risk of obesity-related comorbidities. Thus, although BMI is harder to calculate, and clinicians often use apps to calculate them, this disadvantage is usually outweighed by the facts that a range of target weights can be prescribed and that the ranges are more accurately associated with health outcomes.

These issues lead to the important question of whether IBW equations and BMI are truly irreconcilable or whether there is a way to combine the 2 different approaches of defining target body weights. For the first time, to our knowledge, we unify the concepts of an IBW equation and BMI to define target body weights. We show that a single linear equation can estimate both IBW and target body weight for any BMI and height. In the process, we show that the advantages of IBW equations and BMI can be combined into a single easy-to-use equation.

METHODS

Mathematical derivation

Although the concept of BMI predicts that adult body weight scales as a curvilinear function of height (i.e., Wt ∝ Ht²), this relation can be estimated with a linear equation within the 95% height range for the US population (∼60–75 in or ∼1.5–1.9 m) (13). However, unlike previous approaches to developing IBW equations, we rigorously proved that a linear function is valid with the use of calculus. In the process, we exploited key steps in the derivation to produce a novel body weight equation that is both more accurate than past IBW equations and is generalizable to any BMI and height.

We first rearranged the equation for body weight as a function of height into the form

Then, we rearranged Equation 6 and expanded it about a reference height Ht₀ as follows

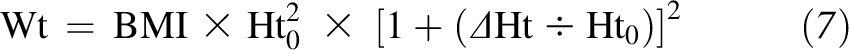where

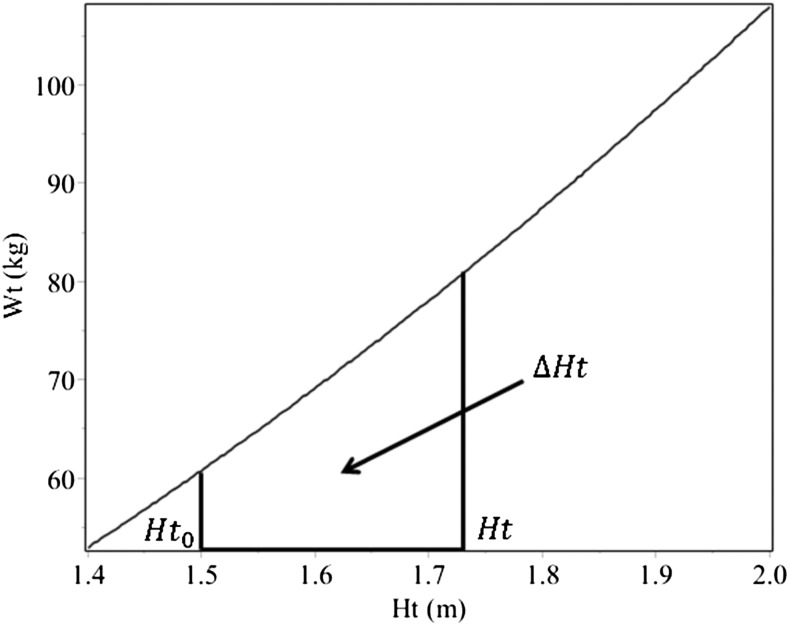
and Ht is the individual’s height (Figure 1). With the use of the calculus technique of Taylor expansion and keeping only the terms linear in ΔHt, we obtained the linear approximation

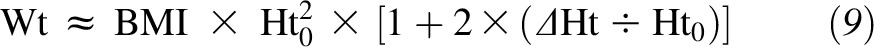This approximation is justified only if the percent error is small. With the curve nearly linear over the 95% height range, the percent error was indeed small (Figure 1). Here, the percent error was determined by the neglected term in the Taylor series expansion

This error can be calculated directly. For example, if the reference height is in the middle of the 95% height range, the maximum percent error is 1.0%.

FIGURE 1.

Wt scales almost linearly with Ht. Although Wt scales as Ht², Wt is a nearly linear function of Ht across the 95% Ht range (∼1.5–1.9 m). The example is for a BMI of 27 kg/m² and shows the reference Ht (Ht₀) of 1.5 m and ΔHt, which is the difference between an individual’s Ht and the reference Ht₀. Ht, height; Wt, weight.

For consistency with past IBW equations, we selected the reference height Ht₀ to be 5 ft (60.0 in or 1.52 m) in the US system and 1.5 m (59.1 in) in the metric system. However, this selection of Ht₀ at the lower end of the 95% height range raised the error. Therefore, we approximated the quadratic term shown in Equation 10 by a compensatory linear term that matched body weight at the upper end of the 95% height range (75 in or 1.9 m). After strategic rounding, our final equation was close to the exact tangent and secant lines but provides a better body weight estimate than either of the lines.

There were 2 key steps in our derivation that made our approach superior to past IBW equations. First, by finding an expression for the slope variable a in Equation 1 in terms of BMI, our equation aligns directly with BMI values. This alignment gives the advantage that our equation can be used to calculate body weight at any target BMI value, which, to our knowledge, has never been done before for an IBW equation. Second, by choosing an appropriate compensatory linear term (as previously described), our IBW equation is both more accurate and easy to remember.

Comparative analysis

We calculated the accuracy of our derived IBW equation through both theoretical and empirical means. The theoretical accuracy was calculated as the absolute error and percent error between the exact and predicted body weights over the 95% height range (60–75 in or 1.5–1.9 m) at BMI values of 20 and 35. The empirical accuracy (both the absolute error and the percent error) was calculated by applying our equation to anthropometric data collected from adults as part of the 1999–2006 NHANES. We also compared how well our body weight equation and other IBW equations align with BMI values. Alignment with BMI values is one method for evaluating the goodness of fit of IBW equations. To determine the alignment, we used the software program Mathematica (version 10.0; Wolfram Research) to calculate the finite integral of the percent error of each IBW equation using body weight predicted by BMI as the true weight. The finite integrals were evaluated over the 95% height range and divided by the difference between the upper and lower bounds of the 95% height range to arrive at a mean accuracy. This process was repeated for each BMI value between 17.0 and 27.0 in increments of 0.1, and the lowest value of the mean percent error over this BMI range was taken as the true percent error for each IBW equation. This method of finding the lowest percent error correctly accounted for the fact that some IBW equations align with higher BMIs, whereas other equations align better with lower BMIs and, thus, avoided unfairly penalizing certain equations on this basis.

RESULTS

Equation in US system

We started by deriving the equation for the US system. After deriving the equation as outlined in Methods, we converted weight to pounds and height to inches and expanded around the reference height of 5 ft (60 in) to get

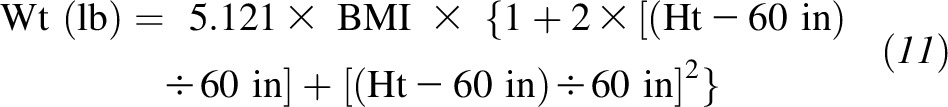Next, we rounded 5.121 to 5 and neglected the second-order term shown in Equation 10. Because neglecting this term slightly underestimated body weight at the upper end of the 95% height range (2.4% error), we found a linear approximation to replace the second-order term. After following the procedure stated in Methods, we found that the correction term for Equation 10 needed to produce the correct weight at the upper end of the 95% height range was

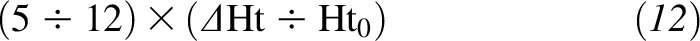After this result was substituted back into the equation, we obtained

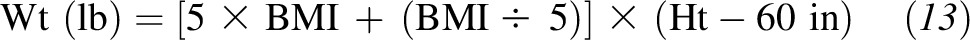Clinical applications

This easy-to-remember formula provides a highly accurate prediction of body weight at any target BMI and height. To determine body weight in pounds, the desired BMI is multiplied by 5 and then add BMI/5 lb for each inch >5 ft in height. For instance, for a BMI of 20, start with 100 lb for a height of 5 ft and add 4 lb for each additional inch of height. For a BMI of 25, start with 125 lb and add 5 lb for each inch of height. Thus, by expressing the slope in terms of BMI, we have developed an equation that is valid for predicting body weight at any given BMI, which makes it a single universal equation.

In the specific case of estimating IBW, one selects an ideal BMI to use in the equation; this selection unifies the concepts of BMI and IBW equations. For example, if one assumes that a BMI of 20 corresponds to IBW, our equation predicts that the IBW would be

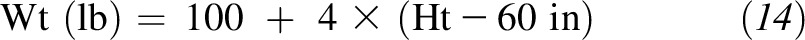Alternatively, BMI values in the range from 18.5 to 25.0 can be taken to represent a range of IBWs. In this case, our equation would give the lower bound (18.5) on IBW as

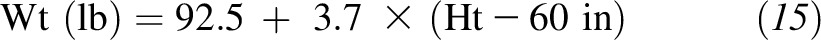and the upper bound (25) as

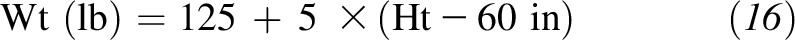Similarly, the other BMI ranges can also be defined by our equation. Table 1 shows the calculations with the use of our equation at the key BMI values of 20, 25, 30, 35, 40, 45, and 50. Each increase in BMI of 5 adds 25 lb to body weight at 5 ft tall and an additional 1 lb for each 1-in increase in height; this calculation provides a convenient way to remember the equation because most key BMI values are multiples of 5.

TABLE 1.

Body weight equation at key BMI values

BMI, kg/m2	US version	Metric version
	Wt (lb) = 5 × BMI + (BMI ÷ 5) × (Ht − 60 in)	Wt (kg) = 2.2 × BMI + 3.5 × BMI × (Ht − 1.5 m)
20	Wt (lb) = 100 + 4 × (Ht − 60 in)	Wt (kg) = 44 + 70 × (Ht − 1.5 m)
25	Wt (lb) = 125 + 5 × (Ht − 60 in)	Wt (kg) = 55 + 88 × (Ht − 1.5 m)
30	Wt (lb) = 150 + 6 × (Ht − 60 in)	Wt (kg) = 66 + 105 × (Ht − 1.5 m)
35	Wt (lb) = 175 + 7 × (Ht − 60 in)	Wt (kg) = 77 + 123 × (Ht − 1.5 m)
40	Wt (lb) = 200 + 8 × (Ht − 60 in)	Wt (kg) = 88 + 140 × (Ht − 1.5 m)
45	Wt (lb) = 225 + 9 × (Ht − 60 in)	Wt (kg) = 99 + 158 × (Ht − 1.5 m)
50	Wt (lb) = 250 + 10 × (Ht − 60 in)	Wt (kg) = 110 + 175 × (Ht − 1.5 m)

Another useful feature of the equation is that each increase of 1 point in an individual’s BMI adds

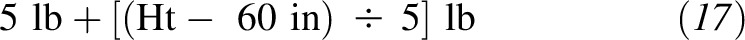of body weight. For example, each 1-point increase in BMI adds 6 lb of body weight to a person whose height is 5 ft 5 in, 7 lb to someone whose height is 5 ft 10 in, and 8 lb to someone whose height is 6 ft 3 in. The knowledge that losing the same consistent number of pounds approximately lowers a person’s BMI by 1 point can be a helpful and motivating target for individuals who are trying to lose weight. Conversely, with the inversion of this relation, a person’s BMI can be estimated by dividing their body weight (in lb) by 6 lb if the individual’s height is 5 ft 5 in, by 7 lb if the individual’s height is 5 ft 10 in, and by 8 lb if the individual’s height is 6 ft 3 in. This method allows a person to quickly estimate BMI.

A practical example that illustrates how this equation can used can be seen in its application to a patient who has a body weight of 225 lb and a height of 5 ft 10 in (or 70 in). If a clinician wants to know if the patient is obese and how much weight the patient would need to lose to reach the upper end of the IBW range, a quick calculation shows that the patient’s weight at the obesity BMI of 30 is

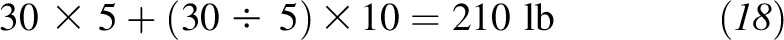whereas at the upper end of the healthy BMI range (<25), the patient would have a weight of

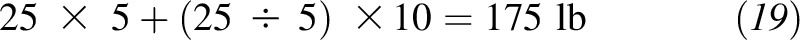Thus, we would classify the patient as obese, and she or he would need to lose 50 lb to be considered within the normal or healthy weight range. Of course, for many patients, a 5–10% weight-loss goal may be a more realistic target, and our equation can take such personalized goals into account because it can estimate body weight for any desired BMI goal. For example, if having a BMI of 28.0 is the patient’s desired goal, the patient’s target weight would be

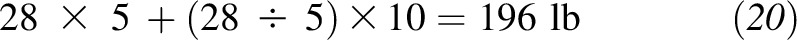Equation in metric system

For the metric system, we followed the same mathematical procedure as that used for the US system. The equation is

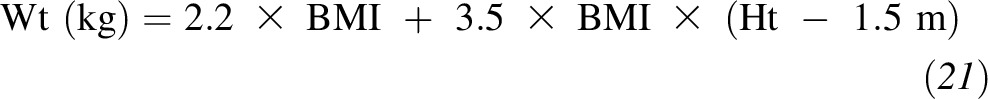where we rounded all terms to one decimal place. For reference, if we took the US version of the equation and directly converted it into metric units, we would have obtained 3.6 instead of 3.5. However, the value of 3.5 yields a lower aggregate percent error over the 95% height range and, thus, is preferred.

Accuracy

Our equation is highly accurate. In Table 2, we illustrate the theoretical accuracy of our equation for BMIs of 20 and 35. Except at heights ≤61 in (≤1.53 m), the equation predicts the correct weight to the nearest 1 lb (0.5 kg) for a BMI of 20 and to the nearest 2 lb (1 kg) for a BMI of 35. The accuracy of our equation as measured by the percent error is independent of BMI; thus, higher BMIs do not result in greater percent errors. The maximum percent error across the 95% height range is 2.4% for both versions of the equation, and the equation is most accurate in the middle of the height range, which is a consequence of the fact that it was designed to minimize the percent error. Finally, when applied to NHANES data, our equation produced mean empirical accuracies of 0.7% (95% CI: 0%, 3.2%) and 0.5% (95% CI: 0.3%, 2.4%) for the US and metric versions, respectively; this corresponded to mean absolute errors of 1.1 lb and 0.4 kg, respectively. The error was driven mostly by individuals at the short and tall ends of the height spectrum, and the effects of covariates such as age were mediated only indirectly through their effect on height.

TABLE 2.

Accuracy of body weight equation¹

	US system				Metric system
BMI	Height, in	Weight, lb	Predicted weight, lb	Absolute error, lb	Height, m	Weight, kg	Predicted weight, kg	Absolute error, kg
20 kg/m2
	60	102	100	−2	1.50	45.0	44.0	−1.0
	61	106	104	−2	1.53	46.8	46.1	−0.7
	62	109	108	−1	1.56	48.7	48.2	−0.5
	63	113	112	−1	1.59	50.6	50.3	−0.3
	64	117	116	−1	1.62	52.5	52.4	−0.1
	65	120	120	0	1.65	54.5	54.5	0.0
	66	124	124	0	1.68	56.4	56.6	0.2
	67	128	128	0	1.71	58.5	58.7	0.2
	68	132	132	0	1.74	60.6	60.8	0.2
	69	135	136	1	177	62.7	62.9	0.2
	70	139	140	1	1.80	64.8	65.0	0.2
	71	143	144	1	1.83	67.0	67.1	0.1
	72	147	148	1	1.86	69.2	69.2	0.0
	73	152	152	0	1.89	71.4	71.3	−0.1
	74	156	156	0	1.92	73.7	73.4	−0.3
	75	160	160	0	—	—	—	—
35 kg/m2
	60	179	175	−4	1.50	78.8	77.0	−1.8
	61	185	182	−3	1.53	81.9	80.7	−1.3
	62	191	189	−2	1.56	85.2	84.4	−0.8
	63	198	196	−2	1.59	88.5	88.0	−0.5
	64	204	203	−1	1.62	91.9	91.7	−0.2
	65	210	210	0	1.65	95.3	95.4	0.1
	66	217	217	0	1.68	98.8	99.1	0.3
	67	224	224	0	1.71	102.3	102.7	0.4
	68	230	231	1	1.74	106.0	106.4	0.4
	69	237	238	1	177	109.7	110.1	0.4
	70	244	245	1	1.80	113.4	113.8	0.3
	71	251	252	1	1.83	117.2	117.4	0.2
	72	258	259	1	1.86	121.1	121.1	0.0
	73	265	266	1	1.89	125.0	124.8	−0.2
	74	273	273	0	1.92	129.0	128.5	−0.6
	75	280	280	0	—	—	—	—

¹Body weights that were predicted by our equation were nearly identical to actual body weights at different heights for BMIs of 20 and 35 kg/m².

Comparison with other IBW equations

Finally, we compared our body weight equation with other IBW equations (Table 3) on the virtue of their alignment with BMI values. As shown in Table 4, the other IBW equations were all best aligned with BMIs in the range from 21.0 to 24.3. For comparison, our equation could be set to align with any BMI value. When we compared each equation to its best-fit BMI, the US version of our equation outperformed IBW equations that estimated body weight in pounds with a 0.5% error for our equation, compared with 3.9% and 2.6% errors for the equations of Hamwi (3) for men and women, respectively. In the metric system, our equation was approximately comparable to the equation of Robinson et al. (5) for men (0.5% error compared with 0.4% error, respectively) but very slightly outperformed the equation of Robinson et al. (5) for women (0.5% error compared with 0.7% error, respectively). All other metric-based IBW equations were not nearly as accurate and had BMI alignment errors ≥2.1%.

TABLE 3.

IBW equations¹

Source and version	Equation
Peterson et al. (current article)
US	Wt (lb) = 5 × BMI + (BMI ÷ 5) × (Ht − 60 in)
Metric	Wt (kg) = 2.2 × BMI + 3.5 × BMI × (Ht − 1.5 m)
Robinson et al., 1983 (5)
Men	Wt (kg) = 52 + 1.9 × (Ht − 60 in)
Women	Wt (kg) = 49 + 1.7 × (Ht − 60 in)
Devine, 1974 (4)
Men	Wt (kg) = 50.0 + 2.3 × (Ht − 60 in)
Women	Wt (kg) = 45.5 + 2.3 × (Ht − 60 in)
Broca, 1871/H-index (1)
Metric	Wt (kg) = Ht − 100 cm
Hamwi, 1964 (3)
Men	Wt (lb) = 106 + 6 × (Ht − 60 in)
Women	Wt (lb) = 100 + 5 × (Ht − 60 in)
Miller et al., 1983 (6)
Men	Wt (kg) = 56.2 + 1.41 × (Ht − 60 in)
Women	Wt (kg) = 53.1 + 1.36 × (Ht − 60 in)
Hammond, 2000 (7)
Men	Wt (kg) = 48 + 1.1 × (Ht − 150 cm)
Women	Wt (kg) = 45 + 0.9 × (Ht − 150 cm)

¹IBW, ideal body weight.

TABLE 4.

Alignment of IBW equations with BMI¹

IBW equation and source	BMI, kg/m2	Error, %
Peterson et al. (current article)
US	All	0.5
Metric	All	0.5
Robinson et al., 1983 (5)
Men	22.5	0.4
Women	21.0	0.7
Devine, 1974 (4)
Men	22.8	2.1
Women	21.3	3.1
Broca, 1871/H-index (1)
Metric	24.3	2.7
Hamwi, 1964 (3)
Men	23.4	3.9
Women	21.2	2.6
Miller et al., 1983 (6)
Men	22.9	3.3
Women	21.7	3.2
Hammond, 2000 (7)
Men	24.3	4.1
Women	21.8	2.7

¹Shown are the alignment of each IBW equation with its best-fit BMI and each equation’s corresponding percentage of error over the 95% height range. IBW, ideal body weight.

DISCUSSION

In this article, we improved on the concept of an IBW equation by increasing its rigor and making it broader in scope. With the use of simple calculus and approximations, we merged the concepts of 1) IBW equations and 2) the use of BMI to define ideal and target body weight ranges. The result is a single universal equation that describes body weight at any BMI value and height in both the US and metric systems. To our knowledge, this is the first time that such an equation has been developed.

Before our work, it was assumed that the concepts of IBW equations and BMI were incompatible. IBW equations predict a single IBW as a linear function of height. By contrast, BMIs are used to prescribe a range of target body weights as quadratic functions of height. We reconciled the 2 contrasting approaches with the use of calculus to linearize the equation that defines BMI. Because we kept the slope a of the linearized equation in terms of BMI (i.e., by leaving the slope as a variable rather than as a constant number), we were able to develop an equation that predicts body weight at any BMI rather than at a single BMI.

Although several IBW equations have been developed over the past few decades, our body weight equation has important advantages. First, as previously articulated, our equation predicts body weight at any BMI value. Therefore, it can be used to prescribe a range of target body weights just like BMI values themselves. Furthermore, if the ideal BMI range is revised upward (or downward) or tailored to a particular demographic or cause-specific outcome, our equation is still valid because it can be used by applying the revised BMI ranges. Similarly, our equation can be adapted to any individual’s weight-loss goal including more realistic BMI targets for the morbidly obese. This special feature makes our equation relevant across a wide range of scenarios and applications.

Second, our equation is highly accurate and avoids the problem of being misaligned with BMI values, which is a problem that plagues other IBW equations. Shah et al. (2) conducted a comparative analysis of IBW equations and concluded that none of the IBW equations were aligned with a single BMI but, rather, spanned from ∼18.5 to ≥25.0. Shah et al. (2) showed that almost all IBW equations underestimated weights at short heights and overestimated weights at taller heights. To arrive at their conclusions, Shah et al. (2) compared the IBW equations with a BMI of 22.0, which is a number that has often been favored by mortality data (14, 15). In the current article, we took a more sophisticated approach to measuring the alignment of IBW equations with BMI. We used calculus to calculate the integrated percent error (an integrated measurement of alignment with BMI values) over the 95% height range and further found the BMI value that minimized the percent error for each IBW equation. Through this method, we compared each equation to the unique BMI that it best fit. As shown in Table 3, with the exception of the IBW equations of Robinson et al. (5), all IBW equations produced misalignment errors ≥2.1%. Both our equation and the equations of Robinson et al. (5) produced the best alignments with BMI values (0.4–0.7% error). However, the equations of Robinson et al. (5) aligned with different BMI values for men and women (22.5 for men compared with 21.0 for women), whereas our equation aligns with the same BMI (chosen by the user) for both sexes. A final attractive feature was that the percent error for our equation was both independent of BMI and was very small, averaging 0.5–0.7% for the US population, as estimated with the use of NHANES data.

Because our body weight equation merges the concepts of IBW equations and BMI, it does share the same limitations as BMI. BMI misclassifies a significant fraction of the population on the basis of adiposity including those with sarcopenic obesity and individuals who are very muscular. Indeed, BMI is best viewed as a first-level anthropometric screen for adiposity. Because our equation is aligned so closely with BMI values over the 95% height range (0.5% error), it suffers from the same limitations in the prediction of body composition. Second, the optimal BMI range may vary by sex, age, ethnicity or race, cause-specific comorbidity or mortality, or other factors.

Despite these drawbacks, body weight and BMI remain the 2 most frequently reported nutrition assessment variables (16). Similarly, IBW equations are still used, albeit less so, to diagnose underweight status and overweight status, to calculate nutrient intakes, and for drug dosing. For drug dosing in particular, IBW is used as a surrogate for lean body mass (5). A common alternative dosing approach is to use IBW plus a multiplier of the difference between total weight and IBW to produce an effective body weight that is intermediate between IBW and actual body weight (17). Our equation may be able to replace this approach to drug dosing because our equation can be used with BMI chosen at an intermediate value between an individual’s ideal and actual BMI, and the chosen value could be tailored to each drug’s lipophobic properties. Therefore, in addition to providing quick estimates of body weight for nutritional and body composition assessments, our equation may have a future use for simplifying drug-dosing calculations.

In conclusion, our universal body weight equation is superior to previous IBW equations because it predicts both IBW and body weight for any BMI and height with a high degree of accuracy. Our equation can be set to align with any BMI value, which makes the equation versatile and relevant across a range of scenarios. Moreover, our equation is sex independent, and the coefficients in the US system are multiples or divisors of 5, thereby making it easy to remember and easy to calculate with the use of mental math or a calculator and without the use of an app. Therefore, our equation should be appealing to health practitioners and the general public.