Overflow metabolism in E. coli results from efficient proteome allocation

Abstract

Overflow metabolism refers to the seemingly wasteful strategy in which cells use fermentation instead of the more efficient respiration to generate energy, despite the availability of oxygen. Known as Warburg effect in the context of cancer growth, this phenomenon occurs ubiquitously for fast growing cells, including bacteria, fungi, and mammalian cells, but its origin has remained mysterious despite decades of research. Here we study metabolic overflow in E. coli and show that it is a global physiological response used to cope with changing proteomic demands of energy biogenesis and biomass synthesis under different growth conditions. A simple model of proteomic resource allocation can quantitatively account for all of the observed behaviors and accurately predict responses to novel perturbations. The key hypothesis of the model, that the proteome cost of energy biogenesis by respiration exceeds that by fermentation, is quantitatively confirmed by direct measurement of protein abundances via quantitative mass spectrometry.

Under anaerobic conditions, organisms ranging from bacteria to mammalian cells excrete large quantities of fermentation products such as acetate or lactate. Strikingly, the excretion of these fermentation products occurs widely even in the presence of oxygen in fast-growing bacteria and fungi^1-4, as well as mammalian cells including stem cells, immune cells, and cancerous cells^5-7. This seemingly wasteful phenomenon, in which fermentation is used instead of the higher ATP-yielding respiration process for energy generation, is generally referred to as “overflow metabolism” (or the Warburg effect in the case of cancer^5-7). Various rationalizations of overflow metabolism as well as regulatory schemes have been proposed over the years^2,5,8-20. However, quantitative tests of the proposed hypotheses as well as systematic characterization of overflow metabolism are generally lacking.

In this study, we provide a quantitative, physiological study of overflow metabolism for the bacterium E. coli. We report an intriguing set of linear relations between the rates of acetate excretion and steady state growth rates for E. coli in different nutrient environments and different degrees of induced stresses. These relations, together with the recently established concept of proteome partition²¹, led us to a simple theory of resource allocation, which can quantitatively account for all of the observed behaviors, as well as accurately predict responses to novel perturbations. Key parameters of the theory regarding the proteome costs of energy biogenesis by respiration and by fermentation were determined by quantitative mass spectrometry following a coarse-graining approach. These results suggest that overflow metabolism is a programmed global response used by cells to balance the conflicting proteomic demands of energy biogenesis and biomass synthesis for rapid growth.

Threshold-linear response of acetate overflow

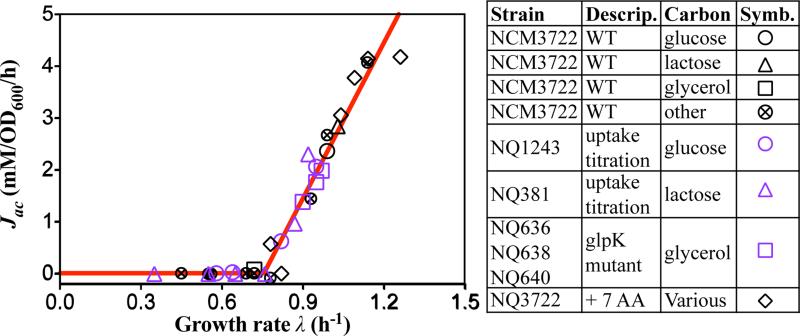
Previous studies have established a strong positive correlation between the rate of acetate excretion and the dilution rate for various strains of E. coli grown in glucose-limited continuous culture^16,22-24 (Extended Data Fig. 1a-e). Here, we measured acetate excretion and growth rates of a wild-type E. coli K-12 strain grown in minimal medium batch culture with a variety of glycolytic substrates as the sole carbon sources (black symbols in Fig. 1). Strikingly, the rate of acetate excretion per biomass, J_ac, exhibits a simple, threshold-linear dependence on growth rate λ,

$$J_{ac}=\{\begin{array}{cc}{S}_{ac}\cdot (\lambda -{\lambda }_{ac})\hfill & \text{for}\lambda \ge {\lambda }_{ac}\hfill \\ 0\hfill & \text{for}\lambda <{\lambda }_{ac}\hfill \end{array}\phantom{\}}$$ [1]

with a linear dependence above a characteristic growth rate (λ_ac ≈ 0.76 h⁻¹, or 55 min per doubling), below which acetate excretion disappears. We refer to this linear relation as the “acetate line” (red line in Fig. 1).

Fig. 1. Acetate excretion under carbon limitation.

Acetate excretion rate (J_ac) is linearly correlated with the growth rate (λ) for WT cells grown in minimal medium with various glycolytic carbon sources (black symbols), and for cells with titratable or mutant uptake systems (purple symbols) (Extended Data Table 1). Black diamonds indicate various carbon sources supplemented with 7 non-degradable amino acids. The red line shows the best-fit of all the data to Eq. [1].

For strains with titratable carbon uptake systems (Extended Data Table 1), the same linear dependence is seen for acetate excretion (purple circles and triangles in Fig. 1). These results suggest that acetate overflow is an innate response that depends on the degree of carbon influx and not specifically on the nature of carbon sources. A vivid demonstration of this effect is seen by the behavior of cells grown on glycerol: Wild type E. coli cells grow in glycerol minimal medium at a rate that is below λ_ac, and do not excrete acetate (black square in Fig. 1) in accordance with Eq. [1]. Three isogenic strains expressing different mutant forms of Glycerol Kinase²⁵ grew at rates faster than λ_ac and excreted acetate with rates dictated by their respective growth rates according to Eq. [1] (purple squares in Fig. 1). Instead of changing the carbon influx, reducing the metabolic demand of cells for carbon by supplementing minimal medium with non-degradable amino acids resulted in significantly enhanced growth rates and concomitantly increased acetate excretion as described by Eq. [1] (black diamonds in Fig. 1).

Coarse-grained model of proteome allocation

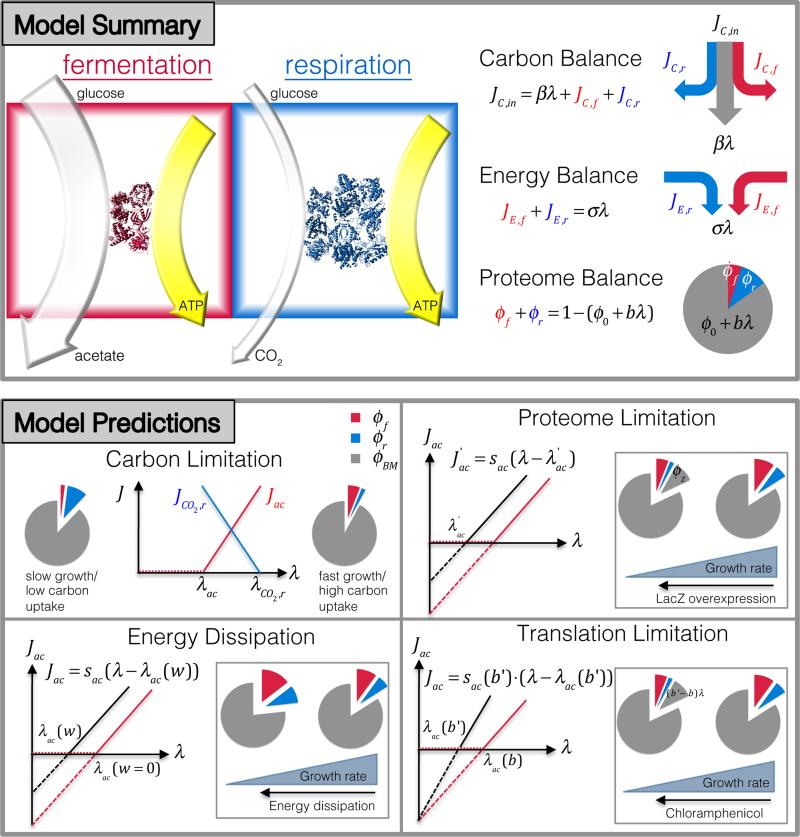
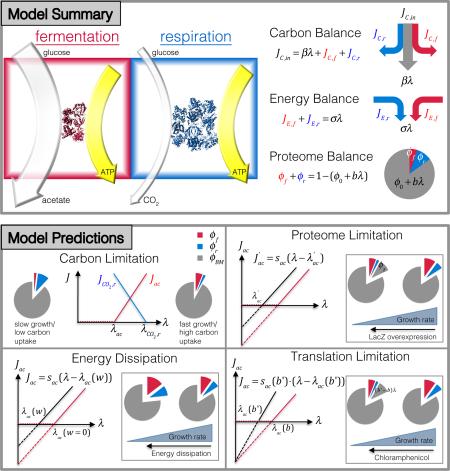
Linear growth rate dependences arose in previous physiological studies^21,26-28 due to the limited capacity of ribosomes to synthesize proteins and the obligatory need for increased ribosomal proteins at faster growth^21,29. Here, we address the problem of acetate excretion with a phenomenological resource allocation model, balancing the demand of the proteome for biomass synthesis with the demand for energy biogenesis.

We focus on acetate excretion for growth on glycolytic substrates (Fig. 1); other substrates metabolized by alternative pathways exhibit similar trends although with quantitative differences (Extended Data Fig. 1f), likely arising from the same underlying principles as those described here. In our model (detailed in Supplementary Note 1 A), acetate excretion is considered as a measure of the carbon flux directed towards energy biogenesis by (oxidative) fermentation, catalyzed by glycolytic enzymes and completed by the oxidative phosphorylation system (for the conversion of NADH to ATP in aerobic environment) (Extended Data Fig. 2a). Energy biogenesis by respiration is catalyzed by enzymes of glycolysis and TCA pathways, and the oxidative phosphorylation system (Extended Data Fig. 2b). Both the fermentation and respiratory pathways draw carbon flux away from biomass synthesis, via the carbon fluxes J_c,f and J_c,r, respectively, and in turn produce the energy fluxes J_E,f and J_E,r (Box 1). Let the abundance of the enzymes used for fermentation and respiration be given by the fraction ϕ_f and ϕ_f, respectively, of the total protein content of the cell. All other metabolic activities, including catabolism, anabolism, ribosome synthesis (referred to as “biomass synthesis”), are provided by the remaining part of the proteome. Previous studies have established the growth-rate dependence of the proteome fraction for biomass synthesis^20,21,27,28, denoted here as ϕ_BM (λ). It is coupled to energy biogenesis via the constraint

$${\varphi }_f+{\varphi }_r+{\varphi }_{BM}\left(\lambda \right)=1.$$ [2]

The total energy flux generated must satisfy the energy demand for cell growth (denoted by J_E(λ)), i.e.,

$$J_{E,f}+J_{E,r}=J_E\left(\lambda \right).$$ [3]

At the same time, not too much carbon should be diverted from the total influx J_C, in order to meet the demand for biomass synthesis (flux denoted by J_C,BM(λ)), i.e.,

$$J_{C,in}\left(\lambda \right)=J_{C,f}+J_{C,r}+J_{C,BM}\left(\lambda \right).$$ [4]

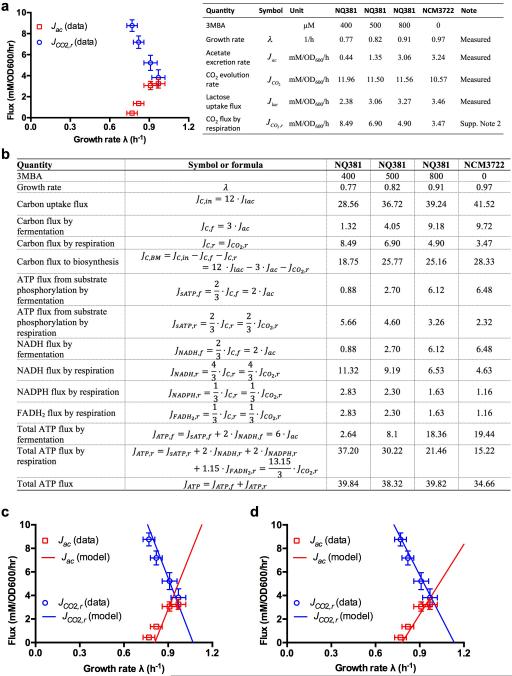
To a large extent, this allocation depends on the efficiencies of the energy biogenesis pathways. There are two very different efficiencies: It is well known that respiration has a much lower carbon cost – the energy flux generated per carbon is larger for respiration than fermentation³⁰, although this advantage of respiration is limited in the presence of oxygen (Extended Data Fig. 2). On the other hand, if respiration has a higher proteome cost, i.e., if the energy flux generated per proteome fraction devoted to the respective pathway, ε_f = J_E,f/ϕ_f, ε_r = J_E,r/ϕ_r, is lower for respiration than fermentation, ε_f > ε_r, as has been suggested previously^14,19,20, then a scenario emerges that may qualitatively explain the observed disappearance of acetate flux at slow growth rates: As illustrated in Box 1, when carbon uptake rate (J_c,in) is high and the cell has the potential to grow rapidly, it is advantageous, i.e., growth rate can be maximized, to generate energy by the more proteome-efficient fermentation pathway, so that more of the proteome can be directed towards biosynthesis as required for rapid growth. Conversely, when carbon uptake is low (small J_c,in), it is advantageous to generate energy by the more carbon-efficient respiration pathway, so that more carbon flux can be directed to biosynthesis and sustain growth. This proteome allocation model predicts the carbon flux for respiration to change in the opposite way from that found for fermentation. Just as the fermentation flux can be read off from acetate excretion, the respiration flux can be deduced by measuring the rate of CO₂ evolution in a bioreactor (Supplementary Note 2). Indeed, this respiration flux exhibits a linear increase with decreasing growth rate as acetate excretion diminishes (Extended Data Fig. 3a).

Testing the model by growth perturbations

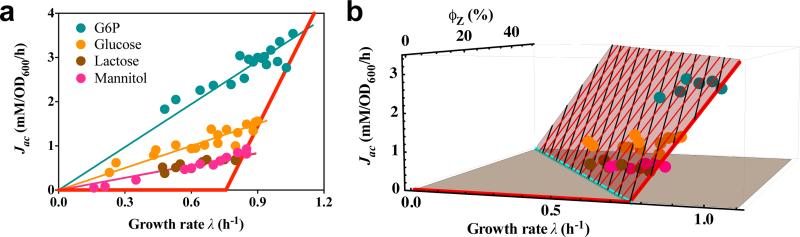
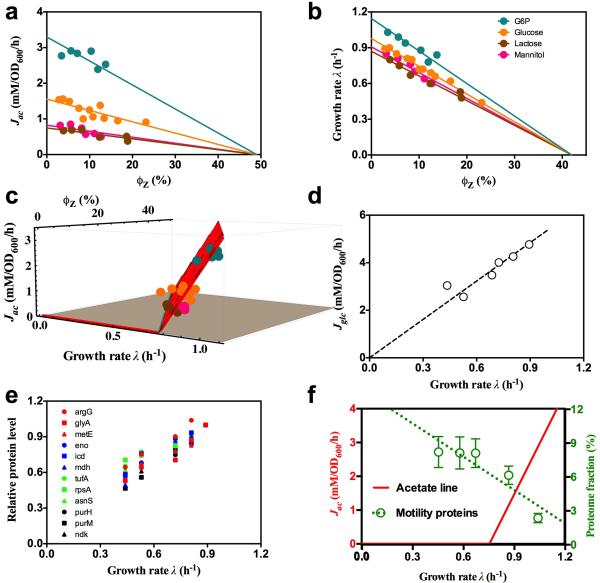
If acetate excretion is the result of the coordination of energy demand with carbon influx given constrained proteomic resources as assumed in the model, then the overexpression of useless proteins, which reduces the proteome fractions available for energy production and biomass synthesis²¹, should yield higher acetate excretion rates. In fact, previous studies reported acetate excretion at slow growth rates with protein overexpression³¹. To systematically test this hypothesis, we expressed large amounts of LacZ by growing strain NQ1389 (Extended Data Table 1) on a number of glycolytic carbon sources. Plotting acetate excretion against growth rate for varying degrees of LacZ overexpression leads to a simple proportionality relation between growth rate and acetate excretion rate for each carbon source tested (Fig. 2a). Moreover, plotting acetate excretion against the corresponding degree of LacZ expression (fraction ϕ_Z of total cellular proteins), we find a similar linear decrease in acetate excretion rate (Extended Data Fig. 4). Finally, in a 3D plot of acetate excretion rates, LacZ abundance and growth rates (Fig. 2b), the different data points are found to lie on a single plane anchored by the acetate line (red) (see also Extended Data Fig. 4c). On this plane, acetate excretion increases linearly with LacZ overexpression at each fixed growth rate (black lines). However, for each fixed level of LacZ abundance, the plane produces a parallel shift of the standard acetate line (thin red lines). These lines are still described by Eq. [1], with an identical slope, but with a reduction of the threshold growth rate, λ_ac, linear with increasing LacZ abundance (cyan line), i.e.

$$\lambda \left({\varphi }_Z\right)={\lambda }_{ac}\cdot (1-{\varphi }_Z∕{\varphi }_{max}),$$ [5]

where ϕ_max ≈ 47% is the extrapolated limit of useless protein expression at which growth rate vanishes (alternatively determined from individual lines in Extended Data Fig. 4), in agreement with previous work^21,27,28. More quantitatively, this result is displayed in Fig. 3a, where interpolated acetate excretion rates for constant LacZ levels are presented.

Fig. 2. Effect of protein overexpression on acetate excretion.

a, Measured acetate excretion rate is plotted against growth rate for increasing degrees of the (useless) expression of LacZ in strain NQ1389, for several carbon sources indicated by circles of different colors. Thick red line is the acetate line of WT cells shown already in Fig. 1, and the thin lines are model predictions (Eq. [S26]), one for each carbon source of respective color. b, 3D plot of the data in panel a. The data lie largely on a plane spanned by the acetate line (thick red line) defined in Fig. 1, and the cyan line, λ_ac(ϕ_z), which defines a linear shift in the threshold growth rate, λ_ac, for different degrees of LacZ expression, as predicted by the model (Eq. [5]).

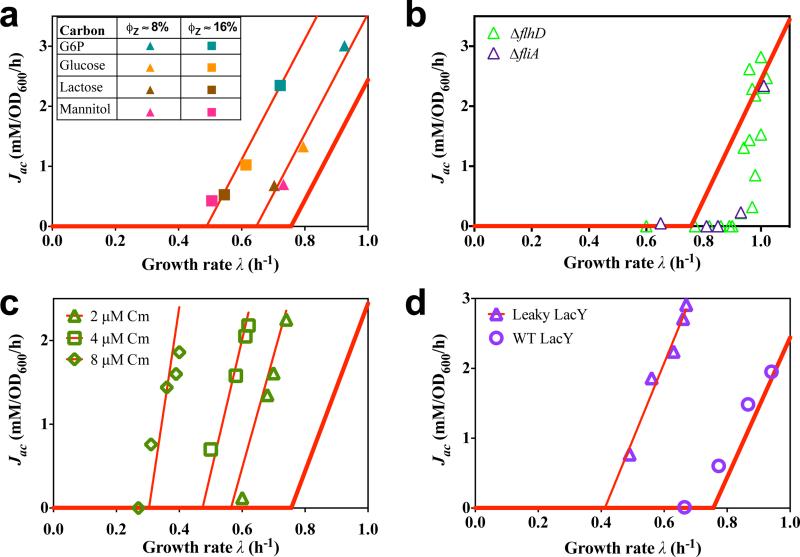
Fig. 3. Effect of genetic and environmental perturbations on the acetate line: model and experiments.

In all subplots, the thick red line represents the acetate line of WT cells (Fig. 1). a, For each fixed level of LacZ expression, growth of the overexpression strain NQ1389 on different carbon sources leads to parallel shifts of the acetate line, as demonstrated by the thin red lines, whose slopes are fixed to that of the WT acetate line and were fitted by only adjusting the threshold growth rates λ_ac. b, Acetate excretion rate with glucose uptake titration (Pu-ptsG, Extended Data Table 1) for a ΔflhD strain (NQ1388) and a ΔfliA strain (NQ1539), both incapable of expressing motility proteins, regarded as “useless” in well-stirred culture. Because the motility proteins are only expressed significantly as growth rate decreases under carbon limitation (Extended Data Fig. 4f), acetate excretion deviates from the acetate line as growth rate decreases. The shift of the threshold growth rate λ_ac in the two strains is quantitatively consistent with the model prediction (Eq. [5]), based on quantification of motility proteins (Extended Data Fig. 4f and Extended Data Table 3). c, For each fixed (sub-lethal) dose of chloramphenicol in the medium, acetate excretion rates were determined for different degrees of lactose uptake by the titratable LacY strain (NQ381, Extended Data Table 1). The thin red lines are model fits with the slope as the only fitting parameter. d, For the energy dissipating mutant (NQ1313) expressing the proton-leaking LacY^A177V, acetate excretion rates (triangles) obtained from titrating the glucose uptake system (Extended Data Table 1) show a parallel shift of the acetate line (thin red line), obtained by fitting the data by adjusting only the threshold growth rate in accordance with model prediction (Eq. [S32]). For comparison, acetate excretion in cells expressing wildtype LacY from the same plasmid system (NQ1312, circles) adheres much closer to the acetate line of wildtype cells.

The concepts represented by Eqs. [2]-[4] are transformed into a quantitative model (as illustrated in Box 1 and detailed in Supp Note 1A) by implementing a simple set of relations: First, the proteome fraction ϕ_BM responsible for biomass synthesis under carbon-limitation follows a linear growth-rate dependence of, i.e., ϕ_BM(λ) = ϕ₀ + bλ, as established by previous studies^21,27,28. Second, empirical evidence²⁸ indicates linear relations between metabolic fluxes and the abundances of the corresponding proteome sectors, which we capture by the equations J_C,f = κ_fϕ_f, J_C,r = κ_rϕ_r, J_E,f = ∈_fϕ_f and J_E,r = ∈_rϕ_r. Finally, we introduce proportionalities of biomass and energy demand to the growth rate (J_C,BM(λ) = βλ, J_E(λ) = σλ), relations that are demonstrated experimentally (see Supplementary Note 1D2 and 1D4). [Maintenance energy is negligible over the growth-rate range studied³².] The detailed meaning of each parameter introduced here is given in Extended Data Table 2. Most important among them are ∈_f and ∈_r, the proteome efficiencies of energy biogenesis by the fermentation and respiration pathways, respectively.

Eqs. [2]-[4], together with the linear relation between the proteome fractions and fluxes, describe all key features of the experimental data as detailed in Supplementary Note 1B, 1C and illustrated in Box 1 (bottom): The model naturally gives rise to the observed threshold-linear form of acetate excretion Eq. [1], with formulae for the threshold λ_ac and the slope s_ac given by Eqs. [S15] and [S16]; the linear decrease in energy-related CO₂ production upon increasing growth rate (Extended Data Fig. 3a) is captured by Eq. [S17], with the corresponding threshold λ_CO2,r and slope S_CO2,r given by Eqs. [S18] and [S19]. Furthermore, the parallel shifts of the acetate line for a constant level of protein overexpression (Fig. 3 a, and thin red lines in Fig. 2b) are captured by Eq. [S30], while the direct proportionalities between acetate excretion rates and growth rate upon varying the degree of overexpression (thin solid lines in Fig. 2a) are captured by Eq. [S26]. Significantly, the data imposes a set of quantitative constraints on the model parameters, in particular,

$$\frac{{ϵ}_f}{{ϵ}_r}\ge \frac{{\lambda }_{C{O}_2,r}}{{\lambda }_{ac}}\approx 1.5,$$ [6]

predicting that fermentation is at least 50% more efficient for energy biogenesis than respiration in terms of proteome cost (see Eqs. [S20-S22] for a derivation).

To quantitatively test the proteome allocation model, we performed additional sets of experiments designed to perturb individual model parameters. To see whether a decrease in acetate excretion is possible, we examined two independent mutants (ΔflhD and ΔfliA) in which motility proteins, ‘useless’ in well-shaken batch culture, are not expressed. These mutants exhibit reductions in acetate excretion (open symbols in Fig. 3b), in accordance with the prediction of the resource allocation model as more proteome becomes available for energy biogenesis. (The nonlinear dependence of acetate excretion arises in this case due to the growth-rate dependence of motility protein expression in wild-type cells²⁸, as shown in Extended Data Fig. 4f) Translational limitation by sub-lethal doses of the antibiotic chloramphenicol inhibits peptide elongation and makes the cell respond by allocating a larger proteome fraction to ribosomes²¹. In our model, this affects the parameter b in ϕ_BM (λ) and therefore predicts an increased slope of the acetate line with an identical y-intercept (Eq. [S14], solid lines in Fig. 3c), which is in good agreement with the data (open symbols in Fig. 3c). We also investigated the effect of energy dissipation on acetate excretion by expressing a mutant lactose transporter LacY^A177V (“leaky LacY”) known to leak protons across the inner membrane³³ (Extended Data Table 1). An energy leakage flux can be added to the right hand side of Eq. [3] and the model predicts a parallel shift of the acetate line to higher excretion rates (Eq. [S32]). This prediction was tested by titrating glucose uptake in a strain (NQ1313) expressing the leaky LacY mutant. As anticipated, a parallel shift to higher acetate excretion rates was obtained (purple triangles and line in Fig. 3d). Similar increases in acetate excretion were obtained with addition of 2,4-Dinitrophenol (DNP), which uncouples oxidative phosphorylation by carrying protons across the cell membrane (Extended Data Fig. 5). A summary of quantitative comparisons between predictions of the proteome allocation model with experimental findings is presented in Extended Data Table 3, showing that the model quantitatively captures the changes of acetate excretion patterns in response to the applied perturbations.

Proteome cost of fermentation and respiration

The theoretical predictions tested so far do not require the knowledge of the values of proteome cost parameters (e.g., ∈_f, ∈_r). However, these parameters are of central importance for theories based on proteome allocation. We have thus developed a coarse-graining approach to directly characterize the proteome cost for fermentation and respiration. First, the absolute protein abundance of individual proteins was obtained using quantitative mass spectrometry²⁸ together with absolute abundance calibration by ribosome profiling³⁴. Next, for each enzyme involved in glycolysis, TCA and oxidative phosphorylation, its abundance was partitioned among the three pathways, fermentation, respiration, and biomass synthesis, in proportion to the three fluxes through the enzyme. Finally, the fractional enzyme amounts partitioned into a pathway were summed up to obtain the total enzyme abundance devoted to the pathway (Fig. 4a); see Supplementary Note 3 for details. In Fig. 4b, the energy production fluxes of fermentation and respiration (Extended Data Fig. 3b) are plotted against their respective proteome fractions determined in this manner. The linearity of the results validates the linear dependences between J_Ef, J_E,r and ϕ_f, ϕ_r assumed in the model, while slopes of these lines directly yield the proteome efficiency of energy biogenesis for glycolytic carbon sources: ∈_f ≈ 750 mM ATP/OD₆₀₀/h and ∈_r ≈ 390mM ATP/OD_600/h. Indeed, the proteome cost of fermentation (1/∈_f) is approximately two-fold lower than that of respiration (1/∈_r), quantitatively validating the key assumption of this approach. Together with similar procedures used to determine the other model parameters (as described in detail in Supplementary Note 1D), we obtained a self-consistent set of parameters (Extended Data Table 2) that successfully recapitulates all our experimental data (Extended Data Fig. 3cd).

Fig. 4. Partition of proteome fractions into flux components.

a, The total abundance of all proteins devoted to glycolysis, TCA, and oxidative phosphorylation (OXPHOS) (defined in Supplementary Note 3), is represented as a fraction of total protein for various degrees of lactose uptake in strain NQ381. Different colors indicate the portions of these proteins dedicated to the biomass production, fermentation and respiration, estimated using the corresponding fraction of fluxes; see Supplementary Note 3. b, Energy fluxes through the fermentation and respiration pathways are plotted against their respective proteome fractions. The lines are linear regression of the data, with the slopes being the proteome efficiencies (∈_f and ∈_r). The steeper slope (for fermentation) indicates higher ATP production per protein devoted to the pathway (lower protein cost), validating the central assumption of the proteome allocation model

The proteome allocation model is able to predict not only acetate excretion patterns but also the expression of dozens of genes in the glycolysis and TCA pathways under different perturbation, as detailed in Supplemental Notes 1C and Extended Data Figs. 6-7. While both proteome limitation and energy dissipation lead to parallel shifts of the acetate line (Fig. 3 a, 3c respectively), this response arises from an opposite response of the energy sectors ϕ_f, ϕ_r as predicted by the model and verified by mass spectrometry: Under LacZ overexpression, cells decreased the expression of enzymes for both fermentation and respiration (orange lines in Extended Data Figs. 6 and 7, as predicted in Eqs. [S26-27]), while under energy dissipation, cells increased the expression of these enzymes (blue lines in Extended Data Figs. 6 and 7, predicted by Eqs. [S36-37]).

Discussion

The notion that fermentation may be more proteome efficient than respiration was hypothesized previously by Molenaar et al¹⁴, extended to the use of Entner-Doudoroff pathway by Flamholz et al³⁵ and to the genome-scale by O'Brien et al¹⁹. Our study directly verifies this hypothesis (Fig. 4b), and establishes the pivotal role proteome efficiency plays in determining the degree of overflow metabolism in E. coli (Fig. 3). Our findings in response to useless protein expression and energy dissipation are difficult to reconcile, even qualitatively, with alternative hypotheses such as the limitation of respiratory capacity⁸, the need for recycling of cofactors², and constraints of the cytoplasmic membrane¹⁷. Models with cell volume constraints¹² are mathematically similar to protein cost models; however, cell volume varies widely between growth conditions with similar densities³⁶, suggesting that it is not a constraint.

Mechanistically, the re-uptake of acetate by Acetyl-CoA Synthase (Acs), upregulated by CRP-cAMP under carbon limitation²⁷, is important for the decrease of acetate excretion under carbon limitation^15,16. However, the linear growth-rate dependence of carbon overflow demands the tight global coordination of energy biogenesis pathways with biosynthesis, which cannot be accounted for by Acs activity alone and requires the coordinated regulation of glycolytic and TCA enzymes. In particular, acetate excretion sharply increased under energy dissipation while the abundance of Acs proteins increased slightly as well (Extended Data Fig. 6). Moreover, the parallel increase of glycolytic and TCA enzymes, in combination with the increase in acetate excretion under energy dissipation, cannot be rationalized from the known actions of CRP regulation (Extended Data Figs. 6 and 7), suggesting the role of additional regulator(s).

We have established how diverse patterns of acetate excretion can be understood as a part of a global physiological response used by E. coli to cope with changing proteomic demands of energy biogenesis and biomass synthesis under different growth conditions³⁷. Our findings can be used to guide approaches to minimizing overflow metabolism in synthetic biology applications^24,38-41, in ways congruent with the fitness of the organism, e.g., by reducing the expression of ‘useless’ proteins (e.g., Fig. 3b). More broadly, a similar physiological rationale may underlie overflow metabolism in rapidly growing eukaryotes including tumor cells^7,42 where the synthesis of mitochondria for TCA reactions is an additional cost. Indeed, scatter plots of ethanol production and sugar uptake in various strains of S. cerevisae and other yeast species point to the existence of a universal response similar to that shown for E. coli (Fig. 1)¹⁸. The quantitative physiological approach developed in this work can be used as a roadmap for characterizing metabolic efficiency and its biological implications in these systems and others.

Methods

Construction of LacY and LacY^A177V strains (NQ1312, NQ1313)

The Ptet-lacY region of the pZE12 Ptet-lacY plasmid⁴³ was amplified with upstream and downstream primers including the digestion sites XhoI and BamHI respectively using the primers Ptet-F and lacY-R (see the primer table below). The resulting DNA fragment was used to replace the corresponding region of Ptet-gfp in the plasmid pZA31-gfp⁴⁴, yielding the plasmid pZA31 Ptet-lacY. This plasmid was transformed into the titratable PtsG strain NQ1243 to yield NQ1312. The same procedure was employed to generate the lacY^A177V mutant (i.e. C531T), but fusion PCR was used to introduce a point mutation Val177 into the lacY sequence³³. For this, two overlapping parts of the Ptet-lacY region were PCR amplified with the primers ptet-F, lacYfusion-R and lacYfusion-F, lacY-R (see the primer table below), where the point substitution C531T leading to the Val177 mutation from Brooker et al.³ was included in the primers lacYfusion-F and lacYfusion-R. These two overlapping DNA fragments were fused together by PCR using primers ptet-F and lacY-R. The resulting Ptet-lacY fragment that carries the desired mutation was inserted into pZA31, yielding pZA31-lacY^A177V. The resulting plasmids were transformed into the titratable PtsG strain NQ1243 to yield NQ1313.

Construction of the flhD and fliA deletion strains (NQ1388, NQ1539)

The ΔflhD deletion allele in strain JW1881-1 (E. coli Genetic Stock Center, Yale Univ.), in which a Km^r gene is substituted for the flhD gene, was transferred to the titratable PtsG strain NQ1243 after deletion of Km^r by phage P1 vir mediated transduction. Similarly, the ΔfliA allele from strain JW1907 (KEIO collection⁴⁵), in which a Km^r gene is substituted for the fliA gene, was transferred to the titratable PtsG strain NQ1243 after deletion of Km^r by phage P1 vir mediated transduction.

Primers used in this study

The primers used for producing the new genetic constructs employed in this work are summarized here.

• ptet-F (sequence ACACTCGAGTCCCTATCAGTGATAGAGATTG) was used for forward amplification of from the Ptet sequence and including an XhoI digestion site for construction of pZE1 Ptetstab-lacZ, pZA31-lacY, pZA31-lacY^A177V.

• lacY-R (sequence TGTGGATCCTTAAGCGACTTCATTCACCTG) was used for reverse amplification of lacY, lacY^A177V and including a BamHI digestion site for construction of pZA31-lacY, pZA31-lacY^A177V.

• lacYfusion-F (sequence CTCTGGCTGTGTACTCATCCTCGCCGTTTTACTCTTTTTCGCCAAAACGG) was used for forward amplification of a fragment of lacY together with the reverse primer lacY-R. This DNA fragment was later used for fusion PCR to construct pZA31-lacY^A177V.

• lacYfusion-R (sequence CCGTTTTGGCGAAAAAGAGTAAAACGGCGAGGATGAGTACACAGCCAGAG) was used for reverse amplification of a fragment of Ptet-lacY together with the forward primer ptet-F. This DNA fragment later was used for fusion PCR to construct pZA31-lacY^A177V.

Growth of bacterial culture

Growth media

Our growth media were based on the MOPS-buffered minimal medium used by Cayley et al⁴⁶ with slight modifications. The base medium contains 40 mM MOPS and 4 mM tricine (adjusted to pH 7.4 with KOH), 0.1 M NaCl, 10 mM NH₄Cl, 1.32 mM KH₂PO₄, 0.523 mM MgCl₂, 0.276 Na₂SO₄, 0.1 mM FeSO₄, and the trace micronutrients described in Neidhardt et al⁴⁷. For ¹⁵N-labeled media, ¹⁵NH₄Cl was used in place of ¹⁴NH₄Cl. The concentrations of the carbon sources and various supplements used are indicated in the relevant tables.

Growth in batch culture

Batch culture growth has been described in detail previously²⁷.

Growth in the bioreactor

To measure CO₂ production from the bacterial growth, cells were grown in a Multifors bioreactor (Infors HT, Switzerland). 400 ml of medium was used in a 750 ml vessel, which has an inlet for compressed air and out outlet for the exhaust gas. The vessel is otherwise closed except during brief period of sample collection. Samples of the cell culture (for reading OD₆₀₀, assaying lactose and acetate, etc) can be taken by using a syringe connected to the vessel. The air flow rate to the inlet was controlled by a mass flow controller (Cole-Parmer, Model #: 32907-67) and maintained at 400 ml/min. The outlet was connected to a BlueInOne Cell sensor unit (BlueSens, Germany) for measuring CO₂ concentration. The stir rate in the growth vessel was set as 800 rpm and temperature was maintained at 37°C.

Glucose assay, Lactose assay, Acetate assay, and β-Galactosidase Assay

Glucose assay

100μL samples were taken for at least 8 different times during exponential growth (typically at OD₆₀₀ between 0.1 and 0.6) and immediately frozen. Before the assay, samples were thawed in water and immediately centrifuged at maximum speed (15,000 rpm) for 2.5min. 7μL of supernatant were used to measure glucose concentrations using the Glucose Assay kit (Product Code GAHK-20, Sigma-aldrich). The slope of the plot of glucose concentrations vs. OD₆₀₀ for all replicates (multiplied with the measured growth rate) was used to determine the glucose uptake rate.

Lactose assay

To assay lactose, ~10μL of the collected supernatant was first digested by β-galactosidase (Sigma-Aldrich) in Z-buffer at 37°C for 20 min. The released glucose was then assayed enzymatically by the kit commercially available (Glucose Assay Kit, GAHK20; Sigma-Aldrich). As a control, the sample was treated in the same way without β-galactosidase. Little glucose was detected in the control.

Acetate assay

200μL samples were taken for at least 3 different times during exponential growth (typically at OD₆₀₀ between 0.1 and 0.6) and immediately frozen. Before the assay, samples were thawed in water and immediately centrifuged at maximum speed (15,000 rpm) for 2.5min. 100μL of supernatant were used to measure acetate concentrations using the Acetate Assay kit (Catalog #: 10148261035, R-Biopharm). The slope of the plot of acetate concentrations vs. OD₆₀₀ for all replicates (multiplied with the measured growth rate) was used to determine the acetate excretion rate.

β-Galactosidase Assay

The assay was performed following a similar protocol as detailed in a previous study²¹.

Proteomic mass spectrometry

Sample collection

Protein mass spectrometry samples were collected from the four bioreactor cultures, a water bath culture of EQ353 grown on glucose minimal medium, and two ¹⁵N labeled water bath cultures of NCM3722 on lactose minimal medium and NQ381 with 200 μM 3MBA. For each of the cultures, 1.8 ml of cell culture at OD₆₀₀=0.4~0.5 during the exponential phase was collected by centrifugation. The cell pellet was re-suspended in 0.2 ml water and fast frozen on dry ice.

Mass spectrometry

Sample preparation and mass spectrometry methods have been described previously²⁸.

Protein identification

The raw mass spectrometry data files generated by the AB SCIEX TripleTOF® 5600 system were converted to Mascot generic format (mgf) files, which were submitted to the Mascot database searching engine (Matrix Sciences, London, UK) against the E. coli SwissProt database to identify proteins. The following parameters were used in the Mascot searches: maximum of two missed trypsin cleavage, fixed carbamidomethyl modification, variable oxidation modification, peptide tolerance ± 0.1 Da, MS/MS tolerance ± 0.1 Da, and 1+, 2+, and 3+ peptide charge. All peptides with scores less than the identity threshold (P=0.05) were discarded.

Relative protein quantitation

The raw mass spectrometry data files were converted to the .mzML and .mgf formats using conversion tools provided by AB Sciex. The .mgf files were used to identify sequencing events against the Mascot database. Finally, results of the Mascot search were submitted with .mzML files to our in-house quantification software⁴⁸. Briefly, intensity is collected for each peptide over a box in RT and m/z space that encloses the envelope for the light and heavy peaks. The data is collapsed in the RT dimension and the light and heavy peaks are fit to a multinomial distribution (a function of the chemical formula of each peptide) using a least squares Fourier transform convolution routine⁴⁹, which yields the relative intensity of the light and heavy species. The ratio of the non-labeled to labeled peaks was obtained for each peptide in each sample.

The relative protein quantitation data for each protein in each sample mixture was then obtained as a ratio by taking the median of the ratios of its peptides. No ratio (i.e., no data) was obtained if there was only one peptide for the protein. The uncertainty for each ratio was defined as the two quartiles associated with the median. To filter out data with poor quality, the ratio was removed for the protein in that sample if at least one of its quartiles lied outside of 50% range of its median; Furthermore, ratios were removed for a protein in all the sample mixtures in a growth limitation if at least one of the ratios has one of its quartiles lying outside of the 100% range of the median.

Absolute protein quantitation using spectral counting data

The spectral counting data used for absolute quantitation were extracted from the Mascot search results. For our ¹⁵N and ¹⁴N mixture samples, only the ¹⁴N spectra were counted. The absolute abundance of a protein was calculated by dividing the total number of ¹⁴N spectra of all peptides for that protein by the total number of ¹⁴N spectra in the sample.

Absolute quantitation of LacZ protein using purified LacZ protein as standard, and determination of the converting factor between Miller Unit and proteome fraction

For the condition of the LacZ overexpression strain (NQ1389) grown on glucose medium with zero cTc level (see source data file of Fig. 2), 15N sample was prepared, i.e., NQ1389 grown on glucose minimal medium with 15NH4Cl. The sample was mixed with a known amount of purified LacZ protein (Roche Diagnostics, Product No. 10745731001), the purity of which was verified both on a SDS-PAGE gel (where a single band was observed) and by checking the spectral counts of 14N peptides in the sample (where ~99% of the 14N peptides are LacZ peptides). With the highly accurate relative protein abundance between the purified 14N LacZ and the 15N LacZ in the sample, the proteome fraction of LacZ in the sample was determined to be 3.3%±0.3%. The average Miller Unit for the same condition was ~20550 (see source data file of Fig. 2), leading to a converting factor of 1.6% of proteome fraction for 10,000 MU.

Error analysis

Uncertainty of individual measurements

Biological replicates show the following typical uncertainties in measured quantities: growth rate, ~5%; acetate excretion rates, ~15%; CO₂ evolution rate, ~5%.

Uncertainties of linear relations

The parameters and their associated standard errors for linear relations were obtained by carrying out linear regression. Following our approach, multiple measurements over wide ranges of conditions from robust data sets revealing underlying relations between variables. The uncertainties are reported in Extended Data Tables 2 and 3, and throughout the text.

Extended Data

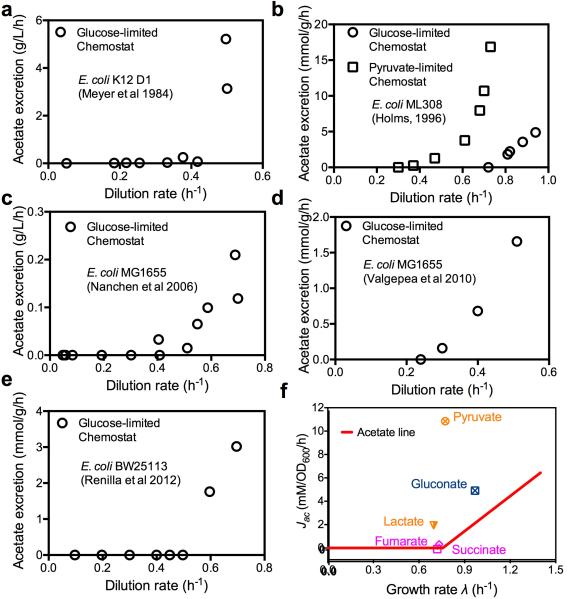
Extended Data Figure 1. Acetate excretion data for E. coli cells grown in chemostat (a-e) and for cells growing on medium with non-glycolytic carbon sources (f).

a, Glucose-limited chemostat data based on the figure 1 of Meyer et al²². b, Glucose-limited and pyruvate–limited chemostat data from Table 7 of Holms⁵⁷. c, Glucose-limited chemostat data based on figure 3 of Nanchen et al²³. Only data with dilution rates less than the apparent washout dilution rate are plotted here. d, Glucose-limited chemostat data from Table 1 of Valgepea et al¹⁵. e, Glucose-limited chemostat data based on figure 4 of Renilla et al¹⁶. f, E. coli K-12 NCM3722 was grown in minimal medium with one of five non-glycolytic carbon sources, including two gluconeogenic substrates (pyruvate and lactate), one substrate of the pentose phosphate pathway (gluconate), and two intermediates of the TCA pathway (succinate and fumarate). Deviation from the acetate line (the red line, as defined in Fig. 1 and Eq. (1) of the main text) is seen most strikingly for pyruvate, which excretes a very large amount of acetate, and to a lesser degree, also lactate and gluconate, which enters glycolysis as pyruvate. In the framework of our model, these deviations result from different proteome efficiencies of fermentation and respiration on these carbon sources.

Note: Acetate excretion measurement was also attempted for growth on LB. However, growth on LB is not characterized by a single exponential steady state growth phase, as various constituents of the medium are depleted during the course of batch culture growth. Assuming exponential growth for OD₆₀₀ data below 0.3 and alternatively from 0.3 for 0.5 gave doubling time of 18 min and 28 min, respectively. The corresponding acetate excretion rates were 14.3 and 3.6 mM/OD₆₀₀/hr. These data should be regarded as semi-quantitative due to the non-steady nature of growth on LB.

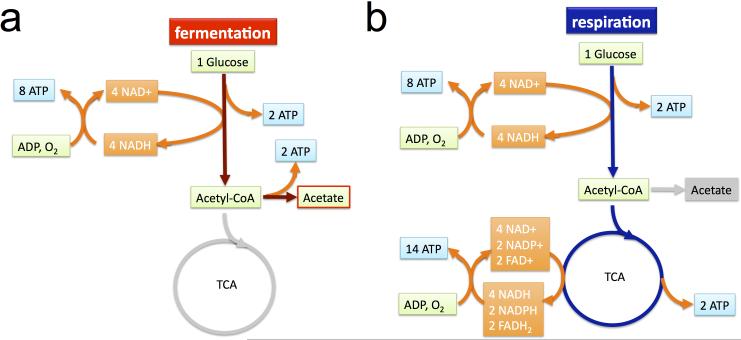
Extended Data Figure 2. The (oxidative) fermentation and respiration pathways.

a, Schematic illustration of the fermentation pathway, using glucose as an exemplary carbon source. The pathway is shown as the colored part. One molecule of glucose is catabolized into two molecules of acetate and two molecules of CO₂ (not shown in the diagram), with 4 molecules of ATP generated via substrate phosphorylation and also 4 molecules of NADH produced. In the aerobic environment, NADH molecules can be converted into ATP molecules. The total number of ATP molecules produced per glucose molecule is therefore 4+4x, where the conversion factor x indicates the number of ATP molecules converted from one NADH molecule (i.e., ATP:NADH = x:1). In the illustration, we assume that 2 molecules of ATP are converted from one NADH molecule, i.e., x=2. b, Schematic illustration of the respiration pathway, using glucose as an exemplary carbon source. The pathway is shown as the colored part. One molecule of glucose is catabolized into 6 molecules of CO₂ (not shown in the diagram), producing 4 molecules of ATP, 6 molecules of NADH, 2 molecules of NADPH, and 2 molecules of FADH₂. Using ATP:NADH = x:1, ATP:NADPH = x:1, and ATP:FADH₂ = x:2, we have the total number of ATP molecules produced as 4+9x for the respiration pathway. Here in the illustration, we assumed x=2.

Note that the ratio of total ATP produced from respiration over total ATP produced from fermentation depends on the conversion factor x, i.e., (4+9x)/(4+4x). The value of this ratio ranges from 1 (for x=0) to 9/4 (for x → ∞).

Extended Data Figure 3. Growth-rate dependence of acetate production and CO₂ evolution in bioreactor: data and comparisons to the model.

a, The rate of CO₂ evolution was determined in a bioreactor setup for wildtype and titratable LacY cells (NCM3722 and NQ381, respectively) grown in lactose minimum medium with various degrees of lactose uptake titration, and the result was used to deduce the CO₂ flux produced by respiration (blue circles). Also plotted (red squares) is the acetate excretion rate measured in the bioreactor. See Supplementary Note 2 for details of this experiment and corresponding analysis. The inducer levels, growth rate, measurements of glucose, acetate, and CO₂, and the deduced CO₂ via respiration are shown in the table on the right. b, Deduced energy production fluxes from fermentation and respiration pathways, based on the measurements presented in panel a. Fluxes are in units of mM/OD₆₀₀/h. c, Comparison of model and experimental data. Using the set of parameters summarized in Extended Data Table 2, the model solution (Eqs. [S14], [S17]) satisfactorily describes the experimental data obtained for acetate excretion (J_ac) and respiratory CO₂ production (J_CO2,r) in the bioreactor for carbon limitation. These results depend on the assumed ratios of ATP-carbon conversion. As described in Sec. D1, the ratios we used in this work are ATP:NADH=2:1, ATP:NADPH=2:1 and ATP:FADH₂=1.15:1. Note that these conversion ratios have never been precisely measured and could be substantially overestimated¹⁵. However, the central results presented in this work are robust with respect to the choice of these conversion ratios. As an illustration, we show in panel d that the model results generated with a very different set of conversion ratios (ATP:NADH=0.5:1, ATP:NADPH=0.5:1 and ATP:FADH₂=0.5:1) even provide a slightly better description of the data. [For these conversion ratios, the energy production of the cell matches the theoretical energy demand for biomass production.] The full model calibration requires the rate of CO₂ evolution, which can only be measured in a bioreactor setup. We note a small discrepancy between acetate fluxes and growth rates obtained for cultures grown in bioreactor as compared to batch cultures, possibly caused by differences in aeration.

Extended Data Figure 4. The effect of useless protein expression on acetate excretion.

a. Acetate excretion rate by strain NQ1389 is plotted against the absolute abundance of the expressed LacZ proteins, reported as a fraction of total protein (ϕ_Z), for each of the four carbon sources described in Fig. 2a of the main text. The solid lines, depicting the linear decrease in acetate excretion, are model predictions (Eq. [S23]), with the lone parameter ϕ_max ≈ 47% (the x-intercept of the line) determined from the least-mean-squares fit of the data in 3D plot of Fig. 2b, by a plane anchored to the acetate line. b, Alternatively, ϕ_max can be determined from linear fits of growth rate vs. ϕ_max for the 4 carbon sources shown. This results in a value ϕ_max = 42% ± 5%. The solid lines in this panel are linear fits using ϕ_max = 42%. [We note that over a broad growth rate range, ϕ_max actually exhibits a growth-rate dependence (manuscript in preparation). Nevertheless, over the narrow growth rate range relevant for acetate excretion, this dependence is negligible. Hence, for the purposes of our paper, we consider ϕ_max to be constant.] c. A different view of the 3D plot in Fig. 2b. d, Glucose uptake rate as a function of growth rate under LacZ overexpression. The circles are the data and the dashed line is the best-fit to the data passing through the origin. e, The relative protein levels of several representative genes, taken from amino acid synthesis (red), central metabolism (blue), protein synthesis genes (green), and nucleotide synthesis (black). As described in Hui et al²⁸, the vast majority of genes exhibited an expression pattern that is linearly proportional to the growth rate when growth is changed by increasing LacZ expression. f. Growth rate dependence of motility proteins under carbon limitation. The proteome fraction data (green symbols) is from the carbon limitation series in Hui et al²⁸, where growth rate was limited by titrating the lactose uptake for the strain NQ381. The motility proteins are proteins that are associated with the Gene Ontology term “GO: 0006810” (with GO name “locomotion”) as defined by the Gene Ontology Consortium⁵⁸. See Hui et al²⁸ for detailed description of the experimental procedure and data processing. Note that the fraction of motility proteins increases the most in the growth range where acetate is excreted. Also note that the energy consumption by chemotaxis comprises a very minor fraction of the total energy budget, estimated to be in the order of 0.1%⁵⁹. Disabling the motility function therefore does not affect the cell's energy requirement.

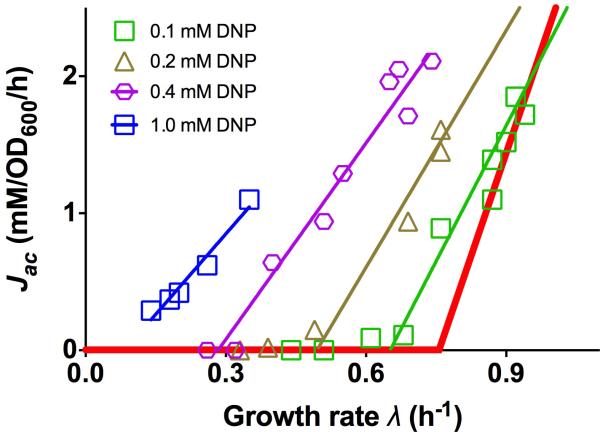
Extended Data Figure 5. Acetate excretion due to energy dissipation by DNP.

DNP is a chemical known to dissipate membrane potential⁶⁰ and thus imposes energy stress on the cell. Acetate excretion rates for the titratable glucose uptake strain (NQ1243) grown in medium with glucose and different concentrations of DNP were measured for different degrees of glucose uptake. The results are qualitatively similar to the data for the leaky LacY mutant NQ1313 (Fig. 3d), except for a systematic difference in the slopes of the resulting acetate lines (thin lines of different colors). The origin of this deviation is presumably a more complex action of DNP with additional effects on the cell as compared to the leaky LacY mutant. Indeed, it is known for instance that in addition to leakage of protons, DNP also causes leakage of osmolites through the membrane⁶¹.

Extended Data Figure 6. The relative expression levels of glycolysis proteins under proteome perturbation (by LacZ overexpression), and energy dissipation (by expressing leaky LacY).

Orange data points and linear fits result from the overexpression experiment (i.e., NQ1389 grown in glucose minimal medium with different induction levels of LacZ expression), and blue data points and fits are the leaky LacY series (i.e., the WT LacY strain NQ1312 and the Leaky LacY strain NQ1313 grown in glucose minimal medium with 200 μM 3MBA). The y-axis denotes relative protein levels, which were obtained by mass spectrometry with the same reference for the two series (see Methods). The x-axis is the growth rate (in units of h⁻¹). The different trends of protein expression for the two series show the distinct nature of the two perturbations, demonstrating that these seemingly similar predictions for the acetate line (parallel shift to slow growth as shown in Fig. 3a and Fig. 3d) for the two perturbations, have distinct origins and exhibit distinctly different patterns of gene expression in accordance with model predictions derived in section C3 of Supplementary Note 1 (see Eqs. [S26] and [S36]). From the perspective of gene regulation, it is not obvious what causes the increased expression levels of glycolysis genes under energy dissipation; The transcription factor Cra in combination with the key central carbon intermediate fructose-1,6-bisphosphate (FBP) is recognized as the major regulator of glycolysis⁶². FBP relieves the repression of glycolytic enzymes expression by Cra⁶³. The observed increase in the abundance of glycolytic enzymes under energy dissipation could be caused by a buildup of FBP, as energy stress limits protein polymerization. However, in this case, it is not clear what signaling pathway gives rise to the opposite responses of glycolytic enzymes to LacZ overexpression. Inset: Corresponding glucose uptake and acetate excretion rates for the two perturbations presented in the main figure. Glucose uptake and acetate excretion rates decreased proportional to growth rate for LacZ OE (as expected from the model Eqs. [S25], [S26] and [S29]). On the other hand, there was a marked increase in acetate excretion with energy dissipation for a roughly constant glucose uptake rate, as correctly anticipated by the model [Eq. S36]. Note that the protein abundance of Acs (main panel) shows that this increase in the acetate excretion rate was not caused by a drop in Acs. Instead, the observed increase of acetate excretion, together with the parallel increase in the expression level of glycolysis and TCA enzymes, points to the coordination of glycolytic and TCA fluxes in response to energy demand.

Extended Data Figure 7. The relative expression level of TCA proteins under proteome perturbations (by protein overexpression) and energy dissipation (by using leaky LacY).

Orange data points and linear fits represent the overexpression experiment (i.e., NQ1389 with different induction levels of LacZ expression), and blue data points and fits are the leaky LacY series (using the strains NQ1312 and NQ1313 with WT LacY expression and with the Leaky LacY expression respectively). The y-axis denotes relative protein levels, which were obtained by mass spectrometry with the same reference for the two series (see Methods). The x-axis is growth rate (in units of h⁻¹). The different trends of protein expression for the two series show the distinct nature of the two perturbations, demonstrating that these seemingly similar predictions on the acetate line (parallel shift to slow growth as shown in Fig. 3a and Fig. 3c) for the two perturbations, have distinct origins and exhibit distinctly different patterns of gene expression in accordance with model predictions derived in section C3 of Supplementary Note 1 (see Eqs. [S27] and [S37]). From the perspective of gene regulation, the transcription factor Crp is thought to be the major regulator of TCA enzyme expression in aerobic conditions⁶³. Crp-cAMP activity, which increases under carbon limitation, is known to activate the expression of most TCA enzymes. Together with the known role of Crp in upregulating the enzyme Acs which takes up acetate^15,16, Crp is considered to be a major candidate for regulating energy metabolism and acetate excretion. However, our findings that the expression of TCA enzymes increased under energy dissipation while acetate excretion also increased (Extended Data Fig. 6 inset) cannot be accounted for by known mechanisms of Crp regulation, and instead suggest an important role of additional regulators in the coordination of energy biogenesis pathways.

Extended Data Table 1. Strains used in this study.

Except for EQ353, all the strains used are derived from E. coli K-12 strain NCM3722^50-52 provided kindly by Sydney Kustu lab. Following is the description of key strains used in this study.

Strain	Genotype	Description
NCM3722	wild-type E. coli K12 strain	parent strain for all strains used here
NQ381	attB::PLlac-O1-xylR, lacY::km-Pu-lacY	titratable LacY
NQ636	glpK g184t	Glpk mutant
NQ638	glpK a218t	Glpk mutant
NQ640	glpK g692a	Glpk mutant
NQ1243	ycaD::FRT:Ptet:xylR PptsG::kan:Pu:ptsG	Titratable PtsG
NQ1312	ycaD::FRT:Ptet:xylR PptsG::kan:Pu:ptsG; pZA31 Ptet-lacY	WT LacY control for NQ1313
NQ1313	ycaD::FRT:Ptet:xylR PptsG::kan:Pu:ptsG; Ptet-lacYA177V on pZA31	leaky LacY mutant
NQ1388	ycaD::FRT:Ptet:xylR Pu:ptsG; ΔflhD-kan	flhD deletion strain
NQ1389	Ptet-tetR on pZA31; Ptetstab-lacZ on pZE1	LacZ over-expression strain
NQ1539	ycaD::FRT:Ptet:xylR Pu.ptsG; ΔfliA-kan	fliA deletion strain
EQ353	wild-type E. coli MG1655 used in Li et al	obtained from Jonathan Weissman lab

NQ1243: Varying glucose uptake by titrating the expression of PtsG, a subunit of the glucose PTS permease. The glucose PTS permease consists of two subunits, PtsG and Crr. Strain NQ1243 was constructed by replacing the ptsG promoter with a titratable Pu promoter from Pseudomonas putida. The activity of the Pu promoter is activated by the regulator XylR upon induction by 3-methylbenzyl alcohol (3MBA). Strain NQ1243 was grown in glucose minimal medium, supplemented with various 3MBA levels (0-800 μM) to stimulate XylR and titrate the expression of PtsG.

NQ381: Varying lactose uptake by titrating the expression of LacY. LacY (or lactose permease) is the primary transporter that allows E. coli to grow on lactose as the sole carbon source. Strain NQ381 was constructed by inserting the same titratable Pu promoter (above) between lacZ stop codon and lacY start codon. See You et al²⁷ details of strain construction.

NQ1389: the titratable LacZ overexpression system. This strain carries two plasmids pZA31 and pZE1. The repressor TetR gene on the pZA31 plasmid is driven by the TetR-repressible P_Ltet-O1 promoter⁵³ while the lacZ gene on the pZE1 plasmid is driven by the modified tet-promoter (more stable with respect to spontaneous mutations). The combination of these two plasmids creates a stable, finely titratable system that can be induced via the addition of chloro-tetracycline (cTc) in the medium⁵⁴. This induction system is tight, highly linear and capable of very high LacZ expression levels (with LacZ constituting up to 42% of the proteome) as seen in Fig. 2 and Extended Data Fig. 4. See Hui et al²⁸ for details of strain construction.

NQ1312 and NQ1313: Strains containing plasmids expressing LacY and LacY^A177V. The leaky LacY mutant (LacY^A177V)³³ or the control wildtype LacY is each driven by the P_Ltet-O1 promoter, harbored on the pZA31 plasmid. Neither strain contains a source of the TetR repressor, hence the plasmid expression system is fully induced. Bacteria use the H⁺ gradient across its inner membrane generated from the electron transport chain to produce ATP using the ATP synthase complex. The leaky LacY protein allows protons to pass through the inner membrane of the cell, thereby ‘draining’ the membrane potential generated by energy production pathways. This in turn leads to reduced energy efficiency or an increased energy demand on the bacterium.

Extended Data Table 2.

Model parameters calibrated from bioreactor.

Parameter (Units)	Description	From literature	Measured
ϕE,max=1-ϕ0 (%)	maximum energy proteome fraction extrapolated to λ = 0		19.0±1.2a
b (% hr)	energy sector growth rate dependence		12.0±1.4b
σ (mM/OD)	energy demand, proportionality constant with growth rate		45.7±2.8c
ef (1)	carbon efficiency, fermentation	2.0d
er (1)	carbon efficiency, respiration	4.4e
εf (mM/OD/hr)	protein efficiency, fermentation		750±30f
εr (mM/OD/hr)	protein efficiency, respiration		390±10g
β (mM/OD)	carbon demand for biomass building blocks, proportionality constant with growth rate		28.5±1.3h
ϕmax (1)	maximum total proteome fraction		0.42±0.05i
Sac (1)	stoichiometric factor for acetate from fermentation	l/3j
SCO2 (1)	stoichiometric factor for CO2 from respiration	l/6k

^aDetermined from Mass Spectrometry data. Offset of linear function fitted to the total energy sector size in Fig. N6 in Supplementary Note 1. Error inferred from this linear fit. See section D.4 in Supplementary Note 1 for details.

^bDetermined from Mass Spectrometry data. Slope of linear function fitted to the total energy sector size in Fig. N6 in Supplementary Note 1. Error inferred from this linear fit. See section D.4 in Supplementary Note 1 for details.

^cDetermined from Energy flux data, assuming energy demand proportional to growth rate. See section D.3 in Supplementary Note 1 and Fig. N5 in Supplementary Note 1.

^dDetermined from Literature. Number of ATP produced per carbon processed in fermentation. A total of 4 ATP and 4 NADH is produced per glucose molecule metabolized in fermentation (EcoCyc⁵⁵). Based on Unden & Dunnwald⁵⁶, a conversion ratio of NADH, NADPH to ATP of 2.0 was assumed. Hence, the equivalent of 2.0 ATP molecules are produced per carbon metabolized in fermentation.

^eDetermined from Literature. Number of ATP produced per carbon processed in respiration. A total of 4 ATP, 2 FADH₂, 2 NADPH and 8 NADH is produced per glucose molecule metabolized in respiration (EcoCyc⁵⁵). Based on Unden & Dunnwald⁵⁶ a conversion ratio of NADH, NADPH to ATP of 2.0 and a conversion ratio of FADH₂ to ATP of 1.15 was assumed. Hence, the equivalent of 4.4 ATP are produced per carbon metabolized in respiration.

^fDetermined from Mass Spectrometry data. Energy flux produced per protein fraction invested in the fermentation pathway. See section D.5 in Supplementary Note 1 for details.

^gDetermined from Mass Spectrometry data. Energy flux produced per protein fraction invested in the respiration pathway. See section D.5 in Supplementary Note 1 for details.

^hDetermined from carbon uptake flux and carbon fluxes by the energy pathways. See section D.2 in Supplementary Note 1 and Fig. N4 in Supplementary Note 1 for details.

ⁱDetermined by LacZ overexpression. Given by the proteome fraction occupied by LacZ, at which the growth rate vanishes. According to the average and the corresponding standard deviation of the fits of the data presented in Fig. 2, growth rate vanishes at (260 000 ± 30 000) MU, which translates into a proteome fraction of (42±5)% given that 100,00 MU corresponds to 1.6% of proteome. Note that this estimate is in good agreement with the estimates in previous works^21,27,28.

^jHere, S_ac = 1/3 simply because of the chemical reaction 6C → 2Acetate + 2CO₂ of the fermentation pathway: the carbon uptake flux J_C,f measured in units of the number of carbon atoms (C), is 3 times of the flux of acetate molecules.

^kS_CO2 = 1/6 simply because of the chemical reaction 6C→ 12CO₂ of the respiration pathway, oxidizing all carbon atoms to CO₂.

Extended Data Table 3.

Comparison between phenomenological model predictions and empirical results.

Parameter	Description	Equations	Figures	Units	Predicted	Empirical
Jac′(λ = 0)	LacZ overexpression, glucose, acetate excretion intercept at λ = 0	S26	2a	mM/OD/hr	0.0a	0.17±0.11b
Jac′(λ = 0)	LacZ overexpression, G6P, acetate excretion intercept at λ = 0	S26	2a	mM/OD/hr	0.0a	0.70±0.25b
Jac′(λ = 0)	LacZ overexpression, lactose, acetate excretion intercept at λ = 0	S26	2a	mM/OD/hr	0.0a	0.13±0.11b
Jac′(λ = 0)	LacZ overexpression, mannitol, acetate excretion intercept at λ = 0	S26	2a	mM/OD/hr	0.0a	−0.18±0.04b
Sac ′	slope acetate line with constant LacZ expression level of 50 000 MU (or ϕz ≈ 8%)	S30	N2a, 3a	mM/OD	10.0c	11.0±1.2d
λ ac ′	threshold growth rate of acetate line with constant LacZ expression level of 50 000 MU (or ϕz ≈ 8%)	S30	N2a, 3a	1/hr	0.61e	0.66±0.05d
Sac ′	slope acetate line with constant LacZ expression level of 100 000 MU (or ϕz ≈ 16%)	S30	N2a, 3a	mM/OD	10.0c	9.1±1.3d
λ ac ′	threshold growth rate of acetate line with constant LacZ expression level of 100 000 MU (or ϕz ≈ 16%)	S30	N2a, 3a	1/hr	0.47e	0.48±0.22d
λ ac ′	threshold growth rate of acetate line with flagella knockout	S14, S28	3b, Extended Data Fig. 4f	1/hr	0.88f	0.96±0.02g
λ ac ′	threshold growth rate of acetate line with 2mM chloramphenicol	S14	N2b, 3b	1/hr	0.59h	0.54±0.02i
λ ac ′	threshold growth rate of acetate line with 4mM chloramphenicol	S14	N2b, 3b	1/hr	0.48h	0.46±0.02i
λ ac ′	threshold growth rate of acetate line with 8mM chloramphenicol	S14	N2b, 3b	1/hr	0.30h	0.26±0.04i
Sac ′	slope of acetate line with LacYA177V	S32	N3, 3c	mM/OD	10.0j	11.1±0.6k

^aEq. S26 predicts direct proportionalities between growth rate λ and acetate excretion rates J_ac′ for LacZ overexpression. Hence, the lines should intercept the origin, with a vanishing acetate excretion rate J_ac′(λ = 0).

^bIntercept J_ac′(λ = 0) of the least-mean-squares fit of a line to the experimental data for different levels of LacZ overexpression presented in Fig. 2a.

^cEq. S30 predicts a slope identical to the standard acetate line for a constant level of LacZ overexpression. The model prediction is illustrated in Fig. N2a in Supplementary Note 1 and presented as the thin red lines in Fig. 3a.

^dFor the four tested carbon sources G6P, glucose, mannitol and lactose, acetate excretion rates and β-galactosidase activities were fitted as linear functions of growth rate. These fits were then used to interpolate growth rates and acetate excretion rates for a fixed level of LacZ overexpression. This resulted in the four points for a fixed LacZ level from each of the different carbon sources presented in Fig. 3a. Resulting slopes and intercepts presented in this table are the result of least-mean-squares fits of lines to these points.

^eEq. S30 predicts the threshold growth rate for a fixed amount of protein overexpression, using the parameter ϕ_max empirically determined in this work and previous works^21,27,28 as input. The model prediction is illustrated in Fig. N2a of Supplementary Note 1 and presented as the thin red lines in Fig. 3a.

^fUsing Eqs. S14, S28, assuming the proteome sector of motility proteins decreases linearly with growth rate, vanishing at λ = 1.1/hr and constituting 10% of the proteome at λ = λ_ac (compare to Extended Data Fig. 4f).

^gEstimated from the data presented in Extended Data Fig. 4a.

^hFor chloramphenicol stress, Eq. S14 predicts an increased slope S_ac′ with an identical offset $s_{ac}^{\prime }{\lambda }_{ac}\prime$, as compared to the standard acetate line. The model predictions (thin red lines, Fig. 3c) arise from using the offset of the standard acetate line given by S_acλ_ac as input and the slope of the modified acetate line as a fitting parameter.

ⁱThreshold growth rate determined from a least-mean-squares fit of a line to the data points presented in Fig. 3c.

^jEq. S32 predicts an identical slope of the modified acetate line with energy dissipation as compared to the standard acetate line. The model prediction is illustrated in Fig. N3 of Supplementary Note 1 and presented as the thin red line in Fig. 3d.

^kSlope is the result of a least-mean-squares fit of a line to the data points presented in Fig. 3d.

Box 1: Resource allocation model for energy biogenesis Top left, Efficiencies of energy production.

Fermentation and respiration pathways for energy biogenesis are shown in the red and blue boxes, respectively. The model assumes that for the same energy flux generated (width of yellow arrows), fermentation needs to draw more carbon flux than respiration (compare the width of light gray arrows), but requires smaller amount of proteins (compare the number of red and blue proteins). Top right, Model summary. The model consists of three resource-balance equations: Carbon flux (J_C,in) is utilized for energy production via fermentation or respiration (J_C,f, J_C,r), and to provide precursors for biomass production (βλ) Fermentation and respiration pathways supply ATP flux (J_E,f, J_E,r) that satisfy the energy demand of the cell (σλ). The proteome fraction required for biomass synthesis (ϕ₀ + bλ) depends linearly on the growth rate, thereby constraining the proteome fraction available for energy biosynthesis (ϕ_f, ϕ_r). Bottom, Model predictions. Under carbon limitation, the model predicts threshold-linear dependences of fermentation and respiration with changing growth rate. Respiration (blue line) gradually replaces fermentation (red line) as growth rate decreases. Proteome limitation by expression of useless proteins results in a horizontal shift of the acetate line. Translational limitation by antibiotics results in an increased slope of the acetate line with a fixed y-intercept. Energy dissipation also leads to a parallel shift of the acetate line. But unlike proteome limitation, which “compresses” both the fermentation and respiration sectors, these two sectors both increase with decreasing growth rate under energy dissipation (for fixed carbon uptake). The behaviors summarized in these plots are derived quantitatively in Supplementary Note 1 and validated in Figs. 1-3.