Significance
In cuprates, when doping is reduced superconductivity weakens and eventually disappears. The sample becomes “insulating” insofar that resistivity increases as the temperature is lowered, but the conductivity remains high, so the nature of this strange insulating state has been a puzzle. Here, we study the superconductor–insulator transition, improving the control of the doping level by 2 orders of magnitude and the sensitivity in probing transport fluctuations by 3 orders of magnitude. Our data reveal that at the lowest temperatures superconductivity competes with a charge-glass state. We propose that the latter is a glassy version of a charge density wave, and that it originates from strong localization due to charge–lattice coupling.
Keywords: high-temperature superconductors, charge glass, superconductor-to-insulator transition, quantum fluctuations, Hall effect
Abstract
Upon doping, cuprates undergo a quantum phase transition from an insulator to a d-wave superconductor. The nature of this transition and of the insulating state is vividly debated. Here, we study the Hall effect in La2-xSrxCuO4 (LSCO) samples doped near the quantum critical point at x ∼ 0.06. Dramatic fluctuations in the Hall resistance appear below TCG ∼ 1.5 K and increase as the sample is cooled down further, signaling quantum critical behavior. We explore the doping dependence of this effect in detail, by studying a combinatorial LSCO library in which the Sr content is varied in extremely fine steps, Δx ∼ 0.00008. We observe that quantum charge fluctuations wash out when superconductivity emerges but can be restored when the latter is suppressed by applying a magnetic field, showing that the two instabilities compete for the ground state.
Clarifying the mechanism of the superconductor–insulator transition (SIT) observed at low doping in cuprates is important per se, and more so because it may help crack the enigma of high-temperature superconductivity (HTS). The key question is the nature of the ground state competing with superconductivity (1, 2). Whereas the answer may not inform directly on the pairing mechanism in the HTS phase, it would reveal the nature of another important (competing) term in the (effective, low-energy) Hamiltonian. However, the physical picture is still contentious at present. Even the widespread use of the adjective “insulating” is problematic here because, although the resistivity (ρ) increases as the temperature is lowered, the sample actually remains quite conductive (3–5). Holes hopping in a Mott insulator may account for the electric transport at very low doping levels of such an “insulator.” However, in the vicinity of the quantum critical point, the physics gets more complex because of the intrinsic inhomogeneity induced by strong localization and significant spin, charge, and phase fluctuations (6–12). As a result, spin glass (6–9), charge glass (or charge-cluster glass) (10, 11), and superconducting vortex liquid/glass (12) all occur in the x-H-T phase diagram near the SIT. For instance, erratic switching in the (longitudinal) resistivity ρ has been observed (11) at very low temperature in two underdoped superconducting LSCO samples, and was taken as a signature of the charge-glass state. However, the measured amplitude of resistivity fluctuations was relatively small (Δρ/ρ ∼1%) even when the sample was deep in the charge-glass state. This raises a question whether the majority of the carriers are localized, or only a small fraction of carriers are in a glassy state while the rest are still itinerant and homogeneously distributed. Alternatively, the small fluctuation amplitude could have resulted from averaging over the measurement time, or over many small domains. Unfortunately, the methodology adopted in previous experiments did not allow making this important distinction. Furthermore, because the quantum critical fluctuations decay abruptly when the doping x moves away from xc, to study the effect of such fluctuations one needs to traverse the SIT in extremely fine steps. This goal is nearly impossible to achieve with the usual one-sample–one-doping strategy because, even with the state-of-art synthesis methods, the uncertainty in controlling the doping level is around ±1% at best, whereas an orders-of-magnitude better accuracy is needed to study the SIT. Moreover, inevitable variations in growth conditions from one sample to another may influence both the density of structural defects and of oxygen vacancies, affecting in turn the electron scattering processes and the density of localized carriers, and distorting the conclusions.
Here we show these difficulties can be overcome by using the combinatorial molecular beam epitaxy (COMBE) technique (13, 14) which enabled us to study the doping dependence as we traverse the SIT in unprecedentedly fine steps, Δx = 0.00008. The transport properties of samples with different doping levels were measured simultaneously, using a single COMBE film with a continuous doping gradient, greatly reducing the variations in growth and measurement conditions.
Next, we show that measuring the transverse (Hall) resistivity, ρH, rather than the longitudinal resistivity ρ, is a much more sensitive probe of charge fluctuations. The charge-cluster glass (CCG) can be envisioned as entailing domains of more-or-less localized charges, which fluctuate greatly in time and space (9–11). The fact that switching can be observed at all in the dc resistance, and even more that it is slow, indicates that at least some of these domains must be relatively large. Thus, we conjecture that such domain fluctuations should also be visible in the ρH, and that the effect could even be much more pronounced.
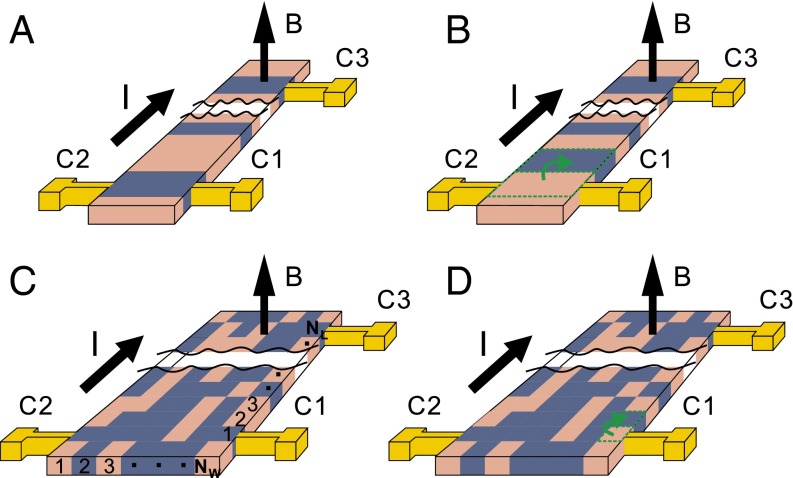
To illustrate our reasoning, we show some cartoons in Fig. 1. Let us assume that in our film there exist two types of domains that differ significantly in their carrier mobility and/or density, e.g., the domain A is significantly more metallic than the domain B, and consider first the extreme case (Fig. 1A) where the domain size is comparable to the strip width W. In this case, if domains fluctuate by jumping up and down the strip, one would expect the Hall resistivity to jump from ρHA to ρHB and back. In the state illustrated in Fig. 1A, the domain A happens to occur between the two Hall voltage contacts, so we observe ρH = ρHA. If domain A jumps up, trading places with domain B (Fig. 1B), the Hall resistivity increases abruptly to ρH = ρHB. Nevertheless, if the distance L between the contacts used to measure the longitudinal resistivity ρ is much larger than the domain size, this jump would cause a small relative change in ρ because it averages over many domains. This can be easily generalized to the situation when the domains are smaller than the strip width W, as sketched in Fig. 1 C and D. In this case, vertical switching between one A and one B domain would still cause a jump in the Hall resistivity, although smaller than in the previous case by a factor on the order of 1/NW, where NW is the number of domains along the strip width. Because in our actual device geometry the total number of domains contributing to ρ is NWNL, the effect on ρ would be much smaller, on the order of 1/NWNL. Of course, these are just cartoons, illustrating one possible way in which the device geometry might make the jumps in ρH appear more pronounced than in ρ. The reality is certainly more complex, because in an inhomogeneous material the Hall voltage is generated by current percolating through a system with a spatially varying Hall coefficient.
Fig. 1.
Schematics showing how the Hall resistance can be more sensitive to domain switching than the longitudinal resistance, for geometric reasons. (A) A narrow strip containing two types of domains that differ significantly in carrier mobility and density—e.g., domains A (dark blue) are more metallic than domains B (pink). When domain A is between the contacts C1 and C2, the Hall voltage is VHA. (B) If domains jump leaving domain B between the contacts C1 and C2, the Hall voltage jumps abruptly to VHB, whereas there is little change in the longitudinal resistance measured between the contacts C1 and C3. (C) The domain size is smaller by a factor NW than the strip width W and by a factor NL than the length L from C1 to C3. (D) Switching of a single domain causes a jump in ρH roughly proportional to 1/NW, whereas in ρ it is on the order of 1/(NLNW) so it can be much smaller.
Our expectations have been solidly confirmed by experiments. When an underdoped LSCO film enters the CCG state, the erratic switching and memory effects in ρH are 1,000× more pronounced, if measured by the ratio of the jump amplitude to the baseline. More importantly, the fluctuations in ρH exceed 100%, i.e., they are strong enough to make ρH change sign. This unambiguously shows that the majority of carriers are in a glassy state and fluctuating in time and space. Therefore, the CCG is a “true” ground state with inhomogeneous local order, fundamentally different from states described by the nearly free electron model or the band theory.
Taking advantage of extremely fine doping steps and high sensitivity in probing fluctuations, we have established the phase diagram in the multidimensional x-H-T phase space covering the complete SIT. We show that at low temperature the insulator state evolves into the CCG state, so the phase that competes at the SIT for the ground state with superconductivity is in fact the CCG state. We also find that even in the ground state this CCG phase hosts quantum fluctuations of the competing superconductive phase; therefore, the nature of the SIT is percolative.
The emergence of the CCG state can be related to the earlier discoveries of static “checkerboard” charge density waves (CDWs) in Bi2Sr2CaCu2O8 (15–17) and Ca2−xNaxCuO2Cl2 (18) and to more recently observed static CDWs in YBa2Cu3O7−x (19–25), Bi2Sr2−xLaxCuO6+δ (26–28), and HgBa2CuO4+δ (29), and dynamic (fluctuating) CDWs in La1.9Sr0.1CuO4 (30). If a well-formed CDW is observed, it implies that the electron–phonon coupling is significant, and moreover, that a single phonon mode with a well-defined wavevector is predominant, usually because of Fermi surface nesting. However, at very low doping levels close to the SIT, the charge excitations no longer have a well-defined quasi-momentum, so no coherent CDW can form. However, the charge–lattice coupling does not go away––in fact, it likely gets stronger as the electron wavefunctions get more localized. Concomitantly, the influence of the randomly distributed charged impurities (e.g., Sr dopants in LSCO) increases. Thus, one can expect that at very low doping levels the CDW may become quite disordered and glassy, giving rise to the observed CCG state. Support for this physical picture can be found in scanning tunneling microscopy (STM) studies of Ca2-xNaxCuO2Cl2 (31, 32) and Bi2Sr2-xLaxCuO6+δ (33), which revealed that doping holes into a Mott insulator creates nanoscale clusters of localized holes within which the CDW is stabilized. These CDW nanoclusters are embedded in an antiferromagnetic matrix, and this two-component mixture persists with increasing hole doping up to the x ∼ 0.06 doping level at which the nanoclusters touch each other, triggering a percolative transition to superconductivity. Together with our results on LSCO, these observations indicate that the presence of the CCG state in the vicinity of the SIT may be intrinsic and generic to the entire HTS cuprate family of compounds.
Experimental Results
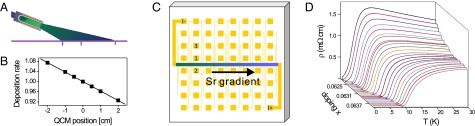
We have measured the dependence of ρ and ρH in LSCO films on temperature, magnetic field, and doping near the quantum critical point (QCP) at x ∼ 0.06. We have traversed the SIT varying x in exquisitely fine steps, Δx = 0.00008, by using the COMBE technique (13, 14), illustrated in Fig. 2 and described in more detail in Materials and Methods. In Fig. 2D, we show ρ(T) measured with the current flowing parallel to the crystallographic a–b plane and along the gradient in Sr doping, in various pixels from a COMBE library with the doping level varied from x = 0.062 to x = 0.065, as a function of temperature T. As a result of the doping gradient, across the library the critical temperature (Tc) varies from 9 K down to less than 0.3 K, the limit of our measurement.
Fig. 2.
COMBE synthesis provides 2-orders-of-magnitude improved resolution in doping. (A) Schematics of the deposition geometry: thermal effusion cell is positioned at a shallow angle (20°) with respect to the substrate. Closer to the source, the deposition rate is higher. (B) The actual deposition rate measured by a quartz crystal microbalance, as a function of the position relative to the rate at the center. The gradient is 4% per 1 cm (the size of our substrates). (C) Schematics of the patterned one-dimensional COMBE library, with 64 gold (yellow) contact pads. This pattern enables simultaneous measurements of ρ at 30 pixels and of ρH at 31 pixels. For example, contacts 1 and 2 provide the Hall voltage, whereas the contacts 1 and 3 provide the longitudinal resistance. (D) The doping dependence of ρ(T) in a COMBE library doped near the QCP at x = 0.06. The chemical composition between two consecutive pixels differs by Δx = 0.00008, enabling a study of the evolution of transport with doping in the vicinity of the QCP with unprecedented precision.
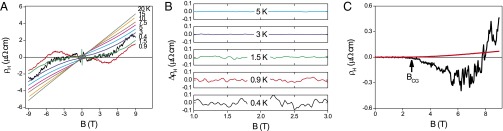
To elucidate our key experimental findings, we first present and discuss the ρH(T) data for one representative doping level, x = 0.063. [The ρ(T) and magnetoresistance data, presented in the Supporting Information, show superconducting fluctuations up to about 10–15 K above Tc, in line with the estimates from NMR (34), terahertz spectroscopy (35), Nernst effect (36), and magnetization measurements (37).] The observed ρH(T) dependence is striking (Fig. 3A). For 3 K < Τ < 20 K, ρH is essentially linear in B, except for a small deviation in the low-B region due to superconducting fluctuations (SFs). However, below TCG = 1.5 K the ρH(B) curves become erratic and exhibit kinks, spikes, and jumps. We emphasize that this is not the instrumental noise, but rather intrinsic behavior of LSCO samples. This can be proven in several ways. First, the instrumental noise of our setup is on the scale of few tens of nV, and it is essentially independent of the sample temperature in the region of interest. In contrast, the erratic jumps in Hall voltage can be as large as 5 μV (using the same probe current I = 10 nA)––at least 2 orders of magnitude larger than our noise floor.
Fig. 3.
Evidence for intrinsic switching in ρH in LSCO near the superconductor–insulator quantum phase transition. (A) The Hall resistivity ρH of La1.937Sr0.063CuO4 as a function of the magnetic field B. The field dependence of ρH is smooth for T > 1.5 K, but it becomes erratic for T < 1.5 K. (B) The same data, normalized to the linear fit, ρH = <RH > B, to emphasize the random switching. The top two curves (at T = 5 K and at T = 3 K) are smooth, showing that the instrumental noise is almost negligible on this scale. However, switching becomes visible at T = 1.5 K and grows dramatically as the sample is cooled down further, exceeding the instrumental noise by 2 orders of magnitude at T = 0.4 K. (C) ρH(B) at T = 0.4 K in the underdoped COMBE library (black curve) and an overdoped LSCO film (red curve) both with Tc = 3 K. For the underdoped curve, switching is absent for low fields, but grows dramatically at high fields, starting from some characteristic field BCG. In contrast, the smooth curve of the overdoped film shows no switching, and the instrumental noise is hardly perceptible on this scale. These data clearly show that the erratic switching observed at very low temperatures does not originate from the instrumental noise in the measurements but rather represents the intrinsic response of LSCO films doped near the QCP.
The second argument is the striking temperature dependence. This can be visualized by comparing the ρH(B) traces recorded at various temperatures. The top two traces in Fig. 3B, recorded at T = 5 K and T = 3 K, respectively, are apparently quite smooth; this gives a clear indication that our noise floor is quite low on this scale. However, when we lower the sample temperature by just a couple of degrees, the traces become visibly erratic, the more so as the temperature is lowered further, becoming quite dramatic at T = 0.4 K.
The third argument is an equally dramatic dependence on the magnetic field. This is illustrated in Fig. 3C, for a sample with slightly higher doping level (black curve), so that Tc = 3 K. For low fields, the ρH(B) trace shows no switching; however, when the field strength exceeds a certain critical value, BCG, the ρH(B) trace becomes quite erratic, with large spikes and jumps. At T = 0.4 K, in the ρ(T) data of this sample we see clear signs of SFs, which are suppressed by the magnetic field of a few T. Concomitantly, switching appears in ρH as well.
The fourth proof is the systematic and dramatic doping dependence. In Fig. 3C, we show the ρH(B) data for an overdoped LSCO film (red curve), with the same Tc = 3 K, taken at the same temperature (T = 0.4 K). In the overdoped film (red curve), the instrumental noise is hardly visible; it is about 2 orders of magnitude lower than in underdoped film (black curve) for B > BCG. This comparison also shows that the dc magnetic field does not affect our instrumental noise, as indeed expected, and as we have also verified directly on many other samples.
Now that we have established that a large switching effect is intrinsic to underdoped LSCO, we proceed with characterizing it in more detail. First, it should be pointed out that as the temperature is lowered toward zero, both the frequency and the magnitude of jumps strongly increase, pointing to the switching of quantum origin. Because this sample is doped very close to the SIT quantum critical point, one indeed expects strong quantum fluctuations.
To explore possible hysteretic and memory effects, we repeated a number of times the measurements of ρH(B) in the same sample under identical experimental conditions, i.e., at a fixed temperature and sweeping the magnetic field in the same way. A comparison of two such traces, taken from the x = 0.063 sample at T = 0.4 K, is shown in Fig. 4A. In repeated measurements, the jumps in ρH(B) occur at different values of the magnetic field, indicating that these jumps are random in nature.
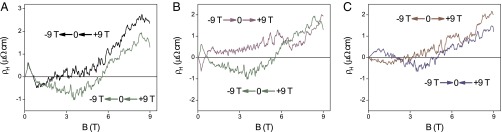
Fig. 4.
Hysteretic behavior and memory effects. The ρH(B) data for La1.937Sr0.063CuO4, measured at T = 0.4 K with different field-ramping histories as indicated by the arrows. To remove the offset due to a small longitudinal component, the Hall voltage is determined by subtracting VH(−) (measured with the field B pointing down) from VH(+) (the field up). (A) The field was decreased from B = 9 T to B = 0 T in two independent experiments performed under exactly the same conditions. The jumps in the ρH curves are different and occur at different field values, indicating that they are random in nature. (B) The purple curve VH(+) = VH(0 T → 9 T) and VH(−) = VH(−9 T → 0 T); the green curve: VH(+) = VH(9 T → 0 T) and VH(−) = VH(0 T → −9 T). (C) The blue curve, VH(+) = VH(9 T → 0 T) and VH(−) = VH(−9 T → 0 T); the red curve: VH(+) = VH(0 T → 9 T) and VH(−) = VH(0 T → −9 T). Note that the ρH curves obtained in this way show significant differences not only in absolute values but also in the sign. The data are suggestive of the existence of many nearly degenerate metastable low-energy states.
Next, we established that the samples show some memory of the magnetic field history, by comparing the results of measurements done over the entire field range, −9 T < B < 9 T, swept in four different ways, as indicated by arrows in Fig. 4 B and C. Apparently, the resulting ρH(B) curves are vastly different. At lower fields (B < 6 T), the four curves show differences not only in the absolute value of ρH but also in its sign. As the field is ramped, every ρH curve changes the sign at least once, but the sign reversals occur at quite different B values. For higher fields, above about 6 T, the ρH(B) curves start to merge, i.e., the hysteresis becomes less pronounced.
Note that at T = 0.4 K we observe switching and memory effects in the longitudinal magnetoresistivity ρ(B) as well, but this effect is less striking; the relative magnitude of random jumps is much smaller, about 0.1% of the average value of ρ(B), so no jumps are clearly visible on the scale of Fig. S1. In contrast, at the same temperature, the amplitude of random jumps in ρH exceeds 100% of the average value of ρH. Thus, the measurement of the Hall effect is a much more (3 orders of magnitude) sensitive method to detect this hysteretic state than the magnetoresistance technique, in line with our expectations.
Fig. S1.
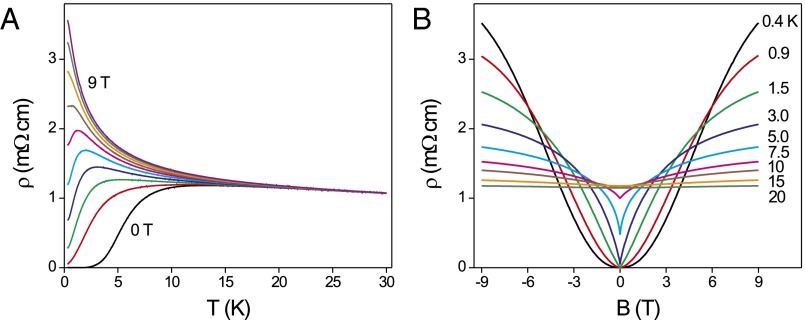
Longitudinal magnetoresistance reveals superconducting fluctuations and their gradual suppression by magnetic field. (A) The resistivity ρ of La1.937Sr0.063CuO4 as a function of temperature, for various values of the external magnetic field B, varied from zero to 9 T in steps of 1 T. The sample is driven from the superconducting (Tc ∼ 2 K) to a nonmetallic state. (B) The same, as a function of B, at various temperatures in the range from 0.4 to 20 K. At low fields, the drop in ρ(Β), i.e., the increase in conductivity, is attributed to superconducting fluctuations.
We turn now to the results of Hall effect measurements for the entire combinatorial library. In Fig. 5A, we show ρH(B) at low temperature (T = 0.4 K) for several representative pixels; it apparently shows the characteristic random jumps in every device. This corroborates that their occurrence is indeed intrinsic to underdoped LSCO over some range of doping levels near the QCP.
Fig. 5.
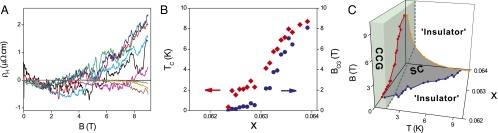
Phase competition in LSCO near the QCP at x = 0.06. (A) The Hall resistivity at T = 0.4 K as a function of the magnetic field, in several representative pixels from the COMBE library under study. (B) The doping dependence of Tc (red diamonds, left scale) and of BCG (blue circles, right scale), the field above which hysteretic switching appears. The fact that erratic switching is observed in every pixel, with the systematic doping dependence, is yet another proof that it is intrinsic to LSCO doped in the vicinity of the QCP. (C) The B-T-x phase diagram determined from the measurements on the entire combinatorial library. The CCG state evolves from the insulator state as the temperature T decreases (the phase boundary is denoted by the dashed lines). The CCG state and the superconductor state (SC) compete for the ground state at zero temperature. By decreasing the doping level x or increasing the applied magnetic field B, LSCO undergoes a quantum phase transition from the SC state to the CCG state.
In Fig. 5B, we show the values of Tc(R = 0) and of the field BCG that destroys any remnants of superconductivity and makes the hysteretic switching appear, measured at a fixed temperature (T = 0.4 K), for different doping levels. The general trend, a monotonic increase of BCG with x, is understandable––a higher doping level corresponds to a higher Tc and to a larger condensation energy, and hence it takes a stronger magnetic field to destroy the superconducting state. (We mention in passing that this is yet another direct proof that the effect is intrinsic; all of the channels are measured simultaneously in the same field and at the same temperature, and show essentially the same instrumental noise, 2 orders of magnitude lower than the jumps in ρH.) The phase diagram of underdoped LSCO, determined by the measurements on the entire combinatorial library, is sketched out in Fig. 5C. The phase characterized by erratic switching in ρH is denoted as the CCG state, for the reasons presented in Discussion below. It is clear that the insulator state evolves into the CCG state when the temperature decreases due to the strong localization at low temperatures. Thus, the ground (zero-temperature) state is determined by competition between the superconducting and CCG states. The so-called “superconductor-to-insulator” transition indeed is a “superconductor-to-CCG” quantum phase transition that can be triggered by decreasing the doping level or by increasing the applied magnetic field, as demonstrated in Fig. 5C.
Discussion
We now outline a physical picture that can account for our experimental results. We have shown that in underdoped LSCO at fixed (low) temperature and magnetic field, the value of ρH can fluctuate by several hundred percent, and even change sign, depending on the sample’s history. This ρH behavior, fundamentally different from the smooth and monotonic magnetic field dependence of ρH in LSCO reported in the literature (38, 39), remained undetected so far because it only occurs at very low temperature (T < 1.5 K) and in a narrow composition range near the QCP at xc ∼ 0.06. This phenomenon cannot be explained within the framework of standard theories of transport in conventional metals and semiconductors. For example, in the Drude model, ρH is inversely proportional to the carrier density, so the reversal of sign of ρH would imply that the carrier type changed from holes to electrons. However, it seems unlikely that one could switch between holes and electrons by just tweaking the magnetic field up and down. Next, we argue that this phenomenon is intrinsic. Whereas atomic and structural defects inevitably occur in any film, this cannot be the origin of the observed switching. First, for fluctuations in ρH by more than 100% to come from impurities and defects, their density would have to be very high, and we would have easily picked up their signature in reflection high-energy electron diffraction (RHEED), atomic force microscopy (AFM), and high-resolution X-ray diffraction (XRD) measurements––which we have not. We monitored the RHEED pattern throughout the growth process and we observed no signals attributable to defects or precipitates. The postgrowth AFM and XRD measurements indicated an atomically smooth single-crystal LSCO film. The upper limit on the density of conceivable defects is orders of magnitude too low to cause jumps by 100% in ρH. Second, the critical field BCG shows continuous and monotonic dependence on the doping (Fig. 5). It is unlikely that this could originate from some random defects (none of which have been observed). In contrast, the doping dependence of BCG can be naturally understood as a consequence of the gradual approach to the SIT. Third, the overall time to ramp the magnetic field in the Hall experiment at one fixed temperature is about 4 h, so the time scale between two local peaks/valleys in ρH is typically a few minutes (Figs. 3–5). The fluctuations under discussion are very slow, indicating that the domains are large, probably on the micrometers scale. Fast fluctuations, as would be caused by atomic defects, may be present as well, but are averaged out and not detectable in our experiment. Fourth, ρH manifests hysteretic behavior and memory effects as shown in Fig. 4. All these findings can be attributed to intrinsic fluctuations in ρH. Moreover, our findings are corroborated by direct STM imaging of localized charge domains in bulk single crystals of NCCOC (31, 32) and BSCCO (33), indicating that the occurrence of CCG is not only intrinsic but also universal to the HTS cuprates.
Therefore, we have to consider more exotic mechanisms, beyond the nearly free electron model. In particular, we should contemplate the Hall effect in a charge-, spin-, or superconducting vortex-glass state, all of which were reported to occur in underdoped cuprates (6–12). Although regrettably a broadly accepted quantitative theory of these phenomena is still missing, we can discriminate between these three glassy states based on qualitative arguments, as follows.
According to the previously reported muon spin rotation and magnetic susceptibility experiments (6–8), our underdoped LSCO films should exhibit spin-cluster-glass behavior at low temperature (TSG ∼ 3 K for x = 0.063). However, in the spin-glass state there should be no long-range order of magnetic moments, and the net moment should vanish after averaging; thus one should not expect the spin degrees of freedom to strongly affect the electric transport.
Superconducting vortex-glass and vortex-liquid states are both expected to appear (12, 40–43) in underdoped LSCO. The vortex motion is involved as long as the SFs are present, which is the case in Fig. S1 for T < 15 K. In the vortex-liquid state, continuous flow of vortices should create no discontinuity in transport properties such as ρH. On the other hand, in the vortex-glass state, at low density and low probe currents the vortices should all be pinned and immobile, thus not contributing to the Hall effect. Whereas the phase transition between the vortex-liquid and the vortex-glass states should be of the first order, in line with the observed hysteretic behavior, this occurs only within a very narrow (∼10-mK wide) temperature window centered at the transition temperature, and in a very narrow field range (41, 42). In contrast, we have shown that for x = 0.063 ρH is hysteretic at all temperatures below T = 1.5 K and in all fields up to 9 T (the maximum available in this setup). Thus, whereas the spin-glass and vortex-glass states likely both occur in our LSCO samples in certain temperature ranges, we conclude that they are not responsible for the fluctuations and hysteresis in ρH reported here.
The only remaining possibility is the CCG––a state where the charges are localized and distributed nonhomogeneously across the sample (9–11). One envisions many different, metastable charge distribution patterns, essentially degenerate in energy––a situation we have illustrated by sketches in Fig. 1. This makes the sample very susceptible to fluctuations, which trigger frequent switching from one metastable pattern to another. This kind of switching can explain random jumps in our ρH. Quantum fluctuations are expected to grow upon approach to the SIT quantum critical point, as observed. The disappearance of the glassy state for T > 1.5 K indicates either that quantum fluctuations diminish rapidly with the temperature, or that thermal fluctuations wipe out glassiness, or both.
We observed, in agreement with ref. 11, that SFs intensify as the temperature is lowered until TCG but then weaken and disappear as the temperature is lowered further. At the same time, hysteretic switching due to charge localization in clusters gets stronger. This is indeed what one would expect from the charge-phase uncertainty relation. An important point is that this clearly indicates that the two orders compete for the ground state.
The key open question is what the effective charge of localized carriers is. STM in Bi2Sr2CaCu2O8 revealed (15, 16) checkerboard patterns of static CDW, with periodicity 4a0 × 4a0. This has been interpreted as a Wigner crystal formed by hole pairs at x = 1/8 doping, dubbed the “pair density wave” or CDW of Cooper pairs (CPCDW) (44–49). In previous experiments (50) with electrolyte gating of LSCO we were able to traverse the SIT using the electric field effect, and found that the transition (in zero magnetic field) occurs at the quantum resistance for pairs, Rc = RQ = h/(2e)2 = 6.5 kΩ. This is suggestive of the existence of pairs on both sides of the SIT, which are localized in the insulator whereas delocalized and condensed in the HTS state.
In summary, we have shown that in LSCO doped near the QCP at x ∼ 0.06 the superconducting state is competing with a quantum CCG state—a glassy version of CDW, clustered but without long-range coherence, pinned on defects such as Sr2+ dopant ions, and subject to massive quantum critical fluctuations. The fact that this strange state of condensed matter occurs in HTS cuprates may not be a mere coincidence.
Materials and Methods
For sample synthesis, we have used the COMBE system at Brookhaven National Laboratory. La2-xSrxCuO4 films, 20 unit cells (26.4 nm) thick, were grown on LaSrAlO4 substrates polished perpendicular to the crystallographic [001] direction. We monitored synthesis in real time by RHEED, which indicated perfect atomic-layer-by-layer growth. Using a single Sr source aimed at a shallow angle (20°) with respect to the heated substrate, we varied the doping level x in the film continuously from 0.062 to 0.065. Two sources each were used for La and for Cu, and their deposition rates and shuttering times were adjusted to preserve accurately the 2:1 ratio between (La + Sr) vs. Cu; this is critically important to avoid nucleation and growth of unwanted precipitates of secondary phases, such as CuO and La2O3. The film as grown is a single crystal, just with a small gradient in Sr doping level (13).
We used photolithography to pattern the film into a Hall bar, 10 mm long and 300 μm wide, with 64 gold contact pads and leads. The sample is thus formed into a one-dimensional combinatorial library with 31 segments (“pixels”), each with a slightly different chemical composition––from one pixel to the next, the doping level x increases in extremely fine steps, Δx = 0.00008. We can estimate the error bars as follows. We measure the deposition rates by quartz crystal monitor and atomic absorption spectroscopy in situ, cross-calibrated by ex situ Rutherford back-scattering spectroscopy and X-ray reflectometry measurements, with compound absolute accuracy conservatively estimated to be better than 3%. Hence, the Sr doping level at the sample center is x = 0.0635 ± 0.0019. However, the doping gradient is continuous, linear, and fixed very accurately by the system geometry at 4% per 1 cm. Hence, the relative (pixel-to-pixel) accuracy is much better. For 1 pixel, the uncertainty in its relative composition (say, compared with its nearest neighbor) is determined by its length, 300 μm, so one can take it to be ±0.00004, although this is not random. Moreover, the width of voltage contacts is just 10 μm, making this (relative) uncertainty 30× smaller in Hall effect measurements. Altogether, these error bars are orders of magnitude smaller than the markers we use in the figures.
Magnetotransport measurements were performed in a Helium-3 cryogenic system equipped with a superconducting magnet, providing field up to 9 T. To enable multichannel data collection, electronic connections to the custom-designed sample-mounting stage are made by 32 pairs of individually twisted and shielded manganin wires. The heat load to the sample is minimized by appropriate thermal anchoring. The temperature can be varied between 300 mK and 300 K, with stability better than ±1 mK. In all transport measurements reported here, the excitation (bias) current density was kept very low, j = 3 × 102 A/cm2. The corresponding voltages are measured by a custom-built, parallel-running, multichannel digital lock-in setup. Thus, ρ and ρH are measured simultaneously at every pixel in the combinatorial library. A multiplex is used for easy switching between the ρ and ρH measurement configurations.
Apart from allowing the study of doping dependence with unprecedented accuracy, the COMBE technique reduces the sample-to-sample variations, because each “sample’ (i.e., pixel) is synthesized on the same substrate under the same thermodynamic conditions and undergoes the same history including lithographic process steps, exposure to atmosphere, etc.
Longitudinal Magnetoresistance in LSCO Doped near the Superconductor–Insulator Transition
We have measured the dependence of the in-plane longitudinal resistivity (ρ) on the magnetic field up to B = 9 T in the same set of samples. To illustrate our main observations, we here present and discuss the data for one representative doping level, x = 0.063––the same sample for which we have shown the Hall effect data in Fig. 3 A and B.
In Fig. S1, we show ρ as a function of temperature T and magnetic field B, respectively. In agreement with earlier experiments in zero field (2, 3), for 20 K < T < 100 K the slope of dρab/dT is negative. This behavior is customarily referred to as insulating (although the sample is actually still quite conductive) and attributed to some sort of charge localization or ordering. Below T ∼ 15 K, superconducting fluctuations become visible, and the superconducting transition occurs at Tc ∼ 2 K. When superconductivity is suppressed by an external magnetic field, the sample shows insulating behavior down to the lowest temperature.
In Fig. S1A, one can see a magnetic-field-driven SIT, occurring for T ∼ 0 at some critical value of sheet resistivity, Rc. This value of Rc is not universal, in contrast to the case of doping-driven SIT where it was found in both LSCO (50) and YBCO (51) that Rc ∼ RQ = 6.5 kΩ. However, Rc is expected (52–55) to be universal only for a strictly 2D SIT, whereas the applied magnetic field makes the carrier motion in CuO2 planes quasi–one-dimensional, and in this case, Rc may depend both on the doping level x and on the sample size.
Fig. S1B highlights the magnetic field dependence. For strong magnetic fields and/or higher temperatures, the field dependence of the magnetoresistance ρ (B) is quadratic in B, as expected for a normal metal. At low fields and low temperatures, the dependence deviates from the B2 behavior, showing significant excess conductivity; this is commonly attributed to SFs (56, 57). Our magnetoresistance data show SFs up to about 10–15 K above Tc, in line with the estimates from NMR (34), terahertz spectroscopy (35), Nernst effect (36), and magnetization measurements (37).
Acknowledgments
This work was supported by the US Department of Energy, Basic Energy Sciences, Materials Sciences and Engineering Division.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1519630113/-/DCSupplemental.
References
- 1.Lee PA, Nagaosa N, Wen X-G. Doping a Mott insulator: Physics of high-temperature superconductivity. Rev Mod Phys. 2006;78(1):17–85. [Google Scholar]
- 2.Zaanen J, et al. Towards a complete theory of high TC. Nat Phys. 2006;2(3):138–143. [Google Scholar]
- 3.Ando Y, Boebinger GS, Passner A, Kimura T, Kishio K. Logarithmic divergence of both in-plane and out-of-plane normal-state resistivities of superconducting La2-xSrxCuO4 in the zero-temperature limit. Phys Rev Lett. 1995;75(25):4662–4665. doi: 10.1103/PhysRevLett.75.4662. [DOI] [PubMed] [Google Scholar]
- 4.Ando Y, et al. Normal-state Hall effect and the insulating resistivity of high-Tc cuprates at low temperatures. Phys Rev B. 1997;56(14):R8530–R8533. [Google Scholar]
- 5.Ono S, et al. Metal-to-insulator crossover in the low-temperature normal state of Bi(2)Sr(2-x)La(x)CuO(6+δ) Phys Rev Lett. 2000;85(3):638–641. doi: 10.1103/PhysRevLett.85.638. [DOI] [PubMed] [Google Scholar]
- 6.Lavrov AN, Ando Y, Komiya S, Tsukada I. Unusual magnetic susceptibility anisotropy in untwinned La2-xSr(x)CuO4 single crystals in the lightly doped region. Phys Rev Lett. 2001;87(1):017007. doi: 10.1103/PhysRevLett.87.017007. [DOI] [PubMed] [Google Scholar]
- 7.Sonier JE, et al. Spin-glass state of individual magnetic vortices in YBa2Cu3Oy and La2-xSrxCuO4 below the metal-to-insulator crossover. Phys Rev B. 2007;76(6):064522. [Google Scholar]
- 8.Stilp E, et al. Magnetic phase diagram of low-doped La2-xSrxCuO4 thin films studied by low-energy muon-spin rotation. Phys Rev B. 2013;88(6):064419. [Google Scholar]
- 9.Julien M-H, et al. Charge segregation, cluster spin glass, and superconductivity in La1.94Sr0.06CuO4. Phys Rev Lett. 1999;83(3):604–607. [Google Scholar]
- 10.Raicević I, Jaroszyński J, Popović D, Panagopoulos C, Sasagawa T. Evidence for charge glasslike behavior in lightly doped La2-xSrxCuO4 at low temperatures. Phys Rev Lett. 2008;101(17):177004. doi: 10.1103/PhysRevLett.101.177004. [DOI] [PubMed] [Google Scholar]
- 11.Shi X, et al. Emergence of superconductivity from the dynamically heterogeneous insulating state in La(2-x)Sr(x)CuO4. Nat Mater. 2013;12(1):47–51. doi: 10.1038/nmat3487. [DOI] [PubMed] [Google Scholar]
- 12.Li L, Checkelsky JG, Komiya S, Ando Y, Ong N-P. Low-temperature vortex liquid in La2-xSrxCuO4. Nat Phys. 2007;3(5):311–314. [Google Scholar]
- 13.Clayhold JA, et al. Combinatorial measurements of Hall effect and resistivity in oxide films. Rev Sci Instrum. 2008;79(3):033908. doi: 10.1063/1.2901622. [DOI] [PubMed] [Google Scholar]
- 14.Wu J, et al. Anomalous independence of interface superconductivity from carrier density. Nat Mater. 2013;12(10):877–881. doi: 10.1038/nmat3719. [DOI] [PubMed] [Google Scholar]
- 15.Hoffman JE, et al. A four unit cell periodic pattern of quasi-particle states surrounding vortex cores in Bi2Sr2CaCu2O8+δ. Science. 2002;295(5554):466–469. doi: 10.1126/science.1066974. [DOI] [PubMed] [Google Scholar]
- 16.Vershinin M, et al. Local ordering in the pseudogap state of the high-Tc superconductor Bi2Sr2CaCu2O(8+δ) Science. 2004;303(5666):1995–1998. doi: 10.1126/science.1093384. [DOI] [PubMed] [Google Scholar]
- 17.da Silva Neto EH, et al. Ubiquitous interplay between charge ordering and high-temperature superconductivity in cuprates. Science. 2014;343(6169):393–396. doi: 10.1126/science.1243479. [DOI] [PubMed] [Google Scholar]
- 18.Hanaguri T, et al. A ‘checkerboard’ electronic crystal state in lightly hole-doped Ca2-xNaxCuO2Cl2. Nature. 2004;430(7003):1001–1005. doi: 10.1038/nature02861. [DOI] [PubMed] [Google Scholar]
- 19.Chang J, et al. Direct observation of competition between superconductivity and charge density wave order in YBa2Cu3O6.67. Nat Phys. 2012;8(12):871–876. [Google Scholar]
- 20.LeBoeuf D, et al. Thermodynamic phase diagram of static charge order in underdoped YBa2Cu3Oy. Nat Phys. 2012;9(2):79–83. [Google Scholar]
- 21.Ghiringhelli G, et al. Long-range incommensurate charge fluctuations in (Y,Nd)Ba2Cu3O(6+x) Science. 2012;337(6096):821–825. doi: 10.1126/science.1223532. [DOI] [PubMed] [Google Scholar]
- 22.Wu T, et al. Emergence of charge order from the vortex state of a high-temperature superconductor. Nat Commun. 2013;4:2113. doi: 10.1038/ncomms3113. [DOI] [PubMed] [Google Scholar]
- 23.Blanco-Canosa S, et al. Momentum-dependent charge correlations in YBa2Cu3O6+δ superconductors probed by resonant X-ray scattering: Evidence for three competing phases. Phys Rev Lett. 2013;110(18):187001. doi: 10.1103/PhysRevLett.110.187001. [DOI] [PubMed] [Google Scholar]
- 24.Blackburn E, et al. X-ray diffraction observations of a charge-density-wave order in superconducting ortho-II YBa2Cu3O6.54 single crystals in zero magnetic field. Phys Rev Lett. 2013;110(13):137004. doi: 10.1103/PhysRevLett.110.137004. [DOI] [PubMed] [Google Scholar]
- 25.Le Tacon M, et al. Inelastic X-ray scattering in YBa2Cu3O6.6 reveals giant phonon anomalies and elastic central peak due to charge-density-wave formation. Nat Phys. 2014;10:52–58. [Google Scholar]
- 26.Rosen JA, et al. Surface-enhanced charge-density-wave instability in underdoped Bi2Sr(2-x)La(x)CuO(6+δ) Nat Commun. 2013;4:1977. doi: 10.1038/ncomms2977. [DOI] [PubMed] [Google Scholar]
- 27.Comin R, et al. Charge order driven by Fermi-arc instability in Bi2Sr(2-x)La(x)CuO(6+δ) Science. 2014;343(6169):390–392. doi: 10.1126/science.1242996. [DOI] [PubMed] [Google Scholar]
- 28.Wise WD, et al. Charge-density-wave origin of cuprate checkerboard visualized by scanning tunneling microscopy. Nat Phys. 2008;4(9):696–699. [Google Scholar]
- 29.Doiron-Leyraud N, et al. Hall, Seebeck, and Nernst coefficients of underdoped HgBa2CuO4+δ: Fermi-surface reconstruction in an archetypal cuprate superconductor. Phys Rev X. 2013;3(2):021019. [Google Scholar]
- 30.Torchinsky DH, Mahmood F, Bollinger AT, Božović I, Gedik N. Fluctuating charge-density waves in a cuprate superconductor. Nat Mater. 2013;12(5):387–391. doi: 10.1038/nmat3571. [DOI] [PubMed] [Google Scholar]
- 31.Kohsaka Y, et al. Visualization of the emergence of the pseudogap state and the evolution to superconductivity in a lightly hole-doped Mott insulator. Nat Phys. 2012;8(7):534–538. [Google Scholar]
- 32.Kohsaka Y, et al. An intrinsic bond-centered electronic glass with unidirectional domains in underdoped cuprates. Science. 2007;315(5817):1380–1385. doi: 10.1126/science.1138584. [DOI] [PubMed] [Google Scholar]
- 33.Cai P, et al. 2015. Visualizing the evolution from the Mott insulator to a charge ordered insulator in lightly doped cuprates. arXiv:1508.05586v1.
- 34.Rybicki D, et al. Electronic spin susceptibilities and superconductivity in HgBa2CuO4+δ from nuclear magnetic resonance. Phys Rev B. 2015;92(8):081115. [Google Scholar]
- 35.Bilbro LS, et al. Temporal correlations of superconductivity above the transition temperature in La2-xSrxCuO4 probed by terahertz spectroscopy. Nat Phys. 2011;7(4):298–302. [Google Scholar]
- 36.Chang J, et al. Decrease of upper critical field with underdoping in cuprate superconductors. Nat Phys. 2012;8(10):751–756. [Google Scholar]
- 37.Kokanovic I, Hills DJ, Sutherland ML, Liang R, Cooper JR. Diamagnetism of YBa2Cu3O6+x crystals above Tc: Evidence for Gaussian fluctuations. Phys Rev B. 2013;88(6):060505. [Google Scholar]
- 38.Hwang HY, et al. Scaling of the temperature dependent Hall effect in La2-xSrxCuO4. Phys Rev Lett. 1994;72(16):2636–2639. doi: 10.1103/PhysRevLett.72.2636. [DOI] [PubMed] [Google Scholar]
- 39.Ando Y, Kurita Y, Komiya S, Ono S, Segawa K. Evolution of the Hall coefficient and the peculiar electronic structure of the cuprate superconductors. Phys Rev Lett. 2004;92(19):197001. doi: 10.1103/PhysRevLett.92.197001. [DOI] [PubMed] [Google Scholar]
- 40.Blatter G, Feigel'man MV, Geshkenbein VB, Larkin AI, Vinokur VM. Vortices in high-temperature superconductors. Rev Mod Phys. 1994;66(4):1125–1388. [Google Scholar]
- 41.Safar H, et al. Experimental evidence for a first-order vortex-lattice-melting transition in untwinned, single crystal YBa2Cu3O7. Phys Rev Lett. 1992;69(5):824–827. doi: 10.1103/PhysRevLett.69.824. [DOI] [PubMed] [Google Scholar]
- 42.Zeldov E, et al. Thermodynamic observation of first-order vortex-lattice melting transition in Bi2Sr2CaCu2O8. Nature. 1995;375(6530):373–376. [Google Scholar]
- 43.Heron DOG, et al. Muon-spin rotation measurements of an unusual vortex-glass phase in the layered superconductor Bi2.15Sr1.85CaCu2O8+δ. Phys Rev Lett. 2013;110(10):107004. doi: 10.1103/PhysRevLett.110.107004. [DOI] [PubMed] [Google Scholar]
- 44.Chen H-D, Hu J-P, Capponi S, Arrigoni E, Zhang SC. Antiferromagnetism and hole pair checkerboard in the vortex state of high T(c) superconductors. Phys Rev Lett. 2002;89(13):137004. doi: 10.1103/PhysRevLett.89.137004. [DOI] [PubMed] [Google Scholar]
- 45.Chen H-D, Vafek O, Yazdani A, Zhang S-C. Pair density wave in the pseudogap state of high temperature superconductors. Phys Rev Lett. 2004;93(18):187002. doi: 10.1103/PhysRevLett.93.187002. [DOI] [PubMed] [Google Scholar]
- 46.Tesanović Z. Charge modulation, spin response, and dual Hofstadter butterfly in high-Tc cuprates. Phys Rev Lett. 2004;93(21):217004. doi: 10.1103/PhysRevLett.93.217004. [DOI] [PubMed] [Google Scholar]
- 47.Pereg-Barnea T, Franz M. Duality and the vibrations modes of a Cooper-pair Wigner crystal. Phys Rev B. 2006;74(1):014518. [Google Scholar]
- 48.Li J-X, Wu C-Q, Lee D-H. Checkerboard charge density wave and pseudogap in high-Tc cuprate. Phys Rev B. 2006;74(18):184515. [Google Scholar]
- 49.Berg E, Fradkin E, Kivelson SA. Charge-4e superconductivity from pair-density-wave order in certain high-temperature superconductors. Nat Phys. 2009;5(11):830–833. [Google Scholar]
- 50.Bollinger AT, et al. Superconductor-insulator transition in La2 - xSrxCuO4 at the pair quantum resistance. Nature. 2011;472(7344):458–460. doi: 10.1038/nature09998. [DOI] [PubMed] [Google Scholar]
- 51.Leng X, Garcia-Barriocanal J, Bose S, Lee Y, Goldman AM. Electrostatic control of the evolution from a superconducting phase to an insulating phase in ultrathin YBa2Cu3O(7-x) films. Phys Rev Lett. 2011;107(2):027001. doi: 10.1103/PhysRevLett.107.027001. [DOI] [PubMed] [Google Scholar]
- 52.Fisher MP, Grinstein G, Girvin SM. Presence of quantum diffusion in two dimensions: Universal resistance at the superconductor-insulator transition. Phys Rev Lett. 1990;64(5):587–590. doi: 10.1103/PhysRevLett.64.587. [DOI] [PubMed] [Google Scholar]
- 53.Fisher MP. Quantum phase transitions in disordered two-dimensional superconductors. Phys Rev Lett. 1990;65(7):923–926. doi: 10.1103/PhysRevLett.65.923. [DOI] [PubMed] [Google Scholar]
- 54.Goldman AM, Marković N. Superconductor-insulator transitions in the two-dimensional limit. Phys Today. 1998;51(11):39–44. [Google Scholar]
- 55.Gantmakher VF, Dolgopolov VT. Superconductor-insulator quantum phase transition. Phys Usp. 2010;53(1):1–49. [Google Scholar]
- 56.Rullier-Albenque F, Alloul H, Rikken G. High-field studies of superconducting fluctuations in high-Tc cuprates: Evidence for a small gap distinct from the large pseudogap. Phys Rev B. 2011;84(1):014522. [Google Scholar]
- 57.Rourke PMC, et al. Phase-fluctuating superconductivity in overdoped La2-xSrxCuO4. Nature Phys. 2011;7(6):455–458. [Google Scholar]