Accumulation of formamide in hydrothermal pores to form prebiotic nucleobases

Significance

The aim of this article is to show that prebiotic nucleobases can be formed in hydrothermal pores, through a significant accumulation of formamide resulting from a combination of thermophoresis and convection. We performed numerical finite element calculations for initial formamide concentrations that correspond to early Earth shallow lake conditions and reveal that formamide accumulates at the bottom of hydrothermal pores in about 45–90 d to high concentrated formamide solutions. The conclusion from these findings is that the combination of thermophoretic mass transport and convection is the missing link, which makes the synthesis of prebiotic nucleobases in porous rocks in contact with shallow lakes under early-earth conditions possible.

Abstract

Formamide is one of the important compounds from which prebiotic molecules can be synthesized, provided that its concentration is sufficiently high. For nucleotides and short DNA strands, it has been shown that a high degree of accumulation in hydrothermal pores occurs, so that temperature gradients might play a role in the origin of life [Baaske P, et al. (2007) Proc Natl Acad Sci USA 104(22):9346−9351]. We show that the same combination of thermophoresis and convection in hydrothermal pores leads to accumulation of formamide up to concentrations where nucleobases are formed. The thermophoretic properties of aqueous formamide solutions are studied by means of Infrared Thermal Diffusion Forced Rayleigh Scattering. These data are used in numerical finite element calculations in hydrothermal pores for various initial concentrations, ambient temperatures, and pore sizes. The high degree of formamide accumulation is due to an unusual temperature and concentration dependence of the thermophoretic behavior of formamide. The accumulation fold in part of the pores increases strongly with increasing aspect ratio of the pores, and saturates to highly concentrated aqueous formamide solutions of ∼85 wt% at large aspect ratios. Time-dependent studies show that these high concentrations are reached after 45–90 d, starting with an initial formamide weight fraction of ${10}^{\mathrm{-}3}$ wt % that is typical for concentrations in shallow lakes on early Earth.

Thermophoresis has been suggested as an active transport mechanism to reach high concentrations of prebiotic molecules to culminate in the formation of RNA (1). A still open question is whether thermophoresis can also be a possible mechanism to form prebiotic nucleobases from simple molecules such as hydrogen cyanide (HCN) and formamide (FA). Already for almost 50 years, FA has been discussed as an important compound from which prebiotic molecules originate (2–7). It has been shown that all known nucleobases can be synthesized from aqueous FA solutions (4). In diluted HCN solutions, polymerization of HCN to form nucleobases becomes favored over hydrolysis of HCN at concentrations of 0.03–0.3 wt % (8). To our knowledge, there are no similar studies of diluted FA solutions. Taking into account the faster hydrolysis of FA (3), we estimated that a 100-times-higher concentration between 3 wt % and 33 wt % should be sufficient for the synthesis of prebiotic molecules in aqueous solutions. In the ocean during the early stages of Earth, the natural occurring concentrations at a low temperature (10 °C) and a pH between 6 and 8 are estimated to be only on the order of ${10}^{-9}$ wt %, whereas, in shallow lakes (depth 10 m), due to vaporization and FA input from the atmosphere, higher concentrations of about ${10}^{-3}$ wt % are possible (3). Still, these natural concentrations are far too small compared with those required for the formation of nucleobases.

In this work, we perform numerical calculations for the spatial and time dependence of the concentration of aqueous FA solutions in hydrothermal pores exposed to a temperature gradient to investigate whether it is possible to reach sufficiently high FA concentrations that are necessary to initiate the synthesis of prebiotic nucleobases. The dependence of the highest FA concentration in part of the pore is analyzed as a function of the initial FA concentration, which is the reservoir concentration within the shallow lake, at various ambient temperatures, initial concentrations, and aspect ratios of the pores. The highest FA concentration within the pore relative to the initial FA concentration defines the so-called accumulation fold. The concentration dependence and temperature dependence of the thermodiffusion and mass diffusion coefficients of FA in aqueous solutions as determined by means of Infrared Thermal Diffusion Forced Rayleigh Scattering (IR-TDFRS), as well as other revelant physical properties of FA solutions, are used as an input to these calculations. In contrast to the previous study (1) for nucleotides and short DNA fragments, we do not find an exponential increase of the accumulation fold with increasing pore aspect ratio. Instead, the accumulation fold increases exponentially only at relatively small aspect ratios, sharply increases at intermediate aspect ratios, and, finally, saturates to highly concentrated FA solutions on the order of 85 wt % at relatively large aspect ratios. The sharp increase of the accumulation fold with increasing pore size is found to be essentially independent of the initial, shallow lake concentration.

Thermophoresis, also known as the Ludwig−Soret effect or thermodiffusion, is the migration of particles or molecules induced by a temperature gradient (9). In a binary fluid mixture, this mass transport is described by a contribution of the form $\mathrm{\sim -}{D}_{\text{T}}\overrightarrow{\nabla }T$ to the mass flux $\overrightarrow{\mathit{j}}$, where $D_{\text{T}}$ is the thermodiffusion coefficient. When $D_{\text{T}}\mathrm{>}0$, mass transport occurs from high to low temperature. The total mass flux is thus given by

$$\overrightarrow{j}=-D\overrightarrow{\nabla }c-c\left(1-c\right)D_{\text{T}}\overrightarrow{\nabla }T,$$ [1]

where the first term describes mass transport due to gradients in the concentration c, with D the Fickian or mass diffusion coefficient. For a time-independent temperature gradient, a steady state is reached when the mass fluxes due the Fickian diffusion and thermodiffusion contributions cancel each other. The ratio of the resulting concentration gradient and the applied temperature gradient is characterized by the Soret coefficient $S_T=D_{\text{T}}/D$. A larger Soret coefficient implies a larger concentration gradient for a given temperature gradient.

Several theoretical approaches exist to describe thermodiffusion (or thermophoresis) of liquid mixtures, polymer solutions, and colloidal suspensions (10–13). The review by Würger (11) introduces theoretical concepts for colloids, and the book chapter by Wiegand (13) gives an overview on the basic physics of the effect. An excellent agreement between experimental results and theoretical models has been found for charged spherical and rod-like colloids (14, 15), whereas the interfacial effects as they occur in microemulsions are still not fully understood (16, 17). So far, no microscopic particle-based theory exists to describe thermophoresis on a microscopic level for liquid mixtures, such as aqueous FA solutions. Simulations have been performed to investigate the effects of attractive and repulsive interactions between uncharged and charged colloidal particles (18, 19), to study the influence of chain length and stiffness of polymers (20), or to study specific interactions as they occur in aqueous mixtures (21). Due to their importance in biotechnology, many aqueous systems have been studied experimentally. Although the charge contributions to the thermophoretic movement of the solute molecules are well understood, the contributions of the hydration layer, although of high importance (for example in protein−ligand interactions), are not yet understood. It is known that the Soret coefficient $S_{\text{T}}$ of the solute molecules increases when hydrogen bonds break. There are two mechanisms that can lead to a breaking of hydrogen bonds between solute and water molecules. One possibility is to add an ingredient with a strong affinity to water, so that the bonds open (22). Alternatively, an increase of the temperature disrupts the hydrogen bonds between water and the solute. This leads, for aqueous solutions of biological and synthetic molecules, to a similar temperature dependence of $S_{\text{T}}$ (23), which can be described by an empirical equation proposed by Iacopini et al. (24).

$$S_{\text{T}}\left(T\right)=S_{\text{T}}^{\mathrm{\infty }}\left[1-\exp \left(\frac{T^{\text{*}}-T}{T_0}\right)\right],$$ [2]

with fitting parameters $S_{\text{T}}^{\infty }$, $T^{\mathrm{*}}$, and $T_0$. Recently, it has been shown that the number of hydrogen bond sites of solute molecules plays a key role for describing the temperature dependence of $S_{\text{T}}$ and the thermodiffusion coefficient $D_{\text{T}}$. It turns out that $S_{\text{T}}$ depends linearly on the difference of donor and acceptor sites of the solute molecule belonging to a homologous series (25). Hydrogen bonding certainly plays an important role also in aqueous FA solutions.

Experimental Results

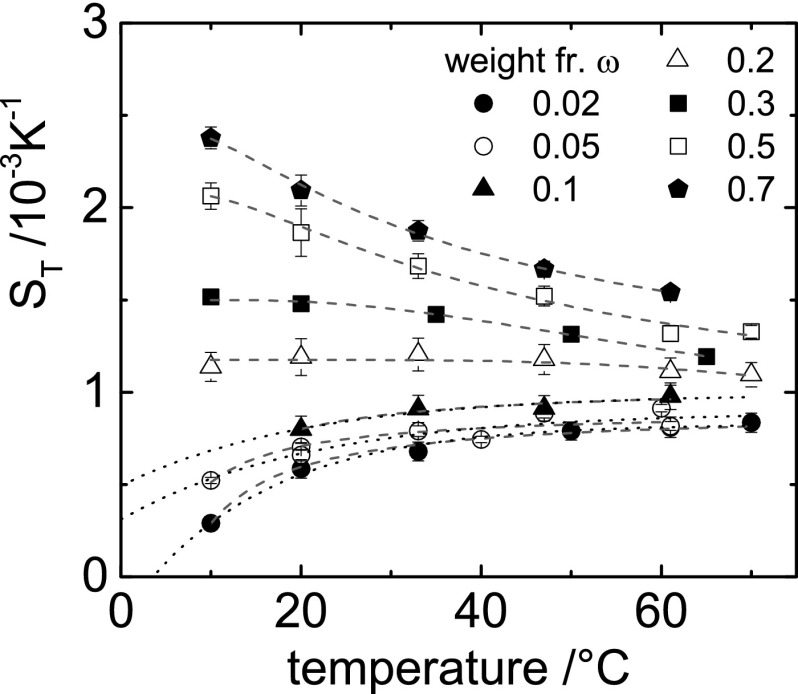
The Soret coefficient of FA/water mixtures was measured by means of IR-TDFRS in the temperature range from 10 °C to 70 °C and in the FA weight fraction range from ω = 0.02 to ω = 0.9. Such measurements require the refractive index of FA solutions as a function of temperature and concentration (SI Appendix, Refractive Index Contrast Measurements). Fig. 1 shows the measured Soret coefficients as a function of temperature for various concentrations. $S_{\text{T}}$ is always positive, which indicates that FA is thermophobic and enriches in the cold regions. Specific to the FA/water system is the sign change of the slope of the temperature dependence from positive to negative on increasing the FA concentration. At low concentrations ($\omega <0.2$), the temperature dependence can be described by Eq. 2 (see the dotted lines in Fig. 1), whereas Eq. 2 is not applicable at higher concentrations, where the Soret coefficient increases with increasing FA concentration. Qualitatively, the often-found temperature dependence of the Soret coefficient as described by Eq. 2 might be explained as follows. At low overall temperatures, the system tries to minimize its local free energy, $F=U-T\mathrm{\cdot }S$, by forming hydrogen bonds, thus minimizing the internal energy U with a relatively small entropic contribution, so that the water molecules accumulate at the cold side. At higher temperatures, where the entropic contribution is dominant, the system minimizes its free energy by maximizing the orientational and translational entropy S, which leads to an enrichment of water molecules on the warm side (26). At higher FA concentrations, Eq. 2 can no longer be used, and it turns out that the temperature dependence can be described empirically by a simple exponential decay,

$$S_{\text{T}}\left(T\right)=S_{\text{T}}^{\infty }+S_{\text{T}}^0\cdot \text{exp}\left(-T/T_0\right),$$ [3]

which corresponds to the dashed curves at high concentrations in Fig. 1. Deviations from Eq. 2 have also been observed for other systems. The most prominent example is the system ethanol/water (27), but, also, dimethyl sulfoxide (DMSO)/water (28) does not follow the general trend at low concentrations. In contrast to FA/water, for high ethanol and DMSO concentrations, an increase of $S_{\text{T}}$ with increasing temperature and a decrease for low concentrations is oberved. Also, Maeda et al. (25) observed a decrease for various types of crown ethers of $S_{\text{T}}$ with increasing concentration.

Fig. 1.

The Soret coefficient as a function of temperature for various FA concentrations (ω is the weight fraction of FA). The dotted lines for the three low concentrations are fits according to Eq. 2, and the dashed lines are fits to Eq. 3.

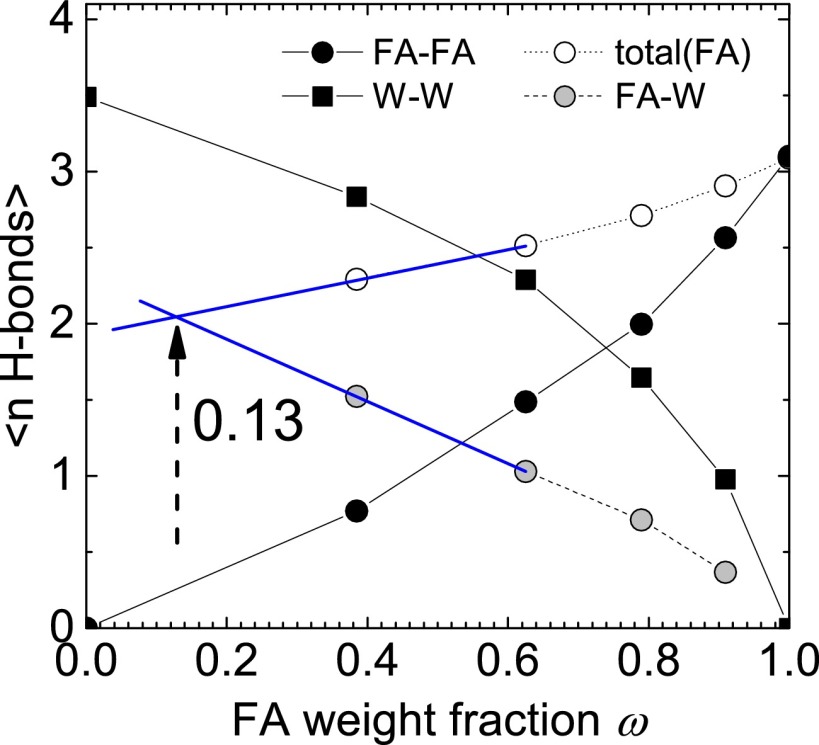
As a consequence of the temperature and concentration dependence shown in Fig. 1, FA accumulates in colder regions for all concentrations, whereas, with increasing concentration, the driving force for accumulation in these regions increases. One could expect that this leads to a self-amplifying mechanism leading to significant FA accumulation. The FA molecule HCONH₂ is a weak base, as it can bind protons to its negatively charged oxygen and the amino group. The pK_a $\mathrm{\approx }$ 20 value of FA is very large, so that the fraction of molecules carrying a positive elementary charge is typically as small as 10⁻¹³. There is thus no measurable charge contribution to the thermodiffusive motion of FA. The molecular dynamic simulations in ref. 29 offer the possibility of understanding the temperature and concentration dependence of aqueous FA solutions in more detail. In Fig. 2, we replot the average number of water−water (W−W), FA−water (FA−W), and FA−FA hydrogen bonds as a function of the FA weight fraction, ω. As expected, the number of hydrogen bonds between water molecules decreases with increasing FA concentration. Accordingly, the number of FA−FA bonds increases. Note that, for pure water, the number of W−W bonds is slightly larger than the number of FA−FA bonds for pure FA, but both solvents show a strong tendency to form hydrogen bonds. With increasing FA concentration, the number of FA−W hydrogen bonds decreases. Around a weight fraction of 0.13, the number of FA−W bonds is equal to the total number of H bonds that FA forms. This is precisely the concentration range where the slope of the temperature dependence of $S_{\text{T}}$ in Fig. 1 changes from positive to negative. This indicates that the temperature dependence as given in Eq. 2 is valid as long as FA molecules are mostly surrounded by water molecules. As soon as FA−FA hydrogen bonds between FA molecules are formed, the temperature dependence of $S_{\text{T}}$ changes from increasing to decreasing with increasing temperature. A possible explanation is that FA at higher concentrations migrates in temperature gradients as entire FA clusters. With increasing concentration, larger and heavier clusters are formed, which have a larger Soret coefficient, whereas, for increasing temperature, the clusters become smaller due to thermal motion, which leads to a decrease of the Soret coefficient.

Fig. 2.

Average number of H bonds in an FA−W mixture as a function of FA weight fraction ω taken from ref. 29. The lines connect the points. The black symbols mark the average number of H bonds between W−W (black squares) and FA−FA (black circles). The total number of FA hydrogen bonds (white circles) is the sum of FA−FA and FA−W bonds. It becomes equal to the average number of H bonds between FA and W (gray circles) in dilute solution around $\omega =0.13$.

As mentioned above, the systems ethanol/water and DMSO/water also do not follow Eq. 2. Compared with FA, both ethanol and DMSO have a much lower hydrogen bond capability, which is only roughly two bonds per molecules, whereas the water hydrogen bond capability lies between 3.5 and 4 per water molecule (30, 31). Both aqueous mixtures show microheterogeneous structures at low concentration (31, 32), which are not formed in the case of FA/water due to their almost equal ability to form hydrogen bonds. As in the case of the crown ethers, the solute molecules are not well interlinked with water molecules. According to computer simulations (33) and near-infrared spectroscopy (34), the water molecules form a clathrate-like structure around the crown ether. Only two water molecules are doubly hydrogen-bonded (bridging) to the crown ether oxygen atoms. In contrast, proteins are often linked to water by 50–100 hydrogen bonds (35), so that the hydrogen bonds of the solute molecules at low concentrations are not influenced by other solute molecules. In conclusion, we can state that Eq. 2 only holds if the solute molecules are well connected to water by hydrogen bonds and no microheterogeneous structures or cages are formed.

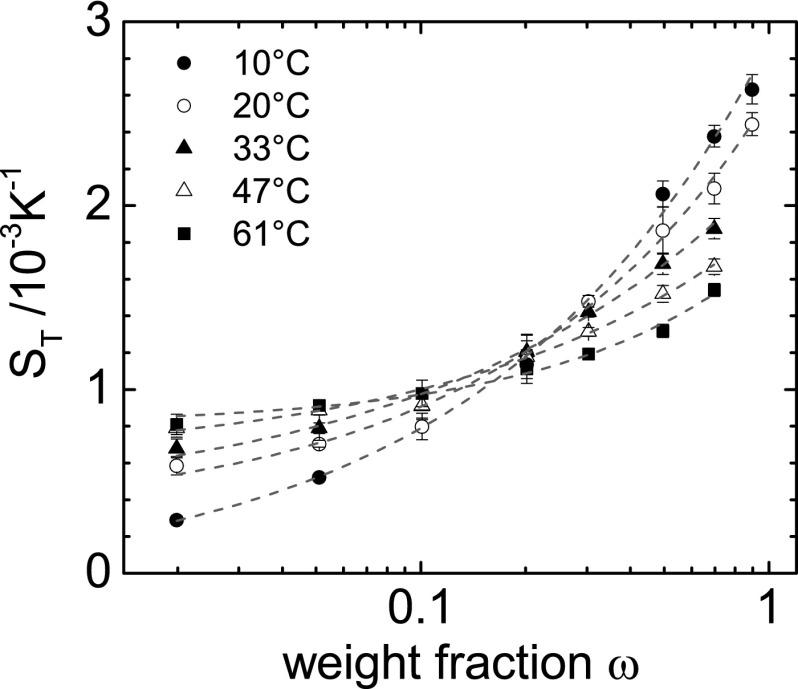
Fig. 3 shows the Soret coefficient of FA as a function of the FA weight fraction ω. The concentration dependence can be described by an empirical equation, which has the form of the so-called Hill equation (36, 37),

$$S_{\text{T}}\left(\omega \right)=\frac{{\omega }^a}{K+{\omega }^a}+S_{\text{T}}^0,$$ [4]

where a, K, and $S_{\text{T}}^0$ are fitting parameters (the dashed lines in Fig. 3). In contrast to many other systems, $S_{\text{T}}$ for FA increases with concentration. The change in the slope of curves at different temperatures leads to a common intersection at a weight fraction of 0.13. Such an intersection point is often found for associated mixtures (28).

Fig. 3.

Soret coefficient as a function of the FA weight fraction, ω, for various temperatures. The solid lines correspond to a fit according to Eq. 4.

Accumulation in Hydrothermal Pores

The stronger accumulation of FA for larger concentrations and lower temperatures raises the question whether it is possible to accumulate sufficient FA by thermophoresis and convection in hydrothermal pores, such that chemical reactions can be initiated to form nucleobases as prebiotic molecules from FA. Using commercial finite element software (COMSOL Multiphysics Modeling Software), we solved the coupled Navier−Stokes, diffusion, and heat transfer equations in two dimensions, and determined the accumulation of FA in similar hydrothermal pores as in ref. 1. The diffusion equation includes both convection and thermophoresis. Numerical calculations use as an input the experimentally determined concentration and temperature dependence of the thermal diffusion and mass diffusion coefficients as obtained from the IR-TDFRS measurements, as well as the viscosity, the specific mass density, the heat conductivity, and the heat capacity of FA/water mixtures (SI Appendix, Temperature and Concentration Dependence). Details on the mesh sizes that were used in the calculations can be found in SI Appendix, Numerical Calculations.

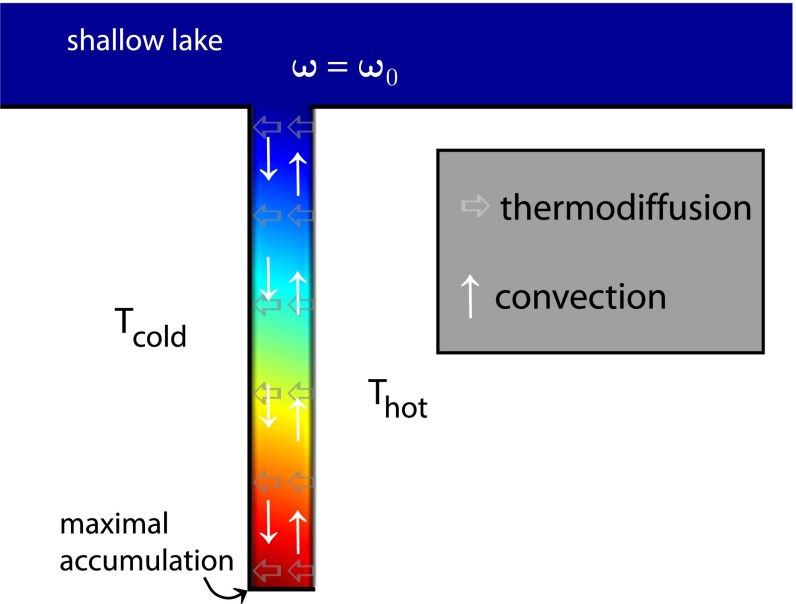
Fig. 4 shows a contour plot of the concentration profile in a pore with aspect ratio 10 in the stationary state. At the top of the pore, the FA concentration is constant, reminiscent of the concentration in a shallow lake. This is also the initial concentration within the pore, before the temperature gradient is switched on. The right side of the pore is warmer compared with the left side, with a temperature difference of 30 K for all calculations. The maximum concentration in the stationary state within the dark red-colored region at the bottom corner of the pore defines the accumulation fold that is of interest here. This is the region where possible formation of nucleobases from FA will take place.

Fig. 4.

Contour plot of the concentration profile in a pore with aspect ratio 10 connected to a reservoir in the stationary state. The vertical and horizontal arrows mark the convective and thermodiffusive flow, respectively.

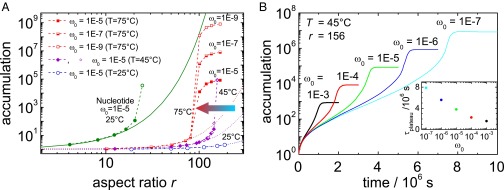
Fig. 5A shows the accumulation fold as a function of the height to width aspect ratio r. For comparison with literature results, we first performed calculations for an aqueous nucleotide solution (see Fig. 5, the green solid dots), with an initial concentration of ${\omega }_0={10}^{-5}$. In this calculation for the nucleotide, literature values for $S_{\text{T}}=0.015\hspace{0.17em}{\text{K}}^{-1}$, as well as for $D=400\hspace{0.17em}\mathrm{\mu }{\text{m}}^2/\text{s}$ were used, whereas the physicochemical properties of pure water were used for the solvent properties, as done in ref. 1. For low aspect ratios, we find good agreement with the exponential function (see Fig. 5, solid line), as proposed in ref. 1. to describe the aspect ratio dependence of the accumulation fold. At high accumulation folds, however, we find the expected deviations from an exponential accumulation as the nucleotide concentration approached 100% saturation. The concentration and temperature dependence of the Soret coefficient and the mass diffusion coefficient of nucleotide solutions for somewhat elevated concentrations is not known. Additionally the solubility of nucleotides is limited, therefore the last data point in Fig. 5A, corresponding to a concentration of 35 wt %, is marked as an open circle to indicate the uncertainty of this data point.

Fig. 5.

(A) Accumulation fold of FA as a function of the aspect ratio r for various initial weight fractions, ${\omega }_0$, and temperatures as indicated in comparison with the accumulation fold for a single nucleotide. The solid line has been calculated using equation 1 in ref. 1, and the dots refer to COMSOL simulations using the physical chemistry properties of water. The accumulation fold of FA at 25 °C, 45 °C, and 75 °C has been determined at a optimal width of 180 μm, 160 μm, and 100 μm, respectively (SI Appendix, Numerical Calculations). All curves show an initial exponential increase, which levels of if the accumulation becomes so strong that it is close to the pure component. (B) Time-dependent study of the accumulation as a function of time for various initial concentrations, ${\omega }_0$, at a width of 160 μm and a height of 25 mm. (Inset) Time to reach the concentration plateau, ${\tau }_{\text{plateau}}$, as a function of the dependence of the accumulation for different initial concentrations ${\omega }_0$.

In contrast to nucleotides, FA and water are miscible at any fraction, so that the entire concentration range is accessible. We studied three different mean temperatures, T_mean = 25 °C, 45 °C, and 75 °C, for the optimal pore widths of 180 μm, 160 μm, and 100 μm, respectively, to achieve an efficient accumulation (SI Appendix, Numerical Calculations). The initial concentration was varied between ${\omega }_0={10}^{-9}$ and ${\omega }_0={10}^{-5}$, corresponding to FA concentrations as predicted for oceans and shallow lakes under early Earth conditions (3). After an initial exponential increase of the accumulation fold with the pore aspect ratio, we observe, for all studies, a steep increase followed by a plateau when the accumulation fold reaches $1/{\omega }_0$ of a pure FA solution, as can be seen from Fig. 5A. This saturation plateau is approached at lower aspect ratios for larger temperatures, thus favoring an accumulation in wider pores at lower ambient temperatures.

Fig. 5B shows the time dependence of the accumulation fold for three initial concentrations ${\omega }_0$, for the same temperature of T_mean = 45 °C and the same pore aspect ratio of 156. For an initial concentration ${\omega }_0={10}^{-5}$, the saturation plateau is reached 45 d after switching on the temperature gradient. Reducing the initial concentration to ${\omega }_0={10}^{-7}$ prolongs the saturation time to 90 d. These are reasonable time ranges to establish regions of sufficiently high FA concentration to synthesize nucleobases.

Discussion

FA is a naturally occurring substance on the early Earth (2–8), with relatively high concentrations on the order of ${10}^{-3}$ wt % in shallow lakes due to the stronger evaporization of water compared with FA, which has a much higher boiling point of $T_{\text{boil}}=210$ °C (3). Numerical finite element calculations for initial FA concentrations that correspond to early Earth shallow lake conditions reveal that FA accumulates at the bottom of hydrothermal pores with aspect ratios between about 100 and 200 and a width in the range of 100–200 μm in about 45 d to high concentrated FA solutions ($\omega \approx 85$ wt %). The conclusion from these findings is that the combination of thermophoretic mass transport and convection may have been at the origin of the synthesis of prebiotic nucleobases in porous rocks in contact with shallow lakes.

The numerical calculations use as an input the experimentally determined concentration and temperature dependence of the Soret coefficient and the mass diffusion coefficient, as obtained by means of IR-TDFRS, of the viscosity, the specific mass density, and the heat conductivity of FA/water mixtures. The positive value of the Soret coefficient for all concentrations leads to an initial accumulation, which is self-enhanced due to the increase of the Soret coefficient with increasing concentration.

Compared with the previously discussed hydrothermal pore accumulation of nucleotides and DNA fragments (1) by thermophoresis and convection, the accumulation of FA is slower and occurs at larger pore aspect ratios. In contrast to FA, the solubility of nucleotides is quite limited, so that the accumulation of nucleotides will be restricted. Besides shallow lakes, mineral surfaces are also proposed to play a role in the origin-of-life concept. These surfaces can act as catalysts in chemical reactions (4) and promote polymerization to form RNA (38–40). Whether such adsorption processes also play a role for the much smaller molecules considered in the present study is an open question. These conditions could affect the accumulation times.

Materials and Methods

Sample Preparation and IR-TDFRS Measurements.

Solutions were prepared using FA ($\mathrm{\ge }99.5$%; Sigma-Aldrich), without further purification, and water (Millipore). All solutions were either used immediately (measurement of contrast factors and density) or kept in a fridge for the duration of the experiment as stock solutions (for the IR-TDFRS measurements). To ascertain the stability of the mixtures against hydrolysis or other chemical reactions, the purity of the stock solution was validated by an accurate determination of the refractive index before each measurement. During the maximum storage time of 8 wk, no significant change was observed.

For the IR-TDFRS measurement, the solutions have been filtered (0.22 μm) directly into the Hellma quartz cells with an optical pass length of 0.2 mm. We used IR-TDFRS, a holographic transient grating technique, to determine the thermophoretic properties. A detailed description of the setup can be found in ref. 41. For analysis of the IR-TDFRS measurement signal, the refractive index contrast factors need to be determined. We measured the refractive index contrast factor with temperature ${\left(\partial n/\partial T\right)}_{p,\omega }$ at constant pressure p and the FA weight fraction ω interferometrically (42) and found, as expected, negative values in the investigated temperature and concentration range. Its magnitude increases with higher FA concentration and decreases with increasing temperature. Measuring the refractive index for various concentrations, we determined ${\left(\partial n/\partial \omega \right)}_{p,T}$. It increases at higher FA concentrations and decreases with rising temperature (see also SI Appendix, Refractive Index Contrast Measurements).

Finite Element Calculations.

To calculate the accumulation of FA in a hydrothermal pore, we solved a combination of Navier−Stokes, heat transfer, and thermodiffusion equations using commercially available finite element software (COMSOL Multiphysics 5.1). The model was built in accordance with the model of Baaske et al. (1). All calculations were done in two dimensions.

In the model, the pore was represented as a rectangle. For the heat transfer equation boundary conditions, the temperatures at the vertical walls (${\mathit{T}}_{\mathrm{left}}\mathrm{=}{T}_{\mathrm{mean}}-\mathrm{\Delta }T$, $T_{\mathrm{right}}=T_{\mathrm{mean}}+\mathrm{\Delta }T$) was fixed, whereas the top and the bottom of the column were considered thermally isolated. The temperature difference, $\mathrm{\Delta }T$, was kept at 30 K for all simulations. For the Navier−Stokes, we used the nonslip boundary conditions for all walls. For the diffusion equation, we fixed the normal flux to zero at the bottom and at the vertical walls, while, at the top of the pore, the concentration was fixed to ${\omega }_0$ as in the simulations by Baaske et al. (1). Fixing the concentration at the top does not contradict the nonslip boundary conditions for the Navier−Stokes equation (top closed for the liquid flow), as the top surface can be, e.g., a porous membrane connected to an external reservoir with concentration ${\omega }_0$. We took into account the temperature and concentration dependence of the thermodiffusion and mass diffusion coefficient, the viscosity, the specific mass density, the heat conductivity, and the heat capacity, part of which is taken from literature (43–49) (SI Appendix, Temperature and Concentration Dependence).

The calculations were done for various aspect ratios of the pore at the optimal pore width. The latter is the width of the column at which the maximum accumulation occurs (1). It was found by running a series of simulations for various widths at a specific height. The optimal width varied with temperature but was constant for all heights. We used three different mean temperatures, T_mean = 25 °C, 45 °C, and 75 °C. The initial concentration ${\omega }_0$ was taken equal to ${10}^{-5}$, ${10}^{-7}$, or ${10}^{-9}$ in accordance with the estimations for the FA concentration at the early Earth conditions (3).