Significance
A central debate in cognitive science concerns the nativist hypothesis: the proposal that universal human behaviors are underpinned by strong, domain-specific, innate constraints on cognition. We use a general model of the processes that shape human behavior—learning, culture, and biological evolution—to test the evolutionary plausibility of this hypothesis. A series of analyses shows that culture radically alters the relationship between natural selection and cognition. Culture facilitates rapid biological adaptation yet rules out nativism: Behavioral universals arise that are underpinned by weak biases rather than strong innate constraints. We therefore expect culture to have dramatically shaped the evolution of the human mind, giving us innate predispositions that only weakly constrain our behavior.
Keywords: nativism, evolution, culture, language
Abstract
A central debate in cognitive science concerns the nativist hypothesis, the proposal that universal features of behavior reflect a biologically determined cognitive substrate: For example, linguistic nativism proposes a domain-specific faculty of language that strongly constrains which languages can be learned. An evolutionary stance appears to provide support for linguistic nativism, because coordinated constraints on variation may facilitate communication and therefore be adaptive. However, language, like many other human behaviors, is underpinned by social learning and cultural transmission alongside biological evolution. We set out two models of these interactions, which show how culture can facilitate rapid biological adaptation yet rule out strong nativization. The amplifying effects of culture can allow weak cognitive biases to have significant population-level consequences, radically increasing the evolvability of weak, defeasible inductive biases; however, the emergence of a strong cultural universal does not imply, nor lead to, nor require, strong innate constraints. From this we must conclude, on evolutionary grounds, that the strong nativist hypothesis for language is false. More generally, because such reciprocal interactions between cultural and biological evolution are not limited to language, nativist explanations for many behaviors should be reconsidered: Evolutionary reasoning shows how we can have cognitively driven behavioral universals and yet extreme plasticity at the level of the individual—if, and only if, we account for the human capacity to transmit knowledge culturally. Wherever culture is involved, weak cognitive biases rather than strong innate constraints should be the default assumption.
A central debate in cognitive science concerns the nativist hypothesis: the proposal that certain universal features of human behavior can be explained by a biologically determined cognitive substrate consisting of “reliably-developing conceptual primitives, content-specialized inferential procedures, representational formats that impose contentful features on different inputs, domain-specific skeletal principles” (ref. 1, p. 309). The nativist hypothesis has been advanced for numerous psychological phenomena, such as concepts (2), folk psychology (3), music perception (4), and religious belief (5).
Perhaps the most widely known example of nativist reasoning comes from Chomsky’s work on language: Linguistic nativism proposes a domain-specific faculty of language that strongly constrains which languages can be learned (6). Linguistic nativism is sometimes taken as the most successful example of nativist reasoning (1), and proof that nativist explanations are necessarily true in at least some domains.
The presence of innate domain-specific constraints on cognition would clearly require an explanation. Such constraints have been persuasively argued to be likely products of natural selection (7). Specifically dealing with constraints on language learning, Pinker and Bloom argue that coordinated constraints on variation may facilitate communication and therefore be adaptive: “the requirement for standardization of communication protocols dictates that …many grammatical principles and constraints must accordingly be hardwired into the [language acquisition] device” (ref. 7, p. 720). This leads naturally to what we will call strong linguistic nativism: an account proposing that there are features of our biologically inherited cognitive machinery that provide hard constraints on what behaviors can be acquired, and that these constraints are domain-specific in the sense that they have evolved via biological evolution under pressure for enhanced communication; in other words, they have evolved for language.
Recent work has questioned the nativist position, either by reassessing the challenges facing language learners (8) or by questioning the evidence for certain types of language universals (9). Here we focus instead on the evolutionary reasoning behind strong nativism. Language, like many other human behaviors, is underpinned by social learning and cultural transmission alongside biological evolution (10, 11): Learners acquire the language of their speech community via a process of learning from observations of the linguistic behavior of that community. Consequently, language is a product of at least two evolutionary processes—biological evolution of the language faculty, and cultural evolution of languages.
In this paper, we test the evolutionary plausibility of strong nativism, by setting out a general model of the interactions between biological and cultural evolution. Two instantiations of this model show that culture can facilitate rapid biological adaptation of the language faculty yet does not deliver hard constraints on learning. Even when strong universal tendencies in behavior emerge, there are few circumstances where strong domain-specific innate constraints on cognition evolve, but many in which culture bootstraps the rapid fixation of weak, defeasible inductive biases.
Evolutionary Perspectives on Linguistic Nativism
How should we expect biology and culture to interact to shape language and the language faculty? One possibility is that the rate of language change far exceeds that of biological evolution, preventing genetic assimilation of linguistic features into the language faculty (12): the “moving target” argument. Chater et al. (12) demonstrate this point convincingly in a series of simulation models showing that biological evolution cannot encode innate constraints for linguistic features that change rapidly as a result of external factors (e.g., language contact). However, some aspects of language exhibit stable statistical regularities, or “language universals”: These are at the center of nativist reasoning and commonly thought to be held stable by constraints on learning (13). Chater et al. also simulate this scenario, finding that, when language is influenced more by the innate constraints of learners than by external factors (a possibility they consider implausible but which might be assumed under the nativist hypothesis), strong constraints on learning do evolve. This work highlights the necessity of understanding how genetic and cultural processes interact to shape language: The plausibility of strong linguistic nativism is contingent on the relationship between individual-level biases and population-level languages.
Another approach to the evolution of constraints on learning is provided by ref. 14, who consider the evolution of constraints on the size of the set of languages considered by learners. They provide two general results. Firstly, there is selection in favor of a language faculty that reduces the size of the search space to levels that allow a population to converge on a shared grammar, as predicted by ref. 7. However, selection will not lead to the most constrained possible learner, because there are costs to being overly constrained (i.e., inability to acquire one of several languages at use in the population). This balance of selective pressures yields learners whose language faculty is permissive, allowing them to learn the largest possible set of languages, but which is nonetheless constraining enough to permit convergence within a population.
Both of these models present important limits on strong nativism. However, both models only consider the evolution of strong constraints on learning: innate mechanisms that effectively dictate whether or not a particular grammar can be acquired. This restriction to “nativism or nothing” rules out a broad class of possible forms of innateness. Many aspects of human cognition (15), and language acquisition in particular (16), may be better characterized by soft constraints: probabilistic inductive biases that can impose a continuum of preferences ranging from weak to strong. Probabilistic inductive biases in acquisition have been proposed to account for universals concerning word order generalizations (13) and hierarchical phrase structure (17) in syntax, suffixing and prefixing asymmetries in morphosyntax (18), and patterns of vowel harmony (19) and velar palatalization (20) in phonology.
A well-known property of cultural evolution is that, under a wide range of circumstances, weak inductive biases acting on learning can have strong effects in the cultural system as the effects of those biases accumulate (10, 21, 22): Given enough time, a weak bias in favor of a particular trait can eventually drive that trait to fixation. Probabilistic constraints combined with culture therefore potentially provide an alternative to nativism or nothing: Behavioral universals can be underpinned by weak biases at the level of the individual.
Here we present two models that allow us to study the biological evolution of a capacity for learning a culturally transmitted behavior. These models combine learning, culture, and evolution in a general way and allow us to look for conditions under which strong nativism might be evolutionarily plausible. We focus on the case where language change is influenced solely by learning, and not by external factors, because it is here that linguistic nativism has received support from evolutionary reasoning, and construct our models around a well-understood, general model of cognition: Bayesian inference. Bayesian models of cognition allow us to explicitly model the influence of innate inductive biases (of various strengths) and environmental input on inference (23, 24), while generalizing over the particular psychological mechanisms that could implement inductive bias. Contemporary approaches to linguistic nativism have cast the debate directly in terms of inductive biases (25, 26), and several core topics of linguistic nativism have been addressed with Bayesian cognitive models.
Our models are maximally abstract: Language learning is reduced to acquisition of a single linguistic feature. Acquisition of natural languages involves learning about many statistically intertwined linguistic features simultaneously; however, this simplification allows us to derive general evolutionary results that relate inductive biases to linguistic structures.
Model 1
In Model 1, we assume a language can be described by a set of discrete absolute principles and potentially variable parameters (27). This perspective has a long pedigree in linguistics, has been described as “the bona fide theory of innateness” (ref. 28, p. 451), and enjoys wide support as a model for nativism, in the broad sense that it posits universal principles and narrowly restricted options for cross-linguistic variation (28–30).
Model Details.
Let F be a linguistic feature that can vary in a binary manner across languages (e.g., F could represent harmony in the ordering of heads and complements across phrasal types). Then, a (potentially infinite) space of possible languages is carved into two possible types, and , based on whether they obey the feature or not (e.g., languages exhibit harmonic ordering across phrase types, whereas languages do not). There are two corresponding classes of utterance, and , which are produced by speakers and portray whether the underlying language is of type or , according to the following likelihood function, where ϵ gives the probability of noise on production,
| [1] |
for . Bayesian learners assess a particular hypothesis h by combining the likelihood of observed dataset d in light of that hypothesis, , with the prior probability of the hypothesis independent of the data observed, , to obtain a posterior probability of that hypothesis: . Here, we interpret the set of hypotheses as the set of possible grammars or language types, so that . Data are sets of utterances from which learners must learn a language: The likelihood of a dataset is simply the product of the likelihood of the individual utterances , with for . The prior probability distribution over grammars reflects the innate biases of learners, and simply assigns probabilities to the two language types: , . Extreme values of α ( or ) would correspond to a principle in standard terminology: a strong or absolute constraint on the type of language that can be acquired by learners, ruling out one type of language; would correspond to an unconstrained learner who can learn either language type.
To model cultural transmission, we use “iterated learning” (21, 22): The data that a learner is exposed to are produced by another individual who learned in the same way. In other words, once the learner has settled on a particular hypothesis, they will produce utterances in line with that hypothesis, from which others can learn.
Finally, we model biological evolution by specifying a set of genes that collectively determine the prior bias of a learner, and which are inherited by new learners, subject to mutation. We treat the prior as a “polygenic” trait (31): The genome of a learner is a set of n genes whose alleles each encode small effects in favor of one language type or the other; the prior probability of a particular hypothesis is simply the proportion of genes that have the allele promoting that hypothesis. If a learner’s genetic endowment includes exactly i genes favoring languages of type (and favor type ), then . Genetic transmission is under selection: In line with other models (14, 32), we assume individuals reproduce with a probability directly proportional to their ability to communicate with the rest of the population; individuals who have the same language type are deemed to communicate successfully. Let be the proportion of the population at generation t made up by learners with prior , and let be the probability that a learner with this prior will acquire a language of type . The fitness of a learner with prior is given by
| [2] |
where c is the population frequency of language type .
Without cultural transmission, the outcome of language acquisition is determined entirely by the learner’s prior preferences, so . However, when cultural transmission is included in the model, the outcome of language acquisition also depends upon the linguistic data a learner encounters, which in turn depend upon the distribution of language types at the previous generation, (see Methods for details of how is calculated in the cultural models). We assume initially that learners acquire their language type by observing utterances produced by a single, randomly chosen individual in the previous generation, and, in Supporting Information, describe a version of our model that relaxes this assumption. We analyze two versions of the cultural model, by contrasting two varieties of Bayesian learner that are known to lead to different cultural evolutionary dynamics (21): “MAP learners” weigh up the posterior probability of both language types and select the winner [i.e., the hypothesis with the highest posterior probability—the maximum a posteriori (MAP) estimate]; “sample learners” pick a language according to its posterior probability. Given the model we have described, the dynamics of biological evolution in the population is given by
| [3] |
where is the probability that the offspring of a learner with prior will, through mutation (see Methods), inherit , and is the average fitness of the population.
Results.
The initial state of each simulation is an unbiased population of learners (i.e., whose genes encode ). A result favoring the strong nativist hypothesis would be one in which natural selection for linguistic coordination leads to the final population’s prior bias consisting of extreme values, or , effectively ruling out one language type.
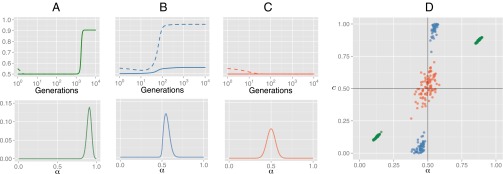
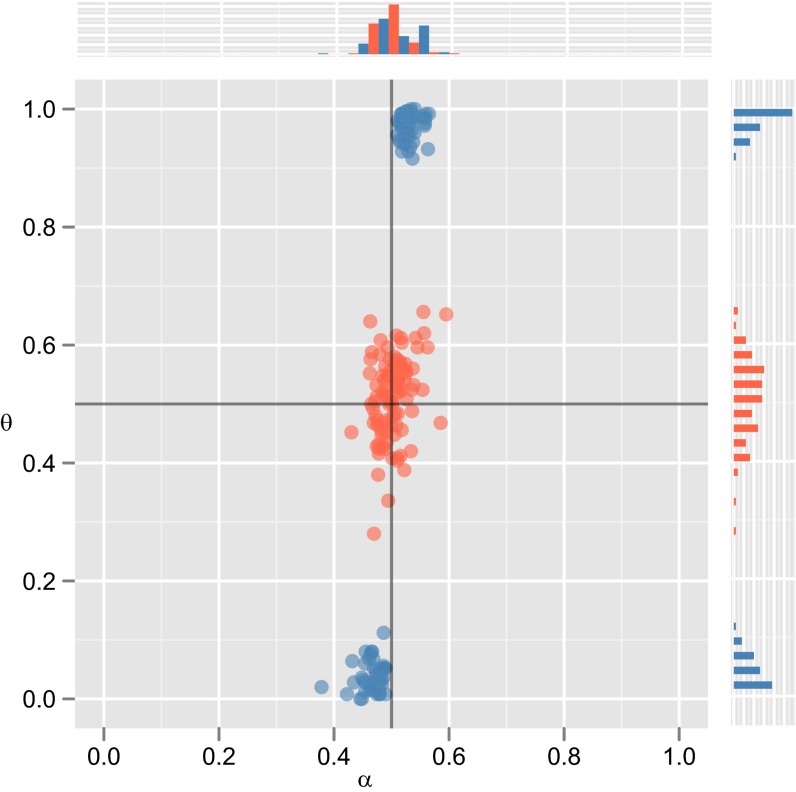
Fig. 1 shows results of numerical and agent-based simulations of these processes. In the baseline model (Fig. 1A) without cultural transmission (comparable to innate signaling in noncultural organisms), after a few thousand generations of gradual change, biological evolution eventually leads to the emergence of strong innate biases for a single language type, which maximizes the communicative utility of that language.
Fig. 1.
Results for the evolutionary model. (A) Results of a numerical model of an infinitely large population, where there is no cultural transmission of language: Individuals select a language with probability given by their genes (i.e., α). (Upper) The evolution of the population’s mean innate bias, α (solid line), which directly determines the proportion of individuals using languages of type (c, dashed line). (Lower) The distribution of α in the population after the model has converged, demonstrating a strong bias in favor of one language type. (B) Results from the model where language is culturally transmitted and in which learners pick the MAP hypothesis (again, solid line shows mean α, and dashed line shows c). (C) The same plots for learners who sample a hypothesis from the posterior distribution. Results of the numerical model give the equilibrium distribution of biases and languages, which reflect the stable outcome of evolution given these conditions. (D) Results from 300 agent-based simulations, giving the values of α and c (the same variables plotted in A−C, Upper) after 10,000 generations in acultural populations (green), and in 1,000 generations in cultural populations of MAP (blue) and sample (red) learners. Results supporting strong universals ( or 1) underpinned by strong nativism ( or 1) would appear in the top left or bottom right corners of this graph but never occur when culture is included in the model; instead, we see strong universals underpinned by weak biases (in MAP populations) or no universals and no constraints on learning (in sampling populations); .
We see a radically different pattern of results when we add cultural transmission to the model. In cultural populations of MAP learners, one language type rapidly comes to dominate the population: Convergence in cultural populations occurs an order of magnitude faster than in acultural populations. However, this strong cultural preference is not directly reflected in the population’s genes. Instead, learners have a very weak bias favoring the majority language type, and could easily acquire the unattested language type given appropriate data. The emergence of a strong cultural universal thus does not imply, nor lead to, nor require, a strong innate constraint. In contrast, under cultural transmission in sampling populations, neither strong innate constraints nor strong language universals emerge. When we include cultural transmission in the model, under no conditions do we see the evolution of strong universals underpinned by strong innate constraints.
Why is this happening? Weak biases in (MAP) individuals are amplified by cultural transmission, driving large effects at the population level (10, 21, 22). In our initial populations, every individual communicates equally well (or poorly): Reproduction occurs at random. Drift of the genes ensues, moving the population away from the perfect equilibrium (in the numerical analysis, we must specify a minor asymmetry in the initial linguistic distribution to mimic this stochastic drift process). At this point, cultural transmission unmasks the tiny biases of individuals, resulting in large effects on the population’s culture: A linguistic universal begins to emerge. Natural selection then favors nonneutrality in the direction of the emerging universal. However, cultural evolution can also mask relative strength of bias (21, 22): Both weak and strong biases can drive strong universals and reliable acquisition of the dominant language; consequently, there is no selection in favor of stronger biases. The combination of unmasking and masking by cultural evolution leads to a balance of forces: Mutation pressure inherent in the genetic model causes drift toward neutrality in the prior, but natural selection keeps individuals away from perfect neutrality. As a result, MAP populations settle on the weakest possible biases that nevertheless ensure convergence on a single language type, leading to universals.
Sampling does not lead to the amplifying effect normally associated with cultural evolution; rather, the culture of sample learners tracks their biases (21). Weak biases provided by drift are never unmasked: There is no consistent selective pressure for a particular bias that would result from a cultural universal generated by unmasking. Neither strong innate constraints nor strong universals emerge: Genes and culture drift, in lockstep, toward a distribution determined by mutation.
Supporting Information presents a range of variations on this model, testing alternative basic assumptions about learning, culture, and biology. We test cases where learners learn from multiple teachers, where genomes vary continuously, where one language is functionally superior, and where both MAP and sample learners exist in the population. In the latter case, as predicted in ref. 33, MAP learners outcompete sample learners, suggesting the pattern of results for MAP learners is the more robust prediction. In none of these variants does evolution lead to nativization (Figs. S1–S5).
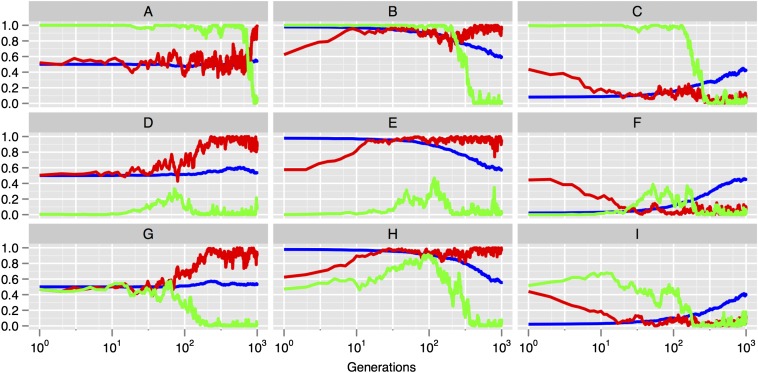
Fig. S1.
Results for the model of the evolution of learning strategies. Natural selection of hypothesis selection strategy, showing weak biases rather than strong innate constraints, are always the end result, regardless of starting conditions. The green line shows the proportion of samplers in the population (they are always removed by natural selection), the red line shows c, the proportion of the population speaking languages of type T1 (this always ends up close to 1 or 0), and the blue line shows α, the strength of the innate bias toward languages of type T1 (this always ends up close to, but not on, 0.5). A–I show results under a range of starting conditions.
Fig. S5.
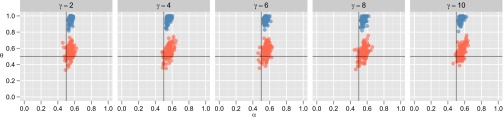
The end points (after 1,000 generations) of our agent-based simulations in which different languages afford their speakers different fitness advantages. Populations of MAP learners (blue) support linguistic universals with weak genetic biases in the direction of language type . Populations of sample learners (red) tend to evolve weak biases toward the fitter language, although these don’t give rise to a linguistic universal. .
Model 2
Model 1 assumes learners acquire a discrete linguistic feature by choosing between just two hypotheses. This discreteness abstracts away from the continuous variation often thought to be characteristic of human learning. To address this limitation, we reformulate the model to reflect an alternative view of linguistic knowledge: Language acquisition reflects statistical inference over probabilistic relationships between grammatical categories.
Model Details.
Let be a simple stochastic grammar that specifies constraints on the possible orderings of grammatical categories X and Y. During acquisition, the learner infers a probabilistic generalization about the ordering of these categories: We could interpret this model of acquisition as applying to proposed universals concerning suffixing and prefixing, or the ordering of verbs and their objects, for example.
Let p be the probability of ordering , such that , and . The learner must make inferences about the underlying probabilities of the two ordering patterns by inducing an estimate : The set of hypotheses a learner considers is infinitely fine-grained, with the learner entertaining all values of p in the range . We consider a noncultural model and the two types of Bayesian learner as before. Methods details the model of Bayesian inference we adopt, and describes a flexible scheme for specifying a prior distribution over this hypothesis space based on the learner’s genes. For direct comparison with Model 1, we explore the case where the expected value of the prior over p reflects the proportion of the learner’s genes promoting ordering XY. Formally, . Again, fitness reflects the ability to communicate by coordinating on an ordering of X and Y.
Results.
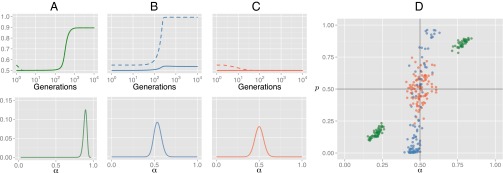
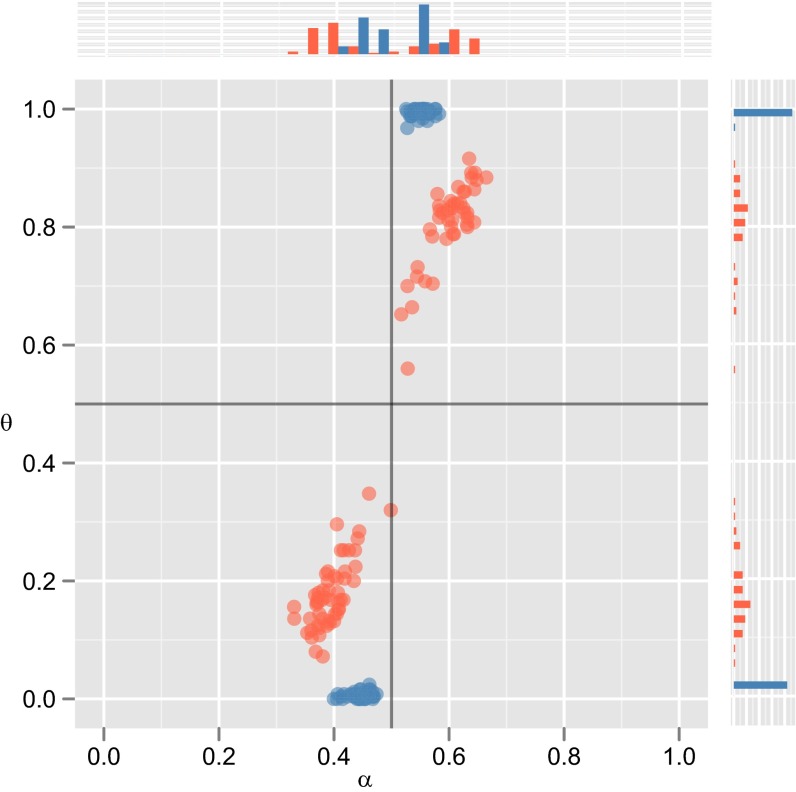
Evolution in Model 2 (Fig. 2) reproduces the key results seen in Model 1. In acultural populations, evolution leads to fixation of strong inductive biases favoring one particular fixed ordering for X and Y. Including culture in the model radically changes the outcome of evolution. In populations of MAP learners, we observe rapid fixation of weak inductive biases that drive a strong cultural universal. In populations of sample learners, again, evolution leads nowhere: no fixation of domain-specific inductive biases and no cultural universals. Again, results hold under a broad parameter range, being particularly robust in MAP populations (see Supporting Information for testing).
Fig. 2.
Evolution in model 2. (A−C) Equilibrium distribution of priors α (Lower) and timecourse dynamics (Upper) for the mean of the population’s prior (α, solid lines) and expected use of ordering (p, dashed lines), in acultural (A), and cultural (B, MAP learners; C, sample learners) populations. (D) Results of 300 agent-based simulations of the model (100 acultural, 100 MAP, 100 Sample) in populations of 100 learners after 1,000 generations: Points show the mean of the population’s prior (α) and expected use of ordering (p) in the final population;.
Discussion
These models show that cultural transmission radically changes the evolution of constraints on learning, rendering strong linguistic nativism untenable on evolutionary grounds. On the one hand, unmasking facilitates rapid evolution of domain-specific biases: Due to culture, the population-level consequences of those biases are amplified and visible to selection. However, masking makes evolving strong constraints unlikely: Given that weak constraints have equivalent effects to strong constraints, there is little or no selection for stronger constraints (34). Note that we do not rule out strong innate constraints on language learning that are domain-general, i.e., have not evolved for the purpose of constraining learning to facilitate communication. For example, we might expect strong evolved constraints that are truly domain-independent [e.g., constraints on statistical learning mechanisms (8) or principles of efficient computation (35) that apply to language and other systems], or which are a consequence of architectural constraints that are a byproduct of our evolutionary history [e.g., spandrels, or developmental constraints (35)]. We may also expect adaptations in the peripheral machinery for language (e.g., vocal anatomy and associated neural machinery), which may follow different evolutionary dynamics (36).
Weak biases are defeasible: The cultural environment can easily overrule these dispositions. This removes any apparent paradox in the idea that we can have biologically driven behavioral universals but nevertheless extreme plasticity at the level of the individual [see, e.g., work demonstrating that the visual cortex can be recruited for language processing in congenitally blind adults (37)]. Under an account assuming that behavioral universals can only be explained in terms of strong innate constraints, such individual-level plasticity is puzzling; however, under an account where cultural evolution mediates between the biases of individuals and behavioral universals, such plasticity is, in fact, predicted.
Weak constraints are also highly evolvable: Evidence for recent rapid adaptation in humans (38) may reflect rapid fixation of weak biases rather than the construction of strongly constraining domain-specific cognitive modules. Our models predict an increase in the rate and number of cognitive adaptations with the onset of culture in human evolution (11) and that the genetic underpinnings of these adaptations may be difficult to detect.
Conclusions
Culture mediates between the biases of individual learners and population-level tendencies or universals. This radically changes the predictions we should make about the language faculty, or any other system of constrained cultural learning: Specifically, the evolution of strong domain-specific constraints on learning is ruled out. Rather, the behavioral universals that these constraints are invoked to explain can instead be produced by weak biases, amplified by cultural transmission. Although we have framed our model in terms of language and linguistic nativism, the same account may be applicable to any behavior that is the product of interactions between culture and biology: Wherever cognition has been shaped to acquire culturally transmitted behaviors, our arguments should apply. We anticipate that cultural transmission may be amplifying the effects of learning biases in many domains of human behavior, mimicking the effects of strong innate constraints and inviting nativist overinterpretation; identifying these domains is a key priority. The default explanation of shared, universal aspects of language or other cultural behaviors should be in terms of weak innate constraints.
Methods
Model 1.
To calculate acquisition probabilities in the model with cultural transmission, we must account for the range of possible datasets d each learner could encounter and the inferences she would make in each case, so that
| [4] |
Assuming a single teacher is randomly sampled from the previous generation, the probability of learning from a speaker of is [and of is ], so the likelihood, , of observing dataset d is
| [5] |
Induction probabilities for sample learners follow posterior probabilities directly, so . For MAP learners, these are
| [6] |
During reproduction, each of a learner’s n genes may mutate with independent probability μ into a gene of the opposite type. Because there are possible genomes with i genes favoring , it is nontrivial to calculate the mutation probabilities between priors. However, it can be shown that
| [7] |
We obtain the equilibrium distribution of biases and language types by specifying initial distributions and , and iterating the recursion Eq. 3 to find the resulting numerical solutions that satisfy , where is a probability vector for the s, and superscripts index time points. In all numerical analyses of both models, for .
Model 2.
The learner’s prior over p follows a Beta distribution with parameters and ,
| [8] |
The data a learner observes consists of N independent utterances that exemplify an ordering pattern for X and Y, of which some number exemplify the specific ordering . The likelihood for is the binomial distribution
| [9] |
The posterior for p given y is also a Beta distribution,
| [10] |
Let give the expected outcome of language acquisition for each class of learner at generation t: is the expected outcome for a learner with i genes promoting ordering XY. Without culture, reflects the expected value when sampling randomly from the prior, given by the prior mean,
| [11] |
With culture, is conditional on the data a learner sees. Summarizing the possible datasets by the possible counts y (which are sufficient statistics), then, in the sample learner model,
| [12] |
where the outcome of acquisition given y reflects the expected value when sampling from the posterior, the posterior mean,
| [13] |
Likewise, in the MAP learner model,
| [14] |
where the outcome of acquisition reflects the maximum a posteriori estimate, or the posterior mode, which is known to be
| [15] |
Fitness can be computed, at the mean field level, with
| [16] |
where is the overall expected value for p in the population. Thus, the recursion for biological dynamics becomes
| [17] |
Finally, we must specify the relationship between genes and prior parameters, and . Let and reflect the ratio of gene types in the genome, smoothed by a constant λ,
| [18] |
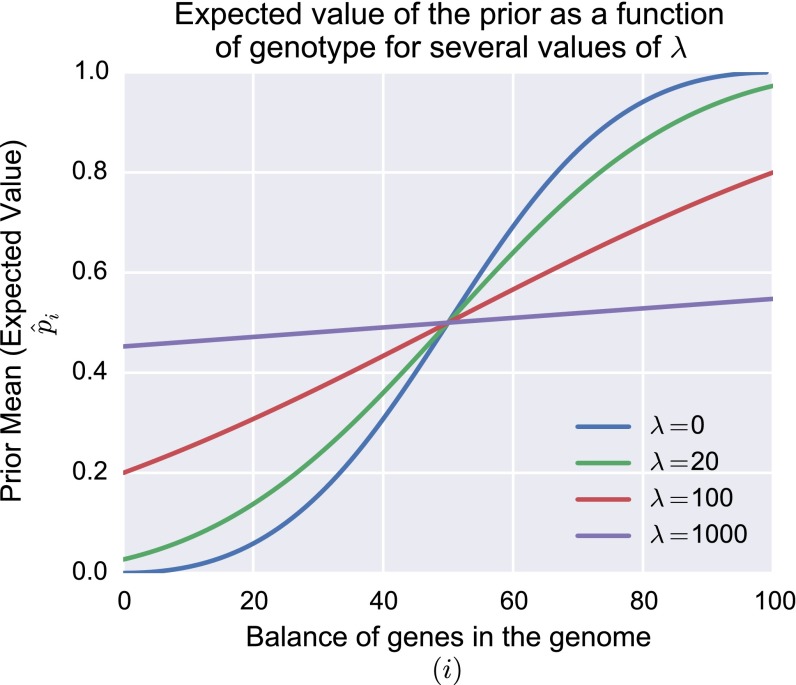
The uniform prior () is given by a uniform distribution of gene types as in Model 1, because . The parameter controls the relationship between asymmetry in the gene distribution and the shape of the prior distribution over p. See Supporting Information for details and analysis (Figs. S6–S8). Here we set , which for our example ensures the approximately linear relationship between the balance of genes in the genome and the prior.
Fig. S6.
The expected value of the prior over p, as a function of gene type distribution (i), for several values of the smoothing parameter λ.
Fig. S8.
Stable evolutionary outcomes in populations of sample learners over a range of values for N and λ. Panels show the average distribution of gene types in the learners’ genomes (Left, genes), the average expected value of the prior distributions over p (Middle, prior), and the average value of p in the population (Right, language).
Variations on Model 1
Agent-based simulations of finite populations offer an alternative way to implement our mathematical model. This method allows us to easily effect and report more considerable variations on the assumptions laid out in Model 1 and Model 2 in the main text. Implementing a computer simulation of our model involves the following steps: (i) initialize—create a population of simulated agents, assign each agent a language at random, and randomly assign each agent a genome from the set of genomes that encode neutral priors; (ii) evaluate and reproduce—each agent is assigned a fitness score, and agents reproduce, to create a new population of agents who have inherited genomes from the previous population; (iii) learn—agents from the old population speak, and, on the basis of this linguistic data, each agent in the new population induces a language, and the old population is discarded; and (iv) iterate—repeat steps ii and iii for a given number of generations.
Our numerical results are maintained using this method (see Fig. 1 —the simulations reported there were set up with parameters ). However, in our simulations with MAP learners, asymmetries in the early distributions of languages and priors, which cause fixation of one language type and of biases that support that universal, are the result of stochastic effects. This means that, because the two language types are arbitrarily distinct, we observe distinct outcomes across simulations. That is, in some simulations, populations converge on language type , and, in others, on type . We present a series of simulations that test pertinent variations of our model. In each case, our assumptions are exactly as described in the main text, except for the elements in focus.
MAP and Sample Learners.
Our first modification is to explore evolutionary outcomes in the case where populations contain both MAP and sample learners. In these simulations, each learner has an additional separate gene that can take one of two possible forms, MAP or sample, and determines whether the learner is a MAP learner or a sample learner. During reproduction, this gene is passed on, along with the agent’s genome, to its offspring. Inheritance of this gene is also subject to mutation: With probability μ, the gene will mutate to the alternative type. The results of these simulations are shown in Fig. S1. MAP learners, and the associated evolutionary dynamic (weak biases driving a universal), always outcompete sample learners. The simulations were set up with parameters .
A Continuous Genome Space.
To rule out the possibility that our results are specific to the polygenic genome model, we explore an alternative method of representing a space of genetic types. Here, a genome is a real number from the set , which determines α directly. We assume, in this case, that genomes, and consequently α values, vary continuously in this range and are distributed according to a beta distribution with matched shape parameters . We implement this assumption through the mutation operator. As before, a parent genome q will mutate during reproduction with probability μ. If q does mutate, a child value is generated from a normal distribution with mean q and SD σ. If the generated value is greater than 1 or less than zero, it is reflected onto the legal range (see ref. 39 for details of this process). This value is then accepted with a probability proportional to its likelihood under our beta distribution. If rejected, a new child value is generated and reflected, and the process repeats until a child value is accepted. Where , all genomes are a priori equiprobable. As , stronger biases become less probable than weaker biases, which are less probable than neutral priors (the distribution is bell-shaped around 0.5). Fig. S2 shows the results of simulations using this genome regime. In MAP populations (blue), we observe the emergence of a linguistic universal supported by weak biases toward that language type. In sample populations (red), no linguistic universals emerge, and no nativization is observed. Our findings generalize to a continuous space of genetic types.
Fig. S2.
The end points of 200 agent-based simulations where learners’ genomes come from a continuous space of possibilities. This pattern of results closely resembles that observed under the polygenic genome model: linguistic universals supported by weak biases in populations of MAP learners (blue points) and no universals and no nativization in populations of sample learners (red points). .
Multiple Teachers.
It has been suggested that fundamental dynamics of language evolution emerge as a result of learners receiving linguistic input from more than one model. Likewise, evolutionary analyses of other traits, such as social learning itself (40), have shown that learning from multiple individuals can lead to dynamics comparable to bias amplification. Because our main model makes the assumption that learners learn from a single teacher, it is possible that our findings may not generalize to the case where learners have multiple teachers. To test this possibility, we adopt two existing models of language evolution through learning from multiple teachers, and modify our simulations to include this element. First, following ref. 41, we simply relax the assumption that each of our learners gets all of their utterances from a single individual. In this case, we assume that each of our learners has N randomly selected teachers from the previous generation, each of whom provides a single utterance to the learner. Smith (41) shows that, in this case, the distribution of languages in a population does not transparently reflect the predispositions of a learner, even in populations of sample learners; rather, cultural transmission amplifies weak biases and historical conditions. Our results support this suggestion. Under these circumstances, both MAP and sampling learning strategies result in amplification of prior biases and patterns of results that generally resemble those observed in MAP populations; consequently, as shown in Fig. S3, we observe the evolution of weak priors (not strong innate constraints) under both MAP and sampling selection when learners learn from multiple teachers, strengthening our conclusion.
Fig. S3.
Results from a model in which learners acquire their language from multiple teachers, and demonstrates that, in a more realistic model where learners have multiple cultural parents, populations of samplers can end up with stronger linguistic universals than in the single-parent model. However, strong innate constraints still do not evolve. , 1,000 generations.
Under Smith’s model of cultural transmission (41), learners are attempting to select a single grammar on the basis of evidence generated by multiple grammars. This violates the rationality of the learners. An alternative model has been proposed that escapes this issue (details in ref. 42). In this model, rather than learning a single language, learners attempt to induce a distribution over languages. Here a learner’s prior has two components: a base distribution over languages , which specifies a learner’s preferences for specific languages and is directly comparable to our parameter α, and a concentration parameter that determines a learner’s expectations about the homogeneity of the linguistic community. For the purposes of our current simulations, we are only interested in evolving the base distribution and so must set the concentration parameter to some fixed value. We fix the concentration parameter low (0.005) and evolve , which we take to be a single parameter characterizing the base distribution such that and . We assume is specified by a genome in exactly the same way as our parameter α, so that . Here θ denotes the average distribution over languages induced by learners in the population. Each member of the population induces a distribution over languages, such that the learner believes languages and are in use with relative proportions and c: We use θ to denote the mean of these individually inferred distributions. The results of our implementation of Burkett and Griffiths’ model are presented in Fig. S4 (this model currently only considers sample learners). Again, we see rapid fixation, in the culture of these populations, of linguistic distributions that are skewed considerably toward one language over the other. As with Smith’s model, these distributions are supported by weak genetic biases toward the majority language.
Fig. S4.
The end results of 100 agent-based simulations where learners induce a distribution over languages (they are multilingual), each run for 1,000 generations. Again we see skews in the cultures of these populations that are not reflected in the genetics: cultural near-universals supported by weak genetic biases. Concentration parameter = 0.005, .
Nonarbitrary Languages.
Our models so far have, in response to trends in the debates surrounding these topics, specifically focused on the case where linguistic variation is arbitrary: Neither language type offers any functional or fitness advantage over the other. Here we add to our model the parameter γ, which regulates the relative fitness advantage that each language affords to its speakers by scaling the fitness advantage afforded to speakers of , so that now
| [S1] |
Where , speakers of language receive an increased fitness advantage. Fig. S5 shows the results of our simulations in which we assume speakers of language receive a fitness advantage greater than that received by speakers of language , for a range of γ values. In the case of populations of MAP learners (blue points), results appear to be unchanged: emergence of a linguistic universal in the direction of the more adaptive language supported by genomes that encode weak biases toward that language. In the case of sample learners (red points), we still see no emergence of linguistic universals, nor any coordinated fixation of nonneutral genetic variants.
Initial Population Composition.
Here we note the effects of assuming a different composition in the initial populations of learners. In particular, it is revealing to consider the case in which initial populations are assumed to already possess a hard constraint against one language type. This is akin to a scenario of exaptation, which, in the main text, we allow as a possible source of strong constraints. In brief, our testing suggests that there may be circumstances where even exaptation may not lead to the maintenance of strong constraints. Specifically, in populations of MAP learners, prebuilt-in initially strong biases are degraded into a shared weak bias over the course of evolution, as a result of masking and mutation pressure, leading to the same result as when biases are constructed from neutrality: stable weak innate constraints supporting a universal. In populations of sample learners, an initial hard constraint is also degraded, but to a lesser extent: The population maintains moderate biases. This demonstrates that shared moderate-strength biases supporting a near-universal could, if preexisting, be maintained in populations of sample learners but, crucially, are not reachable from neutrality: Strong biases are not evolvable. This result is revealing, and a useful validation of the model: It shows that the model doesn’t inherently “build out” the possibility of (near) universals among sample learners; rather, it is the evolutionary dynamics induced by culture that ensure that, unless strong biases are built in from the start for some other reason, the system can’t converge on this solution.
Model 2
In model 2, we must specify the link between the balance of genes in a learner’s genome and the parameters of the Beta prior over p. Although there are many interesting ways to form this link, we choose to let and reflect the ratio of gene types in the learner’s genome, smoothed by a parameter constant λ. For our purposes, we wish to model a smooth linear relationship between the balance of gene types and the expected value of the prior over p. Given the properties of the Beta distribution, our approach allows us to achieve approximately this relationship, and ensure a number of desirable characteristics. As , small imbalances in gene types cause more than proportionally strong inductive biases, because the ratio of i and grows sharply with deviations from neutral. As , the construction of strong innate inductive biases requires many genetic changes, and, in the limit, all genomes encode arbitrarily weak inductive biases. Fig. S6 shows the expected value of the prior over p as a function of i—the number of genes promoting ordering in the genome—for several values of λ. With no smoothing (, blue line in Fig. S6), small genetic imbalances (e.g., ) buy a disproportionately strong cognitive bias, whereas, under higher values (e.g., , red line in Fig. S6), larger asymmetries among gene types are required to construct the same cognitive bias.
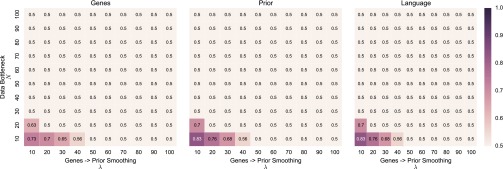
We favor the conservative assumption that more restrictive cognitive specialization requires at least a proportional degree of genetic change, and we confine our analysis in the main text to the proportional case. The impact of this assumption, and its interaction with other parameters, can be straightforwardly tested. Figs. S7 and S8 show, for MAP and sample learner populations, respectively, evolutionary outcomes over a broad parameter range for λ and N (the size of the bottleneck on cultural transmission). The figures show, for each combination of λ and N, the equilibrium distribution obtained numerically in the mathematical model, at the population level, of gene-type asymmetry (Left, squares show), the expected value for p under the prior (Middle, squares show ), and the cultural distribution of (Right, squares show ).
Fig. S7.
Stable evolutionary outcomes in populations of MAP learners over a range of values for N and λ. Panels show the average distribution of gene types in the learners’ genomes (Left, genes), the average expected value of the prior distributions over p (Middle, prior), and the average value of p in the population (Right, language).
Results for MAP populations (Fig. S7) are qualitatively insensitive to changes in these parameters: As we have found in all our analyses, the weak bias − strong universal dynamic brought about by masking and unmasking in these populations appears to be robust even to significant changes in assumption. Results in sample learner populations (Fig. S8) show a similar but weaker insensitivity to these parameters. Under the majority of the parameter range, evolution among sample learners leads nowhere, mirroring our result in the main text. Evolution can only lead to nativization under two conditions: (i) small genetic asymmetries lead to the construction of more than proportionally strong biases (low λ) and (ii) the data bottleneck is tight relative to the continuous space of hypotheses (low N). These results make sense: If strong cognitive biases emerge as a result of minor mutations, and can overpower very limited linguistic data, conditions are highly favorable to nativization. By the first of these conditions, even where strong biases have evolved, we should not expect to find substantial associated genetic changes.
Acknowledgments
B.T. received support from the Engineering and Physical Sciences Research Council and the European Research Council (ABACUS 283435). S.K. received support from the Economic and Social Research Council (ES/G010536/1) and the Arts and Humanities Research Council (AH/F017677/1).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1523631113/-/DCSupplemental.
References
- 1.Tooby J, Cosmides L, Barrett HC. In: The Innate Mind: Structure and Content. Carruthers P, Laurence S, Stich S, editors. Oxford Univ Press; Oxford: 2005. pp. 305–337. [Google Scholar]
- 2.Carey S. The Origins of Concepts. Oxford Univ Press; Oxford: 2009. [Google Scholar]
- 3.Leslie AM. In: Mapping the Domain Specificity in Cognition and Culture. Hirschfeld LA, Gelman SA, editors. Cambridge Univ Press; Cambridge, UK: 1994. [Google Scholar]
- 4.Justus T, Hutsler JJ. Fundamental issues in the evolutionary psychology of music: Assessing innateness and domain specificity. Music Percept. 2005;23(1):1–27. [Google Scholar]
- 5.Boyer P. The Naturalness of Religious Ideas: A Cognitive Theory of Religion. Univ Calif Press; Berkeley, CA: 1994. [Google Scholar]
- 6.Chomsky N. Aspects of the Theory of Syntax. MIT Press; Cambridge, MA: 1965. [Google Scholar]
- 7.Pinker S, Bloom P. Natural language and natural selection. Behav Brain Sci. 1990;13(4):707–784. [Google Scholar]
- 8.Monaghan P, Christiansen MH. In: Corpora in Language Acquisition Research: History, Methods, Perspectives. Behrens H, editor. John Benjamins; Amsterdam: 2008. pp. 139–164. [Google Scholar]
- 9.Evans N, Levinson SC. The myth of language universals: Language diversity and its importance for cognitive science. Behav Brain Sci. 2009;32(5):429–448, and discussion (2009) 32(5):448–494. doi: 10.1017/S0140525X0999094X. [DOI] [PubMed] [Google Scholar]
- 10.Boyd R, Richerson PJ. Culture and the Evolutionary Process. Univ Chicago Press; Chicago: 1985. [Google Scholar]
- 11.Laland KN, Odling-Smee J, Myles S. How culture shaped the human genome: Bringing genetics and the human sciences together. Nat Rev Genet. 2010;11(2):137–148. doi: 10.1038/nrg2734. [DOI] [PubMed] [Google Scholar]
- 12.Chater N, Reali F, Christiansen MH. Restrictions on biological adaptation in language evolution. Proc Natl Acad Sci USA. 2009;106(4):1015–1020. doi: 10.1073/pnas.0807191106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Culbertson J, Smolensky P, Legendre G. Learning biases predict a word order universal. Cognition. 2012;122(3):306–329. doi: 10.1016/j.cognition.2011.10.017. [DOI] [PubMed] [Google Scholar]
- 14.Nowak MA, Komarova NL, Niyogi P. Evolution of universal grammar. Science. 2001;291(5501):114–118. doi: 10.1126/science.291.5501.114. [DOI] [PubMed] [Google Scholar]
- 15.Griffiths TL, Chater N, Kemp C, Perfors A, Tenenbaum JB. Probabilistic models of cognition: Exploring representations and inductive biases. Trends Cogn Sci. 2010;14(8):357–364. doi: 10.1016/j.tics.2010.05.004. [DOI] [PubMed] [Google Scholar]
- 16.Hsu AS, Chater N, Vitányi PMB. The probabilistic analysis of language acquisition: Theoretical, computational, and experimental analysis. Cognition. 2011;120(3):380–390. doi: 10.1016/j.cognition.2011.02.013. [DOI] [PubMed] [Google Scholar]
- 17.Culbertson J, Adger D. Language learners privilege structured meaning over surface frequency. Proc Natl Acad Sci USA. 2014;111(16):5842–5847. doi: 10.1073/pnas.1320525111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.St Clair MC, Monaghan P, Ramscar M. Relationships between language structure and language learning: The suffixing preference and grammatical categorization. Cogn Sci. 2009;33(7):1317–1329. doi: 10.1111/j.1551-6709.2009.01065.x. [DOI] [PubMed] [Google Scholar]
- 19.Finley S, Badecker W. Learning biases for vowel height harmony. J Cogn Sci. 2012;13(3):287–327. [Google Scholar]
- 20.Wilson C. Learning phonology with substantive bias: An experimental and computational study of velar palatalization. Cogn Sci. 2006;30(5):945–982. doi: 10.1207/s15516709cog0000_89. [DOI] [PubMed] [Google Scholar]
- 21.Griffiths TL, Kalish ML. Language evolution by iterated learning with Bayesian agents. Cogn Sci. 2007;31(3):441–480. doi: 10.1080/15326900701326576. [DOI] [PubMed] [Google Scholar]
- 22.Kirby S, Dowman M, Griffiths TL. Innateness and culture in the evolution of language. Proc Natl Acad Sci USA. 2007;104(12):5241–5245. doi: 10.1073/pnas.0608222104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Fitch WT. Toward a computational framework for cognitive biology: Unifying approaches from cognitive neuroscience and comparative cognition. Phys Life Rev. 2014;11(3):329–364. doi: 10.1016/j.plrev.2014.04.005. [DOI] [PubMed] [Google Scholar]
- 24.Spelke ES, Kinzler KD. Innateness, learning, and rationality. Child Dev Perspect. 2009;3(2):96–98. doi: 10.1111/j.1750-8606.2009.00085.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Culbertson J. Typological universals as reflections of biased learning: Evidence from artificial language learning. Lang Linguist Compass. 2012;6(5):310–329. [Google Scholar]
- 26.Pearl L, Sprouse J. Syntactic islands and learning biases: Combining experimental syntax and computational modeling to investigate the language acquisition problem. Lang Acquis. 2013;20(1):23–68. [Google Scholar]
- 27.Chomsky N. Knowledge of Language: Its Nature, Origin and Use. Foris; Dordrecht, The Netherlands: 1987. [Google Scholar]
- 28.Yang CD. Universal Grammar, statistics or both? Trends Cogn Sci. 2004;8(10):451–456. doi: 10.1016/j.tics.2004.08.006. [DOI] [PubMed] [Google Scholar]
- 29.Baker M. The Atoms of Language: The Mind’s Hidden Rules of Grammar. Oxford Univ Press; Oxford: 2001. p. 288. [Google Scholar]
- 30.Crain S, Khlentzos D, Thornton R. Universal Grammar versus language diversity. Lingua. 2010;120(12):2668–2672. [Google Scholar]
- 31.Rockman MV. The QTN program and the alleles that matter for evolution: All that’s gold does not glitter. Evolution. 2012;66(1):1–17. doi: 10.1111/j.1558-5646.2011.01486.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Briscoe T. Grammatical acquisition: Inductive bias and coevolution of language and the language acquisition device. Language. 2000;76(2):245–296. [Google Scholar]
- 33.Smith K, Kirby S. Cultural evolution: Implications for understanding the human language faculty and its evolution. Philos Trans R Soc Lond B Biol Sci. 2008;363(1509):3591–3603. doi: 10.1098/rstb.2008.0145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Deacon TW. Colloquium paper: A role for relaxed selection in the evolution of the language capacity. Proc Natl Acad Sci USA. 2010;107(Suppl 2):9000–9006. doi: 10.1073/pnas.0914624107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Chomsky N. Three factors in language design. Linguist Inq. 2005;36(1):1–22. [Google Scholar]
- 36.de Boer B. Simulating the Evolution of Language. Springer; New York: 2002. pp. 79–97. [Google Scholar]
- 37.Bedny M, Pascual-Leone A, Dodell-Feder D, Fedorenko E, Saxe R. Language processing in the occipital cortex of congenitally blind adults. Proc Natl Acad Sci USA. 2011;108(11):4429–4434. doi: 10.1073/pnas.1014818108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hawks J, Wang ET, Cochran GM, Harpending HC, Moyzis RK. Recent acceleration of human adaptive evolution. Proc Natl Acad Sci USA. 2007;104(52):20753–20758. doi: 10.1073/pnas.0707650104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Bullock S. 2001. Smooth operator? Understanding and Visualising Mutation Bias, eds Kelemen J, Sosik P (Springer, Prague), pp 602–612.
- 40.Perreault C, Moya C, Boyd R. A Bayesian approach to the evolution of social learning. Evol Hum Behav. 2012;33(5):449–459. [Google Scholar]
- 41.Smith K. Iterated Learning in Populations of Bayesian Agents. Cogn Sci Soc; Austin, TX: 2009. pp. 697–702. [Google Scholar]
- 42.Burkett D, Griffiths TL. Iterated Learning of Multiple Languages from Multiple Teachers. In: Smith ADM, Schouwstra M, de Boer B, Smith K, editors. World Sci; Singapore: 2010. pp. 58–65. [Google Scholar]