Necessity of capillary modes in a minimal model of nanoscale hydrophobic solvation

Significance

Hydrophobic effects, which play a crucial role in many chemical and biological processes, originate in the statistics of microscopic density fluctuations in liquid water. Chandler has established the foundation for a simple and unified understanding of these effects, by identifying essential aspects of water’s intermolecular structure while accounting for its proximity to phase coexistence. Here, we show that coarse-grained models based on this perspective, when constructed to include the statistics of capillary waves at interfaces, can achieve remarkable agreement with results of atomistically detailed simulations. Highly efficient and lacking adjustable parameters, such models hold promise as powerful tools for studying multiscale problems in hydrophobic solvation.

Abstract

Modern theories of the hydrophobic effect highlight its dependence on length scale, emphasizing the importance of interfaces in the vicinity of sizable hydrophobes. We recently showed that a faithful treatment of such nanoscale interfaces requires careful attention to the statistics of capillary waves, with significant quantitative implications for the calculation of solvation thermodynamics. Here, we show that a coarse-grained lattice model like that of Chandler [Chandler D (2005) Nature 437(7059):640–647], when informed by this understanding, can capture a broad range of hydrophobic behaviors with striking accuracy. Specifically, we calculate probability distributions for microscopic density fluctuations that agree very well with results of atomistic simulations, even many SDs from the mean and even for probe volumes in highly heterogeneous environments. This accuracy is achieved without adjustment of free parameters, because the model is fully specified by well-known properties of liquid water. As examples of its utility, we compute the free-energy profile for a solute crossing the air–water interface, as well as the thermodynamic cost of evacuating the space between extended nanoscale surfaces. These calculations suggest that a highly reduced model for aqueous solvation can enable efficient multiscale modeling of spatial organization driven by hydrophobic and interfacial forces.

Hydrophobic forces play a crucial role in biological self-assembly, protein folding, ion channel gating, and lipid membrane dynamics (1–9). The origin and strength of these forces are well understood at extreme length scales, based on the recognition that accommodating an ideal volume-excluding hydrophobe in water carries the same thermodynamic cost as evacuating solvent from the corresponding volume. On the scale of a small molecule like methane, density fluctuations that enable such evacuation are Gaussian-distributed to a very good approximation, even far from the mean (10). Linear response theories, such as Pratt–Chandler theory, can thus be quite accurate for assessing solvation of individual small hydrophobic species.

Solvation at much larger scales is, by contrast, dominated by water’s proximity to liquid–vapor coexistence. Hydrophobic forces involving extended substrates are shaped by the physics of interfaces and are quantified by macroscopic parameters like surface tension. In between these extremes, a rich variety of hydrophobic effects results from the combined importance of nearby phase coexistence and details of intermolecular structure. Capturing this interplay, for instance, near a biological macromolecule, presents a significant challenge for theory.

Lum–Chandler–Weeks (LCW) theory represents the modern understanding of hydrophobic solvation, providing a conceptual and mathematical framework to couple interfacial forces with the short-wavelength density fluctuations that determine solvation of small molecules (10, 11). The theory’s physical perspective has inspired the development of coarse-grained lattice models, whose applications have revealed interesting and general mechanisms for the role of water in hydrophobic self-assembly processes (2, 12, 13). Primitive versions of these models, however, long appeared unable to achieve close quantitative agreement with atomistically detailed simulations (e.g., for the probabilities of extreme number density fluctuations in nanometer-scale probe volumes). This shortcoming motivated the construction of more elaborate models, which include interactions between nonadjacent lattice sites (13) and/or explicit coupling between density fluctuations at short and long wavelengths (12). Quantitative accuracy improved as a result of these additions, but close agreement with detailed simulations remained elusive, despite the expanded set of adjustable parameters.

The prominence of interfacial physics in this understanding of hydrophobic effects suggests that the quantitative success of a coarse-grained model hinges on its ability to accurately capture the natural shape fluctuations of a liquid–vapor interface (1, 14–16). We recently showed that doing so with LCW-inspired lattice models requires closer attention to the statistical mechanics of capillary waves than was previously paid (14, 17). These fluctuations are pronounced in molecular simulations but present in lattice models only for sufficiently weak coupling ε between lattice sites [i.e., only at temperatures above the roughening transition $T_{\text{R}}$ (18)]. In this rough regime, the relationship between the microscopic cohesive energy ε and the macroscopic surface tension γ is nontrivial. This previously unrecognized connection, which is essential for faithfully representing the spectrum of capillary waves, yields a lattice model parameterization that is substantially different from that in previous work (17), and has thus presented, to our knowledge, the first primitive LCW-inspired lattice model that fully respects the statistical mechanics of capillary waves.

Here, we put the lattice model of ref. 17 to a number of exacting tests, which probe the models’ ability to accurately describe density fluctuations on the nanometer scales relevant to protein biophysics. Despite its coarseness and lack of adjustable parameters, this model achieves remarkably close agreement with atomistic simulations, even in scenarios with strong spatial heterogeneity. These tests assess the importance of details we have omitted, such as explicit coupling between short- and long-wavelength density fields.

A careful analysis of our results underscores the interplay of length scales accomplished by the coarse-grained model, highlights the importance of capillary fluctuations, and emphasizes the special environment for solvation presented by extended interfaces. Our ultimate conclusion is that diverse hydrophobic phenomena can be captured quantitatively at a coarse-grained level, with minimal attention to atomic-scale intermolecular structure. It is sufficient to capture the correct physics at extreme length scales and link them with simple excluded volume constraints. We illustrate the promise of such models as practical tools with an application to the association of hydrophobic plates.

Coarse-Graining Water

Coarse-grained models motivated by the LCW approach separately account for density fluctuations at small and large length scales. As described by Chandler and coworkers in refs. 12 and 13, long-wavelength variations are represented on a lattice with microscopic resolution on the order of a molecular diameter. In the absence of solutes, walls, or constraints, the corresponding binary occupation variables $n_i$, which indicate either vapor-like ($n_i=0$) or liquid-like ($n_i=1$) density in cell i, are governed by a lattice gas Hamiltonian

$$H=-\mathit{ϵ}{\displaystyle \sum _{\langle i,j\rangle }{n}_i{n}_j}-\mu {\displaystyle \sum _i{n}_i},$$ [1]

where μ is the chemical potential for cell occupation and ${\mathrm{\sum }}_{\langle i,j\rangle }$ indicates summation over all pairs of nearest neighbor cells. We consider ambient thermodynamic conditions, at which liquid is slightly more stable than vapor, $\mu \approx -3\mathit{ϵ}+\delta \mu ,$ where $\delta \mu$ is the chemical potential offset from coexistence (12) unless otherwise specified. As in ref. 17, we set $\mathit{ϵ}/T=1.35,$ within the narrow range that is consistent with the statistical mechanics of rough interfaces yet far from criticality. The lattice spacing $\delta =1.84$ Å is chosen to reproduce the experimentally determined surface tension ${\gamma }_w=72\text{mN}/{\text{nm}}^2$ of the air–water interface, according to the approximate relation

$$\pi \beta {\gamma }_w{\delta }^2={\left(\beta \mathit{ϵ}\right)}^2$$ [2]

derived in ref. 17. In addition to having the correct surface tension, the power spectrum of interfacial height fluctuations of the lattice gas exhibits capillary scaling for this parameter set of $\mathit{ϵ},\delta .$

Regions that are locally liquid-like $(n_i=1)$ additionally support short-wavelength density fluctuations $\delta \rho \left(\mathbf{r}\right),$ which are assumed to obey Gaussian statistics (11). In the absence of constraints, these continuous fluctuations are characterized by the two-point correlation function

$$\chi \left(\mathbf{r}-\mathbf{r}\prime \right)\equiv \langle \delta \rho \left(\mathbf{r}\right)\delta \rho (\mathbf{r}\prime )\rangle ={\rho }_{\ell }\delta \left(\mathbf{r}-\mathbf{r}\prime \right)+{\rho }_{\ell }^2\left(g\left(\mathbf{r}-\mathbf{r}\prime \right)-1\right),$$ [3]

where $\mathbf{r}$ and $\mathbf{r}\prime$ label positions inside the liquid, ${\rho }_{\ell }$ is the macroscopic number density of pure liquid water, and $g\left(r\right)$ is the radial distribution function (19). We use estimates of $g\left(r\right)$ and its Fourier transform obtained from experimental measurements by Narten and Levy (20).

We consider ideal hydrophobic solutes, whose influence on the solvent is to exclude it from a volume v. Weak, smoothly varying attractive interactions between solute and solvent amount to a small perturbation in this context. The effect of, for example, dispersion forces can therefore be reasonably addressed using perturbation theory (12, 13).

We model such idealized solutes by imposing a constraint of solvent evacuation: the total density within v must vanish,

$${\displaystyle \sum _{i\in v}\left[n_i{\rho }_{\ell }{v}_i+{\displaystyle {\int }_{v_i}d\mathbf{r}\hspace{0.17em}\delta \rho \left(\mathbf{r}\right)}\right]}=0,$$ [4]

where the sum runs over all lattice cells i that intersect v, and $v_i$ is the corresponding volume of intersection.

Gaussian fluctuations in the rapidly varying field $\delta \rho \left(\mathbf{r}\right)$ can be integrated out exactly (11), yielding an effective Hamiltonian $H_v\left[\left\{n_i\right\}\right]$ for the lattice occupation variables. In the presence of m ideal volume-excluding solutes (12, 13),

$$H_v\left[\left\{n_i\right\}\right]=-\mathit{ϵ}{\displaystyle \sum _{\langle i,j\rangle }{n}_i{n}_j}-\mu {\displaystyle \sum n_i}+\frac{T}{2}\left[{\overline{N}}^{\mathrm{\top }}{\chi }_{\text{in}}^{-1}\overline{N}+C\right],$$ [5]

where $\overline{N}$ is an m-component column vector with elements

$$N_{\alpha }={\text{Σ}}_i{\rho }_l{n}_i{v}_i^{\left(\alpha \right)}.$$ [6]

$v_i^{\left(\alpha \right)}$ denotes the volume of overlap between the ${\alpha }^{\text{th}}$ solute and lattice cell i, and ${\chi }_{\text{in}}$ is an $m\times m$ square matrix with elements

$${\left({\chi }_{\text{in}}\right)}_{\alpha ,\beta }={\displaystyle {\int }_{\mathbf{r}\in v^{\left(\alpha \right)}}{\displaystyle {\int }_{\mathbf{r}\prime \in v^{\left(\beta \right)}}\mathrm{\Theta }\left(\mathbf{r}\right)\chi \left(\mathbf{r},\mathbf{r}\prime \right)\mathrm{\Theta }(\mathbf{r}\prime )}}.$$ [7]

Here, $\mathrm{\Theta }\left(\mathbf{r}\right)=1$ if the lattice cell containing $\mathbf{r}$ is occupied by solvent and vanishes otherwise. The constant C is given by

$$C=\{\begin{array}{ll}\text{ln}\left(\text{det}\left(2\pi {\chi }_{\text{in}}\right)\right)\hfill & \text{if}\hspace{0.17em}{\displaystyle {\sum }_{\alpha }{\overline{N}}_{\alpha }>1,}\hfill \\ \text{max}\left[\text{ln}\left(\text{det}\left(2\pi {\chi }_{\text{in}}\right)\right),{\displaystyle {\sum }_{\alpha }{\overline{N}}_{\alpha }}\right]\hfill & \text{otherwise}\hspace{0.17em}.\hfill \end{array}$$ [8]

The last two terms in Eq. 5 improve upon previous lattice-based models, providing a computationally tractable yet quantitatively accurate approximation for solute–solute interactions mediated by Gaussian density fluctuations in the surrounding solvent. Starting from a Gaussian field theory (11), the fluctuations may be derived by applying the constraint in Eq. 4 separately to each solute’s excluded volume. Details of this derivation are included in the Supporting Information.

Note that the coarse-grained model defined by Eq. 5 has essentially no free parameters—in light of Eq. 2, there is very little freedom in the choice of ε and δ (17). We only require the surface tension of water and the bulk radial distribution function $g\left(r\right).$ The lattice model also lacks explicit energetic coupling between the density fields $n_i$ and $\delta \rho \left(\mathbf{r}\right).$ The fields’ interdependence arises strictly from the excluded volume constraint expressed in Eq. 4.

Below, we compare calculations based on this coarse-grained model with results of atomistic molecular dynamics (MD) simulations. Molecular simulations were performed using the extended simple point charge (SPC/E) model of water (Methods). Several of these calculations scrutinize the extreme wings of probability distributions, which were accessed using standard techniques of umbrella sampling (Methods).

Results and Discussion

We have performed calculations that stringently assess the ability of an LCW-inspired lattice model to capture details of hydrophobic solvation at small-, large-, and intermediate-length scales. We focus on characterizing and comparing the statistics of density fluctuations within microscopic probe volumes, in part because of the fluctuations’ direct relevance to solubility. Specifically, we calculate the probability $P_v\left(N\right)$ of observing N solvent molecules within a probe volume of size v. The probability distribution’s extreme value determines the excess chemical potential ${\mu }_{\text{ex}}\left(v\right)$ of an ideal hydrophobe with the corresponding excluded volume, ${\mu }_{\text{ex}}\left(v\right)=-T\hspace{0.17em}\ln \hspace{0.17em}{P}_v\left(0\right).$ The behavior of $P_v\left(N\right)$ between this extreme case $(N=0)$ and more typical values $(N\approx {\rho }_{\ell }v)$ reveals much about the physical nature of fluctuations that might be accessed through application of external fields, solute attractions, or changes in thermodynamic state (2, 3). With these implications in mind, we have computed $P_v\left(N\right)$ over its entire meaningful range for a variety of scenarios pertinent to solvation in complex environments.

In addition to atomistically detailed MD simulations and our LCW-inspired lattice model, we present results for several less sophisticated models. These simpler descriptions lack one or more of the physical ingredients underlying LCW theory and thus shed light on their relative importance. For example, short-wavelength fluctuations can be straightforwardly neglected by studying the conventional lattice gas described by Eq. 1, which lacks biases from Gaussian fluctuations in $\delta \rho \left(\mathbf{r}\right).$ In this case, density variations within a probe volume can be achieved only through fluctuations of the binary occupation variables $n_i.$ For the parameterization, we have described $(\mathit{ϵ}/T=1.35,$ $\delta =1.84$ Å), which ensures $T>T_{\text{R}},$ interfaces of this lattice gas exhibit a spectrum of capillary modes comparable to that of a natural liquid–vapor interface. Fluctuations and responses of these capillary modes may contribute significantly to solvation structure and thermodynamics (4–6).

To assess the importance of capillary fluctuations, we examine a different parameterization of Eq. 1 $(\mathit{ϵ}/T=6,$ $\delta =4$ Å), for which $T<T_{\text{R}}.$ This lattice gas too supports interfaces with the correct surface tension. Because its roughening transition lies above ambient temperature, however, the lattice gas with $T<T_{\text{R}}$ lacks fluctuations in the surface-topography characteristic of capillary modes (i.e., the typical amplitude of long-wavelength undulations is not proportional to the undulations’ wavelength). Results from this model thus isolate the contribution of interfacial flexibility to hydrophobic effects, a flexibility that is also neglected in the mean field treatment of LCW theory (17).

Together, these calculations explore the interplay between short- and long-wavelength aspects of hydrophobicity. We find in general that a simple LCW-inspired lattice model can describe with surprising accuracy the statistics of density fluctuations observed in detailed molecular simulations. This success is compromised substantially, in most cases, by omitting the effects of short-wavelength fluctuations and/or capillary waves, suggesting that our coarse-grained model contains a minimum of microscopic detail required to quantitatively capture the solvation and association of nanoscale hydrophobic species.

Statistics of Density Fluctuations in Bulk Water.

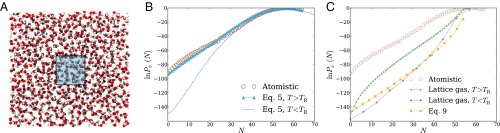
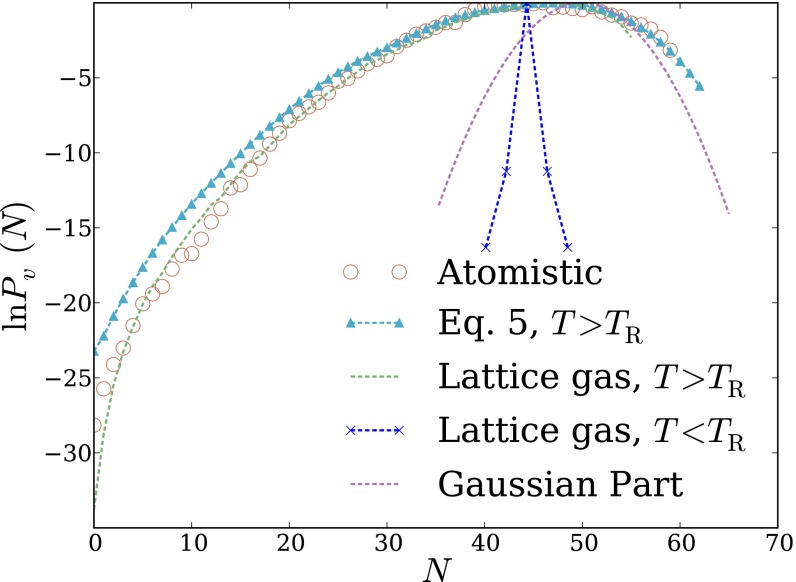
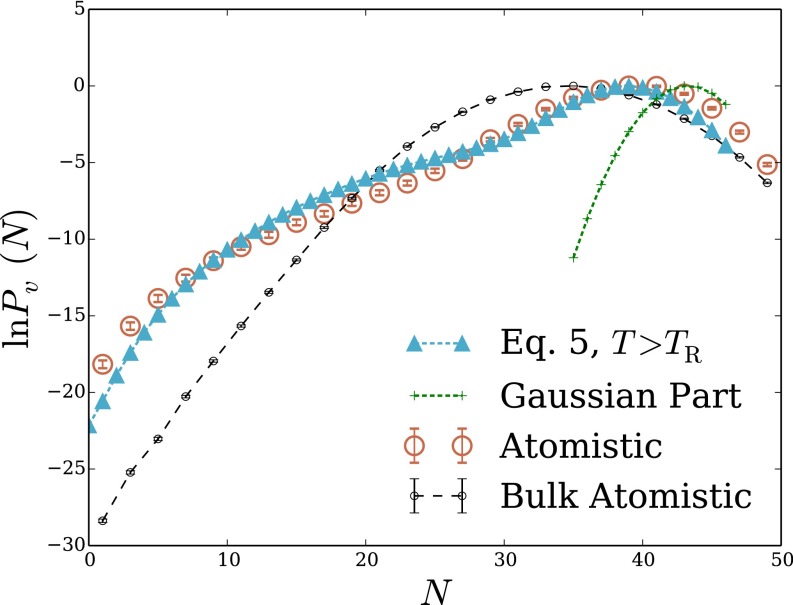
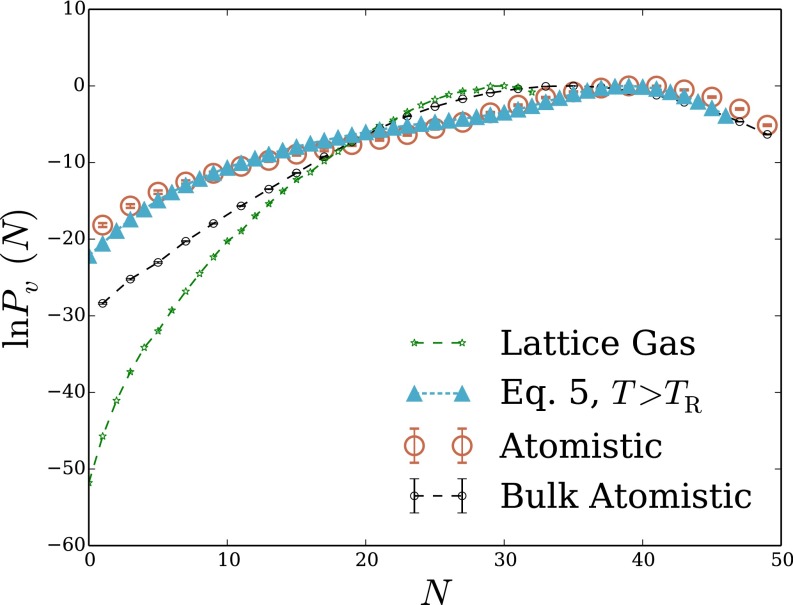
We first examine density fluctuations in the simplest aqueous environment (i.e., bulk liquid water). It has been well established by MD simulations that for small probe volumes $(v\lesssim 0.5$ nm³) in this homogeneous setting, $P_v\left(N\right)$ has a Gaussian form well into the probability distribution’s tails (10). For larger v, low-density fluctuations are strongly biased by the small chemical potential difference between macroscopic liquid and vapor. $P_v\left(N\right)$ then develops an exponential tail, decaying much more slowly than the Gaussian fluctuations near $\langle N\rangle ={\rho }_{\ell }v$ would suggest (13). These basic features of $P_v\left(N\right)$ are essentially built into LCW-inspired models, but the features’ details can be quite sensitive to the way such models are constructed and parameterized. As shown in Fig. 1B, the model of Eq. 5, when parameterized with attention to capillary fluctuations, does an excellent job reproducing distributions obtained from atomistic MD simulations for nanometer-scale cubic probe volumes, over a very wide range of N.

Fig. 1.

Density fluctuations within a cubic probe volume, of size 12 Å $\times$ 12 Å $\times$ 12 Å, in bulk liquid water. (A) Cross-sectional snapshot from an atomistic MD simulation, showing the probe volume v in blue. (B and C) Probability distribution $P_v\left(N\right)$ of the number of water molecules whose center lies in v. Results are shown for atomistic simulations, for the LCW-inspired coarse-grained model of Eq. 5, for the conventional lattice gas of Eq. 1, and for the continuum estimate of Eq. 9. Lattice models were simulated with two parameter sets consistent with the macroscopic surface tension of the air–water interface. The lower temperature case $(T<T_{\text{R}}$ parameters, $\mathit{ϵ}/T=6,$ $\delta =4$ Å) does not support capillary fluctuations. The $T>T_{\text{R}}$ parameters $(\mathit{ϵ}/T=1.35$, $\delta =1.84$ Å), by contrast, describe an interface whose shape fluctuations are consistent with capillary wave theory. Results for Eq. 5 with the $T<T_{\text{R}}$ parameters, plotted in B, data from ref. 13.

Reversibly decreasing N in atomistic simulations from its average value induces formation of a small, roughly cubic cavity that grows to span v as $N\to 0.$ This scenario suggests a simple continuum estimate of $P_v\left(N\right)$ that resolves only the growing interfacial area of the cavity as the probe volume is evacuated. The surface area of a cubic cavity that accommodates an average of N water molecules in bulk is $A=6{\left(N/{\rho }_l\right)}^{2/3},$ which we use as an estimate of the surface area of the cavity that appears as water molecules evacuate the probe volume. Assigning the macroscopic surface tension ${\gamma }_w$ as the free-energy cost per unit area of the microscopic cavity, we obtain a prediction for the decay rate of the exponential tail of $P_v\left(N\right),$

$$\frac{\partial \hspace{0.17em}\ln \hspace{0.17em}{P}_v\left(N\right)}{\partial N}\approx 4\beta {\gamma }_w{\left(\frac{{\rho }_l^2}{\langle N\rangle -N}\right)}^{1/3},$$ [9]

that agrees reasonably well with detailed simulation results. Lacking sensitivity to microscopic fluctuations, this estimate (plotted in Fig. 1C) unsurprisingly fails to capture the Gaussian character of $P_v\left(N\right)$ near $\langle N\rangle .$ Nor does it describe well the overall free-energy scale associated with emptying v, erring by more than 70 $k_{\text{B}}T.$

Fig. 1C also shows results obtained from simulations of the lattice gas with $T<T_{\text{R}}.$ The parameters’ prediction for $P_v\left(N\right)$ closely resembles the simple continuum estimate of Eq. 9, accurately describing the low-density slope, but not the scale or peak behavior, of $\ln \hspace{0.17em}{P}_v\left(N\right).$ This similarity highlights limitations of lattice models at temperatures below the roughening transition temperature. The deficiency of spontaneous fluctuations in interfacial shape begets an overly stiff response to fields or constraints imposed by solutes. Lattice degrees of freedom serve here only to coarsely determine static interfaces when solutes are large enough to induce drying. Lack of capillary modes further renders the surface tension of a lattice gas below the roughening transition temperature anisotropic, introducing the possibility of strong lattice artifacts. In this case of a nanometer-scale cubic probe volume in bulk liquid, correspondence with the continuum estimate suggests that such artifacts are not substantial.

The parameterization of Eq. 1 that we have advocated, which does capture capillary fluctuations at the liquid–vapor interface, significantly improves agreement between atomistic simulations and the conventional lattice gas. Plotted in Fig. 1C, the $T>T_{\text{R}}$ lattice gas result for $P_v\left(N\right)$ manifests low-density fluctuations that are dramatically more probable than for the lattice gas with $T<T_{\text{R}}.$ Agreement with atomistic simulations nonetheless remains very poor, signaling a critical role for short-wavelength modes even in the exponential tail of $P_v\left(N\right).$

The success achieved by the full coarse-grained model of Eq. 5 is thus not a transparent consequence of the limiting behaviors motivating its form. Instead, a subtle cooperation of interfacial fluctuations and thermodynamics, together with Gaussian density statistics at the molecular scale, underlies the equation’s accurate prediction for $P_v\left(N\right)$ across the entire range of N.

LCW-inspired models based on the $T<T_{\text{R}}$ lattice gas are much more difficult to reconcile with atomistic simulations. When parameterized with $T<T_{\text{R}},$ the unadorned form of Eq. 5 accurately predicts $P_v\left(N\right)$ only near its peak, failing dramatically at low N, where interfacial fluctuations figure prominently (Fig. S1). Ref. 13 outlines two strategies to address this shortcoming. Smearing out discrete interfaces with a numerical interpolation scheme improves predictions substantially but still fails to achieve quantitative accuracy in the extreme tail of $P_v\left(N\right).$ Adding as well an estimate of unbalanced attractive forces produces near quantitative agreement (13). These elaborations, however, require introducing interaction potentials and adjustable parameters that are not clearly specified by experimental measurements (13). Our results show that greater accuracy can be achieved much more simply, by using lattice gas parameters that properly represent the statistics of capillary fluctuations.

Fig. S1.

Probability of finding N molecules in a probe volume situated at a liquid–vapor interface. Here, we show the Gaussian part of the Hamiltonian given in Eq. 5 plotted alongside results from atomistic simulations, the coarse-grained model of Eq. 5, a rough lattice gas, and a cold lattice gas at coexistence.

Density Fluctuations at a Liquid–Vapor Interface.

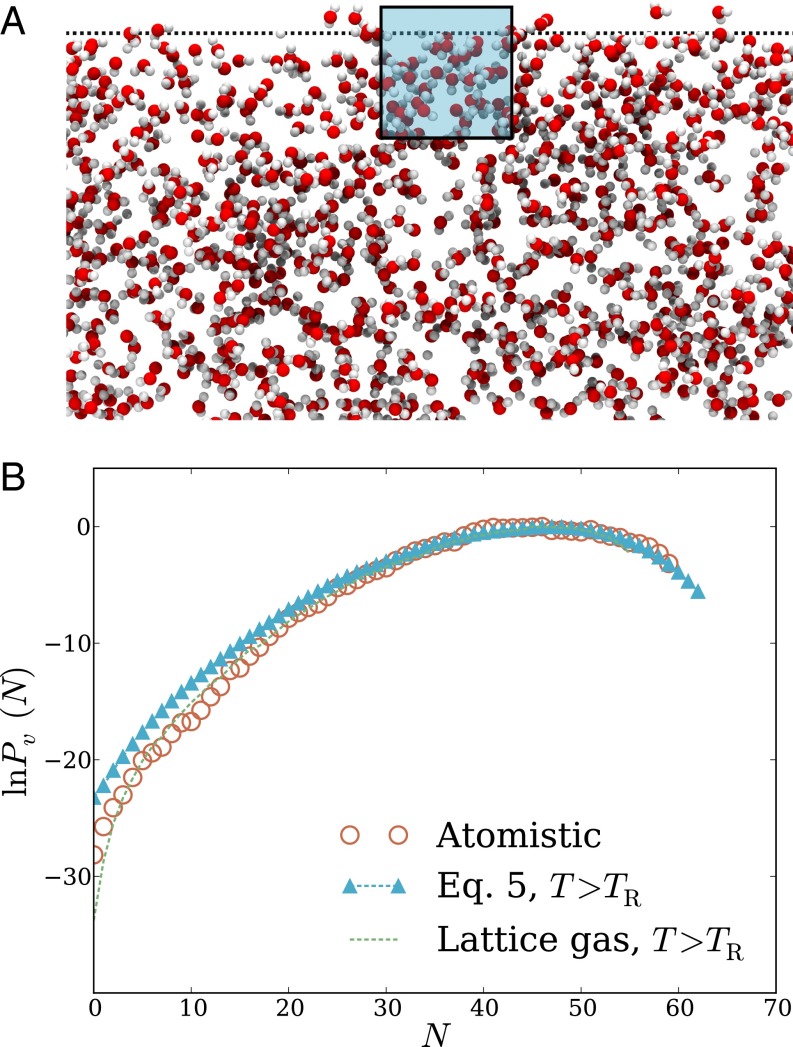
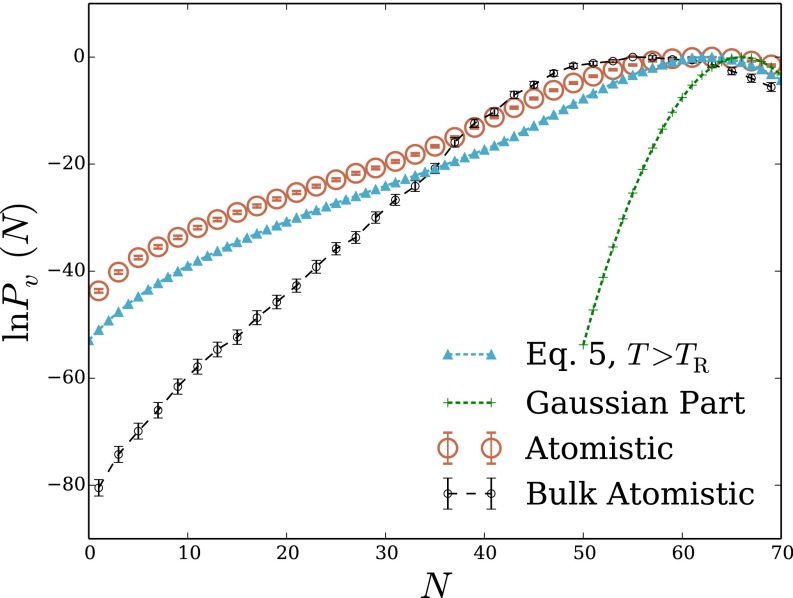
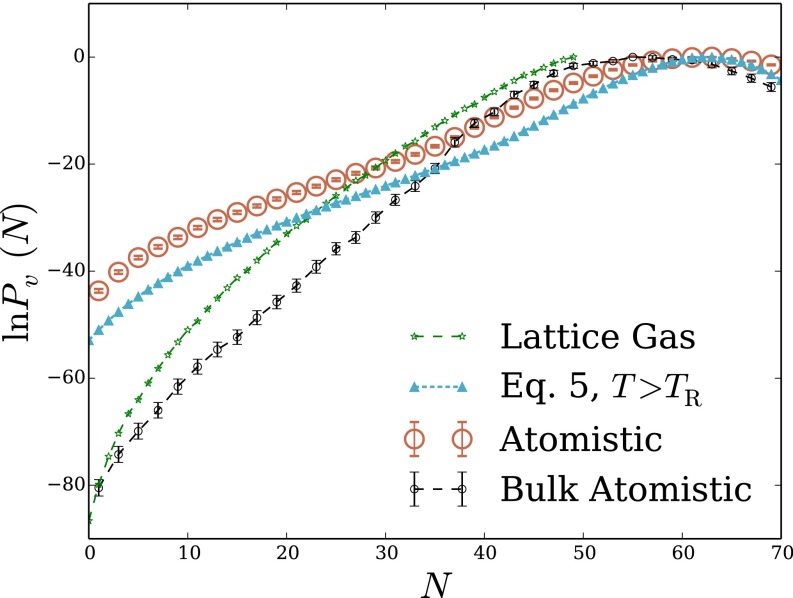
The interplay of physical factors determining hydrophobic solvation can resolve much differently in spatially heterogeneous environments. To explore basic effects of such nonuniformity, we have examined microscopic density fluctuations at the interface between air and water. Specifically, we consider a cubic probe volume that straddles the plane of a macroscopic phase boundary (i.e., the Gibbs dividing surface between liquid and vapor). The overall shape of $P_v\left(N\right)$ in this case is similar to the bulk result, featuring Gaussian statistics near the peak and a more slowly decaying low-density tail. In this case, however, the thermodynamic cost of evacuation is much lower than in bulk, despite a similar value of $\langle N\rangle .$

The LCW-inspired lattice model of Eq. 5 again matches atomistic simulation results very well, both near the mean of $P_v\left(N\right)$ and far into the probability distribution’s low-density wing. Our reduced description is therefore a promising tool for assessing hydrophobic solvation near the liquid’s boundary.

Although the shape of $P_v\left(N\right)$ that we have determined for the interfacial environment resembles that of bulk liquid, the underlying structural fluctuations are quite different. This difference is made clear by considering the simple lattice gas (in its higher-temperature parameterization), whose prediction is also plotted in Fig. 2B. In contrast to our bulk liquid results, neglecting short-wavelength density fluctuations in this case effects only a modest suppression of extreme low-density excursions; the shape and scale of $P_v\left(N\right)$ are in fact captured well by the lattice gas with $T>T_{\text{R}}.$ Correspondingly, a calculation based entirely on short-wavelength fluctuations, with a static, flat interface, fails to capture the shape of $P_v\left(N\right)$ even near the probability distribution’s peak (Fig. S1).

Fig. 2.

Density fluctuations within a cubic probe volume that straddles the interface between liquid water and its vapor. The probe volume, of size 12 Å $\times$ 12 Å $\times$ 12 Å, is centered slightly within the liquid phase, 3.67 Å below the Gibbs dividing surface. (A) Cross-sectional snapshot from an atomistic MD simulation, showing the probe volume v in blue. (B) Probability distribution $P_v\left(N\right)$ of the number of water molecules whose center lies in v. Results are shown for atomistic simulations, for the LCW-inspired coarse-grained model of Eq. 5 at coexistence, and for the conventional lattice gas of Eq. 1 at coexistence. Lattice models were simulated with $T>T_{\text{R}}$ parameters $(\mathit{ϵ}/T=1.35$, $\delta =1.84$ Å) that yield both the correct surface tension and capillary wave scaling.

The long-wavelength density component thus dominates the response of the LCW-inspired model in this spatially heterogeneous scenario, highlighting the key importance of capillary fluctuations at the air–water interface. Evacuation of a probe volume can be inexpensively achieved near a preexisting interface by simply deforming the probe’s shape. Refs. 2 and 21 have also pointed to interfacial deformation as a mechanism for extreme density fluctuations near ideal hydrophobic surfaces and hydrophobic biological molecules.

The statistics of finer scale density variations have nonnegligible quantitative impact on the predictions of Eq. 1 (e.g., reducing the cavitation free energy by roughly 5 $k_{\text{B}}T)$ but do not qualitatively shape the solvent response as in the bulk case. Underscoring the role of surface shape fluctuations, the lower-temperature parameterization of the lattice gas, which lacks capillary waves, fails profoundly to describe occupation statistics for the interfacial probe volume, as shown in Fig. S1.

Association of a Hydrophobic Solute with the Interface.

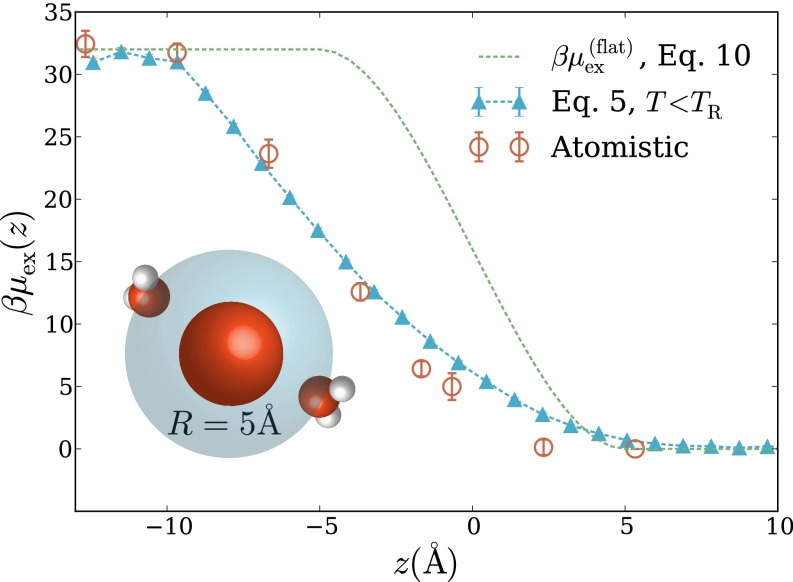
The occupation statistics discussed above hint at thermodynamic driving forces that govern solvation of nonpolar species in interfacial environments. To make this connection explicit, we have computed the excess chemical potential ${\mu }_{\text{ex}}\left(z\right)$ of a spherical hydrophobe as a function of the hydrophobe’s perpendicular displacement z from the air–water interface (with $z\to \infty$ indicating bulk vapor and $z\to -\infty$ bulk liquid). Such interfacial free-energy profiles have been determined from molecular simulations for a variety of solutes (4, 5, 22, 23), including small ions, which can exhibit a surprising tendency to adsorb to the liquid–vapor phase boundary (5). Although charged solutes are distinct in important ways from hydrophobes, the cost of creating solute-sized cavities has been implicated as a key factor in their surface affinity (4, 5). As a simple estimate of this cost, Levin et al. have assigned a fixed solvation free-energy $f_{\text{disp}}$ per unit of solvent volume displaced by the solute (24). For an ideally flat interface, this approximation yields a free-energy profile,

$${\mu }_{\text{ex}}^{\left(\text{flat}\right)}\left(z\right)=f_{\text{disp}}\left[\frac{1}{2}-\frac{z\left(3R^2-z^2\right)}{4R^3}\right],-R\le z\le R,$$ [10]

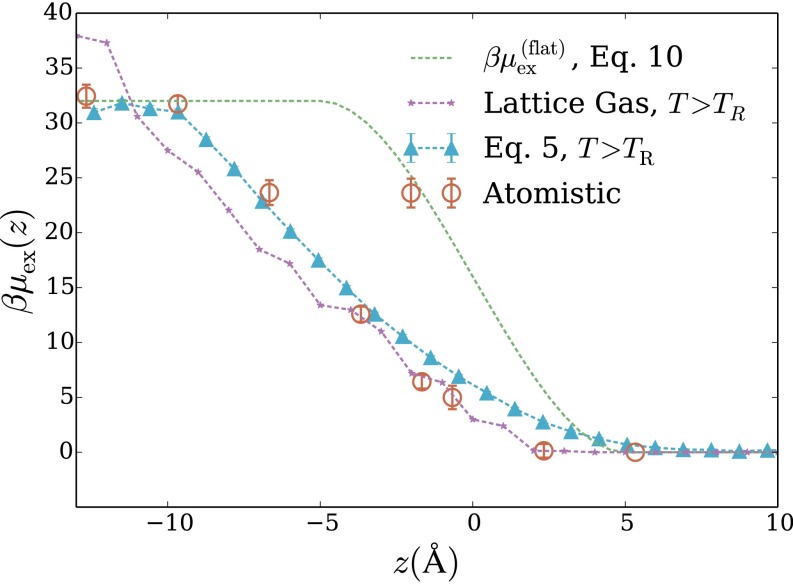
that is antisymmetric about $z=0$ [once ${\mu }_{\text{ex}}\left(z\right)$ has been shifted by its value at $z=0].$ This estimate asserts that the interface influences solubility only for distances $\left|z\right|$ smaller than the solute radius R. The estimate clearly neglects the role of capillary fluctuations, which we have argued can be the dominant mode of solvent response in such scenarios.

Atomistic simulations show that Eq. 10 poorly approximates the free-energy profile for an ideally hydrophobic nanometer-scale solute. As shown in Fig. 3 for $R=5$ Å, the atomistic potential of mean force is highly asymmetric about $z=0.$ On the liquid side $(z<0),$ the interface’s influence extends in distance z well beyond the solute’s radius, with ${\mu }_{\text{ex}}\left(z\right)$ deviating appreciably from ${\mu }_{\text{ex}}\left(-\infty \right)$ out to nearly $z=-2R.$ This extended range strongly implicates variations in surface topography away from the microscopically flat geometry assumed by Eq. 10.

Fig. 3.

Excess chemical potential of a spherical hydrophobic solute as a function of its perpendicular displacement z from the air–water interface. $z\to \infty$ corresponds to bulk vapor, $z\to -\infty$ to bulk liquid, and $z=0$ to the Gibbs dividing surface between the two coexisting phases. Data are shown for atomistic simulations, for the LCW-inspired coarse-grained model of Eq. 5 (with $T>T_{\text{R}}$ parameters $\mathit{ϵ}/T=1.35,$ $\delta =1.84$ Å), and for the estimate in Eq. 10 based on a completely quiescent interface. This solute excludes the center of each water molecule from a sphere of radius $R=5$ Å (as shown in the inset schematic).

Our LCW-inspired lattice model, by contrast, faithfully captures these features of ${\mu }_{\text{ex}}\left(z\right)$ (Fig. 3). The model’s minimal ingredients thus appear sufficient to accurately describe the thermodynamics of accommodating volume-excluding solutes near the liquid’s boundary. Given the dominant role of interfacial softness in determining $P_v\left(N\right)$ for the lattice model, an accounting of capillary fluctuations appears essential for assessing the surface affinity of nonpolar solutes. At the same time, these results suggest that a volume-excluding hydrophobe may be a problematic reference system for understanding interfacial solvation of charged species: as a cavity near the interface is charged, strong response will be induced not only in solvent polarization, as accounted by dielectric continuum theory in ref. 24, but also in interfacial shape, an aspect not addressed in existing theories for interfacial ion solvation. Near the interface, an Ising lattice gas above the roughening transition temperature accurately describes ${\mu }_{\text{ex}}\left(z\right),$ but because the cavitation free energy is not well-described without incorporating Gaussian fluctuations, the bulk free energy of solvation is not captured, as shown in Fig. S2.

Fig. S2.

Excess chemical potential of a spherical hydrophobic solute as a function of its perpendicular displacement z from the air–water interface. $z\to \infty$ corresponds to bulk vapor, $z\to -\infty$ to bulk liquid, and $z=0$ to the Gibbs dividing surface between the two coexisting phases. Data are shown for atomistic simulations, for the LCW-inspired coarse-grained model of Eq. 5 (with $T>T_{\text{R}}$ parameters $\mathit{ϵ}/T=1.35,$ $\delta =1.84$ Å), and for the estimate in Eq. 10 based on a completely quiescent interface. This solute excludes the center of each water molecule from a sphere of radius $R=5$ Å (as shown in the inset schematic). In addition, we show data for an Ising lattice gas with $T>T_{\text{R}}.$ Because it is not possible to implement truly spherical solute in the simple lattice gas system, we used a cubic solute with side length 7.24 Å, so that the surface area is equal to that of the $R=5$ Å sphere.

Density Fluctuations Between Ideal Hydrophobic Plates.

The calculations described so far demonstrate that a simple numerical implementation of the LCW perspective can accurately describe hydrophobic effects involving both microscopic structural response and macroscopic bistability, featuring interfaces that may be preexisting or emergent. This success encourages use of such a model to address more complicated and specific situations that arise in modern biophysics and materials science [e.g., water flow in nanotubes (25), gating of transmembrane ion channels (26), or the development of tertiary and quaternary protein structure (27)]. In each of these phenomena, large-scale atomistic simulations have revealed intriguing functional roles for hydrophobic response as solute configurations rearrange. Toward these frontier applications, we consider as a final example aqueous density fluctuations in a confined hydrophobic environment.

When confined at the nanometer scale or below, water can exhibit physical properties markedly distinct from those of the bulk liquid (28). Interactions with the containing boundaries become a critical consideration, with hydrophilic and hydrophobic walls generating very different structural motifs and susceptibilities. Hydrophobic walls are known to greatly enhance density fluctuations, so that even weak external fields can induce nanoscale drying (3). By poising water near a highly cooperative transition, such constraints can thus be used to engineer switching under minor perturbation, which in turn can sharply modulate functional behaviors like transport and self-assembly (1).

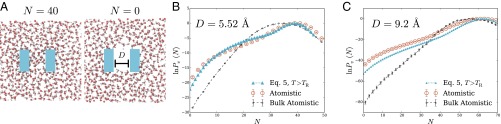
Using atomistic and coarse-grained simulations, we examined a model confinement scenario featuring two ideally hydrophobic parallel plates $(11\delta \times 3\delta \times 5\delta$ in size), separated along the plates’ short dimension by a distance D, immersed in liquid water, as depicted in Fig. 4A. As in our other examples, we focus on occupation statistics of a probe volume, here comprising the space between the two plates (a volume of size $11\delta \times 5\delta \times D)$. Results for $P_v\left(N\right)$ are plotted in Fig. 4 for two separations: $D=3\delta =5.52$ Å (Fig. 4B) and $D=5\delta =9.2$ Å (Fig. 4C). For comparison, we also show the corresponding probability distributions for a probe volume of the same size and shape placed in homogeneous bulk water, obtained from atomistic simulations.

Fig. 4.

Statistics of aqueous density fluctuations between nanometer-scale hydrophobic plates immersed in the liquid phase. (A) Cross-sectional snapshot from an atomistic MD simulation, showing the volume-excluding hydrophobic plates in blue. (B and C) Probability distributions $P_v\left(N\right)$ of the number of water molecules whose center lies between the two plates. Results are shown for atomistic simulations and for the LCW-inspired coarse-grained model of Eq. 5 (with $T>T_{\text{R}}$ parameters $\mathit{ϵ}/T=1.35$, $\delta =1.84$ Å). We also plot results for a probe volume of equivalent size in bulk water, obtained from atomistic simulations. The plates are cuboids that exclude the center of each water molecule from a volume with dimensions 20.24 Å $\times$ 5.52 Å $\times$ 9.2 Å and are separated along their short dimension by a distance D. Plate separations were fixed at $D=5.52$ Å in the simulations of B and at $D=9.2$ Å for C.

The presence of these hydrophobic plates is not sufficient to induce drying for either value of D considered. The plates are not sufficiently large to induce a vapor layer in their vicinity. The average density between plates is in fact greater than in bulk water, because of the tendency of molecules in dense liquids to pack tightly against hard walls. This modest elevation of $\langle N\rangle$ is recapitulated by the LCW-inspired lattice model. Such an increase in local density is also captured by a purely Gaussian model that considers only short-wavelength density fluctuations, underscoring its origin in simple packing effects. The simple Gaussian model, however, considerably overestimates the magnitude of this shift, shown in Figs. S3 and S4—although these plates are not sufficiently confining to evacuate the probe volume with high probability, they do significantly enhance lattice fluctuations in their vicinity.

Fig. S3.

Probability of finding N molecules in a probe volume between two ideal, 20.24 Å $\times$ 5.52 Å $\times$ 9.2 Å hydrophobic plates, separated by a distance of 5.52 Å. Here, we show the Gaussian part of the Hamiltonian given in Eq. 5 plotted alongside results from atomistic simulation, the coarse-grained model of Eq. 5, and the bulk $P_v\left(N\right)$ for a probe volume of the same size as the region between the walls. Note that the Gaussian part of the Hamiltonian overcompensates for the shift toward higher density.

Fig. S4.

Probability of finding N molecules in a probe volume between two ideal, 20.24 Å $\times$ 5.52 Å $\times$ 9.2 Å hydrophobic plates, separated by a distance of 9.2 Å. Here, we show the Gaussian part of the Hamiltonian given in Eq. 5 plotted alongside the results from atomistic simulation, the coarse-grained model of Eq. 5, and the bulk $P_v\left(N\right)$ for a probe volume of the same size as the region between the walls. Note that the Gaussian part of the Hamiltonian overcompensates for the shift toward higher density.

The hydrophobic plates have a much stronger impact on the tails of $P_v\left(N\right).$ For the smaller separation, $D=3\delta ,$ extreme low-density fluctuations are substantially more probable than in the bulk case, reflecting stabilization of the dry state. Typical configurations do not manifest this stabilization; it would instead be apparent in the response to an external field that disfavors occupation of the interplate region. Here, a field strength of just 0.5 T per molecule would be sufficient to induce drying. This profound impact of hydrophobic confinement on susceptibility to weak perturbations, despite negligible influence on typical fluctuations, has been emphasized in previous work and explored in detail in the context of protein complex formation (2, 27, 28).

These behaviors too are well described by the LCW-inspired lattice model. The slope of $\ln \hspace{0.17em}{P}_v\left(N\right)$ in the low-density range, which largely determines the susceptibilities discussed above, is predicted especially accurately. The emergence of an inflection point, a sign of incipient bistability as the plates approach, is also accurately captured by the coarse-grained model. The difficulty of describing solvent-mediated attraction between hydrophobes using linear response theory has been detailed by others (29, 30). For the nanoscale plates considered here, the addition of fluctuating lattice degrees of freedom achieves this goal with striking success.

As in the case of a probe volume of comparable size in bulk solvent (Fig. 1), the conventional lattice gas model (with $n_i$ set to 1 inside the hydrophobic plates) does not give an accurate estimate of $P_v\left(N\right)$ over the probability distribution’s full range (Figs. S5 and S6). At this subnanometer-length scale, Gaussian fluctuations in the field $\delta \rho \left(r\right)$ provide a mechanism for accessing significant deviations from ¡N¿, whose weight is nonnegligible. Increasing plate size should facilitate the formation of extended interfaces, eventually making capillary fluctuations the only relevant source of large deviations in N (as in the case of the preexisting interface of Fig. 2).

Fig. S5.

Probability of finding N molecules in a probe volume between two ideal, 20.24 Å $\times$ 5.52 Å $\times$ 9.2 Å hydrophobic plates, separated by a distance of 5.52 Å. Here, we show the prediction for an Ising lattice gas above the roughening transition temperature in which the constraint the cells occupied by the walls remain empty is imposed.

Fig. S6.

Probability of finding N molecules in a probe volume between two ideal, 20.24 Å $\times$ 5.52 Å $\times$ 9.2 Å hydrophobic plates, separated by a distance of 9.2 Å. Here, we show the prediction for an Ising lattice gas above the roughening transition temperature in which the constraint the cells occupied by the walls remain empty is imposed.

Conclusions

Hydrophobic effects drive the formation of diverse assemblies in biological and materials systems. Our results suggest that the microscopic basis of these effects is thoroughly described by the physical perspective put forth by Lum, Chandler, and Weeks (31). Statistics of extreme fluctuations that determine solvation thermodynamics can be captured with quantitative accuracy in a lattice model based on the LCW perspective. Doing so, however, requires careful attention to the softness of air–water interfaces, a property lacking in many previous models.

The lattice model defined by Eq. 5 appears to be truly minimal for this purpose. Omitting any of the models’ contributions degrades the close agreement with atomistic simulations that we have demonstrated. Moreover, the model’s parameters are highly constrained by basic experimental observations, namely surface tension, molecular pair correlations, and the spectrum of long-wavelength capillary waves.

Notably absent in our model are several ingredients introduced in previous studies to improve agreement with detailed molecular simulations. We have not introduced explicit coupling between the rapidly and slowly varying components of the density field [i.e., between the lattice variables $n_i$ and the Gaussian field $\delta \rho \left(\mathbf{r}\right)].$ Others have motivated such coupling from the form of self-consistent equations in a mean-field treatment of the slowly varying density component (31), which manifest unbalanced attractive forces attributable to the rapidly varying component. Our omission does not, however, imply a lack of unbalanced attraction in the model of Eq. 5. Direct interactions among the lattice variables $n_i$ in Eq. 1 are of course sufficient to stabilize interfaces, the primary and essential role of unbalanced forces in the mean field theories of refs. 31 and 32. Rather, Eq. 5 neglects the specific source of unbalanced attraction attributable to short-wavelength structure, a coupling whose form and strength are not transparent for an associated liquid like water (32). Nor does our omission imply a lack of coupling between $n_i$ and $\delta \rho \left(\mathbf{r}\right).$ The manipulations leading to Eq. 5 permit short-wavelength density fluctuations only in regions that are liquid-like $(n_i=1).$ By correlating the statistics of $\delta \rho \left(\mathbf{r}\right)$ with lattice fluctuations that support phase coexistence, this constraint effects a potent but implicit interaction across length scales. Finally, in LCW-inspired lattice models, explicit length-scale coupling has the side effect of altering statistics of Gaussian density fluctuations in the vicinity of inhomogeneous lattice configurations. According to molecular simulations, short-wavelength fluctuations in liquid regions are in fact quite robust against such heterogeneity, particularly when liquid domains are identified with sensitivity to interfacial fluctuations (21, 33).

The lattice gas on which our model is built includes only nearest neighbor interactions. As emphasized in ref. 13, the ground state of this model possesses unphysical degeneracies in the shape of closed, convex interfaces. These degeneracies can be removed by introducing lattice interactions between nonneighboring cells. In a lattice gas below its roughening transition temperature, the impact of these additional interactions is dramatic, because the interactions suppress the only affordable mode of interfacial shape variation. Our studies of lattice gases above the roughening transition temperature suggest that such degeneracies are much less important in the presence of natural capillary fluctuations.

Such additional couplings may be needed to further improve quantitative predictions or to address more complicated scenarios. These goals may also require attention to molecular details that have not yet been incorporated into LCW-inspired models, for instance, concerning the geometry of hydrogen bonds, coordination statistics, or the specific form of interaction potentials. Pratt has made significant advances toward understanding and quantifying the role of these effects in hydrophobicity (29). Incorporating these advances into a lattice-based model poses significant challenges.

In addition to helping establish a conceptual foundation for complex hydrophobic phenomena, our studies advance the more pragmatic goal of faithfully simulating systems that comprise very large numbers of water molecules. This challenge limits, for example, the scale of biomolecular problems that can be examined by simulation without reducing the description of solvent fluctuations to a gross caricature. For the systems we have discussed, our coarse-grained approach reduces the computational cost of representing explicit solvent fluctuations by more than two orders of magnitude (relative to atomistic simulations), while preserving microscopic realism with surprising accuracy. This advantage should become even more significant for very large systems, whose computational burden scales exactly linearly in Eq. 5. The model we have described could thus enable the study of problems that currently lie outside of the reach of atomistically detailed simulations.

Methods

All atomistic simulations included 6,912 rigid water molecules, interacting through the SPC/E potential (34), in a periodically replicated simulation cell with dimensions 75 Å $\times$ 75 Å $\times$ 100 Å, and held at temperature 300 K using a Nosé–Hoover thermostat (35, 36). These conditions enforce phase equilibrium, with coexisting slabs of liquid and vapor as in ref. 21. Probe volumes were positioned at least 10 Å away from the resulting liquid–vapor interface, except where indicated otherwise. Electrostatic interactions were summed using the particle mesh Ewald algorithm (37). Intramolecular constraints were imposed using the SHAKE algorithm (38). MD trajectories were advanced in time using the LAMMPS software package (39). Probability distributions for occupation statistics of a probe volume were determined with umbrella sampling using the indirect umbrella sampling (INDUS) technique (21).

Coarse-grained simulations were performed with an in-house software package that is available upon request. These systems comprised $30\times 30\times 30$ lattice cells, periodically replicated in each direction. Probability distributions of the lattice-occupation state within a probe volume were determined by straightforward umbrella sampling. Statistics of the total density (including short-wavelength fluctuations) within such probe volumes were then obtained using the method outlined in ref. 13. Simulations with spherical solutes required numerical calculation of the overlap between cubic lattice cells and the solute’s excluded volume. These overlap volumes were computed either with Monte Carlo integration or with analytical expressions detailed in the Supporting Information. Although complicated, these expressions significantly reduce computation time for solutes that move continuously in space.

Integrating Out Gaussian Fluctuations in the Presence of Multiple Ideal Hydrophobes

The presence of a solvent-excluding volume v introduces a constraint on the total solvent density field,

$${\rho }_{l}n\left(\mathbf{r}\right)+\delta \rho \left(\mathbf{r}\right)=0,$$ [S1]

at each point $\mathbf{r}\in v.$ Integrating out small-wavelength Gaussian fluctuations $\delta \rho \left(\mathbf{r}\right)$ in the presence of this constraint requires evaluating

$$Z_v={\displaystyle \int \mathcal{D}\delta \rho \left(\mathbf{r}\right)e^{-\beta H_s}}{\displaystyle \prod _{\mathbf{r}\in v}\delta \left({\rho }_{l}n\left(\mathbf{r}\right)+\delta \rho \left(\mathbf{r}\right)\right)}.$$ [S2]

The product of delta functions enforces the constraint in Eq. S1, and $H_s$ is the unconstrained Hamiltonian for $\delta \rho \left(\mathbf{r}\right),$

$$\beta H_s=\frac{1}{2}{\displaystyle {\int }_{\mathbf{r}}{\displaystyle {\int }_{\mathbf{r}\prime }\delta \rho \left(\mathbf{r}\right){\chi }^{-1}\left(\mathbf{r},\mathbf{r}\prime \right)\delta \rho (\mathbf{r}\prime )}}.$$

A formal expression for $Z_v$ can be easily derived, but numerical evaluation is impractical because of the infinite product of delta functions. For this reason, prior work on coarse-graining water has replaced the pointwise constraint in Eq. S2 by a single constraint on the average density in v, as in Eq. 4. The resulting expression for $Z_v$ is much more manageable and has been applied with great success to systems containing only a single solute with a simple compact geometry. However, for systems with many independently moving solutes that may be separated by large distances, the average constraint in Eq. 4 introduces spurious correlations between solutes that never vanish. If v is the union of m nonintersecting regions,

$$v=v^{\left(1\right)}\mathrm{\cup }{v}^{\left(2\right)}\mathrm{\cup }\dots \mathrm{\cup }{v}^{\left(m\right)},$$

a simple solution is to constrain the average density in each region $v^{\left(\alpha \right)}$ separately (i.e., to apply the constraint expressed in Eq. 4 separately to each solute’s excluded volume). The infinite product of delta functions in Eq. S2 then becomes a product of m delta functions,

$${\displaystyle \prod _{\mathbf{r}\in v}\delta \left({\rho }_{l}n\left(\mathbf{r}\right)+\delta \rho \left(\mathbf{r}\right)\right)}\to {\displaystyle \prod _{\alpha =1}^m\delta \left({\displaystyle {\int }_{\mathbf{r}\in v^{\left(\alpha \right)}}{\rho }_{l}n\left(\mathbf{r}\right)+\delta \rho \left(\mathbf{r}\right)}\right)}.$$

Using the Fourier representation of the delta function, the integral in Eq. S2 becomes

$${\displaystyle \int \mathcal{D}\delta \rho \left(\mathbf{r}\right)e^{-\beta H_s}}{\displaystyle \prod _{\alpha =1}^m{\displaystyle \int \frac{d{\psi }_{\alpha }}{2\pi }}}\hspace{0.17em}\exp \left(-i{\psi }_{\alpha }{\displaystyle {\int }_{\mathbf{r}\in v^{\left(\alpha \right)}}{\rho }_{l}n\left(\mathbf{r}\right)+\delta \rho \left(\mathbf{r}\right)}\right).$$

Defining

$$N_{\alpha }={\displaystyle {\int }_{\mathbf{r}\in v^{\left(\alpha \right)}}{\rho }_{l}n\left(\mathbf{r}\right)\hspace{1em}\text{and}\hspace{1em}\mathrm{\Phi }\left(\mathbf{r}\right)}=\{\begin{array}{ll}i{\psi }_{\alpha },\hfill & \mathbf{r}\in v^{\left(\alpha \right)},\hfill \\ 0,\hfill & \text{else},\hfill \end{array}$$

and rearranging the order of the integrals, we obtain

$${\displaystyle \int \left({\displaystyle \prod _{\alpha =1}^m\frac{d{\psi }_{\alpha }}{2\pi }\hspace{0.17em}{e}^{-i{N}_{\alpha }{\psi }_{\alpha }}}\right)}{\displaystyle \int \mathcal{D}\delta \rho \left(\mathbf{r}\right)}\exp \left(-\beta H_s-{\displaystyle {\int }_{\mathbf{r}}\mathrm{\Phi }\left(\mathbf{r}\right)\delta \rho \left(\mathbf{r}\right)}\right).$$

Evaluating the inner integral over $\delta \rho \left(\mathbf{r}\right)$ results in

$$Z_v=Z_0{\displaystyle \int \left({\displaystyle \prod _{\alpha =1}^m\frac{d{\psi }_{\alpha }}{2\pi }\hspace{0.17em}{e}^{-i{N}_{\alpha }{\psi }_{\alpha }}}\right)}\exp \left(\frac{1}{2}{\displaystyle {\int }_{\mathbf{r}}{\displaystyle {\int }_{\mathbf{r}\prime }\mathrm{\Phi }\left(\mathbf{r}\right)\chi \left(\mathbf{r},\mathbf{r}\prime \right)\mathrm{\Phi }(\mathbf{r}\prime )}}\right).$$

The argument of the rightmost exponent evaluates to

$$-\frac{1}{2}{\left(2\pi \right)}^2{\displaystyle \sum _{\alpha =1}^m{\displaystyle \sum _{\beta =1}^m{\psi }_{\alpha }{\left({\chi }_{\text{in}}\right)}_{\alpha ,\beta }{\psi }_{\beta }}},$$

where ${\left({\chi }_{\text{in}}\right)}_{\alpha ,\beta }$ is given by the double integral

$${\left({\chi }_{\text{in}}\right)}_{\alpha ,\beta }={\displaystyle {\int }_{\mathbf{r}\in v^{\left(\alpha \right)}}{\displaystyle {\int }_{\mathbf{r}\prime \in v^{\left(\beta \right)}}\mathrm{\Theta }\left(\mathbf{r}\right)\chi \left(\mathbf{r},\mathbf{r}\prime \right)\mathrm{\Theta }(\mathbf{r}\prime )}}.$$

With this, $Z_v$ can be expressed compactly in matrix notation,

$$Z_v=Z_0{\displaystyle \int \left({\displaystyle \prod _{\alpha =1}^m\frac{d{\psi }_{\alpha }}{2\pi }}\right)}\text{exp}\left(-\frac{1}{2}{\overline{\psi }}^{\mathrm{\top }}{\chi }_{\text{in}}\overline{\psi }-i{\overline{N}}^{\mathrm{\top }}\overline{\psi }\right),$$

where $\overline{\psi }$ is a column vector with elements ${\psi }_{\alpha },$ $\overline{N}$ is a column vector with elements $N_{\alpha },$ and ${\chi }_{\text{in}}$ is an $m\times m$ matrix with elements ${\left({\chi }_{\text{in}}\right)}_{\alpha ,\beta }.$ This integral is easily evaluated to give

$$Z_v=Z_0\frac{1}{\sqrt{\text{det}\left(2\pi {\chi }_{\text{in}}\right)}}\text{exp}\left(-\frac{1}{2}{\overline{N}}^{\mathrm{\top }}{\chi }_{\text{in}}^{-1}\overline{N}\right).$$

The free-energetic contribution of the small-wavelength field, relative to the unconstrained case, is then given by

$$F_v-F_0=-T\hspace{0.17em}\ln \left(\frac{Z_v}{Z_0}\right)=\frac{T}{2}\left(\ln \left(\text{det}\left(2\pi {\chi }_{\text{in}}\right)\right)+{\overline{N}}^{\mathrm{\top }}{\chi }_{\text{in}}^{-1}\overline{N}\right),$$ [S3]

which are the final two terms in Eq. 5. For two solutes α and β, the off-diagonal matrix element ${\left({\chi }_{\text{in}}\right)}_{\alpha ,\beta }$ gives the coupling between Gaussian fluctuations in regions $v^{\left(\alpha \right)}$ and $v^{\left(\beta \right)}.$ If the solutes are separated by much more than the correlation length of water, this term vanishes. In the limit of infinite separation between all solutes, ${\chi }_{\text{in}}$ becomes a diagonal matrix and the free energy in Eq. S3 reduces to a simple sum of uncoupled terms,

$$F_v-F_0=\frac{T}{2}{\displaystyle \sum _{\alpha =1}^m\left(\ln \left(2\pi {\left({\chi }_{\text{in}}\right)}_{\alpha ,\alpha }\right)+\frac{N_{\alpha }^2}{{\left({\chi }_{\text{in}}\right)}_{\alpha ,\alpha }}\right)}.$$

Exact Expression for the Overlap Between the Lattice and Spherical Solute

The Hamiltonian given in Eq. 5 requires that we compute $v_i,$ the overlap between the solute’s excluded volume and the cubic lattice cells. The overlap can be estimated accurately using Monte Carlo integration when the solute does not move over the course of the simulation. However, it is also possible to compute the overlap analytically, a pragmatic approach when the solute is mobile. This strategy improves accuracy and saves significant computation.

To efficiently compute the overlap between cells of the lattice and spherical objects, we derived an exact formula using ordinary calculus. There are eight distinct cases to consider, each with several subcases. The calculation is a tedious, but straightforward, exercise in enumerating the cases. There are two main, equivalent scenarios. First, if the cubic region lies entirely within the solute, then the overlap is simply ${\delta }^3.$ Otherwise, the diagonal of the cubic cell, which we refer to as the line segment connecting $\left(x_l,y_l,z_l\right)$ to $\left(x_u,y_u,z_u\right)$ throughout, does not lie entirely within the sphere. Every subcase can be rotated and decomposed into one of these two subcases. As such, knowledge of the following specific case is sufficient to compute the overlap in general.

Consider a sphere of radius R centered at the origin. We will work through the case that $R>\delta ,$ where δ is the coarse-graining length (the side length of the cubes that form the lattice). The overlap between the sphere and a cubic lattice cell can always be decomposed into contributions from each of the eight octants of the sphere. Without loss of generality, we will select the first octant $x,y,z>0$ and assume that the diagonal of the cubic lattice cell lies entirely within the octant.

With this particular case fully specified, we now carry out the integral

$${\displaystyle {\int }_0^{\sqrt{R^2-z^2-y^2}}{\displaystyle {\int }_0^{\sqrt{R^2-z^2}}{\displaystyle {\int }_0^{R}dx\hspace{0.17em}dy\hspace{0.17em}dz}}}\hspace{0.17em}-{\displaystyle {\int }_{x_l}^{\sqrt{R^2-z^2-y^2}}{\displaystyle {\int }_{y_l}^{\sqrt{R^2-z^2}}{\displaystyle {\int }_{z_l}^{R}dx\hspace{0.17em}dy\hspace{0.17em}dz}}}.$$ [S4]

This expression is valid when $x_u,y_u,z_u>R.$ If this is not the case, then additional integrals that account for the volume of the sphere in the first octant that lies outside the cubic cell must be subtracted away. These additional integrals have the same form as the integral in Eq. S4.

The integral specifying the overlap can be calculated analytically. We have not been able to simplify the expression into a convenient form, but the analytical result can easily be used within computer code.

The simplified expression for Eq. S4 is

$$\begin{array}{l}\frac{1}{2}[-\frac{1}{3}2\hspace{0.17em}{\tan }^{-1}\left(\frac{x_l{y}_l}{R\sqrt{R^2-x_l^2-y_l^2}}\right)R^3-2x_l{y}_l{z}_l-\frac{1}{3}{x}_l\left(x_l^2-3R^2\right){\tan }^{-1}\left(\frac{y_l}{\sqrt{R^2-x_l^2-y_l^2}}\right)\\ -\frac{1}{2}{y}_l\left(R^2-y_l^2\right){\tan }^{-1}\left(\frac{x_l\sqrt{R^2-x_l^2-y_l^2}}{-R^2+x_l^2+y_l^2}\right)-\frac{1}{6}{y}_l\left(3R^2+y_l^2\right){\tan }^{-1}\left(\frac{x_l\sqrt{R^2-x_l^2-y_l^2}}{-R^2+x_l^2+y_l^2}\right)\\ +\frac{1}{3}{x}_l\left(x_l^2-3R^2\right){\tan }^{-1}\left(\frac{\sqrt{R^2-x_l^2-z_l^2}}{\sqrt{z_l^2}}\right)-z_l\left(R^2-z_l^2\right){\tan }^{-1}\left(\frac{x_l\sqrt{R^2-x_l^2-z_l^2}}{-R^2+x_l^2+z_l^2}\right)\\ +\frac{1}{2}\sqrt{z_l^2}\left(R^2-z_l^2\right){\tan }^{-1}\left(\frac{x_l\sqrt{R^2-x_l^2-z_l^2}}{-R^2+x_l^2+z_l^2}\right)\\ +\frac{2}{3}{x}_l{y}_l\sqrt{R^2-x_l^2-y_l^2}+x_l{z}_l\sqrt{R^2-x_l^2-z_l^2}-\frac{1}{3}{x}_l\sqrt{z_l^2}\sqrt{R^2-x_l^2-z_l^2}]\\ +\frac{1}{2}[\frac{2}{3}{\tan }^{-1}\left(\frac{x_u{y}_l}{R\sqrt{R^2-x_u^2-y_l^2}}\right)R^3+2x_u{y}_l{z}_l+\frac{1}{3}{x}_u\left(x_u^2-3R^2\right){\tan }^{-1}\left(\frac{y_l}{\sqrt{R^2-x_u^2-y_l^2}}\right)\\ +\frac{1}{2}{y}_l\left(R^2-y_l^2\right){\tan }^{-1}\left(\frac{x_u\sqrt{R^2-x_u^2-y_l^2}}{-R^2+x_u^2+y_l^2}\right)+\frac{1}{6}{y}_l\left(3R^2+y_l^2\right){\tan }^{-1}\left(\frac{x_u\sqrt{R^2-x_u^2-y_l^2}}{-R^2+x_u^2+y_l^2}\right)\\ -\frac{1}{3}{x}_u\left(x_u^2-3R^2\right){\tan }^{-1}\left(\frac{\sqrt{R^2-x_u^2-z_l^2}}{\sqrt{z_l^2}}\right)+z_l\left(R^2-z_l^2\right){\tan }^{-1}\left(\frac{x_u\sqrt{R^2-x_u^2-z_l^2}}{-R^2+x_u^2+z_l^2}\right)\\ -\frac{1}{2}\sqrt{z_l^2}\left(R^2-z_l^2\right){\tan }^{-1}\left(\frac{x_u\sqrt{R^2-x_u^2-z_l^2}}{-R^2+x_u^2+z_l^2}\right)\\ -\frac{2}{3}{x}_u{y}_l\sqrt{R^2-x_u^2-y_l^2}-x_u{z}_l\sqrt{R^2-x_u^2-z_l^2}+\frac{1}{3}{x}_u\sqrt{z_l^2}\sqrt{R^2-x_u^2-z_l^2}]\\ +\frac{1}{2}[-\frac{2}{3}{\tan }^{-1}\left(\frac{\frac{x_l{z}_l}{R\sqrt{R^2-x_l^2-z_l^2}}-\frac{x_u{z}_l}{R\sqrt{R^2-x_u^2-z_l^2}}}{\frac{x_l{x}_u{z}_l^2}{R^2\sqrt{R^2-x_l^2-z_l^2}\sqrt{R^2-x_u^2-z_l^2}}+1}\right)R^3\\ -\frac{1}{6}\left(z_l\left(3R^2+z_l^2\right)\right){\tan }^{-1}\left(2z_l\sqrt{R^2-x_l^2-z_l^2},-2x_l{z}_l\right)\\ +\frac{1}{6}\left(z_l\left(3R^2+z_l^2\right)\right){\tan }^{-1}\left(2z_l\sqrt{R^2-x_u^2-z_l^2},-2x_u{z}_l\right)].\end{array}$$ [S5]