Point of impact: the effect of size and speed on puncture mechanics

Abstract

The use of high-speed puncture mechanics for prey capture has been documented across a wide range of organisms, including vertebrates, arthropods, molluscs and cnidarians. These examples span four phyla and seven orders of magnitude difference in size. The commonality of these puncture systems offers an opportunity to explore how organisms at different scales and with different materials, morphologies and kinematics perform the same basic function. However, there is currently no framework for combining kinematic performance with cutting mechanics in biological puncture systems. Our aim here is to establish this framework by examining the effects of size and velocity in a series of controlled ballistic puncture experiments. Arrows of identical shape but varying in mass and speed were shot into cubes of ballistic gelatine. Results from high-speed videography show that projectile velocity can alter how the target gel responds to cutting. Mixed models comparing kinematic variables and puncture patterns indicate that the kinetic energy of a projectile is a better predictor of penetration than either momentum or velocity. These results form a foundation for studying the effects of impact on biological puncture, opening the door for future work to explore the influence of morphology and material organization on high-speed cutting dynamics.

1. Introduction

The field of biomechanics uses physical principles to create a framework for comparing disparate biological systems with similar mechanical behaviours. For example, a venomous snake and stinging jellyfish both use sharp biological features in order to inject venom. The snake's fang and the stinging cells (nematocysts) in jellyfish differ in size by almost seven orders of magnitude and are driven by very different kinematic systems. Snakes generate strike movements of 2–3 m s⁻¹ through a combination of muscle and tendon [1,2], while the nematocyst of jellyfish is powered by hydrostatic pressures which allow them to reach velocities of 38 m s⁻¹ and accelerations in excess of 5 million m s⁻² [3,4]. However, the mechanical goal of both behaviours is the same: create fractures in tissue to allow for penetration of the weapon and injection of venom. Understanding the principles of how size and speed influence puncture mechanics is key to comparing disparate systems such as these. In this study, we attempt to develop a mechanical framework for comparing high-speed biological puncture mechanics across groups using controlled ballistic experiments.

Multiple animals have been identified as using high-speed puncture mechanics, defined here as launching a biological weapon at impact speeds to penetrate a target. Further examples can be found at several orders of magnitude in size and a wide range of speeds. Multiple arthropod groups show high-speed puncture in their mouthparts including mantis shrimp (7 m s⁻¹) [5], trapjaw ants (38 m s⁻¹) [6] and certain termites (56 m s⁻¹) [7]. There are even species of cone snails that attack potential prey using a ‘ballistic’ tooth to inject venom at a minimum velocity of 3 m s⁻¹ [8]. The commonality of puncture mechanics that underlie this wide diversity of biological systems (four phyla: vertebrate, arthropod, mollusc and cnidaria) offers an opportunity to explore how organisms at different scales and with different materials, morphologies and kinematics overcome common mechanical challenges.

However, exploring the biomechanical evolution of these high-speed puncture systems is hampered by the lack of a general framework for how kinematic performance variables in animals, such as velocity, momentum and kinetic energy, influence puncture mechanics. In ballistic penetration (high-speed puncture) experiments on synthetic materials, energy and momentum are typically both examined to determine the effectiveness of a projectile [9]. Momentum is measured because the change in momentum during impact can be used to calculate impact forces. Energy is often used to describe the destructive nature of the projectile. Finally, the velocity is used to characterize materials in terms of resistance with a parameter called the penetration velocity (V50), defined as the velocity at which a projectile will completely penetrate a material. While these variables have all been used to characterize ballistic penetration in during experiments, little is known about how they potentially control crack initiation and propagation itself.

A strong set of theory exists for understanding steady-state cutting in hard and soft materials centred on energy transfer [10]. Energy is required to create new surfaces in materials, so cutting is controlled by the transfer of energy between the cutting tool and the target material [10]. Energy transfer during cutting has been used as a basis for studies examining how tool shape affects fracture creation [11–16], food item reduction (i.e. [17–19]) and wear patterns on cutting implements (i.e. [20–23]). However, the vast majority of studies on cutting mechanics in the biological realm do not take the speed of the cutting weapon into account, assuming constant or near constant, applied forces at slow, steady rates. This ignores the effects of speed and impact on the energetics of surface creation.

Natural selection operates on biological performance, so in order to understand the evolution of biological puncture systems, it is vital to establish a framework linking kinematic performance of the animals with the ability to effectively create puncture. The first step to building this framework is to investigate how the kinematics of a projectile (such as velocity) affects puncture mechanics when that projectile impacts a target. Once this relationship is established, it will be possible to identify what mechanical principles influence the evolution of these puncture systems. For example, smaller animals will have less mass in their projectiles, which translates to less momentum or kinetic energy when launched at a target. If projectile momentum or kinetic energy are important to puncture mechanics, then evolution may select for faster projectiles at smaller sizes. This type of argument ignores the morphology of the projectile and the material properties of the target, both of which are extremely important to cutting and puncture mechanics. However, before the effects of shape and materials can be fully understood in a dynamic behaviour, it is necessary to establish the basic relationship between kinematics and fracture, which is the aim of this study.

In order to establish a mechanical framework for comparing high-speed puncture between disparate groups and exploring the evolution of these systems, we performed a series of ballistic experiments with a custom-built projectile launcher firing arrows into ballistics gelatin. By varying the speed and mass of the projectiles, we are able to relate kinematic performance of the projectile to puncture performance. We tested the hypothesis that measures of puncture performance such as puncture depth would show correlation with one or more measures of kinematic performance. We tested kinetic energy based on the fact that energy is necessary to create new surfaces in materials, and so should correlate with the extent of surface creation during puncture. We tested momentum, based on the relationship between impulse (change in momentum), impact force and stress, the latter of which is a key variable for determining crack propagation. We also tested for correlation between penetration performance and velocity as velocity is the common kinematic link between momentum and kinetic energy. Correlations between puncture and any of these kinematic variables would indicate a link between kinematic performance and puncture ability. We also used high-speed video to capture the behaviour of the material during high-speed puncture and visualize stress wave propagation and deformation at high speeds.

2. Material and methods

2.1. Crossbow apparatus

Puncture tests were performed using a custom-built testing apparatus patterned after a standard crossbow. The custom crossbow was constructed for a previous set of studies [24] and was modified for our purposes. The crossbow was attached to a laboratory bench and stabilized using ratcheted cargo straps to hold the frame in place during testing. Two tandem mounted fibreglass bows (Glassflex^® recurved youth bows, with draw weights of 13.5–16 kg each) were attached horizontally across the front and strung such that both strings could be notched into a single arrow. This allowed for a greater range of draw forces during experiments. We used hollow, carbon fibre archery arrows (Easton, Redline^®, 690) in these experiments. Arrows were launched in a horizontal plane, parallel to the ground with no initial vertical velocity due to gravity. The trajectories of the arrows during flight were partially guided using a metal v-notch supported by a ring stand. The height of this support could be adjusted to account for changes in trajectory arising from using one or both bows.

Projectiles (arrows) were launched into blocks of ballistic gelatin (film cubic inches; see below) placed 0.9 m from the front of the crossbow. These blocks of gelatin were backed by a commercial hard-target (McKenzie Shotblocker, Delta Sports Products LLC, Dike, IA, USA), which was capable of stopping the arrow at all speeds tested.

Two linked Photron (San Diego, CA, USA) high-speed video cameras were used to capture the flight of the arrows and their impact into the ballistics gelatin from multiple angles. The primary camera (FASTCAM SA-Z) was mounted on a tripod and set to capture a lateral view of the horizontal flight path of the arrow. The secondary camera (FASTCAM SA-X2) was mounted on a horizontal platform above the hard-target and a mirror was used to capture a vertical view of the arrows flight. Arrows in both camera views were backlit for ease of digitizing during data analysis. The lateral view was backlit using an LED studio light (Varsa, Nila, Altadena, CA, USA). We also added a sheet of insulation plastic in front of the light to diffuse the emitted light. The vertical view was backlit by a light table (Apollo Audio-Visual, Ronkonkoma, NY, USA) on which the ballistic gelatin targets were placed.

2.2. Materials (ballistic gelatin)

Ballistic gelatin was used as the test material for all projectile experiments. We chose to use this material due to its isotropic, homogeneous nature. Ballistic gelatin is also photoelastic, allowing us to visualize stress within the material during puncture experiments [25]. Such materials have been used in previous studies to analyse a wide range of biological behaviours such as cutting by teeth [14,26], insect locomotion [27] and worm burrowing [28].

Ballistic gelatin was mixed following procedures previously outlined [29,30] using commercial ballistic gelatin powder (Vyse^® Professional Grade Ballistic & Ordnance Gelatin, Custom Collagen, Addison, IL, USA). In order to obtain standardized blocks of gelatin for testing, we used plastic cube containers with dimensions of 4 × 4 × 4 inches (9.6 × 9.6 × 9.6 cm). Liquid gelatin was poured into the cube containers and left to rest for 24 h at room temperature to eliminate bubbles in the gelatin and then placed in a refrigerator for at least another 24 h before use. The cube containers were prepared ahead of time by cutting two opposite edges to allow the gelatin to be peeled out easily. These edges were sealed during casting using modelling clay (Sculpey^®, Polyform Products, Elk Grove Village, IL, USA).

2.3. Experimental protocol

A calibration cube was used before each set of tests to ensure that the two cameras were set perpendicular to each other and to the flight path of the arrow. The calibration cube was a plastic container (the same used for gelatin moulds) with a black and white checkerboard patterns overlaid onto two sides. The cube was set in the same position as the gelatin cubes would be and a single frame of video was captured by each camera. These single frame shots were analysed for shape distortion in order to assess the orientation of the cameras.

Both cameras were set to 40 000 fps (approx. 0.11 mm pixel⁻¹, 25 µs shutter speed). As the two cameras have different specifications, they showed different resolutions. The lateral (SA-Z) camera had a resolution of 1024 × 512 pixels and the vertical camera (SA-X2) had a resolution of 896 × 368 pixels. Some videos were also captured at 20 000 fps to be used for visualizing stress waves (electronic supplementary material, Movie S1). These lower frame rate videos were not used for kinematic or puncture measurements. A polarizing filter was placed in front of the studio light and a second filter was held in front of the lateral camera. These filters were oriented to create cross-polarized light in the lateral view to help visualize stress patterns.

For each puncture experiment, an arrow was notched into both bowstrings and pulled back to predetermined draw strength. The final flight velocity, momentum and kinetic energy of the arrow was controlled by both the extent of draw and the mass of the arrow, which could be altered by placing lead wire into the hollow shaft of the arrow. The arrow was aimed at the upper half of the ballistic gelatin cube guided by the metal guide and released. Each gelatin block was used for two puncture experiments, with the blocks rotated 180° after the first puncture experiment. The two puncture events were at least 2 inches apart in each block and preliminary inspection of the data confirmed that for a given arrow mass and speed the depth of penetration was identical between the first and second shots within the resolution of our analysis.

We also took video of an arrow pressed into a cube of ballistic gelatin at a relatively slow speed (1 mm s⁻¹) using an Instron testing machine (ElectroPuls E1000, Instron, Norwood, MA, USA). These videos were filmed under crossed-polarized light in order to compare stress patterns between slow and high-speed puncture events.

2.4. Data analysis

Position data for the arrow in each frame of the videos was collected using the program ImageJ [31]. These position data were used along with the frame rate data to calculate airborne velocities for the arrows. Average velocity prior to impact for a given experiment was used to calculate momentum and kinetic energy for the arrow. We hypothesize these three variables as having significant influence on puncture during ballistic experiments. Kinetic energy is a measure of the energy the arrow has available to transfer into the target as work; therefore, we might expect kinetic energy to strongly influence surface creation in the target. Momentum transfer, also called impulse, is related to the impact force, which influences the stresses during impact. Velocity is a common link between kinetic energy and momentum and may influence puncture mechanics itself. Arrows ranged in mass from 18.8 to 42.8 g with pre-impact velocities ranging from 8.75 to 13.42 m s⁻¹ (electronic supplementary material, table S1).

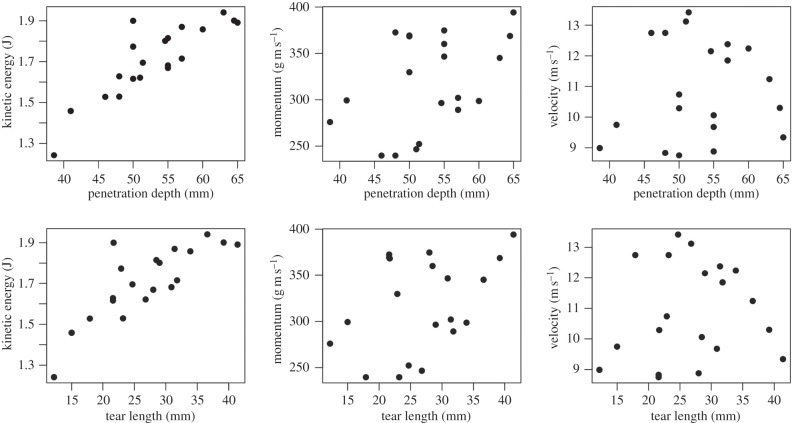
These three kinetic metrics were compared to a series of puncture metrics based on the results of the impact experiments. Figure 1 shows a single frame from one of the puncture experiments, captured at the point where the forward movement of the arrow has completely stopped. The black region seen represents the volume of gelatin affected by the arrow during penetration (figure 1). We call the portion of the black area where the arrow's shape is well defined the tear region and interpret it as the length along the arrow where the gelatin is tearing and new surfaces are being created. These tears can be seen as bright spots in the gelatin along the arrow shaft. Behind the tear region is a larger trapezoidal region that represents the volume of gelatin pulled along by the arrow as it penetrates the cube (figure 1).

Figure 1.

We measured three variables associated with puncture mechanics from high-speed videos of puncture experiments. The gelatin appears as a clear block in the videos, while the arrow is backlit and appears black. (a) Penetration depth: length from the edge of the gelatin to the tip of the arrow. (b) Tear length: length along the edge of the arrow where new surface is being created, denoted by the region where gelatin is no longer being pulled in along the arrow shaft, but is torn instead. Both penetration depth and tear length were measured from single frames at maximum depth. (c) Pull-in area: area of material on the impact surface being deformed during penetration by the arrow. Pull-in area was measured on all frames using a Matlab program that calculated the base length of the trapezoidal region outlined. Frames are from a single video filmed at 40 000 fps at a 1024 × 512 pixel resolution (electronic supplementary material, Movie S2). (Online version in colour.)

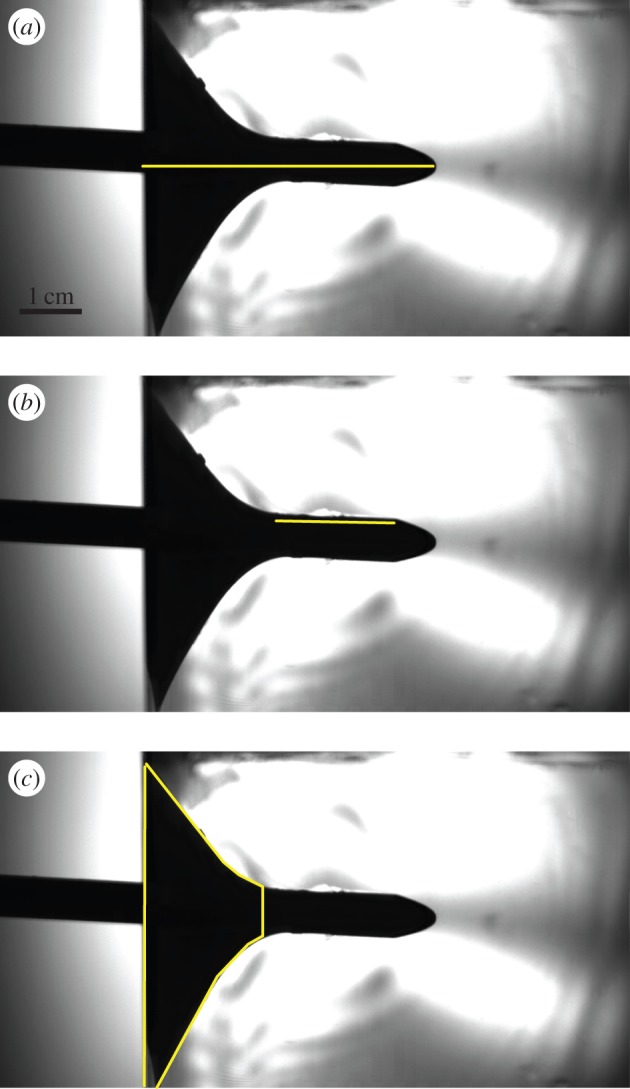
Penetration depth is measured as the distance from the edge of the gelatin first hit by the arrow to the tip of the arrowhead at the point where its forward movement is stopped (figure 1). Tear length is a proxy for the amount of new surface created during puncture and is measured along the upper edge of the arrow shaft along the tear region. Pull-in area is a proxy for the amount of material deformed without fracture during puncture (related to energy dissipated due to deformation) and is measured as the projected surface area on the side of the block being hit that is pulled inwards with the arrow (figure 2). In order to estimate this area, we measured the vertical height of the black region along the impact edge of the cube perpendicular to the arrow during impact (figure 1). The resulting value represents the radius of the projected pull-in area on the block (figure 2).

Figure 2.

Projected pull-in area represents the area on the impact surface of the gelatin block that is deformed or ‘pulled-in’ during impact. The affected region is coloured in while the black oval represents the projected area that was measured for comparison with kinematic variables. (Online version in colour.)

We measured penetration depth and tear length at the point of deepest penetration and compared them to the average kinematic variables (KE, momentum and velocity) using linear regressions and linear mixed models. Linear regressions were used to calculate correlation coefficients between kinematic and puncture variables. We used linear mixed models to determine the significance of these correlations. The random effect was whether the experiment was the first or the second shot into a particular gelatin cube. Although we saw no systematic difference in puncture variables between the first and second shots, we felt it best to account for potential influences. Mixed model regression analyses were performed using the nlme package for R [32]. Because penetration depth varied across experiments and the black deformation region extended beyond the frame in some videos, we did not compare pull-in area at maximum depth. Instead, pull-in area was measured frame by frame in all of the experiments in order to examine the pattern of deformation over time during impact and compare it with velocity. Pull-in area calculations were measured using a custom matlab script (MATLAB and Statistics Toolbox Release 2012b, The MathWorks, Inc., Natick, MA, USA).

3. Results

3.1. Material behaviour

Over the course of 20 ballistic arrow experiments, a pattern emerged of how the material reacted during a high-speed impact event (electronic supplementary material, Movies S1and S2). Upon initial impact with the gelatin, a small pull-in region forms around the arrowhead (figure 3). Stress waves peel off from the front and sides of the arrow immediately and propagate ahead of the arrow as it moves further into the gelatin. Shortly after initial impact, the tear region begins to form as new surfaces are created (figure 3). Sometime after tearing starts (3–4 ms after initial impact) macroscopic deformation of the gelatin block is observed (figure 3). Eventually, the arrow comes to a complete stop, all forward movement is halted. At this point, elastic energy stored in the gelatin during impact is released, leading to backwards movement of the arrow, and in 9 out of 20 experiments, the arrow was fully ejected from the gelatin (figure 3).

Figure 3.

High-speed videos taken under cross-polarized light of arrows impacting ballistics gel illustrates how materials react to puncture events at high speeds. The frames are from high-speed video of a puncture event, taken at 20 000 fps, with an arrow travelling at 12.2 m s⁻¹. Stress waves are clearly visible 3.2 ms after impact and the arrow reached its final penetration depth by 12.9 ms. However, the gelatin did not begin to macroscopically deform until 18.3 ms after impact. Finally, the deformation of the gelatin resulted in the arrow being expunged 48 ms after initial impact (electronic supplementary material, Movie S1).

The stress patterns seen within gelatin blocks undergoing high-speed impact puncture events are markedly different from those seen during steady, slow puncture (1 mm s⁻¹) controlled by an Instron testing machine (figure 4). Stress patterns in the slow experiment spread from the tip of the arrow and create a zone of higher stresses right in front of the encroaching arrow. The high-speed experiments show a series of stress waves created by the impact of the arrow propagating through the gelatin. These stress waves move forward more rapidly than the arrow, which itself slows to a stop. Notably, the block of gelatin does not begin to deform until the stress waves encounter the edges of the block (figure 3). Additionally, the thinner fringes in the dynamic image indicate higher concentrations of stress during dynamic impact relative to the static test. Finally, it can be seen in figure 4b that the transition from normal to shear at the surface for the gel indicates the slower transverse wave and localizations of forces.

Figure 4.

Puncture occurring at high velocities results in a very different strain pattern than puncture occurring at slow, steady rates. (a) Arrow piercing ballistics gelatin at 1 mm s⁻¹ (driven by an Instron testing machine). (b) Arrow piercing ballistics gelatin after being fired from a bow at 12.2 m s⁻¹. The high-velocity impact shows stress waves propagating from the arrow as it pierces the gelatin as the material does not have the ability to come to equilibrium as seen in (a).

3.2. Kinetics versus puncture

Mixed model comparisons between kinematic variables and metrics of puncture effectiveness in gelatin show kinetic energy as the best predictor of puncture effectiveness (table 1 and figure 5). Kinetic energy correlates significantly with both penetration depth and tear length, indicating that KE is a good indicator of the energy available for creating surface area within the material and allowing deeper penetration. Momentum shows border-line significant correlation with penetration depth and no significant correlation with tear length. Velocity shows no correlation with either variable. Full results from linear mixed models can be found in the electronic supplementary material, tables S2–S7.

Table 1.

Kinetic energy is the only kinematic variable that shows significant correlation with both puncture variables (penetration depth and tear length) based on linear mixed models. r² values are based on linear regressions while the p-values are based on linear mixed models (significant values are in bold).

	velocity		momentum		kinetic energy
	r2	p-value	r2	p-value	r2	p-value
penetration depth	0.01	0.7	0.2	0.05	0.74	<0.0001
tear length	0.01	0.7	0.16	0.08	0.65	<0.0001

Figure 5.

The kinetic energy of a weapon fired into ballistics gelatin is a better predictor of puncture depth and tear length than either momentum or velocity. Results from 20 experimental trials with a ballistic testing system varying both the mass and velocity of the projectiles show a strong correlation between the kinetic energy of the projectile arrow in mid-flight and the extent of penetration measured as either overall penetration depth or the length of the fracture zone (tear length). Neither projectile momentum nor speed show as strong of a correlation with puncture depth as energy.

The pattern of pull-in area growth over the course of an experiment shows influences of velocity. When pull-in area is plotted versus penetration depth for a single experiment, the result is an exponential relationship: more material is reacting as the arrow goes further into the block of gelatin (figure 6). Comparing the responses for different impact velocities, it becomes clear that for a given penetration depth, the faster arrows are being resisted with less material (figure 6).

Figure 6.

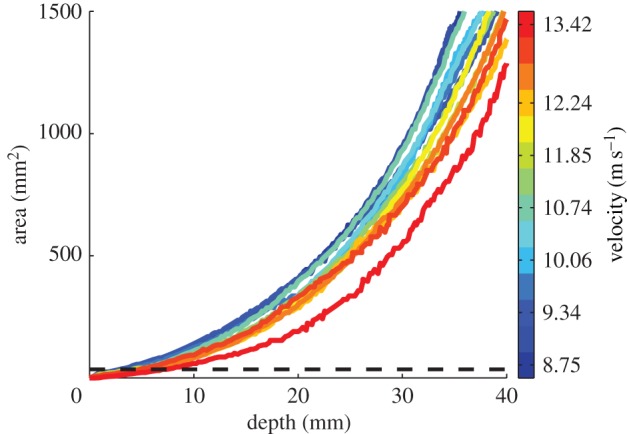
For a given depth of penetration during high-speed puncture experiments, the faster the projectile is moving, the smaller the pull-in area on the impact surface. When pull-in area is plotted against penetration depth across 14 high-speed puncture experiments, an exponential relationship is seen: the farther the arrow penetrates, the larger the pull-in area becomes on the impact surface. However, arrows travelling faster show less area affected than slower arrows as seen by the colour-coding of the lines. (Online version in colour.)

4. Discussion

4.1. Kinematics and puncture

Results from ballistic puncture experiments illustrate that for the range of masses (approx. 18–42 g) and velocities (approx. 8–14 m s⁻¹) studied, kinetic energy is a good predictor of puncture ability as measured by depth of penetration and surface creation (tear length). This result matches our understanding that surface creation during cutting requires energy, so the more energy the projectile has, the more that can be converted into surface area all else being equal. The lack of strong correlation between the puncture variables and momentum is more surprising given both the role of momentum transfer in stress formation and impact force and the fact that kinetic energy and momentum are both calculated from the same measurements: mass and velocity. One explanation is that the material used here, ballistics gelatin, has a low critical stress threshold. None of the experiments resulted in failure to puncture, meaning the range of momentums seen must all fall well above the minimum required for fracture initiation. Momentum may play a more important role at lower speeds or with more resistant materials, where critical stress to fracture is more of a barrier to puncture.

While velocity alone does not correlate with puncture depth or surface creation, it does influence the area affected by impact. For a given depth of penetration, projectiles shot at higher velocities show smaller pull-in area during impact (figure 6). These results indicate that less energy is lost due to deformation when arrows are fired at higher speeds. Higher velocity works to maximize the efficiency of the projectile, ensuring that more of the kinetic energy is transferred into surface creation as opposed to deformation of material. This is similar to how sharpness of a cutting tool focuses energy into a smaller area during cutting, increasing the stress (for a similar discussion of the relationship between projectile energy and impact crater volume in metals, see Christman & Gehring [33]).

The relationship between kinetic energy, velocity and puncture mechanics has implications for the scaling of puncture systems in biology. The energy available for puncture in a biological ballistic system can be altered in one of two ways based on the definition of kinetic energy: either increasing mass or increasing the velocity. However, as noted in the Introduction, there is a sevenfold size range among puncturing animals. As animals get smaller, particularly down to the micro- or nanometre range, the mass of their puncturing weapons will get smaller, which will reduce the kinetic energy available. One way for small animals to compensate for this loss of mass is to increase the speed of the projectile. We see this pattern emerge when reviewing biological examples: the smaller animals (such as termites and the nematocysts of jellyfish) show the highest velocities, especially compared with larger vertebrates such as snakes. Higher velocities can also help by allowing the projectiles to make more efficient use of the energy through reducing the pull-in area of the target affected by impact.

It is important to note that we have only explored a very narrow range of size and speed compared to the biological realm. A size range between 18 and 42 g places us firmly within the vertebrates in terms of weapon size, while the velocities we are looking at (between 8 and 14 m s⁻¹) places us into the invertebrate realm. It is unclear if the patterns we are seeing here will be replicated at much smaller scales (in the mm–μm range) or higher speeds (the 30–60 m s⁻¹). Specifically, when in the size range of a nematocyst (nanometre scale) the hydrodynamics of the system will start to change drastically and may have a strong influence on the mechanics of puncture. In order to address this, future work must explore puncture mechanics at the extremes of both size and speed.

4.2. Material dynamics during puncture

High-speed videos of puncture experiments in ballistic gelatin illustrate major differences between steady cutting mechanics and high-speed puncture. The patterns of stress during steady-state cutting have been observed [14,26] and tend to show a slow spread of strain starting from the point of contact. However, impact at high velocities creates stress waves, which propagate through materials. Videos from our experiments show stress waves propagating out from the arrow after impact (figures 3 and 4; electronic supplementary material, Movies S1 and S2). Two key observations can be made when comparing the two images. The first is that the dynamic experiment shows higher concentrations of stress, indicated by the thinner fringes in the stress waves relative to the stress patterns in the static test. Additionally, the small vertical spread seen in the fringe pattern indicates that the force the material is resisting is more localized.

The dynamics of the stress waves propagating through the gelatin alter how the gelatin responds during puncture. In a slow, non-impact puncture event, malleable materials, like gelatin, will deform when stressed and have time to come to an equilibrium. This deformation can dissipate energy and help blunt crack growth [12]. However, in high-speed events, the stress waves move faster than the material can respond. The stress concentration passes through the material before the material has time to deform allowing only a portion of it to react. This was shown through the effect of velocity on pull-in area that was discussed above. The result is that the gelatin does not act like a malleable, deformable object, but actually acts more like a brittle object [34], which should result in less ability to blunt crack growth [12].

The effect of stress wave speed on fracture growth and deformation has been studied in a number of systems [10,34], but the consequences for biological puncture systems have not yet been explored. It is possible that animals attempting to puncture biological tissues with good crack blunting capabilities (such as tough integument) could potentially overcome these resistances by increasing the speed of strike to a point where the material begins to act in a more brittle manner [34]. Furthermore, attempts to puncture at high speeds can help overcome challenges presented by inertial forces. If a mantis shrimp attempts to spear a fish suspended in the water column, there is nothing to anchor that fish in place. If the strike is too slow, it may just push the fish away as momentum is transferred from the appendage to the fish. However, at higher speeds, where momentum is transferred to a smaller region of the fish, puncture can occur prior to the body of the fish fully reacting to the impact.

In order to understand how high-speed impact will alter cutting mechanics, it is also necessary to explore the effects of rate-dependent material properties in biological tissues. In this study, we specifically focused on the influence of kinematics for a given material: a homogeneous isotropic gelatin. However, the results we found here would likely be altered if we used materials with different properties. While ballistics gelatin is designed to mimic human tissue to an extent, actual human tissue is much more complex. The strain rate of materials is key to understanding how fracture will propagate during impact events [34]. If the strain rate is much slower than the velocity of the stress waves, there would not be time for fractures to extend before the stress field has moved on [34]. Strain rate will also influence how fast the material can deform, directly influencing the patterns seen in our experiments. Some work has been done on strain rates in ballistics gelatin [35] and agarose gel [36]. A good amount of work has also been done on rate-dependency in biological tissues including both bone [37–41] and soft tissues [42–46], particularly brain tissue [47,48].

4.3. Morphology

One major aspect of biological high-speed puncture systems which has not been addressed in this study is morphology. Morphological variation is a cornerstone of evolutionary sciences and a brief review of tooth form across mammals alone illustrates the wide variety of cutting shapes produced by nature [12,49]. Tip morphology in a projectile will alter the relationship between kinematics and puncture found in our study, but it is not clear how. Cone shape has been shown to significantly alter puncture mechanics at slow speeds in relation to mammalian dentition [11,13] and shark teeth [16]. The results from these studies have created a strong basis for characterizing cusp form in relation to puncture, but only in slow, steady-state situations. The effects of tool shape on high-speed puncture have been explored in the evolution of human weaponry [50]. Work in this field has identified measurements such as tip cross-sectional area and perimeter as potentially useful for determining whether collected weapon tips were used on spears or arrows [51–53]. How well metrics like these would work in biological systems is unclear, but these studies present a good starting point for examining morphological influences in high-speed systems.

How morphology will alter puncture performance is also dependent upon the properties and structures of the materials being punctured. While a good deal has been written on the effects of food properties during mastication and grinding [12,19,20,23], much less has been done to investigate how the material properties of biological tissues influence cutting and puncture performance [11,15]. Furthermore, the puncture performance of different morphologies on multi-layered biological composite materials is virtually unknown. Work has been done examining fracture patterns on tooth-like brittle dome structures [54–57], but little is known about how multi-layered structures would alter puncture or cutting patterns [11,14]. The nature of multi-layered bio-composites leads to further questions about the scale of tool morphology and prey material. A theoretical framework for the relationship between food size, tooth size and fracture mechanics has been developed for blunt tools cracking brittle materials [58], but no such theory yet exists for puncture.

While it seems self-evident that tip shape will have an effect on puncture mechanics at high speed, another aspect of morphology may be just as important: surface structure. As the projectile is moving through the material, some energy will be lost due to frictional forces as it moves material aside to make room. Energy lost to friction could potentially be modified by surface structure that reduces contact area between the projectile and the material. A number of studies on biological cutting have focused on the role of surface structures such as serrations [59,60]. Structures such as these in carnivorous vertebrates are usually hypothesized to aide in tearing soft tissues such as muscle using a grip and rip behaviour [59,61]. Whether these surface features could also help with overcoming frictional effects during puncture is not clear. Another potential use for certain serrations (those with more hook-like shapes) is to keep the projectile anchored. In just under half of our experiments, the arrows were expunged from the gelatin after impact due to elastic forces. Serrations could be used to maintain insertion of the projectile in biological systems using puncture for prey capture, such as in the harpoon structures of nematocysts [62].

5. Conclusion

Animals across four phyla and spanning a sevenfold range in size use high-speed projectiles to puncture during prey capture or defensive behaviours. In all cases, the animals must overcome common challenges to create fractures in the target material and insert the projectile weapon. Our experimental work with a controlled ballistic system shows that the kinetic energy of the projectile is a better predictor of puncture mechanics than momentum or velocity, while arrow velocity affects how the material responds to impact. These results form a framework for understanding the relationship between kinematic performance and puncture mechanics. From this basis, future work can begin exploring the effects of strain rate and stress wave propagation in biological materials undergoing high-speed impact, as well as how variation in weapon morphology alters puncture mechanics. Given the breadth of examples found in nature and the commonality of the underlying mechanical principles at work, high-speed puncture offers a good case study for exploring how mechanical principles can influence evolutionary processes across a wide range of animals.

Data accessibility

The data reported in this article have been uploaded on the Dryad digital repository (http://doi.org/10.5061/dryad.25qp5). The kinematic and puncture data taken from videos are available in the electronic supplementary material. The HSV movie files are deposited at the Interface Focus website.

Authors' contributions

P.S.L.A. conceived of the project, designed and performed puncture experiments, analysed high-speed video data, performed statistical analyses and drafted the manuscript; J.L. designed and performed puncture experiments and helped draft the manuscript; M.P. analysed high-speed video data and helped draft the manuscript. All authors gave final approval for publication.

Competing interests

We have no competing interests.

Funding

This research was funded by a National Science Foundation grant (IOS-1149748) awarded to S. Patek.