Understanding spatial distributions: negative density-dependence in prey causes predators to trade-off prey quantity with quality

Abstract

Negative density-dependence is generally studied within a single trophic level, thereby neglecting its effect on higher trophic levels. The ‘functional response’ couples a predator's intake rate to prey density. Most widespread is a type II functional response, where intake rate increases asymptotically with prey density; this predicts the highest predator densities at the highest prey densities. In one of the most stringent tests of this generality to date, we measured density and quality of bivalve prey (edible cockles Cerastoderma edule) across 50 km² of mudflat, and simultaneously, with a novel time-of-arrival methodology, tracked their avian predators (red knots Calidris canutus). Because of negative density-dependence in the individual quality of cockles, the predicted energy intake rates of red knots declined at high prey densities (a type IV, rather than a type II functional response). Resource-selection modelling revealed that red knots indeed selected areas of intermediate cockle densities where energy intake rates were maximized given their phenotype-specific digestive constraints (as indicated by gizzard mass). Because negative density-dependence is common, we question the current consensus and suggest that predators commonly maximize their energy intake rates at intermediate prey densities. Prey density alone may thus poorly predict intake rates, carrying capacity and spatial distributions of predators.

1. Introduction

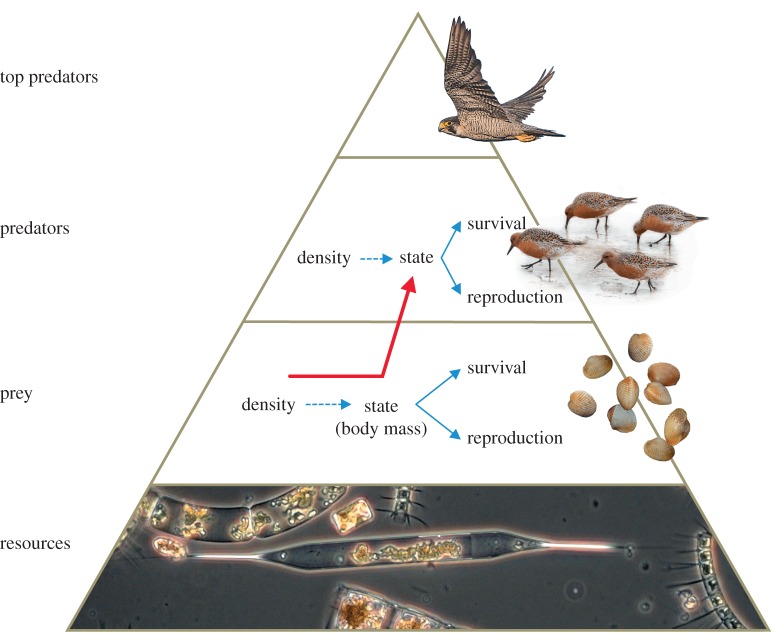
Negative density-dependence in state has mainly been studied within trophic levels in the context of population regulation [1–4]. As density increases, survival and reproduction decrease to a point that mortality and reproduction are at equilibrium, i.e. demographic carrying capacity [2,4]. Negative density-dependent survival and reproduction are population processes mediated by individual states (e.g. body mass [3,5]). As population size increases, intraspecific competition increases and individual body masses decrease, which reduces reproductive output and survival probability [6]. An ignored aspect of these well-studied processes within trophic levels has been the possibility that reduced individual states (body masses) have implications for energy intake rates of foragers at higher trophic levels (figure 1).

Figure 1.

A trophic pyramid for our study system. Within trophic layers, negative density-dependence has been studied in the context of population regulation. For instance, as population size increases an individual's state (e.g. body mass) decreases, which negatively affects their reproductive output and survival probability. Here, we focus on the effect that negative density-dependence among prey has on their predators. Negative density-dependence occurs within all trophic levels. Likewise, the effects of density-dependence occur between all trophic levels. Dashed lines represent negative interaction pathways, and solid lines represent positive interaction pathways. The red arrow represents the focus of this study, i.e. the between trophic-level effect of density-dependence on body mass. Photo courtesy: Jan van de Kam (Falco peregrinus and Calidris canutus), Allert Bijleveld (Cerastoderma edule) and NIOZ (collection of phytoplankton species).

A key concept linking two trophic levels is the ‘functional response’, a function that describes how a predator's per capita intake rate varies with prey density [7]. The functional response is fundamental to spatial distribution modelling [2], estimations of carrying capacity [8,9] and the analysis of population dynamics in predator–prey systems [1]. In the Holling's type II functional response (also known as Holling's disc equation), the most widespread among predators, intake rate increases with prey density towards an asymptote that is set by handling time [10,11]. Intake rates may also decline at high prey densities, which results in a hump-shaped functional response (a so-called type IV functional response [12]). As reviewed in [10], the decline in intake rate at high prey densities has been attributed to a decrease in predator searching efficiency (e.g. owing to increased predator detection, confusion, mobbing), and an increase in associated foraging costs (e.g. owing to the accumulation of toxic prey substances, an increased risk of injury, etc.). However, these processes are particular to specific predator–prey systems. Instead, a more general phenomenon is negative density-dependence [13], which can, through a reduction in the energy state of prey, also cause a declining energy intake rate to predators at high prey densities.

The consequence of negative density-dependence among prey is that predators are faced with a trade-off between the quantity and quality of their prey [14,15]. At low prey densities, predators have difficulty finding prey, but because of low levels of intraspecific competition these prey have a relatively large energy content. At high densities, prey are easier to find, but competition is fierce, and prey have a relatively low energy content. Herbivores are thought to have a type IV functional response, because the digestive quality of forage decreases with an increase in biomass and age [16]. Indeed, some species of herbivores have been shown to select foraging locations of intermediate biomass density where they maximized energy intake rates [17,18]. Conversely, predators (consumers of herbivores and animals of higher trophic levels, figure 1) are generally assumed to maximize energy intake rates at the highest prey densities [2,19].

Aiming to provide a stringent test of this generality, we quantified both the spatial distribution in quantity and quality of a bivalve prey (edible cockles Cerastoderma edule, hereafter called cockles) and foraging distribution of their avian predator (red knot Calidris canutus islandica, hereafter called knots) at high spatial and temporal resolution over a large intertidal area of 50 km². We found that with an increase in cockle density, a cockle's relative flesh mass declined (negative density-dependence). We also showed that a type IV functional response best represented these data and predicted that knots would maximize their energy intake rates on intermediate cockle densities. Knots swallow their prey whole and, because individuals have differently sized gizzards, vary in the amount of shell material they are capable of processing [20]. This in turn means that individuals maximize their intake rates at different cockle densities. To test whether knots indeed selected locations of intermediate cockle densities, we tracked the positions of knots with a novel automated tracking methodology [21] providing high spatial resolution (37 m) and temporal resolution (1 Hz) in the position fixes.

2. Material and methods

(a). Study area and background

Our study site was located in the western Dutch Wadden Sea near the uninhabited islet of Griend (53°15′ N, 5°15′ E) [22]. Griend is surrounded by extensive intertidal mudflats where, during low tide in the non-breeding season, large flocks of knots can be found foraging. In one tidal cycle, knots often fly tens of kilometres in search of buried hard-shelled bivalves or gastropods (Peringia ulvae) [22,23]. Owing to low densities of alternative prey (electronic supplementary material, figure S1), knots in our study area and period mainly foraged on cockles. This was confirmed by a diet analysis on 32 droppings from different individuals, which we collected in the study area between 10 August and 27 September 2011. In these droppings, we found 272 prey items of which 223 were cockles, 46 P. ulvae, and the remaining three prey items were Macoma balthica, Mytilus edulis or Ensis directus. In terms of flesh mass, cockles contributed to more than 99% of ingested biomass. Consequently, we focus on the interaction between knots and cockles.

Cockles can be found in densities of up to several thousand individuals per square metre, and it has been shown that their flesh mass declines with increasing density (negative density-dependence [24,25]). Knots swallow their prey whole, which limits the size of ingestible cockles to those smaller than 16 mm in length [22]. Additionally, their intake rate is constrained by the rate of processing ingested shell material [20]. Owing to this digestive constraint, knots maximize their energy intake rates by selecting individual cockles with large flesh mass compared with their shell mass [20]. Note that the gizzard mass of knots is flexible and, over the course of a week, reflects the rate of shell mass that it has processed [20].

(b). The predators

Between 2 August and 18 September 2011, we tracked 47 knots with the novel and prototype version of the time-of-arrival tracking system [21]. We released all birds between 2 and 5 August 2011, after gluing a 7 g tag (less than 5% of body mass) to their rump with cyanoacrylate (electronic supplementary material, figure S2a). Nineteen of these birds had been captured on Griend in March 2010 and were released after 1.5 years in captivity, and the other 28 were caught on the nearby islet of Richel (53°17′ N, 5°07′ E, electronic supplementary material, figure S2b) between 2 and 4 August 2011. Before releasing the birds, we measured the size of their muscular stomach (gizzard) with ultrasound [26] as described in detail by [27]. The average gizzard mass was 7 g (2.0 s.d.) ranging between 4.0 and 10.4 g.

The tags emitted a radio signal at 1 s intervals, which could be received by nine stations that were set up at fixed locations in the study area (electronic supplementary material, figure S2b). If at least three of the receiver stations registered the tag signal, the position of the bird was estimated (electronic supplementary material, figure S3) via the arrival times of the signal and locations of the receiver stations [28]. To reduce measurement error, we median-filtered the positioning data with a seven-points sliding window (see R-package ‘signal’). Because birds moved out of the area, we lost reception of many tags in the course of our study, and because of technical issues, inherent to the use of prototype systems, signal reception at the receiver stations was sometimes intermittent. Therefore, we restricted our statistical analyses to the period between 12 August and 26 August 2011, and excluded data from the receiver stations on Richel. In this period and area, we had the most regular tracking data and the most individuals. We collected a total of 1341 438 estimated positions across 19 different birds (five that were released from captivity and 14 freshly captured).

To identify intensively used areas and to reduce the computational issues associated with this large dataset (e.g. time-consuming calculations, serial autocorrelation [29]), we summarized our tracking data in ‘residence patches' as follows. We divided an individual's track into sections between two consecutive high tides and calculated residence times for successive positions within these tidal periods [30]. For calculating residence times, we used a time window of 3 h and a patch diameter of 250 m reflecting the grid-spacing for cockle sampling stations. Following [31], we segmented these residence time data automatically, and we refer to [30] for details. To exclude the positions of flying birds as well as infrequently used areas, we disregarded segments with a residence time less than 10 min (n = 165). For each segment, we extracted the median coordinate and residence time. We will refer to each segment as a ‘residence patch’ indicating both the location and the time spent there.

The extent of available mudflat area is restricted by the tide that forces birds to move during parts of the tidal cycle. Because we were interested in foraging behaviour and resource selection without tidal forcing, we restricted our residence-patch data to 3.5 h before and 2.5 h after low tide (electronic supplementary material, figure S4). Additionally, we restricted our analyses to individuals with five or more calculated residence patches. In total, this procedure resulted in data from 13 individuals with 365 residence patches ranging in duration from 10 min to 4.7 h (using 558 781 estimated locations).

(c). The prey

Between 15 and 19 July 2011, we sampled cockle density, flesh mass and shell mass on a 250 m sampling grid, complemented by an additional 20% sampling stations randomly placed on the grid lines (electronic supplementary material, figure S2b). This composite sampling design allowed for accurate spatial interpolations of cockle density, flesh mass and shell mass [32], necessary for predicting these variables at locations where knots were recorded foraging. To reduce laboratory time, we measured flesh and shell mass of individual cockles on roughly 25% of the sampling stations (i.e. on 500 m grid-spacing). At each sampling site, we collected 0.018 m² of mudflat to a depth of 30 cm. Judging their length in the field, we stored cockles less than 8 mm in a 4% formaldehyde solution, and froze larger cockles [33]. In the laboratory, we measured their lengths to the nearest 0.1 mm, ash-free dry mass of the flesh (AFDM_flesh) and dry mass of the shell (DM_shell) [22] (for details see electronic supplementary material, appendix S1). Overall, we sampled 854 stations and collected 15 874 individual cockles. In total, we obtained 663 estimates for AFDM_flesh from 1721 individuals that we collected from 120 sampling cores. For analysing DM_shell, we collected data of 82 individuals from 33 sampling stations.

AFDM_flesh, DM_shell and their variances increase with cockle length (heteroscedasticity). To compare flesh and shell mass between differently sized cockles, we therefore calculated an individual's relative flesh and shell mass by dividing its measured AFDM_flesh or DM_shell by the (predicted) length-specific average [24]. These averages were obtained by fitting nonlinear local regression models (LOESS with local quadratic fitting) between AFDM_flesh or DM_shell, and length on logarithmic scales (electronic supplementary material, figure S5). We back-transformed these residuals to reflect an individual's relative AFDM_flesh and DM_shell compared with the average cockle of identical length.

For each sampling station, we calculated cockle density by counting the number of cockles and dividing that by the surface area of a sampling core. To normalize model residuals, we transformed these counts with the common logarithm (log_10­). To avoid taking the logarithm of zero, we added one before the data transformation.

We analysed the density-dependence on relative AFDM_flesh and DM_shell in linear mixed-effect models with sampling station as a random effect and cockle density (m⁻²) as an explanatory variable. We also investigated effects of length and the interaction of length and density on both relative AFDM_flesh and DM_shell. Cockle length ranged from 1.0 to 41.1 mm. We centred length and log₁₀-transformed density by subtracting their means of 8.9 mm and 3.14, respectively. By parametric bootstrapping (n = 1000), we calculated significance under the null hypothesis that the estimated coefficients are zero.

(d). Interpolating resource landscapes

To calculate resource landscapes for foraging knots, we spatially interpolated cockle densities and relative AFDM_flesh across the study area. For the interpolation of cockle densities, we selected cockles that knots can swallow (length < 16 mm [22]). Because many cockles were too small to separate shell from flesh (electronic supplementary material, appendix S1), the sample sizes of DM_shell were too low for spatial interpolations. To interpolate cockle density and relative AFDM_flesh, we calculated correlograms from the measured values and fitted exponential spatial autocorrelation functions (electronic supplementary material, figure S6) [24,32]. To reduce prediction error in interpolating relative AFDM_flesh, we included spatially interpolated cockle densities as a covariate.

We interpolated measured cockle densities and relative AFDM_flesh on spatial grids with a resolution of 25 × 25 m. These resource landscapes were used to predict a knot's energy intake rate by multiplying the functional response (Holling type II) by the interpolated (density-dependent) energy content of cockles: IR = [(a × N)/(1 + a × N × T_h) ] × e(N), where IR is the energy intake rate (mg AFDM_flesh s⁻¹), a is searching efficiency (m² s⁻¹), N is interpolated cockle density (n m⁻²), T_h is handling time (s) and e(N) is density-dependent AFDM_flesh (mg) of an individual cockle. We used a searching efficiency of 6.4 cm² s⁻¹ [34], and estimated handling time from video recordings collected between 14 August and 24 September. Based on 23 tagged birds handling 637 cockles, handling time was 4.0 s (s.d. 1.7) which compares well with earlier findings [34]. To calculate e(N), we assumed that knots fed on cockles of 7 mm long, which is the size that knots preferentially selected in this area the previous year [24]. We multiplied the spatially interpolated measurements of relative AFDM_flesh by 1.7 mg (the average AFDM_flesh of 7 mm cockles, electronic supplementary material, figure S5a). Note that e(N) (mg) is derived from interpolated measurements of density and relative AFDM_flesh.

We calculated a knot's digestive constraint on shell-mass intake rate (c, mg AFDM_flesh s⁻¹) as q × 0.05 × G² [23], where q is the ratio of AFDM_flesh to DM_shell, and G is gizzard mass (g). Because the sample size was inadequate for spatially interpolating measurements of DM_shell, we predicted relative DM_shell from interpolated densities with the density-dependent model presented in electronic supplementary material, table S1b. To get absolute shell masses, we multiplied relative DM_shell by 24.3 mg (the average DM_shell for cockles of 7 mm, electronic supplementary material, figure S5b). We then calculated a bird's gizzard-mass-dependent intake rate as the minimum of its predicted intake rate without a digestive constraint (IR) and its digestive constraint c [23]. We predicted gizzard-mass-dependent intake rate for average gizzard mass (7 g, IR_avg.gizzard), and for each individual's measured gizzard mass (IR_ind.gizzard). Birds with different gizzard masses have different levels of intake rate (electronic supplementary material, figure S7). To compare IR_ind.gizzard between birds with different gizzard masses, we standardized IR_ind.gizzard by subtracting an individual's mean IR_ind.gizzard and dividing it by its standard deviation (electronic supplementary material, figure S8). Large values of IR_ind.gizzard reflect areas where individuals would achieve a large intake rate given their gizzard mass.

(e). Resource selection analyses

We modelled variation in knot locations as a function of prey-related covariates (cockle density, relative cockle AFDM_flesh, predicted intake rates) within a used-availability design [35]. The values of covariates at the bird's residence patches (used locations) are contrasted with those that were available to them (availability locations). The null model is that resources are selected proportional to their availability, and that deviations from proportionality indicate avoidance or preferential selection. We complemented each residence patch with 15 availability locations resulting in a sample size of 5475 (electronic supplementary material, figure S9). At each used and availability location, we extracted from the resource landscapes: cockle density, relative AFDM_flesh and predicted intake rates without a digestive constraint (IR), with an average digestive constraint (IR_avg.gizzard), and with an individual-specific digestive constraint (IR_ind.gizzard). We analysed the used (1) and availability (0) data in mixed-effect logistic regression models, thus correcting for variation among individuals. To avoid biased estimates of the resource selection functions, we applied infinitely weighted logistic regression by weighing used locations by 1 and availability locations by 1000 [36]. We additionally weighted our used locations by their residence time (h). The resource selection function is defined as the exponent of the predictors of the logistic regression model ignoring the intercept, which is proportional to the density of knot locations. For representation purposes, we scaled the resource selection functions between zero and one.

We calculated a null-model (intercept only) for the used-availability data. For each of the five explanatory resource-related covariates, we fitted two additional models with: (i) an intercept and linear predictor, and (ii) an intercept, a linear and a quadratic predictor. The quadratic term can capture possible trade-offs between resources, e.g. between cockle density and relative AFDM_flesh. High residual spatial and temporal correlation within location observations could lead to overly complex models. We, therefore, used likelihood-based cross validation [37] for selecting between the shapes of resource selection models (i.e. a null-, linear- or quadratic), see electronic supplementary material, table S2.

We analysed our data in R v. 3.1.0 [38] with the packages ‘ncf’ for calculating correlograms, ‘fields' for spatial interpolations, ‘lme4’ for mixed-effect model analyses, and ‘adeHabitatLT’ for calculating residence times. We additionally used the packages ‘RODBC’, ‘PBSmapping’, ‘spatstat’, ‘sp’, ‘raster’, ‘signal’, ‘rgdal’, for working with the (spatial) data. For plotting the spatial data, we used QGIS v. 2.2.0 (http://qgis.osgeo.org). We segmented residence time data with Matlab (code available from http://www.math.u-psud.fr/~lavielle/programmes_lavielle.html).

3. Results

(a). Negative density-dependence in the prey

Both the relative flesh mass (AFDM_flesh) and shell mass (DM_shell) of cockles declined with their density (figure 2a and electronic supplementary material, table S1). Neither length nor its interaction with density, significantly affected a cockle's relative AFDM_flesh and DM_shell. The decline in relative AFDM_flesh was stronger than the decline in relative DM_shell. For this reason, the ratio of flesh to shell mass (digestive quality) also declined with cockle density. Because of the negative density-dependence among cockles, knots had a type IV functional response (figure 2b).

Figure 2.

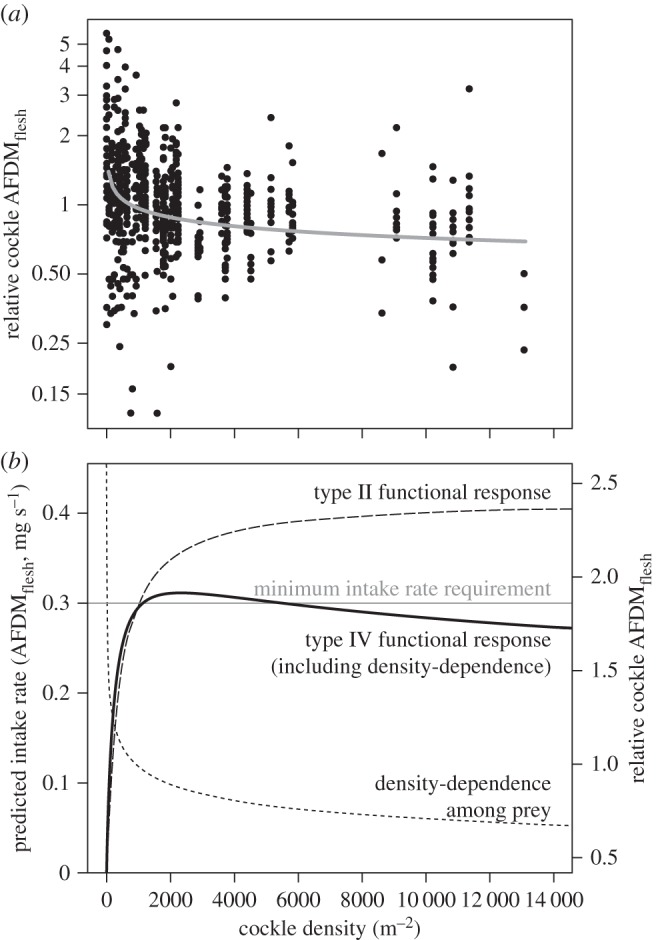
Negative density-dependence in cockle flesh mass caused a hump-shaped functional response for knots (a type IV functional response). (a) A cockle's relative ash-free dry mass of the flesh (AFDM_flesh) plotted against cockle density (m⁻²). The regression line reflects the statistical model presented in electronic supplementary material, table S1a. (b) The predicted energy functional response of knots foraging on 7 mm long cockles (thick black line), which includes the negative density-dependence in relative cockle AFDM_flesh (short-dashed line with units on the right y-axis). We also plotted the Holling's type II functional response without the negative density-dependence among cockles (long-dashed line). For reference, we included the threshold intake rate that knots need to acquire energy balance (grey horizontal line, [34]).

(b). Interpolated resource landscapes

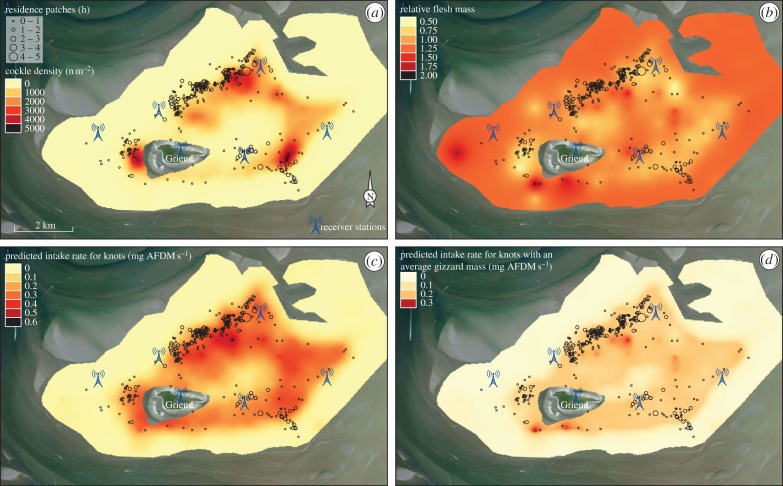
Cockle density (figure 3a) and relative AFDM_flesh (figure 3b) were patchily distributed. Consistent with the analysis of negative density-dependence (figure 2a and electronic supplementary material, table S1a), high cockle densities coincided with low relative AFDM_flesh (figure 3a,b). With interpolated cockle densities (figure 3a) and relative AFDM_flesh (figure 3b), we predicted intake-rate landscapes for knots without a digestive constraint (IR, figure 3c), with an average digestive constraint (IR_avg.gizzard, figure 3d), and with an individual-specific digestive constraint (IR_ind.gizzard, electronic supplementary material, figure S8). Compared with an unconstrained forager, intake rates of digestively constrained foragers are considerably reduced (figure 3d); the smaller the gizzard size, the lower its intake rate (electronic supplementary material, figure S7).

Figure 3.

Resource landscapes with the low-tide distribution of knots. The panels show interpolated (a) cockle densities (m⁻²), (b) relative flesh masses of cockles (AFDM_flesh), (c) predicted intake rates for knots (IR, mg AFDM_flesh s⁻¹) and (d) average gizzard-mass-dependent predicted intake rates (IR_avg.gizzard, mg AFDM_flesh s⁻¹). The panels additionally show the residence patches of all tagged knots. The sizes of these symbols indicate how long a bird had spent in that particular location ranging from 10 min to 4.7 h. The underlying satellite imagery was obtained from Bing in the QGIS OpenLayers plugin.

(c). Resource selection

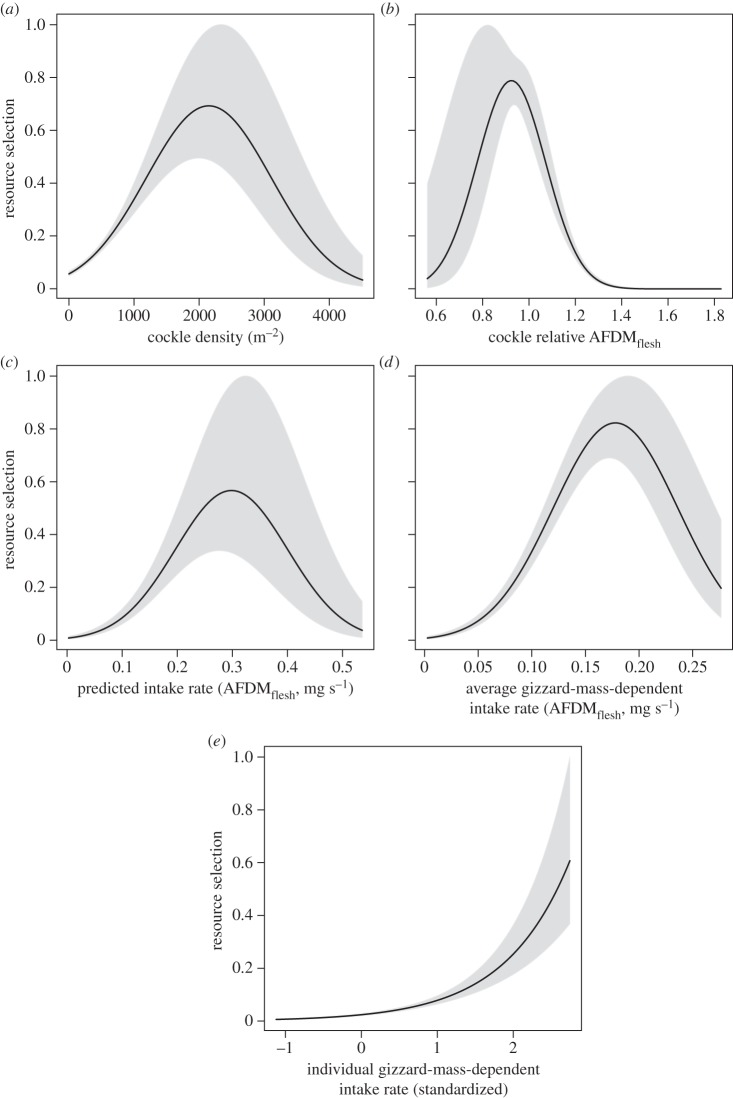
The resource selection analyses (electronic supplementary material, tables S2 and S3) showed that knots preferentially selected locations of intermediate cockle densities (figure 4a). At these locations, the birds encountered cockles with intermediate relative AFDM_flesh (figure 4b). Likewise, they encountered intermediate predicted intake rates when ignoring the digestive constraint (IR, figure 4c) and when considering an average digestive constraint (IR_avg.gizzard, figure 4d). When we incorporated an individual-specific digestive constraint, we found that knots had selected those locations where they maximized their individual gizzard-mass-dependent energy intake rate (IR_ind.gizzard, figure 4e). Birds with large gizzards selected locations with high cockle density but small relative flesh mass, whereas birds with small gizzards selected locations with low cockle density but large relative flesh mass (electronic supplementary material, figure S10).

Figure 4.

Knot resource selection functions. All panels show the resource selection functions on the y-axis, which are proportional to the probability of knot occurrence. The different panels have different prey related predictor variables on the x-axis: (a) cockle density (m⁻²), (b) relative cockle flesh mass (AFDM_flesh), (c) predicted knot intake rates without a digestive constraint (IR, mg AFDM_flesh s⁻¹), (d) average gizzard-mass-dependent predicted intake rates (IR_avg.gizzard, mg AFDM_flesh s⁻¹) and (e) individual gizzard-mass-dependent predicted intake rates (IR_ind.gizzard, standardized). Note that these resource selection functions are the exponent of fitted logistic regression models excluding the intercepts (electronic supplementary material, table S3). As a result, for instance, the linear model in electronic supplementary material, table S3E becomes curved in (e).

4. Discussion

We have shown that negative density-dependence among prey presented their predators with a trade-off between prey quantity and quality. Instead of the general simplification that energy intake rates increase asymptotically with prey density (a type II response), knots feeding on cockles had a type IV functional response. Resource selection analyses confirmed that free-living knots preferentially selected foraging locations with intermediate cockle densities and flesh masses. In fact, knots selected locations where they could maximize their energy intake rates given their phenotype-specific digestive constraint (gizzard mass).

(a). Consistent individual differences in habitat selection and prey quality ingestion

In the past decade, research on consistent individual differences in behaviour (animal personality) has become popular [39–41]. Animal personality limits behavioural flexibility and can correlate with individual resource specialization [42,43], which can have important ecological, evolutionary and conservation implications [44]. In knots, personality variation explains variation in gizzard mass, possibly caused by individual specialization on particular prey qualities [27]. The gizzard mass of knots is flexible and, over the course of a week, reflects the quality of its diet [20]. Birds feeding mainly on high-quality prey maintain small gizzards, whereas birds mainly feeding on low-quality prey maintain large gizzards [26]. That gizzard mass explained resource selection in this study suggests that knots consistently differ in prey quality ingestion.

To guide potential future research improving our understanding of the ecological implications of personality and individual resource specialization, we will provide three non-mutually exclusive hypotheses to explain why knots differ in habitat selection and ingested prey quality.

• (1) At large spatial scales, knots might select foraging locations from habitat characteristics such as prey density, inundation time and/or predation danger. If knots differ in their preference for certain habitat, and if these habitat characteristics are correlated with prey quality (as they often are [14]), knots could consistently ingest particular prey qualities.

• (2) At small spatial scales, knots could have developed different diet specializations during ontogeny [42,43,45]. Because high-quality prey are more difficult to find than low-quality prey, the experience that knots gain feeding on high-quality prey could make it easier for these animals to specialize their feeding [27]. Or they could specialize on more readily available low-quality prey by adapting their physiology to increase processing efficiency. To specialize on particular prey qualities in the single-prey situation studied here, knots need to sense quality variation between individual cockles. A previous study, in which cockle quality was measured before and after predation by knots, shows that cockles that survived knot predation had relatively little flesh mass and large shell mass [24]. Knots thus appear to be able to somehow sense the quality of an individual cockle.

• (3) In line with diet specialization, consistent prey quality ingestion could also originate from competition avoidance [42,46]. Knots are known to avoid explicit interference competition [47], and, when given a choice between equally accessible and available prey types, they prefer high-quality prey [48]. As prey density and quality are inversely related (figure 2a), birds compete over the less abundant high-quality prey. As a result, competitively dominant birds would forage in areas with high-quality prey and obtain small gizzards, while competitively subordinate birds would forage in areas with low-quality prey and obtain large gizzards.

(b). Generality and consequences of a type IV functional response

Holling's type II functional response has long been thought to be the most widespread among predators [10,11]. In this study, we have shown that negative density-dependence among prey results in a type IV functional response. As negative density-dependence is commonly found among prey [13], we predict that most predators will be faced with type IV functional responses. Until now, this might have remained unnoticed because numerical intake rate is often multiplied by an average (size dependent) flesh mass [49]. To investigate the effect of negative density-dependence among prey on a predator's intake rate, flesh mass of individual prey should be measured over a range of densities. We will now discuss two main consequences of ignoring negative density-dependence among prey for predicting a predator's energy intake rates. First, predicted energy intake rates are biased. Second, predators are wrongfully assumed to maximize their energy intake rates at the highest prey densities.

Carrying capacity of an area is often defined as the maximum number of predator-days that can be supported by the local standing stock of prey [8,9]. In the absence of prey growth and recruitment, the number of predators that can be supported depends on their predicted intake rates [9]. Ignoring density-dependence among prey leads to biased predictions of a predator's energy intake rates, which can have consequences for estimating an area's carrying capacity and hence, possibly, management and conservation efforts. In our study, ignoring density-dependence would have led to an underestimation of predicted intake rates by as much as 60% on the lowest prey densities and an overestimation by almost 50% on the highest prey densities (electronic supplementary material, figure S11a). Moreover, given the distribution of prey densities in our study, the surface area of suitable knot habitat (where predicted intake rates were above a knot's minimum requirement, figure 2b) was overestimated by 12.4% when ignoring negative density-dependence among prey.

Foragers are usually assumed to aggregate where predicted intake rates are highest [2,19]. The shape of the functional response, therefore, directly determines where predators will aggregate: they are generally assumed to maximize energy intake rates by foraging at the highest prey densities. Including negative density-dependence into the functional response, however, can substantially lower the prey density at which predators are predicted to maximize energy intake rates. How substantial this effect is depends on the strength of negative density-dependence among prey, and on how fast their functional response (without density-dependence) levels off with prey density. Searching efficiency, handling time and digestion time are positively related to the rate at which the functional response levels off (electronic supplementary material, figure S11b,c). In the presence of negative density-dependence among prey, predators with high searching efficiencies and long handling or digestion times will maximize energy intake rates at substantially reduced prey densities. Moreover, they will have a pronounced hump in their functional response, i.e. their predicted intake rates at intermediate prey densities will be substantially larger than those at the highest prey densities (electronic supplementary material, figure S11b,c).

(c). Type IV functional response allows the ‘gardening of prey’

A type IV functional response may offer interesting predator–prey dynamics. Grazing flocks of barnacle geese (Branta leucopsis), for instance, have been hypothesized to stimulate renewed protein-rich grass growth, thereby providing opportunity for future foraging on high-quality vegetation [50]. Indeed, without lowering biomass, grazing improved the vegetation quality and attracted foraging geese [51]. Consequently, brent geese Branta bernicla have been hypothesized to adopt a cyclic grazing pattern that optimizes their protein intake between locations [52]. We can speculate about this ‘grazing optimization hypothesis' for predators in the context of our study. Thinning of cockle densities reduces competition among cockles and allows the surviving cockles to accumulate flesh mass. Even though it is highly speculative, knots may optimize energy intake rates by ‘gardening’ their cockle prey. However, opposite to grazers, predators kill their prey and reduce their density, which thereby become difficult to find [24], which in turn reduces the benefit from such ‘gardening’. One way to investigate this ‘gardening hypothesis’ is to determine whether knots, after thinning cockle densities, allow time for their prey to increase in flesh mass before revisiting these locations [52]. From a (game) theoretical perspective, an interesting question is if, and under what circumstances, gardening prey is an evolutionarily stable strategy. For instance, will a gardening strategy be outcompeted by a ‘cheater-strategy’ where individuals sneak ahead of the flock and harvest the gardened high-quality prey? Conversely, cheaters, which separate themselves from the main flock, might incur increased predation costs because they lose the safety of numbers.

Data accessibility

Data are available in the Dryad digital repository [53].

Author contributions

A.I.B., J.A.v.G. and T.P. designed the study, A.I.B., Y.C.C., E.P., A.D., S.H., J.t.H. and M.B. collected the data on prey distributions, and A.I.B., Y.C.C., E.P., R.M.G., J.C., E.L.S. and A.D. collected the data on predator distributions for which R.B.M., R.M.G., J.C., E.L.S., A.D. and D.W.W. provided the novel tracking method and technical assistance. A.I.B. analysed the data and wrote a first version of the manuscript, and Y.C.C., J.A.v.G., T.P. and A.I.B. contributed substantially to revisions.

Competing interests

We have no competing interests.

Funding

Our work was supported by core funding of NIOZ to T.P. and grants from NWO-ALW to T.P. (TOP-grant ‘Shorebirds in space’, no. 854.11.004), the Waddenfonds to T.P. (project ‘Metawad’, WF 209925), and a NWO-VIDI grant to J.A.v.G. (no. 864.09.002), as well as funding from ZKO, NWO, NAM, and NIOZ for the benthic sampling programme ‘SIBES’.