Factors influencing the effect size distribution of adaptive substitutions

Abstract

The distribution of effect sizes of adaptive substitutions has been central to evolutionary biology since the modern synthesis. Early theory proposed that because large-effect mutations have negative pleiotropic consequences, only small-effect mutations contribute to adaptation. More recent theory suggested instead that large-effect mutations could be favoured when populations are far from their adaptive peak. Here we suggest that the distributions of effect sizes are expected to differ among study systems, reflecting the wide variation in evolutionary forces and ecological conditions experienced in nature. These include selection, mutation, genetic drift, gene flow, and other factors such as the degree of pleiotropy, the distance to the phenotypic optimum, whether the optimum is stable or moving, and whether new mutation or standing genetic variation provides the source of adaptive alleles. Our goal is to review how these factors might affect the distribution of effect sizes and to identify new research directions. Until more theory and empirical work is available, we feel that it is premature to make broad generalizations about the effect size distribution of adaptive substitutions important in nature.

1. Introduction

The effect sizes of adaptive substitutions, i.e. the replacement of one mutation (or allele) by another with greater fitness, has been a major focus of research since Fisher proposed that adaptation was due exclusively to mutations of small effect [1–6]. Fisher reasoned that large-effect mutations are unlikely to contribute to adaptive evolution because of their deleterious pleiotropic effects. This hypothesis was modified by Kimura [2], who predicted that mutations of intermediate effect size would predominate because adaptive mutations of very small effect may often be lost because of genetic drift.

The view that adaptation was due mainly to mutations of small or intermediate effects was widely accepted until Orr [3] hypothesized that the relative effect sizes of mutations fixed during adaptation will depend upon the initial distance between the current population and its phenotypic optimum. In contrast with both Fisher [1] and Kimura [2], Orr's model [3] considered an entire ‘adaptive walk’ toward a new phenotypic optimum, and predicted that the distribution of effect sizes for adaptive substitutions would approach a negative exponential, with a few mutations of relatively large effect and many of relatively small effect.

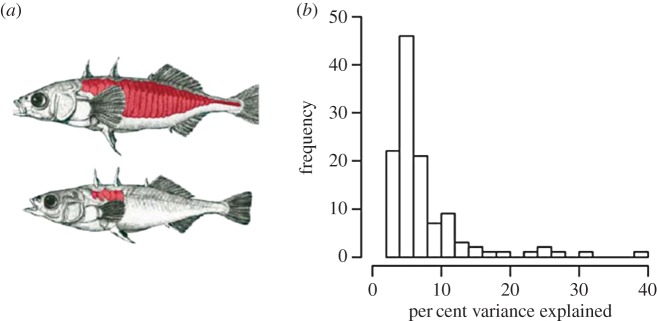
This model has been supported by many quantitative trait locus (QTL) mapping studies that have identified large-effect loci, including the evolution of floral traits in the transition from bee to hummingbird pollination in Mimulus [7], the evolution of light-coloured beach mice from their darker, mainland ancestors [8], and a host shift in Drosophila sechellia [9] from a D. simulans-like ancestor [10]. A particularly compelling case involves the repeated loss of lateral plates in stickleback fish that colonized freshwater from marine habitats (figure 1a). QTL mapping found that a single major locus explains most of the variation in lateral plate pattern and number, and a comprehensive study of multiple skeletal traits finds many small, and some large-effect loci (figure 1b) [12]. Nonetheless, some QTL studies find little evidence for large-effect loci, e.g. mating system divergence in monkeyflowers [13] and host shifts in closely related species of noctuid moths [14].

Figure 1.

Adaptation in sticklebacks. (a) Marine (top) and freshwater (bottom) sticklebacks. Red shading indicates lateral plates (modified by D. M. Kingsley from Cuvier & Valenciennes [11]); (b) effect size distributions for QTL (N = 118) from mapping studies of greater than 100 trophic, armour and skeletal traits in F₂ sticklebacks (N = 370) produced from a cross between marine and freshwater morphs (fig. S2 in [12]).

Without further consideration of the genetic and ecological details, QTL mapping studies are typically not sufficient to test alternate theories for the expected distribution of effect sizes for adaptive substitutions. First, it is widely acknowledged that large mapping populations are required to identify most QTL and to accurately estimate effect sizes [15,16]. Second, QTL studies rarely map the genetic basis of fitness directly (but see [17]), and instead examine putatively adaptive traits. The adaptive value of these traits, i.e. the proportion of variation in overall fitness due to trait variation, is usually unknown. Third, the theory is explicitly about the probability of fixation of new mutations that differ in the magnitude of their effects on fitness, yet with the exception of experimental evolution studies [6], the specific mutations that contribute to adaptation are rarely identified. Instead, QTL mapping studies identify chromosomal regions that often contain hundreds of genes, each of which may harbour multiple mutations [15,18]. Although single genes have been found to underlie large-effect QTL controlling some adaptive traits, e.g. armour in sticklebacks [19] and coat colour in mice [8], there are still few cases where adaptive QTL have been resolved to individual genes and causal mutations.

Given the paucity of studies where the alleles and mutations involved in adaptation in natural populations have been identified, we suggest that it is not yet possible to reach a general consensus on the subject of the distribution of effect sizes. Moreover, the theoretical expectations put forth by Fisher, Kimura and Orr do not adequately capture the full range of biological scenarios that are relevant to understanding the distribution of effect sizes [20–22]. Although Orr's [3] proposal was a paradigm shift for the field of evolutionary genetics, as he acknowledged, his model represents a small subset of the possible alternatives. Here we ask how ecological and evolutionary processes that are known to vary among natural populations might influence the expected distribution of effect sizes. Our goal is to give a broad overview of how the major mechanisms of evolution, i.e. natural selection, genetic drift, mutation and migration might influence the distribution of effect sizes of adaptive substitutions. We hope to motivate further theoretical and empirical study into the many ways in which the genetics and ecology of natural populations and species can influence the effect sizes of adaptive substitutions, and to encourage a consideration of these factors in future work.

Our review extends the idea expressed by Remington [18] that there is no ‘one size fits all’ expectation for the distribution of effect sizes, and examines a range of factors that are expected to influence the distribution of effect sizes for adaptive substitutions. With few exceptions (e.g. [17]), the theory and experimental evolution studies on microbes address effect sizes for fitness itself, while QTL studies address the effect sizes of individual traits that may or may not affect fitness. Additionally, recognizing that alleles may be made up of multiple mutations [18], we reserve the term ‘mutation’ for theoretical models and examples where the causal mutations are known. Our discussion of selection begins with pleiotropy because of its central role in Fisher's geometric model, and then considers the strength and form of selection, the consequences of a fixed versus moving optimum, and the influence of standing variation versus new mutation. Our discussion of mutation and genetic drift examines the interplay between these factors and the source of adaptive genetic variation, and we end with a discussion of how gene flow might influence the distribution of effect sizes.

2. Selection

(a). Pleiotropy

Fisher [1] assumed that, because of pleiotropy (when a single substitution affects multiple traits), mutations with large effects will move a population farther from the phenotypic optimum rather than closer to it, and are thus unlikely to contribute to adaptive evolution. Consistent with the notion that large-effect mutations are more likely to exhibit antagonistic pleiotropy, empirical evidence finds that the degree of pleiotropy in a gene or QTL is positively correlated with its effect size [23–25]. Recent theoretical studies support the prediction that pleiotropy can lead to an increased role of small-effect mutations when many traits are under selection [5] (the ‘cost of complexity’ [26]).

However, the universality of pleiotropy has recently been questioned based on empirical results from studies of gene knockouts [25] and QTL mapping studies [23,24] that suggest that most genes or loci affect only a fraction (less than 10%) of the measured traits. Further, the role of pleiotropy in determining the fixation probability of mutations with different effect sizes may depend upon the trait in question [27]. Trait modularity reduces pleiotropy and is thought to be common [23,25]. Evidence also suggests a substitution bias towards mutations in regulatory regions over those in coding regions, presumably due to their decreased pleiotropic effects [28,29].

Pleiotropy may even facilitate adaptation if a mutation affects multiple traits in the direction of the optimum phenotype [25,30]. A number of putatively adaptive traits map near the Ectodysplasin (EDA) gene in sticklebacks, and pleiotropy among lateral plates and the distribution of sensory organs has been definitively demonstrated [31]. Pleiotropy has also been implicated in floral divergence across multiple plant species [32]. An experimental evolution study using bacteriophage found that selection on multiple traits commonly led to the fixation of mutations with synergistically beneficial effects, rather than constraints on fitness [33].

Large-effect alleles have played a major role in the domestication of plants [34] and animals [35] and are often found to have major pleiotropic effects (e.g. [36]). For example, it has been proposed that selection for increased yield in crops inadvertently results in reduced herbivore defenses [37]. Under domestication, the deleterious effects of pleiotropy are abated by supplying critical resources, thereby potentially reducing constraints on mutational effect sizes. Some evidence suggests that mutations underlying domestication traits have larger effects than those underlying traits subject to natural selection [29], and we suggest further comparisons may provide an opportunity to study whether mitigating the deleterious consequences of pleiotropy allows for the fixation of alleles with larger effect sizes.

(b). Distance to the optimum

In Orr's model [3], the population is initially far from its optimum as might be expected following a major environmental perturbation or after colonization of a new habitat. In the early stages of the adaptive walk, both large and small effect adaptive mutations can move the population closer to the optimum, but as the population approaches the optimum, there is an increased likelihood that large-effect mutations will reduce fitness (figure 2). This leads to Orr's prediction that relative effect sizes will decline with decreasing distance to the optimum.

Figure 2.

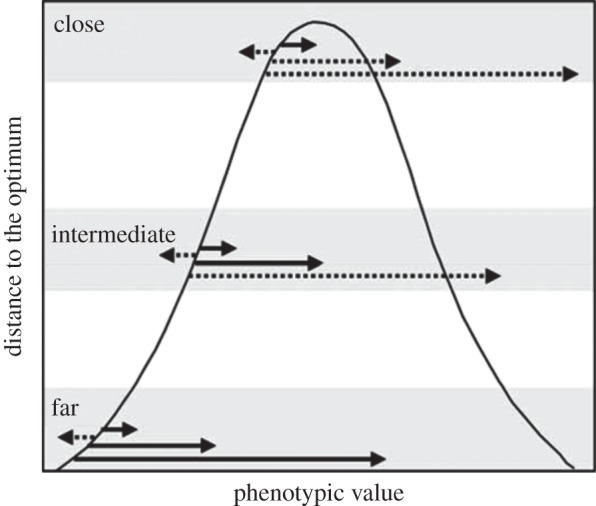
The relationship between distance to the optimum and the possible effect sizes of mutations fixed during a single bout of adaptation, following Orr [3]. A Gaussian fitness function is depicted for natural selection on a single trait with a fixed optimum. The adaptive value of mutations of different effect sizes is given for three different stages of adaptation, reflected as the distance to the optimum (far, intermediate and close). The length of the arrow gives the effect size, solid arrows signify adaptive mutations and dashed arrows signify maladaptive mutations.

This relationship is supported by empirical evidence. Experimental evolution studies in bacteriophage [33], Escherichia coli [38] and the fungus Aspergillus nidulans [39] found that adaptation involved larger effect mutations when populations were farther from the optimum. This hypothesis was also tested in natural populations by comparing the phenotypic effect sizes of QTL underlying body shape and armour among stickleback populations inhabiting freshwater lakes where the phenotypic distance between the ancestral marine form and the local lake forms differed [40]. Consistent with predictions, larger-effect QTL were found in populations adapted to more distant optima.

The use of differentially adapted populations or sister species to study the genetic basis of adaptive traits can allow the identification of alleles fixed over an entire bout of adaptation, and thus are most relevant for evaluating Orr's model [3,18]. The best empirical examples of large effect loci underlying adaptive traits come from studies that examine different populations or closely related species that display clear evidence of adaptive differentiation [7–9,41]. As noted by Remington [18], genetic studies that do not find evidence of large-effect alleles often investigate the genetic basis of trait variation within a population. If these populations are near their optimum, large-effect mutations will be deleterious (figure 2), and are thus unlikely to be maintained at appreciable frequencies.

Human height is a leading example of a trait controlled mainly by small-effect alleles [15] and it is interesting to consider whether the effect sizes of alleles underlying this trait are related to the distance to the optimum. In contemporary European populations, which we might expect are near their optimum, alleles of small effect predominate [42–45]. By contrast, although statistical power was limited, a study that examined differences among a human pygmy population and their agricultural neighbours [46] found evidence for a higher frequency of large-effect alleles. The pygmy form evolved independently at least three times following the colonization of tropical rainforest [44,46,47], suggesting that it might represent an adaptation to a new environment. This example highlights the need to evaluate effect size distributions in light of the evolutionary history of studied populations.

(c). Shape of the fitness function

The geometric model assumes that any phenotypic change in the direction of the optimum increases fitness unless it greatly overshoots the optimum [48]. In some adaptive scenarios however, phenotypic changes of small effect may be selected against, such as in a multi-peaked fitness function when intermediate phenotypes have low fitness. One example is Müllerian mimicry in Heliconius butterflies, which escape bird predation through distinct wing coloration and patterning. Studies of Heliconius hybrid zones suggest that intermediate phenotypes have low fitness [49,50]. Consistent with predictions, large-effect loci contribute to differences in coloration patterns among species [51,52], and might represent the initial steps in adaptation to new optima, followed by the evolution of modifier loci with smaller phenotypic effects [53].

Other examples where adaptation may require one or more large phenotypic steps is edaphic adaptation, such as observed in plants growing on serpentine soils or mine tailings, where there are often abrupt changes in soil type at a microgeographic scale and no intermediate habitat. QTL studies of serpentine adapted Silene vulgaris [54] and copper-tolerant Mimulus guttatus [55] both find large-effect QTL underlying tolerance to nickel and copper, respectively. The shape of the fitness function is likely to be an important contributor to the effect size distribution of adaptive substitutions, but more theoretical and empirical studies are needed.

(d). Moving optimum

Adaptation to a new fixed phenotypic optimum can occur during the colonization of a novel habitat, but other scenarios may lead to adaptation to a moving optimum, such as evolving biotic interactions [56,57] or evolutionary responses to gradual and persistent environmental changes [58]. For a large finite population initially near an optimum which moves deterministically at different rates [21,59], theory predicts an intermediate distribution of effect sizes, with few large- or small-effect mutations. In this scenario, the relative magnitude of effect sizes depends critically on the rate of environmental change. If the environment changes rapidly, the distribution is shifted toward larger-effect mutations [21,59,60]. Additionally, pleiotropy increases the waiting time for beneficial mutations [59] which causes the population to lag behind the optimum, and increases the likelihood of adaptation through the fixation of large-effect mutations [59]. Therefore, with rapid environmental change, relatively larger effect sizes of adaptive mutations are possible under a moving optimum scenario, particularly with increasing pleiotropy.

There is some empirical support for the dependence of the distribution of effect sizes of adaptive alleles on the rate of change in the optimum. In an elegant long-term experimental evolution study of Chlamydomonas, adaptation to slow environmental change involved small-effect mutations, while adaptation to fast environmental change required mutations of large effect [61], consistent with theoretical predictions. While experimental evolution studies have usually investigated adaptation to a fixed optimum [6], they are a promising avenue of future research to further explore theoretical predictions regarding adaptation to a moving optimum.

In reviewing effect sizes for QTL studies of traits likely to be under either abiotic or biotic selection, Louthan & Kay [56] found distributions of effect sizes consistent with Orr's prediction [3] for both types of traits, but there was a shift toward larger effect sizes for traits under biotic selection. If coevolution of biotic interactions is more temporally variable than selection imposed by abiotic factors, these results suggest that adaptation to a moving optimum can influence effect sizes. An interesting extension to current theory would be varying the initial distance to the optimum and/or having the optimum move unpredictably, cf. [56].

3. Standing genetic variation

The theory we have reviewed thus far has modelled adaptation from new mutations. An alternative is adaptation from standing genetic variation (hereafter SGV) [19,20,22,62–66], which in principle could be applied to all the selective scenarios above. The source of SGV in this body of theory is typically modelled as neutral or deleterious alleles underlying fitness maintained in mutation–selection–drift equilibrium [20,22, but see 67]. At some point, the environment changes such that previously deleterious and/or neutral alleles become favourable, and provide the raw material for adaptation to the new phenotypic optimum. Selection on SGV can be more effective than selection on new mutations because the adaptive alleles are already present in the population when the environment changes, and because newly beneficial alleles are at a higher initial frequency than a new mutation, making them less likely to be lost by genetic drift [20,63,68]. However, the equilibrium frequency of SGV depends critically on the population size and mutation rate [65,69], which are likely to differ among species (see below).

Given sufficient mutational input, the likelihood of adaptation from SGV is predicted to depend on the selection coefficients of the alleles before and after the change in the environment [20,22,65,69]. For previously neutral alleles, even those with currently small beneficial effects are predicted to have higher probabilities of fixation relative to new mutations of equal effect sizes because they have escaped loss by drift [20]. The larger the disadvantage of alleles prior to the environmental change, the larger their newly acquired beneficial effects must be for them to fix [20,65]. Theory combining adaptation from SGV and a moving optimum with a very high mutational input predicts more alleles of small effect compared with adaptation from new mutation [22], particularly with more gradual changes in the environment.

There is little information on the selection coefficients of adaptive alleles before and after a change in the environment or the correlation between these effect sizes, but experimental evolution studies give some insight. In studies of the fitness effects of 665 new mutations that confer some degree of antibiotic resistance in Pseudomonas fluorescens, nearly all were deleterious in the absence of antibiotics (prior environment), with most reducing fitness by at least 10% [70]. In Saccharomyces cerevisiae, several mutations that had modest beneficial effects in saline conditions were deleterious, some strongly so, in standard conditions (prior environment) [71]. While it is unknown if such new mutations are representative of SGV in natural populations, these studies do suggest that even strongly deleterious mutations may become beneficial following a major environmental change.

There are several examples consistent with adaptation from SGV in natural populations. In stickleback fish, the allele for low plate number in the EDA gene that characterizes freshwater populations is also present in the ancestral marine population [19,63], and a substantial portion of drug resistance in HIV is thought to be due to SGV (the remainder coming from new mutation) [64]. Both of these examples probably represent systems with high mutational input (large population sizes in sticklebacks, high mutation rates in HIV). Adaptation from SGV and new mutation are not mutually exclusive, but the likelihood of adaptation from SGV (maintained in mutation–selection–drift balance) depends critically on population size and mutational parameters, which we discuss in the next section.

4. Mutation and drift

To contribute to adaptation, mutations must enter the population at an appreciable rate, be beneficial, and escape stochastic loss by genetic drift. The mutation rate and the distribution of effect sizes of mutations determine the initial genetic variation that is then subject to selection and genetic drift. Average per-nucleotide, per-generation mutation rates are of the order of 10⁻⁸ to 10⁻⁹ [72,73], and experimental evidence suggests that many, if not most, new mutations are somewhat deleterious [74,75, but see 76]. Even in a large population, the probability of fixation of most new beneficial mutations is small, approximately equivalent to twice the selection coefficient [77]. This small probability of fixation is reduced further by drift when the effective population size (N_e) is small [78,79]. Many factors influence N_e, including small population size, population bottlenecks and inbreeding; we direct readers to Charlesworth [80] for details. New beneficial mutations are therefore expected to be rare, and most are likely to be lost by drift.

The effect size distribution of adaptive substitutions from new mutations could be influenced by genetic drift. Orr [3] assumed a large (but finite) population, but with decreasing effective population size, small and possibly intermediate effect mutations will be increasingly lost by drift. Thus in small populations we predict fewer small-effect adaptive substitutions, though strong selection could override drift [81]. Small-effect alleles are difficult to detect empirically [16], nevertheless, it has been argued that such alleles underlie much of adaptation [15,82]. To determine the range of parameter space over which small-effect mutations can contribute to adaptation, we suggest modelling adaptive walks for effective population sizes that span the range of empirical estimates from low to mid N_e (see below).

Adaptation from SGV requires that neutral or deleterious alleles be maintained in the population until the environment changes, at which point they become beneficial. The maintenance of SGV depends on both N_e, and the mutation rate (μ), and is modelled as the joint parameter Θ (Theta), which is 2N_eμ for haploids [20] and 4 N_eμ for diploids [22]. Hermisson & Pennings [20] modelled adaptation from SGV for a population with large N_e (25 000), and examined a wide range of Θ (0.4, 0.04 and 0.004; μ's of the order of 10⁻⁶, 10⁻⁷ and 10⁻⁸, respectively). While their results for Θ = 0.4 have been used to support the general importance of SGV in adaptation [15,65], they also found that the probability of fixation from SGV is very low for Θ = 0.004 (figure 2, [20]). As the mutation rate (10⁻⁸) for Θ = 0.004 is the closest to empirical estimates of mutation rates (see above), it would seem that adaptation from SGV should be common only for large population sizes (on the order of 25 000 or more), cf. [69]. Alternatively, the effective mutation rate could in some cases be greater, e.g. a mutational hotspot or a large mutational target size, such that many individual mutations might produce the same phenotype [65]. Matuszewski et al. [22] predict the distribution of effect sizes from SGV for a moving optimum (see above) for very large values of Θ (2.5–10). We suggest that there is a critical need for theoretical predictions about the distributions of effect sizes, and even the likelihood of adaptation from SGV versus new mutation, for the range of values of Θ initially considered (0.4–0.004) by Hermisson & Pennings [20].

Estimates of N_e from sequence data range from approximately 10 000 in humans [83], to approximately 120 000 in Arabidopsis thaliana [84], to over 1 million in Drosophila melanogaster [85,86]. However, caution is needed in interpreting these estimates, because combining samples from populations that are only weakly connected by gene flow will inflate estimates of N_e. This problem is probably less important in organisms with broad dispersal capabilities (e.g. Drosophila), but could be profound in sedentary taxa, particularly those with selfing mating systems (e.g. A. thaliana). Local estimates of N_e, based on approximately 100 SNP markers in A. thaliana from Scandinavia, suggest that N_e may be more commonly of the order of 250–2500 [87].

While adaptation from SGV is plausible for species with moderate to large N_e (or with high mutation rates), adaptation in species with small N_e probably requires new mutations with effect sizes large enough to escape drift. The finding that non-synonymous substitutions are predominantly deleterious in A. thaliana [88] and many other plant species [84] indicates that genetic drift can constrain adaptive evolution, as does the recent finding of several locally maladaptive fitness QTL in a population of A. thaliana with a likely history of population bottlenecks [17]. Generalizations about the distribution of effect sizes of adaptive substitutions will therefore require new theory and empirical examples from organisms that represent the full range of effective population sizes observed in nature.

5. Gene flow

Gene flow between populations in the presence of divergent selection is common in nature, and may impact the effect size distributions of adaptive substitutions. Recent theory has shown that local adaptation in the face of ongoing gene flow, a scenario fundamentally different than the single population model proposed by Orr [3], can favour loci of large effect [89,90]. Griswold et al. [90] predicted that as gene flow between locally adapted populations increases, small-effect mutations become homogenized across populations, thus larger-effect loci are more likely to be detected in QTL studies. Yeaman & Whitlock [89] predicted that alleles with larger selection coefficients have a longer persistence time under gene flow–selection–drift balance, and thus have a higher probability of contributing to local adaptation. The effect size of locally adaptive alleles is therefore predicted to increase over time as segregating alleles with smaller selection coefficients are gradually replaced by larger effect alleles [89]. When gene flow is high, divergent selection is strong and the mutation rate is low, selection may favour linked clusters of small-effect mutations that collectively represent a large-effect locus [89]. Inversion polymorphisms that suppress recombination between small-effect beneficial mutations are one way in which beneficial mutations of small effect become linked [91]. Examples of large-effect adaptive inversion polymorphisms are becoming increasingly common [68,92].

The consequences of gene flow for the distribution of effect sizes of adaptive substitutions has not been directly investigated in natural populations. Experimental evolution studies that manipulate gene flow between populations experiencing divergent selection, and comparative analyses of the effect size distribution of adaptive substitutions reported in organisms with different dispersal capabilities are two possible empirical approaches for testing these theoretical predictions.

6. Conclusion

Owing to its broad importance to evolutionary biology, there is controversy over the expected distribution of effect sizes for adaptive substitutions. Despite recent suggestions that adaptation is due mainly to mutations of small effect [15], there is also evidence that large-effect mutations often contribute to adaptation. Given that natural populations exhibit substantial variation in ecological and genetic factors that are likely to influence the effect size distribution of adaptive mutations, it is not surprising to find substantial variation among taxa in the relative importance of small- versus large-effect mutations. Here we discuss how the expected distribution of effect sizes depends critically on all four evolutionary forces—mutation, gene flow, drift and selection—as well as the extent and magnitude of pleiotropy and the source of adaptive genetic variation. Table 1 provides a summary of some scenarios that involve these factors with predictions that we hope will stimulate future research. Considerable work is needed to develop new theory that reflects the wide range of evolutionary scenarios expected in natural populations. Likewise, the gaps in our empirical understanding are vast, due in large part to the difficulty in identifying adaptive traits and their genetic basis. Given the current limitations of both the theory and empirical evidence, it is not yet possible to make general conclusions about the expected effect size distribution in nature. The challenge for the future is to provide a theoretical framework for predicting the effect size distribution for a variety of situations (table 1) and for a variety of adaptive traits, and to carry out robust empirical tests of the theory.

Table 1.

Scenarios influencing the distribution of effect sizes for adaptive substitutions. This is not intended to be an exhaustive list, but rather a broad overview of some of the theories discussed in the text.

scenario	key features/assumptions	predictions about effect sizes	citation
adaptive walk to a fixed optimum	initially far from a single optimum; new mutation only; large single population; weak selection	exponential distribution of effect sizes; a few large-effect (only while far from the optimum), many small-effect mutations	[3]
multiple fitness optima	intermediate phenotypes have low fitness	at least one large-effect mutation required	verbal model [3,22]
moving optimum	similar to [3] except initially close to moving optimum; new mutation and standing genetic variation	distribution has more intermediate effect sizes; faster moving optimum results in larger effect sizes; slower moving optimum results in smaller effect sizes	[21,22,59,60]
standing genetic variation	variation maintained in a single population in mutation–selection–drift balance before a change in environment	smaller-effect alleles have higher probability of fixation than new mutations of same effect size	[20,22]
small effective population size	small-effect mutations effectively neutral	small-effect mutations lost to drift; intermediate effect size mutations have highest probability of fixation	[2]
migration	divergent selection in the face of gene flow	increased migration leads to larger-effect mutations and/or linked small-effect mutations	[89]

Authors' contributions

E.L.D. and C.G.O. took the lead in writing the paper, but significant contributions were made by all authors.

Competing interests

We declare we have no competing interests.

Funding

Research supported by grants from the National Institutes of Health (5R01GM088805) awarded to H.D. Bradshaw, Jr and D.W.S., and the National Science Foundation (DEB 1022202) to D.W.S., (DEB 1556262) to D.W.S. and C.G.O., and (DEB 0919452) to J.K.C.