Hummingbirds control turning velocity using body orientation and turning radius using asymmetrical wingbeat kinematics

Abstract

Turning in flight requires reorientation of force, which birds, bats and insects accomplish either by shifting body position and total force in concert or by using left–right asymmetries in wingbeat kinematics. Although both mechanisms have been observed in multiple species, it is currently unknown how each is used to control changes in trajectory. We addressed this problem by measuring body and wingbeat kinematics as hummingbirds tracked a revolving feeder, and estimating aerodynamic forces using a quasi-steady model. During arcing turns, hummingbirds symmetrically banked the stroke plane of both wings, and the body, into turns, supporting a body-dependent mechanism. However, several wingbeat asymmetries were present during turning, including a higher and flatter outer wingtip path and a lower more deviated inner wingtip path. A quasi-steady analysis of arcing turns performed with different trajectories revealed that changes in radius were associated with asymmetrical kinematics and forces, and changes in velocity were associated with symmetrical kinematics and forces. Collectively, our results indicate that both body-dependent and -independent force orientation mechanisms are available to hummingbirds, and that these kinematic strategies are used to meet the separate aerodynamic challenges posed by changes in velocity and turning radius.

1. Introduction

Turning is an essential manoeuvre for navigating an aerial environment. During a level arcing turn, an animal must produce enough aerodynamic force to counteract gravity, to maintain forward velocity and to accelerate radially. There are two potential mechanisms that a flapping animal can use to generate the centripetal acceleration necessary for a turn: (i) the body can bank towards the turn to reorient the total aerodynamic force vector inwards or (ii) additional lateral force can be produced through asymmetrical wingbeat kinematics. Aeroplanes perform arcing turns by increasing the total aerodynamic force produced and banking the fuselage and wings towards the turn, directing lift inwards. The bank angle increases during faster or tighter turns, because the centripetal force necessary to complete the turn increases. Despite numerous differences between aircraft and flapping flight in animals, turning studies of cockatiels [1], pigeons [2] and fruit flies [3,4] have shown that these species reorient their bodies and stroke planes into turns, employing largely the same banking strategy as aircraft.

The alternative mechanism to body-dependent force reorientation is to use body-independent asymmetries in wingbeat kinematics, such as differences in stroke amplitude or angle of attack between the left and right wings to produce additional lateral force. Several studies have suggested that flying animals can produce body-independent lateral force through asymmetrical wing kinematics [5–7] and wing asymmetries play a role in generating torques used for yaw turns and saccades [8,9]. However, no studies have shown the exclusive use of asymmetrical wingbeat kinematics to perform arcing turns.

Previous studies of the arcing turns of birds and bats challenged the animals to navigate around a corner [1,10,11]. All of the animals used body-dependent force reorientation by banking their bodies during the turns but simultaneously exhibited body-independent wingbeat asymmetries. The temporal dynamics suggest that the wingbeat asymmetries are used to initiate and maintain body bank; however, kinematic differences between the left and right wings can further contribute to centripetal force. In bats, centripetal force is produced by the body bank during the downstroke, but additional centripetal force is produced by the wingbeat asymmetries during the upstroke [10]. Because these studies did not involve experimental manipulation of the radius or velocity of the turns, the only sources of variation were differences among individuals and between trials. As a result, it is unknown how body-dependent force reorientation and body-independent wingbeat asymmetries are modulated to generate and control centripetal force. Hummingbirds have previously been used to study manoeuvrability, and the wingbeat kinematics of several behaviours have been described including take-off [12], hovering [13], forward flight [14], backward flight [15] and yaw turns [8]. Because hummingbirds can be trained to track a feeder following defined trajectories, they provide an opportunity to experimentally determine the relative contributions of wingbeat and body kinematics to radius and velocity control of arcing turns.

To determine whether hummingbirds direct force into a turn through body-dependent force reorientation or body-independent wingbeat asymmetries, we filmed Anna's hummingbirds (Calypte anna) during hovering flight and four experimental turning treatments. The arcing turn treatments represented four angular velocities and required three levels of centripetal acceleration. We first compare the body and wingbeat kinematics during hovering flight and the arcing turn treatment with the highest angular velocity and centripetal acceleration. During hovering flight, the net force is only needed to counteract gravity, whereas during the turn the hummingbird must also produce forward and inward force components. We expect hummingbirds to orient the wing stroke plane into the turn. If they orient their stroke plane and body in concert, this would support the hypothesis that force is oriented through body bank. If, however, the stroke plane is banked during a turn but the body remains in the hovering orientation, this would support the hypothesis that hummingbirds use asymmetrical wingbeat kinematics to shift the orientation of the net force forward and inward during an arcing turn.

To determine how hummingbirds use body-dependent force reorientation and body-independent wingbeat asymmetries to control arcing turns, we next compare the body and wingbeat kinematics, and associated quasi-steady forces, across the four turning treatments. The quasi-steady model uses independent measurements of the lift and drag coefficients [16] in combination with measurements of wing size and wing velocity. The turning treatments combined slow and fast translational velocities, respectively, with large and small radii to achieve a balanced design for statistical comparison. We test whether body kinematics, wingbeat kinematics or both sets of kinematics are modulated to compensate for increases in centripetal acceleration. If centripetal acceleration is the most important determinant of hummingbird turns, then changes in both radius and velocity should be significantly associated with body and wingbeat kinematics. However, our experimental design also allows for us to determine whether different kinematic features are more strongly associated with changes in radius or velocity.

2. Material and methods

2.1. Animals and marking techniques

Six adult male Anna's hummingbirds were captured at the University of British Columbia with drop-door traps [17] and housed in a vivarium with a 12 L : 12 D cycle (electronic supplementary material, table S1). Each individual was kept in a cage measuring 0.91 × 0.61 × 0.61 m and fed ad libitum with 13% Nektar-Plus (Nekton, Pforzheim, Germany) or 15% sucrose solutions. Immediately prior to filming, Wite-Out correction fluid (Bic, Toronto, Ontario, Canada) markers were applied to the head, back and rump of the birds to facilitate tracking. Wite-Out was reapplied whenever markers showed signs of wear, typically three times for each individual.

2.2. Measurements of arcing turns

Flight was filmed in April and May 2014 within a 0.91 × 0.91 × 0.84 m acrylic chamber that contained a feeder assembly and wooden perch (figure 1). The feeder assembly consisted of a 10 ml syringe attached to an adjustable arm that was rotated by a stepper motor (MDrive 23 Plus; Schneider Electric Motion, Marlborough, CT, USA) in a clockwise circle. Two 0.50 m aluminium bars (80/20, Columbia City, IN, USA) supported the motor and feeder arm. Three high-speed cameras (Miro 120; Vision Research, Wayne NJ, USA) were arranged to provide dorsal and posterior views of individuals during feeding and one camera (Miro 4; Vision Research, Wayne NJ, USA) recorded a lateral view. These cameras were positioned approximately 115–185 cm from the working section of the feeder and were fitted with two 50 mm lenses (AF Nikkor; Nikon, Melville, NY, USA), one 50 mm lens (Nikkor E; Nikon, Melville, NY, USA) and one 24 mm lens (AF Nikkor). The cameras were synchronized at 1000 Hz with a function generator (AFG3021B; Techtronix, Beaverton, OR, USA) and triggered with a common external end trigger. All cameras recorded video at 1000 frames s⁻¹ with an exposure of 200 µs and apertures between f/1.8 and 2.8. Lighting was supplied with four to six 800 W halogen lights configured to minimize shadows over wings and body markers.

Figure 1.

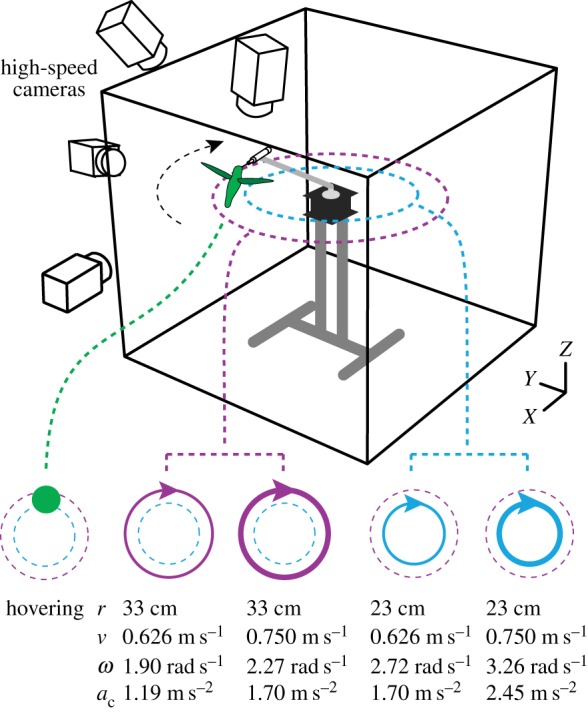
Filming apparatus. Hummingbirds fed from a 10 ml syringe while hovering and turning within an acrylic chamber. The radius and translational velocity of turns varied by adjusting the length of the feeder arm and the speed of the stepper motor's rotation. Experimental treatments and their respective turning radii (r), translational velocities (v), angular velocities (ω) and centripetal accelerations (a_c) are provided and represented by five symbols. Four high-speed cameras provided dorsal, posterior and lateral views of hummingbirds. Representative videos from a camera placed behind the bird during flight through the filming volume are presented in the electronic supplementary materials, videos S1–S5.

Prior to the start of filming, all individuals were given time to acclimatize to the flight chamber, which took no longer than 2 h. After a hummingbird fed regularly from a 10 ml syringe, access to the feeder was restricted with a cover and the individual was allowed to feed only while the feeder revolved. After a successful feeding event, the feeder was stopped and covered for 15–20 min. The feeder's angular velocity increased incrementally with each successful feeding session until individuals were capable of feeding at the experimental velocities. Training took approximately 4 h per individual over the course of 1 day.

Individuals were filmed feeding while hovering and performing four different turns. The four turning treatments had a balanced design with two levels of turn radius (0.23, 0.33 m) and two levels of translational velocity (0.626, 0.750 m s⁻¹). These combinations were selected to determine how body and wingbeat kinematics, and quasi-steady forces, vary with turn radius, velocity and centripetal acceleration. The angular velocity of these turns was calculated as follows:

where ω is angular velocity, v is translational velocity and r is the radius of a turn. Turning treatments had angular velocities of 1.90, 2.27, 2.72 and 3.26 rad s⁻¹. The centripetal acceleration of the treatments was calculated as follows:

where a_c is centripetal acceleration, with values of 1.19 m s⁻² at 1.90 rad s⁻¹, 1.70 m s⁻² at 2.27 rad s⁻¹ and 2.72 rad s⁻¹, and 2.45 m s⁻² at 3.26 rad s⁻¹. Centripetal acceleration was matched for the treatments with angular velocities of 2.27 and 2.72 rad s⁻¹ because one turn had a radius of 0.33 m and was completed at 0.750 m s⁻¹ and the other had a radius of 0.23 m and a translational velocity of 0.626 m s⁻¹.

To perform arcing turns without losing elevation, hummingbirds must increase aerodynamic force production, and redirect a component of the force radially inwards to generate centripetal acceleration. The angle of the force redirection, θ, is given by the equation

where F_c is centripetal force and g is the gravitational constant. From this equation, we calculated the angle of force redirection required to perform the four turning treatments: 6.9° redirection at 1.9 rad s⁻¹, 9.8° redirection at 2.27 rad s⁻¹ and 2.72 rad s⁻¹, and 14° redirection at 3.6 rad s⁻¹. The force redirection may be accomplished by banking the wings and deviations from these predictions would probably reflect the higher degrees of freedom available to flapping animals, such as the ability to perform asymmetrical wingbeat kinematics.

Video of hovering was captured on each day of filming to facilitate body roll calculations, but the order of turning and hovering was alternated among individuals to ensure treatment order was not a confounding variable. At the start of each day and whenever a new individual was used, cameras captured footage of a calibration object and the feeder arm was checked with a level to ensure it was horizontal.

2.3. Kinematic analysis

Sections of video where the bird was at the feeder and maintained a consistent body position were selected for digitization. Fifteen total wingbeats were analysed for each bird in each treatment. These wingbeats were drawn from two to six consecutive wingbeats from three or four different trials. Camera views were calibrated after filming a 36-point calibration object and with a direct linear transformation from DLTcal5 software [18]. Ten points distributed on the head, rump, shoulders, wingtips, fifth primaries and two body points were digitized in every frame of the 15 wingbeats with DLTdv5 software [18].

Digitized points describe 14 kinematic variables during the upstroke and downstroke of each wingbeat. Body angle lateral (body pitch, χ_GR,XZ), body angle frontal (body bank angle, χ_GR,YZ), wing bank angle (WBA), relative wing bank angle (RWBA), average elevation angle (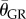), average wingtip speed (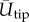), wingtip distance travelled, instantaneous position angle (ϕ_GR), instantaneous elevation angle (θ_GR), angle of attack (α) and the stroke plane angle (β) were calculated with a gravitational frame of reference. A wingstroke-centred frame of reference was used to calculate the stroke amplitude (Φ_SP), elevation amplitude (Θ_SP) and body roll angle (χ_SP,XZ). Frames of reference and kinematic calculations are described in detail in previous studies [8] with the exception of body roll angle, wing bank angle, relative wing bank angle and angle of attack. Roll along the long axis of a bird's body was calculated as a vector extending perpendicularly from a plane comprising the rump and two markers on each individual's back. Body roll was averaged over each wingbeat. To ensure marker placement did not adversely affect roll calculations, body roll was adjusted by subtracting the mean roll observed during a given day's hovering trials from the recorded roll. Wing bank angle was calculated by taking the mean difference of the absolute values of the outside (left) and inside (right) wings. Relative wing bank angle was calculated by adding wing bank angle and body angle frontal. A value of 0° indicates the wings are perpendicular to the body. Angle of attack is calculated as the angle between the plane of the wing and the horizontal for a given wing elevation. The plane of each wing was defined by the shoulder, wingtip and fifth primary. The wing is oriented parallel to the horizon at 0° or 180° and perpendicular at 90°.

2.4. Quasi-steady model

To examine the forces generated during turning, we used a quasi-steady-state aerodynamic analysis based on a blade-element model [19]. This approach does not account for unsteady forces produced during wing turnaround, which could include several mechanisms including rotational lift, wake capture, and clap and fling [20–23] (but see [24,25]). The quasi-steady analysis integrates the lift and drag forces that occur along chord-wise sections of the wing [16,26]. The instantaneous, quasi-steady lift and drag acting on each flapping wing are calculated for each wing stroke as:

where S is the surface area of the wing, ρ is the air density (1.18 kg m⁻³), and R₂ and R₃ are, respectively, the non-dimensional radii of second and third moments of the wing (electronic supplementary material). The coefficients of lift (C_L) and drag (C_D) were calculated using the aerodynamic angle of attack (α_aero, °), which is the angle of attack of the wing relative to the incident velocity (V_incident):

These equations were empirically derived for C. anna [16], but differ here in the sign convention of α_aero for the up- and downstrokes. The incident velocity was calculated as follows:

where V_tip is the velocity of the wingtip calculated from the motion of the wing, V_induced is the velocity of the air induced by the motion of the wings and V_body is the velocity of the bird. The induced velocity was estimated using the Rankine–Froude model, which assumes a flat stroke plane with downward-directed velocity. Because the speed of arcing turns was less than 1 ms⁻¹, the following equation [27] was used to calculate V_induced:

where m is the mass, g is the gravitational constant and A_disc is the area swept out by the actuator disc. The estimate of the actuator disc's area uses wing length (L) and stroke amplitude in the following equation:

Drag acts in the direction of V_incident and lift acts in the direction of the vector provided by the cross product of the leading edge of the wing and V_incident in the positive vertical direction. Instantaneous forces were calculated over each wingbeat and then average forces in the vertical, forward and lateral directions were calculated.

2.5. Statistical analysis

Changes in kinematics between hovering and turning were analysed with turning data from the treatment that required the greatest centripetal acceleration (r = 0.23 m, v = 0.750 m s⁻¹, a_c = 2.45 m s⁻²). Kinematic parameters for hovering were the mean of the left and right wings. Wingstroke differences between hovering and turning were identified with a one-way mixed-model ANOVA that used wing motion (left wing turning, right wing turning, hovering) as the fixed effect and bird as the random effect [28–30]. Models with significant overall ANOVAs (α-level = 0.05) received post hoc comparisons that assessed pairwise differences between each treatment [31]. A separate one-way mixed-model ANOVA quantified changes in parameters related to body kinematics and both wings. This ANOVA used flight mode (hovering versus turning) as the fixed effect and bird as the random effect.

Kinematic changes among the four turning treatments were analysed with a factorial two-way mixed-model ANOVA. This method was also used to identify changes in the vertical, lateral and forward forces generated by the left and right wings among our turning treatments. The two levels of translational speed and turning radius were used as categorical variables in these analyses. These variables, as well as the interaction between the two, also served as the fixed effects in the mixed model, and bird was the random effect.

After completing our statistical analyses, a positive false discovery rate (pFDR) analysis was used to control the false discovery rate [32–34] at 0.05. Our pFDR analysis used the ‘smoother’ option in the R [28] package qvalue [35]. We determined that an adjusted α-level of 0.040 controlled family-wise false discovery at 5% for our 396 statistical tests, and subsequent inferences (electronic supplementary material, tables S2–S5) use this adjusted α-level.

3. Results

Comparing hovering flight to the turning treatment with the highest angular velocity and centripetal acceleration revealed multiple changes in wingbeat and body kinematics. In general, both the body and the stroke plane were banked into turns, but there were also left–right wingbeat asymmetries (figure 2). The time course of the three wing angles revealed more substantial asymmetries for the elevation angle and angle of attack than for the stroke position angle (figure 3).

Figure 2.

Dorsal perspective of a hummingbird performing an arcing turn. A time lapse of images taken during a fast, small radius arcing turn to the right illustrates that the wings and body are banked inwards and that the inner wing rotates faster during the upstroke and slower during the downstroke relative to the outer wing. Images depict (a) supination, (b) mid-upstroke, (c) pronation and (d) mid-downstroke with two full wingbeats elapsed between photos. The sequence comes from the electronic supplementary material, video S5.

Figure 3.

Instantaneous wing measures. Kinematics averaged across all individuals are presented for two wingbeats of hovering (a,d,g) and the turn with the highest centripetal force (b,e,h). (c,f,i) Position angle (a–c), angle of attack (d–f) and elevation angle (g–i). The left wing is shown in red and the right wing is in blue. Lines indicate average values and transparent bands are the standard error of the mean. Downstroke is shaded in grey. Scale bar, 25 ms.

Wingstroke asymmetries in turning flight apparent in instantaneous wing measures translated into statistically significant differences for many of the kinematic parameters (figure 4). Asymmetries in stroke position angle resulted in a small, but significant increase in stroke amplitude in the outer wing (ΔΦ_SP,US 7.7°, ΔΦ_SP,DS 9.1°) and a decrease in the inner wing (ΔΦ_SP,US −5.4°, ΔΦ_SP,DS −10.0°), relative to hovering (figure 4a). The outer wing also had a higher average elevation angle (Δ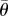_GR,US 14.8°, Δ_GR,DS 14.3°) and lower elevation amplitude (ΔΘ_SP,US −10.6°, ΔΘ_SP,DS −1.9°), relative to hovering, whereas the inner wing has a lower average elevation angle (Δ_GR,US −12.3°, Δ_GR,DS −11.0°) and higher elevation amplitude (ΔΘ_SP,US 15.0°, ΔΘ_SP,DS 13.4°; figure 4d,e). These two measures of wing elevation varied in concert, as has been previously shown for yaw turns [8]. The stroke plane angle of the outer wing was indistinguishable from the hovering wingbeat, but the stroke plane angle of the inner wing was essentially horizontal during the downstroke and was pitched up during the upstroke, such that it was higher at supination than at pronation (figure 4f; electronic supplementary material, figure S2). The time course of angle of attack was analysed at four phases. Overall, the inner wing had advanced timing in wing rotation and the left and right wings were significantly different at all phases except for mid-downstroke (figure 4b; electronic supplementary material, table S2). The analysis of body kinematics demonstrated that body roll angle, body angle frontal and wing bank angle all tilted into the turn with similar magnitude (approx. Δ14°; figure 4h,j,k). As a consequence, there was no significant change in relative wing bank angle between hovering and turning (figure 4l; electronic supplementary material, table S3).

Figure 4.

Analysis of kinematics between hovering and turning. Kinematic parameters describing hovering are shown in green. Box plots from parameters related to the left and right wings of the turning treatment with the highest centripetal force are presented in red and blue, respectively. Parameters related to the body or both wings are shown in purple for turning. Downstroke is shaded in grey. Black bars above each subfigure indicate statistical significance.

Comparisons across the four arcing turn treatments revealed that the wing bank angle titled inwards at values close to what was predicted from physical principles (electronic supplementary material, table S4). For the turning treatment with low velocity and long radius (ω = 1.9 rad s⁻¹), the wing bank angle was 10.2° and 9.3° for the up- and downstrokes, respectively, whereas the predicted angle was 6.9°. For the turning treatments with angular velocities of 2.27 and 2.72 rad s⁻¹ the predicted bank angle was 9.8°. The measured bank angles were 11.5° and 10.5° at 2.27 rad s⁻¹, for up- and downstrokes, respectively, and 10.8° and 10.1° at 2.72 rad s⁻¹. At the angular velocity of 3.26 rad s⁻¹, the predicted bank angle was 14.0°, and the measured wing bank angle was 13.5° and 12.7°, for the up- and downstrokes, respectively.

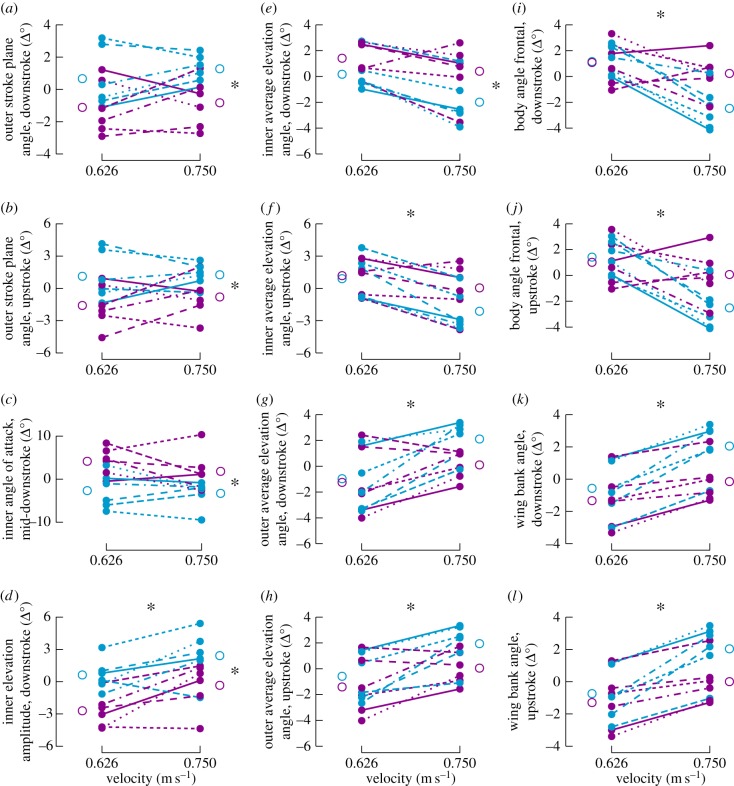
In addition to the overall banking of the body and wings into the turn, analysis of the full set of kinematic variables revealed that some wingbeat kinematic measures varied with radius, some wing and body kinematics varied with velocity, and one wingbeat measure varied with both radius and velocity (figure 5; electronic supplementary material, table S4 and figures S1 and S2). Tighter turns (r = 0.23 m) were associated with tilting of the outer wing's stroke plane angle forward (pronation higher than supination; figure 5a,b), depression of the inner wing (decreased average elevation angle) during downstroke (figure 5e) and decreasing angle of attack of the inner wing at mid-downstroke (figure 5c). Within a radius treatment, translational velocity had no significant effect on these variables. By contrast, both faster and tighter turns were associated with an increase in the inner wing's elevation amplitude during downstroke (figure 5d). Several features of wing elevation were associated exclusively with faster turns. Specifically, the inner wing was more depressed during the upstroke (decreased average elevation angles, figure 5f) and the outer wing was more elevated during both up- and downstrokes (figure 5g,h) at the higher velocity treatments. The overall differences in wing elevation led to the wing bank angle being titled inwards for both up- and downstrokes at high velocity (figure 5k,l). However, because the body angle from the frontal perspective was also titled inwards (figure 5i,j), the relative wing bank angle remained consistent across the turning treatments, just as it did between hovering and the arcing treatment with highest angular velocity and centripetal acceleration (electronic supplementary material, table S4).

Figure 5.

Changes in body and wingbeat kinematics across turning treatments. Kinematic parameters that are significantly influenced by turning radius (a–e) and velocity (d,f–l) are presented for all turning treatments. Plots illustrate how individuals, which are shown as solid points, altered their kinematics with changes in turning radius and speed. Levels of turning radius are indicated with purple (0.33 m) or blue (0.23 m), and velocities are plotted across the horizontal axis. An asterisk above the panel indicates a significant velocity effect. An asterisk to the right of a panel indicates a significant radius effect. The vertical axis indicates the mean change in degrees of a kinematic variable relative to the mean of that individual bird. This calculation most closely approximates the underlying mixed-model ANOVA, in which deviations from the per-bird mean value are analysed across treatment groups. Lines connect an individual's average performance between velocities and offset open circles present the change in kinematic variables averaged across all individuals.

The quasi-steady analysis of the forces produced by wing motion revealed no difference in vertical force across the four turning treatments (figure 6a,b; electronic supplementary material, table S5), which is consistent with their movement in the horizontal plane. Forward force generated by the outer (left) wing increased for tighter turns (figure 6c). The forward force generated by the inner wing did not vary with arcing turn treatment (figure 6d), and neither the outer nor the inner wing forward force was associated with turning velocity. The inwards lateral forces of both the inner and outer wing increased during higher velocity turns, whereas the inwards lateral force of only the inner wing increased during tighter turns (figure 6e,f). Collectively, this analysis indicates that, to perform tighter turns, hummingbirds varied wing force asymmetrically such that the outer wing produced higher forwards force, whereas the inner wing produced more inwards force. To perform faster turns, hummingbirds varied force symmetrically such that both the inner and outer wings produced more inwards lateral force.

Figure 6.

Changes in quasi-steady forces across turning treatments. The quasi-steady force components in the vertical (a,b), forward (c,d) and lateral (e,f) directions are presented for all turning treatments. Forces (in % body weight) generated by the outer (left) wing are shown in (a,c,e) and forces generated by the inner (right) wing are shown in (b,d,f). Plots illustrate how individuals, which are shown as solid points, altered force with changes in turning radius and speed. Changes in turning radius are indicated with purple (0.33 m) or blue (0.23 m), and changes in velocity are plotted across the horizontal axis. An asterisk above the panel indicates a significant velocity effect. An asterisk to the right of a panel indicates a significant radius effect. Lines connect an individual's average performance between velocities and offset open circles present the change in force averaged across all individuals.

4. Discussion

We compared hovering and arcing turns of hummingbirds (figure 1) to determine the relative contribution of body-dependent and -independent force reorientation mechanisms. The time course of wing angles was highly symmetrical during hovering, and differed considerably between inner and outer wings during arcing turns (figures 2 and 3). The differences in instantaneous angles translated into many significant differences among wingbeat and body kinematic variables (figure 4). The overall result was that hummingbirds performed arcing turns both by banking their body and wings into the turn and by using asymmetrical wingbeat kinematics. To determine how body and wingbeat kinematics were being used to control turns, we filmed the birds performing four types of arcing turns that varied in radius and velocity. This analysis revealed that both the wings and the body banked into the turn at close to the predicted angles. In addition, four wingbeat kinematic variables were significantly associated only with changes in radius (figure 5; electronic supplementary material, table S4). Specifically, as the radius decreased, the stroke plane of the outer wing pitched forwards during both strokes, the elevation of the inner wing was lower during the downstroke, and the angle of attack of the inner wing was lower during mid-downstroke. Seven body and wingbeat kinematic variables were significantly associated only with changes in velocity. These can be summarized as tilting inwards of the wing elevation and the body angle with increasing velocity. One wingbeat kinematic variable, the elevation amplitude of the inner wing during the downstroke, increased for both tighter and faster turns. No variables were significantly affected by the interaction of radius and velocity. A quasi-steady analysis revealed a consistent result: changes in radius were associated with asymmetrical forces and changes in velocity were associated with symmetrical forces (figure 6; electronic supplementary material, table S5). Collectively, our results indicate that both body-dependent and -independent force orientation mechanisms are available to hummingbirds, and that these kinematic strategies are used to meet the separate aerodynamic challenges posed by velocity and turning radius.

The ability to use different kinematic strategies within the same manoeuvre illustrates the broad envelope of aerodynamic mechanisms that are available during flapping flight. Unlike in aeroplanes and helicopters in which the wings are fixed either to the fuselage or to a rotating joint, the wings of flapping animals have a much broader range of movement [36]. The hummingbirds in this study exhibited substantial ability to vary the instantaneous wing position, which led to multiple differences in stroke-averaged variables both within and among individuals. However, when the kinematic variables and resultant quasi-steady force estimates are analysed relative to the four turning treatments, a coherent pattern emerges. When challenged with higher velocity turns, hummingbirds increased the inwards bank of both the body and the wings, which led to higher inwards lateral force from both the left (outer) and right (inner) wings. By contrast, when challenged with smaller radius turns, hummingbirds reoriented the stroke plane of the outer wing to produce additional forward thrust that was not matched by the inner wing. The inner, but not the outer, wing was depressed to further reorient the force inwards. Overall, these quasi-steady wing forces resulted in an increased centripetal acceleration and a yawing torque which acts to increase turning performance. If the radius were further decreased, the bird would transition to a pure yaw turn (on axis rotation), which is characterized by high wingbeat asymmetries without body bank [8] and is driven by imbalances in torque [37]. Taken together, these studies illustrate how body-dependent and -independent kinematic mechanisms are employed along a continuum of turning manoeuvres.

Feeder tracking studies provide an experimental approach for manipulating manoeuvring performance in hummingbirds but the range of movements is necessarily limited relative to the diversity of flight trajectories observed in natural conditions [38,39]. The radii used in the current study (0.23 and 0.33 m) are similar to those used by free-flying hummingbirds performing arcing turns in a large laboratory cage (mean = 0.48 m) [40]. With a radius of approximately four wing lengths (electronic supplementary material, table S1), the small radius treatment in this study represents a relatively tight arcing turn. By contrast, the translational velocities used in this experiment (0.63 and 0.75 m s⁻¹) are slower than the average velocities of free flight arcing turns (mean = 1.57 m s⁻¹) but within the range of observed values [40]. The requirement to match centripetal accelerations across turning treatments constrained the range of translational velocities available. Moreover, when the translational velocities were further increased the hummingbirds had a difficult time tracking the feeder consistently. The modest increase in forward velocity may also explain why we did not observe the expected increase in stroke plane angle that normally accompanies higher flight speeds [14]. The arcing turns performed in this study therefore represent a moderate level of performance that is within the range of previously documented manoeuvres.

The combination of body-dependent force reorientation and body-independent wingbeat asymmetries that we observed in hummingbirds is consistent with other studies of arcing turns in bats [10], cockatiels [1] and pigeons [2]. By experimentally varying the velocity and radius of arcing turns, we were able to test the hypotheses that body and wingbeat kinematic variables were modulated in concert to match the requirements for increased centripetal acceleration. Instead we found a set of body-dependent kinematics that varied more in response to changes in velocity, and a different set of wingbeat asymmetries that varied more in response to changes in radius. Because all studies of turning in flapping animals have now demonstrated both kinematic features, their independent use for controlling the velocity and radius of turns may be a common mechanism. This new hypothesis can now be evaluated through comparative study of flapping animals.

Ethics

The Animal Care Committee of the University of British Columbia approved all animal procedures.

Data accessibility

Raw data, including cvs files containing x, y and z coordinates of digitized video sequences as well as python scripts necessary to filter and process raw data into instantaneous wing measurements (e.g. figure 3) are deposited in Dryad (doi:10.5061/dryad.j77h6). This archive also includes R and python scripts that are used for the mixed model ANOVA analyses, multiple comparisons procedures and to generate figures 3, 5, and 6. A README file provides detailed steps for reproducing all analyses.

Authors' contributions

T.J.G.R., P.S.S. and D.L.A. conceived of the study, designed the experiments and wrote the manuscript. T.J.G.R. developed the experimental apparatus and collected the data. T.J.G.R., P.S.S. and K.M.M. analysed the data. All authors gave final approval for publication.

Competing interests

We declare no competing interests.

Funding

This research was supported by a Discovery Grant from the National Science and Engineering Research Council of Canada (402677).