Unifying ecological stoichiometry and metabolic theory to predict production and trophic transfer in a marine planktonic food web

Abstract

Two ecological frameworks have been used to explain multitrophic interactions, but rarely in combination: (i) ecological stoichiometry (ES), explaining consumption rates in response to consumers' demand and prey's nutrient content; and (ii) metabolic theory of ecology (MTE), proposing that temperature and body mass affect metabolic rates, growth and consumption rates. Here we combined both, ES and MTE to investigate interactive effects of phytoplankton prey stoichiometry, temperature and zooplankton consumer body mass on consumer grazing rates and production in a microcosm experiment. A simple model integrating parameters from both frameworks was used to predict interactive effects of temperature and nutrient conditions on consumer performance. Overall, model predictions reflected experimental patterns well: consumer grazing rates and production increased with temperature, as could be expected based on MTE. With decreasing algal food quality, grazing rates increased due to compensatory feeding, while consumer growth rates and final biovolume decreased. Nutrient effects on consumer biovolume increased with increasing temperature, while nutrient effects on grazing rates decreased. Highly interactive effects of temperature and nutrient supply indicate that combining the frameworks of ES and MTE is highly important to enhance our ability to predict ecosystem functioning in the context of global change.

1. Introduction

Given the dramatic global loss of species, numerous ecological studies have addressed the consequences of species diversity loss on ecosystem functioning across multiple trophic levels [1–3]. These multitrophic biodiversity studies, however, yielded inconsistent conclusions regarding the strength and direction of diversity (i.e. richness) effects within and across trophic levels. They indicated that these effects depend on species-specific traits that determine coexistence as well as ecosystem processes and functions (e.g. [4,5]). A number of different traits, such as body size, resource demand and acquisition, constrain fundamental abiotic niches as well as realized niches (coexistence), whereas the same (or additional) traits constrain species contributions to ecosystem functions. These traits thus must guide our understanding of the mechanisms of biodiversity and ecosystem functioning (BEF) relationships in multitrophic systems [6].

Different species-specific traits are also the basis of two major ecological frameworks that have been developed and used to understand multitrophic interactions in food webs, ecological stoichiometry (ES) and metabolic theory of ecology (MTE, [7]). ES acknowledges the importance of material imbalances between consumers and their prey, which is especially profound for herbivore–phototroph interactions. Phototrophs, unlike herbivores, can adjust their elemental composition depending on nutrient stoichiometry, resulting in different food quality and thus affecting consumption rates and consumer nutrient recycling [8]. In community ecology, ES has successfully been used to explain consumer performance (food uptake rate, assimilation, growth rate and efficiency; [9–11]), competition between consumer species [12,13], and consumer effects on prey nutrient composition [14,15]. In contrast to ES, MTE [16] focuses on consumer body mass and temperature as determinants of metabolic rates, which control growth and consumption rates as well as population and community productivity. MTE uses first-order physical principles to extrapolate from basal metabolic rates of individuals to higher levels of biological organization [17], thus providing allometric scaling relationships of body mass and temperature with physiological and ecological processes on cellular, organism and ecological levels. In this context, body size and temperature are generally identified as important determinants of species interactions (e.g. [18]) and community level dynamics and stability [19].

However, both ES and MTE have rarely been applied in the context of BEF so far (for ES and BEF see [20] for a review), or in combination (for exceptions, see [7,21–24]). For instance, Woods et al. [24] demonstrated in a meta-analysis that organismal phosphorus (P) and nitrogen (N) concentrations across various organism groups were higher in cold versus warm environments, as the efficiency of RNA (requiring P) and proteins (requiring N) in biochemical reactions increases with temperature [24]. Therefore, temperature does not only impact the metabolic rates of consumers directly [16], but may also have indirect effects on trophic interactions by changing prey nutrient content and thus food quality [22].

The largest synthesis of ES and MTE so far comprises more than 350 studies in a meta-analysis on the relative explanatory power of both frameworks for herbivore–phototroph interactions [21]. This analysis demonstrated that both temperature and herbivore body size, as well as stoichiometric mismatch (low food quality of prey), constrain herbivory. Overall, per capita grazing rates increased with increasing stoichiometric mismatch between herbivores and their prey (compensating for low food quality), while the population grazing rate decreased (reflecting reduced growth rates due to low food quality).

Given the relevance of interactive effects of producer stoichiometry, consumer size and temperature and the still considerable lack of studies linking the different theories of ES and MTE in a food web context, our study was specifically designed to fill this void. We combined a large laboratory microcosm experiment with ecological modelling to unravel interactive effects of resource stoichiometry and metabolic theory on food web dynamics in a marine prey–consumer system using phyto- and zooplankton. After an initial growth phase of a six-species phytoplankton community under different nutrient and temperature conditions (six different nitrogen to phosphorus (N : P) treatments, three temperatures; figure 1), two zooplankton consumers differing in size, growth and predation characteristics (a ciliate and a rotifer) were added to the system alone and in combination. We investigated interactive effects of resource availability (N and P) and temperature, altering prey stoichiometry and thus prey food quality, on consumer grazing and trophic transfer. Hence, this experiment enabled us to specifically test hypotheses combining elements of both ES and MTE. From these basic frameworks, we obtained the following hypotheses:

• (H1) Before grazer addition, we expect algal biomass to increase with higher overall availability of resources, whereas algal nutrient content reflects the relative availability of resources. Increasing temperature will enhance algal growth rate and thus increase algal biomass, while algal N and P concentrations will decrease with temperature, resulting in elevated C : nutrient ratios.

• (H2) After grazer addition, temperature and nutrient supply interactively affect grazing rates and consumer growth. Increasing temperature will increase consumer grazing and growth rates and also final biovolume after an initial grazing period where consumers have not reached equilibrium yet (9 days in our experiment). We further expect higher consumer grazing rates, but lower consumer growth rates and biovolume with decreasing food quality (increasing algal C : nutrient ratios), with stronger effects for the smaller consumer (see H3).

• (H3) We expect both consumers to grow faster at higher temperatures, but the smaller consumer to be more responsive to temperature and also to stoichiometric change in the algae, as smaller size is supposed to be related to higher P demand (growth rate hypothesis, [25]).

• (H4) The response of the consumer mixture will not be congruent to predictions from the single consumer treatments. A priori, defining concise predictions for this ‘biodiversity effect’ is difficult, as we have no information on the complementarity of the two consumers.

Figure 1.

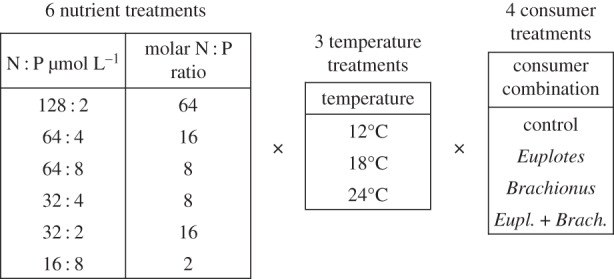
Experimental design: six nutrient treatments with varying N to P concentrations and ratios were combined with three different temperatures and four different consumer treatments, using the ciliate Euplotes vannus, the rotifer Brachionus plicatilis, a combination of both or no consumer (control). Actual temperatures slightly varied from desired temperatures: 13.7°C (±0.59, mean ± s.d.), 19.5 (±1.93) and 23.4 (±0.61).

In order to get a deeper insight into the mechanisms driving the observed experimental patterns, we used a mathematical model, which included components of MTE and ES, and compared the experimental results with theoretically expected dependences of the metabolic rates on temperature, consumer body mass and food stoichiometry.

2. Material and methods

(a). Organisms

Experimental food webs consisted of common and potentially co-occurring marine microzoo- and phytoplankton species (electronic supplementary material, table S1), comprising six microalgae and two differently sized consumers, the ciliate Euplotes vannus and the rotifer Brachionus plicatilis (for culture maintenance and biovolume calculations, see the electronic supplementary material). Phytoplankton species were selected based on feeding preferences of the different consumers. For each consumer, the algal assemblage consisted of five prey and one non-prey organism, the identity of which, however, differed for the consumers (electronic supplementary material, table S1).

(b). Experimental set-up and sampling procedures

For the experimental microcosms, Erlenmeyer flasks were used with an initial experimental volume of 255 ml. The experiment was conducted at three different temperatures and with six growth media, differing in N and P concentrations and ratios (figure 1).

All temperature × nutrient treatment combinations were subject to equal light conditions of 60 µmol photons m⁻² s⁻¹ and a 12 L : 12 D cycle. Different growth media were prepared from sterile filtered natural North Sea water according to f/2 medium (electronic supplementary material), but with different N : P additions (figure 1).

A constant phytoplankton mixture (2 × 10⁶ µm³ ml⁻¹ total initial biovolume) with equal biovolume contribution for each species was added to each Erlenmeyer flask (6 media × 3 temperatures × 4 consumer treatments × 4 replicates = 288 flasks; figure 1). After inoculation, initial samples (10 ml) were taken for microscopy and chlorophyll a fluorescence. The latter parameter was measured every third day throughout the experiment (subsamples of 3 ml) using a fluorometer (Aquafluor handheld fluorometer). After 12 days of phytoplankton growth in different temperature and nutrient treatments, t₁₂ samples were taken to determine algal abundances, composition and particulate nutrients (see below). After that, consumers were added in monoculture and in mixture, respectively, while a quarter of the flasks without consumers served as control for every temperature and nutrient treatment. After grazer addition, the experiment ran for another 9 days, resulting in a total experimental duration of 21 days. Consumers were added in an equal volume of filtered seawater (15 ml) to assure equal dilution of different nutrient treatments. Controls without consumers received an equal volume of sterile filtered seawater. Initial total consumer biovolume varied from 1 to 4 × 10⁶ µm³ ml⁻¹ in mono- and mixed-consumer treatments with equal contribution of each consumer in mixture.

Samples for chlorophyll a fluorescence (3 ml), cell concentrations (10 ml) and dissolved nutrient concentrations (20 ml, N and P) were taken at t₀, at t₁₂ just before the addition of consumers, and then every third day until the end of the experiment (t₂₁). The final experimental volume was approximately 150 ml, which was still sufficiently deep for motile planktonic algae and consumers.

Samples for particulate intracellular nutrients (C, N, P) were taken at t₁₂ just before grazer addition to determine the nutritional status of the algae, and at the end of the experiment (t₂₁) for separate algal and consumer fractions by filtering mixed samples through a 10 µm or 20 µm nylon mesh (for details on dissolved and particulate nutrient analyses, see the electronic supplementary material).

To determine algal and ciliate cell concentrations, samples were preserved with Lugol's iodine solution (1% final concentration) and counted under an inverted microscope (ciliates: whole counting chamber, microalgae: at least 10 fields of view, minimum of 400 cells total). For the rotifer consumer Brachionus, 30 ml subsamples were taken every third day after grazer addition to count Brachionus alive in sterile tissue culture plates, after which the sample was used for dissolved inorganic nutrient determination and further microscopic counts. All cell concentrations were converted to biovolume per millilitre.

In this study, we focus on particulate organic carbon (POC) of the phytoplankton (C ml⁻¹) as a proxy for algal biomass. Unfortunately, 42 out of the total 288 carbon samples from t₁₂ were lost. For these samples, algal biovolume was used to calculate POC according to Menden-Deuer & Lessard [26], to complete the particulate carbon dataset.

Carbon data from t₁₂ (just before grazer addition) and t₂₁ (end of experiment) were used to calculate consumer grazing rates (g = μ − r) per day by subtracting algal growth rates per day with consumers (net growth rate = r) from algal growth rates in the absence of consumers (gross growth rate = μ)

Consumer ratios (ln (biovolume Euplotes/biovolume Brachionus)) were calculated and then statistically tested to investigate whether final consumer biovolume contributions in consumer mixtures differed between different nutrient and temperature treatments.

For the statistical analyses, we used two- and three-way analyses of variances (ANOVA) to test for significant effects across treatment levels and their interactions. The subsequent comparison of differences between single factor levels was conducted using TukeyHSD posthoc tests. In some cases, the ANOVA assumption of variance homogeneity was violated due to differences in variability across temperature treatments. Here, we first applied linear regression based on generalized least squares (gls, R package nonlinear fixed effects model (nlme)) allowing for unequal variance across treatment levels and then performed an ANOVA on the generalized least squares (gls) model. Because commonly used post hoc methods cannot be applied to gls objects that account for differing variances across treatments, we visually compared the effects of different factor levels using box and whisker plots, where differences between factor levels are considered to be significant if the boxes including all values between the lower and upper quartile do not overlap. For details on specific analyses, see the electronic supplementary material.

(c). Theoretical predictions

Grazing and growth rates of consumers depend on the body mass, food stoichiometry and temperature [21,27]. It has been shown that the weight-specific grazing rate scales with a grazer's body mass as m^−0.25 [28,29]. Additionally, grazing rates follow the Arrhenius law as a function of absolute temperature T, and change as (C : N)^0.68 as a function of food stoichiometry [21,27]. As a proxy for the consumer mass, m, we use species biovolume BV (see the electronic supplementary material, table S1).

Combining the three scaling laws, we express the specific attack rate of a consumer in response to its BV at temperature T (K) and food stoichiometry C/N as follows:

2.1

where g₀ is a reference attack rate of a consumer of size BV₀ at a reference temperature T₀ and food stoichiometry C₀ : N₀; E_a is the species activation energy and k = 8.6 × 10⁻⁵ eV is the Boltzmann constant.

We assume that the growth rate of the consumers is proportional to their grazing rate, while their food assimilation efficiency decreases with increasing C : N ratios

2.2

where θ₀ is the reference assimilation efficiency when the food stoichiometry equals C₀ : N₀.

To estimate the activation energies E_a, we fitted the Arrhenius law to the temperature dependences of the consumer maximal growth rates. Although different species can have distinct values for E_a [30], our estimations did not reveal any significant difference between the two consumers in the range below 20°C and we thus used the same value for both species. Note however, that at higher temperature the growth rate of Euplotes reaches a saturation level and does not follow the Arrhenius law (see the electronic supplementary material, figure S3).

We modelled the population dynamics in terms of a consumer–resource system and estimated the parameters (scaling exponent α and coefficients g₀ and θ₀) to minimize the mean square deviations between the model and experimental data. Model fitting was performed using the differential evolution algorithm [31], which provides an efficient way to find a global minimum of a function in multidimensional parameter space. We used the implementation of this method in the GODLIKE procedure for Matlab (see the electronic supplementary material for model details and table S4 for resulting parameters).

3. Results

(a). Phytoplankton response to altered temperature and nutrient conditions in the absence of consumers

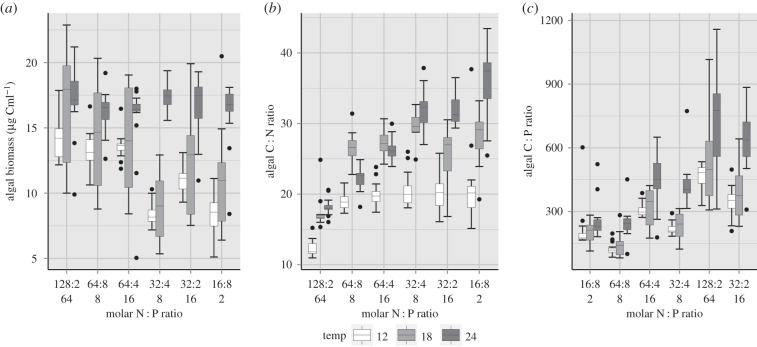
In the absence of consumers, temperature and nutrient conditions significantly and interactively affected phytoplankton biomass production (measured as POC) after 12 days of growth (p < 0.001 for both factors and interaction; electronic supplementary material, table S2; figure 2a). Phytoplankton biomass generally increased with temperature (significant main effect, electronic supplementary material, table S2) and was higher at high N concentrations (greater than or equal to 64 µmol l⁻¹, i.e. N : P = 128 : 2, 64 : 8, 64 : 4) compared with lower N concentrations (N : P = 32 : 4, 32 : 2, 16 : 8). However, this nutrient effect became weaker with increasing temperature. At 12°C, there were significant differences across nutrient treatment levels (based on non-overlapping boxes, see Material and methods), whereas there was hardly any difference in algal biomass at 24°C (figure 2a), reflecting the significant nutrient × temperature interaction (electronic supplementary material, table S2).

Figure 2.

(a) Algal biomass (microgram C per millilitre), (b) algal molar C : N, and (c) algal molar C : P ratios after 12 days of growth (t₁₂, just before consumer addition) at different temperatures (°C) and nutrient supply ratios (molar N : P). Note the different arrangement of nutrient treatments on the x-axes for (c) (arranged in the order of decreasing P concentrations), compared to (a) and (b) (arranged in the order of decreasing N concentrations).

Phytoplankton C : N and C : P ratios were also significantly affected by temperature and nutrient conditions with a significant interaction of both factors (p < 0.001, respectively, electronic supplementary material, table S2; figure 2b,c). Overall, phytoplankton C : N ratios ranged from 11 to 44 and significantly increased with increasing temperature (figure 2b). The nutrient effect strongly depended on temperature: at 12°C and 18°C, C : N ratios were significantly lower at N : P = 128 : 2 compared with all other treatments (Tukey HSD, p > 0.001, see the electronic supplementary material), which were not significantly different from each other. At 24°C, a continuous increase in C : N with decreasing N supply was observed (C : N ratios increase from N : P = 128 : 2 < 64 : 8 < 64 : 4). Below an N supply of 64 µmol N l⁻¹, C : N ratios did not differ significantly, but were significantly higher compared to treatment levels of N ≥ 64 µmol l⁻¹.

Phytoplankton C : P ratios ranged from 81 to 1158 and significantly increased with decreasing P supply and increasing temperature with a significant interaction of both factors (electronic supplementary material, table S2 and figure 2c). The increase in C : P ratios with decreasing P concentrations (8 > 4 > 2 µmol l⁻¹) was enhanced by higher temperature (figure 2c).

Particulate N and P concentrations in the algae were significantly affected by nutrient supply; however, only P concentrations significantly decreased with increasing temperature showing significant differences due to temperature for three out of six nutrient treatments with low P supply (N : P = 128 : 2, 64 : 4 and 32 : 2), while there were no significant differences for the other nutrient treatments. N concentrations, on the other hand, were not affected by temperature (see the electronic supplementary material, figure S1 and table S5). Therefore, increased C : N ratios with increasing temperature only reflected an increase in C and not a decrease in N, while increased C : P ratios with increasing temperature mainly reflected an increase in C, but also a decrease in P at low P supply.

(b). Consumer response to altered temperature, nutrient conditions and feeding on different prey communities

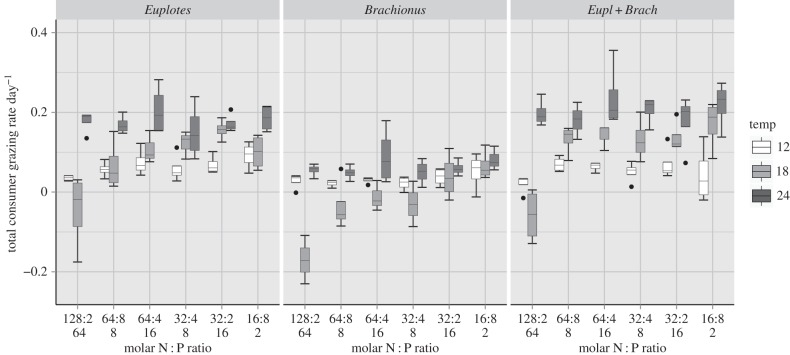
Temperature, nutrient conditions and grazer combination significantly affected total consumer grazing rates (p < 0.001, respectively, electronic supplementary material, table S3; figure 3). Nutrient and consumer effects depended on temperature as indicated by significant interactions of the respective factors (p < 0.001; electronic supplementary material, table S3). Grazing rates were significantly higher for Euplotes and the combined Euplotes + Brachionus treatment compared to Brachionus alone (Tukey HSD, p < 0.001, see the electronic supplementary material). Grazing rates increased with temperature (significant differences between grazing rates at 24°C compared to 18°C and 12°C, Tukey HSD, p < 0.001) for Euplotes alone and in combination with Brachionus, whereas Brachionus in monoculture showed different responses: grazing rates were low at 12°C, even partly negative at 18°C, and only slightly increased at 24°C compared with 12°C (figure 3). Negative grazing rates indicate that phytoplankton growth rates were higher with consumers than without consumers. Algal species composition hardly differed in treatments with negative or positive grazing rates (data not shown), indicating that final elevated algal biovolume in consumer treatments compared with respective controls was not caused by altered competitive interactions due to selective grazing. This, however, may have potentially enhanced algal growth due to nutrient regeneration, which could not be detected in our study with a sampling resolution for dissolved nutrients every third day (data not shown).

Figure 3.

Total consumer grazing rates per day at different temperatures (°C) and nutrient supply ratios (molar N : P) in different consumer treatments (monocultures and mixture).

Across grazer treatments, significantly lower grazing rates were observed for the highest N : P ratio (N : P = 128 : 2) compared with all other nutrient treatments (Tukey HSD, p < 0.001); these were even negative at 18°C for all grazer combinations (figure 3). At 24°C, however, the overall higher grazing rates in the presence of Euplotes hardly differed among different nutrient treatments. The significant two-way interaction thus indicates that the strong positive temperature effect outweighed the negative effect of low P concentrations/high N : P ratios, resulting in higher grazing rates at N : P = 128 : 2 at 24°C compared with intermediate ratios and concentrations at lower temperatures (figure 3). Grazing rates in the combined consumer treatments more or less mirrored the patterns observed for Euplotes alone, as this consumer dominated the consumer mixtures (see below and electronic supplementary material, figure S2 and table S2).

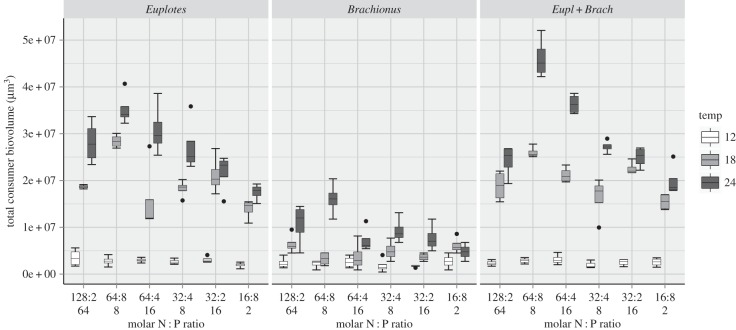
Consumer biovolume at the end of the experiment was significantly and interactively affected by temperature, nutrient conditions and grazer combination (p < 0.01 for all main effects and interactions; electronic supplementary material, table S3; figure 4). A three-way interaction indicated that the effects of all three factors on consumer biovolume production were interrelated (electronic supplementary material, table S3). Consumer biovolume significantly increased with temperature for all consumer combinations (based on non-overlapping boxes, see Material and methods); however, this increase was significantly higher for the consumer combinations including Euplotes (Euplotes and Euplotes + Brachionus). While consumer biovolume hardly differed among nutrient treatments at 12°C, it was strongly affected by nutrients at 18°C and 24°C (again more strongly for consumer treatments including Euplotes), where it peaked at intermediate nutrient ratios.

Figure 4.

Total consumer biovolume at the end of the experiment at different temperatures (°C) and nutrient supply ratios (molar N : P) in different consumer treatments (monocultures and mixture).

The relative contribution of Euplotes biovolume to the consumer mixture significantly increased with temperature, while it only differed slightly among nutrient treatments at 12°C, but not at higher temperatures (non-significant nutrient effect (p = 0.91), significant temperature and interaction effects (p < 0.001, respectively), electronic supplementary material, table S2 and figure S2).

The relative contribution of different algae species to the final total algal biomass did not reveal substantial differences across most nutrient and consumer treatments at 12°C and 18°C, where the diatoms Stauroneis and Chaetoceros contributed the highest portions to algal biomass. Only at 24°C did both consumers alter competitive interactions between the algae, resulting in different species compositions in consumer treatments compared to the control. However, algal community composition is not relevant for the interpretation of the results we focus on in this manuscript, and is therefore not included here or further discussed.

For Euplotes, regression analysis indicated a significant increase of consumer population grazing rates with increasing algal C : N (p = 0.011) and increasing temperature (12°C < 24°C, p < 0.001), while algal C : P did not affect Euplotes population grazing rates. A linear model including only C : N and temperature as predictor variables was able to explain almost 60% of the variation in Euplotes population grazing rates (adjusted r² = 0.5993). For the consumer mixture, only temperature affected grazing rates. When including temperature as the only predictor, the linear model explained almost half of the variation in population grazing rates of the mixed treatment (adjusted r² = 0.4766). Post hoc pairwise comparisons showed significant differences between all temperature levels. For Brachionus, neither C : N, C : P nor temperature showed any effects on consumer grazing rates.

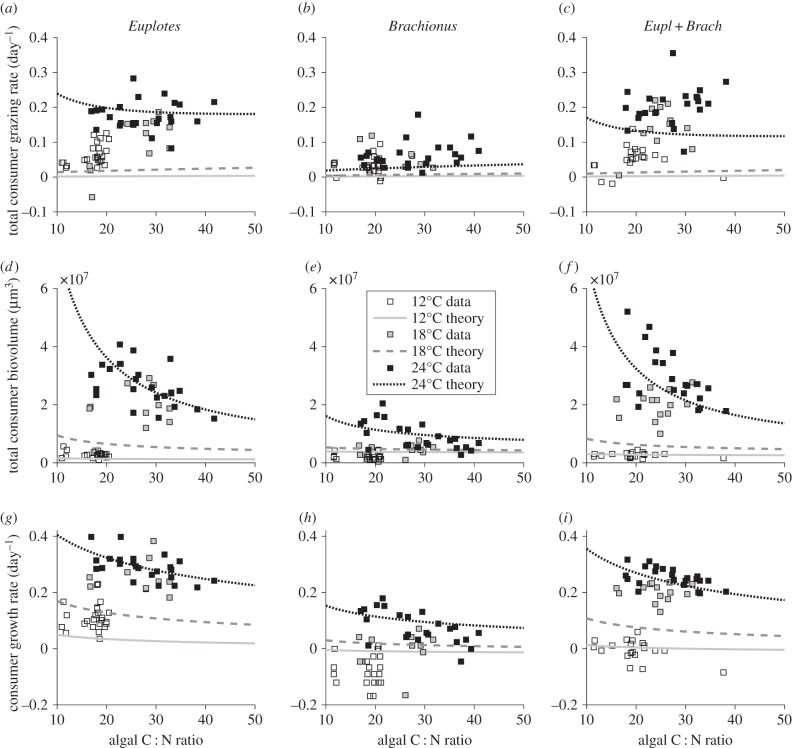
As only algal C : N and not C : P affected consumer grazing rates and final biovolume, we focused in our metabolic model on the effects of algae C : N on consumer growth rates, total consumer population biomass and grazing rates at the end of the experiments (figure 5). The lines in this figure show the best fit of the MTE-ES model (electronic supplementary material, Eq. S1) to the experimental data (squares) at different temperatures. The nonlinear fitting gives α = 1 for the scaling of the assimilation efficiency with food stoichiometry.

Figure 5.

Total consumer grazing rate (a–c), total consumer biovolume (d–f) and consumer growth rate (g–h) at different food qualities, i.e. different molar C : N ratios of the algae after 12 days of growth under different nutrient and temperature conditions before consumer addition. (a,d,g) = Euplotes, (b,e,h) = Brachionus, (c,f,i) = consumer mixture. Different symbols and lines indicate experimental results and model predictions, respectively, obtained at different temperature regimes (see legend in (e)).

The MTE-ES model predictions show that consumer growth rates and final biovolume increase with temperature and decrease with algal C : N for both consumers (figure 5d,e,g,h). Population grazing rates also generally increase with temperature, except for Euplotes at 24°C, where we observed a decrease of grazing rates with increasing C : N ratio. Overall, temperature effects were predicted to be stronger for Euplotes than for Brachionus. As we assumed the same activation energy, this difference is mainly attributed to the difference in the body size.

4. Discussion

(a). Phytoplankton response to altered temperature and nutrient conditions in the absence of consumers (hypothesis H1)

In the absence of consumers, phytoplankton biomass was interactively determined by nutrient supply and temperature, supporting hypothesis H1. Biomass increased with temperature as expected, reflecting increased metabolism, physiological rates and finally growth rates at higher temperature [16]. Phytoplankton biomass also increased with nutrient supply; though responding mainly to higher N irrespective of P concentrations. In fact, the algal stoichiometry observed (see below) indicated a predominantly N-limited system with rather high C : N ratios (C : N > 16) for all nutrient supply treatments except for N : P 128 : 2, where lower C : N and high C : P (consistently > 300) indicated P limitation (e.g. [32]). The nutrient effect on biomass, however, was only evident at lower temperatures (12°C and 18°C), while highest phytoplankton biomass was observed at 24°C irrespective of nutrient conditions. These findings contradict previous studies, which support that the influence of nutrient availability on growth rates of algae and zooplankton increases with temperature [33,34].

Algal C : N and C : P ratios increased with decreasing N and P supply, respectively, also supporting hypothesis H1. Microalgae showed a broad plasticity in elemental composition after 12 days of growth under different nutrient supply conditions. Such broad plasticity can be explained by the physiological separation of nutrient assimilation and photosynthetic C fixation; therefore, fluctuations in resource supply and ratios are partly reflected in a phototroph's elemental composition (e.g. [35]). However, algal C : N and C : P ratios also increased with temperature, i.e. the increase of C : nutrient ratios with decreasing nutrient concentrations was strongest at 24°C. This C : nutrient increase was strongly associated with a higher carbon biomass at 24°C, while there was a decrease of P with increasing temperature only at low P supply. This is consistent with findings by Woods et al. [24], who found a decrease in particulate N and P with increasing temperature in a literature survey across all taxonomic groups. In our study, however, the increase in C : nutrient ratios at higher temperature were mainly due to enhanced carbon fixation per unit resource (N and P), resulting in an increase in algal biomass at 24°C irrespective of nutrient treatments.

(b). Consumer response to altered temperature and nutrient conditions and to feeding on different prey communities (H2–H4)

Temperature and nutrient supply interactively constrained consumer grazing rates and consumer production (final biovolume), supporting hypothesis H2. However, these effects differed for the two consumers (supporting hypothesis H3). Overall, the smaller ciliate consumer, Euplotes, showed higher grazing rates and reached higher final biovolume than the larger rotifer consumer, Brachionus. In treatments containing both consumers, Euplotes dominated, especially at the two higher temperatures; therefore, similar effects could be observed for these mixed treatments compared to treatments containing only Euplotes (refuting hypothesis H4).

(i). Population grazing rates

Consumer grazing rates of both consumers generally increased with temperature as expected by MTE [16,21]. This result was also in accordance with the metabolic model prediction and reflects increased metabolism and physiological rates at higher temperature. Nutrient effects on consumer grazing rates were temperature-dependent, showing stronger effects at lower temperatures compared to the highest temperature (24°C), where grazing was hardly affected by nutrient conditions. This was consistent for all consumer treatments.

In their meta-analysis across different systems and organism groups, Hillebrand et al. [21] generally found increasing per capita grazing rates with decreasing food quality, but decreasing population grazing rates. The capacity of individual consumers to increase food uptake in response to low food quality (compensatory feeding) has been observed for a variety of different herbivores (e.g. [36,37]). At the same time, however, low food quality often reduces herbivore growth efficiency and population growth rates (e.g. [38]), resulting in a decline in population level consumption with decreasing food quality. Therefore, compensatory feeding is only sufficient up to a certain point (regarding time frame or degree of food quality), after which herbivore growth efficiency and abundance decline due to low-quality food, resulting in lower population level herbivory [39,40].

With increasing C : N our metabolic model predicted an increase in population grazing rate for all consumer treatments at all temperatures, except for Euplotes at 24°C, which is congruent with our empirical findings. For Euplotes at 24°C, the metabolic model predicted a decrease in population grazing rate with increasing C : N, while in the experiment, grazing rates were hardly affected by increasing C : N. In contrast to all other organism groups, Hillebrand et al. [21] found in their meta-analysis a positive relationship between population grazing rates and increasing stoichiometric mismatch for zooplankton, which supports the main patterns observed in our study. They attributed this reverse relationship to the high number of short-term laboratory experiments on zooplankton included in their meta-analysis. Such a short time span was presumably not sufficient to lead to strong food quality effects on reproduction and thus abundance. While low food quality may induce enhanced (compensatory) feeding immediately, the 9 days of grazing in our experiment might not have been sufficient for the counteracting negative effects on consumer growth efficiency [11,21] to offset compensatory feeding via reduced population size for most consumer treatments and temperatures. At 24°C, consumer growth was most strongly negatively affected by low food quality in the experiment (see below). Therefore, increased compensatory feeding at low food quality at the individual level might have been balanced by a decrease in population growth, resulting in no observable effects of food quality on grazing at the population level in the experiment at 24°C. In the model, we observed an even stronger decrease of consumer growth with increasing C : N ratios for Euplotes at 24°C, resulting in decreasing population grazing rates, i.e. the decrease in population growth was stronger than compensatory feeding at the individual level [21].

Neither nutrient conditions nor temperature significantly affected grazing rates of Brachionus in the experiment. This might be due to the fact that the smaller consumer Euplotes reproduced much faster, exhibiting much higher population grazing rates compared with Brachionus, for which compensatory feeding activity was low in the time frame of this experiment.

(ii). Consumer biovolume

Consumer growth rates and final consumer biovolume increased with temperature for all consumer combinations, corroborating hypothesis H2 and also predicted by the metabolic model. Based on MTE [16], consumer growth rates are expected to increase with temperature, which resulted in higher total consumer biovolume at the end of our experiment, as consumers had not reached equilibrium after 9 days of growth (at equilibrium steady state, however, population biomass might decline exponentially with temperature for a fixed resource supply, [41]). Overall, both grazing rates and final consumer biovolume were interactively affected by temperature and nutrient conditions. However, the type of interaction of both factors differed. In contrast to consumer grazing rates, final consumer biovolume was more affected by nutrient quality at higher temperatures compared with the lowest temperature, where consumers showed higher biovolume at more balanced resource ratios (N : P = 16 or 8) compared with unbalanced ratios (N : P = 64 or 2). Our model predicted a decrease in consumer growth rates and final consumer biovolume with increasing C : N ratios, which could also be observed in our experiment. Apparently, compensatory feeding by consumers was not sufficient to completely compensate for low food quality by increasing their food uptake, which resulted in lower growth rates and thus lower final biovolume. This negative effect on population growth, however, was not large enough in the time frame investigated to offset population grazing rates (see above). This effect was consistent across all consumer combinations. The intensified effects of low food quality on consumer growth and production at high temperature can be explained by the fact that all biochemical reactions, including protein synthesis, are influenced by temperature by increasing the mean kinetic energy of molecules [42]. Our results are supported by the findings of Persson et al. [33] and Wojewodzic et al. [34], who found that the negative effect of low food quality (high C : P) on growth rates of daphnid and rotifer consumers, respectively, increased with temperature. Persson et al. [33] found no evidence of Daphnia P limitation at the lowest temperature (10°C), indicating that enzyme kinetics or other measures of food quality were more important for somatic Daphnia growth than the demands for P to RNA and protein. By contrast, McFeeters & Frost [43] demonstrated that the effects of high C : P on the growth of Daphnia magna decreased with temperature and noted that contrasting results may suggest that at low temperatures thermal constraints can reduce or mask the effects of poor food quality. All these findings and the results of our study imply that in order to assess stoichiometric food quality effects on natural zooplankton populations, the in situ temperature needs to be taken into account.

Overall, only high C : N ratios limited consumer production (final biovolume) in our study, while increasing C : P ratios had no significant effects on grazing rates or consumer biovolume. The algal food in our experiment was mainly N-limited after 12 days of growth under different nutrient conditions before grazer addition, and this N limitation subsequently affected consumer production.

The interactive effects of temperature and food quality were much stronger for the smaller ciliate consumer Euplotes compared to the rotifer Brachionus, supporting hypothesis H3. MTE predicts higher growth rates and thus higher nutrient demands for smaller consumers compared with larger ones [16], which probably resulted in a stronger dependence on temperature and nutrient supply for Euplotes compared with Brachionus. In accordance with model predictions, experimental data for consumer mixtures thus mostly reflected the patterns observed for Euplotes alone, as this species dominated consumer mixtures especially at higher temperatures.

(c). Outlook

Although global change-induced alterations in temperature and nutrient availability occur in parallel and are recognized as critical aspects of global change, relatively little is known about the interactions of these factors across different levels of organization, ranging from individuals to whole ecosystems [23,44], and across different spatio-temporal scales. The high interdependency of these factors, which also constrained dynamics in our experimental plankton food web, emphasizes that the integration of ES and MTE becomes relevant and necessary in the context of global-change research. The model proposed in our study includes the important predictor variables of consumer body mass, temperature and algal food stoichiometry that determine the outcome of trophic interactions in ES and in MTE. This model was able to explain most of the observed patterns, supporting that the combination of ES and MTE is a powerful tool to make predictions about the effects of temperature and nutrient quality on herbivore dynamics. However, further model development is required (see the electronic supplementary material) to include a wider range of parameters for a better mechanistic understanding of the combined effects of various factors promoting or impairing consumer grazing, growth and production.

Authors' contributions

S.D.M. conceived and designed the experiment. J.A.S., L.P. and M.T. conducted the experiment. D.H. and S.D.M. analysed the data. A.R., B.B. and I.T. formulated the model and made model predictions. S.D.M., D.H. and A.R. wrote the manuscript, all other authors provided content-related and editorial advice. All authors gave final approval for publication.

Competing interests

We have no competing interests.

Funding

A.R. acknowledges support from the Helmholtz Virtual Institute (VH-VI-500, PolarTime); I.T. acknowledges support from DFG-Project RY 143/1–1. J.A.S., D.H. and the project are funded by the Ministry of Science and Culture of Lower Saxony in the project ‘Biodiversity-Ecosystem Functioning across marine and terrestrial ecosystems'.